Ultrafast energy relaxation in single light-harvesting complexes

Significance

The excitation energy transfer in light-harvesting complexes is usually studied either by ultrafast bulk spectroscopy or by single-molecule spectroscopy. These methods are to a high degree complementary: Bulk spectroscopy measures ultrafast processes averaged over thousands of complexes, whereas single-molecule spectroscopy observes much slower dynamics in individual complexes. In this work, we combine these approaches using a recently developed ultrafast single-molecule spectroscopy technique. This enables us, for the first time (to our knowledge), to observe ultrafast energy relaxation with a rate around 100 fs in individual light-harvesting complexes. We determine the distribution of the relaxation times, observe changes of the relaxation time in one complex, and find how the relaxation depends on excitation wavelength.

Abstract

Energy relaxation in light-harvesting complexes has been extensively studied by various ultrafast spectroscopic techniques, the fastest processes being in the sub–100-fs range. At the same time, much slower dynamics have been observed in individual complexes by single-molecule fluorescence spectroscopy (SMS). In this work, we use a pump–probe-type SMS technique to observe the ultrafast energy relaxation in single light-harvesting complexes LH2 of purple bacteria. After excitation at 800 nm, the measured relaxation time distribution of multiple complexes has a peak at 95 fs and is asymmetric, with a tail at slower relaxation times. When tuning the excitation wavelength, the distribution changes in both its shape and position. The observed behavior agrees with what is to be expected from the LH2 excited states structure. As we show by a Redfield theory calculation of the relaxation times, the distribution shape corresponds to the expected effect of Gaussian disorder of the pigment transition energies. By repeatedly measuring few individual complexes for minutes, we find that complexes sample the relaxation time distribution on a timescale of seconds. Furthermore, by comparing the distribution from a single long-lived complex with the whole ensemble, we demonstrate that, regarding the relaxation times, the ensemble can be considered ergodic. Our findings thus agree with the commonly used notion of an ensemble of identical LH2 complexes experiencing slow random fluctuations.

Time-resolved studies of primary events in photosynthetic light harvesting have a decades-long tradition. Usually, the fastest processes observed correspond to the time resolution of the experimental techniques available at the time. Recently, the most popular tool to study ultrafast excitation energy transfer with sub–100-fs resolution is 2D electronic spectroscopy (2DES). This technique has been used to study various light-harvesting complexes (LHCs), such as LH2 and LH1 antennas of purple bacteria (1, 2), the FMO protein of green sulfur bacteria (3, 4), and the major antenna complex LHCII of higher plants (5). It was shown that, after an ultrafast excitation of photosynthetic LHCs, the electronic excitation evolves in a coherent fashion on a 100-fs timescale. These observations sparked a still-ongoing debate on the role of quantum coherence in energy transfer in LHCs.

However powerful the ultrafast techniques have become, they are fundamentally limited by ensemble averaging. Although the 2DES can in principle resolve inhomogeneous and homogeneous line shapes, the observed spectra and system dynamics are still averaged over the whole ensemble of complexes. Another feature of nonlinear spectroscopy such as 2DES is that broadband pulses are used for excitation, which results in simultaneous excitation of many states. Such pulses inevitably excite also superpositions of states, which leads to coherent dynamics. This can provide useful information about the system, especially on the electronic coupling between the pigments and the interplay of electronic and nuclear degrees of freedom. On the other hand, it brings with itself interpretative issues in relation to the relevance of such coherent dynamics for natural light harvesting under incoherent sunlight (6).

At about the same time as ultrafast spectroscopy, also optical microscopy has seen significant advances (7). Nowadays, it is routinely possible to selectively excite and observe individual LHCs. This enables us to overcome the problem of ensemble averaging and observe distributions of single-molecule properties. However, for practical reasons, only single-molecule emission spectroscopy has been possible on biological pigment–protein complexes. Photon counting of the weak luminescence signal becomes a limiting factor for the time resolution, making it possible to observe changes only on a timescale of tens of milliseconds and longer. The standard paradigm is therefore to think about the ultrafast nonlinear ensemble spectroscopy and single-molecule spectroscopy (SMS) as complementary methods that access very different timescales.

In 2005, van Dijk et al. (8) proposed a modification of SMS called single-molecule pump–probe (SM2P), which employs excitation by two pulses. This technique visualizes the initial ultrafast excitation relaxation in single molecules. As they demonstrated on dye monomers (8, 9) and later on dye dimers and trimers (10), it is possible to observe relaxation rates in the 100-fs range. In this work, we explore the possibility of applying this technique to LHCs.

Since 2005, the experimental technique has advanced, and in 2013 the first femtosecond experiment was performed on single LH2 complexes of purple bacteria by Hildner et al. (11). Using pulse shaping, the complexes were coherently excited by two ultrashort pulses of different central wavelengths. Coherent oscillations in the emission signal were then observed when varying the delay between the pulses.

The LHC of choice for our measurement is the LHC 2 (LH2) of the purple bacterium Rhodopseudomonas acidophila. LH2 consists of two rings of bacteriochlorophylls, which result in two distinct absorption bands at roughly 800 and 850 nm, respectively. Both the bands and the rings are referred to as B800 and B850 according to their central absorption wavelength. The pigments in the ring responsible for the B800 band are relatively weakly coupled, whereas the pigments from the B850 ring exhibit strong electronic coupling. This strong interaction results in significant excitonic splitting and formation of delocalized excitonic (vibronic) states (12). Most of the ultrafast studies of energy transfer in LH2 were carried out in the late 1980s and 1990s using variants of transient absorption (TA) and fluorescence up-conversion (12–15). From these and later studies (16, 17), it was concluded that, although the energy transfer from the B800 to the B850 ring is relatively slow, 1–2 ps, the relaxation dynamics after 800-nm excitation are more complex, including faster components due to the overlap of the B800 states with high energetic exciton states of the B850 ring (B850*). These states were found to exhibit ultrafast transfer dynamics on the timescale of hundreds of femtoseconds. Recent results from 2DES spectroscopy furthermore revealed ultrafast sub–200-fs dynamics (1, 18, 19). Meanwhile, SMS studies of LH2 at cryogenic and later at ambient temperatures showed intensity fluctuations and spectral diffusion on a much slower timescale of seconds (20–23). By theoretical modeling, it was shown that most of the spectroscopic observations can be explained by dynamic variations in the realization of the energetic disorder of the pigments (21, 24). These findings highlight the dynamic, fluctuating nature of LHCs. Experimentally, LH2 is a perfect candidate for our proof-of-principle measurement for several reasons. The presence of lower B850 states results in fluorescence emission around 870 nm, which is sufficiently red-shifted with respect to the absorption bands to enable easy excitation and detection separation. Importantly, LH2 shows a high fluorescence yield and significant stability in single-molecule conditions, which is a requirement for our experiment.

Results

The Measurement.

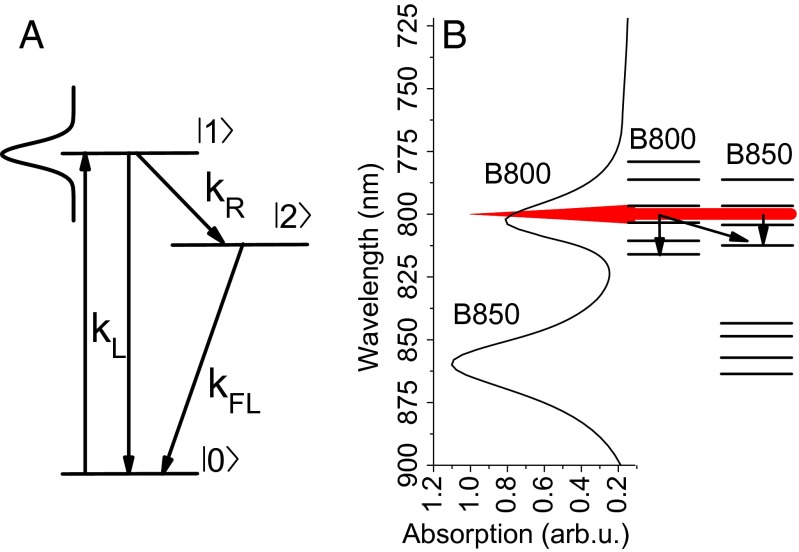
The SM2P principle is based on exciting the system by a near-saturating laser pulse and giving it a time window to relax to some off-resonant state before applying a second pulse. By such relaxation, the excitation in the system can be saved from the stimulated emission caused by the second pulse, and the overall excitation probability therefore rises with the pulse delay. The detected fluorescence signal is proportional to this excitation probability and therefore depends on the delay between the two pulses. The excitation relaxation rate can then be extracted by scanning the pulse delay time and fitting the resulting change in fluorescence intensity. The effective three-level scheme that is used for the SM2P traces analysis is shown in Fig. 1A. It consists of a ground state $|0\rangle$, an excited state $|1\rangle$ resonant with the laser excitation, and an off-resonant excited state $|2\rangle$. This scheme is universal for the technique and can always be used for analysis. It then depends on the measured system how the respective levels should be interpreted. A diagram of the actual situation in LH2, together with the measured absorption spectrum, is presented in Fig. 1B. The depicted excited states manifold qualitatively corresponds to the density of states previously used for theoretical modeling (see, e.g., figure 6 in ref. 17). The main difference between the isolated molecules studied previously in ref. 8 and LHCs is the dense excited states manifold in the latter case. However, it can be shown by numerical simulations that the three-level description still holds as effective. In the case of a dense manifold, the observed relaxation rate is the effective rate with which the excitation escapes the region resonant with the laser. For a more detailed description of the SM2P technique and the analysis procedure, we refer the reader to Supporting Information and the original works by van Dijk et al. (8, 9).

Fig. 1.

(A) The three-level scheme used for the data analysis. $k_L$ is the absorption and stimulated emission rate, $k_{FL}$ is the spontaneous emission rate, and $k_R$ is the relaxation rate that is measured. The Gaussian profile represents the laser pulse, resonant with state $|1\rangle$ and off-resonant with state $|2\rangle$. (B) Excited states available in LH2, schematically shown together with a measured absorption spectrum. The red peak represents the excitation spectrum at 800 nm; the arrows indicate possible relaxation channels.

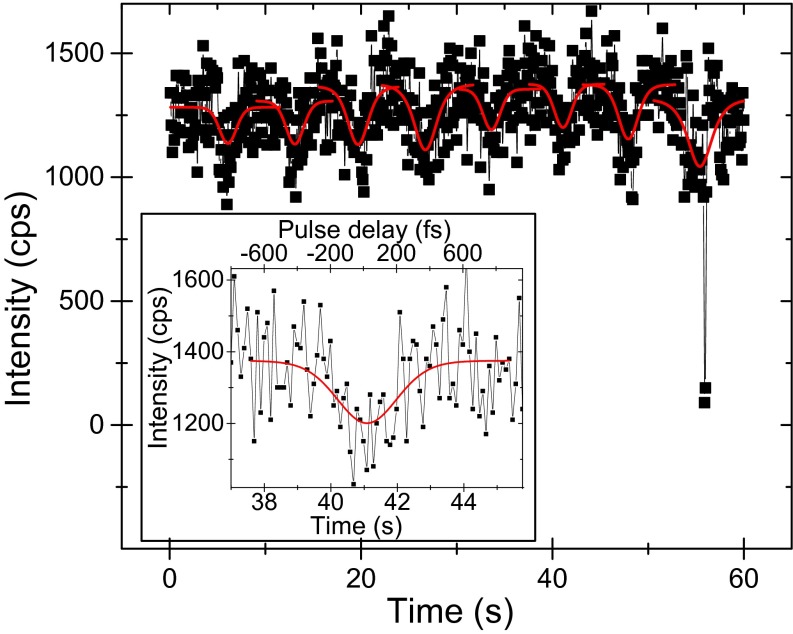
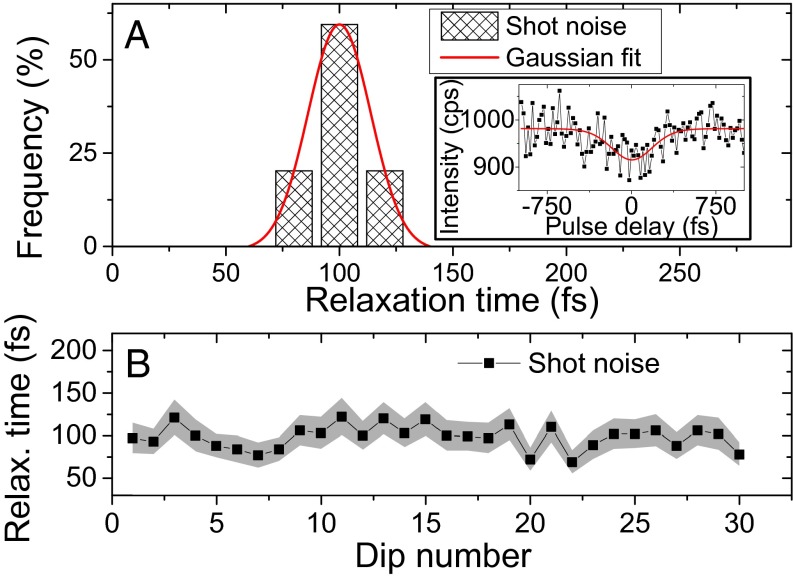
Using a confocal microscope, individual complexes are excited by the two-pulse laser sequence. The pulses with a center wavelength around 800 nm are 200–250 fs long and about 4 nm wide. Thorough preliminary calculations, which can be found in Fig. S1 and text in Supporting Information, indicated that the above-mentioned laser specifications will work to reveal ultrafast dynamics in LH2 complexes. The fluorescence of one complex is collected by the same microscope objective and recorded by an avalanche photodiode. In this way, the fluorescence intensity traces of multiple individual LH2 complexes are recorded one by one. The emission of one complex is measured until it photobleaches, while simultaneously continuously scanning the delay between the two excitation pulses. The first minute of a typical intensity trace from a stable complex is shown in Fig. 2. The signal of about 1,000 cps is characteristic for the given measurement conditions. The data are binned into 100-ms bins, which represents a compromise between the signal-to-noise ratio and the amount of data points available for fitting. The measured intensity modulation results from the pulse delay scanning and each intensity dip can be used to determine the corresponding relaxation time. The Inset in Fig. 2 depicts a single intensity dip from the recorded trace, with an extracted relaxation time of ${\tau }_R=\left(89\pm 25\right)\hspace{0.17em}\text{fs}$. The present noise can be explained by Poissonian shot noise. The good sample stability allowed us to perform multiple pulse delay scanning cycles and therefore to extract multiple subsequent relaxation times from one complex. In the given example, the complex switches into a dark state at $t=55\hspace{0.17em}\text{s}$, a process often called “blinking.” This behavior indicates that the observed signal indeed arises from a single well-connected antenna. It should be noted that not all complexes are such stable emitters. As was observed before (see, e.g., refs. 21 and 23), there can be a significant amount of blinking with different degrees of quenching, which results in switching between different intensity levels. However, no matter what the mechanism of energy dissipation causing these fluctuations is, the fluorescence intensity is still proportional to the excitation probability. Therefore, whenever the emission is stable for a sufficiently long time to perform one pulse delay scan, and the emission intensity is high enough to provide a reasonable signal-to-noise ratio, the relaxation time can be measured. In this way, we can measure several intensity dips for many complexes and extract the relaxation times by fitting with the three-state model.

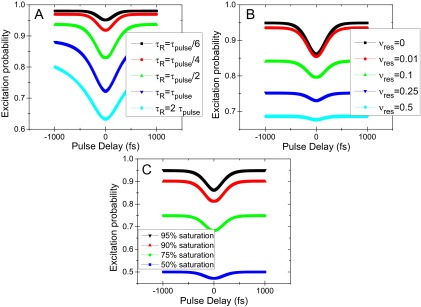
Fig. S1.

Numerical simulations of the intensity dip dependence on (A) the relaxation time, (B) the off-resonance of the relaxed level, and (C) the degree of saturation.

Fig. 2.

First 1 min of a measured fluorescence intensity trace of a single LH2 complex, recorded while continuously scanning the delay between the two excitation pulses. Red lines: data fitted with the three-level model in Fig. 1A. At t = 55 s, the complex briefly switches to a dark state (“blinking”). (Inset) Magnification of one intensity dip with a fitted relaxation time of ${\tau }_R=\left(89\pm 25\right)\hspace{0.17em}\text{fs}$. The bottom axis gives the real recording time, whereas the top axis denotes the delay between the two pulses.

Energy Relaxation.

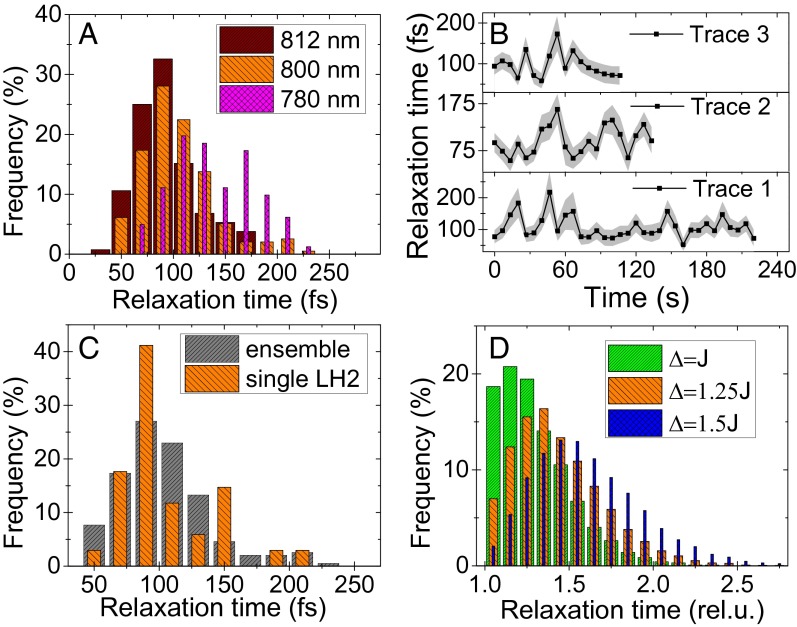
The distributions of relaxation times obtained for excitation wavelengths of 812, 800, and 780 are shown in Fig. 3A. The average recorded relaxation times are 92 fs at 812-nm, 106 fs at 800-nm, and 139 fs at 780-nm excitation. These measured relaxation times agree well with the expected ultrafast timescale.

Fig. 3.

(A) Relaxation time distribution obtained from many measured complexes at three different excitation wavelengths. (B) Relaxation time trajectories of three stable complexes, under 800-nm excitation. The shaded regions indicate the standard error of the fits. (C) The relaxation time distribution obtained from a single complex, trace 1 in B, compared with the ensemble distribution at 800-nm excitation from A. (D) Modeled distribution of the relaxation times in a two-state model using Redfield theory. The distribution shape changes with the ratio of the coupling and energy gap (see text below Eq. 1 for description).

As a result of the already mentioned dense excited states manifold, there are several differences between the original work on dye monomers and the LHCs. In the former case of individual or weakly coupled pigments, the observed ultrafast relaxation is the intramolecular vibrational relaxation, i.e., the dynamic Stokes’ shift. By comparing monomers and dimers, van Dijk et al. (8) showed that this relaxation slows down when the excited states are delocalized and thus more weakly coupled to the environment. In LHCs, the situation is different. First, the pigments are coupled, and thus the vibrational and electronic states become mixed, resulting in a vibronic states manifold. The energy transfer between these states cannot be strictly separated into the intrapigment or interpigment relaxation. Second, unlike the dye molecules, the bacteriochlorophylls present in LH2 have a much smaller Stokes’ shift, typically around 5 nm ($\approx 80$ cm⁻¹) (25). It is thus by itself not enough to escape the 4-nm ($\dot{\approx 65\hspace{0.17em}{\text{cm}}^{-1}}$)-wide excitation pulse. In addition, finally, the measured dependence of the relaxation time on the excitation wavelength is exactly opposite from what would be expected from a Stokes’ shift. In our case, we observe the fastest relaxation in the “red” region with wavelength longer than 800 nm, where the strongly coupled B850* states are present. The relaxation is then slower when exciting in the “blue” region at 780 nm, where the states of weakly coupled B800 pigments play a larger role (Fig. 3A).

Another aspect to consider is that we observe only energy relaxation and not dynamic localization, because of excitation with circular polarized light. The latter contributes mainly to absorption depolarization (17). The observed relaxation rate then effectively describes how fast the excitation escapes the resonant laser excitation range. The next dissimilarity from the case of individual dye molecules is the possible presence of multiple excitations and the related singlet–singlet annihilation. However, because the fluorescence lifetime is orders of magnitude longer than the singlet–singlet annihilation time (26, 27), it is precisely the annihilation which renders the multiply excited states invisible. The annihilation, always present at near-saturating intensities, thus effectively ensures that the three-state model with a single excited state is a good approximation for the observed fluorescence signal. Another concern are higher excited states of the pigments, possibly resulting from multiple excitation of the same pigment. However, these decay to the lowest excited state much faster than the overall excited state lifetime (28, 29). From the discussion above, we can therefore conclude that we indeed observe energy relaxation between the singly excited states within the complex.

Comparing with the literature, we find that our relaxation times are somewhat shorter than those found by previous time-resolved measurements. As mentioned in the Introduction, excitation at 800 nm results in populating states of both the B800 and the B850* bands. Our experimental results indeed indicate that the B850* states contribute significantly to the rather fast observed relaxation rate. The comparably wider excitation pulses of typically 10–15 nm used in TA measurements fail to resolve energy relaxation processes within their bandwidth, resulting in a slower overall relaxation rate. Furthermore, TA and fluorescence decay kinetics are usually fitted with and resolved into several energy transfer components, whereas this study yields an effective “escape” rate comprising all available relaxation channels. As a consequence, the observed relaxation is somewhat faster and the slow components are not visible in our measurement. Our results therefore agree with relaxation times of 150–300 fs reported for 800-nm excitation (14) and furthermore experimentally validate the faster dynamics determined by theoretical modeling of the B850* band (17).

Relaxation Time Fluctuations.

Having discussed the average observed relaxation time, we can focus on the true single-molecule measurement achievements: the relaxation time distribution and fluctuations. We have already mentioned the distributions in Fig. 3A. Due to the anaerobic conditions that increase the sample endurance, we were able to follow several stable complexes for minutes before they photobleached. The obtained relaxation time trajectories can be found in Fig. 3B.

Before we start interpreting these results, we need to make sure that the fluctuations we measure are not just an artifact of the fitting in the presence of shot noise. To this end, we perform numerical simulations of the SM2P signal including Poissonian shot noise. In the Inset of Fig. 4A, we present one of the simulated intensity dips. The distribution of the fitted relaxation times obtained from such simulated dips is presented in Fig. 4A. The signal binning time and the bin size are the same as used in Fig. 3A to illustrate the difference. The calculated relaxation times are symmetrically distributed around the expected value of 100 fs, and the distribution can be excellently fitted by a Gaussian normal distribution with a full width at half maximum (FWHM) of 33 fs. This distribution is much narrower than the experimentally obtained one and also its shape is completely different. In Fig. 4B, we show a “trace” of successively simulated relaxation times that can be compared with its experimental counterpart in Fig. 3B. The extent of the fluctuations caused only by the shot noise is significantly smaller. Together with a clear wavelength dependence of the relaxation time distributions, these simulations convince us that the observed fluctuations are real and not only the result of shot noise.

Fig. 4.

Testing the effect of Poissonian shot noise. The simulated parameters are as follows: a relaxation time of 100 fs, pulses of 200 fs, and a signal of around 1,000 cps. (A) The relaxation time distribution obtained from the simulation, fitted with a Gaussian distribution with a FWHM of 33 fs. (Inset) One of the simulated intensity dips, together with the fitted three-level model curve. The recovered relaxation time was ${\tau }_R=\left(90\pm 17\right)\hspace{0.17em}\text{fs}$. (B) A succession of simulated relaxation times that can be compared with Fig. 3B. The shaded area indicates the SE of the fits.

To qualitatively understand the possible origin of the asymmetric shape of the relaxation time distribution, we can consider the following simple model. Let us describe energy transfer between two excitonic states, originating from two coupled pigments. Using Redfield theory, the relaxation rate $k_R$ between the excitonic levels can be expressed analytically. When we assume, for the sake of simplicity, that the spectral density of bath modes is approximately flat in the considered frequency region, the relaxation rate is proportional to the following:

$$k_R=\frac{1}{{\tau }_R}\propto \frac{1}{1+{\left(\frac{\mathrm{\Delta }}{2J}\right)}^2},$$ [1]

where J is the coupling constant between the pigments and $\mathrm{\Delta }$ is the energy difference between the coupled states. The relaxation time is then determined only by the ratio $\mathrm{\Delta }/2J$, and the distribution arises from the energetic disorder in $\mathrm{\Delta }$. We assume a Gaussian distributed disorder, as is commonly done in such simulations, with a FWHM ${\mathrm{\Delta }}_{\mathrm{dis}}=J$. This is typical for simulations of LHCs, where all three parameters are expected to be in the same range, i.e., $\mathrm{\Delta }\approx J\approx {\mathrm{\Delta }}_{\mathrm{dis}}$. In Fig. 3D, the resulting relaxation time distribution is depicted for different values of the detuning $\mathrm{\Delta }$. We can see that, for strong coupling (or small energy gaps), the relaxation is fastest and the distribution is highly asymmetric. With decreasing coupling (or increasing energy gap), the distribution maximum shifts to longer relaxation times and becomes more symmetric. Our experimentally obtained distributions in Fig. 3A seem to follow this trend: the distribution measured at 812 nm is the most asymmetric one with the shortest relaxation times, the 800-nm distribution is the intermediate case, and the distribution measured at 780-nm excitation is more symmetric and shifted to longer relaxation times. This fully agrees with the discussion above, describing the increasing influence of the strongly coupled B850* ring states when tuning the excitation to longer wavelengths. The shape of the distribution can thus be qualitatively described as originating from a Gaussian energetic disorder of the transitions energies of the antenna pigments.

Finally, we want to comment on the relaxation time trajectories presented in Fig. 3B. The relaxation time clearly varies on a timescale of seconds, which is in agreement with slow fluctuations observed by SMS on LH2 before (20, 21, 24). It should be mentioned that fluctuations in LHCs are observed on almost all timescales, from fast subpicosecond vibrations of the pigments to slow protein structural changes in the range of seconds. Our experiment is able to observe the latter type of fluctuations, where slow motion of the protein causes changes in the local pigment environment resulting predominantly in a shift of their transition energy (24, 30, 31).

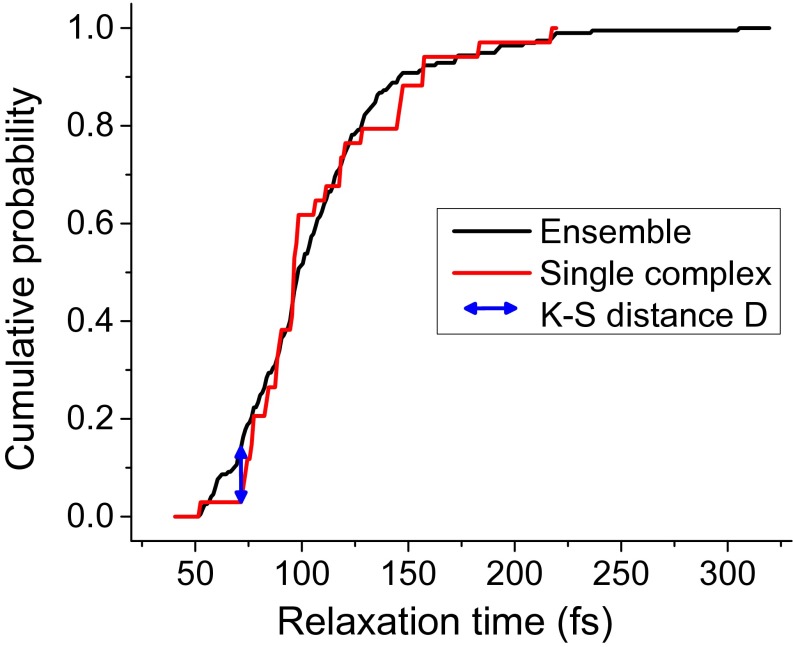
A question arises whether the relaxation times in all complexes experience the same fluctuations, or whether the ensemble is heterogeneous. To investigate this, we compare the relaxation time distribution from a long trace of a single LH2 complex, trace 1 in Fig. 3B, with the distribution from the whole ensemble of many complexes. As is shown in Fig. 3C, the distributions are very similar both in shape and position. Applying the Kolmogorov–Smirnov (K–S) test for quantitative comparison, we find that with 81% probability the single-complex and ensemble relaxation times arise from the same distribution. The cumulative distribution functions, used in the K–S test and further highlighting the distribution similarity, can be found in Fig. S3. This comparison indicates that at least some complexes can likely sample all of the possible relaxation times on a timescale of seconds and that the ensemble can be in this respect considered ergodic. However, this argument does not give an exhaustive answer to the role of disorder in LH2 complexes. Further investigation in this direction would thus certainly be of interest.

Fig. S3.

Cumulative distribution functions for the relaxation time distribution of the whole ensemble and a single complex. The K–S distance is also denoted.

Conclusions

We have successfully applied the SM2P technique to LH2 complexes of purple bacteria. We have demonstrated that it is possible to observe ultrafast energy relaxation in individual LHCs. As such, our work highlights a previously unexplored way to study photosynthetic light harvesting. We have shown how the relaxation time distribution changes when tuning the excitation wavelength. The observed behavior can be explained by a varying influence of the B800 and B850* states of the LH2 rings, in agreement with previous ultrafast spectroscopy studies. By a numerical calculation, we were able to qualitatively explain the shape of the relaxation time distribution as a result of the energetic disorder of the LH2 pigments. The extent of disorder corresponds to the values commonly used in bulk spectroscopy modeling. Our method can be extended to include a detailed excitation wavelength scan, which would enable us to study energy transfer dynamics of single LH2 complexes to an extent similar to bulk transient absorption measurements. Finally, we observed the evolution of the relaxation rate of individual complexes in time. In accordance with previous SMS studies, we attribute its fluctuations to slow protein motion, based on the relevant timescale. Our results thus not only demonstrate the applicability of the incoherent SM2P technique to photosynthetic systems, but also present a fitting piece of evidence to the puzzle of light-harvesting dynamics in the ever-fluctuating antenna complexes.

Materials and Methods

Experimental Setup.

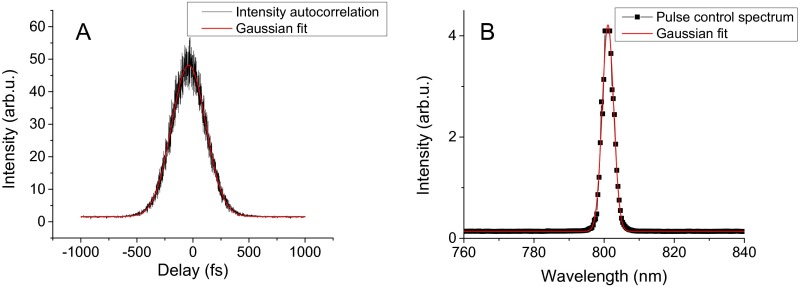
The experimental setup is similar to the one in ref. 8; briefly, a 76-MHz Ti:sapphire laser (Mira 900F; Coherent) is used as a source of 200- to 250-fs, 4- to 5-nm spectrally wide pulses centered at 800 nm. By tuning the laser cavity, the wavelength can be tuned approximately from 750 to 850 nm. The repetition rate is decreased to 2 MHz by a pulse-picker (PulseSelect; APE) to increase the survival time of the complexes and eliminate long-living dark states such as triplet states. The absence of the triplet states is verified by checking the signal drops to one-half when halving the repetition rate. The two pulses are produced by a home-built Michelson interferometer; the delay between them is scanned by a delay line (Newport) in one of the interferometer arms. The pulse length before the microscope is measured by fringe-resolved autocorrelation (32) using the same interferometer and focusing the pulses into a BBO crystal (Eksma Optics). The pulse spectrum is measured by a spectrometer (OceanOptics). Technical details can be found in Fig. S2 and text in Supporting Information. Due to the narrow bandwidth of the pulses, no significant broadening of the pulses in the microscope can be expected. Guild et al. (33) measured the dispersion of common high–numerical-aperture objective microscopes, and for a microscope very similar to ours they find a group delay dispersion of around 4,000 fs², including the beam expander. Using a formula for Gaussian pulse second-order dispersion, we obtain that our 200 fs (lower limit) pulses stretch to 208 fs. This is indeed negligible considering the fluorescence intensity dip fitting error arising from the signal-to-noise ratio. The excitation light is adjusted to a circular polarization by a Berek compensator (New Focus) to avoid complex orientation dependence. The complexes are illuminated and detected by a confocal microscope with a Plan Fluor objective (1.3 N.A.; Nikon) as described elsewhere (21). The detected fluorescence is alternatively dispersed by a grating on a CCD (Princeton Instruments) to measure the emission spectrum or the intensity is measured by an avalanche photodiode (PerkinElmer). The fluorescence spectrum is used to check the integrity of the complexes during the course of the measurement. The excitation intensity is set to be sufficient to nearly saturate the complexes. At 800-nm excitation, we used an excitation power of 0.5 pJ per pulse, focused to a diffraction-limited spot, which is comparable to previous experiments (9). For excitation at different wavelengths, the intensity was increased to compensate for the decreased absorption (see spectrum in Fig. 1B). The measurement is controlled by a custom-made LabView environment.

Fig. S2.

Characterization of the pulses used for the 800-nm excitation measurement. (A) Intensity autocorrelation from using FRAC with vibrating mirror. Gaussian fit yields FWHM = 360 fs; using deconvolution factor $\sqrt{2}$ then gives 255-fs-long pulses. (B) Measured control spectrum (its parameters are not used for the relaxation time extraction). Gaussian fit gives FWHM = 3.8-nm spectral width.

Sample Preparation.

The isolated LH2 complexes from Rhodopseudomonas acidophila are diluted to a concentration of $\sim 10$ pM in a measuring buffer [20 mM Tris, pH 8, and 0.03% (wt/vol) n-dodecyl β-d-maltoside] and then immobilized on a poly-l-lysine (Sigma)–coated cover glass. The dilution is chosen such as to obtain on average ∼10 complexes per 100 μm². To increase the survival time of complexes, the buffer is deoxygenated by the oxygen-scavenging system PCA/PCD (2.5 mM protocatechuic acid, 25 nM protocatechuate-3,4- dioxygenase; Sigma) (34). The experiments were conducted at room temperature.

Relaxation Time Fitting.

The detailed description of the SM2P technique can be found in Supporting Information. When applying the three-level system description as in Fig. 1A, the intensity dip as a function of pulse delay τ can be described as follows:

$$I\left(\tau \right)=I^{\infty }\left\{1-\frac{p_1}{2-p_1}\frac{1}{2}{e}^{\frac{k_R^2{d}^2}{4}}\left[e^{-k_R\tau }erfc\left(\frac{1}{2d}\left(d^2{k}_R-2\tau \right)\right)+e^{k_R\tau }erfc\left(\frac{1}{2d}\left(d^2{k}_R+2\tau \right)\right)\right]\right\},$$ [2]

where $k_R=1/{\tau }_R$ is the relaxation rate, $I^{\infty }$ is the baseline intensity, $p_1$ is the probability of excitation by one pulse ($1/2$ for full saturation), and d is the effective pulse width, related to the pulse FWHM as $d=\left(1/\sqrt{2\ln 2}\right)d_{\mathrm{FWHM}}$. We use this formula to fit the measured dips and extract the relaxation times.

Theoretical Considerations

The SM2P technique is based on exciting the molecules by two near-saturating laser pulses, scanning the delay between them, and observing the correlated change in fluorescence intensity. To understand the resulting signal, we study a model three-level system consisting of a ground state $|0\rangle$, an excited state $|1\rangle$ resonant with the laser excitation, and an off-resonant excited state $|2\rangle$. A schematic illustration is shown in Fig. 1A in the main text. During the interaction with the first pulse, the evolution of the system can be described by the Bloch equations (35). The external electromagnetic field creates a superposition of the ground and excited state, i.e., an optical coherence, and the probability of excitation of state $|1\rangle$ undergoes Rabi oscillations. Because of the strong coupling of the electronic degrees of freedom to the fluctuating environment and fast energy transfer from the excited state, the optical coherence rapidly dephases, typically on the order of 50 fs, and the Rabi oscillations become damped. If the duration of the saturating pulse is longer than the coherence dephasing time, the excitation probability settles at $1/2$. In that case, a description by semiclassical rate equations is appropriate. If the system is excited by the first pulse, it starts to relax to the off-resonant state $|2\rangle$. Now, when the second pulse arrives immediately after the first pulse, the system is still saturated and the excitation probability remains $1/2$. However, when the delay between the pulses is long enough, the excitation can relax to state $|2\rangle$ and thus escape stimulated emission. The system can then interact with the second pulse only if it was not excited by the first pulse. It thus gets a second chance to be excited, and the overall probability of excitation rises to $1/2+1/2\cdot 1/2=3/4$. Scanning the pulse delay and measuring the emission intensity, which is proportional to the excitation probability, allows us to observe a dip in fluorescence (see, e.g., Fig. S1). The width of the dip is related to the time it takes for the system to relax to the off-resonant state. In practice, the excitation starts to relax already during interaction with the exciting pulse, and state $|2\rangle$ might not be completely off-resonant. The dynamics of the system can then be described by coupled equations for the state populations:

$$\frac{\partial P_1\left(t,\tau \right)}{\partial t}=k_L\left(P_0-P_1\right)I_L\left(t,\tau \right)-k_R{P}_1,$$

$$\frac{\partial P_0\left(t,\tau \right)}{\partial t}=-k_L\left(\left(1+{\nu }_{\mathrm{res}}\right)P_0-P_1-{\nu }_{\mathrm{res}}{P}_2\right)I_L\left(t,\tau \right),$$

$$\frac{\partial P_2\left(t,\tau \right)}{\partial t}={\nu }_{\mathrm{res}}{k}_L\left(P_0-P_2\right)I_L\left(t,\tau \right)+k_R{P}_1.$$ [S1]

Here, $k_L$ is the absorption/stimulated emission rate, $k_R$ is the relaxation rate, $I_L\left(t,\tau \right)$ is the intensity of the two laser pulses delayed by τ, and ${\nu }_{\mathrm{res}}$ is the resonance of state $|2\rangle$ (relative to state $|1\rangle$, ${\nu }_{\mathrm{res}}=0$ when state $|2\rangle$ is completely off-resonant). Because the spontaneous emission rate is typically orders of magnitude slower than energy relaxation, the observed fluorescence is proportional to the population of the relaxed state long after interaction with the exciting pulses, $I_{FL}\left(\tau \right)\propto P_2\left(\infty ,\tau \right)$.

Concerning LHCs, several aspects have to be taken into account. Their states, originating from more than one pigment, form a dense excitonic (vibronic) manifold and the energy transfer is ultrafast. It is thus important to verify how sensitive the method is to the actual degree of saturation, how much off-resonant the state $|2\rangle$ has to be, and how the fastest observable relaxation rate depends on the duration of the pulse. To address these questions, we performed numerical simulations varying the respective parameters (Fig. S1). It turns out that the exact saturation level is not critical (Fig. S1C), in agreement with ref. 9. The off-resonance is, however, very important (Fig. S1B). For example, already 75% off-resonance, i.e., ${\nu }_{\mathrm{res}}=0.25$, decreases the intensity dip considerably and, in the presence of Poissonian noise (see below), renders it invisible. Finally, the fastest observable relaxation time is about five times faster than the pulse duration (Fig. S1A). These findings are very encouraging for LHCs. The expected relaxation times are around 100 fs, which can be well resolved by 200-fs laser pulses. These pulses can then be only about 4 nm wide, which, together with a high off-resonance demand, ensures high excitation selectivity. The weak dependence on the degree of saturation furthermore allows to quantitatively measure the relaxation out of the selected narrow excitonic region.

The findings presented above allow us to use an effective description via Eq. S1 with ${\nu }_{\mathrm{res}}=0$. Level $|1\rangle$ then represents the states resonant with the excitation, and level $|2\rangle$, the off-resonant, relaxed states. The effective description by Eq. S1 is therefore still valid even for LHCs with dense excited state manifolds.

For Gaussian pulses, the solution of Eq. S1 can be found analytically by convoluting the result for δ-pulse excitation with both pulse envelopes. This approach, the same as in the original work of van Dijk et al. (9), assumes the pulses are mixed incoherently. This is true for our setup where the vibrations of the rapidly moving delay line safely destroy all phase coherence. (We also tried measuring with a vibrating mirror and obtained comparable results.) The measured fluorescence intensity as a function of the pulse delay τ can then be expressed as follows:

$$I\left(\tau \right)=I^{\infty }\left\{1-\frac{p_1}{2-p_1}\frac{1}{2}{e}^{\frac{k_R^2{d}^2}{4}}\left[e^{-k_R\tau }erfc\left(\frac{1}{2d}\left(d^2{k}_R-2\tau \right)\right)+e^{k_R\tau }erfc\left(\frac{1}{2d}\left(d^2{k}_R+2\tau \right)\right)\right]\right\},$$ [S2]

where $I^{\infty }$ is the baseline intensity, $p_1$ is the probability of excitation by one pulse ($1/2$ for full saturation), k_R is the relaxation rate, and d is the effective pulse width, related to the pulse fFWHM as $d=\left(1/\sqrt{2\ln 2}\right)d_{\mathrm{FWHM}}$. Eq. S2 is used for fitting the data and extraction of the relaxation time ${\tau }_R=1/k_R$.

Pulse Characterization

To characterize the pulses, we use a modified version of fringe-resolved autocorrelation (FRAC) (32). In this interferometric method, we use the same Michelson interferometer as we use for the pulse delay scanning. For the pulse characterization, the pulses are colinearly focused in a BBO crystal to generate a second harmonic signal (SH). The fundamental frequency is then filtered out, and the SH intensity is detected by a slow detector.

Denoting the laser field $E\left(t,\tau \right)=E_0\left(t\right)e^{-i\omega t}+E_0\left(t+\tau \right)e^{-i\omega \left(t+\tau \right)}+c.c.$, the second harmonic is proportional to $E^2\left(t,\tau \right)$, and the measured SH intensity is proportional to the following:

$$\begin{array}{c}{I}_{SH}\left(\tau \right)={\displaystyle \int dt{I}_0^2\left(t\right)}+I_0^2\left(t+\tau \right)+2\mathrm{Re}\left\{E_0^2\left(t\right)E_0^2\left(t+\tau \right)\right\}\cos \left(2\omega \tau \right)\\ +4\left(I_0\left(t\right)+I_0\left(t+\tau \right)\right)\mathrm{Re}\{E_0\left(t\right)E_0\left(t+\tau \right)\cos \left(\omega \tau \right)+4I\left(t\right)I\left(t+\tau \right).\end{array}$$ [S3]

This signal contains a baseline contribution from both pulses, the SH interferogram, envelope-modulated fundamental interferogram, and the intensity autocorrelation that we want to measure. Using this FRAC signal, the pulses can be characterized; however, for pulses as long as ours, the recording requires an impractically long time. By attaching a vibrator to one of the interferometer mirrors, the interference-sensitive part of the SH is averaged out on the detector, which enables us to measure the intensity autocorrelation on a constant background much faster. We checked that this method works by comparing the obtained pulse width with the one from the full recorded interferogram for several pulse lengths.

The characterization of the pulses used for the 800-nm excitation measurement, together with their measured spectrum for control, can be found in Fig. S2.

Ensemble Ergodicity

To check whether it is probable that the relaxation times from a considered single complex trajectory come from the same population as the relaxation times of the whole ensemble of complexes, we use a Kolmogorov–Smirnov (K–S) test to compare their distributions. The K–S test compares the cumulative distribution function (CDF) of the two distributions. The supremum of the distance of the two CDFs over all relaxation times is the K–S distance D. The P value then determines what is the probability of the K–S distance to be this large if the two sets of relaxation times were drawn from the same distribution. The CDF comparison together with the K–S distance is depicted in Fig. S3. The K–S distance is $D=0.11$ and the corresponding P value is $D=0.81$.