Economic irrationality is optimal during noisy decision making

Significance

Healthy individuals appear to display inconsistent preferences, preferring A over B, B over C, and C over A. Inconsistent, intransitive preferences of this form are hallmark manifestations of irrational choice behavior and breach the very assumptions of economic theory. Nevertheless, the neurocognitive mechanisms that mediate the formation of intransitive preferences remain elusive. We show that intransitivity arises from a bottleneck mechanism that blocks the processing of momentarily less valuable information. Although this algorithm is by classical definitions suboptimal (permitting the loss of information), we theoretically and empirically demonstrate that it leads to better decisions when accuracy can be compromised by neural noise beyond the sensory stage. Thus, contrary to common belief, choice irrationality is a by-product of purposeful neural computations.

Abstract

According to normative theories, reward-maximizing agents should have consistent preferences. Thus, when faced with alternatives A, B, and C, an individual preferring A to B and B to C should prefer A to C. However, it has been widely argued that humans can incur losses by violating this axiom of transitivity, despite strong evolutionary pressure for reward-maximizing choices. Here, adopting a biologically plausible computational framework, we show that intransitive (and thus economically irrational) choices paradoxically improve accuracy (and subsequent economic rewards) when decision formation is corrupted by internal neural noise. Over three experiments, we show that humans accumulate evidence over time using a “selective integration” policy that discards information about alternatives with momentarily lower value. This policy predicts violations of the axiom of transitivity when three equally valued alternatives differ circularly in their number of winning samples. We confirm this prediction in a fourth experiment reporting significant violations of weak stochastic transitivity in human observers. Crucially, we show that relying on selective integration protects choices against “late” noise that otherwise corrupts decision formation beyond the sensory stage. Indeed, we report that individuals with higher late noise relied more strongly on selective integration. These findings suggest that violations of rational choice theory reflect adaptive computations that have evolved in response to irreducible noise during neural information processing.

Daily decisions, such as choosing a holiday destination or accepting a job offer, involve comparing alternatives that are characterized by different attributes (1, 2). Understanding how the brain combines information from different attributes into unitary decision values is a key challenge in psychology and the neurosciences (3, 4). From a normative perspective, the value of an alternative should be independent of factors, such as the attractiveness of competing alternatives or the context in which preferences are elicited (5). Thus, the preference relationship between two alternatives ought to remain stable, regardless of changes to the choice set, incurred for example by the addition or removal of other choice alternatives (6).

However, human preferences are often driven by irrelevant factors (7, 8). For instance, an initial preference for one holiday destination (e.g., Bali) over another (e.g., Berlin) can reverse when an inferior alternative (e.g., Dresden) is added to the choice set, even if this “decoy” alternative is never chosen (9, 10). Similarly, an individual preferring a holiday in Bali to Berlin, and Berlin to Boston, will sometimes show a systematic “intransitive” (or inconsistent) preference for Boston over Bali (11). A canonical argument states that such violations of decision theory (hereafter “economic” or “choice irrationality”) disclose fundamental limitations in human processing capacity and of the executive system (12, 13). However, this argument does not have an obvious normative justification. Why did the computations that underlie irrational choices survive millions of years of evolutionary pressure for optimal behaviors that maximize reward? [The term “optimal” is most often used to refer to a policy that yields the highest reward rate, given the likely sources of uncertainty in the environment (e.g., the performance-limiting visibility of a stimulus), and the structure of the task (e.g. the monetary payoff for one action over another). Where independent variables are often economic goods of unknown subjective worth, an optimal policy may be hard to specify, but a rational policy can be defined as one that discloses stable and consistent preferences, as if agents made choices by maximizing a latent subjective utility function.]

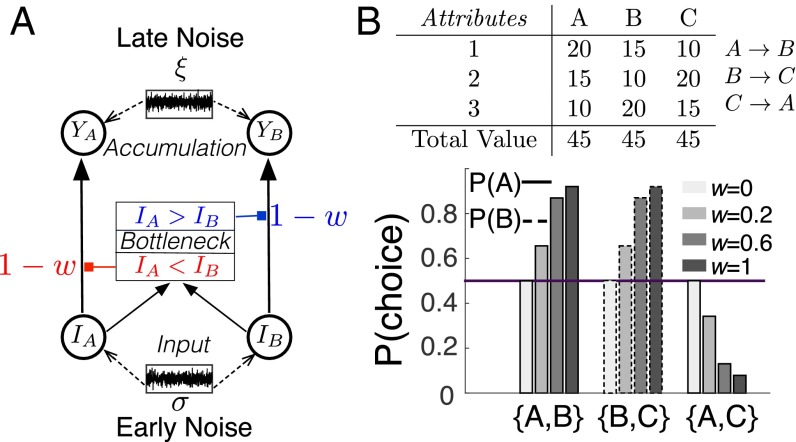
Here, we describe an alternative theory, known as “selective integration” (14), that overcomes this challenge by offering a normative justification of choice irrationality. Building on psychophysical research into the neural and computational mechanisms by which decisions are formed via sequential sampling (15), we assume that choice attributes (e.g., the expense, weather, or culture encountered on holiday) are sampled in turn (2), and integrated toward a cumulative decision variable (16). Under selective integration, the gain of processing on each attribute i of an alternative depends on its rank within that attribute, with a selective gating parameter w (0 < w <1) controlling the reduction in gain for the weakest attribute value (e.g., B_i when A, B are offered and A_i > B_i ). Selective integration thus makes decisions sensitive to the relative ranks of the alternatives within each attribute, over and above their cumulative average value.

Previously, we showed that, when a third (decoy) alternative (D) alters the ranking of two existing alternatives, A and B, the model successfully predicts a preference reversal, despite the fact that the attribute values of A and B remain intact (Table S1) (14). In the current report, we show that selective integration also explains intransitive choice behavior in humans. Using a psychophysical experimental approach, we show that intransitivity can be provoked in most individuals by simple changes to the relative ordering of the decision information, as predicted by selective integration. Critically, however, using a computational simulation based on the sequential sampling framework, we demonstrate that selective integration paradoxically maximizes the accuracy (and subsequent economic outcomes) in the presence of “late” internal noise arising during decision formation, beyond the sensory stage. Importantly, we show that humans with higher estimated late noise are more prone to integrate selectively. Together, these findings offer a biologically viable, descriptively extended, and normatively motivated explanation of economic irrationality.

Table S1.

Qualitative (deterministic) predictions for selective integration for a preference reversal scenario (9) after the addition of an inferior decoy option in the choice set

Decision-relevant quantities	Binary choice				Ternary choice
	Nominal values		Selective integration		Nominal values			Selective integration
	A	B	A	B	A	B	D	A	B	D
Attributes
Weather	35	10	35	0	35	10	5	35	10	0
Expense	15	30	0	30	15	30	25	0	30	25
Total values	50	40	35	30	50	40	30	35	40	25
Choice	$\mathit{A}\succ \mathit{B}$		$\mathit{A}\succ \mathit{B}$		$\mathit{A}\succ \mathit{B}$			$\mathit{A}\prec \mathit{B}$

The alternatives (A, Bali; B, Berlin, D: Dresden) are characterized by two attributes. Here, we used a variant of selective integration that samples attributes in turn and integrates the two highest attribute values with equal gain while discounting the gain of the weakest attribute value (by 1 − w, here w = 1). A smoother version of discounting, where the gains of the second best and worst attribute values are both reduced (by 1 − w₁ and 1 − w₂, respectively), could produce the same qualitative result (provided that w₁ < w₂, i.e., that the gain reduction is stronger for the worst attribute value).

Results

Selective Integration and Intransitivity.

Under a popular computational framework, decisions between competing alternatives are optimized via sequential sampling and integration (17, 18). In choices between multiattribute economic alternatives, such as holidays, this involves sampling attributes in turn (e.g., expense, weather, culture), accumulating their respective values for each alternative (e.g., Bali, Berlin), and comparing the resulting cumulative decision values to select an action (19). We implement selective integration by adding to this framework a “selective gating” parameter, w, which reduces the gain of accumulation for the weaker attribute value (e.g., weather in Berlin) on each sample from 1 (lossless processing, which is optimal according to decision theory) to 1 − w (Fig. 1A and Methods). [An equivalent implementation of selective integration would overweight the stronger attribute value, leaving intact the weaker value. Although this implementation is functionally analogous to the one depicted in Fig. 1A, the two differ in terms of metabolic costs: discounting the value of the local loser engenders a reduction in neural firing rate in contrast to the more costly strategy of amplifying the value (and associated firing rate) of the local winner. Because the experiments presented here were not designed to dissociate these two implementations, we chose to adhere to the less costly one.] After gating (where w > 0), the cumulative value of each alternative is not only a function of its attribute values, as normative theory prescribes, but also a function of the ordinal positions of these values within the different attributes (e.g., Table S1).

Fig. 1.

Selective integration and intransitivity. (A) Schematic of the selective integration model. On each time step, the values of two different alternatives on a single attribute are considered. Input samples (I_A, I_B), corresponding to attribute values, feed to a bottleneck that discounts the gain of the weakest sample (via selective gating, w) before relaying the inputs to the accumulators (Y_A, Y_B). Noise can arise both at the input (σ) and accumulation levels (ξ). (B) Choice probability for different values of w and for σ = ξ = 2, for pairwise comparisons between three equally valued multiattribute alternatives (table). A→B: A wins in more samples than B. WST is violated for w > 0 [i.e., P(A|{A,B}) > 0.5, P(B|{B,C}) > 0.5, P(A|{A,C}) < 0.5, with P(X|{X,Y}) denoting the probability of choosing X over Y].

To illustrate how violations of choice rationality in decisions between two alternatives can arise from selective integration, consider two equally valued alternatives (e.g., A and B in Fig. 1B) that differ along three equally important attributes, which are sampled in turn. For w > 0, the alternative with two (out of three) winning attributes (A) will (on average) be chosen over an alternative that wins by a larger margin on a single attribute (B), because the input to the latter is more often dampened yielding a lower cumulative value. Thus, when the same three values are permuted circularly in three alternatives, the model predicts a violation of “weak stochastic transitivity” (WST) (11, 20): A is chosen more often over B, B over C, and C over A (Fig. 1B; Table S2 for an illustration).

Table S2.

Qualitative (deterministic) predictions of selective integration for all pairwise choices among three equally valued alternatives (Fig. 1B)

Decision-relevant quantities	Nominal values			A vs. B		B vs. C		A vs. C
	A	B	C	A	B	B	C	A	C
Attributes
Weather	20	15	10	20	0	15	0	20	0
Expense	15	10	20	15	0	0	20	0	20
Culture	10	20	15	0	20	20	0	0	15
Total values	45	45	45	35	20	35	20	20	35
Choice				$\mathit{A}\succ \mathit{B}$		$\mathit{B}\succ \mathit{C}$		$\mathit{A}\prec \mathit{C}$

If noise is added (and the model predictions are probabilistic), the model violates WST (Fig. 1B). The selective gating parameter was set to w = 1.

Violations of WST are not only incompatible with normative theories but also with a large class of descriptive theories of choice in which preference tendencies are perturbed by normally distributed noise (16, 21). Thus, when empirically obtained, such violations offer important theoretical constraints. Although WST violations have been reported in humans (11), recent research has shown that the vast majority of these putative violations were not statistically significant when a more appropriate statistical test is applied (20, 22). It is thus an empirical question whether intransitivity, as predicted by our framework, will occur in human observers. Before examining whether humans violate WST in the direction predicted by our model, we first set out to examine how well selective integration characterizes the way humans accumulate evidence over time while forming preferences for different alternatives.

Selective Integration in a Psychophysical Task.

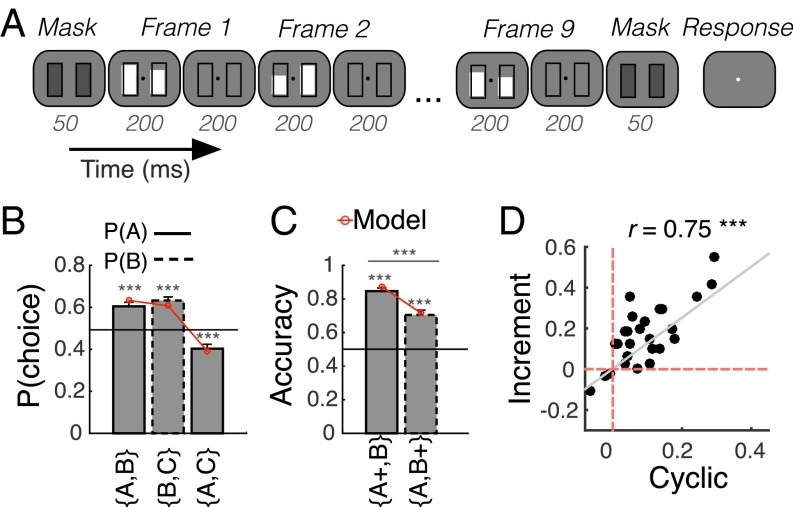
We gathered data from human participants performing a psychophysical choice task with real economic incentives for accurate choices (Fig. 2A; Methods). In experiment 1, participants (n = 28) chose between two alternatives each characterized by nine sequentially occurring bars of different heights, presented in two simultaneous streams (at a rate of 400 ms per frame) on the left and right of the screen (Fig. 2A). Participants were instructed that the two bars in each presentation frame correspond to two “attribute” values as in the example of Fig. 1B. At the end of each trial, they were asked to choose the stream with the larger average height, receiving monetary reward proportional to their choice accuracy. Using the notation A→B to indicate that “alternative A has more winning attributes than B” [here, six vs. three winning attributes], we constructed sequences of equal average value, such that A→B, B→C, and C→A, as in the alternatives in Fig. 1B (“cyclic” trials). Although participants performed the task accurately (range of 62–92% correct on intermixed “standard” trials where the attribute values were randomly generated from Gaussian distributions), they exhibited a higher preference for the frequently winning stream in the cyclic trials, as predicted by the model [Fig. 2B; P(A|{A,B}) = 0.61, P(B|{B, C}) = 0.63, P(C|{A,C}) = 0.62, and P < 0.001 for all comparisons to chance; significant frequent-winner effect in 17 out of 28 participants; SI Results].

Fig. 2.

Behavioral task and selective integration. (A) Trial schematic in experiment 1. Participants (n = 28) viewed two streams of bars and had to choose which stream was overall highest. (B) Mean choices in cyclic trials in experiment 1 (Fig. 1B) revealed a frequent-winner effect: A was chosen more often over B, B over C, and C over A. (C) Accuracy in increment trials, where the samples of either the frequently winning or the frequently losing stream were increased by a constant (A+ vs. B and A vs. B+, respectively). The difference in accuracy between the A+ vs. B and the A vs. B+ trials also revealed a frequent-winner effect. (D) The frequent-winner effect in cyclic ([P(A|{A,B})+P(B|{B, C})+P(C|{A,C})]/3–0.5) and increment trials [P(A₊|{A₊,B}) – P(B₊|{A,B₊})] correlated positively to each other. Filled circles correspond to different participants. Grey curve is the linear regression line. Error bars are 2 SEM. ***P < 0.001.

On a further intermixed set of “increment” trials, we increased the average bar height in either the frequently winning (e.g., A when A→B) or the frequently losing (e.g., B when A→B) streams, breaking the tie without altering the relative proportion of winning attributes (2:1 in favor of A). Participants were more likely to choose the stream with the increment in both cases (Fig. 2C; P < 0.001)—being sensitive to the average height difference and not merely the difference in the number of winning attributes—but accuracy was higher when the increment occurred in the frequently winning than the frequently losing stream (P < 0.001). These “frequent-winner” effects in cyclic and increment trials were highly correlated across the cohort (r = 0.75, P < 0.001; Fig. 2D) and both correlated positively with participants’ estimated w (r = 0.66 in cyclic; r = 0.68 in increment; P < 0.001 in both) (model-fitting procedures and results in SI Methods and Fig. S1).

Fig. S1.

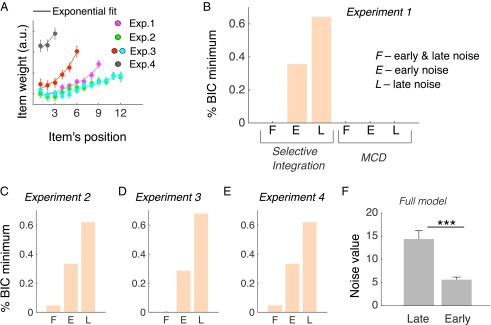
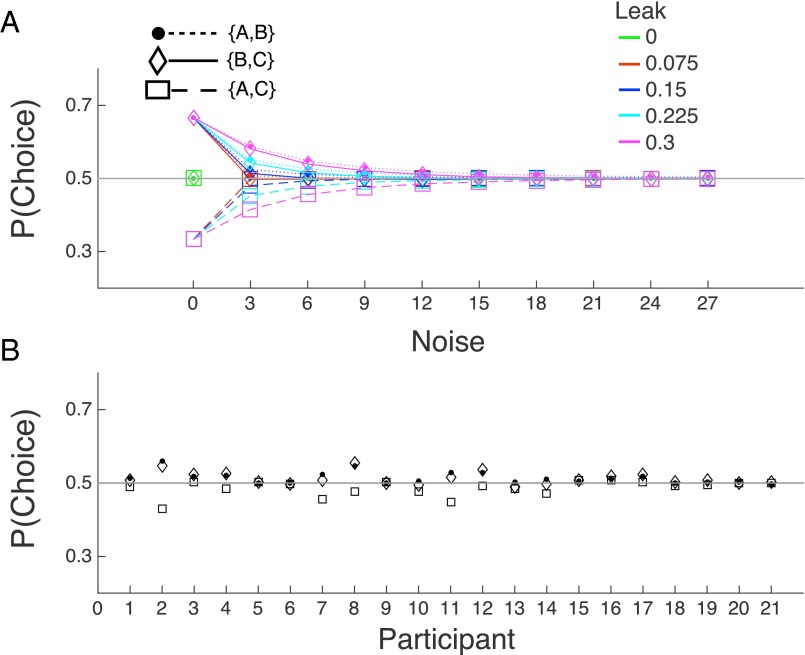
Recency effect and model comparison. (A) A logistic regression assessed the impact of the temporal position of each pair on choice and revealed a recency effect in experiments 1–4. This recency effect necessitated the use of a leak parameter in the models (Methods). (B) Percentage of participants that a given model offered the lowest BIC in experiment 1. Selective integration with late noise only (labeled L; i.e., omitting early noise) scored better. Majority of confirming dimensions (MCD) variants had much higher BIC scores than selective integration variants and consequently failed to score the lowest BIC in any participant. (C) In experiments 2–4, the variant of selective integration with late noise only (L) also scored lower BIC values in more participants compared with the other variants (E: early noise only; F: full model with early and late noise). (D) This three-parameter model that omits early noise is consistent with “late-noise dominance” in the full model (F), which included both early and late noise (mean ± SE of late- vs. early-noise parameter values in the full model across all four experiments: 14.38 ± 1.91 vs. 5.59 ± 0.58). Error bars correspond to 2 SEM. ***P < 0.001.

A tendency to prefer the frequently winning stream could be explained by normalization theories (Table S3) that attribute some aspects of choice irrationality on efficient neural coding schemas [i.e., divisive (23) or range-normalization (24) applied on each pair of values before accumulation]. Similarly, a simpler “majority of confirming dimensions” (MCD) rule that decides based on the total number of local winners (25) could also explain the frequent-winner effect (Table S3). One unique signature of selective integration is that in choices between two alternatives with equal mean value but different variances, it predicts a higher preference for the high-variance alternative. This “provariance” effect has been empirically verified elsewhere (14) but was also observed in the current experiment. When the two alternatives had different variances, accuracy was higher when the high variance was assigned to the correct alternative compared with trials where the correct alternative had low variance [standard conditions 3 and 4 in SI Methods; accuracy difference between 3 and 4: mean ± SEM = 0.23 ± 0.03; P < 0.001]. As shown in Table S4, the provariance effect cannot be captured by normalization theories or by MCD (Fig. S1B).

Table S3.

Qualitative predictions for selective integration, divisive normalization range-normalization models, and majority of confirming dimensions (MCD) for the frequent-winner effect (preference for A over B; Fig. 1B) that underlies intransitivity

Decision-relevant quantities	Nominal values		Selective integration		Divisive normalization		Range normalization		MCD
	A	B	A	B	A	B	A	B	A	B
Attribute 1	20	15	20	0	$\frac{20}{35}$	$\frac{15}{35}$	$\frac{20}{5}$	$\frac{15}{5}$	1	0
Attribute 2	15	10	15	0	$\frac{15}{25}$	$\frac{10}{25}$	$\frac{15}{5}$	$\frac{10}{5}$	1	0
Attribute 3	10	20	0	20	$\frac{10}{30}$	$\frac{20}{30}$	$\frac{10}{10}$	$\frac{20}{10}$	0	1
Total values	45	45	35	20	$\frac{1,580}{1,050}$	$\frac{1,570}{1,050}$	8	7	2	1
Choice	$\mathit{A}\sim \mathit{B}$		$\mathit{A}\succ \mathit{B}$		$\mathit{A}\succ \mathit{B}$		$\mathit{A}\succ \mathit{B}$		$\mathit{A}\succ \mathit{B}$

The divisive normalization model divides each attribute value with the net value on that attribute. The range normalization model divides each attribute value with the absolute difference (range) on that attribute. The MCD counts the number of winning dimensions for each alternative.

Table S4.

Qualitative predictions for selective integration, divisive normalization, range-normalization and MCD models, for the provariance effect (preference for C)

Decision-relevant quantities	Nominal values		Selective integration		Divisive normalization		Range normalization		MCD
	C	D	C	D	C	D	C	D	C	D
Attribute 1	20	15	20	0	$\frac{20}{35}$	$\frac{15}{35}$	$\frac{20}{5}$	$\frac{15}{5}$	1	0
Attribute 2	10	15	0	15	$\frac{10}{25}$	$\frac{15}{25}$	$\frac{10}{5}$	$\frac{15}{5}$	0	1
Total values	30	30	20	15	$\frac{170}{175}$	$\frac{180}{175}$	6	6	1	1
Choice	$\mathit{C}\sim \mathit{D}$		$\mathit{C}\succ \mathit{D}$		$\mathit{C}\prec \mathit{D}$		$\mathit{C}\sim \mathit{D}$		$\mathit{C}\sim \mathit{D}$

For simplicity, we assumed that the high-variance option (C) varies between 10 and 20, whereas the low-variance option (D) has a fixed value of 15 in both attributes.

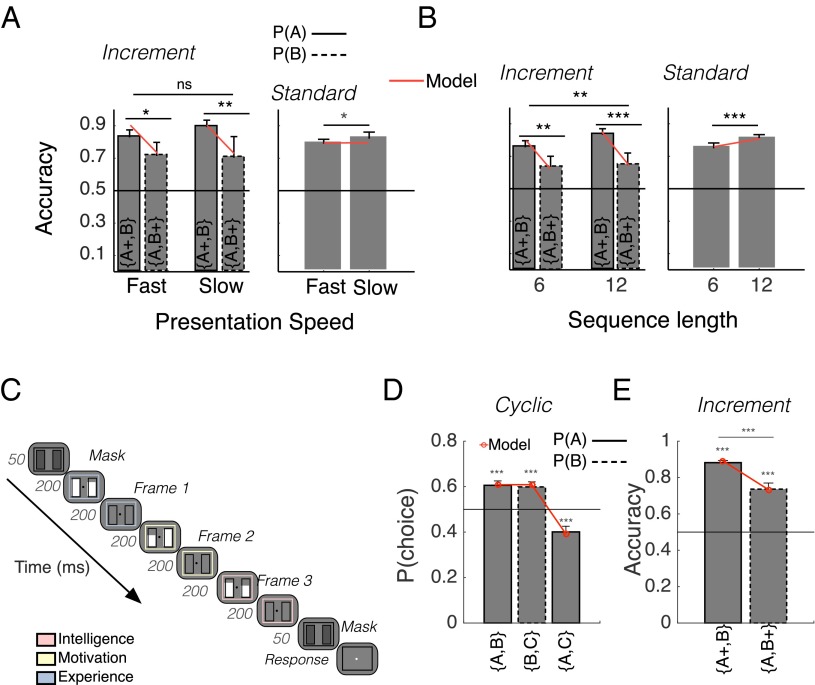
Finally, in two further experiments, we examined whether participants adopted a w > 0 due to the lack of processing resources or the scarcity of information, as theories of bounded rationality would advocate (13). When we slowed the presentation rate to 1 Hz (experiment 2), we obtained a similar frequent-winner effect, suggesting that selective gating does not just reflect a processing bottleneck due to the rapid stimulus presentation (Fig. S2A). When we increased the sequence length from few (6) to many (12) samples (experiment 3), the frequent-winner effect increased in the latter (Fig. S2B), indicating that the tendency to discount losing values does not decrease when more information (samples) is available, contrary to the predictions of heuristic models (26).

Fig. S2.

Behavioral results in experiments 2–4. (A) Accuracy in increment and standard trials in experiment 2 (n = 17) where the presentation speed was manipulated within participants (experiment 2). (B) Accuracy in increment trials and standard trials in experiment 3 (n = 27), where the sequence length changed randomly within an experimental block (experiment 3). (C) Time course of a trial in experiment 4 (n = 21). The colors–dimensions mapping was randomized across participants (SI Methods). (D) Choices in cyclic trials in experiment 4 replicated the frequent-winner effect in experiment 1. WST was significantly violated in 11 out of 21 participants who chose A more often than B, B more often than C, and C more often than A (Table S5). (E) Participants in experiment 4 had above-chance accuracy in both increment conditions, and the frequent-winner effect of experiment 1 was replicated [$P\left(A_{+}|\left\{A_{+},B\right\}\right)>P\left(B_{+}|\left\{A,B_{+}\right\}\right)$]. Error bars correspond to 2 SEM. ***P < 0.001; **P < 0.010; *P < 0.050.

Systematic Violations of WST in Human Observers.

As shown in Fig. 1B, selective integration violates the principle of WST. The preference patterns in the cyclic trials in experiment 1 offer a widely used proxy for the degree of intransitivity; the conclusion that such patterns definitively violate WST can, however, be challenged in statistical grounds (20). [Cyclic trials were created using n different A, B, C triplets (Methods). Participants encountered the three pairwise comparisons for each triplet only once. We could count in how many triplets per participant an intransitive circle was obtained. However, the statistical interpretation of this metric of intransitivity, based on pattern counting, is limited and controversial as explained elsewhere (20). Thus the design of experiment 1 was not suitable for rigorous examination of WST violations.] We thus adjusted the experimental design to rigorously assess WST violations within individuals (experiment 4). Participants (N = 21) chose between pairs of alternatives—each corresponding to a job candidate—characterized by three sequentially presented pairs of bars (Methods). Each pair of bars was presented within a colored outline, with the color indicating an explicitly defined choice dimension (Fig. S2C). The presentation order of the different dimensions was randomized on each trial. The main departure from experiment 1 was that, for each participant, three unique cyclic trials (A vs. B, B vs. C, and A vs. C) were constructed based on a single A–B–C triplet and presented several times, as in multiattribute or risky choice studies of intransitivity (11, 20).

Accuracy in standard trials ranged from 85% to 98%, whereas significant frequent-winner effects were detected in both cyclic (Fig. S2D; P < 0.001 in all three comparisons of the frequent-winning option to chance; frequent-winner effect significant in 15 out of 21 participants; SI Results) and increment trials (Fig. S2E; P < 0.001). As in experiment 1, the two frequent-winner effects were correlated to each other (r = 0.86; P < 0.001) and to the selective gating parameter in the model (r = 0.89 in cyclic; r = 0.96 in increment; P < 0.001 in both). A significant provariance effect was observed in standard trials (0.04 ± 0.01; P < 0.003), ruling out MCD and normalization models. Finally, 11 out of 21 participants violated WST significantly (Table S5). The probability that all these 11 participants corresponded to a type I error is extremely low (P = 1.1 × 10⁻⁹). A detailed presentation of these individual-level analyses is given in SI Methods and SI Results. [It has been recently argued that WST violations can occur spuriously (20). As a remedy, a more stringent test, against the so-called “triangle inequality,” has been prescribed. Three participants were intransitive according to this test. However, this test does not seem suitable for our study. First, the chances that the reported WST violations occurred spuriously in our psychophysical task are negligible (Fig. S3 and SI Results). Second, the test is conservative in the sense that it would fail to detect real intransitivity effects that, although substantial, are below a certain magnitude due to the presence of experimental noise.]

Table S5.

Individual participants’ results and analyses in experiment 4

	Probability of choice
Participant	A over B	B over C	A over C	No. of trials	WST, P value	Triangle ineq., P value
1	0.65	0.62	0.42	162	0.020	1.000
2	0.52	0.60	0.43	162	0.274	1.000
3	0.62	0.58	0.25	162	0.020	1.000
4	0.51	0.52	0.46	162	0.501	1.000
5	0.70	0.69	0.31	162	<0.001	0.119
6	0.57	0.55	0.55	162	1.000	1.000
7	0.49	0.45	0.60	162	0.364	1.000
8	0.61	0.60	0.46	162	0.169	1.000
9	0.80	0.81	0.18	162	<0.001	<0.001
10	0.67	0.80	0.33	162	<0.001	0.015
11	0.60	0.57	0.48	162	0.312	1.000
12	0.48	0.38	0.56	162	0.308	1.000
13	0.55	0.62	0.44	162	0.108	1.000
14	0.50	0.51	0.48	162	1.000	1.000
15	0.66	0.63	0.36	162	<0.001	1.000
16	0.57	0.59	0.38	162	0.030	1.000
17	0.36	0.36	0.60	162	0.006	1.000
18	0.58	0.58	0.38	162	0.021	1.000
19	0.72	0.66	0.29	162	<0.001	0.070
20	0.58	0.60	0.46	81	0.214	1.000
21	0.81	0.69	0.17	81	<0.001	<0.001

Bold indicates significant violations of transitivity tests at $\alpha =0.05$. Number of trials refers to each of the three cyclic conditions. [Two participants (20, 21) completed only one session (i.e., one-half of the trials) due to a technical error.] Details of the statistical tests are provided in SI Methods.

Fig. S3.

Intransitivity predictions of noisy leaky integrator. (A) Probability of choice in the cyclic trials obtained by simulating a noisy leaky integrator (in 5,000 sessions using input sequences as per experiment 4). Leak and noise varied within the range of the corresponding best-fitting parameters. When leak is present, intransitivity can be observed due to the randomization of the sequences and the recency bias. This pattern weakens and eventually dissipates in the presence of noise. (B) Predictions of the noisy leaky integrator (5,000 sessions) using the best-fitting noise and leak parameters per participant and after setting w = 0. Probability of choice on y axes is given for the first alternative in the corresponding binary set (i.e., A in {A, B}).

Selective Integration and Decision Accuracy in the Face of Late Noise.

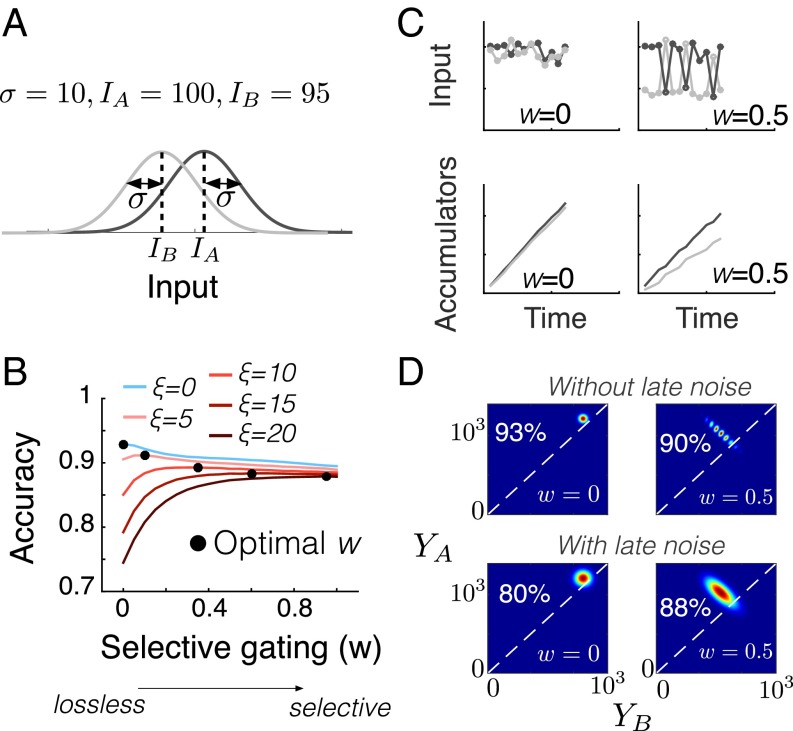
Why do humans discount locally weaker values, provoking intransitive choices (experiment 4) and other violations of economic rationality (14)? We next compared the accuracy (and consequent rewards) that is obtained under selective (w > 0) and lossless integration (w = 0), simulating an experimental setting in which the attribute values of the two alternatives are generated from two Gaussian distributions with the same variance (σ) and different means (Fig. 3A). This setting is equivalent to a two-alternative forced-choice paradigm (15, 17), where one-dimensional quantities (e.g., perceptual signals or economic values of magnitude I_A, I_B) are corrupted by noise, which arises early, before their accumulation (27) (Fig. 1A, lower box). In addition to variability at the input level (which can be both due to early internal noise and due to exogenous fluctuations in the stimuli values), we assumed that noise could also arise late, at the level of accumulation (i.e., decision noise ξ; Fig. 1A, upper box) (28).

Fig. 3.

Selective integration and decision accuracy. (A) The input distributions in a typical two-alternative forced-choice scenario. The SD of the distributions (σ) corresponds to early noise. (B) Decision accuracy in the model for the scenario in A, as a function of w, for different levels of late noise (ξ; curves) and after 12 accumulation steps (t). Black circles indicate the value of w that maximizes accuracy for a given level of late noise. (C) Example input (Top) and single-trial accumulator states (Bottom) for lossless (Left) and selective integration (Right). The input parameters are as in A, and late noise was absent. (D) Bivariate end-state (t = 12) accumulator distributions for the choice problem in A, for lossless (Left) and selective integration (Right). (Top) ξ = 0. (Bottom) ξ = 15. Density to the Left of dashed diagonal corresponds to accuracy (in percentage). Higher density is depicted with red, and lower density with blue.

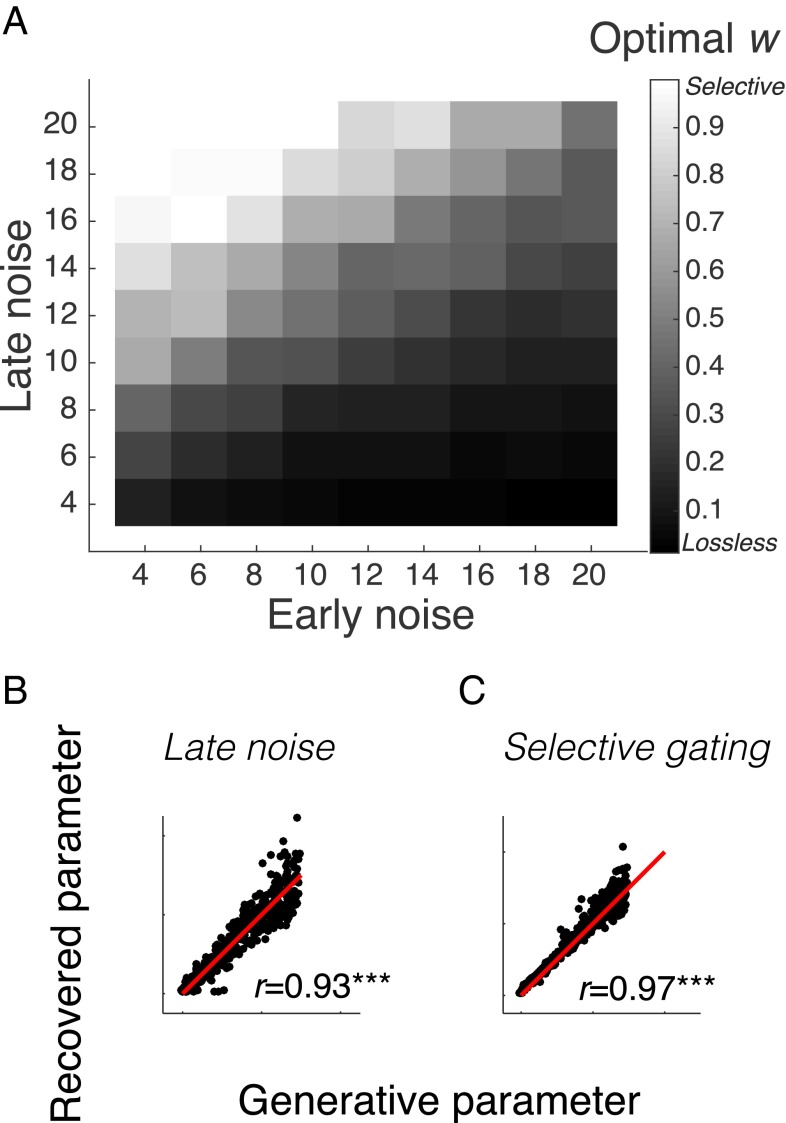
When late noise is absent and early noise is present (Fig. 3B, top blue line), integrating samples with equal gain (w = 0) is optimal as postulated by statistical decision theory (15, 17, 28). Most surprisingly, however, when late noise is also present, maximum accuracy is achieved for w > 0, with the value of w that maximizes accuracy increasing with late noise (Fig. 3B, black circles). [The situation reverses and the optimal w regresses toward 0 as the level of early noise increases. This happens because, when early noise is heightened, selective integration is more costly operating almost at random, given that the “frequency of winning” becomes less predictive of the identity of the correct alternative (Fig. S4A).] Why does selective integration confer an improvement in accuracy in the face of heightened late noise? On average, discounting locally weaker attribute values via selective gating exaggerates the accumulated differences between higher-valued (typically, frequently winning) and lower-valued (typically, frequently losing) alternatives (Fig. 3C for a simulated trial example). This policy occasionally inflates a lower-valued alternative over its higher-valued rival (i.e., when the former is the local winner more often), leading to a slight cost in accuracy relative to lossless integration. When late noise is present, however, the benefit of inflating the accumulated differences offsets this cost.

Fig. S4.

Optimal selective gating for early/late noise and parameter recovery in the model. (A) The optimal selective gating increases (brighter shades) as late noise increases (Fig. 3B) and decreases (darker shades) as early noise increases. The latter effect is due to the fact that, as early noise increases, the local winner becomes less and less predictive of the identity of the correct alternative. As a consequence, selective integration operates almost randomly and at a high cost, which is not balanced out in the absence of strong late noise. Simulation details are described in SI Methods. (B) Generative parameters plotted against recovered parameters for late noise and (C) selective gating in simulated datasets (SI Methods). Red curves are linear regression lines. ***P < 0.001.

In Fig. 3D, we illustrate this point by plotting the bivariate end-state distributions of the two accumulators, under no late noise (top panels) and high (bottom panels) late noise. Relative to lossless integration (w = 0), selective integration (w = 0.5) drives accumulator states away from the equality line (density right to the line corresponds to percentage of choice errors), yielding more robust preference states and thus higher performance under late noise (bottom left/right panels, percent accuracies signaled on each panel). This robustness is comparable to that observed in nonparametric statistics, where inferences depend on the ranked data, whereas the mechanism is related to the heightened signal-to-noise ratio in chains of neural populations when the gain of individual neurons increases (29). Thus, when noise arises at different stages of the processing hierarchy, selective integration—although it ignores part of the input and leads to violations of transitivity—can outperform the lossless integration algorithm (15, 17) by acting against late noise.

Selective Gating and Late Noise Relationship in Human Observers.

Finally, we interrogated the behavioral data to test whether selective integration might be an adaptation specifically evolved to counteract late noise during integration. If so, individuals with higher late noise should have a higher selective gating parameter as depicted in Fig. 3B. We fitted three variants of the selective integration model that differed in their assumptions about the source of internal noise: (i) a full model, having both early and late noise; (ii) a model with early noise only; and (iii) a model with late noise only (SI Methods). The early noise in the model corresponded to extra internal noise applied at the input representation stage, on top of the stimulus external variability. We factored in the latter by fitting the models using the actual stochastic input that participants saw in the experiments. In addition to noise and selective gating (w) parameters, all variants had a leak parameter to capture the recency effect (14) that was observed in all experiments (Fig. S1A).

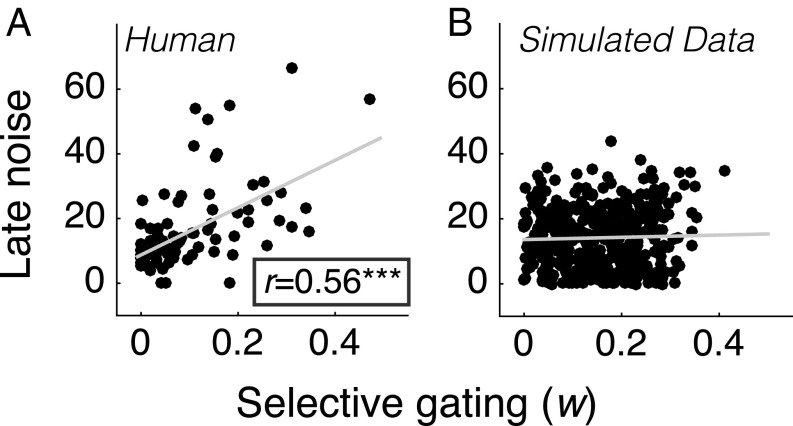
In all experiments, model comparison favored the selective integration variant that omitted early noise (variant iii) (Fig. S1 B–E). Furthermore, examining the noise parameters in the full model (i) revealed that late noise was significantly higher than early noise, with the latter having a negligible magnitude (Fig. S1F). After verifying our fitting method with regards to parameter recovery (Fig. S4 B and C, and SI Methods), we found a positive correlation between participants’ estimated late noise and selective gating in all experiments (experiments 1–4: r = 0.63, P < 0.001, r = 0.80; P < 0.001, r = 0.52; P < 0.006; r = 0.81; P < 0.001; Fig. 4A, scatterplot for all experiments). We ruled out the possibility that this correlation occurred as an artifact of the parameter estimation method, by reporting no relationship (r = 0.03; P = 0.502) between estimated late noise and w in simulated datasets (Fig. 4B and SI Methods). This finding indicates that selective gating has an adaptive role, being adjusted to each individual’s late noise levels, in the service of reward-maximizing decisions.

Fig. 4.

Relationship between selective gating and late noise. (A) Estimated selective gating parameters for each individual (circles) in all four experiments (n = 93) plotted against estimated late noise parameters. (B) Same as A, but for simulated data (see Fig. S4 B and C and SI Methods). Gray curves are linear regression lines. ***P < 0.001.

SI Methods

Stimuli.

The visual stimuli were presented using Psychophysics-3 Toolbox (40) running in Matlab (MathWorks, 2012) on 17” monitors (1,024 × 768-px screen resolution and 60-Hz refresh rate). Participants viewed the stimuli in a dimly lit room from 60-cm distance. The stimuli consisted of two series of white bars presented within two fixed-height black rectangular placeholders (width, 60 px/15 mm/1.5° visual angle; height, 200 px/50 mm/5.0° visual angle) separated by 80 px/20 mm/2.0° visual angle and presented against gray background. The inset bars varied in height over a sequence of a fixed number of samples. The height of each bar was selected depending on the trial condition. In experiment 4 only, a large rectangular outline surrounded the bars at all times. The color of the outline was black during the presentation of masks and after the stimuli presentation, but changed on each presentation frame to indicate the dimension on which the two job candidates were assessed. We used three dimensions (intelligence, motivation, experience) and three colors [r–g–b: C1 = (255–204–204), C2 = (176–196–222), C3 = (255–255–204)]. The mapping between the dimensions and colors was counterbalanced across participants.

Trial Time Course.

Each trial began with two black rectangle outlines (placeholders) for 150 ms and a black central fixation circle (radius, 10 px/2.5 mm/0.25°) that remained on screen during stimulus presentation. The next frame contained a mask stimulus, in which two dark gray bars occupied fully the placeholders (50 ms) followed by a sequence of white bars of varying height presented within the rectangular placeholders (200 ms each, followed by a 200-ms “blank” interval where the outline rectangles appeared empty), and finally a second mask identical to the first (50 ms). In slow trials only, in experiment 2, bars were presented for 800 ms each, followed by a 200-ms blank interval. In all experiments, immediately following the second mask, the fixation circle turned white, prompting participants to respond. In experiment 4, a rectangular outline surrounded the presented bars. The outline changed color on every frame (filled bars and blank periods) signaling the dimension on which the two candidates were assessed (Fig. S2C). The outline was black during the presentation of masks and before for participants’ responses following the presentation of the sequences. Responses in all experiments were made using the keyboard arrow keys, left and right (with index and ring fingers of the dominant hand, respectively), corresponding to the chosen sequence’s screen position. When feedback was provided, the fixation circle turned green for correct and red for incorrect responses (300 ms). When feedback was withheld (44% of trials in experiment 1 and 57% of trials in experiment 4, including in both cases all cyclic trials and 20% of noncyclic trials), the fixation circle turned black regardless of the participant’s response. Participants in experiments 1 and 4 were told that informative feedback is provided in a subset of trials only but performance-based rewards will depend on their accuracy in all trials.

Experimental Conditions.

In experiment 1, cyclic trials were based on a set of prototypical sequences, labeled “A sequences.” Each A sequence (i.e., A_j with j = 1…n) was based on three baseline numbers (corresponding to bar height), labeled $x_{\alpha },\hspace{0.17em}{x}_{\beta }$, and $x_{\gamma }$. These numbers were sampled from a normal distribution with its mean distributed uniformly between 110 and 130 (pixels) and a SD of 4. Each of these sequence-specific numbers was associated with an increment value, labeled $\delta x$ (i.e., ${\delta }_{\alpha },\hspace{0.17em}{\delta }_{\beta }\hspace{0.17em},{\delta }_{\gamma }$), which was sampled from a uniform distribution [$\delta x\sim U(10,20)$].

Each A_j sequence consisted of the following nine samples:

$$A_j=\left\{x_{\alpha }-2{\delta }_{\alpha },\hspace{0.17em}{x}_{\alpha }-{\delta }_{\alpha },\hspace{0.17em}{x}_{\alpha },\hspace{0.17em}{x}_{\beta }-2{\delta }_{\beta },\hspace{0.17em}{x}_{\beta }-{\delta }_{\beta },\hspace{0.17em}{x}_{\beta },\hspace{0.17em}{x}_{\gamma }-2{\delta }_{\gamma },\hspace{0.17em}{x}_{\gamma }-{\delta }_{\gamma },\hspace{0.17em}{x}_{\gamma }\right\}.$$

For each A_j sequence, a corresponding B_j sequence was constructed by performing a right circular shift on each one of the three subsets of the A_j sequence (i.e., a separate shift for $x_{\alpha }-2{\delta }_{\alpha },\hspace{0.17em}{x}_{\alpha }-{\delta }_{\alpha },\hspace{0.17em}{x}_{\alpha }$, for $x_{\beta }-2{\delta }_{\beta },\hspace{0.17em}{x}_{\beta }-{\delta }_{\beta },\hspace{0.17em}{x}_{\beta }$, and for $x_{\gamma }-2{\delta }_{\gamma },\hspace{0.17em}{x}_{\gamma }-{\delta }_{\gamma },\hspace{0.17em}{x}_{\gamma }$):

$$B_j=\left\{x_{\alpha },\hspace{0.17em}{x}_{\alpha }-2{\delta }_{\alpha },\hspace{0.17em}{x}_{\alpha }-{\delta }_{\alpha },\hspace{0.17em}{x}_{\beta },\hspace{0.17em}{x}_{\beta }-2{\delta }_{\beta },\hspace{0.17em}{x}_{\beta }-{\delta }_{\beta },\hspace{0.17em}{x}_{\gamma },\hspace{0.17em}{x}_{\gamma }-2{\delta }_{\gamma },\hspace{0.17em}{x}_{\gamma }-{\delta }_{\gamma }\right\}.$$

Finally, for each B_j sequence, a corresponding C_j sequence was constructed via a right circular shift of the B_j sequence (see above) such that:

$$C_{\mathrm{sequence}}=\left\{x_{\alpha }-{\delta }_{\alpha },\hspace{0.17em}{x}_{\alpha },\hspace{0.17em}{x}_{\alpha }-2{\delta }_{\alpha },\hspace{0.17em}{x}_{\alpha }-{\delta }_{\beta },\hspace{0.17em}{x}_{\beta },\hspace{0.17em}{x}_{\beta }-2{\delta }_{\beta },\hspace{0.17em}{x}_{\gamma }-{\delta }_{\gamma },\hspace{0.17em}{x}_{\gamma },\hspace{0.17em}{x}_{\gamma }-2{\delta }_{\gamma }\right\}.$$

Therefore, streams in cyclic trials had overall equal values, and thus there was no objectively defined correct answer. Also, in each (i) A vs. B, A won locally over B more often; in (ii) B vs. C, B won over C more often; and in (iii) A vs. C, C won over A more often (Fig. 1B). In the long version of experiment 1, 60 unique A–B–C triplets were generated per participant, resulting in 60 trials for each A vs. B, B vs. C, and A vs. C pairwise comparisons. In the short version of the experiment, there were 40 unique triplets.

The two increment conditions were constructed in two ways: (i) by adding a constant of 6 pixels to all samples of the A_j sequences (A+ vs. B), or (ii) by adding a constant of 6 pixels to all samples of the B_j sequences (A vs. B₊).

As in cyclic trials, the presentation order of the pairs within a given trial was randomized.

In standard trials, the bar heights were generated from Gaussian distributions. These trials acted as “fillers” that obscured the trial structure in cyclic and increment trials and also provided an independent measure of accuracy. The mean of the high (i.e., correct) sequence ($S_H$) was randomly sampled from a uniform distribution [${\mu }_H\sim U(80,120)$ in pixels]. The mean of the low sequence ($S_L$) was decreased by 6 pixels (${\mu }_L={\mu }_H-6$). The SDs of the two sequences could be either high or low (${\sigma }_H=20,\hspace{0.17em}{\sigma }_L=10$) resulting in the following four conditions:

$$i)S_H\sim N\left({\mu }_H,{\sigma }_L\right)\hspace{0.17em}\mathrm{and}\hspace{0.17em}{S}_L\sim N\left({\mu }_L,{\sigma }_L\right),$$

$$\mathit{ii})S_H\sim N\left({\mu }_H,{\sigma }_H\right)\hspace{0.17em}\mathrm{and}\hspace{0.17em}{S}_L\sim N\left({\mu }_L,{\sigma }_H\right),$$

$$\mathit{iii})S_H\sim N\left({\mu }_H,{\sigma }_H\right)\hspace{0.17em}\mathrm{and}\hspace{0.17em}{S}_L\sim N\left({\mu }_L,{\sigma }_L\right),\text{and}$$

$$\mathit{iv})S_H\sim N\left({\mu }_H,{\sigma }_L\right)\hspace{0.17em}\mathrm{and}\hspace{0.17em}{S}_L\sim N\left({\mu }_L,{\sigma }_H\right).$$

The sequences generation process was constrained such that the sampled means and SDs did not deviate from the nominal ones more than 3 units (pixels). The Gaussians were truncated such that the sampled height was within the placeholders (range 0–200 pixels). Accuracy differences in iii and iv provide extra leverage in fitting the selective integration model, since the model predicts a “provariance” bias (14), i.e., higher accuracy in iii compared with iv.

Experiments 2 and 3 consisted of standard and increment conditions only (six conditions in total). In experiment 2, we manipulated the presentation rate of the bars in a blockwise fashion (fast/slow). In experiment 3, we randomly interleaved short (six samples) and long sequences. Finally, experiment 4 was analogous to experiment 1, featuring nine conditions overall. There were two differences: (i) that pairs of bars were assigned to specific dimensional labels (intelligence, motivation, and experience of a job candidate), and (ii) that the cyclic trials were created from a single A–B–C triplet (i.e., with fixed dimensional values) per participant. Associating each pair of bars with a different dimension allowed us to randomize the presentation order of the pairs in the cyclic trials, while keeping A–B–C physically intact (i.e., effectively randomizing the presentation order of the three dimensions). In noncyclic trials, pairs of bars were randomly assigned to the three dimensions. Because sequences in experiment 4 had only three items, the mean difference between the two alternatives in noncyclic trials increased to 12 pixels to compensate for the higher difficulty due to the short sequences length. Similarly, to compensate for the larger impact of internal noise due to the short length, the value of the increment ${\delta }_x$ in cyclic trials was set to 30 pixels [compared with ${\delta }_x\sim U(10,20)$ in experiment 1]. In increment trials, the increment value was sampled from ${\delta }_x\sim U(20,40)$_.

Design.

There were two versions of experiment 1 (n = 28) that differed just in the number of trials performed by each participant. Twelve participants performed 400 trials (short group), whereas 16 participants performed 600 trials (long group). In the long group, there were 300 standard trials (75 trials per condition), 120 increment trials (60 in each condition), and 180 cyclic trials (60 per condition). In the short group, there were 200 standard trials, 80 increment trials, and 120 cyclic trials. Behavior between the two groups was indistinguishable. Trials from all conditions were randomly interleaved and presented in eight blocks. The left/right position of the streams was randomized. Feedback was offered following choices in 80% of standard and increment trials, where choice correctness could be objectively defined. Feedback in all cyclic trials was withheld. Because of partial lack of feedback, we indicated midway each block whether accuracy in the preceding trials (excluding cyclic trials where there was no correct answer) increased (an improvement above 5%), decreased (a drop of 5%), or stayed the same (any change in-between) compared with all previous trials thus far.

In experiment 2 (n = 17), we manipulated the presentation rate of the bars in a blockwise fashion. In all trials, participants observed 12 pairs of bars. In “fast” blocks, the pairs were presented at a standard rate (200 ms followed by 200-ms blank), whereas in the “slow” condition the filled white bars stayed on screen for longer (800 ms followed by 200-ms blank interval). Participants performed 432 trials that were divided in eight blocks (54 trials each). There were six conditions (four standard and two increment conditions), resulting in 36 trials per condition and presentation rate. The order of “normal” and slow blocks was controlled such that block type alternated between consecutive blocks. Full feedback was provided. The construction of the prototypical A, B, C sequences was based on four triplets to produce 12 pairs of bars in increment trials.

In experiment 3 (n = 27), we presented participants with standard and increment trials and full feedback. We manipulated the length of the sequences from 6 to 12. The construction of A, B, C sequences was adapted for each sequence length (i.e., using two and four triplets, for sequence length of 6 and 12, respectively). Overall, participants performed 720 trials divided into eight blocks. There were six conditions (four standard and two increment conditions) for each sequence length (60 trials for each condition and sequence length). Trials of different sequence length were randomly interleaved.

Finally, in experiment 4 (N = 21), we presented cyclic, standard, and increment trials as in experiment 1, with partial feedback (in 80% of the noncyclic trials). Procedures and block structure were identical to experiment 1 except that each trial consisted of three pairs of bars, corresponding to three dimensions on which the two hypothetical candidates of each trial were assessed. Each dimension was associated to a unique color (Stimuli). Each frame (i.e., pair of bars) was presented within a colored rectangular outline that described the active dimension. Participants were provided with a hard copy of the dimensions/colors associations and were encouraged to consult this copy as needed during the task. At the end of the experiment, they were asked to match the colors with the dimensions, and all participants were able to do so with 100% accuracy. We presented 1,458 trials in 18 blocks (with each block containing 81 trials and lasting ∼4 min each; a 30-min break was offered after block 9). To ensure that choices in cyclic trials were independent from each other, we pseudorandomized the presentation order of the trials such that two cyclic trials never appeared consecutively. As in experiment 1, we indicated midway each block whether accuracy in the preceding 40 trials (excluding cyclic trials) increased (an improvement above 5%), decreased (a drop of 5%), or stayed the same (any change in-between) compared with all previous trials thus far. Trials were distributed evenly across the nine conditions, resulting in 162 trials per condition.

Statistical Analyses.

Null hypotheses were rejected at $\alpha =0.05$ unless stated otherwise. Mean choice responses in the three cyclic conditions in experiment 1 and 4 were compared with chance level using two-sided one-sample t tests relative to 0.5, and significance was assessed at a Bonferroni-corrected $\alpha =0.05/3$ (Fig. 2B and Fig. S2D). The frequent-winner effect in increment trials in experiments 1 and 4 was assessed via paired t tests in the two increment conditions, using accuracy as dependent variable. In experiments 2 and 3, the strength of the frequent-winner effect in increment trials was assessed and compared across different conditions by inspecting the main effect of trial type and the interaction in the 2 × 2 repeated-measures ANOVA, respectively (e.g., trial type by presentation speed in experiment 2, Fig. S2A; trial type by sequence length in experiment 3, Fig. S2B). The accuracy difference in the standard trials as a function of condition (presentation speed and sequence length in experiments 2 and 3) was assessed with paired t tests and using as dependent variable the pooled accuracy over the four types of standard trials.

In the cyclic trials (experiments 1 and 4), a proxy of selective gating is the deviation from chance of the preference for the frequently winning alternative. To assess the significance of this deviation for each participant, we pooled the number of times that each participant chose A over B, B over C, and C over A, in the corresponding cyclic trials and used a one-sample z test for proportions ($H_0:P\le 0.50;H_1:P>0.50;n=180$ in experiment 1/long group, $n=120$ in experiment 1/short group, and $n=486$ in experiment 4).

For experiment 4, weak stochastic transitivity (WST) was tested within each individual using a recently developed toolbox and the corresponding QTEST (41). Before applying the QTEST, it is necessary to assess whether individual choices in the cyclical trials are independent from each other. We assessed that by applying the relevant test of independence described elsewhere (42). Ultimately, for three alternatives A, B, and C, and the three binary comparisons between them (as in our cyclic trials: A vs. B, B vs. C, and A vs. C), QTEST aims to assess for each participant whether all of the possible transitive preference orders ($A\succ B\succ C;A\succ C\succ B;B\succ A\succ C;B\succ C\succ A;C\succ A\succ B;C\succ B\succ A$, with $X\succ$ Y denoting that X is preferred over Y) are significantly rejected at $\alpha =0.05$. If so, WST is violated significantly. The statistical details and other technicalities of this test are thoroughly discussed elsewhere (22, 41). Here, we used the QTEST for WST, with a supermajority level of 0.5 and a sample size of 1,000. Finally, we asked whether participants violated a more stringent transitivity test, that of triangle inequality. Triangle inequality states that, if $P\left(A\right|\left\{A,B\right\})+P\left(B\right|\left\{B,C\right\})-P\left(A\right|\left\{A,C\right\})\le 1$, then violations of WST can be consistent with a rational mixture model (20) (i.e., a model in which preferences on each moment are sampled from a distribution over transitive preference orders).

In individual analyses, the probability that all participants who showed a significant result at $\alpha =0.05$ (e.g., proportion z test, WST test) constituted “false alarms” was assessed using the binomial distribution function. In particular, we calculated the probability of getting X out of Y significant participants at $\alpha =0.05$ as $1-F\left(X-1;Y,\alpha \right)$, with F being the binomial distribution function.

Model Input and Parameter Values.

For simplicity, in Fig. 3 and Fig. S3, we explored models without leak. In Fig. 3B, the inputs to the two alternatives were distributed around 100 (correct) and 95 (incorrect) with a SD of 10 (corresponding to early noise). Late noise was varied across five levels (lines), whereas w was varied in the 0–1 range in steps of 0.05. Accuracy predictions were obtained by simulating the model for 12 time steps and 1,000,000 trials for each combination of w and late noise. In Fig. 3D, the bivariate distributions of the models’ accumulator states in a trial are depicted after 12 samples are accumulated. These distributions were derived numerically. For the bottom panels, late noise was set to 15. In Fig. S4A, the SD of early and late noise varied between 4 and 20 (in steps of 2). The reward-maximizing w was exhaustively searched in the 0–1 interval in steps of 0.0125. Accuracy predictions were obtained by simulating the model for 12 time steps and 5,000,000 trials for each combination of w, early and late noise.

Alternative Models.

As discussed in the main text, we considered alternative models that could also predict the frequent-winner effect. These models involved divisive and range normalization and a “majority of confirming dimensions” (MCD) heuristic. The divisive normalization model (23), before accumulating the attribute values for each alternative, divides them by the total value on the corresponding attribute. Similarly, the range normalization model (24) divides the attribute values by the range of values (max minus min) on the attribute under consideration. Qualitative predictions of these models are given in Tables S3 and S4.

A third model we considered was an MCD heuristic that tallies up the number of winning attributes for each alternative (25). Because this heuristic appears to be a simple and natural explanation for the frequent-winner effect, besides presenting qualitative predictions of the model in Tables S3 and S4, we implemented and fitted parametric versions of MCD. The model tallies up the number of locally winning samples for each alternative (input: +1 for local winner, 0 for local loser). We created three versions of MCD, which are described below:

• i)a three-parameter model featuring leak (at the accumulators’ level), late noise, and a parameter $\gamma$, which dictated how much larger a target sample needs to be to be counted as a local winner (if the difference was smaller than $\gamma$, both accumulators received 0 input);
• ii)a three-parameter model as above, but with late noise replaced by early noise;
• iii)a four-parameter model including, leak, early and late noise, and $\gamma$.

Without the $\gamma$ parameter MCD models predict that the accuracy in the “infrequent-winner” increment trial (A, B₊) would be below chance. This parameter together with the early- and late-noise parameters were included to improve the quantitative flexibility of the MCD models.

Model-Fitting Procedures.

Variants of the selective integration and MCD models were fitted to each participant’s data separately, using maximum-likelihood (ML) estimation. For each participant in experiment 1, each model was fitted to K = 9 data points corresponding to the mean choices in the nine experimental conditions. Each model was simulated using the actual sequences that participants saw in the experimental trials, repeated 200 times for each trial to increase estimation robustness to simulation noise. For each model, we first constructed an M-dimensional grid search, with M corresponding to the number of free parameters. To illustrate, for the full selective integration model, the 4D grid consisted of the following dimensions: (i) the leak parameter $\lambda$, which varied across 20 values (0, 0.0158, 0.0316, …, 0.3); (ii) the early-noise parameter $\sigma$ that had also 20 values (0, 5.2632, 10.5263, …, 100); (iii) the late-noise parameter $\xi$, having values as per $\sigma$; (iv) the selective integration parameter w that varied across 20 values (0, 0.0526, 0.1053, …, 1). The grid was searched exhaustively, and for each parameter set, ${\vartheta }_j$, the likelihood term was calculated as follows:

$$L\left({\vartheta }_j\right)={\displaystyle \prod _i^K\left(\begin{array}{l}{k}_i\\ y_i\end{array}\right)}{\left(pi\right)}^{y_i}{\left(1-p_i\right)}^{k_i-y_i},$$

where $k_i$ is the number of experimental trials for the ith condition, $y_i$ is the number of correct responses (or responses for A, B, C in the three types of cyclic trials, where correctness is not objectively defined) for a given participant, and $p_i$ is the probability correct (or probability of choice in cyclic trails) predicted by the model. The 30-parameter sets that had the highest likelihood were subsequently fed into a SUBPLEX optimization routine (with the negative log-likelihood being the cost function) (43), which extends the multidimensional simplex Matlab algorithm to better handle noisy functions. At the SUBPLEX stage, each trial was repeated 400 trials to further reduce fluctuations in the cost function due to noise in the models. Parameters were constrained in the range indicated above. We denote the best-fitting parameter set identified by the SUBPLEX with ${\vartheta }_{mle}$.

The same procedure (excluding now the MCD variants from the comparison) was repeated for experiments 2–4. In experiment 2, we fitted K = 6 data points per participant. Data from experiment 2 were not fitted using separate parameters for the two presentation speed conditions due to nonsignificant behavioral differences between slow and fast trials. For experiment 3 and 4, K = 12 and K = 9 data points were fitted, respectively.

Model Comparison.

To quantitatively compare different models (i.e., variants of selective integration and MCD), we calculated the Bayesian information criterion (BIC) for each observer and each model:

$$\mathrm{BIC}=-2\text{l}\mathrm{n}\left(L\left({\vartheta }_{mle}\right)\right)+M\cdot \text{l}\mathrm{n}\left(C\right)$$

(M number of free parameters; C number of trials), and counted the proportion of participants each model yielded the minimum BIC value.

For all experiments (Fig. S1) we compared the following selective integration variants:

• i)the full model consisting of four parameters,
• ii)a three-parameter model without late noise, and
• iii)a three-parameter model without early noise.

For experiment 1 only, we added to the comparison three variants of the MCD model (Alternative Models).

Parameter Recovery.

We tested the ability of the fitting procedure to accurately identify the parameters of the best-fitting selective integration model (the one omitting early noise, see Fig. S1 B–D). Toward this aim, we obtained the model’s mean choice proportions for the nine conditions in experiment 1, using 400 parameter sets. These sets were created by drawing randomly and independently from: $\xi \sim U(0,30),w\sim U(0.7,1),\lambda \sim U(0,0.3)$ (the range of parameter values corresponded roughly to the range of participants’ estimated parameters in all experiments). For each parameter set and each condition, mean choice was obtained by simulating the model for 200 trials (cf. with 60–75 trials in the long version of experiment 1). The artificial mean choice data were fitted with the same procedure used to fit the experimental data.

SI Results

Within-Participants Analyses.

For the cyclic trials in experiment 1, we tested whether each participant chose the frequently winning alternative (A in A vs. B, B in B vs. C, and C in A vs. C) more often than the infrequently winning one by performing a one-samples z test for proportions. This test quantifies the frequent-winner effect and was significant for 17 out of 28 participants. The probability of all these individuals corresponding to type 1 error (under the null hypothesis that there was no frequent-winner effect or, equivalently, that $w=0$ in the selective integration model) was negligible ($P=10\times {10}^{-16}$). For experiment 4, 15 out of 21 participants showed a significant frequent-winner effect with the probability of them corresponding to type 1 error being also negligible ($P=1.2\times {10}^{-15})$.

Before assessing violations of transitivity in experiment 4, we fist examined whether the “independent and identically distributed” assumption held for choices in cyclic trials. Applying the relevant test (42) 62 times (3 cyclic trials × 21 participants), we found deviations outside the 2 SE interval only four times. Proceeding to individual-participants analysis in the cyclic trials revealed significant violations of WST in 11 out 21 participants. The probability of all these participants to constitute type I error was very small ($P=1.1\times {10}^{-9})$. One of these participants violated WST in the opposite direction than the one predicted by selective integration (i.e., C over B, B over A, A over C). This participant was swayed by large differences, perhaps being insensitive (or not perceiving) smaller and more frequent differences. This pattern is not directly obtained within the current implementation of the selective integration model. Notably, some of the participants showed a significant frequent-winner effect (corresponding to $w>0)$ but did not violate WST significantly. These participants had a relatively lower w and/or high noise that masked the behavioral manifestation of intransitivity. The discrepancy between the two effects would be minimized if the experiment contained a larger number of trials (i.e., had higher power) to statistically facilitate the detection of WST violations of smaller magnitude. Individual participants’ choice probabilities, number of trials performed, and transitivity tests are given in Table S5.

Ruling Out Spurious Explanations of Intransitivity.

It has been recently argued that some probabilistic choices that violate WST can derive from preferences that are transitive on each trial but change across trials under the influence of latent variables (20). For example, a rational agent could prefer A to B to C in one-third of the trials, B to C to A in another third of the trials, and C to A to B in the rest of the trials. When averaging choice behavior across trials, this agent will prefer two out of three times A to B, B to C, and C to A, appearing thus to violate WST (an analog of the Condorcet paradox in voting theory, hereafter “aggregation artifact”). In response to that possibility, Regenwetter et al. (20) suggest that “true intransitivity” occurs only when aggregation artifacts are ruled out and preferences are intransitive on specific times or trials. Such artifacts are certainly ruled out when the triangle inequality is violated (20), i.e., intransitivity occurs when P(A over B) + P(B over C) – P(A over C) > 1 is satisfied. Although 3 of 21 of our participants violated this stricter triangle inequality criterion, most of the other participants showed weaker violations (Table S5). This may raise concerns that the WST violations in those participants are an artifact of averaging. In our paradigm, the only obvious factor that could potentially generate preference variability across trials is the recency effect (Fig. S1A) in conjunction with the randomized presentation order of the different dimensions. Due to recency, the three dimensions will be weighted differently on different trials (i.e., the dimension that is presented last will be overweighted). Additionally, the frequently winning alternative, having a higher value in two out of three samples, will end up with a winning sample two out of three times. We thus examined whether the mere presence of a recency effect could produce a frequent-winner effect (and consequently WST violations) of the magnitude observed in our data.

In the absence of any processing noise, a recency bias due to leaky integration will produce a frequent-winner effect without necessitating selective gating. When noise is present, however, the leak-induced frequent-winner effect dissipates fast (Fig. S3A). In Fig. S3B, we plot the choice probabilities in cyclic trials predicted by the selective integration model in the absence of selective gating (w = 0) (i.e., using the best-fitting leak and late-noise parameters for each participant; we treat this as a leak-only control simulation). Across participants, the predicted choice probabilities show negligible deviations from chance, suggesting that WST violations due to an aggregation artifact are unlikely. Simulating 2,000 experimental sessions with the leak-control model for the two “worst-case” participants, whose predicted probabilities diverged the most from chance (participants 2 and 8), revealed a negligible number of significant WST violations, well within the conventional type I error rate (3.2% in participant 2 and 0.15% in participant 8). A complementary argument against leak-induced WST violations comes from a partial correlation among the selective integration model parameters and the frequent-winner effect. This analysis revealed a significant and strong correlation between the frequent-winner effect and w (r = 0.84; P < 0.001) and no correlation between the frequent-winner effect and the leak parameter (r = −0.05; P = 0.836). This is not surprising because a model with leak and no selective gating fails to explain other empirical aspects, such as the provariance effect, and thus would not provide a good fit.

In sum, we have no indication that the violations of WST in our task were obtained as an aggregation artifact from a pure leaky integrator. Beyond the recency bias, it can still be argued that WST violations occur as an averaging artifact (over temporally changing transitive preferences) due to subjective reasons or exogenous factors that are not under experimental control. For example, in real-life decisions, an individual may prefer meat to fish to salad on Mondays, fish to salad to meat on Wednesdays, and salad to meat to fish on Fridays, knowing that on Mondays the meat specialist is in charge, on Wednesdays that the fish is fresh, and on Fridays that the salad is on special offer. Such subjective reasons and exogenous factors are implausible in the context of our well-controlled psychophysical experiment. Given that, as well as the excellent fit of our model to the data (including additional aspects such as the provariance effect), we maintain that the evidence presented here strongly supports the thesis that intransitivity in our task is due to selective integration rather than due to aggregation artifacts.

Correlation Between Late Noise and Selective Gating.

When calculating the correlation between estimated late noise and selective gating (w), we used the parameters of the best-fitting variants of selective integration. In all experiments, this was the variant that omitted early noise (Fig. S1 B–E). The superiority of this variant was consistent with the fact that in the full model (i) the early-noise parameter was estimated to negligible values as opposed to the late-noise parameter that was much higher (Fig. S1F). When including the leak parameter in a partial correlation with late noise and w, the results remained unaffected: w and late noise remaining correlated (r = 0.48; P < 0.001), and leak and w were uncorrelated (P = 0.238).

Discussion

Violations of the axioms of choice rationality have been exhaustively documented in the decision-making literature (2, 7, 9–11, 24). Numerous studies have found that the subjective value of an economic prospect depends not only on its own attribute values but also on the irrelevant context provided by competing alternatives. Although this relative (rather than absolute) valuation schema is incorporated in descriptive theories of choice (3), and is reflected in neural signals recorded both from single cells (30) and whole-brain areas (31), it currently lacks a plausible normative explanation. Instead, violations of choice rationality appear to have negative repercussions, potentially leading to a continuous drain on resources, for example to what economic theory knows as a “money pump” (6).

Here, we argue that choice irrationality occurs because of selective integration, a policy that explicitly discards some information about the rival choice alternatives but paradoxically maximizes reward in the face of decision noise. Selective integration builds on an established framework for understanding both perceptual (15, 17) and economic decisions (16, 32), in which momentary decision values (e.g., sensory samples of a noisy stimulus, or attributes values for an economic prospect) are accumulated in parallel for two or more alternatives, corrupted by noise that could arise either during encoding or during information integration (28). The additional assumption of the model is that, where attributes compete locally, the winner can be integrated with relatively higher gain. Thus, when contemplating the (excellent) weather in Bali, the (reasonable) weather in rival Berlin appears poor by comparison, and does not drive a positive evaluation of a Berlin holiday as much as it should.

Selective integration predicts that violations of transitivity will occur when choice alternatives differ circularly in their number of winning attributes. Here, we verified this prediction empirically, showing that humans performing a magnitude discrimination task make intransitive choices about alternatives with equal cumulative value. Normalization or heuristic models could explain a tendency to choose a frequently winning alternative and hence intransitive choices in our task, but they fail to explain other aspects of the data such as why participants prefer high-variance to low-variance alternatives. It has been recently shown that most of the past instances of intransitivity could have been caused by spurious factors and not necessarily by decision processes that violate economic rationality (20, 22). Our well-controlled psychophysical task together with computational modeling suggests that the systematic intransitivity reported here is not caused by spurious factors but by the tendency to integrate information selectively.

In sharp contrast to the mainstay in decision theory—which considers reward-rate optimal the algorithm that accumulates all available information without loss (17)—selective integration maximizes accuracy (and subsequent rewards) in the face of heightened late noise. The model achieves so by implicitly exaggerating monetary differences (i.e., via weakening the losing input), inflating the average accumulated difference between the correct and incorrect alternative. Fitting the model to human data revealed a strong positive correlation between late noise and the tendency to integrate selectively. This correlation suggests that observers use selective integration as a compensatory mechanism to alleviate the potentially negative impact of elevated accumulation noise. Violations of the axioms of choice rationality emerge as a side effect of this policy and occur when alternatives are structured in unusual ways [e.g., when the number of winning attributes differ circularly or when dominated decoys are introduced in the choice set (9)].

It is conceivable that explicit and equal increase of the gain of processing for both inputs, if strong enough, could outperform selective integration by cancelling out late noise. In our analyses, however, we assumed that such direct and unbounded gain amplification is not plausible because organisms operate within computational and metabolic constraints (33). Due to these constraints, even under conditions of increased vigilance behavioral and neural variability perseveres (34), indicating that a portion of internal noise is virtually irreducible. The way our model acts against this (otherwise-irreducible) noise presents a paradox for decision theory analogous to “less-is-more” effects in other domains (35), whereby ignoring part of the available information leads to better performance. Thus, in contrast to normalization theories (23, 24), in which accuracy and metabolic efficiency trade off against each other, selective integration increases choice accuracy while reducing the cost of information processing.

Our account of choice irrationality is not only normatively motivated but also builds on well-established psychological and neural principles. First, as in models of selective attention and visual search (36), our explanation incorporates selective processing. Although selective processing has been recently added to an influential evidence accumulation model to explain the increased accumulation rate for visually fixated alternatives (32), our approach differs in that gain modulation is determined by the value of the incoming information rather than merely by the (random) locus of fixation. Second, our account is biologically plausible, building upon two widely accepted neurobiological facts: that decisions are realized in a hierarchy of cortical layers and that processing at each layer is corrupted by independent neuronal noise (29, 37). It is the distributed and noisy nature of neural information processing that allows nonnormative choice algorithms, such as selective integration, to practically outperform the normative benchmark.

Why humans make irrational choices has puzzled economists and psychologists for decades. The findings described here suggest that violations of choice rationality are a natural consequence of selective gating—a processing bottleneck that discounts locally weaker samples when evidence is accumulated over time. We demonstrated that this bottleneck could protect decisions from the pernicious influence of late noise—that arising downstream from the input representation stage. Such late noise may be an indispensable feature of neural computation, perhaps because it promotes learning and exploratory behavior (38). Fitting selective integration to human choices, we indeed showed that selective gating was stronger in those individuals with higher late noise. This finding calls into question the long-standing argument that humans are irrational because they lack the computational resources to engage in effortful executive processes and fall back instead on less costly, intuitive strategies or heuristics (12). We suggest instead that apparently irrational choices may stem from an evolutionary pressure for reward-maximizing decisions, realized in a hierarchy of noisy cortical layers (29). This calls for a broader theory of ecological rationality (39) that is bounded by neurophysiological constraints.

Methods

Participants.

Ninety-three participants (42 females; age range: 18–50; N₁ = 28, N₂ = 17, N₃ = 27, and N₄ = 21 in experiments 1–4, respectively) were recruited from Oxford University (experiments 1–3) and Warwick University (experiment 4) participant pools and gave informed consent to take part. All participants reported normal or corrected-to-normal vision and no history of neurological or psychiatric impairment. The experimental procedures were approved by the Oxford University Medical Sciences Division Ethics Committee (approval no. MSD/IDREC/C1/2009/1) and Warwick University Humanities and Social Sciences Research Ethics Sub-Committee (approval no. 83/14-15:DR@W). Participants received £8/h for their participation and a bonus of £15 that was subject to task performance.

Task.

In all experiments, participants viewed two streams of bars of varying height presented simultaneously left and right from a central fixation point. Bar height was described as indicating the scores of two job candidates on different dimensions. In all experiments, participants were instructed that all dimensions are equally important. The dimensions were explicitly specified (i.e., intelligence, motivation, experience of a job candidate) and explicitly announced during stimuli presentation via changes in the color of a rectangular outline only in experiment 4 (SI Methods). After a fixed number of pairs of bars presented at a fixed rate, participants were asked to choose which stream (candidate), the left or the right, had on average higher bars (scores). Participants received partial feedback in experiments 1 and 4, and full feedback in experiments 2 and 3 (SI Methods) in 8 (experiments 1–3) or 18 (experiment 4) blocks (each lasting less than 10 min). At the end of the experiment, participants viewed their average accuracy on the screen, and if it fell within the 85th percentile of the cohort, they received a bonus of £15. A detailed description of the visual stimuli and trial time course is provided in SI Methods.

Outline of Experimental Conditions.

Experiment 1 consisted of nine conditions that differed in the way the two sequences were constructed. We classify the different conditions into cyclic (three conditions), increment (two conditions), and standard (four conditions). Cyclic trials were constructed based on a set of sequences that resembled the A–B–C alternatives in Fig. 1B. Cyclic trials were divided in three conditions: (i) A vs. B, (ii) B vs. C, and (iii) A vs. C. There were n unique A_j–B_j–C_j triplets (j = 1…n), with each triplet yielding one set of cyclic (i–iii) trials. Twelve participants performed a short version of the task with cyclic trials being generated by n = 40 unique triplets, whereas 16 participants performed a longer version with n = 60 (SI Methods). In each A_j–B_j–C_j triplet, the three sequences had identical values, but their order was reshuffled as per the example in Fig. 1B (i.e., B_j was created via a right circular shift of A_j, whereas C_j via a right circular shift of B_j ; see SI Methods). The two increment conditions were created by modifying i above, by increasing by 6 pixels either the height of all bars of A_j (A+ vs. B) or all bars of B_j (A vs. B+). Finally, in standard trials, the two alternatives consisted of normally distributed values. Two levels of mean and variance (high/low) were resampled with replacement, yielding overall four conditions. Experiments 2 and 3 consisted only of increment and standard trials (six conditions). Experiment 4 was similar to experiment 1 and had all nine conditions. However, cyclic trials in experiment 4 were constructed from a unique (per participant) A–B–C triplet, with each A–B–C sequence having the very same dimensional values in the whole experiment. The dimensions in experiment 4 were explicitly specified and announced alongside the presentation of the bars. Details about the experimental conditions, the sequences construction, and the number of trials per condition in the four experiments are provided in SI Methods.

Selective Integration.

Two accumulators (Y_A and Y_B) integrate the attribute values (i.e., pixels representing the heights of the two bars) of the two sequences (A and B) according to the following difference equations:

$$\begin{array}{l}{Y}_A\left(t\right)=\left(1-\lambda \right)\cdot Y_A\left(t-1\right)+I_A\left(t\right)+\xi \cdot {\zeta }_A\left(t\right),\\ Y_B\left(t\right)=\left(1-\lambda \right)\cdot Y_B\left(t-1\right)+I_B\left(t\right)+\xi \cdot {\zeta }_B\left(t\right).\end{array}$$ [1]

In the above, t denotes the current discrete time step, $\lambda$ is integration leak, $\xi$ is late noise, and ${\zeta }_{A,B}\left(t\right)$ are random standard Gaussian samples independent of each other and across t. The leak parameter was introduced to capture the recency-weighting profile (Fig. S1A) that was obtained in all experiments (see also ref. 14).

The two accumulators are initialized at 0:

$$Y_A\left(0\right)=Y_B\left(0\right)=0.$$

The momentary inputs to the accumulators, I_{A, B}(t), are defined as follows:

$$\begin{array}{l}{I}_A\left(t\right)=\theta \left(X_A\left(t\right)-X_B\left(t\right)\right)\cdot X_A\left(t\right),\\ I_B\left(t\right)=\theta \left(X_B\left(t\right)-X_A\left(t\right)\right)\cdot X_B\left(t\right).\end{array}$$ [2]

The gain function $\theta$ is a step function defined as follows:

$$\theta \left(x\right)=\{\begin{array}{l}1,\hspace{0.17em}\mathrm{if}\hspace{0.17em}x>0\\ w,\hspace{0.17em}\mathrm{if}\hspace{0.17em}x<0\end{array},$$ [3]

with w in [0, 1] being the selective gating parameter. Finally, X_{A, B}(t) correspond to the incoming stimuli corrupted by internal (early) noise:

$$\begin{array}{l}{X}_A\left(t\right)=\sigma \cdot {\rho }_A\left(t\right)+s_A\left(t\right),\\ X_B\left(t\right)=\sigma \cdot {\rho }_B\left(t\right)+s_B\left(t\right),\end{array}$$ [4]

where $\sigma$ is the early noise parameter, ρ_{A, B}(t) are random standard Gaussian samples independent of each other and across t, and s_{A, B}(t) are the presented stimuli on time step t (bar heights, in pixels).

At the end of stimuli presentation (e.g., t = 9, in experiment 1), the model chooses sequence A if $Y_A\left(t\right)>Y_B\left(t\right)$, sequence B if $Y_B\left(t\right)>Y_A\left(t\right)$, and randomly between A and B if $Y_A\left(t\right)=Y_B\left(t\right)$. Overall, the full selective integration model has four free parameters: leak ($\lambda$), early noise ($\sigma$), late noise ($\xi$), and selective gating parameter (w). Noise parameters are expressed in pixels.

Model-fitting procedures and model parameters in the various simulations reported in the main text are given in SI Methods.