Marine mixotrophy increases trophic transfer efficiency, mean organism size, and vertical carbon flux

Significance

Marine plankton commonly combine the autotrophic use of light and inorganic resources with the heterotrophic ingestion of prey. These mixotrophs blur the strict boundary between producers and consumers and allow energy and biomass to enter the food web across multiple trophic levels. Incorporating this flexibility into a global simulation of the surface ocean food web reveals that mixotrophy enhances the transfer of biomass to larger organisms at higher trophic levels, which in turn increases the efficiency of oceanic carbon storage through the production of larger, faster-sinking, and carbon-enriched organic detritus.

Abstract

Mixotrophic plankton, which combine the uptake of inorganic resources and the ingestion of living prey, are ubiquitous in marine ecosystems, but their integrated biogeochemical impacts remain unclear. We address this issue by removing the strict distinction between phytoplankton and zooplankton from a global model of the marine plankton food web. This simplification allows the emergence of a realistic trophic network with increased fidelity to empirical estimates of plankton community structure and elemental stoichiometry, relative to a system in which autotrophy and heterotrophy are mutually exclusive. Mixotrophy enhances the transfer of biomass to larger sizes classes further up the food chain, leading to an approximately threefold increase in global mean organism size and an ∼35% increase in sinking carbon flux.

Marine ecosystems provide essential nutrition to more than half the world’s population via fisheries (1) and mediate global cycles of climatically important elements including carbon (2). Current models of marine biogeochemical cycles assume that the plankton can be clearly divided into two mutually exclusive guilds: the autotrophic phytoplankton and the heterotrophic zooplankton. According to this view, phytoplankton are responsible for all photosynthetic carbon fixation, ultimately controlled by the supply and consumption of inorganic nutrients.

There is clear evidence that such a strict dichotomy between producers and consumers does not reflect the true nature of marine microbial communities. Autotrophic and heterotrophic traits are not mutually exclusive, and a large and increasing number of plankton taxa have been shown to simultaneously exploit both inorganic resources and living prey (3). These mixotrophic plankton, found throughout the eukaryotic tree of life (4), and particularly in the 2- to 200-µm size range (5–7), can sustain photosynthesis even when chronically outcompeted for the most-limiting inorganic nutrient, in clear contrast to the way we typically describe and model marine systems (8).

Although mixotrophy is known to be common throughout the global ocean (6, 7), its contribution to net community production is difficult to quantify, and its integrated impact on global biogeochemical cycles remains unknown. Numerical simulations provide a platform to address these questions, but to date, no global ocean models have resolved this important lifestyle. Here, we examine the global role of mixotrophy in a numerical “thought experiment,” comparing two simulations of the marine plankton food web in the global ocean (9) that differ only in their representation of trophic strategy (Fig. 1). The traditional “two-guild” model encapsulates the default view of the marine ecosystem, with each of the 10 simulated size classes divided into separate phytoplankton and zooplankton populations. In the alternative “mixotrophy” model, this unrealistically strict distinction is not made, and each size class contains just one population that is capable of both inorganic resource uptake and predation, dependent on resource availability. A detailed model description can be found in the Supporting Information, Tables S1 and S2, and ref. 9.

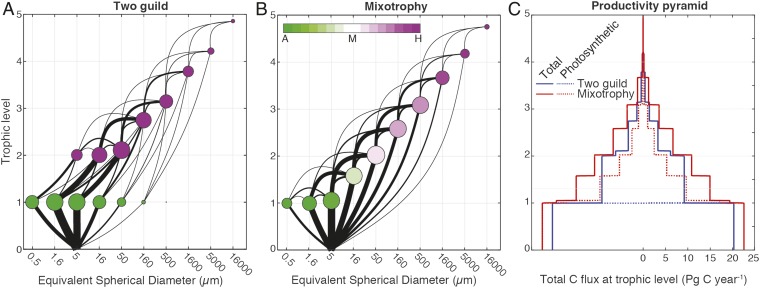
Fig. 1.

Emergent global mean community structure in the two-guild (A) and mixotrophy (B) models. Circular nodes represent global carbon biomass (surface area proportional to the annual mean), and black links represent global carbon fluxes (thickness proportional to the square root of the annual mean, with all fluxes directed upwards). The horizontal position of the nodes denotes plankton size, whereas the vertical position denotes trophic level (T). For each population, T is calculated as 1 plus the average trophic level of each prey item, weighted by the contribution of each prey to the total carbon intake, including photosynthesis (T is calculated sequentially from small to large; Methods). Colors represent the balance of autotrophic and heterotrophic carbon assimilation in each population (Inset, color scale). (C) Representation of the total annual carbon flux across each trophic level in the two-guild (blue) and mixotrophy (red) models. The fluxes were calculated for each value of T by summing all fluxes beginning at a lower level and ending at a higher level. Solid lines represent the total flux, whereas dotted lines represent only the photosynthetic flux.

Table S1.

Size-independent model parameters

Parameter	Symbol	Value	Units
Nutrient uptake
Ammonium inhibition	$\mathrm{\Psi }$	4.6	(mmol N m−3)−1
Nutrient quotas
Minimum nitrogen:carbon quota	$Q_{\text{N}}^{\text{min}}$	5.0$\times {10}^{-2}$	mmol N (mmol C)−1
Maximum nitrogen:carbon quota	$Q_{\text{N}}^{\text{max}}$	1.7$\times {10}^{-1}$	mmol N (mmol C)−1
Minimum phosphate:carbon quota	$Q_{\text{P}}^{\text{min}}$	2.1$\times {10}^{-3}$	mmol P (mmol C)−1
Maximum phosphate:carbon quota	$Q_{\text{P}}^{\text{max}}$	1.1$\times {10}^{-2}$	mmol P (mmol C)−1
Minimum iron:carbon quota	$Q_{\text{Fe}}^{\text{min}}$	5.0$\times {10}^{-6}$	mmol Fe (mmol C)−1
Maximum iron:carbon quota	$Q_{\text{Fe}}^{\text{max}}$	2.0$\times {10}^{-5}$	mmol Fe (mmol C)−1
Temperature
Reference temperature	$T_{\text{ref}}$	20	$°\text{C}$
Temperature dependence	A	0.05	dimensionless
Photosynthesis
Maximum Chl a-to-nitrogen ratio	${\theta }_{\text{N}}^{\text{max}}$	3.0	mg Chl a (mmol N)−1
Initial slope of P-I curve	α	3.83$\times {10}^{-7}$	mmol C (mg Chl a)−1 (μEin m−2)−1
Cost of biosynthesis	ξ	2.33	mmol C (mmol N)−1
Grazing
Optimum predator:prey length ratio	${\vartheta }_{\text{opt}}$	10	dimensionless
Geometric SD of ϑ	${\sigma }_{\text{graz}}$	2.0	dimensionless
Total prey half-saturation	$k_{\text{C}}^{\text{prey}}$	5.0	mmol C m−3
Maximum assimilation efficiency	${\lambda }^{\text{max}}$	0.7	dimensionless
Grazing refuge parameter	$\mathrm{\Lambda }$	−1	dimensionless
Assimilation shape parameter	h	0.1	dimensionless
Mortality
Plankton mortality	m	0.05	d−1
Particulate organic matter
POM remineralization rate	$r_{\text{POM}}$	0.04	d−1
POM sinking rate	$w_{\text{POM}}$	10.0	m d−1
DOM
DOM remineralization rate	$r_{\text{DOM}}$	0.02	d−1
DOM sinking rate	$w_{\text{DOM}}$	0	m d−1

Table S2.

Size-dependent model parameters and scaling coefficients

Parameter	Symbol	a	b	Parameter units
Inorganic nutrient uptake
Maximum uptake rate	$V_{{\text{NO}}_3}^{\text{max}}$	0.44	−0.12	mmol N (mmol C)−1 d−1
	$V_{{\text{NO}}_2}^{\text{max}}$	0.44	−0.12	mmol N (mmol C)−1 d−1
	$V_{{\text{NH}}_4}^{\text{max}}$	0.22	−0.12	mmol N (mmol C)−1 d−1
	$V_{{\text{PO}}_4}^{\text{max}}$	4.4$\times {10}^{-2}$	0.06	mmol P (mmol C)−1 d−1
	$V_{\text{Fe}}^{\text{max}}$	1.4$\times {10}^{-6}$	−0.09	mmol Fe (mmol C)−1 d−1
Half-saturation concentration	$k_{{\text{NO}}_3}$	0.14	0.33	mmol N m−3
	$k_{{\text{NO}}_2}$	0.14	0.33	mmol N m−3
	$k_{{\text{NH}}_4}$	0.07	0.33	mmol N m−3
	$k_{{\text{PO}}_4}$	0.04	0.41	mmol P m−3
	$k_{\text{Fe}}$	8.0$\times {10}^{-6}$	0.27	mmol Fe m−3
Carbon quotas
Cell carbon content	$Q_{\text{C}}$	1.45$\times {10}^{-11}$	0.88	mmol C cell−1
Grazing
Maximum prey ingestion rate	$G_{\text{C}}^{\text{max}}$	21.9	−0.16	d−1

$a{V}^b$, parameter value; V, cell volume.

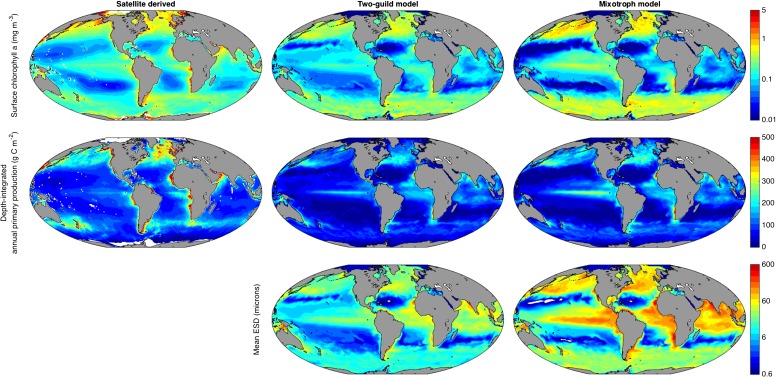
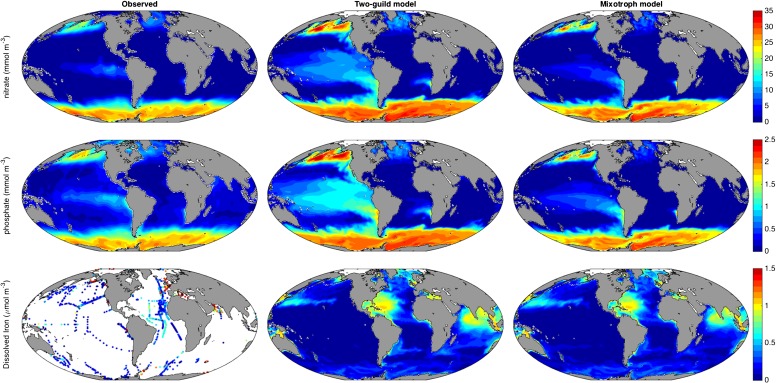
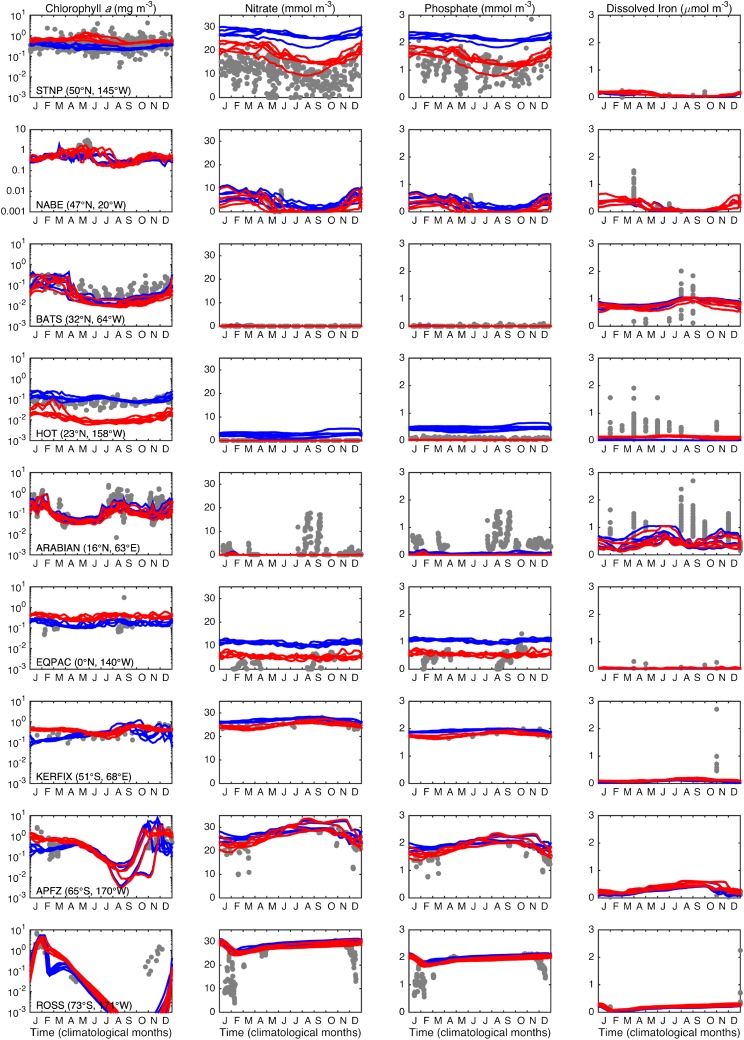
Despite the removal of a distinction that is central to all current global-scale ecosystem and biogeochemistry simulations (9–12), the emergent community structure shown in Fig. 1B allows the mixotrophy model to reliably reproduce observed, global distributions of chlorophyll a, primary production and nutrients (Figs. S1 and S2). At specific time-series sites where in situ empirical data are available (Fig. S3), the two simulations show only minor differences in terms of their fidelity to observed seasonal cycles of chlorophyll a and limiting nutrients, whereas the mixotrophic model is better able to reproduce the concentrations of nonlimiting nutrients, which are often overestimated by the two-guild model.

Fig. S1.

Observed and modeled global annual mean distributions of surface chlorophyll a (0–10 m), depth-integrated primary productivity (48), and geometric mean plankton size.

Fig. S2.

Observed (49, 50) and modeled global annual mean surface (0–10 m) nutrient distributions.

Fig. S3.

Observed and modeled seasonal cycles of surface chlorophyll a and nutrients. Gray dots correspond to all observations, regardless of year. Each line represents one of an additional 5 y of model integration (years 11–15), with the two-guild model in blue and the mixotrophy model in red. Chlorophyll, nitrate, and phosphate observations correspond to the exact time-series locations (51). Dissolved iron data within the surface 50 m were taken from a global database (50), with observations matched to time-series sites if they fall within 2$°$ latitude and longitude.

Although the two model configurations make no prior assumptions with regard to the balance of autotrophic and heterotrophic nutrition in each size class, both model communities show a clear and credible (7, 9, 13) trophic structure, with a general shift from autotrophy to heterotrophy with increasing organism size and trophic level (Fig. 1 A and B). In each case, the smallest plankton are too small to ingest prey, whereas the largest plankton have very low affinities for inorganic nutrients. Alongside these similarities, there are also important differences, the most obvious being the strong disconnect between the first and second trophic levels seen in the two-guild model. With a strict dichotomy between phytoplankton and zooplankton, photosynthesis is restricted to the base of the food web, as shown in Fig. 1C. The flux of energy and biomass up the food chain decreases at each trophic level because the energetic demands of consumers can only be met by the catabolic respiration of ingested biomass. In the mixotrophic model, consumers can dramatically increase their apparent trophic transfer efficiency by using photosynthesis to compensate for respiratory losses. [An alternative mechanism not included in the model is the harvesting of light energy to decrease the need for catabolic respiration (14).]

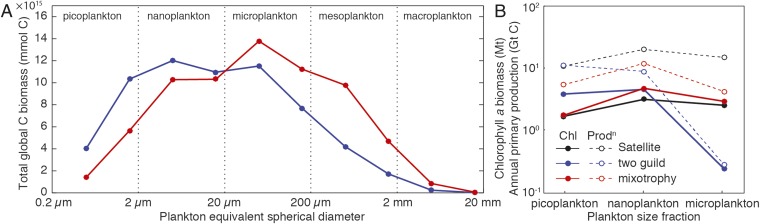
Either mechanism allows greater transfer of energy and biomass across each trophic level, which ultimately supports greater biomass among larger size classes further up the food chain (15). Fig. 2A shows that the total global biomass distribution is shifted toward larger size classes in the mixotrophy model, with an approximately threefold increase in global geometric mean plankton diameter (from 17 to 46 µm). Noting that both models neglect a range of other mechanisms that may also support photosynthetic growth among larger plankton (16), the inclusion of mixotrophy allows the model community to support much higher global values of primary production and chlorophyll a biomass in the 20- to 200-µm microplankton size range (Fig. 2B). This shift in community structure brings the mixotrophic model into closer agreement with empirical estimates derived from a synthesis of in situ and satellite observations (17, 18).

Fig. 2.

(A) Total annual mean size distribution of carbon biomass in the two-guild (blue) and mixotrophy (red) models. (B) Global size-fractionated annual mean chlorophyll a biomass and annual primary production from the two-guild (blue) and mixotrophy (red) models in comparison with empirical estimates (black). Empirical estimates were derived from a synthesis of in situ and satellite observations (17, 18).

The shift toward larger plankton is ultimately driven by an increased competitive ability of mixotrophs relative to phytoplankton or zooplankton specialists. In general, the nutrient affinity of plankton decreases with increasing organism size (19), and in the two-guild paradigm, highly efficient uptake by the smallest phytoplankton leaves insufficient nutrients to support photosynthesis in the larger groups. In the mixotrophy model, photosynthesis is supported among larger size classes because mixotrophs can exploit both inorganic nutrient resources and prey. Specifically, analytic solutions to a highly simplified version of the ecological model (Methods) show that the ability of mixotrophs to ingest prey not only provides an additional source of the nutrients required to support photosynthesis, but also provides an additional source of carbon as a supplement to photosynthesis. This double benefit decreases their dependence on inorganic nutrients and allows mixotrophs to survive at nutrient concentrations that would be unable to support specialist phytoplankton of equivalent size (Methods and Eq. 4). The fact that this advantage is derived by eating smaller competitors (20) has the complementary effect of decreasing the biomass of smaller groups (Fig. 2A), further shifting the community mean toward larger sizes.

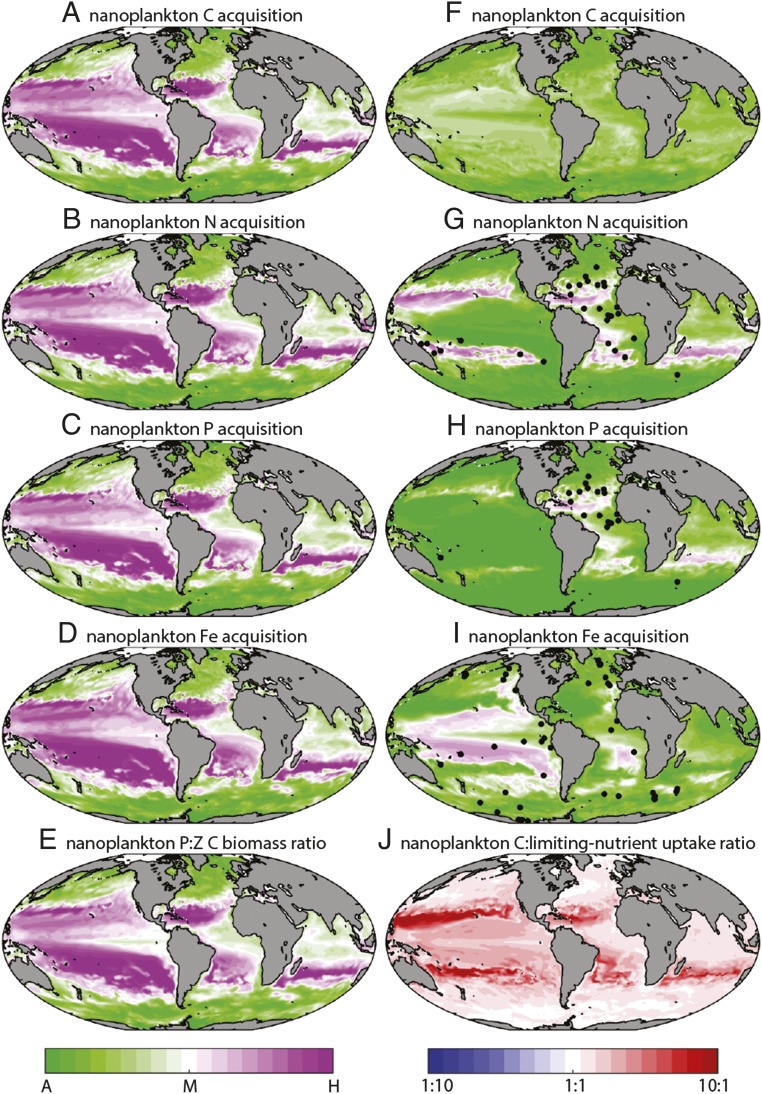
The flexible use of both inorganic and prey resources by mixotrophs is highlighted in Fig. 3, which shows the balance of autotrophy and heterotrophy in the nanoplankton size class (selected because this intermediate size class is relatively evenly balanced between the two trophic strategies; Fig. 1 A and B). In the two-guild model, Fig. 3E shows that nanoplankton biomass is dominated at low latitudes by zooplankton. In these more stratified regions, and particularly at the centers of the subtropical gyres, the scarcity of any one nutrient resource allows the smaller picophytoplankton to outcompete the larger nanophytoplankton, in accordance with Liebig’s law. The exclusion of nanophytoplankton leaves heterotrophy as the only viable strategy in the nanoplankton class, and all resources, including carbon, are acquired primarily by ingestion of prey (Fig. 3 A–D).

Fig. 3.

(A–D and F–I) Depth-integrated balance of autotrophic and heterotrophic acquisition of C, N, P, and Fe by nanoplankton in the two-guild (A–D) and mixotrophy (F–I) models. Black dots in G–I indicate sites where in situ nutrient addition experiments have identified (at least occasional) limitation by that nutrient element (30). (E) Global balance of depth-integrated nanophytoplankton and nanozooplankton C biomass in the two-guild model. (J) Relative change between the two models in the molar ratio of photosynthetic C acquisition to the uptake of the most-limiting nutrient (N, P, or Fe; Supporting Information).

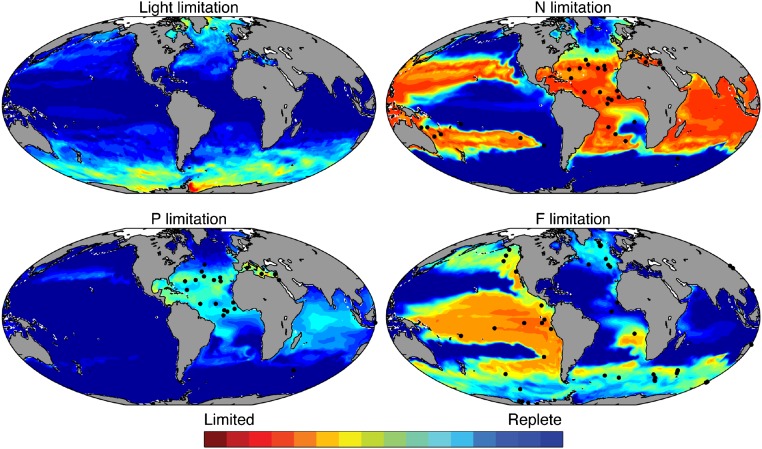
In the mixotrophic model, the nanoplankton mixotrophs are still outcompeted for limiting nutrients by the picoplankton at low latitudes, but the essential resource elements can be acquired instead by ingestion of prey (20). This flexibility is confirmed in Fig. 3 G–I, which shows that in regions where a nutrient is strongly limiting, the nanoplankton mixotroph community acquires that resource by grazing, for example, in the subtropical gyres for nitrogen and phosphorus, or in the equatorial Pacific for iron [black dots in Fig. 4 G–I show regions where each nutrient has been observed to be limiting, and model nutrient limitation is shown in Fig. S4]. This emergent feature of the simulations is consistent with experimental findings in the field and laboratory (5, 6, 21, 22). For example, equatorial Pacific isolates of Ochromonas species acquire iron by phagotrophy under iron-limited conditions (21), whereas photosynthetic protists acquire limiting N and P by phagotrophy in the North Atlantic (5, 6).

Fig. 4.

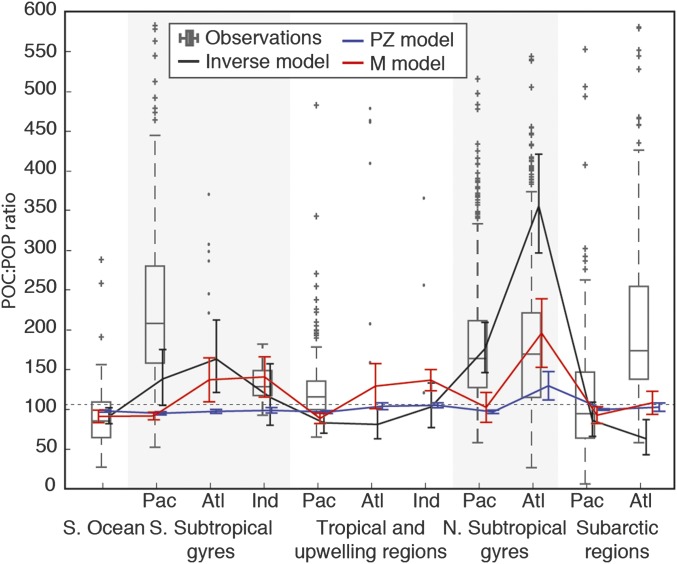
Modeled and observed large-scale variation in C:P ratios of particulate organic matter. Blue and red lines show regional C:P in the surface 100 m, with error bars showing ±1 SD. Observed particulate C:P ratios from ref. 23 are shown, with boxes marking the 25th, 50th, and 75th percentiles and whiskers covering ∼99.3% of the data. The remaining points are represented by plus symbols. Observations in regions with <10 data points are plotted individually (dots). Inverse model estimates of exported C:P ratios are also shown by black lines (24), with error bars again showing ±1 SD. The global mean “Redfield” (31) C:P ratio of 106 is shown by a horizontal dashed line.

Fig. S4.

Limitation terms in the mixotroph model. Annual mean community light limitation within the mixed layer and annual mean community N, P, and Fe limitation in the surface (0–10 m) layer (from ${\gamma }_{\text{I}}$, ${\gamma }_{\text{N}}$, ${\gamma }_{\text{P}}$, and ${\gamma }_{\text{Fe}}$ in Eqs. S14, S6, and S7). Community means are biomass-weighted. Black circles indicate sites where in situ nutrient addition experiments have identified (at least occasional) limitation by the nutrient element in question (30).

The key difference in the mixotrophy model is that ingested nutrients are available to directly support photosynthesis in the nanoplankton (and larger) size classes in regions where light is abundant but nutrients are scarce. In contrast to the two-guild simulation, for which the nanoplankton are dominated by heterotrophs that must respire carbon for energy, the switch to mixotrophy allows this size class to support photosynthetic plankton that can accumulate much higher ratios of carbon to limiting nutrient elements. This broad shift in the trophic status of the larger plankton underpins the increased carbon content of particulates in the mixotrophic world.

Fig. 3F confirms that carbon acquisition by the mixotrophic nanoplankton is dominated by phototrophy throughout the surface ocean, regardless of whether the supply of inorganic N, P, or Fe is limiting to growth. This result is in clear contrast to the two-guild model, for which a shortage of any one of these inorganic nutrients is sufficient to suppress photosynthesis (Fig. 3A). The supplemental resources derived from prey allow the mixotrophic nanoplankton community to sustain higher levels of photosynthesis for a given supply of limiting inorganic nutrient, relative to the two-guild model. This can be seen quite clearly in Fig. 3J, which shows that mixotrophy universally increases the ratio of photosynthetic carbon fixation to the uptake of limiting inorganic nutrients. In a balanced system, this extra source of exogenous carbon leads to elevated carbon stoichiometry (Eq. 5), and Fig. 4 confirms that this mechanism allows the mixotrophy model to better reproduce the elevated C:P ratios seen in both suspended particulate (23) and exported (24) organic matter in the oligotrophic subtropical gyres.

The ability to supplement scarce nutrients through grazing allows mixotrophs greater flexibility to balance supply and demand (25) and leads to increased accumulation of carbon (and nonlimiting nutrients) relative to limiting nutrients. Coupled with the shift toward larger plankton size classes, which drives increased production of larger and faster sinking organic detritus, the increased relative carbon content of sinking organic material leads to an ∼35% increase in global carbon export, relative to the two-guild model (from 7.2 to 9.8 Gt C yr⁻¹). It is likely, however, that this enhancement represents an upper limit, because in this initial simulation, mixotrophy was incorporated without consideration of any potential costs, and it seems intuitively unlikely that a mixotroph generalist could simultaneously achieve the same essential rates as similar phytoplankton and zooplankton specialists (26, 27).

The likely impacts of these potential tradeoffs were examined with additional simulations in which mixotrophs were placed in direct competition with phytoplankton and zooplankton specialists (i.e., with three competing populations within each size class). Across a number of model experiments (Supporting Information and Table S3), mixotrophy was associated with a range of costs, in the form of decreased resource acquisition rates relative to specialists. Fig. 5 confirms that increasing the assumed costs decreases both the relative importance of mixotrophy and the inferred ecological and biogeochemical effects (Table S4). Nonetheless, Fig. 5 indicates that regardless of the tradeoffs, there is a clear positive relationship between the prevalence of mixotrophs and their impact on mean plankton size and carbon export. Given that mixotrophs are observed to be a ubiquitous component of marine food webs, Fig. 5 suggests that this prevalence should translate to significant ecological and biogeochemical impacts.

Table S3.

Resource acquisition tradeoffs under different assumptions

Parameter	Symbol	Definition	Multiplication factor		Units
			Handling, A+S	Encounter, S
Maximum photosynthetic rate	$P_{\text{C}}^{\text{max}}$		${\omega }^{\tau }$	${\omega }^{\tau }$	d−1
Maximum uptake rate	$V_{{\text{NO}}_3}^{\text{max}}$		${\omega }^{\tau }$	${\omega }^{\tau }$	mmol N (mmol C)−1 d−1
	$V_{{\text{NO}}_2}^{\text{max}}$		${\omega }^{\tau }$	${\omega }^{\tau }$	mmol N (mmol C)−1 d−1
	$V_{{\text{NH}}_4}^{\text{max}}$		${\omega }^{\tau }$	${\omega }^{\tau }$	mmol N (mmol C)−1 d−1
	$V_{{\text{PO}}_4}^{\text{max}}$		${\omega }^{\tau }$	${\omega }^{\tau }$	mmol P (mmol C)−1 d−1
	$V_{\text{Fe}}^{\text{max}}$		${\omega }^{\tau }$	${\omega }^{\tau }$	mmol Fe (mmol C)−1 d−1
Nutrient affinity	${\alpha }_{{\text{NO}}_3}$	$V_{{\text{NO}}_3}^{\text{max}}/k_{{\text{NO}}_3}$	${\omega }^{\tau }$	1	m3 d−1 (mmol C)−1
	${\alpha }_{{\text{NO}}_2}$	$V_{{\text{NO}}_2}^{\text{max}}/k_{{\text{NO}}_2}$	${\omega }^{\tau }$	1	m3 d−1 (mmol C)−1
	${\alpha }_{{\text{NH}}_4}$	$V_{{\text{NH}}_4}^{\text{max}}/k_{{\text{NH}}_4}$	${\omega }^{\tau }$	1	m3 d−1 (mmol C)−1
	${\alpha }_{{\text{PO}}_4}$	$V_{{\text{PO}}_4}^{\text{max}}/k_{{\text{PO}}_4}$	${\omega }^{\tau }$	1	m3 d−1 (mmol C)−1
	${\alpha }_{\text{Fe}}$	$V_{\text{Fe}}^{\text{max}}/k_{\text{Fe}}$	${\omega }^{\tau }$	1	m3 d−1 (mmol C)−1
Maximum grazing rate	$G_C^{\text{max}}$		${\left(1-\omega \right)}^{\tau }$	${\left(1-\omega \right)}^{\tau }$	d−1
Prey clearance rate	${\omega }_C^{\text{prey}}$	$G^{\text{max}}/k_C^{\text{prey}}$	${\left(1-\omega \right)}^{\tau }$	1	m3 d−1 (mmol C)−1

If resource uptake is limited by the rate of resource handling (A+S), both the resource affinity and the saturated uptake rate are affected by τ. If resource acquisition at low concentrations is limited by the rate of resource encounters (S), only the saturated rate is affected by τ (32).

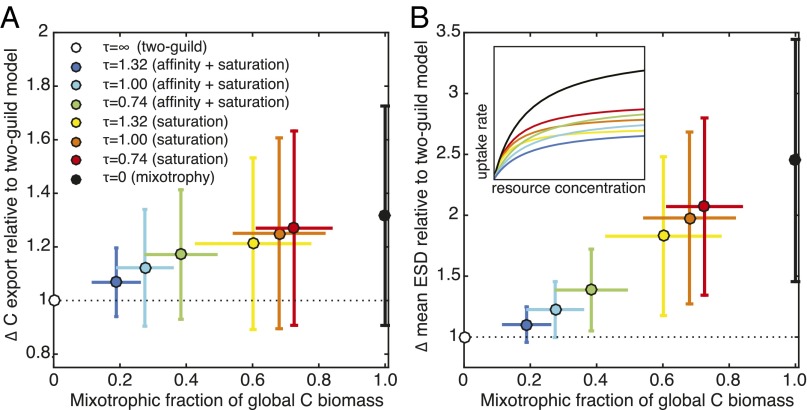
Fig. 5.

Relationship between mixotrophic dominance and the relative increase in global carbon export (A) and global geometric mean plankton size (B) in the sensitivity experiments (Supporting Information), relative to the two-guild model. Dots represent the global average from each simulation, whereas the error bars show the degree of spatial variability in the annual average for each simulation. In the legend, the parameter $\tau$ describes the strength of the tradeoff (a larger number represents a stronger penalty for mixotrophy). This penalty may be applied to the resource affinities and the maximum resource uptake rates (affinity and saturation) or just to the maximum resource uptake rates (saturation) (Supporting Information and ref. 32). The relative uptake functions for the mixotrophs in each experiment are illustrated schematically in B (Inset). With no tradeoff, the mixotrophs have identical uptake functions to the specialists (black line).

Table S4.

Summary statistics for the main simulations and sensitivity experiments

Simulation	Total biomass, Pg C	Mean ESD, μm	Total abundance, individuals	Primary productivity, Pg C y−1	Carbon export, Pg C y−1	Mixotrophic fraction of total C, %
						Biomass	Autotrophy	Heterotrophy
τ =$\infty$, Two-guild	0.75	16.7	3.5$\times$ 1027	28.0	7.24	0	0	0
τ = 1.32, A+S	0.78	18.4	2.9$\times$ 1027	28.7	7.68	18.9	21.3	12.3
τ = 1.00, A+S	0.78	20.5	2.5$\times$ 1027	29.1	8.01	27.5	31.3	20.3
τ = 0.74, A+S	0.80	23.3	2.1$\times$ 1027	29.5	8.38	38.4	41.3	31.8
τ = 1.32, S	0.79	31.5	1.5$\times$ 1027	28.9	8.67	60.2	47.3	61.8
τ = 1.00, S	0.80	34.5	1.4$\times$ 1027	29.3	8.95	68.0	54.0	71.0
τ = 0.74, S	0.81	36.5	1.4$\times$ 1027	29.7	9.14	72.6	58.6	75.9
τ = 0, Mixotrophy	0.82	45.9	1.3$\times$ 1027	30.7	9.76	100	100	100

Although these numerical experiments suggest the potential importance of mixotrophy at the global scale, our representation of the mixotroph community is highly simplified, and many uncertainties remain. In particular, we have not differentiated among the wide diversity of different lifestyles and ecological strategies (such as the acquisition and use of ingested chloroplasts) that fall under the very broad classification of mixotrophy (4). In addition, computational constraints limited our global simulations to decadal timescales, and we did not address any longer-term feedbacks associated with the modified export of organic material. Alongside the increased export ratio of carbon to limiting nutrients, the simulations reveal increased export of nonlimiting nutrients, with elevated downward fluxes of organic N and P in regions where those elements are not limiting to growth. Over centennial and millennial timescales, this increased export may feedback on the supply of resources to the surface ocean, potentially modulating any short-term changes in C export. Further work in a simpler, less computationally expensive framework will be required to assess the potential for such indirect feedbacks.

Here we have presented a first effort to resolve mixotrophy in a global model of ocean ecology and biogeochemistry. The simulations are highly idealized and dependent on a number of uncertain physiological and ecological assumptions. Nonetheless, the results indicate a significant role for mixotrophy in shaping not only the structure of marine ecosystems but also the ecosystems’ global-scale biogeochemical function. We suggest that existing carbon cycle models do not faithfully capture key mechanisms that shape trophic dynamics, elemental stoichiometry, and carbon export. An integrated approach combining targeted empirical studies with the explicit incorporation of mixotrophs into marine biogeochemical and global change models will therefore improve our quantitative understanding of marine food webs and the global carbon cycle.

Methods

Trophic Level.

We use a standard definition of trophic level (28, 29), defined in terms of carbon and modified slightly to allow for mixotrophic nutrition. For a community of N plankton populations, the trophic level $T_i$ of population $i$ is given by

$$T_i=1+{\displaystyle \sum }_{j=1}^N{T}_j{p}_{ij}.$$ [1]

Here, $T_j$ is the trophic level of each prey population $j$, and $p_{ij}$ is the relative contribution of prey population $j$ to the total carbon assimilation by population $i$ (including photosynthesis). Whereas strict autotrophs have a trophic level of exactly 1, the trophic levels of mixotrophic or heterotrophic plankton are computed sequentially from the smallest to the largest groups. According to this definition, a strict herbivore consuming only strict autotrophs is assigned T = 2. Drawing nutrition from sources across multiple trophic levels allows populations to occupy intermediate trophic levels. For example, a mixotroph gaining exactly half of its organic carbon from photosynthesis and half through grazing on a strict autotroph (T = 1) would be assigned T = 1.5.

Simplified Analytic Model.

The emergent behavior of the global model can interpreted under a number of simplifying assumptions. Eq. S2 (Supporting Information) describes the rate of change of biomass for each plankton class, and we focus here in particular on carbon and phosphorus biomass $(B_C$ and $B_P)$. For simplicity, we look at the behavior of just one plankton size class in a homogenous physical environment, and we neglect mortality from higher predators to consider the balance between resource acquisition and basal mortality $\left(m\right).$ Photosynthetic carbon fixation and predatory carbon assimilation are both down-regulated when the cellular quota becomes carbon enriched (phosphorus starved), whereas phosphate uptake and predatory phosphorus assimilation are up-regulated. Here, for simplicity, we assume that both the autotrophic and heterotrophic regulation terms are identical in each case.

$$\frac{d{B}_P}{dt}=\left(V_P^{\text{max}}\frac{P}{P+k_P}+G_C^{\text{max}}\frac{F_C}{F_C+k_g}\lambda Q_F\right)\left(\frac{Q_{\text{max}}-Q}{Q_{\text{max}}-Q_{\text{min}}}\right)B_C-m{B}_P,$$ [2]

$$\frac{d{B}_C}{dt}=\left(V_C+G_C^{\text{max}}\frac{F_C}{F_C+k_g}\right)\left(1-\frac{Q_{\text{min}}}{Q}\right)B_C-m{B}_C.$$ [3]

Here, $V_C$ represents the light-limited rate of photosynthesis, whereas $Q$ represents the cellular P:C ratio, bounded by minimum and maximum values $Q_{\text{min}}$ and $Q_{\text{max}}.$ Phosphorus uptake is dictated by the maximum uptake rate, $V_P^{\text{max}},$ the half-saturation concentration $k_P,$ and the ambient phosphate concentration $P.$ The grazing rate, $G_C,$ is a function of the available prey carbon biomass, $F_C,$ and the half-saturation concentration for grazing $k_g.$ Here, $\lambda$ is the maximum prey assimilation efficiency, and the P:C ratio of prey items is denoted as $Q_F.$

Shift Toward Larger Cells.

Assuming equilibrium, we can solve Eqs. 2 and 3 for $P=R_P^{\ast },$ which represents the minimum resource concentration required for the population to overcome the basal mortality $m.$ For a phytoplankton population, $R_P^{\ast }$ is simply a function of the organisms physiology, the light-limited growth rate $V_C,$ and the mortality rate. Typically, in size-structured phytoplankton communities, $R_P^{\ast }$ increases with organism size, such that the smallest phytoplankton are able to exclude larger groups that are outcompeted for scarce nutrients. For a mixotroph population, $R_P^{\ast }$ is given by a very similar function, but we must also account for the ingestion of prey, as represented by $G_C=G_C^{\text{max}}[F_c/(F_c+k_g)]$:

$$R_P^{\ast }=\frac{k_P}{V_P^{\text{max}}{\left(m{Q}_{\text{min}}\mathrm{\Delta }Q{\left[Q_{\text{max}}\left(1-\frac{m}{V_C+G_C\lambda }\right)-Q_{\text{min}}\right]}^{-1}-G_C\lambda Q_F\right)}^{-1}-1}.$$ [4]

On the right-hand side of Eq. 4, the terms $G_C\lambda$ and $G_C\lambda Q_F$ are unique to the mixotroph, whereas the other terms are common to the phytoplankton and mixotroph. Positive values for $G_C\lambda$ and $G_C\lambda Q_F$ will always decrease $R_P^{\ast },$ demonstrating that the additional carbon and phosphorus acquired by grazing both serve to make the mixotrophs more competitive.

Smaller Equilibrium P:C Quota.

Eq. 2 can be solved to find the equilibrium P:C ratio, $\overline{Q}$:

$$\overline{Q}=\frac{Q_{\text{min}}}{1-\frac{m}{\left(G_C\lambda +V_C\right)}}.$$ [5]

Eq. 5 gives the equilibrium stoichiometry of the cell when photosynthetic and predatory carbon assimilation are balanced by mortality. Relative to a specialist zooplankton (frequently dominant in the two-guild model), the additional carbon acquisition term $V_C$ serves to decrease $\overline{Q}$ (i.e., increase C:P).

Model Description

The global plankton food-web model is as previously described (9, 33) but with a number of modifications to simplify the representation of the plankton and with phosphorus now included in inorganic, planktonic, and detrital forms. The number of unique plankton size classes is reduced to 10 [compared with 35 previously (9, 33)]. This simplification initially reduced model stability but was counteracted by extending the active switching term (Eq. S23) to all available prey (34) and by increasing the geometric SD of the predator:prey grazing ratio (Table S1).

Environmental concentrations of inorganic nutrients ([R_ii]), plankton biomass ([B_ib,j]), and organic matter ([OM_io,k]) have units of mmol element m⁻³ or mg chlorophyll m⁻³ and appear inside square brackets. Subscript $i_i$ refers to a distinct inorganic nutrient. All plankton are described using the same general biomass equations, with subscript j denoting an individual population, and with subscript $i_b$ denoting either carbon, nitrogen, phosphorus, iron, or chlorophyll (Chl) biomass. Subscript k indicates either dissolved (DOM) or particulate (POM) organic matter, and subscript $i_o$ denotes the organic nutrient element.

The model equation for inorganic nutrients is as follows:

$$\begin{array}{c}\frac{\partial \left[{\text{R}}_{i_i}\right]}{\partial t}=-\nabla \cdot \left(\mathbf{u}\left[{\text{R}}_{i_i}\right]\right)+\nabla \cdot \left(\mathbf{K}\nabla \left[{\text{R}}_{i_i}\right]\right)-{\displaystyle \sum _{j=1}^J\left[{\text{B}}_{\text{C},j}\right]V_{i_i,j}+S_{i_i}^{\text{R}}}.\end{array}$$ [S1]

The model equation for plankton (phytoplankton and zooplankton, or mixotrophs) is as follows:

$$\frac{\partial \left[{\text{B}}_{i_b,j}\right]}{\partial t}=-\nabla \cdot \left(\mathbf{u}\left[{\text{B}}_{i_b,j}\right]\right)+\nabla \cdot \left(\mathbf{K}\nabla \left[{\text{B}}_{i_b,j}\right]\right)+\left[{\text{B}}_{\text{C},j}\right]V_{i_b,j}+\left[{\text{B}}_{\text{C},j}\right]{\lambda }_{i_b,j}{\displaystyle \sum _{j_{\text{prey}}=1}^J{G}_{i_b,j,j_{\text{prey}}}}-{\displaystyle \sum _{j_{\text{pred}}=1}^J\left[{\text{B}}_{\text{C},j_{\text{pred}}}\right]G_{i_b,j_{\text{pred}},j}}-\left[{\text{B}}_{i_b,j}\right]m.$$ [S2]

The model equation for organic matter (dissolved and particulate) is as follows:

$$\begin{array}{c}\frac{\partial \left[{\text{OM}}_{i_o,k}\right]}{\partial t}=-\nabla \cdot \left(\mathbf{u}\left[{\text{OM}}_{i_o,k}\right]\right)+\nabla \cdot \left(\mathbf{K}\nabla \left[{\text{OM}}_{i_o,k}\right]\right)\\ -\frac{\partial }{\partial z}{w}_k\left[{\text{OM}}_{i_o,k}\right]\\ -r_{i_o,k}\left[{\text{OM}}_{i_o,k}\right]+S_{i_o,k}^{\text{OM}},\end{array}$$ [S3]

where:

• u indicates 3D velocity field $\left(u,v,w\right)$ from the physical model.

• K indicates 3D mixing coefficients from the physical model.

• z indicates depth.

• t indicates time.

• $V_{i_i,j}$ indicates uptake rate of inorganic nutrient $i_i$ by plankton j.

• $V_{i_b,j}$ indicates uptake rate of nutrient element $i_b$ by plankton j.

• $G_{i_b,j_{\text{pred}},j_{\text{prey}}}$ indicates grazing rate for predator $j_{\text{pred}}$ on biomass $i_b$ of prey $j_{\text{prey}}.$

• ${\lambda }_{i_b,j_{\text{pred}}}$ indicates assimilation efficiency of predator $j_{\text{pred}}$ on biomass element $i_b.$

• m indicates linear mortality rate of plankton.

• $w_k$ indicates sinking rate of organic matter type k.

• $r_{i_o,k}$ indicates remineralization rate of organic matter type k, element $i_o.$

• $S_{i_i}^{\text{R}}$ indicates additional sources and sinks of inorganic nutrient $i_i.$

• $S_{i_o,k}^{\text{OM}}$ indicates additional sources and sinks of organic matter type k, element $i_o.$

Previous versions of the model (9, 33) applied different nitrogen quotas and mortality rates to the phytoplankton and zooplankton. Here, the same background mortality and size-independent scalings for minimum and maximum quotas were applied to all plankton. Maximum nutrient uptake rates and half-saturation concentrations for N and P were updated according to recently published allometries (19, 35) (parameters are listed in Tables S1 and S2).

Biomass and Nutrient Quotas

Growth of plankton type j is calculated as the acquisition of carbon and other essential elements. The proportion in which these elements are assimilated is variable but within finite limits that prevent excessive accumulation of any one type. The ratio of cellular nitrogen, phosphorus, iron, and chlorophyll a to cellular carbon can be specified in terms of the cellular quota Q:

$$Q_{i_b,j}=\frac{\left[{\text{B}}_{i_b,j}\right]}{\left[{\text{B}}_{\text{C},j}\right]}.$$ [S4]

The uptake and assimilation of each nutrient element decreases to zero as the respective quota becomes full, preventing excessive accumulation of N, P, or Fe biomass in relation to carbon. The generic form of the uptake regulation term for element $i_b$ ($\ne \hspace{0.17em}\text{Chl}$) is given by a linear function of the nutrient status, modified by an additional shape parameter (h = 0.1) that allows greater assimilation under intermediate resource limitation:

$$Q_{i_b,j}^{\text{stat}}={\left(\frac{Q_{i_b,j}^{\text{max}}-Q_{i_b,j}}{Q_{i_b,j}^{\text{max}}-Q_{i_b,j}^{\text{min}}}\right)}^h.$$ [S5]

Nutrient limitation is given by the internal nutrient status (36–38), according to a linear function for N,

$${\gamma }_{\text{N},j}=\frac{Q_{\text{N},j}-Q_{\text{N},j}^{\text{min}}}{Q_{\text{N},j}^{\text{max}}-Q_{\text{N},j}^{\text{min}}},$$ [S6]

and a normalized hyperbolic function for P and Fe ($i_b=$ P or Fe),

$${\gamma }_{i_b,j}=\frac{1-Q_{i_b,j}^{\text{min}}/Q_{i_b,j}}{1-Q_{i_b,j}^{\text{min}}/Q_{i_b,j}^{\text{max}}}.$$ [S7]

Temperature affects a wide range of metabolic processes through an Arrhenius-like equation that is here set equal for all plankton:

$${\gamma }_{\text{T}}=e^{A\left(\text{T}-T_{\text{ref}}\right)}.$$ [S8]

The parameter A describes the temperature sensitivity, T is the ambient water temperature in °C, and $T_{\text{ref}}$ is a reference temperature (also in °C) at which ${\gamma }_{\text{T}}=1$.

Autotrophy

Nitrogen Uptake.

Nitrogen uptake $\left(V_{\text{N},j}\right)$ is the sum of ammonium (NH₄), nitrite (NO₂), and nitrate (NO₃) uptake. Thus, the overall N uptake rate is given by

$$V_{\text{N},j}=V_{{\text{NH}}_4,j}+V_{{\text{NO}}_2,j}+V_{{\text{NO}}_3,j},$$ [S9]

where

$$V_{{\text{NH}}_4,j}=V_{{\text{NH}}_4,j}^{\text{max}}\frac{\left[{\text{NH}}_4\right]}{\left[{\text{NH}}_4\right]+k_{{\text{NH}}_4,j}}{Q}_{\text{N},j}^{\text{stat}}\cdot {\gamma }_{\text{T}},$$ [S10]

$$V_{{\text{NO}}_2,j}=V_{{\text{NO}}_2,j}^{\text{max}}\frac{\left[{\text{NO}}_2\right]}{\left[{\text{NO}}_2\right]+k_{{\text{NO}}_2,j}}{Q}_{\text{N},j}^{\text{stat}}\cdot {\gamma }_{\text{T}}\cdot e^{-\mathrm{\Psi }\left[{\text{NH}}_4\right]},$$ [S11]

$$V_{{\text{NO}}_3,j}=V_{{\text{NO}}_3,j}^{\text{max}}\frac{\left[{\text{NO}}_3\right]}{\left[{\text{NO}}_3\right]+k_{{\text{NO}}_3,j}}{Q}_{\text{N},j}^{\text{stat}}\cdot {\gamma }_{\text{T}}\cdot e^{-\mathrm{\Psi }\left[{\text{NH}}_4\right]}.$$ [S12]

Uptake of all three forms of nitrogen is modified according to the quota status and the temperature function. Ammonium represents the most energetically efficient form of nitrogen, followed by nitrite and nitrate, and preferential uptake of ammonium is included in the model by exponentially reducing the uptake rates for nitrite and nitrate with increasing environmental ammonium (39, 40).

Phosphorus and Iron Uptake.

Phosphate and dissolved iron $(i_i=i_b=$ P or Fe) are taken up as functions of environmental availability $\left(\left[{\text{R}}_{{\text{i}}_i}\right]\right),$ maximum uptake rate $\left(V_{i_i,j}^{\text{max}}\right),$ the half-saturation concentration for uptake $\left(k_{i_i,j}\right),$ quota satiation $\left(Q_{i_b,j}^{\text{stat}}\right),$ and temperature limitation $\left({\gamma }_{\text{T}}\right):$

$$V_{i_i,j}=V_{i_i,j}^{\text{max}}\frac{\left[{\text{R}}_{{\mathrm{i}}_{\text{i}}}\right]}{\left[{\text{R}}_{{\mathrm{i}}_{\text{i}}}\right]+k_{i_i,j}}{Q}_{i_b,j}^{\text{stat}}\cdot {\gamma }_{\text{T}}.$$ [S13]

Photosynthesis.

The photosynthesis and photoacclimation model is modified from refs. 41 and 42. The light-limitation term $\left({\gamma }_{I,j}\right)$ is calculated as a Poisson function of local irradiance (I), modified by the iron-dependent initial slope of the P-I curve $\left(\alpha {\gamma }_{\text{Fe},j}\right)$ and the chlorophyll a-to-carbon ratio $\left(Q_{\text{Chl},j}\right):$

$${\gamma }_{I,j}=\left[1-\exp \left(\frac{-\alpha \cdot {\gamma }_{\text{Fe},j}{Q}_{\text{Chl},j}\cdot \text{I}}{P_{\text{C},j}^{\text{sat}}}\right)\right].$$ [S14]

The gross carbon-specific photosynthetic rate $\left(P_{\text{C},j}^{\text{sat}}\right)$ is modified from an absolute maximum reference value $\left(P_{\text{C},j}^{\text{max}}\right)$ by light and temperature dependence, as well as the cellular status of the most limiting nutrient:

$$P_{\text{C},j}=P_{\text{C},j}^{\text{max}}\cdot {\gamma }_{I,j}\cdot {\gamma }_{\text{T}}\cdot \text{min}\left[{\gamma }_{\text{N},j},{\gamma }_{\text{P},j},{\gamma }_{\text{Fe},j}\right].$$ [S15]

Net carbon uptake, after removal of the metabolic cost of biosynthesis, is given by

$$V_{\text{C},j}=P_{\text{C},j}-\xi \cdot V_{\text{N},j}.$$ [S16]

Photoacclimation.

The chlorophyll-to-carbon ratio is regulated as the cell attempts to balance photon capture with the maximum rate at which energy can be used to fix carbon. Depending on this ratio, a certain fraction of newly assimilated nitrogen is diverted to the synthesis of new chlorophyll a:

$${\rho }_{\text{Chl},j}={\theta }_{\text{N}}^{\text{max}}\frac{P_{\text{C},j}}{\alpha \cdot {\gamma }_{\text{Fe},j}\cdot Q_{\text{Chl},j}\cdot \text{I}},$$ [S17]

where ${\rho }_{\text{Chl},j}$ is the amount of chlorophyll a that is synthesized for every mmol of nitrogen assimilated [mg Chl (mmol N)⁻¹]. If nitrogen is assimilated at carbon-specific rate $V_{\text{N},j}$ [mmol N (mmol C)⁻¹ d⁻¹], then the carbon-specific rate of chlorophyll a synthesis [mg Chl (mmol C)⁻¹ d⁻¹ is

$$V_{\text{Chl},j}={\rho }_{\text{Chl},j}\cdot V_{\text{N},j}.$$ [S18]

Monomodal Size Dependence of Maximum Photosynthetic Rate.

Contrary to other size-dependent parameters, which are all monotonic power law functions of plankton volume (V) (Table S2), a monomodal function was used to relate the maximum photosynthetic rate to plankton size (35, 43, 44):

$$P_{\text{C}}^{\text{max}}=\frac{p_a+{\log }_{10}\left(V\right)}{p_b+p_c{\log }_{10}\left(V\right)+{\log }_{10}{\left(V\right)}^2},$$ [S19]

where $p_a=3.08,$ $p_b=5.00,$ and $p_c=-\mathrm{3.80.}$ The equation was fit to log-transformed empirical data (35) with $r^2=0.79,$ as shown in Fig. S5.

Fig. S5.

Size dependence of $P_C^{\text{max}}.$ Black dots represent data from ref. 35, and gray dots indicate the model size classes. The equation for the curve is given in Eq. S19.

Heterotrophy

Predator–Prey Interactions.

The predator biomass-specific grazing rate of predator $\left(j_{\text{pred}}\right)$ on prey $\left(j_{\text{prey}}\right)$ is given by

$$G_{\text{C},j_{\text{pred}},j_{\text{prey}}}=\underset{\mathit{max}\mathit{.}\hspace{0.17em}\mathit{rate}}{\underbrace{{\gamma }_{\text{T}}\cdot G_{\text{C},j_{\text{pred}}}^{\text{max}}}}\cdot \underset{saturation}{\underbrace{\frac{{\mathcal{F}}_{\text{C},j_{\text{pred}}}}{{\mathcal{F}}_{\text{C},j_{\text{pred}}}+k_{\text{C},j_{\text{pred}}}}}}.\underset{switching}{\underbrace{{\mathrm{\Phi }}_{j_{\text{pred}},j_{\text{prey}}}}}.\underset{\mathit{prey}\hspace{0.17em}\mathit{refuge}}{\underbrace{\left(1-e^{\mathrm{\Lambda }\cdot {\mathcal{F}}_{\text{C},j_{\text{pred}}}}\right)}},$$ [S20]

where ${\gamma }_{\text{T}}\cdot G_{\text{C},j_{\text{pred}}}^{\text{max}}$ is the temperature-dependent maximum grazing rate. This variable is modified by a saturating function of total food availability $\left({\mathcal{F}}_{\text{C},j_{\text{pred}}}\right)$ and the predator specific “half-saturation” constant for grazing $k_{\text{C},j_{\text{pred}}},$ where

$${\mathcal{F}}_{\text{C},j_{\text{pred}}}={\displaystyle \sum _{j_{\text{prey}}=1}^J{\varphi }_{j_{\text{pred}},j_{\text{prey}}}\left[{\text{B}}_{\text{C},j_{\text{prey}}}\right]}.$$ [S21]

The relative availability of each prey population is given by ${\varphi }_{j_{\text{pred}},j_{\text{prey}}},$ which is an approximately log-normal function of the predator-to-prey length ratio, ${\vartheta }_{j_{\text{pred}},j_{\text{prey}}},$ with an optimum ratio of ${\vartheta }_{\text{opt}}$ and a geometric SD ${\sigma }_{j_{\text{pred}}}:$

$${\varphi }_{j_{\text{pred}},j_{\text{prey}}}=\exp \left[-{\left(\ln \left(\frac{{\vartheta }_{j_{\text{pred}},j_{\text{prey}}}}{{\vartheta }_{\text{opt}}}\right)\right)}^2/\left(2{\sigma }_{j_{\text{pred}}}^2\right)\right].$$ [S22]

Predators are assumed to preferentially attack prey that are relatively more available (i.e., with larger ${\varphi }_{j_{\text{pred}},j_{\text{prey}}}\left[{\text{B}}_{\text{C},j_{\text{prey}}}\right])$, according to an active prey switching function:

$${\mathrm{\Phi }}_{j_{\text{pred}},j_{\text{prey}}}=\frac{{\left({\varphi }_{j_{\text{pred}},j_{\text{prey}}}\left[{\text{B}}_{\text{C},j_{\text{prey}}}\right]\right)}^2}{{\displaystyle {\sum }_{j_{\text{prey}}=1}^J{\left({\varphi }_{j_{\text{pred}},j_{\text{prey}}}\left[{\text{B}}_{\text{C},j_{\text{prey}}}\right]\right)}^2}}.$$ [S23]

Finally, a prey refuge function is incorporated, such that the overall grazing rate is reduced when the availability of all prey $\left({\mathcal{F}}_{\text{C},j_{\text{pred}}}\right)$ is low. The size of the prey refuge is dictated by the coefficient $\mathrm{\Lambda }.$

The overall grazing response is calculated on the basis of prey carbon. Grazing losses of other prey elements are simply calculated from their stoichiometric ratio to prey carbon, with different elements assimilated according to the predator’s nutritional requirements (see Prey Assimilation below).

Prey Assimilation.

Prey biomass is assimilated into predator biomass with an efficiency of ${\lambda }_{i_b,j_{pred}}$ $(i_b\ne$ Chl). This has a maximum value of ${\lambda }^{\text{max}}$ that is modified according the quota status of the predator (Eq. S5). For elements $i_b$ = N, P, or Fe, prey biomass is assimilated as a function of the respective predator quota. If the quota is full, the element is not assimilated. If the quota is empty, the element is assimilated with maximum efficiency $\left({\lambda }^{\text{max}}\right):$

$${\lambda }_{i_b,j_{\text{pred}}}={\lambda }^{\text{max}}{Q}_{i_b,j_{\text{pred}}}^{\text{stat}}.$$ [S24]

C assimilation is regulated according to the status of the most limiting nutrient element (N, P, or Fe), modified by the same shape-parameter, h, that was used to modify $Q_{i_b,j_{\text{pred}}}^{\text{stat}}$ (Eq. S5). If all three quotas are full, C is assimilated at the maximum rate. If any are empty, C assimilation is down-regulated until sufficient quantities of the limiting element(s) are acquired:

$$Q_{i_b,j_{\text{pred}}}^{\text{lim}}={\left(\frac{Q_{i_b,j_{\text{pred}}}-Q_{i_b,j_{\text{pred}}}^{\text{min}}}{Q_{i_b,j_{\text{pred}}}^{\text{max}}-Q_{i_b,j_{\text{pred}}}^{\text{min}}}\right)}^h,$$ [S25]

$${\lambda }_{C,j_{\text{pred}}}={\lambda }^{\text{max}}\min \left(Q_{\text{N},j_{\text{pred}}}^{\text{lim}},Q_{\text{P},j_{\text{pred}}}^{\text{lim}},Q_{\text{Fe},j_{\text{pred}}}^{\text{lim}}\right).$$ [S26]

Sources of Organic Matter.

Plankton mortality and grazing are the only two sources of organic matter, with partitioning between nonsinking dissolved and sinking particulate phases determined by the parameter ${\beta }_j,$ as a function of organism size. For $x={\text{log}}_{10}\left(V_j\right),$

$${\beta }_j=0.9-\frac{0.7}{1+e^{\left(2.0-x\right)}}$$ [S27]

and

$$S_{i_o,\text{DOM}}^{\text{OM}}=\underset{\text{mortality}}{\underbrace{{\displaystyle \sum _{j=1}^J\left[{\text{B}}_{i_o,j}\right]{\beta }_j{m}_{\text{P}}}}}+\underset{\text{messy}\hspace{0.17em}\text{feeding}}{\underbrace{{\displaystyle \sum _{j_{\text{pred}}=1}^J\left[{\text{B}}_{\text{C},j_{\text{pred}}}\right]}{\displaystyle \sum _{j_{\text{prey}}=1}^J{\beta }_{j_{\text{prey}}}\left(1-{\lambda }_{i_b,j_{\text{pred}}}\right)G_{i_o,j_{\text{pred}},j_{\text{prey}}}}}},$$ [S28]

$$S_{i_o,\text{POM}}^{\text{OM}}=\underset{\text{mortality}}{\underbrace{{\displaystyle \sum _{j=1}^J\left[{\text{B}}_{i_o,j}\right]\left(1-{\beta }_j\right)m_{\text{P}}}}}+\underset{\text{messy}\hspace{0.17em}\text{feeding}}{\underbrace{{\displaystyle \sum _{j_{\text{pred}}=1}^J\left[{\text{B}}_{\text{C},j_{\text{pred}}}\right]}{\displaystyle \sum _{j_{\text{prey}}=1}^J\left(1-{\beta }_{j_{\text{prey}}}\right)\left(1-{\lambda }_{i_b,j_{\text{pred}}}\right)G_{i_o,j_{\text{pred}},j_{\text{prey}}}}}}.$$ [S29]

Biogeochemistry.

The biogeochemical component of the model is as described in refs. 40 and 45.

Physical Environment.

State variables in the food-web model are transported according to daily resolved advection and diffusion fields from an empirically constrained version of the Massachusetts Institute of Technology General Circulation Model (46) with 1$°$ horizontal resolution and 24 vertical levels (47). The model was run for 15 y, from 1992 to 2006. Global maps and averages are based on output from 2003. The seasonal cycles of chlorophyll a and nutrients shown in Fig. S3 include years 2003 to 2007. Further details can be found in refs. 9 and 40.

Resource Uptake Diagnostics.

The carbon fluxes shown in Fig. 1 represent carbon assimilation. Autotrophic carbon assimilation is given by photosynthesis minus the cost of biosynthesis (Eq. S16). Heterotrophic carbon assimilation is given by the overall grazing rate (Eq. S20) multiplied by the carbon assimilation efficiency (Eq. S26).

The balance (${\nu }_{a:h}$) of autotrophic and heterotrophic nutrition for nutrient element $i_b$ in the nanoplankton size class (Fig. 4) is given by the ratio of depth-integrated inorganic nutrient uptake (or photosynthetic carbon assimilation) and assimilated grazing:

$${\nu }_{a:h,i_b}=\frac{{\nu }_{a,i_b}}{{\nu }_{a,i_b}+{\nu }_{h,i_b}},$$ [S30]

where

$${\nu }_{a,i_b}={\displaystyle \underset{0}{\overset{\infty }{\int }}{\displaystyle \sum _{j=j_{\text{nano}}}{V}_{i_b,j}\hspace{0.17em}dz}}$$ [S31]

is depth-integrated assimilated photosynthesis or inorganic uptake of element $i_b$, and

$${\nu }_{h,i_b}={\displaystyle \underset{0}{\overset{\infty }{\int }}{\displaystyle \sum _{j=j_{\text{nano}}}{\lambda }_{i_o}{G}_{i_b,j}\hspace{0.17em}dz}}$$ [S32]

is depth-integrated assimilation of element $i_b$ from grazing on prey. Here, $j_{\text{nano}}$ is an index of all members of the nanoplankton size class.

The ratio of nanoplankton photosynthesis to uptake of the most-limiting nutrient applied in Fig. 3J requires knowledge of the most limiting nutrient X at each grid point, which is found for the mixotrophic model, according to a nanoplankton carbon biomass-weighted, water-column average of the nutrient limitation terms given in Eqs. S6 and S7, such that

$$X=\{\begin{array}{cc}\text{N},& \text{if}\hspace{0.17em}{\gamma }_{\text{N}}<{\gamma }_{\text{P}}\&{\gamma }_{\text{N}}<{\gamma }_{\text{Fe}}\\ \text{P},& \text{if}\hspace{0.17em}{\gamma }_{\text{P}}<{\gamma }_{\text{Fe}}\&{\gamma }_{\text{P}}<{\gamma }_{\text{N}}\\ \text{Fe},& \text{if}\hspace{0.17em}{\gamma }_{\text{Fe}}<{\gamma }_{\text{N}}\&{\gamma }_{\text{Fe}}<{\gamma }_{\text{P}}.\end{array}$$

The community nutrient exploitation efficiency shown in Fig. 3J is calculated as the ratio of depth-integrated photosynthetic carbon fixation to the depth-integrated uptake of the most-limiting inorganic nutrient.

$$\text{C}:X_{\text{uptake}}=\frac{{\displaystyle {\int }_0^{\infty }\left({\displaystyle {\sum }_{j=j_{\text{nano}}}{V}_{\text{C},j}}\right)dz}}{{\displaystyle {\int }_0^{\infty }\left({\displaystyle {\sum }_{j=j_{\text{nano}}}{V}_{\text{X},j}}\right)dz}}.$$ [S33]

Sensitivity to Tradeoffs.

In the mixotrophy model used in Figs. 1–4 of the main text, it is assumed that all plankton have both autotrophic and heterotrophic traits, with no physiological penalty associated with being a mixotroph. The conceptual view that mixotrophs are generalists relative to specialist phytoplankton and zooplankton suggests that there should be a metabolic cost associated with supporting both autotrophic and heterotrophic metabolism (26). This possibility is explored here in a sensitivity experiment, in which six additional model runs were performed, each resolving three trophic strategies in each size class: specialist phytoplankton, specialist zooplankton, and mixotrophs. The two specialist guilds were parameterized as in the two-guild model, and the mixotroph class was parameterized as for the mixotrophy model but with an additional penalty imposed on autotrophic and heterotrophic resource-acquisition parameters. In this way, mixotroph generalists are made to compete directly with specialists.

In practice, the balance between autotrophic and heterotrophic traits is described by a parameter ω, which is set to 1 for phytoplankton, 0 for zooplankton, and 0.5 for mixotrophs. To allow for different tradeoffs, ω is modified by an exponent τ. Within each size class, the autotrophic parameters listed in Table S3 are multiplied by ${\omega }^{\tau },$ whereas the heterotrophic parameters are multiplied by ${\left(1-\omega \right)}^{\tau }$ (32). The tradeoffs involved in mixotrophy are not empirically well constrained, so we apply three different values for τ (0.74, 1.00, and 1.32), such that mixotrophs are assigned autotrophic and heterotrophic traits that are ∼40%, 50%, or 60% of the specialist values (32). [The mixotroph model used in Figs. 1–4 of the main text essentially assumes that $\tau =0$, such that the mixotrophs have the full resource acquisition traits of both specialists (which are assumed to be fully outcompeted), whereas the two-guild model assumes the limit $\tau \to \infty ,$ such that the mixotrophs have zero resource acquisition traits.]

Additionally, the tradeoffs for nutrient affinity (maximum uptake rate/half-saturation concentration) and grazing clearance rate (maximum grazing rate/half-saturation concentration) depend on whether uptake at low resource concentrations is limited by the rate of encounters with resources (scenario S, only the maximum uptake rate is affected by τ) or the rate of handling of resources once successfully captured (scenario A+S, both the resource affinity and the maximum uptake rate are affected by τ) (32). We examine both possibilities, as outlined in Table S3. These tradeoffs result in six alternative parameterizations for the mixotrophs.

Fig. 5 and Table S4 show that the ecological and biogeochemical effects of adding mixotrophs are somewhat sensitive to their relative success, as a function of the imposed tradeoffs. The weaker the tradeoff, the more mixotrophs dominate the global plankton community and the stronger the effects on carbon export and mean plankton size. Although the results presented in Figs. 1–4 of the main text outline a scenario where mixotrophs have the strongest ecological and biogeochemical impact, the effects are still relatively large when mixotrophs are assigned a reasonably strong tradeoff, as long as no tradeoff is imposed on the nutrient affinities and grazing clearance rates (32). For example, when the mixotroph maximum uptake and maximum grazing rates are reduced to 40% of equivalent specialist values (yellow colors in Fig. 5), global C export is still increased by 20%, relative to the two-guild model, whereas mean plankton ESD is still almost doubled.