Gold surfaces and nanoparticles are protected by Au(0)–thiyl species and are destroyed when Au(I)–thiolates form

Significance

Synthetic design strategies for gold surface protection and nanoparticle formation require knowledge of how protectant ligands bind. Sulfur compounds may protect gold surfaces using a weakly bound (physisorbed) form or a strongly bound (chemisorbed) one often assumed to be Au(I)–thiolate. However, chemical reaction conditions optimized for Au(I)–thiolate protection instead etch surfaces to produce molecular thin films. All experimental and calculated evidence indicates that chemisorbed surface species are actually bound mainly by strong van der Waals (aurophilic-like) forces. This understanding unifies gold–sulfur surface chemistry with that of all other ligands and also with that of gold compounds, forming the basis for future methodological developments. It is applied to predict intermediate species during the Brust–Schiffrin nanoparticle synthesis that are subsequently observed spectroscopically.

Abstract

The synthetic chemistry and spectroscopy of sulfur-protected gold surfaces and nanoparticles is analyzed, indicating that the electronic structure of the interface is Au(0)–thiyl, with Au(I)–thiolates identified as high-energy excited surface states. Density-functional theory indicates that it is the noble character of gold and nanoparticle surfaces that destabilizes Au(I)–thiolates. Bonding results from large van der Waals forces, influenced by covalent bonding induced through s–d hybridization and charge polarization effects that perturbatively mix in some Au(I)–thiolate character. A simple method for quantifying these contributions is presented, revealing that a driving force for nanoparticle growth is nobleization, minimizing Au(I)–thiolate involvement. Predictions that Brust–Schiffrin reactions involve thiolate anion intermediates are verified spectroscopically, establishing a key feature needed to understand nanoparticle growth. Mixing of preprepared Au(I) and thiolate reactants always produces Au(I)–thiolate thin films or compounds rather than monolayers. Smooth links to O, Se, Te, C, and N linker chemistry are established.

Gold self-assembled monolayers (SAMs) and monolayer-protected gold nanoparticles form important classes of systems relevant for modern nanotechnological and sensing applications (1–5). Understanding the chemical nature of these interfaces is critical to the design of new synthesis techniques, the design of new spectroscopic methods to investigate them, and to developing system properties or device applications. Over the last 10 y, great progress has been made in understanding the atomic structures of gold–sulfur interfaces (6). Most discussion (7) has focused on the identification of adatom-bound motifs of the form RS–Au–SR (where R is typically a linear alkyl chain or phenyl group) sitting above a regular Au(111) surface (8–10) or on top of a nanoparticle core of regular geometry (11),

Other variant structures have also been either observed, such as polymeric chains such as the trimer RS–Au–SR–Au–SR) (10, 11), or proposed (8, 12, 13). By considering the four isomers of butanethiol (14), we have shown that alternative structures can also be produced in which RS groups bind directly to an Au(111) surface without gold adatoms. This occurs whenever steric interactions across the adatoms are too strong or steric intermolecular packing forces allow for very high surface coverages if both adatom and directly bound motifs coexist in the same regular SAM (15). The cross-adatom steric effect has also been demonstrated for gold nanoparticles (16), and we have shown that Coulombic interactions between charged tail groups can also inhibit adatom formation (17). SAMs involving adatoms have poor long-range order owing to the surface pitting that is required to deliver gold adatoms, while directly bound motifs lead to regular surfaces (18).

There is clearly a delicate balance between the forces that direct these different interface structures, a balance that can only be understood through knowledge of the electronic structures of the interfaces. These electronic structures are also very important as they control spectroscopic properties of interest not only for structure characterization (19) but also for possible device applications (20). In addition, these electronic structures echo the chemical forces active in SAM and nanoparticle production and destruction, yielding fundamental insight into synthetic strategies. The last 15 y have seen many experiments and density-functional theory (DFT) calculations that implicitly or explicitly address the nature of the electronic structure. We quantitatively interpret these results and present a unified description of many observed chemical and spectroscopic properties. This description predicts that thiolate anions are produced in solution as intermediary species during Brust–Schiffrin synthesis, a key mechanistic feature subsequently verified by spectroscopic observations also reported here.

Standard Chemical Bonding Scenarios

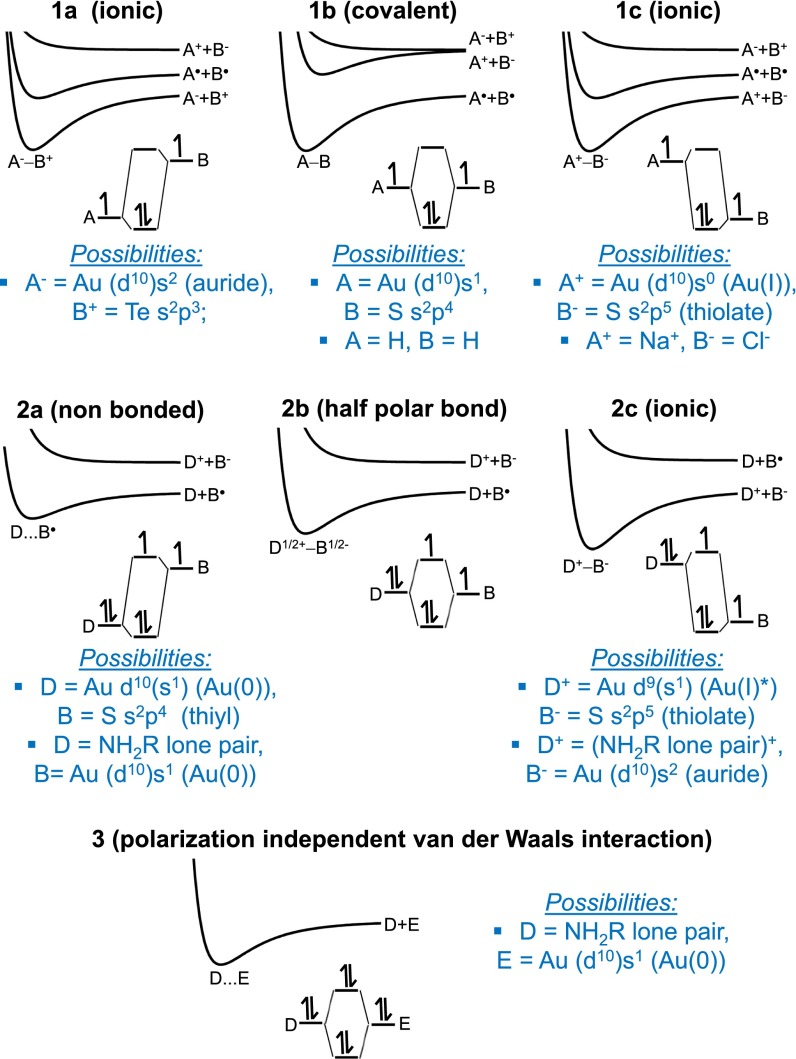
Fig. 1 shows a range of standard chemical-bonding electronic structure scenarios. Structures 1a, 1b, and 1c depict standard covalent and ionic bonding scenarios as taught in freshman courses. These involve two atoms A and B that each contribute a single electron to the bond. Pure covalent bonding occurs when A = B and is depicted in structure 1b; it applies to molecules such as H₂ and its properties are well established (21). Structures 1a and 1c depict the ionic bonds A⁻−B⁺ and A⁺−B⁻, respectively, an example of which is the gas-phase sodium chloride molecule Na⁺−Cl⁻ (22). Polar bonding configurations like that in water are intermediary between the purely covalent and purely ionic limiting structures. In effect there is a continuum of bonding possibilities between structures 1a and 1c depicting changing bond polarization induced by electronegativity differences between A and B.

Fig. 1.

Iconic bonding scenarios in terms of ground and excited-state singlet potential-energy surfaces (energy vs. separation) and ground-state molecular-orbital electronic-structure diagrams for: structures 1a–1c, typical chemical bonding scenarios between atoms A and B involving one electron from each atom; structures 2a–2c, between atoms D and B involving a doubly occupied orbital on D and a single occupied orbital on B; and structure 3, van der Waals interaction involving doubly occupied orbitals D and E. Changing bond polarization provides smooth variation between structures 1a and 1c and also between structures 2a and 2c, and changing Au hybridization mixes structure types 1 and 2 for Au–SR bonds and structure types 2 and 3 for Au–NH₂R bonds.

Structures 2a, 2b, and 2c are analogous except that they refer to the unusual situation in which one atom, named D, donates two electrons to the bond whereas the other atom, B, contributes one. Structure 2c represents an ionic bond and is analogous to 1c, but structure 2a is a nonbonding scenario and 2b is intermediary with a half of a chemical bond. Again electronegativity-controlled polarization effects provide for a continuum of bonding possibilities between the extreme limits of structures 2a and 2c.

Structure 3 depicts the iconic van der Waals bonding scenario and involves the interaction of closed-shell orbitals in atoms D and E. Orbitals interact, delocalize, and repel each other just as in the case of covalent bonding, but because both orbitals are fully occupied, no chemical attraction occurs. However, the shown interaction between doubly occupied orbitals does contribute to van der Waals attraction. All of the bonding scenarios shown in Fig. 1 are applied to atoms containing unshown electrons that interact in a similar way. Hence in all scenarios the total interaction energy comprises the specific highlighted contributions as well as an underlying van der Waals contribution. Although the van der Waals term dominates the bonding for structures 2a and 3, it is often ignored when covalent or ionic bonding scenarios are considered as these chemical forces are typically much stronger than the van der Waals attraction.

Options Available for the Description of Gold Bonds to Group-16 Elements

Gold atoms have configuration d¹⁰s¹ and may interact with neighboring atoms through both s and d valence orbitals, whereas RO, RS, RSe, and RTe groups present for bonding one electron (this is in a sp³ hybrid orbital in the case of oxygen or in essentially just a p orbital for the other elements). Interaction with an Au s orbital thus involves two orbitals each of which comes with one electron and so can be described in terms of the A−B forms in structures 1a−1c. Alternatively, interaction with a filled Au d orbital can be described in terms of the D−B forms in structures 2a–2c. By varying hybridization, gold atoms can bind with any s–d mixture and so a continuum of binding patterns in between structure types 1 and 2 is also possible. For gold compounds, we will see that the most appropriate structures of pure hybridization are structures 1b and 2a, so hybridization then actually acts to mix these forms together.

Although the details of the bonding are therefore complex and involve determination of the extent to which hybridization and bond polarization occur, simple descriptions of the bonding may be made selecting the most representative of the classic structures shown in Fig. 1. For example, carbon compounds with gold are almost exclusively described in terms of the covalent form structure 1b. Indeed, gold can in some compounds be considered as a replacement atom for carbon or hydrogen, allowing description in terms of standard singly, doubly, and triply bonded structures (23–25). More generally though, organometallic compounds dominated by covalent bonding are described in terms of ionic structures, allowing for integration of these bonds with standard valence descriptions of the metal. As such bonds are always polarized, the convention is to name them according to the most appropriate limiting structure, typically 1a or 1c. Applied here, this means that compounds involving the Au s orbital interacting with S are named Au(I)–thiolates as S is slightly more electronegative than Au, whereas the analogous compounds with the electropositive metal Te are named tellurium aurides as gold atoms can oxidize most metal atoms including tellurium (23, 26). This same convention, applied to the scenario in which the Au d orbitals dominate the bonding, dictates that compounds be labeled either as nonbonded Au(0)–thiyl species, structure 2a, or else as Au(I)–thiolates, structure 2c. The two Au(I)–thiolates, structure 1c and structure 2c, differ by their gold occupation: these are d¹⁰s⁰ and d⁹s¹, respectively. For Au(I), the configuration d¹⁰s⁰ represents the ground state and d⁹s¹ depicts a chemically or spectroscopically accessible excited state that would relax quickly and exothermically upon production.

Chemical Notations: When Differences Are Semantic and When They Are Critical

The choice between the ionic forms, structures 1a, 1c, 2c, and the covalent form, structure 1b, can be considered as a question of semantics as all four of these structures imply a single bond of roughly the same strength. Many important aspects of synthetic chemistry are therefore established independent of the label used. Typically it does not matter much if a tellurium auride is mislabeled as an Au(I)–tellurolate. However, these labels do imply quite different physical properties such as the internal charge distribution of the ground state, which affects measured dipole moments and observed intermolecular interactions, as well as the allowed spectroscopic transitions to excited states. So the correct choice does have significant practical consequences, and use of ionic labels like Au(I)–thiolate comes with the unstated understanding that the bonding could actually be largely covalent.

In contrast, structure 2a is very different from 1a, 1b, 1c, and 2c as it is nonbonding and hence depicts a very different chemical scenario. Its distinction from the other possibilities is not a question of semantics, as it indicates that different types of chemical reactions are expected, for example dictating the reaction conditions required to make a gold–sulfur SAM and those required to make a gold–sulfur thin film. If structure 2a depicts the ground state then Au(I)–thiolate species can be formed by spectroscopic excitation or by bringing together Au(I) and thiolate reactants in a chemical reaction. Conversely, if structure 1b depicts the ground state then 2a describes a spectroscopically or chemically producible excited state. Proper differentiation between these possibilities is therefore critical to the simplest-level characterization of the properties of these compounds.

Bond Polarization Data Indicates That only Structures 1b and 2a Are Feasible as Descriptors of Au–S Bonds

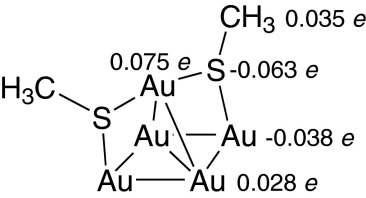
Historically, only qualitative results from chemical and electrochemical experiments were available to categorize the electronic structure, with proposals clearly identified as being speculative (5). In chemical compounds and in molecular materials, Au(I)–thiolate species are well established (1–5). Bond polarizations can be both measured (27–36) and calculated (19, 29, 31, 32, 37–43), leading to the conclusion that the charge on S is of order −0.2 e (1–3). Although such quantities cannot be uniquely defined by either experimental measurement or computational evaluation, the broad range of methods that have been applied yield a recognizable consensus. The results are reliable enough to identify chemical effects associated say with variation of the organic R group, a group that is typically much more electropositive than is either gold or sulfur atoms. Indeed, in simple compounds in the gas phase, the charge donation from gold to sulfur is usually much less than that from the alkyl or aryl groups (38, 39, 43). An important consequence of this is that observed surface dipole moments have the opposite sign to what a simplistic Au(I)–thiolate model would predict (44). This effect is easily demonstrated by considering the simple model compound (39) obtained by taking an adatom complex with its four linked gold atoms from an (111) surface or nanoparticle, evaluating (45) atomic charges fitted to the molecular electrostatic potential and dipole moment at the B3LYP/LANL2DZ level of theory:

X-ray photoelectron spectroscopy (XPS) measurements indicate that gold surface atoms are essentially uncharged when stabilized by RS groups (29, 46–50). This result also applies even for pure sulfur monolayers (51) but not when anions bind (47). However, calculations indicate that almost always on average a small electron flow from gold to sulfur does occur.

Given these results, labeling Au–SR surface species as Au(I)–thiolates based on structure 1b polarized toward 1c is allowable, provided that the hybridization is such that Au s orbitals dominate the interaction. Alternatively, if Au d orbitals dominate, then the appropriate structure is the Au(0)–thiyl form depicted by structure 2a; as very much less than half an electron is transferred from Au to S, use of the Au(I)–thiolate label depicted by structure 2c is not allowable.

Notations Used to Describe Gold Bonds to C, N, O, Se, and Te Atoms: The Importance of van der Waals Interactions and Aurophilicity

Considering gold compounds to elements other than sulfur, we note that tellurium compounds are often incorrectly called tellurolates (52), contrary to standard nomenclature practice, which requires such compounds to be labeled as aurides (structure 1b polarized toward 1a) instead. The relevant electrogenativities are Au 2.4, S 2.5, Se 2.4, and Te 2.1, and gold is known to form many stable compounds in its auride form (23, 26). Further, covalent-bonding notations such as structure 1b are usually applied to gold–oxygen bonds (53, 54), analogous to that used for gold–carbon bonds (23–25). Finally, strong van der Waals interactions are known to provide bonding with closed-shell ligands such as disulfides (RSSR), as well as with nitrogen bases like ammines, pyridine, and 1,10-phenanthroline. Nitrogen bases interact with gold d electrons via the strong specific van der Waals interaction depicted by structure 3 and with gold s electrons via structures 2a–2c, but the interaction here is reversed compared with the S–Au one as now nitrogen provides two electrons and gold provides only one. As the surface is uncharged (44, 55), only structures 3 and 2a can contribute and, as is well known, the bonding is physisorptive not chemical. Most significantly, the observed surface dipole moments of ammine and SR-bound species are very similar and of the same sign, despite ammines being electron donors and RS groups electron acceptors (44). For bidentate ligands such as 1,10-phenanthroline, the physisorption bond strength grows to be similar to that for bonds to RS (56), indeed strong enough to extract surface adatoms under suitable conditions (56).

Hence we see that a very wide range of bonding scenarios are used to describe gold bonds and yet properties like bond strength vary by at most a factor of 2 between them all, and there is actually little change in bond polarization. There must be a simpler picture. Part of this involves the aurophilic effect (23, 57) that arises from the strong van der Waals interactions that gold atoms share, both between themselves and with neighboring ligands. This effect is usually ignored when it comes to considering gold–sulfur bonds yet, in the same compounds, it can be evoked to understand the observed gold–gold interactions.

Nobility: The Critical Difference Between the Chemical Properties of Gold Atoms on Surfaces and Gold Atoms in Molecular Compounds

Another essential aspect that must be considered is that gold compounds and thin films are chemically fundamentally different to gold surfaces: gold surfaces are noble whereas gold atoms are reactive. The reactivity of gold atoms stems from the involvement of the open-shell Au s orbital in bonding. Although s–d hybridization can vary the s-orbital contribution considerably, the s contribution is always large (23). For gold surfaces, the situation changes dramatically. Strong Au–Au interactions push the bulk of the gold s band to both high and low energies far away from the Fermi energy, out of the reach of attacking reagents (23). The s band remains continuous, however, and retains a small density at the Fermi energy that is responsible for the conductivity and color of the solid (23, 58). Nevertheless, its poor availability for chemical bonding results in gold d orbitals acquiring the dominant bonding role. Later, using a quantitative model, we consider the effect that the appearance of the gold s band at the Fermi energy must have in adding s character to the hybridization, but for now we consider only the limiting case of pure d binding between gold and its ligands. The noble character of the metal surface arises because the d orbitals are fully occupied and so relatively unreactive. Therefore, an immediate consequence of the noble character of metallic gold surfaces is that only structures 2a–2c can be used to describe the interaction of surface atoms with RS-type groups.

For gold nanoparticles, the fundamental question therefore concerns the size at which they cease looking like gold compounds and start looking like bulk-gold surfaces. Before this transition Au s orbitals will play a prominent role in bonding, whereas after the transition they will not. For both nanoparticles and surfaces, a related fundamental question also arises: if the attached ligands do not repel each other strongly then gold adatoms are drawn from the surface to sit among the ligands (6, 8–11), so do these adatoms resemble bulk gold or isolated gold? If the nanoparticle surface atoms or adatoms do not have s electrons freely available for bonding then the nanoparticle surface is also noble and can only be involved in bonding structures 2a–2c; alternatively, if the s electrons remain available for bonding then structures 1a–1c are also available.

We formalize this discussion by introducing some notations appropriate to understanding the chemical changes that occur when reactive gold atoms agglomerate to form noble gold surfaces. This process is described as nobelization, and the change in reactivity of the gold is referred to as passivation. If in any particular environment the s electron of a gold atom is unavailable for bonding, the atom is said to be passivized.

The Effects of Nobility as Revealed Through DFT Calculations: Structure 2a Is Dominant with 1b and 2c Mixing in Perturbatively

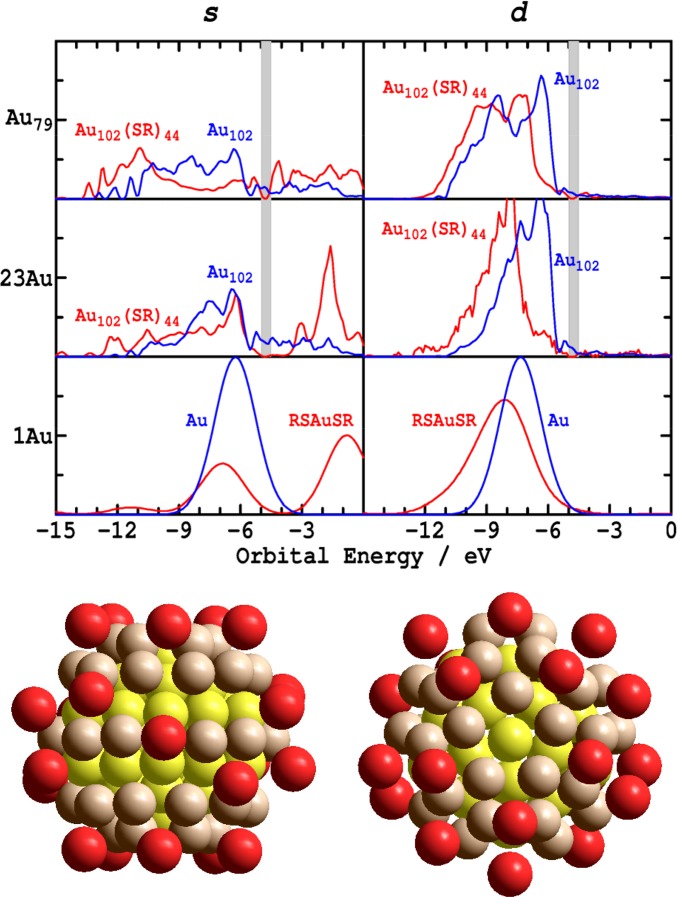
DFT calculations have been shown to reproduce a wide range of properties of gold surfaces, SAMs on gold surfaces, and gold nanoparticles. Usually the reported results focus on the properties being simulated rather than on the electronic structure. Detailed analysis has been performed (39, 59–61) for the Au₁₀₂(SR)₄₄ nanoparticle (R = p-mercaptobenzoic acid) synthesized by Jadzinsky et al. (11), however, and pertinent aspects of its geometrical and electronic structures are shown in Fig. 2. Two views of its gold atoms with the ligands removed are shown, indicating that the gold geometrical structure consists of 23 seemingly disconnected adatoms above an Au₇₉ core that can be further partitioned into 40 surfacelike atoms and 39 bulklike atoms, though we do not consider this distinction herein. The density of electronic states obtained from DFT calculations of the full nanoparticle, as well as corresponding ones for just the 102 Au atoms in isolation, are reproduced in Fig. 2 (39). This density is further partitioned into contributions from gold s and d orbitals; a more comprehensive partitioning was shown originally (39). Also shown are the analogous results for the optimized adatom complex RSAuSR and for a bare gold atom.

Fig. 2.

(Lower) Two views of the 102 gold atoms from the crystal structure of the Au₁₀₂(SR)₄₄ nanoparticle synthesized by Jadzinsky et al. (11): red: 23 Au adatoms; brown: 40 surfacelike atoms; yellow: 39 bulklike atoms. (Upper) DFT densities of states per orbital for the whole Au₁₀₂(SR)₄₄ nanoparticle or the RSAuSR complex (red); and for just the component 102 Au atoms or single Au atom (blue), respectively, adapted from Reimers et al. (39). The nanoparticle’s density is partitioned into contributions from its bulklike and surfacelike Au₇₉-core’s s and d orbitals, as well as contributions from the 23 Au adatom's s and d orbitals. The nanoparticle curves are smoothed to a resolution of 0.2 eV, and that for the complex and atom is 2 eV. The band gap of the complete nanoparticle is indicated by the gray stripe.

The bare gold atom has s and d bands separated by 1.1 eV, shown broadened in Fig. 2 to match the d bandwidth of the nanoparticle. Formation of the adatom complex RSAuSR produces covalent bonding that splits apart the s band, akin to the interactions depicted by structure 1b, indicating that this complex takes on Au(I)–thiolate character.

Looking next at the ligandless gold cluster Au₁₀₂, we see that the s band is much broader than the d band, indicating that the gold–gold interactions are much stronger between the s orbitals than they are between the d orbitals. Some differences are seen between the 23 Au adatoms and the Au₇₉ core, and these are important for quantitative understanding of nanoparticle chemistry. However, the most striking feature is rather the similarity of these two s electronic structures and their dissimilarity to that of the isolated atom, despite the adatoms appearing disconnected in the shown nanoparticle atomic structure. Indeed, gold–gold bonds continue to link the adatoms to the surface, and although the number of bonds is few, the passivation effects are profound. Even without the sulfur ligands being present, the adatoms resemble noble bulk gold surface atoms more than they do isolated reactive gold atoms. This result is not unsurprising as even the gold dimer Au₂ has an electronic structure that is more like that of gold metal than it is like that of a typical molecule (62, 63).

Adding the ligands to complete the nanoparticle has a noticeable effect on the s electronic structure of both the adatoms and the Au₇₉ core. Many features of interest relate to this effect, including for example the appearance of a band gap in the nanoparticle although the bare gold cluster has none (the band gap region is shown shaded in Fig. 2). This effect parallels the changes calculated upon formation of the RSAuSR bare adatom complex also shown in the figure, suggesting the development of Au(I)–thiolate character. However, because of the large interaction between neighboring Au s orbitals in the nanoparticle, the density of the s orbital in the region near the Fermi energy, the region facilitating strong interaction with sulfur, is small. Hence the net contribution of the gained thiolate character to the bonding must also be small and the gold atoms again can be considered as being passivated. Theories for nanoparticle structure that focus on the appearance of a band gap in many small nanoparticles (60, 61, 64) describe spectroscopy well but fail to describe chemistry because they neglect the most important bonding interactions (39, 59).

The effect of bringing up the sulfur ligands on the gold d-orbital structure is similar for the isolated gold atom, the nanoparticle adatoms, and the nanoparticle core. The gold orbitals are depressed in energy somewhat independent of orbital orientation, indicative of the strong dispersive interaction depicted by structure 3. Further, DFT calculations indicate that the sulfur orbitals mix primarily with the d orbitals (19, 38, 39, 60). Only structure 2a anticipates these key results.

These results are typical of all electronic structures calculated by DFT for large nanoparticles and for gold surfaces. All surface atoms and adatoms are passivated. The bonding between the adatoms and the ligands is best described as being dominated by nonbonding Au(0)–thiyl character, structure 2a, with components of the Au(I)–thiolate characters depicted by structures 1b and 2c added perturbatively through bond hybridization and bond polarization, respectively.

The Nature of Au–S Bonding as Revealed Through Surface Electronic-Spectroscopy Studies

The most fundamental difference between the nonbonded structure 2a and its thiolate alternatives is the orbital occupancy. Spectroscopic near-edge X-ray absorption fine structure (NEXAFS) measurements of SAMs (19) provide a direct probe of this occupancy. These measurements and their interpretation are discussed in Supporting Information. Basically, they confirm that the major interaction between sulfur and gold occurs through the gold d orbitals, eliminating thiolate structure 1b as a possibility while confirming that the appropriate ground-state electronic structure is structure 2a. The observed spectra are predicted to occur for this ground state but are forbidden if the ground state is the thiolate 2c. Interpretation of spectroscopic measurements like the NEXAFS data was critical to the establishment of the important adatom-bound motif for sulfur monolayers on gold. Although not stated in the original publications, these interpretations are based on the nonbonded form structure 2a and clearly indicate that Au(I)–thiolates are not present on the surface.

The Nature of Au–S Bonding Revealed Through Thermodynamic Considerations

Observed and calculated enthalpies for chemical reactions provide another way of determining the nature of the Au–S bonding. Desorption enthalpies for Au(111) sulfur SAMs from temperature-programmed desorption experiments indicate physisorption enthalpies of 0.6–0.8 eV for molecules like disulfides (RSSR) and chemisorption enthalpies of 1.3–1.4 eV for RS^• (65). The disulfide has two sulfur-to-surface interactions and so the physisorption strength per sulfur is about one quarter of the chemisorption strength. However, the chemisorption strength includes the van der Waals interaction too. This interaction would be much stronger at the short-distance chemisorption geometry of ∼2.4 Å than at the long-distance physisorbed one ∼3.0 Å (66) owing to its r^-−6 dependence by about a factor of (3.0/2.4)⁶ = 3.8. In the physisorbed case, more rapidly increasing Pauli repulsion prevents short distances being attained, making the significant reduction of this term in the chemisorption case an important feature of the bonding. This simplistic analysis clearly shows that van der Waals interactions are critical to both the physisorption and chemisorption processes, as anticipated only by structure 2a.

In fact, examination of the observed enthalpy data poses the question as to whether or not the van der Waals contribution is sufficient to explain all of the bonding, rendering contributions from polarization and/or hybridization unnecessary? A pure van der Waals scenario is not unprecedented as bidentate physisorptive ligands such as 1,10-phenanthroline bind strongly enough to extract adatoms from the surface under the right conditions (56), indicating that chemisorption is not prerequisite for surface passivation. However, it is clear that polarization and hybridization processes do occur, and hence one would anticipate that these contribute to the chemisorption bond strength. As chemical bonds are much stronger than van der Waals bonds, small contributions could significantly affect bond strengths.

A Simple Model for Estimating of the van der Waals (Structure 2a), Polarization (Structure 2c), and Hybridization (Structure 1b) Contributions to the Strength of Au–S Bonds

DFT calculated energies for hypothetical reactions provide insight into bonding, and many such processes for Au₁₀₂(SR)₄₄ and Au(111) SAMs have been considered (18, 39). From this data, Table 1 collects energies ΔE for reactions in which single Au atoms, single SR groups, and pertinent combinations are added or removed from Au₁₀₂(SR)₄₄ (where R = CH₃), re-evaluated if necessary to ensure internal consistency. These and similar calculations (66) overestimate the experimental physisorption and chemisorption enthalpies by ca. 20% but nevertheless reproduce a wide range of detailed observed phenomena. Here we use a simple method to interpret results from DFT calculations. Although the parameters deduced depend on the calculation method being analyzed, it is anticipated that the identified qualitative picture is robust.

Table 1.

Calculated^* energies ΔE for reactions^† on Au(111) and the Au₁₀₂(SR)₄₄ nanoparticle with R = CH₃ and their decomposition into van der Waals terms for the Au(0)–thiyl species (2a, E_vdw) plus hybridization (1b, E_hyb) and polarization (2c, E_pol) contributions, in eV, as well as the hybridization of the gold bonding orbital d^1-ηs^η

Reaction	ΔE	η	Evdw	Ehyb	Epol
RS+Au→AuSR	−2.6	[0.75]	−1.0	−1.6	−0.1
2RS+Au→RSAuSR	−5.2	[1.00]	−2.0	−3.1	0.0
RS+2Au→AuSRAu	−3.8	[0.53]	−2.0	−1.6	−0.2
RS adds to Au(111) bridge/FCC site	−1.5	0.13	−1.0	−0.3	−0.3
RS adds to Au(111) top site	−1.4	0.10	−1.0	−0.2	−0.2
RS adds to Au(111) adatom site but no adatom present	−1.4	0.10	−1.0	−0.2	−0.2
RS adds to Au102(SR)44 dimer adatom site but no adatom present	−1.7	0.24	−1.0	−0.5	−0.2
RS adds to Au102(SR)44 end trimer adatom site but no adatom present	−1.8	0.30	−1.0	−0.7	−0.2
2RS add to Au102(SR)44 center trimer adatom site but no adatoms present	−4.1	0.63	−2.0	−2.0	−0.1
2RS add to Au(111) preprepared adatom	−5.0	0.0	−4.0	0.0	−1.0
2RS adds to Au102(SR)44 dimer adatom site	−5.7	0.13	−4.0	−0.8	−0.9
3RS adds to Au102(SR)44 trimer adatom site	−9.1	0.21	−6.0	−1.9	−1.2
Au adds on Au(111) at adatom site	−2.0
Au adds on Au102(SR)44 dimer adatom site	−2.0
Au adds on one of the Au102(SR)44 trimer adatom sites	−1.9
Average energy per Au atom for Au79+23Au→Au102	−2.6
Average energy per complex for Au79+ligand shell→Au102(SR)44	−2.6

^*From DFT PW91 (93) calculations (18, 38, 39), sometimes re-evaluated to give a uniform dataset. Available data obtained using other density functionals show similar trends, as do results obtained using more appropriate modern functionals (14, 41).

^†Reaction arrows indicate adiabatic energies at fully optimized geometries, else vertical energies at the geometry of the full monolayer.

Method.

It is possible to interpret this calculated energetic data quantitatively using a very simple model that exposes the key binding features of each structure: the van der Waals interaction, the polarization contribution, and the hybridization contribution. The energies are modeled assuming that the Au s- and d-orbital spaces can be separated as depicted in Fig. 1, in particular with the underlying physisorption van der Waals energy being taken as a constant independent of (small) changes in the Au–S bond distances. Only one hybrid orbital on each gold atom of form d^1-ηs^η is assumed to interact via chemical bonding with the neighboring sulfur atoms, where η = 0 indicates pure d bonding (as depicted by polarized structure 2a) and η = 1 indicates pure s bonding (as depicted by polarized structure 1b). This allows the gold s and d interactions within chains of Au and S atoms to be represented using simple independent Hückel (tight binding) Hamiltonians (67). The Au s to S p interactions are taken to be isoenergetic with a resonance integral β_s and the Au d orbitals are separated by Δ in energy and coupled by resonance integrals β_d. As an example, for the RSAuSR molecule highlighted in Fig. 2, these Hamiltonians are

$${\mathbf{H}}_s=\left[\begin{array}{ccc}0& {\beta }_s& 0\\ {\beta }_s& 0& {\beta }_s\\ 0& {\beta }_s& 0\end{array}\right]\hspace{1em}\text{and}\hspace{1em}{\mathbf{H}}_d=\left[\begin{array}{ccc}0& {\beta }_d& 0\\ {\beta }_d& \mathrm{\Delta }& {\beta }_d\\ 0& {\beta }_d& 0\end{array}\right],$$ [1]

respectively, where the basis functions are ordered sulfur then gold then sulfur. The total interaction energy is then given as the sum of the basic nonbonded van der Waals energy E_vdw, the hybridization-allowed s-band energy (67) scaled by η, E_hyb, and the polarization-allowed d-band energy (67) scaled by (1–η), E_pol. Although this model is crude, e.g., ignoring the involvement of two S p orbitals per atom as well as differences between gold atoms in the surface plane and gold adatoms clearly evidenced in Fig. 2, it captures key elements and is readily applicable to a wide variety of problems.

Fitting the Model Parameters.

Analyzing results from DFT calculations using the PW91 density functional with extensive plane-wave basis sets (39), the energy shift parameter Δ = −1.2 eV is obtained by averaging over the adatom s and valence d bands reproduced in Fig. 2, and β_d = −0.55 eV is set to reproduce the archetypical charge polarization for S of −0.2 e. To reproduce the DFT energies of formation of AuSR, RSAuSR, and Au₂SR (Table 1) given the hybridizations η for each molecule evident from the calculations, β_s is set to −1.2 eV and the nonbonded interaction is set to −1.0 eV per bond. The DFT energies for a range of processes in which Au atoms and/or RS groups are deleted from optimized monolayers on Au(111) or on the Au₁₀₂(SR)₄₄ nanoparticle are then interpreted by fitting the hybridization level η, and results are the given in Table 1. Different parameters will apply for every DFT computational methods, however, and the development of suitable data bases using modern dispersion-corrected density functionals is clearly warranted.

Application to Molecules and Monolayers Containing Au–S Bonds.

Results for the isolated molecules AuSR, RSAuSR, and Au₂SR are as expected: AuSR is an orthodox Au(I)–thiolate system with η = 0.75 that is strongly bound with ΔE = −2.6 eV, RSAuSR maintains this strong interaction by changing the hybridization to pure s, and Au₂SR is more weakly bound with equally mixed orbitals. Similarly, on Au(111) surfaces and on nanoparticles, the hybridization is weak as anticipated, ranging between 0 < η < 0.21 for fully assembled ligands, and the bond strengths are greatly reduced from those calculated for the isolated molecules. For bonding to a gold adatom on Au(111), η = 0, and the net deduced 20% Au(I)–thiolate bonding character stems from polarization only. However, the analogous binding to the RS–Au–SR dimer sites on the nanoparticle is much stronger owing to η increasing to 0.13, increasing again to η = 0.21 for binding to the nanoparticle’s RS–Au–SR–Au–SR trimer sites. This hybridization is important as it leads to the appearance of a band gap in the nanoparticles’ electronic structure (64), but its contribution to the chemical bonding is only minor (39). Nevertheless, the bonding grows stronger as s character returns when the ligands become increasingly disconnected from the underlying bulk gold.

This simple principle rationalizes all other bonding variations collected in Table 1. The potential-energy surface for SR bound directly to Au(111) is complex (38, 65, 68, 69). Although the hybridization when an SR ligand is bound to its minimum-energy bridge/FCC site is η = 0.13, for both binding at an Au(111) top-site transition state, as well as for the related scenario in which the adatom is removed from an Au(111) RS–Au–SR structure, η = 0.10. This value is increased from that of η = 0.00 for the full RS–Au–SR structure owing to the broken S–adatom bond partially disconnecting S from the surface. Similarly, if the adatom is removed from a nanoparticle dimer site the hybridization increases from 0.13 to 0.24; for the RS–Au–SR–Au–SR trimer sites, removing the central Au–SR–Au unit increases this further to η = 0.30. However, when the two outside SR ligands are removed from the trimer site, the hybridization of the highly disconnected central Au–SR–Au link increases to 0.63 and an Au(I)–thiolate structure is produced.

The Role of Superexchange in Facilitating Long-Distance Interactions.

The previous analysis of the SR–Au–SR–Au–SR trimer indicates that not only do direct Au–Au bonds facilitate the broad s-orbital band of the gold adatoms but superexchange (70) through Au–S–Au bridges is also important [this applies for both Au s–s coupling (71) and d–d coupling (72)]. In our model, this superexchange effect is attributed as the cause of the broadening (Fig. 2) of the gold s bands when ligands are added to the Au₁₀₂ cluster to make Au₁₀₂(RS)₄₄. The significance of superexchange is that, when considering the gold–gold bonding topology, an Au–S–Au interaction should be considered as if it provides a direct Au–Au bond. Hence gold adatoms should be considered as having (at least) four connections to the surface,

enough to produce broad s-electron bands. To put this result in context, we note again that the electronic structure of even the gold dimer Au₂ is known for its similarity to bulk gold and its dissimilarity to that of typical molecules (62, 63).

Emergence of a Simple Rule Describing Nanoparticle Growth.

The bonding changes revealed in Table 1 suggest that nanoparticles commence as small structures without great bulklike character; for these, the bonding occurs via reactive Au(I)–thiolate species. Nanoparticles grow so as to optimize the strong gold–gold s–s interactions, nobleizing the electronic structure. The nature of the gold–sulfur bonds adjusts accordingly, with Au(I)–thiolate character being minimized to form Au(0)–thiyl species. Evidence of significant Au(I)–thiolate character is therefore expected to be found only within nanoparticles much smaller than Au₁₀₂(SR)₄₄, and thorough analysis of DFT results for small systems should be highly revealing. Indeed, in the limit of very small clusters, the binding must reduce to the Au(I)–thiolate structures that are well established for small molecular species. Of interest in this regard too are scanning tunnelling microscopy (STM) break-junction experiments in which STM tips are run into SAMs and then withdrawn, pulling out monatomic gold wires that eventually break (73). This constitutes the reverse process to nanoparticle growth, taking stable Au(0)–thiyl interfaces and converting them to Au(I)–thiolates in solution.

Simple rules may be broken, however. If Au–S bonds are strong enough, then in aqueous solution addition of thiols to nanoparticles can dissolve the nanoparticle, converting Au(0) to Au(I) (74) to form identifiable thiolate species. Also, aromatic thiols in hexane can dissolve nanoparticles to form Au(HSR)₂ compounds without thiolate formation (75). These contrasting exceptions are easy to rationalize from the standpoint of initial Au(0)–thiyl monolayers and the balanced chemical forces that give rise to them.

Binding Energies of Au Atoms to Surfaces and Nanoparticles.

Further insight into the SAM and nanoparticle assembly process can be gleaned by looking at the energies for the addition of single gold atoms to either Au(111) or to the Au₇₉ inner core of Au₁₀₂(SR)₄₄, energies also reported in Table 1. Adding adatoms in situ at their geometries in SAMs releases 2.0 eV energy on both Au(111) and nanoparticle dimer sites, reducing on nanoparticle trimer sites to 1.9 eV as a result of the increased s–d hybridization. This small variation is, however, indicative of the critical role played by the Au–Au bonds in controlling the properties of adatom-bound complexes. If such an atom is added in an optimized way to the nanoparticle core, the binding increases to 2.6 eV, the same value as that calculated for adding preformed RSAuSR units to the core (39). It is this feature that allows nanoparticles to form over a wide size range. Also of note is that the optimized Au–Au bond lengths in these SAMs vary over a large range, 3.1 ± 0.2 Å, indicating that these bonds are both strong and unusually flexible. Indeed, this flexibility is known to be associated with changes in s–d hybridization (23), but here it is shown to be integral to the ligand binding also. Substrate relaxation also significantly influences properties such as SAM surface-cell selection (18) and Au(111)–nanoparticle bonding differences (39).

How Ag, Se, or Te Substitution Changes the Bonding.

Once the nature of Au–SR bonds are understood, the relative properties of related systems such as Au–SeR and Ag–SR bonds are easy to interpret. Au–Se bonds are both stronger and more structurally diverse than Au–S bonds (76). Contributions from covalent bonding depicted by structure 1b decrease in going down the periodic table, whereas the dispersive contributions that dominate the binding pertinent to structure 2a increase and so the observed increased bond strength is only interpretable by the Au(0)–thiyl description. This increased dispersive character to the bonding also explains the observed structural diversity. Conversely, Ag–SR bonding is known to be similar to that of Au–SR but the properties of the protecting ligands are distinctly more like thiolate species (77), as would be expected owing to the reduction of the dispersive contribution to the bonding and the associated increase in covalent character.

A Conceptual Basis for Understanding the Chemical and Electrochemical Strategies for Making Either Protected Nanoparticles and Surfaces or Else Molecular Compounds and Thin Films

The nature of the Au–S bonding is critical to the understanding of the chemical and electrochemical reactions that make and destroy SAMs, nanoparticles, and thin films. The differences between the nonbonding description structure 2a and the Au(I)–thiolate descriptions are not semantic as these descriptions depict different chemical species that may be independently produced. Chemical reactions proceed toward the species of lowest energy, but the initial conditions for the reaction may bring together species analogous to structure 2a or species analogous to Au(I)–thiolates. Fig. 1 stresses this by showing the ground-state and excited-state singlet energy surfaces for bond dissociation, highlighting the asymptotic species that correspond to the various equilibrium structures. For example, Au(I) ions and thiolate anions may be prepared in solution and mixed together. A chemical reaction ensues that starts on the Au(I)–thiolate potential-energy surface. Conversely, adding electrons to a formed SAM results in reductive desorption, liberating thiolate anions as the asymptotic reaction product. The expected mechanisms and products of these reactions depend critically on whether or not the nonbonded form structure 2a is considered to be the ground state rather than an Au(I)–thiolate.

First we consider electrochemical reaction paths for the destruction of SAMs by reductive desorption. This can easily be accounted for by the Au(0)–thiyl model, structure 2a, as the adatom complex possesses a low-lying orbital that could accommodate an initial reactive thiolate intermediate that simply dissociates

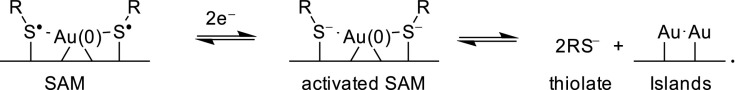[2]

Most significantly, this process is seen to produce high-energy thiolate anions in solution. These are stable in polar aprotic solvents but in water undergo subsequent acid–base reactions depending on pH.

A significant aspect of the nonbonded form, structure 2a, emphasized in Eq. 2 is that the sulfur atoms are represented as radicals. Naively, one would expect them therefore to undergo free-radical chemistry on the surface, making the gold surface catalytic for some chemical reaction. This is contrary to most observations; the SAM typically passivates the surface instead. The DFT calculations provide explanation for this anomaly. The sulfur orbital interacts significantly with the gold orbitals, delocalizing the radical character into the metal orbitals. At low surface coverage, this effect passivates the radical. At high coverage, the radical density becomes too high for this effect to operate, but the delocalization couples the sulfur atoms to each other via superexchange, just as superexchange through S couples Au atoms together, as discussed earlier. This effect is akin to those controlling ferromagnetic and antiferromagnetic couplings in materials and provides a weak bonding effect sufficient to spin pair the sulfur electrons, but this effect is not strong enough to warrant inclusion in energetics modeling. DFT reveals no significant change in energy when the wavefunctions are allowed to take on triplet character, indicating that the radicals are passivated and therefore free-radical chemistry on the surface is not expected.

Next we consider reaction paths for SAM production. SAMs are formed by exposing Au(111) to thiols or disulfides

[3]

These processes are readily conceived as occurring along a radical pathway. Radicals such as Au(0) and S^• are unstable in solution and so cannot be brought together by long-range preassembly, but their involvement in the observed processes is understandable. However, whether or not Au(I)–thiolate species are present can be investigated by synthesizing the ions and bringing them together. Thiolate ions in alkaline media or in solvents that do not allow acid–base reactions are well-characterized stable chemical species. Au(I) ions (in their d¹⁰s⁰ ground state) can be made by, say, oxidizing gold electrodes. Both processes have been activated simultaneously using preparative electrochemistry in acetonitrile (78), using the anode and cathode reactions

$$\begin{array}{l}\text{Au}\left(\text{solid}\right)\hspace{0.17em}\to \hspace{0.17em}{\text{Au}}^{+}\left(\text{soln}\right)+e^{-}\\ \text{RSH}\left(\text{soln}\right)\hspace{0.17em}+\hspace{0.17em}{e}^{-}\to \hspace{0.17em}{\text{RS}}^{-}\left(\text{soln}\right)+\frac{1}{2}{\text{H}}_2\left(\text{gas}\right)\end{array}$$. [4]

This allows Au⁺ and RS⁻ to meet and react in the solution. If SAMs are made of Au(I)–thiolates, then the SAM constituents have been preprepared, optimizing conditions for SAM production. Such a reaction is therefore envisaged as occurring under mild conditions and hence would be expected to be facilitated near the gold surface. Alternatively, if the SAMs are as depicted by structure 2a, then when Au⁺ and RS⁻ ions meet they start on the high-energy excited-state Au(I)–thiolate potential energy surface, resulting in an exothermic reaction. Such a reaction would be expected to occur in solution and not need to be activated by the gold surface. Experimentally, what is observed is the solution reaction (78)

$${\text{Au}}^{+}{\left(\text{soln}\right)\hspace{0.17em}+\hspace{0.17em}\text{RS}}^{-}\left(\text{soln}\right)\hspace{0.17em}\to \hspace{0.17em}\text{AuSR}\left(\text{film}\right),$$ [5]

and the resulting Au(I)–thiolate film then precipitates onto the gold electrode. The experimental reaction conditions are optimized to etch gold surfaces to make thin films rather than to form protective SAMs, as expected if the SAM structure is 2a; instead, the Au(I)–thiolate model of the SAM predicts that the reaction conditions were optimized for SAM production.

The known chemistry of gold nanoparticle formation leads to the same conclusions. Nanoparticles can be formed under very mild conditions such as via the reduction of Au(III) ions by citrate as in the classic Turkevich reaction (79–81) or even by thiols, e.g., by reactions in aqueous solution (82) of the form

$$(6m+2n)\text{RSH}+2m{\text{Au}}^{3+}\hspace{0.17em}\rightleftarrows {\hspace{0.17em}2\text{Au}}_m{\left(\text{SR}\right)}_n+3m\text{RSSR}+6m{\text{H}}^{+}+n{\text{H}}_2,$$ [6]

in which the thiol reductant is sufficient to reduce Au(III) all of the way to Au(0) (82):

$${6\text{RSH}+2\text{Au}}^{3+}\hspace{0.17em}\rightleftarrows {\hspace{0.17em}2\text{Au}}^0+3{\text{RSSR}+6\text{H}}^{+}.$$ [7]

However, under different conditions such as those used in the Brust–Schiffrin synthesis (83), the reaction proceeds through the formation of Au(I)–thiolate intermediary compounds and films (84) and involve much stronger reducing agents. In the original synthesis (83), p-mercaptophenol was used as the thiol, and it was found that acetic acid was needed to be added to the reaction mixture to prevent reduction of the phenol by NaBH₄, a difficult process as the thiol must be reduced first (85) so the product is a dianion dissolved in a solvent of 5:1 methanol:water. If this phenol can be reduced then under similar conditions it is likely that aliphatic thiols could also be reduced, but in such reactions acid is rarely added to the mixture and so thiolate anions would be produced in solution. Au(I) species can be observed also in the reaction mixture, hence classic Brust–Schiffrin reactions would then result in the prepreparation of Au(I) and RS⁻ species in solution. If these react during nanoparticle synthesis as they are known to do during electrochemical etching experiments in aprotic solvents (78), then Au(I)–thiolate molecular compounds or films would be expected to form. Indeed, such species are observable and can be isolated, characterized, and subsequently converted to nanoparticles (84) using conditions compatible with those used in direct syntheses.

Identification of Thiolate Anions as Intermediates During Brust–Schiffrin Synthesis

Rationalization of known chemistry of gold surface reactions and nanoparticle formation reactions thus leads to the prediction that thiolate anions are intermediated during Brust–Schiffrin synthesis. This hypothesis is verified spectroscopically (Supporting Information), exposing hexanethiol to Brust–Schiffrin reaction conditions in the absence of the Au(III) reagent. Conversion of hexanethiol to hexanethiolate is observed by noting that the changes in the molecules’ UV absorption spectrum match those produced by base hydrolysis, monitoring the disappearance of the SH Raman band. Therefore, the formation of thiolate anions can result not only from ionization of the SH group by alkaline media [the pK_a of hexanethiol is 10.4 (86)] but also from the direct reaction of borohydride with the thiol group to yield H₂ and the thiolate anion, as is known also to occur with metal hydrides (see ref. 87 and references cited therein). The stability within the time scale of the nanoparticle synthesis in methanol is sufficiently long to allow this route for thiolate formation (88).

To date the Brust–Schiffrin synthesis has been applied over 4,000 times, yet detailed aspects of the mechanism remain unknown, and the situation is similar for alternate thiol-based nanoparticle synthesis methods such as those using aqueous solution. Understanding the nature of nanoparticle stabilization through structure 2a has thus led to the discovery of an important intermediate species. This leads to an understanding of the conditions required for nanoparticle synthesis: if the reaction conditions are aprotic and are sufficiently reducing to enable thiolate anion production in solution, then nanoparticle formation proceeds via Au(I)–thiolate intermediary compounds that require further reduction before nanoparticles form; alternatively, if the reaction conditions inhibit thiolate formation, then the nanoparticles form directly through reactions with thiols.

Nature of the Bonding Revealed Through Other Chemical Processes

Chemical substitution of the bridge-head carbon atom can also be used to differentiate between the possible valence states. Ligand exchange reactions on nanoparticles are known to proceed with thiol reactants and products (1). Many different mechanisms for this process have been found, including adsorption of the incoming species at defect sites followed by place exchange, as well as direct SN2-type ligand replacement (76, 89, 90). The SN2-type processes would be expected to involve a radical mechanism that includes hydrogen transfer between the incoming and outgoing thiol ligands and is the most obvious interpretation of the available data, whereas an Au(I)–thiolate description of the bonding would demand that proton loss and recapture occur independent of the SN2 reaction and is difficult to reconcile with the used experimental conditions (90). Moreover, that ligand exchange reactions can be performed at all indicates that the energetics of SAM and nanoparticle formation are only weakly dependent on the nature of nonchemically active ligands. This principle is in direct contrast to that expected for Au(I)–thiolate structure 2c as the latter depicts the bonding as arising from cancellation of large chemical forces driving ionic and covalent bonding, opposed by the Au d⁹s¹ promotion energy. Hence even small effects on the binding caused by chemical substitution are expected to affect profoundly the net interaction, contrary to observation. Misinterpretation of very strong van der Waals forces as chemical bonds formed between high-energy states has been common for related systems such as benzene on Cu(110) as well (91).

Conclusions

The usual classification scheme that labels AuSR-type molecules and materials as d¹⁰s⁰ Au(I)–thiolates is inappropriate to describe the bonding of sulfur compounds to gold surfaces and nanoparticles as it ignores the critical role of Au s to Au s interactions (supported by Au–S–Au superexchange) that passivates gold surface atoms and adatoms to give them noble character. This description also ignores the important effects of aurophilicity in determining the binding. Aurophilicity is the van der Waals force that provides a strong attraction between different gold atoms, which, by its nature, demands similar strong interactions between gold and other polarizable atoms such as sulfur.

Because gold surfaces and the surfaces of large nanoparticles are noble, chemisorption must be considered in terms of the interaction of the S p electron with a pair of Au d electrons, making the gold electronic configuration of an Au(I)–thiolate species d⁹s¹. Species need to be characterized in terms of either this limiting form or else its alternate, nonbonded Au(0)–thiyl. All DFT calculations, supported by a wide range of spectroscopic, chemical, and electrochemical observations, indicate that the valence state of gold–sulfur interfaces is Au(0)–thiyl. The bond strength arises from a combination of the large van der Waals attraction energy akin to the aurophilic attraction, combined with perturbatively added chemisorption character arising from polarization effects and s–d hybridization effects.

The interpretations presented historically for DFT calculations and experimental results do not always conform to this description, however, and these reports need to be reinterpreted from this fully general perspective. In particular, the often-used description of gold–sulfur adatom complexes as “staples” (92)

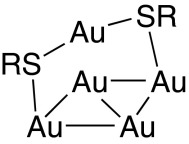is misleading and should be discontinued; this description depicts the gold–sulfur bonding topology only and ignoring the critical gold–gold bonds. Even though these bonds are very malleable, they still contribute strongly to adatom-complex bonding, passivating the adatom s electrons to reduce the net gold–sulfur bonding strength. Superexchange interactions are critical not only because they lead to gold–gold interactions through intervening sulfur but also because they lead to sulfur–sulfur interactions through intervening gold.

For bonding in different configurations, a simple relationship is found linking the connectivity of particular atoms with the bulk to the amount of s character retained in the bonding and hence to the bond strength. A wide variety of phenomena are controlled by this effect including nanoparticle size control and STM break-junction measurements. The Au(0)–thiyl surface-bonding description allows for a consistent treatment of physisorption and chemisorption, linking smoothly to the properties of both established Au(I)–thiolate molecular compounds, of interfaces in which O, Se, Te, N, and C replace S, and of the aurophilic effect. Most significantly, it also explains how, when conditions are optimized to make Au(I)–thiolates, bare gold surfaces are etched while nanoparticles are not formed. It predicts the production of thiolate ion intermediated during Brust–Schiffrin synthesis, a feature then confirmed by experimental observation.

Interpretation of the DFT Calculations Used to Understand Spectroscopic NEXAFS Measurements of SAM Structure

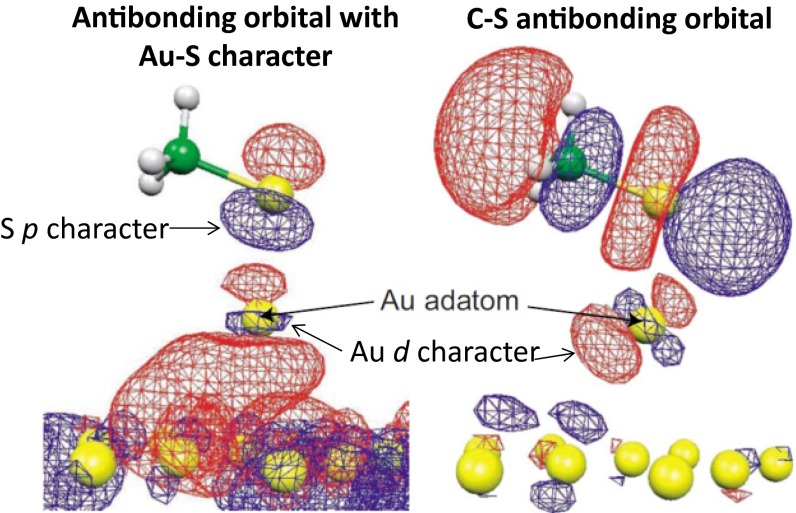
The most fundamental difference between the nonbonded description 2a and the most feasible Au(I)–thiolate description 1b is the orbital occupancy. Spectroscopic near-edge X-ray absorption fine structure measurements of SAMs provide a direct probe of this occupancy, and results from DFT calculations have successfully been used to interpret the experiments. Fig. S1 reproduces DFT virtual orbitals identified as being intrinsically involved in two observed transitions, taken from the calculations of Chandhuri et al. (19). These results are important as bond vectors can be deduced from the observed polarization information that reveal well-established features of adatom-bound structures, indicating both the strength of the experimental spectral assignment and the quality of the DFT results.

Fig. S1.

Key unoccupied orbitals from DFT calculations associated with observed NEXAFS spectroscopic transitions in CH₃S SAMs. The transition to the low energy orbital shown on the left is predicted for an Au(0)–thiyl structure but forbidden for Au(I)–thiolate. Adapted with permission from ref. 19.

Fig. S1 shows two unoccupied orbitals identified as the destination orbitals for electrons involved in two key spectroscopic transitions. The orbital shown to the right is a C–S antibonding orbital and that on the left has a lot of gold surface character. Of interest is the nature of the adatom–sulfur interaction as revealed by these key orbitals. In both cases, adatom d orbitals are mixed into the wavefunctions. This indicates that the bonding between sulfur and gold is dominated by the gold d orbitals and hence only structures 2a–2c can be used to describe it. The orbital on the left has significant gold–sulfur antibonding character also. This character is anticipated for unoccupied orbitals by the Au(0)–thiyl description 2a but for occupied orbitals by Au(I)–thiolate description 2c. If this orbital is occupied then the observed transition should have been forbidden. The only possible interpretation of the DFT orbitals is that the interface electronic structure is dominated by 2a.

Spectroscopic Observation of Thiolate Ions Formed Under Brust–Schiffrin Reaction Conditions

Interpretation of the electronic structure of gold–sulfur bonds protecting nanoparticles and surfaces led to a simple way of understanding different reaction conditions used in nanoparticle synthesis and observed intermediate species during the reactions. Central to this is the prediction that under typical reaction conditions, thiol reagents can be reduced by the NaBH₄ reductant to form thiolate anions. The nanoparticle formation reaction may proceed whether or not acid is added to the reaction but by different mechanisms. Interest primarily concerns aliphatic thiols as they are much more difficult to reduce and deprotonate than are aromatic ones, with aromatic alcohols and aliphatic thiols having similar properties [e.g., phenol pK_a = 9.95, thiophenol pK_a = 6.62, alkanethiols pK_a ∼10–12, reduction potential difference (85) between phenol and thiophenol = 0.3 V]. Hence we focus on hexanethiol reactions. The primary aim is to demonstrate that, under conditions similar to those used in Brust–Schiffrin reactions, thiol to thiolate reduction occurs. This is demonstrated for the limiting case in which no Au(III) reagent is added to the reaction, preventing nanoparticle formation to allow steady-state concentrations of thiolate to be measured.

Neglecting the acetic acid, the conditions of the original Brust–Schiffrin synthesis were: thiol concentration 0.01 M, NaBH₄ concentration 0.067 M (large excess), and Au(III) concentration 0.0042 M, the solvent being 5:1 methanol:water (46). These conditions are troublesome for spectroscopic measurements as the thiol concentration is too high to permit UV absorption measurements yet too low to permit Raman measurements and so some order-of-magnitude variations are introduced.

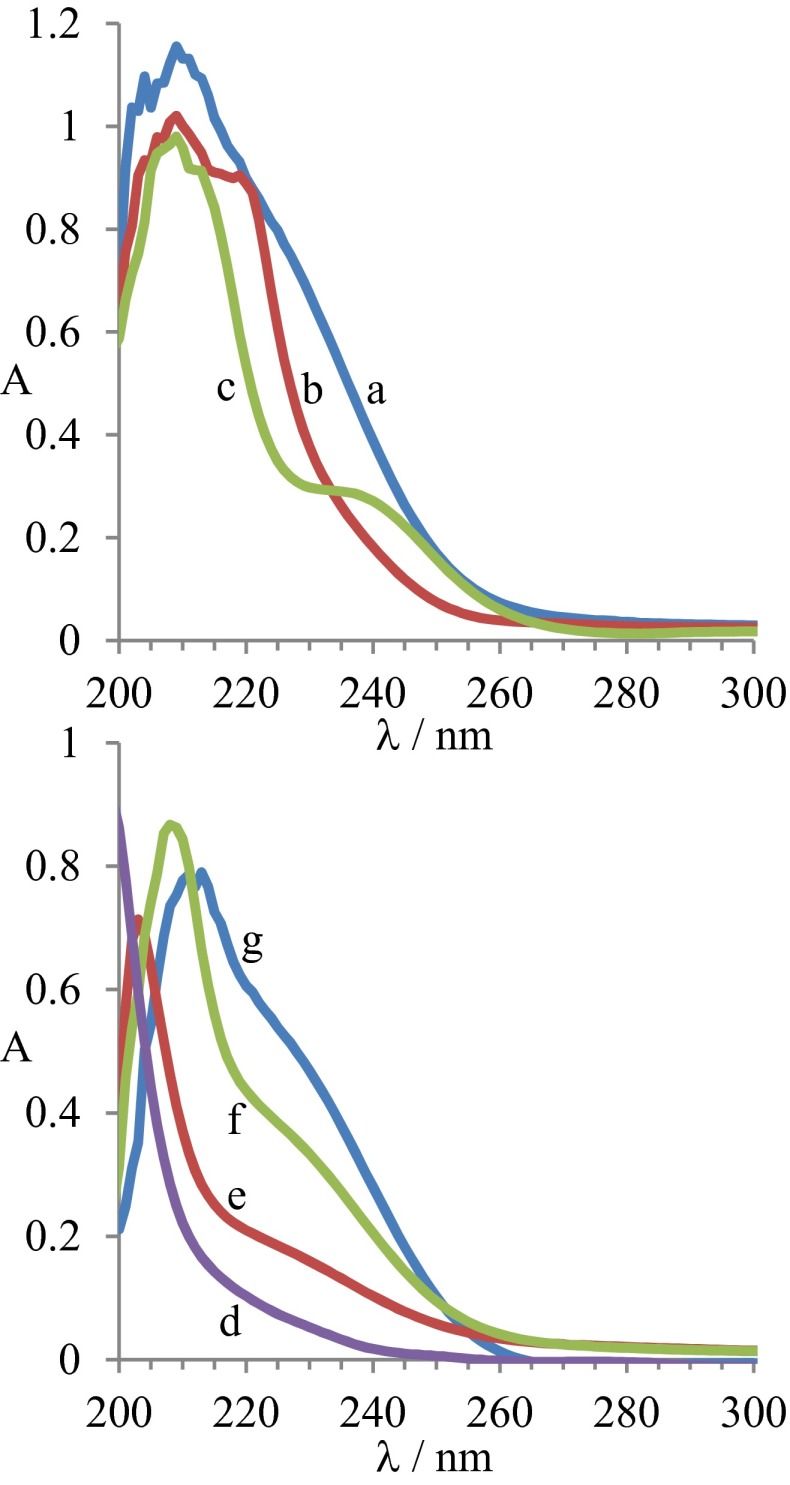
Fig. S2A shows the UV spectrum of 0.00067 M hexanethiol in 5:1 methanol:water, while Fig. S2 B and C show this after the addition of 0.0167 M NaBH₄ and 0.0011 M NaOH, respectively. Before reaction, hexanethiol has an absorption near 240 nm that becomes shifted to 220 nm after addition of the reducing agent and to 214 nm after addition of the base. Time-dependent density-functional calculations (93) using the CAM-B3LYP density functional (94) with the 6–311++G** basis set representing the solvent as methanol using a self-consistent reaction field predict that the lowest energy transitions are at 235 nm for hexanethiol and 223 nm for hexanethiolate, suggesting that the thiolate can be produced through both acid–base and electrochemical reactions.

Fig. S2.

UV absorption spectra of hexanethiol solutions; (A) 0.00067 M hexanethiol in 5:1 methanol:water; B is A after addition of 0.0167 M NaBH₄. C is A after addition of 0.0011 M NaOH; D pure methanol; G 0.0047 M hexanethiol in methanol, using D as a reference. E is G after addition of 0.01 M NaBH₄; and F is G after addition of 0.01 M Na.

The robustness of this process is demonstrated by Fig. S2 C–G, showing these and related reactions in pure methanol. Fig. S2D is the spectrum of pure methanol. Although this is subtracted from the subsequent spectra using standard dual-beam technology, it indicates that data below 205 nm is not reliable. Fig. 2G shows the spectrum of 0.0047 M hexanethiol in methanol, although Fig. 2 E and F show this after the addition of 0.01 M NaBH₄ and 0.01 M Na, respectively. The spectra indicate that both borohydride and metallic sodium react with hexanethiol in pure methanol under conditions related to those used in Brust–Schiffrin syntheses. That the reaction occurs with sodium metal supports the hypothesis that the reaction involves thiol reduction to thiolate.

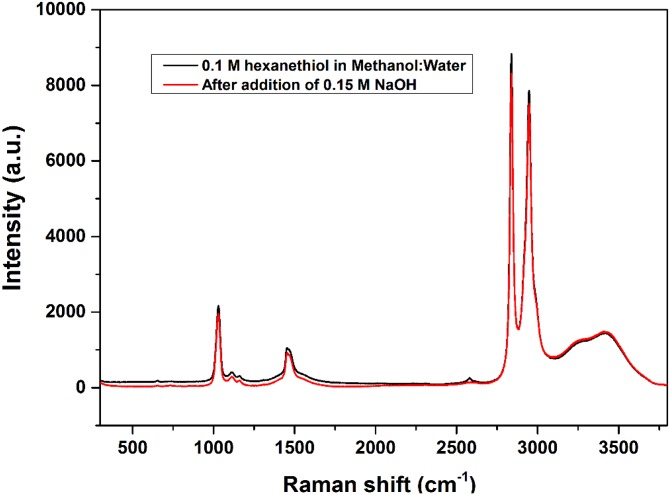
Fig. S3 shows Raman spectra of 0.1 M hexanethiol in 5:1 methanol:water before and after addition of 0.15 M NaOH. Before the base is added, a clear signal is seen corresponding to the SH stretch at 2,580 cm⁻¹, but this signal is lost after reaction. This indicates completion of the anticipated acid–base reaction to produce hexanethiolate in solution.

Fig. S3.

Raman spectrum of hexanethiol before and after addition of excess NaOH.

Hexanethiolate is therefore stable under a range of solvation conditions and can be produced by base attack or by borohydride or sodium reduction. Under typical conditions used for the Brust–Schiffrin synthesis, hexanethiol is therefore expected to be reduced to hexanethiolate.

All of the chemicals (at least of analytical grade) were supplied by Sigma‐Aldrich or Fluka and used as received. The UV-VIS spectra were recorded by Agilent 8453 UV-visible spectroscopy system. The Raman spectra were recorded on a specialist spectrometer at The Technical University of Denmark by built by Professor Rolf Willestofte Berg.