Abstract
Understanding stable patterns of interpersonal movement coordination is essential to understanding successful social interaction and activity (i.e., joint action). Previous research investigating such coordination has primarily focused on the synchronization of simple rhythmic movements (e.g., finger/forearm oscillations or pendulum swinging). Very few studies, however, have explored the stable patterns of coordination that emerge during task-directed complementary coordination tasks. Thus, the aim of the current study was to investigate and model the behavioral dynamics of a complementary collision-avoidance task. Participant pairs performed a repetitive targeting task in which they moved computer stimuli back and forth between sets of target locations without colliding into each other. The results revealed that pairs quickly converged onto a stable, asymmetric pattern of movement coordination that reflected differential control across participants, with 1 participant adopting a more straight-line movement trajectory between targets, and the other participant adopting a more elliptical trajectory between targets. This asymmetric movement pattern was also characterized by a phase lag between participants and was essential to task success. Coupling directionality analysis and dynamical modeling revealed that this dynamic regime was due to participant-specific differences in the coupling functions that defined the task-dynamics of participant pairs. Collectively, the current findings provide evidence that the dynamical coordination processes previously identified to underlie simple motor synchronization can also support more complex, goal-directed, joint action behavior, and can participate the spontaneous emergence of complementary joint action roles.
Keywords: joint action, movement coordination, task-dynamics, perception-action
Many of our physical actions and movements are performed together with other individuals and can be characterized as interpersonal or joint actions.1 Although there is a growing body of research investigating the neural and cognitive mechanisms that play a role in joint action (e.g., Bekkering et al., 2009; Gallese, 2003; Graf, Schütz-Bosbach, & Prinz, 2009; Newman-Norlund, Noordzij, Meulenbroek, & Bekkering, 2007; Vesper, Butterfill, Knoblich, Sebanz, 2010), identifying the dynamical processes of motor coordination by which individuals are mutually responsive to one another in time and space is also crucial to understanding such behavior (Schmidt, Fitzpatrick, Caron, & Mergeche, 2011; van der Wel, Knoblich, & Sebanz, 2011; Vesper, van der Wel, Knoblich, Sebanz, 2013). Indeed, the dynamics of interpersonal motor coordination appear to provide the fundamental structure for joint activity by forming the embodied context for shared intentions (e.g., Coey, Varlet & Richardson, 2012; Marsh, Richardson & Schmidt, 2009; Oullier & Basso, 2010; Sebanz & Knoblich, 2009). Moreover, stable motor coordination can increase rapport and cooperation between individuals (Hove & Risen, 2009), reduce perceived social differences and prejudice (Miles, Lumsden, Richardson, & Macrae, 2011), and has been shown to break down in pathologies such as premature birth, autism, and schizophrenia (Goldfield, Richardson, Lee, Margetts, 2006; Fitzpatrick, Diorio, Richardson & Schmidt, 2013; Varlet et al., 2012).
Given the importance of understanding the dynamics of joint coordination, it is perhaps surprising that the majority of the existing research has only investigated the presence of these dynamic processes in tasks in which intentional or unintentional coordination was observed between highly stereotyped or non-functionally directed oscillatory limb or body movements (e.g., finger/forearm oscillations, pendulum swinging; e.g., Oullier, De Guzman, Jantzen, Lagarde, & Kelso, 2008; Richardson, Marsh, & Schmidt, 2005; Schmidt, Carello, & Turvey, 1990; Schmidt & O’Brien, 1997).2 The significance of this research is that it demonstrates that the rhythmic movements of informationally coupled individuals are dispositionally constrained to inphase (a stable 0° relative phase relation) and antiphase (a stable 180° relative phase relation) patterns of one-to-one behavioral synchrony,3 and can be understood and modeled using the same coupled oscillator dynamic known to underlie intrapersonal interlimb coordination (see Kelso, 1995; Schmidt & Richardson, 2008 for a review). Although pertinent to understanding the coordination dynamics of the spontaneous movement synchronization that occurs, say between the leg movements or full-body movements of two individuals while walking or sitting side-by-side (e.g., Harrison & Richardson, 2009; Richardson, Marsh, Isenhower, Goodman & Schmidt, 2007; van Ulzen, Lamoth, Daffertshofer, Semin, & Beek, 2008; Varlet, Marin, Lagarde, & Bardy, 2011), the extent to which the conclusions drawn from these interpersonal coordination studies can be generalized to more natural joint actions remains to be determined. Everyday joint actions typically require that coactors coordinate goal-directed movements in a complementary manner, such that each actor adopts a different action role to jointly accomplish the task at hand (Bosga, Meulenbroek, & Cuijpers, 2010; Graf et al., 2009). In other words, the mutual responsiveness or spatial-temporal patterning of coactors’ movements (i.e., who does what and when) is often asymmetric rather than symmetric.4 Furthermore, natural joint actions are often nonstationary and adaptive, with a temporal and spatial patterning evolving in real time as the interaction between the coacting agents and their environment unfolds (Sebanz & Knoblich, 2009). Accordingly, the current study investigated the dynamics of a more complex joint action rhythmic coordination task, in which individuals had to perform goal-directed movements without colliding into one another.
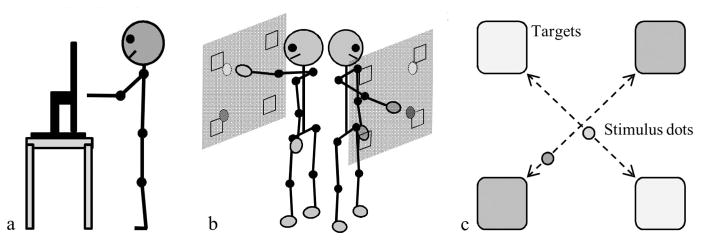
A continuous repetitive targeting task with a collision-avoidance requirement was chosen and is illustrated in Figure 1. The task required a pair of participants to continuously and repetitively move computer stimuli (visual stimulus dots) back and forth between diagonally opposed target locations (i.e., bottom-left to top-right for one participant, bottom-right to top-left for the other participant) at a comfortable, self-paced tempo without the stimuli colliding into each other. The stimulus display (i.e., targets and controlled stimuli) was presented to participants on large computer monitors and participants used a hand-held motion-tracking sensor to control and move the stimuli back and forth between their respective target locations (see the Method section below for more details). This task was chosen because many joint actions involve the continuous production of repetitive movements over time. For instance, the same or similar movements are performed in a repetitive manner when two individuals are loading a dishwasher, stacking a pile of blocks or magazines, dancing, or fighting together. These social activities, however, do not involve the incidental inphase or antiphase movement synchronization that has been the focus of the majority of previous studies of social coordination. On the contrary, they require that individuals explicitly avoid colliding into each other and establish a more complex or complementary pattern of movement coordination—since prototypical inphase or antiphase coordination patterns can often be detrimental to task performance. In a similar fashion, the current task was designed so that prototypical inphase or antiphase patterns of movement coordination would result in task failure. More specifically, if both participants were to move in a straight-line path between targets, then their stimulus dots would collide if they coordinated in an inphase or antiphase manner because they would pass the position located equal distance from their respective target locations at the same time (i.e., their stimulus dots would cross the center of the task space at the same time). This can be discerned from an inspection of Figure 1c. It is important to appreciate that because the target locations that each participant had to move back and forth between were positioned near the ends of the workspace’s major diagonal axis (for one participant) and minor diagonal axis (for the other participant), inphase and antiphase coordination can only be defined arbitrarily. That is, synchronously arriving at the top and bottom targets together or synchronously arriving at the left and right targets together can both be considered to define either “inphase” or “antiphase” patterns of coordination.
Figure 1.
Representations of the experimental setup for each (a) individual in a pair and (b) for the pair together, as well as for the (c) task display.
The implication of designing the task such that straight-line inphase coordination would result in failure (i.e., collision) was that the task entailed a conflict between the natural tendency of coactors to coordinate their movements in a synchronous manner (e.g., Richardson et al., 2007; Richardson, Campbell, & Schmidt, 2009; Schmidt & O’Brien, 1997) and the task goal of avoiding collision. A natural question, therefore, is how would the task be completed? What, if any, stable patterns of movement coordination would ensure task success? One task solution would be for participants in a pair to maintain straight-line trajectories between their respective targets, but coordinate their movements with a non-0° or non-180° phase relation. For example, a 90° relative phase relation, with one participant moving a ¼ cycle in front or behind their coparticipant (here the term cycle refers to a single back and forth movement; e.g., a participant going from their bottom target to their top target and then back to their bottom again). Thus, when one participant was arriving at a target location the other participant would be midway between target locations. It is well known, however, that for rhythmic or repetitive movement tasks a 90° relative phase relation (or any non-0° or non-180° relative phase relation) is inherently unstable and therefore quite difficult to learn and maintain (e.g., Haken, Kelso, & Bunz, 1985; Kelso, 1995; Zanone, & Kelso, 1992). We therefore expected that it would be more likely for one or both participants to deviate from a strict straight-line path and converge on a set of more elliptical movement trajectories that minimized the chance of a collision (i.e., created a path of safe travel) but that, at the same time, also allowed subjects to move between or arrive at the target locations in a synchronous (i.e., inphase) manner. In truth, the novelty of the repetitive collision avoidance task employed here precluded making a specific a priori prediction about the kinematic details of this movement pattern (i.e., because the task solution space is too large). However, we did expect that participant pairs would quickly learn to perform the task effectively and would converge onto a stable pattern of behavior. Of particular interest was (a) whether all participant pairs converged on the same spatiotemporal pattern of behavioral coordination (task solution) and (b) what, if any, complementary roles emerged during stable task performance.
Method
Participants
Twelve pairs (24 participants in total) of undergraduate students from the University of Cincinnati participated for partial course credit. All participants were right-handed and had normal or corrected-to-normal vision. All of the procedures and data collection tools employed for the current study were approved by the University of Cincinnati IRB.
Materials
Each participant in a pair stood facing a 50-inch computer monitor (operating at a 60-Hz refresh rate), with the screens positioned so that participants were back-to-back and could not see each other (see Figure 1a and 1b). The stimulus controlled by each participant was a small red dot 3.5 cm in diameter. The targets were 10 cm squares and were positioned in each of the four corners of the monitor, with one participant moving their stimulus between the bottom-left and top-right target set, and the other participant moving their stimulus between the bottom-right and top-left target set (Figure 1c). A Polhemus FASTRACK magnetic motion tracking system was used to record and track the movements of each participant at 60 Hz. Participants held a 1.5 × 2 cm motion-tracking sensor in their dominant (right) hand to control their stimulus. Each monitor displayed the real-time motion of the participant’s own stimulus and targets, as well as the real-time motion of their coparticipant’s stimulus and targets. That is, the data from the Polhemus motion tracking sensors was used to control the stimulus in real-time. A custom C/C++ program, using the OpenGL graphics library, was written to present the stimuli and record the data from the motion tracking sensors. The data collection stream was synchronized with the refresh rate of the monitor (i.e., 60 Hz); hence, the delay between the participants arm/hand movements and the controlled visual stimulus dot was less than or equal to 16.66 ms. Stimulus collisions were deemed to have occurred if any part of the participants’ stimuli would have overlapped as a function of the current and previous two sample locations. Extensive pilot testing was completed to verify the accuracy of data collection and collision detection.
Procedure
Participants were informed that the experiment was investigating multiperson rhythmic coordination and that each of them would be required to move a computer stimulus continuously between two sets of targets while not letting their stimuli collide. Following these brief instructions, the participants were positioned in front of their respective monitor, handed their motion sensors, and randomly assigned to a target pair along either the major or minor diagonal axis of the monitor. Each participant then completed a 40-s practice trial alone, in which they were instructed to “move their stimulus back and forth between their target locations continuously and at a comfortable speed.” During these practice trials, the participant who was not moving their stimulus closed their eyes and placed their hands by their sides.
After completing the practice trials, participants were informed that they were to begin the joint coordination task. Participants were instructed to start each trial at their bottom target and that “the goal of the task is to move your stimulus back and forth between your target locations continuously and at a comfortable speed and to coordinate your movements with each other so that your stimuli do not collide, hit, or bump into each other.” No other instructions as to the pattern or form of the coordination were provided. Participants were also told to not converse during the experiment. Once participants indicated that they understood the task instructions, they were informed that the trial-by-trial procedure was designed as a game. Specifically, they were told that if they continuously moved between their respective targets without their stimuli colliding into each other for the entire length of a trial—40 seconds—they would receive 1 point and that the experiment would end when they reached a score of 15 points. After completing 15 successful trials, participants were debriefed and thanked for their cooperation.
Data Reduction and Processing
One pair was unable to complete the task within the allotted time for the experimental session (40 minutes)—only reaching a score of 7 of 31 trials—and was therefore dropped from the analysis. The data from the last successful trial (i.e., Trial 15) of another pair was also dropped due to equipment malfunction. Thus, there were a total of 164 successful trials completed by participant pairs. On average, the 11 pairs retained for analysis took 21 trials to reach a score of 15 (range 15–36 trials, median = 19), with 8 of the 11 pairs reaching a score of 15 in less than 22 trials (i.e., 7 or fewer failed trials). Given the relatively small number of failed trials, compared to successful trials, and the fact that 69% of failures occurred within the first 20 s of a trial (mean failure time of 14.65 s), only data from successful trials were analyzed.
Prior to analysis, movement time-series from successful trials were low-pass filtered using a 10 Hz Butterworth filter and the first 5 s of each trial was removed to eliminate startup movement transients. The movement and coordination patterns that emerged during successful task completion were determined using (a) movement frequency analysis, (b) principal components analysis, (c) measures of relative phase; and (d) coupling directionality (see below for more details).
Results
Movement Frequency
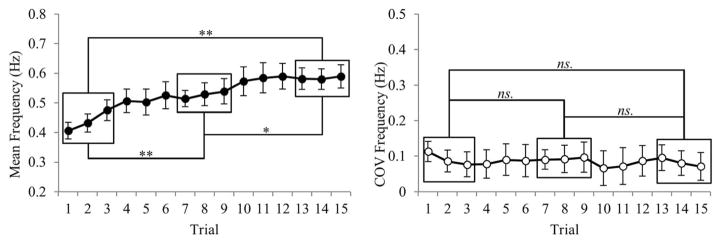
For each participant on each trial, average movement frequency was computed separately for the x (horizontal/frontal plane) and y (vertical/sagittal plane) movement time-series as the average of the sequence of inverse peak-to-peak durations in the respective x and y time series. An inspection of these movement frequencies revealed that there was no meaningful difference between the movement frequencies of participants’ x and y time series (Mean difference = 0.004 Hz), nor was there a meaningful difference between the movement frequencies of coparticipants on a given trial (Mean difference = 0.005 Hz). Thus, the mean and COV (i.e., the coefficient of variation of movement frequency = SD of movement frequency normalized by the mean movement frequency) for each pair on each trial was calculated as the average of the coparticipants’ pooled sets of movement frequencies from both the x (horizontal/frontal plane) and y (vertical/sagittal plane) movement time-series. As can be seen from an inspection of Figure 2, in which the across-pair mean and COV of frequency are plotted as a function of trial, participant pairs increased their frequency of movement across trials from approximately 0.4 Hz for the first trial to approximately 0.58 Hz in the 15th trial, while maintaining the same magnitude of frequency variability. To determine whether the changes in the mean and COV of movement frequency over trials were significant, the difference between the data averaged within the first, middle, and last three trials (i.e., Trials 1–3, 7–9, and 13–15, respectively) was compared using a one-way repeated measures ANOVA. This analysis revealed a significant difference in mean frequency, F(2, 20) = 47.22, p < .01, , across trial blocks, but no difference in the COV of frequency, F(2, 20) < 1. With respect to the former mean frequency analysis, Bonferroni post hoc tests revealed that the first, middle, and last trial blocks were all significantly different from each other (ps < .02).
Figure 2.
Across-pair mean and COV of movement frequency as a function of trial. Error bars indicate standard error of the mean (* p < .05; ** p < .01; ns. p > .05).
Principal components analysis (PCA)
PCA was conducted on the movement data from each trial as a whole (i.e., not to each individual movement cycle) and was used to calculate the normalized spread or width (δ) of each participant’s cyclic movement paths about the principal axis of movement. δ equals the ratio of the eigenvalues (λ) from the covariance matrix between a participant’s x (horizontal/frontal) and y (vertical/sagittal) data (i.e., δ = λ2/λ1). As a normalized ratio of the excursions perpendicular to the principal axis of motion, δ provides a measure of movement “straightness” or “spread” relative to the angular direction of motion (Duarte & Zatsiorsky, 2002). For the current data, the larger the value of δ, the greater the deviation from a straight-line trajectory between targets (i.e., the more elliptical a participant’s movements).
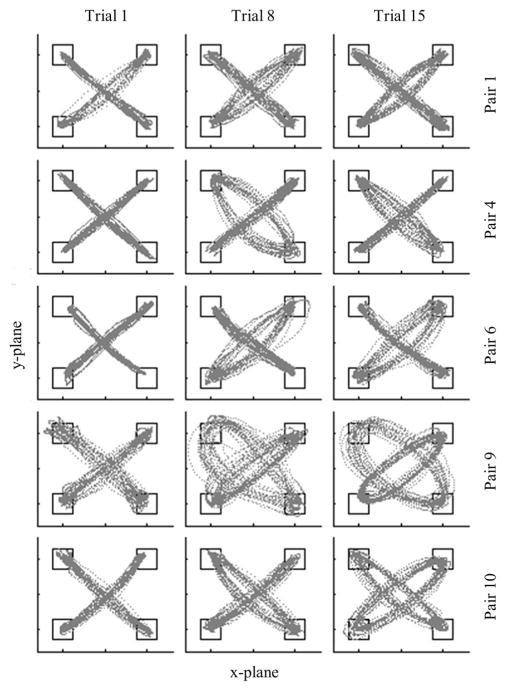
The importance of δ for understanding the movement patterns adopted by participants to successfully perform and complete the task can be seen from an inspection of Figure 3, in which the movement time-series trajectories for Trials 1, 8, and 15 for five different pairs of participants are displayed. The data is a representative sample of the movement patterns observed across all pairs and captures the characteristic changes in the trajectories of participants from the first to the last successful trial. Two distinct features of the movements displayed in Figure 3 should be noted.
Figure 3.
Example movement data. Trials 1, 8, and 15 for five different pairs.
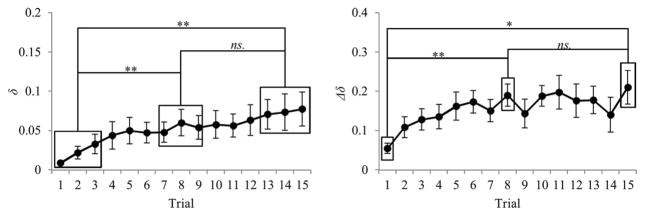
First, one or both participants in a pair tended to adopt a more elliptical or oval movement trajectory over the course of the experiment, particularly within the first ½ of the successfully completed trials. A one-way repeated measures ANOVA comparing pairs’ mean δ for the first, middle, and last blocks of trials was significant, F(2, 20) = 8.40, p < .01, , with Bonferroni post hoc tests revealing that the first trial block was significantly lower (i.e., less elliptical movement paths) than the middle and last trials blocks (both p < .05; see Figure 4, left panel).
Figure 4.
Mean δ and Δδ as a function of trial. Error bars indicate standard error of the mean (* p < .05; ** p < .01; ns. p > .05).
Second, one participant in a pair tended to adopt a greater degree of movement ellipticality than their coparticipant. The differentiation of participants with respect to the degree of elliptical motion can also be identified from an examination of the data in Table 1, in which the mean and SD of δ for each participant in a pair (averaged across trials) is reported along with the percentage of trials a given participant displayed a greater degree of elliptical motion than their coparticipant. Interestingly, not only did the participants within a pair adopt differing degrees of movement ellipticality across trials, but for nine of the 11 pairs, this movement trajectory differentiation remained constant or increased across trials. An inspection of the data revealed that this interparticipant movement differentiation occurred for most pairs within the first five trials and remained that way for the remainder of the experimental session. For the two pairs in which the participants exhibited an approximately equal number of trials with a greater magnitude of curvature (i.e., pair 7 and 10)—that is they switch between roles over the course of successful trials—it was still the case that on any given trial one participant adopted a more curvilinear motion between targets. It is also important to note that once differentiation occurred very few collision trials occurred for the remainder of the experimental session. In fact, nine of the 11 pairs had no more than five collisions (5 pairs had 0 or 1 collisions) after differentiation occurred. The other two pairs had six and 15 collision trials after differentiation respectively.
To further determine whether the increased interparticipant differentiation in movement ellipticality was a significant factor across trials, a δ difference score was calculated for each trial by taking the difference in δ between the participant with the straighter (less elliptical, smaller δ) trajectory δpS and the participant with the more elliptical (larger δ) trajectory δpE, (i.e., Δδ = δpE − δpS). The resulting Δδ scores are displayed in Figure 4 (right panel) and, although there was an increase in the between-pair variability of Δδ across trials, there was also a clear increase in Δδ. Although this increase in average Δδ was only found to be marginally significant between the first, middle, and last trial blocks, F(2, 20) = 3.02, p = .07, , a subsequent one-way ANOVA comparing Δδ for the single Trials 1, 8, and 15 was found to be significant, F(2, 20) = 4.552, p < .05, . For this latter analysis, Bonferroni post hoc tests revealed that Δδ for Trial 1 was significantly lower compared to Trial 8 (p < .01) and marginally lower compared to Trial 15 (both p < .095). There was no difference between Trial 8 and 15 (p > .95).
Relative phase analysis
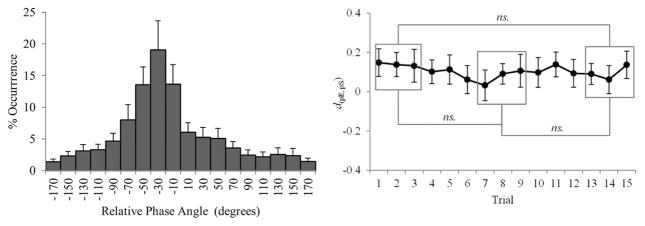
Given the PCA results, the relative phase, ϕ, of a pair’s movement was calculated with respect to the principal axis of each participant’s movements in the x–y plane (i.e., at each point in time, a participant’s actual cursor position was projected onto the diagonal between his or her designated targets) where the phase of the participant with the smaller value of δ (more straight-line: θpS) for the corresponding trial was subtracted from the phase of the participant with the greater value of δ (more elliptical: θpE), that is, ϕ = θpE − θpS. For each trial of each participant pair, we first computed a relative phase time-series between the principal axis movement of pairs. This was done by calculating the difference between the instantaneous phase angles of each participant’s movement along their principal axis using the Hilbert transform (see Pikovsky, Rosenblum, & Kurths, 2001 for details about this transformation). For each relative phase time-series, we constructed a frequency distribution of relative phases, or DRP, using all samples in the trial. The binning procedure for constructing each trial’s DRP consisted of assigning each sample to one of 18 20°-wide bins between 0° and 360° according to its relative phase value, and then dividing the number of samples in each bin by the total number of samples in the trial (see Richardson et al., 2005; Schmidt & O’Brien, 1997). We then computed a mean DRP across all pairs and trials in order to index the overall patterning of relative phase in the experiment. Phase-entrainment is indicated by a concentration of relative phase angles in a portion of the distribution. Given the way in which the relative phase time-series were calculated (i.e., ϕ = θpE − θpS; see above), negative relative phases correspond to the participant with the greater δ (δpE associated with the participant with a more elliptical trajectory) following the phase of the participant with the lower δ (δpS associated with the participant with a straighter or less elliptical trajectory).
What is apparent from an inspection of Figure 5 (left) is that, as expected, most participants did not coordinate in a canonical inphase pattern. Rather, the peak in the relative phase histogram was at −30°, indicating that, for the largest number of participant pairs, the participant who adopted the more elliptical movement trajectory (δpE) typically phase lagged the participant with the straighter or less elliptical movement trajectory (δpS) by approximately 10° to 40°. In other words, the participant who adopted the straighter movement path tended to be the phase-leader.
Figure 5.
(Left) Mean frequency distribution of relative phases (DRP). (Right) Index of coupling directionality, d(pE,pS). Error bars indicate standard error of the mean (* p < .05; ** p < .01; ns. p > .05).
Directionality of coupling
Finally, we estimated the directionality of the coupling between the participants using the evolution map approach proposed by Rosenblum and Pikovsky (2001; see also Rosenblum, Cimponeriu, Bezerianos, Patzak, & Mrowka, 2002). Briefly stated, the method provides a measure of the directionality of the coupling between two self-sustained oscillatory movements by estimating the ratio of the coupling terms from the phase angle time series of the movements (i.e., from θ1 and θ2). This coupling or directionality index, d(1,2), varies from + 1 in the case of unidirectional coupling (θ1 → θ2 only) to −1 in the opposite case (θ2 → θ1 only), with d(1,2) = 0 corresponding to symmetric bidirectional coupling (θ2 ↔ θ1). As with the calculations of relative phase above, the directionality index, d, was calculated for each trial with respect to the value of δ for that trial, with the phase angle time series of the participant with the greater value of δ (i.e., δpE) labeled as θpE, and the phase angle time series of the participant with the lower value of δ (i.e., δpS) labeled as θpS. The average d(pE,pS) values across participant pairs as a function of trial are displayed in Figure 5 (right). Interestingly, there was a small but consistent asymmetry in the coupling between θpE and θpS, with slightly positive d(pE,pS) values for each trial. There was no difference in d(pE,pS) between the first, middle, and last trial blocks, F(2, 20) < 1, and d(pE,pS) averaged across all trials was significantly different from zero, t(10) = 3.46, p < .01. This indicates that on any given trial the participant with the straighter trajectory, (θpS), drove the movements of the participant with the more elliptical trajectory, (θpE), more strongly than vice versa.
Dynamical Modeling
The results of the collision avoidance task investigated here revealed that pairs converged onto a stable relative phase relationship that averaged −30°, with one participant spontaneously adopting and maintaining a more straight-line trajectory between targets, and with the other participant in the pair adopting a more elliptical trajectory between targets. The deviation from straight-line trajectories (i.e., the appearance of ellipticality) can be interpreted as the recruitment of a movement degree-of-freedom orthogonal to the straight-line principal motion axis between targets. Indeed, if pairs attempted to move using straight-line trajectories, they nearly always collided or had to perform the task very slowly. As discussed in the Introduction, such ellipticality would be sufficient to avoid collisions while still allowing a canonical inphase relationship to be maintained between the participants’ principal motion axes. Therefore, why a noncanonical and typically difficult-to-perform noninphase relation emerged in addition to ellipticality as part of the interpersonal dynamic synergy that implemented the complementary task solution in which the symmetry of participants’ roles was broken.
The reason for the asymmetry and phase shift becomes apparent when one attempts to model the steady-state behavioral dynamics (Warren, 2006) for this collision avoidance task. Here we modeled the behavioral dynamics observed in this task using a simple task-dynamic model (Saltzman & Kelso, 1987), which captured the terminal movement objectives (goals) of the actors by means of a functionally defined task space that included the minimal number of relevant task dimensions (i.e., task variables or task-space axes) and a minimal set of task-dynamic equations of motion. We developed the model in three steps.
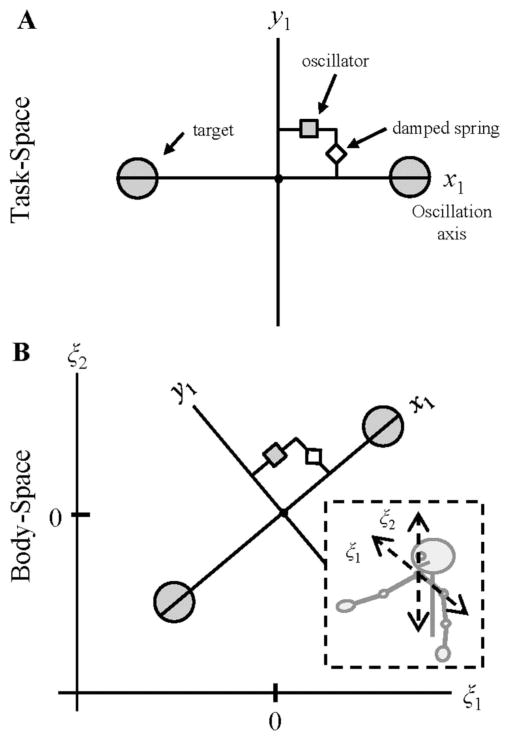
First, we defined the task space for a single participant. For this task, the actor was instructed to control and move a stimulus between two targets along a primary axis of motion (i.e., diagonally between two designated targets) using a motion sensor held to their hand. We modeled this task as one that involved oscillating a point-mass within a two-dimensional plane; the corresponding two-dimensional task space is illustrated in Figure 6. Axis x1 corresponds to the axis of instructed oscillation for the participant, using limit cycle dynamics to generate a self-sustained oscillation of the point-mass (endeffector) along this axis between the two targets. The orthogonal axis, y1, corresponds to deviations away from the oscillatory motion axis. Given that the most efficient path between a participant’s two targets is a straight-line trajectory along the primary motion axis, x1, a simple point-attractor dynamics (damped mass-spring equation) was used along y1 to minimize deviations away from the primary motion axis.
Figure 6.
(a) 2-dimensional task space for an individual instructed to perform a simple point-mass (end-effector) rhythmic movement task. (b) The 2-dimensional task space embedded at a 45° angle within a shoulder-centered, body-space coordinate system. For the task space, x1 corresponds to the axis of instructed direction of oscillation, with movement along this axis defined by a limit cycle oscillator. x2 corresponds to orthogonal deviations away from the principal movement axis, such that movement along the orthogonal axis can be defined by a simple damped mass-spring function. ξ1 and ξ2 correspond to the horizontal (frontal) and vertical (sagittal) dimensions of the task movements with respect to shoulder-centered body-space.
Assuming a point-mass of 1 (for simplicity), the dynamics in this functionally defined task space can be defined by the following set of motion equations:
| (1a) |
where x1 and y1, ẋ1 and ẏ1, ẍ1 and ÿ1 correspond to the position, velocity and acceleration of the end effector along each axis, respectively, kx1 and ky1 are stiffness coefficients for axis x1 and y1, respectively, bx1 and by1 are the damping coefficients for axis x1 and y1, respectively, and ( ) is the van der Pol (limit cycle oscillator) escapement function for axis x1. It is important to note that Equation 1a has been previously employed as an abstract task-dynamic model of rhythmic reaching between two target locations (Saltzman & Kelso, 1987).
Our second step was to extend Equation 1a to an interpersonal rhythmic coordination situation. This required: (a) the addition of a second system of equations to describe the task-dynamics of the second participant
| (1b) |
where x2 and y2, ẋ2 and ẏ2, ẍ2. and ÿ2 correspond to the position, velocity and acceleration of the point-mass along each axis for the second participant; and (b) a set of coupling functions to link the point-mass movements of the coactors. For the generalized rhythmic coordination task being captured here, this was achieved by adding the linear, dissipative coupling functions
| (2a) |
and
| (2b) |
to the equations that define each actor’s instructed axes of motion (i.e., x1 and x2). The reader should note that some previous models of rhythmic interpersonal coordination have employed a more complex coupling function, namely one that captures situations in which inphase and antiphase coordination reflect two nonarbitrarily defined, stable modes of coordination that differ in stability (i.e., the function captures the fact that inphase coordination is typically more stable that antiphase coordination)—as is the case in the Haken et al. (1985) model of rhythmic coordination (commonly referred to as the HKB model). Given the arbitrary nature of defining inphase and antiphase coordination for the current task (as discussed in the Introduction), we felt that the more complex HKB coupling function was not necessary to model the behavior under consideration in the present study. However, such coupling functions could easily be incorporated for other collision avoidance tasks in which inphase and antiphase movements can be nonarbitrarily defined.
The combination of Equations 1a and 1b with Equations 2a and 2b results in the coupled system
| (3) |
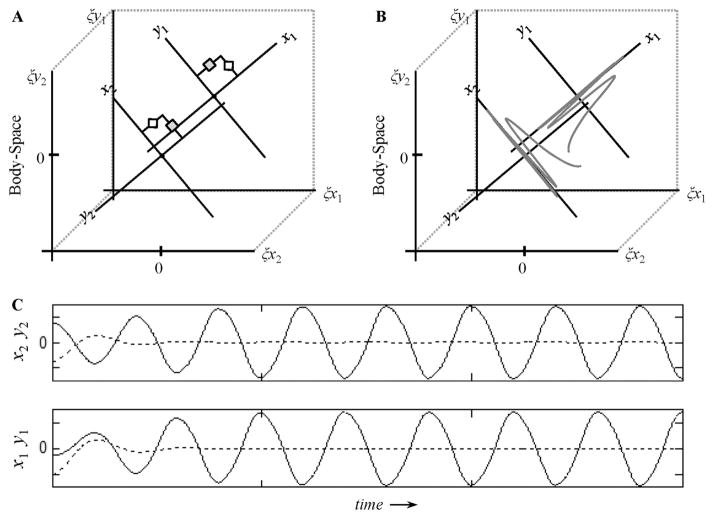
and reflects an idealized model of synchronous inphase interpersonal rhythmic coordination. For clarification purposes, an abstract representation of this preliminary system (Equation 3), as well as simulated time-series are provided in Figure 7. For the sake of illustration, the implementation of Equation 3 in Figure 7a models the task of two actors instructed to rhythmically coordinate inphase with each other at a fixed amplitude and at a fixed diagonal angle of 45° with respect to their shoulder/body plane. The simulated time-series presented in Figure 7c and their embedding as movement trajectories in body-space in Figure 7b together reveal how Equation 3 results in the synchronized movement of x1 and x2 after an initial transient period. During the transient period, initial deviations away from perfect inphase coordination along the x1 and x2 axes are damped out, as are initial deviations away from the instructed axis of motion (i.e., deviations along y1 and y2) that resulted from the arbitrarily chosen initial conditions. Note that although in the current experiment both participants started with the same initial conditions on each trial (at their respective bottom targets with zero velocity), different initial conditions were chosen for each participant in the simulation to illustrate the equifinality of the dynamical solution (i.e., the solution is attained independently of initial conditions).
Figure 7.
(a) Abstract representation of the coupled rhythmic coordination system captured by Equation 2—for a task in which two actors are instructed to coordinate a point-mass (end-effector) at the 45° angle with respect to a shoulder-centered coordinate system. (b) Example rhythmic movement trajectories projected in body-space (shoulder-centered) coordinates. (c) Simulated time-series for arbitrary initial conditions using parameter settings: bx1 = bx2 = 1, by1 = by2 = 2, kx1 = kx2 = ky1 = ky2 = 2π, cx1 = cx2 = .5 and αx1 = αx2 = .5.
In many respects, Equation 3 captures the dynamics observed between many of participant pairs at the beginning of the experimental session. Indeed, most pairs typically failed in the first few trials because they were naturally attracted toward a pattern of inphase synchronization along straight-line trajectories on each participant’s instructed motion axis. As we detailed in the introduction, this natural tendency of interacting individuals to synchronize their movements when visually (informationally) coupled is, of course, well known (for a review, see Schmidt & Richardson, 2008) and has been modeled in a similar manner by numerous researchers in the past (e.g., Mörtl et al., 2012; Varlet et al., 2012), using systems of equations similar to those employed by Kelso and colleagues to capture intrapersonal interlimb synchrony (e.g., Haken et al., 1985; Schöner, Haken, Kelso, 1986; see Kelso, 1995 for a review).
A third step was needed, however, to capture the behavioral dynamics that would produce behavior qualitatively similar to that produced by participant pairs at the end of an experimental session. Given that the task instructions were to “avoid bumping or colliding into each other,” the simplest modification was to create a repelling coupling force that acted on participant-i’s end-effector, and whose strength was a function of the body-space displacement vector from participant-j’s (“origin”) end-effector to participant-i’s (“target”) end-effector (see Figure 8). This was accomplished using repeller functions partially derived from the obstacle avoidance couplings previously employed by Fajen and Warren (see, e.g., Fajen & Warren, 2003; Warren & Fajen, 2008; Warren, 2006). The repeller functions took the form
Figure 8.
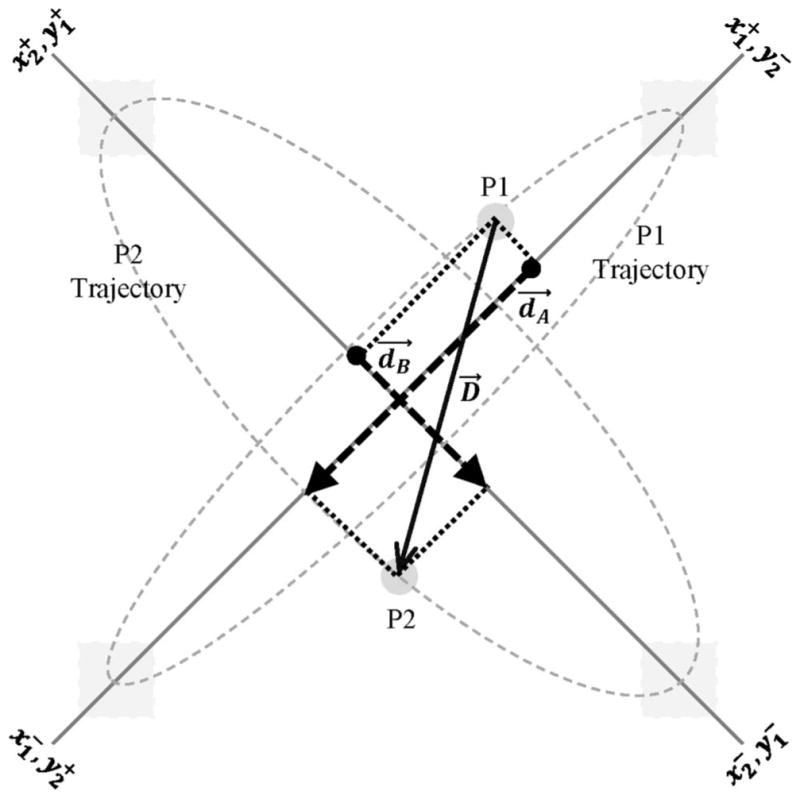
Illustration of how the displacement vector between participants’ on-screen end-effector locations is projected onto the appropriate task-dynamic axes for defining the repeller coupling functions in Equations 4a–d. The target locations (gray squares) are located at the corners of the screen. The solid gray lines along the screen’s intertarget diagonals represent the primary (limit cycle) task-space motion axes (x1 and x2) and orthogonal (point-attractor) motion axes (y1 and y2) of the participants, P1 and P2. The task axes of P1 are rotated CCW 45° from the screen’s right-horizontal axis, and the task axes of P2 are rotated CCW 135° from the screen’s right-horizontal axis; thus, the labels and at the ends of the intertarget on-screen diagonals denote the positive-going directions for motions along the corresponding xi and yi axes of the ith participant. The gray dashed lines reflect idealized on-screen movement trajectories of the participants, with the gray disks representing the current on-screen locations of P1 and P2 along these movement trajectories. In this example, the solid black line with open arrow heads, D, is the displacement vector from P1 to P2, and the dashed black lines with closed arrow heads, dA and dB, represent the projections of D onto the relevant task axes of P2, that is, dA = y2 − (− x1) = y2 + x1 as in Eq. 4d, and dB = x2 − y1 as in Equation 4b. Note that the displacement vector from P2 to P1 would be represented by −D, and its projections onto the task axes of P1 would be defined by −dA = x1 − (− y2) = x1 + y2 as in Eq. 4a and −dB = y1 − x2 as in Eq. 4c.
| (4a) |
and
| (4b) |
for the primary task axes, x1 and x2, respectively, and
| (4c) |
and
| (4d) |
for the secondary task axes, y1 and y2, respectively. There are three terms in these coupling functions. The leftmost γ terms are participant-dependent constants that scale the strength of the repelling force along each participant’s task-axes. The middle terms in parentheses are the projections of the relevant body-space displacement vector onto the task-space axes of the vector’s “target” participant; these projections specify the direction, and contribute to the magnitude, of the displacement-dependent repelling force along these axes (see Figure 8 and its caption for details regarding these projections and the sign conventions used to compute these terms). The leftmost terms scale the magnitude of the repelling forces as a decreasing exponential function of the length of these projections onto the task-axes, that is, small projection lengths specify stronger repelling forces. Accordingly, if γi for a given participant is set to zero or close to zero, the effect of the repeller coupling terms is null or minimal, and a straight-line trajectory will be created that is aligned along the systems principal axis—the participant will behave in a manner similar to Equation 1. If γi is set to a value greater than zero, however, the repeller coupling terms will add forces along both task-axes of participant-i, resulting not only in greater ellipticality (due to forces added along the point-attractor task axis), but also in a greater phase lag relative to participant-j (due to forces added along the limit cycle axis). It is important to note that the increased ellipticality should not be considered to result from the “recruitment” of a previously quiescent kinematic degree of freedom (e.g., recruitment of a biomechanical degree of freedom, as in studies by Kelso, Buchanan, de Guzman, & Ding, 1993; Fink, Kelso, Jirsa & de Guzman, 2000). Rather, both the increased ellipticality and increased phase lag result from the “recruitment” of repeller dynamics onto both axes of the participant’s two-dimensional task-space, such that these dynamics are added to the point-attractor and limit cycle dynamics of Equation 3 that was used to define a synchronization task with no collision-avoidance constraint.
Combining the coupling functions in Equations 4a–d with Equation 3 resulted in the following system of equations
| (5) |
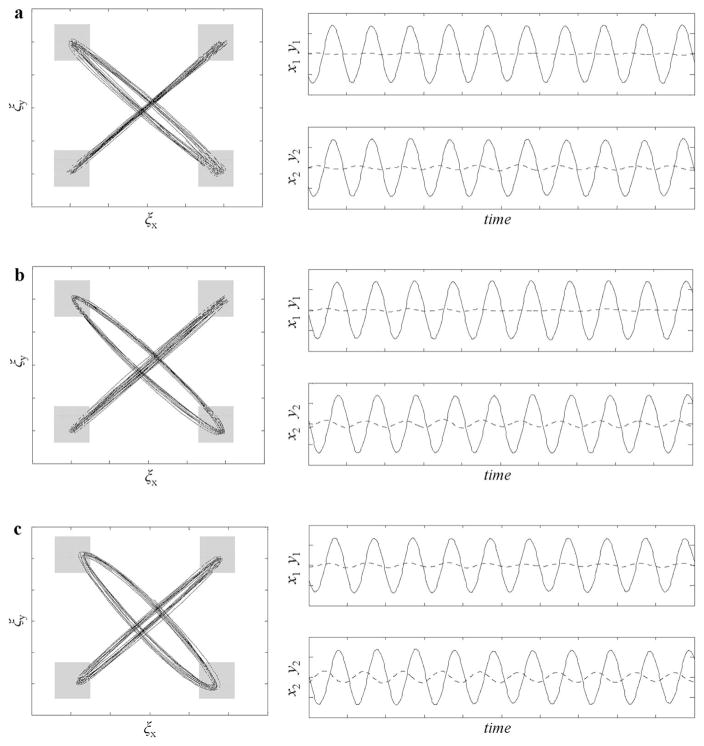
which can successfully capture the stable task solution adopted by participants when successfully performing the composite task (rhythmic synchronization + collision avoidance). An example of the movement trajectories and time-series data generated from Equation 5 are displayed in Figure 9, using various settings for γx1 = γy1 and γx2 = γy2. Consistent with the proposal that participants adopted an asymmetric relation in coupling in order to avoid collisions while simultaneously synchronizing their between target movements, when γx1 = γy1 ≠ γx2 = γy2 an asymmetry in the movement trajectory emerges, as well as a phase lag between the more-elliptical and the more-straight-line trajectory. This asymmetry is qualitatively similar to that observed in the experimental data reported above. In fact, by modulating the magnitudes of γx1= γy1 and γx2 = γy2 and the ratio γx1 = γy1 ≠ γx2 = γy2, Equation 5 can generate a range of movement trajectory patterns that match the range of coordinated movement patterns exhibited by participants and displayed in Figure 3. Note also that: a) if γx1 = γy1 = γx2 = γy2 = 0, then no motion is created along y1 or y2 (i.e., ẏ1 = ẏ2 = 0), which makes the behavior of Equation 5 equivalent to the behavior of Equation 3; and b) if γx1 = γy1 = γx2 = γy2 > 0, then equivalent motion patterns are created along y1 and y2 resulting in elliptical trajectories that are symmetric across participants with oscillations along x1 and x2 that are synchronized with zero phase lag. The potential significance of such symmetric across-participant γ values will be discussed in more detail below, as this situation also results in a stable collision avoidance solution, especially for γx1 ≫ 0, but one that does not include a phase lag along the principal motion axes (i.e., trajectories are coordinated inphase with a 0° relative phase relationship along these axes).
Figure 9.
Examples of how modulating the symmetry and strength of the repulsive coupling parameters γx1 = γy1 and γx2 = γy2 in Equation 3 can produce movement trajectories qualitatively similar to those observed between real participants pairs. The simulated time series in panels a, b, and c were generated using arbitrary initial conditions and the parameter settings bx1 = bx2 = 1, by1 = by2 = 2, kx1 = kx2 = ky1 = ky2 = 2π, cx1 = cx2 = .5 and αx1 = αx2 = .5. In panel a, γx1 = γy1 = 0 and γx2 = γy2 = 7.5; in panel b, γx1 = γy1 = 0 and γx2 = γy2 = 15; and in panel c, γx1 = γy1 = 7.5 and γx2 = γy2 = 20. A small amount of Gaussian noise was also added at each time-step (taken from a normal distribution with a mean of 0 and an SD of 5) to all four equations in (5). In the right column, solid lines denote x1 and x2 trajectories, and dashed lines denote y1 and y2 trajectories.
Discussion
The experimental study presented here was designed to investigate the dynamics of the interpersonal movement coordination that occurred between a pair of participants completing a rhythmic collision avoidance task. Participants were instructed to control and move a computer stimulus back and forth between sets of diagonally positioned targets without colliding into one another. Although no specific instructions were provided to participants about how they should coordinate their movements, the results revealed that nearly all pairs converged onto the same stable pattern of coordination. More specifically, pairs converged onto a stable relative phase relationship of 10° to 40° between their primary motion axes, with one participant maintaining a straight-line trajectory between targets and the other participant tending to exhibit a more elliptical trajectory. There also appeared to be an asymmetry in coupling strength between coactors, with the movements of the participant who adopted a more elliptical trajectory being more coupled to (driven by) the movements of the participant who adopted a more straight-line trajectory.
Of particular significance, task success was dependent on the participants discovering this complementary task solution. If pairs tried to move using equally straight movement trajectories, they nearly always collided into one another or, alternatively, had to perform the task exceptionally slowly. This is because pairs were unable to maintain a phase difference large enough to avoid collision when adopting similarly straight-line shaped between-target movement trajectories. Essentially, participants faced a conflict between the natural attraction toward synchronizing their movements’ inphase and the fact that such synchronization would result in task failure (i.e., a collision). Both the asymmetry in participant path shapes and the nonzero relative phase between participant’s principal motion axes enabled pairs to overcome this conflict.
Our simulations support the hypothesis that both of the asymmetries that contribute to task success (i.e., asymmetry in path ellipticality, and deviations from 0° relative phase) are the result of interparticipant asymmetries in the strength of repeller dynamics between the participants’ end-effectors. Consistent with these modeling results is the experimental finding that, in a participant pair, the participant who adopted a more elliptical trajectory tended to display a greater phase lag relative to the participant who adopted a more straight-line trajectory. Interestingly, a correlational analysis between the path shape asymmetry measure, Δδ, and the coupling directionality index, d(pE,pS ), for the first, middle, and last trial blocks revealed an increasing positive relationship between these two measures across trials, going from r = .08, to r = .37, to r = .85, respectively (with only the latter correlation significant at p < .05). With regard to the coupling directionality index, d(pE,pS), the interparticipant directional asymmetry in coupling strength was by no means large, and future research will be required to determine whether this could have been a result of attentional differences between participants in a pair or a functional consequence of adopting a more elliptical versus straight-line movement trajectory.
With regard to the task dynamic model that was developed to capture the steady-state dynamics observed between pairs, this model produced a similar pattern of asymmetric behavior when the repeller coupling weights of the experimentally motivated repel- ling functions were manipulated. More specifically, creating an asymmetry in the weights of the repeller (collision-avoidance) functions that were used to modulate movements along both the primary axis (between targets) and secondary axis (orthogonal to the primary axis) of each participant produced the same pattern of behavior observed experimentally. Essentially, the interparticipant repeller asymmetry produced a sufficient degree of elliptical difference between participants and a sufficiently large nonzero relative phase relationship, both of which contributed to a safe collision-avoiding distance between the participants’ stimulus dots throughout the task.
As mentioned above in the Dynamical Modeling section, the parameters γ1 and γ2, which determine the strength of the repeller coupling functions in Equations 4a–d, are not control parameters with respect to the state-dynamics of the system. That is, scaling γ1 or γ2 beyond some critical value does not result in a bifurcation or spontaneous symmetry break of task solutions (i.e., a sudden qualitative change in the symmetry of the movement trajectories). Rather, scaling the value of γ1 or γ2 simply increases the strength of the repeller force that pushes the end-effectors away from each other, which serves to increase the ellipticality of path shapes and, when γ1 ≠ γ2, to increase the deviation from 0° relative phase in the two-participant oscillatory system. We hypothesize that the repeller coupling functions may have arisen during and across trials as a discovered solution to the collision-avoidance component of the current task, consistent with the proposal that task enactment and behavioral exploration can lead to the discovery of the behavioral/task dynamics and parametric solutions required for successful task performance (Warren, 2006). In particular, it seems likely that the globally stable joint action behavior observed here emerged from participants experiencing both task failures (i.e., collisions), which ended a trial, and task-relevant movement fluctuations (i.e., close calls and near misses) during an ongoing trial. Further, we hypothesize that these repeller functions are not built from scratch but are recruited from a task-dynamic repertoire that includes collision-avoidance functions that have been active in related situations encountered in everyday life, for example, avoiding collisions with other pedestrians on a crowded sidewalk. We view the recruitment of these repeller functions as inducing a change (addition) to the underlying system graph5 (e.g., Saltzman & Munhall, 1992) that governs performance of the rhythmic coordination component of the task. Once the composite graph, which includes both repeller and synchronizing coupling terms, has been created, the differential strengths of the repeller functions are then “tuned” over trials in order to enhance task performance.
It is likely that alternative models exist that can capture the differential behavior of participants observed in the current study. The modeling choices made here, however, were motivated by: (a) the nature of the overall task objective (i.e., synchronized rhythmic motions + collision avoidance); (b) a desire to keep the model as consistent as possible with the task-relevant aspects of previous dynamical models of rhythmic coordination (e.g., Haken et al., 1985; Mörtl et al., 2012; Schmidt & Richardson, 2008; Varlet et al., 2012) and obstacle avoidance (Fajen & Warren, 2003, 2007; Warren & Fajen, 2008); and (c) the patterns of kinematic asymmetries (path shapes and relative phase) displayed by the participant pairs, which led us to hypothesize corresponding asymmetries in the strength of interparticipant repeller coupling functions. Indeed, the modeling strategy detailed here reflects a task specific implementation of the more general task/behavioral dynamics approaches proposed by Saltzman & Kelso, (1987) and Warren, (2006). Thus, the abstract task space and mathematical functions introduced here could be easily generalized or adapted to capture a range of different rhythmic joint action tasks, including interpersonal rhythmic movement interference tasks (e.g., Kilner, Paulignan, & Blakemore, 2003; Richardson et al., 2009; Romero, Coey, Schmidt, & Richardson, 2012) or other repetitive joint-action targeting or object pick-and-place tasks (e.g., Riley, Richardson, Shockley, & Ramenzoni, 2011; Vesper & Richardson, 2014; Vesper, Soutchek, & Schubö, 2009).
Although the data and model provide converging evidence that the movement roles that emerged between participants were the result of an asymmetry in underlying dynamics, one is left with the question of why this asymmetry emerged. As noted at the end of the Dynamical Modeling section, our simulations indicate that participants could have avoided collisions simply by both producing equally elliptical trajectories, without producing deviations from 0° relative phase along their primary motion axes. That is, the production of symmetrical elliptical movement trajectories is sufficient for collision-avoidance, and the addition of deviations from 0° relative phase synchronization is not necessary. This scenario can be simulated using symmetric values of γ (i.e., repeller coupling strengths) across participants. However, simulations also indicated that asymmetric values of γ could generate, in addition to path ellipticality, phase lags between the participants’ primary motion axes that induce a greater margin of safety from collisions. Additionally, for the extreme case of γ-asymmetry, in which participant-i’s γi = 0 and participant-j’s γj > 0, task success (rhythmic synchronization + collision avoidance) can be attained with only participant-j modifying his or her task-dynamic strategy away from the simpler straight-line synchronization-only strategy. In fact, as indicated above, the task solution observed in the experimental data was likely due to one participant spontaneously discovering the elliptical movement solution due to task-relevant movement fluctuations (i.e., close calls and near misses), which then established the asymmetric solution as the successful task solution from the first completed successful (no-collision) trial. Furthermore, while it is possible that participant pairs may have converged on the symmetric elliptical solution given enough practice, there is no evidence to suggest that this symmetric solution would be more stable than the asymmetric solutions observed. In fact, given that the symmetric solution is a special case of a much larger set of asymmetric solutions, it seems more likely for the asymmetric solution to spontaneously emerge in the current joint-action task context.
Clearly, further empirical research is required to investigate the latter issue. A somewhat related issue that also needs to be explored in future research concerns whether the changes in the behavioral order of a pair prior to and after the emergence of differential movement trajectories was due to a spontaneous symmetry break6 in the system’s state-dynamics that resulted from the change in some to-be-identified control parameter, rather, than as modeled here, the result of an induced change in structure of the system’s underlying task-dynamic graph. As noted above, the choice to model the observed symmetry break as an induced asymmetry in the respective strengths, γ, of the repulsive coupling functions defined for Participant 1 (i.e., Equations 4a and 4c) and Participant 2 (i.e., Equations 4b and 4d) was by no means arbitrary. In many respects the asymmetric movement patterns in the current data that are generated by interparticipant differences in γ seem analogous to the symmetry-breaking effects in bimanual synchronization tasks that are induced by differences in the natural frequencies (detunings, Δω) of the tasks’ component rhythmic limb movements. Such detunings affect both the mean value and variability of relative phase in 1:1 frequency-locked interlimb coordination patterns (i.e., detunings induce a shift away from symmetric inphase coordination to an asymmetric lead/lag relationship; see Kelso, Delcolle, & Schoner, 1990; Schmidt & Richardson, 2008 for more details). The implication is that interparticipant differences in the strategies adopted for dealing with the collision-avoidance aspect of the overall task are reflected in corresponding differences (asymmetries) in the degree to which repeller dynamics are incorporated into each participant’s overall task-dynamics. Moreover, these interparticipant asymmetries in the γ coupling strength appear to induce a symmetry break in the behavioral dynamics of ongoing behavior in the same way that physical or informational detuning differences or imperfections do (Amazeen, Amazeen, Treffner, & Turvey, 1997; Park & Turvey, 2008; Romero et al., 2012; Turvey, 2007; Vesper et al., 2013; Vesper & Richardson, 2014).
The preceding discussion highlights how asymmetries in the behavioral intentions, skill or perceptual attunement of coactors can influence the behavioral dynamics of a joint-action task in much the same way as physical asymmetries do. Several other recent studies have also demonstrated the key role that such symmetry breaks play in defining the behavioral dynamics of joint-action. For instance, Vesper and colleagues (Vesper et al., 2013; Vesper & Richardson, 2014) have demonstrated how asymmetries in actor role (leader–follower) and task-relevant information resulted in between-actor asymmetries in behavior, including the spontaneous emergence of behavioral modifications that operated to enhance and stabilize synchronous interpersonal coordination. More specifically, when two coacting individuals were instructed to jump or move between different target locations at the same time, individuals with more information about a future target location spontaneously modulate their movement dynamics to ensure synchronous coordination. The constructive emergence of asymmetric movement patterns and complementary participant roles in joint action tasks has also been observed in research examining the dynamics of an interpersonal balance board task (Bosga et al., 2010). Similar to what was observed here, pairs learned to stabilize the interpersonal balance board by imposing a differential “leader–follower” type solution, with the intrapersonal control of one individual operating in a subordinate and compensatory role with respect to the control of their coparticipant. Interestingly, the spontaneous emergence of complementary, role type strategies has also been observed in research examining the dynamics of a social binary search task (Roberts & Goldstone, 2011; Theiner, Allen, & Goldstone, 2010). In this latter work, Internet-connected groups of individuals were required to collectively guess a target number between 51 and 100. Each individual in the group chose a number between 0 and 50, with the sum of the individual choices equaling the group’s guess. After each guess, the groups were informed of whether the collective sum was higher or lower than the target number. The results revealed that over the course of repeated attempts some individuals in the group started to adopt the role of “reactor” (i.e., always changed their individual number choice over attempts/trials), whereas other individuals adopted the role of “nonreactor” (i.e., stuck with the same number choice over attempts/trials). Moreover, the degree of differential “reactivity” across participants in the group was positively correlated with a group’s overall performance (Theiner et al., 2010). In other words, an emergent asymmetry of individual behavior—of complementary reactor and nonreactor roles— enhanced the collective success of the group as a whole.
Finally, it is important to note that participant pairs in the current task discovered the observed coordination pattern implicitly. Although it is possible that the spontaneous emergence of trajectory differentiation and the persistence with which participants maintained a specific role (or switched between roles in the case of two pairs) could have reflected a greater drive or motivation of one (or both) participant to adopt a more or less responsive role in achieving task success (or vice versa), postexperimental debriefing revealed that most participants were not aware of the role they played nor could they articulate how the collective organization was controlled. Participants were also not allowed to converse during the experiment. Thus, the control of “who-did-what-and-when” emerged over trials and was determined by the dynamics of trial outcomes with respect to the task goal. In this sense, the emergent distinctions between participants’ roles not only stabilized task performance, but also operated to control the future real-time activity and success of participants. In fact, the persistence with which participants adopted a specific role (i.e., maintained a more straight-line or a more elliptical trajectory after differentiation occurred; see Table 1) within and across trials would seem to indicate that the emergent social structure shaped the behavioral organization of the interacting individuals. This implies that any “strategic decision” or “intention” of one or both participants in pair to adopt a specific role was also a spontaneous and emergent consequence of the task dynamics. A provocative question that could be examined in future research is whether the emergence of such asymmetric action roles persists and generalizes to other joint action tasks, instantiating an asymmetric structure of responsiveness or rapport that influences the structure of each participant’s future activity during other joint action tasks.
Table 1.
δ Statistics for Each Pair Averaged Across Trials
| Pair no. | Participant A
|
Participant B
|
||||
|---|---|---|---|---|---|---|
| Mean δ | SD δ | δ > % | Mean δ | SD δ | δ > % | |
| 1 | 0.0062 | 0.0016 | 100.00 | 0.0103 | 0.0033 | 0.00 |
| 2 | 0.0044 | 0.0014 | 100.00 | 0.0132 | 0.0065 | 0.00 |
| 4 | 0.0643 | 0.0425 | 0.00 | 0.0045 | 0.0017 | 100.00 |
| 5 | 0.0071 | 0.0024 | 66.67 | 0.0072 | 0.0021 | 33.33 |
| 6 | 0.0093 | 0.0036 | 100.00 | 0.0253 | 0.0088 | 0.00 |
| 7 | 0.1369 | 0.1277 | 40.00 | 0.0612 | 0.0567 | 60.00 |
| 8 | 0.0600 | 0.0362 | 86.67 | 0.0985 | 0.0464 | 13.33 |
| 9 | 0.1102 | 0.0512 | 20.00 | 0.0628 | 0.0394 | 80.00 |
| 10 | 0.0247 | 0.0110 | 53.33 | 0.0258 | 0.0148 | 46.67 |
| 11 | 0.0320 | 0.0266 | 80.00 | 0.0695 | 0.0381 | 20.00 |
| 12 | 0.1083 | 0.0523 | 100.00 | 0.1836 | 0.0530 | 0.00 |
In conclusion, the current findings provide evidence that the dynamical coordination processes previously known to underlie incidental motor synchronization can also support more complex goal-directed joint action, and that complementary action roles can naturally emerge during ongoing joint action behavior. The current findings also highlight how complementary joint actions are functionally related to the spatiotemporal symmetry of interagent coupling, as well as movement and task constraints, and that understanding the symmetries that define a joint action task space is fundamental to understanding the dynamic order of complex joint action behavior (Lagarde, 2013). Indeed, the dynamical processes that support complex joint action behavior may well be characterized by the induction and maintenance of asymmetric interagent relations, with changes in the symmetry of joint action behavior marking the emergence of higher or lower orders of complex and complementary social activity and coordination.
Acknowledgments
The research was supported by National Institutes of Health, R01GM105045. Special thanks to Ryan May for help with data collection. Thanks also to Charles Coey and Manu Varlet for methodological suggestions and pilot testing.
Footnotes
Throughout this article the term joint action is used to label the cooperative physical activity displayed between two individuals participating in a task together. It does not refer to movement coordination at the level of individual joints in the musculoskeletal system.
Research investigating the dynamics of interpersonal and mutliagent coordination in sport is the exception (see, e.g., Lagarde, Peham, Licka, & Kelso, 2005; Hristovski, Davids, & Araujo, 2006; Okumura et al., 2012; Passos et al., 2009). Also see Mottet, Guiard, Ferrand, and Bootsma (2001) for an example of research examining an interpersonal Fitts Law task.
Inphase or 0° relative phase synchronization refers to the movements that oscillate in the same direction at the same time. Antiphase or 180° relative phase synchronization refers to the movements that oscillate in opposite directions at the same time.
Throughout this article we use the term symmetry to refer to an equivalence of some kind. This equivalence could be a spatial or temporal equality or an invariant correspondence under some form of functional transformation. The term symmetry can also apply to mathematical objects, operations or functions that result in an equivalence in the state(s) or changes in state(s) of a mathematical variable or system. An asymmetry or break in the symmetry of an object or system, therefore, refers to a relationship of nonequivalence (or one that has fewer equalities or invariant relations) with respect to some form of spatial, temporal, functional or mathematical transformation.
In this context, the term graph refers to the graph-theoretic node-link architecture that defines the system’s equation of motion for the overall task. Viewed as a circuit diagram (e.g., as when using Matlab’s Simulink toolbox), one can identify: a) nodes with system parameters (e.g., k, b, γ) and operator-elements of the circuit (e.g., defining operations such as summation, multiplication, integration); and b) links with internode connections that transmit parameterized functions of state variables. From this perspective, the component force terms of an equation of motion (e.g., spring force, repeller force) are defined as subgraphs of the overall system graph.
The term symmetry break does not mean that the system goes from a completely symmetric state to a highly asymmetric state, but rather that the symmetry of the system (the number of transformations that leave the system or the system’s solution states unchanged) has simply been reduced or redistributed in some way.
Contributor Information
Michael J. Richardson, University of Cincinnati
Steven J. Harrison, University of Nebraska
Rachel W. Kallen, University of Cincinnati
Ashley Walton, University of Cincinnati.
Brian A. Eiler, University of Cincinnati
Elliot Saltzman, Boston University and Haskins Laboratories, New Haven, Connecticut.
R. C. Schmidt, College of the Holy Cross
References
- Amazeen EL, Amazeen PG, Treffner PJ, Turvey MT. Attention and handedness in bimanual coordination dynamics. Journal of Experimental Psychology: Human Perception and Performance. 1997;23:1552–1560. http://dx.doi.org/10.1037/0096-1523.23.5.1552. [Google Scholar]
- Bekkering H, de Bruijn ERA, Cuijpers RH, Newman-Norlund R, Van Schie HT, Meulenbroek R. Joint action: Neurocognitive mechanisms supporting human interaction. Topics in Cognitive Science. 2009;1:340–352. doi: 10.1111/j.1756-8765.2009.01023.x. http://dx.doi.org/10.1111/j.1756-8765.2009.01023.x. [DOI] [PubMed] [Google Scholar]
- Bosga J, Meulenbroek RGJ, Cuijpers RH. Intra- and interpersonal movement coordination in jointly moving a rocking board. Motor Control. 2010;14:440–459. doi: 10.1123/mcj.14.4.440. [DOI] [PubMed] [Google Scholar]
- Coey C, Varlet M, Richardson MJ. Coordination dynamics in a socially situated nervous system. Frontiers in Human Neuroscience. 2012;6:164. doi: 10.3389/fnhum.2012.00164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duarte M, Zatsiorsky VM. Effects of body lean and visual information on the equilibrium maintenance during stance. Experimental Brain Research. 2002;146:60–69. doi: 10.1007/s00221-002-1154-1. http://dx.doi.org/10.1007/s00221-002-1154-1. [DOI] [PubMed] [Google Scholar]
- Fajen BR, Warren WH. Behavioral dynamics of steering, obstacle avoidance, and route selection. Journal of Experimental Psychology: Human Perception and Performance. 2003;29:343–362. doi: 10.1037/0096-1523.29.2.343. [DOI] [PubMed] [Google Scholar]
- Fajen BR, Warren WH. Behavioral dynamics of intercepting a moving target. Experimental Brain Research. 2007;180:303–319. doi: 10.1007/s00221-007-0859-6. [DOI] [PubMed] [Google Scholar]
- Fink PW, Kelso JAS, Jirsa VK, de Guzman G. Recruitment of degrees of freedom stabilizes coordination. Journal of Experimental Psychology: Human Perception and Performance. 2000;26:671–692. doi: 10.1037//0096-1523.26.2.671. http://dx.doi.org/10.1037/0096-1523.26.2.671. [DOI] [PubMed] [Google Scholar]
- Fitzpatrick P, Diorio R, Richardson MJ, Schmidt RC. Dynamical methods for evaluating the time-dependent unfolding of social coordination in children with autism. Frontiers in Integrative Neuroscience. 2013;7:21. doi: 10.3389/fnint.2013.00021. http://dx.doi.org/10.3389/fnint.2013.00021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gallese V. The manifold nature of interpersonal relations: The quest for a common mechanism. Philosophical Transactions of the Royal Society of London Series B, Biological Sciences. 2003;358:517–528. doi: 10.1098/rstb.2002.1234. http://dx.doi.org/10.1098/rstb.2002.1234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldfield EC, Richardson MJ, Lee KG, Margetts S. Coordination of sucking, swallowing, and breathing and oxygen saturation during early infant breast-feeding and bottle-feeding. Pediatric Research. 2006;60:450–455. doi: 10.1203/01.pdr.0000238378.24238.9d. http://dx.doi.org/10.1203/01.pdr.0000238378.24238.9d. [DOI] [PubMed] [Google Scholar]
- Graf M, Schütz-Bosbach S, Prinz W. Motor involvement in action and object perception similarity and complementarity. In: Semin G, Echterhov G, editors. Grounding sociality: Neurons, minds, and culture. New York, NY: Psychology Press; 2009. pp. 27–52. [Google Scholar]
- Haken H, Kelso JAS, Bunz H. A theoretical model of phase transitions in human hand movements. Biological Cybernetics. 1985;51:347– 356. doi: 10.1007/BF00336922. [DOI] [PubMed] [Google Scholar]
- Harrison SJ, Richardson MJ. Horsing around: Spontaneous four-legged coordination. Journal of Motor Behavior. 2009;41:519–524. doi: 10.3200/35-08-014. [DOI] [PubMed] [Google Scholar]
- Hove MJ, Risen JL. It’s all in the timing: Interpersonal synchrony increases affiliation. Social Cognition. 2009;27:949–960. http://dx.doi.org/10.1521/soco.2009.27.6.949. [Google Scholar]
- Hristovski R, Davids K, Araújo D. Affordance-controlled bifurcations of action patterns in martial arts. Nonlinear Dynamics, Psychology, and Life Sciences. 2006;10:409–444. [PubMed] [Google Scholar]
- Kelso JAS. Dynamic patterns. Cambridge, MA: MIT Press; 1995. [Google Scholar]
- Kelso JAS, Buchanan JJ, de Guzman GC, Ding M. Spontaneous recruitment and annihilation of degrees of freedom in biological coordination. Physics Letters A. 1993;179:364–371. http://dx.doi.org/10.1016/0375-9601(93)90692-S. [Google Scholar]
- Kelso JAS, DelColle JD, Schoner G. Action–perception as a pattern formation process. In: Jeannerod M, editor. Attention and performance XIII: Motor representation and control. Hillsdale, NJ: Erlbaum; 1990. pp. 139–169. [Google Scholar]
- Kilner JM, Paulignan Y, Blakemore SJ. An interference effect of observed biological movement on action. Current Biology. 2003;13:522–525. doi: 10.1016/s0960-9822(03)00165-9. http://dx.doi.org/10.1016/S0960-9822(03)00165-9. [DOI] [PubMed] [Google Scholar]
- Lagarde J. Challenges for the understanding of the dynamics of social coordination. Frontiers in Neurorobotics. 2013;7:18. doi: 10.3389/fnbot.2013.00018. http://dx.doi.org/10.3389/fnbot.2013.00018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lagarde J, Peham C, Licka T, Kelso JAS. Coordination dynamics of the horse-rider system. Journal of Motor Behavior. 2005;37:418–424. doi: 10.3200/JMBR.37.6.418-424. http://dx.doi.org/10.3200/JMBR.37.6.418-424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marsh KL, Richardson MJ, Schmidt RC. Social connection through joint action and interpersonal coordination. Topics in Cognitive Science. 2009;1:320–339. doi: 10.1111/j.1756-8765.2009.01022.x. http://dx.doi.org/10.1111/j.1756-8765.2009.01022.x. [DOI] [PubMed] [Google Scholar]
- Miles LK, Lumsden J, Richardson MJ, Macrae CN. Do birds of a feather move together? Group membership and behavioral synchrony. Experimental Brain Research. 2011;211:495–503. doi: 10.1007/s00221-011-2641-z. http://dx.doi.org/10.1007/s00221-011-2641-z. [DOI] [PubMed] [Google Scholar]
- Mörtl A, Lorenz T, Vlaskamp BN, Gusrialdi A, Schubö A, Hirche S. Modeling inter-human movement coordination: Synchronization governs joint task dynamics. Biological Cybernetics. 2012;106:241–259. doi: 10.1007/s00422-012-0492-8. http://dx.doi.org/10.1007/s00422-012-0492-8. [DOI] [PubMed] [Google Scholar]
- Mottet D, Guiard Y, Ferrand T, Bootsma RJ. Two-handed performance of a rhythmical Fitts task by individuals and dyads. Journal of Experimental Psychology: Human Perception and Performance. 2001;27:1275–1286. doi: 10.1037//0096-1523.27.6.1275. [DOI] [PubMed] [Google Scholar]
- Newman-Norlund RD, Noordzij ML, Meulenbroek RGJ, Bekkering H. Exploring the brain basis of joint action: Coordination of actions, goals and intentions. Social Neuroscience. 2007;2:48–65. doi: 10.1080/17470910701224623. http://dx.doi.org/10.1080/17470910701224623. [DOI] [PubMed] [Google Scholar]
- Okumura M, Kijima A, Kadota K, Yokoyama K, Suzuki H, Yamamoto Y. A critical interpersonal distance switches between two coordination modes in kendo matches. PLoS ONE. 2012;7(12):e51877. doi: 10.1371/journal.pone.0051877. http://dx.doi.org/10.1371/journal.pone.0051877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oullier O, Basso F. Embodied economics: How bodily information shapes the social coordination dynamics of decision-making. Biological Sciences. 2010;365:291–301. doi: 10.1098/rstb.2009.0168. http://dx.doi.org/10.1098/rstb.2009.0168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oullier O, de Guzman GC, Jantzen KJ, Lagarde J, Kelso JAS. Social coordination dynamics: Measuring human bonding. Social Neuroscience. 2008;3:178–192. doi: 10.1080/17470910701563392. http://dx.doi.org/10.1080/17470910701563392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park H, Turvey MT. Imperfect symmetry and the elementary coordination law. In: Fuchs A, Jirsa VK, editors. Coordination: Neural, behavioral and social dynamics. Heidelberg, Germany: Springer-Verlag; 2008. pp. 3–25. http://dx.doi.org/10.1007/978-3-540-74479-5_1. [Google Scholar]
- Passos P, Araújo D, Davids K, Gouveia L, Serpa S, Milho J, Fonseca S. Interpersonal pattern dynamics and adaptive behavior in multiagent neurobiological systems: Conceptual model and data. Journal of Motor Behavior. 2009;41:445–459. doi: 10.3200/35-08-061. http://dx.doi.org/10.3200/35-08-061. [DOI] [PubMed] [Google Scholar]
- Pikovsky A, Rosenblum M, Kurths J. Synchronization: A universal concept in nonlinear sciences. New York: Cambridge University Press; 2001. [Google Scholar]
- Richardson MJ, Campbell WL, Schmidt RC. Movement interference during action observation as emergent coordination. Neuroscience Letters. 2009;449:117–122. doi: 10.1016/j.neulet.2008.10.092. http://dx.doi.org/10.1016/j.neulet.2008.10.092. [DOI] [PubMed] [Google Scholar]
- Richardson MJ, Marsh KL, Isenhower RW, Goodman JR, Schmidt RC. Rocking together: Dynamics of intentional and unintentional interpersonal coordination. Human Movement Science. 2007;26:867–891. doi: 10.1016/j.humov.2007.07.002. http://dx.doi.org/10.1016/j.humov.2007.07.002. [DOI] [PubMed] [Google Scholar]
- Richardson MJ, Marsh KL, Schmidt RC. Effects of visual and verbal interaction on unintentional interpersonal coordination. Journal of Experimental Psychology: Human Perception and Performance. 2005;31:62–79. doi: 10.1037/0096-1523.31.1.62. http://dx.doi.org/10.1037/0096-1523.31.1.62. [DOI] [PubMed] [Google Scholar]
- Riley MA, Richardson MJ, Shockley K, Ramenzoni VC. Interpersonal synergies. Frontiers in Psychology. 2011;2:38. doi: 10.3389/fpsyg.2011.00038. http://dx.doi.org/10.3389/fpsyg.2011.00038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roberts ME, Goldstone RL. Adaptive group coordination and role differentiation. PLoS ONE. 2011;6(7):e22377. doi: 10.1371/journal.pone.0022377. http://dx.doi.org/10.1371/journal.pone.0022377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Romero V, Coey C, Schmidt RC, Richardson MJ. Movement coordination or movement interference: Visual tracking and spontaneous coordination modulate rhythmic movement interference. PLoS ONE. 2012;7(9):e44761. doi: 10.1371/journal.pone.0044761. http://dx.doi.org/10.1371/journal.pone.0044761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenblum MG, Cimponeriu L, Bezerianos A, Patzak A, Mrowka R. Identification of coupling direction: Application to cardiorespiratory interaction. Physical Review E. 2002;65:041909. doi: 10.1103/PhysRevE.65.041909. http://dx.doi.org/10.1103/PhysRevE.65.041909. [DOI] [PubMed] [Google Scholar]
- Rosenblum MG, Pikovsky AS. Detecting direction of coupling in interacting oscillators. Physical Review E. 2001;64:45202. doi: 10.1103/PhysRevE.64.045202. http://dx.doi.org/10.1103/PhysRevE.64.045202. [DOI] [PubMed] [Google Scholar]
- Saltzman EL, Kelso JAS. Skilled actions: A task dynamic approach. Psychological Review. 1987;94:84–106. [PubMed] [Google Scholar]
- Saltzman E, Munhall KG. Skill acquisition and development: The roles of state-, parameter-, and graph-dynamics. Journal of Motor Behavior. 1992;24:49–57. doi: 10.1080/00222895.1992.9941600. [DOI] [PubMed] [Google Scholar]
- Schmidt RC, Carello C, Turvey MT. Phase transitions and critical fluctuations in the visual coordination of rhythmic movements between people. Journal of Experimental Psychology: Human Perception and Performance. 1990;16:227–247. doi: 10.1037//0096-1523.16.2.227. http://dx.doi.org/10.1037/0096-1523.16.2.227. [DOI] [PubMed] [Google Scholar]
- Schmidt RC, Fitzpatrick P, Caron R, Mergeche J. Understanding social motor coordination. Human Movement Science. 2011;30:834–845. doi: 10.1016/j.humov.2010.05.014. http://dx.doi.org/10.1016/j.humov.2010.05.014. [DOI] [PubMed] [Google Scholar]
- Schmidt RC, O’Brien B. Evaluating the dynamics of unintended interpersonal coordination. Ecological Psychology. 1997;9:189–206. http://dx.doi.org/10.1207/s15326969eco0903_2. [Google Scholar]
- Schmidt RC, Richardson MJ. Dynamics of interpersonal coordination. In: Fuchs A, Jirsa V, editors. Coordination: Neural, Behavioral and Social Dynamics. Heidelberg, Germany: Springer-Verlag; 2008. pp. 281–308. http://dx.doi.org/10.1007/978-3-540-74479-5_14. [Google Scholar]
- Schöner G, Haken H, Kelso JAS. A stochastic theory of phase transitions in human hand movement. Biological Cybernetics. 1986;53:247–257. doi: 10.1007/BF00336995. http://dx.doi.org/10.1007/BF00336995. [DOI] [PubMed] [Google Scholar]
- Sebanz N, Knoblich G. Prediction in joint action: What, when, and where. Topics in Cognitive Science. 2009;1:353–367. doi: 10.1111/j.1756-8765.2009.01024.x. http://dx.doi.org/10.1111/j.1756-8765.2009.01024.x. [DOI] [PubMed] [Google Scholar]
- Theiner G, Allen C, Goldstone RL. Recognizing group cognition. Cognitive Systems Research. 2010;11:378–395. http://dx.doi.org/10.1016/j.cogsys.2010.07.002. [Google Scholar]
- Turvey MT. Action and perception at the level of synergies. Human Movement Science. 2007;26:657–697. doi: 10.1016/j.humov.2007.04.002. http://dx.doi.org/10.1016/j.humov.2007.04.002. [DOI] [PubMed] [Google Scholar]
- van der Wel RP, Knoblich G, Sebanz N. Let the force be with us: Dyads exploit haptic coupling for coordination. Journal of Experimental Psychology: Human Perception and Performance. 2011;37:1420–1431. doi: 10.1037/a0022337. http://dx.doi.org/10.1037/a0022337. [DOI] [PubMed] [Google Scholar]
- van Ulzen NR, Lamoth CJC, Daffertshofer A, Semin GR, Beek PJ. Characteristics of instructed and uninstructed interpersonal coordination while walking side-by-side. Neuroscience Letters. 2008;432:88–93. doi: 10.1016/j.neulet.2007.11.070. http://dx.doi.org/10.1016/j.neulet.2007.11.070. [DOI] [PubMed] [Google Scholar]
- Varlet M, Marin L, Lagarde J, Bardy BG. Social postural coordination. Journal of Experimental Psychology: Human Perception and Performance. 2011;37:473–483. doi: 10.1037/a0020552. http://dx.doi.org/10.1037/a0020552. [DOI] [PubMed] [Google Scholar]
- Varlet M, Marin L, Raffard S, Schmidt RC, Capdevielle D, Boulenger JP, … Bardy BG. Impairments of social motor coordination in schizophrenia. PLoS ONE. 2012;7(1):e29772. doi: 10.1371/journal.pone.0029772. http://dx.doi.org/10.1371/journal.pone.0029772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vesper C, Butterfill S, Knoblich G, Sebanz N. A minimal architecture for joint action. Neural Networks. 2010;23:998–1003. doi: 10.1016/j.neunet.2010.06.002. http://dx.doi.org/10.1016/j.neunet.2010.06.002. [DOI] [PubMed] [Google Scholar]
- Vesper C, Richardson MJ. Strategic communication and behavioral coupling in asymmetric joint action. Experimental Brain Research. 2014;232:2945–2956. doi: 10.1007/s00221-014-3982-1. http://dx.doi.org/10.1007/s00221-014-3982-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vesper C, Soutschek A, Schubö A. Motion coordination affects movement parameters in a joint pick-and-place task. The Quarterly Journal of Experimental Psychology. 2009;62:2418–2432. doi: 10.1080/17470210902919067. http://dx.doi.org/10.1080/17470210902919067. [DOI] [PubMed] [Google Scholar]
- Vesper C, van der Wel RP, Knoblich G, Sebanz N. Are you ready to jump? Predictive mechanisms in interpersonal coordination. Journal of Experimental Psychology: Human Perception and Performance. 2013;39:48–61. doi: 10.1037/a0028066. http://dx.doi.org/10.1037/a0028066. [DOI] [PubMed] [Google Scholar]
- Warren WH. The dynamics of perception and action. Psychological Review. 2006;113:358–389. doi: 10.1037/0033-295X.113.2.358. http://dx.doi.org/10.1037/0033-295X.113.2.358. [DOI] [PubMed] [Google Scholar]
- Warren WH, Fajen BR. Behavioral dynamics of visually guided locomotion. Coordination: Neural, Behavioral and Social Dynamics. Heidelberg: Springer-Verlag; 2008. pp. 45–75. [Google Scholar]
- Zanone PG, Kelso JAS. Evolution of behavioral attractors with learning: Nonequilibrium phase transitions. Journal of Experimental Psychology: Human Perception and Performance. 1992;18:403–421. doi: 10.1037//0096-1523.18.2.403. http://dx.doi.org/10.1037/0096-1523.18.2.403. [DOI] [PubMed] [Google Scholar]