Parallelization and Improvements of the Generalized Born Model with a Simple sWitching Function for Modern Graphics Processors

Abstract

Two fundamental challenges of simulating biologically relevant systems are the rapid calculation of the energy of solvation, and the trajectory length of a given simulation. The Generalized Born model with a Simple sWitching function (GBSW) addresses these issues by using an efficient approximation of Poisson–Boltzmann (PB) theory to calculate each solute atom's free energy of solvation, the gradient of this potential, and the subsequent forces of solvation without the need for explicit solvent molecules. This study presents a parallel refactoring of the original GBSW algorithm and its implementation on newly available, low cost graphics chips with thousands of processing cores. Depending on the system size and nonbonded force cutoffs, the new GBSW algorithm offers speed increases of between one and two orders of magnitude over previous implementations while maintaining similar levels of accuracy. We find that much of the algorithm scales linearly with an increase of system size, which makes this water model cost effective for solvating large systems. Additionally, we utilize our GPU-accelerated GBSW model to fold the model system chignolin, and in doing so we demonstrate that these speed enhancements now make accessible folding studies of peptides and potentially small proteins.

Introduction

An accurate representation of solvent in molecular dynamics simulations plays a vital role in recapitulating molecular conformation and energetics. This is especially true for studying biological macromolecules such as nucleic acids and proteins, where the solvent environment can be a driving force of observed phenomena.^1-5 Traditionally in biomolecular simulations, the solvent (generally water) is represented by atomically-detailed molecules and counterions that surround a solute molecule. While such explicitly-represented solvent models are often considered the most detailed approach to molecular simulations, they can be cost-prohibitive when used for long timescales and large systems.⁶ In order to reduce boundary-condition artifacts and to better describe experiments, a given system may comprise of as much as 95% water-related atoms.^7,8 The computational load of accounting for non-bonded pairwise interactions and the need to equilibrate configurations of water and counterions can make many systems prohibitively expensive to simulate.⁶

For purposes of exploring conformational equilibria of a large solute molecule, implicit solvent models can be used to mimic solvent effects without requiring the computational load of simulating a large bulk of solvent.^9-13 Although implicit solvent omits atomic-level interactions between the solvent and solute, such as hydrogen bonding, such setups offer straightforward methods of calculating solvation free energy, salt effects, and continuous changes to pH.^11,13-17 Additionally, continuum solvent obviates the need to maintain structural equilibria of water and counterions, so conformational changes of the solute often occur on shorter timescales. For instance Tsui and Case have shown that A-form DNA converges into a more optimal B-form conformation within 20 ps as compared to 500 ps when using explicit solvent.^7,12 Such enhanced dynamics have been useful in exploring protein folding mechanisms and protein-protein interactions.^4,18

Many successful implicit solvent models are based on the assumption that a protein's interior is a uniform, low dielectric region of space filled with partially-charged atoms, and that this protein is surrounded by a featureless high-dielectric solvent.^19,20 The exact solution of this approximation is given by the numerical solution of the finite-difference Poisson-Boltzmann (PB) equation. Although PB implicit solvation grants simulation speed gains by reducing the system size, its poor scalability has been a principle bottleneck in exploring the dynamics of large biological systems.^21-23

In the pursuit of finding a more efficient method of solvating bio-macromolecules, the generalized Born (GB) implicit solvent model has been developed as a computationally cheaper approximation of PB solvent.^13,19,20 This method of calculating a system's electrostatic free energy relies upon the solute atom's locations, atomic partial charges, and the effective distance between an atom and the solvent-solute dielectric boundary, or Born radius. The most accurate GB formula for calculating the electrostatic free energy of solvation (ΔG^elec) was first proposed by Still et al., and follows the form²⁰

$$\Delta G^{elec}=-\frac{1}{2}\sum _a\sum _b\tau \frac{q_a{q}_b}{f_{ab}^{GB}}$$ (eq. 1)

where

$$f_{ab}^{GB}={\left[r_{ab}^2+R_a^{Born}{R}_b^{Born}\exp (-r_{ab}^2∕\left(4R_a^{Born}{R}_b^{Born}\right))\right]}^{1∕2}$$ (eq. 2)

Here $R_a^{Born}$ represents the Born radius of atom a, r_ab is the distance between atoms a and b, and q is the partial charge of the atoms. τ is the conversion factor that scales the Born energy by the difference in dielectric values at the dielectric boundary.

$$\tau =1∕{\epsilon }_p-1∕{\epsilon }_s$$ (eq. 3)

Here ε_p and ε_s are the dielectric values of inside the solute molecule (such as a protein) and solvent respectively. Should a low concentration of salt be present in the simulation, the electrostatic energy can be modified by a Debye-Huckel screening parameter κ as follows,¹⁷

$$\tau =1∕{\epsilon }_p-\exp \left(-\kappa f_{GB}\right)∕{\epsilon }_s$$ (eq. 4)

The accuracy and speed of GB implicit solvent models depend heavily on the method used for calculating the Born radius, and those various methods are what distinguish each model. Some popular models include using an empirically-driven spatial symmetry function of atom placement such as in the Fast Analytical Continuum Treatment of Solvation (FACTS);²⁴ atom-atom pairwise potentials as in Generalized Born Surface Area from Onufriev, Bashford, and Case (GBSA/OBC);^11,25 atom-atom pairwise potentials with surface area interaction potentials as in the Analytical Generalized Born plus NonPolar 2 model (AGBNP2);²⁶ and atomic volume exclusion such as in the Generalized Born with a Simple sWitching function (GBSW)¹³ and Generalized Born using Molecular Volume (GBMV).²⁷ Atomic volume exclusion algorithms make few assumptions regarding the shape of molecules and the placement of atoms. As we will develop later in this study, these algorithms integrate energy contributions from groups of neighboring atoms, which is effective at capturing atomic overlap and buriedness. As such, they often excel at reproducing solvation free energies, but usually at a higher computational cost and lower scalability relative to other models.²⁸ In this study we will look at improving the speed and scalability of the accurate GBSW model.

GBSW has over a decade of research and parameterization. Aside from gaining a well-characterized set of atomic and fitting parameters, its functionality has been extended to include pH, implicit membranes, and coarse-graining.^{4,13,14,29-33} Unfortunately GBSW scales poorly with system size, and systems larger than 1,000 atoms running on one central processing unit (CPU) core proceed at speeds of less than 1 nanosecond (ns) per day. Several methods of improving its speed include using more processing cores, improving the algorithm, or improving the hardware. With additional CPU cores modest speed improvements can be seen, and systems of up to 10,000 atoms can be simulated for single ns/day. When using additional cores, few speed increases are seen above about 20 cores. Additionally, systems with more than 8 cores today are expensive, and cost-limiting to many research groups. Thus we focus on algorithmic improvements to allow GBSW to utilize more cores, and on hardware improvements to take advantage of newer and more affordable parallel processing hardware.

With the availability of graphics processing units (GPUs) carrying up to thousands of parallel processing cores and their newer ability to compute complex mathematical functions using C-like languages such as Open Computing Language (OpenCL) and Compute Unified Device Architecture (CUDA), a new frontier of GPU-powered ultra-parallel molecular dynamics software has come into being. Programs such as CHARMM,⁶ AMBER,³⁴ OpenMM,³⁵ GROMACS,³⁶ and NAMD³⁷ all offer GPU-accelerated options for many types of simulations, all of which can replace the computational power of much larger computer networks with a single graphics card. Despite the fantastic improvements in molecular mechanics simulations afforded by GPUs, some algorithms remain challenging to parallelize. Notable among these are implicit solvent models, which either rely on recursive data processing or are inefficiently split into parallel functions. From the variety of implicit solvent methods for calculating solvation free energy, only those that use an uncoupled summation of Cramer-Truhlar-type atom-atom pairwise interactions,³⁸ such as GBSA/OBC,^11,25 have been implemented in GPU languages. Such implementations only required a retooled version of the neighboring atom interaction processes that were already developed for all-atom molecular mechanics.^11,35-37 This study represents the first implementation of a parallel, atom-coupled volumetric integration approach to calculating solvation free energy using the GBSW algorithm.

Due to OpenMM's achievements and effectiveness in harnessing GPUs, the CHARMM-OpenMM interface was developed to combine the capabilities of the two software packages. As such, the robust algorithms and range of methods supported in CHARMM are used to design new simulation methods, and these methods are run using OpenMM's efficient processes that have been developed and optimized for modern GPU architectures^6,35 Additionally, the GBSA/OBC model already in place in OpenMM offers a GB framework that forms a basis for our new GBSW code. In this study we outline a highly-parallelized version of the Generalized Born implicit solvent model with a Simple sWitching function within the CHARMM-OpenMM interface.¹⁴ First we present some of the underlying theory of how GBSW calculates the solvation free energy and Born radii. Then we delve into the implementation of the algorithm in its original Fortran90 format, and how functions were refactored for a parallel CUDA implementation in the OpenMM software package. Supporting information (SI) accompanies this study to explain why particular numerical cutoffs were chosen, and to describe the hardware setup used for benchmarking. Figures were generated using the PyMOL and MATLAB software packages. Finally we review the speed improvements achieved by the new algorithm, its ability to fold chignolin a linear peptide chain, and future directions for developing the model.

Theory

Effective Born Radii

Like many other GB solvent models, GBSW uses the atomic self-contribution of the Still equation (eq. 1) to calculate the Born radius from the electrostatic free energy. The self-term for atom a reduces eq. 1 to

$$\Delta G_a^{elec}=\frac{-\tau }{2}\frac{q_a^2}{R_a^{Born}}$$ (eq. 5)

The self-energy is then approximated in two energy terms, the Coulomb field approximation term $\Delta G_a^{elec,0}$, and an empirical correction term ΔG^{elec, 1}, in the following relationship:²⁷

$$\Delta G_a^{elec}\approx {\alpha }_0\Delta G_a^{elec,0}+{\alpha }_1\Delta G_a^{elec,1}$$ (eq. 6)

where α₀ and α₁ are empirical fitting coefficients. By default, these coefficients are −0.1801 and 1.81745 respectively.¹³ The first interaction term is derived from the Coulomb-field approximation for electric displacement, and it calculates the work function for removing the partial charge of an atom a a distance from a dielectric boundary. This term is evaluated to

$$\Delta G_a^{elec,0}=\frac{-\tau q_a^2}{8\pi }{\int }_{solvent}\frac{1}{{\left(r_{a,\mathbf{r}}\right)}^4}dV$$ (eq. 7)

Here the integral is evaluated over all solvent volume V, and r_{a, r} is the radial distance between the point in space r and atom a. The Coulomb-field approximation from equation 7 systematically underestimates the electrostatic solvation free energy as calculated by exact Poisson-Boltzmann methods, and consequently overestimates atomic Born radii.²⁷ Lee et al. demonstrated that this underestimation could be greatly reduced by adding the Born energy correction term ΔG^{elec, 1},^27,39 which is computed as follows.¹³

$$\Delta G_a^{elec,1}=\frac{-\tau q_a^2}{2}{\left[\frac{1}{4\pi }{\int }_{solvent}\frac{1}{{\left(r_{a,\mathbf{r}}\right)}^7}dV\right]}^{1∕4}$$ (eq. 8)

Finally we solve for the Born radius using eq. 5 – 8 and we arrive at

$${\left(R_a^{Born}\right)}^{-1}={\alpha }_0\left[\frac{1}{4\pi }{\int }_{solvent}\frac{1}{{\left(r_{a,\mathbf{r}}\right)}^4}dV\right]+{\alpha }_1{\left[\frac{1}{4\pi }{\int }_{solvent}\frac{1}{{\left(r_{a,\mathbf{r}}\right)}^7}dV\right]}^{1∕4}$$ (eq. 9)

Thus we have the basic construction for evaluating Born radii. Next we explain the details of the switching function that define the dielectric boundary in GBSW.

Switching Function

In GBSW, the solvent volume is defined as the region of space excluded by the van der Waals spheres of the solute molecule's atoms. Rather than integrate over all space to infinity, we integrate the volume of the solute molecule and calculate the volume inclusive function V_solute(r–r_a), where r–r_a is a location in Cartesian space centered on atom a. Then 1–V_solute(r–r_a) becomes the solvent exclusion function, and we get the following equation for the Born radius.

$${\left(R_a^{Born}\right)}^{-1}\approx {\alpha }_0\left[\frac{1}{4\pi }\int d\mathbf{r}\frac{1-V_{solute}(\mathbf{r}-{\mathbf{r}}_a)}{{\left(r_{a,\mathbf{r}-{\mathbf{r}}_a}\right)}^4}\right]+{\alpha }_1{\left[\frac{1}{4\pi }\int d\mathbf{r}\frac{1-V_{solute}(\mathbf{r}-{\mathbf{r}}_a)}{{\left(r_{a,\mathbf{r}-{\mathbf{r}}_a}\right)}^7}\right]}^{1∕4}$$ (eq. 10)

Here, r_{a, r–ra} is the radial distance between the point in space (r–r_a) and atom a. Being a function of all atoms of the solute, V_solute(r–r_a) can be expressed as a product of each atom's volume as follows.

$$V_{solute}(\mathbf{r}-{\mathbf{r}}_a)=\prod _b^{soluteatoms}{v}_b\left(r_{b,\mathbf{r}-{\mathbf{r}}_a}\right)$$ (eq. 11)

Here r_{b, r–ra} is the distance between atom b and the point in space r–r_a, and ν_b is the atomic volume-inclusive function. This function determines whether a given point in space is inside (0), or outside (1) an atom. Since discontinuities in the dielectric boundary can cause numerical instability in calculations of solvation forces, we employ a simple switching function in ν_b from which GBSW derives its name. The switching function blurs the hard boundary with a cubic function, and continuously links the interior and exterior of an atom in the following relationship.

$$v_a\left(r\right)=\{\begin{array}{cc}0\hfill & r\le R_a^{atom}-s_w\hfill \\ \frac{1}{2}+\frac{3}{4s_w}\left(r-R_a^{atom}\right)-\frac{3}{4{s_w}^3}{\left(r-R_a^{atom}\right)}^3\hfill & R_a^{atom}-s_w<r<R_a^{atom}+s_w\hfill \\ 1\hfill & r\ge R_a^{atom}+s_w\hfill \end{array}\phantom{\}}$$ (eq. 12a)

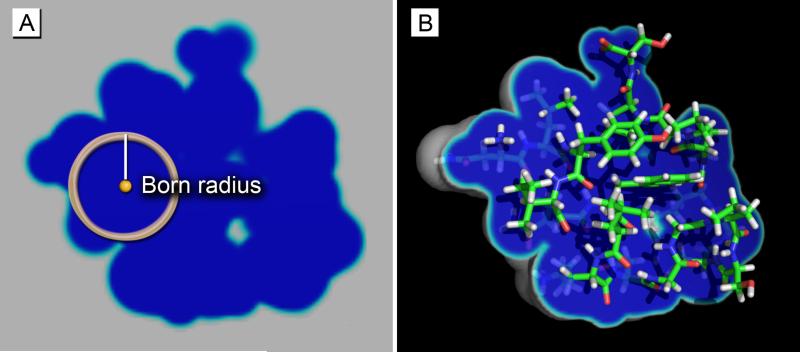
The term ν_a is a function of distance r from the center of atom a. $R_a^{atom}$ is the atomic radius of atom a that defines a dielectric boundary that is consistent with PB calculations, and s_w is the switching length that determines the thickness of the switching function. The default switching length in GBSW is 0.3 Å.¹³ One of the most noticed benefits of the switching length is it fills small voids with atomic density, which in turn corrects for an underestimation on the Born radius when integrating over small crevices. Figure 1a illustrates the Born radius relative to an atom inside a molecule, and figure 1b shows a cross-section of the switching function.

Figure 1.

A) The Born radius (white line) of an atom (yellow ball) is shown with respect to the molecular surface cross-section of a Trp-Cage miniprotein. Notice it is the approximate distance to the solvent. B) The same protein is shown with a partially-removed isosurface of atom density, which ranges from “solute” (dark blue) to “solvent” (white). The switching function exists in between (cyan), which makes the solute-solvent transition continuous.

Interestingly, when the atomic radii are optimized to recapitulate the exact Born energy from PB calculations, they differ from the van der Waals radius used for Lennard-Jones potentials. Chen et al. have produced the latest such modifications to atomic radii for amino acid side chains, which include larger radii for methyl carbons and zero radii for hydrogens.^30,40

In equation 12a we find a method for including the low-dielectric environment of an implicit membrane. Much like how the solvent volume exclusion functions (eq. 11 and 12a) simulate the low dielectric of a protein's interior by removing atom-sized volumes from the solvent, the low dielectric environment inside of a membrane is simulated by removing a slab of solvent volume in the following manner:^13,33

$$v_{mem}\left({\mathbf{r}}^z\right)=\{\begin{array}{cc}0\hfill & \mid {\mathbf{r}}^z\mid \le R^{mem}-s_w\hfill \\ \frac{1}{2}+\frac{3}{4s_w}\left(\mid {\mathbf{r}}^z\mid -R^{mem}\right)-\frac{3}{4{s_w}^3}{\left(\mid {\mathbf{r}}^z\mid -R^{mem}\right)}^3\hfill & R^{mem}-s_w<\mid {\mathbf{r}}^z\mid <R^{mem}+s_w\hfill \\ 1\hfill & \mid {\mathbf{r}}^z\mid \ge R^{mem}+s_w\hfill \end{array}\phantom{\}}$$ (eq. 12b)

Here we see that if the absolute value of the z-coordinate of a point in space r^z is such that it is less than the membrane's half-thickness, R^mem, then the membrane's switching function applies to that point in space. This option enables a membrane-like low dielectric to interact with the solute molecule, which scales an atom's Born radius by both its buriedness in a solute molecule, and by its buriedness in a membrane. This setup has been useful in predicting structures of transmembrane domains of G protein-coupled receptors.⁴¹

Numerical Quadrature

Im et al.¹³ optimized a spherical quadrature method for calculating the Born radii as a means to sample the atomic density surrounding each atom, and rapidly calculate the volume exclusion functions 1–V_solute(r–r_a). The setup involves placing points of integration (quadrature points) around each atom, determining the ν_a values for each atom near those quadrature points, calculating the value of 1–V_solute(r–r_a), and scaling the result of each point by a corresponding volumetric weight. Retooling equation 9 with quadrature points results in

$${\left(R_a^{Born}\right)}^{-1}\approx {\alpha }_0\left[\sum _{quad}{w}_{quad}\frac{1-V_{solute}({\mathbf{r}}_{quad}+{\mathbf{r}}_a)}{{\left(r_{a,{\mathbf{r}}_{quad}+{\mathbf{r}}_a}\right)}^2}\right]+{\alpha }_1{\left[\sum _{quad}{w}_{quad}\frac{1-V_{solute}({\mathbf{r}}_{quad}+{\mathbf{r}}_a)}{{\left(r_{a,{\mathbf{r}}_{quad}+{\mathbf{r}}_a}\right)}^5}\right]}^{1∕4}$$ (eq. 13)

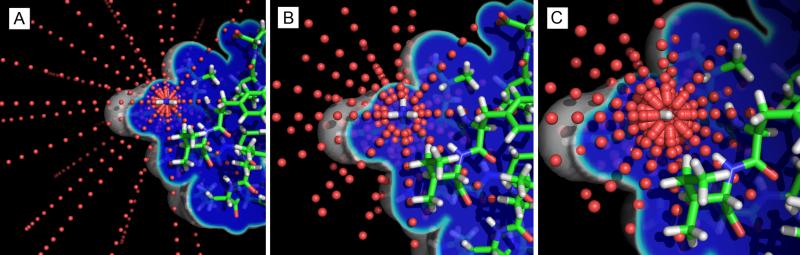
Here w_quad is the integration weight for a quadrature point, and r_quad+r_a is the placement of that quadrature point in space as projected from atom a. Meanwhile, r_{a, rquad+ra} is the distance between atom a and the quadrature point r_quad+r_a. The default quadrature point cloud of GBSW is comprised of 1200 points that are determined by the combination of a 50-point Lebedev quadrature⁴² and two second-order Gaussian-Legendre quadratures.⁴³ The angular Lebedev quadrature distributes 50 points on the surface of a unit sphere, and each radius of both Gaussian-Legendre quadratures scales a Lebedev quadrature to sample a volume. The 24 radii are determined by a 5-radius Gaussian-Legendre quadrature from 0.5 Å to 1 Å, and another 19-radius quadrature from 1 Å to 20 Å. The result is 1200 points that sample a spherical volume around each atom, and 500 points within a 1 Å radius around each atom. In addition to offering a high sampling rate near each atomic center, the quadrature setup also provides an integration process that is straightforward to parallelize: the integration value at each point can be performed independently from the others. Figure 2 illustrates the quadrature point cloud around each atom. Notice that the (4π)⁻¹ from eq. 13 is included in the weights of the Levadev quadrature.

Figure 2.

A) The original 1200 quadrature point cloud (red dots) around the R1 N atom of Trp-Cage miniprotein. Each point samples its local atom density V_solute(r) as being 1 (dark blue; inside an atom), 0 (outside an atom), or in between (cyan), and offers a contribution to the atom's Born radius. B) The modified 350 quadrature point cloud which retains the quadrature points that most contribute to the Born energy and Born force. Points near the atom's center are assumed to have V_solute(r)=1, and points far from the atom are assumed to have V_solute(r)=0. The remaining points recapitulate greater than 99.5% of the original force vectors and atom-wise energy. C) The modified 500 quadrature point cloud for hydrogen atoms, here around the R1 HT2 atom of Trp-Cage. Similarly to the nitrogen atom's quadrature scheme, points very close and very far from the atom's center are unnecessary to calculate explicitly. Since hydrogen has a smaller atomic radius than nitrogen, fewer quadrature points near the atom's center could be omitted.

As we will discuss later, not all the quadrature points contribute equally to solvation free energy. Figure SI2 illustrates the effects on solvation free energy associated with omitting radial shells of integration points from the Gaussian-Legendre quadratures. In Figure 2b and 2c we show the actual quadrature point clouds used in the algorithm developed in this study.

Nonpolar energy

The nonpolar contribution ΔG^np represents the energy used to cavitate a solvent around a solute. Although physically relevant, this component of the energy is not included in the GBSW model by default. Nevertheless, we discuss its implementation.

Schaefer and coworkers along with modifications from Jay Ponder calculated the nonpolar energy of solvation with the following relationship,^35,44

$$\Delta G^{np}=\sum _a\Delta G_a^{np}=4\pi \gamma \sum _a{\left(R_a^{atom}+R^{probe}\right)}^2{\left(\frac{R_a^{atom}}{R_a^{Born}}\right)}^6$$ (eq. 14)

Here ΔG^np is a sum of nonpolar contributions from each atom a, each of which is derived from a relationship among the atomic radii $R_a^{atom}$, Born radii $R_a^{Born}$, the phenomenological constant γ, and the “probe radius” R^probe, which corresponds to the radius of a water-molecule-sized sphere. The original fraction had an exponent of 1 but unpublished work from Ponder found that a higher-order exponent of 6 better captured the solute molecule's solvent-accessible surface area. This equation establishes that the smaller the Born radius of an atom, the closer it is to the solvent, and thus it has a larger contribution to the surface area. Conversely an atom with a large Born radius is far from the solvent-accessible surface area, and thus gives a smaller surface area contribution. The higher exponent greatly enhances this relationship, and better removes the contributions to the surface area from buried atoms with larger Born radii. Again we note that the nonpolar contribution to solvation free energy is small, and ignored by default in GBSW. Should the nonpolar energy and forces be enabled during a simulation, we adopted the formalism already used in OpenMM to calculate it.³⁵

Calculating the forces

Calculating the forces of implicit solvation becomes complicated because the effective Born radius of an atom is a function of all solute atoms in the system. Thus the force on any atom also depends on the placement of every other atom in the system. When we deconvolve the force with respect to atom-atom distances and Born radii, we arrive at,

$$\frac{\partial \Delta G^{elec}}{\partial {\mathbf{r}}_a}=\frac{\partial \Delta G^{elec}}{\partial r_{ab}}\frac{\partial r_{ab}}{\partial {\mathbf{r}}_a}+\sum _b\frac{\partial \Delta G^{elec}}{\partial R_b^{Born}}\frac{\partial R_b^{Born}}{\partial {\mathbf{r}}_a}$$ (eq. 15)

Here we find two terms. The first force component is centralized on atom a, and is a Coulomb-like interaction between atom pairs. When expressed in greater detail, it becomes

$$\frac{\partial \Delta G^{elec}}{\partial r_{ab}}\frac{\partial r_{ab}}{\partial {\mathbf{r}}_a}=\frac{\tau }{4}\sum _{ab}\frac{q_a{q}_b\left[4-\exp \left(-D_{ab}\right)\right]}{{\left(f_{ab}^{GB}\right)}^3}\left({\mathbf{r}}_b-{\mathbf{r}}_a\right)$$ (eq. 16a)

where

$$D_{ab}=\frac{r_{ab}^2}{R_a^{Born}{R}_b^{Born}}$$ (eq 17)

For systems with a low salt concentration, and a non-zero Debye-Huckel screening parameter, we instead arrive at

$$\frac{\partial \Delta G^{elec}}{\partial r_{ab}}\frac{\partial r_{ab}}{\partial {\mathbf{r}}_a}=\frac{1}{4}\sum _{ab}\frac{q_a{q}_b\left[4-\exp \left(-D_{ab}\right)\right]}{{\left(f_{ab}^{GB}\right)}^3}\left({\mathbf{r}}_b-{\mathbf{r}}_a\right)\left(\frac{\tau }{f_{bc}^{GB}}+\kappa \frac{e^{-\kappa f_{bc}^{GB}}}{{\epsilon }_s}\right)$$ (eq. 16b)

Here the r_b–r_a gives direction to the force vector. Meanwhile, the atomic charges, distances, and Born radii scale the force. We note that when a and b are equal, the force of this component is zero. The second component arises from the electric displacement of solute atoms in a continuous dielectric, and effectively is the interaction between an atom and the molecular surface. When interpreted in the context of GBSW's quadrature, we see that it emerges as an atom-quadrature point interaction. The force is scaled first by deriving the Still equation (eq 1) with respect to the change in neighboring atoms’ Born radii:

$$\frac{\partial \Delta G^{elec}}{\partial R_b^{Born}}=\frac{\tau }{2}\sum _{bc}\frac{q_b{q}_c\exp \left(-D_{bc}\right)}{{\left(f_{bc}^{GB}\right)}^3}\left(R_c^{Born}+\frac{r_{bc}^2}{4R_b^{Born}}\right)$$ (eq. 18a)

For systems with a non-zero Debye-Huckel screening parameter we alternatively arrive at

$$\frac{\partial \Delta G^{elec}}{\partial R_b^{Born}}=\frac{1}{2}\sum _{bc}\frac{q_b{q}_c\exp \left(-D_{bc}\right)}{{\left(f_{bc}^{GB}\right)}^2}\left(R_c^{Born}+\frac{r_{bc}^2}{4R_b^{Born}}\right)\left(\frac{\tau }{f_{bc}^{GB}}+\kappa \frac{e^{-\kappa f_{bc}^{GB}}}{{\epsilon }_s}\right)$$ (eq. 18b)

The remaining component of the force computes the atom-molecular surface interaction as atom-quadrature point $\partial R_b^{Born}∕\partial {\mathbf{r}}_a$ contributions. This becomes

$$\frac{\partial R_b^{Born}}{\partial {\mathbf{r}}_a}={\left(R_b^{Born}\right)}^2\sum _{quad}{w}_{quad}\left[\frac{a_0}{{\left(r_{b,{\mathbf{r}}_{quad}+{\mathbf{r}}_b}\right)}^2}-\frac{a_1}{32{\left(r_{b,{\mathbf{r}}_{quad}+{\mathbf{r}}_b}\right)}^5}{\left(\frac{\tau q_b^2}{\Delta G_b^{elec,1}}\right)}^3\right]\frac{-\partial V_{solute}\left({\mathbf{r}}_{quad}+{\mathbf{r}}_b\right)}{\partial {\mathbf{r}}_a}$$ (eq. 19)

where

$$\frac{\partial V_{solute}({\mathbf{r}}_{quad}+{\mathbf{r}}_b)}{\partial {\mathbf{r}}_a}=\sum _{b\ne a}\frac{V_{solute}({\mathbf{r}}_{quad}+{\mathbf{r}}_b)}{v\left(r_{a,{\mathbf{r}}_{quad}+{\mathbf{r}}_b}\right)}\left(\frac{3}{4s_w}-\frac{3}{4{s_w}^3}{(r_{a,{\mathbf{r}}_{quad}+{\mathbf{r}}_b}-R_a^{atom})}^2\right)\frac{{\mathbf{r}}_{quad}+{\mathbf{r}}_b-{\mathbf{r}}_a}{\mid {\mathbf{r}}_{quad}+{\mathbf{r}}_b-{\mathbf{r}}_a\mid }+\sum _{a=b,a\ne c}\frac{V_{solute}({\mathbf{r}}_{quad}+{\mathbf{r}}_a)}{v\left(r_{c,{\mathbf{r}}_{quad}+{\mathbf{r}}_a}\right)}\left(\frac{3}{4s_w}-\frac{3}{4{s_w}^3}{(r_{c,{\mathbf{r}}_{quad}+{\mathbf{r}}_a}-R_c^{atom})}^2\right)\frac{{\mathbf{r}}_{quad}+{\mathbf{r}}_a-{\mathbf{r}}_c}{\mid {\mathbf{r}}_{quad}+{\mathbf{r}}_a-{\mathbf{r}}_c\mid }$$ (eq. 20)

The derivative of the volume exclusion function V_solute is split between one part where quadrature points from an atom a mediate an interaction with atoms b, and the inverse where atom a is interacting with a quadrature point of another atom c. Notice that for quadrature points where V_solute(r_quad)={0, 1} there will always be at least one switching function such that ∂ν(r)/∂r_a=0. Thus eq. 20 only receives contributions from quadrature points residing at the dielectric boundary where there is a nonzero slope of the volume exclusion function in eq. 12 and 13. We have arrived at the equations GBSW uses to generate both the solvation free energy, and its derivative force on all solute atoms. The most computationally-demanding portion of this algorithm is calculating the quadrature point contributions. The demand arises both from the great number of quadrature points in the system, and their potential interaction with any atom in the solute. Fortunately these challenges were met well by the nature of GPU architecture. Now we explore the framework used to perform this calculation both efficiently and in parallel.

Function Design and Parallelization

The GPU languages CUDA and OpenCL are designed for massively-parallel processes, or kernels, that execute efficiently when a problem can be divided into many smaller parallel pieces. Due to their architecture, processing time is both related to the speed of each processing core as well as the number of processing cores. Graphics chips of today can have up to many tens of multiprocessors, each consisting of up to 64 discrete processing cores. Thus kernels at minimum must be split into thousands of parallel tasks to take full advantage of the parallel architecture of today's GPUs.

The overall structure of a kernel running on a GPU is divided into blocks and threads, and data is stored in a hierarchical memory structure of increasing speed and decreasing capacity: global, shared, and local memory. Blocks are parallel processes that can ideally run in any order, and only communicate to each other on global memory. These processes are analogous to the multi-processor tasks in C++, Fortran, and other multi-processor CPU languages. Unlike the CPU, however, each of these parallel tasks can be further subdivided into groups of related threads on a GPU. On graphics cards, each thread has its own local memory, and threads can communicate through a high-speed shared memory as they process a calculation. Additionally, threads can initiate, stop, and synchronize with other threads, allowing for a precise level of control over both data management and speed. For instance, this study covers a kernel used for quadrature integration that designates one block for each atom, and one thread for each quadrature point. Midway through the calculation, all threads in a block share Born radii calculation results and intermediate values to compute Born radius gradients.

Although a fast implementation of GBSW can be built directly from CUDA, a myriad of complexities arise if the code is to be robust on all computing systems. Depending on the year a GPU was manufactured, available memory, number of processors, and thread management capabilities are different. The OpenMM software toolkit developed by Eastman et al.³⁵ addresses this complexity through a rapid update cycle, and an execution step that effectively redesigns kernels to suit the available hardware. Its accomplishments were notable enough to the CHARMM community that a CHARMM-OpenMM interface was developed so that CHARMM could take advantage of GPUs in an efficient manner. Simulations can now be designed using CHARMM's robust algorithms for processing macromolecules, and through the software interface, CHARMM controls OpenMM's kernels to run the dynamics of a simulation. The GBSW algorithm was developed as a stand-alone solvent model within OpenMM, and as part of the CHARMM-OpenMM interface. This way the GBSW kernels are slightly tailored to different GPU hardware under the guidance of OpenMM, and effectively utilize a wide range of available hardware.

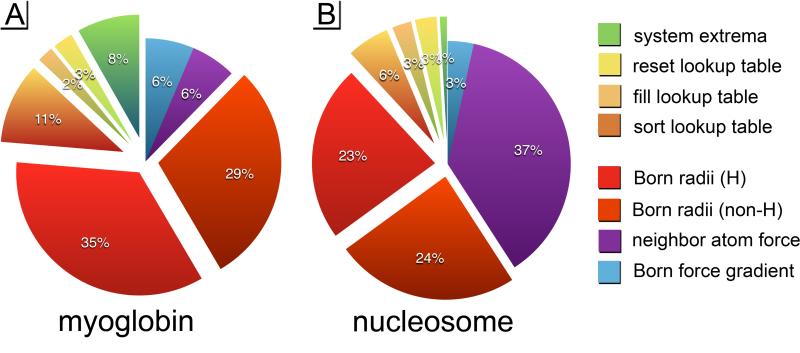
The GBSW calculation is broken up into a total of 8 kernels, 4 of which organize an atom-lookup table, and the other 4 calculate the Born energies and forces on each atom. The lookup table is a multidimensional array that facilitates the rapid calculation of the Born radii, and is the most memory-intensive part of the calculation. Meanwhile calculating the Born energy and forces are the most computationally-intensive. In the next few sections we discuss the details of those kernels, and overcoming the challenges associated with them. The approximate time spent per kernel is shown in Figure 3.

Figure 3.

These are the approximate distributions of GPU time spent on two systems when run the CUDA-GBSW algorithm: A) myoglobin with 2459 atoms, and B) the eukaryotic nucleosome with 22481 atoms. Notice that the neighbor lookup table is the only kernel that doesn't scale approximately with O(N) complexity. In larger systems the neighbor-atom force becomes the most expensive part of the solvent model calculation.

Baseline of Error

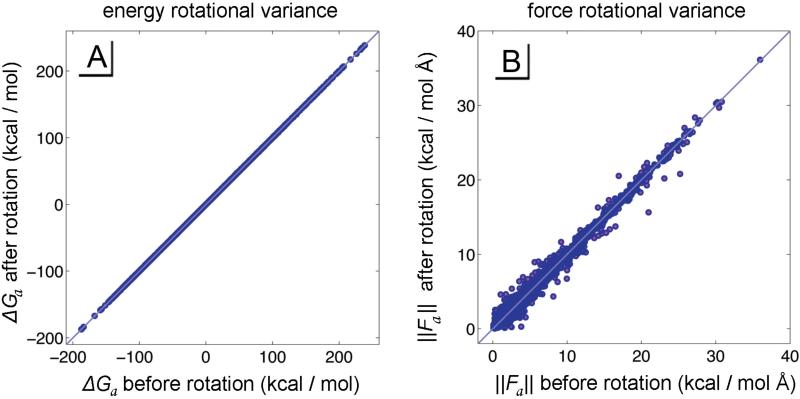
As we explore the various alterations and assumptions made in this iteration of the GBSW algorithm, we must ensure that it accurately recapitulates the original algorithm. Since the quadrature points are fixed along Cartesian coordinates, they do not rotate with the system's atoms. Consequently there is an inherent rotational variance in the energy and force vectors produced by the integration algorithms, as shown in Figure 4. Rotational variance was explored by comparing 100 rotations of a 4,107-atom system generated from the small ribosome subunit proteins S1, S2, and S3 from the PDB 4V88. The standard deviation in forces and angles caused by rotational variance provide a baseline of accuracy for the GBSW algorithm: 0.00029 kcal/mol in system energy, 0.233 kcal/mol Å in atomic magnitudes of force (9.23 % of the magnitude), and 8.01 degrees in atomic angles of force. As we develop the CUDA-GBSW algorithm we use these numbers as qualifiers of accuracy while we refactor the algorithm for parallel processing.

Figure 4.

The rotational variance of the original GBSW model was explored by randomly rotating a 4,107-atom system and observing the resulting changes in forces and energies of each atom. Shown here are the variations for one rotation in A) energy magnitudes and B) force magnitudes of individual atoms (small light blue dots). These data provided a minimum baseline of accuracy for GBSW as we altered the algorithm and made it suitable for parallel processing.

Atom Lookup Table

An important assistant to calculating the Born radii is an atom-lookup table that returns the resident atoms at a given point in space. We found the most efficient memory structure is a voxelized representation of 3-dimensional Cartesian coordinates, where each XYZ grid coordinate contains an array of atoms residing at that gridpoint. An atom a is identified as residing inside all voxels that meet the distance criteria

$$r_{atom,voxel}\le R_a^{atom}+s_w+L_{voxel}\left(\sqrt{3}∕2\right)$$ (eq. 21)

where the atom's distance to a voxel r_{atom, voxel} is small enough that part of the atom (or its switching function) may reside inside a cubic voxel of side length L_voxel. In the Fortran90 implementation of GBSW, the lookup table was a 3D rectangular array with index locations, another 3D rectangular array containing the length of the atom list at a gridpoint, and a large 1-dimensional (1D) array containing the concatenated atom lookup lists at each gridpoint. The two 3D grids provided the location of the local resident atom array within the large 1D array. Because the arrays were resized and reshaped with every timestep, this method gave a small footprint in computer memory.

Unfortunately, the dynamic rearrangement of data within a large 1D array is not efficiently parallelizable, and dynamically allocating memory is not possible inside of a GPU process. To solve these problems we allocate a large 4-dimensional array that holds a small 1D array for every location in 3D space. By converting a point in space to a voxel in the first 3 dimensions, the lookup array returns the small 1D array containing the number of resident atoms at that location, and the atom indices of those atoms. An isosurface representation of the 3D portion of the lookup table is shown in Figure 5. The caveat of this method of data storage is that it requires enough memory to contain all reasonable configurations of the system before any kernels are executed (dimensions X * dimensions Y * dimensions Z * number of voxels per gridpoint). Consequently, this lookup array is the single largest memory requirement for most, if not all, GPU simulations using the GBSW implicit water model. Thankfully, though, graphics memory is relatively cheap and seems to be more plentiful with each new generation of GPU's. We find the parallelized 4D array requires about 11 times the memory footprint of the previous algorithm, but now each voxel can be processed in parallel.

Figure 5.

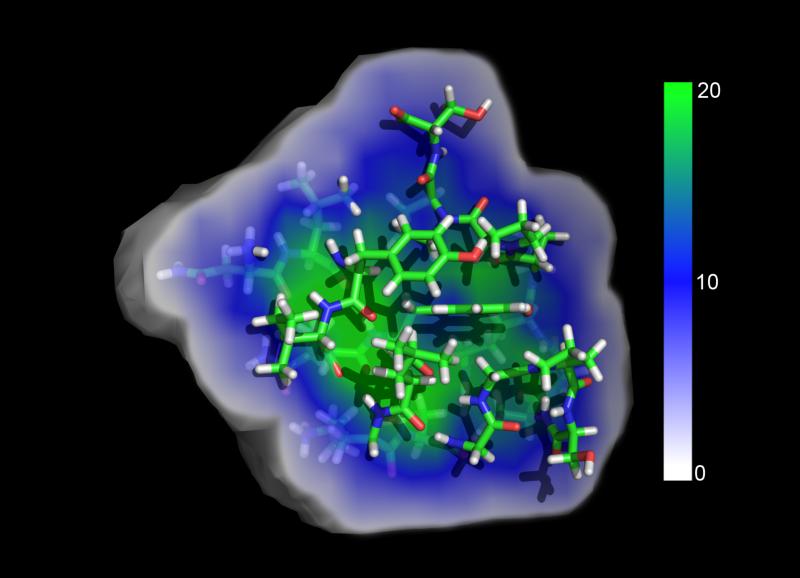
The lookup table is a multidimensional array that tracks which atoms exist in what part of space by using a 3D grid. Each grid voxel is a cube with a side length of 1.5 Å. Shown here is a cutaway representation of the number of atoms at each gridpoint, ranging from white (0 atoms) to green (20+ atoms). The condition that determines whether or not an atom resides in a voxel is shown in eq. 21.

A cubic voxel length L_voxel of 1.5 Å is used for the lookup table, which allows for a rapid filling of the lookup table, a smaller 1D atom list in each voxel, and ultimately a smaller memory footprint of the array. Decreasing this length increases memory requirements exponentially, but decreases the time spent calculating the energies and forces. This value may change as memory on GPU chips becomes more abundant. Meanwhile, the length of the 1D atom list at each voxel was set to 25 atoms. This length was found to contain a sufficient number of atom indices for an accurate GBSW calculation as shown in Figure 5. Although some regions of space may contain more than 25 atoms, there is a diminishing influence on Born forces and Born energy when additional atoms are accounted for. As shown in the Supporting Information (SI) Figure SI1, setting 23 as the maximum number of atoms still provides accurate calculations of Born forces and energies.

Adding a buffer or an extension to the radial parameter L_voxel($\sqrt{3}∕2$) can reduce the need to update the lookup table with every timestep. This change, however, not only increases the burden on memory allocation, but also increases the amount of time needed for the expensive Born radii calculation. Ultimately the GBSW algorithm is fastest when each voxel stores the shortest atom list possible. As a side note, the nearest-neighbor atom lookup tables used for Lennard-Jones and electrostatic force calculations can also be used to calculate a correct set of Born radii. This form of calculating GBSW requires that all quadrature points around an atom need to check their distance from all neighboring atoms of atom a. This arrangement would make the Born radius calculation prohibitively inefficient, and was only explored as a means of checking the accuracy of the calculations.

The lookup table kernels run in O(N) time, where for 2 kernels N is the number of atoms, and for the other 2 N is the number of voxels in the system. Because there are volume-dependent components to this calculation, conformation can change the speed of creating the atom lookup table. Despite its complexity, this CUDA algorithm is approximately 90 times faster than its previous CPU iteration, and it owes most of its speed increase to the fact that it now runs in parallel. A full description of the lookup table kernels follows in Table 1.

Table 1.

Layout of the 4 lookup table kernels.

kernel	no. blocks	no. threads per block	description
System extrema	1	64	Calculate the maximum and minimum dimensions of the system, define the size and shape of the lookup table. When periodic boundaries are used, these calculations only need to be performed once and this kernel is ignored.
Reset lookup table	dimX * dimY * dimZ	1	Each block attends one voxel, and the single thread in each block sets the number of atoms per voxel to 0.
Fill lookup table	number of atoms	256	Each block attends one atom, and each thread attends one voxel near that atom. If the atom resides in this voxel (see eq. 21), then this atom's index is recorded.
Sort lookup table	dimX * dimY * dimZ	25	Each block sorts one voxel of space. Each thread sorts one atom in the 1D lookup list at the block's voxel. Atoms are sorted by distance to the voxel's center ratom, voxel using a parallel bubble-sort. Although O(N2) comparisons take place during the sort, the parallel architecture allows it to run in O(N) time. Since the sorted array finds quadrature points inside atoms faster than unsorted arrays, it speeds up the Born radius calculation by about 40 % over using an unsorted lookup table.

Born Radii, Forces, and Energy Calculation

The Born radii calculation consists of calculating the volume exclusion function V_solute for each quadrature point in parallel, and then combining those values to integrate the Born radii using equations 11 through 13. When is portion of the work is combined with a well-designed and sorted lookup table, parallel graphics processing offers a speedup of more than an order of magnitude over the single-core iteration of the algorithm.

Although the Born radii calculation is the most parallelizable part of the GBSW algorithm, it still remains the most computationally expensive kernel as shown in Figure 3. The end goal of this study is to speed up GBSW as much as possible while preparing it for a future of parallel processors, so we set out to determine precisely how many of the quadrature points need to be calculated. The contribution to the Born energy and forces diminishes with r⁻² and r⁻⁵ as shown in eq. 13. Additionally, the default coefficients α₀ and α₁ indicate that the r⁻⁵ term provides the greatest contribution to the calculation. Noting these aspects, we can explore reducing the maximum for quadrature radius r_a,rquad+ra by assuming that V_solute(r)=0 for various integration radii. Additionally, since many quadrature points are guaranteed to reside within atomic radii $R_a^{atom}$, quadrature points closest to the atom centers can be pre-integrated by assuming that V_solute(r)–1. Figure SI2 illustrates the effects on energy and forces from pre-integrating quadrature points near the atom's center, and reducing the maximum for quadrature radius.

We conclude that an accurate calculation of Born energies and forces only requires 500 quadrature points for hydrogens and 350 points for heavier, non-hydrogen atoms. Not only do we reduce the total number of points needed for the algorithm, we also significantly reduce the number of threads required per block. When implemented on the GPU, this new integration setup is roughly 30 times faster than the previous single-core calculations of Born radii. For a visual reference, Figure 2b and 2c show these integration points around atoms.

After calculating the Born radii, neighboring-atom facilities already exist in OpenMM that efficiently calculate (∂ΔG^elec/∂r)(∂r/∂r) and (∂ΔG^elec/∂R^Born) from eq. 16 and eq. 18, respectively, in a single kernel. Additionally, this same kernel calculates the free energy of solvation $\Delta G_a^{elec}$ for each atom, which greatly speeds the majority of the force calculation. These facilities vary greatly in efficiency depending on input parameters and system configuration, but in general marginalize the time requirements for neighboring-atom interactions for solute systems smaller than 20,000 atoms, as shown in Figure 3.

The final component of GBSW is calculating the Born radius gradient ∂R^Born/∂r from eq. 19. The original algorithm for GBSW was optimized for a minimum memory footprint, and consequently favored recalculating values over saving them to memory. As such the Born radius gradient was a stand-alone function that required a similar time as calculating the Born radii. In this parallel iteration of GBSW we calculate the Born radius gradient at the same time as the Born radii, and then we save the resulting $\partial R_b^{Born}∕\partial {\mathbf{r}}_a$ values in a vector array. As with the lookup table, this array was capped with a maximum number of gradient contributions per atom. Figure SI3 shows that a maximum of 196 quadrature interactions per atom does not significantly alter the force calculation, and so a generous cap of 256 interactions was used. The result is a rapid, parallel calculation of both the Born radii and their gradients from which we gain yet more speed improvement over the original algorithm.

With the exception of the neighbor-atom force kernel which runs in O(N) to O(N²) depending on the system configuration and input parameters, the GBSW Born radii and Born force calculations all operate on O(N) time where N is the number of atoms. As we will discuss in the next section, GBSW shows promise in scaling well with system size. For sufficiently large systems, GBSW emerges as one of the fastest solvent methods available at the time of this study. A full description of the Born radii kernels follows in Table 2.

Table 2.

Layout of the 4 Born energy kernels.

kernel	no. blocks	no. threads per block	description
Calculate Born radii for hydrogens	number of atoms	500	Each block attends one hydrogen atom, each thread attends one quadrature point. The atom density Vsolute at each quadrature point is calculated. Then those densities are integrated to generate the Born radius RBorn and the derivative ∂RBorn / ∂r from eq. 13 and eq. 19 respectively.
Calculate Born radii for heavy atoms	number of atoms	350	Each block attends one non-hydrogen atom, each thread attends one quadrature point. This kernel functions the same as the “Calculate Born radii for hydrogens” kernel and calculates RBorn, and the derivative ∂RBorn / ∂r for heavier atoms. The differences lie in the integration offsets and number of threads used to accommodate the larger radii of heavier atoms.
Calculate neighbor-atom force	number of neighbor-atom tiles	256	Each block attends one atom-atom comparison tile of the OpenMM neighbor-atom list, and each thread attends one atom-atom pair in that tile. The atom-atom interactions of all atoms, their Born radii, and charges are combined to calculate (∂ΔGelec / ∂r)(∂r / ∂r) and (∂ΔGelec / ∂RBorn) from eq. 16 and eq. 18 respectively. Additionally, the GBSW free energy of solvation ΔGelec is calculated for the system.
Born force gradient	number of atoms	256	Each block attends an atom, and each thread attends a contribution of $\Delta R_b^{Born}∕\Delta {\mathbf{r}}_a$. The final value of (∂ΔGelec / ∂RBorn)(∂RBorn / ∂r) from eq. 15 is calculated and added to the total force on each atom. If the option for calculating the nonpolar contribution to the solvation free energy is requested, it is calculated in this kernel following eq. 14.

Accuracy and speed gains exhibited by CUDA-GBSW

We have outlined the basic setup of a new parallel CUDA-GBSW algorithm that shows great speed increases over the original Fortran90 GBSW. Although the new algorithm shows the same size-dependent scaling as the original, the new algorithm maintains useful speeds of nanoseconds per day even when used to solvate systems greater than 100,000 atoms. During this study we subdivided the GBSW algorithm into many thousands of parallel tasks, all of which would benefit well with the addition of more processing cores in future graphics chips. This new solvation method is expected to gain speed benefits until each quadrature point thread has its own core. In a smaller system of 1000 atoms with 500 hydrogens, 250,000 parallel threads are used to calculate the Born radii of the hydrogen atoms. Such a system presumably would receive no speed improvements only when more than a quarter-million cores exist on a single GPU.

We benchmarked the CUDA-GBSW algorithm and observed its ability to recapitulate the original GBSW algorithm in CHARMM as shown in Figure 6. The specifications of the benchmarking computer are listed in the Table SI1. For each point in Figure 6E a subselection of the small ribosomal subunit (PDB code 4V88) was used for the benchmark. Since these subselections were not necessarily as dense or compact a system as a folded protein, there was an added cost of processing a large, empty atom lookup grid. With this in mind, the log plot benchmarks slightly underestimate the CUDA-GBSW performance for more compact systems containing the same number of atoms.

Figure 6.

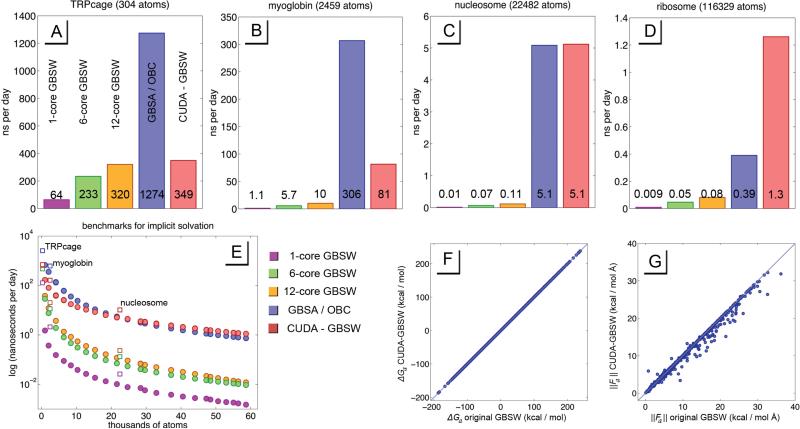
Above in plots A-D are benchmarks for specific systems in nanoseconds per day, which include benchmarks for the original CHARMM algorithm with 1, 6, and 12 cores (purple, green and yellow respectively), a benchmark for the GBSA / OBC algorithm running in OpenMM (blue), and the CUDA-GBSW algorithm discussed in this study (red). Plot E shows a logarithmic benchmark for various system sizes, all of which are comprised of one or more proteins from the small eukaryotic ribosomal subunit. The result is a smooth curve highlighting what system sizes receive what speed gains for various systems. The square icons represent benchmarks for the specific systems in plots A-D. These systems were TRPcage, myoglobin, nucleosome, and the small eukaryotic ribosomal subunit, with PDB codes 1L2Y, 1BVC, 1AOI, and 4V88 respectively. Plots F and G show the accuracy of CUDA-GBSW in recapitulating the forces and energies of the original GBSW algorithm in CHARMM.

We find that for smaller systems such as TRPcage (304 atoms), the CUDA-GBSW algorithm was only slightly faster than the 12-core multiprocessing GBSW, and less than one-third the speed of the CUDA-GBSA/OBC solvation method. However, CUDA-GBSW solvation scales mostly through O(N) scaling. It is an expensive calculation for each member N, but for large enough systems the better scaling compensates for its algorithmic complexity. We find that for systems greater than 22,000 atoms, CUDA-GBSW emerges as a more efficient implicit solvation method than GBSA/OBC, and over an order of magnitude faster than a multiprocessing Fortran90 GBSW solvation. When simulating large systems such as the small ribosomal subunit (116,329 atoms), CUDA-GBSW solvation is over 3 times faster than GBSA/OBC running on the same GPU.

We also reflect that CUDA-GBSW, despite its assumptions and simplifications, reproduces the original GBSW algorithm with less error than its inherent rotational variation. The differences between the two implementations are 0.0027 kcal/mol in system energy, 0.0779 kcal/mol Å in atomic magnitudes of force (1.39 % of the magnitude), and 0.896 degrees in atomic angles of force. These changes amount about a one percent difference between the two version of GBSW. We also note that while the error in calculating system energy is greater than the rotational variance, this error is smaller than one part per one million from an average system energy of −12,255 kcal / mol. Since the CUDA-GBSW algorithm uses single precision calculations, such error in energy calculations is expected. As we observe the error in force calculations in Figure 6G, we see 56 outliers of the 4,107 atom system where the difference in force magnitudes between the GBSW and CUDA-GBSW algorithms exceeds 1 kcal / mol Å. These outliers are both rare, and negligibly affect sidechain dynamics. Thus we conclude that CUDA-GBSW accurately recapitulates the original algorithm of GBSW from CHARMM, and represents a good first iteration of the algorithm in modern parallel graphics processing languages.

Folding Chignolin

Chignolin is a 10-residue peptide consisting of 137 atoms, and when solvated with CUDA-GBSW runs at 438 ns/day in our computer setup. We simulated chignolin starting from in a linear, unfolded state in 8 replicas, each for 1 microsecond. The simulations were run using the CHARMM22 forcefield^45,46 using the Leapfrog Verlet integrator with an integration time step of 2 fs. These were NT simulations in an unbounded volume at a temperature of 298K using a Langevin heat bath. Atomic radii were optimized through work by Chen et al.³⁰ These simulations tested both the numerical stability of CUDA-GBSW during long simulations, and whether the algorithm and force field could find a reasonable structure for the native peptide. We analyzed the trajectories using unbiased k-means clustering to find the dominant conformation, and compared the trajectories to the crystal structure PDB 1UAO through backbone-atom root mean squared deviation (RMSD).

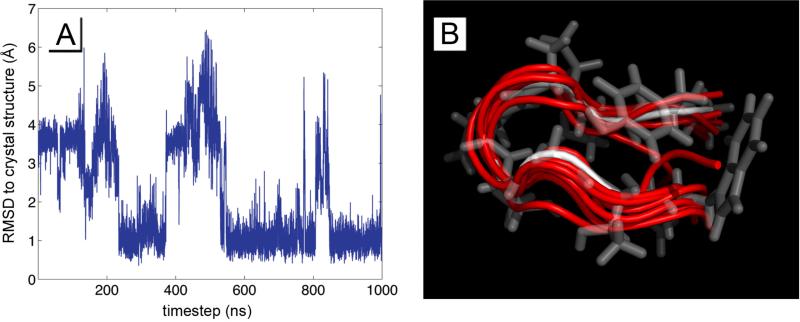
We found that of the 8 replicas, all trajectories explored configurations that were within 0.5 Å RMSD from the crystal structure. Additionally, the k-means clustering reported that 6 out of 8 trajectories were dominated by a structure within 1.5 Å RMSD of the crystal structure. Two simulations reported structures within 0.7 Å RMSD of PDB 1UAO. Figure 7 illustrates an RMSD trajectory, and a backbone-atom overlay of the k-means clustering results.

Figure 7.

Chignolin was simulated in 8 replicas for 1 microsecond, and each trajectory was analyzed by RMSD to the PDB crystal structure 1UAO by backbone carbon atoms, and through an unbiased k-means clustering algorithm. A) shows a typical RMDS trajectory of comparing chignolin to the crystal structure, and B) overlays the dominant configurations from the k-means clustering (red) with the structure from 1UAO (white and transparent).

This exploration was designed only with testing the numerical stability of CUDA-GBSW in mind, and was not optimized for efficiency or accuracy. Nevertheless, it shows that CUDA-GBSW solvation is comparably efficient to other GPU-based GB models in folding chignolin,⁴⁷ and that GBSW running on GPUs remains appropriate for folding small proteins when starting from a linear chain.^48-50 Additionally, these data indicate that the algorithm remains appropriate for exploring the conformational equilibria of small proteins.^48-50

Future Directions

One of the greatest sources of accuracy and error of the GBSW algorithm lies in the placement of quadrature points around each atom. Through the better placement of each point, one may reduce the calculation time of the algorithm or enhance spatial sampling and reduce rotational variance. Each variation on quadrature point placement, though, carries the risk of requiring a full recalibration of the atomic radii and phenomenological constants. For instance, a variation of the Gaussian-Legendre quadrature was explored by using a single radial quadrature rather than two. This implementation, however, reduced sampling near the atomic centers and poorly recapitulated the PB free energies of solvation for each atom.

One possibility of increasing speed is by restricting the Lebedev quadrature only to integrate points away from neighboring atoms. Hydrogen atoms, for example, often lie inside the atomic radii of heavier atoms, and don't require a complete quadrature point cloud. Another option is to scan the solute molecule before a simulation to determine an optimal quadrature point setup for each atom. Such an option could begin the radial Gaussian-Legendre integration at an atom's switching function ($R_a^{atom}-s_w$), rather than the arbitrary distance of 0.5 Å from an atomic center as currently implemented in GBSW.

Although many more variations and improvements upon GBSW remain to be explored, what has been established is a parallel version that will improve greatly with each new generation of graphics chips for many years to come. Finally, we note that another highly accurate, volumetric integration-based generalized Born model, GBMV,²⁷ has a similar algorithmic construction to the GBSW model we studied here. By applying similar GPU-based approaches, such as the CUDA-GBSW lookup table kernels, to the GBMV model, there is potential for giving the algorithm significant speed improvements. This remains a topic for future explorations.