Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2016 Mar 22;6:23186. doi: 10.1038/srep23186

Hybrid metamaterial switching for manipulating chirality based on VO2 phase transition

T T Lv 1,4, Y X Li 1, H F Ma 2, Z Zhu 1, Z P Li 1, C Y Guan 1, J H Shi 1,3,a, H Zhang 3,b, T J Cui 2,c
PMCID: PMC4802382  PMID: 27000427

Abstract

Polarization manipulations of electromagnetic waves can be obtained by chiral and anisotropic metamaterials routinely, but the dynamic and high-efficiency modulations of chiral properties still remain challenging at the terahertz range. Here, we theoretically demonstrate a new scheme for realizing thermal-controlled chirality using a hybrid terahertz metamaterial with embedded vanadium dioxide (VO2) films. The phase transition of VO2 films in 90° twisted E-shaped resonators enables high-efficiency thermal modulation of linear polarization conversion. The asymmetric transmission of linearly polarized wave and circular dichroism simultaneously exhibit a pronounced switching effect dictated by temperature-controlled conductivity of VO2 inclusions. The proposed hybrid metamaterial design opens exciting possibilities to achieve dynamic modulation of terahertz waves and further develop tunable terahertz polarization devices.

Polarization provides a controllable degree of freedom in the field of light propagation and information processing. Polarization devices are crucial in many optical systems. As a fundamental phenomenon, optical activity, that is the ability to rotate the polarization state of light, has acquired great importance in many fields of science including physics, life-sciences and chemistry1. This effect usually occurs in naturally chiral structures that lack mirror symmetry such as DNA, sugar solution and bio-molecules. However, chiral effect in natural media is normally weak and the devices are bulky. Recently, the advent and deep investigations of metamaterials and plasmonics open a promising platform to control the polarization states of light2,3,4. The artificial chirality in metamaterials is much stronger than that in natural media, therefore the corresponding polarization devices are possibly ultrathin and miniaturized that are suitable for lab-on-chip integration. Much attention has been paid to the chiral metamaterials5,6,7,8,9,10,11,12, as significant candidates, for flexibly manipulating the polarization state.

Terahertz (THz) wave occupies a large portion of the electromagnetic spectrum between microwave and infrared frequencies. A variety of metamaterials have been proposed to offer a strong engineered THz response and fill the so-called THz gap13,14,15,16,17,18,19,20,21,22. Many interesting phenomena have been studied in the THz regime, for instance, artificial magnetism13, negative refractive index14, anomalous refraction15, giant optical activity16,17 and asymmetric transmission18. Strong THz fields in metamaterials can lead to promising nonlinear and quantum responses for ultrafast, nonlinear THz photonics and plasmonics19,20,21,22. Remarkably, dynamic THz responses of graphene, liquid crystal, GeSbTe (GST), vanadium dioxide (VO2) and semiconductors enable active THz metamaterials that are excited by external stimuli via electric bias23,24,25,26,27, temperature28,29,30,31,32, photo excitation33,34,35,36,37,38 or MEMS39,40, which are capable of dynamic and flexible modulation of THz waves. Although chiral metamaterials were widely studied5,6,7,8,9,10,11,12,16,17,18, there are only a few attempts to realize dynamic modulation of the optical activity in the THz frequency35,36,37,38. The THz chiral metamaterials integrated with photoactive inclusions can accomplish tunable optical activity35,36, chirality switching37 and tunable linear polarization conversion38, which are controlled by external light illumination. At present, thermal-controlled chirality has been seldom reported32,41. The mid-infrared chiral metamaterials have been demonstrated to show the reversal of the circular dichroism sign and ultrafast tuning of pronounced circular conversion dichroism, respectively, enabled by temperature-controlled phase change materials Ge3Sb2Te632 and Ge2Sb2Te541. As one of the most important phase change materials, VO2 can exhibit an insulator-to-metal phase transition that can be electrically27, thermally28,29,30,31,42,43,44,45, or optically46 tuned. Generally, the temperature controlled phase transition of VO2 is much more preferable28,29,30,31,42,43,44,45. It is interestingly found that the VO2 transition behavior could be tailored by extreme nanogap42,43,44. The hysteresis curve can be narrowed and shift to a low temperature. Hybridizing VO2 with a metamaterial has been shown a large temperature activated tuning of the transmission without polarization conversion in the THz range. It is possible and worthwhile that the asymmetric transmission of linearly polarized wave and circular dichroism can be efficiently modulated by the phase transition effect of VO2, which provides an alternative route to realize switchable and functional THz devices. Actually, some other efficient approaches have been also presented to manipulate the polarization state with metasurfaces. For instance, broadband anomalous deflection can be observed with phase discontinuities47,48. Starting from the fundamental amplitude and phase, the polarization state of light can be tuned by controlling the time retardation with L-shaped microstructured surface49. However, they are not involved in the dynamic and flexible manipulation of the polarization state. A strategy will be demonstrated to realize a dynamic control of polarization conversion and asymmetric transmission in our scheme.

In this work, we report a novel metamaterial-based thermal switch to control artificial chirality and THz wave propagation exploiting the mechanism of VO2 phase transition. The hybrid THz metamaterial is comprised of an array of 90°-twisted E-shaped resonators with incorporated VO2 films. The orthogonal arrangement leads to a strong asymmetric transmission and circular dichroism in the bilayered metamaterial. The insulator-to-metal transition in VO2 films changes the resonator structure as well as the resonant frequency. The hybrid chiral metamaterial allows us to dynamically modify its chiral properties by controlling the temperature-dependent conductivity of VO2. Therefore, the thermal switching of the asymmetric transmission and circular dichroism can be implemented. Such dynamic control of phase transition metamaterials is of importance to acquire a variety of functionalities in the THz regime, such as filters, modulators and switches.

Results

Metamaterial design and simulation method

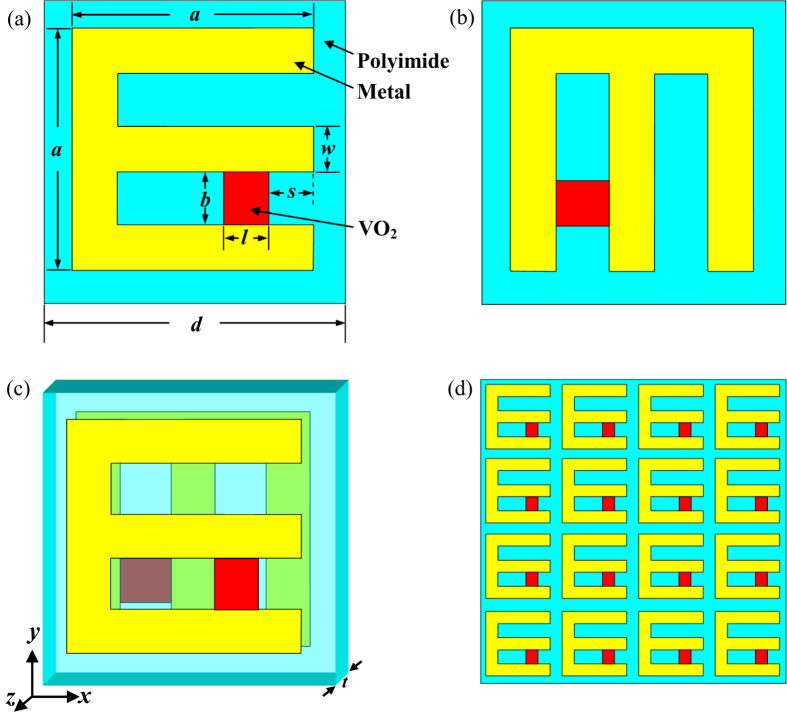
The proposed metamaterial configuration is sketched in Fig. 1. This hybrid metamaterial can be regarded as an array of square stereo E-shaped dimers embedded with VO2 inclusions. The period of the unit cell is d = 100 μm. Each dimer is composed of two spatially separated E-shaped gold resonators with a thickness of tm = 200 nm. The two E-shaped resonators are geometrically identical, but the back layer is twisted by θ = 90° along the z axis with respect to the front one. The spacer dielectric layer is polyimide with a thickness of t = 16 μm. The E shape is square with a length of a = 80 μm. The width of the metallic strip is w = 15 μm. In order to realize a tunable THz metamaterial, VO2 films with a size of b = 17.5 μm and l = 15 μm are incorporated into one of the gaps of E-shaped resonators. The thickness of VO2 films is identical to that of metal layers, i.e., 200nm. The displacement of VO2 is described by s. VO2 film layer can be deposited on the polyimide dielectric by the reactive magnetron sputtering technique28, while VO2 islands and E-shaped metallic resonators can be fabricated by CF4/O2 plasma etching and the photolithography technique28,30. Under an external thermal excitation, VO2 film integrated into the chiral metamaterial will undergo an insulator-metal phase transition process, accompanied by conductivity change up to several orders of magnitude30. Therefore, the associated cross-polarization transmission properties can be modulated in this way. Compared with previous designs such as multilayered rosettes, swastikas and helix, the proposed 90°-twisted E-shaped resonators with incorporated VO2 films has relatively simple geometry, easy integration and more flexibly switching function for the cross-polarization transmission. Besides, a flat cross-polarization transmission and asymmetric transmission can be easily achieved with respect to other simple metamaterial structures. In addition, switching functionality based on phase transition property of VO2 can be applied to other metamaterial designs in microwave, THz and near-infrared frequencies28,29,30,50,51.

Figure 1. Schematic of the hybrid chiral metamaterial.

Figure 1

Open in a new tab

(a) The front layer. (b) The back layer. (c) A unit cell in chiral metamaterial. (d) The top view of the metamaterial.

For a linearly polarized wave beam normally incident on the structure along the -z direction, Jones matrix is used to explore the polarization properties of the hybrid metamaterial. Jones matrix links the complex amplitudes of the incident to the transmitted field:

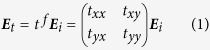graphic file with name srep23186-m1.jpg

where the vectors Ei and Et denote the incident and transmitted electric field, the matrix tf represents the transmission matrix along forward propagation. The matrix tf consists of 2 × 2 elements, in which tjk and |tjk| indicate the transmission complex coefficients and amplitudes. The subscripts j and k correspond to the polarization states of the transmitted and the incident waves, which could be either x or y linear polarization. Here, the two layers are structurally identical, while the second layer structure is twisted clockwise by 90° around the z axis. So, txx is equal to tyy. Since the reciprocal theorem is applied, the transmission matrix tb for backward propagation (along +z direction) can be derived as9,52:

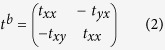graphic file with name srep23186-m2.jpg

In order to further quantify the polarization properties of the metamaterial, the circular transmission coefficients can be inferred from the linearly polarized transmission matrix according to the following equation:

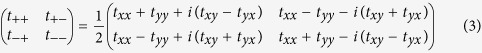graphic file with name srep23186-m3.jpg

where “+” and “−” denote the right-handed (RCP) and left-handed circularly polarized waves (LCP), respectively.

Numerical simulations were performed in the THz range by means of the commercial software CST Microwave Studio, where the lossy polyimide spacer was assumed to have a relative permittivity εp = 2.4 + 0.005i 53 and gold was taken as a lossy metal with the conductivity of σAu = 4.561 × 107 S/m. Generally, the complex dielectric properties of VO2 films in the THz range can be described by the Bruggeman effective-medium theory (EMT)54,

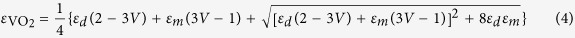graphic file with name srep23186-m4.jpg

where εd and εm, respectively, are dielectric constants of the insulating and metallic phase VO2 films, and V is the volume fraction of the metallic regions. For simplicity, the temperature-dependent conductivity 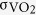Inline graphic can alternatively qualify dynamic insulator-to-metal phase transition of VO2 films28,29,30. The relative permittivity of VO2 films in the insulating state is about 9, while the conductivity in the insulating state is smaller than 200 S/m and as high as an order of 105 S/m in the metallic state55.

Thermal switching properties of 90°-twisted E-shaped metamaterials embedded with VO2 films

VO2 films embedded into the bilayered E-shaped chiral metamaterial experience an insulator-to-metal phase transition under thermal excitation, further modulate the polarization conversion and asymmetric transmission due to the structure change of resonant elements. The electromagnetic responses of the hybrid metamaterials with VO2 films at different temperatures were modeled using the conductivity 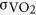Inline graphic. The change of VO2 conductivity from 200 to 105 S/m corresponds to the insulator-to-metal phase transition28,29,30,55. The phase transition occurs on a picosecond timescale, as the VO2 conductivity reaches the value of the metallic state29. The thermal control of the THz metamaterial can be implemented by an attached thin Peltier heater/cooler30.

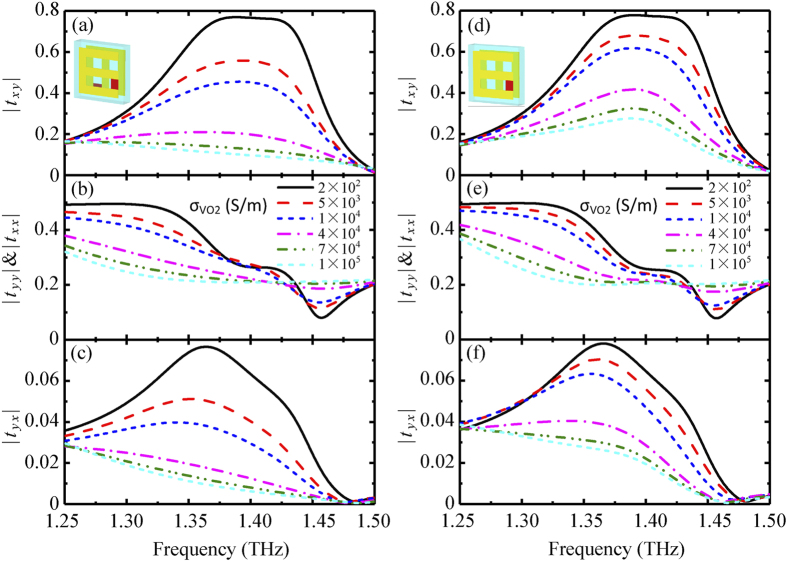
Figures 2(a–c) show the simulated temperature dependence of transmission properties in the hybrid metamaterial incorporated by bilayered VO2 films for forwardly propagating electromagnetic waves along −z direction, where the displacement s = 0. In Fig. 2(a), when the VO2 film is in the insulating state with 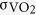Inline graphic  = 200 S/m, corresponding to the temperature of about 25 °C, the E-shaped metamaterial reveals flat y-to-x cross-polarization transmission spectrum in the region centered at 1.4 THz. The transmission maximum is close to |txy| = 77%. Interestingly, this dispersion-free property of the cross-polarization transmitted light only occurs at a specific dielectric layer thickness. The dispersion-free property can be well engineered by the metamaterial’s parameters56,57,58. The intrinsic dispersion of the E-shaped metallic structure with embedded VO2 could actually be cancelled out by the thickness–dependent dispersion of the dielectric layer56. Hence, the cross-polarization transmission has dispersion free within a certain frequency range by properly choosing the thickness of the dielectric layer. As the temperature progressively increases, VO2 film undergoes a change from the insulator phase to the metal phase accompanied by an increasing conductivity. Accordingly, the y-to-x cross-polarization transmission has an obvious reduce. The complete insulator-to-metal phase transition of the metamaterial makes the y-to-x cross-polarization conversion into the “OFF” state. When 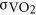Inline graphic reaches 105 S/m, corresponding to the temperature of about 85 °C, the y-to-x cross-polarization conversion |txy| almost decreases less than 0.1 at about 1.4 THz. Particularly, the modulation depth of the y-to-x cross-polarization transmittance is as high as MOD = 96.6%, calculated by Inline graphic.

Figure 2. Simulated thermal switching properties of hybrid chiral metamaterials with s = 0 in forward propagation direction.

Figure 2

Open in a new tab

(a–c) Cross-polarization and co-polarization transmission of hybrid chiral metamaterial incorporated by bilayered VO2 films in either layer as a function of VO2 conductivity. (d–f) Cross-polarization and co-polarization transmission of hybrid chiral metamaterial incorporated by single-layer VO2 film in the front layer as a function of VO2 conductivity. Insets indicate the hybrid metamaterials with bilayered and single-layer VO2 films.

On the contrary, no pronounced switching effect occurs for three other transmission coefficients. The co-polarization transmission tyy and txxdepend weakly on 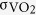Inline graphic and are only thermally modulated in the range of 0.2–0.3 in Fig. 2(b). In Fig. 2(c), the other cross-polarization transmission tyx is totally suppressed below 0.1 in the frequency range of 1.25–1.50 THz no matter what the conductivity 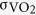Inline graphic is. Considering the sample fabrication easiness, the transmission spectra of hybrid chiral metamaterial incorporated by single-layer VO2 film in the front layer are shown in Fig. 2(d–f). Similarly, an obvious thermal switching effect in single-layer VO2 film integrated metamaterial is available. However, the modulation depth of the y-to-x cross-polarization transmittance decreases to 76% due to slightly high transmission in the metallic state of VO2 film, here the metamaterial can be regards as a combination of E-shaped and 6-shaped resonators. Therefore, the hybrid chiral metamaterial incorporated with single-layer VO2 film can alternatively realize a thermal switching effect of the cross-polarization transmission.

Next, we mainly focus on the chiral switching response of the hybrid metamaterial with bilayered VO2 films. To visualize the thermal controlled polarization effect, the polarization rotation angle θ and its ellipticity angle η of the transmitted wave are calculated according to Eq. 5.

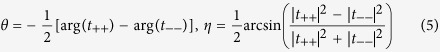graphic file with name srep23186-m12.jpg

Figure 3(a) clearly shows that such hybrid metamaterial is capable of effectively modulating both the polarization rotation angle θ and its ellipticity angle η. When VO2 film is insulating, at about 1.42 THz the transmitted wave is linearly polarized since the polarization rotation angle nearly approaches 60° and the ellipticity angle is close to 0, while at about 1.37 THz the transmitted wave is circularly polarized due to η = 45°. But VO2 film is metallic with its conductivity 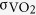Inline graphic = 105 S/m, both the polarization rotation angle θ and its ellipticity angle η are almost 0, thus its chirality is thermally switched off. The giant chirality modification results from the change of the effective metallic geometry when VO2 film experiences a phase transition. Importantly, the hybrid metamaterial can realize thermally controlled linear-to-circular polarization conversion at around 1.37 THz.

Figure 3. Simulated thermally controlled chirality in the hybrid metamaterial with bilayered VO2 inclusions for s = 0.

Figure 3

Open in a new tab

(a) Polarization rotation azimuth angle θ and ellipticity η. (b) Asymmetric transmission parameter Δ. (c) Circular dichroism. The electric field of RCP light rotates anti-clockwise when looking into the coming beam.

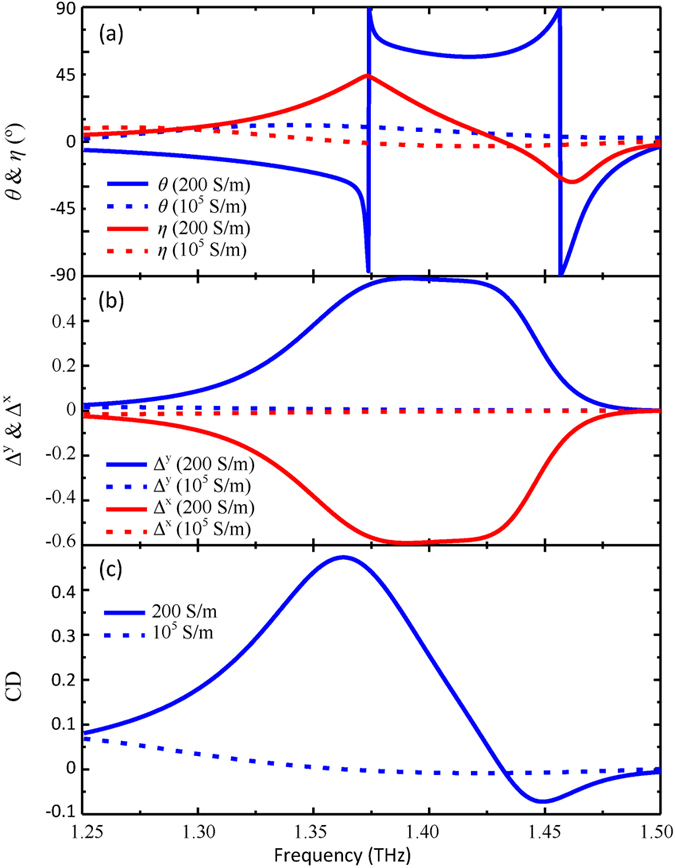
Since |txy| ≠ |tyx| and |txx| = |tyy|, the hybrid metamaterial will reveal the asymmetric transmission of linearly polarized wave. Asymmetric transmission for the linearly polarized wave refers to total intensity difference between two opposite directions and the associated asymmetric transmission parameter can be expressed as:

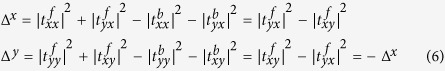graphic file with name srep23186-m14.jpg

The insulator-to-metal phase transition of VO2 films enables this hybrid metamaterial to efficiently switch the asymmetric transmission of linearly polarized waves as shown in Fig. 3(b). Δx and Δy are exactly contrary to each other. Remarkably, the asymmetric transmission parameter can be thermally modulated between 0.6 and 0 in the frequency band of 50 GHz centered at 1.40 THz. Generally, the metamaterial exhibiting asymmetric transmission of linearly polarized wave is anisotropic and 3D chiral. Thus, the hybrid VO2 metamaterial can also thermally control its circular dichroism. The circular dichroism refers to differential transmittance between RCP and LCP waves, which can be calculated by CD = |t++|2 − |t−−|2. Interestingly, the circular dichroism strongly depends on the conductivity of the VO2 film shown in Fig. 3(c). The insulator-to-metal phase transition of the VO2 film leads to a complete switching effect of the circular dichroism with a maximum change of 0.45 at around 1.36 THz. Our demonstration could be of importance to modulate THz wave propagation and recognize interaction between the external stimuli and matter by detecting its chiral properties. The scheme could be exploited for developing novel highly efficient THz polarization modulators and thermal sensors.

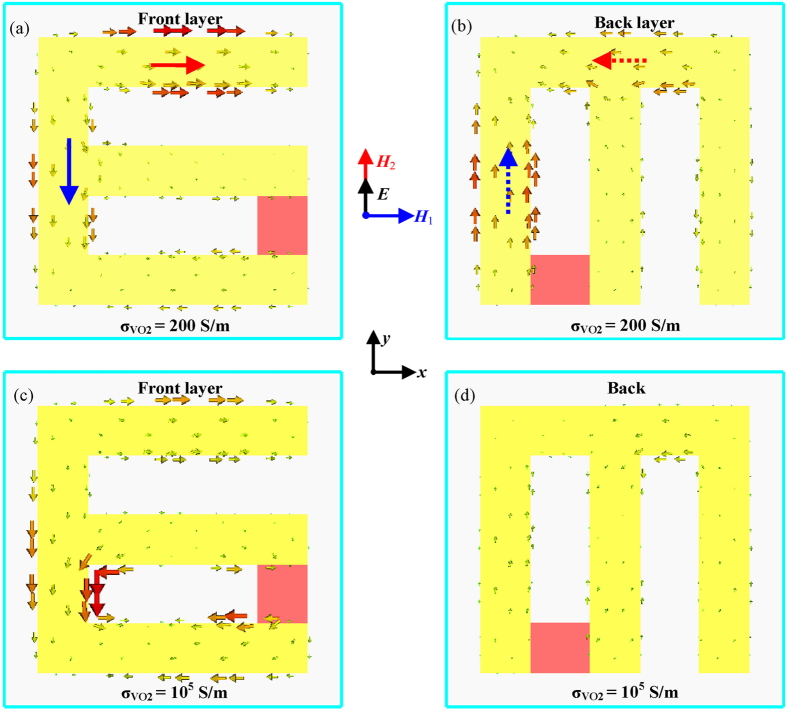
To clarify the physical origin of thermal-controlled switching polarization effect, the Born-Kuhn model can be recalled, in which two charged oscillators couple with each other2,7. The distributions of the instantaneous induced surface currents in the bilayered hybrid VO2 metamaterial at 1.4 THz are simulated and presented in Fig. 4. Without thermal excitation, VO2 film has a very low conductivity and the resonator is E-shaped. The strong antiphase current pairs excited by incident y-polarized wave can result in a magnetic response between the two layers shown in Fig. 4(a,b). The cross coupling happens between the induced magnetic field H2 and the incident electric field E. Therefore, the strong chirality can be observed. While with thermal excitation, VO2 film behaves as metal material and the resonator is 6-shaped. In this case, no strong antiphase current pairs and magnetic response are excited in Fig. 4(c,d). Thus, no strong chirality can be observed. It can be well understood that the thermal switching effect occurs due to the phase change of VO2.

Figure 4. Distributions of induced surface currents of the bilayered hybrid VO2 metamaterial for y polarized incident wave at 1.4 THz.

Figure 4

Open in a new tab

(a,b) Surface currents of the front and back layers without thermal excitation. (i.e., corresponding to 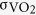Inline graphic = 200 S/m). (c,d) Surface currents of the front and back layers with thermal excitation (i.e., corresponding to 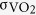Inline graphic = 105 S/m). The bold solid and dashed arrows indicate instantaneous directions of the current flow.

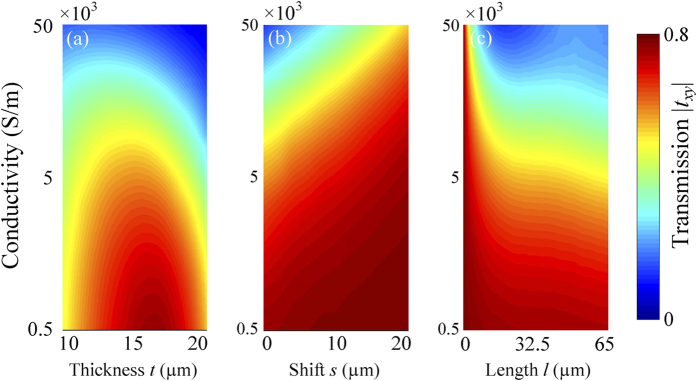
In order to know how geometrical parameters of the metamaterial affect the thermal switching effect, we also perform numerical simulations of the hybrid metamaterial, in which the only one parameter is variable and the others are kept unchanged. The dependence of the switching properties at resonant frequency 1.4 THz is individually investigated on the thickness of polyimide dielectric layer, the displacement and length of VO2 film, shown in Fig. 5(a–c). When the thickness of polyimide dielectric layer increase from 10 to 20 μm, the hybrid metamaterial has an obvious thermal effect since the transmission strongly depends on the VO2 conductivity. In addition, the hybrid metamaterial has the largest switching modulation depth as the thickness of polyimide is about 17 μm. When the displacement s is less than 10 μm and the length l of VO2 films is larger than 10um, the thermal switching effect can be observed in Fig. 5(b,c). Particularly, the thermal switching effect can be engineered to work at other frequencies by changing geometrical parameters.

Figure 5.

Figure 5

Open in a new tab

Geometrical dependence of the thermal switching phenomenon at the resonant frequency 1.4 THz by varying (a) the thickness of polyimide dielectric layer, (b) the shift of VO2 film and (c) the length of VO2 film.

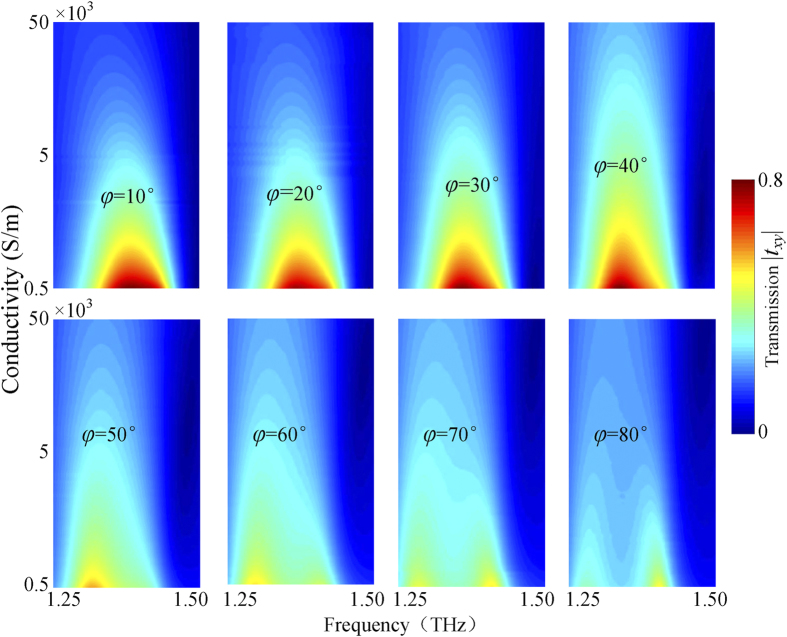
In general, extrinsic 2D and 3D chirality in intrinsically non-chiral metamaterials can be dominated and enhanced by increasing angles of incidence6,11. However, the oblique incidence usually weakens chiral properties in intrinsically chiral metamaterials. Therefore, it is necessary to investigate acceptable angle range for achieving such thermal switching effect. The angular dependence of the thermal switching effect is shown in Fig. 6. When the angle of incidence increases from 0° to 40°, the modulation depth of the cross-polarization transmission txy is almost kept unchanged, but the resonant frequency shifts slightly to red. For angles ranging from 50° to 80°, the modulation depth of the cross-polarization transmission txy has a rapid damping. As a result, no thermal switching effect can be observed in the hybrid chiral metamaterial at a large angle of incidence. It is worth mentioning that the thermal switching functionality in our metamaterial remains fairly available for a wide range of angles up to 40° and thus our design is robust and flexible to manipulate THz wave propagation.

Figure 6. Angular dependence of the thermal switching effect in the bilayered hybrid metamaterial as a function of incident angle φ.

Figure 6

Open in a new tab

Discussion

In conclusion, we have demonstrated a thermal-controlled chiral switching in a hybrid THz metamaterial and the modulation depth of 96.6% is observed at about 1.4 THz for the linear cross-polarization transmittance. The insulator-to-metal phase transition of VO2 films embedded in two 90°-twisted E-shaped resonators promises a dynamic control on polarization rotation angle, circular dichroism and asymmetric transmission of linearly polarized light under external thermal excitation. The transmission maximum is close to |txy| = 77% at about 1.4 THz. Particularly, our simulations show that the thermal switching functionality remains fairly available for a wide range of angles up to 40°. In addition, thermal switching effect can be engineered to work at other frequencies by changing geometrical parameters. Most importantly, the phase change material VO2 can be easily completed. Our work offers flexible polarization modulation in the THz frequency that would be highly beneficial for potential applications such as thermal switching and polarization sensitive detection.

Methods

Numerical simulations were performed in the THz range by means of the commercial software CST Microwave Studio. In the model, the hybrid metamaterial is freestanding that could be possibly fabricated15. The boundary conditions in the x and y directions is set to unit cell boundary conditions due to its periodic structure. The lossy polyimide spacer was assumed to have a relative permittivity εp = 2.4 + 0.005i53 and gold can be taken as a lossy metal with the conductivity of σAu = 4.561 × 107 S/m. Generally, the complex dielectric properties of VO2 films in the THz range can be described by the Bruggeman effective-medium theory (EMT)54. For simplicity, the temperature-dependent conductivity 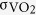Inline graphic can alternatively qualify dynamic insulator-to-metal phase transition of VO2 films28,29,30. The relative permittivity of VO2 films in the insulating state is about 9, while the conductivity in the insulating state is smaller than 200 S/m and as high as an order of 105 S/m in the metallic state55.

Additional Information

How to cite this article: Lv, T. T. et al. Hybrid metamaterial switching for manipulating chirality based on VO2 phase transition. Sci. Rep. 6, 23186; doi: 10.1038/srep23186 (2016).

Acknowledgments

This work is supported by the National Science Foundation of China (Grant Nos. 61275094, U1231201, 613111156), the Natural Science Foundation of Heilongjiang Province in China under Grant No. A2015014, the Heilongjiang Postdoctoral Funds for Scientific Research Initiation (Grant No. LBH-Q15036), the Fundamental Research Funds for the Central Universities and the 111 Project (Grant No. B13015). H.F. Ma acknowledges the support from the Natural Science Foundation of Jiangsu Province under BK20150020. T.J. Cui acknowledges the support from the National Science Foundation of China (Grant Nos. 61302018, 61401089, 61571117, 61501112, and 61501117), and the 111 Project (Grant No. 111-2-05).

Footnotes

Author Contributions J.H.S., H.Z. and T.J.C. conceived the idea, wrote the paper and supervised the work; T.T.L. and Y.X.L. designed the metamaterial; H.F.M. and Z.Z. performed numerical analysis; Z.P.L. and C.Y.G. carried out the EM simulations and prepared the figures; all authors discussed the results and analyzed the data.

References

  1. Barron L. D. Molecular Light Scattering and Optical Activity. Cambridge University Press (2004).
  2. Rogacheva A. V., Fedotov V. A., Schwanecke A. S. & Zheludev N. I. Giant gyrotropy due to electromagnetic-field coupling in a bilayered chiral structure. Phys. Rev. Lett. 97, 177401 (2006). [DOI] [PubMed] [Google Scholar]
  3. Mousavi S. A., Plum E., Shi J. H. & Zheludev. N. I. Coherent control of optical polarization effects in metamaterials. Sci. Rep. 5, 8977 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Ma H. F., Wang G. Z., Kong G. S. & Cui T. J. Independent controls of differently-polarized reflected waves by anisotropic metasurfaces. Sci. Rep. 5, 9605 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Decker M., Klein M. W., Wegener M. & Linden S. Circular dichroism of planar chiral magnetic metamaterials. Opt. Lett. 32, 856 (2007). [DOI] [PubMed] [Google Scholar]
  6. Plum E. et al. Metamaterials: optical activity without chirality. Phys. Rev. Lett. 102, 113902 (2009). [DOI] [PubMed] [Google Scholar]
  7. Yin X., Schäferling M., Metzger B. & Giessen H. Interpreting chiral nanophotonic spectra: the plasmonic born–kuhn model. Nano Lett. 13, 6238–6243 (2013). [DOI] [PubMed] [Google Scholar]
  8. Fedotov V. A. et al. Asymmetric propagation of electromagnetic waves through a planar chiral structure. Phys. Rev. Lett. 97, 167401 (2006). [DOI] [PubMed] [Google Scholar]
  9. Menzel C. et al. Asymmetric transmission of linearly polarized light at optical metamaterials, Phys. Rev. Lett. 104, 253902 (2010). [DOI] [PubMed] [Google Scholar]
  10. Shi J. H. et al. Dual-band asymmetric transmission of linear polarization in bilayered chiral metamaterial. Appl. Phys. Lett. 102, 191905 (2013). [Google Scholar]
  11. Cao T. et al. Extrinsic 2D chirality: giant circular conversion dichroism from a metal-dielectric-metal square array. Sci. Rep. 4, 7442 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Shi J. H. et al. Broadband chirality and asymmetric transmission in ultrathin 90°-twisted Babinet-inverted metasurfaces. Phys. Rev. B 89, 165128 (2014). [Google Scholar]
  13. Yen T. J. et al. Terahertz magnetic response from artificial materials. Science 303, 1494–1496 (2004). [DOI] [PubMed] [Google Scholar]
  14. Zhang S. et al. Negative refractive index in chiral metamaterials, Phys. Rev. Lett. 102, 023901 (2009). [DOI] [PubMed] [Google Scholar]
  15. Grady N. K. et al. Terahertz Metamaterials for linear polarization conversion and anomalous refraction. Science 340, 1304 (2013). [DOI] [PubMed] [Google Scholar]
  16. Singh R., Plum E., Zhang W. & Zheludev N. I. Highly tunable optical activity in planar achiral terahertz metamaterials. Opt. Express 18, 13425–13430 (2010). [DOI] [PubMed] [Google Scholar]
  17. Xiong X. et al. Construction of a chiral metamaterial with a U-shaped resonator assembly. Phys. Rev. B 81, 075119 (2010). [Google Scholar]
  18. Singh R. et al. Terahertz metamaterial with asymmetric transmission. Phys. Rev. B 80, 153104 (2009). [Google Scholar]
  19. Lange C. et al. Extremely nonperturbative nonlinearities in GaAs driven by atomically strong terahertz fields in gold metamaterials. Phys. Rev. Lett. 113, 227401 (2014). [DOI] [PubMed] [Google Scholar]
  20. Kim J. Y. et al. Terahertz quantum plasmonics of nanoslot antennas in nonlinear regime. Nano Lett. 15, 6683–6688 (2015). [DOI] [PubMed] [Google Scholar]
  21. Bahk Y. M. et al. Electromagnetic saturation of angstrom-sized quantum barriers at terahertz frequencies. Phys. Rev. Lett. 115, 125501 (2015). [DOI] [PubMed] [Google Scholar]
  22. Yoshida K. et al. Terahertz field enhancement and photon-assisted tunneling in single-molecule transistors. Phys. Rev. Lett. 115, 138302 (2015). [DOI] [PubMed] [Google Scholar]
  23. Chen H. T. et al. Active terahertz metamaterial devices. Nature 444, 597–600 (2006). [DOI] [PubMed] [Google Scholar]
  24. Chen H. T. et al. A metamaterial solid-state terahertz phase modulator. Nat. Photonics. 3, 148–151 (2009). [Google Scholar]
  25. Mao Z. Q. et al. Widely tunable terahertz phase modulation with gate-controlled graphene metasurfaces. Phys. Rev. X 5, 041027 (2014). [Google Scholar]
  26. Buchnev O. et al. Electrically controlled nanostructured metasurface loaded with liquid crystal: toward multifunctional photonic switch. Adv. Optical Mater. 3, 674–679 (2015). [Google Scholar]
  27. Driscoll T. et al. Memory metamaterials. Science 325, 1518–1521 (2009). [DOI] [PubMed] [Google Scholar]
  28. Wen Q. Y. et al. Terahertz metamaterials with VO2 cut-wires for thermal tunability. Appl. Phys. Lett. 97, 021111 (2010). [Google Scholar]
  29. Liu M. K. et al. Terahertz-field-induced insulator-to-metal transition in vanadium dioxide metamaterial. Nature 487, 345–348 (2012). [DOI] [PubMed] [Google Scholar]
  30. Wen Q. Y. et al. A tunable hybrid metamaterial absorber based on vanadium oxide films. J. Phys. D: Appl. Phys. 45, 235106 (2012). [Google Scholar]
  31. Appavoo K. & Haglund R. F. Polarization selective phase-change nanomodulator. Sci. Rep. 4, 6771 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Yin X. H. et al. Active chiral plasmonics. Nano Lett. 15 (7), 4255–4260 (2015). [DOI] [PubMed] [Google Scholar]
  33. Padilla W. J. et al. Dynamical electric and magnetic response at terahertz frequencies. Phys. Rev. Lett. 96, 107401 (2006). [DOI] [PubMed] [Google Scholar]
  34. Chen H.-T. et al. Experimental demonstration of frequency-agile terahertz metamaterials. Nat. Photonics 2, 295–298 (2008). [Google Scholar]
  35. Kanda N., Konishi K. & Kuwata-Gonokami M. Light-induced terahertz optical activity. Opt. Lett. 34, 3000 (2009). [DOI] [PubMed] [Google Scholar]
  36. Zhou J. et al. Terahertz chiral metamaterials with giant and dynamically tunable optical activity. Phys. Rev. B. 86, 035448 (2012). [Google Scholar]
  37. Zhang S. et al. Photoinduced handedness switching in terahertz chiral metamolecules. Nat. Commun. 3, 942 (2012). [DOI] [PubMed] [Google Scholar]
  38. Lv T. T. et al. Optically controlled background-free terahertz switching in chiral metamaterial. Opt. Lett. 39, 3066–3069 (2014). [DOI] [PubMed] [Google Scholar]
  39. Tao H. et al. Reconfigurable terahertz metamaterials. Phys. Rev. Lett. 103, 147401 (2009). [DOI] [PubMed] [Google Scholar]
  40. Zhu W. M. et al. Microelectromechanical Maltese-cross metamaterial with tunable terahertz anisotropy. Nat. Commun. 3, 1274 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Cao T. et al. Numerical study of achiral phase-change metamaterials for ultrafast tuning of giant circular conversion dichroism. Sci. Rep. 5, 14666 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Seo M. et al. Active terahertz nanoantennas based on VO2 phase transition. Nano Lett. 10, 2064–2068 (2010). [DOI] [PubMed] [Google Scholar]
  43. Jeong Y. G. et al. A vanadium dioxide metamaterial disengaged from insulator-to-metal transition. Nano Lett. 15, 6318–6323 (2015). [DOI] [PubMed] [Google Scholar]
  44. Thompson Z. J. et al. Terahertz-triggered phase transition and hysteresis narrowing in a nanoantenna patterned vanadium dioxide film. Nano Lett. 15, 5893–5398 (2015). [DOI] [PubMed] [Google Scholar]
  45. Kim H. et al. Active terahertz metamaterials based on the phase transition of VO2 thin films. Thin Soild Films 596, 45–50 (2015). [Google Scholar]
  46. Zhang Y. X. et al. Photoinduced active terahertz metamaterials with nanostructured vanadium dioxide film deposited by sol-gel method. Opt. Express 22, 11070–11078 (2014). [DOI] [PubMed] [Google Scholar]
  47. Zhang X. Q. et al. Broadband terahertz wave deflection based on C-shaped complex metamaterials with phase discontinuities. Adv. Mater. 24, 4567–4572 (2013). [DOI] [PubMed] [Google Scholar]
  48. Yu N. F. et al. Light propagation with phase discontinuities: generalized law of reflection and refraction. Science 334, 333–337 (2011). [DOI] [PubMed] [Google Scholar]
  49. Jiang S. C. et al. Tuning the polarization state of light via time retardation with a microstructured surface. Phys. Rev. B 88, 161104 (2013). [Google Scholar]
  50. Zhu Y. H. et al. Tunable dual-band terahertz metamaterial bandpass filters. Opt. Lett. 38, 2382–2384 (2013). [DOI] [PubMed] [Google Scholar]
  51. Duan X. Y. et al. Dynamically tunable plasmonically induced transparency by planar hybrid metamaterial. Opt. Lett. 38, 483–485 (2013). [DOI] [PubMed] [Google Scholar]
  52. Menzel C. et al. Advanced Jones calculus for the classification of periodic metamaterials. Phys. Rev. A 82, 053811 (2010). [Google Scholar]
  53. Ma Y. et al. A terahertz polarization insensitive dual band metamaterial absorber. Opt. Lett. 36, 945 (2011). [DOI] [PubMed] [Google Scholar]
  54. Jepsen P. U. et al. Metal-insulator phase transition in a VO2 thin film observed with terahertz spectroscopy. Phys. Rev. B 74, 205103 (2006). [Google Scholar]
  55. Zhu Y. H. et al. Tunable dual-band terahertz metamaterial bandpass filters. Opt. Lett. 38, 2382–2384 (2013). [DOI] [PubMed] [Google Scholar]
  56. Jiang S. C. et al. Controlling the polarization state of light with a dispersion-free metastructure. Phys. Rev. X 4, 021026 (2014). [Google Scholar]
  57. Sieber P. E. & Werner D. H. Reconfigurable broadband infrared circularly polarizing reflectors based on phase changing birefringent metasurface. Opt. Express 21, 1087–1100 (2013). [DOI] [PubMed] [Google Scholar]
  58. Zhao Y. et al. Tailoring the dispersion of plasmonic nanorods to realize broadband optical meta-waveplates. Nano Lett. 13(59), 1086–1091 (2013). [DOI] [PubMed] [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES