Abstract
This paper presents robot-aided intraocular laser surgery using a handheld robot known as Micron. The micromanipulator incorporated in Micron enables visual servoing of a laser probe, while maintaining a constant distance of the tool tip from the retinal surface. The comparative study was conducted with various control methods for evaluation of robot-aided intraocular laser surgery.
Index Terms: Medical robotics, micromanipulator, surgery, visual servoing
I. Introduction
Intraocular laser photocoagulation is used to treat many common ocular conditions such as diabetic retinopathy [1] and retinal breaks [2]. For optimal clinical outcomes, high accuracy is required, since inadvertent photocoagulation of unintended nearby structures can cause permanent vision loss [3].
To improve accuracy and reduce operating time in laser photocoagulation, automated systems have been developed [4], [5]. However, these systems treat through the pupil, and are designed for the outpatient clinic rather than the operating room [6]. During intraocular surgery, pupil size and media opacity can be controlled by the surgeon; however, manipulation of an intraocular laser probe for precise and efficient treatment of intraocular target is challenging.
Therefore, robot-assisted techniques have been introduced using an active handheld robot known as Micron [6], [7]. Since Micron incorporates a miniature micromanipulator that can maneuver a laser probe, lesions can be treated automatically via visual servoing of the aiming beam emitted from the laser probe. The first demonstration used a three-degree-of-freedom (3-DOF) prototype of Micron [6], whose limited range of motion required a semiautomated coarse/fine approach, with the operator moving the laser probe to within a few hundred microns of each target. Moreover, the distance between the laser probe and the retinal surface was manually controlled, relying on the operator’s depth perception, since the axial range of motion was even smaller than the lateral. Recently, we proposed automated intraocular laser surgery using an improved prototype of Micron [7]. Since the new system provides much greater range of motion, intraocular laser treatment can be automated, while automatically maintaining a constant distance from the retina. Thus, the operator only needs to hold the instrument without further deliberate maneuver. In addition, the 6-DOF manipulation can accommodate the sclerotomy. Consequently, automated laser photocoagulation was demonstrated in a realistic eye phantom, while compensating for eye motion using a retina-tracking algorithm.
However, the initial prototype of the automated system still entails several drawbacks. First, the system requires accurate camera calibration and stereo reconstruction for position-based visual servoing; performance can vary substantially depending on the calibration accuracy. Furthermore, the automated system is susceptible to actuator saturation, since manual drift is compensated and thus invisible to the operator. Accordingly, the preliminary work was limited to a single demonstration in the eye phantom without further quantitative evaluation.
This paper, therefore, introduces hybrid visual servoing for robot-aided intraocular laser surgery, incorporating an adaptive framework to mitigate calibration problems and to improve control. Hand-eye coordination is also maintained by providing the operator with guidance cues during the time of robot-aided operation. Finally, we experimentally compare automated, semiautomated, and unaided manual intraocular laser surgery.
II. Materials and Methods
A. Robot-aided Laser Photocoagulation System
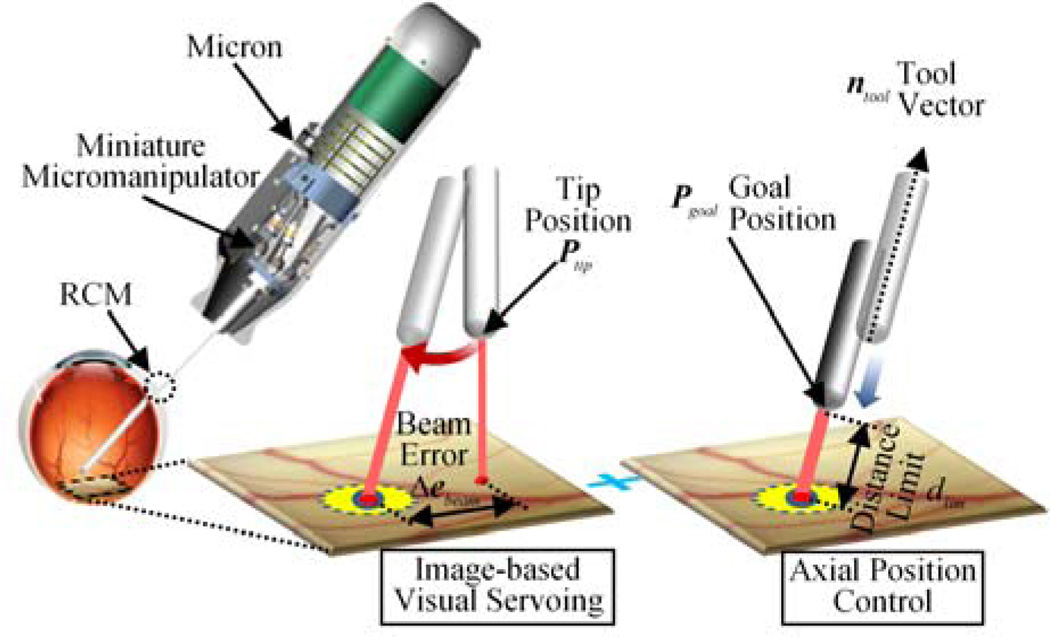
The robot-aided intraocular laser photocoagulation system primarily comprises the active handheld robot, Micron, the vision system, and the laser with the endoprobe, as shown in Fig. 1(a). Micron, presented in Fig. 1(b), incorporates a miniature micromanipulator that provides 6-DOF actuation of an end-effector within a cylindrical workspace 4 mm in diameter and 4 mm high [8]. It thus allows for a remote center of motion (RCM) at the point of entry through the sclera. Micron is also equipped with a custom-built optical tracking system (“Apparatus to Sense Accuracy of Position,” or ASAP). ASAP tracks the position and orientation of the end-effector and handle for control at a sampling rate of 1 kHz with less than 10 µm RMS noise [9]. Hence, the laser probe attached to the micromanipulator can be controlled accurately according to a specified 3D goal position for the laser tip, regarding undesired handle motion as a disturbance. The remaining degrees of freedom in actuation are independently controlled at the RCM by the operator. The vision system consists of a stereomicroscope, two CCD cameras, and a desktop PC. A pair of images is captured by the CCD cameras at 30 Hz and streamed to the PC for further processing. Given the image streams, 2D tip and aiming beam positions are detected by image processing. The 2D tip position is then used for system calibration between the cameras and the Micron control system. The aiming beam of the laser is used for visual servoing of the laser tip. In addition, the vision system is capable of tracking the retinal surface using the ‘eyeSLAM’ algorithm [10] for compensation of eye movement. For laser photocoagulation, an Iridex 23-gauge EndoProbe is attached to the tool adaptor of Micron, and an Iridex Iriderm Diolite 532 Laser is interfaced with the Micron controller.
Fig. 1.
System setup for robot-aided intraocular laser surgery. (a) Overall system setup. (b) Micron with the eye phantom. (c) Guidance cues overlaid on the display screen.
Once patterned targets are placed on a preoperative image, the laser probe is then deflected to correct error between the aiming beam and the given target. During the operation, the system also maintains a constant standoff distance of the laser probe from the retinal surface. As the distance between the aiming beam and the target comes within a specified targeting threshold, the laser is triggered. Once laser firing is detected via image processing, the procedure is repeated until completion of all targets. Alternatively, the robot-aided execution can use a fixed repeat rate in place of a targeting threshold, as is normally used for manual operation. This control mode thus allows direct comparison with unaided operation. For this comparative study, we also implemented the semiautomated control algorithm used in [6], in which automatic control engages whenever the aiming beam comes within 200 µm of an untreated target.
To maintain hand-eye coordination during the time of robot-aided operation, two guidance cues are overlaid on the monitor screen, as shown in Fig. 1(c). The first circular cue on the top of the screen represents the current displacement of the tool tip with respect to the nominal position in the manipulator. Hence, the cue is useful to prevent the manipulator from being saturated by reaching out of its workspace. The second cue shows the displacement of the null position with respect to the initial null position given at the beginning of a trial, where the null position is what the tip location would be if the actuators were turned off. The second cue is thus informative to keep hand-eye coordination, providing the operator with a virtual representation of the displacement of the instrument. Each circle encodes 3D displacement, as a combination of the 2D location and diameter of the circle; these correspond to lateral and vertical displacements, respectively. For seamless robot-aided operation, the operator is instructed to perform a holding-still task by keeping the second red circle centered as much as possible and maintaining a fixed size of the circle, with the blue circle as a reference. However, following these instructions is not strictly required as long as the manipulator is operating inside its workspace, as indicated in the first cue.
B. Hybrid Visual Servoing
We propose a hybrid control scheme for robot-aided intraocular laser surgery, in order to address the issues raised by position-based visual servoing, specifically, due to inaccurate stereo-reconstruction of the aiming beam and retinal surface, including placed targets. Any large error in the calibration procedure may lead to failure of the servoing, which is a weakness of such position-based visual servoing [11]. In the hybrid control, only selected degrees of freedom are controlled using visual servo control, and the others use position servo control. Castaño and Hutchinson introduced a hybrid vision/position control structure called visual compliance [12]. Specifically, the 2-DOF motion parallel to an image plane is controlled using visual feedback, and the remaining degree of freedom (perpendicular to the image plane) is controlled using position feedback provided by encoders.
To apply such a partitioned control scheme to our system, the 3-DOF motion of the tool tip is decoupled into the 2-DOF planar motion parallel to the retinal surface and the 1-DOF motion along the axis of the tool. The decoupled 2-DOF motion is then controlled via image-based visual servoing, to locate the laser aiming beam onto a target position using a monocular camera. The 1-DOF axial motion is controlled to maintain a constant standoff distance from the estimated retinal surface.
The first step is to register the CCD cameras with the Micron control coordinates (called herein the “ASAP coordinates”) by sweeping the tool above the retinal surface as described in [7]. Given multiple correspondences between 2D and 3D tip positions, projection matrices are obtained for the left and right cameras Mc as in (1).
| (1) |
Where and are 2D and 3D ASAP tip positions, respectively. We also reconstruct the 3D beam points that belong to the retinal surface via triangulation of aiming beams detected on images. The retinal surface is then described as a plane by linear least squares fitting on the 3D points, assuming a small area of interest within the eyeball. The resulting plane is thus defined in the ASAP coordinates in terms of a point P0 belonging to the surface, and principal components, u, v, and n. The orthonormal vectors u and v lies on the plane, and n indicates a surface normal.
For image-based visual servoing, we formulate an analytical image Jacobian instead of using image feature points, since it is extremely challenging to robustly extract the feature points during intraocular operation. We first assume that the image plane is parallel to the retinal surface (regarded as a task plane), resulting in an interaction matrix Jp ∈ ℝ2×2 for differential motions, as in (2).
| (2) |
where Δximage and ΔΘtask are differential motions in image and task planes, respectively. To derive the interaction matrix Jp, two differential motions are taken in the task plane with respect to the 3D point P0 lying on the surface, using the orthonormal bases of the plane, u and v :
| (3) |
The corresponding differential motions in the image plane, Δpu and Δpv are then defined, using the projection matrix of the left camera in (1):
| (4) |
Hence, the matrix Jp between the task and image coordinates is composed by the two vectors, Δpu and Δpv, as in (5).
| (5) |
where I2×2 is an identity matrix; the differential motions in the task space, u and v, are subject to canonical bases with respect to the task plane coordinates. The inverse of the interaction matrix, , is obtained by taking the inverse of the matrix [Δpu Δpv] that has full rank.
To control the tool tip in the ASAP coordinates, we extend the 2D vector ΔΘtask to the 3D vector ΔXplane using the orthonormal bases of the plane described in the ASAP coordinates as in (6).
| (6) |
Since the tool tip is located above the plane by dsurf, the actual displacement of the tool tip, corresponding to the motion of the aiming beam on the plane, is scaled down by the ratio of the lever arms, rlever = dRCM / (dRCM + dsurf):
| (7) |
where dRCM is the distance of the tool tip from the RCM. Small angular motion pivoting around an RCM is assumed, as the displacement of the aiming beam is much smaller than the distance of the tool tip from the RCM. Finally, an image Jacobian J is derived for visual servoing, given an error between target and current beam positions on the image plane:
| (8) |
| (9) |
The goal position of the tool tip is set by a PD controller as in (10), subject to minimizing the error between the current aiming beam and the target positions.
| (10) |
When the aiming beam reaches the target via visual servoing, we still have a remaining degree of freedom along the axis of the tool in control. Hence, this 1-DOF motion is regulated to maintain a specific distance dlim between the tool tip and the retinal surface. Consequently, we incorporate a depth-limiting feature with image-based visual servoing in our control to fully define the 3-DOF motion of the tool tip, as in (11).
| (11) |
where ntool is a unit vector describing the axis of the tool. As a result, the 2D error is subject to being minimized via the visual servoing loop, while the distance of the tool tip from the retinal surface is regulated by the position control loop. The corresponding parameters and control procedure are also depicted in Fig. 2.
Fig. 2.
Visualization of the hybrid visual servoing scheme.
C. Image Jacobian Update
Our control scheme also incorporates an image Jacobian update during control in order to compensate any error in deriving such an analytical and static Jacobian. Although image-based visual servoing is achievable with an inaccurate Jacobian, the update framework is still beneficial to increase operation speed and particularly to avoid erroneous movement of the tool tip in microsurgery.
An initial goal position for the tip is set primarily by the image Jacobian derived as in (8), which acts as an open-loop controller. The feedback controller in (10) is then applied, in order to correct the remaining error between the target and current beam positions. This switching scheme is particularly crucial to address issues raised by unreliable beam detection, especially saturation in images at the instant of laser firing. Accordingly, accurate Jacobian mapping would reduce error in the open-loop control, leading to minimal closed-loop control. In addition, the accurate Jacobian allows us to apply high gains to the control without losing stability, which is desirable for control of such a handheld manipulator.
Hence, we update the inverse of the partial Jacobian primarily to compensate the error given by the open-loop control. First, we define a desired displacement of the aiming beam from a previous target to the next one.
| (12) |
The actual displacement of the tool tip is also defined as in the ASAP coordinates as below.
| (13) |
Using Broyden’s method [13], a new inverse Jacobian is formulated:
| (14) |
| (15) |
III. Experiments and Results
We investigated the performance of robot-aided intraocular laser surgery for both “automated” and “semiautomated” operations under a board-approved protocol. Performance was evaluated in terms of accuracy and speed of operation, compared to unaided operation (with Micron turned off). The aided operation was controlled by setting a targeting threshold or a fixed repetition rate. We conducted the experiments under two test conditions: unconstrained (or “open-sky”) and constrained (eye phantom) environments. The open-sky test focuses primarily on the control performance of the robot-aided operation itself, while eliminating effects caused by the retinal tracking algorithm. On the other hand, the eye phantom provides much similar environment to realistic intraocular surgery. However, the overall performance may be affected by disturbance at the RCM, and the accuracy and robustness of the retinal tracking algorithm. Moreover, in the unconstrained experiment, the operator is allowed to freely move the instrument (e.g., both translation and rotation). However, in the constrained experiment, rotation (pivoting around the RCM) and axial motions are rather desirable, since transverse motion leads to the movement of the eye ball, resulting in the movement of the targets.
We introduced triple ring patterns in our experiments, as a typical arrangement for the treatment of diabetic retinopathy [14]. The targets were preoperatively placed on along the circumferences of multiple circles with 600-µm spacing: 1, 2, and 3 mm in diameter. As an indication of the targets, 200-µm green dots were printed on a paper slide, which were used for targeting cues in unaided trials. In addition, four fiducials were introduced to align the preoperative targets with the printed green dots before the procedure. The fiducials were also postoperatively used to provide the ground truth for error analysis, taking into account error resulting from both the servo control and the retinal tracking. To burn targets on the paper slide, the power of the laser was set as 3.0 W with a duration of 20 ms, which yields distinct black burns on the paper. To evaluate the accuracy of operation for each trial, the resulting image was binarized to find black dots and then underwent K-means clustering to find the center of each burn. Error between the burn and the target locations was measured.
A. Open-Sky
A slip of paper was fixed on a flat surface under the operating microscope. In automated trials, five targeting thresholds were set in a range of 30–200 µm, in order to characterize the resulting error and speed of operation, depending on the thresholds. The same setting was also adopted in semiautomated trials. For unaided operation, repetition rates were set to be 0.5–2.5 Hz with a step increment of 0.5 Hz, as acceptable results were attainable only with the rate below 2.5 Hz. We also repeated these tests for four trials and averaged errors, resulting in a total of 128 burns.
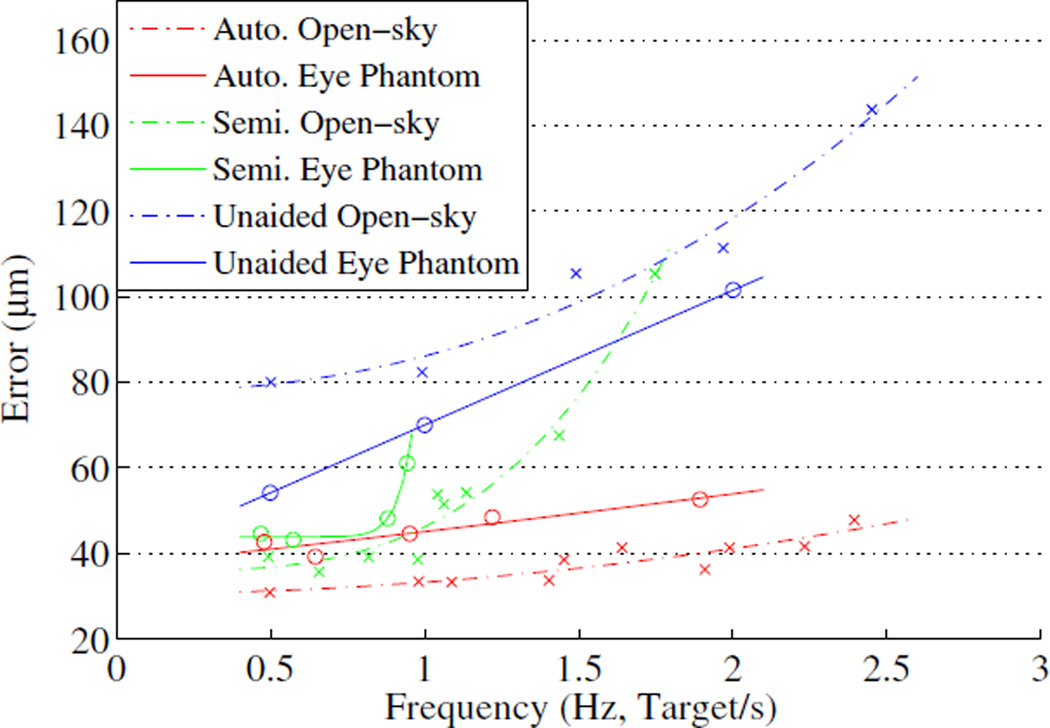
The mean error in automated operation slightly increases as the targeting threshold increases, whereas the execution time drops significantly from 29.4 to 14.3 s with higher thresholds. Similar trends are also found in the automated trials with fixed repeat rates. However, the mean error in semiautomated operation exponentially increases as the execution time decreases, as shown in Fig. 3. Interestingly, the semiautomated operation could not be performed at a 2.5 Hz repetition rate, while the unaided operation could marginally be done. This is because the operator instantaneously loses the hand-eye coordination, while the tip is being deflected to correct the aiming beam error, which requires extra time to accommodate the transition for switching the control back to the manual operation.
Fig. 3.
Targeting error vs. effective frequency in both open-sky and eye phantom tasks.
Representative results for the 1.0 Hz repetition rate are presented in Fig. 4(a)–(c). The overall results are summarized in Table I, including statistical analysis for three possible combinations via the ANOVA tests: automated/semiautomated, automated/unaided, and semiautomated/unaided. Statistically significant differences between the automated and the unaided trials are found across all repetition rates (p < 1.0×10−20).
Fig. 4.
Representative figures for a 1.0 Hz repetition rate in the open-sky and the eye phantom tasks. The top row shows the results from the open-sky task: (a) automated, (b) semiautomated, and (c) unaided trials. The bottom row shows the results from the eye phantom task: (d) automated, (e) semiautomated, and (f) unaided trials.
TABLE I.
Summary of Experimental Results in Open-sky Task
| Control Setting |
Time (s) (Auto/Semi or All) |
Auto Error (µm) |
Semi Error (µm) |
Unaided Error (µm) |
Error Reduction (%) | ||
|---|---|---|---|---|---|---|---|
| Auto /Semi |
Auto /Unaided |
Semi /Unaided |
|||||
| 30 µm | 29.4/48.6 | 33 | 36 | - | 6.7 | - | - |
| 50 µm | 22.8/39.1 | 34 | 39 | - | 13.9 | - | - |
| 100 µm | 19.5/30.7 | 41 | 54 | - | 23.0 | - | - |
| 150 µm | 16.1/30.1 | 41 | 52 | - | 19.7 | - | - |
| 200 µm | 14.3/28.2 | 42 | 54 | - | 23.1 | - | - |
| 0.5 Hz | 64.0 | 31 | 39 | 80 | 21.1* | 61.4*** | 51.0** |
| 1.0 Hz | 32.0 | 33 | 39 | 82 | 13.2 | 59.3*** | 53.1** |
| 1.5 Hz | 21.3 | 39 | 68 | 105 | 42.9** | 63.4*** | 35.9* |
| 2.0 Hz | 16.0 | 36 | 105 | 111 | 65.6*** | 67.4*** | 5.4 |
| 2.5 Hz | 12.8 | 48 | - | 142 | - | 66.2*** | - |
“Auto” and “Semi” stand for automated and semiautomated, respectively.
Statistical significances from the ANOVA tests:
p < 1.0×10−20,
p < 1.0×10−10, and
p < 1.0×10−2.
B. Eye Phantom
We used an eye phantom made of a hollow polypropylene ball with 25-mm diameter. The portion presenting the cornea was open, and the sclerotomy locations for insertion of a light-pipe and the tool were formed by rubber patches. In addition to the targets, artificial blood vessels were also printed on the paper, in order to track the movement of the eye using the eyeSLAM algorithm [10].
In the eye phantom task, we selectively adopted a few control settings from the open-sky task, considering the effectiveness of operation in terms of accuracy and execution time. As a result, the targeting thresholds were set to 50 and 100 µm for automated and semiautomated trials. The repetition rate was varied up to 2.0 Hz, at which the unaided operation could marginally be performed in the eye phantom, since maneuverability of the tool was limited by the fulcrum at the scleral entry.
The interruption of hand-eye coordination became pronounced, specifically, in semiautomated operation, as the operation speed increased, due to limited dexterity in the eye phantom. As a result, semiautomated trials were possible only up to 1.0 Hz. Noticeably, the mean error is increased in both automated and semiautomated trials, compared to the results operation are lower. It is considered that the fulcrum supports the laser probe during the unaided operation, resulting in stabilization of the tool. On the other hand, the fulcrum degrades control performance in the aided operation by applying external force to the tool, creating a disturbance to the control system. Due to these effects, the semiautomated trials do not show any statistically significant difference from the unaided trials. On the other hand, high accuracy is still achieved in the automated trials, all of which were significantly better than unaided performance.
Representative results for the 1.0 Hz repetition rate in the eye phantom are shown in Fig. 4(d)–(f), and the overall results are summarized in Table II.
TABLE II.
Summary of Experimental Results in Eye Phantom Task
| Control Setting |
Time (s) (Auto/Semi or All) |
Auto Error (µm) |
Semi Error (µm) |
Unaided Error (µm) |
Error Reduction (%) | ||
|---|---|---|---|---|---|---|---|
| Auto /Semi |
Auto /Unaided |
Semi /Unaided |
|||||
| 50 µm | 49.6/55.8 | 39 | 43 | - | 8.9 | - | - |
| 100 µm | 26.2/36.3 | 48 | 48 | - | 0.0 | - | - |
| 0.5 Hz | 64.0 | 43 | 45 | 54 | 4.2 | 21.1* | 17.7 |
| 1.0 Hz | 32.0 | 45 | 61 | 70 | 27.0* | 36.3* | 12.7 |
| 2.0 Hz | 16.0 | 53 | - | 102 | - | 48.2** | - |
IV. Discussion
The proposed hybrid control scheme is well suited to robot-aided intraocular laser surgery, as it deals well with inaccuracy in 3D reconstruction. The image Jacobian update also improves the control performance by allowing the increment of gains used for visual servoing. As a result, it is found that the hybrid control approach improves the accuracy of robot-aided operation, compared to the position-based visual servo control [7]; the average error is reduced by 26.2%. The visual cues designed to maintain hand-eye coordination were useful in robot-aided operation, allowing repeatable experiments in both in the open-sky and eye phantom tasks, alleviating the limitations of previous work [7].
The fixed-repeat-rate control in aided operation allowed direct comparison to unaided operation at equal firing rates. Hence, it is found that the automated operation still shows significantly lower errors, compared to the unaided operation, although the performance is slightly degraded by constraints in the eye phantom.
Compared to semiautomated laser surgery using the 3-DOF Micron [6], the performance was significantly improved in terms of the mean error: from 129 to 39 µm at the 1.0 Hz repeat rate. As a result, the error is reduced by 53.1%, whereas the error reduction with the 3-DOF Micron was only 22.3%. The investigation of the semiautomated operation under both constrained and unconstrained environments would be meaningful for design of a human-in-the-loop system. Transition between unaided and aided operations should be considered for further study.
The comparative study presented in this paper could be a general guideline for development of robot-aided intraocular surgery using handheld instruments. Further experiments will be performed on biological tissues ex vivo and in vivo.
Acknowledgments
Research supported by the U. S. National Institutes of Health (grant no. R01EB000526) and the Kwanjeong Educational Foundation.
Contributor Information
Sungwook Yang, Robotics Institute, Carnegie Mellon University, Pittsburgh, PA 15213 USA; Center for BioMicrosystems, Korea Institute of Science and Technology, Seoul, Korea.
Robert A. MacLachlan, Robotics Institute, Carnegie Mellon University, Pittsburgh, PA 15213 USA
Joseph N. Martel, Department of Ophthalmology, University of Pittsburgh, Pittsburgh, PA 15213 USA
Louis A. Lobes, Jr., Department of Ophthalmology, University of Pittsburgh, Pittsburgh, PA 15213 USA
Cameron N. Riviere, Email: camr@ri.cmu.edu, Robotics Institute, Carnegie Mellon University, Pittsburgh, PA 15213 USA.
References
- 1.Diabetic Retinopathy Study Research Group. Photocoagulation treatment of proliferative diabetic retinopathy: clinical application of Diabetic Retinopathy Study (DRS) findings, DRS Report Number 8. Ophthalmology. 1981 Jul.88(7):583–600. [PubMed] [Google Scholar]
- 2.Davis JL, Hummer J, Feuer WJ. Laser photocoagulation for retinal detachments and retinal tears in cytomegalovirus retinitis. Ophthalmology. 1997;104(12):2053–2061. doi: 10.1016/s0161-6420(97)30059-1. [DOI] [PubMed] [Google Scholar]
- 3.Frank RN. Retinal laser photocoagulation: Benefits and risks. Vision Res. 1980 Jan.20(12):1073–1081. doi: 10.1016/0042-6989(80)90044-9. [DOI] [PubMed] [Google Scholar]
- 4.Blumenkranz MS, Yellachich D, Andersen DE, Wiltberger MW, Mordaunt D, Marcellino GR, Palanker D. Semiautomated patterned scanning laser for retinal photocoagulation. Retina. 2006 Mar.26(3):370–376. doi: 10.1097/00006982-200603000-00024. [DOI] [PubMed] [Google Scholar]
- 5.Wright CHG, Barrett SF, Welch AJ. Design and development of a computer-assisted retinal laser surgery system. J. Biomed. Opt. 2006 Jan.11(4):041127. doi: 10.1117/1.2342465. [DOI] [PubMed] [Google Scholar]
- 6.Becker BC, MacLachlan RA, Lobes LA, Riviere CN. Semiautomated intraocular laser surgery using handheld instruments. Lasers Surg. Med. 2010;42(3):264–273. doi: 10.1002/lsm.20897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Yang S, MacLachlan RA, Riviere CN. Toward automated intraocular laser surgery using a handheld micromanipulator; IEEE/RSJ Int. Conf. Intell .Robot. Syst; 2014. pp. 1302–1307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Yang S, MacLachlan RA, Riviere CN. Manipulator design and operation of a six-degree-of-freedom handheld tremor-canceling microsurgical instrument. IEEE/ASME Trans. Mechatron. 2015;20(2):761–772. doi: 10.1109/TMECH.2014.2320858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.MacLachlan RA, Riviere CN. High-speed microscale optical tracking using digital frequency-domain multiplexing. IEEE Trans. Instrum. Meas. 2009 Jun.58(6):1991–2001. doi: 10.1109/TIM.2008.2006132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Becker BC, Riviere CN. Real-time retinal vessel mapping and localization for intraocular surgery; Proc. IEEE. Int. Conf. Robot. Autom; 2013. pp. 5360–5365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Hutchinson S, Hager GD, Corke PI. A tutorial on visual servo Control. IEEE Trans. Robot. Autom. 1996;12(5):651–670. [Google Scholar]
- 12.Castaño A, Hutchinson S. Visual compliance: Task-directed visual servo control. IEEE Trans. Robot. Autom. 1994;10(3):334–342. [Google Scholar]
- 13.Jägersand M, Fuentes O, Nelson R. Experimental evaluation of uncalibrated visual servoing for precision manipulation; Proc. IEEE Int. Conf. Robot. Autom; 1997. pp. 2874–2880. [Google Scholar]
- 14.Bandello F, Lanzetta P, Menchini U. When and how to do a grid laser for diabetic macular edema. Doc. Ophthalmol. 1999 Jan.97:415–419. doi: 10.1023/a:1002499920673. [DOI] [PubMed] [Google Scholar]