Dirichlet-Laplace priors for optimal shrinkage

Abstract

Penalized regression methods, such as L₁ regularization, are routinely used in high-dimensional applications, and there is a rich literature on optimality properties under sparsity assumptions. In the Bayesian paradigm, sparsity is routinely induced through two-component mixture priors having a probability mass at zero, but such priors encounter daunting computational problems in high dimensions. This has motivated continuous shrinkage priors, which can be expressed as global-local scale mixtures of Gaussians, facilitating computation. In contrast to the frequentist literature, little is known about the properties of such priors and the convergence and concentration of the corresponding posterior distribution. In this article, we propose a new class of Dirichlet–Laplace priors, which possess optimal posterior concentration and lead to efficient posterior computation. Finite sample performance of Dirichlet–Laplace priors relative to alternatives is assessed in simulated and real data examples.

1. INTRODUCTION

The overwhelming emphasis in the literature on high-dimensional data analysis has been on rapidly producing point estimates with good empirical and theoretical properties. However, in many applications, it is crucial to obtain a realistic characterization of uncertainty in estimates of parameters, functions of parameters, and predictions. Usual frequentist approaches to characterize uncertainty, such as constructing asymptotic confidence regions or using the bootstrap, can break down in high-dimensional settings. For example, in regression when the number of subjects n is equal to or larger than the number of predictors p, one cannot naively appeal to asymptotic normality and resampling from the data may not provide an adequate characterization of uncertainty.

Most penalized estimators correspond to the mode of a Bayesian posterior distribution. For example, Lasso/L₁ regularization [28] is equivalent to maximum a posteriori (MAP) estimation under a Gaussian linear regression model having a double exponential (Laplace) prior on the coefficients. Given this connection, it is natural to ask whether we can use the entire posterior distribution to provide a probabilistic measure of uncertainty. In addition to providing a characterization of uncertainty, a Bayesian perspective has distinct advantages in terms of tuning parameter choice, allowing key penalty parameters to be marginalized over the posterior distribution instead of relying on cross-validation.

From a frequentist perspective, we would like to be able to choose a default shrinkage prior that leads to similar optimality properties to those shown for L₁ penalization and other approaches. However, instead of showing that a penalized estimator obtains the minimax rate under sparsity assumptions, we would like to show that the entire posterior distribution concentrates at the optimal rate, i.e., the posterior probability assigned to a shrinking neighborhood of the true parameter value converges to one, with the neighborhood size proportional to the frequentist minimax rate.

An amazing variety of shrinkage priors have been proposed in the Bayesian literature; however with essentially no theoretical justification in the high-dimensional settings for which they were designed. [14] and [6] provided conditions on the prior for asymptotic normality of linear regression coefficients allowing the number of predictors p to increase with sample size n, with [14] requiring a very slow rate of growth and [6] assuming p ≤ n. These results required the prior to be sufficiently flat in a neighborhood of the true parameter value, essentially ruling out shrink-age priors. [3] considered shrinkage priors in providing simple sufficient conditions for posterior consistency in linear regression where the number of variables grows slower than the sample size, though no rate of contraction was provided.

In studying posterior contraction in high-dimensions, several properties of the prior distribution are critical, including the prior concentration around sparse vectors and the implied dimensionality of the prior. Studying these properties of shrinkage priors is challenging due to the lack of exact zeros, with the prior draws being sparse in only an approximate sense. This technical hurdle has prevented any previous results on posterior concentration in high-dimensional settings for shrinkage priors. Investigating these properties is critical not just in studying frequentist optimality properties of Bayesian procedures but for Bayesians in obtaining improved insight into prior elicitation. Without such a technical handle, prior selection remains an art. Our overarching goal is to obtain theory allowing design of novel priors, which are appealing from a Bayesian perspective while having frequentist optimality properties.

2. A NEW CLASS OF SHRINKAGE PRIORS

2.1 Bayesian sparsity priors in normal means problem

For concreteness, we focus on the normal means problem ([9, 11, 20]); although the methods developed in this paper generalize trivially to high-dimensional linear and generalized linear models. In the normal means setting, one aims to estimate a n-dimensional mean¹ based on a single observation corrupted with i.i.d. standard normal noise:

$$y_i={\theta }_i+{\epsilon }_i,{\epsilon }_i~\mathrm{N}(0,1),1\le i\le n.$$ (1)

Let l₀[q; n] denote the subset of ℝⁿ given by

$$l_0[q;n]=\{\theta \in {ℝ}^n:\#(1\le j\le n:{\theta }_j\ne 0)\le q\}.$$

For a vector x ∈ ℝ^r, let ‖x‖₂ denote its Euclidean norm. If the true mean θ₀ is q_n-sparse, i.e., θ₀ ∈ l₀[q_n; n], with q_n = o(n), the squared minimax rate in estimating θ₀ in l₂ norm is 2q_n log(n/q_n)(1+ o(1)) [11], i.e.²

$$\underset{\mathrm{\theta ̂}}{\text{inf}}\underset{{\theta }_0\in l_0[q_n;n]}{\text{sup}}{E}_{{\theta }_0}{\Vert \mathrm{\theta ̂}-{\theta }_0\Vert }_2^2\asymp q_n\text{log}(n/q_n).$$ (2)

In the above display, E_θ0 denotes an expectation with respect to a N_n(θ₀, I_n) density. In the presence of sparsity, one looses a logarithmic factor in the ambient dimension for not knowing the locations of the zeroes. Moreover, (2) implies that one only needs a number of replicates in the order of the sparsity to consistently estimate the mean. Appropriate thresholding/penalized estimators achieve the minimax rate (2); see [9] for detailed references.

For a subset S ⊂ {1, …, n}, let |S| denote the cardinality of S and define θ_S = (θ_j : j ∈ S) for a vector θ ∈ ℝⁿ. Denote supp(θ) to be the support of θ, the subset of {1, …, n} corresponding to the non-zero entries of θ. For a vector θ ∈ ℝⁿ, a natural way to incorporate sparsity is to use point mass mixture priors:

$${\theta }_j~(1-\pi ){\delta }_0+\pi g_{\theta },j=1,\dots ,n,$$ (3)

where π = Pr(θ_j ≠ 0), 𝔼{|supp(θ)| | π} = nπ is the prior guess on model size (sparsity level), and g_θ is an absolutely continuous density on ℝ. These priors are highly appealing in allowing separate control of the level of sparsity and the size of the signal coefficients. If the sparsity parameter π is estimated via empirical Bayes, the posterior median of θ is a minimax-optimal estimator [20] which can adapt to arbitrary sparsity levels as long as q_n = o(n).

In a fully Bayesian framework, it is common to place a beta prior on π, leading to a beta-Bernoulli prior on the model size, which conveys an automatic multiplicity adjustment [27]. In a recent paper, [9] established that prior (3) with an appropriate beta prior on π and suitable tail conditions on g_θ leads to a minimax optimal rate of posterior contraction, i.e., the posterior concentrates most of its mass on a ball around θ₀ of squared radius of the order of q_n log(n/q_n):

$$E_{{\theta }_0}\mathbb{P}({\Vert \theta -{\theta }_0\Vert }_2<M{s}_n|y)\to 1,\text{as}n\to \infty ,$$ (4)

where M > 0 is a constant and $s_n^2=q_n\text{log}(n/q_n)$. [24] obtained consistency in model selection using point-mass mixture priors with appropriate data-driven hyperparameters.

2.2 Global-local shrinkage rules

Although point mass mixture priors are intuitively appealing and possess attractive theoretical properties, posterior sampling requires a stochastic search over an enormous space, leading to slow mixing and convergence [26]. Computational issues and consideration that many of the θ_js may be small but not exactly zero has motivated a rich literature on continuous shrinkage priors; for some flavor refer to [3, 8, 16, 18, 25]. [26] noted that essentially all such shrinkage priors can be represented as global-local (GL) mixtures of Gaussians,

$${\theta }_j~\mathrm{N}(0,{\psi }_j\tau ),{\psi }_j~f,\tau ~g,$$ (5)

where τ controls global shrinkage towards the origin while the local scales {ψ_j} allow deviations in the degree of shrinkage. If g puts sufficient mass near zero and f is appropriately chosen, GL priors in (5) can intuitively approximate (3) but through a continuous density concentrated near zero with heavy tails.

GL priors potentially have substantial computational advantages over point mass priors, since the normal scale mixture representation allows for conjugate updating of θ and ψ in a block. Moreover, a number of frequentist regularization procedures such as ridge, lasso, bridge and elastic net correspond to posterior modes under GL priors with appropriate choices of f and g. For example, one obtains a double-exponential prior corresponding to the popular L₁ or lasso penalty if f is an exponential distribution. However, many aspects of shrinkage priors are poorly understood, with the lack of exact zeroes compounding the difficulty in studying basic properties, such as prior expectation, tail bounds for the number of large signals, and prior concentration around sparse vectors. Hence, subjective Bayesians face difficulties in incorporating prior information regarding sparsity, and frequentists tend to be skeptical due to the lack of theoretical justification.

This skepticism is warranted, as it is clearly the case that reasonable seeming priors can have poor performance in high-dimensional settings. For example, choosing π = 1/2 in prior (3) leads to an exponentially small prior probability of 2⁻ⁿ assigned to the null model, so that it becomes literally impossible to override that prior informativeness with the information in the data to pick the null model. However, with a beta prior on π, this problem can be avoided [27]. In the same vein, if one places i.i.d. N(0, 1) priors on the entries of θ, then the induced prior on ‖θ‖ is highly concentrated around $\sqrt{n}$ leading to misleading inferences on θ almost everywhere. Although these are simple examples, similar multiplicity problems [27] can transpire more subtly in cases where complicated models/priors are involved and hence it is fundamentally important to understand properties of the prior and the posterior in the setting of (1).

There has been a recent awareness of these issues, motivating a basic assessment of the marginal properties of shrinkage priors for a single θ_j. Recent priors such as the horseshoe [8] and generalized double Pareto [3] are carefully formulated to obtain marginals having a high concentration around zero with heavy tails. This is well justified, but as we will see below, such marginal behavior alone is not sufficient; it is necessary to study the joint distribution of θ on ℝⁿ. With such motivation, we propose a class of Dirichlet-kernel priors in the next subsection.

2.3 Dirichlet-kernel priors

Let ϕ₀ denote the standard normal density on ℝ. Also, let DE(τ) denote a zero mean double-exponential or Laplace distribution with density f(y) = (2τ)⁻¹e^−|y|/τ for y ∈ ℝ. Integrating out the local scales ψ_j’s, (5) can be equivalently represented as a global scale mixture of a kernel 𝒦(·),

$${\theta }_j\stackrel{\mathrm{i}.\mathrm{i}.\mathrm{d}.}{~}𝒦(·,\tau ),\tau ~g,$$ (6)

where $𝒦(x)=\int {\psi }^{-1/2}{\varphi }_0(x/\sqrt{\psi })g(\psi )d\psi$ is a symmetric unimodal density on ℝ and $𝒦(x,\tau )≔{\tau }^{-1/2}𝒦(x/\sqrt{\tau })$. For example, ψ_j ~ Exp(1/2) corresponds to a double-exponential kernel 𝒦 ≡ DE(1), while ψ_j ~ IG(1/2, 1/2) results in a standard Cauchy kernel 𝒦 ≡ Ca(0, 1).

These choices lead to a kernel which is bounded in a neighborhood of zero. However, if one instead uses a half Cauchy prior ${\psi }_j^{1/2}~{\text{Ca}}_{+}(0,1)$, then the resulting horseshoe kernel [7, 8] is un-bounded with a singularity at zero. This phenomenon coupled with tail robustness properties leads to excellent empirical performance of the horseshoe. However, the joint distribution of θ under a horseshoe prior is understudied and further theoretical investigation is required to understand its operating characteristics. One can imagine that it concentrates more along sparse regions of the parameter space compared to common shrinkage priors since the singularity at zero potentially allows most of the entries to be concentrated around zero with the heavy tails ensuring concentration around the relatively small number of signals.

The above class of priors rely on obtaining a suitable kernel 𝒦 through appropriate normal scale mixtures. In this article, we offer a fundamentally different class of shrinkage priors that alleviate the requirements on the kernel, while having attractive theoretical properties. In particular, our proposed class of Dirichlet-kernel (Dk) priors replaces the single global scale τ in (6) by a vector of scales (ϕ₁τ, …, ϕ_nτ), where ϕ = (ϕ₁, …, ϕ_n) is constrained to lie in the (n − 1) dimensional simplex ${𝒮}^{n-1}=\{x={(x_1,\dots ,x_n)}^{\mathrm{T}}:x_j\ge 0,{\sum }_{j=1}^n{x}_j=1\}$ and is assigned a Dir(a, …, a) prior:

$${\theta }_j|{\varphi }_j,\tau ~𝒦(·,{\varphi }_j\tau ),\varphi ~\text{Dir}(a,\dots ,a).$$ (7)

In (7), 𝒦 is any symmetric (about zero) unimodal density with exponential or heavier tails; for computational purposes, we restrict attention to the class of kernels that can be represented as scale mixture of normals [32]. While previous shrinkage priors obtain marginal behavior similar to the point mass mixture priors (3), our construction aims at resembling the joint distribution of θ under a two-component mixture prior.

We focus on the Laplace kernel from now on for concreteness, noting that all the results stated below can be generalized to other choices. The corresponding hierarchical prior given τ,

$${\theta }_j|\varphi ,\tau ~\mathrm{D}\mathrm{E}({\varphi }_j\tau ),\varphi ~\text{Dir}(a,\dots ,a),$$ (8)

is referred to as a Dirichlet–Laplace prior, denoted θ | τ ~ DL_a(τ).

To understand the role of ϕ, we undertake a study of the marginal properties of θ_j conditional on τ, integrating out ϕ_j. The results are summarized in Proposition 2.1 below.

Proposition 2.1. If θ | τ ~ DL_a(τ), then the marginal distribution of θ_j given τ is unbounded with a singularity at zero for any a < 1. Further, in the special case a = 1/n, the marginal distribution is a wrapped Gamma distribution WG(τ⁻¹, 1/n), where WG(λ, α) has a density f(x; λ, α) ∝ |x|^α−1 e^−λ|x| on ℝ.

Thus, marginalizing over ϕ, we obtain an unbounded kernel 𝒦, so that the marginal density of θ_j | τ has a singularity at 0 while retaining exponential tails. A proof of Proposition 2.1 can be found in the appendix.

The parameter τ plays a critical role in determining the tails of the marginal distribution of θ_j’s. We consider a fully Bayesian framework where τ is assigned a prior g on the positive real line and learnt from the data through the posterior. Specifically, we assume a gamma(λ, 1/2) prior on τ with λ = na. We continue to refer to the induced prior on θ implied by the hierarchical structure,

$${\theta }_j|\varphi ,\tau ~\mathrm{D}\mathrm{E}({\varphi }_j\tau ),\varphi ~\text{Dir}(a,\dots ,a),\tau ~\text{gamma}(na,1/2),$$ (9)

as a Dirichlet–Laplace prior, denoted θ ~ DL_a.

There is a frequentist literature on including a local penalty specific to each coefficient. The adaptive Lasso [31, 34] relies on empirically estimated weights that are plugged in. [23] instead sample the penalty parameters from a posterior, with a sparse point estimate obtained for each draw. These approaches do not produce a full posterior distribution but focus on sparse point estimates.

2.4 Posterior computation

The proposed class of DL priors leads to straightforward posterior computation via an efficient data augmented Gibbs sampler. The DL_a prior (9) can be equivalently represented as

$${\theta }_j~\mathrm{N}(0,{\psi }_j{\varphi }_j^2{\tau }^2),{\psi }_j~\text{Exp}(1/2),\varphi ~\text{Dir}(a,\dots ,a),\tau ~\text{gamma}(na,1/2).$$

We detail the steps in the normal means setting noting that the algorithm is trivially modified to accommodate normal linear regression, robust regression with heavy tailed residuals, probit models, logistic regression, factor models and other hierarchical Gaussian cases. To reduce auto-correlation, we rely on marginalization and blocking as much as possible. Our sampler cycles through (i) θ | ψ, ϕ, τ, y, (ii) ψ | ϕ, τ, θ, (iii) τ | ϕ, θ and (iv) ϕ | θ. We use the fact that the joint posterior of (ψ, ϕ, τ) is conditionally independent of y given θ. Steps (ii) – (iv) together give us a draw from the conditional distribution of (ψ, ϕ, τ) | θ, since

$$[\psi ,\varphi ,\tau |\theta ]=[\psi |\varphi ,\tau ,\theta ][\tau |\varphi ,\theta ][\varphi |\theta ].$$

Steps (i) – (iii) are standard and hence not derived. Step (iv) is non-trivial and we develop an efficient sampling algorithm for jointly sampling ϕ. Usual one at a time updates of a Dirichlet vector lead to tremendously slow mixing and convergence, and hence the joint update in Theorem 2.2 is an important feature of our proposed prior; a proof can be found in the Appendix. Consider the following parametrization for the three-parameter generalized inverse Gaussian (giG) distribution: Y ~ giG(λ, ρ, χ) if f(y) ∝ y^λ−1e^{−0.5(ρy+χ/y)} for y > 0.

Theorem 2.2. The joint posterior of ϕ | θ has the same distribution as (T₁/T, …, T_n/T), where T_j are independently distributed according to a giG(a − 1, 1, 2|θ_j|) distribution, and $T={\sum }_{j=1}^n{T}_j$.

Summaries of each step are provided below.

1. To sample θ | ψ, ϕ, τ, y, draw θ_j independently from a $\mathrm{N}({\mu }_j,{\sigma }_j^2)$ distribution with

   $${\sigma }_j^2={\{1+1/({\psi }_j{\varphi }_j^2{\tau }^2)\}}^{-1},{\mu }_j={\{1+1/({\psi }_j{\varphi }_j^2{\tau }^2)\}}^{-1}y.$$

2. The conditional posterior of ψ | ϕ, τ, θ can be sampled efficiently in a block by independently sampling ψ_j | ϕ, θ from an inverse-Gaussian distribution iG(μ_j, λ) with μ_j = ϕ_jτ/|θ_j|, λ = 1.

3. Sample the conditional posterior of τ | ϕ, θ from a $\text{giG}(\lambda -n,1,2{\sum }_{j=1}^n|{\theta }_j|/{\varphi }_j)$ distribution.

4. To sample ϕ | θ, draw T₁, …, T_n independently with T_j ~ giG(a − 1, 1, 2|θ_j|) and set ϕ_j = T_j/T with $T={\sum }_{j=1}^n{T}_j$.

3. CONCENTRATION PROPERTIES OF DIRCHLET–LAPLACE PRIORS

In this section, we study a number of properties of the joint density of the Dirichlet–Laplace prior DL_a on ℝⁿ and investigate the implied rate of posterior contraction (4) in the normal means setting (1). Recall the hierarchical specification of DL_a from (9). Letting ψ_j = ϕ_jτ for j = 1, …, n, a standard result (see, for example, Lemma IV.3 of [33]) implies that ψ_j ~ gamma(a, 1/2) independently for j = 1, …, n. Therefore, (9) can be alternatively represented as³

$${\theta }_j|{\psi }_j~\mathrm{D}\mathrm{E}({\psi }_j),{\psi }_j~\mathrm{G}\mathrm{a}(a,1/2).$$ (10)

The formulation (10) is analytically convenient since the joint distribution factors as a product of marginals and the marginal density can be obtained analytically in Proposition 3.1 below. The proof follows from standard properties of the modified Bessel function [15]; a proof is sketched in the Appendix.

Proposition 3.1. The marginal density Π of θ_j for any 1 ≤ j ≤ n is given by

$$\mathrm{\Pi }({\theta }_j)=\frac{1}{2^{(1+a)/2}\mathrm{\Gamma }(a)}{|{\theta }_j|}^{(a-1)/2}{K}_{1-a}\left(\sqrt{2|{\theta }_j|}\right),$$ (11)

where

$$K_{\nu }(x)=\frac{\mathrm{\Gamma }(\nu +1/2){(2x)}^{\nu }}{\sqrt{\pi }}{\int }_0^{\infty }\frac{\text{cos}t}{{(t^2+x^2)}^{\nu +1/2}}dt$$

is the modified Bessel function of the second kind.

Figure 3 plots the marginal density (11) to compare with common shrinkage priors.

Figure 3.

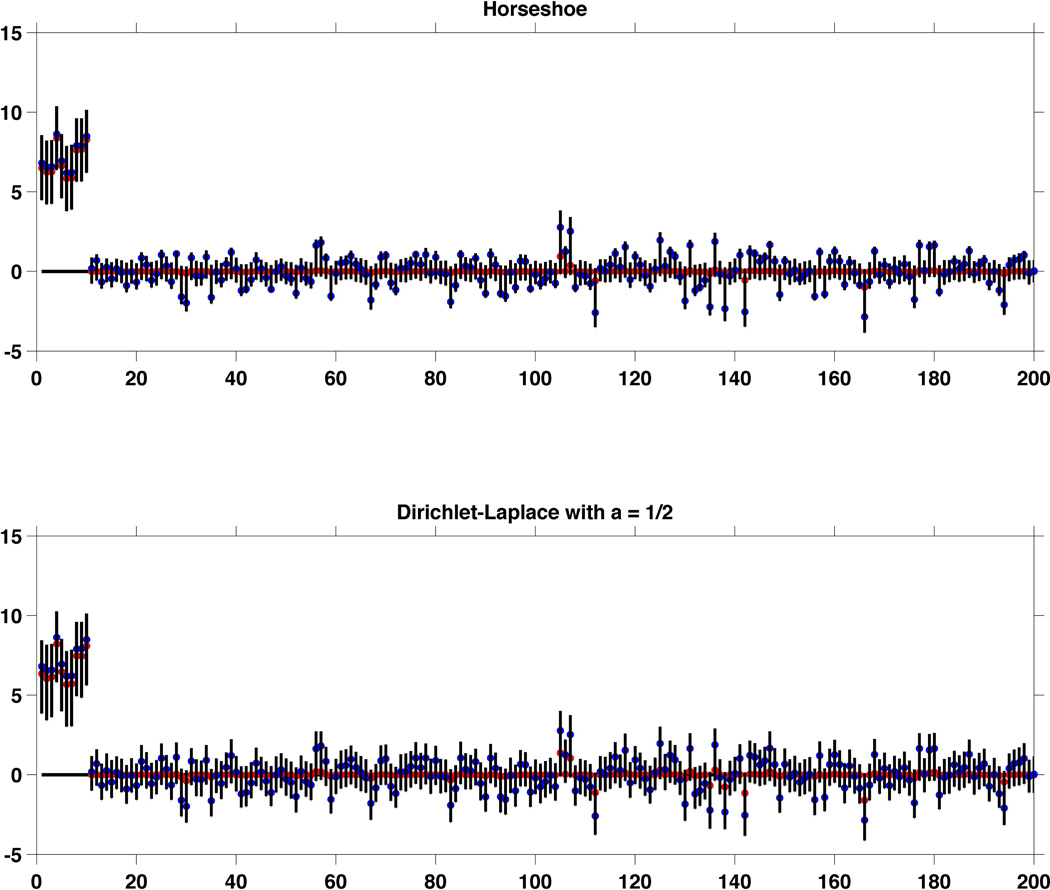
Simulation results from a single replicate with n = 200, q_n = 10, A = 7. Blue circles = entries of y, red circles = posterior median of θ, shaded region: 95% point wise credible interval for θ. Left panel: Horseshoe, right panel: DL_1/2 prior

We continue to denote the joint density of θ on ℝⁿ by Π, so that $\mathrm{\Pi }(\theta )={\prod }_{j=1}^n\mathrm{\Pi }({\theta }_j)$. For a subset S ⊂ {1, …, n}, let Π_S denote the marginal distribution of θ_S = {θ_j : j ∈ S} ∈ ℝ^|S|. For a Borel set A ⊂ ℝⁿ, let ℙ(A) = ∫_A Π(θ)dθ denote the prior probability of A, and ℙ(A | y⁽ⁿ⁾) the posterior probability given data y⁽ⁿ⁾ = (y₁, …, y_n) and the model (1). Finally, let E_θ0/P_θ0 respectively indicate an expectation/probability w.r.t. the N_n(θ₀, I_n) density. We now establish that under mild restrictions on ‖θ₀‖, the posterior arising from the DL_a prior (9) contracts at the minimax rate of convergence for an appropriate choice of the Dirichlet concentration parameter a.

Theorem 3.1. Consider model (1) with θ ~ DL_an as in (9), where a_n = n^−(1+β) for some β > 0 small. Assume θ₀ ∈ l₀[q_n; n] with q_n = o(n) and ${\Vert {\theta }_0\Vert }_2^2\le q_n{\text{log}}^{4}n$. Then, with $s_n^2=q_n\text{log}(n/q_n)$ and for some constant M > 0,

$$\underset{n\to \infty }{\text{lim}}{E}_{{\theta }_0}\mathbb{P}({\Vert \theta -{\theta }_0\Vert }_2<M{s}_n|y)=1.$$ (12)

If a_n = 1/n instead, then (12) holds when q_n ≳ log n.

A proof of Theorem 3.1 can be found in Section 6. Theorem 3.1 is the first result obtaining posterior contraction rates for a continuous shrinkage prior in the normal means setting or the closely related high-dimensional regression problem. Theorem 3.1 posits that when the parameter a in the Dirichlet–Laplace prior is chosen, depending on the sample size, to be n^−(1+β) for any β > 0 small, the resulting posterior contracts at the minimax rate (2), provided ${\Vert {\theta }_0\Vert }_2^2\le q_n{\text{log}}^{4}n$. Using the Cauchy–Schwartz inequality, ${\Vert {\theta }_0\Vert }_1^2\le q_n{\Vert {\theta }_0\Vert }_2^2$ for θ₀ ∈ l₀[q_n; n] and the bound on ‖θ₀‖₂ implies that ‖θ₀‖₁ ≤ q_n(log n)². Hence, the condition in Theorem 3.1 permits each non-zero signal to grow at a (log n)² rate, which is a fairly mild assumption. Moreover, in a recent technical report, the authors showed that a large subclass of global-local priors (5) including the Bayesian lasso lead to a sub-optimal rate of posterior convergence; i.e., the expression in (12) converges to 0 whenever ${\Vert {\theta }_0\Vert }_2^2/q_n\to \infty$. Therefore, Theorem 3.1 indeed provides a substantial improvement over a large class of GL priors.

The choice a_n = n^−(1+β) will be evident from the various auxiliary results in Section 3.1, specifically Lemma 3.3 and Theorem 3.4. The conclusion of Theorem 3.1 continues to hold when a_n = 1/n under an additional mild assumption on the sparsity q_n. In Tables 1 & 2 of Section 4, detailed empirical results are provided with a_n = 1/n as a default choice. Based on empirical experience, we find that a = 1/n may have a tendency to over-shrink the signals in cases where there are several relatively small signals. In such settings, depending on the practitioner’s utility function, the singularity at zero can be softened using a DL_a prior for a larger value of a. We report the results for a = 1/2 in Section 4, whence computational gains arise as the distribution of T_j in (iv) turns out to be inverse-Gaussian (iG), for which exact samplers are available. A fully Bayesian procedure with a discrete hyper prior on a is considered in the real data application.

Table 1.

Squared error comparison over 100 replicates. Average squared error across replicates reported for DL (Dirichlet–Laplace) with a = 1/n and a = 1/2, LS (Lasso), EBMed (Empirical Bayes median), PM (Point mass prior), BL (Bayesian lasso) and HS (horseshoe). Signal strength A = 5, 6.

n	100						200
$\frac{{\mathrm{q}}_{\mathrm{n}}}{\mathrm{n}}\%$	5		10		20		5		10		20
A	5	6	5	6	5	6	5	6	5	6	5	6
DL1/n	21.90	14.09	32.43	21.81	55.26	38.71	44.86	31.57	50.24	35.39	95.14	85.54
DL1/2	14.77	12.54	21.79	18.26	37.13	31.06	28.52	25.46	43.74	37.45	75.37	65.29
LS	22.21	20.67	36.41	36.54	65.91	66.60	43.37	43.51	74.05	75.98	139.20	137.94
EBMed	15.42	13.68	28.26	27.86	57.93	58.00	28.94	27.50	56.03	57.65	120.67	119.85
PM	14.50	11.99	24.97	23.66	49.92	49.16	26.66	24.86	49.96	50.89	103.40	101.69
BL	30.84	31.61	44.32	46.65	61.23	63.46	59.70	62.30	88.10	94.02	125.89	128.72
HS	12.50	9.31	21.63	17.63	39.60	35.89	23.41	18.75	42.95	38.21	81.07	74.31

Table 2.

Squared error comparison over 100 replicates. Average squared error across replicates reported for DL (Dirichlet–Laplace) with a = 1/n and a = 1/2, LS (Lasso), EBMed (Empirical Bayes median), PM (Point mass prior), BL (Bayesian lasso) and HS (horseshoe). Signal strength A = 7, 8.

n	100						200
$\frac{{\mathrm{q}}_{\mathrm{n}}}{\mathrm{n}}\%$	5		10		20		5		10		20
A	7	8	7	8	7	8	7	8	7	8	7	8
DL1/n	8.20	7.19	17.29	15.35	32.00	29.40	16.07	14.28	33.00	30.80	65.53	59.61
DL1/2	11.77	11.87	17.57	18.36	30.24	30.42	20.30	22.70	36.51	35.30	61.43	65.79
LS	21.25	19.09	38.68	37.25	68.97	69.05	41.82	41.18	75.55	75.12	137.21	136.25
EBMed	13.64	12.47	29.73	27.96	60.52	60.22	26.10	25.52	57.19	56.05	119.41	119.35
PM	12.15	10.98	25.99	24.59	51.36	50.98	22.99	22.26	49.42	48.42	101.54	101.62
BL	33.05	33.63	49.85	50.04	68.35	68.54	64.78	69.34	99.50	103.15	133.17	136.83
HS	8.30	7.93	18.39	16.27	37.25	35.18	15.80	15.09	35.61	33.58	72.15	70.23

In the regression setting y ~ N_n(Xβ, I_n) with the number of covariates p_n ≤ n, it is typically assumed that the eigenvalues of (X^TX)/n are bounded between two absolute constants [4, 19]. In such cases, Theorem 3.1 can be used to derive posterior convergence rates for the vector of regression coefficients β in l₂ norm. [4] studied posterior consistency in this setting for a class of shrinkage priors but did not provide contraction rates. While our methods can be extended trivially to the ultra high-dimensional regression setting, substantial work will be required to establish theoretical properties under standard restricted isometry type conditions on the design matrix commonly used to prove oracle inequalities for frequentist penalized methods [29]. Even with point mass mixture priors, such contraction results are unknown with the exception of a recent technical report [10]. While we propose a heuristic variable selection method which seems to work well in practice, obtaining model selection consistency results similar to [19, 24] is challenging and will be addressed elsewhere.

3.1 Auxiliary results

In this section, we state a number of properties of the DL prior which provide a better understanding of the joint prior structure and also crucially help us in proving Theorem 3.1. We first provide useful bounds on the joint density of the DL prior in Lemma 3.2 below; a proof can be found in the Appendix.

Lemma 3.2. Consider the DL_a prior on ℝⁿ for a small. Let S ⊂ {1, …, n} and η ∈ ℝ^|S|.

If min_1≤j≤|S| |η_j| > δ for δ small, then

$$\text{log}{\mathrm{\Pi }}_S(\eta )\le C|S|\text{log}(1/\delta ),$$ (13)

where C > 0 is an absolute constant.

If ‖η‖₂ ≤ m for m large, then

$$-\text{log}{\mathrm{\Pi }}_S(\eta )\le C\{|S|\text{log}(1/a)+|S{|}^{3/4}{m}^{1/2}\},$$ (14)

where C > 0 is an absolute constant.

It is evident from Figure 3 that the univariate marginal density Π has an infinite spike near zero. We quantify the probability assigned to a small δ-neighborhood of the origin in Lemma 3.3 below.

Lemma 3.3. Assume θ₁ ∈ ℝ has a probability density Π as in (11). Then, for δ > 0 small,

$$\mathbb{P}(|{\theta }_1|>\delta )\le C\text{log}(1/\delta )/\mathrm{\Gamma }(a),$$

where C > 0 is an absolute constant.

A proof of Lemma 3.3 can be found in the Appendix.

In case of point mass mixture priors (3), the induced prior on the model size |supp(θ)| follows a Binomial (n, π) prior (given π), facilitating study of the multiplicity phenomenon [27]. However, ℙ(θ = 0) = 0 for any continuous shrinkage prior, which compounds the difficulty in studying the degree of shrinkage for these classes of priors. Letting supp_δ(θ) = {j : |θ_j| > δ} to be the entries in θ larger than δ in magnitude, we propose |supp_δ(θ)| as an approximate measure of model size for continuous shrinkage priors. We show in Theorem 3.4 below that for an appropriate choice of δ, |supp_δ(θ)| doesn’t exceed a constant multiple of the true sparsity level q_n with posterior probability tending to one, a property which we refer to as posterior compressibility.

Theorem 3.4. Consider model (1) with θ ~ DL_an as in (9), where a_n = n^−(1+β) for some β > 0 small. Assume θ₀ ∈ l₀[q_n; n] with q_n = o(n). Let δ_n = q_n/n. Then,

$$\underset{n\to \infty }{\text{lim}}{E}_{{\theta }_0}\mathbb{P}(|{\text{supp}}_{{\delta }_n}(\theta )|>A{q}_n|y^{(n)})=0,$$ (15)

for some constant A > 0. If a_n = 1/n instead, then (15) holds when q_n ≳ log n.

The choice of δ_n in Theorem 3.4 guarantees that the entries in θ smaller than δ_n in magnitude produce a negligible contribution to ‖θ‖. Observe that the prior distribution of |supp_δn(θ)| is Binomial(n, ζ_n), where ζ_n = ℙ(|θ₁| > δ_n). When a_n = n^{− (1+β)}, ζ_n can be bounded above by log n/n^1+β in view of Lemma 3.3 and the fact that Γ(x) ≥ 1/x for x small. Therefore, the prior expectation 𝔼 |supp_δn(θ)| ≤ log n/n^β. This implies an exponential tail bound for ℙ(|supp_δn(θ) | > Aq_n) by Chernoff’s method, which is instrumental in deriving Theorem 3.4. A proof of Theorem 3.4 along these lines can be found in the Appendix.

The posterior compressibility property in Theorem 3.4 ensures that the dimensionality of the posterior distribution of θ (in an approximate sense) doesn’t substantially overshoot the true dimensionality of θ₀, which together with the bounds on the joint prior density near zero and infinity in Lemma 3.2 delivers the minimax rate in Theorem 3.1.

4. SIMULATION STUDY

To illustrate the finite-sample performance of the proposed DL prior, we tabulate the results from a replicated simulation study with various dimensionality n and sparsity level q_n in Tables 1 and 2. In each setting, we sample 100 replicates of a n-dimensional vector y from a N_n(θ₀, I_n) distribution with θ₀ having q_n non-zero entries which are all set to be a constant A > 0. We chose two values of n, namely n = 100, 200. For each n, we let the model size q_n to be 5, 10, 20% of n and vary A over 5, 6, 7, 8. This results in 24 simulation settings in total; for each setting the squared error loss corresponding to the posterior median averaged across simulation replicates is tabulated. The simulations were designed to mimic the setting in Section 3 where θ₀ is sparse with a few moderate-sized coefficients.

Based on the discussion in Section 3, we present the results for the DL prior with a = 1/n and a = 1/2. To offer grounds for comparison, we have tabulated the results for Lasso (LS), Empirical Bayes median (EBMed)⁴ [20], posterior median with a point mass prior (PM) [9], posterior median corresponding to the Bayesian lasso [25] and the horseshoe [8]. For the fully Bayesian analysis using point mass mixture priors, we use a complexity prior on the subset-size, π_n(s) α exp{−κs log(2n/s)} with κ = 0.1 and independent standard Laplace priors for the non-zero entries as in [9].⁵ A wide difference between most of the competitors and the proposed DL_1/n is observed in Table 2. As evident from Tables 1 and 2, DL_1/2 is robust to smaller signal strength as is the horseshoe.

We also illustrate a high-dimensional simulation setting akin to an example in [8], where one has a single observation y from a n = 1000 dimensional N_n(θ₀, I_n) distribution, with θ₀[1 : 10] = 10, θ₀[11 : 100] = A, and θ₀[101 : 1000] = 0. We then vary A from 2 to 7 and summarize the squared error averaged across 100 replicates in Table 3. We only compare the Bayesian shrinkage priors here; the squared error for the posterior median is tabulated. Table 3 clearly illustrates the need for prior elicitation in high dimensions.

Table 3.

Squared error comparison over 100 replicates. Average squared error for the posterior median reported for BL (Bayesian Lasso), HS (horseshoe) and DL (Dirichlet–Laplace) with a = 1/n and a = 1/2 respectively.

n	1000
A	2	3	4	5	6	7
BL	299.30	385.68	424.09	450.20	474.28	493.03
HS	306.94	353.79	270.90	205.43	182.99	168.83
DL1/n	368.45	679.17	671.34	374.01	213.66	160.14
DL1/2	267.83	315.70	266.80	213.23	192.98	177.20

For visual illustration and comparison, we present the results from a single replicate in the first simulation setting with n = 200, q_n = 10 and A = 7 in Figure 2 & 3. The blue circles indicate the entries of y, while the red circles correspond to the posterior median of θ. The shaded region corresponds to a 95% point wise credible interval for θ.

Figure 2.

Simulation results from a single replicate with n = 200, q_n = 10, A = 7. Blue circles = entries of y, red circles = posterior median of θ, shaded region: 95% point wise credible interval for θ. Left panel: Bayesian lasso, right panel: DL_1/n prior

5. PROSTATE DATA APPLICATION

We consider a popular dataset [12, 13] from a microarray experiment consisting of expression levels for 6033 genes for 50 normal control subjects and 52 patients diagnosed with prostate cancer. The data take the form of a 6033 × 102 matrix with the (i, j)th entry corresponding to the expression level for gene i on patient j; the first 50 columns correspond to the normal control subjects with the remaining 52 for the cancer patients. The goal of the study is to discover genes whose expression levels differ between the prostate cancer patients (treatment) and normal subjects (control). A two sample t-test with 100 degrees of freedom was implemented for each gene and the resulting t-statistic t_i was converted to a z-statistic z_i = Φ⁻¹(T₁₀₀(t_i)). Under the null hypothesis H_0i of no difference in expression levels between the treatment and control group for the ith gene, the null distribution of z_i is N(0, 1). Figure 4 shows a histogram of the z-values, comparing it to a N(0, 1) density with a multiplier chosen to make the curve integrate to the same area as the histogram. The shape of the histogram suggests the presence of certain interesting genes [12].

Figure 4.

Histogram of z-values

The classical Bonferroni correction for multiple testing flags only 6 genes as significant, while the two-group empirical Bayes method of [20] found 139 significant genes, being much less conservative. The local Bayes false discovery rate (fdr) [5] control method identified 54 genes as non-null. For detailed analysis of this dataset using existing methods, refer to [12, 13].

To apply our method, we set up a normal means model z_i = θ_i + ε_i, i = 1, …, 6033 and assign θ a DL_a prior. Instead of fixing a, we place a discrete uniform prior on a supported on the interval [1/6000, 1/2], with the support points of the form 10(k + 1)/6000, k = 0, 1, …, K. Such a fully Bayesian approach allows the data to dictate the choice of the tuning parameter a which is only specified up to a constant by the theory and also avoids potential numerical issues arising from fixing a = 1/n when n is large. Updating a is straightforward since the full conditional distribution of a is again a discrete distribution on the chosen support points.

A referee pointed out that the z-values for 6033 genes obtained using n = 102 observations are unlikely to be independent and recommended investigating robustness of our approach under correlated errors. We conducted a small simulation study to this effect to evaluate the performance of our method when the error distribution is misspecified. We generated data from the model y_i = θ_i + ε_i with (ε₁, …, ε_n)^T ~ N_n(0, Ω), where Ω corresponds to the covariance matrix of an auto-regression sequence with pure error variance σ² and auto-regressive coefficient ρ. We placed a discrete uniform prior on a supported on the interval [1/1000, 1/2], with the support points of the form 10(k + 1)/1000, k = 0, 1, …, K. We observe that the mean squared error of the posterior median for 50 replicated datasets with n = 1000, q_n = 50, A = 4, 5, 6, σ² = 1 increases by only 3% on average when ρ increases from 0 to 0.1. Therefore, the proposed method is robust to mild misspecification in the covariance structure. However, if further prior information is available regarding the covariance structure, that should be incorporated in the modeling framework.

For the real data application, we implemented the Gibbs sampler in Section 2.4 for 10,000 draws discarding a burn-in of 5,000. Mixing and convergence of the Gibbs sampler was satisfactory based on examination of trace plots, with the 5,000 retained samples having an effective sample size of 2369.2 averaged across the θ_i’s. The computational time per iteration scaled approximately linearly with the dimension. The posterior mode of a was at 1/20.

In this application, we expect there to be two clusters of |θ_i|s, with one concentrated closely near zero corresponding to genes that are effectively not differentially expressed and another away from zero corresponding to interesting genes for further study. As a simple automated approach, we cluster |θ_i|s at each MCMC iteration using kmeans with 2 clusters. For each iteration, the number of non-zero signals is then estimated by the smaller cluster size out of the two clusters. A final estimate (M) of the number of non-zero signals is obtained by taking the mode over all the MCMC iterations. The M largest (in absolute magnitude) entries of the posterior median are identified as the non-zero signals.

Using the above selection scheme, our method declared 128 genes as non-null. Interestingly, out of the 128 genes, 100 are common with the ones selected by EBMed. Also all the 54 genes obtained using FDR control form a subset of the selected 128 genes. Horseshoe is overly conservative; it selected only 1 gene (index: 610) using the same clustering procedure; the selected gene was the one with the largest effect size (refer to Table 11.2 in [13]).

6. PROOF OF THEOREM 3.1

We prove Theorem 3.1 for a_n = 1/n in details and note the places where the proof differs in case of a_n = n^−(1+β). Recall θ_S ≔ {θ_j, j ∈ S} and for δ ≥ 0, supp_δ(θ) ≔ {j : |θ_j| > δ}. Let E_θ0/P_θ0 respectively indicate an expectation/probability w.r.t. the N_n(θ₀, I_n) density.

For a sequence of positive real numbers r_n to be chosen later, let δ_n = r_n/n. Define ${𝒟}_n=\int {\prod }_{i=1}^n{f}_{{\theta }_i}(y_i)/f_{{\theta }_{0i}}d\mathrm{\Pi }(\theta )$. Let

$${𝒜}_n=\{{𝒟}_n\ge e^{-4r_n^2}\mathbb{P}({\Vert \theta -{\theta }_0\Vert }_2\le 2r_n)\}$$

be a subset of σ(y⁽ⁿ⁾), the sigma-field generated by y⁽ⁿ⁾, as in Lemma 5.2 of [9] such that $P_{{\theta }_0}({𝒜}_n^c)\le e^{-r_n^2}$. Let 𝒮_n be the collection of subsets S ⊂ {1, 2, …, n} such that |S| ≤ Aq_n. For each such S and a positive integer j, let {θ^S,j,i : i = 1, …, N_S,j} be a 2jr_n net of Θ_S,j,n = {θ ∈ ℝⁿ : supp_δn(θ) = S, 2jr_n ≤ ‖θ − θ₀‖₂ ≤ 2(j + 1)r_n} created as follows. Let {ϕ^S,j,i : i = 1, …, N_S,j} be a jr_n net of the |S|-dimensional ball {‖ϕ − θ_0S‖ ≤ 2(j+1)r_n}; we can choose this net in a way that N_S,j ≤ C^|S| for some constant C (see, for example, Lemma 5.2 of [30]). Letting ${\theta }_S^{S,j,i}={\varphi }^{S,j,i}$ and ${\theta }_S^{S,j,i}=0$ for k ∈ S^c, we show this collection indeed forms a 2jr_n net of Θ_S,j,n. To that end, fix θ ∈ Θ_S,j,n. Clearly, ‖θ_S − θ_0S‖ ≤ 2(j +1)r_n. Find 1 ≤ i ≤ N_S,j such that $\Vert {\theta }_S^{S,j,i}-{\theta }_S\Vert \le j{r}_n$. Then,

$${\Vert {\theta }^{S,j,i}-\theta \Vert }_2^2={\Vert {\theta }_S^{S,j,i}-{\theta }_S\Vert }_2^2+{\Vert {\theta }_{S^c}\Vert }_2^2\le {(j{r}_n)}^2+(n-q_n)r_n^2/n^2\le 4j^2{r}_n^2,$$

proving our claim. Therefore, the union of balls B_S,j,i of radius 2jr_n centered at θ^S,j,i for 1 ≤ i ≤ N_S,j cover Θ_S,j,n. Since E_θ0ℙ(|supp_δn(θ)| > Aq_n | y⁽ⁿ⁾) → 0 by Theorem 3.4, it is enough to work with E_θ0ℙ(θ : ‖θ − θ₀‖₂ > 2Mr_n, supp_δn(θ) ∈ 𝒮_n | y⁽ⁿ⁾). Using the standard testing argument for establishing posterior convergence rates (see, for example, the proof of Proposition 5.1 in [9]), we arrive at

$$E_{{\theta }_0}\mathbb{P}(\theta :{\Vert \theta -{\theta }_0\Vert }_2>2M{r}_n,{\text{supp}}_{{\delta }_n}(\theta )\in {𝒮}_n|y^{(n)})I_{{𝒜}_n}\le \sum _{S\in {𝒮}_n}\sum _{j\ge M}\sum _{i=1}^{N_{S,j}}2\sqrt{{\beta }_{j,S,i}}{e}^{-C{j}^2{r}_n^2},$$ (16)

where

$${\beta }_{S,j,i}=\frac{\mathbb{P}(B_{S,j,i})}{e^{-4r_n^2}\mathbb{P}(\theta :{\Vert \theta -{\theta }_0\Vert }_2<2r_n)}.$$

Let $r_n^2=q_n\text{log}n$. The proof of Theorem 3.1 is completed by deriving an upper bound to β_S,j,i in the following Lemma 6.1 akin to Lemma 5.4 in [9].

Lemma 6.1. $\text{log}{\beta }_{S,j,i}\le |S|\text{log}(2j)+C(|S|+|S_0|)\text{log}n+C\prime r_n^2$.

Proof.

$${\beta }_{S,j,i}\le \frac{\mathbb{P}(\theta \in {ℝ}^n:{\text{supp}}_{{\delta }_n}(\theta )=S,{\Vert {\theta }_S-{\mathrm{\theta ̃}}_S^{S,j,i}\Vert }_2<2j{r}_n)}{e^{-4r_n^2}\mathbb{P}(\theta \in {ℝ}^n:{\Vert \theta -{\theta }_0\Vert }_2<2r_n)}\le \frac{\mathbb{P}(\theta \in {ℝ}^n:|\theta {|}_j\le {\delta }_n\forall j\in S^c,|{\theta }_j|>{\delta }_n\forall j\in S,{\Vert {\theta }_S-{\mathrm{\theta ̃}}_S^{S,j,i}\Vert }_2<2j{r}_n)}{e^{-4r_n^2}\mathbb{P}(\theta \in {ℝ}^n:{\Vert {\theta }_{S_0}-{\theta }_{0S_0}\Vert }_2<r_n,\Vert {\theta }_{0S_0^c}\Vert <r_n)}\le \frac{e^{4r_n^2}\mathbb{P}{(|{\theta }_1|<{\delta }_n)}^{n-|S|}\mathbb{P}(|{\theta }_j|>{\delta }_n\forall j\in S,{\Vert {\theta }_S-{\mathrm{\theta ̃}}_S^{S,j,i}\Vert }_2<2j{r}_n)}{\mathbb{P}{(|{\theta }_1|<{\delta }_n)}^{n-q_n}\mathbb{P}({\Vert {\theta }_{S_0}-{\theta }_{0S_0}\Vert }_2<r_n)}.$$ (17)

Next, we find an upper bound to

$$R_{S,j,i}=\frac{\mathbb{P}(|{\theta }_j|>{\delta }_n\forall j\in S,{\Vert {\theta }_S-{\mathrm{\theta ̃}}_S^{S,j,i}\Vert }_2<2j{r}_n)}{\mathbb{P}({\Vert {\theta }_{S_0}-{\theta }_{0S_0}\Vert }_2<r_n)}.$$ (18)

Let υ_q(r) denote the q-dimensional Euclidean ball of radius r centered at zero and |υ_q(r)| denote its volume. For the sake of brevity, denote υ_q = |υ_q(1)|, so that |υ_q(r)| = r^qυ_q. The numerator of (18) can be clearly bounded above by |υ_|S|(2jr_n)| sup_{|θj|>δn ∀ j∈S} Π_S(θ_S). Since the set {‖θ_S0 − θ_0S0‖₂ < r_n} is contained in the ball υ_|S0|(‖θ_0S0‖₂ + r_n) = {‖θ_S0‖₂ ≤ ‖θ_0S0‖₂ + r_n} and ‖θ_0S0‖₂ = ‖θ₀‖₂, the denominator of (18) can be bounded below by |υ_|S0|(r_n)| inf_υ|S0|(tn) Π_S0(θ_S0), where t_n = ‖θ₀‖₂ + r_n. Putting together these inequalities and invoking Lemma 3.2, we have

$$R_{S,j,i}\le \frac{{(2j{r}_n)}^{|S|}{\upsilon }_{|S|}\text{exp}\{C|S|\text{log}(1/{\delta }_n)\}}{r_n^{|S_0|}{\upsilon }_{|S|}\text{exp}\{-C(|S_0|\text{log}n+{|S_0|}^{3/4}{t}_n^{1/2})\}}.$$ (19)

Using υ_q ≍ (2πe)^q/2q^−q/2−1/2 (see Lemma 5.3 in [9]) and $r_n^2\ge q_n=|S_0|$, we can bound $\text{log}\{r_n^{|S|}{\upsilon }_{|S|}/(r_n^{|S_0|}{\upsilon }_{|S_0|})\}$ from above by $C(|S|\text{log}n+r_n^2)$. Therefore, we have

$$\text{log}{R}_{S,j,i}\le |S|\text{log}(2j)+C\{|S|\text{log}n+r_n^2+|S_0|\text{log}n+|S|\text{log}(1/{\delta }_n)+|S_0{|}^{3/4}{t}_n^{1/2}\}.$$ (20)

Now, since ${\Vert {\theta }_0\Vert }_2^2\le q_n{\text{log}}^{4}n$ and $r_n^2=q_n\text{log}n$, we have $t_n\lesssim q_n^{1/2}{\text{log}}^{2}n$ and hence $|S_0{|}^{3/4}{t}_n^{1/2}\lesssim q_n\text{log}n=r_n^2$. Substituting in (20), we have

$$\text{log}{R}_{S,j,i}\le |S|\text{log}(2j)+C(|S|+|S_0|)\text{log}n+C\prime r_n^2.$$

Finally, ℙ(|θ₁| < δ_n)^n−|S|/ℙ(|θ₁| < δ_n)^n−q_n ≤ ℙ(|θ₁| < δ_n)^−|S|. Using Lemma 3.3, ℙ(|θ₁| < δ_n) ≥ (1 − log n/n), which implies that ℙ(|θ₁| < δ_n)^−|S| ≤ e^{log n}.

Substituting the upper bound for β_S,j,i obtained in Lemma 6.1, and noting that |S| ≤ Aq_n and |N_S,j| ≤ e^C|S|, the expression in the left hand side of (16) can be bounded above by

$$2\sum _{S\in {𝒮}_n}\sum _{j\ge M}\sum _{i=1}^{N_{S,j}}\text{exp}\{A{q}_n\text{log}(2j)/2+C/2(A+1)q_n\text{log}n+C\prime 2r_n^2/2\}{e}^{-C{j}^2{r}_n^2}\le 2\sum _{S\in {𝒮}_n}\sum _{j\ge M}\text{exp}\{C{q}_n+A{q}_n\text{log}(2j)/2+C/2(A+1)q_n\text{log}n+C\prime r_n^2/2\}{e}^{-C{j}^2{r}_n^2}.$$

Since $|{𝒮}_n|\le A{q}_n\left(\begin{array}{c}\hfill n\hfill \\ \hfill A{q}_n\hfill \end{array}\right)\le A{q}_n{e}^{A{q}_n\text{log}(ne/A{q}_n)}$, it follows that E_θ0ℙ(θ : ‖θ − θ₀‖₂ > 2Mr_n, supp_δn(θ) ∈ 𝒮_n | y⁽ⁿ⁾) → 0 for large M > 0.

When a_n = n^−(1+β), the conclusion of Lemma 6.1 remains unchanged and the proof of Theorem 3.4 does not require q_n ≳ log n. The rest of the proof remains exactly the same.

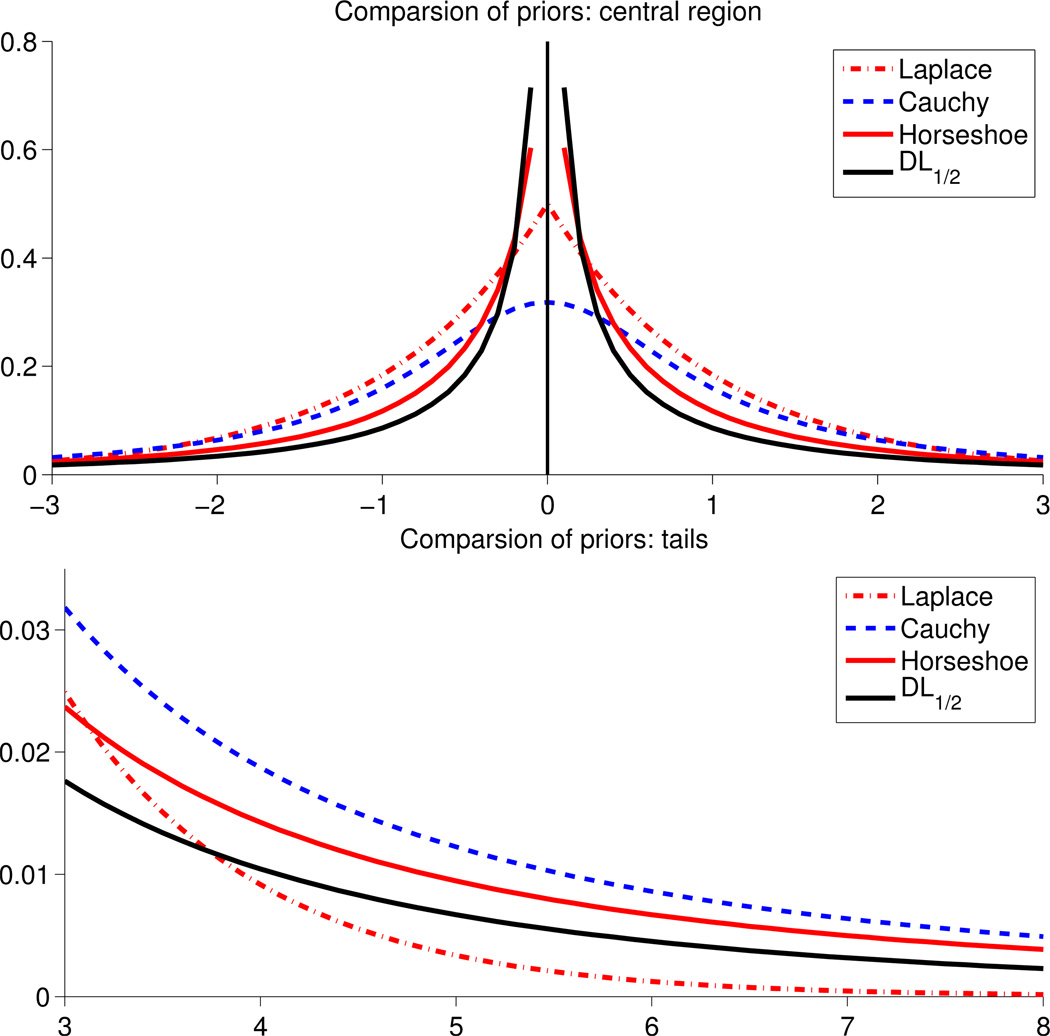
Figure 1.

Marginal density of the DL prior with a = 1/2 in comparison to other shrinkage priors.

APPENDIX

Proof of Proposition 2.1

When a = 1/n, ϕ_j ~ Beta(1/n, 1 − 1/n) marginally. Hence, the marginal distribution of θ_j given τ is proportional to

$${\int }_{{\varphi }_j=0}^1{e}^{-|{\theta }_j|/({\varphi }_j\tau )}{\left(\frac{{\varphi }_j}{1-{\varphi }_j}\right)}^{1/n}{\varphi }_j^{-2}d{\varphi }_j.$$

Substituting z = ϕ_j/(1 − ϕ_j) so that ϕ_j = z/(1 + z), the above integral reduces to

$$e^{-|{\theta }_j|/\tau }{\int }_{z=0}^{\infty }{e}^{-|{\theta }_j|/(\tau z)}{z}^{-(2-1/n)}dz\propto e^{-|{\theta }_j|/\tau }{|{\theta }_j|}^{1/n-1}.$$

In the general case, ϕ_j ~ Beta(a, (n − 1)a) marginally. Substituting z = ϕ_j/(1 − ϕ_j) as before, the marginal density of θ_j is proportional to

$$e^{-|{\theta }_j|/\tau }{\int }_{z=0}^{\infty }{e}^{-|{\theta }_j|/(\tau z)}{z}^{-(2-a)}{\left(\frac{1}{1+z}\right)}^{na-1}dz.$$

The above integral can clearly be bounded below by a constant multiple of

$$e^{-|{\theta }_j|/\tau }{\int }_{z=0}^1{e}^{-|{\theta }_j|/(\tau z)}{z}^{-(2-a)}dz.$$

The above expression clearly diverges to infinity as |θ_j| → 0 by the monotone convergence theorem.

Proof of Theorem 2.2

Integrating out τ, the joint posterior of ϕ | θ has the form

$$\pi ({\varphi }_1,\dots ,{\varphi }_{n-1}|\theta )\propto \prod _{j=1}^n[{\varphi }_j^{a-1}\frac{1}{{\varphi }_j}]{\int }_{\tau =0}^{\infty }{e}^{-\tau /2}{\tau }^{\lambda -n-1}{e}^{-{\sum }_{j=1}^n|{\theta }_j|/({\varphi }_j\tau )}d\tau .$$ (A.1)

We now state a result from the theory of normalized random measures (see, for example, (36) in [22]). Suppose T₁, …, T_n are independent random variables with T_j having a density f_j on (0,∞). Let ϕ_j = T_j/T with $T={\sum }_{j=1}^n{T}_j$. Then, the joint density f of (ϕ₁, …, ϕ_n−1) supported on the simplex 𝒮ⁿ⁻¹ has the form

$$f({\varphi }_1,\dots ,{\varphi }_{n-1})={\int }_{t=0}^{\infty }{t}^{n-1}\prod _{j=1}^n{f}_j({\varphi }_{j}t)dt,$$ (A.2)

where ${\varphi }_n=1-{\sum }_{j=1}^{n-1}{\varphi }_j$. Setting $f_j(x)\propto \frac{1}{x^{\delta }}{e}^{-|{\theta }_j|/x}{e}^{-x/2}$ in (A.2), we get

$$f({\varphi }_1,\dots ,{\varphi }_{n-1})=\left[\prod _{j=1}^n\frac{1}{{\varphi }_j^{\delta }}\right]{\int }_{t=0}^{\infty }{e}^{-t/2}{t}^{n-1-n\delta }{e}^{-{\sum }_{j=1}^n|{\theta }_j|/({\varphi }_{j}t)}dt.$$ (A.3)

We aim to equate the expression in (A.3) with the expression in (A.1). Comparing the exponent of ϕ_j gives us δ = 2 − a. The other requirement n − 1 − nδ = λ − n − 1 is also satisfied, since λ = na. The proof is completed by observing that f_j corresponds to a giG(a − 1, 1, 2|θ_j|) when δ = 2 − a.

Proof of Proposition 3.1

By (10),

$$\mathrm{\Pi }({\theta }_j)=\frac{{(1/2)}^a}{2\mathrm{\Gamma }(a)}{\int }_{{\psi }_j=0}^{\infty }{e}^{-|{\theta }_j|/{\psi }_j}{\psi }_j^{a-2}{e}^{-{\psi }_j/2}d{\psi }_j=\frac{{(1/2)}^a}{2\mathrm{\Gamma }(a)}{\int }_{z=0}^{\infty }{e}^{-z|{\theta }_j|}{z}^{-a}{e}^{-2/z}dz.$$

The result follows from 8.432.7 in [15].

Proof of Lemma 3.2

Letting h(x) = log Π(x), we have logΠ_S(η) = ∑_1≤j≤|S| h(η_j).

We first prove (13). Since Π(x), and hence h(x), is monotonically decreasing in |x|, and |η_j| > δ for all j, we have log Π_S(η) ≤ |S|h(δ). Using K_α(z) ≍ z^−α for |z| small and Γ(a) ≍ a⁻¹ for a small, we have from (11) that Π(δ) ≍ a⁻¹|δ|^(a−1) and hence h(δ) ≍ (1 − a) log(δ⁻¹) − loga⁻¹ + C ≤ C log(δ⁻¹).

We next prove (14). Noting that K_α(z) ≳ e^−z/z for |z| large (section 9.7 of [1]), we have from (11) that $-h(x)\le \text{log}{a}^{-1}+3/2\text{log}|x|+\sqrt{2}\sqrt{|x|}$ for |x| large. Using Cauchy–Schwartz inequality twice, we have ${({\sum }_{j=1}^{|S|}\sqrt{|{\eta }_j|})}^4\le {|S|}^3{\Vert \eta \Vert }_2^2$, which implies ${\sum }_{j=1}^{|S|}\sqrt{|{\eta }_j|}\le {|S|}^{3/4}{\Vert \eta \Vert }_2^{1/2}\le {|S|}^{3/4}{m}^{1/2}$.

Proof of Lemma 3.3

Using the representation (9), we have ℙ(|θ₁| > δ | ψ₁) = e^−δ/ψ₁, so that,

$$\mathbb{P}(|{\theta }_1|>\delta )=\frac{{(1/2)}^a}{\mathrm{\Gamma }(a)}{\int }_0^{\infty }{e}^{-\delta /x}{x}^{a-1}{e}^{-x/2}dx=\frac{{(1/2)}^a}{\mathrm{\Gamma }(a)}\{{\int }_0^{4\delta }{e}^{-\delta /x}{x}^{a-1}{e}^{-x/2}dx+{\int }_{4\delta }^{\infty }{e}^{-\delta /x}{x}^{a-1}{e}^{-x/2}dx\}\le \frac{{(1/2)}^a}{\mathrm{\Gamma }(a)}\{C+{\int }_{4\delta }^{\infty }\frac{e^{-x/2}}{x}dx\}\le \frac{{(1/2)}^a}{\mathrm{\Gamma }(a)}\{C+{\int }_{2\delta }^{\infty }\frac{e^{-t}}{t}dt\},$$ (A.4)

where C > 0 is a constant independent of δ. Using a bound for the incomplete gamma function from Theorem 2 of [2],

$${\int }_{2\delta }^{\infty }\frac{e^{-t}}{t}dt\le -\text{log}(1-e^{-2\delta })\le -\text{log}(\delta ),$$ (A.5)

for δ small. The proof is completed by noting that (1/2)^a is bounded above by a constant and C + log(1/δ) ≤ 2 log(1/δ) for δ small enough.

Proof of Theorem 3.4

For θ ∈ ℝⁿ, let f_θ(·) denote the probability density function of a N_n(θ, I_n) distribution and f_θi denote the univariate marginal N(θ_i, 1) distribution. Let S₀ = supp(θ₀). Since |S₀| = q_n, it suffices to prove that

$$\underset{n\to \infty }{\text{lim}}{E}_{{\theta }_0}\mathbb{P}(|{\text{supp}}_{{\delta }_n}(\theta )\cap S_0^c|>A{q}_n|y^{(n)})\to 0.$$

Let ${ℬ}_n=\{|{\text{supp}}_{{\delta }_n}(\theta )\cap S_0^c|>A{q}_n\}$. By (10), $\{{\theta }_i,i\in S_0^c\}$ is independent of {θ_i, i ∈ S₀} conditionally on y⁽ⁿ⁾. Hence

$$\mathbb{P}({ℬ}_n|y^{(n)})=\frac{{\int }_{{ℬ}_n}{\prod }_{i\in S_0^c}\frac{f_{{\theta }_i}(y_i)}{f_0(y_i)}d\mathrm{\Pi }({\theta }_i)}{\int {\prod }_{i\in S_0^c}\frac{f_{{\theta }_i}(y_i)}{f_0(y_i)}d\mathrm{\Pi }({\theta }_i)}≔\frac{{𝒩}_n^{\prime }}{{𝒟}_n^{\prime }},$$ (A.6)

where ${𝒩}_n^{\prime }$ and ${𝒟}_n^{\prime }$ respectively denote the numerator and denominator of the expression in (A.6). Observe that

$$E_{{\theta }_0}\mathbb{P}({ℬ}_n|y^{(n)})\le E_{{\theta }_0}\mathbb{P}({ℬ}_n|y^{(n)})1_{{𝒜}_n^{\prime }}+P_{{\theta }_0}({𝒜}_n^{\prime c}),$$ (A.7)

where ${𝒜}_n^{\prime }$ is a subset of σ(y⁽ⁿ⁾) as in Lemma 5.2 of [9] (replacing θ by ${\theta }_{S_0^c}$ and θ₀ by 0) defined as

$${𝒜}_n^{\prime }=\{{𝒟}_n^{\prime }\ge e^{-r_n^2}\mathbb{P}({\Vert {\theta }_{S_0^c}\Vert }_2\le r_n)\},$$

with $P_{{\theta }_0}({𝒜}_n^{\prime c})\le e^{-r_n^2}$ for some sequence of positive real numbers r_n. We set $r_n^2=q_n$ here. With this choice, from (A.7),

$$E_{{\theta }_0}\mathbb{P}({ℬ}_n|y^{(n)})\le \frac{\mathbb{P}({ℬ}_n)}{e^{-r_n^2}\mathbb{P}({\Vert {\theta }_{S_0^c}\Vert }_2\le r_n)}+e^{-r_n^2}.$$ (A.8)

We have $\mathbb{P}({\Vert {\theta }_{S_0^c}\Vert }_2\le r_n)\ge \mathbb{P}(|{\theta }_j|<r_n/\sqrt{n}\forall j\in S_0^c)=\mathbb{P}{(|{\theta }_1|<r_n/\sqrt{n})}^{n-q_n}$, with the equality following from the representation in (10). Using Lemma 3.3, $\mathbb{P}(|{\theta }_1|<r_n/\sqrt{n})\ge 1-\text{log}n/n$, implying $\mathbb{P}({\Vert {\theta }_{S_0^c}\Vert }_2\le r_n)\ge e^{-C\text{log}n}$. Next, clearly ℙ(ℬ_n) ≤ ℙ(|supp_δn(θ)| > Aq_n). As indicated in Section 3.1, |supp_δn (θ)| ~ Binomial(n, ζ_n), with ζ_n = ℙ(|θ₁| > δ_n) ≤ log n/n in view of Lemma 3.3. A version of Chernoff’s inequality for the binomial distribution [17] states that for B ~ Binomial(n, ζ) and ζ ≤ a < 1,

$$\mathbb{P}(B>an)\le {\left\{{\left(\frac{\zeta }{a}\right)}^a{e}^{a-\zeta }\right\}}^n.$$ (A.9)

When a_n = 1/n, q_n ≥ C₀ log n for some constant C₀ > 0. Setting a_n = Aq_n/n, clearly ζ_n < a_n for some A > 1/C₀. Substituting in (A.9), we have ℙ(|supp_δn (θ)| > Aq_n) ≤ e^{Aq_n log(e log n)−Aq_n log Aq_n}. Choosing A ≥ 2e/C₀ and using the fact that q_n ≥ C₀ log n, we obtain ℙ(|supp_δn(θ)| > Aq_n) ≤ e^{−Aq_n log 2}. Substituting the bounds for ℙ(ℬ_n) and $\mathbb{P}({\Vert {\theta }_{S_0^c}\Vert }_2\le r_n)$ in (A.8) and choosing larger A if necessary, the expression in (A.7) goes to zero.

If a_n = n^−(1+β), ζ_n ≤ log n/n^1+β in view of Lemma 3.3. In (A.9), set a_n = Aq_n/n as before. Clearly ζ_n < a_n. Substituting in (A.9), we have ℙ(|supp_δn(θ) | > Aq_n) ≤ e^{−CAq_n log n}. Substituting the bounds for ℙ(ℬ_n) and $\mathbb{P}({\Vert {\theta }_{S_0^c}\Vert }_2\le r_n)$ in (A.8), the expression in (A.7) goes to zero.