Abstract
The nephron in the kidney regulates its fluid flow by several autoregulatory mechanisms. Two primary mechanisms are the myogenic response and the tubuloglomerular feedback (TGF). The myogenic response is a property of the pre-glomerular vasculature in which a rise in intravascular pressure elicits vasoconstriction that generates a compensatory increase in vascular resistance. TGF is a negative feedback response that balances glomerular filtration with tubular reabsorptive capacity. While each nephron has its own autoregulatory response, the responses of the kidney's many nephrons do not act autonomously but are instead coupled through the pre-glomerular vasculature. To better understand the conduction of these signals along the pre-glomerular arterioles and the impacts of internephron coupling on nephron flow dynamics, we developed a mathematical model of renal haemodynamics of two neighbouring nephrons that are coupled in that their afferent arterioles arise from a common cortical radial artery. Simulations were conducted to estimate internephron coupling strength, determine its dependence on vascular properties and to investigate the effect of coupling on TGF-mediated flow oscillations. Simulation results suggest that reduced gap-junctional conductances may yield stronger internephron TGF coupling and highly irregular TGF-mediated oscillations in nephron dynamics, both of which experimentally have been associated with hypertensive rats.
Keywords: haemodynamics, tubuloglomerular feedback, myogenic response, afferent arteriole, non-linear dynamics
1. Introduction
The fundamental role of the kidney is to remove metabolic waste from the body while
maintaining a balance of volume, electrolytes and acid–base (Eaton & Pooler, 2004). That balance is achieved,
in large part, by processes that take place in the individual functional unit of the
kidney, the nephron. Each nephron consists of a filtering component, termed glomerulus
and a renal tubule. A single afferent arteriole delivers blood to the glomerulus. About
one-fifth of the blood plasma is filtered through the glomerular capillaries to become
filtrate that enters the renal tubule. The epithelial transport processes along the
tubule continuously modify the composition of the filtrate, such that eventually most of
the filtered water and electrolytes are reabsorbed and returned to general circulation.
The number of nephrons in a kidney depends on body size. A rat kidney is composed of
 30,000–40,000 nephrons
(Han et al., 1992); a human
kidney contains up to a million nephrons (Nyengaard
& Bendtsen, 1992).
30,000–40,000 nephrons
(Han et al., 1992); a human
kidney contains up to a million nephrons (Nyengaard
& Bendtsen, 1992).
Epithelial transport and tubular luminal fluid composition are influenced substantially by fluid flow, which is in turn determined, in part, by the glomerular filtration rate (GFR). Thus, regulation of the GFR is essential for proper kidney function. One regulatory mechanism is the myogenic response, in which the afferent arteriolar muscles respond to perturbations in intraluminal pressure or stretch with active force development, thereby enabling the arteriole to constrict, reducing glomerular blood delivery and the GFR (Holstein-Rathlou & Marsh, 1994; Just, 2007).
Another contributing mechanism is a negative feedback system, termed tubuloglomerular
feedback (TGF), by which the nephron controls incoming blood flow and the GFR by
responding to variations in the ionic composition of loop of Henle outflow (Holstein-Rathlou & Marsh, 1994; Just, 2007). A specialized cluster of cells, termed
macula densa (MD), senses the Cl concentration in the
tubular fluid flowing past that area and generates a signal that adjusts the GFR by
changing the afferent arteriole smooth muscle tone. Taken in isolation, a higher GFR
results in a higher tubular fluid Cl
concentration in the
tubular fluid flowing past that area and generates a signal that adjusts the GFR by
changing the afferent arteriole smooth muscle tone. Taken in isolation, a higher GFR
results in a higher tubular fluid Cl concentration. The
MD cells respond by inducing a constriction of smooth muscles in the afferent arteriole
to increase vascular resistance, thereby lowering blood flow and thus the GFR.
Conversely, the TGF system responds to a low [Cl
concentration. The
MD cells respond by inducing a constriction of smooth muscles in the afferent arteriole
to increase vascular resistance, thereby lowering blood flow and thus the GFR.
Conversely, the TGF system responds to a low [Cl ] by
dilating the afferent arteriole to increase blood flow and the GFR.
] by
dilating the afferent arteriole to increase blood flow and the GFR.
In a series of studies, we developed a detailed mathematical model of renal
haemodynamics (Chen et al., 2011;
Sgouralis & Layton, 2012, 2014a, b).
The model by Sgouralis & Layton (2014b)
represents an afferent arteriole, glomerular filtration, Cl transport along the proximal segments of a short-loop nephron and TGF. The model
afferent arteriole is myogenically active and represents smooth muscle membrane
potential and gap-junctional coupling. The activity of non-selective cation channels is
assumed to be shifted by changes in intravascular pressure, and thus the smooth muscle
membrane depolarizes with increasing intravascular pressure, such that elevation in
pressure induces vasoconstriction which increases resistance to blood flow. We used that
model to assess the individual contributions of TGF and myogenic response to GFR
regulation in the rat kidney.
transport along the proximal segments of a short-loop nephron and TGF. The model
afferent arteriole is myogenically active and represents smooth muscle membrane
potential and gap-junctional coupling. The activity of non-selective cation channels is
assumed to be shifted by changes in intravascular pressure, and thus the smooth muscle
membrane depolarizes with increasing intravascular pressure, such that elevation in
pressure induces vasoconstriction which increases resistance to blood flow. We used that
model to assess the individual contributions of TGF and myogenic response to GFR
regulation in the rat kidney.
The model by Sgouralis & Layton (2014b)
represents an isolated nephron with the associated vasculature, whereas, as noted above,
 30,000–40,000 nephrons are
packed inside a rat kidney. Indeed, experimental observation in rats has indicated that
individual nephrons do not operate independently but interact constantly with the
neighbouring nephrons. This coupling effect is mediated by the propagation of
TGF-induced electrotonic signals along the pre-glomerular vasculature (Holstein-Rathlou, 1987; Källskog & Marsh, 1990; Yip et al., 1992). For instance, if two afferent arterioles
associated with two nephrons are fed by a common cortical radial artery, then the
contraction of one nephron's afferent arteriole likely causes the other afferent
arteriole to contract too.
30,000–40,000 nephrons are
packed inside a rat kidney. Indeed, experimental observation in rats has indicated that
individual nephrons do not operate independently but interact constantly with the
neighbouring nephrons. This coupling effect is mediated by the propagation of
TGF-induced electrotonic signals along the pre-glomerular vasculature (Holstein-Rathlou, 1987; Källskog & Marsh, 1990; Yip et al., 1992). For instance, if two afferent arterioles
associated with two nephrons are fed by a common cortical radial artery, then the
contraction of one nephron's afferent arteriole likely causes the other afferent
arteriole to contract too.
Results of previous modelling studies have suggested that internephron coupling may have
a significant impact on the TGF-mediated dynamics of nephron flow and other variables
(Pitman et al., 2004; Layton et al., 2006, 2009, 2011).
While those studies represent Cl transport along the
thick ascending limb in detail, the afferent arteriole is not represented explicitly,
and the conduction of the TGF signal via the coupled afferent arterioles is represented
only phenomenologically. A goal of this study is to better characterize the coupling, in
the context of TGF, between two neighbouring nephrons.
transport along the
thick ascending limb in detail, the afferent arteriole is not represented explicitly,
and the conduction of the TGF signal via the coupled afferent arterioles is represented
only phenomenologically. A goal of this study is to better characterize the coupling, in
the context of TGF, between two neighbouring nephrons.
To that end, we extend the renal haemodynamics model of Sgouralis & Layton (2014b) to a pair of nephrons whose afferent arterioles arise from the same cortical radial artery. We use the coupled nephron model to study the conduction of TGF signals along the afferent arterioles, and we investigate how TGF-mediated tubular flow dynamics is impacted by internephron coupling.
2. Mathematical model
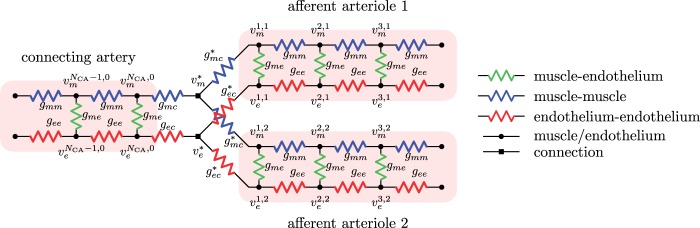
A schematic diagram of the coupled-nephron model is given in Fig. 1. The model represents a connecting artery that branches off the
cortical radial artery and divides into a pair of afferent arterioles. Model geometry is
based on anatomic findings by Casellas et
al. (1994). Each afferent arteriole is connected to a model
glomerulus and a short-loop nephron segment. The representation of model components is
based on our previous work (Sgouralis & Layton,
2014b). Below we describe the vascular and tubular components. The two
nephrons are indexed by  , where
, where 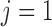 or
2.
or
2.
Fig. 1.
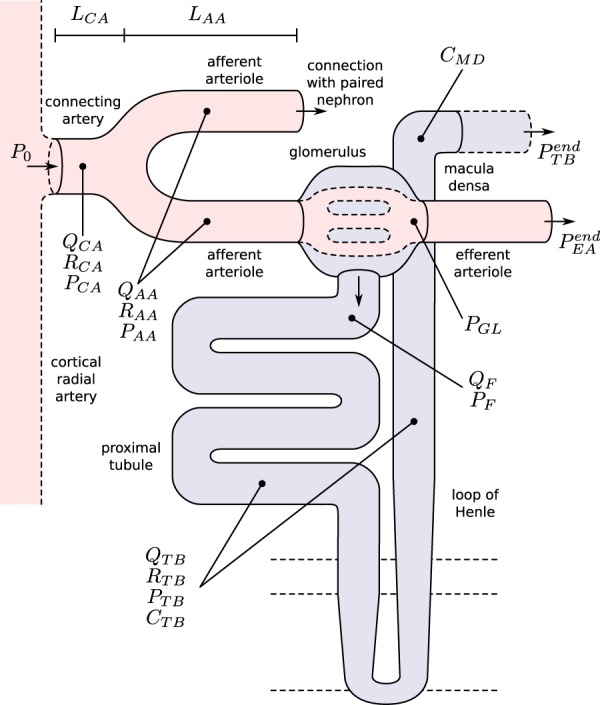
Schematic representation of the coupled nephrons model. Both afferent
arterioles are shown, while glomerulus and tubular segments are shown only for
one of the paired nephrons. 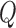 , fluid
flow;
, fluid
flow; 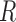 , tubular or vascular radius;
, tubular or vascular radius;
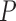 , fluid pressure. Subscripts
‘CA’ denote connecting artery; ‘AA’, afferent
arteriole; ‘EA’, efferent arteriole; ‘GL’,
glomerulus; ‘F’, proximal tubule entrance; ‘TB’,
renal tubule.
, fluid pressure. Subscripts
‘CA’ denote connecting artery; ‘AA’, afferent
arteriole; ‘EA’, efferent arteriole; ‘GL’,
glomerulus; ‘F’, proximal tubule entrance; ‘TB’,
renal tubule. 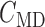 , tubular fluid
[Cl
, tubular fluid
[Cl ] at the macula densa.
] at the macula densa.
2.1. Vascular submodel
The 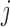 th model afferent arteriole
consists of a series of smooth muscle cell models (Sgouralis & Layton, 2012, 2014a, b), electrically coupled via
gap-junctions and via an endothelial layer. The cellular ionic transport dynamics of
each smooth muscle cell, influenced by the autoregulatory mechanisms, determine the
local vascular tone. The resulting vascular resistance is the main determinant of
blood flow and single-nephron glomerular filtration rate (SNGFR).
th model afferent arteriole
consists of a series of smooth muscle cell models (Sgouralis & Layton, 2012, 2014a, b), electrically coupled via
gap-junctions and via an endothelial layer. The cellular ionic transport dynamics of
each smooth muscle cell, influenced by the autoregulatory mechanisms, determine the
local vascular tone. The resulting vascular resistance is the main determinant of
blood flow and single-nephron glomerular filtration rate (SNGFR).
Each smooth muscle cell model incorporates cell membrane potential, transmembrane
ionic transport, cytosolic Ca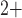 regulation
and muscle contraction. The interactions between the Ca
regulation
and muscle contraction. The interactions between the Ca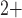 and K
and K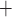 fluxes, which are mediated by
voltage-gated and voltage–calcium-gated channels, respectively, give rise to
the development of spontaneous oscillations in membrane potential. This in turn
results in oscillations in cytoplasmic Ca
fluxes, which are mediated by
voltage-gated and voltage–calcium-gated channels, respectively, give rise to
the development of spontaneous oscillations in membrane potential. This in turn
results in oscillations in cytoplasmic Ca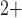 concentration and muscle tone. Details of the ionic transport,
Ca
concentration and muscle tone. Details of the ionic transport,
Ca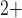 dynamics, crossbridges
phosphorylation and muscle mechanics can be found in Chen et al. (2011), Sgouralis & Layton (2012) and Sgouralis & Layton (2014a, b).
Below we summarize key model components.
dynamics, crossbridges
phosphorylation and muscle mechanics can be found in Chen et al. (2011), Sgouralis & Layton (2012) and Sgouralis & Layton (2014a, b).
Below we summarize key model components.
2.1.1. Smooth muscle cell membrane potential
The smooth muscle cells that form the 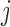 th afferent
arteriole are indexed by
th afferent
arteriole are indexed by 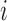 , where
, where
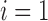 and
and 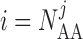 denote the cells
closest to the connecting artery (
denote the cells
closest to the connecting artery (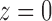 ) and
glomerulus (
) and
glomerulus (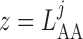 ), respectively.
The associated endothelial compartments are indexed analogously. Throughout this
study, let subscripts
), respectively.
The associated endothelial compartments are indexed analogously. Throughout this
study, let subscripts 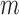 and
and 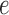 denote the muscle and endothelial
cells, respectively. The rate of change of the membrane potentials of the
denote the muscle and endothelial
cells, respectively. The rate of change of the membrane potentials of the
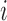 th smooth muscle and endothelial
cells, denoted by
th smooth muscle and endothelial
cells, denoted by 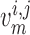 and
and
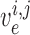 , respectively, are
given by
, respectively, are
given by
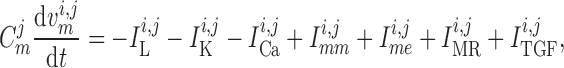 |
(2.1) |
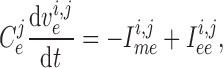 |
(2.2) |
where 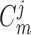 and
and
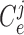 denote cellular
capacitances, assumed spatially independent but may differ between arterioles. By
denote cellular
capacitances, assumed spatially independent but may differ between arterioles. By
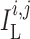
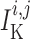 , and
, and
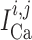 we denote
transmembrane leak current, potassium current and calcium current, respectively;
we denote
transmembrane leak current, potassium current and calcium current, respectively;
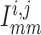 ,
,
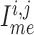 and
and
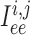 are gap-junctional
currents; and
are gap-junctional
currents; and 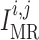 and
and
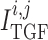 are myogenic-
and TGF-induced currents.
are myogenic-
and TGF-induced currents.
The transmembrane currents are given by
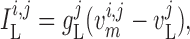 |
(2.3) |
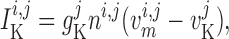 |
(2.4) |
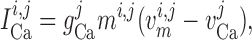 |
(2.5) |
where 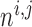 and
and
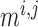 denote the fraction of
open K
denote the fraction of
open K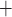 and
Ca
and
Ca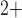 channels, respectively.
The model assumes that
channels, respectively.
The model assumes that 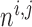 depends
on
depends
on 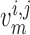 as well as on cytosolic
[Ca
as well as on cytosolic
[Ca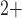 ], whereas
], whereas
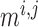 depends only on
depends only on
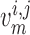 . For details see Chen et al. (2011) and Sgouralis & Layton (2014a). The remaining
currents,
. For details see Chen et al. (2011) and Sgouralis & Layton (2014a). The remaining
currents, 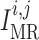 and
and
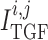 , arise from the
operation of the myogenic response and TGF (see below).
, arise from the
operation of the myogenic response and TGF (see below).
Neighbouring afferent arteriole smooth muscle cells communicate via homocellular
and heterocellular gap-junctions (Brink,
1998; Wagner, 2008). We consider
gap-junctional currents passing between smooth muscles, denoted by
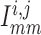 , between smooth
muscles and the endothelium, denoted by
, between smooth
muscles and the endothelium, denoted by 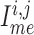 ,
and between endothelial cells, denoted by
,
and between endothelial cells, denoted by 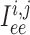 . (Recall subscripts
. (Recall subscripts
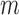 and
and 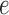 indicate smooth muscle and
endothelial cells, respectively.) The smooth muscle–endothelium
gap-junction current in Equation (2.2) is given by Ohm's law
indicate smooth muscle and
endothelial cells, respectively.) The smooth muscle–endothelium
gap-junction current in Equation (2.2) is given by Ohm's law
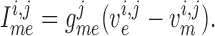 |
(2.6) |
Similarly, away from the boundaries, i.e. for 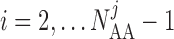 , the
gap-junction currents
, the
gap-junction currents 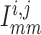 and
and
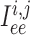 are, respectively,
given by
are, respectively,
given by
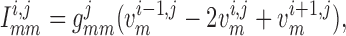 |
(2.7) |
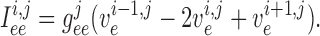 |
(2.8) |
To implement electrotonic coupling of the two nephrons, we assume that, at the
junction with the connecting artery (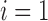 ), the two
afferent arterioles are attached to a common node with potentials
), the two
afferent arterioles are attached to a common node with potentials
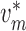 and
and
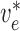 , with gap-junctional
conductances denoted by
, with gap-junctional
conductances denoted by 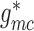 and
and
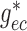 , respectively; see Fig.
2. (The subscript
, respectively; see Fig.
2. (The subscript
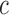 indicates
‘connection’.) This yields the boundary conditions
indicates
‘connection’.) This yields the boundary conditions
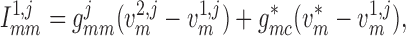 |
(2.9) |
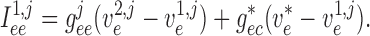 |
(2.10) |
In the base case, 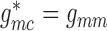 and
and
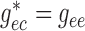 .
.
Fig. 2.
Equivalent circuit of intercellular coupling near the vascular junction. For simplicity, only gap-junctional currents are shown. Both homocellular and heterocellular interfaces are represented.
The boundary condition at 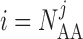 ,
which represents current leakage out of the vessel, can be found in Sgouralis & Layton (2012, 2014a).
,
which represents current leakage out of the vessel, can be found in Sgouralis & Layton (2012, 2014a).
2.1.2. Myogenic response
We assume that the activity of non-selective cation channels responds to changes
in intravascular pressure, such that elevations in intravascular pressure
depolarize the smooth muscle membrane and vice versa. To induce
pressure-dependent changes in membrane potential, we apply a current
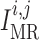 in Equation
(2.1), which is described by
in Equation
(2.1), which is described by
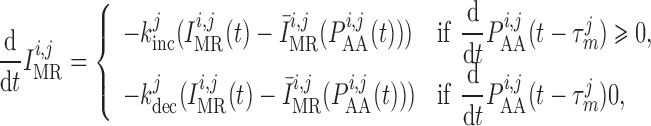 |
(2.11) |
where 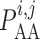 denotes the
intravascular pressure. Equation (2.11) describes a rate-dependent myogenic response, in which
denotes the
intravascular pressure. Equation (2.11) describes a rate-dependent myogenic response, in which
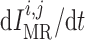 at time
at time 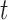 depends on the
direction that
depends on the
direction that 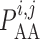 is changing at an earlier time
is changing at an earlier time 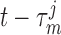 , as
indicated by experimental observations (Loutzenhiser et al., 2002, 2004). The asymmetric rate constants
, as
indicated by experimental observations (Loutzenhiser et al., 2002, 2004). The asymmetric rate constants 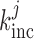 and
and
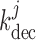 are set to 0.55 and
0.13 s
are set to 0.55 and
0.13 s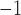 for both nephrons,
consistent with experimental measurements (Loutzenhiser & Loutzenhiser, 2000). Similarly, the response delay
for both nephrons,
consistent with experimental measurements (Loutzenhiser & Loutzenhiser, 2000). Similarly, the response delay
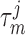 of both nephrons is set
to 0.3 s for pressure increases and to 1 s for pressure decreases
(Loutzenhiser et al.,
2002, 2004).
of both nephrons is set
to 0.3 s for pressure increases and to 1 s for pressure decreases
(Loutzenhiser et al.,
2002, 2004).
To represent a depolarizing current at elevated blood pressure, we assume that the
target current 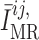 is an
increasing function of luminal pressure having the saturable form
is an
increasing function of luminal pressure having the saturable form
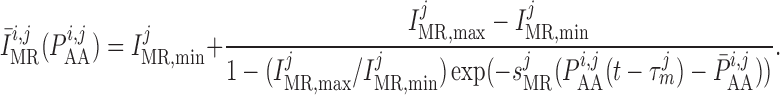 |
(2.12) |
The reference pressure 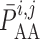 is chosen such
that at baseline perfusion pressure
is chosen such
that at baseline perfusion pressure 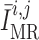 is zero.
is zero.
2.1.3. Tubuloglomerular feedback
The TGF current is applied to the smooth muscles spanning only the distal
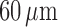 of the afferent
arterioles (Christensen & Bohle, 1978).
The current
of the afferent
arterioles (Christensen & Bohle, 1978).
The current 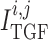 is assumed to
exhibit a sigmoidal dependence on intratubular macula densa
[Cl
is assumed to
exhibit a sigmoidal dependence on intratubular macula densa
[Cl ] (denoted by
] (denoted by
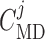 ),
),
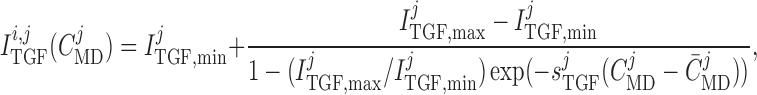 |
(2.13) |
where 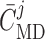 denotes the
operating macula densa [Cl
denotes the
operating macula densa [Cl ], set to
32 mM for both nephrons (Layton et
al., 1991). The parameters
], set to
32 mM for both nephrons (Layton et
al., 1991). The parameters 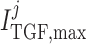 ,
,
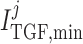 and
and
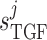 determine the
dynamic range and open-loop gain of TGF; for details see Sgouralis & Layton (2014b).
determine the
dynamic range and open-loop gain of TGF; for details see Sgouralis & Layton (2014b).
2.1.4. Connecting artery
Representation of the connecting artery follows that of the afferent arteriole. Smooth muscle membrane and endothelium potentials are given by
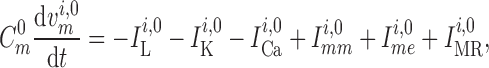 |
(2.14) |
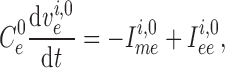 |
(2.15) |
where 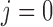 denotes the connecting
artery. At the junction with the arterioles (
denotes the connecting
artery. At the junction with the arterioles (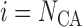 ), muscle and
endothelial potentials are connected to
), muscle and
endothelial potentials are connected to 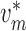 and
and
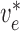 with conductances
with conductances
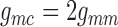 and
and
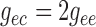 , respectively; see
Fig. 2. The values of
, respectively; see
Fig. 2. The values of
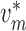 and
and
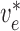 are determined by
conservation of current
are determined by
conservation of current
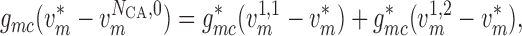 |
(2.16) |
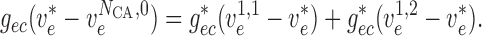 |
(2.17) |
2.1.5. Blood flow
Blood enters the cortical radial artery at the renal perfusion pressure
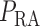 , which is assumed
known a priori and is given by
, which is assumed
known a priori and is given by
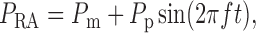 |
(2.18) |
where 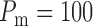 mmHg is the mean
arterial pressure,
mmHg is the mean
arterial pressure, 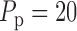 mmHg is the pulse
amplitude and
mmHg is the pulse
amplitude and 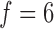 Hz is the heart rate typical
of a rat. The pulse amplitude
Hz is the heart rate typical
of a rat. The pulse amplitude 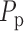 is
chosen to be smaller than the heart beat amplitude to reflect the damping that
occurs upstream of the connecting artery and the afferent arterioles.
is
chosen to be smaller than the heart beat amplitude to reflect the damping that
occurs upstream of the connecting artery and the afferent arterioles.
We assume simple Poiseuille flow so that blood flow can be computed from the
pressure drop along the vessel and the vascular resistance. Let
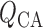 and
and
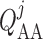 denote blood flow
along the connecting artery and the
denote blood flow
along the connecting artery and the 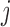 th afferent
arteriole, respectively. Then
th afferent
arteriole, respectively. Then
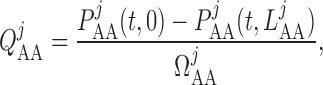 |
(2.19) |
where 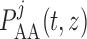 is the pressure
profile along the
is the pressure
profile along the 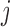 th afferent arteriole.
Conservation of mass implies
th afferent arteriole.
Conservation of mass implies
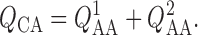 |
(2.20) |
The overall resistance of each afferent arteriole is computed from the radius profile
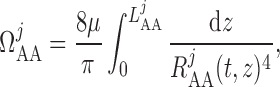 |
(2.21) |
where 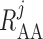 denotes arteriolar
radius and
denotes arteriolar
radius and 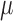 denotes the apparent blood
viscosity.
denotes the apparent blood
viscosity.
We assume that each model afferent arteriole is connected in series to a
post-glomerular resistor 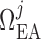 at the end of
which pressure is
at the end of
which pressure is 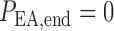 mmHg.
Post-glomerular blood flow is given by the difference between arteriolar flow
mmHg.
Post-glomerular blood flow is given by the difference between arteriolar flow
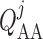 and SNGFR (denoted
by
and SNGFR (denoted
by 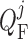 ), and is related to
pressure drop and vascular resistance according to
), and is related to
pressure drop and vascular resistance according to
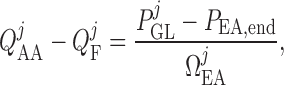 |
(2.22) |
where 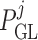 is the blood
pressure at the end of the glomerular capillary. The relation between
is the blood
pressure at the end of the glomerular capillary. The relation between
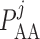 and
and
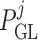 can be found in
Sgouralis & Layton (2014b). The
values of
can be found in
Sgouralis & Layton (2014b). The
values of 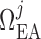 are chosen
such that, in the base case, they account for 47% of the pressure drop
between
are chosen
such that, in the base case, they account for 47% of the pressure drop
between 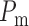 and
and
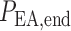 .
.
The pressure gradient along the vascular lumens is given by the Poiseuille equation
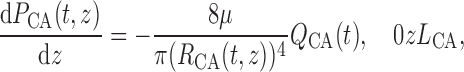 |
(2.23) |
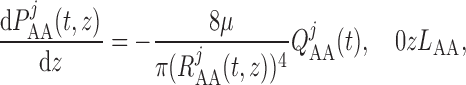 |
(2.24) |
where 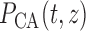 is the pressure
along the connecting artery. Before entering the connecting artery, blood is
assumed passing through a fixed resistor
is the pressure
along the connecting artery. Before entering the connecting artery, blood is
assumed passing through a fixed resistor 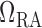 , thus pressure
at the connecting artery's inlet is given by
, thus pressure
at the connecting artery's inlet is given by 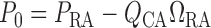 .
The value of
.
The value of 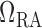 is chosen such
that at baseline it accounts for a pressure drop of 5 mmHg, (Sgouralis & Layton, 2014b). At the
vascular junction, continuity of blood pressure implies
is chosen such
that at baseline it accounts for a pressure drop of 5 mmHg, (Sgouralis & Layton, 2014b). At the
vascular junction, continuity of blood pressure implies 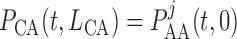 for
for 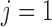 and 2.
and 2.
To represent the differences in the geometric dimensions between the afferent arterioles and the connecting arteries, as seen in Casellas et al. (1994) and Wagner et al. (1997), the baseline vascular tone of the smooth muscles forming the connecting artery is adjusted to yield a baseline luminal radius that is 20% larger than that of the arterioles.
2.2. Tubule submodel
The tubule model represents a proximal tubule followed by a short-loop of Henle,
extending from 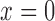 (connection with the glomerulus)
to
(connection with the glomerulus)
to 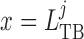 (site of the macula
densa). The model predicts intratubular pressure (
(site of the macula
densa). The model predicts intratubular pressure ( ), water flow rate
(
), water flow rate
(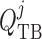 ) and
Cl
) and
Cl concentration
(
concentration
(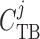 ). Tubular walls are
assumed to be compliant, with a radius that depends passively on the transmural
pressure gradient
). Tubular walls are
assumed to be compliant, with a radius that depends passively on the transmural
pressure gradient
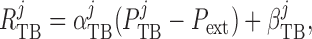 |
(2.25) |
where 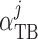 characterizes
tubular compliance and
characterizes
tubular compliance and 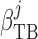 is the
unpressurized radius.
is the
unpressurized radius.
2.2.1. Water transport
Tubular water flow is assumed to be pressure driven. The proximal tubule and the
initial segment of the descending limb of Henle's loop are water permeable.
Taking the transmural water flux 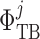 into account,
pressure and flow rate along the model nephron are, respectively, given by
into account,
pressure and flow rate along the model nephron are, respectively, given by
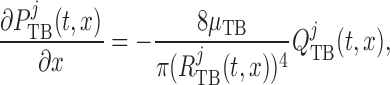 |
(2.26) |
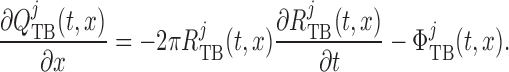 |
(2.27) |
At its outlet (site of the macula densa), the model tubule is connected to a
resistance 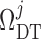 , at the end of
which pressure is assumed to be fixed at
, at the end of
which pressure is assumed to be fixed at 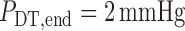 .
Thus, tubular outlet pressure and flow are related by
.
Thus, tubular outlet pressure and flow are related by
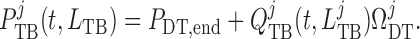 |
(2.28) |
For details see Sgouralis & Layton (2014b).
Transmural water flux depends on the SNGFR:
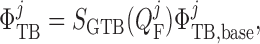 |
(2.29) |
where 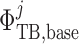 is the
baseline water flux profile. The factor
is the
baseline water flux profile. The factor 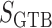 is
a dimensionless scaling that models glomerulotubular balance (Thomson et al., 2001; Thomson & Blantz, 2008), which is given by
is
a dimensionless scaling that models glomerulotubular balance (Thomson et al., 2001; Thomson & Blantz, 2008), which is given by
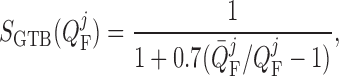 |
(2.30) |
where 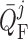 is the operating
point, set to 30 nl/min for both nephrons.
is the operating
point, set to 30 nl/min for both nephrons.
2.2.2. Chloride transport
Chloride concentration along the tubule is given by conservation of mass
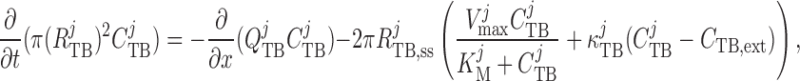 |
(2.31) |
where 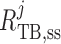 is the
steady-state tubular radius. Interstitial Cl
is the
steady-state tubular radius. Interstitial Cl concentration, denoted by
concentration, denoted by
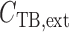 , is set to
115 mM in the cortex and increases to 275 mM at the
outer–inner medullary boundary (Layton
et al., 1991). The first term in the last pair of
parentheses corresponds to active solute transport characterized by
Michaelis–Menten-like kinetics, and the second term represents
transepithelial diffusion with transmural permeability
, is set to
115 mM in the cortex and increases to 275 mM at the
outer–inner medullary boundary (Layton
et al., 1991). The first term in the last pair of
parentheses corresponds to active solute transport characterized by
Michaelis–Menten-like kinetics, and the second term represents
transepithelial diffusion with transmural permeability 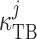 . Strictly
speaking, Na
. Strictly
speaking, Na ion is actively transported
via the Na
ion is actively transported
via the Na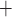 /K
/K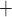 -ATP pump, with
Cl
-ATP pump, with
Cl ion transported passively
through the basolateral membrane. On the apical side, the NKCC2 transporter binds
one Na
ion transported passively
through the basolateral membrane. On the apical side, the NKCC2 transporter binds
one Na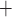 ion for each
K
ion for each
K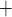 or
NH
or
NH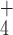 ion plus two
Cl
ion plus two
Cl ions. Thus, the
Michaelis–Menten term in Equation (2.31) is an approximation and appears to be sufficient. At the entrance
of the proximal tubule (
ions. Thus, the
Michaelis–Menten term in Equation (2.31) is an approximation and appears to be sufficient. At the entrance
of the proximal tubule (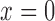 ), tubular
fluid [Cl
), tubular
fluid [Cl ] is set to 115 mM.
] is set to 115 mM.
The proximal tubule exhibits glomerulotubular balance, whereby NaCl and water
reabsorption along the proximal tubular varies in tandem. To
represent glomerulotubular balance, we assume that, along the proximal tubule,
maximum active Cl transport
transport
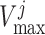 exhibits an
analogous dependence upon the SNGFR as the transmural water flux
exhibits an
analogous dependence upon the SNGFR as the transmural water flux
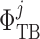 . That dependence
is given by
. That dependence
is given by
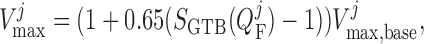 |
(2.32) |
where 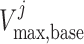 is the
baseline maximum transport rate along the proximal tubule. Note that the above
relation applies only along the proximal tubule, not the downstream segments.
is the
baseline maximum transport rate along the proximal tubule. Note that the above
relation applies only along the proximal tubule, not the downstream segments.
2.3. Model parameters
The model involves a large number of parameters, which have been adopted from Sgouralis & Layton (2014b) unless specified otherwise. A list of selected key parameter values can be found in Table 1.
Table 1.
Baseline parameter values. Superscripts  refer to connecting
artery, afferent arteriole
refer to connecting
artery, afferent arteriole  and
afferent arteriole
and
afferent arteriole  respectively. References:
respectively. References:  present
study,
present
study,  Casellas et al. (1994),
Casellas et al. (1994),
 Chilton et al. (2008),
Chilton et al. (2008),
 Sgouralis & Layton (2014b),
Sgouralis & Layton (2014b),
 Sgouralis & Layton (2012),
Sgouralis & Layton (2012),  Sgouralis & Layton (2014a),
Sgouralis & Layton (2014a),
 Chen et al. (2011)
Chen et al. (2011)
| Description | Parameter | Value | Units |  |
|---|---|---|---|---|
Afferent arteriole size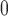
|
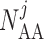 |
81 | — | 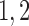 |
Connecting artery size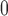
|
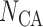 |
20 | — | — |
Afferent arteriole length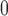
|
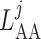 |
243 | 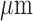 |
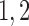 |
Connecting artery length
|
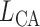 |
60 | 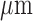 |
— |
Muscle membrane capacitance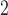
|
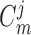 |
6.5 | pF |  |
Endothelium compartment capacitance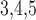
|
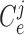 |
0.41 | pF | 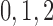 |
Muscle–muscle gap-junctional
conductance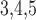
|
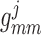 |
6175 | pS | 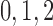 |
Muscle–endothelium gap-junctional
conductance
|
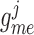 |
553 | pS | 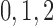 |
Endothelium–endothelium gap-junctional
conductance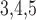
|
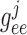 |
12350 | pS |  |
Whole muscle leak conductance
|
 |
6.5 | pS |  |
Whole muscle potassium conductance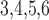
|
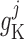 |
26 | pS |  |
Whole muscle calcium conductance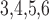
|
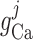 |
13 | pS | 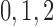 |
Leak reversal potential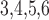
|
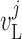 |
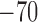 |
mV | 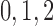 |
Potassium reversal potential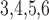
|
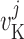 |
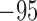 |
mV | 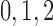 |
Calcium reversal potential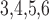
|
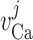 |
80 | mV |  |
Myogenic response minimum current
|
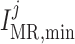 |
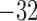 |
fA | 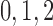 |
Myogenic response maximum current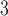
|
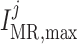 |
195 | fA | 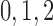 |
Myogenic response sensitivity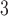
|
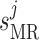 |
0.06 | mmHg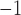
|
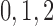 |
Tubuloglomerular feedback minimum current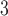
|
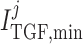 |
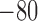 |
fA | 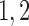 |
Tubuloglomerular feedback maximum current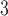
|
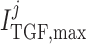 |
60 | fA | 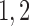 |
Tubuloglomerular feedback sensitivity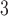
|
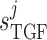 |
0.16 | mM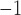
|
 |
3. Results
3.1. Effect of coupling on TGF-mediated dynamics
We first consider two isolated nephrons. The goal is to understand the behaviours of
blood flow and solute transport in the absence of internephron coupling, and how
those behaviours are affected by TGF. Similar to previous modelling studies, the
afferent arterioles are assumed to be 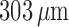 long (Sgouralis & Layton, 2012, 2014a, b).
The connecting artery is not represented; instead, perfusion pressure
long (Sgouralis & Layton, 2012, 2014a, b).
The connecting artery is not represented; instead, perfusion pressure
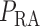 is applied at the
entrance of separate pre-arteriolar resistors
is applied at the
entrance of separate pre-arteriolar resistors 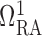 and
and
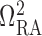 , with each one
having half the baseline value of
, with each one
having half the baseline value of 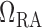 .
With this configuration, the nephrons are fed by non-overlapping vasculatures, and
thus each one operates independently of the other.
.
With this configuration, the nephrons are fed by non-overlapping vasculatures, and
thus each one operates independently of the other.
In nephron 1, the TGF parameter 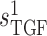 is
set to 0. This corresponds to an open-loop gain of 0, and thus complete absence of
TGF. SNGFR and macula densa luminal [Cl
is
set to 0. This corresponds to an open-loop gain of 0, and thus complete absence of
TGF. SNGFR and macula densa luminal [Cl ] time courses,
shown in Fig. 3(A1 and A2) (blue line), exhibit
limit-cycle oscillations at a frequency of
] time courses,
shown in Fig. 3(A1 and A2) (blue line), exhibit
limit-cycle oscillations at a frequency of 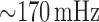 . Those
oscillations arise from the spontaneous vasomotion of the afferent arteriole, which,
in turn, results from the interactions between cellular ionic fluxes and membrane
potential (for a detailed explanation of the origin of the spontaneous vasomotion,
see Chen et al., 2011).
Spontaneous vasomotion yields oscillations in arteriolar resistance, and thus the
SNGFR.
. Those
oscillations arise from the spontaneous vasomotion of the afferent arteriole, which,
in turn, results from the interactions between cellular ionic fluxes and membrane
potential (for a detailed explanation of the origin of the spontaneous vasomotion,
see Chen et al., 2011).
Spontaneous vasomotion yields oscillations in arteriolar resistance, and thus the
SNGFR.
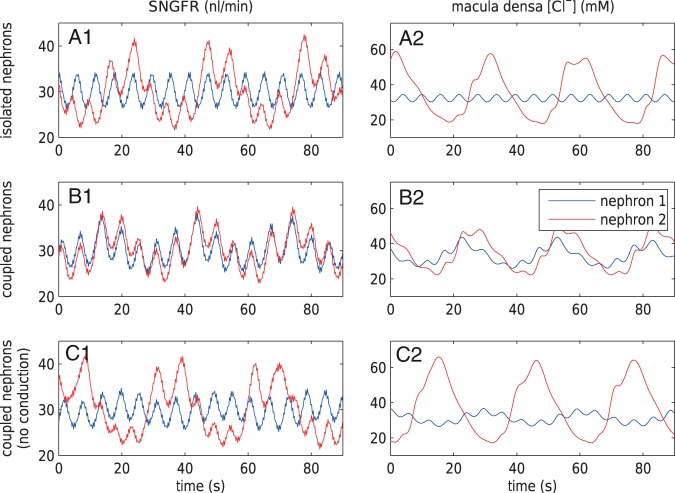
Fig. 3.
Effect of internephron coupling on SNGFR and macula densa
[Cl ]. TGF is disabled in
nephron 1; TGF gain is set to 3.1 in nephron 2. (A1 and A2) Isolated
nephrons. TGF-mediated oscillations are seen in nephron 2. (B1 and B2) Fully
coupled nephrons show synchronization of myogenic and TGF-mediated
oscillations. (C1 and C2) Electrotonic conduction disabled. Oscillations in
nephron 1 are induced by hydrodynamic coupling and are much weaker compared
with the fully coupled case (B1 and B2).
]. TGF is disabled in
nephron 1; TGF gain is set to 3.1 in nephron 2. (A1 and A2) Isolated
nephrons. TGF-mediated oscillations are seen in nephron 2. (B1 and B2) Fully
coupled nephrons show synchronization of myogenic and TGF-mediated
oscillations. (C1 and C2) Electrotonic conduction disabled. Oscillations in
nephron 1 are induced by hydrodynamic coupling and are much weaker compared
with the fully coupled case (B1 and B2).
In nephron 2, 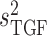 is set to
0.16 mM
is set to
0.16 mM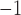 , which gives an open-loop gain
of 3.1. At this gain, TGF-mediated oscillations in blood flow and related variables
emerge, at a frequency of
, which gives an open-loop gain
of 3.1. At this gain, TGF-mediated oscillations in blood flow and related variables
emerge, at a frequency of 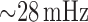 ; see Fig. 3(A1 and A2) (red line).
; see Fig. 3(A1 and A2) (red line).
Another frequency signature (6 Hz) in the blood flow arises from the heart beat (Equation (2.18)). Those oscillations are significantly attenuated by the glomerular filtration process, and then further damped by the compliance of the renal tubule. As a result, oscillations at heart rate are distinguishable only at the SNGFR (Fig. 3A1) and entirely removed from the time courses at the site of the macula densa (Fig. 3A2).
In the next set of simulations, the two nephrons are connected to a common connecting
artery, as shown in Fig. 1. The SNGFR and the
macula densa [Cl ] of each nephron are shown in
Fig. 3(B1 and B2). The oscillating TGF signal in
nephron 2 propagates along the two arterioles and drives nephron 1, whose TGF has
been inhibited, to oscillate too.
] of each nephron are shown in
Fig. 3(B1 and B2). The oscillating TGF signal in
nephron 2 propagates along the two arterioles and drives nephron 1, whose TGF has
been inhibited, to oscillate too.
The propagation of the TGF signal is mediated by two pathways: (i) electrotonic
conduction along the smooth muscle and endothelium layers of the arteriolar walls,
and (ii) blood flow hydrodynamics. Electrotonic conduction (i) induces simultaneous
vasoconstriction in both nephrons, whereas, owing to mass conservation, hydrodynamic
coupling (ii) induces opposing changes in the two nephrons. Both pathways are
represented in Fig. 3(B1 and B2). Synchronicity
of the oscillations suggests the dominance of the electrotonic pathway over
hydrodynamics. To further clarify the importance of electrotonic conduction, we set
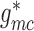 and
and
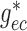 to zero, thereby
completely disabling pathway (i). The resulting SNGFR and macula densa
[Cl
to zero, thereby
completely disabling pathway (i). The resulting SNGFR and macula densa
[Cl ] are shown in Fig. 3(C1 and C2). The TGF-mediated macula densa
[Cl
] are shown in Fig. 3(C1 and C2). The TGF-mediated macula densa
[Cl ] oscillations become out of
phrase and significantly weaker relative to those in Fig. 3(B1 and B2).
] oscillations become out of
phrase and significantly weaker relative to those in Fig. 3(B1 and B2).
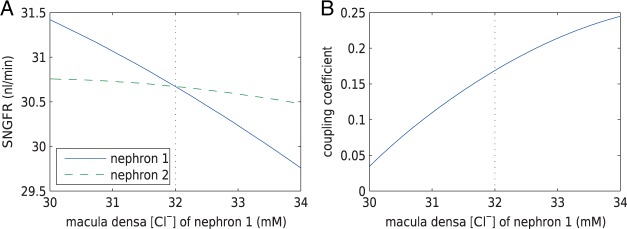
3.2. Estimation of internephron coupling coefficient
In the next set of simulations, we determine 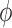 , which quantifies the ability of
one nephron to influence the other nephron's SNGFR via TGF. To that end, we
disable TGF in nephron 2 (by fixing
, which quantifies the ability of
one nephron to influence the other nephron's SNGFR via TGF. To that end, we
disable TGF in nephron 2 (by fixing 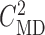 at
32 mM), vary
at
32 mM), vary 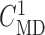 values from 30 to
34 mM, and compute changes in the two nephrons’ SNGFR. As previously
noted, even in the absence of TGF, tubular flow and other variables exhibit
oscillations owing to the spontaneous vasomotion and, to a lesser extent due to heart
beat. Thus, to estimate internephron coupling strength, we use time-averaged SNGFR
values for each nephron. The predicted SNGFR of both nephrons, as functions of
values from 30 to
34 mM, and compute changes in the two nephrons’ SNGFR. As previously
noted, even in the absence of TGF, tubular flow and other variables exhibit
oscillations owing to the spontaneous vasomotion and, to a lesser extent due to heart
beat. Thus, to estimate internephron coupling strength, we use time-averaged SNGFR
values for each nephron. The predicted SNGFR of both nephrons, as functions of
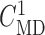 , are shown in Fig.
4(A). Owing to the decay of the electrotonic
signal along the afferent arterioles, perturbations in
, are shown in Fig.
4(A). Owing to the decay of the electrotonic
signal along the afferent arterioles, perturbations in 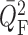 are smaller than in
are smaller than in
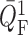 . Fig. 4(B) shows the ratio of these perturbations. This
ratio provides an estimation of the internephron coupling coefficient
. Fig. 4(B) shows the ratio of these perturbations. This
ratio provides an estimation of the internephron coupling coefficient
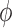 , which is defined as this ratio
evaluated at the operating macula densa [Cl
, which is defined as this ratio
evaluated at the operating macula densa [Cl ], i.e.
], i.e.
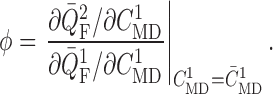 |
(3.1) |
The baseline coupling coefficient is 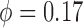 , which
is consistent with experimental observation (Chen
et al., 1995).
, which
is consistent with experimental observation (Chen
et al., 1995).
Fig. 4.
Open-loop simulations to estimate internephron coupling coefficient. (A)
SNGFR for the two nephrons as a function of 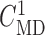 , with
, with
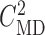 set to
32 mM. (B) Corresponding coupling coefficient, given by the ratio of
the two SNGFR values.
set to
32 mM. (B) Corresponding coupling coefficient, given by the ratio of
the two SNGFR values.
3.2.1. Effect of afferent arteriole length on internephron coupling
Because the electrotonic signal decays along the afferent arterioles,
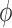 is expected to be a
decreasing function of vessel length. Figure 5(A) shows
is expected to be a
decreasing function of vessel length. Figure 5(A) shows 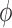 as a
function of total afferent arteriole length (sum of the lengths of the two
arterioles). These results were obtained with the assumption that the two model
arterioles are of identical length. Anatomic findings have yielded a range of
afferent arteriole lengths,
as a
function of total afferent arteriole length (sum of the lengths of the two
arterioles). These results were obtained with the assumption that the two model
arterioles are of identical length. Anatomic findings have yielded a range of
afferent arteriole lengths, 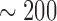 –
–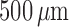 (Casellas et al., 1994; Nordsletten et al., 2006).
Given these estimates, our model suggests that
(Casellas et al., 1994; Nordsletten et al., 2006).
Given these estimates, our model suggests that 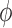 ranges in an approximately
linear fashion, from nearly 90% at a total arteriolar length of
ranges in an approximately
linear fashion, from nearly 90% at a total arteriolar length of
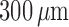 , to nearly 0 at
, to nearly 0 at
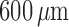 . It is
interesting that for sufficiently long arterioles,
. It is
interesting that for sufficiently long arterioles, 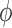 becomes negative, which
indicates a shift in the dominant pathway from electrotonic conduction to
hydrodynamics.
becomes negative, which
indicates a shift in the dominant pathway from electrotonic conduction to
hydrodynamics.
Fig. 5.
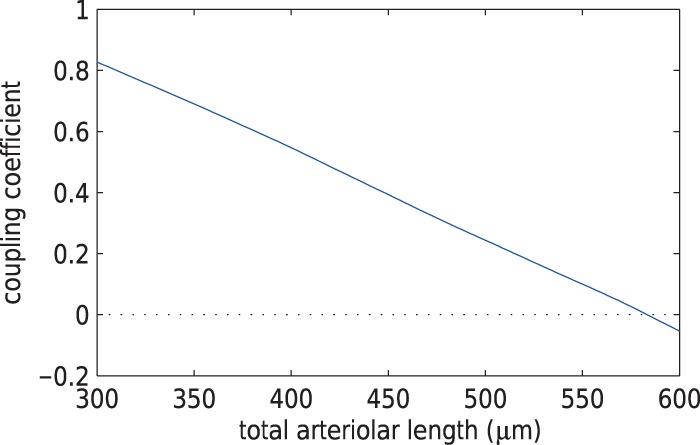
Internephron coupling coefficient as a function of total arteriolar length. Dependence is approximately linear.
3.2.2. Internephron coupling sensitivity on gap-junctions
Electrotonic signal propagation between the two nephrons is mediated by
gap-junctions developed at the interfaces of smooth muscle and endothelium cells.
Each interface is associated with a different conductance, and thus impacts
 differently. To assess the
impact of these conductances on
differently. To assess the
impact of these conductances on 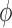 , we
conducted simulations where we separately varied each conductance by
, we
conducted simulations where we separately varied each conductance by
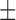 20% of its baseline
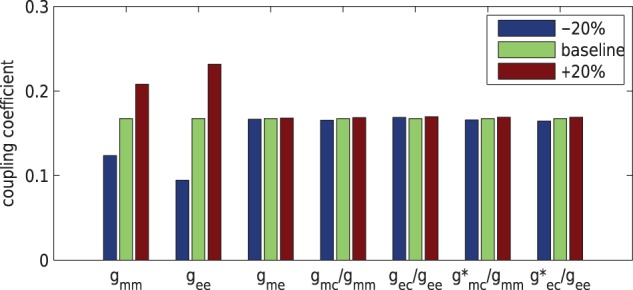
value. Results, which are summarized in Fig. 6, indicate that
20% of its baseline
value. Results, which are summarized in Fig. 6, indicate that 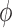 is most
sensitive to
is most
sensitive to 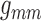 and
and
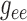 . In contrast,
. In contrast,
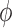 appears relatively
insensitive to conductances developed near the vascular junction (i.e.
appears relatively
insensitive to conductances developed near the vascular junction (i.e.
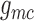 ,
, 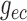 ,
, 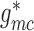 ,
, 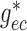 ). This suggests that
geometric considerations near the vascular junction do not have a significant
impact on overall coupling strength.
). This suggests that
geometric considerations near the vascular junction do not have a significant
impact on overall coupling strength.
Fig. 6.
Percentage changes in coupling coefficient changes as gap-junctional
parameters are varied by 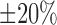 from baseline
values. Coupling strength is most sensitive to
from baseline
values. Coupling strength is most sensitive to 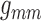 and
and
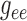 .
.
Next we compare the relative contributions of the smooth muscle and endothelial
pathways in the conduction of the TGF signal. To that end, we individually vary
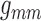 and
and
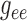 , from 10% to about
200% its baseline value, and compute the resulting coupling coefficient
, from 10% to about
200% its baseline value, and compute the resulting coupling coefficient
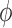 . As can be observed from
Fig. 7, the dependence of
. As can be observed from
Fig. 7, the dependence of
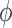 on
on 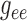 is significantly stronger
than that on
is significantly stronger
than that on 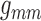 . This implies the majority
of the TGF signal is conducted via the endothelial layer. This is further
illustrated in Fig. 8, which shows the
membrane potential of the smooth muscle and endothelial cells along the
arterioles, as well as the connecting artery, under maximal stimulation of TGF.
One can see that the signal decays more rapidly along the smooth muscle layer,
owing to its lower gap-junctional conductance, relative to the endothelial layer.
. This implies the majority
of the TGF signal is conducted via the endothelial layer. This is further
illustrated in Fig. 8, which shows the
membrane potential of the smooth muscle and endothelial cells along the
arterioles, as well as the connecting artery, under maximal stimulation of TGF.
One can see that the signal decays more rapidly along the smooth muscle layer,
owing to its lower gap-junctional conductance, relative to the endothelial layer.
Fig. 7.
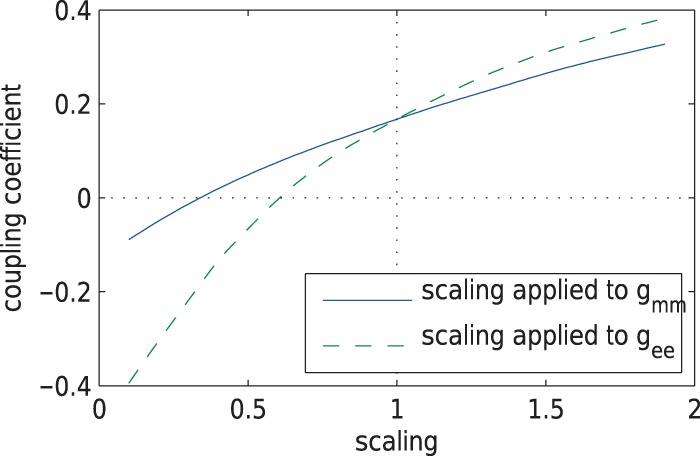
Internephron coupling coefficient 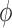 as a function of
scaling applied to either
as a function of
scaling applied to either 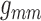 or
or 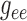 .
.
Fig. 8.
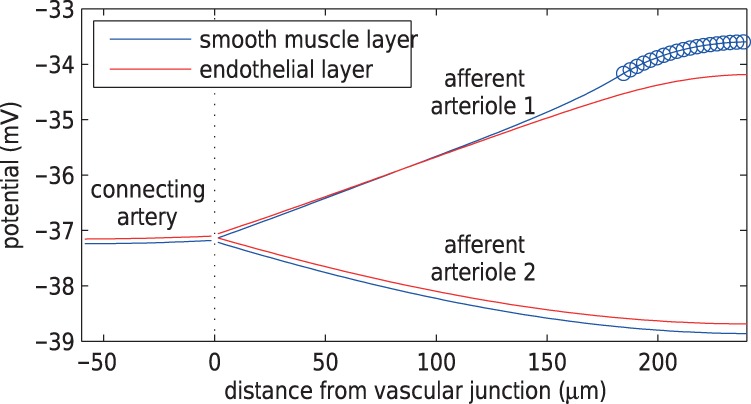
Time average smooth muscle and endothelium potential profiles under maximal stimulation of TGF at nephron 1. Circles denote the TGF application site. Length constant of depolarization is longer in endothelium than in smooth muscle.
3.3. Effect of gap-junctions on TGF responses
As noted above, the baseline model exhibits regular oscillations with key frequencies
at 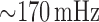 and
and
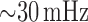 (Fig. 3), which correspond to oscillations mediated by
spontaneous ionic fluxes and TGF, respectively. Those oscillations are transmitted to
blood and solute flows through the contractile mechanics of the vascular smooth
muscles of the arteriolar walls. Fluctuations in the myogenic tone of a given smooth
muscle is initiated by changes in its membrane potential, which is coupled to that of
the neighbouring smooth muscles via the gap-junctions.
(Fig. 3), which correspond to oscillations mediated by
spontaneous ionic fluxes and TGF, respectively. Those oscillations are transmitted to
blood and solute flows through the contractile mechanics of the vascular smooth
muscles of the arteriolar walls. Fluctuations in the myogenic tone of a given smooth
muscle is initiated by changes in its membrane potential, which is coupled to that of
the neighbouring smooth muscles via the gap-junctions.
Gap-junctional coupling is known to be altered in hypertension (Rummery & Hill, 2004; Figueroa et al., 2006; Wagner, 2008; Brisset et
al., 2009; Figueroa &
Duling, 2009), and blood flow in spontaneously hypertensive rats has been
observed to exhibit highly irregular oscillations (Holstein-Rathlou & Marsh, 1994). Thus, we seek to investigate the role
of gap-junctional coupling in maintaining or disrupting the regularity of flow
oscillations. To that end, we computed the time courses of proximal tubule pressure
for a range of gap-junctional conductance values. Two selected cases are shown in
Fig. 9: (A) corresponds to baseline
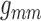 ,
,  ,
, 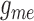 , and (B) to the same parameters
reduced by 55% of the baseline values. As can be seen, the lower conductances
yield highly irregular oscillations. In none of the simulations with conductances
higher than baseline did we observe similarly irregular oscillations (results not
shown).
, and (B) to the same parameters
reduced by 55% of the baseline values. As can be seen, the lower conductances
yield highly irregular oscillations. In none of the simulations with conductances
higher than baseline did we observe similarly irregular oscillations (results not
shown).
Fig. 9.
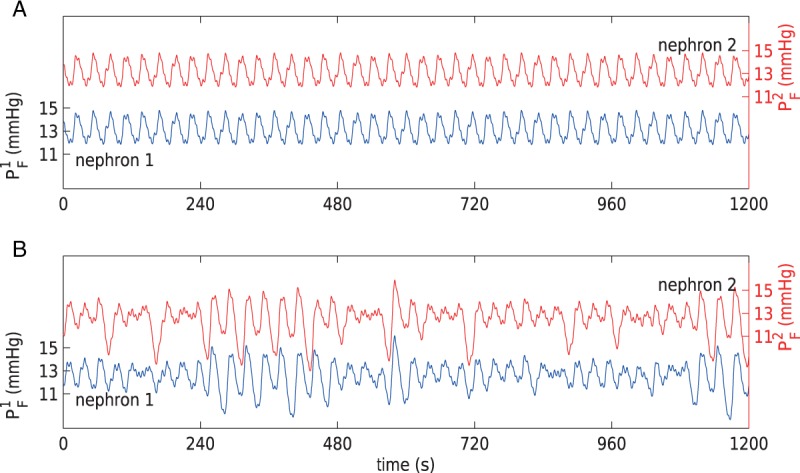
Proximal tubule pressure oscillations for baseline (A) and reduced (B) gap-junctional conductances. Irregular oscillations are obtained for the lower conductances.
The spontaneously hypertensive rats that exhibit irregular oscillations (Holstein-Rathlou & Marsh, 1994) have also
been found to exhibit stronger vasomotor coupling among neighbouring nephrons (Wagner et al., 1997). To better
understand the relation between gap-junctional conductance and vasomotor coupling
strength, we conducted open TGF-loop simulations for conductances at baseline values
and reduced by 55%, as above. In both simulations, 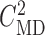 was kept at 32 mM,
and
was kept at 32 mM,
and 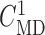 was chosen to yield a
local vasoconstriction of
was chosen to yield a
local vasoconstriction of 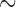 20%.
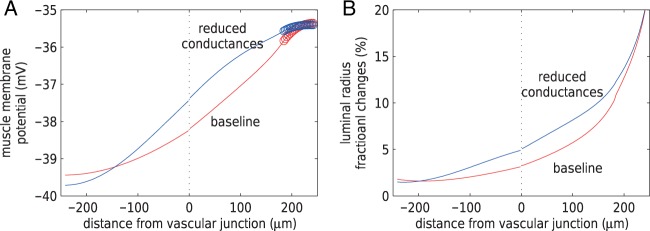
Figure 10 shows the resulting profiles of
time-averaged muscle potential and vasoconstriction along the afferent arterioles.
Reduced gap-junctional conductances appear to yield stronger conducted responses in
both membrane potential and vasoconstriction.
20%.
Figure 10 shows the resulting profiles of
time-averaged muscle potential and vasoconstriction along the afferent arterioles.
Reduced gap-junctional conductances appear to yield stronger conducted responses in
both membrane potential and vasoconstriction.
Fig. 10.
(A) Time-averaged muscle potential profiles for baseline
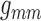 ,
,
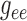 ,
,
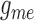 values, and for
conductances reduced by 55%. Circles denote TGF application sites.
Stimulated nephron is shown on the right (positive distance); paired nephron
on the left (negative distance). Dotted line indicates the location of the
vascular junction. (B) Corresponding vasomotor responses. Reduced
conductances yield stronger coupling.
values, and for
conductances reduced by 55%. Circles denote TGF application sites.
Stimulated nephron is shown on the right (positive distance); paired nephron
on the left (negative distance). Dotted line indicates the location of the
vascular junction. (B) Corresponding vasomotor responses. Reduced
conductances yield stronger coupling.
To understand the above predictions, which may appear counter-intuitive, we revisit
the spontaneous limit-cycle oscillations of the smooth muscle membrane potential,
which arise from the interactions between the membrane potential, and the
voltage-gated Ca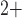 and
K
and
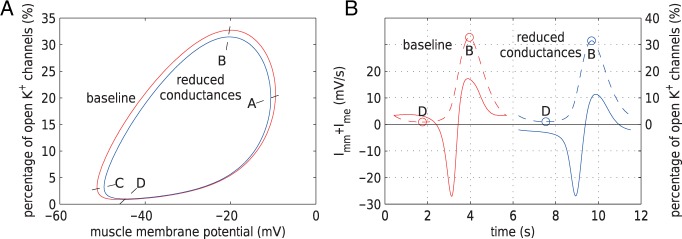
K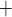 channels (Equations (2.4) and (2.5)). Figure 11(A) shows
the limit cycles of the smooth muscle located
channels (Equations (2.4) and (2.5)). Figure 11(A) shows
the limit cycles of the smooth muscle located 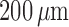 upstream of the TGF
application site, for the simulations with baseline and reduced conductances. Each
cycle can be divided into four regions, according to the open state of the
Ca
upstream of the TGF
application site, for the simulations with baseline and reduced conductances. Each
cycle can be divided into four regions, according to the open state of the
Ca and
K
and
K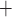 channels:
A
channels:
A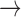 B, where
Ca
B, where
Ca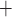 channels close and
K
channels close and
K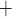 channels open;
B
channels open;
B C, where
Ca
C, where
Ca and K
and K channels close;
C
channels close;
C D, where
Ca
D, where
Ca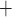 channels open and
K
channels open and
K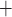 channels close;
D
channels close;
D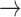 A, where
Ca
A, where
Ca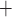 and K
and K channels open. Clearly, the
electrotonic influence is stronger along A
channels open. Clearly, the
electrotonic influence is stronger along A B
B C, which is associated with the
closing of K
C, which is associated with the
closing of K channels, than along
C
channels, than along
C D
D A, which is associated with the
opening of K
A, which is associated with the
opening of K channels. Owing to the
gap-junctional communications among the smooth muscles, different conductances yield
different deformations of the limit cycles. In particular, the reduced conductances
case yield a smaller limit cycle. How does this explain the stronger
vasoconstriction?
channels. Owing to the
gap-junctional communications among the smooth muscles, different conductances yield
different deformations of the limit cycles. In particular, the reduced conductances
case yield a smaller limit cycle. How does this explain the stronger
vasoconstriction?
Fig. 11.
(A) Limit cycles of muscle potential and K channels opening of
afferent arteriole smooth muscle cells located
channels opening of
afferent arteriole smooth muscle cells located 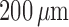 upstream
of the TGF application site. Trajectories are counterclockwise for both
cycles. (B) Time courses of net gap-junctional current
upstream
of the TGF application site. Trajectories are counterclockwise for both
cycles. (B) Time courses of net gap-junctional current
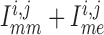 (solid lines) and fraction of open K
(solid lines) and fraction of open K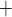 channels (dashed
lines).
channels (dashed
lines).
To answer this question, we consider the net gap-junctional currents (between two
smooth muscle cells, and between smooth muscle and endothelial cells,
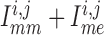 ). As shown
in Fig. 11(B), the reduced conductance values
yield smaller currents than the base case (compare maximum currents at 11.3 (reduced)
versus 17.2 mV/s (baseline), minimum currents at
). As shown
in Fig. 11(B), the reduced conductance values
yield smaller currents than the base case (compare maximum currents at 11.3 (reduced)
versus 17.2 mV/s (baseline), minimum currents at 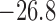 (reduced) versus
(reduced) versus
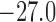 mV/s (baseline)). This is to be
expected and does not explain the stronger coupling in the reduced conductance case.
However, consider point B, which marks the beginning of the closing of the
K
mV/s (baseline)). This is to be
expected and does not explain the stronger coupling in the reduced conductance case.
However, consider point B, which marks the beginning of the closing of the
K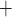 channels. Coincidentally, B is
close to the peaks of
channels. Coincidentally, B is
close to the peaks of 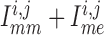 in both
cases. That current is depolarizing, which opposes the closing of the
K
in both
cases. That current is depolarizing, which opposes the closing of the
K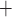 channels. Thus, the stronger the
current, the slower is the closing of K
channels. Thus, the stronger the
current, the slower is the closing of K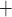 channels.
Because
channels.
Because 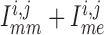 is
stronger with the baseline conductances, K
is
stronger with the baseline conductances, K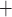 channels are
prone to slower closing. To quantify these observations, we compute the time-averaged
fraction of open K
channels are
prone to slower closing. To quantify these observations, we compute the time-averaged
fraction of open K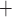 channels
channels
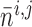 by
by
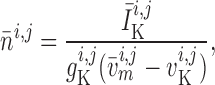 |
(3.2) |
where 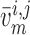 and
and
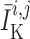 are the
corresponding time averages of
are the
corresponding time averages of 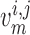 and
and
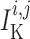 . For the muscles
shown in Fig. 11,
. For the muscles
shown in Fig. 11, 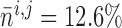 and
11.2% for baseline and reduced conductances, respectively. Consequently, the
time-averaged membrane potentials are
and
11.2% for baseline and reduced conductances, respectively. Consequently, the
time-averaged membrane potentials are 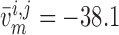 and
and
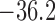 mV, respectively. That is, the
reduced conductances result in a larger degree of depolarization, and a stronger
vasoconstrictive response (radius
mV, respectively. That is, the
reduced conductances result in a larger degree of depolarization, and a stronger
vasoconstrictive response (radius 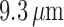 compared with
compared with 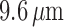 in the base
case).
in the base
case).
4. Discussion
We have extended our previous detailed model of renal haemodynamics (Sgouralis & Layton, 2014b) to represent two coupled nephrons. The resulting coupled nephron model is used to study electrotonic conduction of TGF signal between coupled nephrons, factors that impact the coupling strength, and the effect of internephron coupling on TGF-mediated dynamics.
4.1. Comparison with previous modelling studies
In a series of studies (Layton et al., 2009, 2011; Ryu & Layton, 2014), we have previously used mathematical models to investigate the effects of internephron coupling on TGF-mediated dynamics. A major difference between the present study and the previous studies is that the latter represent only electrical coupling, whereas by including the afferent arterioles and connecting artery, the present study represents both hydrodynamic and electrical coupling.
Another major difference is that the previous models (Layton et al., 2009, 2011; Ryu & Layton, 2014) do
not explicitly incorporate the afferent arterioles. Instead, internephron coupling is
represented by applying a fraction (determined by a coupling parameter,
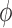 ) of the TGF signal of the
initiating nephron to its paired nephron. This implies that the coupling strength is
known a priori. In contrast, the present model explicitly represents
two paired afferent arterioles, along which the TGF signal propagates. This allows us
to determine the internephron coupling strength. The base case coupling strength,
) of the TGF signal of the
initiating nephron to its paired nephron. This implies that the coupling strength is
known a priori. In contrast, the present model explicitly represents
two paired afferent arterioles, along which the TGF signal propagates. This allows us
to determine the internephron coupling strength. The base case coupling strength,
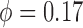 , agrees well with values
assumed in our previous studies (Layton et
al., 2009, 2011; Ryu & Layton, 2014).
, agrees well with values
assumed in our previous studies (Layton et
al., 2009, 2011; Ryu & Layton, 2014).
In a pioneering study, Marsh et al. (2013) published a similarly comprehensive model of a nephrovascular network that incorporates a large number of afferent arterioles, loops of Henle and TGF. In that model, each afferent arteriole is represented by only two myogenically active segments. Thus, each submodel represents a rather long segment along the afferent arteriole, whereas in the present study, each afferent arteriolar cell submodel has the dimensions of a renal smooth muscle cell (Loutzenhiser & Loutzenhiser, 2000). Also, the model of Marsh et al. (2013) uses a phenomenological representation of TGF signal propagation; the TGF input is applied to both arteriolar segments with a predefined decay based on the distance from the glomerulus. In contrast, in the current model TGF input is applied only to the distal smooth muscles of each arteriole and the signal propagates along the arterioles via electronic conduction.
4.2. Internephron coupling and hypertension
In the cardiovascular system, gap-junctions are made up of one or more of four connexin proteins: Cx37, Cx40, Cx43 and Cx45. Changes in Cx expression in hypertensive animal models have been reported, although those results are not always consistent. Cx40 and Cx45 are consistently reduced in endothelial cells, but results for Cx43 are mixed (Haefliger et al., 2000; Yeh et al., 2006). An interesting and likely relevant observation is that normalization of blood pressure in the spontaneously hypertensive rats using an angiotensin-converting enzyme inhibitor or candesartan restores endothelial connexin expression to normal in parallel with the normalization of blood pressure (Kansui et al., 2004; Rummery et al., 2005).
Our simulation results suggest that a reduction in gap-junctional conductances
elevates internephron coupling, in the sense that it yields a stronger conducted TGF
response (Fig. 11). This rather surprising
prediction is a result of the interactions between the gap-junctional voltage signal
and the K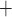 channels. Assuming that
gap-junctional conductances are indeed reduced in spontaneously hypertensive rats,
our result may explain the observed stronger TGF coupling (Wagner et al., 1997). There is experimental
evidence which suggests that gap-junctional conductances may vary in different
disease states (Heberlein et al.,
2009). The relation between gap-junctional conductances and TGF coupling
strength predicted by the present model can be tested provided these quantities can
be measured in health and disease states.
channels. Assuming that
gap-junctional conductances are indeed reduced in spontaneously hypertensive rats,
our result may explain the observed stronger TGF coupling (Wagner et al., 1997). There is experimental
evidence which suggests that gap-junctional conductances may vary in different
disease states (Heberlein et al.,
2009). The relation between gap-junctional conductances and TGF coupling
strength predicted by the present model can be tested provided these quantities can
be measured in health and disease states.
Additionally, our simulation results suggest that reduced conductances give rise to
irregular TGF-mediated oscillations in nephron flows and related variables (Fig.
9). Similar patterns have been observed in
spontaneously hypertensive rats (Holstein-Rathlou
& Marsh, 1994). This prediction is also consistent with findings by
de Wit et al. (2003), which
indicate that the absence of vascular Cx40 is associated with hypertension and
irregular vasomotion. In particular, de Wit et al. reported diameter
fluctuations reaching as low as 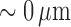 in
Cx40
in
Cx40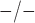 arterioles. Similarly, our
model predicts fluctuations reaching near complete occlusion when gap-junctional
conductances are reduced to ≥40% of
baseline values (results not shown).
arterioles. Similarly, our
model predicts fluctuations reaching near complete occlusion when gap-junctional
conductances are reduced to ≥40% of
baseline values (results not shown).
Note, however, that we have limited our consideration to the effects of altered gap-junctional conductances. Other differences between hypertensive and normotensive animals, e.g. perfusion pressure, TGF gain (Dilley & Arendshorst, 1984), pressure natriuretic and diuretic responses (Granger et al., 2002; Beard & Mescam, 2012), etc. have not been incorporated. These factors will be considered in a future, more comprehensive study that focuses on autoregulation in a hypertensive kidney.
4.3. Myoendothelial gap-junction expression
The proper conduction of vasomotor responses relies on a high density of myoendothelial gap-junctions, which provide electrical communication between endothelial cells and smooth muscle cells. The expression of myoendothelial gap-junctions have been reported to be heterogeneous, among different vascular beds, with density inversely related to arteriolar size (Sandow et al., 2012). In a modelling study, Hald et al. (2014) show that heterogeneous distributions of myoendothelial gap-junction properties may have a profound impact on system behaviour. However, spatial heterogeneity in myoendothelial gap-junction expression within a given afferent arteriole has yet to be demonstrated, and direct measurements of myoendothelial gap-junction conductances do not exist. Given these uncertainties, we have assumed constant gap-junction conductances in the present model. Nonetheless, the impact of heterogeneous myoendothelial gap-junction distributions is a worthwhile consideration in a future study.
Funding
This research was supported by the National Institutes of Health: National Institute of Diabetes and Digestive and Kidney Diseases, Grant DK089066. Part of the work was conducted while I.S. was a Postdoctoral Fellow at the National Institute for Mathematical and Biological Synthesis, an Institute sponsored by the National Science Foundation through NSF Award #DBI-1300426, with additional support from The University of Tennessee, Knoxville.
References
- Beard D., Mescam M. (2012) Mechanisms of pressure-diuresis and pressure-natriuresis in Dahl salt-resistant and Dahl salt-sensitive rats. BMC Physiol., 12, 6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brink P. (1998) Gap junctions in vascular smooth muscle. Acta Physiol. Scand., 164, 349–56. [DOI] [PubMed] [Google Scholar]
- Brisset A., Isakson B., Kwak B. (2009) Connexins in vascular physiology and pathology. Antioxid Redox Signal, 11, 267–282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Casellas D., Dupont M., Bouriquet N., Moore L., Artuso A., Mimran A. (1994) Anatomic pairing of afferent arterioles and renin cell distribution in rat kidneys. Am. J. Physiol., 267, F931–F936. [DOI] [PubMed] [Google Scholar]
- Chen J., Sgouralis I., Moore L., Layton H., Layton A. (2011) A mathematical model of the myogenic response to systolic pressure in the afferent arteriole. Am. J. Physiol. Renal Physiol., 300, F669–F681. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Y., Yip K., Marsh D., Rathlou N. H. (1995) Magnitude of TGF-initiated nephron-nephron interaction is increased in SHR. Am. J. Physiol., 269, F198–F204. [DOI] [PubMed] [Google Scholar]
- Chilton L., Loutzenhiser K., Morales E., Breaks J., Kargacin G., Loutzenhiser R. (2008) Inward rectifier k(+) currents and kir2.1 expression in renal afferent and efferent arterioles. J. Am. Soc. Nephrol., 19, 69–76. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christensen J., Bohle A. (1978) The juxtaglomerular apparatus in the normal rat kidney. Virchows Arch. A Path Anat. and Histol., 379, 143–150. [DOI] [PubMed] [Google Scholar]
- de Wit C., Roos F., Bolz S.-S., Pohl U. (2003) Lack of vascular connexin 40 is associated with hypertension and irregular arteriolar vasomotion. Physiol. Genom., 13, 169–177. [DOI] [PubMed] [Google Scholar]
- Dilley J., Arendshorst W. (1984) Enhanced tubuloglomerular feedback activity in rats developing spontaneous hypertension. Am. J. Physiol., 247, F672–F679. [DOI] [PubMed] [Google Scholar]
- Eaton D., Pooler J. (2004) Vander's Renal Physiology, 6th edn New York: McGraw-Hill Medical. [Google Scholar]
- Figueroa X., Duling B. (2009) Gap junctions in the control of vascular function. Antioxid Redox Signal, 11, 251–266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Figueroa X., Isakson B., Duling B. (2006) Vascular gap junctions in hypertension. Hypertension, 48, 804–811. [DOI] [PubMed] [Google Scholar]
- Granger J., Alexander B., Llinas M. (2002) Mechanisms of pressure natriuresis. Curr. Hypertens Rep., 4, 152–159. [DOI] [PubMed] [Google Scholar]
- Haefliger J., Polikar R., Schnyder G., Burdet M., Sutter E., Pexieder T., Nicod P., Meda P. (2000) Connexin37 in normal and pathological development of mouse heart and great arteries. Dev. Dyn., 218, 331–344. [DOI] [PubMed] [Google Scholar]
- Hald B., Jacobsen J., Sandow S., Holstein-Rathlou N.-H., Welsh D. (2014) Less is more: minimal expression of myoendothelial gap junctions optimizes cell-cell communication in virtual arterioles. J. Physiol., 15, 3243–3255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han J., Thompson K., Chou C., Knepper M. (1992) Experimental tests of three-dimensional model of urinary concentrating mechanism. J. Am. Soc. Nephrol., 2, 1677–1688. [DOI] [PubMed] [Google Scholar]
- Heberlein K., Straub A., Isakson B. (2009) The myoendothelial junction: breaking through the matrix? Microcirculation, 16, 307–322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holstein-Rathlou N. (1987) Synchronization of proximal intratubular pressure oscillations: evidence for interaction between nephrons. Pflügers Arch., 408, 438–443. [DOI] [PubMed] [Google Scholar]
- Holstein-Rathlou N., Marsh D. (1994) Renal blood flow regulation and arterial pressure fluctuations: a case study in nonlinear dynamics. Physiol. Rev., 74, 637–681. [DOI] [PubMed] [Google Scholar]
- Just A. (2007) Mechanisms of renal blood flow autoregulation: dynamics and contributions. Am. J. Physiol. Regul. Integr. Comp. Physiol., 292, R1–R17. [DOI] [PubMed] [Google Scholar]
- Källskog Ö., Marsh D. (1990) TGF-initiated vascular interactions between adjacent nephrons in the rat kidney. Am. J. Physiol., 259, F60–F64. [DOI] [PubMed] [Google Scholar]
- Kansui Y., Fujii K., Nakamura K., Goto K., Oniki H., Abe I., Shibata Y., Iida M. (2004) Angiotensin II receptor blockade corrects altered expression of gap junctions in vascular endothelial cells from hypertensive rats. Am. J. Physiol. Heart Circ. Physiol., 287, H216–H224. [DOI] [PubMed] [Google Scholar]
- Layton A., Bowen M., Wen A., Layton H. (2011) Feedback-mediated dynamics in a model of coupled nephrons with compliant thick ascending limbs. Math. Biosci., 230, 115–127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Layton A., Moore L., Layton H. (2006) Multistability in tubuloglomerular feedback and spectral complexity in spontaneously hypertensive rats. Am. J. Physiol. Renal Physiol., 291, F79–F97. [DOI] [PubMed] [Google Scholar]
- Layton A., Moore L., Layton H. (2009) Multistable dynamics mediated by tubuloglomerular feedback in a model of coupled nephrons. Bull. Math. Biol., 71, 515–555. [DOI] [PubMed] [Google Scholar]
- Layton H., Pitman E., Moore L. (1991) Bifurcation analysis of TGF-mediated oscillations in SNGFR. Am. J. Physiol., 261, F904–F919. [DOI] [PubMed] [Google Scholar]
- Loutzenhiser R., Bidani A., Chilton L. (2002) Renal myogenic response: kinetic attributes and physiologic role. Circ. Res., 90, 1316–1324. [DOI] [PubMed] [Google Scholar]
- Loutzenhiser R., Bidani A., Wang X. (2004) Systolic pressure and the myogenic response of the renal afferent arteriole. Acta Physiol. Scand., 181, 404–413. [DOI] [PubMed] [Google Scholar]
- Loutzenhiser K., Loutzenhiser R. (2000) Angiotensin ii-induced ca(2+) influx in renal afferent and efferent arterioles: differing roles of voltage-gated and store-operated ca(2+) entry. Circ. Res., 87, 551–557. [DOI] [PubMed] [Google Scholar]
- Marsh D., Wexler A., Brazhe A., Postnov D., Sosnovtseva O., Rathlou N. H. (2013) Multinephron dynamics on the renal vascular network. Am. J. Physiol. Renal Physiol., 304, F88–F102. [DOI] [PubMed] [Google Scholar]
- Nordsletten D., Blackett S., Bentley M., Ritman E., Smith N. (2006) Structural morphology of renal vasculature. Am. J. Physiol. Heart Circ. Physiol., 291, H296–H309. [DOI] [PubMed] [Google Scholar]
- Nyengaard J., Bendtsen T. (1992) Glomerular number and size in relation to age, kidney weight, and body surface in normal man. Anat. Rec., 232, 194–201. [DOI] [PubMed] [Google Scholar]
- Pitman E., Zaritski R., Kesseler K., Moore L., Layton H. (2004) Feedback-mediated dynamics in two coupled nephrons. Bull. Math. Biol., 66, 1463–1492. [DOI] [PubMed] [Google Scholar]
- Rummery N., Grayson T., Hill C. (2005) Angiotensin-converting enzyme inhibition restores endothelial but not medial connexin expression in hypertensive rats. J. Hypertens., 23, 317–328. [DOI] [PubMed] [Google Scholar]
- Rummery N., Hill C. (2004) Vascular gap junctions and implications for hypertension. Clin. Exp. Pharmacol. Physiol., 31, 659–667. [DOI] [PubMed] [Google Scholar]
- Ryu H., Layton A. (2014) Tubular fluid flow and distal NaCl delivery mediated by tubuloglomerular feedback in the rat kidney. J. Math. Biol., 68, 1023–1049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sandow S., Senadheera S., Bertrand P., Murphy T., Tare M. (2012) Myoendothelial contacts, gap junctions, and microdomains: anatomical links to function? Microcirculation, 19, 403–415. [DOI] [PubMed] [Google Scholar]
- Sgouralis I., Layton A. (2012) Autoregulation and conduction of vasomotor responses in a mathematical model of the rat afferent arteriole. Am. J. Physiol. Renal Physiol., 33, F229–F239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sgouralis I., Layton A. (2014a) Control and modulation of fluid flow in the rat kidney. Bull. Math. Biol., 306, F1357–F1371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sgouralis I., Layton A. (2014b) Theoretical assessment of renal autoregulatory mechanisms. Am. J. Physiol. Renal Physiol., 306, F1357–F1371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomson S., Blantz R. (2008) Glomerulotubular balance, tubuloglomerular feedback, and salt homeostasis. J. Am. Soc. Nephrol., 19, 2272–2275. [DOI] [PubMed] [Google Scholar]
- Thomson S., Deng A., Bao D., Satriano J., Blantz R., Vallon V. (2001) Ornithine decarboxylase, kidney size, and the tubular hypothesis of glomerular hyperfiltration in experimental diabetes. J. Clin. Invest., 107, 217–224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagner C. (2008) Function of connexins in the renal circulation. Kidney Int., 73, 547–555. [DOI] [PubMed] [Google Scholar]
- Wagner A., Holstein-Rathou N., Marsh D. (1997) Internephron coupling by conducted vasomotor responses in normotensive and spontaneously hypertensive rats. Am. J. Physiol., 272, F372–F379. [DOI] [PubMed] [Google Scholar]
- Yeh H., Lee P., Su C., Tian T., Ko Y., Tsai C. (2006) Reduced expression of endothelial connexins 43 and 37 in hypertensive rats is rectified after 7-day carvedilol treatment. Am. J. Hypertens., 19, 129–135. [DOI] [PubMed] [Google Scholar]
- Yip K., Holstein-Rathlou N., Marsh D. (1992) Dynamics of TGF-initiated nephron-nephron interactions in normotensive rats and SHR. Am. J. Physiol., 262, F980–F988. [DOI] [PubMed] [Google Scholar]