EMPIRICAL AVERAGE-CASE RELATION BETWEEN UNDERSAMPLING AND SPARSITY IN X-RAY CT

Abstract

In X-ray computed tomography (CT) it is generally acknowledged that reconstruction methods exploiting image sparsity allow reconstruction from a significantly reduced number of projections. The use of such reconstruction methods is inspired by recent progress in compressed sensing (CS). However, the CS framework provides neither guarantees of accurate CT reconstruction, nor any relation between sparsity and a sufficient number of measurements for recovery, i.e., perfect reconstruction from noise-free data. We consider reconstruction through 1-norm minimization, as proposed in CS, from data obtained using a standard CT fan-beam sampling pattern. In empirical simulation studies we establish quantitatively a relation between the image sparsity and the sufficient number of measurements for recovery within image classes motivated by tomographic applications. We show empirically that the specific relation depends on the image class and in many cases exhibits a sharp phase transition as seen in CS, i.e., same-sparsity images require the same number of projections for recovery. Finally we demonstrate that the relation holds independently of image size and is robust to small amounts of additive Gaussian white noise.

1. Introduction

In X-ray computed tomography (CT) an image of an object is reconstructed from projections obtained by measuring the attenuation of X-rays passed through the object. Motivated by reducing the exposure to radiation, there is a growing interest in low-dose CT, cf. [40] and references therein. This is relevant in many fields, for example, in medical imaging to reduce the risk of radiation-induced cancer, in biomedical imaging where high doses can damage the specimen under study, and in materials science and non-destructive testing to reduce scanning time.

Classical reconstruction methods are based on closed-form analytical or approximate inverses of the continuous forward operator; examples are the filtered back-projection method [28] and the Feldkamp-Davis-Kress method for cone-beam CT [13]. Their main advantages are low memory demands and computational efficiency, which make them the current methods of choice in commercial CT scanners [30]. However, they are known to have limitations on reduced data.

Alternatively, an algebraic formulation can be used, in which both object and data domains are discretized, yielding a large sparse system of linear equations. This approach can handle non-standard scanning geometries for which no analytical inverse is available. Furthermore, data reduction arising from low-dose imaging can sometimes be compensated for by exploiting prior information about the image, such as smoothness or as in our case sparsity, i.e., having a representation with few non-zero coefficients.

Developments in compressed sensing (CS) [4, 8] show potential for a reduction in data while maintaining or even improving reconstruction quality. This is made possible by exploiting image sparsity; loosely speaking, if the image is “sparse enough,” it admits accurate reconstruction from undersampled data. We refer to such methods as sparsity-exploiting methods. Under specific conditions on the sampling procedure, e.g., incoherence, there exist guarantees of perfect recovery.

Different types of sparsity are relevant in CT. For blood vessels [25] the image itself can be considered sparse, and reconstruction based on minimizing the 1-norm can be expected to work well. The human body consists of well-separated areas of relatively homogeneous tissue and many materials, such as metals, consist of non-overlapping uniform sub-components. In these cases the image gradient is approximately sparse, and reconstruction based on minimizing total variation (TV) of the image [35] is often a good choice. Empirical studies using simulated as well as clinical data, using standard highly structured, i.e., non-random, sampling patterns, have demonstrated that sparsity-exploiting methods indeed allow for reconstruction from fewer projections [2, 18, 34, 37, 38].

However, as will be explained in Section 2.2, CS guarantees of recovery from undersampled data are far from generalizing to the sampling done in CT. Therefore, in spite of the positive empirical results, we still lack a fundamental understanding of conditions—especially in a quantitative sense—under which such methods can be expected to perform well in CT: How sparse images can be reconstructed and from how few samples?

The present paper demonstrates empirically an average-case relation between image sparsity and the sufficient number of CT projections enabling image recovery. Inspired by work of Donoho and Tanner [7] we use computer simulations to empirically study recoverability within well-defined classes of sparse images. Specifically, we are interested in the average number of CT projections sufficient for exact recovery of an image as function of the image sparsity. To simplify our analysis we focus on images with sparsity in the image domain and reconstruction through minimization of the image 1-norm subject to a data equality constraint, as motivated by CS. These studies set the stage for forthcoming studies of other regularizers, such as TV, as well as other types of sparsity. We believe that our findings shed light on the connection between sparsity and sufficient sampling in CT and that they suggest the existence of a yet unknown theoretical foundation for CS in CT.

The paper is organized as follows. Section 2 presents the reconstruction problem of interest, describes relevant previous work and results from CS and discusses the application to CT. Section 3 describes all aspects of the experimental design, including the CT imaging model, generation of sparse images, and how to robustly solve the optimization problem of reconstruction. Section 4 contains our results establishing quantitatively a relation between image sparsity and sufficient sampling for recovery. Section 5 presents results for the noisy case and is followed by a discussion in Section 6.

2. Sparsity-exploiting reconstruction methods

This section describes our choice of sparsity-exploiting reconstruction method and explains how existing recovery guarantees from CS do not prove useful in the setting of CT.

2.1. Reconstruction based on 1-norm minimization

We consider the discrete inverse problem of recovering a signal x_orig ∈ ℝ^N from data b ∈ ℝ^M. The imaging model, which is assumed to be linear and discrete-to-discrete [1], relates the image and the data through a system matrix A ∈ ℝ^M×N,

$$Ax=b,$$ (1)

where the elements of x ∈ ℝ^N are pixel values stacked into a vector. We focus in the present work on the “undersampled” and consistent case where M < N such that (1) has infinitely many solutions and hence is ill-posed [17, 20]. To restrict the solution set we consider the problem

$$\mathbf{L}\mathbf{1}:\hspace{1em}\hspace{1em}\underset{x}{\text{min}}{\Vert x\Vert }_1\mathrm{s}.\mathrm{t}.Ax=b,$$ (2)

which seeks to recover a sparse solution, i.e., one with few non-zero components. More generally, one could consider other forms of regularization based on prior knowledge or assumptions to restrict the set of solutions. A common type of regularization takes the form:

$$\underset{x}{\text{min}}J(x)\mathrm{s}.\mathrm{t}.{\Vert Ax-b\Vert }_2\le \epsilon ,$$ (3)

where J(x) is the regularizer. The regularization parameter ε controls the level of regularization and in the limit ε → 0 we obtain the equality-constrained problem.

The inequality-constrained problem (3) is of more practical interest than (2) because it allows for noisy and inconsistent measurements, but its solution depends in a complex way on the noise and inconsistencies in the data, as well as the choice of the parameter ε. Studies of the equality-constrained problem, on the other hand, provide a basic understanding of a given regularizer’s reconstruction potential, independent of specific noise. Furthermore, many of the initial CS recovery guarantees deal with the equality-constrained formulation, and as such the equality-constrained problem in CT is the most natural place to first attempt to establish recovery results in CT. Therefore, we focus for the major part of the present work on the equality-constrained problem, however we conclude with a brief study of robustness with respect to additive Gaussian white noise.

2.2. Existing recovery guarantees do not apply to CT

We call a pair (x_orig, A) a problem instance and say that x_orig is recoverable if the L1 solution with b = A x_orig is identical to x_orig. A caveat is that L1 does not necessarily have a unique solution. The solution set may consist of a single image or an entire hyperface or hyperedge on the 1-norm ball in case this set is aligned with the affine space of feasible points {x | Ax = b}. For being recoverable we therefore require that x_orig be the unique L1 solution.

CS establishes guarantees of recovery of sparse signals from a small number of measurements. An important concept is the restricted isometry property (RIP): A vector x ∈ ℝ^N with k ≤ N non-zero elements is called k-sparse. A matrix A satisfies the RIP of order k if a constant δ_k ∈ (0, 1) exists such that

$$(1-{\delta }_k){\Vert x\Vert }_2^2\le {\Vert Ax\Vert }_2^2\le (1+{\delta }_k){\Vert x\Vert }_2^2$$ (4)

for all k-sparse vectors x. If the RIP-constant δ_k is small enough, then recovery of sparse signals is possible; more precisely, if ${\delta }_{2k}<\sqrt{2}-1$ then the L1 solution x^⋆ for data b = Ax_orig recovers the original image x_orig [5]. There also exist RIP-based guarantees for TV [29]. Such results are sometimes referred to as uniform or strong recovery guarantees [14] since recovery of all vectors of a given sparsity is ensured.

Unfortunately, the RIP is impractical to use because computing the RIP-constant for a given matrix is NP-hard [39]. RIP-constants have been established only for few, very restricted classes of matrices, e.g., with independent identically distributed Gaussian entries [4]. In [36] the authors computed lower bounds close to 1 on the RIP-constant for very low sparsity values for X-ray CT system matrices, thereby excluding the possibility of RIP-based guarantees in tomography for other than extremely sparse signals.

Other CS guarantees rely on incoherence [3], the spark [9] or the null-space property [6] but also fail to give useful guarantees, either due to being extremely pessimistic or NP-hard to compute, see, e.g., [12]. In fact, it is possible to construct examples of very sparse vectors that cannot be recovered from CT measurements [32], implying that we cannot hope for uniform recovery guarantees for CT.

Instead, recoverability can be studied in an average-case sense. This can be motivated by a desire to ensure recovery of “typical” images of a given sparsity, but not all possible pathological images. Such results are sometimes referred to as non-uniform or weak recovery guarantees [14]. Donoho and Tanner [7] derived weak recovery guarantees, i.e., established a relation between image sparsity and the critical average-case sampling level for recovery for example for Gaussian matrices. Their so-called phase diagram demonstrated agreement of the theoretical sampling level for a given sparsity with empirical recovery experiments by revealing a sharp phase transition between recovered and non-recovered images.

Weak recovery guarantees have been established for discrete tomography [31] using very restrictive sampling patterns (essentially only rays perfectly aligned with pixels) and for discrete-valued tomography [15]. These results, however, do not apply to the general case of X-ray CT, see [21] for background on discrete tomography. To our knowledge recovery guarantees for X-ray CT remain an open question.

2.3. Our contribution

In the present paper we empirically establish a quantitative relation between the number of measurements and the image sparsity sufficient for average-case recovery. We generate random images from specific classes of images motivated by tomographic applications and determine the average critical sampling level for recovery by L1 as function of image sparsity. Our empirical study is inspired by the Donoho-Tanner (DT) phase diagram, however we use a slightly modified diagram in which the quantities of our interest, namely sparsity and sampling, can be read directly off the axes.

With this approach we provide extensive empirical evidence of an average-case relation between sampling and sparsity occurring across different image classes, image sizes as well as showing robustness to noise.

3. Design of numerical experiments

In this section we describe our overall empirical study design after presenting the chosen imaging model, generation of sparse test images and numerical optimization for the reconstruction problem.

3.1. CT imaging geometry

We consider a typical 2D fan-beam geometry with 360° circular source path and N_v equi-angular projections, or views, onto a curved detector. We consider a square domain of N_side × N_side pixels, and due to rotational symmetry we restrict the region-of-interest to be within a disk-shaped mask inside the square domain consisting of approximately $N=\lceil \pi /4·N_{\text{side}}^2\rceil$ pixels. The source-to-center distance is 2N_side, and the fan-angle 28.07° is set to precisely illuminate the disk-shaped mask. The detector consists of 2N_side bins, so the total number of measurements is M = 2N_sideN_v. The M × N system matrix A is computed by means of the MATLAB package AIR Tools [19].

3.2. Sparse image classes

By an image class we mean a set of test images described by a set of specifications, such that we can generate random realizations from the class. We refer to such an image as an image instance from the class, and multiple image instances from the same class form an image ensemble.

For the spikes image class, given an image size N and a target sparsity k, we generate an image instance as follows: starting from the zero image, randomly select k pixel indices, and set each select pixel value to a random number from a uniform distribution over [0, 1]. Figure 1 shows examples of spikes image instances of varying sparsity percentage. This class is deliberately designed to be as simple as possible and it does not model any particular application; it is solely used to study the generic case of having a sparse image. The spikes class, which is known as “random-valued impulse noise” in the signal processing literature, is often considered in CS studies, e.g., [7], and therefore studying it in the setting of CT is natural.

Figure 1.

Top, middle, bottom: Sparse image instances from spikes, 1-power, 2-power classes. Left to right: 5%, 10%, 20%, 40%, 60%, 80% non-zeros. Gray-scale [0, 1].

The p -power class is a more realistic image class that models background tissue in the female breast as described and illustrated in [33]. The idea is to introduce structure to the pattern of non-zero pixels by creating correlation between neighboring pixels. Our procedure is based on [33], followed by thresholding to obtain many zero-valued pixels. The amount of structure is governed by a parameter p:

1. Create an N_side × N_side phase image P with values drawn from a Gaussian distribution with zero mean and unit standard deviation.

2. Create an N_side × N_side amplitude image U with pixel values

   $$U(i,j)={({(\frac{2i-1}{N}-1)}^2+{(\frac{2j-1}{N}-1)}^2)}^{-p/2},i,j=1,\dots ,N_{\text{side}}.$$

3. For all pixels (i, j) compute F(i, j) = U(i, j)e^{2πι̂P (i,j)}, with $\widehat{ɩ}=\sqrt{-1}$.

4. Compute the square image as the magnitude of the DC-centered 2D inverse discrete Fourier transform of F.

5. Restrict the square image to the disk-shaped mask.

6. Keep the k largest pixel values and set the rest to 0.

Figure 1 shows examples of images from classes 1-power and 2-power. Both have more structure than the spikes images, and the structure increases with p.

We do not claim that our image classes are fully realistic models. As our goal is to study how image sparsity affects the number of projections sufficient for recovery, we simply consider a selection of qualitatively different image classes. Development of more realistic image classes for specific applications is beyond the scope of the present work.

3.3. Robust solution of optimization problem

Our interest in the present work is to robustly assess whether an image x_orig in a given problem instance is recoverable. The approach we take is to solve L1 numerically and compare the achieved solution with x_orig. The robustness of the decision regarding recovery naturally depends on the accuracy of the solution. False conclusions may result from incorrect or inaccurate solutions. To robustly solve the optimization problem L1 we must therefore use a numerical method which gives a reliable indication of whether a correct solution, within a given accuracy, has been computed. Our choice is the package MOSEK [27], which uses a primal-dual interior-point method and issues warnings in the rare case that an accurate solution can not be computed. For all problem instances in our studies, MOSEK returned a certified accurate solution.

To solve L1 using MOSEK we recast it as the linear program

$$\underset{x,w}{\text{argmin}}{\mathbf{1}}^{T}w\mathrm{s}.\mathrm{t}.Ax=b\text{and}-w\le x\le w,$$ (5)

where 1 denotes the vector of all ones in ℝ^N and “≤” denotes elementwise inequality.

3.4. Simulations

Using the presented imaging model, method for generating sparse test images, and robust optimization algorithm we carry out simulation studies of recoverability within an image class. A single recovery simulation consists of the following steps, assuming image sparsity k and number of projections N_v:

1. Generate k-sparse test image x_orig,

2. generate system matrix A using N_v projections,

3. compute perfect data b = Ax_orig,

4. solve L1 numerically to obtain x^⋆, and

5. test for recovery numerically using

   $$\frac{{\Vert x^{\star }-x_{\text{orig}}\Vert }_2}{{\Vert x_{\text{orig}}\Vert }_2}<\tau ,$$ (6)

where the threshold τ is chosen based on the chosen accuracy of the optimization algorithm; empirically we found τ = 10⁻⁴ to be well-suited in our set-up.

We wish to study how the number of projections sufficient for L1 recovery depends on the image sparsity. In order to make comparisons across image size we introduce the following normalized measures of sparsity and sampling. For a given problem instance, we define the relative sparsity as

$$\mathbf{\text{relative sparsity}}:\hspace{1em}\kappa =k/N.$$ (7)

In our studies we will generate test images of a desired relative sparsity κ and set the sparsity as k = round(κN). We let the sufficient projection number $N_{\mathrm{v}}^{\text{suf}}$ denote the smallest number of projections that causes A to have full column rank. At $N_{\mathrm{v}}\ge N_{\mathrm{v}}^{\text{suf}}$ the original image is the unique feasible point and hence minimizer no matter what objective is minimized and we therefore use $N_{\mathrm{v}}^{\text{suf}}$ as a reference point of full sampling. For a given problem instance, the number of projections for L1 recovery $N_{\mathrm{v}}^{\mathbf{L}\mathbf{1}}$ denotes the smallest number of projections for which recovery is observed for all $N_{\mathrm{v}}\ge N_{\mathrm{v}}^{\mathbf{L}\mathbf{1}}$. We define the

$$\mathbf{\text{relative sampling}}:\hspace{1em}\hspace{1em}\mu =N_{\mathrm{v}}/N_{\mathrm{v}}^{\text{suf}},$$ (8)

$$\mathbf{\text{relative sampling for}}\mathbf{L}\mathbf{1}\mathbf{\text{recovery}}:\hspace{1em}\hspace{1em}{\mu }^{\mathbf{L}\mathbf{1}}=N_{\mathrm{v}}^{\mathbf{L}\mathbf{1}}/N_{\mathrm{v}}^{\text{suf}}.$$ (9)

For the test problems considered here, existence of an L1 solution is guaranteed by the way we generate data. As mentioned in Section 2.2, uniqueness is not guaranteed and for a given problem instance it cannot be known in advance whether the solution is unique. The computed solution depends on the optimization algorithm, and therefore our conclusions of recoverability by L1 are, in principle, subject to our use of MOSEK. We do not specifically check for uniqueness; however, in the event of infinitely many solutions, it is unlikely that any optimization algorithm will select precisely the original image, so we believe that our observations of recoverability based on solving L1 correspond to existence of a unique solution.

4. Simulation results

In this section we present our numerical results. We first establish that L1 indeed can recover the original image from fewer than $N_{\mathrm{v}}^{\text{suf}}$ projections. We then systematically study how $N_{\mathrm{v}}^{\mathbf{L}\mathbf{1}}$ depends on the image sparsity, image size, image class and finally the robustness to noise.

4.1. Recovery from undersampled data

To verify that L1 is capable of recovering an image from undersampled CT measurements in our set-up, we use a spikes image x_orig with N_side = 64, leading to N = 3228 pixels in the disk-shaped mask. The relative sparsity is set to κ = 0.20, which yields 646 non-zeros. We consider reconstruction from data corresponding to 2, 4, 6, …, 32 projections; the smallest and largest system matrices are of sizes 256×3228 and 4096×3228, respectively. At N_v = 24, the matrix is 3072×3228 and rank(A) = 3052, at N_v = 25 it is 3200×3228 and has rank 3185, while at N_v = 26, the matrix is 3328×3228 and full-rank; hence $N_{\mathrm{v}}^{\text{suf}}=26$. Selected L1 reconstructed images x^⋆ are shown in Figure 2 along with the error images x^⋆ − x_orig to better visualize the abrupt drop in error when the image is recovered. L1 recovery occurs already at $N_{\mathrm{v}}=N_{\mathrm{v}}^{\mathbf{L}\mathbf{1}}=12$, where A has size 1536 × 3228 and rank 1524, i.e., a substantial undersampling relative to the full-sampling reference point of $N_{\mathrm{v}}^{\text{suf}}=26$.

Figure 2.

L1 reconstructions of spikes image with N_side = 64, relative sparsity κ = 0.20. Top row: L1 reconstructions, gray-scale [0, 1]. Bottom row: L1 minus original image, gray-scale [−0.1, 0.1]. Columns: 4, 8, 10, 12 ($=N_{\mathrm{v}}^{\mathbf{L}\mathbf{1}}$, i.e., the number of projections for L1 recovery), 24 and 26 ($=N_{\mathrm{v}}^{\text{suf}}$, i.e., the sufficient projection number) projections.

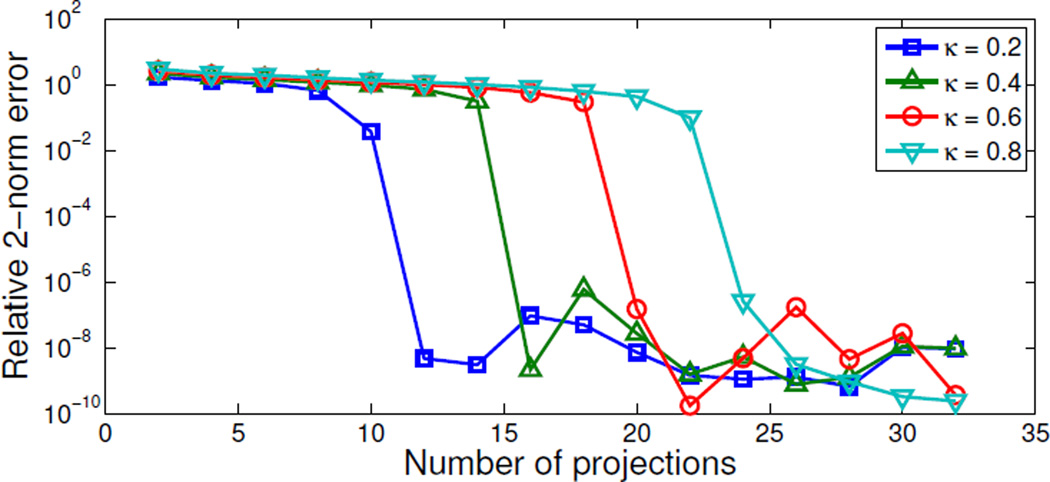
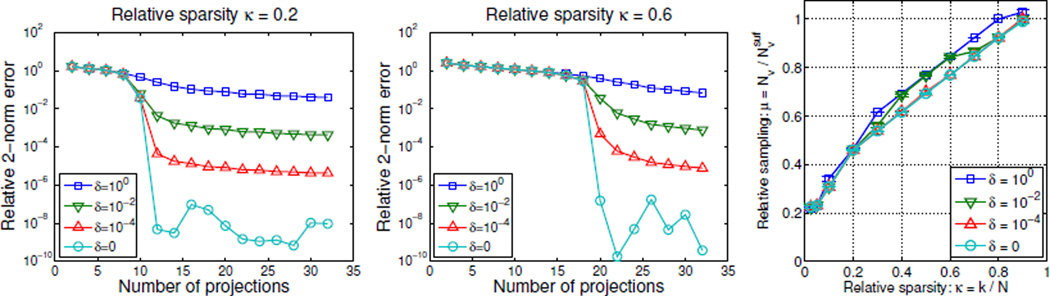
To see how relative sparsity affects recovery, we repeat the experiment for κ = 0.4, 0.6 and 0.8. Figure 3 shows the relative 2-norm error from (6) for the L1 reconstructions as a function of N_v. In all cases an abrupt drop in error to a numerically accurate reconstruction is observed and the relative sampling for L1 recovery $N_{\mathrm{v}}^{\mathbf{L}\mathbf{1}}$ changes from $N_{\mathrm{v}}^{\mathbf{L}\mathbf{1}}=12$ at κ = 0.2 to 16, 20 and 24. This indicates a very simple relation between sparsity and number of projections for L1 recovery.

Figure 3.

Relative 2-norm error from (6) of L1 reconstructions vs. number of projections for spikes images with relative sparsity values κ = 0.2, 0.4, 0.6, 0.8. The κ = 0.2 image is recovered at N_v = 12 as also seen in Fig. 2. The relative errors of recovered images are non-zero due to the numerical accuracy chosen for MOSEK.

4.2. Recovery phase diagram

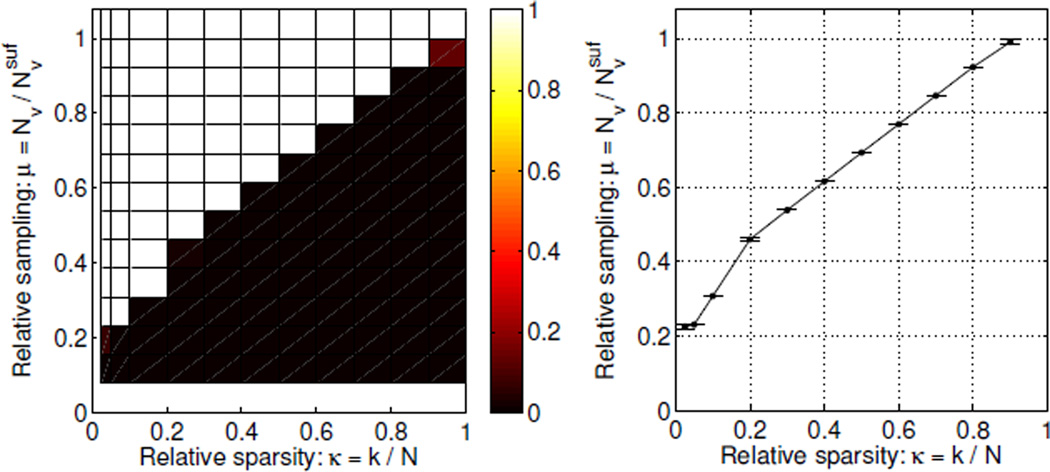
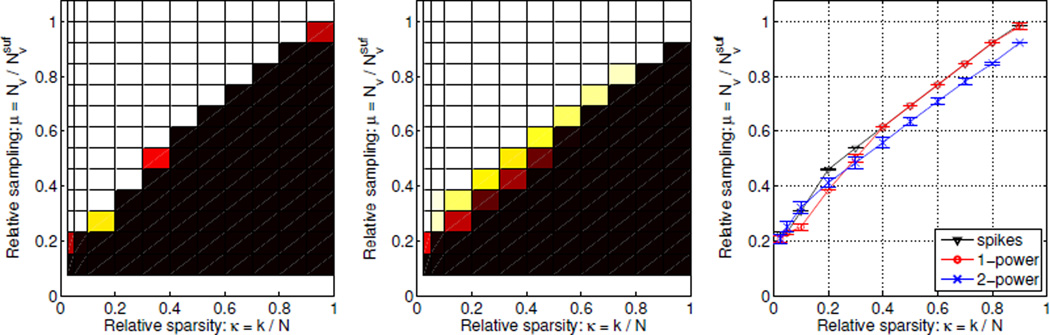
In general, we can not expect all image instances of the same relative sparsity to have the same $N_{\mathrm{v}}^{\mathbf{L}\mathbf{1}}$. We can study the variation within an image class by determining the number of projections for L1 recovery of an ensemble of images of different sparsity. At each of the relative sparsity values κ = 0.025, 0.05, 0.1, 0.2, …, 0.9 we create 100 image instances of the spikes class. For each instance we compute the L1 reconstruction from N_v = 2, 4, …, 32 projections. Based on the relative 2-norm error in (6) we assess whether the original is recovered. Figure 4 (left) shows the fraction of recovered instances as function of relative sparsity κ and relative sampling μ. Each square corresponds to the κ value at the left edge of the square and the μ value at the bottom edge. We refer to this plot as a phase diagram. The phase diagram shows two distinct regions: the lower right black one, in which no image instances were recovered, and the upper left white one, in which all images were recovered.

Figure 4.

Left: Phase diagram for spikes images (N_side = 64) showing fraction of image instances recovered by L1 as function of relative sparsity and relative sampling. Each square corresponds to the κ value at the left edge of the square and the μ value at the bottom edge. The color ranges from black (no images recovered) to white (all images recovered). Right: Average relative sampling for L1 recovery and its 99% confidence interval to better show the location and width of the transition from non-recovery to recovery.

An important observation is the sharp phase transition from non-recovery to recovery, meaning that the number of projections for L1 recovery is essentially constant for same-sparsity images of the spikes class. A sharp phase transition is often seen in CS [7], but to the best of our knowledge has not been reported for CT-matrices before, and we therefore believe the sharp transition to be a novel observation. The sharpness of the transition is perhaps better appreciated in Figure 4 (right), which shows the average μ^L1 over all instances at each κ and its 99% confidence interval estimated using the empirical standard deviation, illustrated by errorbars. The confidence intervals are very narrow, in fact, in several cases of width zero, due to zero variation of $N_{\mathrm{v}}^{\mathbf{L}\mathbf{1}}$, which agrees with the visual observation of a sharp transition.

The relative sampling for recovery μ^L1 increases monotonically with the relative sparsity κ. As κ → 0, also μ^L1 → 0, showing that extremely sparse images can be recovered from very few projections, i.e., highly undersampled data. As κ → 1, μ^L1 → 1, confirming that L1 does not admit undersampling for non-sparse signals. Furthermore, the phase diagram makes these observations quantitative. Assume, for example, that we are given an image of relative sparsity κ = 0.1, how many projections would suffice for recovery? The phase diagram shows that at κ = 0.1 the average μ^L1 = 0.31, corresponding to $N_{\mathrm{v}}^{\mathbf{L}\mathbf{1}}=8$ projections. Or conversely, the maximal relative sparsity that, on average, allows recovery from 8 projections is κ = 0.1.

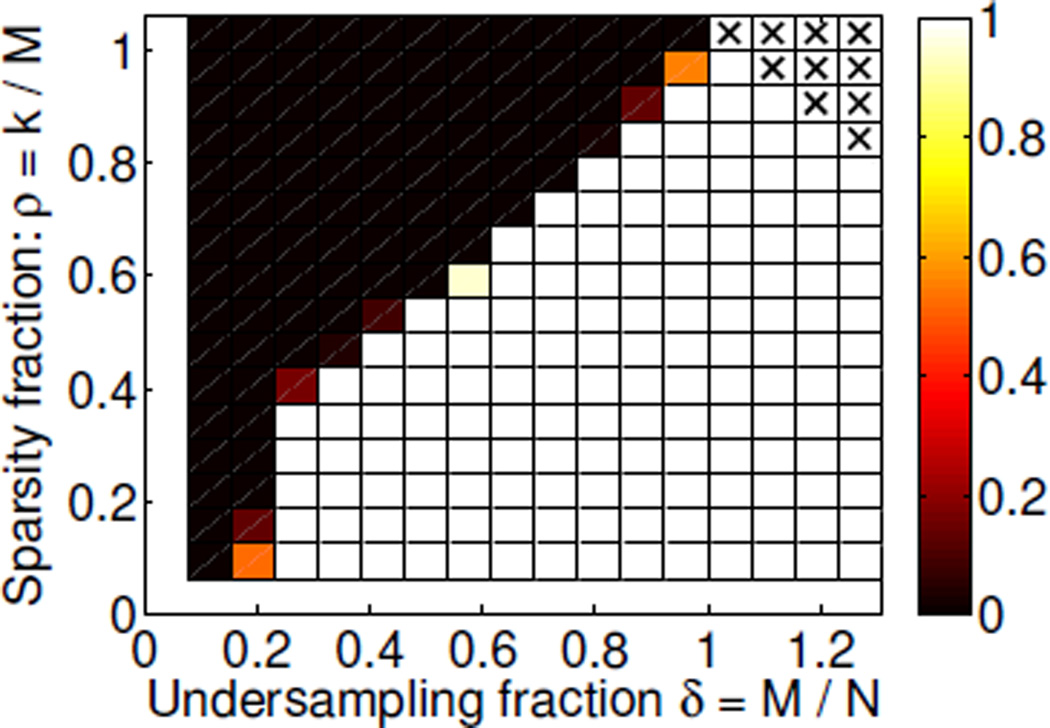
We note that the phase diagram introduced by Donoho and Tanner [7] is slightly different from the one presented here. The DT diagram is parametrized by the sparsity fraction ρ = k/M, i.e., normalized by the number of measurements, not pixels, and undersampling fraction δ = M/N. We create a DT phase diagram for our set-up by assessing recovery for 100 instances at N_v = 2, 4, …, 32 and ρ = 1/16, 2/16, …, 16/16, see Figure 5. The DT phase diagram confirms the observations from Figure 4, in particular the sharp phase transition.

Figure 5.

Donoho-Tanner phase diagram for spikes images: fraction of image instances recovered by L1 as function of δ and ρ. Each square corresponds to the δ value at the left edge of the square and the ρ value at the bottom edge. The color ranges from black (no images recovered) to white (all images recovered). Crosses indicate unreliazable configurations.

We find that phase diagrams such as the one in Figure 4 are more intuitive to interpret because the quantities of interest, namely sparsity and sampling, can be read more directly off the axes. Furthermore, normalizing the sparsity by the number of samples as in the Donoho-Tanner phase diagrams leads to two minor issues: First, where in Figure 4 each column is based on 100 specific instances of a certain sparsity, each square in the Donoho-Tanner diagram contains 100 new instances, and hence sufficient sampling for specific instances is not addressed. Second, having M ≥ N is common in CT, for example if using a large number of projections compared to the number of pixels, but as k cannot be larger than N, the upper right corner cannot be realized, so they are marked by crosses. In summary, we consider phase diagrams of the former type more convenient in the setting of CT, and for the remainder of the paper we will only show this type of phase diagram.

4.3. Dependence on image size

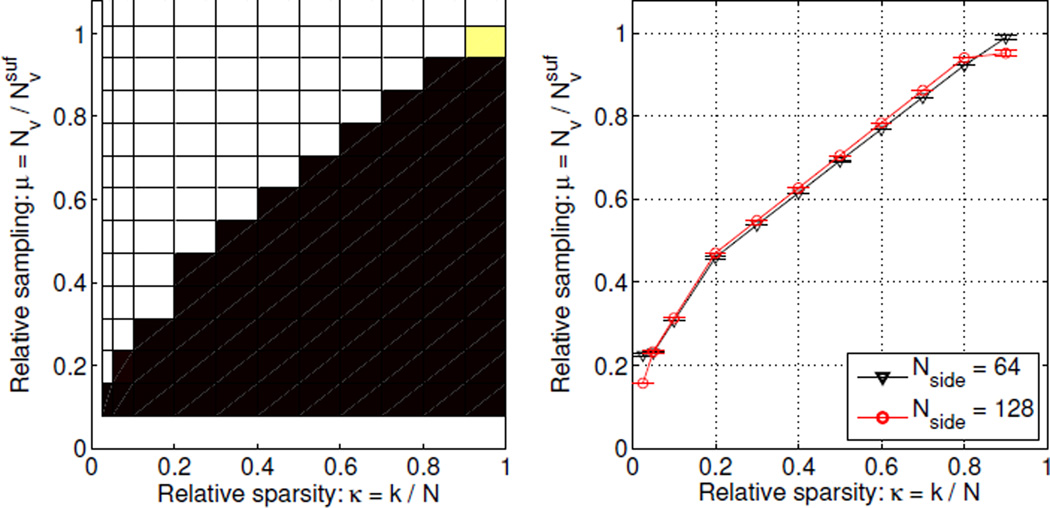
To study how recoverability depends on image size, we construct the phase diagram for N_side = 128, see Figure 6. For N_side = 128 we have $N_{\mathrm{v}}^{\text{suf}}=51$, so by taking N_v = 4, 8, …, 64 we obtain approximately the same relative sampling values as for N_side = 64.

Figure 6.

Phase diagram dependence on image size for spikes images with N_side = 128, see caption of Fig. 4 for detailed explanation. Left: Phase diagram. Right: Average relative sampling for L1 recovery and 99% confidence intervals indicating that the transition is independent of image size.

Overall, for N_side = 128 we see the same monotone increase in μ^L1 with increasing κ as we did for N_side = 64. The only differences are a generally sharper transition, i.e., narrower confidence intervals, as well as slightly better recovery at the extreme κ-values. We conclude that, with appropriate normalization, the observed relation between the average number of projections for L1 recovery and the image sparsity does not depends on the image size. Moreover, N_side = 64 is sufficiently large to give representative results that can be extrapolated to predict the sparsity-sampling relation for larger images.

4.4. Dependence on image class

Next, we study how the image class affects recoverability. Figure 7 shows phase diagrams for the 1-power and 2-power classes for N_side = 64. Comparing with spikes in Figure 4 we observe similar overall trends but also some differences, which are more clearly seen in the plot of the average μ^L1 for all classes in Figure 7 (right). For 1-power the transition from non-recovery to recovery occurs at almost exactly the same (κ, μ)-values, except around κ = 0.2 where μ^L1 is slightly lower, and is almost as sharp as for the spikes class. For 2-power the transition is more gradual, and occurs at lower μ-values for the mid and upper range of κ.

Figure 7.

Phase diagram dependence on image class, see caption of Fig. 4 for detailed explanation. Left: 1-power. Center: 2-power. Right: Average sampling for L1 recovery and 99% confidence intervals showing similar transitions but with some differences in both location and width.

Based on these results we conclude that image classes with increasing structure on average admit recovery from a smaller number of projections but the in-class recovery variability is larger. Thus, while recoverability is clearly tied to sparsity, the spatial correlation of the non-zero pixel locations also plays a role.

5. Robustness to noise

In the previous section we have empirically established a relation between the number of projections for L1 recovery and image sparsity in the noise-free setting. A natural question is whether and how the results generalize in the case of noisy data. Noise and inconsistencies in CT data are complex subjects arising from many different sources including scatter and preprocessing steps applied to the raw data before the reconstruction step. A comprehensive CT noise model is very application-specific and beyond our scope; rather we wish to investigate how recovery changes when subject to simple Gaussian white noise.

We consider the reconstruction problem

$$\mathbf{L}{\mathbf{1}}_{\epsilon }:\hspace{1em}\hspace{1em}\underset{x}{\text{min}}{\Vert x\Vert }_1\hspace{1em}\mathrm{s}.\mathrm{t}.\hspace{1em}{\Vert Ax-b\Vert }_2\le \epsilon ,$$ (10)

which can be solved in MOSEK by introducing a quadratic constraint:

$$\underset{x,w,t}{\text{argmin}}{\mathbf{1}}^{T}w\mathrm{s}.\mathrm{t}.t=Ax-b\text{and}{\Vert t\Vert }_2^2\le {\epsilon }^2\text{and}-w\le x\le w.$$ (11)

We model each CT projection to have the same fixed X-ray exposure by letting the data in each projection b_p, p = 1, …, N_v be perturbed by an additive zero-mean Gaussian white noise vector e_p of constant magnitude ‖e_p‖₂ = δ, p = 1, …, N_v, p = 1, …, N_v. Hence, the noisy data are b = Ax_orig+e, where e is the concatenation of noise vectors for all projections. We use three noise levels, δ = 10⁻⁴, 10⁻², 10⁰, corresponding to relative noise levels ‖e‖₂/‖Ax_orig‖₂ of 0.00016%, 0.016% and 1.6%. We reconstruct using L1_ε with $\epsilon ={\Vert e\Vert }_2=\sqrt{N_{\mathrm{v}}}·\delta$ and show the relative reconstruction errors from (6) in Figure 8.

Figure 8.

Left, center: Relative errors of L1_ε reconstructions vs. number of projections at different noise levels. Same spikes image instances as in Fig. 3 with relative sparsity values κ = 0.2 (left) and κ = 0.6 (center). Right: Average relative sampling for L1_ε recovery and 99% confidence intervals for different noise levels showing similar transitions. The “δ = 0” case is the noise-free L1 result for reference.

For δ = 10⁻⁴ and 10⁻² the abrupt error drop when the image is recovered is observed at the same number of projections as in the noise-free case. The limiting reconstruction error is now governed by the choice of δ and not by the numerical accuracy of the algorithm as in the noise-free case. For the high noise level of δ = 10⁰ no abrupt error drop can be observed. However, the reconstruction error does continue to decay after the number of projections for L1 recovery seen at the lower noise levels and approach a limiting level consistent with the lower noise-level error curves.

In order to set up phase diagrams we must choose appropriate thresholds τ to match the limiting reconstruction error at each noise level. In the noise-free case we used τ = 10⁻⁴ chosen to be roughly the midpoint between the initial and limiting errors of the order of 10⁰ and 10⁻⁸, respectively. Using the same strategy we obtain thresholds 10^−2.5, 10^−1.5, 10^−0.5 for increasing noise level δ. We determine the phase diagrams and for brevity and ease of comparison we only show the average sampling plots in Figure 8. The low-noise phase transition is essentially unchanged from the noise-free case. With increasing noise level we see that the location of the transition is gradually shifted to higher μ values for the medium and large κ values. At the high noise level and the largest κ = 0.9 we even see that there are instances that are not recovered (to the chosen threshold τ) at $N_{\mathrm{v}}^{\text{suf}}$.

We conclude that the sparsity-sampling relation revealed by the phase diagram in the noise-free case is robust to low levels of Gaussian white noise. For medium and high levels of noise, the phase diagram shows that a sharp transition continues to hold (for the particular noise considered) but the location of the transition changes to require more data for accurate reconstruction.

6. Discussion

Our simulation studies for X-ray CT show that for several image classes with different sparsity structure it is possible to observe a sharp transition from non-recovery to recovery in the sense that, on average, same-sparsity images require essentially the same sampling for recovery. This is similar to what is observed in CS, but as explained in Section 2.2 no theory predicts that this should be the case for X-ray CT. Based on the empirical evidence we conjecture that an underlying theoretical explanation exists.

The use of a robust optimization algorithm limits the possible image size; with MOSEK, we found N_side > 128 to be impractical. Faster algorithms applicable to larger problems exist, however in our experience MOSEK is extremely robust in delivering an accurate L1 solution, and the use of less robust optimization software may affect the decision of recoverability. Furthermore, we found the relation between relative sparsity and relative sampling to hold independently of image size, so we expect that larger images can be studied indirectly through extrapolation.

The present work considers an idealized CT system, by focusing on recovery with L1 rather than L1_ε, and as such the quantitative conclusions are only valid for the specific CT geometry and image classes. Nevertheless we believe that our results can provide some preliminary guidance on sampling in a realistic CT system, as Section 5 indicates robustness of the relation between sparsity and sampling.

During the time the present work was under review we made progress in two directions, see [22]. First, we compared the empirically observed phase transitions for X-ray CT with theoretical phase transitions valid in the case of Gaussian sensing matrices, see, e.g., [10, 11]. Interestingly, we found in many cases almost identical phase-diagram performance of X-ray CT and using Gaussian sensing matrices. A similar observation has been made empirically for certain special sensing matrices [26] but to our knowledge not for practical sensing matrices such as those occurring in X-ray CT. Second, we did a preliminary study of how well the phase-transition behavior observed on small test images can be used to predict sufficient sampling for a realistically sized CT image. In the study the sufficient number of projections for accurate reconstruction was predicted quite well from the test object’s gradient-domain sparsity, see [22] for details.

6.1. Future work

The phase diagram allows for generalization to increasingly realistic set-ups. For example, more realistic image classes, sparsity in, e.g., gradient or wavelet domains, and other types of noise and inconsistencies can be considered by changing the optimization problem accordingly. We expect that such studies will lead to improved understanding of the role of sparsity in CT.

Our earlier studies of TV reconstructions [23] indicate a relation between the sparsity level in the image gradient and sufficient sampling for accurate reconstruction, but due to the complexity of the test problems in that study we found it difficult to establish any quantitative relation. An investigation based on the phase diagram could provide more structured insight. In a follow-up work [24] to the present we have demonstrated that indeed it is possible to observe similar phase diagram behavior in the case of TV-regularized reconstruction for images sparse in the gradient domain.

With the present reconstruction approach we always face the problem of possible non-unique solutions to L1, leading to phase diagrams that, in principle, depend on the particular choice of optimization algorithm. Uniqueness of the L1 solution can be studied by numerically verifying a set of necessary and sufficient conditions [16]. We did not pursue that idea in the present work in order to focus on an empirical approach easily generalizable to other penalties for which similar uniqueness conditions may not be available. In our follow-up work [24] we did carry out uniqueness tests and observed identical phase diagrams, thus validating the reconstruction approach used in the present work.

Finally, it would be interesting to study the in-class recovery variability, i.e., why the 2-power class transition from non-recovery to recovery is more gradual. Can differences be identified between instances that were recovered and ones that were not, e.g., in the spatial location of the non-zero pixels? In [31] it is found that the number of zero-measurements affects recoverability. In our case, the structure of 2-power leads to a higher and more variable number of zero-measurements, which might be connected with the larger in-class recovery variability.

7. Conclusion

We demonstrated empirically in extensive numerical studies a pronounced average-case relation between image sparsity and the number of CT projections sufficient for recovering an image through L1 minimization. The relation allows for quantitatively predicting the number of projections that, on average, suffices for L1 recovery of images from a specific class, or conversely, to determine the maximal sparsity that can be recovered for a certain number of projections.

The specific relation was found to depend on the image class with a smaller, but also more variable, number of projections sufficing for an image class of more structured images. Classes of less-structured images were found to exhibit a sharp phase transition from non-recovery to recovery. We further demonstrated empirically that the sparsity-sampling relation is independent of the image size and robust to small amounts of additive Gaussian white noise.

With these initial results we have taken a step toward better quantitative understanding of undersampling potential of sparsity-exploiting methods in X-ray CT.