What does gamma coherence tell us about inter-regional neural communication?

Abstract

Neural oscillations have been measured and interpreted in multitudinous ways, with a variety of hypothesized functions in physiology, information processing and cognition. Much attention has been paid in recent years to gamma-band (30–100 Hz) oscillations and synchrony, with an increasing interest in ‘high gamma’ (>100 Hz) signals as mesoscopic measures of inter-regional communication. The biophysical origins of the measured variables are often difficult to precisely identify, however, making their interpretation fraught with pitfalls. Here we discuss how measurements of inter-regional gamma coherence can be prone to misinterpretation and suggest strategies for deciphering the roles that synchronized oscillations across brain networks may play in neural function.

Neural circuits often undergo oscillatory activity patterns, and temporally coordinated input can facilitate the transmission and integration of information within neurons, leading researchers to hypothesize about the functions of synchronized oscillations^1-4 (but see, for example, ref. 5). A mesoscopic variable that is relatively easy to record is the local field potential (LFP), which reflects coordinated transmembrane currents summed across nearby neurons^6,7. Numerous studies in recent years have used LFP measurements to investigate the role of gamma-band (30–100 Hz) oscillations in inter-regional communication^8,9, with several groups extending their analyses to high gamma signals of varying definitions, ranging from 60 to 500 Hz (refs. 10-13). Gamma rhythms resist a precise definition, as they exist in multiple forms and exhibit a diverse set of characteristic frequencies depending on brain region, species, network state and even cycle-by-cycle excitation–inhibition balance^8,14. In general, however, the periodicity of gamma oscillations reflects a competition between excitation and inhibition in local cortical circuits, and the LFP generated by the synaptic currents involved in this balancing act can be used as a proxy indicator of increased spiking activity in a given network.

Studies of gamma oscillations often attempt to link changes in synchrony and/or coherence across brain regions between signals in this frequency band to perceptual, behavioral and cognitive processes thought to involve long-distance network coordination. But despite this developing into a prominent area of both theoretical and experimental research, considerable controversy remains over the interpretation of the available experimental data. To understand oscillatory neural signals, it is useful to distinguish two components: the origins of the periodic rhythm and the sources of the transmembrane currents that give rise to the LFP. In this Perspective, we focus on the use of LFP gamma rhythms as an indirect way of gaining insights into neuronal communication across brain regions. By analyzing specific examples, we illustrate why the neural origins of LFP gamma signals may often remain opaque in complex networks, making conclusions drawn from these limited observations vulnerable to erroneous assumptions about the physiology underlying them.

Ambiguity in coherence measures: which variables are synchronized?

Consider the task of determining the direction and timescale of communication between networks A and B (Fig. 1). Network A is unidirectionally connected to network B so that, by design, the direction of neuronal communication is known. To identify the impact of network A on the computation carried out in network B, the most informative measurements would record and distinguish representatively large fractions of principal cells and inhibitory interneurons in both networks. Alternatively, combining extracellular population recordings of network A with whole-cell recordings in multiple neurons in network B would yield direct insight into synaptic communication between these populations. Such measurements in behaving animals are often prohibitively difficult, however, so one would like to make such an inference from measuring either the mesoscopic LFPs or a combination of LFPs and spikes.

Figure 1.

An idealized experimental layout to identify communication by gamma frequency coupling within and across networks. (a) A_DEND and B_DEND recordings designate recordings from the superficial dendritic layers of networks A and B, while A_SOMA and B_SOMA are recording from the deep somatic layers. Tick marks, output action potentials from interneurons (red) and pyramidal cells (blue); lines, LFP traces from electrodes of matching colors. Traces are shown in their respective physical locations on the left and are aligned for easier comparison on the right. In real networks with multiple afferents, high spatial resolution recording techniques from dendritic and somatic layers are needed to obtain interpretable results about the direction of communication. (b) List of signal pairs and the typical coherence measurements found between them.

To achieve the above goal, recording electrodes are placed in both networks. But where exactly should they be located? Cortical networks have multiple layers, including different dendritic domains, which often receive distinct afferent inputs, and somatic layers, where output spikes can be detected. One possibility for observing neural transmission from network A to network B is to record the output spikes in the somatic layer of network A (electrode A_SOMA) and monitor the transmembrane currents in the extracellular space in the target dendritic layer (electrode B_DEND). This measurement allows one to calculate the spike→LFP coherence¹⁵ between the two electrodes. Assuming that at least some neurons in network A are periodically synchronized within the timescale of synaptic currents, this coherence will typically be high because the spikes in network A cause postsynaptic currents in the dendrites of B that generate extracellular voltage fluctuations⁷ (that is, LFP). In the converse direction, LFP→spike coherence from electrode A_DEND to electrode B_SOMA is typically low because the output spikes of network B are not expected to exert any influence on dendritic currents in network A. In the remaining configurations, gamma band coherence can vary from low to moderate, depending on various conditions. Spike→LFP coherence between spikes in A_SOMA and LFP in B_SOMA and spike-spike coherence between principal cells in the respective regions are typically low and decrease as a function of frequency. This is because fast dendritic currents may not reliably propagate to the soma and influence the spike timing of the principal neurons in network B owing to the low-pass filtering properties of distal dendrites^16,17 (Fig. 2). The target neurons may still respond to strong excitation from network B, and while some temporal entrainment of pyramidal cells in network B may be mediated through perisomatically targeting interneurons receiving feed-forward input from network A (red neuron in Fig. 1), their spikes will often not be phase-locked to the same gamma oscillatory patterning impinging on the dendrites¹⁸. For the same reason, LFP-LFP and spike-LFP gamma coherence between dendritic and somatic layers in the same network (A_SOMA versus A_DEND and B_SOMA versus B_DEND) is also typically low^18-20 (Fig. 3), though volume-conducted currents and passive return currents across layers may result in significant levels of coherence in these signals^21,22. Finally, LFP-LFP coherence between electrode A_DEND and electrode B_DEND is also likely to be low, unless the distal dendrites of principal cells in networks A and B receive coordinated input from a third network. The A_DEND-B_DEND configuration corresponds roughly to the often-used brain surface recordings by subdural grid electrodes²³, although their typically larger electrode areas result in less local signals. Such measurements are often referred to as intracranial EEG, but many of the issues raised here relating to LFP-LFP coherence are equally applicable to them.

Figure 2.

Fast synaptic patterns delivered to the dendrites may not propagate to the soma. Current injected directly into distal dendrites is low-pass filtered between the input site and the soma. Modified from ref. 17 with permission of Nature Publishing Group.

Figure 3.

Dendritic target domains are characterized by gamma coherence. Coherence maps of gamma activity (30–90 Hz) in the hippocampus during exploration. Cell body layers from histological sectioning are overlaid in gray. The 10 seed sites (black dots) served as reference sites, and coherence was calculated between the reference site and the remaining 255 locations recorded by an 8-shank, 256-site silicon probe. LFP-LFP coherence within the same layer is consistently high because the dendritic segments in a given layer receive inputs from a temporally coordinated upstream neuron population. In contrast, gamma coherence across layers is low because upstream populations that target the distinct layers are not necessarily coordinated. The central map does not display coherence but instead indicates groups of electrodes that displayed high coherence with each other, with each group represented by a different (arbitrary) color. Modified from ref. 19 with permission of the American Physiological Society.

Examples of unidirectionally connected feed-forward networks (Fig. 1) can be found in the visual and entorhinal-hippocampal systems. Experiments in these networks reveal that gamma coupling is consistently high between spikes of upstream regions and LFPs in their dendritic target layers in the downstream region^{12,18,20,24-26}. For the same reason, LFP-LFP coherence between electrodes placed far apart within the same layer are high since the dendritic segments in a given layer receive synchronous input across distributed axon terminals of a coordinated upstream neuron population^19,27 (Fig. 3). In contrast, gamma coherence across layers (just tens to hundreds of micrometers apart) is consistently low^18-20 (Fig. 3), especially when current source density or independent component analysis techniques are employed^18,27, because spikes of neurons in the respective upstream regions, which project to the different dendritic layers, are often not coordinated at gamma timescales. Neocortical circuits also exhibit laminar segregation of gamma patterns^19,28-30, although multilayer architecture and recurrent and reciprocal connections may complicate our ability to infer mechanisms of interlayer coordination in the gamma frequency band without additional spike or other information. The scenarios above can be complicated further by volume-conducted currents^6,21,24 because larger amplitude gamma fields from other layers can spread to the recording layer. As a result, LFP coherence values may become inflated and/or independent gamma rhythms may be mixed. Low-coherence scenarios can certainly be informative, but when coherence values fall below 0.1 extra care should be devoted to their analysis and interpretation³¹.

In the somatic layer, LFP gamma patterns display higher variability than other layers because there the LFP reflects a mixture of passive return currents (and volume-conducted currents) from the multiple dendritic domains, synaptic currents brought about by perisomatic inhibition, and spikes and spike afterpotentials^6,18,32,33 (Fig. 4a). As a result, LFPs recorded from near the somata typically display broadband spectral power. Objective separation of distinct frequency bands and removing spike ‘contamination’ may require sophisticated measurements and analyses, including simultaneous recording from several input structures, high-density recordings across multiple layers, current source density techniques, independent component analysis, de-spiking, cross-frequency coupling analyses and spike-LFP phase-locking^{11,18,21,24,33-35}.

Figure 4.

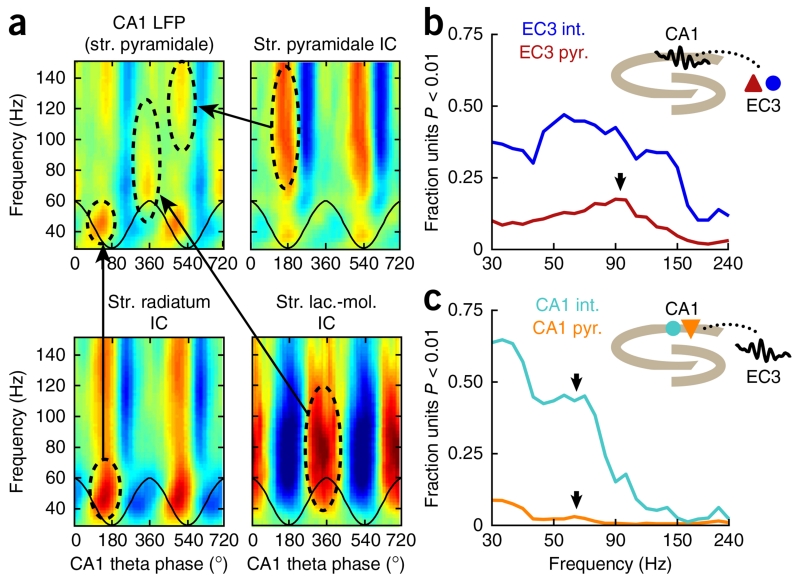
The origins of gamma LFP patterns can be revealed with simultaneous multisite recordings of LFP and spiking activity. (a) Multiple gamma patterns in the rat CA1 stratum (str.) pyramidale LFP (top left) are discernible at different frequencies and theta phases during locomotion. High-density silicon electrode arrays spanning multiple layers provide sufficient coverage and spatial resolution to employ independent component analysis to decompose CA1 LFPs into different physiological components. Arrows indicate independent components (ICs) corresponding to currents in str. pyramidale (top right), str. radiatum (bottom left) and str. lacunosum-moleculare (lac.-mol., bottom right) that were at matching frequencies and theta phases to the three gamma sub-bands visible in the str. pyramidale LFP. (b) The fraction of EC3 pyramidal cells (pyr.; red) and interneurons (int.; blue) significantly phase-locked (Rayleigh test P < 0.01) are plotted as a function of frequency for CA1 LFPs. The greatest proportions of EC3 pyramidal cells are locked near 90–100 Hz (arrow). (c) Same as in b, but for CA1 units relative to EC3 LFPs. Few CA1 pyramidal cells (orange) are significantly synchronized with EC3 gamma oscillations, although a larger proportion of CA1 interneurons (cyan) are modulated by slow to medium gamma waves recorded in EC3. Peaks in the phase-locked proportions for both cell types can be seen near 60 Hz (arrows), which is far from the peak locking frequency in the opposite direction (b). Modified from ref. 18 with permission of Elsevier.

Often the exact anatomical connections between the recorded neurons and their targets are not known, yet one would like to infer the mechanisms of information flow between these areas. As compared to the idealized situation (Fig. 1), most cortical networks are mutually connected and have multiple interconnected layers³⁶. Inserting just one or a few electrodes in each of the networks and comparing the LFP phase and/or power relationships may provide useful indicators of dynamical changes in network activity, but their physiological meaning will often be inherently ambiguous. For instance, suppose that network A in Figure 1 contains local recurrent connections in addition to sending projections to network B. In that case, even if there is only a single oscillation in network A, coherent LFP gamma oscillations may be detected in dendritic layers of both networks A and B. However, whether the coherent oscillations are due to the transferred gamma patterns from network A to B or coherent coupling of two independent oscillators with similar frequencies in the two networks remains ambiguous using simple coherence measures.

As should be clear from the examples in Figure 1, the frequently used term “spike-field coupling” has at least two implied physiological mechanisms: spikes of an upstream network can generate a coherent LFP pattern in their target dendritic domains (spike→LFP coupling) or, in the reverse direction, spikes of the downstream population can be phase-locked to the oscillations in the upstream network^18,37 (LFP→spike coupling). Finally, when the spike times of two distant neuronal populations are temporally coordinated, one finds spike-spike coupling^30,38,39. Not knowing the exact anatomical wiring, the origin of the recorded LFP and other factors, it is difficult to arrive at reliable conclusions about the direction of communication without further information.

Communication with gamma oscillations

In addition to its role in local computation^9,40, a postulated function of gamma oscillations is selective and flexible coupling of neighboring or distant cortical regions^1,3. An influential model of gamma frequency coupling across layers/regions is referred to as communication through coherence⁴¹. The idea behind this hypothesized mechanism of selective coupling is that if a neuron is receiving input from multiple afferent populations, each of which is oscillating at distinct frequencies and/or phases relative to each other, that neuron may tune into one of those input streams if its excitability is modulated coherently at the proper phase relationship to the preferred input⁴². Such a mechanism can be supported by dynamic frequency modulation of gamma oscillations mediated by perisomatic interneurons^14,29, which has been proposed as a possible way to multiplex neural codes⁴³. The efficacy of coherence-based communication depends on the temporal coordination of the upstream and downstream networks⁴⁴. However, as discussed earlier, demonstration of coherent LFP-LFP or spike-LFP coherence in an upstream and target regions without further information is not sufficient for the explicit demonstration of input selection per se because such measures can reflect (i) an open channel of feed-forward communication^26,39 (see A_SOMA-B_DEND in Fig. 1), (ii) coupling of two phase-locked network oscillations or (iii) the co-modulating effect of an upstream network (that is, an unmonitored ‘third party’) common to both recorded networks. Furthermore, inter-regional spike-spike coupling at gamma time-scales detected in single- or multi-unit activity may often reflect feed-forward entrainment of interneurons rather than synchronization of principal cells^18,45,46. Efforts to cluster and classify single units by cell type can therefore provide additional insight into the roles of oscillatory coherence.

Extension of the communication though coherence model⁴¹ to fast gamma frequencies, however, is especially problematic^43,47. ‘High’ or ‘fast’ gamma loosely refers to high frequency bands above 60–100 Hz, depending on which terminology the authors adopt. In the hippocampus, slow (30–80 Hz), medium (60–120 Hz) and fast or high (>100 Hz) gamma (or epsilon) sub-bands have been distinguished by means of cross-frequency coupling^33,48 and independent component analysis¹⁸, though some authors have combined or relabeled these sub-bands^12,49,50. The precise boundaries between distinct frequency bands, however, will vary across regions, brain states, animals and species because of hitherto undetermined factors. In layers with dense cell bodies or axon terminals, irregular wide-band signals resulting from spikes and spike afterpotentials^22,32,51 can strongly influence estimates of high-gamma power and phase, but true fast oscillations in the excitability of neuronal populations, including hippocampal and neocortical ripples^52-54, also occupy this band. Separation of true and spurious gamma oscillations may not be possible with spectral methods alone and often requires techniques capable of quantifying the periodic modulation of neuronal activity⁵⁵.

An explicit model of communication via gamma rhythms has been advanced in the hippocampus, where selective coupling of the CA1 region to one of its two main inputs, area CA3 and the layer III pyramidal cells of the medial entorhinal cortex (EC3), was suggested to be mediated through coherent oscillations at either slow or fast gamma frequencies, respectively, at different phases of the theta cycle¹². Several aspects of this general framework have important merits: namely, that different gamma patterns may reflect distinct inputs and/or modes of operation^49,50 and that the theta-phase segregation of inputs and the resulting CA1 response may correspond to different computations^50,56. However, other aspects of the model may be criticized on both functional and biophysical grounds. The first difficulty arises when one examines the directionality of coupling in the circuit. CA3 and EC3 pyramidal cells project to different CA1 dendritic layers, and their synapses generate a large portion of CA1 LFP power in the theta and gamma frequency bands. Both of these upstream structures can concurrently generate their own LFP signals. As a result, the recipient CA1 dendritic layers can be coherent with CA3 or EC3 LFPs on account of their common cause—namely, the gamma phase-locked activity of the feed-forward projection neurons in each upstream region (Fig. 3). Consistent with this interpretation, a sizeable fraction of pyramidal neurons in CA3 and EC3 are phase-locked to gamma-band LFPs both locally and in CA1 (refs. 12,18) (Fig. 4a,b). If the CA1 pyramidal cells couple to these input oscillations by exhibiting coherent modulation of their excitability, one would expect to also see CA1 spikes to be phase-locked to the upstream LFP or spikes. However, such coupling is rare and very weak at frequencies above ~50 Hz (ref. 18) (Fig. 4c).

The weak coupling at higher frequencies may largely be due to biophysical causes, as the synapses of the EC3 input are located on the most electrotonically distant portions of the CA1 pyramidal cell dendrites. The low-pass filtering properties of neuronal dendrites preclude the synchronized entrainment of spikes to rapidly varying depolarizations of the distal dendritic compartments^16,17 (Fig. 2). Perisomatically targeting interneurons receiving EC3 input, such as chandelier cells⁵⁷, could conceivably mediate the timing signal from EC3 to the axon initial segment of CA1 pyramidal neurons (Fig. 1), similarly to the entrainment of CA3 and CA1 basket cells by gamma phase-locked CA3 pyramidal neurons^24,45. Depending on the efficacy of the EC3-interneuron synapses and subsequent perisomatic inhibition, a low to moderate level of LFP→spike coherence may be present between CA1 neurons and gamma LFP in EC3. Although a considerable fraction of putative CA1 interneurons are locked to EC3 gamma phase, this occurs predominantly for mid-gamma but not higher frequencies¹⁸ (Fig. 4c), and such phase-locking is rare for CA1 pyramidal cells. Complementing the gamma coupling measurements, the CA1 network is most active at the trough (that is, negative peak) of the local theta cycle, which is separated from the theta phases of maximum spiking for both CA3 (descending phase) and EC3 (positive peak) pyramidal cells^18,58, in contrast to what one would predict from the communication through coherence model.

Thus, while important clarifications are still needed concerning the nature and function of long-distance gamma synchronization in general, the available evidence demonstrates that gamma coherent entrainment of spikes has a strong frequency-dependent limitation. The LFP signature in the target region can indicate the occurrence of strong, gamma-synchronized input, which can influence the state, or processing mode, in the target region^27,39,49,50 but does not necessarily reflect spike-spike coordination in the same frequency range between the two networks. It will therefore be important for future studies to determine which cell types—principal neurons or various interneuron subtypes—are responsible for the experimentally observed bidirectional (spike-LFP and LFP-spike) gamma coherence.

Potential artifactual sources of high-frequency LFP coherence

Broadband, high-frequency coherence and zero phase–synchronous fluctuations of fast gamma waves have been regarded as a signature of coupled neural oscillations^12,25,59. Synchronized oscillations can occur in reciprocally connected networks⁶⁰, such as between homologous layers of the two cortical hemispheres^31,38 (Fig. 5). However, even though zero-phase coherence can signify important physiological mechanisms, caution should be used when zero-time-lag LFPs are detected in distant brain regions, especially in the high gamma band.

Figure 5.

Interhemispheric, zero-phase-lag coherence of gamma oscillations. (a) LFPs recorded from the left (L) and right (R) CA1 pyramidal layer of the mouse hippocampus. (b) Co-modulation of theta and gamma power in the two hemispheres. Note that theta power in one hemisphere is co-modulated with gamma power of the other hemisphere (yellow band at 9 Hz and 40–100 Hz, white arrowheads). (c) Spectral power of the LFP from the left hippocampus during wheel running (red) and REM sleep (blue). (d) Coherence spectra between signals derived from the two hippocampi. Note rapidly decreasing coherence in the gamma frequency band (40–100 Hz) and negligible coherence above 100 Hz (high gamma). (e) Phase spectra of the LFP signals derived from the left and right hippocampi. Reproduced from ref. 31 with permission of Elsevier.

An often-neglected ‘artifactual’ source (that is, not generated by local neural activity) of intracranial high gamma power and zero-lag synchrony is the electromyogram (EMG) activity volume-conducted from head and neck muscles⁶¹. EMG activity can produce high spurious LFP coherence with zero time/phase lag, even during times when clear large-amplitude artifacts are not apparent¹⁸. Another spurious source of gamma LFP in nonhuman primates and humans is oculomotor activity, which can result in widespread and zero-phase-lag synchronized, artifactual ‘gamma’ activity⁶². Even the modulation of high gamma power by the phase of lower frequency rhythms cannot be taken as definitive evidence against EMG contamination, since head and neck movements, as well as saccadic eye movements, can be significantly theta modulated^18,63,64. Care must therefore be taken to control for the many potential sources of nonspecific and artifactual signals in attempts to infer functional properties of circuits from LFP signals.

Another spurious source of gamma coherence is amplitude covariations between signals in the same frequency band⁶⁵. Given that power increases at gamma frequencies can also be brought about by both spiking activity and nonoscillatory transient events⁶⁶, this is another artificial source of increased gamma coherence.

Measuring and exploiting LFP data

LFP data can serve as an extremely useful mesoscopic measurement of neuronal cooperation, with gamma band and higher frequency activities providing signatures of local processing within neural circuits. However, effective exploitation and interpretation of the LFP and especially its role in inter-regional communication entail several requirements. (i) Because coherence of physiological high frequency activity can vary dramatically across various afferent-efferent domains of principal cells, high-density sampling of the somato-dendritic layers provides crucial information for signal localization. This is especially critical in the neocortex, where the somatic and dendritic domains of multiple layers show considerable overlap. (ii) Simultaneous recording of LFP and spiking of isolated pyramidal cells and interneurons confers a greater ability to assess both the involvement of different cell populations in the coordinated activity reflected in the LFP and the directionality of communication. (iii) Prior knowledge of anatomical connectivity may assist in placing the recording electrodes in appropriate layers for testing hypotheses about how excitation propagates through the network. (iv) Prevention or removal, or at least consideration, of spike contamination of high-frequency LFP power and phase is an absolute necessity. (v) Very low coherence values, even when significant, should be treated with caution and divorced from possible spike-induced increase of the LFP power. (vi) For high-frequency LFP components, detecting and characterizing signatures of (or directly recording) EMG and/or eye movements and, ideally, its effective removal by appropriate offline analysis (for example, using current source density or independent component analysis methods) is an important prerequisite. Zero-time synchrony of high gamma activity at multiple locations is often a telltale of such artifactual contamination of the LFP signals, and so alternative explanations must be ruled out. Measurements that do not meet all of these conditions can still be highly informative, but it is critical to understand that compromise will complicate the physiological interpretation of the data.

Assuming that the above conditions are met, sophisticated multivariate methods are available for teasing out cause-effect relationships, including directed coherence, Granger causality and dynamic causal modeling^67,68, and independent component analysis³⁵ might be harnessed to extract functionally important physiological interactions between different parts of neural circuits. Many of these techniques are deployed with the intention of overcoming limitations in the measurements, but these computational methods are only as good as the physiological recordings. No amount of math can substitute for a good experimental design. However, these promising methods may be further refined and placed on firmer footing if they can be tested on data sets with less physiological ambiguity.

We conclude that the best route forward may therefore be to deploy more advanced recording techniques that allow simultaneous monitoring of both principal cell and interneuron spiking activity across larger portions of the circuit. Targeted perturbation of specific circuit elements may provide crucial tests of the resulting hypotheses, although manipulating the temporal characteristics of network activity without altering the balance between competing circuit elements is not trivial. Such combined experimental approaches, complemented with appropriate computational methods^7,69,70, will allow us to disentangle the activities of distinct neural populations, their emergent interactions in the gamma frequency band, and the relationships between their dynamics and behavior.

Conclusions

We have attempted to elucidate the purposes and limitations of methods commonly employed to investigate inter-regional communication through gamma oscillations. We do so in the hope that, armed with a fuller understanding of their tools, neuroscientists will soon be able to decipher the precise mechanisms and roles of oscillations, synchrony and inter-regional coordination in carrying out the sophisticated neural operations underlying cognition and behavior. Gamma oscillations provide a means to temporally organize neural activity, especially in conjunction with oscillations at slower timescales^9,40. Their ubiquity and robustness in neuronal networks is a consequence of the multiple interacting mechanisms that give rise to them, and the resulting circuit dynamics have numerous theoretical advantages. Definitively identifying the roles and physiological significance of gamma rhythms in inter-regional communication and neural information flow, however, remains a persistent challenge.