Effects of conservation policy on China’s forest recovery

China’s forest cover exhibited a positive trend that was significantly related with the implementation of a national conservation policy.

Abstract

Forest loss is one of the most pervasive land surface transformations on Earth, with drastic effects on global climate, ecosystems, and human well-being. As part of biodiversity conservation and climate change mitigation efforts, many countries, including China, have been implementing large-scale policies to conserve and restore forests. However, little is known about the effectiveness of these policies, and information on China’s forest dynamics at the national level has mainly relied on official statistics. In response to international calls for improved reliability and transparency of information on biodiversity conservation and climate change mitigation efforts, it is crucial to independently verify government statistics. Furthermore, if forest recovery is verified, it is essential to assess the degree to which this recovery is attributable to policy, within the context of other relevant factors. We assess the dynamics of forest cover in China between 2000 and 2010 and evaluate the effectiveness of one of the largest forest conservation programs in the world—the Natural Forest Conservation Program (NFCP). Results indicate that forest cover has significantly increased in around 1.6% of China’s territory and that the areas exhibiting forest gain experienced a combined increase in net primary productivity (ca. 0.9 Tg of carbon). Among the variables evaluated at county level, the NFCP exhibited a significantly positive relation with forest gain, whereas reduction in rural labor showed a negative relationship with both forest loss and gain. Findings such as these have global implications for forest conservation and climate change mitigation efforts.

INTRODUCTION

Human activities have transformed up to half of Earth’s land surface, particularly through the often intertwined processes of agricultural expansion and deforestation (1, 2). Because forests provide crucial services to society, including soil and water conservation, climate regulation, and carbon storage, among many others (3, 4), degradation and outright conversion of forests constitute some of the most detrimental anthropogenic land surface processes (5). Yet, although degradation of forests continues in many parts of the world, an opposite trend has also emerged. This “forest transition” from loss to gain at the national level began to occur during the 18th century in Western Europe (6) and has since emerged in other developed (7) and developing (8) countries around the world. Forest scarcity and economic development are considered two of the most common pathways to forest recovery (9). The former involves the planting of trees in response to a demand for timber and other forest products, whereas the latter is associated not only with industrialization leading to the concentration of population in urban centers and consequent rural depopulation and spatial contraction of increasingly intensive agricultural production, but also with changing ecological or aesthetic goals, as wealthy societies come to value natural landscapes and can afford to invest in biodiversity conservation (10). The forest transition literature also recognizes the important role of government policy, particularly in developing countries (11). The challenge is quantifying the actual role of government programs against the background of other (for example, social, economic, and ecological) factors.

The fate of forests in China, the most populous nation on Earth, has global consequences by virtue of the country’s sheer magnitude and the rapidity of its development (12). According to Chinese government statistics, the country’s forests have been recovering over the past three decades (13, 14). This has taken place in the context of exceptionally rapid economic growth over the same time period (15), which suggests that China is on the economic development pathway to the forest transition (because harvests from many of these forests are not currently allowed, the forest scarcity pathway is not a sufficient explanation in this case). However, during the same period, the Chinese government also implemented other environmental programs (16). In particular, since the beginning of the 21st century, China has been implementing one of the largest forest conservation and restoration programs in the world—the Natural Forest Conservation Program (NFCP). This program bans logging in many natural forests and supports monitoring activities to prevent illegal harvesting. In the first decade of implementation, total investment in the NFCP exceeded 93 billion yuan (US$1 = 6.8 yuan in 2010) (17). Although this program was largely motivated by the need to control soil erosion following massive floods in 1998, the consequent increase in forest cover also has important implications for other ecosystem services such as carbon sequestration. In fact, China’s president pledged to increase forest cover by 40 million hectares by 2020 (from the 2005 level), and the NFCP is a key measure for fulfilling the country’s commitment to global climate change mitigation (18). Although widespread environmental and socioeconomic benefits are anticipated from program implementation (17, 19), actual benefits have so far only been assessed in a few localized areas (20, 21), and not on a national scale. This study evaluates the effectiveness of the NFCP on a national scale during the first decade of the 21st century and its contribution to changes in net primary productivity (NPP).

RESULTS

Over the 2000–2010 period, around 1.6% (ca. 157,315 km²) of China’s territory displayed a significant gain in percent tree cover, whereas ca. 0.38% (ca. 37,268 km²) experienced a significant loss (Fig. 1). Among the areas exhibiting gains and losses, the average percent tree cover in the year 2000 was 24.81% (SD, 12.76%) and 53.57% (SD, 12.94%), respectively (fig. S1), suggesting that forest gain tends to occur more often in areas of lower initial tree cover, whereas forest loss tends to occur more often in areas of higher initial tree cover.

Fig. 1. Forest cover dynamics in China.

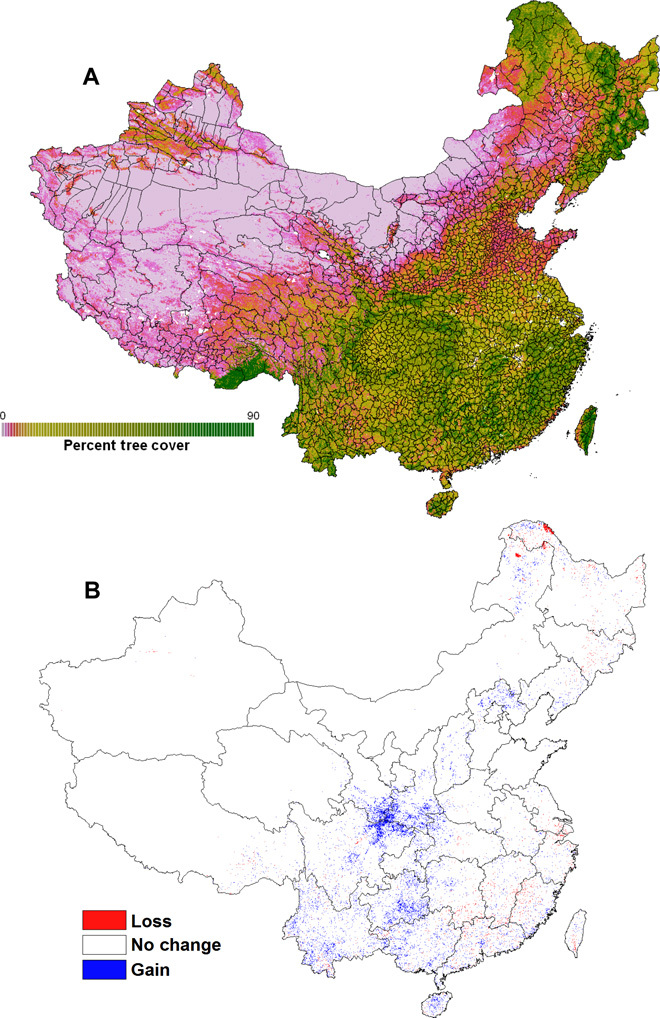
(A) Pixel-based (250 m per pixel) percent tree cover across China in 2000. The map was derived from the VCF tree cover product based on surface reflectance data collected by MODIS. Polygons correspond to county boundaries. (B) Pixels exhibiting a significant gain or loss in percent tree cover [that is, changes higher than or equal to |20%| and with statistically significant (P < 0.05) positive and negative monotonic trends in percent tree cover] between 2000 and 2010. Polygons correspond to province boundaries.

Stepwise multilevel models show that, at the pixel level, the initial percent tree cover, elevation, and total annual precipitation were statistically significant in the forest loss model (Table 1), whereas northing, distance to main roads, gridded population density in 2000, elevation, mean annual temperature, and the compound topographic index (CTI) were statistically significant in the forest gain model (Table 2). At the county level, the NFCP evidenced a statistically significant (P < 0.001) positive relationship with forest gain, whereas change in rural labor between 2000 and 2010 exhibited a statistically significant negative relation with both forest loss (P < 0.05) and forest gain (P < 0.01) (Table 3). The gross domestic product (GDP) per capita exhibited a statistically significant (P < 0.05) positive relation with forest loss (Table 3).

Table 1. Coefficients of the pixel-based forest loss model.

Maximum likelihood estimates of the coefficients of the predictor variables obtained in a logistic regression model to assess the probability of forest loss during the 2000–2010 period. See Materials and Methods for details on the logistic regression models developed in the study.

Parameter	Estimate	SE	Wald χ2	P > χ2
Intercept	−11.1959	3.0388	13.5744	0.0002
Easting	2.997 × 10−7	2.66 × 10−7	1.2701	0.2598
Northing	3.768 × 10−7	5.27 × 10−7	0.5113	0.4746
Initial tree cover	0.0534	0.00614	75.4652	<0.0001
Distance to main roads	−0.00233	0.00275	0.7168	0.3972
Population density in 2000	0.000012	7.466 × 10−6	2.7208	0.0991
CTI	0.0591	0.0597	0.9814	0.3219
Elevation	−0.00019	0.000086	4.9686	0.0258
Slope	0.000960	0.0205	0.0022	0.9627
Aspect	−0.00111	0.0179	0.0038	0.9506
Precipitation	0.0275	0.00846	10.5727	0.0011
Temperature	−0.0876	0.0682	1.6494	0.1990

Table 2. Coefficients of the pixel-based forest gain model.

Maximum likelihood estimates of the coefficients of the predictor variables obtained in a logistic regression model to assess the probability of forest gain during the 2000–2010 period. See Materials and Methods for details on the logistic regression models developed in the study.

Parameter	Estimate	SE	Wald χ2	P > χ2
Intercept	1.2464	1.1394	1.1966	0.2740
Easting	1.528 × 10−7	1.02 × 10−7	2.2462	0.1339
Northing	−5.61 × 10−7	1.652 × 10−7	11.5298	0.0007
Initial tree cover	0.00415	0.00295	1.9723	0.1602
Distance to main roads	−0.00488	0.00174	7.8691	0.0050
Population density in 2000	−0.00005	0.000015	10.4924	0.0012
CTI	−0.2077	0.0349	35.4714	<0.0001
Elevation	−0.00023	0.000044	27.1876	<0.0001
Slope	−0.00523	0.00781	0.4485	0.5031
Aspect	0.0114	0.00830	1.8695	0.1715
Precipitation	−0.00257	0.00405	0.4027	0.5257
Temperature	0.0743	0.0216	11.7815	0.0006

Table 3. Coefficients of county-based spatial autoregressive models.

Estimates of the coefficients of the spatial autoregressive models developed to assess the relationship between county-based independent variables and significant gain and loss of forest cover [presented as coefficient (SE)]. See Materials and Methods for details on these spatial autoregressive models.

Parameter	Forest loss	Forest gain
R2	0.478	0.742
Intercept	2.61 × 10−5 (0.0006)	−0.0004 (0.0019)
NFCP	−0.0007 (0.0004)	0.0070* (0.0015)
GDP per capita in 2000	0.0014† (0.0005)	−0.0023 (0.0018)
Change (2010–2000) in GDP	−2.04 × 10−7 (6.109 × 10−7)	1.36 × 10−7 (2.02 × 10−6)
Grain production in 2000	4.01 × 10−6 (1.91 × 10−5)	−1.10 × 10−5 (6.32 × 10−5)
Change (2010–2000) in grain production	8.43 × 10−7 (2.20 × 10−6)	−2.77 × 10−6 (7.18 × 10−6)
Meat production in 2000	−2.29 × 10−5 (0.0001)	6.21 × 10−5 (0.0003)
Change (2010–2000) in meat production	−2.17 × 10−6 (1.73 × 10−6)	4.10 × 10−6 (5.72 × 10−6)
Total population in 2000	1.34 × 10−5 (2.13 × 10−5)	8.30 × 10−5 (7.03 × 10−5)
Change (2010–2000) in total population	4.47 × 10−7 (1.48 × 10−5)	−3.10 × 10−5 (4.88 × 10−5)
Rural labor in 2000	−3.94 × 10−5 (4.00 × 10−5)	−0.0002 (0.0001)
Change (2010–2000) in rural labor	−1.31 × 10−6‡ (6.21 × 10−7)	−6.45 × 10−6† (2.05 × 10−6)
Spatial autoregressive term	0.6922* (0.0195)	0.8493* (0.0122)

*P < 0.001.

^†P < 0.01.

^‡P < 0.05.

Among the pixels exhibiting a gain in forest cover, the average per-pixel relative NPP gain over the 2000–2010 period was 14.7% (SD, 17.4%) (Fig. 2). NPP accumulated across all pixels exhibiting a significant gain in forest cover rose by a total of ca. 0.91 Tg (that is, from 45.12 Tg in 2000 to 46.03 Tg in 2010).

Fig. 2. NPP dynamics.

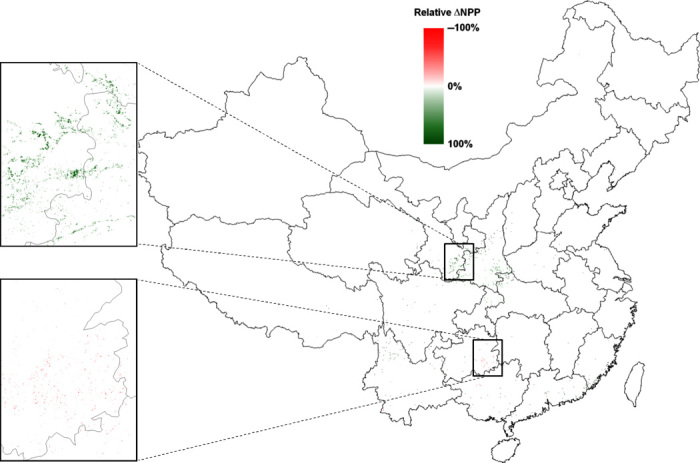
Per-pixel relative (that is, percent) change in NPP between 2000 and 2010 among pixels exhibiting a significant gain in forest cover (Fig. 1B). Insets: Areas that exhibited particularly wide-ranging positive/negative trends.

DISCUSSION

Our results suggest that, among the factors considered at the county level and after accounting for pixel-level biophysical and demographic variables, the implementation of the NFCP exhibited a significant relationship with forest gain in China during the first decade of the 21st century. This significant relationship suggests that government intervention—in the form of logging bans and monitoring activities to prevent illegal logging—was instrumental in enhancing forest recovery. Other conservation policies implemented at the national level (such as the Grain-to-Green Program, which encourages farmers to convert steep hillside cropland into forest by providing cash, grain, and tree seedlings) (17, 22), as well as other forest management measures (for example, fire prevention and stand thinning), may also have had significant effects on China’s forest cover (for example, promotion of forest regeneration). However, they were not evaluated because their implementation generally concerns small cropland parcels (usually <1 ha) that may be difficult to detect at the 250-m resolution of the Moderate Resolution Imaging Spectroradiometer (MODIS) sensor and because 10 years may not be sufficient to detect their effects owing to the longer time required for trees to establish sufficient canopies from seeds or seedlings (21).

Many of the areas that exhibited significant gains in forest cover constituted some of the most recently logged areas and thus may be showing the most dramatic responses to NFCP implementation. For instance, an area exhibiting prominent gains in forest cover in central China [located between the Qinling Mountains (in Gansu and Shaanxi provinces to the north) and the Daba Mountains (in Sichuan province to the south)] (Fig. 1B) was the locus of major timber extraction activities before the year 2000. In fact, Sichuan and Gansu provinces exhibited some of the highest rates of deforestation during the 1990s (23). With the implementation of the NFCP, thousands of people employed by the timber industry were laid off and sought alternative employment opportunities. Dramatic abandonment of rural livelihood activities had also been spurred by new employment opportunities in urban centers such as Chengdu in Sichuan province and Xi’an in Shaanxi province. Thus, economic growth (as exemplified by the change in rural labor between 2000 and 2010) may have played a significant role in forest recovery. Nevertheless, the effects of economic growth are not completely clear, given that the other metric of economic growth used in the study (that is, GDP per capita) showed a significant positive relationship with forest loss.

Previous studies have shown that the forest recovery observed during the last two decades of the 20th century had significant effects on standing biomass and NPP in the forests of China (24, 25), but the effects of forest recovery during the first decade of the 21st century are not clear. We analyzed the change in NPP in the pixels exhibiting significant forest recovery, and our results showed a significant increase in NPP across all pixels exhibiting a significant gain in forest cover. Thus, in addition to the local and regional benefits it may accord the country in terms of soil and water conservation, the NFCP seems to significantly contribute to carbon sequestration in China’s forested areas, with potentially important effects on global carbon budgets.

Although China’s forest conservation policy may exert positive effects on China’s forests, it may exert negative effects on other forested areas around the world. At the same time that China’s conservation policy bans logging of natural forests, China has become one of the world’s leading timber importers and has also been importing more food and other agricultural products (13). Thus, China’s conservation policy may be exacerbating forest degradation (through both legal and illegal logging) in other regions such as Southeast Asia, Africa, and Northern Eurasia from which China has been importing forest and agricultural products (13, 26). For example, between 2000 and 2010, China imported forest products from Vietnam (ca. US$695 million), Burma (ca. US$62 million), Indonesia (ca. US$880 million), Madagascar (ca. US$18 million), and Russia (ca. US$887 million) (27). Therefore, at least some of the carbon sequestration in China’s forested areas may have come at the cost of carbon emissions elsewhere (3, 28). In addition, if the associated forest cover losses elsewhere occur in areas with high biodiversity, the expansion of forests in China may also be entailing a significant net loss of biodiversity. These considerations pose important challenges for current territory-based strategies for global climate change mitigation and biodiversity conservation. A systems approach that simultaneously considers the tradeoffs and synergies among conservation, production, and consumption in both importing and exporting countries (29) is urgently needed to address these challenges.

MATERIALS AND METHODS

Forest cover dynamics

Although some authors deem necessary the use of medium spatial resolution imagery acquired by satellite sensors such as Landsat TM, Landsat ETM+, or SPOT (Satellite Pour l’Observation de la Terre) for forest cover change assessments (30), many areas around the world experience frequent cloud cover. Thus, insufficient cloud-free medium spatial resolution imagery is available for forest change assessments (31, 32), particularly when evaluating the effects of conservation policy implementation over short temporal windows. In addition, Landsat-based products, such as the Global Forest Change 2000–2013 (3), map forest cover as an internally homogeneous land cover type, which is inadequate for assessing forest cover dynamics that do not necessarily correspond with complete land surface transformations (that is, from forest to nonforest or vice versa). Therefore, we assessed the spatiotemporal dynamics of China’s forest cover using the annual Vegetation Continuous Fields (VCF) tree cover product derived from surface reflectance data acquired by NASA’s MODIS (33). This product represents the percentage of annual per-pixel tree cover at a spatial resolution of approximately 250 m and has successfully been used to quantify forest cover dynamics, exhibiting results comparable with those derived using medium spatial resolution imagery (for example, Landsat-based) (34).

Using the MODIS VCF, we evaluated changes in forest cover from 2000 to 2010. We chose this period to capture the first decade of NFCP implementation and to match the availability of relevant socioeconomic data. Because changes in forest cover at a MODIS VCF pixel may not necessarily account for actual changes in forest cover on the ground, we performed two different procedures to assess the change in forest cover, which were later combined to produce a final change output.

In the first procedure, we assessed the change in forest cover by thresholding the VCF to separate forest from nonforest pixels and estimated the minimum magnitude of the percent change required to assess a significant change in forest cover. To find the optimal VCF threshold to separate forest from nonforest pixels and to validate the MODIS VCF tree cover product, we developed a data set of 4000 “ground-truth” polygons of the same size as a MODIS pixel (ca. 0.0625 km²), randomly distributed throughout China. Within each of these polygons, we randomly distributed 25 points. Using the high spatial resolution imagery available in Google Earth, we visually ascertained the number of points per polygon coinciding with a tree canopy. The horizontal positional accuracy of Google Earth’s high-resolution imagery has been established to vary between 0.4 and 171.6 m, with average accuracies of 24.1 m in developed countries and 44.4 m in developing countries (35). Such horizontal positional accuracies are much lower than the spatial resolution of a MODIS pixel (ca. 250 m per pixel) and thus are suitable for assessing the classification accuracy of the MODIS VCF product.

We considered a polygon to be forested if three or more points (that is, >10%) coincided with a tree canopy, on the basis of the classification of forested areas established by the United Nations Food and Agriculture Organization (36). To assess the reliability of the interpretation of the Google Earth imagery, two image interpreters independently performed the point counts for each polygon. The average point count between the two interpreters was obtained, and only those polygons exhibiting a point count difference of less than 20% between the two interpreters were used in the validation. Google Earth imagery acquired between 2000 and 2005 was used to validate the 2000 MODIS VCF data set, whereas Google Earth imagery acquired between 2006 and 2010 was used to validate the 2010 MODIS VCF data set. Thus, given that not all of China’s territory is covered by Google Earth high-resolution imagery, not all polygons were used in the validation. In addition, because high-resolution image availability between 2000 and 2005 is considerably lower than that between 2006 and 2010, the final number of ground-truth polygons used in the validation was 569 (14.2% of the polygons) for the 2000 MODIS VCF data set and 1973 (49.3% of the polygons) for the 2010 MODIS VCF data set (fig. S2).

With these data, we conducted threshold-dependent and threshold-independent validation procedures. The threshold-dependent procedure was the κ statistic, which is a chance-corrected measure of agreement (37). Using equality in sensitivity and specificity as a criterion (reported to be the most reliable criterion for cumulative threshold selection) (38), we found that a percent tree cover of 24 and 23% in the 2000 and 2010 MODIS VCF data sets, respectively, constitutes the optimal threshold for separating forest from nonforest pixels, and we obtained κ coefficients of 0.64 (overall accuracy, 90%) and 0.60 (overall accuracy, 87%) for the 2000 and the 2010 MODIS VCF data sets, respectively. The threshold-independent procedure was the area under the receiver operating characteristic curve (AUC) (39). The AUC ranges from 0 to 1, where a score of 1 indicates perfect discrimination, a score of 0.5 is expected from a random prediction, and a score lower than 0.5 indicates discrimination that is worse than random. The AUC values obtained were ca. 0.94 for both the 2000 and the 2010 MODIS VCF data sets (fig. S3), which were significantly different (P < 0.0001) from 0.5 (that is, a random prediction). Both of these validation procedures (that is, threshold-dependent and threshold-independent) demonstrate that the MODIS VCF tree cover product constitutes an accurate depiction of forest cover in China.

The per-pixel change in forest cover was then obtained by calculating the Δ in the VCF tree cover between 2000 and 2010 (that is, Tree Cover Δ_2010–2000 = Tree Cover₂₀₁₀ − Tree Cover₂₀₀₀). To validate this change, we used the Δ in the percent tree cover of the ground-truth polygons, obtained using Google Earth. Validation of the change in forest cover was based on the threshold-dependent κ statistic, which suggested a percent change in tree cover of ±20% as the optimal threshold for detecting changes in percent tree cover. The κ coefficients obtained were 0.39 (overall accuracy, 68.2%) and 0.40 (overall accuracy, 69.8%) for forest recovery and forest loss, respectively.

In the second procedure, we assessed per-pixel annual trends in the VCF percent tree cover over the decade (that is, 2000–2010). This was performed not only because a change in forest cover in a MODIS VCF pixel may not necessarily represent the same areal change in forest cover on the ground but also because the values of the VCF tree cover product may change from year to year as a result of changes in climate conditions accumulated over time (for example, annual precipitation and incoming radiation). To assess the significance of per-pixel trends (monotonic increases and decreases in the VCF between 2000 and 2010), we used the Spearman rank correlation coefficient. The significance of the Spearman rank correlation coefficient was determined through a permutation analysis in which the order of the ranks was randomly permuted 99 times. The significance measure corresponds to the number of times the correlation coefficient of the permuted data set exceeded the original (that is, nonpermuted) coefficient. When fewer than 5 of 99 permutations yielded higher correlation coefficients, these pixels were determined to exhibit significant positive (for r > 0) or negative (r < 0) trends.

Finally, we combined the two procedures to assess the number of pixels that exhibited a significant change (that is, gain or loss) in forest cover. To this effect, among the pixels exhibiting an absolute change in percent forest cover equal to, or larger than, 20% (assessed through the validation of the change in percent tree cover) between 2000 and 2010, we only selected those exhibiting significant positive/negative trends based on the significance of the Spearman rank correlation coefficient. Although the combination of these two procedures noticeably reduced the number of pixels considered to exhibit significant positive and negative changes in forest cover, it was preferred because it reduces the potential effects of the coarse pixel resolution of the MODIS VCF and accounts for the effects of accumulated climate conditions on the MODIS VCF tree cover product. Our estimates of forest cover dynamics are therefore conservative but reduce potential overestimations of forest gain or loss, yielding more robust analytical findings. The use of such combination of approaches to assessing changes in forest cover takes advantage of the fuzzy classification nature of the VCF tree cover product, together with its annual frequency. This constitutes an alternative to recent procedures designed to incorporate land cover classification errors into areal estimates of land cover change (40). Figure 3 shows a summary of the procedures used.

Fig. 3. Methodological steps.

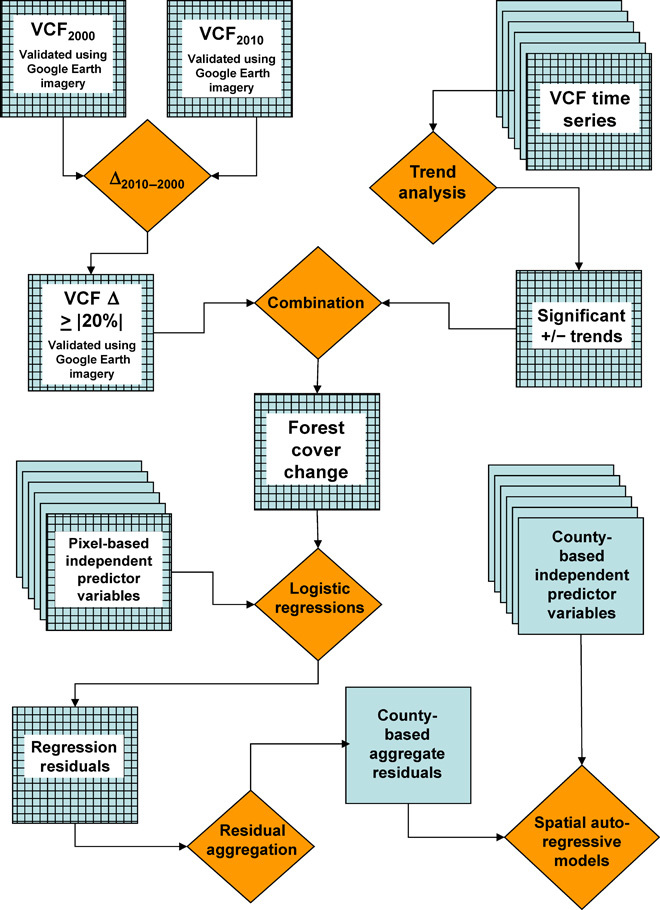
Flow chart depicting the major steps in the procedures used in the study. For details, see Materials and Methods.

Dynamics of NPP

To assess the changes in NPP between 2000 and 2010 among the pixels exhibiting a significant gain in forest cover, we used the Terra/MODIS NPP MOD17A3 product, which was obtained through the online data pool at the NASA Land Processes Distributed Active Archive Center, U.S. Geological Survey/Earth Resources Observation and Science Center, Sioux Falls, SD (https://lpdaac.usgs.gov/data_access). This data set was resampled and coregistered to the MODIS VCF product (that is, 250 m per pixel). Pixels exhibiting a significant gain in forest cover between 2000 and 2010 were evaluated to determine whether they exhibited significant (P < 0.01) trends in decadal (2000–2010) NPP values. Pixels with no significant NPP trends were assumed not to have changes in NPP between 2000 and 2010. Accumulated NPP per year in all pixels exhibiting a significant gain in forest cover was obtained as the cumulative sum of NPP gain across space.

Statistical analyses

To assess the relationship between forest loss or gain and the implementation of the NFCP, we used a stepwise multilevel approach, which accommodates data acquired at different scales. Figure 3 shows a summary of the procedures used. In the first step, we developed logistic regression models (41) to assess the probability of forest loss and gain at the pixel level during the 2000–2010 period. We randomly selected 30,000 pixels across China that have a minimum sampling distance of 5 km to limit potential spatial autocorrelation effects. Two-thirds of these pixels were used to calibrate a pair of logistic regression models (41), whereas the remainder were reserved for validating them. The dependent binary variable (either forest loss or gain) was set to 1 if the pixel exhibited a significant positive (or negative) change [that is, a percent tree cover Δ equal to, or higher than, 20% (equal to, or lower than, −20%) and with significant positive (negative) trends in percent tree cover] and to 0 if the pixel exhibited significant negative (or positive) change or no change. Biophysical and demographic factors that were shown to be strongly correlated with forest cover dynamics in previous spatially explicit models [for example, Rudel et al. (9), Geist and Lambin (42), and Rudel (43)] were selected for use as predictor variables. These included the geographic position of each pixel (that is, easting and northing), elevation, slope, aspect [converted into soil moisture classes (44)], and the CTI [a measure of soil water accumulation (45)] derived from a digital elevation model constructed from data acquired by the Shuttle Radar Topography Mission (46), initial tree cover (that is, VCF in 2000), distance to main roads [obtained from the Digital Chart of the World Dataset (47)], gridded population density in 2000 (48), and mean annual temperature and total annual precipitation in grid format obtained from the WorldCLIM database (49). We acknowledge that, like almost all other data sets, these global data sets have limitations (for example, lack of uniformity across different regions) that may reduce their reliability. However, given that standardized procedures have been applied in their production and that they are publicly available, their use not only allows replication and verification but also allows rapid updates of the analyses as more data become available. As a result, such data sets have been widely used in numerous publications over the last several years [for example, Yang et al. (50), Zheng et al. (51), and Zhang et al. (52)]. All grids were resampled and coregistered to match the MODIS VCF product (that is, 250 m per pixel). Model validation was conducted using the AUC procedure (39). These logistic regression models registered AUC scores of 0.71 and 0.67, respectively, which were significantly different (P < 0.0001) from 0.5 (that is, a random prediction). Using the coefficients obtained in these logistic regression models, we calculated the probability of forest loss and gain for all pixels comprising mainland China. Logistic regression model residuals were then obtained by subtracting these probability values from the observed forest loss and gain values, with the latter expressed in binary format [that is, 1 for any significant negative (positive) change and 0 for any significant positive (negative) change or no change] (fig. S4). These pixel-level residuals represent the unexplained variance of the logistic regression models.

In the second step, we obtained aggregate model residual values on a per-county basis by averaging the pixel-level residuals (both positive and negative) within the county divisions (including city districts) of China (Fig. 1). These per-county aggregate residuals (county-based aggregate of the unexplained variance of the logistic regression models) were used as the dependent variables in spatial autoregressive models (53, 54). Independent predictor variables included implementation of the NFCP [expressed in binary format; that is, 1 for counties where the NFCP was implemented and 0 for counties where it was not (17)], county-based per-capita GDP for 2000, change in county-based per-capita GDP (that is, GDP 2010 − GDP 2000), agricultural production (in the form of total grain and meat production) for 2000 and its change (that is, 2010 − 2000), total population in 2000 and its change (that is, 2010 − 2000), and rural labor in 2000 and its change (that is, 2010 − 2000). These data were obtained from the China Data Center (55). Spatial weighting matrices at the county level were created, defining a neighbor based on both the Queen and the Rook contiguity approaches (56). We report results obtained using the Queen contiguity approach, although results using the two approaches were similar. Using these data, we developed lag and error spatial autoregressive models (53, 54) for each dynamic (that is, forest loss and gain, respectively). We report the results of the lag model for both forest loss and gain (Table 1) because these exhibited the best (that is, lowest) Akaike information criterion values (53, 54).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/2/3/e1500965/DC1

Fig. S1. Histogram of dynamic pixels.

Fig. S2. Distribution of validation polygons.

Fig. S3. Validation of the MODIS VCF.

Fig. S4. Distribution of model residuals.