Abstract
The human motor system is capable of remarkably precise control of movements—consider the skill of professional baseball pitchers or surgeons. This precise control relies upon stable representations of movements in the brain. Here, we investigated the stability of cortical activity at multiple spatial and temporal scales by recording local field potentials (LFPs) and action potentials (multiunit spikes, MSPs) while two monkeys controlled a cursor either with their hand or directly from the brain using a brain–machine interface. LFPs and some MSPs were remarkably stable over time periods ranging from 3 d to over 3 years; overall, LFPs were significantly more stable than spikes. We then assessed whether the stability of all neural activity, or just a subset of activity, was necessary to achieve stable behavior. We showed that projections of neural activity into the subspace relevant to the task (the “task-relevant space”) were significantly more stable than were projections into the task-irrelevant (or “task-null”) space. This provides cortical evidence in support of the minimum intervention principle, which proposes that optimal feedback control (OFC) allows the brain to tightly control only activity in the task-relevant space while allowing activity in the task-irrelevant space to vary substantially from trial to trial. We found that the brain appears capable of maintaining stable movement representations for extremely long periods of time, particularly so for neural activity in the task-relevant space, which agrees with OFC predictions.
SIGNIFICANCE STATEMENT It is unknown whether cortical signals are stable for more than a few weeks. Here, we demonstrate that motor cortical signals can exhibit high stability over several years. This result is particularly important to brain–machine interfaces because it could enable stable performance with infrequent recalibration. Although we can maintain movement accuracy over time, movement components that are unrelated to the goals of a task (such as elbow position during reaching) often vary from trial to trial. This is consistent with the minimum intervention principle of optimal feedback control. We provide evidence that the motor cortex acts according to this principle: cortical activity is more stable in the task-relevant space and more variable in the task-irrelevant space.
Keywords: brain–machine interface, LFPs, minimum intervention, motor cortex, optimal feedback control, stability
Introduction
Animals perform complex learned movements countless times with little error. This consistent performance implies some level of stability within movement representations in the motor cortex. However, several experiments have also shown substantial variability in individual neuronal representations (Padoa-Schioppa et al., 2004; Carmena et al., 2005; Rokni et al., 2007). Here, we face an unanswered question of fundamental importance: at what spatial and temporal scales do stable representations exist? More specifically, do neurons have a constant relationship with a given movement or is there some other mechanism through which highly variable neuronal signals produce consistent movements?
The stability of motor cortical signals is also an important issue in the design of brain–machine interfaces (BMIs), which translate brain signals into controls for external devices such as prosthetic arms. Stable BMI performance depends, at least partly, on the stability of the input signals. However, it remains unclear whether movement representations at the single-neuron level are stable over long time periods (months to years). Prior studies have found conflicting evidence of single-unit stability, with some showing variability (Carmena et al., 2005; Rokni et al., 2007) and others showing stable properties over the course of a few hours (Stevenson et al., 2011), days (Chestek et al., 2007), or weeks (Ganguly and Carmena, 2009). Recently, numerous studies have used unsorted threshold crossings (multiunit spikes, or MSPs) in both scientific and neuroprosthetic experiments (Fraser et al., 2009; Chestek et al., 2011; Flint et al., 2013; Todorova et al., 2014), yet the level of stability of these signals has not been investigated. Local field potentials (LFPs) have long been postulated to be more stable than spikes (Pesaran et al., 2002). Indirect evidence of LFP stability over months to a year was suggested by stable ensemble decoding performance both during reaching (Chao et al., 2010) and in an online BMI (Flint et al., 2013). However, it is still desirable to obtain direct evidence of this stability in terms of the information that each individual signal provides.
Here, we examine directly the stability of LFPs and MSPs in the primary motor cortex (M1) of monkeys controlling a cursor using either arm movements (hand control) or BMI control over a period of months to years. Because the BMI translates M1 activity directly into cursor movement, it removes any variability that could be introduced along the efferent pathway between motor cortex and muscles. Therefore, we can assess directly the stability of M1 signals with respect to cursor movement. Overall, we find that LFPs, and to a lesser extent MSPs, maintain stable representations of cursor movement over very long time periods.
How can this finding be reconciled with reports of motor cortical variability? The framework of optimal feedback control (OFC) provides one potential explanation. OFC postulates that the brain controls movement in a given task by correcting only those errors that interfere with task objectives—the minimum intervention principle (MIP). This is achieved by limiting variability in a “task-relevant” space (the space relevant to objectives) and ignoring variability in a task-irrelevant or “task-null” space (Scholz and Schöner, 1999; Todorov and Jordan, 2002). Here, we investigated the differential stability of both LFPs and MSPs in task-relevant and task-null spaces. We found that, over the long term, stability is extremely high in the task-relevant space and lower in the task-null space. These findings provide important and novel cortical population-level evidence supporting OFC in the neural control of movement.
Materials and Methods
Experimental methods.
All procedures were approved by the Northwestern University Institutional Animal Care and Use Committee. The behavioral training, surgical implantation, and recording methods for the current study were described in detail in Flint et al. (2013). Briefly, two adult rhesus macaques, one male and one female (Monkeys C and M), were each trained to use a two-link manipulandum to move a cursor (1-cm-diameter circle) within a rectangular planar workspace (20 × 20 cm) to sequential targets in a random target pursuit task (Fig. 1A). The choice of a random target task was motivated by our desire to sample more of the kinematic workspace than would be sampled by a center-out task. In each monkey, we surgically implanted a 96-electrode silicon array (Blackrock Microsystems) into the primary motor cortex contralateral to the arm used to control the cursor. We recorded LFPs and unsorted threshold crossings (which we term here MSPs) during the reaching behavior and built Wiener cascade decoders consisting of a linear Wiener filter cascaded with a third-order polynomial (Westwick et al., 2006) to relate end-point 2D velocity to MSP or LFP signals. LFP decoders were built using features extracted from the continuous LFP signal (Flint et al., 2012a). For each electrode, we calculated the local motor potential (LMP) by averaging the time domain signal in 50 ms bins (Schalk et al., 2007) and the spectral power in 5 frequency bands (0–4, 7–20, 70–110, 130–200, and 200–300 Hz) by using a fast Fourier transform on Hanning-windowed, 256 ms segments. These features, binned at 50 ms intervals, were used to train a Wiener cascade BMI decoder. MSP decoders were built from spike counts binned at 50 ms. LFP and MSP decoders for BMI control were built on early epochs (10 min blocks) of hand-controlled reaching behavior and then held static until the end of all data collection for the entire study (hundreds of days). Monkeys C and M used each static decoder for BMI control typically two or three times per week. On most days, the monkeys had epochs of both hand control and one or more types of BMI control (Flint et al., 2013). The monkeys' arms used in hand control were not restrained during BMI control, but the manipulandum was removed. Their arm movements during BMI control were not stereotyped, differed from those when under hand control, and tended to attenuate slightly in amplitude over days.
Figure 1.
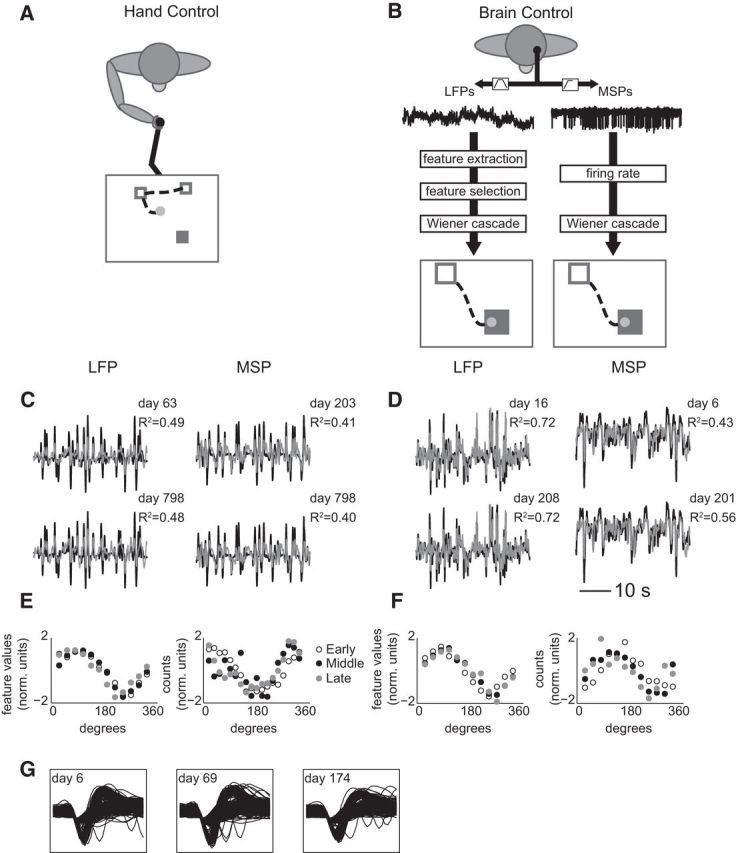
Random target pursuit behavior in hand control (A) and BMI control (B). BMI control was performed with either LFP features (B, left) or MSP firing rates (B, right). C, D, Brief examples of decoding actual Y velocity on the last day using single feature decoders built from 2 prior days (labeled “day” to the right of each trace) for hand (C) and brain (D) control. R2 refers to the fit between the actual velocity (black) and the predicted velocity (gray). E, F, Example tuning curves in hand (E) and brain (F) control. As in C and D, LFP curves are on the left and MSP curves are on the right. Each plot shows three example curves as open circles or filled gray or black circles. For display, we normalized each tuning curve by subtracting its mean across bins and dividing by the SD. G, Example MSP waveforms from one representative electrode during days 6, 69, and 174 of recording.
The dataset used in this study includes BMI control data that were presented in a previous study (Flint et al., 2013), as well as hand control data. Days 180–380 (Monkey C) and 50–250 (Monkey M) of hand control were recorded concurrently with the BMI control study.
Stability of single feature decoders.
We used two measures of stability in this study (see “Stability of ensemble tuning” section for details on the second measure). The first approach is based on single feature decoders (SFDs), which had been used earlier to evaluate single-unit stability over 1–2 d (Chestek et al., 2007). SFDs are constructed by treating each feature of each input signal as an independent input and calculating the ability of that single feature to predict the output. Here, we built SFDs using the data from each recording epoch over a period of 6 months for each feature (frequency band power or LMP) used in LFP control and for each electrode used in MSP control. SFDs were trained separately for hand control epochs, LFP control epochs, and MSP control epochs. After each SFD was trained, we calculated SFD prediction accuracy using that SFD to predict the actual velocity in five recording epochs from the end of the study's data collection period (which lasted months to years) and averaged the accuracy over those five epochs. Prediction accuracy was defined as the coefficient of determination (R2) between the actual cursor velocity (either hand- or brain-controlled) and the velocity predicted by the SFD. Testing epochs were not used for SFD training and training epochs were never used for prediction accuracy testing. In the Results, we report SFD R2 values for each day of the study. To calculate the prediction accuracy for a day, we computed the average R2 obtained by using the SFDs trained on all epochs from that day. Examples of single-feature predictions are shown in Figure 1, C and D. Figure 2A shows SFD prediction accuracy for each day as a single column; for example, the leftmost column in Figure 2A shows the SFD prediction accuracy for all features on day 1 of the study. During hand control, SFD R2 values measured the accuracy of predictions made by a single feature. During BMI control, the R2 value for each SFD estimated the contribution of that feature to the BMI (population-level) decoder.
Figure 2.
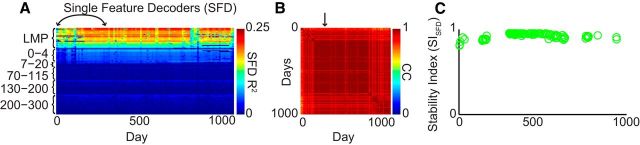
Calculation of SISFD, the mean pairwise correlation of LFP (or MSP) single-feature performance over all recording days. A, LFP SFD map for Monkey C during hand control. Color shows the R2 value between actual and decoded movements. Features (rows) are sorted within each feature type in descending order of average SFD performance. B, Correlation map for LFP SFD R2 performance. Each point in this color map represents the correlation coefficient between 2 d of the study (i.e., two columns of the maps in A). For example, the point in the top row of B designated with an arrow corresponds to the correlation of the two columns in A designated with a double arrow. C, SISFD over time for Monkey C; each circle is the average over all rows in a given column in the ensemble correlation map from B.
The entire hand control dataset spanned 1040 d for Monkey C and 800 d for Monkey M. Figure 2A shows an example color plot of R2 values (for y-velocity) with N rows and D columns, where N is the number of included features and D is the number of days in the study. Each column represents the average performance for all SFDs trained on that day; the performance of each SFD is obtained as an average over the five testing epochs. We computed the correlation coefficient between each pair of columns in the N × D matrix of Figure 2A, producing the D × D color map of correlations shown in Figure 2B. The SFD stability index (SISFD) was then calculated as the mean of the correlation map across rows (or equivalently across columns), as seen in Figure 2C (see also Fig. 3C,F); this is similar to the measure in Ganguly and Carmena (2009). Overall, the color map (Fig. 2B) provides detailed information about the stability of the individual features and the SISFD provides a summary of stability over all features over time.
Figure 3.
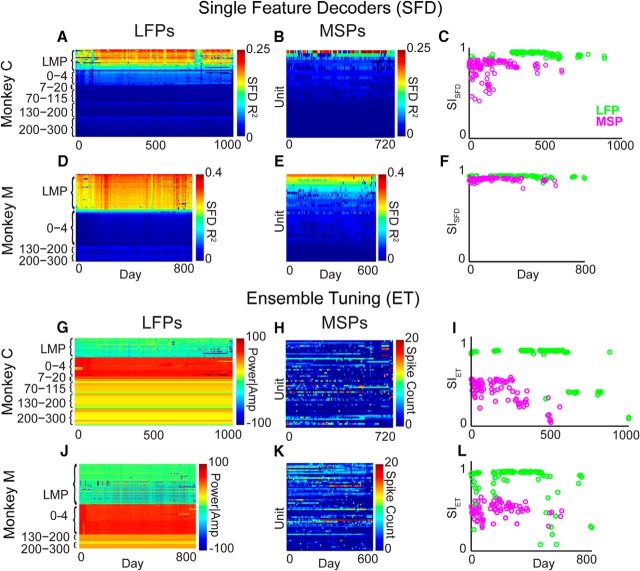
Stability of LFPs and MSPs during hand control. A, LFP SFD performance map for Monkey C. Rows are sorted within feature type by descending average SFD performance. B, MSP SFD performance map for Monkey C. C, SISFD values reflect high stability for LFPs (green circles) and MSPs (magenta circles) during hand control in Monkey C. D, E, Same as A and B but for Monkey M. F, Stability of LFPs was also slightly greater than that of MSPs in Monkey M. G, LFP ET map for Monkey C sorted by feature type. H, MSP ET map for Monkey C. I, Using SIET, LFPs were still highly stable and MSPs less stable. J, K, Same as G and H but for Monkey M. L, SIET showing that the stability of LFPs was also greater than that of MSPs in Monkey M.
Features included in the analysis.
In this study, we analyzed the performance of only those LFP features that were included in the decoder for LFP-based BMI control. When analyzing MSP stability, we included only those channels that corresponded to included LFP features so that stability indices calculated for both LFPs and MSPs would be based on signals from the same electrodes. As the multielectrode arrays aged, they developed leakage (or shunting) between some of the electrodes, likely due to insulation degradation (Barrese et al., 2013). This shunting manifested itself as an unusually high correlation in the signals recorded from pairs of electrodes, usually those that were physically adjacent on the array. In our analysis for this study, we removed from consideration all channels that were shunted with any other channel.
Stability of ensemble tuning.
The second measure of stability used here was based on the directional tuning of individual features, as in Ganguly and Carmena (2009). Because movement velocities were in random directions, we evaluated movement direction every 100 ms and grouped these directions into 12 bins of 30° each. In each 10 min epoch, we computed the mean of each spike rate and LFP feature value over all movements that corresponded to each binned direction. This resulted in a tuning curve with 12 components for each feature/spike in each epoch. We computed the stability of the ensemble of tuning curves over all features/spikes used in BMI control (as in Fig. 3 of Ganguly and Carmena, 2009). In other words, we calculated the correlation coefficient between the ensemble of tuning curves of all features from each day (averaged over all epochs in that day) and the ensemble of curves from all other days to produce a color map of correlations over days (as for SFDs in Fig. 2B). The ensemble tuning stability index (SIET) was then calculated as the mean of these correlations across days (Fig. 3, bottom).
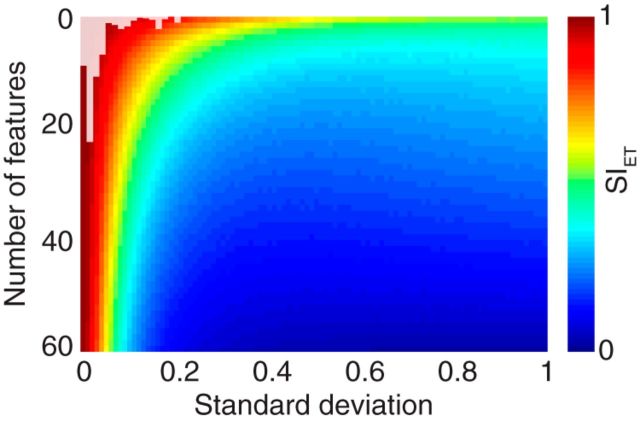
To provide an intuition about the meaning of a given value of SISFD or SIET, we performed an analysis using simulated data. We started with an actual ensemble tuning curve (the first column from Fig. 4K), added noise with SD σ to n of N total features, and computed the SI value for each value of σ (ranging from 0 to 1) and n (ranging from 2 to N). We then plotted these SI values in a color plot (Fig. 5). We also calculated the σ that was actually observed in our results from the single features (Fig. 5, histogram overlay). Therefore, Figure 5 demonstrates how many features must vary, and by how much, to arrive at a particular value of the stability index. We repeated the simulation for SISFD with similar results.
Figure 4.
Stability of LFPs and MSPs during BMI control. A, Monkey C's LFP SFD performance (R2) during LFP BMI control. B, Monkey C's MSP SFD performance during MSP BMI control. C, SISFD values reflect high stability for LFPs (green circles) and MSPs (magenta circles) in Monkey C. D, E, Same as A and B but for Monkey M. F, LFP stability was also higher than MSP stability in Monkey M. G, LFP ET map for Monkey C sorted by feature type. H, MSP ET map for Monkey C. I, Using SIET, LFPs remained highly stable, whereas MSPs were less stable. J–L, Same as G–I but for Monkey M. SIET shows that the stability of LFPs was noticeably higher than that of MSPs during BMI control.
Figure 5.
Simulated data show changes in SIET with number and variability of features. The color map shows a surface of SIET values as we systematically changed the number of simulated features that were influenced by noise (y-axis), and the SD (σ) of the noise (x-axis). The histogram overlay shows the σ values for the actual single feature ensemble tuning (Monkey M, MSP control, taken from Fig. 4K).
Singular value decomposition analysis.
To investigate the variability of neural activity during BMI control in a more principled manner, we performed a singular value decomposition (SVD) of the Wiener filter matrix H. This was an M × (10N) matrix, where M is the number of outputs (two in this case, for the two components of the velocity vector) and 10N is the number of inputs, given by the number N of neurons (or features) multiplied by the 10 time lags (the number of taps in the Wiener filter). At each time lag, the Wiener filter maps N inputs onto two outputs using the transform h, where h is the subset of H that corresponds to a single time lag. We used SVD to decompose h into a task-relevant space (of dimension two) and a task-null space (of dimension N-2). Because there were 10 time lags in our decoder, we calculated the SVD 10 times (once for each h) and combined them as described below.
For each time lag, SVD decomposed h into a left orthonormal matrix U, a scaling matrix ∑ that contained the singular values along the diagonal, and a right orthonormal matrix V, such that:
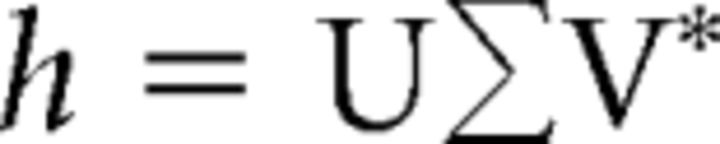 |
Where V* refers to the transpose of V. Intuitively, U and V can be thought of as rotation matrices and ∑ as a scaling matrix. Therefore, SVD can be thought of as a sequence of three geometrical transformations: a rotation in input space (V*), a scaling along the new axes (∑), and a rotation in output space (U). This resulted in 10 V matrices, one for each lag, denoted as Vi, 1 ≤ i ≤ 10. In each case, the matrix Vi captured the corresponding task-relevant neural space through its first two singular vectors; that is, its first two columns: vji or j = 1,2. The SVD has only two nonzero eigenvalues because the linear filter maps the N dimensional neural space into a 2D velocity space. For each lag i, the corresponding null space, is the one spanned by the remaing N − 2 singular vectors, the columns vji for 3 ≤ j ≤ n.
We projected each N-dimensional neural vector x, a vector of either firing rates (during MSP-based BMI control) or LFP features (during LFP-based BMI control), onto each of the singular vectors vji The projections αji were thus defined as follows:
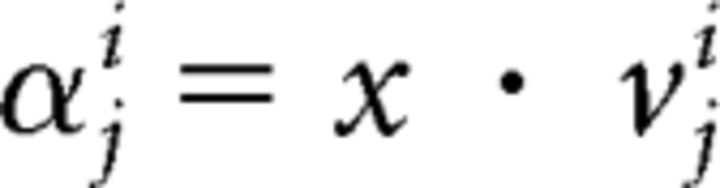 |
In a similar manner to the SFD analysis, for each BMI control epoch, we built two decoders of the BMI-controlled cursor velocity, one based on the first two projections {α1i, α2i}, for 1 ≤ i ≤ 10, and one based on the remaining projections {α3i, …, αNi}, for 1 ≤ i ≤ 10. We evaluated the performance of these decoders, one for each epoch, based on their ability to predict the BMI-controlled cursor velocity in the last five epochs—the same metric as in the SFD analysis. We measured the R2 performance of each of these decoders and averaged this performance over all epochs in a given day. We performed this analysis in congruent control modes: only on MSPs for MSP-based BMI control and only on LFP features for LFP-based BMI control. We used the coefficient of variation (CV) of the performance over all days to quantify variability.
Results
We recorded LFPs and threshold crossings (MSPs) for an extended time period while two monkeys controlled a computer cursor using either hand control with a 2D manipulandum (>3 years) or direct brain (BMI) control with LFPs or MSPs (∼7 months). Table 1 summarizes the monkeys' behavioral performance during the hand control and BMI control tasks.
Table 1.
Summary statistics of reaching behavior (median ± interquartile range) in each epoch
| Reaches/epoch | Peak speed (cm/s) | |
|---|---|---|
| Monkey C | ||
| Hand control | 659 ± 137 | 27 ± 13 |
| LFP BMI control | 85 ± 22 | 35 ± 20 |
| MSP BMI control | 121 ± 33 | 31 ± 20 |
| Monkey M | ||
| Hand control | 561 ± 92 | 23 ± 14 |
| LFP BMI control | 71 ± 17 | 38 ± 37 |
| MSP BMI control | 164 ± 58 | 22 ± 16 |
LFP and spike movement representations are stable during reaching
We first investigated how long neural representations of movement remain stable in the brain during natural motor tasks. SFD performance for all LFP features and MSP units (the ensemble “map”) in Monkey C is shown in Figure 3, A and B. During hand control, both signal types were highly stable in Monkey M (Fig. 3D,E), whereas MSPs were less stable than LFPs in Monkey C. This was true both on a single-feature level (each row in Fig. 3A,D) and for the ensemble as a whole (Fig. 3C,F). LFPs were significantly more stable than MSPs during hand control for Monkey C. The mean (±SD) of the SISFD over all days was 0.92 ± 0.05 for LFPs versus 0.77 ± 0.10 for MSP (p = 10−33, t test). LFPs were also more stable than MSPs for Monkey M, by a small but statistically significant amount (SISFD 0.98 ± 0.02 vs 0.95 ± 0.02; p = 10−31).
Ensemble tuning (ET), or directional tuning, of all LFP features and MSP units during hand control is shown in Figure 3, G, H, J, and K. The SIET for all LFP features and MSP units is shown in Figure 3I (Monkey C) and Figure 3L (Monkey M). LFPs were significantly more stable than MSPs in both monkeys during hand control. The mean (±SD) of SIET over all days for LFPs was 0.75 ± 0.20 and 0.38 ± 0.14 for MSPs for Monkey C (p = 10−30). The mean of SIET over all days for LFPs was 0.79 ± 0.19 and 0.45 ± 0.08 for MSPs for Monkey M (p = 10−30).
LFP and spike movement representations are stable during BMI control
We next analyzed the stability of each signal type during BMI control (Fig. 4). Similar to our results during hand control, we found that SISFD values indicated stable movement representations in both LFPs and MSPs (Fig. 4C,F). For Monkey C, LFPs were significantly more stable than MSPs (SISFD 0.94 ± 0.03 and 0.80 ± 0.09, respectively; p = 10−19). Monkey M exhibited very stable signals, with an SISFD of LFPs (0.99 ± 0.001) that was slightly but significantly greater than that of MSPs (0.98 ± 0.01; p = 10−33). Using ensemble tuning, a subpopulation of spikes was still stable over time (Fig. 4H,K), but the population was notably less stable than LFPs. For Monkey C, SIET was 0.97 ± 0.01 and 0.51 ± 0.01 for LFPs and MSPs, respectively (p = 10−81). For Monkey M, SIET was 0.97 ± 0.03 and 0.57 ± 0.02 (p = 10−50).
To help clarify the meaning of SIET values, we computed the SIET as we introduced different levels of noise into a simulated MSP dataset (Fig. 5). As an example, a value of 0.5 for SIET means that if half the population (∼30 features) is changing, then those signals are varying with an SD (σ) of ∼0.11. Alternatively, if the average σ were ∼0.2, an SIET of 0.5 would mean that ∼20% of the population is changing. For reference, we have superimposed actual σ values taken from our data (Fig. 5, histogram overlay). Similar color maps and histograms were found for SISFD for MSPs as well as for LFPs (data not shown).
LFPs are highly stable in the time domain and high-frequency bands
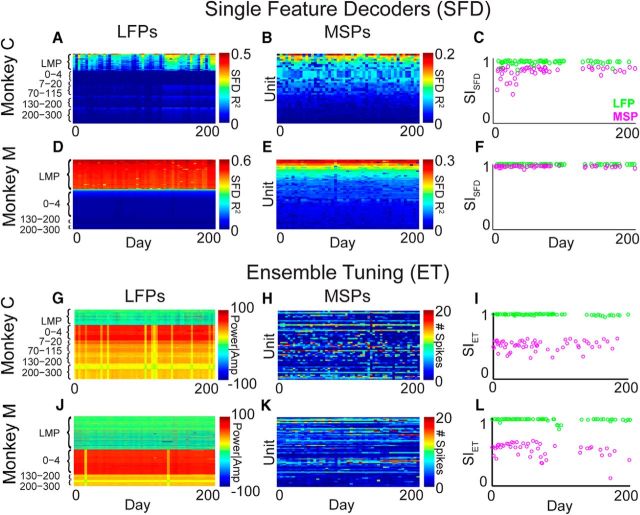
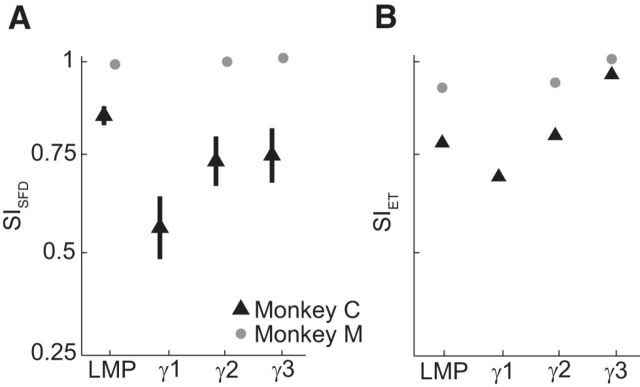
The above results reflect the aggregate of multiple-frequency bands and time domain (LMP) LFP features. The high-gamma (70–300 Hz) band and LMP features contained most of the information about movement and contributed most to our decoders (Flint et al., 2012b). Therefore, we investigated the stability of the LMP and the three high gamma bands (γ1: 70–115 Hz, γ2: 130–200 Hz, and γ3: 200–300 Hz) that were used in the BMI decoders by the monkeys during LFP-based BMI control (Fig. 6). As anticipated from the monkeys' stable BMI performance, the LMP and high-gamma features were highly stable. This mirrored the stability of the overall population (cf. mean values over time in Fig. 4C). Interestingly, the γ2 and γ3 bands were even more stable than the γ1 band for Monkey C. This could suggest that high-gamma signals, in particular, might provide highly stable signals for studying neurophysiology and for controlling BMIs.
Figure 6.
Stability of selected LFP feature types during LFP-based BMI control. A, Mean (±SD) SISFD over all days for Monkey C (triangles) and Monkey M (circles). B, Mean SIET for Monkey C (triangles) and M (circles). Some error bars are not visible because they are smaller than the marker sizes. Overall, LMP and high-gamma features were highly stable.
LFP stability increases during early BMI decoder learning
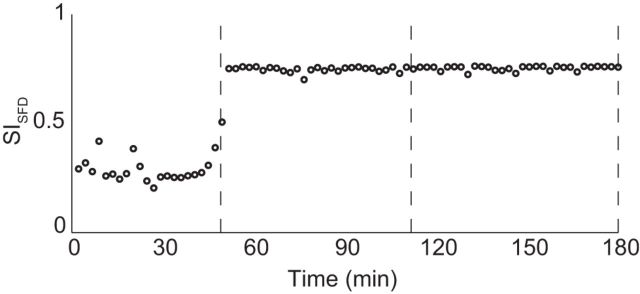
The prior analyses examined the stability of LFPs during long-term BMI use. To gain insight into what happens during the early learning of a new LFP-based BMI decoder and to facilitate comparison with prior studies, we also examined the stability over a short timescale. We selected data from the first 3 d of Monkey C's use of an LFP-based BMI decoder different from the one used in the above analyses. We calculated the SISFD by dividing the data in those 3 d into 80 epochs of ∼2 min each and performing the SFD stability analysis as described previously. The LFPs stabilized on day 2, after an accumulated task time of ∼50 min. This was followed by an extended period of high stability across days 2 and 3 (Fig. 7). This timescale of days for achieving stability is similar to the timescale of map stabilization found using small ensembles of spikes to control a BMI (Ganguly and Carmena, 2009).
Figure 7.
LFP stability increases quickly after the introduction of a new decoder. After the introduction of a new decoder, the SISFD increased sharply after ∼45 min of BMI control. Dashed lines denote boundaries between days of recording.
Stability measures remain high even when using very few features
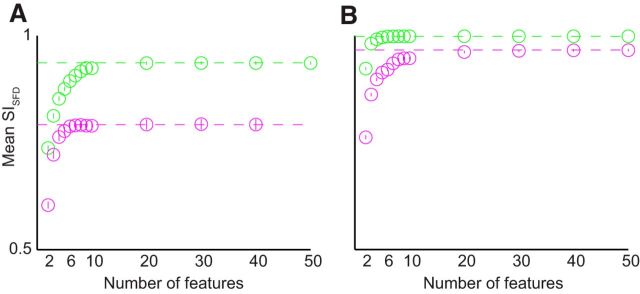
Because we computed stability by simultaneously using a large number of features with more LFP features than spikes, one possible concern could be that stability was overestimated due to averaging effects. We therefore sought to determine how many features must be included to approach the level of stability achieved by the entire population. We conducted a feature-dropping analysis to answer this question. We randomly sampled F features from the population of LFP or MSP features, where F varied from 1 to 50. For each group of features, we calculated the SISFD and repeated this 500 times. We found that a small number of features, <20 in each case, sufficed to achieve the SISFD found for the entire population (Fig. 8). Therefore, our metric was unlikely to overestimate stability due to the large number of features in the ensemble.
Figure 8.
LFPs (green points) and MSPs (magenta points) achieved stability with a small number of features. A, B, Feature-dropping curves for Monkey C (A) and Monkey M (B). Each point represents SISFD values for a feature set of size F (horizontal axis), averaged across days. Vertical lines show SD values, which were very small. For both LFPs and MSPs, the SISFD indicates remarkable stability even with very few features, approaching its population level (dashed horizontal lines) with the inclusion of as few as 10–20 features.
Cortical stability is higher in the task-relevant space than in the null space
The above analyses showed that LFPs and MSPs were stable overall, yet some neurons and features were more stable than others (Fig. 3B,E). To investigate these differences in a principled manner, we examined the projections of LFP features and spikes into two neural subspaces: task-relevant and task-null subspaces. We hypothesized that, if the cortex used a strategy like the MIP of OFC to control the BMI, then the activity in the task-null space (or neural null space) should be much less stable than that in the task-relevant space.
The mean R2 of the α1,2 decoders (task-relevant space) was much higher than that of the α3, …,N decoders (Fig. 9C–F, null space). Stability of the decoders based on task-relevant space features was not surprising because, by definition, the task-relevant space should be an excellent predictor of the full Wiener filter output. What was not certain, however, was whether the variability of the predictions would be lower in the task-relevant space than in the task-null space (Fig. 9A). An alternative possibility could have been for the variability to be equally low in both spaces, which would have indicated that all components of cortical activity were controlled with equal precision regardless of task relevance (Fig. 9B).
Figure 9.
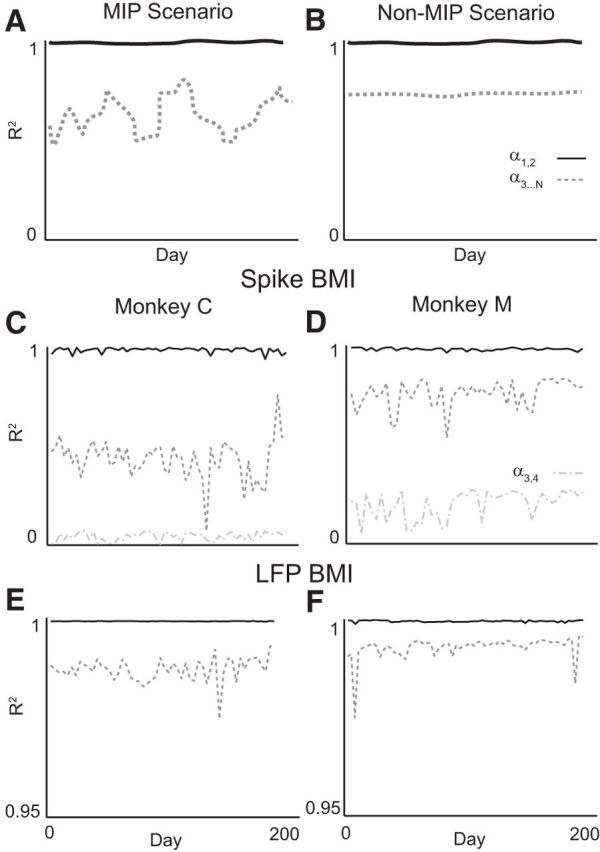
Stability in the task-relevant and task-null neural spaces. A, Expected decoding performance if cortical activity adheres to the MIP in the task-relevant (using the α1,2 decoder; solid line) and null spaces (using the α3…N decoder; dashed line). Mean null space performance is lower than that in the task-relevant space and null space performance is much more variable. B, Expected decoding performance if cortical activity does not adhere to the MIP. Here, null space performance has lower mean but the same variance as performance in the task-relevant space. C, D, Actual decoding performance in the task-relevant (α1,2), full task-null (α3…N), and partial task-null (α3,4) spaces using MSP-based BMI data in Monkeys C and M, respectively. The task-relevant space performance was extremely high and stable, whereas the null space performances were much more variable. The same was true for LFP-based BMI (E, F), but the null space decoder in this case had much higher performance than for the MSP-based BMI.
We found that the task-relevant SFD performance showed low variability, as measured by the CV (CV = 0.010 and 1.8 × 10−4 for Monkeys C and M, respectively; see Fig. 9C,D). This would be expected from the stable and accurate BMI performance previously reported by Flint et al. (2013). In contrast, the null space SFD performance had much higher variability (CV = 0.23 and 0.0026, respectively, using spikes). Similar, but smaller, differences were found for LFPs between null space (CV = 0.060 and 0.091) and task-relevant space (CV = 10−5 and 6.7 × 10−3) SFD performances (Fig. 9E,F).
Principal components analysis of the LFP features used in the decoders showed that 13 (Monkey C) and 17 (Monkey M) principal components were needed to account for 80% of the variance in these features. This suggested that LFP activity in the null space did indeed covary substantially with that in the task-relevant space. This would explain the higher performance and lower variability of the null space predictions for LFPs than for spikes.
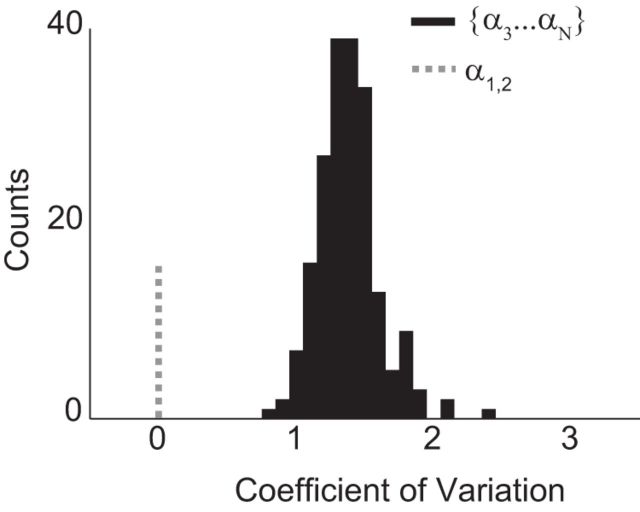
We next tested whether any pair of null space projections provided as stable an input to a decoder as the pair of task relevant projections. This allowed us to determine whether the large difference in the number of α inputs to the decoder (2 vs 83) biased the stability of the decoding. We repeated the decoder calculation using a random subsampling of two α projections in the null space of LFP control in Monkey C. We repeated this random subsampling 200 times to obtain a distribution of CVs and compared it with the CV value obtained using {α1, α2} as decoder input. The entire distribution of predictions based on 2D null space projections had significantly higher CVs than those based on task-relevant space projections (p = 0.005 using the cumulative empirical distribution; Fig. 10). Therefore, the increased variability found in the null space was not due to bias from the higher number of α inputs to the decoder.
Figure 10.
Variability in the null space versus the task-relevant space. The CVs of the decoding performance over time for decoders based on two randomly selected null-space projections (black bars) were significantly higher than the CV for a decoder based on the two task-relevant projections (dashed line).
Discussion
The long-term stability of individual MSPs and LFPs in the motor cortex had not been established previously. We found LFPs to be highly stable, and MSPs somewhat less stable, over time scales ranging from 3 d to 3 years. In general, LFPs and MSPs behaved stably with respect to cursor movement controlled by either the hand or the brain. LFPs were somewhat more stable than MSPs during hand control and substantially more stable than MSPs during BMI control. In particular, we found that signal stability was much higher in the task-relevant space than the task-null space, an observation consistent with the hypothesis of optimal feedback control at the cortical level.
Stability at different spatial scales
Stability of movement representation would seem to be important for overlearned, daily activities such as reaching for food. However, it has been debated whether this high behavioral stability requires highly stable activity at the neuronal level (Chestek et al., 2007; Ganguly and Carmena, 2009; Stevenson et al., 2011) or if stability is a network-level phenomenon that arises despite unstable representations in single neurons (Cohen and Nicolelis, 2004; Carmena et al., 2005; Rokni et al., 2007). Here, we found evidence for stability of both MSPs and LFPs at the single-feature level. Stability was higher at the mesoscopic (LFP) scale than at the MSP scale and a subset of MSPs were much less stable. This could suggest that the brain is capable of different levels of control on mesoscopic (LFPs) and single-neuron scales (Ganguly and Carmena, 2009), although it could also be due to signal averaging at the mesoscopic scale.
Some apparent contradictions about stability in published reports are likely due to differences in methods or analysis. For example, Rokni et al. (2007) found variable preferred directions (PDs) during a movement task, but measurement noise may have played an important role in the apparent amount of PD variation in that study (Stevenson et al., 2011). Two prior studies found lower stability in ensemble-level, offline decoding (Flint et al., 2013; Perge et al., 2014) than we saw previously with online BMI control (Flint et al., 2013) or here using single-feature analyses. In addition, movement representations may change with learning of a task (Cohen and Nicolelis, 2004; Chestek et al., 2007; Mandelblat-Cerf et al., 2009). Ganguly and Carmena (2009) showed that this phenomenon also occurs when learning a BMI task using a small ensemble of neurons while requiring the hand to remain stationary. In our study, as in Chestek et al. (2007), monkeys performed overlearned control tasks. In addition, our BMI decoders were biomimetic (trained on actual reaches) and the monkeys' arms were not required to remain stationary during BMI control. These differences may account for the minimal and rapid early learning required for our BMI task based on both behavioral performance (Flint et al., 2013) and on SISFD (Fig. 7). These aspects of our experiment also may have contributed to the highly stable movement representations that we found.
One potential concern with our approach could be that our stability indices were calculated across a large number of features (or spikes), so the actual stability of individual signals may be overestimated. To validate our population-level analysis, we repeatedly eliminated randomly selected inputs and recalculated SISFD (“feature dropping”). We found that the high degree of signal stability observed for LFPs and MSPs was preserved even when using a very low number of features to compute SISFD (Fig. 8). In some cases, even as few as five to six features provided remarkably high stability and, generally, 20 features sufficed to achieve population-level stability. We found a similar trend for hand control results (data not shown).
Evidence supporting the minimal intervention principle
According to the MIP, the brain minimizes effort by controlling only those movement components that are relevant to the task goals while allowing variability in those movement components that are unrelated to the task goals. This principle accounts for the simultaneous observation of highly accurate control of movements in a particular task with substantial trial-to-trial variability in the way the limb or body moves while achieving the task goal (Todorov, 2004). The principle predicts low variability in the task-relevant space and higher variability in the task-null space, a phenomenon that can be explained by optimal feedback control (Todorov, 2004) among other models (Martin et al., 2009). Substantial evidence for this concept was found in modeling and behavioral studies (Pandy et al., 1990; Scholz and Schöner, 1999; Latash et al., 2001; Todorov and Jordan, 2002; Scott, 2004) and in a myoelectric interface study (Nazarpour et al., 2012), although some evidence against it also exists (Mosier et al., 2005; de Rugy et al., 2012). Cortical electrophysiological evidence supporting the OFC framework, but not the MIP, was presented previously in the context of long-latency stretch responses (Pruszynski and Scott, 2012). In the current study, direct BMI control using signals from primary motor cortex provided a unique opportunity to study cortical control strategies during voluntary, goal-oriented behavior without the intervening levels of the neuromuscular system (spinal cord, muscle activations, joint biomechanical constraints, etc.). Although somatosensory feedback was intact during BMI control, it did not inform the monkeys about their performance in the BMI task. Therefore, we were able to assess directly the relative variabilities in the “neural” null and task spaces.
Neural patterns during BMI control were extremely stable in the task-relevant space and more variable in the task-null space. Although we expected that the task-relevant space would be high performing and stable and that the null space would be lower performing on average, there was no a priori reason that the variability in the null space had to be greater. For example, the brain could have controlled all of the neural signal components with equal precision and this would have resulted in a neural null space with low mean and low variance in performance (Fig. 9B). Instead, we found low mean but high variance in the neural null space performance (Fig. 9A). This finding is consistent with the MIP.
This result was not due to bias from unequal dimensionality of the input space. None of the 2D combinations of neural patterns in the null space was as stable as those in the task-relevant space (Fig. 10). These findings could provide an explanation for the conflicting evidence of neuronal stability presented in some prior studies. More importantly, this result provides evidence in support of the minimal intervention principle in the motor cortex itself. More direct evidence of cortical signals' consistency with the OFC framework would require an examination of trial-by-trial variability in the task and null spaces. Because our experiments were not designed to track trial-to-trial variability, further investigation of short-term variability in the neural null and task spaces is warranted.
Implications for decoding motor intent over long time periods
By leveraging the ability to decode limb kinematics (Georgopoulos et al., 1982; Moran and Schwartz, 1999) or kinetics (Evarts, 1968; Fagg et al., 2007; Flint et al., 2014) from cortical activity, BMIs have the potential to restore lost function to individuals with paralysis (Hochberg et al., 2006; Collinger et al., 2013; Ethier et al., 2012). However, single-neuron action potentials are difficult to record over long time scales with silicon-based arrays and those that are recorded over long times can exhibit substantial nonstationarity in their amplitudes and waveforms (Chestek et al., 2011; Simeral et al., 2011). This variability represents a significant roadblock to clinically viable BMIs. These issues have fueled a push toward examining unsorted spikes (MSPs, also called threshold crossings) and LFPs for decoding movement (Pesaran et al., 2002; Mehring et al., 2003; Stark and Abeles, 2007; Jarosiewicz et al., 2008; Zhuang et al., 2010; Bansal et al., 2011; Chestek et al., 2011; Slutzky et al., 2011; Flint et al., 2012a; Flint et al., 2012b; Gilja et al., 2012; Flint et al., 2013; Nuyujukian et al., 2014; Perge et al., 2014; Todorova et al., 2014). The results reported here, and our prior results showing high long-term BMI performance (Flint et al., 2013), indicate that it should be possible to decode intended movement accurately over clinically useful time spans, limited only by recording hardware rather than by inherent instabilities in the neural signals. Although LFPs were more stable than MSPs, this did not translate to higher BMI performance (Flint et al., 2013), possibly because spikes were slightly more informative overall. Adaptive decoding algorithms (Gilja et al., 2012; Orsborn et al., 2014) may provide a way to counteract changes that do occur in neural representations. Further, adaptation to BMI decoders is greatly facilitated when the cortical modulations required to achieve control are within the “intrinsic manifold” of the cortical activity (Sadtler et al., 2014). This result was based solely on the analysis of neural activity and did not take into account the decoder. The findings of Sadtler et al. (2014), when combined with the results reported here, suggest that a more judicious design of BMIs may make them both easier to learn and more stable to use over long periods of time.
Footnotes
This work was supported by the National Institutes of Health (Grant K08 NS060223 to M.W.S. and Grants R25 GM79300 and T32 HD057845 to M.R.S.) and the Defense Advanced Research Projects Agency (Grant N66001121-4023 to M.W.S.).We thank Lee Miller for the use of recording equipment.
The authors declare no competing financial interests.
References
- Bansal AK, Vargas-Irwin CE, Truccolo W, Donoghue JP. Relationships among low-frequency local field potentials, spiking activity, and three-dimensional reach and grasp kinematics in primary motor and ventral premotor cortices. J Neurophysiol. 2011;105:1603–1619. doi: 10.1152/jn.00532.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barrese JC, Rao N, Paroo K, Triebwasser C, Vargas-Irwin C, Franquemont L, Donoghue JP. Failure mode analysis of silicon-based intracortical microelectrode arrays in non-human primates. J Neural Eng. 2013;10 doi: 10.1088/1741-2560/10/6/066014. 066014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carmena JM, Lebedev MA, Henriquez CS, Nicolelis MA. Stable ensemble performance with single-neuron variability during reaching movements in primates. J Neurosci. 2005;25:10712–10716. doi: 10.1523/JNEUROSCI.2772-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chao ZC, Nagasaka Y, Fujii N. Long-term asynchronous decoding of arm motion using electrocorticographic signals in monkeys. Front Neuroeng. 2010:3. doi: 10.3389/fneng.2010.00003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chestek CA, Batista AP, Santhanam G, Yu BM, Afshar A, Cunningham JP, Gilja V, Ryu SI, Churchland MM, Shenoy KV. Single-neuron stability during repeated reaching in macaque premotor cortex. J Neurosci. 2007;27:10742–10750. doi: 10.1523/JNEUROSCI.0959-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chestek CA, Gilja V, Nuyujukian P, Foster JD, Fan JM, Kaufman MT, Churchland MM, Rivera-Alvidrez Z, Cunningham JP, Ryu SI, Shenoy KV. Long-term stability of neural prosthetic control signals from silicon cortical arrays in rhesus macaque motor cortex. J Neural Eng. 2011;8 doi: 10.1088/1741-2560/8/4/045005. 045005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen D, Nicolelis MA. Reduction of single-neuron firing uncertainty by cortical ensembles during motor skill learning. J Neurosci. 2004;24:3574–3582. doi: 10.1523/JNEUROSCI.5361-03.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collinger JL, Wodlinger B, Downey JE, Wang W, Tyler-Kabara EC, Weber DJ, McMorland AJ, Velliste M, Boninger ML, Schwartz AB. High-performance neuroprosthetic control by an individual with tetraplegia. Lancet. 2013;381:557–564. doi: 10.1016/S0140-6736(12)61816-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Rugy A, Loeb GE, Carroll TJ. Muscle coordination is habitual rather than optimal. J Neurosci. 2012;32:7384–7391. doi: 10.1523/JNEUROSCI.5792-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ethier C, Oby ER, Bauman MJ, Miller LE. Restoration of grasp following paralysis through brain-controlled stimulation of muscles. Nature. 2012;485:368–371. doi: 10.1038/nature10987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evarts EV. Relation of pyramidal tract activity to force exerted during voluntary movement. J Neurophysiol. 1968;31:14–27. doi: 10.1152/jn.1968.31.1.14. [DOI] [PubMed] [Google Scholar]
- Fagg AH, Hatsopoulos NG, de Lafuente V, Moxon KA, Nemati S, Rebesco JM, Romo R, Solla SA, Reimer J, Tkach D, Pohlmeyer EA, Miller LE. Biomimetic brain machine interfaces for the control of movement. J Neurosci. 2007;27:11842–11846. doi: 10.1523/JNEUROSCI.3516-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flint RD, Ethier C, Oby ER, Miller LE, Slutzky MW. Local field potentials allow accurate decoding of muscle activity. J Neurophysiol. 2012a;108:18–24. doi: 10.1152/jn.00832.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flint RD, Lindberg EW, Jordan LR, Miller LE, Slutzky MW. Accurate decoding of reaching movements from field potentials in the absence of spikes. J Neural Eng. 2012b;9 doi: 10.1088/1741-2560/9/4/046006. 046006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flint RD, Wright ZA, Scheid MR, Slutzky MW. Long term, stable brain machine interface performance using local field potentials and multiunit spikes. J Neural Eng. 2013:10. doi: 10.1088/1741-2560/10/5/056005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flint RD, Wang PT, Wright ZA, King CE, Krucoff MO, Schuele SU, Rosenow JM, Hsu FP, Liu CY, Lin JJ, Sazgar M, Millett DE, Shaw SJ, Nenadic Z, Do AH, Slutzky MW. Extracting kinetic information from human motor cortical signals. Neuroimage. 2014;101:695–703. doi: 10.1016/j.neuroimage.2014.07.049. [DOI] [PubMed] [Google Scholar]
- Fraser GW, Chase SM, Whitford A, Schwartz AB. Control of a brain–computer interface without spike sorting. J Neural Eng. 2009;6 doi: 10.1088/1741-2560/6/5/055004. 055004. [DOI] [PubMed] [Google Scholar]
- Ganguly K, Carmena JM. Emergence of a stable cortical map for neuroprosthetic control. PLoS Biol. 2009;7:e1000153. doi: 10.1371/journal.pbio.1000153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Georgopoulos AP, Kalaska JF, Caminiti R, Massey JT. On the relations between the direction of two-dimensional arm movements and cell discharge in primate motor cortex. J Neurosci. 1982;2:1527–1537. doi: 10.1523/JNEUROSCI.02-11-01527.1982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilja V, Nuyujukian P, Chestek CA, Cunningham JP, Yu BM, Fan JM, Churchland MM, Kaufman MT, Kao JC, Ryu SI, Shenoy KV. A high-performance neural prosthesis enabled by control algorithm design. Nat Neurosci. 2012;15:1752–1757. doi: 10.1038/nn.3265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hochberg LR, Serruya MD, Friehs GM, Mukand JA, Saleh M, Caplan AH, Branner A, Chen D, Penn RD, Donoghue JP. Neuronal ensemble control of prosthetic devices by a human with tetraplegia. Nature. 2006;442:164–171. doi: 10.1038/nature04970. [DOI] [PubMed] [Google Scholar]
- Jarosiewicz B, Chase SM, Fraser GW, Velliste M, Kass RE, Schwartz AB. Functional network reorganization during learning in a brain-computer interface paradigm. Proc Natl Acad Sci U S A. 2008;105:19486–19491. doi: 10.1073/pnas.0808113105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latash ML, Scholz JF, Danion F, Schöner G. Structure of motor variability in marginally redundant multifinger force production tasks. Exp Brain Res. 2001;141:153–165. doi: 10.1007/s002210100861. [DOI] [PubMed] [Google Scholar]
- Mandelblat-Cerf Y, Paz R, Vaadia E. Trial-to-trial variability of single cells in motor cortices is dynamically modified during visuomotor adaptation. J Neurosci. 2009;29:15053–15062. doi: 10.1523/JNEUROSCI.3011-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin V, Scholz JP, Schöner G. Redundancy, self-motion, and motor control. Neural Comput. 2009;21:1371–1414. doi: 10.1162/neco.2008.01-08-698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mehring C, Rickert J, Vaadia E, Cardosa de Oliveira S, Aertsen A, Rotter S. Inference of hand movements from local field potentials in monkey motor cortex. Nat Neurosci. 2003;6:1253–1254. doi: 10.1038/nn1158. [DOI] [PubMed] [Google Scholar]
- Moran DW, Schwartz AB. Motor cortical activity during drawing movements: population representation during spiral tracing. J Neurophysiol. 1999;82:2693–2704. doi: 10.1152/jn.1999.82.5.2693. [DOI] [PubMed] [Google Scholar]
- Mosier KM, Scheidt RA, Acosta S, Mussa-Ivaldi FA. Remapping hand movements in a novel geometrical environment. J Neurophysiol. 2005;94:4362–4372. doi: 10.1152/jn.00380.2005. [DOI] [PubMed] [Google Scholar]
- Nazarpour K, Barnard A, Jackson A. Flexible cortical control of task-specific muscle synergies. J Neurosci. 2012;32:12349–12360. doi: 10.1523/JNEUROSCI.5481-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nuyujukian P, Kao JC, Fan JM, Stavisky SD, Ryu SI, Shenoy KV. Performance sustaining intracortical neural prostheses. J Neural Eng. 2014;11 doi: 10.1088/1741-2560/11/6/066003. 066003. [DOI] [PubMed] [Google Scholar]
- Orsborn AL, Moorman HG, Overduin SA, Shanechi MM, Dimitrov DF, Carmena JM. Closed-loop decoder adaptation shapes neural plasticity for skillful neuroprosthetic control. Neuron. 2014;82:1380–1393. doi: 10.1016/j.neuron.2014.04.048. [DOI] [PubMed] [Google Scholar]
- Padoa-Schioppa C, Li CS, Bizzi E. Neuronal activity in the supplementary motor area of monkeys adapting to a new dynamic environment. J Neurophysiol. 2004;91:449–473. doi: 10.1152/jn.00876.2002. [DOI] [PubMed] [Google Scholar]
- Pandy MG, Zajac FE, Sim E, Levine WS. An optimal control model for maximum-height human jumping. J Biomech. 1990;23:1185–1198. doi: 10.1016/0021-9290(90)90376-E. [DOI] [PubMed] [Google Scholar]
- Perge JA, Zhang S, Malik WQ, Homer ML, Cash S, Friehs G, Eskandar EN, Donoghue JP, Hochberg LR. Reliability of directional information in unsorted spikes and local field potentials recorded in human motor cortex. J Neural Eng. 2014;11 doi: 10.1088/1741-2560/11/4/046007. 046007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pesaran B, Pezaris JS, Sahani M, Mitra PP, Andersen RA. Temporal structure in neuronal activity during working memory in macaque parietal cortex. Nat Neurosci. 2002;5:805–811. doi: 10.1038/nn890. [DOI] [PubMed] [Google Scholar]
- Pruszynski JA, Scott SH. Optimal feedback control and the long-latency stretch response. Exp Brain Res. 2012;218:341–359. doi: 10.1007/s00221-012-3041-8. [DOI] [PubMed] [Google Scholar]
- Rokni U, Richardson AG, Bizzi E, Seung HS. Motor learning with unstable neural representations. Neuron. 2007;54:653–666. doi: 10.1016/j.neuron.2007.04.030. [DOI] [PubMed] [Google Scholar]
- Sadtler PT, Quick KM, Golub MD, Chase SM, Ryu SI, Tyler-Kabara EC, Yu BM, Batista AP. Neural constraints on learning. Nature. 2014;512:423–426. doi: 10.1038/nature13665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schalk G, Kubánek J, Miller KJ, Anderson NR, Leuthardt EC, Ojemann JG, Limbrick D, Moran D, Gerhardt LA, Wolpaw JR. Decoding two-dimensional movement trajectories using electrocorticographic signals in humans. J Neural Eng. 2007;4:264–275. doi: 10.1088/1741-2560/4/3/012. [DOI] [PubMed] [Google Scholar]
- Scholz JP, Schöner G. The uncontrolled manifold concept: identifying control variables for a functional task. Exp Brain Res. 1999;126:289–306. doi: 10.1007/s002210050738. [DOI] [PubMed] [Google Scholar]
- Scott SH. Optimal feedback control and the neural basis of volitional motor control. Nat Rev Neurosci. 2004;5:532–546. doi: 10.1038/nrn1427. [DOI] [PubMed] [Google Scholar]
- Simeral JD, Kim SP, Black MJ, Donoghue JP, Hochberg LR. Neural control of cursor trajectory and click by a human with tetraplegia 1000 days after implant of an intracortical microelectrode array. J Neural Eng. 2011;8 doi: 10.1088/1741-2560/8/2/025027. 025027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slutzky MW, Jordan LR, Lindberg EW, Lindsay KE, Miller LE. Decoding the rat forelimb movement direction from epidural and intracortical field potentials. J Neural Eng. 2011;8 doi: 10.1088/1741-2560/8/3/036013. 036013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stark E, Abeles M. Predicting movement from multiunit activity. J Neurosci. 2007;27:8387–8394. doi: 10.1523/JNEUROSCI.1321-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stevenson IH, Cherian A, London BM, Sachs NA, Lindberg E, Reimer J, Slutzky MW, Hatsopoulos NG, Miller LE, Kording KP. Statistical assessment of the stability of neural movement representations. J Neurophysiol. 2011;106:764–774. doi: 10.1152/jn.00626.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Todorova S, Sadtler P, Batista A, Chase S, Ventura V. To sort or not to sort: the impact of spike-sorting on neural decoding performance. J Neural Eng. 2014;11 doi: 10.1088/1741-2560/11/5/056005. 056005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Todorov E. Optimality principles in sensorimotor control. Nat Neurosci. 2004;7:907–915. doi: 10.1038/nn1309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Todorov E, Jordan MI. Optimal feedback control as a theory of motor coordination. Nat Neurosci. 2002;5:1226–1235. doi: 10.1038/nn963. [DOI] [PubMed] [Google Scholar]
- Westwick DT, Pohlmeyer EA, Solla SA, Miller LE, Perreault EJ. Identification of multiple-input systems with highly coupled inputs: application to EMG prediction from multiple intracortical electrodes. Neural Comput. 2006;18:329–355. doi: 10.1162/089976606775093855. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhuang J, Truccolo W, Vargas-Irwin C, Donoghue JP. Decoding 3-D reach and grasp kinematics from high-frequency local field potentials in primate primary motor cortex. IEEE Trans Biomed Eng. 2010;57:1774–1784. doi: 10.1109/TBME.2010.2047015. [DOI] [PMC free article] [PubMed] [Google Scholar]