A review of trabecular bone functional adaptation: what have we learned from trabecular analyses in extant hominoids and what can we apply to fossils?

Abstract

Many of the unresolved debates in palaeoanthropology regarding evolution of particular locomotor or manipulative behaviours are founded in differing opinions about the functional significance of the preserved external fossil morphology. However, the plasticity of internal bone morphology, and particularly trabecular bone, allowing it to respond to mechanical loading during life means that it can reveal greater insight into how a bone or joint was used during an individual's lifetime. Analyses of trabecular bone have been commonplace for several decades in a human clinical context. In contrast, the study of trabecular bone as a method for reconstructing joint position, joint loading and ultimately behaviour in extant and fossil non‐human primates is comparatively new. Since the initial 2D studies in the late 1970s and 3D analyses in the 1990s, the utility of trabecular bone to reconstruct behaviour in primates has grown to incorporate experimental studies, expanded taxonomic samples and skeletal elements, and improved methodologies. However, this work, in conjunction with research on humans and non‐primate mammals, has also revealed the substantial complexity inherent in making functional inferences from variation in trabecular architecture. This review addresses the current understanding of trabecular bone functional adaptation, how it has been applied to hominoids, as well as other primates and, ultimately, how this can be used to better interpret fossil hominoid and hominin morphology. Because the fossil record constrains us to interpreting function largely from bony morphology alone, and typically from isolated bones, analyses of trabecular structure, ideally in conjunction with that of cortical structure and external morphology, can offer the best resource for reconstructing behaviour in the past.

Introduction

The goal of palaeoanthropologists, and palaeontologists in general, is to reconstruct behaviour in the past. The accuracy with which behaviour can be reconstructed has obvious implications for understanding the evolutionary history, environment, diet or phylogenetic relationships of past and present species. However, a primary problem when investigating fossil morphology is that one is limited by the functional inferences one can make from the preserved external morphology alone. The external shape of a bone largely reflects a genetic blueprint in the sense that, for example, a gorilla femur or metacarpal is distinct from those of a chimpanzee or a human. Furthermore, the similarities in external morphology shared among gorillas, chimpanzees and humans compared with other primates also reflect their shared phylogenetic history.

The external shape of a bone is also obviously functional. For example, the length and degree of curvature of long bones correlate well with habitual locomotor behaviours (e.g. quadrupedalism vs. suspension vs. bipedalism; Jungers et al. 1997; Fleagle, 2013). Furthermore, the shape and size of articular facets are strongly correlated with joint mobility (Ruff, 1988; Ruff & Runestad, 1992; Ruff et al. 1994; Currey, 2002). However, articular facets are also functionally and physiologically constrained by the need for congruence with articulating bones and the interdependence of all the components of a particular joint that allow it to function effectively (Ruff & Runestad, 1992; Lieberman et al. 2001; Currey, 2002). As such, the external size and shape of articular facets remain relatively constant throughout life (apart from pathological conditions; Ruff & Runestad, 1992; Lieberman et al. 2001). Other aspects of external bone shape are more malleable and can reflect differences in function during one's lifetime, such as variation in the position or robusticity of muscle attachments (Churchill & Morris, 1998; Hawkey, 1998; Eshed et al. 2004; Zumwalt, 2006), but the utility of such skeletal markers for inferring behaviour has been questioned (Eliot & Jungers, 2000; Djukic et al. 2015; Miszkiewicz et al. 2015; Rabey et al. 2015). In short, although external morphology provides a wealth of functional information, it encompasses both primitive and derived features influenced by both genetic and non‐genetic factors that can make it challenging to determine which aspects of external shape and size are functionally important for reconstructing the finer details of behaviour, particularly in fossils (Lieberman, 1997).

This confounding nature of external bony morphology has caused much debate among palaeoanthropologists regarding the behavioural reconstructions of many fossil hominoid (Madar et al. 2002; Susman, 2004; Moyà‐Solà et al. 2005; Begun & Kivell, 2011) and hominin taxa (Stern, 1975; Rose, 1991; Richmond & Strait, 2000; Dainton, 2001; Lovejoy, 2009; Wood & Harrison, 2011; Almécija et al. 2013). The clearest example of this debate is the over 40‐year‐long discussion about the degree of arboreality in Australopithecus afarensis (for review, see Ward, 2002, 2013; Niemitz, 2010 ). Some view the primitive features of external morphology as retentions from a more arboreal ancestor that were either in the process of being lost or were selectively neutral and, as such, were considered largely non‐functional and adaptively insignificant (Lovejoy et al. 1973; Latimer & Lovejoy, 1989). Other researchers aim to reconstruct behaviour as a whole and thus consider the primitive features as functionally useful with adaptive value retained under stabilizing selection (Stern, 1975; Rose, 1991; Stern & Susman, 1991). Palaeoanthropologists run into similar problems when interpreting the unusual morphology of Miocene apes like Oreopithecus (Moyà‐Solà et al. 2005; Susman, 2004) and Sivapithecus (Madar et al. 2002; Begun & Kivell, 2011), or the mosaic morphology of Australopithecus sediba (Berger et al. 2010; Kivell et al. 2011a; DeSilva et al. 2013) and Homo naledi (Berger et al. 2015; Kivell et al. 2015). Thus, fossilized morphology often leaves us questioning which features are functionally important for reconstructing behaviour and exactly how extinct taxa interacted with their environments.

Resolution of this debate requires a better understanding of aspects of bony morphology that are more sensitive to loading (i.e. force or stress) during life than external bone shape and size and, as such, can better reflect how a bone was used during an individual's lifetime (Ruff & Runestad, 1992; Lieberman, 1997). Analyses of internal bone structure – both the compact cortical shell and the spongy trabecular (also called cancellous) bone found underneath joints – can offer this functional insight (Fig. 1). There is a general consensus that all bone is initially formed via a genetic blueprint but, because bone remodels throughout life, it can adapt to the magnitude and direction of mechanical loading during one's lifetime (Martin et al. 1998; Carter & Beaupré, 2001; Currey, 2002). This is true for both external and internal bony morphology. However, variation in the internal cortical and trabecular structure reflects more directly how a joint or bone was used during life because it is more responsive to the predominant directions of mechanical stress (which cause strain in the bone; Lieberman, 1997; Ruff et al. 2006). Furthermore, it is argued here that trabecular structure in particular is especially informative for inferring function and behaviour in the past for several reasons.

Figure 1.

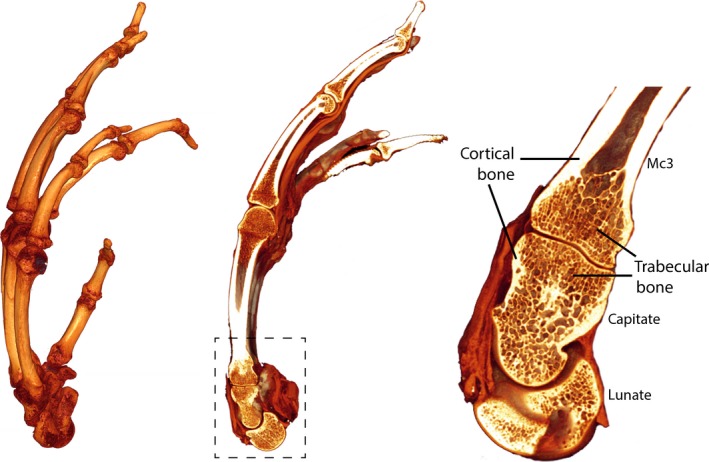
Trabecular and cortical bone structure in a chimpanzee hand. A 3D rendering from a micro‐CT scan of an extant chimpanzee hand (Pan troglodytes; left), a sagittal cross‐section through the third ray, revealing the internal bone structure (middle) with the area outlined in the dashed box blown up (right) to show the dense cortical shell and the trabecular meshy network inside. Note that trabeculae fill just the epiphyses of long bones, like the third metacarpal (Mc3), while short bones, like the capitate and lunate, are filled completely with trabeculae.

Trabecular bone is more porous than cortical bone. As such, trabecular bone has greater surface area and an increased number of bone cells that make it more metabolically active than densely‐packed cortical bone (Huiskes et al. 2000; Jacobs, 2000; Currey, 2002). Trabecular bone typically remodels at a faster rate than cortical bone; the annual turnover rate of trabecular bone is approximately 25% compared with only about 2–3% of cortical bone in adult humans (Eriksen, 1986, 2010). Therefore, it is generally accepted that trabecular bone is more responsive and malleable to variations in magnitude and direction of load throughout life than cortical bone and, as such, may more clearly reflect function (Jacobs, 2000; Carter & Beaupré, 2001; Rubin et al. 2001, 2002; but see Lovejoy et al. 2003 and below). In vivo experimental studies of trabecular remodelling show that the basic genetic blueprint of trabecular structure can be subsequently changed by variation in load and/or habitual activities of an individual (Biewener et al. 1996; Guldberg et al. 1997; Mittra et al. 2005; Pontzer et al. 2006; Chang et al. 2008; Polk et al. 2008; Barak et al. 2011; Harrison et al. 2011). These experimental studies are further supported by computational analyses modelling trabecular bone response to variation in load (Huiskes et al. 2000; Jacobs, 2000; Fox & Keaveny, 2001). Thus, quantifying how trabecular structure varies (e.g. trabecular bone volume or BV/TV, mean thickness or spacing of trabecular struts, degree of anisotropy) across individuals or species could reveal differences in how a particular joint or bone was used during an individual's lifetime. As such, variation in trabecular structure can hold more detailed functional information than can be gleaned from external morphology alone and, when trabeculae are preserved, can be particularly informative for reconstructing behaviour in extinct taxa.

The dynamic adaptability of trabecular bone can help shed new light on several challenges that inherently come with analyses of (often unusual and fragmentary) fossilized morphology and, in particular, the longstanding palaeoanthropological debates founded on differing functional interpretations of external morphology. For example, recent studies, reviewed in more detail below, using comparative and/or experimental analyses, have demonstrated the functional insight that can be gained from analyses of trabecular structure when applied to fossil hominin morphology (Barak et al. 2013b; Su et al. 2013; Skinner et al. 2015). A more precise insight into how bones and joints were loaded in extinct taxa can, in turn, provide a greater understanding of the functional significance (or lack thereof) of variation in their external morphology (Ryan & Ketcham, 2002b). The behavioural and mechanical flexibility (Wainwright et al. 2008) that characterizes extant primates means that external morphology does not always predict or reflect behaviour. This is particularly important for the numerous extinct Miocene and Pliocene taxa that are characterized by combinations of morphologies for which we have no good modern analogues (e.g. Sivapithecus, Ardipithecus ramidus, Australopithecus sediba). Furthermore, in fragmentary fossil specimens in which an epiphysis (and its underlying trabeculae) are preserved (e.g. a femoral head or distal ulna), more functional information can be gleaned about joint loading and potential behaviour than might be possible from just the external morphology alone. Trabecular analyses are non‐invasive and can provide additional functional insight that, in combination with cortical and external morphology, can allow one to make the most out of such rare finds (Fig. 1).

This paper will review what is known about trabecular bone's functional response to load, how this has been applied to primate taxa, with a focus on extant hominoids and, finally, how this information can be (and has been) used to infer behaviour in fossil hominoids and hominins. Ideally, reconstructions of behaviour from bone should incorporate both trabecular and cortical bone structure, in combination with functional analyses of external morphology. Although the underlying physiological processes responsible for modelling and remodelling of trabecular and cortical bone are generally the same (Eriksen, 2010), there are several insightful reviews on the complexity of cortical bone functional adaption (Lieberman, 1997; Pearson & Lieberman, 2004; Ruff et al. 2006; Judex & Carlson, 2009; Robling, 2009) and thus this will only be discussed briefly here.

The history of trabecular bone functional adaptation

The concept that the structure of bone (be that cortical or trabecular bone) can adapt over time to mechanical loading throughout life is commonly referred to as ‘Wolff's law’ (Wolff, 1892; Cowin, 2001; Pearson & Lieberman, 2004). However, Julius Wolff was not the first to recognize the correlation between bone structure and mechanical use. Nearly 50 years before Wolff, Julius Ward (1838) compared the distinct trabecular pattern of the human femoral neck to the support bracket of a street lamp, which is the origin of ‘Ward's triangle’ for the sparse triangular area of trabeculae within the ‘bracket’ (Fig. 2; Koch, 1917; Martin et al. 1998). In 1867, Georg Hermann von Meyer, a Swiss anatomist, was the first to recognize variation in trabecular orientation within different bones. When German engineer Karl Culmann saw von Meyer's trabecular illustrations, he noticed that the orientation of the trabecular struts within the human femoral neck was remarkably similar to the internal compressive and tensile stress lines of a crane (similar to a cantilevered beam) he was designing at the time (Fig. 2; Martin et al. 1998; Hammers, 2015). The collaboration between von Meyer and Culmann has been called the ‘first cooperation in the field of bone biomechanics’ (Roesler, 1987: 1029). However, it was Wolff that made the concept popular (Wolff, 1870, 1892), and his ‘trajectorial theory’ of how forces are distributed throughout bone was well accepted by many in the scientific community at the time (Jacobs, 2000; but see Roux, 1881).

Figure 2.

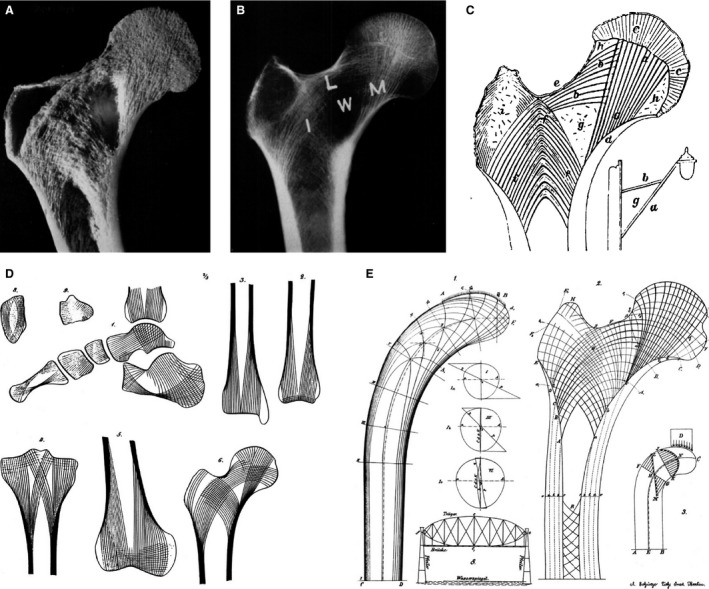
Historical description of trabecular bone functional adaptation. (A) Coronal cross‐section and (B) radiograph of a human proximal femur showing the distinct trabecular pattern related to bipedal loading. (C) Ward's (1838) drawing of the trabecular structure that he related structurally to the bracket street lamp post. The sparse area of trabeculae in the femoral neck is equivalent to the empty space within the bracket (‘g’), which is known as ‘Ward's triangle’ (W). (D) von Meyer's (1867) stylized illustrations of trabecular patterns in human bones. (E) Wolff's (1870) composite diagram including the compressive and tensile strain patterns in Culmann's cantilevered beam and ‘crane’ (left), and the similarity to the trabecular patter in the human proximal femur (right). Images (A–C) adapted from Garden (1961), and images (D and E) adapted from Skedros & Baucom (2007).

Wolff, however, considered there to be a static mathematical relationship between trabecular structure and stress trajectories, i.e. that they must be perpendicular to each other (Wolff, 1986; Jacobs, 2000; Hammers, 2015). Wolff also focused solely on adult structure, and made no reference to growth and development or processes that may have formed the ‘final’ adult structure, as he had no understanding of bone modelling and remodelling as we know them today (Townsley, 1948; Wolff, 1986; Martin et al. 1998; Pearson & Lieberman, 2004). Thus, Wolff's idea of how trabecular bone reflected mechanical loading was actually quite different from our current understanding that we still regularly subsume under the title ‘Wolff's law’. In fact, it was Roux (1881) that recognized that bone cells were capable of responding to local mechanical stresses and that organisms had the ability to adapt their bony structure to new environments. These two important principles are much more similar to the general understanding and use of Wolff's law today, so much so that many researchers have suggested that the more general version of Wolff's law be called ‘Roux's law’ instead (Cowin, 2001; for further historical review, see Roesler, 1987; Martin et al. 1998).

Although many have found fault in Wolff's specific mathematical explanation for how bone adapts to mechanical loads (Pauwels, 1980; Carter et al. 1989; Frost, 1990; Bertram & Swartz, 1991; Cowin, 2001; Lovejoy et al. 2003), the current, more general version of ‘Wolff's law’ is well accepted (Cowin, 2001; Currey, 2002; Ruff et al. 2006). Thus, given that Wolff himself did not fully recognize the potential dynamic adaptability of bone, more appropriate terms are the ‘mechanical adaptability hypothesis’ (Martin et al. 1998) or ‘bone functional adaptation’ (Roux, 1881; Cowin et al. 1985; Lanyon & Rubin, 1985; Ruff et al. 2006), the latter of which will be used from here on in.

Evidence of trabecular bone functional adaptation

The general functional role of trabecular bone is to provide strength and transfer external load away from the joint and toward the cortical bone (Currey, 2002; Barak et al. 2008). The relative amount of trabecular bone (BV/TV, sometimes also referred to as ‘density’) and its degree of alignment (i.e. anisotropy) are the most biomechanically informative aspects of trabecular architecture (Goldstein et al. 1993; Odgaard et al. 1997; van Rietbergen et al. 1998); 88% of trabecular stiffness (Young's modulus of elasticity) can be explained by BV/TV (Stauber et al. 2006), while an additional 10% can be explained by degree of anisotropy (Maquer et al. 2015). Indeed, Odgaard et al. (1997) demonstrated that the fabric (i.e. a characterization of the anisotropy) and mechanical (or elastic) principal directions are closely aligned. Thus, BV/TV and degree of anisotropy are among the most commonly quantified parameters in trabecular studies, often in concert with other variables that can provide more detailed information about variation in shape and size of the trabecular struts (Table 1; Odgaard, 1997, 2009). These descriptive variables, such as trabecular thickness or number, are quantified in an effort to better understand heterogeneity in trabecular strength and/or the optimization of its structure. However, little is known about the effect these descriptive parameters have on the mechanical properties of the trabecular structure as a whole. For example, the number of trabeculae is thought to have no importance (Gibson, 1985; Gibson & Ashby, 1997), while the interconnectedness (i.e. connectivity; Hodgskinson & Currey, 1990) or shape of the individual struts (plate‐ vs. rod‐shape; Liu et al. 2008) seem to play a more substantial mechanical role. In short, some descriptive parameters may be unimportant (Maquer et al. 2015), while others may be highly correlated with BV/TV and anisotropy, making their specific mechanical role challenging to identify (Hodgskinson & Currey, 1990; Goldstein et al. 1993).

Table 1.

Commonly used trabecular parameters

Parameter	Symbol (unit)	Description
Bone volume fraction	BV/TV	The proportion of trabecular bone voxels relative to the total number of voxels in a given region or volume of interest (VOI)
Degree of anisotropy	DA	DA describes the trabecular orientation in 3D space. Anisotropic structure has a preferred orientation to the trabecular struts, while isotropic structures show symmetry of the orientation in all directions. DA is usually calculated using the mean intercept length (MIL) algorithm (see Harrigan & Mann, 1984), where the eigenvectors give the main directions. DA is reported as a dimensionless value, with fully isotropic structure represented by 0 or 1, and higher values representing relatively more anisotropic structures
Trabecular thickness	Tb.Th (mm)	The mean thickness of the trabecular struts in a given region or VOI. This is typically measured via ‘sphere‐fitting’, i.e. by the diameter of spheres that can be fully contained within the structure
Trabecular separation	Tb. Sp (mm)	The mean width of the spaces between adjacent trabeculae in a given region or VOI
Trabecular number	Tb.N (mm−1)	The number of trabecular struts per mm. It is calculated as the inverse of the mean distance between the mid‐axes of the trabecular struts
Structure model index	SMI	SMI is a dimensionless measure of the relative proportion of plate‐like vs. rod‐like structures in a given region or VOI. Values typically range from 0 (idealised plates) to 3 (idealised rods), and can be positive or negative values. Negative values indicate a more concave or closed structure, like a honeycomb; positive values indicate a more convex and open structure
Connectivity density	Conn.D	The number of interconnected trabeculae per unit volume (Odgaard & Gundersen, 1993)
Trabecular bone pattern factor	Tb.Pf (mm−1)	A proxy measure of trabecular connectivity within a given region or VOI. Lower values indicate greater connectivity and structural integrity within the trabecular structure; higher values indicate greater fragmentation and the presence of isolated trabecular struts. It can also have positive (connected structures are more convex) or negative (connected structures are more concave) values and the basis of its calculation is similar to SMI (Hahn et al. 1992). Thus, changes in SMI and Tb.PF values are closely correlated. Importantly, Odgaard (1997) demonstrates that quantification of Tb.Pf in 2D is not representative of connnectivity in 3D
Bone surface density	BS/BV	The ratio of trabecular bone surface area relative to total trabecular bone volume in a given region or VOI

Regardless of the potential limitations of describing and quantifying trabecular structure, the concept that trabecular bone structure can adapt to its mechanical environment has been demonstrated by numerous empirical studies. Firstly, several comparative studies of primate trabecular bone across individuals or species have revealed variation in trabecular structure that fits well with predictions of differences in habitual mechanical loading during locomotion (Fajardo & Müller, 2001; Ryan & Ketcham, 2002a, 2005; Ryan & Shaw, 2012, 2015; Scherf et al. 2013; Tsegai et al. 2013; Matarazzo, 2015; but see below). Within humans, for example, more mobile, foraging populations show significantly greater BV/TV and thicker trabeculae in their proximal femur than that of less mobile, agricultural populations (Ryan & Shaw, 2015). The distinctive trabecular pattern of the adult proximal femur (Fig. 2) appears between the ages of 1 and 2 years, when human infants develop independent bipedal walking and the femur becomes weight‐bearing in a human‐like way (Townsley, 1948; Ryan & Krovitz, 2006; but see Cunningham & Black, 2009a,b). Raichlen et al. (2015) have recently followed on this study, suggesting that subtle changes in trabecular structure of the human distal tibia reflect the increased biomechanical stability during bipedalism that is gained between the ages of 1 and 8 years.

Secondly, several computational studies can explain the maintenance of a particular trabecular structure as optimal for the mechanical load it experiences (Levenston et al. 1994; Huiskes et al. 2000; Fox & Keaveny, 2001; Keaveny et al. 2001; Gupta et al. 2007). For example, in one of the first computer simulations of trabecular bone remodelling, Huiskes et al. (2000) showed that there is a balance in the metabolic process of bone resorption (osteoclasts) and bone formation (osteoblasts) that is governed by mechanical load. When mechanical load remained stable (i.e. homeostasis), remodelling continued without affecting the overall bone mass or structure. However, when the external load was rotated by 30 °, the main orientation of the trabeculae gradually reoriented as well to align with the external load and optimize mechanical strength. A 20% decrease or increase in the external loading reduced or increased trabecular bone mass by a comparable degree (15.8% and 17.5%, respectively). When the original homeostatic loading conditions were applied again, the trabecular structure and bone mass gradually returned to its original form (Huiskes et al. 2000).

Since the 1990s, finite element (FE) modelling has been used successfully in various ways to quantify and validate the mechanical properties and functional significance of trabecular bone (Hollister et al. 1994; van Rietbergen et al. 1995, 1999; Kabel et al. 1999; Ulrich et al. 1999; Homminga et al. 2004; Ryan & van Rietbergen, 2005; Nguyen et al. 2013, 2014). For example, Homminga et al. (2004) used micro‐FE modelling to show that osteoporotic human vertebrae were just as resistant to normal daily loading as healthy vertebrae. The osteoporotic trabeculae were more longitudinally oriented, compensating for the effects of bone loss and ensuring adequate stiffness for normal daily loading (although they were less resistant to non‐normal loads; Homminga et al. 2004).

Thirdly, and most convincingly, are in vivo experimental analyses that test directly trabecular bone functional adaptation (Lanyon, 1974; Skerry & Lanyon, 1995; Biewener et al. 1996; Mittra et al. 2005; Pontzer et al. 2006; Chang et al. 2008; Polk et al. 2008; Barak et al. 2011; Harrison et al. 2011). Many of the initial experimental studies focused on the mammalian calcaneus due to its predictable loading environment (Lanyon, 1973, 1974; Skerry & Lanyon, 1995; Biewener et al. 1996; Skedros et al. 2004, 2012; Sinclair et al. 2013). In mammals in which the calcaneus does not touch the ground during locomotion, it experiences a regular cantilever‐like loading (i.e. bending) from the Achilles tendon during ankle extension. These studies found that the trabeculae underlying the Achilles tendon attachment were aligned with the compressive (and tensile) principal direction of stress (Lanyon, 1974; Biewener et al. 1996). Furthermore, after 8 weeks of disuse (in individuals in which the Achilles tendon was detached from the calcaneus), there was a reduction in BV/TV, trabecular thickness and number (although the orientation did not change) that reflected the absence of an external load (Biewener et al. 1996).

More recent in vivo studies have expanded on this work to test how variation in the direction and magnitude of the external load affect trabecular structure (Pontzer et al. 2006; Chang et al. 2008; Barak et al. 2011; Harrison et al. 2011). For example, Barak et al. (2011) showed that trabecular orientation varied predictably in the hindlimb joints of sheep that were loaded differently through daily exercise on level and inclined treadmills. The inclined sheep had a more extended ankle joint by 3.6 ° at midstance (i.e. at peak ground reaction force). After roughly 1 month, these sheep showed a change in trabecular orientation 2.7–4.3 ° in the distal tibia, corresponding closely with the change in the orientation of the external load at the ankle. In contrast, the carpal joint remained at a stable orientation in both groups and there were no significant differences in the trabecular orientation in the distal radius. Thus, even small changes in joint angle can be reflected in the trabecular structure. Pontzer et al. (2006) also found a strong correspondence between changes in the orientation of external joint loading of the knee and trabecular orientation of the distal femur in guinea fowl.

Similar results have also been found in in vivo studies of humans. Elite athletes whom engage in sports that cause irregular‐impact loading of the femur (i.e. forces from high acceleration/deceleration and from varied directions, such as during soccer or squash), showed approximately 10% higher trabecular bone density (i.e. bone mineral density quantified in vivo via magnetic resonance imaging), compared with elite athletes who engaged in sports of high‐magnitude but primarily vertical loading (e.g. power‐lifting), and 20% higher than non‐athletes (Harrison et al. 2011). Trabecular bone mass (i.e. increased BV/TV and trabecular number, decreased trabecular spacing) was also higher in the knee in both gymnasts (Modlesky et al. 2008a) and Olympic fencers (Chang et al. 2008) compared with the respective control groups. Conversely, trabecular bone structure has been shown to be severely underdeveloped in children with cerebral palsy (Modlesky et al. 2008b), and to decrease in non‐gravitational environments (Jee et al. 1983; Bikle & Halloran, 1999).

Altogether, there is a large body of empirical evidence across a variety of different animals from the last several decades supporting trabecular bone functional adaptation. Trabecular bone structure is clearly capable of responding during life, often within a relatively short period of time, to the magnitude and direction of load (or unloading). However, there is still much that we do not understand about trabecular bone, including the genetic and developmental role in shaping trabecular architecture, if and how trabecular bone might respond differently to variation in the duration, frequency or magnitude of the external load, or how all of these factors might vary depending on the species, age, anatomical region or differences in body mass. All of these factors can confound our interpretations of joint loading and bone function from trabecular structure in extant and, particularly, fossil taxa.

The complexity of trabecular bone functional adaptation

Despite the evidence described above, there are also several empirical studies that have found that trabecular bone does not respond to mechanical stimuli in ways that one might predict. For example, Carlson et al. (2008) conducted an experimental analysis on mice to see how trabecular structure varied in the distal femur with differences in locomotion during growth. They had three groups of mice: (i) a free‐ranging control group; (ii) a ‘linear’ group, which were encouraged to travel through a straight tube; and (iii) a ‘turning’ group, in which the mice moved through a twisting tube. Despite their predictions that there should be variation in external load on the femur in the ‘linear’ vs. ‘turning’ mice, the trabecular structure did not significantly differ between the two groups. Furthermore, the ‘free‐ranging’ control mice had significantly higher BV/TV than the exercised linear/turning mouse groups, which was also counterintuitive (Carlson et al. 2008). These results highlight some of the complexity of trabecular bone functional adaptation and the challenges of testing hypotheses in living animals. For example, the Carlson et al. (2008) results may suggest that the free‐ranging mice were actually more active than the ‘linear/turning’ mice, or that the trabecular structure of such small animals scales differently (Barak et al. 2013a,b; Christen et al. 2015) or experiences less strain (and thus there is less response) than that of larger animals (Biewener, 1990), especially when the cortical bone has responded to the changes in midshaft loading (Carlson & Judex, 2007), or reflect differences in bone modelling and remodelling based on anatomical location (Bass et al. 1999; Morgan & Keaveny, 2001; Morgan et al. 2003; Yeni et al. 2011; Räth et al. 2013) or species (Chow et al. 1993; Erben, 1996; Turner, 2001; Barak et al. 2013a). Below, some of the complicating factors that suggest trabecular bone functional adaptation is not as straightforward as functional morphologists might wish it to be are discussed.

When, how and to what kind of load does trabecular bone respond?

There is ongoing debate regarding what kind of external load trabecular bone is most responsive to. Is it primarily loading from muscles (i.e. contractile forces) or gravitational loading (i.e. substrate reaction forces; for review, see Robling, 2009; Judex & Carlson, 2009, respectively)? Is there a minimum magnitude of loading that is required to stimulate bone growth and remodelling (Frost, 1987)? Is trabecular structure reflecting more frequent but low‐magnitude loading, or rare but high‐magnitude loading? How much does adult trabecular structure reflect loading that occurred during earlier development when bone was still growing? There are several studies that have tried to address these issues and have yielded conflicting results (for review, see Bertram & Swartz, 1991).

Many of the in vivo experiments described above (Pontzer et al. 2006; Carlson et al. 2008; Barak et al. 2011) are conducted on juvenile animals because bone is both actively modelling and remodelling during this time, and is considered to be more responsive to mechanical stimuli than adult bone (Pearson & Lieberman, 2004). Indeed, Pettersson et al. (2010) found that variation in physical activity during growth (i.e. childhood and adolescence) was the strongest predictor for differences in adult trabecular bone density (i.e. bone mineral density) in the calcaneus of a large sample of men. Thus, this work highlights how activity during growth can have a lasting effect on trabecular structure later in life, even in inactive adults (Pettersson et al. 2010; but see Karlsson et al. 2000).

However, trabecular bone modelling and remodelling throughout ontogeny are influenced by a number of factors, such as the underlying genetic patterning (Cunningham & Black, 2009a,b), vascular patterning and the positioning of growth plates (Cunningham & Black, 2010), changes in hormone levels (Simkin et al. 1987; Karlsson et al. 2001; Yeni et al. 2011), and variation in cellular processes and constraints on bone design, that go beyond the scope of this paper (for review, see Lieberman, 1997). In early ontogeny, several studies have demonstrated that trabecular bone (and bone in general) follows particular patterns of growth during the modelling and remodelling process. For example, in a sample of healthy human children and adults, Parfitt et al. (2000) found that trabecular bone in the ilium (analysed via biopsy) formed with a roughly uniform trabecular number that was retained throughout life in healthy individuals (e.g. without osteopenia). In other words, between the ages of 1.5 and 23 years, there was an increase in BV/TV and trabecular thickness, but trabecular number did not change (Parfitt et al. 2000). In addition, during early ontogeny BV/TV and trabecular thickness tend to increase first, during periods of more dramatic increases in body mass, while trabecular orientation (i.e. anisotropy) is adapted later in development (Parfitt et al. 2000; Tanck et al. 2001). For example, in humans, trabecular structure of the femur and tibia reaches an adult‐like pattern (BV/TV, anisotropy) at approximately 8 years old (Ryan & Krovitz, 2006; Gosman & Ketcham, 2009; Raichlen et al. 2015). The same ontogenetic pattern is found in the trabecular structure of human vertebrae (Roschger et al. 2001). Thus, overall trabecular architecture appears to be optimized later in life (Huiskes et al. 2000; Nafei et al. 2000; Tanck et al. 2001; Ryan & Krovitz, 2006; Cunningham & Black, 2009a).

However, this does not imply that adult trabecular bone is not also capable of responding and adapting to changes in external load. To the contrary, several in vivo experimental studies have been conducted on adult animals demonstrating changes in trabecular structure in response to variation in mechanical stress (Smith et al. 1989; Biewener et al. 1996; Rubin et al. 2001, 2002). Trabecular structure can respond to increased load even late in life, such as in postmenopausal women (Simkin et al. 1987; Smith et al. 1989) or, conversely, resorbing with removal of load, such as in quadriplegics (Frey‐Rindova et al. 2000). However, adult trabecular structure seems to respond to external mechanical stimuli in different ways than during earlier ontogeny. Saparin et al. (2011) noted that in areas of higher loading in the adult primate femoral neck, BV/TV was higher due to increased trabecular thickness, while trabecular number did not change. In contrast, in areas of lower loading, BV/TV was lower due to a reduction in trabecular number, but trabecular thickness remained constant (Saparin et al. 2011; see also Rubin et al. 2001, 2002; Shaw & Ryan, 2012). The latter result is contrary to the finding that trabecular number remains uniform throughout life (Parfitt et al. 2000). However, Saparin et al. (2011) suggest that in areas of lower loading, reducing trabecular number is ‘safer’ than reducing trabecular thickness because of risk that resorption during remodelling will weaken or sever a trabecula, thus making it non‐functional (Skedros et al. 2012). Instead, the reduction in trabecular number is not random, but is associated with increased anisotropy, thus preferentially removing specific and mechanically unnecessary trabeculae (Saparin et al. 2011; Skedros et al. 2012). This hypothesis is also consistent with the in vivo experimental results of Biewener et al. (1996).

There also appears to be a minimum load (either in magnitude, frequency and/or duration) that is required to stimulate trabecular bone remodelling. Frost's (1987) ‘mechanostat’ hypothesis puts forth strain thresholds for bony response: strains below 100–300 microstrain (με) elicit remodelling of trabecular (and cortical) bone, while much higher strains (1500–3000 με) stimulate bone modelling to increase cortical bone mass (Burr, 1985; Rubin & Lanyon, 1985). However, the duration of the strain (or external stress) is also important. For example, Skerry & Lanyon (1995) immobilized the calcaneus in several sheep, reducing the external load significantly. In a subset of these sheep, the immobilization device was removed and they were allowed to walk on the treadmill for 20 min/day. Even though the strain experienced by the calcaneus during this short time was ‘normal’ (Lanyon, 1973, 1974) and supposedly enough to stimulate trabecular remodelling (147 με), after 12 weeks both groups of sheep showed the same degree of trabecular bone loss in the calcaneus. This result suggests that the magnitude and/or duration of load experienced during the short periods of walking were not sufficient to reduce the degree of trabecular bone loss due to immobilization. Barak et al. (2011) found a similar result; loading during ‘normal’ activity in non‐exercised sheep wearing shoes that altered their ankle joint angle was not enough to stimulate the reorientation of the trabecular alignment that was found in exercised sheep. In an experimental study on mice, Lambers et al. (2013) found that it required 10 weeks for trabecular bone (quantified as BV/TV and bone stiffness) within the vertebrae to ‘fully adapt’ to a new increased external load (applied at a high frequency for 5 min, three times/week). The BV/TV and stiffness values remained the same after 10 weeks, and the remodelling rates returned to those of the control group by this time as well (Lambers et al. 2013). Such studies suggest that bone functional adaptation requires both a minimum magnitude and duration of loading to affect trabecular growth and remodelling (Rubin & Lanyon, 1985; Skerry & Lanyon, 1995; Biewener et al. 1996; Barak et al. 2011), but determining what these minimum thresholds are, in particular skeletal elements or particular species, especially in primates, is challenging.

That being said, many experimental studies (Simkin et al. 1989; Smith et al. 1989; Bassey & Ramsdale, 1994), including several discussed above (Pontzer et al. 2006; Barak et al. 2011; Lambers et al. 2013), have shown that relatively short periods of external loading can, sometimes dramatically, affect changes in trabecular structure if the orientation or magnitude is ‘unusual’ compared with that of normal daily activity. Thus, bone adaptation may be driven by an animal's most infrequent but dynamic behaviours, rather than habitual loading (Burr, 1990). If so, this has important implications for interpreting function and behaviour from trabecular structure in fossils. If only 10 or 15 min/day [as was the case in Pontzer et al. (2006) and Barak et al. (2011), respectively] of loading from a particular ‘unusual’ behaviour is enough to significantly alter trabecular structure, what can we infer about the overall locomotor behaviour of a fossil hominoid or hominin? Might the trabecular structure primarily retain a functional signal for those behaviours that loaded the skeleton in relatively rare and unusual ways, overriding the functional signal of the most common daily behaviours?

Rubin et al. (2001, 2002) tested this hypothesis specifically; is bone functional adaptation dependent on peak skeletal stress or can very low‐level stress during less vigorous but much more frequent activities (e.g. standing) influence trabecular bone structure? In an experiment with adult sheep, they constrained some individuals and exposed their hindlimbs to extremely low‐level (0.3 g) external loads at a high frequency (30 Hz) using an oscillation plate for 20 min/day for 1 year. These sheep showed a 34.2% increase in the trabecular bone density (decreasing trabecular spacing by 36.1% and increasing trabecular number by 45.6%) compared with the control group. Furthermore, there was no significant difference in cortical structure in any of the hind‐ or forelimb bones, demonstrating that trabecular bone is more responsive to low‐magnitude but high‐frequency loading than the cortex [Rubin et al. 2001, 2002; but see Carlson & Judex, 2007; Carlson et al. 2008 for the opposite results]. These results suggest that very low‐level external loading during habitual activities can be a determining factor of the overall trabecular pattern.

Trabecular bone and body mass

The relationship between variation in trabecular structure and body mass has been recently well studied in primates (Scherf, 2008; Cotter et al. 2009; Hernandez et al. 2009; Fajardo et al. 2013; Ryan & Shaw, 2013), and across a wider variety of mammals and birds (Swartz et al. 1998; Doube et al. 2011; Barak et al. 2013a; Christen et al. 2015). Generally, larger primates (and mammals) have absolutely thicker and more widely‐spaced trabeculae but, relative to body mass, their trabecular struts are thinner and more tightly packed (Swartz et al. 1998; Doube et al. 2011; Barak et al. 2013a; Ryan & Shaw, 2013; Fig. 3). In other words, these aspects of trabecular structure scale with negative allometry across primates and mammals (but not within a particular taxon). In fact, the trabeculae of a whale are not much wider or more widely spaced than that of a human (Odgaard et al. 1997). In contrast, BV/TV scales with weak positive allometry while the degree of trabecular anisotropy shows no significant relationship with body mass (Doube et al. 2011; Barak et al. 2013a; Ryan & Shaw, 2013; but see Fajardo et al. 2013). However, scaling of specific trabecular parameters with body mass does seem to vary depending on bone (e.g. femur vs. vertebra) and taxonomic group (e.g. hominoids vs. strepsirrhines; Cotter et al. 2009; Fajardo et al. 2013; Ryan & Shaw, 2013).

Figure 3.

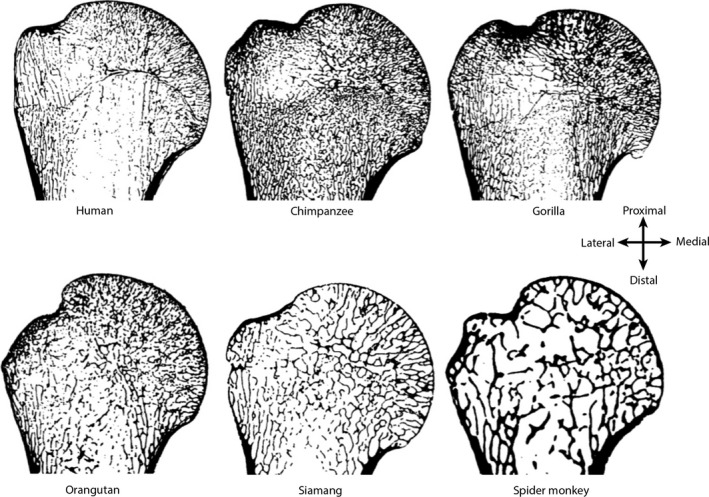
Trabecular bone in the primate humerus. Coronal cross‐section of the proximal humerus showing variation in trabecular structure, particularly in relation to body size. All humeri are scaled to approximately the same size. Note that the trabeculae in larger‐bodied primates (e.g. chimpanzee, gorilla and orangutan) tends to be thinner and more densely‐packed compared with smaller‐bodied primates (siamang and spider monkey), which have relatively thicker trabeculae that are more spaced out. Humans are unique in having thin and somewhat densely‐packed trabeculae, but have a comparatively low trabecular bone volume (BV/TV) compared with other great apes.

The relationship between trabecular structure and body mass suggests that there are a number of constraining metabolic and biomechanical factors that govern trabecular architecture in general. Swartz et al. (1998) proposed that relative differences in trabecular structure between small and large animals may be driven by requirements to maintain an adequate surface area for the release and deposition of calcium (Kerschnitzki et al. 2013). Furthermore, trabecular thickness is constrained by the size of the regions that can be effectively regulated by osteocytes (Mullender & Huiskes, 1995; Mullender et al. 1996; Cowin, 2001; Christen et al. 2015). For example, there appears to be a minimum trabecular thickness, regardless of how small the animal, because the lacunae created by osteoclasts are about 30–60 μm in depth (Eriksen et al. 1985; Cowin, 2001; McNamara et al. 2006; Mulvihill et al. 2008; Eriksen, 2010). Trabeculae any thinner than this would simply be cut in two with remodelling, and thus would not be functional (Barak et al. 2013a). Conversely, there also appears to be a maximum trabecular thickness (i.e. approximately 460 μm; Lozupone, 1985; Lozupone & Favia, 1990) that allows for optimal positioning of the osteocytes relative to bone surface while also maintaining the necessary biomechanical strength (i.e. stiffness; Ryan & Shaw, 2013). Indeed, Christen et al. (2015) recently demonstrated via computer modelling that the underlying mechanism for negative allometric trabecular bone scaling in terrestrial mammals may be variation in osteocyte density and the distance an osteocyte signal can travel towards osteoblasts at the bone surface (i.e. influence distance).

Larger animals experience relatively higher skeletal loading than smaller animals (Biewener, 1989, 1990). Given the metabolic constraints on trabecular size outlined above, the trabecular structure of larger animals must mitigate these increased loads in other ways. For example, they can alter other aspects of trabecular structure, such as increasing the BV/TV or trabecular anisotropy, or changing the shape of trabecular struts (i.e. plates vs. rods; Ryan & Shaw, 2013). It is also important to remember that trabeculae do not exist independently but within bones, such that larger animals may adapt the cortical distribution instead, highlighting the importance of studying both trabecular and cortical structure together (see below). Finally, it is also well documented that larger animals alter their locomotor kinematics [e.g. more extended limb postures (Biewener, 1983, 1989) or complaint gaits (Schmitt, 1999; Polk, 2002)], which would reduce joint loading and, ultimately, strain on the trabecular structure. Such metabolic and biomechanical constraints should be considered when interpreting function from trabecular bone, especially in comparative analyses of extant and fossil primates that vary greatly in body size.

Systemic skeletal patterns of trabecular bone

A well‐known experimental study by Lieberman (1996) investigated the potential reasons for variation in cranial vault thickness across hominins. Although this study investigated cortical bone only, the results raise an important and potentially confounding issue with regards to making functional inferences from internal bony morphology: a systemic response of bone throughout the skeleton. Lieberman (1996) had young pigs run on a treadmill for 60 min/day for 3 months and compared their cortical structure with that of controls (confined to walking in a small pen all day). Predictably, the exercised pigs had significantly higher cortical thickness in their limb bones compared with that of the controls. However, they also had significantly thicker (28%) cranial vault bones, as well as thicker cortex in the caudal vertebrae and the last and penultimate ribs, neither of which are weight‐bearing during locomotion or would indirectly incur higher external loading from running (Lieberman, 1996). Similar systemic patterns have been found in non‐weight‐bearing skeletal elements (e.g. mandible) in rats when external loads are reduced (e.g. absence of gravity; Simmons et al. 1983). Thus, these results make a strong argument for systemic adaptations of bone that are unrelated to load.

However, trabecular bone functional adaption appears to be more localized than that of cortical bone (Rubin et al. 2001, 2002; Judex et al. 2004; Barak et al. 2011). For example, in the sheep experiment by Rubin et al. (2001, 2002) described above, the externally loaded hindlimb bones showed increased trabecular bone mass, but the radius (which did not experience the low‐magnitude, high‐frequency oscillations) did not. Judex et al. (2004) have shown in different genetic strains of inbred mice that changes in trabecular bone due to disuse varied not only across the mouse groups, but also varied depending on anatomical location (more so than changes in cortical bone).

That being said, this does not mean that there are not underlying systemic and genetic factors that must be considered in functional analyses of trabecular structure. All bone growth is mediated by hormones at both localized and systemic levels (Lieberman, 1996). Studies have found that certain aspects of trabecular structure, primarily BV/TV and its mechanical properties (i.e. Young's modulus), are strongly influenced by genetics in baboons (Havill et al. 2010) and rodents (Alam et al. 2005). Furthermore, there appear to be systemic patterns in trabecular bone density or BV/TV that are consistent throughout several skeletal elements within a particular taxon and that are distinctive across different primate taxa (Chirchir et al. 2015). For example, compared with other extant primates and fossil hominins, modern humans may have recently evolved a remarkably low trabecular bone density throughout the epiphyses of both the upper limbs and, counterintuitively, the weight‐bearing lower limbs as well (Chirchir et al. 2015; but see Ryan & Shaw, 2015). Independent analyses of trabecular structure across extant hominoids have revealed that there are consistent differences in BV/TV in several elements of the skeleton, with Pan, and particularly bonobos, having especially high BV/TV in the metacarpals (Tsegai et al. 2013), humerus (Davenport, 2013), manual phalanges and talus (TL Kivell, unpublished data) compared with Gorilla and Pongo, and much higher than humans (Maga et al. 2006; Cotter et al. 2009; Hernandez et al. 2009; Griffin et al. 2010; Ryan & Shaw, 2012; Scherf et al. 2013). Thus, there appears to be an underlying blueprint of trabecular structure that is systemic throughout the skeleton, at least in some taxa, which is not fully understood. Such systemic patterns could bias functional inferences when only one anatomical element is being investigated, which is often the case in trabecular studies (Maga et al. 2006; DeSilva & Devlin, 2012; Su et al. 2013; Ryan & Shaw, 2015).

Lovejoy et al. (2003) take a more extreme view. They critique the concept of ‘Wolff's law’ [referring to the strict version of this concept (i.e. that the bones’ response is based on mathematical laws), rather than the more generalized version accepted by most researchers today] from a genetic and developmental perspective, suggesting that the structure and distribution of bone (both trabecular and cortical) reflects primarily the expression of positional information from mesenchymal cells during early growth. While the material properties and maintenance of bone structure can also be influenced by localized strain, this process is relatively minor compared with the genetic and development underpinnings of bone morphology, particularly in adults (Lovejoy et al. 2003). In other words, ‘bones of the … skeleton are almost entirely determined by the PI (positional information) of their original cartilage anlagen’ (Lovejoy et al. 2003: 96). Their view has some empirical support; Skedros et al. (2004) found that the characteristic arched trabecular pattern of the adult deer calcaneus, which is ideal for resisting bending stress, is already present in the calcanei of foetal deer. Cunningham & Black (2009a,b) also found correspondence between the trabecular pattern of the human newborn ilium (i.e. prior to weight‐bearing bipedalism) and the distinctive pattern found in adults. However, the position of Lovejoy et al. (2003) generally runs counter to the vast experimental literature showing bone's response to variation in load, even in adults. The value of their critique is the recognition of the significant genetic role in establishing and constraining (at least to some degree) bony morphology and that we still have much to learn about the mechanosensory mechanisms of bone in general.

Bone functional adaptation is not sufficient (but is all we have)

The numerous influences on how bone may (or may not) respond and adapt to mechanical stimuli discussed above demonstrate the complexity of drawing functional inferences from bone structure. In addition, Hall (1985) cautioned: ‘Theoretical approaches which treat bones as idealized, isolated units … simply fall short of reality. A particular bone's response to altered mechanical stress might be compromised by the simultaneous response of the attached muscles or connective tissue … by altered blood flow, by associated mineral requirements, etc. ’ (Hall, 1985: xxvi–xxvii). Thus, in analyses of trabecular bone structure, one should ideally consider the broader context of cortical bone (both its external and internal morphology), the muscles and connective tissues acting on the bone, and the articulating bones and joints that together provide the environment in which bone may respond to mechanical stimuli.

The human femoral neck is a particularly good example of the increased biomechanical understanding one can gain when trabecular bone is not investigated in isolation. Trabecular bone density in the femoral neck has an upper threshold due to weight constraints and limitations on energy absorption and haematopoietic function (Gibson & Ashby, 1997; Currey, 2002). However, there is also a lower threshold of trabecular bone density, clearly demonstrated by increased risk of fracture when trabecular stiffness is reduced (Lotz et al. 1995; Fox & Keaveny, 2001). There are kinematic limitations on the cortical thickness and maximum neck diameter that ensure the necessary range of motion at the hip joint (Fox & Keaveny, 2001). Therefore, trabecular bone in the human femoral neck is among the stiffest in the human skeleton, capable of coping with the significantly higher compressive strain compared with the proximal tibia, vertebrae and femoral trochanter (Morgan & Keaveny, 2001; Morgan et al. 2003; also see Amling et al. 1996) and carry approximately 50% of the compressive load at midneck (Lotz et al. 1995).

However, in the world of palaeontology, we are limited to the information that is preserved in the fossil record. Associated or articulated skeletal remains are rare within palaeoanthropology (Napier & Davis, 1959; Moyà‐Solà & Köhler, 1996; White et al. 2009; Berger et al. 2010, 2015), and information regarding soft tissues, metabolism or genetics is at best ambiguous and usually absent. Thus, contrary to Hall's valid caveat, palaeontologists are generally forced to treat bones as isolated units. To move forward with any inferences about behaviour in the past, we must assume that there is at least some correlation between bone form and function, that bone responds to external load by minimizing bone mass and risk of fracture, while simultaneously optimizing stiffness, even if we are not exactly sure if this is true or how it works (Martin et al. 1998). Because trabecular bone appears to be particularly sensitive to mechanical stimuli during life, it can provide greater insight into bone and joint function, and ultimately behaviour, than analyses of external morphology alone.

What we already know about primate trabecular bone

The overwhelming majority of studies on trabecular bone morphology are on humans, usually within the context of better understanding osteopenia and osteoporosis (Eriksen, 1986; Simkin et al. 1987; Smith et al. 1989; Dempster, 2000). Living or cadaveric/osteological human samples are abundant, come with ethical consent and can be studied via radiography, such as dual‐energy X‐ray absorptiometry (DEXA) or peripheral quantitative computed tomography (pQCT) that can measure bone mineral density with relatively minimal effort. However, non‐human primate osteological samples are much more rare, and the use of radiography on living individuals is usually ethically and logistically unfeasible. Thus, much less is known about trabecular bone in non‐human primates. Pauwels (1948), Kummer (1966, 1972) and Oxnard (1972, 1982, 1993) pioneered new 2D methods for assessing stress trajectories in relation to trabecular structure, focusing primarily on human vertebrae or ilia but often within a broader, comparative and/or evolutionary context. Some of the first 2D studies of trabecular morphology in non‐human primates were on the femur and vertebrae of a rhesus macaque (Beddoe, 1978), and talus and calcaneus of two sympatric species of lemur (Ward & Sussman, 1979). It was not until much later that Rafferty (1996; Rafferty & Ruff, 1994) conducted the first extensive comparative 2D trabecular analysis, looking at the humerus and femur in a large sample of prosimian and anthropoid primates.

However, 2D analyses provide only a single image of trabecular structure within an entire epiphysis or bone, and thus are limited in what can be inferred with regards to trabecular architecture and ultimately function. If one wishes to investigate trabecular structure in 3D in any extant or fossil primate, access to high‐resolution (e.g. voxel size of ~30 μm) micro‐CT is required. The resolution limits of medical CT (e.g. ~200 μm) are usually greater than the thickness of individual trabeculae and thus cannot reliably reproduce trabecular architecture (for a review of technological limitations, see Scherf, 2008). Limited access to micro‐CT and the time‐consuming and costly nature of dealing with large 3D data sets were the main limitations on 3D analyses of trabecular bone in non‐human primates. Furthermore, when it comes to fossils, one can only study trabecular structure if the trabeculae themselves are sufficiently preserved.

Fajardo & Müller (2001) conducted one of the first 3D analyses of non‐human hominoid trabecular bone using micro‐CT. They investigated how differences in trabecular morphology of the proximal humerus and femur varied with arboreal and terrestrial locomotor behaviour in one gibbon, spider monkey, rhesus macaque and baboon. Fajardo & Müller (2001) found that variation in the degree of anisotropy correlated with locomotor differences in a predictable way: the more arboreal gibbon and spider monkey, which presumably have more variable loading of their humerus and femur, had more isotropic (i.e. less aligned) trabecular structure than the macaque and baboon with more stereotypical loading at the shoulder and hip. This research also laid important groundwork for investigating trabecular bone across different species that can vary greatly in morphology and body size; in particular, the challenges associated with making sure one is comparing homologous trabecular morphology with regards to anatomical location and amount of trabeculae being quantified [i.e. size and location of a volume of interest (VOI); Fajardo & Müller, 2001; Kivell et al. 2011a,b; Lazenby et al. 2011].

However, Fajardo et al. (2007) conducted a more extensive analysis of trabecular structure in the proximal femur (superior and inferior femoral neck) on a larger primate sample that contradicted the results of their previous study (Fajardo & Müller, 2001). They did not find a clear correlation between variation in trabecular structure and differences in locomotor behaviour. Instead, they found a high degree of overlap in trabecular parameters (including, among others, BV/TV and degree of anisotropy) across quadrupedal (Colobus, Macaca, Papio) and climbing/suspensory (Ateles, Symphalangus, Alouatta) taxa. Despite the addition of potential inherent differences in body size and phylogeny across the sample, ‘taxa in this study share more similarities in femoral neck trabecular structure than differences and these similarities belie any correlation of structure with locomotor mode’ (Fajardo et al. 2007: 431). They suggested that there may be greater similarity in hip joint loading across quadrupedal and climbing/suspensory primates than previously considered and/or that current models of anthropoid hip joint mechanics are overly simplistic.

The absence of a clear correlation between trabecular structure and predicted loading differences based on locomotor behaviour found by Fajardo et al. (2007) is just one of many studies on extant primates, or hominoids specifically, that have yielded equivocal results (Viola, 2002; Maga et al. 2006; Scherf, 2007, 2008; Cotter et al. 2009; Ryan et al. 2010; Ryan & Walker, 2010; DeSilva & Devlin, 2012; Shaw & Ryan, 2012; Schilling et al. 2014). For example, Ryan & Walker (2010) investigated variation in proximal humeral and femoral trabecular structure in relation to relative differences in forelimb and hindlimb use across five anthropoid primates. Despite predictions of higher loading of the humerus in brachiators (Symphalangus), higher loading of the femur in climbing arboreal quadrupeds (Pan and Alouatta) and equal loading of both limbs in terrestrial quadrupeds (Papio and Presbytis), all taxa had significantly higher BV/TV in the femur and greater isotropy in the humerus (see also Shaw & Ryan, 2012). Thus, similar to the findings of Fajardo et al. (2007), these results also suggest broad similarities in trabecular bone structure of the humerus and femur across anthropoid primates.

Although most trabecular studies to date have focused on the proximal humerus and femur (Rafferty & Ruff, 1994; Rafferty, 1996; MacLatchy & Müller, 2002; Ryan & Ketcham, 2002a,b, 2005; Viola, 2002; Ryan & van Rietbergen, 2005; Ryan & Krovitz, 2006; Fajardo et al. 2007; Scherf, 2007, 2008; Saparin et al. 2011; Ryan & Shaw, 2013; Scherf et al. 2013), equivocal results are not limited to just these bones. For example, Ryan et al. (2010) also found no significant differences in the trabecular structure of the mandible in platyrrhines that habitually engage in gouging feeding behaviour (Callithrix) vs. non‐gouging species (Sanguinus and Saimiri). Schilling et al. (2014) found that variation in wrist bone (scaphoid, lunate and capitate) trabecular structure did not correlate with predicted loading differences from locomotor behaviour. Similar equivocal results have been found in the hominoid calcaneus (Maga et al. 2006), talus (DeSilva & Devlin, 2012) and thoracic vertebrae (Cotter et al. 2009; but see Oxnard & Yang, 1981; Oxnard, 1997).

In contrast to hominoids and studies of anthropoid primates more generally, more clear functional signals have been found in the trabecular structure of extant strepsirrhines (MacLatchy & Müller, 2002; Ryan & Ketcham, 2002a, 2005). Leaping galagines (Galago), indriids (Avahi) and tarsiers (Tarsius), predicted to have more stereotypical hip joint loading than quadrupedal or slow climbing taxa, have more anisotropic trabeculae than non‐leaping taxa (Cheirogaleus, Loris, Perodicticus and Otolemur; Ryan & Ketcham, 2002a, 2005). An earlier study by MacLatchy & Müller (2002) on a smaller sample (Perodicticus and Galago) found similar results. Furthermore, a comparative analysis of two fossil omomyid (Omomys and Shoshonius) femora showed variation in the trabecular structure suggesting important differences in joint loading and locomotor behaviour not revealed by the external morphology (Ryan & Ketcham, 2002b). Although Ryan & Ketcham (2002a) also noted a large degree of intraspecific variation in all taxa, suggesting that the trabecular structure was potentially also responding to subtle differences in individual behaviour, these results suggest that the locomotor behaviours of strepsirrhines may engender more divergent and/or stereotypical loading of the joints than is typical of a comparable sample of anthropoid primates (Demes et al. 1994; Hirasaki et al. 2000; Schmitt & Hanna, 2004).

Why so many equivocal results in analyses of hominoid trabecular bone?

Within primates, most trabecular studies have focused on hominoids, in part because of their close relationship to humans and their potential to help infer behaviour in fossil hominoids and hominins (Macchiarelli et al. 1999; Rook et al. 1999; Griffin, 2008; DeSilva & Devlin, 2012; Shaw & Ryan, 2012; Barak et al. 2013b; Scherf et al. 2013; Su et al. 2013; Tsegai et al. 2013; Schilling et al. 2014; Raichlen et al. 2015). Despite substantial variation in locomotion across extant hominoids, including highly specialized brachiation and suspension in Asian apes, and distinct knuckle‐walking locomotion in African apes, many of these studies have yielded results that neither fit specific predictions of differences in external joint loading, nor broader ‘suspensory’ or ‘quadrupedal’ signals when compared with other non‐hominoid primates that engage in similar behaviours (e.g. Ateles or Alouatta; DeSilva & Devlin, 2012; Shaw & Ryan, 2012; Schilling et al. 2014). There may be several reasons for these ambiguous results.

First, locomotion and body size are highly variable within hominoids. This includes variation in frequency of certain behaviours, even between species (e.g. Gorilla vs. Pan or P. troglodytes vs. P. paniscus), that are generally categorized in the same broad locomotor categories (e.g. ‘knuckle‐walkers’; Hunt, 1991; Doran, 1993; Remis, 1995). Reasons for variation in certain locomotor behaviours can relate to ecology (Doran & Hunt, 1994), body size (Cant, 1992; Hunt, 1994) or even social rank (Hunt, 1992; Remis, 1995), which is often information not associated with osteological specimens. If, for example, trabecular bone is responding to more infrequent but dynamic loads (Burr, 1990) rather than habitual daily activity, then slight differences in the frequency of certain behaviours (e.g. suspension, climbing) may have significant effects on the overall trabecular structure, creating greater intraspecific variation and greater overlap among different locomotor groups. Indeed, several recent trabecular studies demonstrate a high degree of intraspecific variation in trabecular structure in many taxa, such as Pongo (Tsegai et al. 2013) and humans (Ryan & Shaw, 2012, 2015). Furthermore, there can be substantial intraspecific variation in body mass between sexes (Plavcan & van Schaik, 1997), which can be challenging to accommodate and investigate in the typically small samples available for micro‐CT scanning. Although most trabecular parameters have recently been shown to be negatively allometric across different primate or mammalian taxa (Doube et al. 2011; Ryan & Shaw, 2013), potential variation in scaling within a taxon [i.e. between sexes and in the absence of broad‐scale differences in body mass, such as when comparing dwarf shrews and elephants (Doube et al. 2011) or galagos and gorillas (Ryan & Shaw, 2013)] is not well understood.

Second, the majority of trabecular studies to date have focused on the proximal humerus and/or femur. Although their globular epiphyses makes them relatively easy anatomical structures in which to analyse trabeculae, the shoulder and hip are complex joints, loaded in multiple directions from both soft tissues and substrate reaction forces. The kinematics of these joints during different types of locomotion, particularly arboreal behaviours, is not well understood (Bergmann et al. 1984; Larson, 1995; Chan, 2007, 2008). Our predictions of joint loading across different species may be either too simplistic (Fajardo et al. 2007) or, alternatively, loading at these joints may actually be more similar than we would instinctively expect. For example, there are broad similarities in hip joint loading between bipeds and quadrupeds (Bergmann et al. 1984, 1993, 1999). Finally, the proximal humerus and femur are relatively removed from the external loading of substrate reaction forces compared with more distal skeletal elements (e.g. metacarpals or distal tibia), which may obscure the adaptive response of trabecular bone. In short, it may be that the trabecular structure of the hip and shoulder are limited in their value for containing a strong locomotor‐specific functional signal (Rafferty, 1996; Fajardo et al. 2007; Shaw & Ryan, 2012).

Third, such problems understanding joint loading at the shoulder and hip highlight a more general problem in trabecular studies: that most trabecular analyses are based on relatively simplistic and coarse biomechanical models (Fajardo et al. 2007; Ryan & Walker, 2010; Ryan & Shaw, 2012; Tsegai et al. 2013). Collection of the necessary biomechanical data, such as the kinematics of joint movement, ground reaction forces or electromyography of muscles, are all inherently challenging in extant primates for a number of logistical and ethical reasons (Vereecke et al. 2011). Thus, in the absence of specific biomechanical data, researchers are often forced to make predictions about how trabecular structure might vary based on relatively crude assumptions about habitual joint postures. The coarseness of the biomechanical models is in direct contrast to the incredibly precise information on trabecular structure that one can gain from micro‐CT.

Fourth, phylogeny may also confound potential functional signals in trabecular bone, particularly in studies that have focused mainly on closely related taxa like hominoids. Only recently have trabecular studies addressed the influence of phylogeny on individual parameters (that also account for variation in body size) using, for example, independent contrasts (Doube et al. 2011), the K statistic (Ryan & Shaw, 2012), phylogenetic generalized least squares (Ryan & Shaw, 2013) or independent evolution and phylogenetic general least squares (Smaers & Vinicius, 2009; Tsegai et al. 2013). Some studies found only a minor phylogenetic influence (Doube et al. 2011), while others found a more complex pattern of influence that varied across elements and taxonomic groups (Ryan & Shaw, 2013). Thus, the potential influence of phylogeny and how this might confound functional interpretations should not be ignored in comparative primate studies.

Finally, some of the equivocal results from trabecular studies may be, in part, a consequence of methodology. Over the last decade, the traditional method of analysing trabecular structure in 3D is to quantify trabecular bone in a VOI, such as a sphere or cube within an epiphysis (Fig. 4A). The main advantage of the VOI method is that it is computationally feasible; it allows one to extract and quantify a portion of a complex structure from a much larger and cumbersome micro‐CT data set. There have been varied methods of determining VOI size and positon (Ryan & Ketcham, 2002a; Griffin et al. 2010; Schilling et al. 2014), and further discussion about the potential bias resulting from variation in VOI size and position (Fajardo & Müller, 2001; Maga et al. 2006; Kivell et al. 2011a,b; Lazenby et al. 2011). Studies using VOIs aim to quantify a functionally informative trabecular subsection that is considered representative of the region or epiphysis being analysed.

Figure 4.

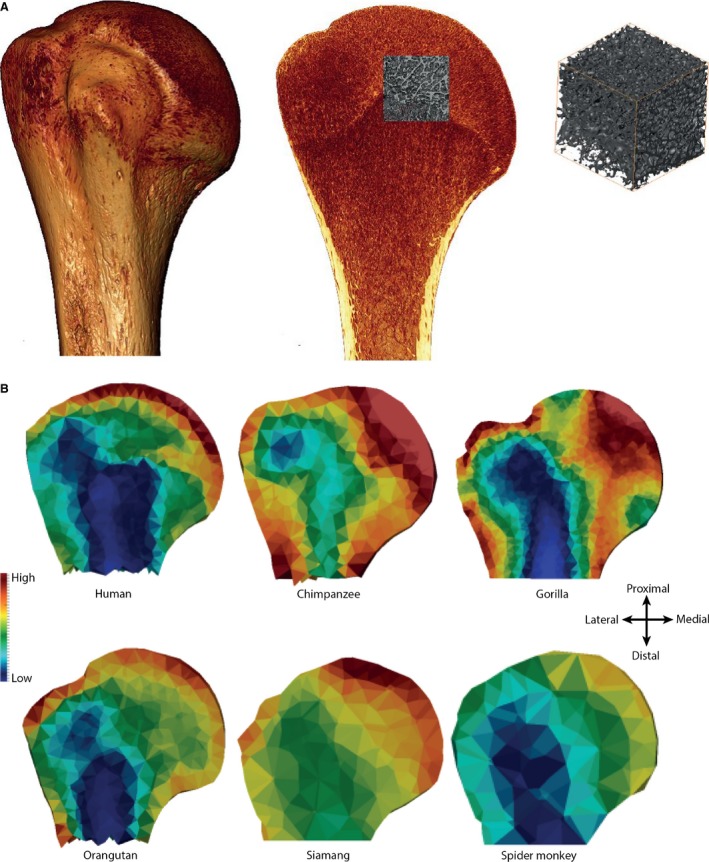
Different methodological approaches to investigating trabecular bone. (A) The traditional volume of interest (VOI) method that analyses trabecular structure in a subsection of the epiphysis or bone. Here, an example is shown in the human proximal humerus in which the VOI is 30% of the geometric mean of the articular dimensions. (B) A new, holistic method [medtool (Pahr & Zysset, 2009a; Gross et al. 2014)] that quantifies and visualizes variation in trabecular bone distribution (BV/TV) and stiffness throughout the entire epiphysis or bone. Here, variation in BV/TV is shown in a coronal cross‐section throughout the proximal humerus in the same taxa and specimens shown in Fig. 3. Red indicates high BV/TV; blue indicates low BV/TV.

However, there are several inherent limitations to the VOI method that are difficult to avoid. VOI size and position are constrained by the trabecular morphology itself, such that a VOI must be large enough to quantify a meaningful amount of trabecular structure (e.g. at least four trabecular struts; Gross et al. 2014), but small enough that it quantifies only trabeculae (i.e. avoiding cortical bone or anatomical features such as foramena). Therefore, it is often challenging to position VOIs near the subarticular surface where external joint loading is initially incurred, and the trabecular structure can be different from that deeper within the epiphysis (Singh, 1978; Currey, 2002). Positioning of VOIs is particularly difficult in small, irregular‐shaped bones, such as tarsals and carpals (Schilling et al. 2014). Furthermore, there are several challenges associated with determining anatomically and/or biomechanically ‘homologous’ VOIs across a sample, especially when morphology is complex or there is a large degree of morphological and size variation (Maga et al. 2006; Kivell et al. 2011a,b; Lazenby et al. 2011). Although such methodological issues have been recognized by many researchers (Fajardo & Müller, 2001; Ryan & Ketcham, 2002a,b; Maga et al. 2006), these traditional methods have remained the standard in non‐human primate studies due to computational limitations and the lack of alternative methods (see below).

A way forward

Recently, methods of analysing trabecular structure have evolved and improved. Several studies have taken an approach of placing multiple VOIs within an anatomical region with the aim of quantifying more detailed information about joint loading, albeit with varied success (DeSilva & Devlin, 2012; Su et al. 2013). Analysis of multiple trabecular parameters (derived from a single VOI) together using, for example, principal components analysis, has revealed combined patterns of trabecular structure that more clearly differentiate primate locomotor behaviour than specific parameters in isolation (Kivell et al. 2012; Ryan & Shaw, 2012; Scherf et al. 2013; Matarazzo, 2015). For example, Scherf et al. (2013) found a clear separation in the humeral trabecular structure across humans, orangutans and chimpanzees when BV/TV, rod‐ vs. plate‐like trabeculae, trabecular number and spacing were considered together. Ryan & Shaw (2012), in a much larger anthropoid sample, also found that distinct combinations of variation in similar trabecular parameters could reasonably differentiate (via discriminant functional analysis) between different primate locomotor groups in the femur and, to a lesser degree, in the humerus. However, Ryan & Shaw (2012) also found that there was still a large degree of overlap in trabecular morphology, even across locomotor groups that would presumably have quite distinct loading of their shoulder and hip joints [e.g. bipeds (humans), quadrumanus climbers (orangutans) and arboreal quadrupeds (crab‐eating macaques)].

The recent use of both comparative and experimental data in trabecular analyses by Barak et al. (2013b) is an ideal approach for better understanding the potential functional significance of variation (both inter‐ and intraspecific) in trabecular structure in extant and fossil taxa. They used kinematic and ground reaction force data collected on chimpanzees during terrestrial knuckle‐walking and humans during bipedalism (with both extended‐ and bent‐hip‐bent‐knee gaits) to interpret variation in the trabecular structure of the distal tibia. They found that the principal trabecular orientation in chimpanzees was more obliquely angled than in humans, reflecting a more dorsiflexed tibiotalar joint at midstance than the more extended ankle joint in normal (i.e. extended hip and knee) human bipedal walking. Furthermore, they used these results to interpret the trabecular structure of fossil hominin distal tibae; the principal trabecular orientation of the fossil hominin specimens was most similar to that of normal human bipedalism than the more dorsiflexed ankle joint loading of the bent‐hip‐bent‐knee gait, suggesting that Australopithecus africanus (and a tibia putatively assigned to early Homo) likely used an extended‐hip‐extended‐knee bipedal gait (Barak et al. 2013a,b).

More recently, a method originally developed for in vivo clinical studies of osteoporosis (Pahr & Zysset, 2009a,b) has been adapted for analyses of high‐resolution trabecular bone across primates (Gross et al. 2014). This method uses an in‐house script written for medtool (http://www.dr-pahr.at/index_en.php) that allows one to visualize and quantify trabecular (and cortical) morphology throughout the entire epiphysis or bone, rather than just a small VOI subsection of trabeculae (Fig. 4B). In particular, one can visualize via colour maps the distribution of trabecular bone and how BV/TV or stiffness vary throughout the epiphysis/bone, including just below the cortical bone where external load is first incurred. Thus, this method provides the ability to better reconstruct joint position of peak loading during habitual behaviours than is possible from, for example, a VOI positioned within the centre of an epiphysis (Shaw & Ryan, 2012; Scherf et al. 2013) or bone (Schilling et al. 2014). The downside of medtool, however, is that it does not yet provide the ability to statistically compare differences in trabecular structure across individuals or taxa, which is possible with traditional VOI methods.

The holistic medtool approach has been applied successfully to hominoid metacarpals (Stephens, 2012; Tsegai et al. 2013; Skinner et al. 2015), humeri (Davenport, 2013) and carpal bones (Bird, 2014; Fig. 4B). For example, the region of greatest BV/TV and trabecular stiffness throughout the third metacarpal head (Mc3) fits predictions of peak loading during habitual locomotor and manipulative behaviours across hominoids; a more dorsal concentration of trabecular bone on the Mc3 head in Pan and Gorilla is consistent with the extended metacarpophalangeal joint position during knuckle‐walking (Jenkins & Fleagle, 1975), while a more palmar concentration is found in Pongo, hylobatids and humans, consistent with a flexed metacarpophalangeal joint during arboreal grasping (Asian apes) and manipulation (humans; Tsegai et al. 2013). A similar correlation between trabecular bone distribution and inferred joint position was also found in the Mc1 and Mc5 epiphyses; in particular, highlighting a distinct pattern in humans consistent with forceful opposition between the thumb and the fingers (Stephens, 2012; Foote, 2013; Skinner et al. 2015). A human‐like distribution of trabecular bone in some fossil hominins was used to suggest the ability for forceful precision or power squeeze gripping in Australopithecus africanus (Skinner et al. 2015). Although the average BV/TV or trabecular thickness values derived from the entire epiphyses revealed some overlap across extant (and fossil) hominoids (Tsegai et al. 2013; Skinner et al. 2015), similar to the results of previous VOI studies (Shaw & Ryan, 2012), the ability to visualize how trabecular structure varies throughout the bone can be more informative for reconstructing joint position, and ultimately behaviour, in fossil taxa. Currently, medtool is limited to quantifying BV/TV and trabecular stiffness (Gross et al. 2014), but can be used in conjunction with traditional VOI methods to quantify additional trabecular parameters (e.g. trabecular thickness or number) in regions of interest (Davenport, 2013) and calculate mean values for the entire trabecular structure using freeware, such as BoneJ (Doube et al. 2010; Tsegai et al. 2013).

Trabecular bone functional adaptation in fossils

The decades‐long debates regarding fossil hominoid or fossil hominin behaviour can only be resolved, at least to some degree, with analyses of bony morphology that is more responsive to load during life than the external bone shape and size. Trabecular bone can provide this insight. However, to move forward, palaeoanthropologists must make some assumptions about trabecular bone functional adaptation, despite the caveats and ambiguity from analyses of extant taxa discussed above. For example, we generally assume that the patterns and variation we see in trabecular bone structure in fossil taxa reflect loading from habitual behaviours, rather than more rare, but dynamic loading. Several comparative and experimental studies support this assumption (Rubin et al. 2001, 2002; Barak et al. 2013b; Tsegai et al. 2013), but others do not (Barak et al. 2011). We must also assume that the general genetic, developmental or metabolic factors that influence trabecular bone structure, growth and remodelling in extant taxa are the same in fossil taxa as well. The general similarity in some of these processes across different mammals provides support for this assumption (Turner, 2001), but important exceptions have been noted (Chow et al. 1993; Erben, 1996; Aerssens et al. 1998; Barak et al. 2013a). Furthermore, for ethical reasons, those interested in primates are forced to rely on other animal models (e.g. rodents, sheep) for in vivo testing of trabecular bone functional adaptation, or computer simulation methods. Thus, there will always be some degree of the ‘unknown’ in analyses of extant and fossil primates that cannot be avoided.

However, the disconnect between trabecular bone functional adaptation and variation in hominoid trabecular bone that has been prevalent in the last decade of research can be improved upon. Access to micro‐CT is now easier and more affordable. Thus, larger extant samples that accommodate intraspecific variation in sex, body size or locomotor behaviour may help tease out functional signals in trabecular bone that have been previously obscured (Kivell et al. 2012). We continue to increase our understanding of variation in ecology and behaviour across different extant hominoid (and primate) taxa, particularly subspecies (Thorpe & Crompton, 2006; Pruetz & Bertolani, 2009; Wich et al. 2009) that were once lumped together into a sample of, for example, ‘Pan’ or ‘Pongo’. Although rare, the use of behavioural and ecological data that has been collected on specific individuals (e.g. Taï chimpanzees; Carlson et al. 2006) may further help to elucidate how particular frequencies of behaviours might be reflected in trabecular structure.

Methodological advancements in the analyses of bone structure are now more accessible and can provide more informed functional interpretations of fossil morphology. Holistic approaches such as medtool (Pahr & Zysset, 2009a; Gross et al. 2014) provide clear and specific information about individual and species differences in joint loading, and when used in combination with traditional VOI methods that allow for statistical comparisons we are much better equipped to quantify and interpret variation in trabecular structure. In vivo validation testing of trabecular strength (i.e. Young's modulus) is not possible in fossil specimens, but micro‐FE modelling of fossil morphology within the context of a comparative, validated extant sample can be used to test the effectiveness of fossilized morphology (both internal and external) in different loading regimes (Richmond et al. 2005; Nguyen et al. 2014) that can ultimately shed light on behaviour (Fig. 5).

Figure 5.

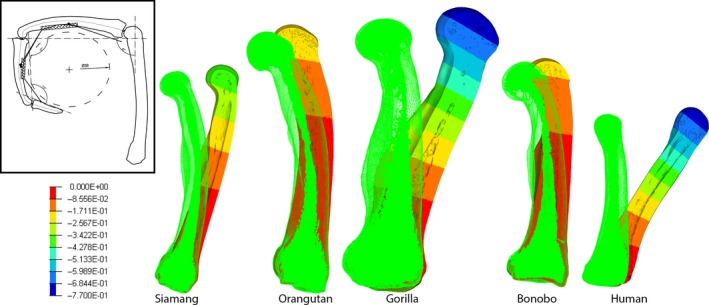
Micro‐finite element (μFE) modelling of the primate phalanx. Using micro‐CT, the true trabecular and cortical structure of the third proximal phalanx is modelled using μFE in a static, suspensory posture (left inset image). The biomechanical model was validated by Richmond (2007) and tested via μFE (Nguyen et al. 2014) on siamang phalanges. Here, this model is used to look at the displacement (how much the bone deforms under loading) across different extant hominoid taxa. Here, the displacement is 30 × greater than actual so the deformation can be visualized. Due to variation in trabecular structure, cortical thickness and phalangeal curvature, one can see substantial variation in how well each phalanx copes with the external loading during a suspensory posture. Orangutans and bonobos show the least displacement, while gorilla and humans show the most. Adding fossil phalanges to this comparative context will provide greater insight into how well their external and internal morphology could cope with the compression and bending stress of suspensory grasping.

Kinematic data on joint posture and loading (e.g. force and pressure) during primate locomotor and manipulative behaviours are essential for accurately interpreting the functional significance of variation of trabecular structure across extant and fossil primates. There have been numerous studies over the last few decades, particularly on quadrupedal or bipedal gaits on horizontal substrates (Schmitt, 1999, 2003; Vereecke et al. 2003; D'Août et al. 2004; Hanna et al. 2006; Wunderlich & Jungers, 2009). However, there have been far fewer studies on arboreal primate behaviours, such as climbing and suspension (Isler, 2002a,b, 2004; Schoonaert et al. 2006; Channon et al. 2010). To better reconstruct behaviour in fossil hominoids and hominins, more detailed analyses on joint kinematics and loading in primates engaged in more naturalistic locomotor behaviours, particularly arboreal locomotion (Vereecke et al. 2011), and manipulative behaviours (Shaw et al. 2012; Williams et al. 2012) are needed. Such data will improve on the simplistic biomechanical models that are used, by necessity, in most trabecular studies to date. Together, incorporating biomechanical data and new trabecular methods into analyses of extant taxa, as well as knowing the potential limitations of trabecular bone structure and remodelling discussed above, will provide a better comparative context in which to make more informed functional interpretations of fossil specimens.

Although this review argues that trabecular bone is particularly informative for reconstructing behaviour in the past, it is, of course, not an isolated structure. Trabecular bone exists within a bone and its cortical shell that together, with soft tissues, serve to optimize biomechanical function within the skeleton as a whole. Thus, there are trade‐offs between trabecular and cortical bone that, if analysed together, will provide a more informed reconstruction of behaviour in the past. Several studies of extant taxa have shown that cortical cross‐sectional shape largely reflects biophysical loads rather than genetic factors (Jones et al. 1977; van der Meulen et al. 1993; Ruff et al. 1994, 2006; van der Meulen & Carter, 1995; van der Meulen et al. 1996). The cortical cross‐sectional shape of long bones has been shown to differentiate locomotor behaviours across primates (Marchi, 2005; Ruff, 2009), or variation in behaviour and mobility across different human populations (Stock & Pfeiffer, 2001; Shaw & Stock, 2013). However, because of the denser structure and slower remodelling rate of cortical bone (Eriksen, 1986), functional signals can be more ambiguous than that of trabecular bone. For example, in vivo studies in a variety of animals have shown that limb bone shaft cross‐sections are not always reinforced in the planes in which they are habitually loaded (Lanyon & Rubin, 1985; Judex et al. 1997; Demes et al. 1998; Lieberman et al. 2004; Wallace et al. 2014; but see Brassey et al. 2013). Thus, many have suggested caution when inferring functional loading patterns from cross‐sectional shape, especially when one does not know the habitual loading behaviour or how bone may respond, such as in fossil taxa (Demes et al. 1998; Pearson & Lieberman, 2004; Wallace et al. 2014; but see Ruff et al. 2006; Brassey et al. 2013).

Regardless of the inherent complexity of cortical bone functional adaptation, the few primate studies that have analysed trabecular and cortical bone together have revealed interesting compensatory effects between the two structures (Skedros et al. 2004, 2012; Carlson & Judex, 2007; Carlson et al. 2008; Lazenby et al. 2008; Shaw & Ryan, 2012). For example, Shaw & Ryan (2012) showed in a sample of anthropoid primates that as trabecular bone increases in the humeral head, cortical diaphyseal strength also increases. Thus, even though loading at the shoulder joint and humeral midshaft is biomechanically distinct, when the humerus as a whole is loaded there is a morphological response in both trabecular and cortical bone. However, in other anatomical regions, the relationship between cortical and trabecular bone is more complex. In contrast to their humeral results, Shaw & Ryan (2012) found no correlation between trabecular structure in the femoral head and midshaft cross‐sectional geometry of the femur across their sample. In the femoral neck, variation in cortical bone may reflect more clearly differences in external load than trabecular bone across anthropoid primates (Fajardo et al. 2007), while in the specialized bipedal loading of human femoral neck, trabecular bone seems to play a more specific biomechanical role. The external loads elicit a pattern of ‘trabecular eccentricity’; the asymmetrical (i.e. non‐central) distribution of trabecular bone within the human femoral neck helps to reduce stress on the inferior aspect of the neck where strain and fracture risk is typically highest (Fox & Keaveny, 2001). Thus, analyses of both trabecular and cortical structure in extant taxa will provide a more holistic biomechanical interpretation and allow for more informed behavioural reconstructions in fossil taxa.

Concluding remarks

Like external bone morphology, trabecular bone architecture is the product of both genetic and non‐genetic influences (Judex et al. 2004; Havill et al. 2010; Barak et al. 2011; Raichlen et al. 2015). However, it can be argued that the ability for trabecular bone to respond and adapt to mechanical stimuli throughout life, more so than external bone shape and size, makes it a particularly important source of functional information for reconstructing behaviour in the past. Teasing out the relevant functional signals (from the genetic, developmental or metabolic influences) in trabecular structure is not straightforward, as many of the comparative, experimental and computational modelling studies have demonstrated. However, variation in trabecular structure is our best source of morphological information that is preserved in the fossil record, particularly when analysed in conjunction with cortical bone, for reconstructing actual, rather than potential, behaviours in fossil hominoids and hominins.