Fast Search of Thousands of Short-Read Sequencing Experiments

Abstract

We introduce Sequence Bloom Trees, a method for querying thousands of short-read sequencing experiments by sequence 485 times faster than existing approaches. The approach searches large data archives for all experiments that involve a given sequence. We use Sequence Bloom Trees to search 2652 human blood, breast, and brain RNA-seq experiments for all 214,293 known transcripts in under 4 days using less than 239 MB of RAM and a single CPU.

The NIH Sequence Read Archive (SRA)¹ contains ~3 petabases of sequence information that can be used to answer biological questions that single experiments do not have the power to address. However, searching the entirety of such a database for a sequence has not been possible in reasonable computational time.

Some progress has been made toward enabling sequence search on large databases. The NIH SRA provides a sequence search functionality²; however, the search is restricted to a limited number of experiments. Existing full-text indexing data structures such as Burrows-Wheeler transform³, FM-index⁴, or others^5–7 are currently unable to mine data of this scale. Word-based indices^8,9, such as those used by Internet search engines, are not appropriate for edit-distance-based biological sequence search. The sequence-specific solutions caBLAST and its variants^10–12 require an index of known genomes, genes, or proteins and so cannot search for novel sequences. Further, none of these existing approaches are able to match a query sequence q that spans many short reads.

We use an indexing data structure, Sequence Bloom Tree (SBT), to identify all experiments in a database that contain a given query sequence q. A query is an arbitrary sequence, such as a transcript. The SBT index is independent of eventual queries, so the approach is not limited to searching for known sequences. The SBT index can be efficiently built and stored in limited additional space. It also does not require retaining the original sequence files, and the index can be distributed separately from the data. SBTs are dynamic, allowing insertions and deletions of new experiments. A coarse-grained version of a SBT can be downloaded and subsequently refined as more specific results are needed. They can be searched using low memory for the existence of arbitrary query sequences.

SBTs create a hierarchy of compressed bloom filters^13,14, which efficiently store a set of items. Each bloom filter contains the set of kmers (length-k subsequences) present within a subset of the sequencing experiments. SBTs are binary trees in which the sequencing experiments are associated with leaves, and each node v of the SBT contains a bloom filter that contains the set of kmers present in any read in any experiment in the subtree rooted at v (Supplementary Fig. 1). We reduce the space usage by using bloom filters that are compressed via the RRR¹⁵ compression scheme (see Online Methods). Hierarchies of bloom filters have been used for data management on distributed systems¹⁶. However, they have not previously been applied to sequence search, and we find that this allows us to tune the bloom filter error rate much higher than in other contexts (see Theorem 2, Online Methods), vastly reducing the space requirements. Bloom filters have also been used for storing implicit de Bruijn graphs^17,18 and one view of SBTs is as a generalization of this to multiple graphs.

We used SBTs to search RNA-seq experiments for expressed isoforms. We built a SBT on 2652 RNA-seq experiments in the SRA for human blood, breast, and brain tissues (Supplementary Table 1). The entire SBT requires only 200 GB (2.3% of the size of the original sequencing data) (Supplementary Table 2). For these data, construction of the tree takes ≈2.5 min per file (Supplementary Table 3).

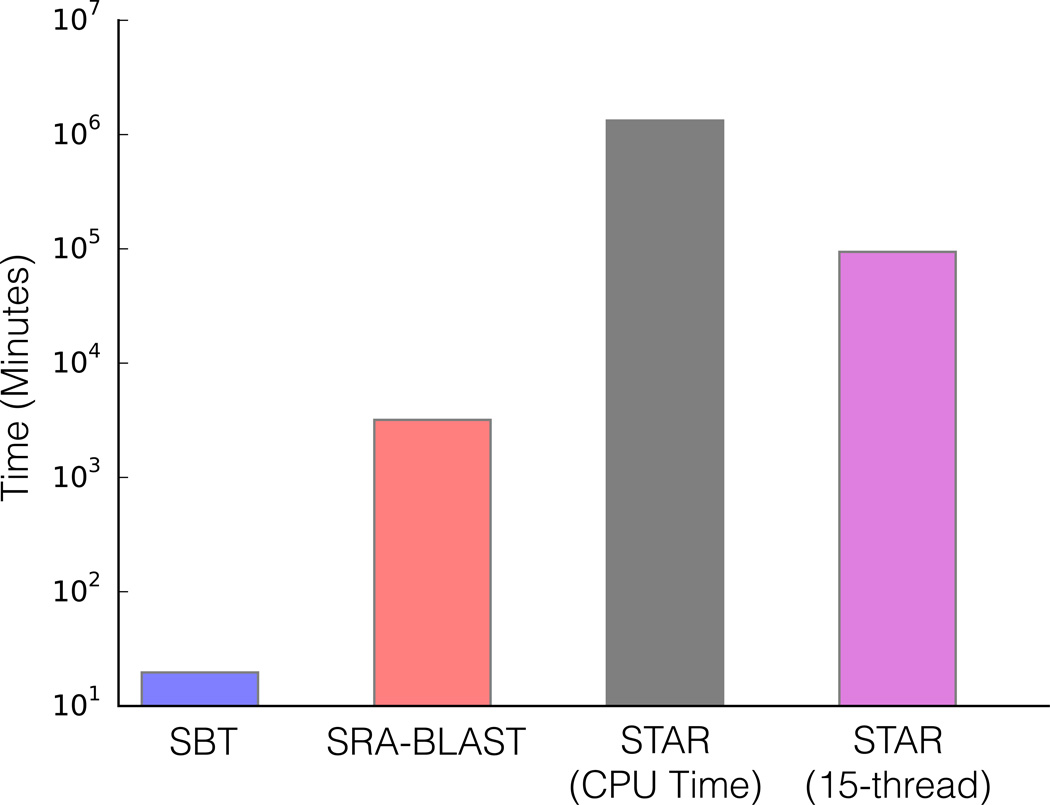
We find these experiments can be searched for a single transcript query in on average 19 min (Fig. 1) using less than 239 MB of RAM with a single thread (see Online Methods). The comparable search time using SRA-BLAST² or mapping via STAR²⁰ is estimated to be 6.4 days and 456 days respectively (see Online Methods), though SRA-BLAST and STAR return alignments while SBT does not. However, even a very fast aligner such as STAR cannot identify query-containing experiments as fast as SBT. We also tested batches of 100 queries and found SBT is an estimated 3650 times faster than a batched version of the mapping approach (Supplementary Fig. 2). These queries were performed over varying sensitivity threshold θ as well as the TPM threshold used to select the query set (Supplementary Fig. 3 and Supplementary Fig. 4). For a majority of queries, the upper levels of the SBT hierarchy provide substantial benefit, particularly on queries that are not expressed in any experiment (Supplementary Fig. 5 and Supplementary Table 4).

Figure 1.

Estimated running times of search tools for one transcript. The SBT per-query time was recorded using a maximum of a single filter in active memory and one thread. The other bars show the estimated time to achieve the same query results using SRA-BLAST and STAR (see Online Methods).

SBTs can speed up the use of algorithms, such as STAR or SRA-BLAST, by first ruling out experiments in which the query sequences are not present. This allows the subsequent processing time to scale with size of the number of hits rather than the size of the database. We find that first filtering the database with SBT reduces the overall query time of STAR or SRA-BLAST by a factor of ≈3.5 (Supplementary Fig. 6).

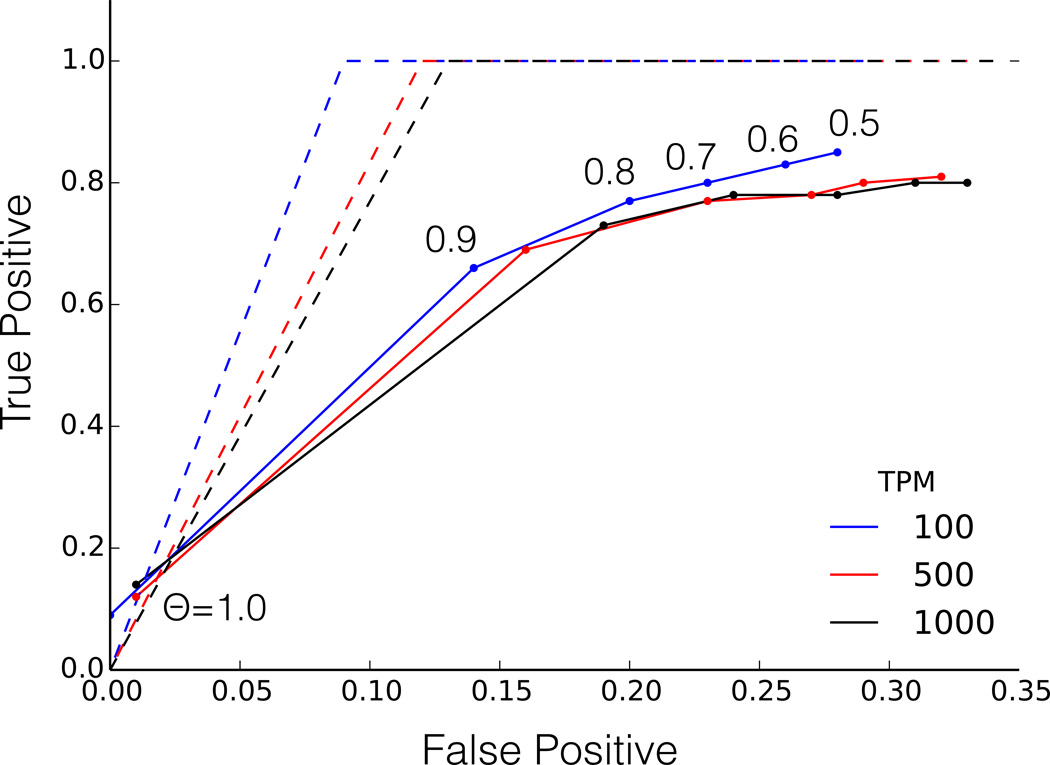
To analyze the accuracy of the SBT filter, we compare the experiments returned by SBT with those in which the query sequence is estimated to be expressed using Salmon¹⁹. Because it is impractical to use existing tools to estimate expression over the entire set of experiments, we query the entire tree but estimate accuracy on a set of 100 random files on which we ran Salmon (Fig. 2).

Figure 2.

ROC curve averaged over 100 queries with estimated expression > 100, > 500 and > 1000 TPM and variable θ (see Online Methods). Solid lines represent mean TP and FP rates, dashed lines represent the median rates on the same experiments. Relaxing θ leads to a higher sensitivity at the cost of specificity. In more than half of all queries, 100% of true positive hits can be found with θ as high as 0.8.

Both false positives (FP) and false negatives (FN) can arise from a mismatch between SBT’s definition of present (coverage of kmers over a sufficient fraction of the query) and Salmon’s definition of expressed (as estimated via read mapping and an expectation-maximization inference). These two definitions are related, but not perfectly aligned, resulting in some disagreement that is quantified by the FP and FN rates of Fig. 2. The observed false negatives are primarily driven by a few outlier queries for which the SBT reports no results but their expression is above the TPM threshold as estimated by Salmon. This is supported by the fact that the average true positive rate at θ = 0.7 for queries that return at least one file is between 96 – 99%, and the median true positive rate across all queries is between 90 – 100% for all but the strictest θ (Fig. 2).

We use SBT to search all blood, brain, and breast SRA sequencing runs for the expression of all 214,293 known human transcripts and use these results to identify tissue-specific transcripts (Supplementary Table 5 and Supplementary Fig. 7. This search takes 3.3 days using a single thread (Supplementary Fig. 8). We estimate an equivalent search using Salmon would take 76 days.

The speed and computational efficiency of SBTs will enable both individual labs and sequencing centers to support large-scale sequence searches. SBTs may be useful to search genomic and metagenomic collections as well. An open-source prototype implementation of SBT is available at http://www.cs.cmu.edu/~ckingsf/software/bloomtree (Supplementary File 1).

Online Methods

Sequence Bloom Tree construction and insertion

A Sequence Bloom Tree is a binary tree that is built by repeated insertion of sequencing experiments. Given a (possibly empty) Sequence Bloom Tree T, a new sequencing experiment s can be inserted into T by first computing the bloom filter b(s) of the kmers present in s and then walking from the root along a path to the leaves and inserting s at the bottom of T in the following way. When at node u, if u has a single child, a node representing s (and containing b(s)) is inserted as u’s second child. If u has two children, b(s) is compared against the bloom filters b(left(u)) and b(right(u)) of the left left(u) and right right(u) children of u. The child with the more similar filter under the Hamming distance between the filters becomes the current node, and the process is repeated. If u has no children, u represents a sequencing experiment s′. In this case, a new union node v is created as a child of u’s parent. This new node has two children: u and a new node representing s.

Each filter consists of a bit vector of length m and a set of h hash functions h₁ : U → [0, m) that map items to bits in the bit vector. Insertion of k ∈ U is performed by setting to 1 the bits specified by h_i(k) for i = 1, …, h. Querying for membership of k in b(k) checks these same bits; if they are all 1, the filter is reported to contain k. Because of overlapping hash results, bloom filters have one-sided error: they can report a kmer k is present when it is not. This error, and its effect on overall query accuracy of Sequence Bloom Trees, can be made quite small with the appropriate choice of parameters (see below). Bloom filters have been used in several others contexts in bioinformatics (e.g. [21, 22]). Hierarchies of Bloom filters have been used in other applications [23].

As s is walked down the tree, the filters at the nodes that are visited are unioned with b(s). This unioning process can be made fast (and trivially parallelized for large filters) since the union of two bloom filters can be computed by ORing together the bit vectors. This is particularly beneficial where GPU or vector computations can be used for these single instruction, multiple data (SIMD) operations. SBTs are different than cascading bloom filters [24, 25], which aim to reduce false positive rates of a single set query by recursively storing false positives in their own bloom filters. SBT works when word based indices fail [26, 27].

The insertion process is designed to greedily group together sequencing experiments with similar bloom filters. This is important for two reasons. First, it helps to mitigate the problem of filter saturation. If too many dissimilar experiments are present under a node u, then b(u) tends to have many bits set. In addition, by placing similar experiments in similar subtrees, more subtrees are pruned at an earlier stage of a query, reducing query time.

A primary challenge with scaling Sequence Bloom Trees to terabytes of sequence is saturation of the filters at levels of the tree near the root. The filter at any node v is the union of the filters of its children. However, this means as one moves from the leaves to the root, the filters will tend to contain more and more bits set to 1, increasing their false positive rate. This saturation can be overcome using several techniques: appropriate parameter selection (see Setting the bloom filter size), grouping of related experiments during insertion into the tree as above, and including only k-mers that have a minimum coverage count (see Building bloom filters). Note that filters with poor false positive rates at high levels of the tree only affect query time: accuracy is governed entirely by the false positive rate of the leaf filters.

Querying

Given a query sequence q and a Sequence Bloom Tree T, the sequencing experiments (at the leaves) that contain q can be found by breaking q into its constituent set of kmers K_q and then flowing these kmers over T starting from the root. At each node u, the bloom filter b(u) at that node is queried for each of the kmers in K_q. If more than θ|K_q| kmers are reported to be present in b(u), the search proceeds to all of the children of u, where θ is a cutoff between 0 and 1 governing the stringency required of the match. The parameter θ governs a query’s tolerance to errors. Ignoring the effects of sequence boundaries, a general SBT query with N kmers and kmer size k tolerates at least N (1 − θ)/k kmer mismatches, between the query and the stored data.

If fewer than that number of kmers are present, the subtree rooted at u is not searched further (it is pruned). It has been shown that kmer similarity is highly correlated to the quality of the alignments between sequences [28, 29, 30, 31], and SBT guarantees that if the query sequence is present (at sufficient coverage), it will be found.

When a search proceeds to the children, the children are added to a queue for eventual processing. Even though there may be a large frontier of nodes that are currently active, the memory usage for querying is the trivial amount of memory needed to store the tree topology plus the memory needed to store the single current filter. The Sequence Bloom Tree timings reported here are all for single-threaded operation.

If several queries are to be made, they can be batched together so that a collection C = {K_q1, …, K_qt } of queries starts at the root, and only queries for which |b(u) ∩ K_qi| > θ|K_qi| are propagated to the children. When C becomes empty at a node, the subtree rooted at that node is pruned and not searched further. The main advantage of batching queries in this way is locality of memory references. If b(u) must be loaded from disk, it need be loaded only once per batch C rather than once per query. Batch queries can be parallelized in the same way as non-batched queries by storing with the nodes on the queue the indices of query sets that remain active at that node. Additionally, batch queries offer an alternative means of parallelization where the query collection C is split evenly among active threads that merge results for the final query results.

Our implementation of SBT allows a user to specify a weight w_a between 0 and 1 for each kmer a in their query K_q. When these weights are specified, a subtree rooted at u is searched if ∑_{a∈Kq∩b(u)} w_a ≥ θ ∑_a∈Kq w_a. That is, a subtree is searched if greater than θ fraction of the possible total kmer weights are observed. Kmers that the user considers essential to their query (e.g. those spanning an exon junction) can be given higher weight than others. For all experiments here, we use unweighted kmers (w_a = 1 for all a).

Setting the bloom filter size

There are two important parameters that need to be set when constructing the bloom filters contained in a Sequence Bloom Tree. These are the bloom filter length (m) and the number of hash functions (h) used in the filter. We also must choose the kmer threshold θ for our queries. We explore below the relationship between m, h, θ, and the resulting false positive rate ξ of the filters.

Let S be a collection of r sequencing experiments with the property that each s ∈ S contains n distinct kmers. We analyze the behavior of a union of filters under the simplifying assumption that the kmer overlap between all pairs of experiments in S is uniform. Specifically, assume that the probability that two different experiments s_i and s_j in S share any given kmer is p. In other words, the expected number of kmers that appear in s_j that do not appear in s_i is d(1 − p), where d is the number of kmers in the experiments. We can then estimate the expected number of unique kmers:

Lemma 1

Let U = ⋃_s∈S s be the union of sequencing experiments in S as described above. The expected number of distinct kmers in the union is n(1 − (1 − p)^r)/p.

Proof

We have 𝔼[|U|] = 𝔼[|S₁|] + 𝔼[|S₂ \ S₁|] + 𝔼[|S₃ \ S₁ \ S₂|] + …. Each kmer in S_i is absent from ⋃_j<i S_j independently with probability (1 − p)ⁱ⁻¹. Therefore 𝔼[|S_i \ ⋃_j<i S_j|] = n(1 − p)^{i − 1}, and we have:

$$𝔼[|U|]={\sum }_{i=1}^{r}n{(1-p)}^{i-1}=n(1-{(1-p)}^r)/p$$ (1)

The assumptions of a uniform kmer count n and uniform overlap probability p do not hold in practice. However, under idealized assumptions, Lemma 1 formalizes the intuition that the expected number of elements in the SBT is the union set of all kmers. In practice, this allows us to define the size of the bloom filter to be equal to an estimate of the total number of unique kmers. Under the theoretical assumptions, it also shows that when the overlap is large (p is close to 1), the number of elements of U approaches that of a single experiment. Using this relationship, we can select the optimal number of hash functions for such a union as in Theorem 1.

Theorem 1

The number of hashes that minimizes the false positive rate of a union filter U with the expected number of elements is

$$h^{*}=(m(\text{ln }2)/(n(1-{(1-p)}^r/p))=(p\text{ ln }2)/(1-{(1-p)}^r)\mathit{\text{load}})$$ (2)

where load = n/m. Under this setting of h, the FPR of U is

$${\left(\frac{1}{2}\right)}^{h^{*}},$$ (3)

which is at most 1/2 so long as h* ≥ 1.

Proof

Follows directly by treating U as a single filter containing n(1 − (1 − p)r)/p items.

In the case of Sequence Bloom Trees, we have an advantage that we are not ultimately interested in a single bloom filter query on a kmer, but rather a set of queries of the kmers contained in the longer query string q. Thus, we are concerned mostly with the FPR on queries rather than FPR on kmers. Theorem 2 explores the connection between the two.

Theorem 2

Let q be a query string containing ℓ distinct kmers. If we treat the kmers of q as being independent, the probability that > ⌊θℓ⌋ false positive kmers appear in a filter U with FPR ξ is

$$1-{\sum }_{i=0}^{\lfloor \theta \ell \rfloor }\left(\begin{array}{c}\ell \hfill \\ i\hfill \end{array}\right){\xi }^i{(1-\xi )}^{\ell -i}$$ (4)

The above expression is nearly 0 when ξ ≪ θ.

Proof

Treating each kmer in q independently allows us to model the repeated queries using a binomial distribution, yielding (4). A false positive in q occurs when > ⌊θℓ⌋ false positive kmers occur in U. Let X be the number of false positive kmers, and let Y be the number of correctly determined kmers. Then Pr[X > θℓ] = Pr[Y ≤ ℓ − θℓ]. When θ ≥ ξ, we have ℓ − θℓ ≤ ℓ(1 − ξ) = E[Y], and the following bound holds by Chernoff’s inequality:

$$\mathrm{Pr}[Y\le \ell -\theta \ell ]\le \text{exp}\left(\frac{-{(\ell (1-\xi )-(\ell -\theta \ell ))}^2}{2(1-\xi )\ell }\right)=\text{exp}\left(\frac{-\ell {(\theta -\xi )}^2}{2(1-\xi )}\right).$$ (5)

In our search application, it is natural to require that at least 1/2 the kmers of a query are present; if < 1/2 are present it is fair to say that the query is not contained within the experiment. Therefore θ will typically be ≫ 0.5. In this case, if we choose the FPR of the bloom filters to be 0.5, by Theorem 2, we will be unlikely to observe > θ fraction of false positive kmers in the filter. A bloom filter FPR of 0.5 is much higher than typical applications of bloom filters, in which very low false positive rates are sought. The above analysis assumes independence of the kmers, which is of course unrealistic. Nevertheless, it formalizes the intuition that choosing a high FPR can still lead to few errors. By choosing such a high filter FPR, we can use smaller filters, limiting the memory footprint of the Sequence Bloom Tree.

To set the bloom filter size, we follow the intuition of Lemma 1, and use an estimate of the total number of unique kmers across as an estimate of the number of items any individual filter will contain. As it is computationally expensive to quantify this across all 2652 files, the total was estimated by counting the combined kmer content of 100 random files using Jellyfish 2.0, yielding an estimate of 1,902,731,933 kmers. Because we use a filter FPR of 0.5 and h = 1, as suggested by the above theorems, a single element in the SBT has a storage cost of ≤ 1 bit. Therefore, we set the size m of each bloom filter (in bits) to approximately equal this estimate of number of kmers. This offers an approximation that, by under-counting kmers, sacrifices some accuracy at the highest levels of the tree for a reduced bloom filter size. This value is also substantially higher than the number of kmers expected in any individual leaf filter and allows leaf filters (where accuracy is most important) to be less saturated and easily compressed. This leads to an uncompressed filter size of 239 MB, and any kmer of sufficient coverage that is shared between two files will correspond to a shared bit.

Experiments selected for inclusion in the SBT

A Sequence Bloom Tree was constructed from 2652 human, RNA-seq short-read sequencing runs from the NIH SRA. These 2652 files represented the entire set of publicly available, human RNA-seq runs from blood, brain, and breast tissues stored at the SRA at the time of download as determined by keywords in their metadata and excluding files sequenced using the SOLID technology. Files where the metadata was unclear about tissue type or experimental setup were discarded. This tree was used for all experiments described in the manuscript.

Building bloom filters

The construction of the Sequence Bloom Tree involves 3 major tasks: creation of bloom filters for each of the experiments included at its leaves, the construction of the tree and internal bloom filters, and the RRR compression [15] of each of the filters. Timing for each stage is given in Supplementary Table 4.

In the experiments here, bloom filters were constructed using the Jellyfish kmer counting library [32] from short-read FASTA files downloaded from the NIH SRA by counting canonical kmers (the lexicographically smaller kmer between a kmer and its reverse complement). We choose k = 20 as these kmers are reasonably unique within the human genome. Jellyfish was allowed to use 20 threads — all other computation reported here was run with a single thread.

To select only kmers from sufficiently expressed transcripts and to avoid counting kmers resulting from sequencing errors, we built trees containing kmers that occur greater than a file-dependent threshold. This threshold count(s_i) was determined using the file size of experiment s_i as follows: count(s_i) = 1 if s_i is 300 MB or less, count(s_i) = 3 for files of size 300–500 MB, count(s_i) = 10 for files of size 500 MB–1 GB, count(s_i) = 20 for files between 1 GB and 3 GB, and count(s_i) = 50 for files > 3 GB or larger FASTA files. These cutoffs were determined via the analysis of a small set of 18 sequence experiments of various sizes and tissue types and were chosen such that at least 60% of the transcripts expressed at a non-zero level in each of these files had an estimated uniform coverage above this number. In practice, we found these thresholds to outperform two naïve thresholds (count(s_i) = 0 and count(s_i) = 3 for all i) in speed and accuracy. We report only the results from the file-dependent threshold for this reason.

We can use a cutoff based on file size here because all the experiments sequenced the human transcriptome. In a situation where experiments of mixed organism origin are included, a more sophisticated scheme based directly on sequencing coverage would be needed to avoid counting sequencing errors.

After the Sequence Bloom Tree is built, the filters (both leaf and internal) are compressed using the RRR [15] bit vector compression scheme as implemented in the succinct data structures library [33]. This permits querying a bit without decompression and incurs only a O(log m) factor increase in access time (where m is the size of the bloom filter).

Hardware used for computational experiments

All times in all experiments reported here were obtained on a shared computer with Intel Xeon 2.60GHz CPUs using a single thread (or 15 threads in the case of STAR and 20 in the case of Jellyfish). The SBT queries were limited to keeping a single compressed filter in memory at any one time, leading to memory usage of < 239 megabytes of RAM.

Representative query sets and ground truth results

To determine the accuracy of Sequence Bloom Trees, we selected a subset of 100 random read files and used Salmon (the latest version of Sailfish [19]; see [34]) to quantify the expression of all transcripts in each of these experiments. All Sequence Bloom Tree queries are queried on the full set of 2652 files but the accuracy is computed based only on the random subset of files for which we computed expression results from Salmon.

Note that Sequence Bloom Tree returns no false negatives in the sense that if a query is covered by kmers in sufficient depth over θ-fraction of its length then the experiment will be returned. The “false negatives” in Figure 2 are those experiments where Salmon indicated the transcript was sufficiently expressed but SBT indicated that it was not sufficiently present. In this context, present and expressed are different concepts: “present” means sufficient coverage of the transcript at a given depth, while “expression” is estimated using Salmon’s expectation-maximization approach to allocate mapped reads to isoforms. These are related, but not identical notions. SBT has a 0% FN rate and a very low false positive rate identifying present transcripts (false positives identifying present transcripts are due to the one-sided bloom filter errors and kmer shredding of the reads). Figure 2 shows SBT’s false negative and false positive rates identifying expressed transcripts, which are partially due to the mismatch between the definitions of present and expressed.

Three collections of representative queries were constructed, denoted by High, Medium, and Low, that include transcripts that are likely to be expressed at a higher, medium, or low level in at least one experiment contained in the tree. To create these sets, Salmon was run on 100 random sequencing experiments to estimate transcript expression. The High set was chosen to be 100 random transcripts of length > 1000 nt with an estimated abundance of > 1000 transcripts per million (TPM). The Medium and Low query sets were similarly chosen randomly from among transcripts with > 500 and > 100 TPM, respectively. These Salmon estimates were taken as the ground truth of expression for the query transcripts.

SRA-BLAST

There are presently no search or alignment tools that can solve the sequence search problem in short-read sequencing files at the scale we attempt here. However, as alignments can be used to determine query coverage and thus the presence of transcripts in sequence files, we compare with SRA-BLAST [2]. SRA-BLAST has a limitation on the total nucleotide count that can be searched at once and requires specifying SRX (experiment) files rather then SRR (run) files. Because it is impractical to use SRA-BLAST at the SBT scale, we estimated an average SRA-BLAST query time from 100 random queries of a transcript against a single SRX experiment set using the SRA-BLAST webtool [2]. Specifically, we randomly selected a short read file from the total 2652 set and a query from the Low representative query set and recorded the time it took SRA-BLAST to return an alignment. Some publicly available SRR files cannot be searched using this webtool and random queries containing these files were discarded. The extrapolated time to process one > 1000 nt query against one megabase of sequence read file was recorded at 0.0696 seconds per-megabase-per-query.

The comparison with SRA-BLAST is not meant to indicate that SBT can provide the same information as SRA-BLAST. In fact, the tools provide complementary information: a list of experiments identified with SBT can be searched for individual read alignments with SRA-BLAST, thereby partially overcoming SRA-BLAST’s limitation on the number of experiments that can be searched.

STAR

We also compare our search times with an alignment-based approach using a read mapping algorithm, STAR [20]. To do this, we built a separate STAR index for each of the 100 sequence queries in the Low query set using a size-6 pre-index string. Reads from the 100 files analyzed by Salmon (our ground truth set) were mapped to these indices, allowing zero mismatches during the alignment and a single thread. After 5 days of 15-threaded continuous run-time, only 4 STAR queries had completed, and from these an average STAR query time of 4.9 seconds per-megabase-per-query was calculated by normalizing the time it takes to perform a STAR alignment against the total size of each sequence file and number of queries. While these single-query indices are more representative of the standard search use case, they represent an index size smaller than is typically used with STAR. To estimate batched times, a single STAR index was built from all 100 sequences queries in the Low query set using a size-11 pre-index string. In this case, an average STAR query time of 0.0093 seconds per-megabase-per-query was calculated. Note in either case, the time per-megabase-per-query does not include the time to build the STAR index. Although STAR was designed to perform efficient alignments, it represents one of the most competitive existing tools that could be adapted to the general search problem we solve. The comparison with STAR is not intended to indicate that SBT provides the same information as STAR, but rather to show that even a very fast aligner such as STAR cannot identify experiments that contain a query sequence as quickly as SBT.