Comparison of multiple AMBER force fields and development of improved protein backbone parameters

Abstract

The ff94 force field that is commonly associated with the AMBER simulation package is one of the most widely used parameter sets for biomolecular simulation. After a decade of extensive use and testing, limitations in this force field, such as over stabilization of α-helices, were reported by us and other researchers. This led to a number of attempts to improve these parameters, resulting in a variety of “AMBER” force fields and significant difficulty in determining which should be used for a particular application. We show that several of these continue to suffer from inadequate balance between different secondary structure elements. In addition, the approach used in most of these studies neglected to account for the existence in AMBER of two sets of backbone φ/ψ dihedral terms. This led to parameter sets that provide unreasonable conformational preferences for glycine. We report here an effort to improve the φ/ψ dihedral terms in the ff99 energy function. Dihedral term parameters are based on fitting the energies of multiple conformations of glycine and alanine tetrapeptides from high level ab-initio quantum mechanical calculations. The new parameters for backbone dihedrals replace those in the existing ff99 force field. This parameter set, which we denote ff99SB, achieves a better balance of secondary structure elements as judged by improved distribution of backbone dihedrals for glycine and alanine with respect to PDB survey data. It also accomplishes improved agreement with published experimental data for conformational preferences of short alanine peptides, and better accord with experimental NMR relaxation data of test protein systems.

Introduction

Molecular modeling studies of biologically important molecules usually require the evaluation of potential energies for alternate conformations. The most accurate approach would encompass the use of the quantum mechanical (QM) wave function. Unfortunately, due to the large sizes of biological macromolecules, such calculations are extremely time consuming and can only be applied to a limited number of conformations. Therefore, most simulation projects employ classical molecular mechanics (MM) energy functions. Due to the need to evaluate these functions a large number of times during the simulation, these functions are relatively simple and utilize many adjustable empirical parameters. These are most often obtained by fitting to data from experiments or from high level quantum mechanical calculations. The energy function together with the set of empirical parameters is known as a force field.

In spite of persistent yet slow emergence of force fields that explicitly account for charge polarization¹, the fixed charge additive force fields remain popular due to computational efficiency. For a more in-depth overview of current force fields and trends in force field development, the reader is referred to recent review articles^2–4. In this report, we focus on the existing AMBER fixed charge additive force fields.

The “Cornell et al” force field⁵ (denoted ff94 in AMBER) has been the most widely used with the AMBER suite of programs^6,7 since its publication over a decade ago. It introduced the set of parameters for all-atom simulations suitable for protein simulations in the condensed phase, largely inspired by the OPLS potentials⁸. Some characteristic features of ff94 include fixed partial charges on atom centers, explicit use of all hydrogen atoms, no specific functional form for hydrogen bonding, and dihedral parameters fit to relative quantum-mechanical (QM) energies of alternate rotamers of small molecules. In particular, the protein φ/ψ dihedrals have specific rotational parameters that affect relative energies of alternate backbone conformations. These were fit to optimize agreement with QM relative energies for several conformations of glycine and alanine. The partial atomic charges were derived by fitting the (gas phase) electrostatic potential calculated at the Hartree-Fock 6–31G* level. This approach intentionally “overpolarizes” bond dipoles as present in the gas phase, such that the resulting charge distribution approximates that occurring in aqueous condensed phase⁹.

Due to limited computational resources at the time, dihedral parameters were fit to a small number of low-energy conformations of glycine and alanine dipeptides. A possible limitation of using dipeptides is that their gas phase energy surfaces do not have a local minimum in the α-helical region, which occurs with high frequency in protein structures. This was addressed in subsequent modifications of ff94, such as ff96¹⁰ and, more recently, ff99¹¹. In ff96, identical parameters were used for φ and ψ terms, which were empirically adjusted to reproduce the energy difference between extended and constrained α-helical energies for alanine tetrapeptide. ff99 reflects another attempt at refitting backbone dihedral parameters by including eleven representative structures of alanine tetrapeptide along with the alanine dipeptides. During this process, however, a new problem was introduced in the way ff96/ff99 φ/ψ dihedral parameters were optimized (discussed in detail below), resulting in incorrect conformational preferences for glycine. In addition to changes in backbone dihedral parameters, ff99 also generalized and extended atom types to compounds beyond amino and nucleic acids.

Even though both ff99 and, particularly, ff94 parameter sets have been successfully used for many years, improvement in conformational sampling due to increased computer power and algorithmic advances revealed that both force fields over-stabilize α-helical peptide conformations^12,13. On the other hand, the changes introduced in the less frequently used ff96 were observed to overestimate β-strand propensity^14–17. Because the backbone dihedral parameters are shared by all amino acids, regardless of the type of sidechain, their cumulative effect is most likely responsible for the bias towards the specific secondary structure. This recently motivated us^12,18 and others^13,19 to revisit backbone dihedral parametrization for ff94/ff99. Garcia and Sanbonmatsu¹³ simply zeroed the torsion potential for φ and ψ (although as we explain below, only some of the φ/ψ terms were removed) and noted improved agreement with experimental helix-coil parameters. More recently, Sorin and Pande^19,20 modified ff99 by replacing its φ dihedral parameters with the ones from ff94. This improved the agreement with experimental kinetic and thermodynamic measurements for folding of two 21-residue α-helical peptides. Our own modification of ff99 published previously¹⁸ specifically addressed strong helical bias and, in this respect, succeeded to achieve better balance of major secondary structures.

All these previous modifications were aimed at correcting an apparent problem encountered with a specific system. The heuristic approaches that were employed might have improved that specific weakness but a more systematic revision was clearly necessary to quantify the problem and address the issue with generality and transferability in mind.

Much of the confusion and suboptimal performance of recent AMBER protein force field variants may have been caused by a somewhat non-intuitive parameterization of protein backbone dihedral angles. In AMBER, each dihedral profile is defined by a set of four atoms. The set of atoms used to define φ and ψ for glycine is as expected, following φ and ψ along the main chain (φ = C-N-C^α-C, ψ = N-C^α-C-N). Importantly, for other amino acids that have a side chain, an additional set of dihedrals also influences rotation about the φ/ψ bonds connecting the C^α atom to the amide C and N atoms. This extra set of terms corresponds to dihedral angles branched out to the C^β carbon, which in this work we identify as φ′ = C-N-C^α-C^β and ψ′ = C^β-C^α-C-N.

This definition of dihedrals was originally implemented in ff94, with φ and ψ fit independently to glycine data and φ′ and ψ′ used to adjust the behavior for alanine. Later modifications of ff94, such as ff96, ff99, Garcia’s¹³, Pande’s¹⁹ and ours^12,18 only changed the first set of φ/ψ terms, using them to adjust backbone preferences for alanine. Thus the new ϕ and ψ parameters were fit in the presence of the ff94 alanine-based φ′ and ψ′, and will only give their intended behavior when they accompany these φ′ and ψ′ dihedrals. Importantly, φ′ and ψ′ are not present in glycine. For example, ff99 modified the backbone φ and ψ terms in order to reproduce relative energies for alanine. However, the alanine residue also had the φ′ and ψ′ dihedral parameters present during the φ/ψ modification. These optimizations may perform well for non-glycine residues that possess the φ′/ψ′ terms. However, when these modified backbone dihedral parameters are applied to glycine, the result has little physical justification since they were fit in the presence of φ′ and ψ′. A similar inconsistency is present in Garcia’s modification; only the φ and ψ terms were zeroed, thus while glycine has no backbone dihedral potential all other amino acids retain the ff94 φ′ and ψ′ terms which were fit in the presence of the glycine-based φ and ψ terms and thus have no meaning when applied without them.

We show below that these modifications result in unreasonable sampling of dihedral space for several post-ff94 AMBER force fields. These problems are in addition to the overstabilization of helical conformations present in ff94 and ff99. AMBER and other popular force fields (e.g. CHARMM22 and GROMOS96 variants and OPLS-AA) were previously compared^21,22 in terms of conformational sampling of blocked glycine and alanine dipeptide and noted to disagree to various degrees (particularly for glycine²¹) with simulations employing combined QM/MM force field as well as with statistical analysis of high resolution protein crystal structures. In another study, all force fields were also shown to perform very differently with respect to a number of properties of trialanine compared to NMR and infrared observables²³.

We also show that our reparametrization of backbone dihedral parameters improves conformational preferences for typical secondary structures. It should be noted that this work does not attempt to create yet another variant of AMBER force field, but strives to improve the existing ff94 and ff99 force fields as well as specifically address the problem with glycine sampling. Thus rather than contributing to the diverging set of AMBER force fields, we extend the evolution started with ff94, followed by ff99 and subsequently refined in this report. This is also reflected by naming this modified force field ff99SB. We attempted to maximally improve the methodology that we used to derive our new parameters while still following the same general philosophy as was used with ff94/ff99.

A different approach was taken by Duan et al²⁴, who recently introduced a more extensive modification of ff94/ff99 (called ff03), in which a fundamentally different concept to derivation of partial atomic charges was used. Instead of relying on the HF/6–31G* approach to provide aqueous-phase charges, a low-dielectric continuum model corresponding to an organic solvent environment was included directly in the QM calculation of the dihedral parameters and electrostatic potential (from which the charges are obtained). Due to these differences, ff03 should be considered a distinct force field model rather than extension of previous AMBER force fields.

AMBER force fields are not the only ones undergoing such evolutionary changes brought about by discovery of limitations through improved conformational sampling capabilities. Similar efforts have recently been reported by MacKerell et al²⁵, improving the backbone parameters in the CHARMM force field, specifically removing the bias toward π-helical peptide conformations^26,27. In this case, the CHARMM22 alanine dipeptide dihedral energy surface was corrected using a grid-based difference map (CMAP) to achieve an almost perfect match with LMP2/cc-pVQZ(-g) energy surface. Likewise, dihedral terms in the original OPLS-AA force field²⁸ were also reparametrized to improve the agreement with high level QM data²⁹.

Methods

Optimization of backbone dihedral parameters

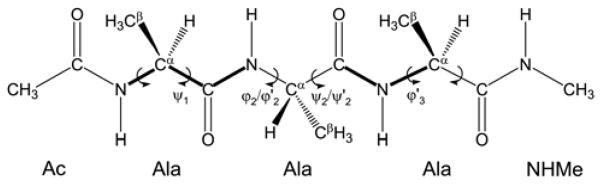
To better understand the procedure we used for obtaining a new set of backbone dihedral parameters, we first outline the general procedure originally used in ff94⁵. Even though it may at first seem more straightforward to have a single set of backbone φ/ψ parameters for all amino acids, the different nature of glycine (no C^β carbon), motivated the following approach: there is indeed a single set of backbone φ/ψ parameters for glycine (defined as φ =C-N-C^α-C, ψ =N-C^α-C-N), but any other amino acid has an additional set of φ/ψ parameters which are added to the glycine ones (here defined as φ′ = C-N-C^α-C^β, ψ′ = C^β-C^α-C-N). In other words, for any non-glycine amino acid, the dihedral energy is the sum of dihedral energies calculated for φ/ψ and φ′/ψ′. Note however, that φ′/ψ′ is calculated for a dihedral angle shifted by ~120° because that is the offset of the two torsions (as follows from their definitions using different sets of four atoms). Figure 1 demonstrates the definition of these two sets of dihedral angles on Ala₃ tetrapeptide.

Figure 1.

Blocked alanine tetrapeptide (three alanine residues but four peptide bonds) used in the optimization procedure. Note the definition of dihedral angles: φ =C-N-C^α-C, ψ =N-C^α-C-N, φ′ = C-N-C^α-C^β, ψ′ = C^β-C^α-C-N. There are three φ/ψ pairs and three additional φ′/ψ′ pairs in this tetrapeptide. Glycine tetrapeptide would only have the φ/ψ dihedrals due to the absence of C^β carbon. As an example, ψ₁ and φ′₃ are shown in bold.

The glycine φ/ψ parameters were optimized first, usually based on the best reasonable fit of QM and MM energies for a set of glycine conformers. These are total potential energies for the molecule, where backbone dihedral parameters are the adjustable variables in the optimization. For example, if we optimized the absolute difference of QM and MM energies for glycine tetrapeptide (Gly₃), we would minimize the absolute error (ae) between the MM and QM energies (Equation 1):

$$ae=1/N\sum _{i=1}^N\left|E_{QM}(i)-E_{MM}(i)\right|$$ (1)

where E_QM(i) and E_MM(i) correspond to the QM and MM energies respectively for i-th glycine tetrapeptide conformer and N is the number of all glycine conformers. In our case, MM energy for a given conformer is given by the AMBER energy function (see ff94⁵):

$$E_{MM}=E_{\mathit{bond}}+E_{\mathit{angle}}+E_{\mathit{non}-\mathit{bond}}+E_{\mathit{dihedral}}$$ (2)

where the dihedral energy term is:

$$E_{\mathit{dihedral}}(\theta )=\sum _{n=1}^3{V}_n\left(1+cos\left(n\theta -{\gamma }_n\right)\right)$$ (3)

V_n is dihedral force constant (amplitude), n is dihedral periodicity, and γ_n is a phase of the dihedral angle θ (which would be either φ or ψ for backbone dihedral terms). The Fourier series in E_dihedral is approximated using a small number of terms. Our choice of three terms in the expansion is consistent with the AMBER philosophy of using dihedral terms that can be physically rationalized ³⁰ and yields a reasonable number of terms per single dihedral (six) that need to be optimized.

Dihedral energy parameters in Equation 3 corresponding to backbone φ/ψ dihedrals (i.e. V_n and γ_n) are the adjustable parameters. We seek values of these parameters that minimize the function in Equation 1. Once the glycine parameters are optimized, they are held fixed and used in a second round of fitting where φ′/ψ′ parameters are optimized. This is carried out by fitting the parameters to best reproduce QM and MM energies for a set of alanine tetrapeptide (Ala₃) conformations. This second round of φ′/ψ′ optimization was initially misunderstood by us and by others who modified the original ff94. The use of a single round fitting in which the glycine φ/ψ dihedral parameters were modified to improve agreement for alanine data where the ‘real’ φ′/ψ′ alanine parameters were untouched led to incorrect parametrization (primarily for glycine) and overall confusion about the effect of dihedral parameters on the backbone conformation.

In the following, we describe the specifics of this general procedure that were employed for the present study. All optimizations were carried out with blocked (acetyl and N-methylamine groups at the N- and C-termini, respectively) glycine and alanine tetrapeptides (Gly₃, Ala₃) as shown in Figure 1. A set of Gly₃ and Ala₃ tetrapeptide conformers was chosen to represent local minima on the ff94 energy surface (ff99 was not used here due to apparent flaws in the ff99 energy function for glycine). Because the 6-dimensional dihedral space of tetrapeptides is too large to be represented exhaustively (as would be possible for simple 2-dimensional surface of dipeptides), we chose to optimize the relative depths of local minima on the energy surface, because these are most relevant to the thermodynamic stability of alternate secondary structure types. Each point in this dihedral space corresponds to a specific tetrapeptide conformation. Local minima were identified through a stochastic search in φ/ψ dihedral space followed by local minimization.

All conformations corresponding to the proposed minima were optimized at the Hartree-Fock level with 6–31G* basis set. After discarding the conformers that converged to the same geometry, we ended up with 28 glycine and 51 alanine tetrapeptide conformers (with a maximum range ff94 energy cutoff of 10 kcal/mol). The energies of these conformations were calculated using higher level (gas phase) QM LMP2/cc-pVTZ(-f) in Jaguar³¹ employing the methodology described by Beachy³², who showed that inclusion of electron correlation (in this case using LMP2) is important and has a significant effect on relative energies of peptide conformations. Tables of all Gly₃/Ala₃ conformers and their QM energies are provided in the supplementary material (Tables S1 and S2). Note that we only used these energies to refit backbone dihedral parameters, and no change was made to the ff94 partial atomic charges.

The optimization of dihedral parameters was done in two steps. First, the φ/ψ torsion parameters for Gly₃ were optimized as follows. We used an exhaustive grid search in 12-dimensional dihedral parameter space: three amplitudes (V₁, V₂, V₃) and three phases (γ₁, γ₂, γ₃) for each φ and ψ. Amplitudes were systematically varied between 0 and 2 kcal/mol with a step of 0.2, phases were set to either 0 or π radians. Thus the total number of grid points in the initial search was 11⁶ x 2⁶ (over 100 million).

As the initial grid spacing was 0.2 kcal/mol for amplitudes (V_n), that would be the maximum precision of optimized parameters. To improve this, we employed ‘grid focusing’ by repeating the grid search with finer grid spacing centered on the parameters resulting from the initial course grid. Our refined grid had a spacing of 0.01 kcal/mol for amplitudes, thus that is the ultimate precision of our optimized grid parameters.

The function we used for optimization is somewhat more complicated than that shown in Equation 1. Since the zero of the MM energy function is arbitrary, the optimization should be performed using energy differences between alternate conformations. This was achieved in ff99 by setting one of the energies (the lowest one) to zero, and all other energies were assigned values relative to this “zero energy” reference. However, we observed that the optimized parameter set changes depending on which conformer’s energy is used as a reference. Therefore the function we optimized was calculated as an average of QM and MM energy differences with each conformer’s energy set as a reference in turn. This gives an average absolute error (aae) defined as follows:

$$\mathit{aae}=1/N(N-1)\sum _{i=1}^N\sum _{j>i}^N\left|E_{QM}^{o,i}(j)-E_{MM}^{o,i}(j)\right|$$ (4)

where $E_{QM}^{o,i}(j)$ is the QM energy of conformer j with conformer i as a reference, and $E_{MM}^{o,i}(j)$ is the MM energy of conformer j with conformer i as a reference, N is number of conformers, which is 28 for Gly₃. Another possibility to define a function for optimization is to concentrate on what the maximum absolute error (mae) might be when we consider all individual QM and MM differences and, again, take into account that any conformer may serve as a reference “zero energy”. This would give a function of the following form:

$$\mathit{mae}=\underset{i,j>i}{max}\left|E_{QM}^{o,i}(j)-E_{MM}^{o,i}(j)\right|$$ (5)

Here, we would search for such set of dihedral parameters that give the smallest mae. As it turns out, there are many sets of dihedral parameters with very similar aae. However, inspecting mae reveals that this parameter is much more sensitive to different parameter sets and therefore the selection of the final set was based on this error estimate. In general, small values of mae always correlate with small values of aae, such that the best parameter set picked based on mae will also have one of the lowest aae values.

For Gly₃ optimization, an additional constraint was introduced, requiring the first phase for φ (i.e. γ₁ for φ) to be 0. This was necessary to obtain physically reasonable dihedral functions with energy barrier located at φ ≈ 0° on the glycine Ramachandran map. Even though glycine parameter sets without this constraint achieved slightly better fit of QM and MM data, the resulting dihedral energy function would have a physically unreasonable minimum in the φ ≈ 0° region of Ramachandran map (where we also did not have any QM data). This arises from our use of only local minima to train the dihedral correction terms.

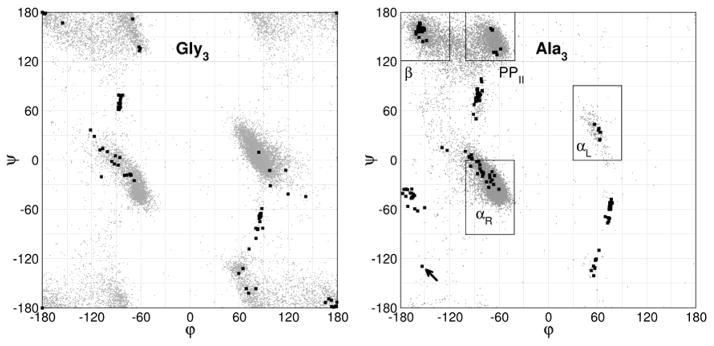
Once the Gly₃ parameter set was obtained, the same procedure was repeated with 51 Ala₃ conformers, and parameter sets corresponding to φ′/ψ′ dihedrals were obtained. While the resulting set of parameters appeared satisfactory, a more detailed analysis of errors revealed that Ala₃ conformer number 16 was repeatedly responsible for the largest fitting errors (as measured by aae or mae). This conformer also falls into the unusual region of the Ramachandran map (see Figure 2 below), therefore it was excluded from the optimization of Ala₃ dihedral parameters.

Figure 2.

Ramachandran plot of 28 Gly₃ (left) and 51 Ala₃ (right) conformers as obtained from QM geometry optimization of structures that were acquired using stochastic search with MM energies. All three dihedral pairs are shown for each conformer (black squares). The gray points in the background are φ/ψ values of glycine and alanine residues collected from a subset of the PDB. Typical secondary structure regions are outlined by boxes in the Ala₃ plot (see Methods for additional details). Ala₃ conformer number 16 (outlier) in the lower left of Ala₃ plot is designated by an arrow.

The resulting parameters in the form suitable for use with AMBER are provided in supplementary material (Table S3).

Simulations in explicit water

All molecular dynamics simulations for Gly₃ and Ala₃ tetrapeptides were carried out with the sander module in AMBER8⁷ using several different force fields as discussed in the main text: ff94⁵, ff99¹¹, Garcia’s modification of ff94¹³ with C-N-C^α-C and N-C^α-C-N terms zeroed (denoted ff94gs in the text), Pande’s modified ff99¹⁹ with C-N-C^α-C term replaced by the one from ff94 (denoted ff99ϕ), ff03²⁴ (as present in AMBER8 distribution) and ff99SB developed as described above. The time step was 2 fs, and all bonds involving hydrogen were constrained by SHAKE with a tolerance of 10⁻⁴Å. Glycine and alanine tetrapeptide systems were solvated by approximately 520 TIP3P³³ water molecules in a periodic box. Simulations were carried out in the NPT ensemble at 300 K. A cutoff of 8 Å was used for nonbonded interactions, and long-range electrostatic interactions were treated with the particle mesh Ewald (PME) method³⁴.

Replica exchange molecular dynamics (REMD) simulations³⁵, as implemented in AMBER8, were run for Ala₃ using explicit water solvation and the ff99SB and ff03 force fields. REMD simulations were set up under similar conditions as the corresponding standard MD runs. Ala₃ was solvated in a truncated octahedral box using 595 TIP3P water molecules. 26 replicas were used to span the temperatures range of 267 K to 571 K. Temperatures were optimized to give a uniform exchange acceptance ratio of ~30%. Exchange between neighboring temperatures was attempted every picosecond and each REMD simulation was run for ~30,000 exchange attempts (30 ns). Due to the high temperatures of some replicas, the NVT ensemble was employed.

Calculation of NMR order parameters

Hen egg white lysozyme (PDB code 6LYT³⁶) and ubiquitin (PDB code 1UBQ^37,38) simulations were run under the same conditions as the short peptides described above, but with truncated octahedral periodic boundary conditions including 4350 and 3300 water molecules respectively. Equilibration was done in multiple steps, with positional restraints on all heavy atoms in the crystal structure gradually released from 2 to 0 kcal/mol-Ų. The production run trajectories were 30 ns long. These trajectories were used to calculate the N-H internuclear vector autocorrelation functions with ptraj module. Order parameters (S²) were obtained from a plateau region of autocorrelation functions³⁹. Specifically, the autocorrelation function was calculated up to time of half of trajectory length and the mean of last 5 ns was taken as S². Standard deviation of the mean was used to plot the error bars. Since autocorrelation functions for a few backbone amides typically do not converge well (meaning that they do not show clear plateau), the mean will be a less reliable estimate of S² for these amides, which will be reflected by larger standard deviations (i.e. larger error bars).

Dihedral plots and free energy surfaces

A Ramachandran plot showing the distribution of glycine or alanine φ/ψ angles in protein crystal structures was constructed based on a subset of proteins from a PDB database, with high resolution (<1.6 Å), small R-factor (<0.25) and less than 20% sequence homology^40,41. Dihedral plots based on this statistical survey of the PDB provide experimental indication of which values of backbone torsions are commonly found in proteins.

Gly₃/Ala₃ simulations were used to produce free energy surfaces (or potential of mean force, PMF, maps) for backbone dihedral angles, assuming that φ/ψ are represented in the ensembles according to a Boltzmann distribution. First, the values of all φ/ψ dihedral pairs over the production portions of simulations were collected. Then, 2-dimensional φ/ψ normalized histograms were constructed from these values and converted to free energies using equation 6:

$$\mathrm{\Delta }{G}_i=-\mathit{RT}ln\left(N_i/N_0\right)$$ (6)

where N_i is the population of a particular histogram bin for specified values of φ/ψ, and N₀ is the most populated bin. Thus the global free energy minimum always has a value of 0 kcal/mol.

The φ/ψ histograms were also used to evaluate populations in different regions of secondary structures. The definitions of the four principal regions were as follows: right-handed α-helix (α_R): (φ, ψ) ≈ (−70±30°, −45±45°), left handed α-helix (α_L): +60±30°/+45±45°, poly-proline II (PP_II): −70±30°, +150±30°, and extended β-strand conformation (β): −150±30°, +150±30°. Most ranges are ±30° except from the ψ range of α_R and α_L, which were slightly wider (±45°) to capture the shift in these regions that resulted from using the ff94gs parameter set. The number of structures in individual regions were summed and divided by the total number of structures to obtain population fractions. Relative fractions are also reported; these differ in that the populations in the secondary structure basins were normalized by the total number of structures in just the four regions.

The convergence of Ala₃ simulations was estimated by comparing the first and second half of the trajectories in terms of differences of population fractions. The fractions were calculated independently for the two parts of the trajectory and the resulting values are given as averages, with deviations reflecting the differences of the two independent calculations.

Decoy analysis

Similar to work that we previously published¹² for ff94 and ff99, we used “decoy analysis” to test the capability of the force field to identify the experimentally determined native structure as that with the lowest potential energy. Three systems were used for decoy analysis: trpzip2⁴² (SWTWENGKWTWK-NH₂), Baldwin type⁴³ alanine based α-helical peptide⁴⁴ (Ace-GGG(KAAAA)₃K-NH₂) and trpcage miniprotein⁴⁵ (NLYIQWLKDGGPSSGRPPPS). The decoys for the three systems were generated by a number of unrestrained as well as forced MD simulations at 300K as described previously¹². The sets cover structures generated in simulations started from various initial structures, such as native, extended, and multiple unfolded or partially folded structures from intermediary stages of folding trajectories. The decoy ensembles thus contain local and global structural variation with a greater diversity of structures than could be obtained from a single simulation. The sizes of the three decoy sets are as follows: 177,000 for trpzip2, 70,000 for the helical peptide, and 118,000 for trpcage. The energies of these decoy sets were analyzed with different force fields using a Generalized Born solvation model⁴⁶ implemented in AMBER. For each force field, the potential energy and RMSD from the experimentally determined structure were plotted for each of the decoy structures. The expectation for a “correct” force field is that the lowest energies are obtained for structures with low RMSDs, i.e. for native folds.

Because many different structures can have similar RMSD values, and because different force fields may favor slightly different conformations in each RMSD range, we performed a further simplification of the data. Since we are primarily interested in structures with low energies, we only plot one energy value, which is the average of the 20 lowest energies in that particular RMSD bin. This results in a curve that outlines the lowest energies sampled for the RMSD range (“lowest energy profile”), which can be more easily interpreted as being representative of the underlying energy surface for the force field. This approach has several limitations, including neglect of entropic contributions to the actual free energy, and also uses an implicit solvation model which may have its own effects on the stability of different conformations. Nevertheless, this methodology is useful for fast qualitative screening of many variations of a force field on larger peptides.

Results and Discussion

The unique conformations of 28 Gly₃ and 51 Ala₃ that resulted from QM optimization are shown in Figure 2. In general, these conformers overlap the regions outlined by PDB survey data. There are several distinct clusters that fall within the regions of typical protein secondary structures, such as right handed (α_R) and left handed (α_L) α-helix, polyproline II (PP_II) and extended β-strand conformations.

Following the procedure described in Methods, we optimized a set of dihedral parameters (Table I). The root mean square difference (RMSD) between the QM and MM energies for glycine tetrapeptide using these parameters is 1.17 kcal/mol. The average absolute error and maximum error are 0.93 and 2.71 kcal/mol, respectively. Alanine tetrapeptide calculations used the glycine φ/ψ backbone parameters as well as the φ′/ψ′ dihedral terms. In this case, the root mean square difference, absolute average error and maximum error are 1.31, 1.05 and 3.43 kcal/mol. This is comparable to similar fitting errors obtained in ff99¹¹ and ff03²⁴. For comparison, the values of backbone dihedral parameters for many other variants of AMBER force field are given in the supplementary information (Table S4). It should be noted again that RMSD, absolute average error (aae) and maximum absolute error (mae) are calculated such that each conformer in turn is set as a “zero energy” reference, and thus all pairs of energy differences are used in the average. The sensitivity of errors (RMSD, aae, mae) to the choice of reference can be demonstrated by calculating these errors for all 51 Ala₃ conformers with a reference conformation fixed to each conformer in turn. Such evaluation of errors produces best RMSD of 0.94 if conformer #31 is a reference and worst RMSD of 1.97 for conformer #45 as a reference. Similarly, depending on the choice of conformer as a reference, aae ranges between 0.77 and 1.82, and mae between 1.74 and 3.43 kcal/mol. Thus, averaging over all pair wise differences should provide a more stringent error estimation (e.g. mae is always the largest of all pair wise differences when using all pairs) and yields an independence of results with respect to which conformer is chosen as a reference.

Table I.

Optimized dihedral parameters: amplitudes (V) and phases (γ) for backbone dihedral angles. The φ/ψ terms are always used by all residues, φ′/ψ′ are used by all residues except glycine. Phases are in radians and amplitudes are in kcal/mol.

		V1	γ1	V2	γ2	V3	γ3
φ	C-N–Cα–C	0.00	0	0.27	0	0.42	0
ψ	N-Cα–C–N	0.45	π	1.58	π	0.55	π
φ′	C-N–Cα–Cβ	2.00	0	2.00	0	0.40	0
ψ′	N-C–Cα–Cβ	0.20	0	0.20	0	0.40	0

Force field validation

Explicit water simulations of Gly₃/Ala₃

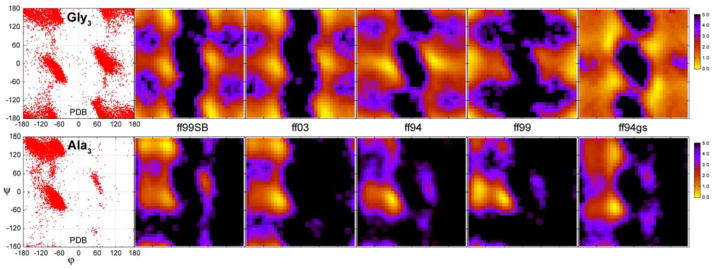
We performed molecular dynamics simulations on the same systems we used for parameter optimization, i.e. Gly₃ and Ala₃ peptides, with different AMBER force fields. All simulations were fully solvated with explicit water and extended to ~80ns. Histogram analysis was used to calculate relative free energies of different conformers with respect to φ/ψ backbone angles. These free energy (PMF) surfaces are shown in Figure 3 for both Gly₃ and Ala₃.

Figure 3.

Free energy φ/ψ maps for Gly₃ (top row) and Ala₃ (bottom row) from 80ns simulations with explicit TIP3P water. The energies are color coded from 0 up to 5 kcal/mol. PDB survey data is represented by a simple Ramachandran plot. Individual force fields are designated as: ff99SB (this work), ff03²⁴, ff94⁵, ff99¹¹ and ff94gs¹³.

The correspondence of the distributions obtained from PDB and simulations has been used extensively in force field validation and development^21,24–26. This is the basis for our first test and qualitatively evaluates our dihedral parameter set. PDB survey data are presented here as simple Ramachandran maps, not as free energy surfaces. One might expect that the φ/ψ regions sampled in crystal structures should be also accessible to solvated Gly₃/Ala₃ peptides. However, it would be wrong to assume that the relative populations of φ/ψ angles in static crystal structures should match populations in small tetrapeptides solvated in water. Not only are the two environments very different but also populations in crystal structures will certainly be biased by occurrence of common secondary structures, such as α-helices and β-sheets. Furthermore, there is no obvious choice for temperature associated with the PDB distribution, which would make any free energy calculation difficult.

We first discuss the plots for Gly₃. The plots obtained from the Gly₃ simulations are symmetric with respect to the origin, while alanine plots are not due to the presence of the chiral center on the alanine α-carbon. A certain amount of asymmetry in the glycine PDB data arises from the influence of chiral centers in other residues, which are not present in the Gly₃ simulations.

The analysis of glycine conformations in the PDB data reveals that both right- and left-handed α-helical regions are densely populated. PP_II and extended β-strand regions are also found with high frequency. One should expect similar conformational preferences resulting from MD simulations (Figure 3). This is largely true for ff99SB and ff03 and to a lesser extent for ff94 (which is missing PP_II and β, and has strong bias favoring α). However, ff99 and ff94gs both show unexpected patterns for glycine conformations, sampling regions which are not represented in PDB survey data. As we noted before, these likely arise from lack of treatment of both sets of backbone parameters (φ/ψ and φ′/ψ′). The ff99 glycine parameters were fit using alanine data and favor conformations that show no population in the PBD data (φ = −180° and ψ = 0°). The ff94gs surface is also in significant disagreement with PDB data, with a surface that has minima and low barrier heights that appear highly dissimilar to the PDB data and to any of the force fields that do include φ and ψ terms. This may artificially increase the glycine conformational transition rates. The plots for ff96, ff99ϕ as well as the plots obtained from simulations that used our previous modification of dihedral parameters^12,18 are shown in Figure S6 (supplementary material) and, similarly to ff99 and ff94gs, exhibit incorrect sampling for glycine dihedrals due to the lack of explicit treatment of both sets of backbone parameters.

Alanine free energy maps for the different force fields (Figure 3) show more similarity to each other, with major regions represented by right handed α-helix, PP_II and extended β conformations. Once again, differences in the relative free energies of the basins are readily apparent in the different force fields. While ff99SB and ff03 show a reasonable balance between α_R and PP_II, ff94 and ff99 show clear bias in favor of α_R. ff99 also shows the same tendency to adopt too-low (close to −180°) values of φ that was seen in its corresponding Gly₃ data. ff94gs samples both α_R and PP_II, but little population of extended β is present; α_R is also shifted low in ψ. The α_L conformation (with a positive backbone φ value) is sampled most in ff99SB and least in ff03. This conformation occurs in several types of β-turns⁴⁷, particularly those found in β-hairpins, and thus reproducing α_L region may be important for modeling β-hairpins.

In order to better interpret such significant differences in relative populations of various secondary structure elements, we turned to available experimental data that provide more direct evidence concerning the dominant structure of short alanine dipeptides in aqueous solution. All of these observations have important implications for the varied conformational states of proteins and therefore should be captured in the force field if it should ever be used for the description of unfolded proteins or for protein folding studies.

A recent two-dimensional infrared spectroscopy study of alanine dipeptide in aqueous solution⁴⁸ estimated backbone dihedral angles in the range (−70±25°, +120±25°), corresponding to PP_II-like conformation. Another structural study of alanine dipeptide using ¹³C NMR⁴⁹ confirmed the presence of PP_II conformation, but also suggests that a mixture of PP_II and α_R is more likely in water. The dominance of PP_II in trialanine was reiterated by two-dimensional vibrational spectroscopy studies of Woutersen & Hamm^50,51 and later modified by the same authors to include around 20% of α_R apart from PP_II ⁵². The experimental studies of Schweitzer-Stenner & Eker on trialanines^53,54 and tetraalanines⁵⁵ in water using polarized Raman, FT-IR and VCD spectroscopy confirm the dominance of PP_II conformation in tetraalanines, while a 50:50 mixture of PP_II and extended β-strand-like conformations was observed for trialanines. Other studies^56–58, mostly from Kallenbach and colleagues, have confirmed that short alanine peptides form predominantly PP_II conformation, which is in temperature dependent equilibrium with extended β-strand conformations. Taken together, these experimental findings suggest that short alanine peptides are found predominantly in PP_II-like structures with varying degree of extended β-strand, and possibly smaller fractions of α-helical conformations.

We analyzed the Ala₃ simulation data obtained from each force field in terms of fractional population of local conformational basins corresponding to the four prevalent secondary structure elements. The frequent transitions between PP_II, α_R and β regions result in relatively rapid thermalization of these basins during the simulations. However, the α_L region is separated from the other basins by a higher barrier near φ =0, resulting in much less frequent transitions from other regions (see Figure S5 in the supplementary information for further details). To ensure that the relative populations in that region were determined reliably, we ran replica exchange molecular dynamics (REMD) for ff99SB and ff03, which were the two force fields that provided conformational ensembles most consistent with the PDB data. All results are summarized in Table II. Comparison of standard and replica exchange molecular dynamics for ff99SB and ff03 demonstrates that relative populations in the four regions are essentially unchanged, which indicates that the results are well converged and that the differences do not arise from poor sampling.

Table II.

Fractions (percentages) of the four secondary structures in Ala₃ MD simulations in explicit water. See Methods for definitions of secondary structure regions. Numbers in parentheses are relative fractions, only considering populations within the four regions.

force field	Region
	PPII (%)	β (%)	αR (%)	αL (%)
ff99SB	38.1±1.2 (51.9±1.7)	20.1±0.7 (27.4±0.5)	13.0±1.6 (17.8±2.6)	2.1±0.9 (2.8±1.2)
ff99SB (REMD)	36.9±0.1 (50.1±0.3)	20.5±0.8 (27.9±1.0)	12.7±0.5 (17.2±0.7)	3.4±0.1 (4.6±0.1)
ff03	28.0±0.4 (37.8±0.4)	12.4±0.5 (16.7±0.5)	33.6±0.5 (45.4±0.9)	0.0±0.0 (0.0±0.0)
ff03 (REMD)	28.6±0.6 (38.2±0.6)	12.6±0.4 (16.9±0.5)	33.4±0.7 (44.7±1.1)	0.1±0.0 (0.1±0.0)
ff94	2.7±0.5 (3.5±0.7)	0.8±0.1 (1.1±0.2)	72.0±0.5 (94.6±0.6)	0.5±0.2 (0.7±0.3)
ff99	1.0±0.0 (2.5±0.1)	2.4±0.3 (6.3±0.8)	35.8±0.4 (90.8±0.5)	0.1±0.1 (0.3±0.3)
ff94gs	20.7±3.1 (30±6.0)	2.3±0.3 (3.4±0.7)	46.3±6.8 (66.0±6.5)	0.4±0.2 (0.6±0.2)
ff99ϕ	1.6±0.7 (2.2±0.9)	0.4±0.2 (0.5±0.2)	68.8±0.5 (96.6±0.6)	0.4±0.4 (1.2±1.2)

Simulations with ff99SB produce ensembles that are largely PP_II (38%) with significant fraction of β (20%) and lower population of α_R (13%). Compared to other force fields, this appears to be in best agreement with experimental observations, in that PP_II is the most favorable conformation with lower presence of extended β and even lower fraction of α-helical structures.

ff94 and ff99 show clear preference towards α_R (72% and 36% respectively), with the relative fractions of α_R as compared to the other basins being over 90% for both force fields. The lower absolute fraction in ff99 (36%) arises from the unusually high population of structures around (−150°, 0°) which do not correspond to any of the four canonical secondary structure basins and are also much less populated in other force fields. Overall, the data from ff94 and ff99 are both at variance with experimental observations.

ff03 behaves most similarly to ff99SB, but it may still be slightly over stabilizing α-helices as the most populated basin is the α_R conformation (34%). It is also somewhat unsettling that ff03 samples very poorly the α_L region that is important for β-turn conformations. We obtained no sampling of α_L in standard 80ns long MD simulations (0.0% fraction) indicating that this region is at least 5 kcal/mol (this is based on our cutoff for free energy plots, see Figure 3) less stable than the most populated α_R region. However, REMD simulations do sample α_L region with 0.06% population fraction. The sampling is insufficient to make a reliable estimate (see φ versus time plots in Figure S5 of supplementary material) of free energy difference between α_R and α_L, but based on the populations in those regions, α_L is at least 3.8 kcal/mol higher than α_R. Even though ff99SB only adopts 2–3% population in that region, it is still the largest compared to other force fields.

Simulations with ff99ϕ result in essentially the same behavior as was obtained for ff94, with the relative basin populations overwhelmingly dominated by α_R conformations (97 vs. 95% for ff94, see relative fractions of individual secondary structures in Table II and free energy surfaces in Figure S6 of supplementary material). Thus, at least at the level of glycine/alanine tetrapeptide, the small change of a single φ term in ff99ϕ does not seem to result in significantly different or improved behavior.

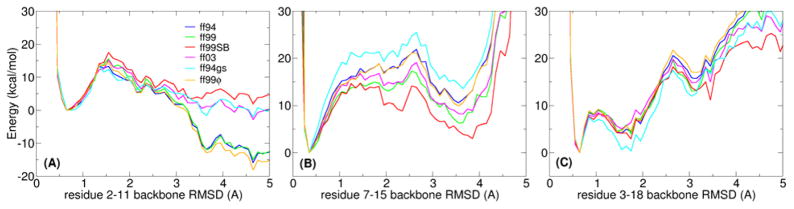
Decoy analysis of longer peptides

A critical property of the energy function is whether it can distinguish the native state such that it corresponds to the lowest (free) energy. We previously employed “decoy analysis”¹² as a rapid test of how well the energy function identifies the native structure. By plotting the potential energy against RMSD from the native structure one can readily see if the native state generally has lowest energies. This has the advantage that energy profiles for multiple force fields can be compared without obtaining converged ensembles for each peptide/force field combination. As a result of neglecting entropy and the use of an implicit water model, however, the results do not provide quantitative stability data for any of the peptides simulated.

We show the “lowest profile” (see Methods) of energies plotted versus RMSD from the native structure (Figure 4) with the expectation to see lowest potential energies (including solvation free energy) for small RMSD values, reflecting that the native basin indeed can be distinguished based merely on the energy function. We performed decoy screening using several peptides that have been experimentally demonstrated to adopt stable secondary and/or tertiary structures. Trpzip2 represents an exceptionally well-defined β-hairpin⁴², stabilized by cross-strand pairs of indole rings. The Baldwin type alanine-based peptide⁴⁴ was designed to adopt α-helix. Lastly, the trpcage mini-protein⁴⁵ has a mixture of secondary structure elements (α, 3¹⁰ and polyproline).

Figure 4.

“Lowest energy” profiles for three prototypical decoy systems, each tested with six AMBER force field variants (ff94, ff99, ff99SB, ff03, ff94gs, ff99ϕ): (A) trpzip2, which is known to adopt a β-hairpin, (B) a Baldwin-type sequence as a representative of an α-helix, and (C) trpcage as a representative of mixed secondary structures. RMSD values are calculated using the experimentally determined structure as a reference. Ideally, a force field should show lowest energies for the lowest RMSD values.

We previously used decoy analysis of the trpzip2 β-hairpin to demonstrate the extreme helical bias of the ff94/ff99 force fields¹², showing that non-native α-helical decoys had the lowest energies and were also the most populated in simulations. Therefore it comes as no surprise that the present decoy plots again clearly reveal the inadequacy of the ff94 and ff99 force fields to identify the native state of the hairpin. Indeed the pronounced minimum around 4–5 Å (Figure 4A) represents a large set of helical structures. Consistent with our observations from the tetrapeptide simulations, ff99ϕ behaves much like ff94. The native trpzip2 structure scores as lowest in potential energy only with ff99SB. ff03 also performs much better than ff94/ff99 but, as we noted before, may still be slightly too favorable for helices. ff94gs behaves similarly to ff03.

On the other hand, all tested force fields successfully score the α-conformation of the Baldwin helix with lowest energy. As expected, the energy gap between the helical conformation and those with larger RMSD values is greater for the force fields with strong helical bias (ff94, ff99, ff99ϕ). Even though ff94gs performed almost as well as ff99SB for trpzip2, it scores the Baldwin helix even more favorably than the ff94/ff99 force fields that are known to over stabilize α-helix conformations. Likewise, all of the force fields correctly identify the trpcage native fold.

Overall, both ff99SB and ff03 perform well in all three decoy cases. ff99ϕ follows very closely the behavior of ff94. Since ff94gs and ff99ϕ have not been used as extensively as the original AMBER force fields upon which they are based (ff94/ff99), and did not perform well on the tetrapeptide and decoy screens, we will not consider them in further validation.

Comparison with NMR parameters for lysozyme and ubiquitin

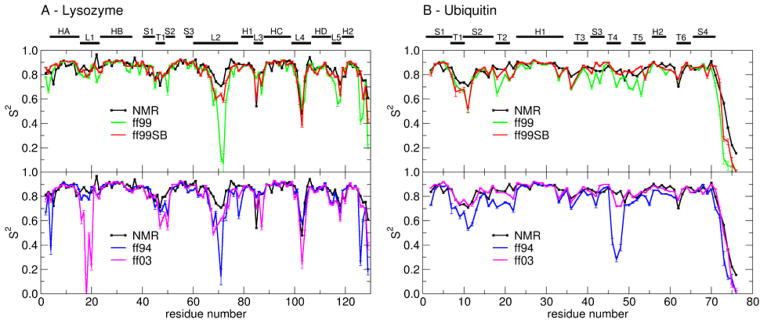
Hen egg white lysozyme has become a standard for evaluating the quality of force fields by comparing internal dynamics parameters calculated from MD simulations to NMR relaxation experiments^59–63. The degree of backbone flexibility is specified by experimentally derived order parameters S², which correspond to amide bond N-H librational motion. Lower S² values reflect increased backbone flexibility. We generated 30ns MD simulations of lysozyme with explicit water using four different parameter sets: ff94, ff99, ff99SB and ff03. Order parameters calculated from these simulations are compared to experimentally derived values in Figure 5A. The root mean square difference and the correlation coefficient between experimental and calculated S² are given in Table III. It can be seen that the agreement of ff99SB derived values with the experiment is very good, with the best correlation to experimental data and only half of the root mean square difference (RMSD) compared to all other force fields.

Figure 5.

Order parameters (S²) derived from experiment (black line) and calculated from MD simulations in explicit water with different force field parameter sets: ff99 (green), ff99SB (red), ff94 (blue) and ff03 (magenta). Error bars reflect the convergence of calculated S² values. (A) Lysozyme. Secondary structures of lysozyme are labeled: helix A (HA: residues 4–15), loop 1 (L1: 16–23), helix B (HB: 24–36), strand 1 (S1: 41–45), turn 1 (T1: 46–49), strand 2 (S2: 50–53), strand 3 (S3: 58–60), long loop 2 (L2: 61–78), 3₁₀ helix 1 (H1: 80–84), loop 3 (L3: 85–89), helix C (HC: 89–99), loop 4 (L4: 100–107), helix D (HD: 108–115), loop 5 (L5: 116–119) and 3₁₀ helix 2 (H2: 120–124). (B) Ubiquitin. Secondary structure elements in ubiquitin: strand 1 (S1: residues 1–7), turn 1 (7–10), strand 2 (S2: 10–17), turn 2 (T2: 18–21), helix 1 (H1: 23–34), turn 3 (T3: 37–40), strand 3 (S3: 41–44), turn 4 (T4: 45–48), turn 5 (T5: 51–54), helix 2 (H2: 56–59), turn 6 (T6: 62–65) and strand 4 (S4: 66–71). Differences are described in the text.

Table III.

Correlation of experimental and calculated order parameters (S²) for several AMBER force fields.

	ff94	ff99	ff99SB	ff03
	lysozyme
RMSD	0.11	0.12	0.06	0.13
Ra	0.61	0.62	0.83	0.62
	ubiquitin
RMSD	0.13	0.10	0.07	0.05
R	0.83	0.93	0.95	0.96

^alinear correlation coefficient

ff99SB describes well the increased flexibility of residues in loops L2 and L4 as well as residue 84 in L3 (which is not described well by other force fields). As has been noted previously⁶⁴, molecular mechanics force fields perform most poorly in the loop regions, usually exaggerating the flexibility of loop residues. This is confirmed by our simulations where the most obvious disagreements with experimental order parameters occur in loops. Some of these discrepancies might be explained by a particular bias/weakness of the specific force field that was revealed in our model system studies. For example, we demonstrated that ff03 did not sample the α_L region of φ/ψ space for alanine tetrapeptide. The pronounced failure of ff03 to match experimental data in the L1 loop (with simulated S² values much too low) may be a result of the α_L conformation that is adopted by several L1 residues in the crystal structure. The local instability in this conformation may give rise to increased structural dynamics in the ff03 simulations. Interestingly, significantly lower order parameters specifically in regions with glycines occupying the α_L conformation were also noted for CHARMM22 force field by its developers²⁶.

We also showed that ff94/ff99 are both biased towards helical structures, lacking sampling in PP_II and β regions. This is likely the cause for increased flexibility in the middle of the long L2 loop, where several residues occupy the extended β-like conformation. This problem may be exacerbated in ff99 due to the presence of two glycines; we showed above that the glycine free energy surface in ff99 is highly distorted. Overall, many of the problematic regions are found to contain glycines, further supporting our assertion of the inadequacy of glycine parameters in many AMBER force field variants.

We repeated the same type of analysis for another protein, human ubiquitin. This is another small and well characterized protein of 76 residues with a known crystal structure^37,38, for which NMR relaxation parameters were also determined experimentally⁶⁵. Based on the crystal structure, the C-terminal region extends away from and makes few contacts with the remainder. This is reflected by very low S² parameters for the four terminal residues. Again, Figure 5B graphically compares the ability of the four force fields to reproduce experimental S² parameters. The quantitative indicators for the agreement with experimental data is given in Table III. For this system, all four AMBER force fields work reasonably well, with no large discrepancies with the exception of the region near turn T4 when using ff94. All force fields but ff03 exaggerate flexibility of turn T1 connecting strands S1 and S2. Overall, ff03 performs best, even though ff99SB still provides slight improvement over ff94/ff99. Examination of trajectories did not reveal any specific structural differences; rather the variations appear to arise from the magnitude of fluctuations about similar average structures.

Overall, these simulations serve as a good example of sensitivity of internal dynamics, as measured by NMR order parameters, to particular details of the molecular mechanics force field. Also, it is clear from these two sets of simulations that the quality of agreement to experimental relaxation data is somewhat system dependent. All force fields achieved better agreement with S² values for ubiquitin than for lysozyme.

Conclusions

We have shown that several variants of AMBER force field have deficiencies arising from inadequate backbone dihedral term parametrization. The original ff94 force field introduced backbone dihedral treatment to be able to reproduce relative energies of selected glycine and alanine dipeptide conformers. Due to limited computational resources at the time, only a few conformers were included in the fitting procedure. We have shown here and previously that ff94 strongly favors helical conformations. More recent modifications of ff94 attempted to rectify the problem, but only partially succeeded. All of them failed to recognize that not just one, but two sets of dihedral parameters control backbone preferences in ff94. The first set is optimized solely for glycine. Any other amino acid will use both glycine set of parameters and a second set of dihedral parameters which are usually parametrized using alanine. Prior modifications of ff94, such as ff96, ff99, ff94gs, ff99ϕ, and our previous modification of ff99¹⁸ only changed the first set of dihedrals, effectively overwriting glycine dihedral parameters with the ones intended for alanine, unaware that there existed a set of alanine dihedral parameters that do not use the traditional definition of φ and ψ. This resulted in incorrect parametrization of glycine. Our data demonstrate (Figure 3, Figure S6) that these parameter sets result in conformational ensembles for glycine peptides that are in significant disagreement with both the PDB data and with force fields that explicitly include glycine in the fitting process. We therefore recommend against using these parameter sets for protein simulations.

The modification of ff94/ff99 force field presented in this work aims to rectify the problems caused by misunderstanding of parametrization procedure, but also endeavors to improve the parametrization initially done in ff94. This was primarily achieved through two courses of action. First, we used a large number of glycine and alanine tetrapeptide local minima instead of a small number of dipeptide conformations when fitting QM and MM energies. We believe that, unlike the dipeptide, tetrapeptide dihedral space bears closer resemblance to that found in proteins, and also has a local minimum for the α-helical conformation, permitting direct fitting to avoid over stabilization that was observed in earlier variants. Second, we used a procedure that avoids biasing the outcome of the dihedral parameters optimization with respect to a single a priori chosen reference conformation.

The resulting parameter set was shown to result in better balance of prevalent secondary structures, such as PP_II, α-helix and extended/β-strand in simulations of short glycine and alanine peptides in water. This was supported by better agreement of dihedral angle regions sampled in the simulations with regions generated from PDB survey data. Here, the improvement for glycine residue is most noticeable, where some of the force fields produced free energy surfaces that bore no resemblance to those observed for real proteins. The relative sampling of the typical secondary structure regions in simulations of alanine tetrapeptide using the new force field is in good agreement with experimental data which used various techniques to infer the prevalent states of short alanine peptides. Beyond short glycine and alanine peptides, the qualitative performance of the new parameters was tested on several larger systems representing typical secondary structures: trpzip2 β-hairpin, Baldwin type α-helix and the trpcage miniprotein. ff99SB correctly identified native structure as that with the lowest energy in all three cases, which was not observed for any of the other force field variants. Finally, we performed long explicit water simulations of lysozyme and ubiquitin and tested the performance of different force field variants by comparing relaxation order parameters calculated from simulations to experimental NMR values. Once again, the newly derived parameters performed the best. The changes we introduced with ff99SB modification are extremely minimal and therefore excellent compatibility should be preserved with existing parameters developed to be compatible with ff94/ff99. This is in contrast to the ff03 protein parameters, for which no compatible parameters currently exist for small molecules and most importantly nucleic acids. It is therefore unclear whether ff03 could be used for simulations of these complexes (which would include potentially incompatible charge models).

As usual, caution should be taken when any force fields are used beyond their range of validity. For example, one can expect a substantial effect of solvation model used. Implicit solvation models, such as Generalized Born, may shift the balance between different secondary structure elements. If, for example, PP_II is indeed stabilized by specific interactions with explicit water as recently suggested^57,66–68, such stabilization is not possible with implicit solvents, and thus structural preference may change. In fact, we recently reported that GB solvation models increase α-helical propensity⁶⁹. Different approaches in force field development might be needed to account for these effects, and force fields should likely be tested with the particular characteristics (and perhaps idiosyncrasies) of these models in mind.

Force field development is a complex process in which many approximations are typically required. In the present case, conformational energies from high-level gas-phase QM calculations were used to fit dihedral parameters for a force field in which the partial charges should more closely represent those in aqueous solution. Additionally, the large difference in the size of systems that are used to train biomolecular force fields and those for which they are intended to be used results in a slow maturation period, often with deficiencies becoming apparent only after extensive use. For this reason, we extensively used these parameters on a variety of systems not discussed here before making this report. For example, the improved glycine parametrization was important in our recent simulations of HIV-1 protease⁷⁰, where glycine rich “flaps” play an essential role in protease dynamics. Another study⁶⁹ reported a hybrid replica exchange method, where ff99SB was used to test the methodology based on conformational sampling of polyalanine peptides of varying lengths. Our recent simulations⁷¹ of fragments of the villin headpiece with ff99SB also achieved good agreement with experimental trends⁷² in calculated J-coupling constants and helical propensities. These studies have supplied further evidence that the ff99SB parameter set provides a reasonable parameter set for protein simulations, in the context of an efficient, additive molecular mechanics model.