The Unfolded State of the Villin Headpiece Helical Subdomain: Computational Studies of the Role of Locally Stabilized Structure

Summary

The 36 residue villin headpiece helical subdomain (HP36) is one of the fastest cooperatively folding proteins, folding on the microsecond timescale. HP36’s simple three helix topology, fast folding and small size have made it an attractive model system for computational and experimental studies of protein folding. Recent experimental studies have explored the denatured state of HP36 using fragment analysis coupled with relatively low resolution spectroscopic techniques. These studies have shown that there is apparently only a small tendency to form locally stabilized secondary structure. In this study, we complement the experimental studies by using Replica Exchange Molecular Dynamics (REMD) with explicit solvent to investigate the structural features of these peptide models of unfolded HP36. To ensure convergence, two sets of simulations for each fragment were performed with different initial structures, and simulations were continued until these generated very similar final ensembles. These simulations reveal low populations of native-like structure and early folding events which cannot be resolved by experiment. For each fragment, calculated J-coupling constants and helical propensities are in good agreement with experimental trends. HP-1, corresponding to residues 41 to 53 and including the first α-helix, contains the highest helical population. HP-3, corresponding to residues 62 through 75 and including the third α-helix, contains a small population of helical turn residing at the N-terminus while HP-2, corresponding to residues 52 through 61 and including the second α-helix, formed little to no structure in isolation. Overall, HP-1 was the only fragment to adopt a native-like conformation, but the low population suggests that formation of significant structure only occurs after formation of specific tertiary interactions.

Introduction

Structure in the unfolded state may play a significant role in the rapid folding of proteins by limiting the conformational search. Recent experimental work from the Fersht and Oas labs has highlighted the role of unfolded state structure in the rapid folding of helical proteins.^{1; 2} Other work has suggested the importance of polyproline II conformations (PPII) structure in the unfolded ensemble^{3; 4; 5; 6; 7}. Unfortunately, direct experimental studies of the unfolded state are difficult because the most relevant unfolded state is that which is in equilibrium with the folded state under native conditions. The normal high cooperativity of folding together with the free energy balance of folding means that this state is only sparsely populated at equilibrium. Experimental difficulties also arise because of the short lifetime of the denatured state in refolding experiments. Consequently, indirect methods have to be employed but many approaches fail to examine the unfolded state under equilibrium conditions. ^{8; 9; 10; 11; 12}

One indirect approach to studying the denatured state under native conditions is to analyze peptide fragments corresponding to elements of secondary structure derived from the whole protein. Peptide fragment analysis provides the local propensity for secondary structure formation and a potential glimpse at structures that may form in the early stages of folding. Such locally stabilized structure can play a role in rapid folding by limiting the early stages of the conformational search. For example, one popular model for folding, the diffusion collision model, postulates a critical role for locally stabilized microdomains. The determination of these structural details are potentially of great importance for the folding of helical proteins.^{2; 13; 14}

The villin headpiece helical subdomain (HP36), the C-terminal portion of the villin headpiece, is the shortest naturally occurring sequence which has been shown to fold cooperatively (Figure 1). Its rapid folding, small size and simple topology of three helices have made this domain an extremely popular system for computational and theoretical studies.^{3; 13; 15; 16; 17; 18; 19; 20; 21; 22; 23} These studies have largely focused on generation of the correct native topology and have not investigated the details of the folding mechanism or the role of residual structure in the unfolded state.

Figure 1.

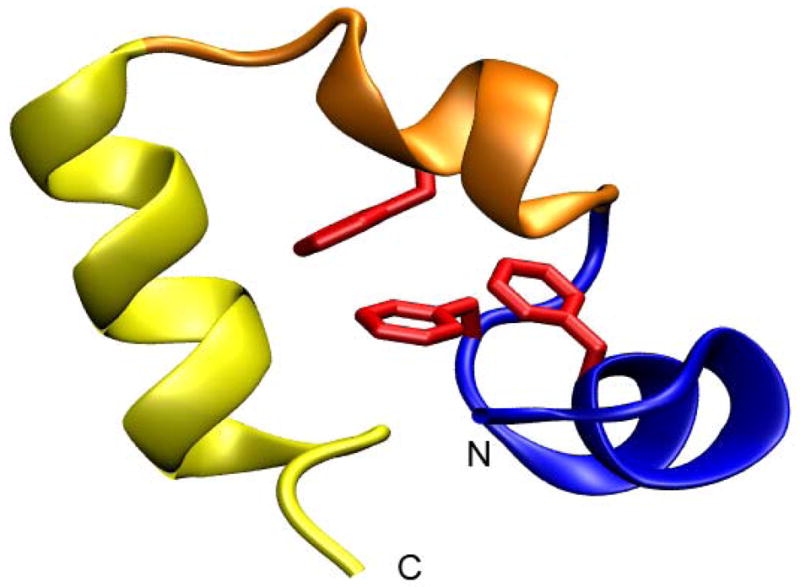
Structure of the Villin headpiece subdomain (pdb code 1vii). HP-1 is in blue, HP-2 is in orange and HP-3 is in yellow. Phe47, Phe51, and Phe58 are shown in red. The N and C-termini are labeled.

Recent experimental work has explored the possibility of residual structure in the unfolded state of HP36.²⁴ In that work, a set of fragments corresponding to the three α-helices were studied as well as a larger fragment containing the first two helices. None of the individual peptide fragments showed significant helical content as judged by Circular Dichroism (CD) spectroscopy. However, two of the helices in HP36 are quite small in fragments 1 (HP-1) and 2 (HP-2) and the CD spectra of short helices are not well understood. ^{25; 26; 27} Thus it is not clear how best to interpret CD studies of the small helices that may be formed by these fragments, particularly when NMR studies hint at some tendency to form non-random structure. The experimentally measured ¹H-alpha chemical shift deviations from random coil (approximately 0.25 ppm upfield) observed for the HP36 fragments suggest either sparsely populated helical conformations or ring current effects in HP-1 and fragment 3 (HP-3). These potential ambiguities are due to the limitations that exist with experimental methods.

Simulations can help overcome these limitations and allow for the observation of structure at the level of individual molecules instead of the ensemble averages typically provided by experiments. Computational studies can also provide atomic level detail concerning specific interactions that may not be readily available from experimental studies of rapidly interconverting ensembles. This enhances the understanding of mechanistic details of protein folding and structure. However, conformational sampling remains a significant obstacle in molecular dynamics (MD) simulations. Generation of precise populations at equilibrium is difficult due to the protein folding time scale being much longer than is typically accessible to simulation. Hence, the study of partially populated states through simulation is hampered by poor convergence.

Replica exchange molecular dynamics (REMD) is an enhanced sampling technique^{28; 29; 30} that can help overcome the limited time scale issues, yet it remains a challenging task to obtain converged results, particularly for large systems. Many different studies have used REMD to study folding in smaller model peptide systems^{31; 32; 33; 34; 35; 36} however studies of unfolded state structure have been more limited. ^26;37

In this paper, we analyze the same set of short fragments of HP-36 that were studied experimentally in an attempt to clarify the extent of locally stabilized secondary structure. We conducted REMD simulations using both an implicit and explicit solvent model for each fragment. The results demonstrate that explicit solvent is the more accurate approach for studying these small peptides. We find HP-1 possesses the most native-like structure of the three fragments, and the potential role that locally stabilized structure may play a role in the fast folding of HP36 is discussed.

Results

Convergence of Simulations Allows For Reliable Populations of Low Levels of Structure

When the goal of a simulation study is simply to identify a low-energy conformation, it is typically unnecessary to generate a Boltzmann-weighted ensemble with conformations populated according to relative energies. However, when one wishes to use these results to gain insight into the relationship of the unfolded state to the folding process, it is necessary to obtain a reliable and quantitative estimation of the extent to which any residual structure is present in the unfolded state, with well defined limits.

In the present case, we investigate the role of locally stabilized structure in the unfolded state ensemble of the villin headpiece protein. In order to ensure that the simulations are robust and that the populations that we observe are precise, all of the simulations were repeated with two different initial starting structures. For each fragment, one simulation was initiated from a fully extended structure while another was started from a helical structure. Since it has been demonstrated that different properties converge at different rates³⁸, we use as our convergence metric the fractional populations of alternate conformations which are the main focus of our analysis. As described in the Methods, conformation families are defined based on the combined set of structures from all simulations, and the populations of each conformation family are then calculated for the ensemble obtained from each of the two alternate simulations. For all fragments, the absolute populations sampled in the two independent runs in the TIP3P³⁹ explicit water model demonstrated a high correlation (R² = .994 (HP-1), .993 (HP-2), .863 (HP-3)), indicating that the populations of each conformational basin are independent of initial coordinates. For the simulations in implicit solvent, there was a high correlation between runs 1 and 2 for HP-1 (0.999) and HP-3 (0.996), but HP-2 showed poor convergence (0.279). The explicit solvent simulations clearly provide more data precision for all three fragments; this may arise from slower convergence in the implicit model due to high barriers to conformational change arising from salt bridges that are too strong in the implicit model.⁴⁰

Comparison of structural ensembles obtained using explicit and implicit solvent models

Accurate treatment of solvation is essential for meaningful simulation of biological molecules in solution. Explicit solvent models can be highly effective, particularly when water has non-bulk properties and interacts directly with the solute⁴¹. Implicit models such as the semi-analytical generalized Born model (GB)⁴² are attractive because they are computationally less expensive and can converge more rapidly than simulations in explicit water due to lack of solvent viscosity. While GB has been widely used for protein folding studies, others have reported poor results including secondary structural bias and ion pairing issues.^{34; 43; 44} We note, however, that many variants of the GB model exist and relatively few studies comparing their performance for protein folding have been published. ^{45; 46; 47}

In this study, both the GB and TIP3P solvent models share the same largest cluster in HP1, indicating the same most preferred structure. Nevertheless they differ significantly in the contribution of this conformation to the overall ensemble (90 % in GB vs. 25 % in TIP3P). Overall the populations of the conformation families for HP-1 show a poor correlation between TIP3P and GB ensembles (R² = .67 and a slope of .26). This arises primarily from a ~1.5 kcal/mol overstabilization of the α-helical region of the Ramachandran region in the GB simulations as compared to TIP3P. The other fragments showed similarly poor agreement between the solvent models. We therefore focus on results obtained using TIP3P and discuss GB data only to illustrate specific shortcomings observed with that model in the discussions.

Summary of data analysis approaches

Data from the two independent sets of simulations were combined for analysis of each fragment as described in Methods. Differences between the data sets provide a low bound to the actual uncertainty. Analysis included calculation of root mean square deviation (RMSD) of structures as compared to the conformation of the fragment in intact HP36, radius of gyration (Rg), torsion angles, secondary structure types using the dictionary of secondary structure prediction (DSSP) algorithm⁴⁸, Lifson-Roig (LR) analysis of the distribution of helix lengths^{49; 50}, and conformational cluster analysis.

Simulations of Ala₁₀

A simulation of Ala₁₀ in explicit solvent was run as a control. This particular system was chosen due to a similar size to the three fragments and the fact that Ala has the smallest sidechain (other than Gly). Comparison of the Ala₁₀ structural ensemble to those from the fragments provides insight into the role of specific side-chain interactions in the HP36 fragments.

The central residue of Ala₁₀ samples local backbone conformations which are located in all 4 basins of the Ramachandran plot: α helix, PPII, anti-parallel beta sheet and the left handed helical basin. Furthermore, DSSP analysis of Ala₁₀ resulted in an average α-helical content of only 1.3 %. Since Ala10 lacks any intrinsic structure, we conclude that any helical content observed in the fragments are the result of the sequence. In addition, the lack of significant helical content in Ala₁₀ suggests that the force field employed does not suffer from over-stabilization of α-helices, as has been reported for previous versions of the Amber force field.^{51; 52}

Analysis of Conformational Preferences for Fragment HP-1 Suggests Locally Stabilized Structure in the Unfolded State

HP-1 (M41LSDEDFKAVFGM53) contains the sequence that forms the N-terminal helix of HP36, (between D44 and K48), located near the center of the fragment, with 3 backbone α-helical hydrogen bonds in intact HP36. The fragment includes a stretch of predominantly basic and acidic residues and several residues that can perform helix N-capping. We first present properties of the entire ensemble of structures sampled, followed by more detailed discussion of specific preferred conformations.

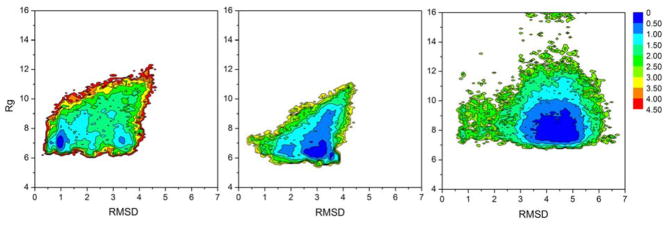
Figure 2a shows the free energy landscape at 300 K for HP-1 along coordinates of the Rg and the RMSD to the backbone of the NMR structure of HP36. The global free energy minimum has a low RMSD (1.0Å) and an Rg value of 7.0Å, similar to HP-1 in the native state of HP36 (Rg = 6.7Ǻ). The broad shape of the minimum with respect to Rg indicates that the compactness of the fragment is variable, while the relatively narrow shape with respect to RMSD suggests that the structures remain quite native-like during these fluctuations. Overall, the consistency between the RMSD and native like Rg in this landscape indicate that at least half (discussed later in cluster analysis) of the ensemble of structures populated by HP-1 have a high similarity to the conformation adopted by the fragment in intact HP36, suggesting that residual native structure in this region is fairly well populated in the unfolded state of HP36.

Figure 2.

Free energy landscapes of three fragments at 300K from REMD explicit water simulations. (A) Rg vs RMSD (backbone 43 – 49) to the native HP36 structure for HP-1 (B) Rg vs RMSD (backbone 54–59) to the native HP36 for HP-2 (C) Rg vs. RMSD (backbone 64–70) to the native HP36 for HP-3. While all three fragments remain compact as in HP36, only HP-1 has a free energy minimum located at a low RMSD. The other two fragments occupy minima with higher RMSDs and more broad minima than HP-1.

Figure 3a shows the Ramachandran free energy surfaces at 300K for three residues in the HP-1 ensemble, selected from the terminal regions and the center of the fragment. As expected, the termini are more flexible, with the N-terminal Leu42 predominantly sampling the PPII and helical basins, while the C-terminal V50 samples shallow, broad minima in the PPII, and α-helical basins (approximately 1.0 – 1.5 kcal/mol in depth) (Figure 5c). In contrast, the central D46 is stabilized in the helical region by approximately 2.0 kcal/mol relative to other basins (Figure 5b). D46 adopts local backbone angles which correspond to the ones seen in the native state of HP36.

Figure 3.

Free energy profiles of residues at 300 K from REMD explicit water simulations in (A) HP-1 (L42, D46, V50); (B) HP-2 (T54, A57, L61) and (C) HP-3 (W64, L69, K73). HP-1 and HP-3 have global free energy minima in the helical region for residues D46 in HP-1 and W64 in HP-3. All three residues in HP-2 occupy shallow local minima, which suggest significant conformational flexibility.

Figure 5.

DSSP Analysis of (A) HP-1; (B) HP-2; (C) HP-3 at 300 K. (Black = 3₁₀; Red = α-helix; Green = π-helix; Blue = parallel β-strand; Yellow = antiparallel β-strand; Magenta = turn). HP-1 contains the most helical content of all three fragments.

LR and DSSP analysis were employed to evaluate the relationship between local and long range helical structure in HP-1 (Figure 4 & 5a). The most probable helix length is 3 to 4 residues, but longer helices of 5–6 residues are still found in 5 - 10% of the structures in the ensemble. This is similar to the length of the first helix in the native HP36. DSSP shows that the α-helical content of the ensemble increases rapidly from the N-terminus toward the center of the fragment, then drops sharply towards the C-terminus (average α-helicity of 35 % and 8 % at N and C-termini respectively). This is consistent with the trend seen in the free energy surfaces which show that the relative depth of the helical basin increases towards the center of the sequence and decreases toward the C-terminus. Importantly, the high α-helical propensity observed in the center of the fragment (35 %) is in the same region as the α-helix in the native HP36 structure (D44 – K48). Other types of secondary structure are less prevalent and the propensities are fairly consistent across the sequence, in contrast to the increase in helical content in the middle of the fragment.

Figure 4.

Probability of finding helices of a particular length in the ensembles at 300K for (A) HP-1(black), (B) HP-2 (red), and (C) HP-3 (green). The populations show that HP-2 has little probability (2–4%) of forming even a single turn of helix with 3 residues. HP-3 does form very short helices, but only HP-1 shows significant population of helices that are 5–7 residues in length

Cluster analysis was performed on the backbone of HP-1 from residues 43 to 49 (Figure 5). The two most populated conformational clusters, which account for approximately 59 and 13 % of the structures respectively, contain the most α-helical structure. The first cluster contains structures with modest population of α-helix from S43 to A49, while cluster 2 features a shorter α-helical turn from L42 to E45. The population of cluster 3 (9 % of the ensemble) is made up of helix-turn-helix structures displaying a helical content of 20 and 15 % at the N and C-termini respectively, however there is greater variation in the structures within the entire cluster than in the first two clusters. These structural populations are in agreement with the DSSP results which showed that the N-terminus is more helical than the C-terminus. It is impressive to note that the most populated cluster forms the full helical conformation seen in HP36.

HP-2 shows no significant residual structure

HP-2 (G52MTRSAFANL61) contains the shortest helix in HP36, comprising residues R55 through F58 and containing only one α-helical hydrogen bond between T54-F58. This fragment contains N-capping residues that might favor helix formation, however the small number of residues in HP-2 may not be sufficient to stabilize the native helical conformation. Figure 2b shows the free energy surface at 300K in explicit solvent along the Rg and RMSD to the HP36 structure. The distribution of the minima is much broader and not as well defined as was observed for HP-1. This landscape shows one broad, shallow global free energy minimum centered at RMSD of 2.5 Ǻ and Rg of ~ 6.0 Ǻ. Similar to HP-1, this Rg value is comparable to that seen for this compact region in native HP36 (6.0 Å). In contrast to our HP-1 results, however, the structures sampled for HP-2 are quite different than the structure in the corresponding helical region in native HP36, averaging an RMSD of 2.9 Å for the residues comprising the native helix. These observations show that HP-2 is less structured than HP-1 and does not form an appreciable amount of the structure seen in HP36.

Figure 3b shows Ramachandran free energy surfaces for three residues of HP-2 at 300K. Thr54 and Ala57 sample all 4 major basins, while Leu61 occupies a broader basin in the α-helical region, and to a lesser extent the PPII and anti-parallel β-strand regions. DSSP analysis shows that the N-terminal portion of HP-2 is more helical than the C-terminal region, however the total helical content is significantly lower for HP-2 (2.2 ± .7 %) than for HP-1 (19.8 %) (Figure 5b). LR analysis indicates that HP-2 does not adopt significant helical content, with less than 5% population even for short 3-residue helices (Figure 4). Instead, HP-2 contains a modest population of turn (22.0 ± 1.8 %) in the center of its sequence and a small population of anti-parallel β-strand at each of the termini. The high turn population could indicate nascent helix initiation or transient β–turn structure.

Cluster analysis was performed on the backbone of HP-2 from residues 55 to 59 since this region contains the native helix of HP36 and DSSP indicates significant turn population in the fragment. In Figure 7, we show representative structures for the top five clusters, each of which makes up 10–30 % of the entire ensemble of HP-2. This is unlike HP-1, in which more than half of the entire ensemble is comprised of a single structure cluster. All of the clusters have very low α-helicity, except for the second cluster which has structures that are most helical in the center (approximately 10 %). The smaller clusters appear to sample random coil and turn-like structures.

Figure 7.

Representative structures for the five most populated clusters of HP-2. (A) 1^st cluster (25.2 %) (B) 2^nd cluster (21 ± 3 %) (C) 3^rd cluster (13.1 ± .6 %) (D) 4^th cluster (13 ± 2 %) (E) 5^th cluster (11.0 ± .6 %). All five clusters sample random coil and turn-like structure.

Overall, HP-2 does not show strong evidence of any well-defined structure. It appears that the residues in HP-2 are more flexible and this region of HP36 relies on tertiary contacts and packing constraints to stabilize secondary structure. Vermeulen et al. have suggested that the second helix should not be stable without residues from the third helix which favorably interact with the second helix’s dipole. ⁵³

Analysis of HP-3

HP-3 (P62LWKQQNLKKEKGL75) contains the longest helix in the native structure of HP36 (L63 to E72), with 7 stable α-helical hydrogen bonds, a proline that promotes helix initiation in native HP36, and a patch of acidic and basic residues that serve as part of the actin binding domain. Figure 2c shows the free energy landscapes for the entire ensemble of HP-3 at 300K along the radius of gyration (Rg) and RMSD to the HP36 structure. Despite the relatively large number of helical hydrogen bonds in the HP36 structure, the distribution of the minima for HP-3 is the broadest of all three fragments, centered at an RMSD of 4.0 Å and Rg of 8.0 Å. The structures are also somewhat less compact than in HP36 (Rg of 9.0 ± 2.0 Å compared to 7.0 Å in native HP36). While HP-1 showed significant sampling of native-like backbone structure (RMSD = 1.0 Ǻ), and HP-2 showed a larger average RMSD of 2.9 Ǻ, HP-3 shows even larger deviations from the HP36 native structures with an average RMSD of 4.5 ± 1.9 Å. These larger values may indicate further deviation from native structure as compared to HP-2, or they may arise from the larger size of this fragment.

Unlike HP-1 but similar to HP-2, HP-3 shows little residual helical content despite being the longest helix in HP36. Figure 3c shows Ramachandran free energy surfaces for three residues (W64, N68, and K73) selected from different parts of HP-3. W64 has the global free energy minimum in the helical region of the free energy surface while N68 occupies all 4 major basins at nearly equal free energies, unlike the well-defined α-helical conformation observed for this residue in the middle of helix 3 in HP36. Similar shallow minima are sampled by K73, which is consistent with the low level of structure seen at the C-termini of all three fragments.

Figure 4 shows results of LR analysis on HP-3, which indicate a 5–10% probability of forming short 3–4 residue helices, larger than was seen in HP-2. This is in agreement with DSSP calculations that show limited population of helical turns in the N-terminal region (W64 is approximately 20 % α-helical). This lack of helical structure in the C-terminus is consistent with the free energy surfaces of L69 and K73 which show shallow local minima sampled in the 4 major basins (figure 3b & 3c). Unlike HP-1, nearly no propensity to form longer helices of 5–6 residues is observed. Instead, many structures in the ensemble of HP-3 have a high local turn population (20 ± 2 %) (Figure 5c). In the intact HP36, helix 3 makes extensive hydrophobic contacts with residues from helix 1 and helix 2. In the absence of these interactions, the helical structure is not stable.

Further evidence of significant conformational variability is obtained from cluster analysis, where the five largest clusters account for only 69% of the ensemble (Figure 8). DSSP analysis shows that the center of HP-3 samples a significant amount of turn conformation, with the only significant helical content being 3₁₀ structure near the N-terminus that is present in clusters 1, 3 and 4. Clusters 1 and 4 are made up of α-helical structures at the N-terminus from L63 to Q66 while cluster 5 appears to be somewhat native-like, sampling a long helix between residues L63 and K72, with an average α-helicity per residue of 34 %. However, cluster 5 only comprises only 10 % of the structures and therefore it does not make a significant contribution to the ensemble average. Unlike HP-2, however, it does indicate that HP-3 has a small propensity to adopt a native-like conformation.

Figure 8.

Representative structures for the five most populated clusters of HP-3. (A) 1^st cluster (19 ± 2 %) (B) 2^nd cluster (15 ± 2 %) (C) 3^rd cluster (14.1 ± .7 %) (D) 4^th cluster (10.5 ± .9 %) (E) 5^th cluster (10 ± 5 %). Cluster 5 contains the most native-like helix, however the population is quite small.

Discussion

What may stabilize the high population of helical structure in HP-1?

We examined the entire HP-1 ensemble to identify contacts that may be playing a part in stabilizing the helical structure. Approximately 50 % of the ensemble had ion-pair contacts between D44 - K48 (27 ± 4%), E45 - K48(8 ± 2 %), and both D44 and E45 with K48 (14.0 ± .03 %). Another contact was present (85.0 ± .5 %) between the D44 backbone carbonyl and the charged sidechain of K48; this is present alone (56 ± 4 %) and with the charged sidechain of D44 (30 ± 6 %). These contacts are not observed in the NMR and the x-ray structures where the charged groups of these residues are more than 6 Ǻ apart in space. These interactions appear to desolvate the backbone hydrogen bonds, resulting in stabilization of α-helical structure. These types of interactions have been shown to favor helical structure in various peptide systems.⁵⁴

Comparison with experimental data

The tendency of the three fragments to adopt helical structure in simulations is in good agreement with the trends seen in CD experiments (HP-1 > HP-3 > HP-2). These differences observed in the experiment are small due to the length and the low population of helix. Figure 9 shows the theoretical and experimental J-coupling values for the residues in all three fragments. The calculated J-couplings match most of the experimental trends with the exception of a few residues whose deviation from experiment is quite small (<1.5 Hz). HP-1 and HP-3 have calculated J-couplings that are lower than 7 Hz (shifted to the helical region) in the N-terminal region, consistent with analysis of their ensembles. The calculated J-couplings of HP-2 are 7.0 ± 0.5 Hz, consistent with an average ensemble that has no specific structural preference. While the results do not show any strong conformational preferences, they show that the ensembles generated in the simulations are able to reasonably reproduce experimental parameters.

Figure 9.

J-coupling values for residues in (A) HP-1 (B) HP-2; (C) HP-3. Experimental values are shown in red and calculated values are shown in black. Calculations for all three fragments followed the relative trends and were in good agreement of the experimental data. Some residues are missing because either the J-coupling constants were not measured or the results were ambiguous.

Some differences exist between the simulation data and previous solid state NMR freeze quench studies that also suggested some non-random structure.⁵⁵ Those studies are consistent with V50 in HP-1 adopting a relatively well ordered local polyproline II (PPII) conformation; A57 in HP-2 is more conformationally disordered, but retains significant helix content; and L69 in HP-3 is the most disordered of these three labeled residues in unfolded 35-residue villin headpiece subdomain (HP35). Those experiments suggested that local structure is present for HP-1 and HP-2 but only disordered structures are populated for HP-3⁵⁵. Our study showed no backbone conformational preference at 300 K for V50 in HP-1, A57 in HP-2, and L69 in HP-3 (Figures 5c, 9b &12b). However, the solid state NMR experiments are performed at cold temperatures which might induce these residues to adopt more a rigid backbone conformation. Our analysis evaluated the ensembles generated at 300 K, conditions that were similar to the original fragment study, and the structural populations are more relevant to folding at this temperature.

Implications for folding

This study suggests that the HP-1 has the highest tendency to adopt helical structure among the three fragments, and these have high similarity to the structure of the fragment in HP36. HP-3 also samples fully formed structure as adopted in the native state of HP36, but at a significantly smaller overall probability than HP-1. HP-2 contains the least residual structure and samples a wide variety of conformations, all in low population. These isolated structures need to be stabilized by other contacts to form native helical structure. All of the fragments are more helical than Ala₁₀, suggesting that the side chains play an important role and that observed tendency to form helices does not arise from over-stabilization of helical structure that has been reported for earlier versions of the Amber force field.

Overall, the geometric ensemble properties of HP-1 are remarkably similar to that found in the HP36 native state, but with a much lower overall propensity to form well-defined structure. In previous studies, the Pande lab has proposed the “mean-structure hypothesis” which states that the geometry of the collapsed unfolded state of small peptides and proteins in an average sense corresponds to the native equilibrium state even though individual structures in the ensemble demonstrate unfolded, random coil properties.³ The presence of a significant population of HP-1 structures with low RMSD values suggests that at least some of the individual structures sampled may also be highly (although locally) native-like.

Preformed structure in the unfolded state has been implicated for potentially favoring very rapid folding. Residual structure might help guide proteins to fold into the native state. Recent studies of model helical bundles have suggested that such residual structure is essential in aiding the protein folding process.^{1; 12} The presence of low levels of highly native-like structure in the HP-1 fragment may play a role in the fast folding of HP36. This residual helical content in the HP-1 fragment varies only weakly with temperature, with average α-helical content of 19% at 300K and 17% at 340K (considering all helix lengths). This is consistent with experimental studies for larger fragments and with the intact protein, which have shown that there is considerable structure in the unfolded state at higher temperatures.²⁴ We note, however, that force fields of the type used in this study are not parameterized to quantitatively reproduce temperature-dependent behavior.

The diffusion collision model has often been applied to helical proteins. However, Islam et al. has noted that this model is ineffective at describing the folding of HP36 due to the relatively small size of the helices in the subdomain.¹³ Residual structure in isolated helices may not be enough to drive the folding process. Gianni et al.⁵⁶ and Daggett et al.⁵⁷ have suggested that some proteins can form unstable secondary structure that will become stable once tertiary contacts are secured around a nucleus of hydrophobic contacts. This mechanism seems to relate better to HP36.

Much experimental work has focused on the contacts that stabilize the native state. The work by McKnight’s group has stressed the importance of three phenylalanines in maintaining the hydrophobic core.¹⁶ Experimental fragment studies²⁴ have shown the fragment containing the first two helices of HP36 and all three of these phenylalanines maintains a considerable amount of residual structure, presumably due to these hydrophobic interactions. The crystal structure of HP35 has also suggests some hydrogen bonding interactions between the first two helices that may influence the compactness of the structure in HP36’s unfolded state.⁵⁸ These interactions stabilize the first and second helix and allow them to form more structure than seen in the individual fragments.

In summary, REMD simulations using explicit solvent have been used as a method for studying the propensity to populate locally stabilized unfolded state structure in HP36. Two simulations using explicit solvent were run for each fragment and both converged to the same population of structures. HP-1 was shown to contain the most helical structure with a low RMSD to the native HP36 structure, implying that this region may be partially structured in the unfolded state of HP36. The low tendency to adopt helical structure in the other two fragments indicates that these rely on contacts from each other for stability. This is in agreement with experimental studies which demonstrate that tertiary contacts are necessary to form stable, detectable structure.

Methods

Three fragments were built from the sequence of HP36: M41–F76 (MLSDEDF KAVFGMTRSAFANLPWKQQNLKKEKGLF). HP-1 (M41-M53) corresponds to the N-terminal helix of HP36. HP-2 (G52-L61) contains the second helix and HP-3 (P62-L75) contains the C-terminal helix. HP-1 has a free N-terminus while HP-2 and HP-3 have acetylated N-termini. All C-termini were amidated. These sequences and termini correspond to those used in the experimental studies.²⁴ All sidechains for Asp, Glu, Lys, and Arg were charged during the simulation. Ala₁₀ was acetylated and amidated at the N and C termini respectively. All simulations were performed in Amber version 8 ⁵⁹ and used the Amber ff99 force field^{60; 61}, with modifications to eliminate α-helical bias.⁶² These parameters have been provided elsewhere,⁶³ are denoted “ff99SB” in Amber version 9 and are available for download from the Amber web site (amber.scripps.edu). SHAKE ⁶⁴ was used to constrain bonds involving hydrogen. The time step was 2 fs. Temperatures were maintained using weak Berendsen coupling.⁶⁵ All simulations were initiated from both an extended and a helical structure, with comparison of the two runs providing a lower bound for the uncertainty in resulting data.

Explicit solvent simulations

Explicit water simulations were performed in a truncated octahedral box using periodic boundary conditions and particle mesh Ewald⁶⁶ (PME) to calculate long range electrostatic interactions. The structures were equilibrated at 300 K for 50 ps with harmonic restraints on solute atoms, followed by minimization with gradually reduced positional restraints and three 5 ps MD simulations with gradually reduced restraints at constant pressure (1 atm) and temperature (300 K) to generate starting structures. To improve sampling, we use REMD as implemented in Amber 8. Each system is represented by multiple simulations which are coupled to baths at different temperatures. Periodically an exchange of replicas is attempted using a Metropolis-type criterion. The target exchange acceptance ratio for all simulations was approximately 20 % between temperatures ranging from 260 – 580 K. Exchanges between neighboring temperatures was attempted every 1 ps.

The initially extended and helical HP-1 fragments were surrounded by 1387 TIP3P waters and 1029 TIP3P waters respectively. The extended structure used 38 replicas ranging from 257 to 533 K while the folded structure used 34 replicas ranging from 262 to 531 K. Each simulation was run for 42 ns. The extended and helical HP-2 fragments were surrounded by 1092 waters and 849 waters respectively. The extended structure used 34 replicas ranging from 269 to 548 K while the helical structure used 30 replicas ranging from 265 to 543 K. Both were simulated for 32 ns. The extended and partially helical HP-3 fragments were surrounded by 1250 waters. Both were simulated with 40 replicas ranging from 266 to 578 K for 41 ns. The first 10 ns of each simulation were discarded to reduce bias caused by the initial structure.

The Ala₁₀ peptide in an α-helical and an extended conformation was solvated using 983 TIP3P water molecules for a total of 3058 atoms. 40 replicas were used at temperatures ranging from 267K to 571K, which were optimized to give a uniform exchange acceptance ratio of ~30%.

Implicit solvent simulations

The implicit solvent effects were calculated using the Generalized Born continuum model⁴² using pairwise descreening⁶⁷ with mbondi radii.⁶⁸ Simulations were initiated with the same two initial conformation ensembles as were used for the explicit solvent REMD calculations. Both initial structures were minimized, followed by a brief equilibration. The same force field and target exchange ratios in the explicit solvent were implemented in the GB runs.

The first 5 ns was discarded to remove initial structure bias in each run. The HP-1 simulations used 8 replicas from 272 to 539 K, for approximately 50 ns each. Simulations of HP-2 ran for 40 ns with 8 replicas between 268 and 587 K and HP-3 simulations ran for 60 ns using 10 replicas between 277 and 571 K. For Ala₁₀, 8 replicas were used at temperatures ranging from 270 to 571 K. Exchanges were attempted every 1 ps and the REMD simulation was run for 50000 exchanges (50 ns).

Data analysis

Cluster analysis was performed on each simulation with MOIL-View ⁶⁹, using backbone RMSD as a similarity criterion with average linkage. Clusters were formed with a bottom-up approach using a similarity cutoff of 2.5 Ǻ; the populations of the resulting clusters for each fragment are discussed in the main text. The portions of the backbone were selected according to the region of the fragment where the HP36 native helix was located. DSSP analysis of the fragments confirmed that these regions were the most structured portions of the fragments. Conformational families were defined based on the combined set of structures from all simulations of the fragment (both initial structures and both solvent models), and the populations of each family were then calculated for the ensemble obtained from each simulation. Comparison of the populations of each structure type in the ensembles obtained from independent initial structures was used as a convergence metric.

DSSP analysis⁴⁸ and calculation of distances, RMSDs, and radius of gyration were done using the ptraj module in Amber. Distances between sidechains were calculated using heavy atoms of the charged atoms. Free energy histograms were calculated at 300 K according to equation 1

$$\mathrm{\Delta }{\mathrm{G}}_{\mathrm{i}}=-\text{RT}ln({\mathrm{N}}_{\mathrm{i}}/{\mathrm{N}}_0)$$ (1)

where N_i is the population of a particular histogram bin along the reaction coordinates that were employed and N₀ is the most populated bin.

LR analysis was implemented to calculate the probability of forming helices of a particular length. Backbone torsion (φ/Ψ) angles were used to evaluate whether a residues was helical or non-helical. Using the Garcia and Sanbonmatsu definition⁷⁰, a residue was considered helical if φ = 60 ± 30 and Ψ = 47 ± 30. Helical populations were calculated using the equation:

$$\text{Hp}=({\mathrm{H}}_{\mathrm{l}}/\mathrm{N})$$ (2)

where Hp is the population of a helix at a particular length, H_l is the amount of that helix of a particular length L and N is the total number of structures in the ensemble. We note that this provides absolute helical content and formation of several short helices in single structure is possible.

J-coupling constants were calculated using a version of the Karplus equation previously employed for analysis of small peptides:

$$\mathrm{J}=\mathrm{A}{cos}^2(\mathrm{\phi }-60)+\mathrm{B}cos(\mathrm{\phi }-60)+\mathrm{C}$$ (1)

where A = 6.51, B = −1.76, and C = 1.60.⁷¹ All calculations were performed on the combined data set including simulations started with the extended and folded starting structures.

Figure 6.

Representative structures for the five most populated clusters of HP-1. (A) 1^st cluster (59 ± 6 %) (B) 2^nd cluster (13 ± 2 %) (C) 3^rd cluster (8 ± 1 %) (D) 4^th cluster (5.4 ± .4 %) (E) 5^th cluster (5.0 ± .3 %). The most populated cluster contains helical content similar to helix 1 in the native HP36.

Abbreviations

CD

DSSP

GB

HP-1

HP-2

HP-3

HP12

HP35

HP36

LR

MD

PPII

REMD

Rg

RMSD