Clusterless Decoding of Position From Multiunit Activity Using A Marked Point Process Filter

Abstract

Point process filters have been applied successfully to decode neural signals and track neural dynamics. Traditionally, these methods assume that multiunit spiking activity has already been correctly spike-sorted. As a result, these methods are not appropriate for situations where sorting cannot be performed with high precision such as real-time decoding for brain-computer interfaces. As the unsupervised spike-sorting problem remains unsolved, we took an alternative approach that takes advantage of recent insights about clusterless decoding. Here we present a new point process decoding algorithm that does not require multiunit signals to be sorted into individual units. We use the theory of marked point processes to construct a function that characterizes the relationship between a covariate of interest (in this case, the location of a rat on a track) and features of the spike waveforms. In our example, we use tetrode recordings, and the marks represent a four-dimensional vector of the maximum amplitudes of the spike waveform on each of the four electrodes. In general, the marks may represent any features of the spike waveform. We then use Bayes’ rule to estimate spatial location from hippocampal neural activity.

We validate our approach with a simulation study and with experimental data recorded in the hippocampus of a rat moving through a linear environment. Our decoding algorithm accurately reconstructs the rat’s position from unsorted multiunit spiking activity. We then compare the quality of our decoding algorithm to that of a traditional spike-sorting and decoding algorithm. Our analyses show that the proposed decoding algorithm performs equivalently or better than algorithms based on sorted single-unit activity. These results provide a path toward accurate real-time decoding of spiking patterns that could be used to carry out content-specific manipulations of population activity in hippocampus or elsewhere in the brain.

1 Introduction

Neural systems encode information about external stimuli in temporal sequences of action potentials. Because action potentials have stereotyped, impulse waveforms, they are most appropriately modeled as point processes (Brillinger, 1992). Neural systems are moreover dynamic in that the ensemble firing of populations of neurons, representing some biologically relevant variable, continually evolves. Decoding algorithms based on adaptive filters have been developed to study how the firing patterns maintain dynamic representations of relevant stimuli. More specifically, both discrete-time and continuous-time point process filter algorithms have been applied with great success to address problems of estimating a continuous state variable (Eden et al., 2004; Smith & Brown, 2003; Smith et al., 2004), such as the location of an animal exploring its environment (Brown et al., 1998; Huang et al., 2009; Koyama et al., 2010).

A prerequisite for these increasingly efficient decoding methods is the application of spike-sorting: the waveforms recorded extracellularly at electrodes must be clustered into putative single neurons. Therefore, the accuracy of the spike-sorting critically impacts the accuracy of the decoding (Brown et al., 2004). Many algorithms for spike-sorting, whether real-time and automatic or offline and manual, have been developed since the 1960s (Lewicki, 1998; Wild et al., 2012). The majority of these algorithms are clustering-based methods, allocating each spike to a putative single cell based on the characteristics of spike waveforms. These types of pure waveform, hard boundary spike-sorting algorithms, suffer from many sources of error such as nonstationary noises, non-Gaussian clusters, and synchrony (Lewicki, 1998; Harris et al., 2000; Quiroga, 2012). In addition, they also have been shown to yield biased and inconsistent estimates for neural receptive fields (Ventura, 2009b). Another clustering method, soft or probabilistic spike assignment, has been incorporated into some decoding paradigms and analyses have shown that these algorithms can yield unbiased estimates of stimulation parameters (Ventura, 2008, 2009a). Nonetheless, these algorithms, like most hard sorting methods, are not well suited to real-time implementations, both because the algorithms are too computationally intensive and because they rely on having the entire dataset available for the clustering algorithm.

More recently, decoding methods without a spike-sorting step have been investigated (Luczak & Narayanan, 2005; Stark & Abeles, 2007; Fraser et al., 2009; Chen et al., 2012; Kloosterman et al., 2014). Chen et al. (2012) and Kloosterman et al. (2014) developed a spike feature decoding paradigm for unsorted spikes using a time-homogeneous spatio-temporal Poisson process. It incorporates a covariate-dependent method to estimate a nonparametric distribution of the animal’s position. This improves decoding performance by using information that is otherwise excluded by sorting spikes into discrete clusters. However, this method does not incorporate a model of the animal’s position trajectory, and therefore the decoding results can depend substantially on specific model parameters such as the choice of a discrete time bin width: if the time scale is too broad, the algorithm cannot track the stimuli fast enough; if too narrow, it cannot integrate information provided by spikes nearby in time. Additionally, this algorithm extracts information from spike intervals, but does not optimally incorporate information from intervals that contain no spikes. In the Extensions and Discussion to Chen et al. (2012), they suggested the possibility of applying a state-space framework with a temporal prior, but do not provide a complete algorithm or an implementation of this method.

To address these issues, we generalize and extend this decoding paradigm for unsorted spikes to allow for general marked point process models. In doing so, we develop an iterative algorithm that solves the marked point process filter problem. In particular, this allows us to model neural activity that is dependent on the timing and mark values of previous spikes. In the current work, we propose a novel algorithm for adaptive decoding of spiking activity which avoids the clustering problem of spike-sorting entirely by defining a joint model for the spike waveform and receptive field structure, and uses a state-space model to incorporate knowledge of the properties of the signal to decode. The resulting algorithm is a general marked point process filter.

The goal of the proposed algorithm is to decode an adaptive state variable, in this case the dynamic trajectory of the rat along a track, by computing the posterior distribution of the state process conditioned on the set of observations up until the current time. Our algorithm takes directly as inputs the recorded spikes where each spike is associated with a vector of characteristic features selected from the raw waveforms. Such inputs can be mathematically described by a marked point process, where the points are the spike times and the marks are their corresponding waveform. In their seminal book on point processes in 1980, D. R. Cox and V. Isham have already explicitly suggested that “in the neurophysiological example mentioned […] the mark could be the magnitude of the peak signal at the point in question” (Cox & Isham, 1980).

In this paper, we first characterize the spiking activity of an ensemble of neurons using the conditional intensity function for marked point processes. Next, we construct a stochastic state marked point process filter to iteratively calculate the full posterior probability for the state variable. We illustrate our approach in a simulation study where the decoding algorithm is used to reconstruct an animal’s position from unsorted multiunit place cell spiking activity. We also apply the algorithm to experimental data recorded in the hippocampus of a rat navigating a linear environment. We then compare the quality of fit of our clusterless decoding algorithm to that of a traditional spike-sorting and decoding algorithm.

2 Methods

Any orderly point process can be fully characterized by its conditional intensity function (Daley & Vere-Jones, 2003). A conditional intensity function describes the instantaneous probability of observing a spike, given previous spiking history. By relating the conditional intensity function to specific biological and behavioral signals we can specify a spike train encoding model. The conditional intensity function also generalizes to the marked case, in which a random vector, termed a mark, is attached to each point. In the case of tetrode recordings, for example, the mark could be a length four vector of the maximum amplitudes on each of the four electrodes at every spike time. A marked point process is completely defined by its joint mark intensity function

$$\lambda (t,\overrightarrow{m}\mid H_t)=\underset{\Delta \to 0}{\lim }\frac{\mathrm{Pr}\left(\text{a spike with mark vector}\overrightarrow{m}\text{in}\right(t,t+\Delta ]\mid H_t)}{\Delta },$$ (1)

where H_t is the history of the spiking activity up to time t. $\lambda (t,\overrightarrow{m}\mid H_t)$ represents a joint stochastic model for the marks as well as the arrivals of the point process.

The joint mark intensity function characterizes the instantaneous probability of observing a spike with mark $\overrightarrow{m}$ at time t as a function of factors that may influence spiking activity. We posit that the spiking activity depends on some underlying internal state variable x(t), such as an animal’s location in space, that varies across time. We can therefore model the spiking activity as $\lambda (t,\overrightarrow{m}\mid H_t)=g\left(x\right(t),\overrightarrow{m}\mid H_t)$. When taking an integral of $\lambda (t,\overrightarrow{m}\mid H_t)$ over the mark space $\mathcal{M}$, we get the probability of observing a spike regardless of the mark value:

$$\Lambda (t\mid H_t)={\int }_{\mathcal{M}}\lambda (t,\overrightarrow{m}\mid H_t)d\overrightarrow{m}.$$ (2)

Λ(t|H_t) can be understood as the conventional conditional intensity function of a temporal point process. For a marked point process, Λ(t|H_t) is called the intensity function of the ground process (Daley & Vere-Jones, 2003). The mark space $\mathcal{M}$ can be of any dimension.

The goal of our decoding algorithm is to compute, at each time point, the posterior distribution of the state variable given observed marked spiking activity. To do this, we apply the theory of state-space adaptive filters (Haykin, 1996). Recursive filter equations can be solved in both discrete-time and continuous-time (Eden et al., 2004; Eden & Brown, 2008). In this paper we present an algorithm in discrete-time.

To describe the discrete-time filters, we partition an observation interval [0, T] into {t_k : 0 ≤ t₁ < ⋯ < t_N ≤ T} and let Δ_k = t_k − t_k−1. The posterior density for the state variable at time t_k can be derived simply using Bayes’ rule,

$$p(x_k\mid \Delta N_k,{\overrightarrow{m}}_k,H_k)=\frac{p(x_k\mid H_k)p(\Delta N_k,{\overrightarrow{m}}_k\mid x_k,H_k)}{p(\Delta N_k,{\overrightarrow{m}}_k\mid H_k)},$$ (3)

where x_k = x(t_k) is the state variable at time t_k, ΔN_k is the number of spikes observed in the interval (t_k−1, t_k], and H_k is the spiking history up to time t_k. ${\overrightarrow{m}}_k$ represents a collection of mark vectors ${\overrightarrow{m}}_{k_i}$, i = 1, ⋯ ,ΔN_k, observed in the interval (t_k−1, t_k].

The first term in the numerator on the right hand side of equation (3), p(x_k|H_k), is the one-step prediction density defined by the Chapman-Kolmogorov equation as

$$p(x_k\mid H_k)=\int p(x_k\mid x_{k-1})p(x_{k-1}\mid \Delta N_{k-1},{\overrightarrow{m}}_{k-1},H_{k-1}){\mathit{dx}}_{k-1}.$$ (4)

Here we have assumed that given the past state value, x_k−1, the distribution of the current state does not depend on past spiking activity. The integral in equation (4) typically cannot be solved analytically, but multiple numerical and approximation methods are available to compute its value at each time point. In this case, we performed numerical integration over a one-dimensional state space using a simple Riemann sum. If the state variable is high-dimensional, alternative methods can be considered to improve computational efficiency. In particular, when prior knowledge allows us to assume unimodality of the posterior density, a linear recursive Gaussian approximation to the posterior density can be constructed (Brown et al., 1998; Eden et al., 2004; Smith & Brown, 2003). Alternatively, when the posterior distribution is unknown, sequential Monte Carlo methods, also called particle filters, can provide efficient estimation (Doucet et al., 2001; Ergun et al., 2007). We show the construction of these two types of algorithms in the Appendix.

Equation (4) has two components: p(x_k|x_k−1), which is given by a state evolution model under the Markovian assumption, and $p(x_{k-1}\mid \Delta N_{k-1},{\overrightarrow{m}}_{k-1},H_k)$, which is the posterior density from the last iteration step. We multiply this probability density function with the posterior distribution of the state variable at the previous time step t_k−1, and numerically integrate the product over all possible values of the previous state, x_k−1. The resulting integral is the a one-step prediction density at the current time t_k.

The second term in equation (3), $p(\Delta N_k,{\overrightarrow{m}}_k\mid x_k,H_k)$, is the likelihood or observation distribution at the current time, and can be fully characterized by the joint mark intensity function $\lambda (t,\overrightarrow{m}\mid H_t)$:

$$p(\Delta N_k,{\overrightarrow{m}}_k\mid x_k,H_k)\propto \{\begin{array}{cc}\exp [-{\Delta }_k\Lambda (t_k\mid H_k\left)\right],\hfill & \Delta N_k=0;\hfill \\ \prod _{i=1}^{\Delta N_k}\left[\lambda \right(t_k,{\overrightarrow{m}}_{k_i}\mid H_k\left){\Delta }_k\right]\exp [-{\Delta }_k\Lambda (t_k\mid H_k\left)\right],\hfill & \Delta N_k>0.\hfill \end{array}\phantom{\}}$$ (5)

We can interpret equation (5) by separating the product on the right hand side into two terms. The ${\prod }_{i=1}^{\Delta N_k}\left[\lambda \right(t_k,{\overrightarrow{m}}_{k_i}\mid H_k\left){\Delta }_k\right]$ term characterizes the distribution of firing ΔN_k spikes, such that the mark value of the i^th spike in the interval (t_k−1, t_k] is m_ki, where i = 1, ⋯ ,ΔN_k. If no spike occurs, i.e., ΔN_k = 0, this term equals 1. The exp [−Δ_kΛ(t_k|H_k)] term gives the probability of not firing any other spikes in the observation interval, where $\Lambda (t_k\mid H_k)={\int }_{\mathcal{M}}\lambda (t_k,{\overrightarrow{m}}_k\mid H_k)d{\overrightarrow{m}}_k$ as defined in equation (2).

The discrete-time likelihood or observation distribution defined by equation (5) assumes that within a small time step Δ_k, conditional on the history H_k and the current value of the state vector x_k, spiking activity for the neural ensemble is independent. However, the spiking activity at a given time step can explicitly depend on the past history of activity from the entire population, including dependencies between neurons.

The observation distribution is then multiplied by the one-step prediction density to get the posterior density at the current time. Note that we can drop the normalization term, $p(\Delta N_k,{\overrightarrow{m}}_k\mid H_k)$ because it is not a function of x_k. Substituting equation (4) into equation (3) yields a recursive expression for the evolution of the unnormalized posterior density:

$$p(x_k\mid \Delta N_k,{\overrightarrow{m}}_k,H_k)\propto p(\Delta N_k,{\overrightarrow{m}}_k\mid x_k,H_k)\int p(x_k\mid x_{k-1})p(x_{k-1}\mid \Delta N_{k-1},{\overrightarrow{m}}_{k-1},H_{k-1}){\mathit{dx}}_{k-1}.$$ (6)

3 Simulation Study

We first tested this approach on simulated data corresponding to the activity of two “place cells” firing as an animal traverses a linear track. Place cells are neurons in the hippocampus that are activity primarily when an animal is located in a certain portion of it’s environment (O’Keefe & Dostrovsky, 1971; O’Keefe, 1979). Substantial amount of information about the position carried by place cells have been reliably quantified with a formal statistical algorithm and used to reconstruct the trajectory and predict the future position of the rat (Muller & Kubie, 1989; Wilson & McNaughton, 1993; Zhang et al., 1998; Brown et al., 1998).

In this section, we apply the clusterless decoding algorithm to the problem of decoding a one-dimensional position of a rat on a linear track using a marked point process arising from two hippocampal place cells, where the one-dimensional mark represents the peak height of the spike waveform. Here we note that accurate decoding of position based on place cell activity normally requires many cells. Our goal here is therefore not to test the accuracy of decoding, but rather to provide intuition about how our approach works in a simple case. First, we simulate the rat’s trajectory using an autoregressive process and the joint mark intensity function of the two cells using a mixture of two bivariate Gaussian distributions. Then, we use marked point process filter to reconstruct the location of the rat at each time step. We show that the filter yields exact full posterior densities that are often multimodal. We also reconstruct the trajectory using a traditional algorithm in which decoding was applied after spike-sorting. Last, we compare the performance of the clusterless decoding algorithm to the traditional decoding algorithm.

3.1 Data Simulation

We simulated the movement of a rat running back and forth along a linear track with the following transition probability

$$p(x_k\mid x_{k-1})\sim N(\alpha x_{k-1},\sigma ),$$ (7)

where we set α = 0.98 and σ = 0.05 to generate an autoregressive process whose steady-state standard deviation is 1.26.

We defined the joint mark intensity of two hippocampal place cells using a bivariate Gaussian mixture function,

$$\lambda (t,\overrightarrow{m})=\sum _{c=1}^2\exp \left\{{\alpha }^c-{\left(\begin{array}{c}\hfill x\left(t\right)-{\mu }_x^c\hfill \\ \hfill \overrightarrow{m}-{\mu }_{\overrightarrow{m}}^c\hfill \end{array}\right)}^T{\left[\begin{array}{cc}\hfill 2{\left({\sigma }_x^c\right)}^2\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 2{\left({\sigma }_{\overrightarrow{m}}^c\right)}^2\hfill \end{array}\right]}^{-1}\left(\begin{array}{c}\hfill x\left(t\right)-{\mu }_x^c\hfill \\ \hfill \overrightarrow{m}-{\mu }_{\overrightarrow{m}}^c\hfill \end{array}\right)\right\}.$$ (8)

This model assumes that spikes originate from an ensemble of two cells and that the joint mark intensity function for each cell’s place field and marks is a multivariate Gaussian function. In other words, each cell has a place field with a Gaussian shape, and the marginal distribution of the marks given the rat’s position is a multivariate Gaussian distribution.

The parameters for this model include α^c for c = 1, 2, which controls the maximum in-field firing rate for the c^th neuron. x(t) is the animal’s linearized position at time t and $\overrightarrow{m}$ is the one-dimensional mark value. ${\mu }_x^c$ is the center of the place field and ${\mu }_{{\overrightarrow{m}}_c}$ is the mean of the density function for marks for neuron c. ${\sigma }_x^c$ and ${\sigma }_{\overrightarrow{m}}^c$ are the standard deviations of the place field and the mark space for neuron c respectively. In this illustrative example, we set the centers of the place field at ${\mu }_x^1=-1.5$ and ${\mu }_x^2=1.5$ respectively, with a ${\left({\sigma }_x^1\right)}^2={\left({\sigma }_x^2\right)}^2=0.1$ variance. We set the maximum in-field firing rate of both neurons to α¹ = α² = 100 spikes per second. The one-dimensional mark space for the two neurons are centered at ${\mu }_{\overrightarrow{m}}^1=10$ and ${\mu }_{\overrightarrow{m}}^2=13$ respectively, with standard deviations ${\sigma }_{\overrightarrow{m}}={\sigma }_{\overrightarrow{m}}^1={\sigma }_{\overrightarrow{m}}^2$ varying between 0.01 and 5.

By plugging in the simulated position trajectories, x(t), into Equation (8), we computed the instantaneous intensity at each time step. The underlying unmarked spike trains are generated under an inhomogeneous Poisson process model with rate Λ(t|H_t) given by equation (2). The marks associated with the spike trains are sampled from the probability density $f(\overrightarrow{m}\mid t)=\frac{\lambda (t,\overrightarrow{m})}{\Lambda (t\mid H_t)}$.

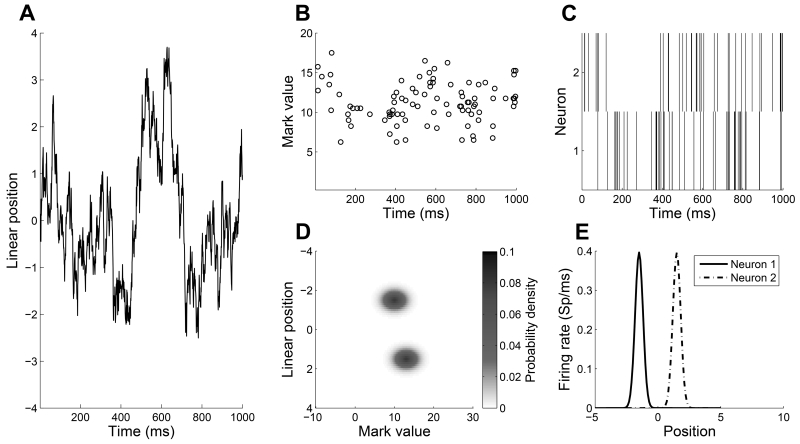
Figure 1 displays the results of a representative, one-second trial where spiking activity of two neurons with moderate mark space overlap ${\sigma }_{\overrightarrow{m}}=2$ was simulated. Figure 1(A) shows the simulated trajectory of the animal with the linear location on the y-axis. Figure 1(B) plots the simulated spike train with the mark value on the y-axis. Visually, we cannot identify a clear clustering of the mark values. Figure 1(D) shows the true joint mark intensity function $\lambda (t,\overrightarrow{m})$ used to simulate the marked spike train in Figure 1(B). The two simulated neurons overlap over a moderate amount of mark space, but are fairly localized in space, with little overlap of their place fields.

FIGURE 1.

(A) Simulated trajectory of the animal running back and forth on a linear track. (B) One second unsorted spike train with marks from two simulated neurons. (C) One second raster plot of spikes without marks where the spikes were sorted via a linear discriminant function on their mark values. (D) True joint mark intensity of the two simulated neurons as a function of linear position on the y-axis and mark value on the x-axis. The place fields center at −1.5 and 1.5 respectively, with a 0.1 variance. The mark spaces are one-dimensional with mean of 10 and 13 respectively, and standard deviation of 2. (E) True rate of each of the two simulated neurons as a function of linear position. It represents the place field of each neuron.

3.2 Decoding Results

In this subsection, we present the decoding results of the simulated data described in subsection 3.1 Data Simulation using the clusterless decoding algorithm described in the Methods section. When calculating the observation distribution defined in Equation (5), we used the true joint mark intensity function specified in Equation (8). In real data, we will need to estimate an encoding model for the joint mark intensity function. However, this simulation study affords us the opportunity to explore errors due purely to the decoding algorithms.

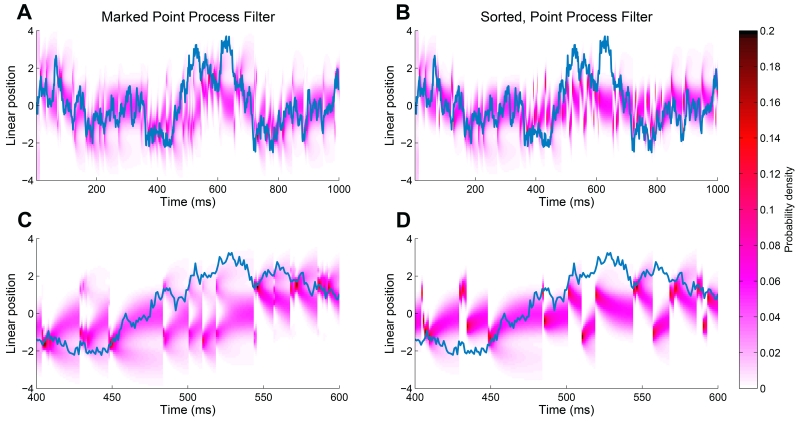
Figure 2(A) shows the posterior density for the position of the animal during a one-second trial as a function of time, using the clusterless decoding algorithm. The blue line shows the true position of the animal, and the red region is the estimated posterior density at that time step. We can see that the estimate tracks the true position relatively closely, and the region of high posterior density covers the true position most of the time.

FIGURE 2.

Decoding results for two simulated neurons. (A) Posterior density of the animal’s linear position using the clusterless decoding algorithm. The blue line represents the actual position of the animal. The red represents the posterior density at each time step. (B) Posterior density of the animal’s linear position using the decoding with spike-sorting. (C) Clusterless decoding results zoomed in at time between 400 and 600 ms, showing the multimodality of the posterior around 430 ms. (D) Decoding with spike-sorting results zoomed in at time between 400 and 600 ms.

In order to compare with the traditional approach where decoding is applied after spike-sorting, we also implemented a decoding algorithm on individual neurons after classifying the spikes into clusters using linear discriminant functions (Bishop, 2006). Here we assume the number of neurons being recorded is known and that we have true knowledge of the rate function λ^c(t) about neuron c. This is more knowledge than is typically available for clustering and decoding, where both the number of neurons and place fields must be estimated. The time-dependent rate function for individual neuron, λ^c(t), takes the following form:

$${\lambda }^c\left(t\right)=\exp \left\{{\alpha }^c-\frac{1}{\sqrt{2{\left({\sigma }_x^c\right)}^2}}{\left(x\right(t)-{\mu }_x^c)}^2\right\}.$$ (9)

Note that λ^c(t) represents the conventional rate function for an inhomogeneous Poisson process, not the joint mark intensity process we have used to define our marked point process model.

Figure 1(C) plots the spike raster of the two simulated neurons sorted using a linear discriminant function on their marks. Figure 1(E) shows the true condition intensity function λ^c(t) for each neuron c, i.e., the place field of each neuron.

In this case, the unnormalized posterior density is of the form

$$p(x_k\mid \Delta N_k^1,\Delta N_k^2)\propto \prod _{c=1}^2\mathrm{Pr}(\Delta N_k^c\mid H_k)\int p(x_k\mid x_{k-1})p(x_{k-1}\mid \Delta N_{k-1}^1,\Delta N_{k-1}^2){\mathit{dx}}_{k-1}.$$ (10)

The probability of seeing $\Delta N_k^c$ spikes from neuron c during the time interval (t_k−1, t_k] is

$$\mathrm{Pr}(\Delta N_k^c\mid H_k)\propto {\left({\lambda }_k^c{\Delta }_k\right)}^{\Delta N_k^c}\exp \{-{\lambda }_k^c{\Delta }_k\},$$ (11)

where, for simplicity, ${\lambda }_k^c$ denotes λ^c(t_k).

Figure 2(B) and 2(D) are results using decoding with spike-sorting where the decoder is applied after classifying the spikes into two clusters. Figure 2(B) shows the posterior density using decoding with spike-sorting. Visually, we obtained comparable tracking for the animal’s trajectory.

To illustrate the advantage of using a clusterless decoding algorithm when clear clustering of neurons is difficult, we zoomed in on the decoding results at times between 400 ms and 600 ms, shown in Figure 2(C) and 2(D). From Figure 1(B) and 1(C), we can see that even though the rat’s position is positive, and therefore only Neuron 2 is spiking, the spike waveforms cannot be perfectly resolved. This leads to incorrect decoding results using the presorted spiking activity. However, the marked point process decoder results in a bimodal posterior distribution that accurately reflects the uncertainty due to the waveform overlap. Figure 2(C) demonstrates the multimodality of the posterior estimated by a clusterless decoder. For example, at time around 430 ms when a new spike arrives, the posterior density splits into two modes, one near a linearized position of −1 and another around a linearized position at 1.5. The posterior density is slightly higher in the region correctly predicting the animal’s position in the negative regime. For the decoding with spike-sorting results shown in Figure 2(D), the algorithm has some trouble tracking the trajectory after new spikes from both neurons arrive because the posterior density in this case is not multimodal. For example at time around 430 ms, the posterior density incorrectly estimates the animal’s position at a positive value near 1.

3.3 Goodness-of-Fit Analysis

In order to compare the quality of fit between the two decoding algorithms, we simulated 100 trials of spiking activity for different degrees of overlap between the two neurons in the mark space. We evaluate the ability of these two algorithms to track the location of the animal when the overlaps in the mark space between the joint mark intensity functions of the simulated neural ensemble vary from low (${\sigma }_m^c=0.01$) to high (${\sigma }_m^c=5$) in units of the number of standard deviations, using two different measures: the root-mean-squared error (rMSE) between the true positions of the animal and their estimated values and the percentage of the time that the true position values were covered by the 99% highest posterior density (HPD) region (Casella & Berger, 2001).

To calculate the 99% HPD region, we find the largest value y₀ such that

$${\int }_{\{x:{\rho }_k(x)>y_0\}}{\rho }_k\left(x\right)\mathit{dx}=0.99,$$ (12)

where ρ_k denotes the posterior density at time step t_k as defined in equation (3) for marked point processes and in equation (10) for the unmarked case. The 99% HPD region is thus given by {x : ρ_k(x) > y₀}. Because an HPD region indicates the region of highest posterior probability regardless of contiguity, it is a useful measure of uncertainty when the posterior density can be multimodal. If the state space model is correct, the 99% HPD region should contain the true position of the animal at any time step with probability 0.99.

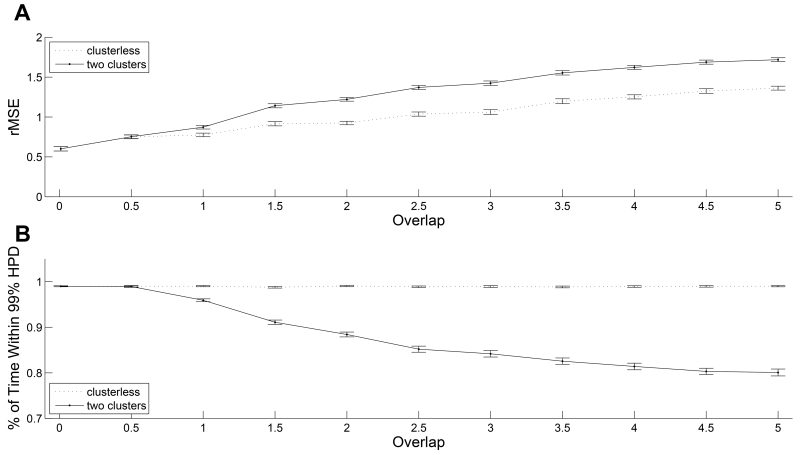
Figure 3(A) shows the rMSEs between the true positions of the animal and their estimated values averaged across 100 trials as a function of σ_m. Error bars represent 2 standard deviations from the mean rMSE. The dotted line represents the performance of the clusterless decoding method. The solid line represents the performance of the decoding with spike-sorting method. When the standard deviations of both mark spaces exceed 1, the clusterless decoder consistently gives the lower mean rMSE and there is no overlap between the error bars for the two algorithms.

FIGURE 3.

Quality of fit comparison between the two decoding algorithms. (A) Root-mean-squared error (rMSE) between the true positions of the animal and their estimated values averaged across 100 trials as a function of the overlap between mark spaces of two simulated neurons. Error bars represent 2 standard deviations from the mean rMSE. The dotted line represents the performance of clusterless decoding method. The solid line represents the performance of decoding with spike-sorting method. (B) Fraction of time that the true position values were covered by the 99% highest posterior density (HPD) region averaged across 100 trials as a function of the overlap between mark spaces of two simulated neurons. Error bars represent 2 standard deviations from the mean coverage probability. The dotted line represents the performance of clusterless decoding method. The solid line represents the performance of decoding with spike-sorting method.

The comparison of the rMSEs shows that as the overlap between the marks for the individual neurons increases and clustering of the spike waveforms becomes more difficult, the clusterless decoding algorithm provides a consistently more accurate estimate of the rat’s position than the decoding algorithm using presorted spikes.

Figure 3(B) shows the fraction of time that the true position values were covered by the 99% HPD region averaged across 100 trials as a function of σ_m, which measures how well each algorithm characterizes their uncertainty. The flat dotted line with narrow error bars illustrates that regardless of the degree of the overlap between mark spaces, the true trajectory stays in the 99% HPD region of the clusterless decoding method around 99% of the time with very little variance about this percentage of time across the 100 repeated trials of the simulation. The descending solid line with widening error bars illustrates that, for decoding with spike-sorting, as the degree of the overlap between mark spaces increases, the fraction of time that the true trajectory stays in the 99% HPD region is decreasing from 99% to 80% with an increasing variance.

The comparison of the 99% HPD region illustrates two advantages of the clusterless decoding algorithm regarding the uncertainty of the state estimates. First, the width of a 99% HPD describes the degree of uncertainty in the estimates. As the overlap between the mark spaces increases, the width of the 99% HPD region of the decoding algorithm using presorted spikes increases, indicating decreasing certainty in the estimated position. However, the clusterless decoding algorithm provides a narrower 99% HPD region regardless of the mark space overlap. This means that the clusterless decoding algorithm provides more estimates of the rat’s position and is less influenced by the degree of overlap in the mark space. Second, the percentage of time within the 99% HPD represents the accuracy of uncertainty in the estimates. As the overlap in the mark distribution between the neurons increases, the decoding with presorted spikes estimates the uncertainty in position with less accuracy, while the estimated certainty of the clusterless decoding algorithm remains the correct at around 99%. Therefore the estimated certainty for the clusterless decoding algorithm is both higher and more accurate than the estimated certainty for decoding with presorted spikes.

4 An Application to Position Decoding from Multiunit Activity in Rat Hippocampus

We also applied the clusterless decoding algorithm to experimental data recorded using a multi-electrode array in the hippocampus of a rat running back and forth on a linear track. The data used in this analysis were recorded from 5 tetrodes in the dorsal CA1 and CA2 regions of the hippocampus. Manual clustering of spike waveforms above a 40 μV threshold during the linear track session yielded fifteen distinct unit clusters. Four units with less than 100 spikes during the 840 second recording session were excluded. One of the remaining units was a putative interneuron, identified by firing rate exceeding 7 Hz and exceptionally narrow spikewidth. In the clusterless decoding, all of the thresholded spikes above the 40 μV threshold, including this putative interneuron, were included. Details of the experimental preparation, data acquisition and choice of spike-sorting method can be found in the Appendix.

When recording from multi-electrode arrays, each electrode records the signals from nearby neurons, and these signals can be combined across electrodes. Thus, by combining tetrodes together, we can gain additional spatial information about each signal. In this case, assuming that conditional on the spiking history and the current state variable the spiking activity is independent between tetrodes, we can augment the observation distribution in equation (5) to be

$$p(\Delta N_k,{\overrightarrow{m}}_k\mid x_k,H_k)\propto \{\begin{array}{cc}\prod _{s=1}^S\exp [-{\Delta }_k{\Lambda }^s(t_k\left)\right],\hfill & \Delta N_k=0;\hfill \\ \prod _{s=1}^S\prod _{i=1}^{\Delta N_k^s}\left[{\lambda }^s\right(t_k,{\overrightarrow{m}}_{k_i}\left){\Delta }_k\right]\exp [-{\Delta }_k{\Lambda }^s(t_k\left)\right],\hfill & \Delta N_k>0,\hfill \end{array}\phantom{\}}$$ (13)

where S is the number of groups of recordings, in this case the number of tetrodes. $\Delta N_k^s$ is the number of spikes observed from neurons on tetrode s during (t_k−1, t_k]. ${\Lambda }^s\left(t_k\right)={\int }_{\mathcal{M}}{\lambda }^s(t_k,{\overrightarrow{m}}_k)d{\overrightarrow{m}}_k$, where ${\lambda }^s(t_k,{\overrightarrow{m}}_k)$ defines the joint mark intensity function for neurons on tetrode s, where s = 1, ⋯ , S.

In this analysis, we propose a marked Poisson, nonparametric clusterless encoding model to estimate the joint mark intensity function $\lambda (t,\overrightarrow{m})$, given an observation interval t ∈ (0, T] with a sequence of N spike times 0 < u₁ < ⋯ < u_i < ⋯ < u_N ≤ T:

$$\widehat{\lambda }(t,\overrightarrow{m})=\frac{\frac{1}{N}\sum _{i=1}^N\frac{1}{B_x}\frac{1}{\det \left(B_{\overrightarrow{m}}\right)}\mathcal{K}\left(\frac{x\left(t\right)-x_{u_i}}{B_x},B_{\overrightarrow{m}}^{-1}(\overrightarrow{m}-{\overrightarrow{m}}_{u_i})\right)}{\frac{1}{T}\sum _{j=1}^T\frac{1}{b_x}K\left(\frac{x\left(t\right)-x_j}{b_x}\right)},$$ (14)

where N is the total number of spikes, u_i is the time of i^th spike, and T is the total time of the experiment. $\mathcal{K}$ is a multivariate kernel in both the place field and the mark space whose smoothness depends on both the smoothing parameter B_x and the bandwidth matrix $B_{\overrightarrow{m}}$ (Ramsay & Silverman, 2010). K is a univariate kernel on the spatial component only and its smoothing parameter is b_x.

Here we used Gaussian kernels for both $\mathcal{K}$ and K:

$$\mathcal{K}=\left\{\frac{1}{\sqrt{2\pi }}\exp \left[-\frac{1}{2}{\left(\frac{x\left(t\right)-x_{u_i}}{B_x}\right)}^2\right]\right\}\cdot \left\{\frac{1}{{\left(\sqrt{2\pi }\right)}^d}\exp \left[-\frac{1}{2}{(\overrightarrow{m}-{\overrightarrow{m}}_{u_i})}^T{B}_{\overrightarrow{m}}^{-T}{B}_{\overrightarrow{m}}^{-1}(\overrightarrow{m}-{\overrightarrow{m}}_{u_i})\right]\right\},$$ (15)

$$K=\left\{\frac{1}{\sqrt{2\pi }}\exp \left[-\frac{1}{2}{\left(\frac{x\left(t\right)-x_j}{b_x}\right)}^2\right]\right\},$$ (16)

where d = 4 is the dimension of the mark space. The bandwidths were chosen based on previous knowledge of two things: variability in the waveform structure for a single neuron and prior information about spatial extent of a place field. For this analysis, b_x and B_x were set to 1.5% of the linear track length, and $B_{\overrightarrow{m}}$ was set to a 4-dimensional scalar matrix whose diagonal entries equal 20 mV. We found that our results remain consistent for a wide range of bandwidths.

We then compare the results to decoding based on sorted data. These data included a total of 11 active place cells across an 840 second recording session. To assess whether the models generalize well to unobserved data as well as to limit overfitting, both algorithms are carried out using a 5-fold cross-validation.

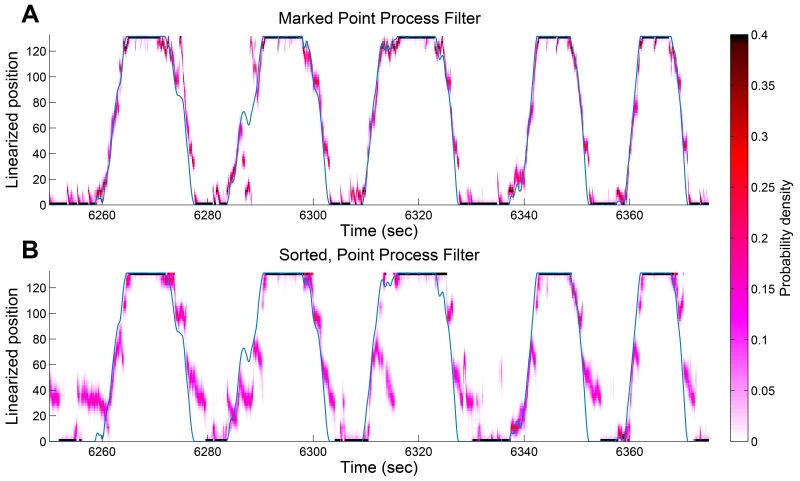
Figure 4 illustrates the decoding results from signals recorded from 5 tetrodes in the CA1 and CA2 regions of the hippocampus using the two different algorithms. Here we display the first 125 seconds of decoding results in both panels. Figure 4(A) are decoding results using the clusterless decoding algorithm. Figure 4(B) are decoding results where the decoder is applied after the spikes have been manually sorted into clusters. The blue line shows the true position of the animal, and the red region shows the estimated posterior density at that time step. We can see that the estimate tracks the true position closely, and the region of highest posterior density covers the true position most of the time. In contrast, as shown in Figure 4(B), the posterior density using decoding with spike-sorting has some trouble tracking the true trajectory, for example between time 6250 seconds and 6260 seconds.

FIGURE 4.

Decoding results for hippocampus data. (A) Posterior density of the rat’s linear position using the clusterless decoding algorithm. The blue line represents the actual position of the rat. The red represents the posterior density at each time step. The posterior density computed through the clusterless decoding algorithm has an rMSE of 14.3 cm and remains within the 99% HPD region 74.25% of the time. (B) Posterior density of the rat’s linear position using decoding with manual spike-sorting. The posterior density computed by first spike-sorting and then decoding has a rMSE of 26.0 cm and remains within the 99% HPD region 70.76% of the time.

To assess quality of fit, we calculated the root-mean-square error (rMSE) in centimeters and the percentage of the time that the true position values fall within the 99% HPD region. We compared the rMSE and percentage of time within 99% HPD region for the decoding results on the entire 840 seconds of recording. The posterior density computed through the clusterless decoding algorithm has an rMSE of 14.3 cm and remains within the 99% HPD region 74.25% of the time. The size of the 99% HPD region for the clusterless decoding algorithm has a mean of 10.5 cm and a standard deviation of 6.96 cm. The posterior density computed by first spike-sorting and then decoding has a rMSE of 26.0 cm and remains within the 99% HPD region 70.76% of the time. The size of the 99% HPD region for the decoded with sorted spikes has a mean of 17.2 cm and a standard deviation of 13.14 cm.

The clusterless algorithm has narrower 99% HPD region, more accurately reflecting the uncertainty of the decoding estimates. The algorithm that uses spike-sorting has wider 99% HPD region, suggesting less certainty in the estimates. Therefore the estimated certainty for the clusterless decoding method is both higher and more accurate than the estimated certainty for the spike-sorting based method. Both visually and numerically, we showed that our proposed clusterless algorithm performs as well as or better than algorithm based on sorted spikes.

5 Discussion

We previously used point process theory to develop efficient decoding algorithms based on spike train observations (Brown et al., 1998; Eden et al., 2004; Huang et al., 2009; Koyama et al., 2010). In each of these cases, a key assumption is that the signals have been accurately sorted into single units before the decoding algorithm is applied. Although new spike-sorting algorithms are actively being developed, spike-sorting still remains a time-consuming, difficult task, suffers from many sources of errors, and likely provides biased estimates (Lewicki, 1998; Harris et al., 2000; Quiroga, 2012). In this article, we have proposed a novel clusterless decoding algorithm that maintains the accuracy of previous methods, but avoids spike-sorting.

The proposed clusterless decoding algorithm has several important advantages. First, this algorithm does not require that the multiunit activity has been accurately sorted into single units. Instead, by using the theory of marked point processes, the algorithm characterizes directly the relationship between a desired variable and features of the spike waveforms. We bypass spike-sorting by modeling the spiking activity as a joint function of the state variable to decode and of features of the spike waveforms. Therefore, this new algorithm can incorporate information from spikes that, in previous decoders that relied on spike sorting, may have been thrown out because of difficulties in clustering, or misclassified. Indeed, in a recent analysis of the effects of spike-sorting schemes on decoding performance, Todorova and colleagues confirmed that discarding waveforms that do not match any template—the “hash”—systematically degrades decoding (Todorova et al., 2014), consistent with previous studies (Stark & Abeles, 2007; Fraser et al., 2009).

Another advantage of the marked point process approach is that the joint intensity mark function defines a population level place receptive field structure, which will typically have multimodal structure. That is, the joint intensity mark function is expected to have multiple peaks in the joint place and mark space. Previous work by Huang et al. has shown that decoding algorithms that allow for highly non-Gaussian and multimodal posterior densities perform better at reconstructing the animal’s trajectory and predicting future decisions (Huang et al., 2009).

Last, formulating the decoding problem within a state-space paradigm offers a number of specific benefits. It allows us to incorporate knowledge about the system we are decoding, in this case the rat’s position trajectory. This also imposes an implicit continuity constraint, preventing large fluctuations in the state estimates. This allows us to track the state variable smoothly without high dependence on the choice of time step during decoding. Moreover, due to the state-space approach, the resulting decoding algorithm incorporates information from both spike intervals and non-spike intervals.

We tested the new decoding algorithm on tetrode recordings from the hippocampus of a rat running back and forth on a linear track. We showed that the clusterless decoding algorithm provided a slightly improved accuracy than that of the decoding with manual spike-sorting approach. The intention of this example is to demonstrate comparable decoding accuracy without the additional, time-consuming spike-sorting step, thus making this algorithm a suitable candidate for real-time application.

There are a number of directions in which this work may be extended. The numerical integration we used to compute the filtering is efficient when decoding low-dimensional signals. When the desired variable is high-dimensional, alternative adaptive algorithms can be used to ensure efficiency, such as sequential Monte Carlo methods or Gaussian approximate filters.

In the application example, we presented a nonparametric encoding model to estimate the joint mark intensity function based on kernel methods. We have found that our results remain consistent for a wide range of bandwidths. Therefore, in real-time decoding, it is reasonable to set the smoothing parameter and bandwidth matrix before-hand. We also recognize for non-parametric kernel based encoding, the computation time increases with the total number of spikes. In the interest of real-time applications, it is possible to explore other more efficient models as well. Within the family of non-parametric encoding model, one can include a time dimension with receding horizon to reduce the number of spikes encoded at any given time.

Another choice of encoding model is semi-parametric models, for example, a multi-dimension grid interpolated for the joint distribution of mark and place field. This grid can serve as a kind of look-up table for the estimated joint mark intensity function. By calculating this grid beforehand, we can perform real-time clusterless decoding without any computation time spent in encoding. A more general approach to reduce encoding time is to perform dimension reduction on the multi-dimensional mark space before encoding.

Finally, as we move away from the prerequisite of spike-sorting, multivariate marked point process models can be developed to describe coupling between neurons (Ba et al., 2014).

Another future role for these methods is in the development of new types of closed-loop experiments. Traditionally, experiments designed to study the role of specific spike patterns in stimulus-response tasks take one of two forms: observational studies that characterize statistical properties of neural activity during such tasks or interventional studies that broadly alter neural activity over an entire neural population or brain region. However, new closed-loop experiments designed based on the content of neural signals aim to characterize causal relationships between neural activity and the biological and behavioral signals they encode. The proposed algorithm can allow investigators to manipulate millisecond-timescale spike patterns in a content-specific way, altering spiking activity related to certain neural patterns while leaving activity related to other patterns intact.

In conclusion, we develop a novel method for modeling neural response properties and decoding biological and behavioral signals by expanding the class of neural models to incorporate marked point processes. We found that the resulting decoding signals were estimated with higher accuracy and more confidence than traditional spike-sorting based methods. We believe this work has broad implications, allowing for better neural coding models across a wide range of brain areas and neural systems.

6 Appendix

6.1 Hippocampal data collection and preprocessing

The hippocampal data in this paper are from a single male Long-Evans rat (500-600 g) trained to alternate in a linear track for liquid reward (condensed milk). A microdrive array containing 21 independently movable tetrodes was implanted targeting the hippocampal cell layers according to University of California San Francisco Institutional Animal Care and Use Committee and US National Institutes of Health guidelines. All neural signals were recorded relative to a reference tetrode in the corpus callosum. Following data collection, electrode locations were verified histologically to localize to the CA1–CA2 region of the hippocampus.

Data were collected using the NSpike data acquisition system (L.M.F. and J. MacArthur, Harvard Instrumentation Design Laboratory). An infrared diode array with a large and a small cluster of diodes was attached to the preamps during recording. Following recording, the rats position on the track was reconstructed using a semi-automated analysis of digital video of the experiment. Individual units (putative single neurons) were identified by clustering spikes using peak amplitude, principal components, and spike width as variables (MatClust, M. Karlsson) (Karlsson & Frank, 2008).

6.2 Gaussian approximation to the posterior density

Because in this paper the state variable is low-dimensional, we used a simple Riemann sum to perform numerical integration over the state space in order to solve the one-step prediction density in equation (4). If the state variable is high-dimensional and the posterior density can be assumed to be approximately Gaussian, a stochastic state point process filter (SSPPF) can be used. The SSPPF is constructed using a Gaussian approximation to the posterior density. Detailed derivation of approximate Gaussian filters for temporal point processes can be found in (Brown et al., 1998; Eden et al., 2004). Here we provide an extension of the SSPPF to the marked case.

For estimating higher-dimensional state variables, a linear recursive Gaussian approximation to the posterior density at each time step, p(x_k|ΔN_k, m_k) can be constructed with the estimated conditional mean x_k|k and variance W_k|_k as follows:

$$W_{k\mid k}^{-1}={(F_k{W}_{k-1\mid k-1}{F}_k^T+Q_k)}^{-1}+{\left[\frac{{\partial }^2{\Lambda }_k}{\partial x_k\partial x_k^T}{\Delta }_k-\sum _{i=1}^{\Delta N_k}\frac{{\partial }^2\log {\lambda }_k^i}{\partial x_k\partial x_k^T}\right]}_{x_k=F_k{x}_{k-1\mid k-1}}$$

$$x_{k\mid k}=F_k{x}_{k-1\mid k-1}+W_{k\mid k}{\left[\sum _{i=1}^{\Delta N_k}{\left(\frac{\partial \log {\lambda }_k^i}{\partial x_k}\right)}^T-{\left(\frac{\partial {\Lambda }_k}{\partial x_k}\right)}^T{\Delta }_k\right]}_{x_k=F_k{x}_{k-1\mid k-1}},$$

where, for simplicity, ${\lambda }_k^i$ denotes $\lambda (t_k,{\overrightarrow{m}}_{k_i}\mid H_k)$ and Λ_k denotes $\Lambda (t_k\mid H_k)={\int }_{\mathcal{M}}\lambda (t_k,{\overrightarrow{m}}_k\mid H_k)\mathrm{d}{\overrightarrow{m}}_k$. In the posterior mean equation, the innovation includes two terms. The first term, $\frac{\partial \log {\lambda }_k^i}{\partial x_k}$, depends on the marks of the observed spikes. The second term $\frac{\partial {\Lambda }_k}{\partial x_k}$ includes Λ_k, which is the intensity function of the ground process and relates to the intensity of observing any spikes regardless of the mark.

6.3 Sequential Monte Carlo decoding algorithm

When the state variable is high-dimensional and the posterior density cannot be assumed to be approximately Gaussian, another computationally efficient alternative is a sequential Monte Carlo algorithm. Point process adaptive filters using sequential Monte Carlo approximations to the posterior density have been developed in previous literature (Ergun et al., 2007; Meng et al., 2011). Here we provide a pseudo-code description of the algorithm with extension to marked point processes. This is a bootstrap filter, so the proposal distribution is based on the one-step prediction density from the previous time step.

At each time step t, the algorithm produces a collection of weighed samples, or particles, each containing proposed values for the state variable x_t. We construct estimates for the state variable by computing their sample means over all the particles, and construct approximate 95% confidence intervals.

1. Initialization:

Set t = 0 and for i = 1, ⋯ , n particles, draw the initial states and parameters from an initial probability distribution and set the importance weight of the i^th particle $w_0^i=n^{-1}$ for all i. Set t=1.

2. Importance sampling:

Using the particles from the previous step which represent the one-step prediction density defined in equation (4) as the sampling distribution, update all of the states x_t.

Evaluate the importance weight of the i^th particle

$$w_t^i=w_{t-1}^{t}p(\Delta N_t,{\overrightarrow{m}}_k\mid H_t),$$

where $p(\Delta N_t,{\overrightarrow{m}}_k\mid H_t)$ is computed by equation (5) or (13).

Normalize the importance weights

$${\tilde{w}}_t^i=\frac{w_t^i}{\sum _j{w}_t^j}.$$

3. Resampling:

Resampling can be performed at any fixed interval. Draw n particles $\{{\tilde{x}}_t^i:i=1,\cdots ,n\}$ from $\{s_t^i:i,\cdots ,n\}$ using the residual resampling approach. Reset the weights to ${\tilde{w}}_t^i=n^{-1}$ to obtrain the Monte Carlo estimate of the probability density

$$p({\tilde{x}}_t\mid N_t)\approx n^{-1}\sum _{i=t}^n\delta ({\tilde{x}}_t-{\tilde{x}}_t^i),$$

where δ(·) is the Dirac delta function, indicating a point mass at 0.

4. Repeat steps 2–3.