Abstract
To investigate the electroencephalograph (EEG) background activity in patients with Alzheimer’s disease (AD), power spectrum density (PSD) and Lempel–Ziv (LZ) complexity analysis are proposed to extract multiple effective features of EEG signals from AD patients and further applied to distinguish AD patients from the normal controls. Spectral analysis based on autoregressive Burg method is first used to quantify the power distribution of EEG series in the frequency domain. Compared with the control group, the relative PSD of AD group is significantly higher in the theta frequency band while lower in the alpha frequency bands. In order to explore the nonlinear information, Lempel–Ziv complexity (LZC) and multi-scale LZC is further applied to all electrodes for the four frequency bands. Analysis results demonstrate that the group difference is significant in the alpha frequency band by LZC and multi-scale LZC analysis. However, the group difference of multi-scale LZC is much more remarkable, manifesting as more channels undergo notable changes, particularly in electrodes O1 and O2 in the occipital area. Moreover, the multi-scale LZC value provided a better classification between the two groups with an accuracy of 85.7 %. In addition, we combine both features of the relative PSD and multi-scale LZC to discriminate AD patients from the normal controls by applying a support vector machine model in the alpha frequency band. It is indicated that the two groups can be clearly classified by the combined feature. Importantly, the accuracy of the classification is higher than that of any one feature, reaching 91.4 %. The obtained results show that analysis of PSD and multi-scale LZC can be taken as a potential comprehensive measure to distinguish AD patients from the normal controls, which may benefit our understanding of the disease.
Keywords: Electroencephalogram, Alzheimer’s disease, Power spectrum density, Lempel–Ziv complexity, Multi-scale Lempel–Ziv complexity
Introduction
Alzheimer’s disease (AD) is a progressive, disabling neuro-degenerative disorder that affects mainly older persons beyond the age of 70. Experimental studies show that it is may be caused by the degeneration of synapses and death of neurons in the brain regions, such as hippocampus, entorhinal cortex, neocortex. It usually results in a loss in cognition, memory, judgment, even language and functional skills (Dauwels et al. 2009, 2010a, 2011; Mattson 2004). It is asserted that a definite diagnosis is only possible by necropsy (Dauwels et al. 2010a). Because the symptoms in early state are easily neglected as normal consequences of aging, discriminating AD patients from the normal is difficult.
Electroencephalogram (EEG) could record multi-channel neural electrical signals in different areas of the brain simultaneously with high temporal resolution. Scalp recordings are related to underlying processes, although spatial information is lost due to the blurring effects of high skull conductivity (Dauwels et al. 2010a; Koenig et al. 2005; Claus et al. 1999; Schoenberg and Speckens 2015; Yang and Lin 2013; Han et al. 2013). Due to the high temporal resolution, non-invasiveness, simplicity, and relatively low cost, EEG is still one irreplaceable brain research technique although some structural and functional imaging techniques developed quickly (Han et al. 2013; Kowalski et al. 2001; Jonkman 1997; Babiloni et al. 2006). Now it is widely used as auxiliary diagnosis method for clinician to detect normal brain and brain with neurological disorders, such as Alzheimer’s disease (AD; Dauwels et al. 2009, 2010a, b, 2011; Wang et al. 2014) According to the rather widely held view, the development of AD is associated with perturbations in EEG synchrony (Stam et al. 2003; Park et al. 2008), reduction of complexity in EEG (Dauwels et al. 2010a; Stam 2005) and the slowing of EEG (Dauwels et al. 2011; Moretti et al. 2009).
Among various EEG analysis methods, the spectral analysis methods are especially important because the frequencies and characteristics of brain waveform change depending on the brain function affected from disorders and physiological state (Akin and Kiymik 2000; Nunez et al. 2001). By dividing the whole frequency spectrum into a sum of pure frequency components via wavelet decomposition, each EEG signal can be analyzed in terms of its power spectral density (PSD) based on parametric autoregressive (AR) model, which provides information on the signal power at each relatively narrow frequency band (Dauwels et al. 2010a, 2011; Akin and Kiymik 2000). Compared with traditional spectrum estimation methods, AR-Burg algorithm could perform better with less spectral losses and higher frequency resolution (Akin and Kiymik 2000; Yi et al. 2013). Nowadays, the most frequently observed spectral change of AD is the “slowing” of the EEG, which supposedly correlates with the degree of cognitive decline (Bennys et al. 2001; Dringenberg 2000; Jeong 2004; Schreiter-Gasser et al. 1994). Czigler et al. (2008) have found a significant power increase of the theta band and decrease of alpha band in AD EEG. Gianotti et al. and Jeong et al. have further proved that power decrease occurs in high frequency band (alpha and beta band) with a simultaneous increase in low frequencies (delta and theta band) in AD patients, which is closely related to the development of the disease (Jeong 2004; Gianotti et al. 2007). On the whole, AD is associated with an increase of power in low frequencies (delta and theta band, 0–8 Hz) and a decrease of power in higher frequencies (alpha and beta band 8–30 Hz).
PSD based on AR model could characterize the group differences between AD patients and the normal controls in frequency domain (Wang et al. 2015a, b). However, it focuses on the linearity within EEG signals (Zhou et al. 2008). In fact, it has been extensively reported that the EEG signals are naturally nonlinear due to the nonlinearity of the brain at the neuronal level. Moreover, previous works have shown that nonlinear analysis of EEG is useful to characterize different pathological states like epilepsy (Lehnertz et al. 2003), schizophrenia (Roschke et al. 1995) and Parkinson’s diseases (Stam et al. 1995). This gives rise to the possibility that the underlying mechanisms of the brain function maybe explained by nonlinear dynamics. Hence, non-linear analysis techniques may be a better approach than traditional linear methods to obtain a better understanding of abnormal electrophysiological behavior of AD patients in EEG signals (Escudero et al. 2006). In AD associated with neuropathological deficits, owing to the decreased capability to process information the neural complexity appears to be reduced by the analysis of approximate entropy, sample entropy, Lempel–Ziv complexity (LZC), chaos analysis and so on (Gu et al. 2003; Hornero et al. 2009).
Correlation dimension (D2) and the largest Lyapunov exponent (LLE) are the first nonlinear techniques applied to EEG (Jeong et al. 2001). It has been shown that AD patients have lower values of D2 and LLE than the normal controls. However, the calculation of D2 and LLE requires the data series to be stationary and long enough, which cannot be achieved for physiological data (Jeong et al. 1998; Jelles et al. 1999; Grassberger and Procaccia 1983; Eckmann and Ruelle 1992; van Cappellen et al. 2003). Other nonlinear methods such as entropy index are mostly parametric and need to choose appropriate parameters, which may increase the calculation burden. Besides, LZC is a non-parametric measure of complexity in a one-dimensional signal related to the number of distinct substrings (equal to the number of different patterns in a sequence) and the rate of their recurrence (Lempel and Ziv 1976). It is better suited for EEG analysis than D2 and more precise than LLE for characterizing order or disorder (Kaspar and Schuster 1987). The use of this quantitative complexity measure can help us gain a better insight into the system dynamics (Zhang et al. 2001). However, the traditional LZC method cannot describe the relationship between adjacent points during the coarse-graining which transfers the original signal into a binary time series, leading to a great loss of detailed information from the original signal.
On the other hand, quantitative analysis of EEG based on classification evaluation and ROC curves have also been widely applied to distinguish AD group and the control group. For instance, Besthorn et al. (1997) achieved an accuracy of 69.5 % with D2 (using 50 AD patients and 42 controls). Abasolo et al. (2006a) achieved an accuracy of 77.3 % with sample entropy (using 11 patients with AD and 11 controls). Moreover, Escudero et al. (2006) used multi-scale entropy and obtained an accuracy of 90.4 %. However, these methods were mainly based on single feature and could only reflect one aspect of the scalp-recorded EEG signals.
In this work, we introduce the multi-scale LZC method and demonstrate its advantages by comparing it with the traditional LZC analysis. We aim to detect and assess the abnormalities of EEG signals from ADs based on spectrum and complexity analysis. Multiple efficient features: relative PSD and multi-scale LZC values are extracted and applied to discriminate AD from normal control by applying a support vector machine model. We also seek to combine the two classes of features to discriminate the spontaneous EEG recordings of the two groups. Accordingly, the subsequent parts of this paper are organized as follows: in “Experiment and EEG recording” section, we give a description of the experimental design and the EEG recording, including information of the subjects, the EEG data recording and preprocessing; in “Analysis methods” section, we formulate the estimation of PSD, LZC and multi-scale LZC, extract the EEG features, and explain the statistical analysis in detail; in “Results” section, analysis results of the two groups are presented; which is followed by discussion in “Discussion” section and conclusion in “Conclusions” section.
Experiment and EEG recording
The subjects of experiment are separated into two groups: AD group and the control group. The mean age of twenty-four AD patients (ten females and fourteen males) was 78, and the Mini-Mental-Status examination (MMSE) scores were between 11.5 and 14.2. As for the control group, the mean age of twenty-four controls (ten females and four males) was 75, and the MMSE scores were ranged from 27.2 to 29.7. The MMSE test is a reliable 30-point questionnaire that is used extensively in clinical research to measure cognitive impairment associated with the severity of AD. Generally, any test scores greater than or equal to 27 points (out of 30) indicates a normal cognition. Below this, the scores can also indicate mild (19–24 points), moderate (10–18 points) or severe (≤9 points) cognitive impairment. All the subjects were right-handed and free from other neurological or psychological disorders, neurological active medication, or any other factor that may affect EEG activity. During the experiment, the subjects were seated upright in a relaxed state with eyes closed, and they were told in advance that any movements should be avoided during the experiment, such as body movements, eye movements and blinks.
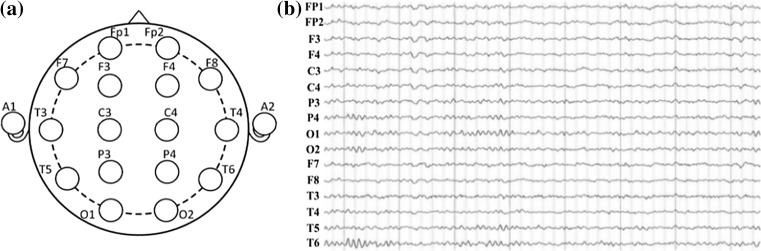
A 16-channel Symptom system was used to set on the scalp according to the international widely used 10–20 system. The electrode impedances were kept under 30 kΩ, and the sampling frequency was 1024 Hz. The linked ears A1 and A2 were used as a reference, and the 16 Ag–AgCl scalp electrodes were channels Fp1, Fp2, F3, F4, C3, C4, P3, P4, O1, O2, F7, F8, T3, T4, T5, T6, as shown in Fig. 1a, and the real EEG signals recorded were shown in Fig. 1b. The digitized EEG data were processed in a MATLAB environment (version 7.12.0.635, R2011a).
Fig. 1.
The distribution of electrode loci in the modified 10–20 electrode configuration for 16-channel EEGs marked in a brain is represented in a, and the real EEG recordings of 16-channels in b
Analysis methods
Wavelet decomposition
In order to achieve high confidence of the data, we intercept five EEG epochs which last for 8 s from EEG data of each subject so to investigate the effect of AD on the brain. First all selected epochs are digitally filtered with cut-off frequencies at 0.5–30 Hz by set the lower and upper limit of the FIR filter which is band-passed to eliminate artifacts induced by residual EMG and noise. Then, following Adeli et al. and Ahmadlou et al. who decompose the whole frequency band into different sub-bands, a three-level wavelet decomposition is used to decompose the band-limited EEG (0.5–30 Hz) into four sub-bands: delta (0.5–4 Hz), theta (4–8 Hz), alpha (8–15 Hz), and beta (15–30 Hz; Adeli et al. 2007; Ahmadlou et al. 2010).
Power spectral density estimation
In our study, the PSD for each epoch is estimated using AR Burg method. There are two steps in the spectrum estimation procedure. Firstly, estimate the parameters of the model-based method from a given data sequence x(n), 0 ≤ n ≤ N − 1. Secondly, compute the PSD estimated from these estimations. The AR method, which is one of the most frequently used parametric methods, is based on modeling the data sequence x(n) as the output of a causal and discrete filter whose input is white noise. Thus the AR method of order p is expressed as follows
| 1 |
where a(k) are the AR coefficients and ω(n) is the white noise of variance equal to σ2. The AR method of order p can be characterized by AR parameters {a[1], a[2],…, a[p], σ2}. Then PSD is defined as follows
| 2 |
where
In our work, AR coefficients are estimated by the recursive Burg method, which is based on minimizing the forward and backward prediction errors. From the estimates of AR parameters by the Burg algorithm, PSD estimation is formed as
| 3 |
where is the total least squares error. The model order p of the AR method is determined by using Akaike information criterion (AIC). In our study, the model order is taken as p = 10. Then the PSD results of each frequency band are normalized to obtain the relative PSD of one band to the whole frequency band.
| 4 |
where [fL, fH] = [0.5, 40] and [f1, f2] is determined by the frequency sub-band selected (Akin and Kiymik 2000; Bennys et al. 2001; Dringenberg 2000).
Furthermore, in order to observe the topographical distribution of the power of different rhythms, 16-channel EEG signals of all subjects are analyzed specifically in the four bands.
Lempel–Ziv complexity
Lempel–Ziv complexity
The complexity of signal can be quantified by Lempel–Ziv complexity (LZC; Lempel and Ziv 1976). As a nonlinear complexity measure, LZC is well suited for characterizing the development of spatio-temporal activity patterns in high-dimensionality nonlinear systems, and it could reveal the regularity and randomness in an epoch of time varying EEG and gain the information regarding the dynamics of the specific regional brain subsystem, such as brain function, movement prediction, anesthetized depth, and so on (Czigler et al. 2008; Gianotti et al. 2007; Shaw et al. 1999).
LZC analysis is based on a coarse graining of the measurements. First, the EEG signal with 8192 samples is coded about the median by a binary sequence of zeros and ones in the calculation of LZC. Then, the symbol sequence is scanned from left to right and the complexity counter c(n) is increased by one unit every time a new subsequence of consecutive characters is encountered in the scanning process, which is a useful measure describing the sequence with length n and reflects the relative complexity of the string . c(n) tends to the value:
| 5 |
where b(n) gives the asymptotic behavior of c(n) for a random string. c(n) is normalized by b(n):
| 6 |
Obviously, 0 ≤ C(n) ≤ 1. After normalization, the complexity measure reflects the rate of occurrences of new pattern along with time increasing. The higher LZ complexity value is, the higher complexity of the EEG signal is.
Multi-scale Lempel–Ziv complexity
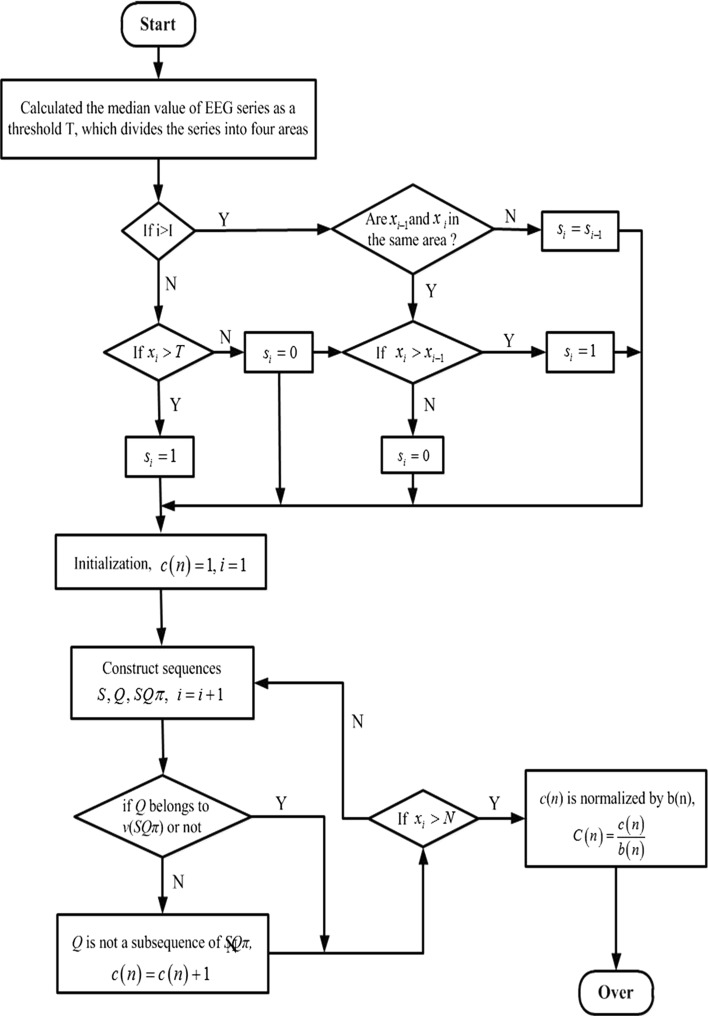
In order to retain most of the detailed information during the feature extraction, multi-scale Lempel–Ziv complexity is introduced. Multi-scale LZC could overcome the disadvantage that the excessive coarse-graining leads to detailed information lost too much in the traditional LZC. The difference of the two LZC methods exists in the approach of coarse-graining, and the steps of coarse-graining in the multi-scale LZC can be described as follows.
First, median value of EEG series is calculated as a threshold T, which divides the series into two areas according to the numerical relationship of each value of EEG series and the median value. Moreover, each area is divided into two areas in the same way. Thus, the EEG series is divided into four areas.
Then, by comparison with the threshold T, the value of the first point is converted into 0 or 1. If it is larger than the median value, it is assigned 1, and vice versa.
| 7 |
From the second point of the EEG series, the results of encoding depend on the comparisons with the previous point. If the value of EEG series is increased to another area, then the value of this point is assigned to 1; if it is decreased to another area, then the value of this point assigned to 0; otherwise, if the two points are in the same area, then the encoding value of the point equals to the value of the previous point. Then the EEG series are converted into a 0–1 sequence , with si defined by
| 8 |
where After extracting the features of EEG signals using multi-scale LZC analysis, it is possible to keep more detailed information, and improve the accuracy of the feature extraction. The steps of the multi-scale LZC analysis are depicted as a block diagram shown in Fig. 2.
Fig. 2.
Multi-scale LZC block diagram
Statistical analysis
One-way ANOVA test was used to assess significant changes in the power spectral density and Lempel–Ziv complexity for AD group and the control group. A smaller P value and a larger F value indicate a higher group difference, and vice versa. Generally, P < 0.01 was considered as the significance level in statistics.
The ability of the two methods to discriminate AD patients from the normal controls where P < 0.01 by ANOVA was evaluated using receiver operating characteristic (ROC) curves (Zweig and Campbell 1993), which was based on the support vector machine (SVM) classifier. SVM is a supervised classifier whose main objective is to find an optimal separating hyperplane that can maximize the distance between this hyperplane and the nearest data point of each class (called the support vectors). In the case of non-linear classification, kernel functions can be used to map the nonlinear features to a higher dimensional space where the features become linearly separable. In this work, we used the radial basis function kernel. To improve the performance of the classifier, a grid search approach was used to find proper parameters for the SVM algorithm.
Results were showed in terms of sensitivity (i.e., proportion of all AD patients who tests positive), specificity (i.e., percentage of the normal controls correctly classified), and accuracy (i.e., total fraction of AD and the normal controls well classified) for all the available thresholds of the SVM classifier [not the threshold T in Eq. (7)]. The highest accuracy (minimal false negative and false positive results) could be obtained at the optimum threshold which was determined from the ROC curve as the closest value to the left top point (100 % sensitivity, 100 % specificity). Moreover, the area under the ROC curve (AUC) characterized the performance of classification, for a perfect classification the area is 1 while an AUC of 0.5 represented a worthless test.
Results
Power spectrum density estimation
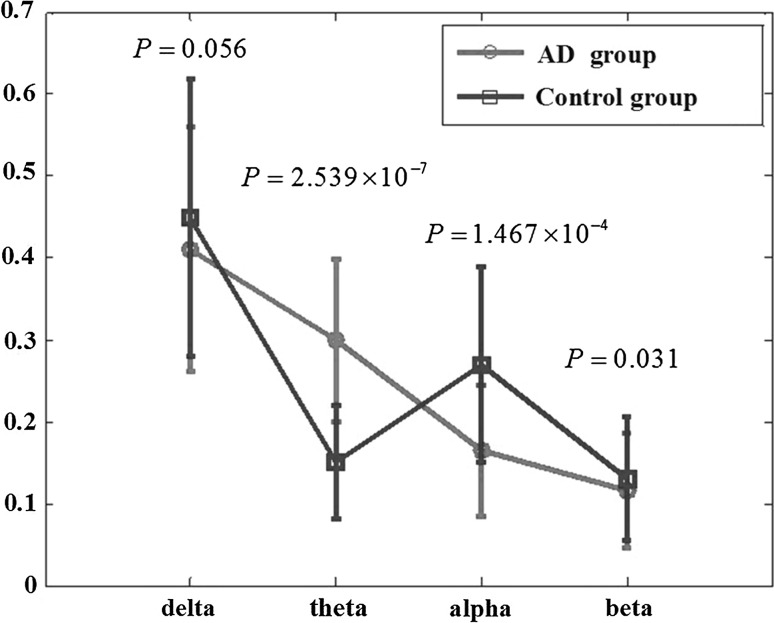
In this work, the relative power in each sub-band was obtained by the ratio of the power in each sub-band and the total power in the whole band. Figure 3 shows the relative PSD values of AD group and the control group averaged over 16 electrodes, the results of one way ANOVA is also included in the figure. It can be observed that for both two groups, the relative PSD decreased with the increase of the frequency, except for the value of the control group in the alpha frequency band. Moreover, the relative PSD in the beta band was the lowest indicating that the energy distributed in this sub-band was lowest owing to that the beta rhythm had something to do with less movement high attention which was seldom occurred in eye-closed relax state, neither AD patients nor normal subjects. Compared with the control group, it was found that, the relative PSD in the theta frequency band was increased, whereas decreased in the remaining three frequency bands, such as the delta, alpha, and beta frequency bands. Moreover, it was shown that the group differences of the relative PSD estimated by the AR Burg method were statistically significant in the theta (P = 1.467 × 10−4 < 0.01) and alpha frequency bands (P = 2.539 × 10−7 < 0.01).
Fig. 3.
The relative PSD values averaged over the 16 electrodes in the four frequency bands for AD group and control group. Standard errors are represented with error bars. P values returned by one way ANOVA are also displayed
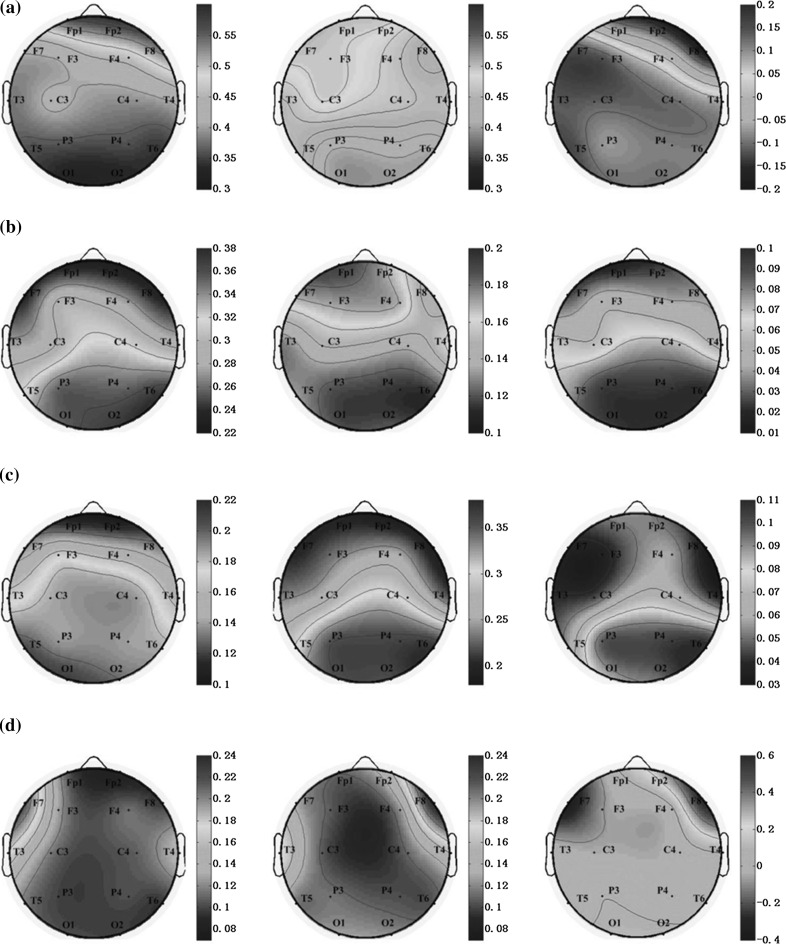
To investigate the difference of energy distribution between AD group and the control group in different brain regions, the topographic maps of two groups in four sub-bands are displayed in Fig. 4. In Fig. 4a, delta power was activated at the frontal areas in AD group, but in control group the power was almost distributed over the whole brain, so the normalized differences between two groups were distributed in the whole brain except the frontal regions. In the Fig. 4b, the theta power was mainly activated in the parietal and occipital regions in AD group and activated in the frontal and parietal occipital regions in control group. After normalization, the differences between two groups were centered on parietal and occipital regions. The alpha power (Fig. 4c) was widely distributed in the brain except the frontal regions, whereas it was almost centered in the occipital in control group and the normalized difference group. The distribution of the beta power (Fig. 4d) was mainly at the left frontal- temporal in AD group, while located at right frontal- temporal in the other two groups. It was a noteworthy contrast that when the frequency increased from delta, theta, alpha, to beta rhythms, the activated areas of both AD and control group were transferred from the frontal regions of brain to the parietal regions, and then transferred to the occipital regions, and finally traveled to the frontal-temporal regions.
Fig. 4.
Topographic maps of PSD values for AD group (left), the control group (middle), and the normalized differences between two groups (right) in a delta, b theta, c alpha and d beta sub-band, respectively
Lempel–Ziv complexity analysis
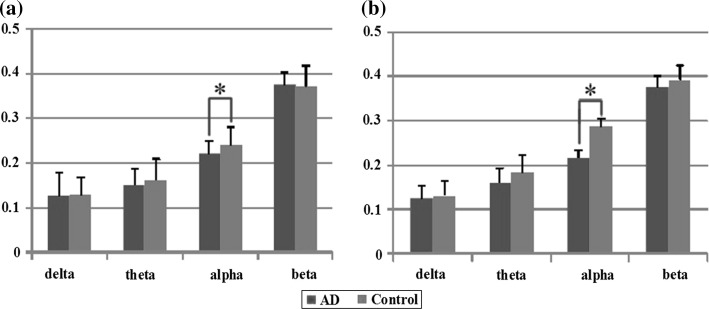
LZC and the multi-scale LZC were calculated for 16 channels: Fp1, Fp2, F3, F4, C3, C4, P3, P4, O1, O2, F7, F8, T3, T4, T5 and T6 to quantify the complexity in the EEG data of AD and control groups. The results have been averaged based on all the artefact-free 8 s epochs (N = 8023 points) within the 5-min period of EEG recordings. Figure 5 and Table 1 showed the statistical results of LZC and multi-scale LZC analysis in the delta, theta, alpha and beta frequency bands for the two groups. It was noted that, the group difference was all significant in the alpha frequency band, returning P = 0.0002, F = 16.72 with LZC analysis and P = 0.0000169, F = 24.23 with multi-scale LZC analysis. However, the group difference by multi-scale LZC method was much more remarkable.
Fig. 5.
The average traditional LZC values (a) and the average multi-scale LZC values (b) averaged over the 16 electrodes in the four frequency bands for AD group and control group. Standard errors are represented with error bars. Asterisk represents significant difference between two groups with P < 0.01 by ANOVA analysis
Table 1.
Results of ANOVA analysis for traditional LZC and multi-scale LZC of the four frequency bands between AD and control group
| Method | Sub-band | F value | P value |
|---|---|---|---|
| LZC | Delta | 0.11 | 0.7367 |
| Theta | 1.47 | 0.2322 | |
| Alpha | 16.72 | 0.0002 | |
| Beta | 1.22 | 0.2756 | |
| Multi-scale LZC | Delta | 0.22 | 0.6466 |
| Theta | 6.63 | 0.0124 | |
| Alpha | 24.23 | 1.69e−05 | |
| Beta | 0.63 | 0.4318 |
Significant group differences (P < 0.01) are shown in boldface
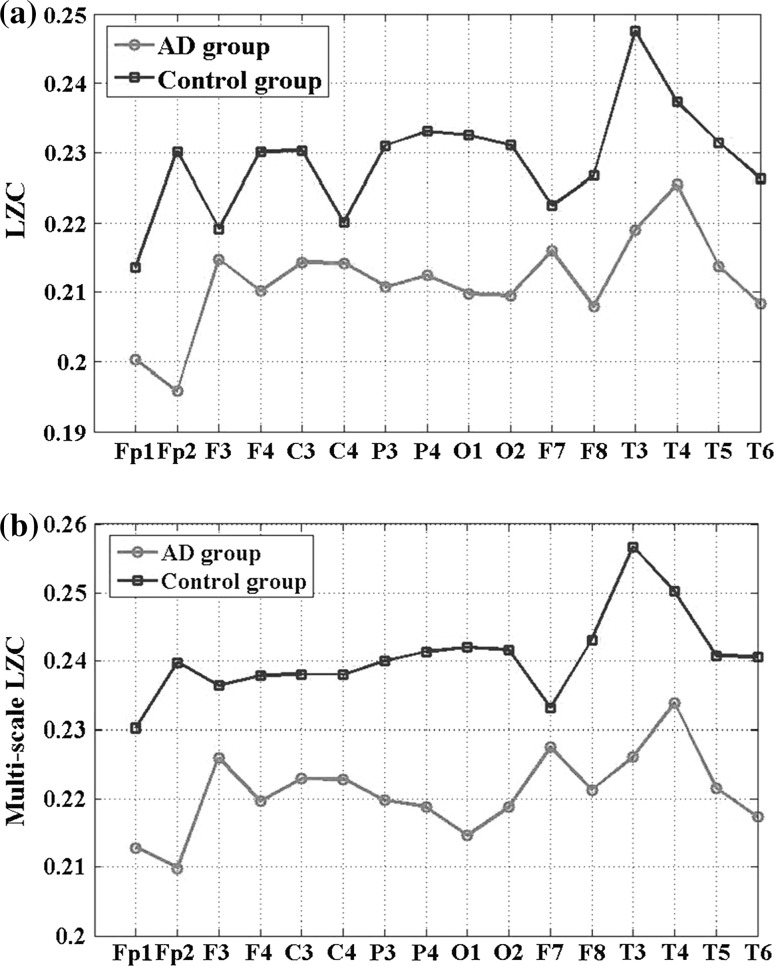
LZC and multi-scale LZC analysis were further applied to all pair-wise EEG channels for AD group and the control group in the alpha frequency band, where the relative PSD and LZC mentioned above all had significant group difference. As shown in Fig. 6, for the both methods, the values of AD group were much lower than that of the control group. However, the group difference of the multi-scale LZC values was higher than the LZC values. Moreover, the trends of the multi-scale LZC values were similar the trends of the LZC values for AD group, while slight different for the control group, particularly in the channel F3 and C4. These results suggest that EEG activity of AD patients is markedly less complex in certain regions than in a normal brain, indicating the number of different patterns in EEG signal of AD is smaller than the EEG of normal controls.
Fig. 6.
The average traditional LZC values (a) and the average multi-scale LZC values (b) of the EEGs in AD group and control group for all channels
The average LZC and multi-scale LZC values and standard deviations for AD groups and the control group for the 16 electrodes are summarized in Tables 2 and 3. The AD group has significantly lower LZ complexity values (P < 0.01) at electrodes FP2, F4, P3, P4, O1, O2, F8, T3, T5 and T6 for the traditional two-symbol sequence conversion, particularly in O1 and O2, where the group difference was much more significant with P < 0.001. While the group difference was significant in all channels except F3 by the multi-scale LZC method. Especially, the channel FP2, P3, P4, O1, O2, F8, T3, T5 and T6 obtained the significance level P < 0.001. Obviously, the multi-scale LZC method was much more sensitive than the traditional LZC method to evaluate the group difference.
Table 2.
The average LZC values of the EEGs in all channels for AD group and the control group
| Electrode | AD group (mean ± SD) | Control group (mean ± SD) | P value |
|---|---|---|---|
| Fp1 | 0.229 ± 0.026 | 0.238 ± 0.019 | 0.1944 |
| Fp2* | 0.223 ± 0.019 | 0.247 ± 0.026 | 0.0018 |
| F3 | 0.232 ± 0.016 | 0.246 ± 0.017 | 0.0159 |
| F4* | 0.228 ± 0.015 | 0.247 ± 0.023 | 0.0041 |
| C3 | 0.237 ± 0.013 | 0.246 ± 0.017 | 0.0651 |
| C4 | 0.231 ± 0.017 | 0.244 ± 0.034 | 0.1506 |
| P3* | 0.230 ± 0.015 | 0.245 ± 0.014 | 0.0027 |
| P4* | 0.227 ± 0.019 | 0.247 ± 0.017 | 0.0015 |
| O1** | 0.225 ± 0.017 | 0.246 ± 0.014 | 0.0001 |
| O2** | 0.226 ± 0.016 | 0.247 ± 0.014 | 0.0001 |
| F7 | 0.241 ± 0.020 | 0.243 ± 0.015 | 0.7967 |
| F8* | 0.235 ± 0.013 | 0.250 ± 0.020 | 0.0099 |
| T3* | 0.240 ± 0.019 | 0.265 ± 0.032 | 0.0051 |
| T4 | 0.245 ± 0.017 | 0.258 ± 0.022 | 0.0603 |
| T5* | 0.232 ± 0.018 | 0.250 ± 0.015 | 0.0022 |
| T6* | 0.225 ± 0.019 | 0.247 ± 0.021 | 0.0013 |
* and ** represent significant difference between the two groups with P < 0.01 and P < 0.001 respectively
Table 3.
The average multi-scale LZC values of the EEGs in all channels for AD group and the control group
| Electrode | AD group (mean ± SD) | Control group (mean ± SD) | P value |
|---|---|---|---|
| Fp1* | 0.213 ± 0.019 | 0.230 ± 0.019 | 0.0073 |
| Fp2** | 0.210 ± 0.021 | 0.240 ± 0.020 | 3.48e−05 |
| F3 | 0.226 ± 0.016 | 0.236 ± 0.014 | 0.0350 |
| F4* | 0.220 ± 0.016 | 0.238 ± 0.020 | 0.0027 |
| C3* | 0.223 ± 0.015 | 0.238 ± 0.014 | 0.0023 |
| C4 | 0.223 ± 0.017 | 0.238 ± 0.032 | 0.0681 |
| P3** | 0.220 ± 0.013 | 0.240 ± 0.011 | 6.14e−06 |
| P4** | 0.219 ± 0.019 | 0.241 ± 0.012 | 7.51e−05 |
| O1** | 0.215 ± 0.016 | 0.242 ± 0.011 | 3.23e−07 |
| O2** | 0.219 ± 0.016 | 0.242 ± 0.014 | 3.10e−05 |
| F7 | 0.228 ± 0.019 | 0.233 ± 0.013 | 0.2861 |
| F8** | 0.221 ± 0.014 | 0.243 ± 0.019 | 2.32e−04 |
| T3** | 0.226 ± 0.017 | 0.257 ± 0.030 | 3.91e−04 |
| T4* | 0.234 ± 0.016 | 0.250 ± 0.021 | 0.0099 |
| T5** | 0.222 ± 0.016 | 0.241 ± 0.013 | 1.87e−04 |
| T6** | 0.217 ± 0.019 | 0.241 ± 0.015 | 1.62e−04 |
* and ** represent significant difference between the two groups with P < 0.01 and P < 0.001 respectively
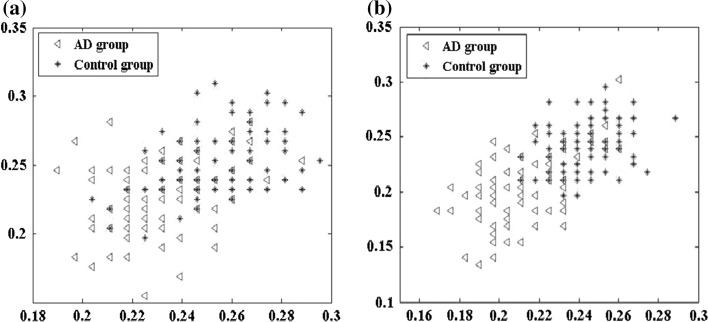
The effects of the traditional LZC and multi-scale LZC analysis on O1 and O2 channel in the alpha frequency band were exhibited in Fig. 7, on which significant groups differences of both relative PSD and LZC analysis existed (Tables 2, 3; Fig. 6). Seen from Fig. 6, both the LZC and the multi-scale LZC value of the control group for O1 and O2 was much higher than that of AD group. However, the multi-scale LZC achieved a better result in the clustering compared with the results of traditional LZC method, manifested as smaller overlap area between AD group and the control group. This may be due to the fact that the multi-scale LZC conversion could keep more detailed information of the EEG during the coarse-graining process.
Fig. 7.
Scatter plots of average a LZC and b multi-scale LZC values of the EEGs on O1 and O2 channel for AD group and the control group in the alpha frequency band
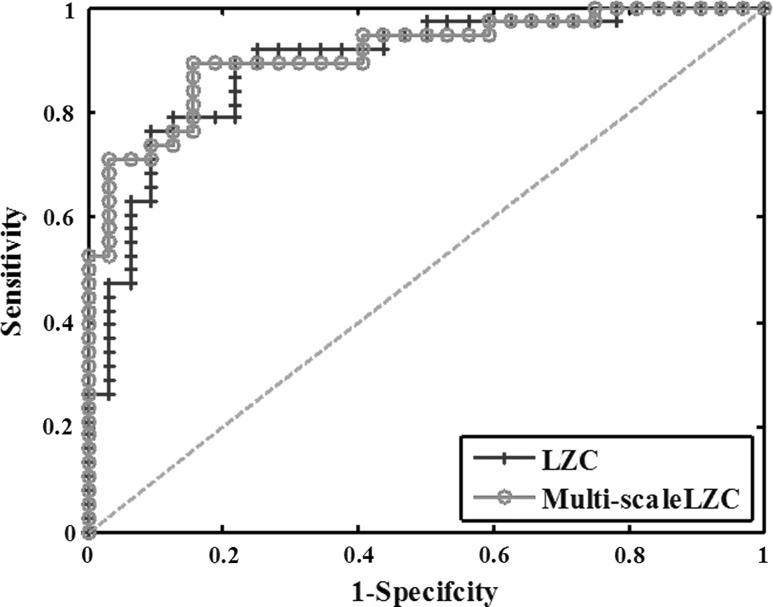
In order to make a comparison of LZC and multi-scale LZC methods, the classification of AD and the control group by the two LZC methods was further executed. The corresponding ROC curves which summarized the performance of a two-class classifier were shown in Fig. 8. Each point of the curves corresponds to a classification threshold. We calculated the areas under the ROC curve (AUC) of the features in the figure. Generally, the larger the AUC is, the better the classification is. From Fig. 9, it was shown that the AUC of the multi-scale LZC value in the alpha frequency was larger than that of LZC value. In addition, the results of the sensitivity, specificity, AUC and accuracy for the two methods were shown in the first two lines of Table 4. It was found that multi-scale LZC value provided a better classification between the two groups with an accuracy of 85.7 %. Moreover, the sensitivity, specificity and AUC reached were 86.8, 84.3 and 91.12 %, respectively.
Fig. 8.
ROC curves which assesses the classification performance between AD patients and the normal controls in the alpha band with LZC and multi-scale LZC. In addition, the green dotted line is known as the “no-discrimination line” and corresponds to a classifier which returns random guesses. (Color figure online)
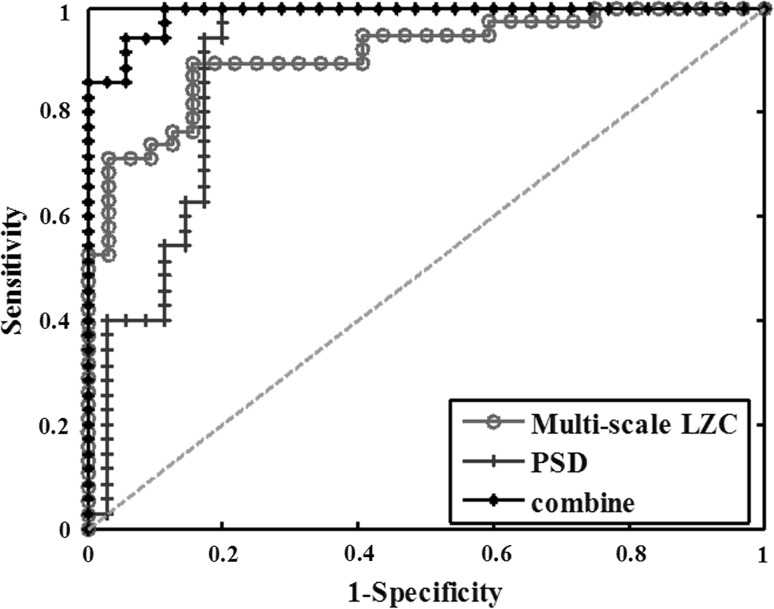
Fig. 9.
ROC curves for discriminating AD patients and normal controls with PSD, multi-scale LZC and their combined feature
Table 4.
Results of the ROC analysis for the PSD, LZC, multi-scale LZC and the combined features of PSD and multi-scale LZC, including sensitivity, specificity, area under the ROC curve (AUC) and accuracy
| Method | Sensitivity (%) | Specificity (%) | AUC | Accuracy (%) |
|---|---|---|---|---|
| LZC | 80.0 | 78.1 | 0.8921 | 78.5 |
| Multi-scale LZC | 86.8 | 84.3 | 0.9112 | 85.7 |
| PSD | 97.1 | 80.0 | 0.8955 | 88.5 |
| Multi-scale LZC + PSD | 100.0 | 82.9 | 0.9886 | 91.4 |
Finally, the classification results of the two groups by the multi-scale LZC, PSD and the combined feature were displayed in Fig. 9 and Table 4. The best classification was achieved using the combined feature with an accuracy of 91.4 %. Moreover, the highest sensitivity, specificity and AUC were reached, which are 100, 82.9 and 98.86 %, respectively. It could be concluded that the combined feature provided a better classification between the two groups than any other features.
Discussion
In this study, we analyzed the EEG background activity of 14 AD patients and 14 age-matched normal controls. Relative PSD and Lempel–Ziv complexity were calculated to quantify the abnormalities of spectrum and complexity in AD patients. PSD has been applied in order to investigate the topographical differences in EEG power distributions and LZC due to its possible relation to non-linear dynamics of the EEG signal.
Compared with the normal controls, the relative PSD values of AD patients were significantly increased in the theta frequency band while markedly decreased in the alpha frequency band, particularly in the parietal and occipital regions. Considering the fact that the relative PSD is correlated with the energy, the results obtained suggest that brains affected by AD show a slower rhythmic behavior. These alterations could reflect two different pathophysiological changes: the relative PSD decrease of the higher frequencies (alpha frequency band) could be related to alterations in cortico-cortical connections, whereas the increase of the lower frequencies (theta frequency band) could be related to the lack of influence of subcortical cholinergic structures on cortical electrical activity (Moretti et al. 2009; Jeong 2004). Our findings are also in accordance with other studies showing spectral “slowing” in AD. For instance, Jeong have observed a higher power in the theta frequency band in the resting EEG in AD patients (Jeong 2004). Dauwels et al. have further demonstrated that AD patients showed an increase of delta and theta spectrum and a decrease of alpha and beta spectrum (Dauwels et al. 2010a).
In addition to the spectrum analysis, the LZC and multi-scale LZC methods are employed to investigate the complexity abnormalities in the EEG of AD patients. It was observed that both LZC and multi-scale LZC values are significantly decreased in the alpha band, indicating a loss of EEG complexity in AD patients. This alteration might be a result of neurotransmitter deficiency, neuronal death and loss of connectivity (Gómez et al. 2007; Stam et al. 2007). In spite that both nonlinear methods could distinguish AD group from the control group, the multi-scale LZC showed better discriminating ability, manifested as greater group difference and higher classification accuracy. This may be due to the fact that the LZC method ignores the relationship between adjacent points during the coarse-graining process, leading to a great loss of detailed information, especially when the point is close to the threshold (median value), and the converted 0–1 sequence could only reflect the amplitude change characteristics based on the median value.
The obtained results are consistent with the previous studies that have revealed that the development of AD is associated with the reduction of complexity in EEG. By now, many non-linear methods have been applied to analyze the features of brain activity of AD and a significant amount of interesting results are reported. For instance, Besthorn et al. have found that D2 values are significantly lower in the EEG of AD patients than in those of the controls. Additionally, it has been suggested that the decrease of D2 values was associated with the severity of dementia (Besthorn et al. 1997). Jeong et al. (1998) also have found lower D2 and L1 values in AD group compared with the control group. Moreover, entropy, a key index to measure the disorder degree of signal, is also widely employed for studies of the cognitive mental states and chaotic behavior of AD brain activity. Escudero et al. (2006) have shown that AD patients usually have lower sample entropy values than the normal by multi-scale entropy analysis. Abasolo et al. further found significant decrease of sample entropy values in the parietal and occipital regions when compared with the normal controls (Abasolo et al. 2006a), and a decrease of approximate entropy values in the parietal region for AD patients also was observed (Abasolo et al. 2005). Compared with these nonlinear methods, LZ complexity is non-parametric and very easy to compute. Only the differences between activity patterns that make a difference to the underlying system itself are considered. Therefore, the LZ complexity based method may be a convenient and fast technique in the analysis of bioelectricity signals.
It has also been found that both the relative PSD and LZC values of AD group are lower than that of control group in the alpha frequency band, particularly in parieto-occipital brain areas, which might represent the cognitive dysfunction. Our findings are similar to the previous studies which have shown a slowing and complexity decrease of EEG. However, these studies only applied one separate feature, either PSD or LZC, to classify AD patients and the normal controls. Here, we attempted to improve the accuracy of the classification of the two groups by combining the relative PSD and multi-scale LZC features. A ROC curve was used to assess the ability of the combined feature in discriminating AD patients from the normal controls. With the combined feature, an accuracy of 91.4 % (100 % sensitivity; 82.9 % specificity) was achieved, which was higher than the accuracy with only relative PSD or multi-scale LZC. This implies that a combined feature could characterize the abnormalities of EEG in AD patients in a more comprehensive way.
Classification evaluation has been widely used to distinguish AD group and the control group in previous works. For instance, Besthorn et al. (1997) achieved an accuracy of 69.5 % using D2, which is actually not suitable for the non-stationary signals such as EEG. Abasolo et al. further obtained an accuracy of 77.3 % with sample entropy at electrode P3, P4, O1 and O2 (Abasolo et al. 2006a) and 81.8 % with conventional LZC at electrode P3, P4, O1 (Abasolo et al. 2006b). However, their results are based on single electrode and the whole frequency band rather than the specific bands with significant group difference between AD patients and the normal controls. In addition to the above classification difference between this study with the previous researches, the difference of sex, age and severity of disease between AD groups may be another important reason for the differences in the classification results.
Conclusions
In this paper, we have investigated the abnormalities of corticocortical response of AD patients by analyzing relative PSD, Lempel–Ziv complexity and multi-scale Lempel–Ziv complexity of scalp-recorded EEG signals. By the analysis of relative PSD, significant energy abnormalities were found in the theta and alpha band of AD EEG. And through the analysis of LZC and multi-scale LZC, the complexity of EEG in AD patients was found significantly decreased in most brain regions. In addition, the multi-scale LZC method is more suitable for the discrimination of AD patients and the normal controls. Finally, the combined feature of relative PSD and multi-scale LZC was used to improve the classification of the two groups. The results indicated that the combined feature performed better than any one feature. Therefore, the slowing of power and the loss of complexity may well represent a significant aspect of cognitive dysfunction in AD. The abnormalities of AD brain in the alpha frequency band, as revealed through the relative PSD and multi-scale LZC features could be used as potential features to distinguish AD patients from the normal effectively. Moreover, a larger cohort of clinical patients with different stages of AD may be necessary in our further study of the disease.
Acknowledgments
This work is supported by the Tangshan Technology Research and Development Program (Grant Nos. 14130223B and 14130224B).
References
- Abasolo D, Hornero R, Espino P, Poza J, Sanchez CI, de la Rosa R. Analysis of regularity in the EEG background activity of Alzheimer’s disease patients with approximate entropy. Clin Neurophysiol. 2005;116:1826–1834. doi: 10.1016/j.clinph.2005.04.001. [DOI] [PubMed] [Google Scholar]
- Abasolo D, Hornero R, Espino P, Poza J. Entropy analysis of the EEG background activity in Alzheimer’s disease patients. Physiol Meas. 2006;27(3):241–253. doi: 10.1088/0967-3334/27/3/003. [DOI] [PubMed] [Google Scholar]
- Abasolo D, Hornero R, Gómez C, Garcia M, Lopez M. Analysis of EEG background activity in Alzheimer’s disease patients with Lempel–Ziv complexity and Central Tendency Measure. Med Eng Phys. 2006;28:315–322. doi: 10.1016/j.medengphy.2005.07.004. [DOI] [PubMed] [Google Scholar]
- Adeli H, Ghosh-Dastidar S, Dadmehr N. A wavelet-chaos methodology for analysis of EEGs and EEG subbands to detect seizure and epilepsy. IEEE Trans Biomed Eng. 2007;54(2):205–211. doi: 10.1109/TBME.2006.886855. [DOI] [PubMed] [Google Scholar]
- Ahmadlou M, Adeli H, Adeli A. New diagnostic EEG markers of the Alzheimer’s disease using visibility graph. J Neural Transm. 2010;117(9):1099–1109. doi: 10.1007/s00702-010-0450-3. [DOI] [PubMed] [Google Scholar]
- Akin M, Kiymik MK. Application of periodogram and AR spectral analysis to EEG signals. J Med Syst. 2000;24:247–256. doi: 10.1023/A:1005553931564. [DOI] [PubMed] [Google Scholar]
- Babiloni C, Vecchio F, Bultrini A, Romani GL, Rossini PM. Pre- and poststimulus alpha rhythms are related to conscious visual perception: a high-resolution EEG study. Cereb Cortex. 2006;16:1690–1700. doi: 10.1093/cercor/bhj104. [DOI] [PubMed] [Google Scholar]
- Bennys K, Rondouin G, Vergnes C, Touchon J. Diagnostic value of quantitative EEG in Alzheimer’s disease. Neurophysiol Clin. 2001;31:153–160. doi: 10.1016/S0987-7053(01)00254-4. [DOI] [PubMed] [Google Scholar]
- Besthorn C, Zerfass R, Geiger-Kabisch C, Sattel H, Daniel S, Schreiter-Gasser U, Forstl H. Discrimination of Alzheimer’s disease and normal aging by EEG data. Electroencephalogr Clin Neurophysiol. 1997;103:241–248. doi: 10.1016/S0013-4694(97)96562-7. [DOI] [PubMed] [Google Scholar]
- Claus JJ, Strijers RL, Jonkman EJ, Ongerboer de Visser BW, Jonker C, Walstra GJ, Scheltens P, van Gool WA. The diagnostic value of electroencephalography in mild senile Alzheimer’ disease. Clin Neurophysiol. 1999;110:825–832. doi: 10.1016/S1388-2457(98)00076-5. [DOI] [PubMed] [Google Scholar]
- Czigler B, Csikós D, Hidasi Z, Gaál ZA, Csibri E, Kiss E, Salacz P, Molnár M. Quantitative EEG in early Alzheimer’s disease patients-power spectrum and complexity features. Int J Psychophysiol. 2008;68:75–80. doi: 10.1016/j.ijpsycho.2007.11.002. [DOI] [PubMed] [Google Scholar]
- Dauwels J, Vialatte F, Latchoumane C, Jeong J, Cichocki A (2009) Loss of EEG synchrony in early-stage AD patients: a study with multiple synchrony measures and multiple EEG data sets. In: Proceedings of the 31st annual international conference of the IEEE engineering in medicine and biology society, 2009 [DOI] [PubMed]
- Dauwels J, Vialatte F, Cichocki A. Diagnosis of Alzheimer’s disease from EEG signals: where are we standing? Curr Alzheimer Res. 2010;7:487–505. doi: 10.2174/156720510792231720. [DOI] [PubMed] [Google Scholar]
- Dauwels J, Vialatte F, Musha T, Cichocki A (2010b) A comparative study of synchrony measures for the early diagnosis of Alzheimer’s disease based on EEG. Neuroimage 49(1):668–693 [DOI] [PubMed]
- Dauwels J, Srinivasan K, Reddy MR, Musha T, Vialatte FB, Latchoumane C, Jeong J, Cichocki A (2011) Slowing and loss of complexity in Alzheimer’s EEG: two sides of the same coin? Int J Alzheimers Dis 539621 [DOI] [PMC free article] [PubMed]
- Dringenberg HC. Alzheimer’s disease: more than a ‘cholinergic disorder’-evidence that cholinergic-monoaminergic interactions contribute to EEG slowing and dementia. Behav Brain Res. 2000;115:235–249. doi: 10.1016/S0166-4328(00)00261-8. [DOI] [PubMed] [Google Scholar]
- Eckmann JP, Ruelle D. Fundamental limitations for estimating dimensions and Lyapunov exponents in dynamical systems. Phys D. 1992;56:185–187. doi: 10.1016/0167-2789(92)90023-G. [DOI] [Google Scholar]
- Escudero J, Abásolo D, Hornero R, Espino P, López M. Analysis of electroencephalograms in Alzheimer’s disease patients with multiscale entropy. Physiol Meas. 2006;27(11):1091–1106. doi: 10.1088/0967-3334/27/11/004. [DOI] [PubMed] [Google Scholar]
- Gianotti LR, Künig G, Lehmann D, Faber PL, Pascual-Marqui RD, Kochi K, Schreiter-Gasser U. Correlation between disease severity and brain electric LORETA tomography in Alzheimer’s disease. Neurophysiol Clin. 2007;118:186–196. doi: 10.1016/j.clinph.2006.09.007. [DOI] [PubMed] [Google Scholar]
- Gómez C, Hornero R, Abásolo D, Fernández A, Escudero J. Analysis of the magnetoencephalogram background activity in Alzheimer’s disease patients with auto-mutual information. Comput Methods Programs Biomed. 2007;87(3):239–247. doi: 10.1016/j.cmpb.2007.07.001. [DOI] [PubMed] [Google Scholar]
- Grassberger P, Procaccia I. Characterization of strange attractors. Phys Rev Lett. 1983;50(5):346–349. doi: 10.1103/PhysRevLett.50.346. [DOI] [Google Scholar]
- Gu FJ, Meng X, Shen EH, Cai ZJ. Can we measure consciousness with EEG complexities? Int J Bifurc Chaos. 2003;13:733–742. doi: 10.1142/S0218127403006893. [DOI] [Google Scholar]
- Han CX, Wang J, Yi GS, Che YQ. Investigation of EEG abnormalities in the early stage of Parkinson’s disease. Cogn Neurodyn. 2013;7(4):351–359. doi: 10.1007/s11571-013-9247-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hornero R, Abásolo D, Escudero J, Gómez C. Nonlinear analysis of electroencephalogram and magnetoencephalogram recordings in patients with Alzheimer’s disease. Philos Trans A Math Phys Eng Sci. 2009;367(1887):317–336. doi: 10.1098/rsta.2008.0197. [DOI] [PubMed] [Google Scholar]
- Jelles B, van Birgelen J, Slaets J, Hekster R, Jonkman E, Stam C. Decrease of non-linear structure in the EEG of Alzheimer patients compared to healthy controls. Clin Neurophysiol. 1999;110:1159–1167. doi: 10.1016/S1388-2457(99)00013-9. [DOI] [PubMed] [Google Scholar]
- Jeong J. EEG dynamics in patients with Alzheimer’s disease. Neurophysiol Clin. 2004;115:1490–1505. doi: 10.1016/j.clinph.2004.01.001. [DOI] [PubMed] [Google Scholar]
- Jeong J, Kim SY, Han SH. Non-linear dynamical analysis of the EEG in Alzheimer’s disease with optimal embedding dimension. Electroencephalogr Clin Neurophysiol. 1998;106:220–228. doi: 10.1016/S0013-4694(97)00079-5. [DOI] [PubMed] [Google Scholar]
- Jeong J, Chae JH, Kim SY, Han SH. Nonlinear dynamic analysis of the EEG in patients with Alzheimer’s and vascular dementia. J Clin Neurophysiol. 2001;18:58–67. doi: 10.1097/00004691-200101000-00010. [DOI] [PubMed] [Google Scholar]
- Jonkman EJ. The role of the electroencephalogram in the diagnosis of dementia of the Alzheimer type: an attempt at technology assessment. Clin Neurophysiol. 1997;27:211–219. doi: 10.1016/S0987-7053(97)83777-X. [DOI] [PubMed] [Google Scholar]
- Kaspar F, Schuster HG. Easily calculable measure for the complexity of spatiotemporal patterns. Phys Rev A. 1987;36:842–848. doi: 10.1103/PhysRevA.36.842. [DOI] [PubMed] [Google Scholar]
- Koenig T, Prichep L, Dierks T, Hubl D, Wahlund LO, John ER, Jelic V. Decreased EEG synchronization in Alzheimer’s disease and mild cognitive impairment. Neurobiol Aging. 2005;26:165–171. doi: 10.1016/j.neurobiolaging.2004.03.008. [DOI] [PubMed] [Google Scholar]
- Kowalski JW, Gawel M, Pfeffer A, Barcikowska M. The diagnostic value of EEG in Alzheimer Disease: correlation with severity of mental impariment. J Clin Neurophysiol. 2001;18:570–575. doi: 10.1097/00004691-200111000-00008. [DOI] [PubMed] [Google Scholar]
- Lehnertz K, Mormann F, Kreuz T, Andrzejak R, Rieke C, David P, Elger C. Seizure predictionby nonlinear EEG analysis. IEEE Eng Med Biol. 2003;22:57–63. doi: 10.1109/MEMB.2003.1191451. [DOI] [PubMed] [Google Scholar]
- Lempel A, Ziv J. On the complexity of finite sequences. IEEE Trans Inf Theory. 1976;22:75–81. doi: 10.1109/TIT.1976.1055501. [DOI] [Google Scholar]
- Mattson MP. Pathways towards and away from Alzheimer’s disease. Nature. 2004;430:634–639. doi: 10.1038/nature02621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moretti DV, Fracassi C, Pievani M, Geroldi C, Binetti G, Zanetti O, Sosta K, Rossini PM, Frisoni GB. Increase of theta/gamma ratio is associated with memory impairment. Clin Neurophysiol. 2009;120:295–303. doi: 10.1016/j.clinph.2008.11.012. [DOI] [PubMed] [Google Scholar]
- Nunez PL, Wingeier BM, Silberstein RB. Spatial-temporal structures of human alpha rhythms: theory, microcurrent sources, multiscale measurements, and global binding of local networks. Hum Brain Mapp. 2001;13:125–164. doi: 10.1002/hbm.1030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park YM, Che HJ, Im CH, Jung HT, Bae SM, Lee SH. Decreased EEG synchronization and its correlation with symptom severity in Alzheimer’s disease. Neurosci Res. 2008;62(2):112–117. doi: 10.1016/j.neures.2008.06.009. [DOI] [PubMed] [Google Scholar]
- Roschke J, Fell J, Beckmann P. Non-linear analysis of sleep EEG data in schizophrenia: calculation of the principal Lyapunov exponent. Psychiatry Res. 1995;56:257–269. doi: 10.1016/0165-1781(95)02562-B. [DOI] [PubMed] [Google Scholar]
- Schoenberg PLA, Speckens AEM. Multi-dimensional modulations of α and γ cortical dynamics following mindfulness-based cognitive therapy in Major Depressive Disorder. Cogn Neurodyn. 2015;9(1):13–29. doi: 10.1007/s11571-014-9308-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schreiter-Gasser U, Gasser T, Ziegler P. Quantitative EEG analysis in early onset Alzheimer’s disease: correlations with severity, clinical characteristics, visual EEG and CCT. Electroencephalogr Clin Neurophysiol. 1994;90:267–272. doi: 10.1016/0013-4694(94)90144-9. [DOI] [PubMed] [Google Scholar]
- Shaw FZ, Chen RF, Tsao HW, Yen CT. Algorithmic complexity as an index of cortical function in awake and pentobarbital-anesthetized rats. J Neurosci Methods. 1999;93:101–110. doi: 10.1016/S0165-0270(99)00133-8. [DOI] [PubMed] [Google Scholar]
- Stam CJ. Nonlinear dynamical analysis of EEG and MEG: review of an emerging field. Clin Neurophysiol. 2005;116:2266–2301. doi: 10.1016/j.clinph.2005.06.011. [DOI] [PubMed] [Google Scholar]
- Stam CJ, Jellesa B, Achtereektea HAM, Romboutsa SARB, Slaetsb JPJ, Keunena RWM. Investigation of EEG non-linearity in dementia and Parkinson’s disease. Electroencephalogr Clin Neurophysiol. 1995;95:309–317. doi: 10.1016/0013-4694(95)00147-Q. [DOI] [PubMed] [Google Scholar]
- Stam CJ, van der Made Y, Pijnenburg YAL, Scheltens PH. EEG synchronization in mild cognitive impairment and Alzheimer’s disease. Acta Neurol Scand. 2003;108:90–96. doi: 10.1034/j.1600-0404.2003.02067.x. [DOI] [PubMed] [Google Scholar]
- Stam CJ, Jones BF, Nolte G, Breakspear M, Scheltensc P. Small-world networks and functional connectivity in Alzheimer’s disease. Cereb Cortex. 2007;17(1):92–99. doi: 10.1093/cercor/bhj127. [DOI] [PubMed] [Google Scholar]
- van Cappellen YAL, van Walsum AM, Pijnenburg Y, Berendse H, van Dijk B, Knol D, Scheltens P, Stam C. A neural complexity measure applied to MEG data in Alzheimer’s disease. Clin Neurophysiol. 2003;114:1034–1040. doi: 10.1016/S1388-2457(03)00072-5. [DOI] [PubMed] [Google Scholar]
- Wang R, Wang J, Yu H, Wei X, Yang C, Deng B. Decreased coherence and functional connectivity of electroencephalograph in Alzheimer’s disease. Chaos. 2014;24(3):033136. doi: 10.1063/1.4896095. [DOI] [PubMed] [Google Scholar]
- Wang R, Wang J, Yu H, Wei X, Yang C, Deng B. Deng B., Power spectral density and coherence analysis of Alzheimer’s EEG. Cogn Neurodyn. 2015;9(3):291–304. doi: 10.1007/s11571-014-9325-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang R, Wang J, Li S, Yu H, Deng B, Wei X. Multiple feature extraction and classification of electroencephalograph signal for Alzheimers’ with spectrum and bispectrum. Chaos. 2015;25(1):013110. doi: 10.1063/1.4906038. [DOI] [PubMed] [Google Scholar]
- Yang CY, Lin CP. Coherent activity between auditory and visual modalities during the induction of peacefulness. Cogn Neurodyn. 2013;7(4):301–309. doi: 10.1007/s11571-012-9234-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yi G, Wang J, Bian H, Han C, Deng B, Wei X, Li H. Multi-scale order recurrence quantification analysis of EEG signals evoked by manual acupuncture in healthy subjects. Cogn Neurodyn. 2013;7(1):79–88. doi: 10.1007/s11571-012-9221-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang XS, Roy RJ, Jensen EW. EEG complexity as a measure of depth of anesthesia for patients. IEEE Trans Biomed Eng. 2001;48:1424–1433. doi: 10.1109/10.966601. [DOI] [PubMed] [Google Scholar]
- Zhou SM, Gan JQ, Sepulveda F. Classifying mental tasks based on features of higher-order statistics from EEG signals in brain–computer interface. Inf Sci. 2008;178(6):1629–1640. doi: 10.1016/j.ins.2007.11.012. [DOI] [Google Scholar]
- Zweig MH, Campbell G. Receiver-operating characteristic (ROC) plots: a fundamental evaluation tool in clinical medicine. Clin Chem. 1993;39:561–577. [PubMed] [Google Scholar]