Variable Field Analytical Ultracentrifugation: II. Gravitational Sweep Sedimentation Velocity

Abstract

Sedimentation velocity (SV) analytical ultracentrifugation is a classical biophysical technique for the determination of the size-distribution of macromolecules, macromolecular complexes, and nanoparticles. SV has traditionally been carried out at a constant rotor speed, which limits the range of sedimentation coefficients that can be detected in a single experiment. Recently we have introduced methods to implement experiments with variable rotor speeds, in combination with variable field solutions to the Lamm equation, with the application to expedite the approach to sedimentation equilibrium. Here, we describe the use of variable-field sedimentation analysis to increase the size-range covered in SV experiments by ∼100-fold with a quasi-continuous increase of rotor speed during the experiment. Such a gravitational-sweep sedimentation approach has previously been shown to be very effective in the study of nanoparticles with large size ranges. In the past, diffusion processes were not accounted for, thereby posing a lower limit of particle sizes and limiting the accuracy of the size distribution. In this work, we combine variable field solutions to the Lamm equation with diffusion-deconvoluted sedimentation coefficient distributions c(s), which further extend the macromolecular size range that can be observed in a single SV experiment while maintaining accuracy and resolution. In this way, approximately five orders of magnitude of sedimentation coefficients, or eight orders of magnitude of particle mass, can be probed in a single experiment. This can be useful, for example, in the study of proteins forming large assemblies, as in fibrillation process or capsid self-assembly, in studies of the interaction between very dissimilar-sized macromolecular species, or in the study of broadly distributed nanoparticles.

Introduction

The goal of gravitational sweep sedimentation velocity is the detection of all particles in solution over a very large size range by continuously increasing the centrifugal field, causing sequentially smaller particles to sediment. Although this is conceptually straightforward, sedimentation velocity (SV) has usually been carried out at constant rotor speed, due to experimental difficulties in the precise implementation of a centrifugal field schedule in SV, and the difficulty of solving the Lamm equation—the master equations for sedimentation and diffusion in the centrifugal field—for a time-dependent rotor speed. Sedimentation in a time-varying centrifugal time field was first considered 1965 in a technical report by Gehatia (1), and in 1970 in a communication by Nossal and Weiss (2), who presented approximate analytical Lamm equation solutions for sedimentation and diffusion for arbitrary rotor speed profiles. A key element in this work was the transformation of the time variable to a temporal integral over the centrifugal field, which defines an effective sedimentation time. Although the stated purpose of this entirely theoretical work was the elucidation of elastic properties of macromolecules (1), and studying the sedimentation of small proteins already during the extended rotor acceleration phase to high speeds (2), respectively, the implications of time-varying centrifugal fields went far beyond this scope.

Shortly after, in 1972 the first experiments systematically exploiting time-variable rotor speeds were reported for characterizing broad particle size distributions of latex suspensions (3). In their comprehensive work, Scholtan and Lange (3) described how the signal from a fixed-radius detector could be transformed directly into an apparent particle size distribution of nondiffusing particles, after corrections for Mie scattering. This idea was later termed “gravitational sweep sedimentation” by Mächtle (4) (and restated again in Mächtle (5)), using a stepwise approximation of an exponential rotor speed profile. With the sedimentation analysis resting on the time-integral of the centrifugal field, which is a sufficient transformation for nondiffusing particles, this allowed a very wide range of particle sizes to be observed, but it failed in the presence of particles below 10 nm (4).

In the realm of biomacromolecules, so far, variable field SV only found a few documented applications. Its use was described first 1981 by Runge et al. (6) in studies on samples of tubulin and neurofilaments, applying three discrete steps of sequentially higher rotor speeds in a single SV run to cover a large particle size range. Even though not further elaborated, their transformation of signal to apparent sedimentation coefficient distributions g(s) rests on the relationship mentioned above between the temporal integral of the centrifugal field and the migration of nondiffusing particles. This approach was later integrated by Stafford and Braswell (7) as wide distribution analysis into time-derivative analysis, and Mach and Arvinte (8) have analogously used a variation of radial-derivative analysis to observe a large range of s values from the analysis of scans acquired in time-varying centrifugal fields.

In the last two decades, modern computational resources and numerical algorithms for differential and integral equations have completely eliminated previous restrictions in considering time-varying centrifugal fields. Our laboratory originally became interested in time-varying rotor speeds due to the necessity to account for the rotor acceleration phase of the experiment even in conventional constant-speed SV (2, 9). Unfortunately, for achieving highest precision in both sedimentation and diffusion, the effective sedimentation time approach (via the temporal integral of the centrifugal field) is not optimal. This problem is exacerbated when carrying out experiments with slow rotor acceleration schedules for isothermal centrifugation (10). Therefore, we incorporated a discretized approximation of the rotor acceleration into the explicit numerical finite element Lamm equation solutions (11, 12, 13) used in our SEDFIT software. Recently we have extended the consideration of time-varying rotor speeds from merely modeling the acceleration phase to the modeling of the approach to equilibrium in an arbitrarily changing centrifugal field, with the goal to calculate a rotor speed schedule minimizing the time required to attain sedimentation equilibrium at a target speed (14). While the previous work was in a largely diffusion-dominated regime, in this work we have focused on the sedimentation-dominated regime to simulate and model sedimentation velocity experiments of particles over a large size-range in time-varying fields. Incorporated as a kernel into the well-established diffusion-deconvoluted sedimentation coefficient distributions (15) allows us to revisit the idea of gravitational sweep sedimentation.

The explicit consideration of diffusion addresses previous limitations and results in an extended size range and hydrodynamic resolution of medium to small particles. To facilitate the experimental application of gravitational sweep SV in practice, we have implemented ancillary tools to prepare centrifugal speed steps schedules for today’s analytical ultracentrifuges, tools to compensate for field-dependent rotor stretching before the data analysis, and tools to reconstruct experimental field profiles from experimental scan data. As a result, great freedom in the application of time-varying centrifugal fields over a large range of conditions is achieved for SV analysis. We believe these developments warrant revisiting the idea and practical utility of gravitational sweep sedimentation. To this end, this work analyzes properties of different possible rotor speed schedules, and demonstrates the application to mixtures of several model proteins and nanoparticles.

Materials and Methods

Theory and computational

For a simple prediction of the behavior of particles of different size in time-varying centrifugal fields, it is useful to consider the differential equation of motion for an ideal nondiffusing point particle, r^(p)(t), which follows from the definition of the s value as a normalized velocity

$$\frac{d{r}^{\left(p\right)}}{dt}=s\omega {\left(t\right)}^2{r}^{\left(p\right)},$$ (1)

where s is the sedimentation coefficient, and ω is the rotor angular velocity. (For readability of the article we follow the custom in the field and will use units of Svedbergs for s, noting that 1 S equals 10⁻¹³ s, and units of rpm for the angular velocity, noting that 1 rpm is 0.1047 rad/s.) They are therefore exponentially expelled radially with

$$r^{\left(p\right)}\left(t\right)=m\text{exp}\left[s\underset{0}{\overset{t}{\int }}\omega {\left(t^{\prime }\right)}^{2}d{t}^{\prime }\right],$$ (2)

assuming they are initially located at the meniscus m. This is the basis for the approximation of the effective sedimentation time t^(sed) that may be attributed to a scan acquired at time t^∗ at a rotor speed ω^∗,

$$t^{\left(\text{sed}\right)}={\left(\frac{1}{{\omega }^{\ast }}\right)}^2\underset{0}{\overset{t^{\ast }}{\int }}\omega {\left(t^{\prime }\right)}^{2}d{t}^{\prime },$$ (3)

such that Eq. 2 conforms to the conventional expression at constant rotor speed:

$$r^{\left(p\right)}\left(t\right)=m\text{exp}\left[s{\omega }^{\ast 2}{t}^{\left(\text{sed}\right)}\right].$$ (4)

This simplification correctly predicts the sedimentation for any ω(t) but is incorrect for the diffusion process (10). It may be used, however, in the approximation that diffusion is negligible, such as in the dc/dt approach to calculate g(s^∗) (7, 16) or in the fixed radius transformation of time to s value applied in Mächtle (5). In practice, this approach is greatly facilitated by the fact that the analytical ultracentrifuges used in this study keep track of not only the elapsed time since start of the experiment, but also of $\int {\omega }^{2}dt$ and report this quantity in scan time files. (It should be noted that in reported scan files this quantity is subject to the same errors as the reported elapsed time (17, 18).) This eliminates the need to maintain an independent record of precise rotor speed schedules (see below).

A more accurate description of the migration in the centrifugal field is achieved when considering both sedimentation and diffusion in the Lamm equation (19)

$$\frac{\partial \chi }{\partial t}=-\frac{1}{r}\frac{\partial }{\partial r}\left(\chi s\omega {\left(t\right)}^2{r}^2-D\frac{\partial \chi }{\partial r}r\right),$$ (5)

where χ(r,t) denotes the radial and temporal evolution of macromolecular concentration of a species with sedimentation coefficient s and diffusion coefficient D in a sector-shaped solution column rotating with angular velocity ω(t). The solution of this equation has been implemented in SEDFIT for time-varying fields, in a modification of the finite element algorithm described in Brown and Schuck (12), where the adaptive radial grid size is eliminated and the grid truncations are carried out only for depleted regions. For species with sedimentation coefficients in excess of 1000 S, this necessitates an increase of the default radial grid size or neglect of diffusion. The time-dependence of the angular velocity ω(t) was approximated by discretization into 10 s intervals of constant rotor speed.

The predicted sedimentation profiles are compatible with standard distribution analysis models. Briefly, normalized solutions of Eq. 1 were taken as the kernel of the integral equation

$$a\left(r,t\right)\cong \underset{s_{\text{min}}}{\overset{s_{\max }}{\int }}{\chi }_1\left(r,t,s,D\left(s\right)\right)c\left(s\right)ds,$$ (6)

directly fitted by least-squares to the experimental data a(r,t), to determine the sedimentation coefficient distribution c(s) (15). As in the conventional c(s) method, diffusion is considered in the approximation of a scaling law D(s) based on an average frictional coefficient, and therefore high-resolution diffusion-deconvoluted sedimentation coefficient distributions c(s) are achieved (15, 20). Using standard techniques for integral equations, Tikhonov or maximum entropy regularization is applied (15, 20). Extension to size-and-shape distributions is seamlessly possible (21)—where sufficient information is present to determine these (22)—as is the incorporation of prior knowledge by Bayesian regularization (23). For the limiting case of very large particles where D(s) ≈ 0, the c(s) distribution will converge to the apparent sedimentation coefficient distribution ls-g^∗(s) (24). Furthermore, the model Eq. 6 can be combined with systematic noise decomposition to account for time-invariant and radial-invariant (RI) baseline contributions (25, 26).

Before analysis via Eq. 6, it is important to correct the experimental scans for the rotor-speed dependent rotor stretching. This requires two steps: 1) the translation of the solution column from the detector reference frame to a reference frame at constant meniscus position using a previously measured stretching modulus E; and 2) the compensation of the ensuing changes in the centrifugal field by using an apparent rotor speed (to keep ω²r constant),

$$r^{\prime }=r-E{\omega }^2\text{and}{\omega }^{\prime }=\omega \sqrt{\frac{r_{\text{mid}}}{r_{\text{mid}}-E{\omega }^2},}$$ (7)

with r_mid denoting the middle of the solution column.

The question arises what choice of ω(t) would be most desirable. In the absence of other knowledge, when studying potentially extremely broad size distributions, it may be reasonable to aim at logarithmically spaced resolution in s values to cover the largest possible range. This can be achieved, for example, when particles transit past the highest observable radius r_max with exponentially decreasing s value with time. If Eq. 2 is solved with regard to the s value and an exponential time-course is imposed, it can be shown that this requires a rotor speed profile using a power-law

$$\omega \left(t\right)={\omega }_{\text{low}}{\left(\frac{{\omega }_{\max }}{{\omega }_{\text{low}}}\right)}^{\frac{\left(t-t_{\text{low}}\right)}{t_{\max }-t_{\text{low}}}},$$ (8)

with ω_low and ω_max representing lower and upper limits of rotor speed assumed at times t_low and t_max, respectively. Alternatively, another rational choice for the rotor speed schedule would be

$$\omega \left(t\right)=\sqrt{{\omega }_{\text{low}}^2+\left({\omega }_{\text{max}}^2-{\omega }_{\text{low}}^2\right)\frac{\left(t-t_{\text{low}}\right)}{t_{\max }-t_{\text{low}}}},$$ (9)

based on the idea of a constant increase in centrifugal field.

A special case for a variable-field sedimentation experiment is sometimes experimentally implemented inadvertently when carrying out the initial adjustment of data acquisition at a rotor speed of 3000 rpm, before acceleration to the target rotor speed of the experiment. This was discouraged in the context of Lamm equation analysis due to the deviations it creates from the constant rotor acceleration model assumed previously in Zhao et al. (27). However, in the framework of variable rotor speed SV this step can now be naturally accounted for. Even though the scan files do not contain sufficient information to establish and model the speed schedule, with input of the rotor speed ω_low (usually 3000 rpm) it is possible to determine the approximate time the rotor was held at the lower speed from the t and $\int {\omega }^{2}dt$ entries of the files, as

$$t_{\text{low}}=\left(t-t^{\left(\text{sed}\right)}\right)\frac{{\omega }_0^2}{{\omega }_0^2-{\omega }_{\text{low}}^2}+\frac{{\omega }_{\text{low}}}{\dot{\omega }}-\frac{2{\omega }_0^3}{3\dot{\omega }\left({\omega }_0^2-{\omega }_{\text{low}}^2\right)},$$ (10)

with $\dot{\omega }$ the constant rotor acceleration (which is not adjustable on our instrumentation) and t^(sed) as defined in Eq. 3. Accordingly, SEDFIT has been extended to deduce the presence of an initial low-speed phase from the t and $\int {\omega }^{2}dt$ entries of the files, and after user entry of ω_low, will create a speedsteps.txt file to accurately model this rotor speed profile.

Similarly, it may be possible to extract the entire history of rotor speed changes from experimental scan data: provided that at least one scan is available at each rotor speed, then the known fixed rotor acceleration $\dot{\omega }$, jointly with the ω, t, and $\int {\omega }^{2}dt$ entries of the files, allows us to calculate the time τ when the rotor acceleration from the previous speed was commenced,

$${\tau }_i=\left({\left(\int {\omega }^{2}dt\right)}_i-{\left(\int {\omega }^{2}dt\right)}_{i-1}+{\omega }_{i-1}^2\left(t_{i-1}-t_{a,i}\right)-{\omega }_i^2\left(t_i-t_{a,i}\right)-{\omega }_{i-1}\dot{\omega }{t}_{a,i}^2-\frac{1}{3}{\dot{\omega }}^2{t}_{a,i}^3\right){\left({\omega }_{i-1}^2-{\omega }_i^2\right)}^{-1},$$ (11)

for ω_{i >} ω_i−1, with i enumerating the scans, using the abbreviation $t_{a,i}=\left({\omega }_i-{\omega }_{i-1}\right)/\dot{\omega }$ for the time required to change the rotor speed. A new utility function in SEDFIT was implemented to extract in this way the entire rotor speed history from sets of loaded scans and assemble the necessary speedsteps.txt file required for the analysis.

Experimental

The proteins used in this study were purchased from Amersham Biosciences (kits No. 17-0441-01 and 17-0442-01; Piscataway, NJ). Lyophylized proteins were dissolved in phosphate-buffered saline and dialyzed overnight in the same buffer. DNA-coated gold nanoparticles were prepared as described in Ko et al. (28), and streptavidin-coated 15-nm gold nanoparticles were from Ted Pella (Redding, CA), both diluted into Tris(hydroxymethyl)aminomethane buffered saline. It should be noted that the nanoparticle samples used were stressed from extended storage past their stable lifetime; however, the resulting polydispersity presents no detriment to their use as rapidly sedimenting particles in this study. A quantity of 400 μL sample volumes were matched with reference buffer and placed in charcoal-filled Epon double-sector centerpieces.

Analytical ultracentrifugation experiments were carried out in instruments subjected to external temperature and radius calibrations (18, 29), and using the standard sedimentation velocity protocol (27) except for the following modifications. After thorough temperature equilibration of the samples and the resting rotor in the evacuated rotor chamber, scans with standard SV settings of 0.003 cm intervals and single acquisition per radius in continuous mode were initiated through the sedimentation equilibrium method in the data acquisition program. This engages the automatic scheduler for scans and rotor speed changes.

The experimental rotor speed schedule was specified in speedsteps.txt files introduced previously in Ma et al. (14), containing a table of elapsed times when rotor speed changes are planned to be initiated, the new target rotor speed, and the rotor acceleration (usually 280 rpm/s). For data analysis, this file will be automatically recognized by SEDFIT when it is located in the corresponding scan data folder, if scans acquired at different rotor speeds are loaded. Before the experiment, such a file can be created as an ASCII text file, and utility functions in SEDFIT can create from this a scanning schedule readable by the Optima XLA/I analytical ultracentrifuge operating system (Beckman Coulter, Brea, CA) using the equilibrium mode to establish precise experimental timing. Dependent on the scan parameters, different numbers of scans may be taken in each rotor speed step. This number has to be adjusted for each step such as not to delay scheduled changes to the next speed steps. However, if at least one scan was taken at each speed step, the actual experimental speed steps can be extracted later from the scan time information, replacing the scheduled speed steps.

Disclaimer

Certain commercial equipment, instruments, or materials are identified in order to specify the experimental procedure adequately. Such identification is not intended to imply recommendation or endorsement by the National Institute of Standards and Technology, nor is it intended to imply that the materials or equipment identified are necessarily the best available for the purpose.

Results

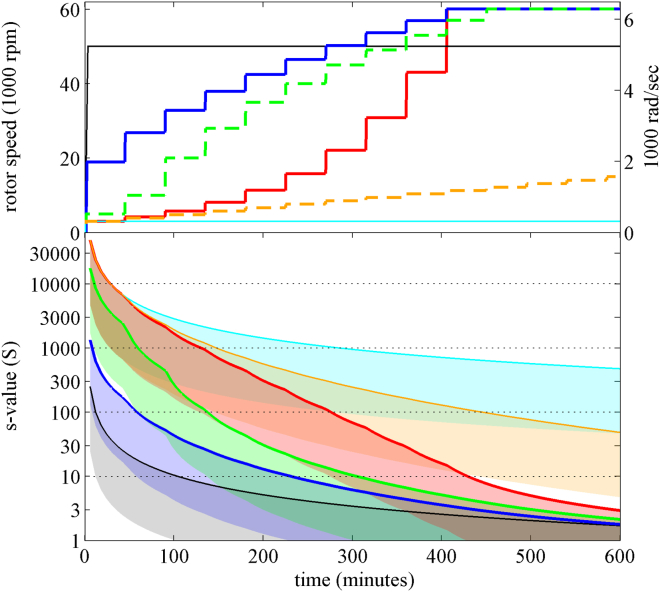
First, we were interested in examining properties of different centrifugal field schedules and their impact on the sedimentation coefficient range. To this end we considered Eq. 2 and determined the s value of nondiffusing particles initially at the meniscus that would transition 1 mm into the solution column, and those that migrate out of the observation window assuming the radial range to be from 6.1 to 7.1 cm of a 12-mm solution column in double sector centerpieces. This will reflect the boundary position of particles with the smallest and largest s value that can just be observed at any given point in time. We calculated these extreme s values as a function of time for a 10 h SV experiment for different rotor speed schedules (Fig. 1; see Table S1 in the Supporting Material). Essentially due to geometrical constraints, at any given time, approximately a factor of 10 in the s-value range can be sampled in the observation window at once.

Figure 1.

Range of observable sedimentation coefficients as a function of time for different rotor speed schedules. (Top) Rotor speed models using a constant field increase model (blue), a power-law model (red), an ad hoc model consisting of two lower speed steps at 5000 and 10,000 rpm followed by a constant field increase (green dashed), and a model with slowly linearly increasing rotor speed (orange dashed). Rotor speed changes were initiated in 45-min intervals, with rotor acceleration of 280 rpm/s, with ω_low = 3000 rpm and ω_max = 60,000 rpm. For comparison, constant speed data are shown for a conventional constant speed experiment at 50,000 rpm (black solid) and 3000 rpm (cyan solid). (Bottom) Observable range of s values for nondiffusing particles located between 6.1 and 7.1 cm in a 12 mm column, indicated with patches colored corresponding to the rotor speed schedules on the top. To see this figure in color, go online.

As a reference, Fig. 1 shows the conventional constant rotor speed (except for the unavoidable acceleration phase) result. At a relatively high rotor speed of 50,000 rpm (black line/gray patch) the fastest particles will be observable only for a very short time, severely constraining the opportunity for their reliable detection and characterization. Within the existing initial delay for the onset of scanning (caused by delay calibrations and/or requirement for optical adjustments) on the order of a few minutes, this limits observations of particles to those sedimenting more slowly than a few hundred S. With the lowest limit for detectable sedimentation coefficients being ∼0.1 S, the standard experiment therefore spans ∼3 decades of s values. On the other extreme, if a very low rotor speed of 3000 rpm is used in a conventional constant-field experiment (cyan), very large s values of ∼10,000 S and higher can be detected (30), but the lower limit is ∼100 S.

The rotor speed scheme designed to maximize the range is the power-law model equation (Eq. 8), shown in red. As it starts at the lowest rotor speed and ends at the highest rotor speed, it can combine the range of the low- and high-speed experiments above, spanning a detection range of approximately five orders of magnitude. While this is ideal for extremely broadly distributed particle sizes, a disadvantage appears when the predominant interest is in the smallest particles of typical macromolecular size (1–100 S) or average protein size range (1–10 S), because it takes several hours before the centrifugal field grows strong enough to cause their sedimentation. Another rational choice was outlined in the constant field to increase the model equation, Eq. 9 (blue). Due to the initially lower fields, it can achieve an approximately 10-fold larger maximal s value as compared to the conventional high-speed model, while decaying continuously toward the latter. This choice would satisfy a focus on the detection of intermediate particles, macromolecular assemblies, and protein-sized particles. However, it would seem to sacrifice detection of the extremely large particles. Conversely, a slow linear rotor speed increase (orange) will improve the range for the large particles, but still sacrifice detection of small particles. An intermediate model consisting of a constant field increase preceded ad hoc by two low-speed steps (green) appears as a compromise, capturing migration of very large particles but at the same time homing in much faster on the medium/small sizes than the power law.

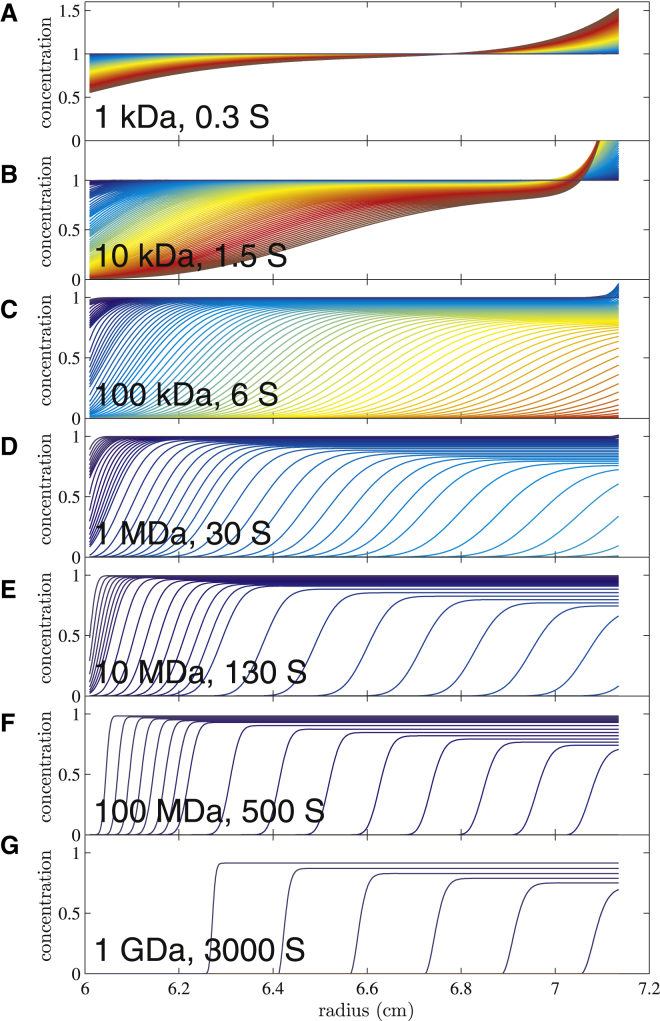
A second question when attempting to model the entire sedimentation/diffusion process is how the sedimentation profiles will be shaped in gravitational sweep SV. As an example, we imposed the ad hoc field schedule combining the low-speed steps with a constant field increase, as shown in green in Fig. 1, in a simulation of the sedimentation process for single species across a 10,000-fold range of molecular sizes. Fig. 2 shows the simulated concentration distributions for representative species, in a superposition of 100 scans in equally spaced 5-min intervals for the duration of 8.5 h. The same color temperature scheme is used for all to indicate later times with higher color temperature, with green being centered at ≈4 h. In some plots, different rotor speed steps may be discerned from regions of different line density, which reflects the rate of boundary migration in this field. The most striking feature of Fig. 2 is how the boundaries from different size species peel off the meniscus and migrate into the cell at their characteristic time while they will remain spatially well separated. A salient feature of the direct boundary modeling is that data from the entire time-course can be modeled at once, and this will allow the natural combination of information from particles of all sizes.

Figure 2.

Calculated boundary profiles of discrete species sedimenting in variable field SV under conditions of the ad hoc schedule shown in green in Fig. 1. Radial concentration profiles are calculated for a time-period from ≈9 min to 8.5 h, in 100 scans of 5-min intervals. All panels show the radial profiles using the same color scheme with increasing color temperature indicating later time. For reference, the green range is approximately in the middle of the experiment where the rotor speed is 40,000 rpm. Sedimentation was simulated for particles with partial-specific volume of 0.73 mL/g in water, with frictional ratios between 1.2 and 1.5. Sedimentation parameters are for species of (A) 1 kDa, 0.3 S; (B) 10 kDa, 1.5 S; (C) 100 kDa, 6 S; (D) 1 MDa, 30 S; (E) 10 MDa, 130 S; (F) 100 MDa, 500 S; and (G) 1 GDa, 3000 S. To see this figure in color, go online.

Another interesting aspect of the sedimentation boundary shapes is that all exhibit significant boundary broadening with time, despite their very dissimilar diffusion coefficients. This is clearly due to the different timescales involved in their sedimentation process, where large particles are observed at low speed, such that the rate of diffusional transport remains significant relative to sedimentation. In fact, even for moderate and small particles, boundary broadening is exacerbated by the slow migration at the earlier times at lower centrifugal fields. To quantify this, we considered the data from Fig. 2 C (simulated for a 100 kDa protein with 6 S) during the 40,000 rpm step, which comprises scans 45–53 that show in green the boundary midpoint between 6.3 and 6.45 cm. When we subjected this data set to a simplistic Lamm equation analysis on the basis of effective sedimentation times derived through Eq. 3, the best-fit sedimentation coefficient is 5.95 S, as expected very close to the value of 6 S underlying the simulation. However, the best-fit molar mass is only 57 kDa rather than the 100 kDa underlying the gravitational sweep SV simulation. This discrepancy is caused by increased diffusion time during the prolonged low speed phases of the experiment, which is not accounted for in the approximation of effective sedimentation times from Eq. 3. Thus, the analysis of variable field SV profiles cannot be carried out with naïve approximations based on effective sedimentation time (or, equivalently, by a Gaussian fit to an apparent sedimentation coefficient distribution g^∗(s)). However, it can be carried out easily with full consideration of the true centrifugal field schedule (Eq. 5).

On the other hand, the question arises whether diffusional boundary broadening for very large particles can be distinguished from polydispersity. To test this, we can try to fit the simulated data of single diffusing species from Fig. 2 with an impostor distribution model ls-g^∗(s) describing polydisperse nondiffusing particles. For example, the data from Fig. 2 G (with 3000 S) can be fit well with a distribution of nondiffusing particles (with a square root of the second moment of 60 S) producing a root-mean-square deviation (RMSD) of the boundary profiles of only 0.32% (with maximum error <6%) of the loading signal (data not shown). This value is below the signal/noise level of typical data acquisition, and therefore diffusion of this large particle would be indistinguishable from polydispersity. By contrast, the data from the 500 S particle in Fig. 2 F cannot be fit well with a distribution of nondiffusing particles, with an impostor ls-g^∗(s) fit to this data producing an RMSD of 2% (with maximum error >25%) of the loading signal, and even less so the 130 S data of Fig. 2 E, for which an impostor ls-g^∗(s) fit will produce an RMSD of 3.2% (with maximum error >30%) of the loading signal. For these smaller particles, therefore, the presence of diffusion contributions should be discernable even for particles with continuous size distributions.

Finally we tested the experimental application of gravitational sweep SV. For the implementation of a rotor speed schedule, the accurate timing of rotor speed changes is important. It is generally preferable to avoid manual adjustments by taking advantage of the preprogrammed rotor speed changes in the sedimentation equilibrium method data acquisition mode of the graphical user interface of the Beckman Coulter analytical ultracentrifuge. The main characteristic of this data acquisition mode is that it can execute sedimentation steps serially at different rotor speeds and temperature, and initiate scans at each step at preset time intervals. Although the rules for the precise timing of speed changes and scans are nonobvious, in the previous communication on variable-field analytical ultracentrifugation (14) we have reported on a new utility function in SEDFIT that can convert between speedsteps.txt files and sedimentation equilibrium method .equ files that can be directly loaded into the analytical ultracentrifuge user interface (see tutorial video https://sedfitsedphat.nibib.nih.gov/tools/Protocols/TOSE_implementation.wmv). However, for the desired timing to be honored it is important that the total time for the sequence of scans at each step—including delay calibration—does not exceed the allotted total time for the rotor to reside at this speed; otherwise speed changes will be delayed. This requires a conservative estimate for the scan time, which depends on radial resolution, number of replicates, scanning mode, number of cells, number of wavelengths, and rotor speed at low speeds. It can be determined before the gravitational sweep SV experiment. For example, at rotor speeds >5000 rpm, an estimate at standard SV scan settings of 0.003 cm target radial interval with a single acquisition in velocity mode in our instruments is ≈2 min for the first scan (requiring delay calibration) and ≈1 min for the following scans per cell.

Fortunately, one can also retroactively extract the rotor speed schedule from experimental data files via Eq. 11 provided each rotor speed is represented by at least a single scan. When applied to experimental data preprogrammed for the ad hoc schedule in Fig. 1 (green), the reconstructed time points of rotor speed changes were consistent with the preprogrammed time-points within 0.5% or better. With time-stamp errors accounted for (17), the source of the remaining small discrepancy is unclear, but the magnitude is within the typical relative accuracy of s values (29). Thus, this approach provides a useful fallback for inconsistent preprogrammed schedules, or when speed schedules are adjusted ad hoc in real-time.

Before data analysis, preprocessing of scans is an essential step to eliminate the translation of the solution column due to rotor stretching via Eq. 7. At this stage, residual scan time errors can also be removed (17, 18). A very sensitive measure for radial alignment is the successful elimination of time-invariant residual features across all scans, as visualized by the absence of vertical features from the residuals bitmap after fit. This worked well using the predetermined stretching modulus (31) as implemented in SEDFIT. Some residual small shifts at low rotor speed remained (Figs. 3 and S1), possibly reflecting rotor-speed-dependent shifts in the axis of rotation not accounted for in Eq. 7. Such shifts were examined for the Model E ultracentrifuge and found to impact translation of the solution column ∼10-fold less than the effect of rotor stretching (33, 34).

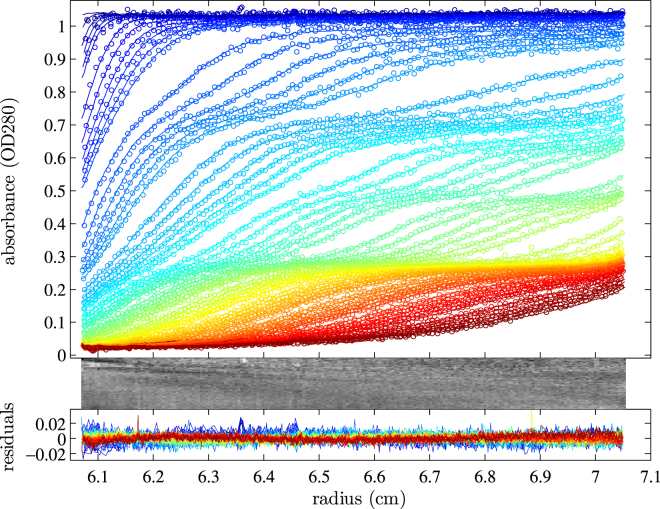
Figure 3.

Variable-field SV experiment using a mixture of four proteins (chymotrypsinogen A, catalase, thyroglobulin, and ferritin) subjected to the extended power-law rotor speed schedule shown in green in Fig. 1. (Top, circles) Experimental data points (only every third point shown) in 66 scans acquired from 8 to 489 min in ≈6 min intervals, and approximately twice this delay after acceleration phases, which can be recognized from the apparent gaps in scan pattern. The line is the best-fit c(s) distribution model, as shown in Fig. 4. The c(s) model describes diffusion on the basis of a best-fit average frictional ratio (here refined to 1.36) as in the standard constant-speed c(s) approach. (Middle and bottom panels) Bitmap and overlay of the residuals, which have a root-mean-square deviation of 0.0050 OD and a relative deviation from normal distribution (32) of H = 1.0%. To see this figure in color, go online.

To investigate the performance of gravitational sweep SV for a highly polydisperse protein mixture covering a wide range of sizes, we carried out an experiment using as model proteins samples of chymotrypsinogen A sedimenting at 2.5 S, catalase at 10.8 S, thyroglobulin at 18.8 S with oligomers in the 25–40 S range, and ferritin—the latter exhibiting a broad distribution with weighted average s value of 68 S in addition to oligomers and aggregates spanning up to 200 S. For the centrifugal field profile, the ad hoc model shown in green in Fig. 1 A was used. (Simulations of the sedimentation boundaries for this mixture with other field profiles can be found in Fig. S2.) Fig. 3 shows the resulting absorbance profiles after radial alignment. A clear separation of the boundaries for all proteins can be discerned. Each protein sample was inserted into the mixture at concentrations producing an absorbance of 0.25 in the 12-mm-pathlength solution, which corresponds well to the observed boundary heights. In control experiments at 20,000 rpm and 50,000 rpm constant speed, as expected, no simultaneous observation of the largest and smallest species was possible (data not shown).

An excellent fit could be achieved with the standard c(s) model. For covering large s-value ranges we applied a logarithmically spaced grid. We found it necessary to increase the P value for regularization, applying a stronger constraint for parsimony of the distribution than usually achieved from relying on F-statistics allowing for a 1 or 2 SD increase in the RMSD. We believe this is related to the fact that information on any given s range rests only on a subset of scans, constituting a much smaller fraction of the total number of data points than in constant speed SV. As mentioned above, unstretching absorbance scans allowed a good description of time-invariant noise. In some experiments, we observed clear shifts in baseline associated with rotor speed changes (data not shown). This can be captured with an RI noise offset model. Therefore, although RI noise is ordinarily not required for modeling absorbance data (27), it was included for modeling variable-field SV absorbance data.

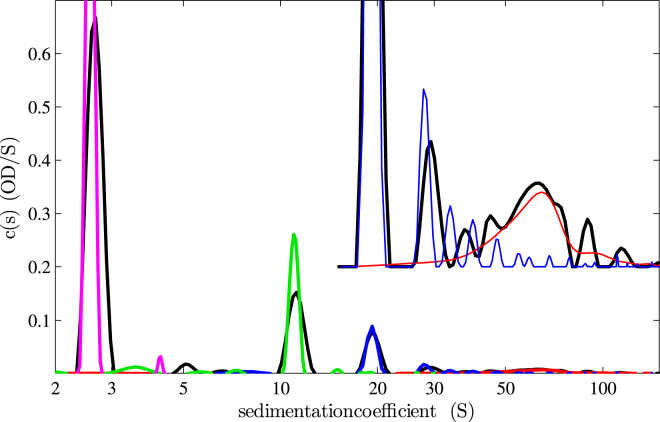
The resulting c(s) distribution is shown as a bold black line in Fig. 4. We compared the distribution with c(s) distributions obtained from conventional constant-speed SV experiments of the individual samples conducted at 20,000 rpm (ferritin and thyroglobulin) and 50,000 rpm (catalase and chymotrypsinogen A). The results of the individual c(s) traces is consistent with the gravitational sweep results. Lower resolution appears to be achieved in the gravitational speed experiment for the oligomers of thyroglobulin where trace dimer and trimer seems to be merged, but ferritin oligomers could be better resolved in the gravitational sweep. Generally, due to the broader boundaries in the gravitational sweep configuration, especially for small species, we would expect lower resolution of closely spaced s values; however, hydrodynamically well-separated faster-sedimenting species may be better resolved in gravitational sweep sedimentation than in a single compromise rotor speed.

Figure 4.

Diffusion-deconvoluted sedimentation coefficient distribution c(s) corresponding to the fit of the variable-field SV experiment shown in Fig. 3 (black line). To better visualize the distribution at larger s values, it was repeated with 20-fold amplification and offset by 0.2 OD. For comparison with the variable-field experiment (black), also shown are the distributions of chymotrypsinogen A (magenta) and catalase (green) obtained in a conventional constant-speed SV experiment at 50,000 rpm, and the distributions of thyroglobulin (blue) and ferritin (red) obtained in a constant-speed SV experiment at 20,000 rpm. To see this figure in color, go online.

Finally, to explore further the dynamic range of gravitational sweep SV, we carried out experiments with samples expected to have even higher s values: a sample of DNA-coated gold nanoparticles with modal s values of ∼350 S (Fig. S1), and samples of streptavidin-coated gold nanoparticles with a modal s value of ∼950 S (Fig. S3) could both be resolved using the same extended-constant-field-increase speed schedule as applied for the protein mixture. Interestingly, in the latter sample a small 2.6 S species—consistent with the expected size of free streptavidin—could be resolved cosedimenting with the nanoparticles ranging in size up to a few thousand Svedbergs.

Discussion

Previous approaches (5, 7) of gravitational sweep or multispeed SV were successful in demonstrating the detection of large particles over a very wide range of sizes, but the lack of consideration of diffusion limited the size resolution that could potentially be achieved, as well as the smallest particle sizes that could be distinguished. This problem is exacerbated in the variation of the wide distribution analysis (7), where the time-derivative method to calculate an apparent sedimentation coefficient distribution g(s^∗) (16) is subject to additional artificial broadening from the discrete approximation of dc/dt even for very large, nondiffusing particles (24), which restricts the choice of rotor speeds and number of scans that can be included into such an analysis, and thereby the range of particle sizes that can be reliably assessed.

In this work, we have addressed these limitations by solving the Lamm equation for the coupled sedimentation/diffusion process in a time-varying centrifugal field, to be used as a kernel in diffusion-deconvoluted sedimentation coefficient distributions c(s) (15) or size-and-shape distributions (21). This approach inherits the lower size-limit of detectable sedimentation in Lamm equation modeling, along with the exquisite hydrodynamic resolution of c(s)—for example, routinely providing baseline separation of monomers and dimers of small proteins—and all the advantages in data range, statistical accuracy, noise analysis, and quality control of direct boundary modeling in the raw data space. Although we have experimentally demonstrated only a ≈1000-fold range of sedimentation coefficients, the considerations in this work suggest that particles across the entire spectrum of size ranges detectable by SV should be accessible in a single gravitational sweep experiment: with sedimentation coefficients ranging from 0.1 to 10,000 S, this comprises eight orders of magnitude in mass, starting at the smallest detectable species such as buffer salts and small molecules of ∼10² Da sedimenting at the high rotor speeds (35, 36), up to entire organisms in the 10¹⁰ Da range sedimenting ahead already at the lowest rotor speeds (30).

To apply the c(s) analysis to gravitational sweep SV data, some prior knowledge about an approximate relationship between sedimentation and diffusion is useful. In standard SV this is often accomplished with a scaling law for compact particles, with an average frictional ratio as an adjustable parameter (15, 20), although a few other, and more general scaling models are currently implemented in SEDFIT (37). Dependent on the sample, not all detectable particles in gravitational sweep SV may follow the same scaling law. This may be addressed with the multimodal models, or tabulated relationships, or with future extensions as needed for the study of particular samples. However, it should be noted that the significance of diffusion—and therefore the required precision for approximate description—will decrease with increasing particle size. Our experience so far suggests that this is not critical as long as the focus remains on the sedimentation coefficient distribution, as opposed to molar mass distributions, which will be far less reliable, particularly for large particles. Size-and-shape distributions expressed as c(s,D) will completely circumvent this problem, especially when the ill-defined diffusion dimension is collapsed to the general c(s,∗) (21).

The new method discussed here has virtually no restrictions in shape and number of scans that can be included, and virtually no restrictions in the selection of rotor speed profiles. This offers a great freedom of experimental design. We have explored several centrifugal field schedules, which may be chosen dependent on the system under study. Because an extended dynamic range comes at the price of reduced information content on a particular species, as compared to a conventional SV experiment at suitably chosen constant speed, we do not anticipate gravitational sweep SV to become the method of choice when species of interest are known to fall within a narrow s range (e.g., within a factor 10). Even though a 100-fold or larger range of s values is easily detectable during the course of a constant speed experiment, faster particles migrate rapidly through the solution column and are therefore observed only for a short time. The application of field schedules with constant rate of rotor speed increase (for large particles) or constant rate of field increase (for small particles), permit a ≈100-fold range of s values to be explored more thoroughly. The widest range possible with uniform resolution can be achieved with a power-law model. However, deviations from these models are easily possible, such as the ad hoc extended-constant-field-increase model used for the experiments in this study; it has a wide range but focuses more on the smaller sizes. There is virtually complete freedom; a much simpler application enhancing standard SV could consist, for example, in a single moderate speed step at 20,000 rpm for the duration of 1 h—to better capture possible large aggregates—followed by the standard high-speed condition at 50,000 rpm for the remaining time to sediment medium and small proteins.

The time-varying centrifugal fields can be implemented either in a preprogrammed mode, or be adjusted ad hoc, with the limitation that at least one scan must report on each speed step to allow reconstruction of the field variation. Similar to potential rotor speed adjustments in the software TOSE, it is conceivable that real-time c(s) analysis (which might show, for example, the apparent lack of particles migrating at the momentary speed) could automatically lead to decisions to increase rotor speeds, creating a dynamic feedback for optimal analysis of unknown samples. Unfortunately, this is not possible with current instrumentation due to the absence of accessible speed and scan control interfaces in the centrifugal operating software.

Besides enabling gravitational sweep analysis, the variable field extension of SV has implications for how conventional experiments can be conducted. First, it appears sometimes desirable to use an initial single low-speed step, typically at 3000 rpm, to allow time for leak tests and optical adjustments. This can now be naturally accounted for in the framework of time-varying centrifugal fields, without causing detrimental effects on the accuracy of the data analysis. With knowledge of the rotor speed and the standard acceleration, it is possible to reconstruct the exact duration of the low-speed step. Temperature equilibration, however, should still be carried out with the rotor at rest, before any centrifugation, in order not to cause convective disturbances of any sedimentation and diffusion processes. With respect to temperature accuracy, another side effect of the extension of SV to time-varying centrifugal fields is the opportunity to carry out slow rotor acceleration phases in isothermal mode, avoiding adiabatic cooling during the rapid stretching of the rotor through radiative heat flow (10).

We believe gravitational sweep SV in conjunction with c(s) analysis introduced in this communication will be particularly useful in the study of proteins that self-assemble into large structures, such as virions or fibrils, which cannot be easily characterized simultaneously with their free building blocks. Similarly, equilibria between very dissimilar sized macromolecules or particles should be better accessible without compromising the detection of either a small or large reactant. Finally, a natural field of applications are broadly distributed nanoparticles (38), in biotechnology (8), and samples of entirely unknown distribution.

Author Contributions

J.M. designed experiments, performed research, and analyzed data; J.S. and J.A.L. provided materials; and H.Z. and P.S. designed experiments, analyzed data, contributed analytical tools, and wrote the article.

Editor: Elizabeth Komives.