Abstract
Phospholipid self-assembly is the basis of biomembrane stability. The entropy of transfer from water to self-assembled micelles of lysophosphatidylcholines and diacyl phosphatidylcholines with different chain lengths converges to a common value at a temperature of 44°C. The corresponding enthalpies of transfer converge at ∼−18°C. An equation of state for the free energy of self-assembly formulated from this thermodynamic data depends on the heat capacity of transfer as the sole parameter needed to specify a particular lipid. For lipids lacking calorimetric data, measurement of the critical micelle concentration at a single temperature suffices to define an effective heat capacity according to the model. Agreement with the experimental temperature dependence of the critical micelle concentration is then good. The predictive powers should extend also to amphiphile partitioning and the kinetics of lipid-monomer transfer.
Introduction
Spontaneous self-assembly of phospholipids in water is essential to the stability of biological membranes, and indeed to life itself. It is driven by thermodynamics, specifically the tendency of hydrophobic lipid chains to segregate from contact with water, coupled with the structural requirement to form a thin, flexible membrane that functionally forms a tight permeability barrier to polar solutes in the aqueous environment. The latter aspects require a strong interplay of the lipid polar headgroups and their hydrocarbon acyl chains. This results in formation of bilayer membranes or, in the case of shorter or single lipid chains, topologically equivalent normal micelles. Because the lipid chains are highly flexible, the membrane interior provides a fluid microphase of uniquely graded properties. Thus, thermodynamics of lipid assembly are important when considering incorporation and stability of membrane proteins, and also such aspects as partitioning and transmembrane transport of hydrophobic drugs and the interaction with other amphiphiles, in both pharmacological and biotechnological applications.
Until recently, considerably more attention has been paid to thermodynamic analysis of protein folding than to that of lipid-membrane assembly. For a restricted set of globular proteins, it was found that thermal unfolding is characterized by denaturation entropies and enthalpies per residue that extrapolate to common values at temperatures in the region of 110°C (1). Also, the entropy for transfer of hydrocarbons to water goes to zero at a temperature close to this range (2). These features led to a thermodynamic description of protein unfolding in terms of the linear dependence of denaturation entropy and enthalpy on heat capacity of unfolding (3). Although entropy and enthalpy convergence is not preserved with an expanded set of thermodynamic data on protein unfolding (4), it still holds for the simpler process of transferring small apolar molecules from hydrophobic environments to water (see, e.g., (5)).
Here, I explore to what extent these common features of the hydrophobic effect, namely entropy and enthalpy convergence coupled with a large heat capacity for transfer from water to apolar environments, can be used to describe the self-assembly of phospholipids into micelles or membranes. Lipid assembly relates more directly to small-molecule transfer processes than does the structurally more complex situation accompanying protein unfolding. My aim is to establish an equation of state for self-assembly of lipid monomers in water that applies with reasonable generality to all phospholipids. In addition to the fixed parameters that we need to define this equation of state, the thermodynamics for a particular lipid are determined by a single further parameter, the heat capacity of transfer to the micelle, or alternatively, the value of the critical micelle concentration (CMC) at a single temperature. It is to be expected, and is found, that the thermodynamic parameters for lipid self-assembly differ significantly from those for the hydrophobic effect alone, because of contributions from the structurally necessary phospholipid polar headgroups.
Similar thermodynamic principles should apply to the partitioning of aqueous amphiphiles into membranes, which is directly analogous to incorporation into the membrane of constituent lipid monomers. They are relevant also to the kinetics of transfer of lipid monomers into and out of micelles or membranes, because these depend partly on the thermodynamics of partitioning. Both of these aspects are discussed in the context of the equation of state.
Results
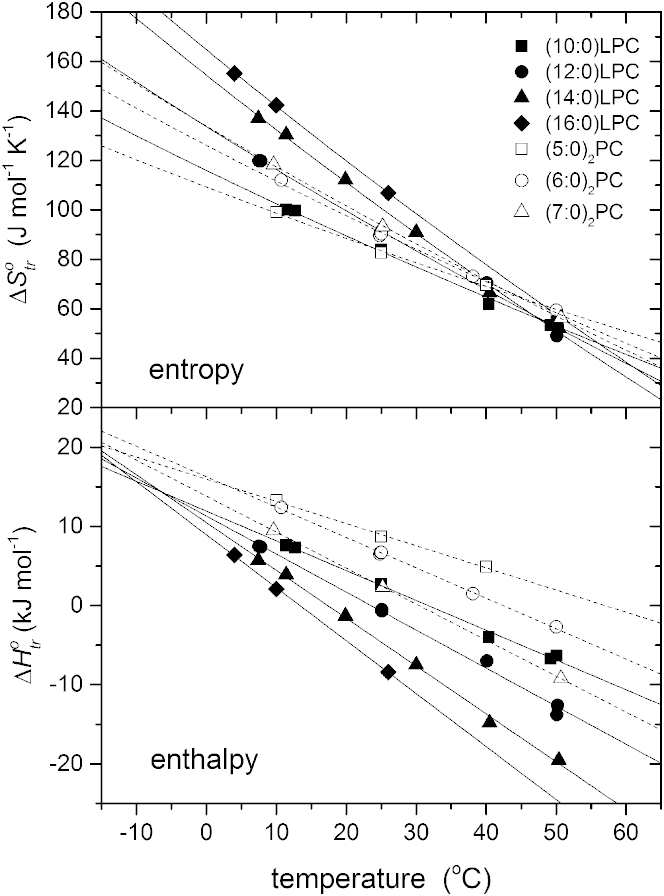
Fig. 1 shows the temperature dependence of the entropy and enthalpy for transfer of saturated acyl lysophosphatidylcholines (n:0)LPC and diacyl phosphatidylcholines (n:0)2PC of different chain lengths, n, from the monomeric state in water to their respective micelles. This data is obtained from isothermal titration calorimetry by Heerklotz and Epand (6). In this type of experiment, a concentrated aqueous suspension of micelles is injected into a fixed volume of water, and the heat evolved or absorbed on dissociation of the micelles into monomers dissolved in water is measured. Both the enthalpy and entropy of transfer are strongly dependent on temperature, implying a large heat capacity. To a reasonable degree of approximation, the transfer entropies reach a common value of 50−60 J mol−1 K−1 in the region of 50°C, whereas the enthalpies extrapolate to a common value of 15 kJ mol−1 at a temperature below 0°C. There are slight differences between the convergence for lysolipids and for short-chain diacyl lipids, which might be attributable to some difference in structure of their micelles.
Figure 1.
Temperature dependence of the entropy (upper panel) and enthalpy (lower panel) of lipid monomer transfer from water to micelles of saturated 1-acyl lysophosphatidylcholines (n:0)LPC (solid symbols and lines) and 1,2-diacyl phosphatidylcholines (n:0)2PC (open symbols and dashed lines) of different chain lengths, n. Experimental data from Heerklotz and Epand (6).
Following the treatment of protein unfolding by Murphy et al. (3), I assume that the enthalpy of transfer, , of a lipid monomer from water into the aqueous micellar assembly converges to a common value ΔH+ at temperature ,
| (1) |
where is the (temperature-independent) heat capacity of transfer. In Eq. 1, ΔH+ is independent of the lipid chain length nCH, and therefore at the convergence temperature . Similarly, I assume that the entropy change () in this same transfer process converges to a common value ΔS+ at temperature ,
| (2) |
where ΔS+ is independent of lipid chain length, and therefore at T = . Note that for limited temperature ranges (T – T+ << T+), expansion of the logarithm in Eq. 2 gives a linear temperature dependence: ln(T/T+) ≅ (T – T+)/T+. According to Eqs. 1 and 2, a direct consequence of convergence is that, at any fixed temperature, both enthalpy and entropy should be linearly dependent on the heat capacity of transfer, with a common gradient and intercept for the family of compounds under question (3).
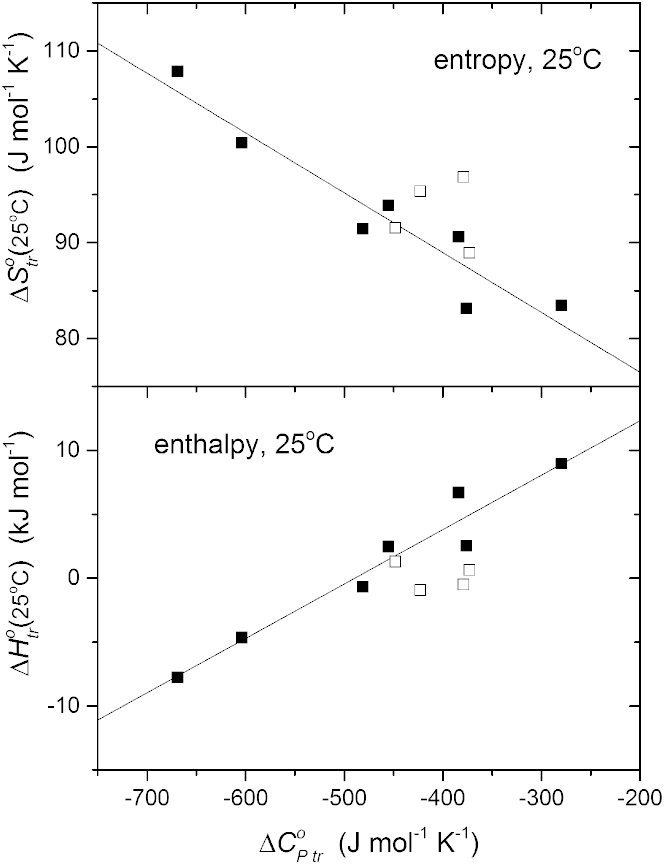
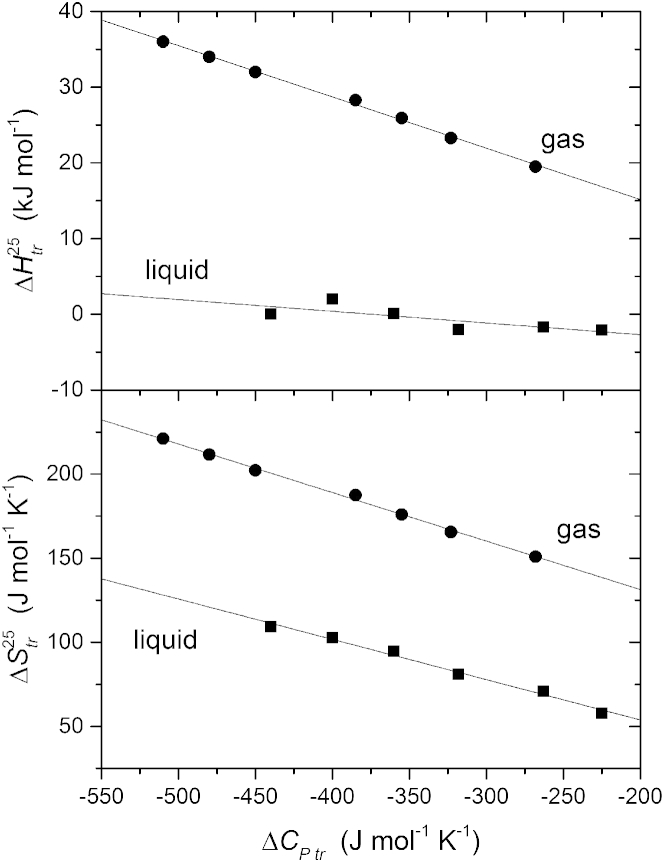
Fig. 2 plots the values of and at 25°C, interpolated from the data of Fig. 1, against the constant heat capacity that is deduced from the temperature dependence in the same figure (see also (7, 8)). Both entropy and enthalpy are approximately linear with respect to the heat capacity for the combined data from lysophosphatidylcholines and diacyl phosphatidylcholines, which are given by the solid symbols in Fig. 2. Linear regression according to Eqs. 1 and 2 gives the following aggregate parameters for these zwitterionic phospholipids: ΔH+ = 20.8 ± 2.3 kJ mol−1, = −17.6 ± 4.7°C, ΔS+ = 64.0 ± 4.3 J mol−1 K−1, and = 44.2 ± 2.8°C. The open symbols in Fig. 2, which are not part of the linear regression, are corresponding data for the negatively charged diacyl phospholipids phosphatidylglycerol (8:0)2PG and phosphatidylserine (8:0)2PS, in 0 and 0.15 M NaCl (7). These data suggest that the parameters for phosphatidylcholines might also represent other phospholipids reasonably well.
Figure 2.
Dependence of the transfer entropy (upper panel) and enthalpy (lower panel), from water into micelles at 25°C, on heat capacity of transfer for the lysophosphatidylcholines and diacyl phosphatidylcholines of Fig. 1 (solid squares). Solid lines are linear regressions according to Eqs. 1 and 2 (regression coefficients: 0.971 and −0.952, respectively). Open squares are corresponding data for charged lipids (8:0)2PG and (8:0)2PA in 0 and 0.15 M NaCl, from Marsh (7).
From Eqs. 1 and 2, the free energy for transfer of a phospholipid monomer from water into the micelle becomes
| (3) |
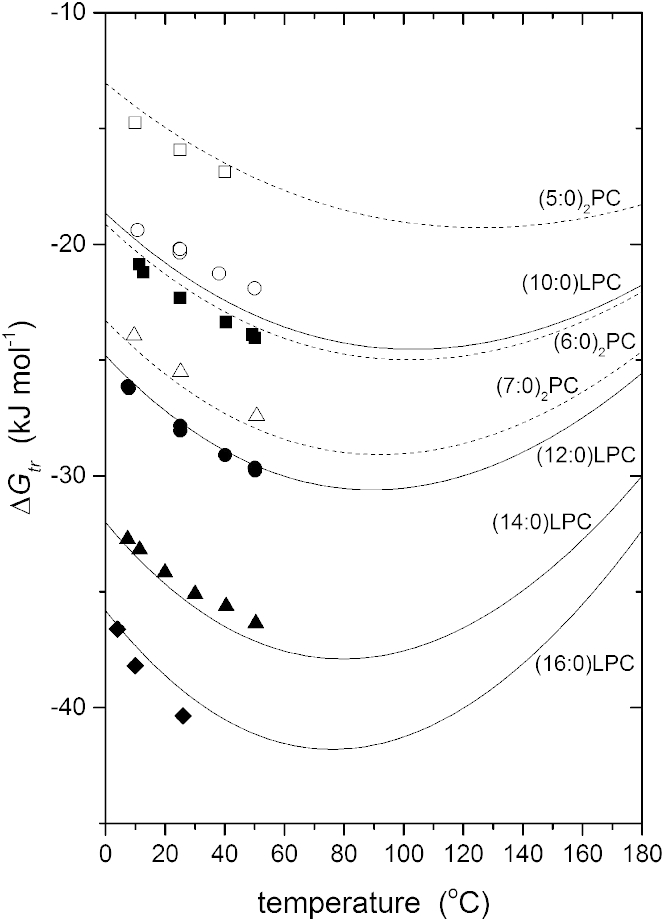
which is determined by the value of the heat capacity for the particular lipid, together with the aggregate parameters that are obtained from Fig. 2. Equation 3 therefore constitutes an equation of state for the self-assembly of aqueous phospholipids into micelles or membranes. Fig. 3 shows the temperature dependence of the free energy of transfer that is predicted by Eq. 3 for the different phosphatidylcholines from their heat capacities. The free energy displays a minimum that occurs at the temperature Tmin,ΔG = , at which the entropy of transfer, , is zero. This is the temperature at which the self-assembled state is most stable, and varies systematically between phospholipids according to their heat capacity of transfer. As can be seen from the data points that are also included in the figure, the predictions of Eq. 3 describe the experimental temperature dependence reasonably well over the range of measurement (6). The agreement is not perfect, as might be anticipated from the scatter about the linear regressions in Fig. 2, but we see that Eq. 3 serves quite well in the spirit of a global approximation.
Figure 3.
Temperature dependence of the free energy of lipid monomer transfer from water into micelles of 1-acyl lysophosphatidylcholines (n:0)LPC (solid symbols and lines) and 1,2-diacyl phosphatidylcholines (n:0)2PC (open symbols and dashed lines). Symbols defined as in Fig. 1. Lines are predictions from Eq. 3 with the parameters obtained from Fig. 2 and heat capacities of transfer, for each phosphatidylcholine as indicated on the figure.
With fixed parameters ΔS+, ΔH+, ,and , for the two convergence points, Eq. 3 reasonably describes the temperature dependence for the whole range of phosphatidylcholines, without further adjustable parameters. However, offsets in absolute values of the free energy are observed for certain lipids. In particular, the absolute values for (10:0)LPC and (6:0)2PC are rather close, but their predicted relative positions are reversed compared with experiment. This suggests that a slight adjustment in effective heat capacity for particular lipids could remove these minor offsets. For instance, decreasing the absolute value of for (6:0)2PC by 6%, and increasing that of (10:0)LPC by 2%, reverses the predicted order and brings the free energies close to the experimental values. Indeed, we can extend this method to apply the equation of state with phospholipids for which we lack calorimetric measurements. In principle, the CMC determined at a single temperature (as is often the case) should suffice.
For large micelles, or extended bilayers, the free energy for incorporating monomers from water is related to the CMC by (see, e.g., Cevc and Marsh (9))
| (4) |
where XCMC is the critical micelle concentration of the lipid monomer, in mole fraction units with respect to water. Rearranging Eqs. 3 and 4, we can then calculate an effective heat capacity of transfer from the CMC measured at temperature T:
| (5) |
Table 1 lists the effective heat capacities for lysophosphatidylcholines and diacyl phosphatidylcholines that we obtain in this way. Where heat capacity measurements are available, these are also listed for comparison (cf. Fig. 2). In most cases, we see that the adjusted values of the heat capacity lie within the uncertainty limits of the experimental measurements. Note that the shorter-chain diacyl phosphatidylcholines in Table 1 form micelles, whereas those with longer chains form bilayers. This point is addressed in the Appendix.
Table 1.
Effective Heat Capacity of Transfer Matched to the Measured CMC, According to Eq. 5, for Zwitterionic Lipids
| Lipid | T (°C) | CMC (M) | (J mol−1 K−1) | (J mol−1 K−1)a | Reference |
|---|---|---|---|---|---|
| (5:0)2PC | 25 | 9 × 10−2 | −289 | −280 ± 12 | (6) |
| (6:0)2PC | 24.9 | 1.5 × 10−2 | −362 | −384 ± 9 | (6) |
| (7:0)2PC | 25.2 | 1.9 × 10−3 | −445 | −455 ± 2 | (6) |
| (8:0)2PC | 2.7 × 10−4 | −524 | (10, 11) | ||
| (9:0)2PC | 2.9 × 10−5 | −614 | (10, 11) | ||
| (10:0)2PC | 25 | (5 ± 2) × 10−6 | −686 | (12) | |
| (12:0)2PC | R.T. | (2.5 ± 0.5) × 10−8 | −897 | (13) | |
| (16:0)2PC | 20 | 4.6 × 10−10 | −1057 | (14) | |
| (12:0/4-DOXYL5:0)PC | 20 | 1.2 × 10−4 | −558 | (15) | |
| (8:0)LPC | 37 | 5.7 × 10−2 | −304 | (16) | |
| (10:0)LPC | 25 | 6.8 × 10−3 | −394 | −386 ± 9 | (6) |
| (12:0)LPC | 25.1 | 7.1 × 10−4 | −485 | −481 ± 10 | (6) |
| (14:0)LPC | 30 | 5.0 × 10−5 | −595 | −604 ± 10 | (6) |
| (16:0)LPC | 26 | 5 × 10−6 | −687 | −669 ± 10 | (6) |
| (18:0)LPC | R.T. | (4.0 ± 0.1) × 10−7 | −785 | (17) |
R.T., room temperature; , effective heat capacity of transfer.
Direct measurements of the heat capacity for transfer of monomers from water.
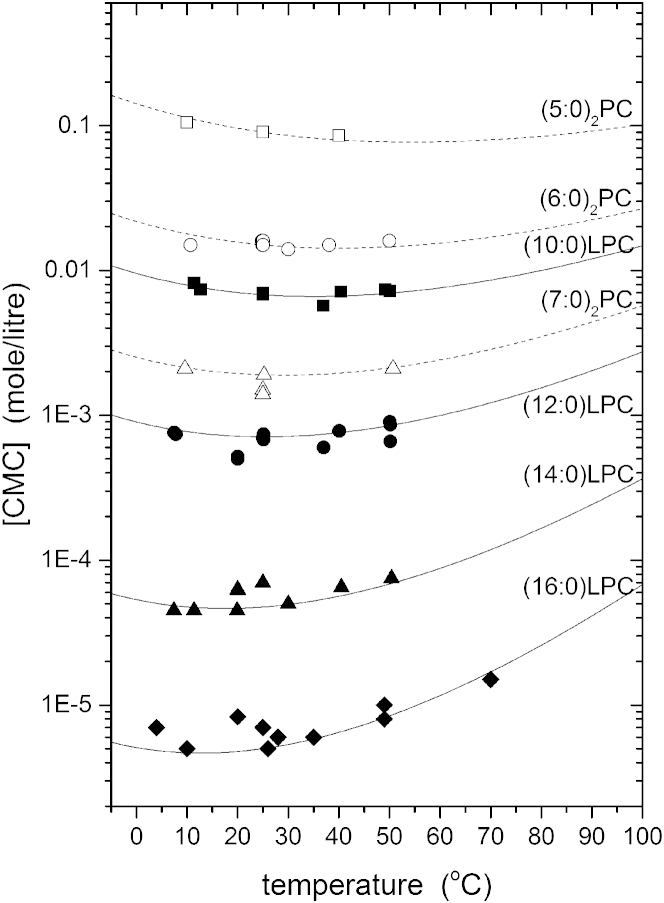
Fig. 4 shows the temperature dependence of the CMC that is calculated from Eqs. 3 and 4, by using the effective heat capacities of transfer for the different phosphatidylcholines from Table 1. The CMC reaches a minimum value at a temperature Tmin,CMC = , at which the enthalpy of transfer, = −RT2(∂lnXCMC/∂T), is zero. This behavior is very reminiscent of liquid hydrocarbons dissolving in water, where the minimum solubility occurs in a similar temperature range (27). As with the free energy, the temperature of the minimum varies systematically depending on heat capacity of transfer of the particular lipid, but note that Tmin,CMC is much lower than Tmin,ΔG. Experimental values for the CMC are also plotted in Fig. 4. These include not only the calorimetric data that was used for the linear fits in Fig. 2, but also other independent determinations of the CMC for the same lipids (see legend to Fig. 4, and Marsh (8)). This increases the experimental scatter but the equation of state given by Eq. 3, with the effective heat capacities, provides a satisfactory description of the CMC throughout the measured range of temperature. Again, as in Fig. 3, the temperature dependence is satisfactorily described with the same fixed set of parameters for the two convergence points.
Figure 4.
Temperature dependence of the critical micelle concentration, [CMC] in molar units, of 1-acyl lysophosphatidylcholines (n:0)LPC (solid symbols and lines) and 1,2-diacyl phosphatidylcholines (n:0)2PC (open symbols and dashed lines). Data from Heerklotz and Epand (6), with additional points from the literature (10, 11, 16, 18, 19, 20, 21, 22, 23, 24, 25, 26)—see Marsh (8). Symbols and annotations as in Fig. 3. Lines are predictions from Eqs. 3 and 4, with fixed parameters as in Fig. 3 and effective heat capacities from Table 1.
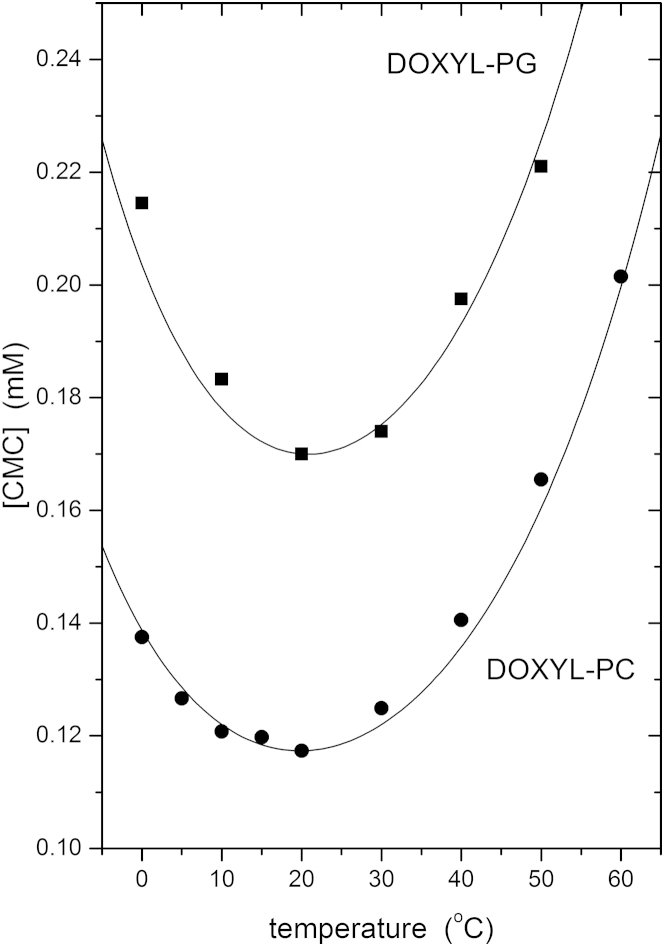
Table 2 gives data analogous to Table 1, but for the charged lipids phosphatidylglycerol, phosphatidylserine, and phosphatidic acid. Using the fixed parameters for the equation of state that are established with phosphatidylcholines, we see that the effective heat capacities calculated from a single CMC sometimes do not agree so well with direct measurement as does the same comparison for phosphatidylcholines in Table 1. However, the number of temperature points for those anionic lipids where the heat capacity has been measured is less than for phosphatidylcholines, and the experimental scatter is greater. Nevertheless, we can test whether the parameters established for phosphatidylcholine are appropriate for a different phospholipid by using a systematic comparison of the temperature dependence for spin-labeled phosphatidylglycerol and the corresponding phosphatidylcholine that was obtained with electron paramagnetic resonance spectroscopy (15). Fig. 5 compares the experimental temperature dependence of the CMCs for (12:0/4-DOXYL5:0)PG and (12:0/4-DOXYL5:0)PC with predictions from Eq. 3 that use the effective heat capacities found for these lipids in Tables 2 and 1, respectively. For both phospholipids, the sn-1 chain is lauroyl (C12:0), and the sn-2 chain is valeroyl (C5:0) with the DOXYL (4′,4′-dimethyloxazolidine-N-oxyl) spin label attached at the 4-C atom. As we see, the temperature dependence is well described for the anionic phosphatidylglyerol with the same fixed parameters in the equation of state as for the zwitterionic phosphatidylcholine. Note that these spin-labeled lipids have a short sn-2 chain and both form micelles in water.
Table 2.
Effective Heat Capacity of Transfer Matched to the Measured CMC, According to Eq. 5, for Anionic Lipids
| Lipid | [NaCl] (M) | T (°C) | CMC (M) | (J mol−1 K−1) | (J mol−1 K−1)a | Reference |
|---|---|---|---|---|---|---|
| (8:0)2PG | 0 | 21.5 | 1.21 × 10−3 | −464 | −373 ± 40 | (7) |
| 0.15 | 40 | 1.5 × 10−2 | −510 | −379 ± 18 | (7) | |
| (10:0)2PG | 21.5 | 4.2 × 10−4 | −507 | (28) | ||
| (12:0)2PG | 21.5 | 1.3 × 10−4 | −554 | (28) | ||
| (14:0)2PG | 21.5 | 1.1 × 10−5 | −653 | (28) | ||
| (12:0/4-DOXYL5:0)PG | 0.15 | 20 | 1.7 × 10−4 | −543 | (15) | |
| (6:0)2PS | 0 | 25 | 2.9 × 10−2 | −335 | (29) | |
| (8:0)2PS | 0 | 25 | 1.7 × 10−3 | −450 | −448 ± 19 | (7) |
| 0.15 | 40 | 3.89 × 10−4 | −513 | −423 ± 29 | (7) | |
| (10:0)2PS | 21.5 | 9.6 × 10−5 | −566 | (28) | ||
| (8:0)2PA | pH 8.2 | 5 | 4.21 × 10−3 | −422 | −547 ± 11 | (7) |
, effective heat capacity of transfer.
Direct measurements of the heat capacity for transfer of monomers from water.
Figure 5.
Temperature dependence of the critical micelle concentration of spin-labeled phosphatidylglycerol (12:0/4-DOXYL5:0)PG in 0.15 M NaCl (squares), and phosphatidylcholine (12:0/4-DOXYL5:0)PC in water (circles). Data from King and Marsh (15). Lines are predictions from Eqs. 3 and 4, with fixed parameters as in Fig. 3 and effective heat capacities from Tables 1 and 2.
Discussion
The equation of state derived here is for assembly/disassembly of lipid micelles or membranes in water. It refers directly to the thermodynamics that govern the stability of biomembranes. On the other hand, theoretical analyses of the hydrophobic effect often are based on the transfer of an apolar molecule from a fixed position in an ideal gas to a fixed position in bulk water (see, e.g., Graziano and Lee (5)). This differs significantly from the process actually involved in self-assembly of lipids in water. A major part of the entropy change accompanying this gas-to-solution transfer is attributed to cavity formation in water (5, 30, 31). Quite apart from the specific role played by the lipid polar headgroups, we do not expect the convergence temperatures found here to correspond with those predicted by theoretical models for the hydrophobic effect, because the reference states involved are so different. It is known, for instance, that lipid membrane surfaces have a pronounced influence on the ordering of water molecules, which among other things markedly affects the thermodynamics of lipid chain melting and gives rise to strong repulsive forces between zwitterionic bilayers (see, e.g., Cevc and Marsh (9,32)).
Table 3 gives the thermodynamic parameters for convergence that are derived from plots such as those given in Fig. 2 for different transfer processes, and for the original limited data set on protein thermal unfolding that gave rise to this type of analysis. Whereas the entropy and enthalpy of protein unfolding both converge at ∼100°C, this is not the case for the various transfer processes. Also, the convergence temperatures differ between the different transfer processes, particularly for the enthalpy. We see this clearly in Fig. 6, which compares entropies and enthalpies for transferring n-alkanes from the gas phase to water with those for transfer of different aliphatic and aromatic hydrocarbons from the neat liquid to water. The slopes of the dependences on (which determine the convergence temperatures according to Eqs. 1 and 2) for transfer to the gas phase obviously differ from those for transfer to the neat liquid. This demonstrates directly that convergence temperatures depend on the reference state chosen, because this introduces further chain-length-dependent contributions that result in different dependences on (see Eqs. 7−9 given later below). Note the large difference in absolute values of the thermodynamic quantities for the two reference states in Fig. 6. Taking the gaseous phase as reference results in most of the enthalpy and a large part of the entropy coming from transfer from the gas to a condensed phase, a process entirely unrelated to lipid self-assembly in water. Indeed, for the liquid alkanes that are included in both data sets in Fig. 6, the gas-phase values are obtained by adding the large heat or entropy of vaporization (36).
Table 3.
Parameters for the Equation of State, Eq. 3, Applied to Different Thermodynamic Processes
| Processa | (°C) | ΔS+(J mol−1 K−1) | (°C) | ΔH+ (kJ mol−1) | Reference |
|---|---|---|---|---|---|
| PC transfer | 44 ± 3 | 64 ± 4 | −18 ± 5 | 21 ± 2 | (6) |
| Protein unfold | 110 ± 6 | 18 ± 1 | 102 ± 5 | 5.7 ± 0.3 | (33)b |
| Peptide transfer | 104 ± 12 | 15 ± 3 | 72 ± 9 | 11.5 ± 0.8 | (34) |
| HC transfer | 106 ± 5 | −6 ± 4 | 40 ± 6 | 6 ± 2 | (27)c |
| 124 ± 3 | 74 ± 3 | 93 ± 2 | 1.6 ± 0.7 | (35)d |
PC transfer is the transfer of diacyl phosphatidylcholine and lysophosphatidylcholine monomers to micellar aggregates. Protein-unfold is the thermal unfolding of globular proteins per residue. Peptide transfer is the dissolution of solid cyclic dipeptides, GG, AG, AA, LG, and VV, per residue in water. HC transfer is the dissolution of liquid aromatic and aliphatic hydrocarbons in water (27), or of gaseous n-alkanes (35).
CnH2n+2 for n = 2−8.
Figure 6.
Dependence of the enthalpy (upper panel) and entropy (lower panel), for transfer from water into the gas phase (circles) or neat liquid phase (squares) at 25°C, on heat capacity of transfer for gaseous n-alkanes (circles, from Abraham and Matteoli (35)) and liquid aromatic and aliphatic hydrocarbons (squares, from Gill and Wadsö (27)).
The convergence temperatures found here for phospholipid self-assembly depart most from those of the other systems listed in Table 3 (and from theoretical estimates of the hydrophobic effect (5, 30)). This is most likely because the reference state for transfer is very different, namely either membrane or micelle, and not simply a homogeneous condensed phase. As mentioned already, the divergent value of for the transfer entropy most likely originates from ordering of water molecules at the membrane/micelle surface.
Having established that phospholipid self-assembly might reasonably be represented by Eq. 3, it now remains to ask why and to what extent. Lee (37) has shown that entropy and enthalpy converge if each is a bilinear function of temperature and some intensive property of the solute (such as chain length, nCH). On the other hand, Gill and Wadsö (27) have derived an expression for the free energy of dissolving aliphatic and aromatic hydrocarbons in water that is based on linear dependences on the number of H-atoms in the solute that are directly bonded to carbon. For our case of lipid self-assembly, the free energy for transfer of lipid monomers from water into micelles that we derive from the experimental CMC depends approximately linearly on the number of aliphatic carbon atoms, nCH, in the chains ((8) and see Fig. 7 later in the Appendix),
| (6) |
where specifies the end contributions, which are given by the intercept of the linear dependence. This linearity with chain length corresponds to the conventional interpretation of the hydrophobic effect: that the free energy of transfer is directly determined by the surface area of hydrocarbon in contact with water (38, 39, 40). Correspondingly, we find experimentally that the enthalpy for transfer of lipid monomers from water to micelles or membranes also depends linearly on the phospholipid hydrocarbon chain length (6):
| (7) |
From Eqs. 6 and 7, it therefore follows that the entropy of transfer is also linear with lipid chain length,
| (8) |
in agreement with experiment (8). Also, a linear dependence of the heat capacity for lipid monomer transfer from water to micelles/membranes is found experimentally (6):
| (9) |
with relatively little temperature dependence.
Figure 7.
Chain-length dependence of the standard free energy of transfer (see Eq. 4) of 1,2-diacyl phosphatidylcholines (n:0)2PC from water to micelles (or bilayers) at 21−25°C. (Circles) All experimental data points collected in Marsh (8), which includes those in Table 1. (Solid line) Linear regression to all data points; (dashed line) linear regression for data with n ≤ 10. Uncertainty range without symbol is extrapolated to from the linear regression.
Because , , and depend linearly on chain length, both and must be linearly dependent on , as given by Eqs. 1 and 2, respectively. Identifying the gradient of the transfer enthalpy with respect to in Eq. 7 with that in Eq. 1 requires the relation = between the chain-length dependences in Eqs. 7 and 9. If << in Eq. 9, then the constant term in Eq. 1 is given by ΔH+ ≡ = , which is independent of nCH. By an analogous procedure, we arrive at Eq. 2 for the entropy of transfer, where ΔS+ = is independent of nCH. Therefore, the condition for convergence is that the chain-length-dependent part of the heat capacity of transfer must be much larger than other contributions. For self-assembly of lipids, the dependence of on nCH is dominated by the hydrophobic effect, which is characterized by a particularly high heat capacity, hence satisfying the condition for convergence.
We thus find that convergence for a given lipid type is linked to the linear dependence of the free energy and heat capacity of self-assembly on chain length. As is evident in Fig. 1, convergence is somewhat better within the lysophosphatidylcholine or diacyl-phosphatidylcholine data sets individually than between the two data sets. This suggests that slight differences in convergence temperature might also be expected between species with different headgroups. However, as seen already in Fig. 4, this discrepancy is compensated by using the effective heat capacity obtained from the measured CMCs with the definition given in Eq. 5. Note that the approach is rather general and might also work with surfactants. For instance, micelle formation by homologous alkyl glucosides (41), and alkyl dimethylphosphine oxides (42), appears to display approximate enthalpy convergence.
Similar principles should apply to the partitioning of amphiphiles into membranes. We expect an equation of state that has the same form as Eq. 3, but the effective heat capacity of transfer is given by replacing [CMC] with 1/Kp in Eq. 5, where Kp is the mole-fraction partition coefficient. The equation of state also contributes to the kinetics of monomer transfer from micelles or vesicles. For micellar self-assembly, the off-rate constant k_ is related to the on-rate constant k+ by detailed balance (see. e.g., Cevc and Marsh (9)),
| (10) |
where [CMC] is expressed as a molar concentration when the units of k+ are M−1 s−1. The activation energies Ea,− and Ea,+ are therefore related by
| (11) |
where given by Eq. 5 is the free energy for transfer from water to micelle, and the factor 10−3 m3 corrects the concentration units. The preexponential coefficients, ko,− and ko,+, can be estimated by using Kramers’ theory (43), and by assuming a diffusion-controlled on-rate (15), respectively. We then get ln(ko,−/ko,+) = ΔS#/R – , where σcoll is the effective collision diameter, lb ≈ 0.07 nm (44) is the width of the transition-state barrier for leaving the aggregate, and ΔS# is the transition-state entropy.
Thermodynamics of the hydrophobic effect are characterized by an unusually large heat capacity (27). This is true also of phospholipid self-assembly, dealt with here, and the folding/unfolding of proteins (4). An inevitable consequence is that the enthalpy of transfer will go to zero at some particular temperature, as also will the entropy of transfer, although at a different temperature (cf. Figs. 3 and 4). Any claims for a nonclassical hydrophobic effect that are based on relative enthalpic and entropic contributions to the free energy at a fixed arbitrary temperature are therefore inappropriate. As seen in connection with Fig. 4, the enthalpy goes to zero and the transfer free energy becomes totally entropic at the special temperature , which depends both on the lipid chain length and on the reference state chosen for the transfer process. The isoentropic and isoenthalpic temperatures nearly coincide using the limited data set for protein folding, but not for phospholipid self-assembly or simpler transfer processes that involve the hydrophobic effect (see Table 3). This probably has its origin in the difference in configurational entropy between lipid chains in a micelle and amino-acid side chains in the core of a globular protein. The high heat capacity also gives rise to considerable entropy-enthalpy compensation; this results in a relatively shallow temperature dependence of the CMC needed to achieve self-assembly, as is observed (see Fig. 4).
Acknowledgments
I thank the Hans Christian Andersen Foundation (University of Southern Denmark), and Christian Griesinger and the Department of NMR-Based Structural Biology (Max Planck Institute), for financial assistance.
Editor: Markus Deserno.
Appendix: Micelle-Forming and Bilayer-Forming Lipids
The treatment given in this article assumes that the self-assembled lipids are in thermodynamically equivalent states, independent of whether the aggregated state is a micelle or an extended bilayer. Which of the two types of aggregate forms, is determined by packing restrictions that depend on the lipid chain length. Fig. 7 shows the chain-length dependence of the transfer free energy of 1,2-diacyl phosphatidylcholines (n:0)2PC from monomers in water to the self-assembled state. The shorter-chain lipids (n = 5–8) form micelles, albeit of progressively increasing size, and the longer-chain lipids, n = 9–12, form bilayers (28, 45). Nonetheless, there is a progressive increase in negative transfer free energy with increasing chain length. Buboltz and Feigenson (13) point out that the transfer free energy for n = 12 lies significantly below the linear extrapolation (dashed line) from the lipids with shorter chains, including those forming bilayers. The situation for the longest chains, n = 16, is somewhat uncertain because this involves an extrapolation from measurements in methanol-water mixtures (14). The available data therefore suggest that, to lowest order, the lipids assembled in micelles and bilayers are in comparable states thermodynamically, but there may be differences in stability of the bilayer aggregates when the lipid chains become longer. Note that chain order in the liquid-crystalline bilayer state of diacyl phosphatidylcholines with different chain lengths is comparable when at the same temperature (46).
References
- 1.Privalov P.L. Stability of proteins: small globular proteins. Adv. Protein Chem. 1979;33:167–241. doi: 10.1016/s0065-3233(08)60460-x. [DOI] [PubMed] [Google Scholar]
- 2.Baldwin R.L. Temperature dependence of the hydrophobic interaction in protein folding. Proc. Natl. Acad. Sci. USA. 1986;83:8069–8072. doi: 10.1073/pnas.83.21.8069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Murphy K.P., Privalov P.L., Gill S.J. Common features of protein unfolding and dissolution of hydrophobic compounds. Science. 1990;247:559–561. doi: 10.1126/science.2300815. [DOI] [PubMed] [Google Scholar]
- 4.Robertson A.D., Murphy K.P. Protein structure and the energetics of protein stability. Chem. Rev. 1997;97:1251–1268. doi: 10.1021/cr960383c. [DOI] [PubMed] [Google Scholar]
- 5.Graziano G., Lee B. Entropy convergence in hydrophobic hydration: a scaled particle theory analysis. Biophys. Chem. 2003;105:241–250. doi: 10.1016/s0301-4622(03)00073-5. [DOI] [PubMed] [Google Scholar]
- 6.Heerklotz H., Epand R.M. The enthalpy of acyl chain packing and the apparent water-accessible apolar surface area of phospholipids. Biophys. J. 2001;80:271–279. doi: 10.1016/S0006-3495(01)76012-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Marsh D. Thermodynamics of phospholipid self-assembly. Biophys. J. 2012;102:1079–1087. doi: 10.1016/j.bpj.2012.01.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Marsh D. CRC Press; Boca Raton, FL: 2013. Handbook of Lipid Bilayers. [Google Scholar]
- 9.Cevc G., Marsh D. Wiley-Interscience; New York: 1987. Phospholipid bilayers: Physical Principles and Models. [Google Scholar]
- 10.Tausk R.J.M., Karmiggelt J., Overbeek J.T.G. Physical chemical studies of short-chain lecithin homologues. I. Influence of the chain length of the fatty acid ester and of electrolytes on the critical micelle concentration. Biophys. Chem. 1974;1:175–183. doi: 10.1016/0301-4622(74)80004-9. [DOI] [PubMed] [Google Scholar]
- 11.Tausk R.J.M., van Esch J., Overbeek J.T.G. Physical chemical studies of short-chain lecithin homologues. II. Micellar weights of dihexanoyl- and diheptanoyllecithin. Biophys. Chem. 1974;1:184–203. doi: 10.1016/0301-4622(74)80005-0. [DOI] [PubMed] [Google Scholar]
- 12.Reynolds J.A., Tanford C., Stone W.L. Interaction of L-α-didecanoyl phosphatidylcholine with the AI polypeptide of high density lipoprotein. Proc. Natl. Acad. Sci. USA. 1977;74:3796–3799. doi: 10.1073/pnas.74.9.3796. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Buboltz J.T., Feigenson G.W. Phospholipid solubility determined by equilibrium distribution between surface and bulk phases. Langmuir. 2005;21:6296–6301. doi: 10.1021/la047086k. [DOI] [PubMed] [Google Scholar]
- 14.Smith R., Tanford C. The critical micelle concentration of L-α-dipalmitoylphosphatidylcholine in water and water-methanol solutions. J. Mol. Biol. 1972;67:75–83. doi: 10.1016/0022-2836(72)90387-7. [DOI] [PubMed] [Google Scholar]
- 15.King M.D., Marsh D. Head group and chain length dependence of phospholipid self-assembly studied by spin-label electron spin resonance. Biochemistry. 1987;26:1224–1231. doi: 10.1021/bi00379a004. [DOI] [PubMed] [Google Scholar]
- 16.Kumar V.V., Baumann W.J. Lanthanide-induced phosphorus-31 NMR downfield chemical shifts of lysophosphatidylcholines are sensitive to lysophospholipid critical micelle concentration. Biophys. J. 1991;59:103–107. doi: 10.1016/S0006-3495(91)82202-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kramp W., Pieroni G., Hanahan D.J. Observations on the critical micellar concentration of 1-O-alkyl-2-acetyl-sn-glycero-3-phosphocholine and a series of its homologs and analogs. Chem. Phys. Lipids. 1984;35:49–62. doi: 10.1016/0009-3084(84)90032-x. [DOI] [PubMed] [Google Scholar]
- 18.Johnson R.E., Wells M.A., Rupley J.A. Thermodynamics of dihexanoylphosphatidylcholine aggregation. Biochemistry. 1981;20:4239–4242. doi: 10.1021/bi00517a044. [DOI] [PubMed] [Google Scholar]
- 19.Burns R.A., Roberts M.F., Mendelsohn R. Monomer-to-micelle transition of dihexanoylphosphatidylcholine—13C NMR and Raman studies. J. Am. Chem. Soc. 1982;104:430–438. [Google Scholar]
- 20.Lin T.L., Chen S.H., Roberts M.F. Use of small-angle neutron scattering to determine the structure and interaction of dihexanoylphosphatidylcholine micelles. J. Am. Chem. Soc. 1986;108:3499–3507. [Google Scholar]
- 21.Lin T.L., Chen S.H., Roberts M.F. Small-angle neutron scattering techniques applied to the study of polydisperse rodlike diheptanoylphosphatidylcholine micelles. J. Phys. Chem. 1987;91:406–413. [Google Scholar]
- 22.Lewis K.A., Bian J.R., Roberts M.F. Asymmetric short-chain phosphatidylcholines: defining chain binding constraints in phospholipases. Biochemistry. 1990;29:9962–9970. doi: 10.1021/bi00494a029. [DOI] [PubMed] [Google Scholar]
- 23.Stafford R.E., Fanni T., Dennis E.A. Interfacial properties and critical micelle concentration of lysophospholipids. Biochemistry. 1989;28:5113–5120. doi: 10.1021/bi00438a031. [DOI] [PubMed] [Google Scholar]
- 24.Nakagaki M., Komatsu H., Handa T. Estimation of critical micelle concentrations of lysolecithins with fluorescent probes. Chem. Pharm. Bull. (Tokyo) 1986;34:4479–4485. [Google Scholar]
- 25.Gow A., Auton W., Smith R. Interactions between bovine myelin basic protein and zwitterionic lysophospholipids. Biochemistry. 1990;29:1142–1147. doi: 10.1021/bi00457a007. [DOI] [PubMed] [Google Scholar]
- 26.Gow A., Winzor D.J., Smith R. Equilibrium binding of myristoyllysophosphatidylcholine to bovine myelin basic protein: an example of ligand-mediated acceptor association. Biochemistry. 1987;26:982–987. doi: 10.1021/bi00378a002. [DOI] [PubMed] [Google Scholar]
- 27.Gill S.J., Wadsö I. An equation of state describing hydrophobic interactions. Proc. Natl. Acad. Sci. USA. 1976;73:2955–2958. doi: 10.1073/pnas.73.9.2955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kleinschmidt J.H., Tamm L.K. Structural transitions in short-chain lipid assemblies studied by 31P-NMR spectroscopy. Biophys. J. 2002;83:994–1003. doi: 10.1016/S0006-3495(02)75225-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Walker J.M., Homan E.C., Sando J.J. Differential activation of protein kinase C isozymes by short chain phosphatidylserines and phosphatidylcholines. J. Biol. Chem. 1990;265:8016–8021. [PubMed] [Google Scholar]
- 30.Hummer G., Garde S., Pratt L.R. An information theory model of hydrophobic interactions. Proc. Natl. Acad. Sci. USA. 1996;93:8951–8955. doi: 10.1073/pnas.93.17.8951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Graziano G. Entropy convergence in the hydration thermodynamics of n-alcohols. J. Phys. Chem. B. 2005;109:12160–12166. doi: 10.1021/jp051460n. [DOI] [PubMed] [Google Scholar]
- 32.Cevc G., Marsh D. Hydration of noncharged lipid bilayer membranes. Theory and experiments with phosphatidylethanolamines. Biophys. J. 1985;47:21–31. doi: 10.1016/S0006-3495(85)83872-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Privalov P.L., Gill S.J. Stability of protein structure and hydrophobic interaction. Adv. Protein Chem. 1988;39:191–234. doi: 10.1016/s0065-3233(08)60377-0. [DOI] [PubMed] [Google Scholar]
- 34.Murphy K.P., Gill S.J. Thermodynamics of dissolution of solid cyclic dipeptides containing hydrophobic side groups. J. Chem. Thermodyn. 1989;21:903–913. [Google Scholar]
- 35.Abraham M.H., Matteoli E. The temperature variation of the hydrophobic effect. J. Chem. Soc., Faraday Trans. I. 1988;84:1985–2000. [Google Scholar]
- 36.Gill S.J., Nichols N.F., Wadsö I. Calorimetric determination of enthalpies of solution of slightly soluble liquids. II. Enthalpy of solution of some hydrocarbons in water and their use in establishing the temperature dependence of their solubilities. J. Chem. Thermodyn. 1976;8:445–452. [Google Scholar]
- 37.Lee B. Isoenthalpic and isoentropic temperatures and the thermodynamics of protein denaturation. Proc. Natl. Acad. Sci. USA. 1991;88:5154–5158. doi: 10.1073/pnas.88.12.5154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Tanford C. Wiley; New York: 1980. The Hydrophobic Effect. [Google Scholar]
- 39.Reynolds J.A., Gilbert D.B., Tanford C. Empirical correlation between hydrophobic free energy and aqueous cavity surface area. Proc. Natl. Acad. Sci. USA. 1974;71:2925–2927. doi: 10.1073/pnas.71.8.2925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Marsh D. Lateral pressure in membranes. Biochim. Biophys. Acta. 1996;1286:183–223. doi: 10.1016/s0304-4157(96)00009-3. [DOI] [PubMed] [Google Scholar]
- 41.Opatowski E., Kozlov M.M., Lichtenberg D. Heat evolution of micelle formation, dependence of enthalpy, and heat capacity on the surfactant chain length and head group. J. Colloid Interface Sci. 2002;246:380–386. doi: 10.1006/jcis.2001.8050. [DOI] [PubMed] [Google Scholar]
- 42.Kresheck G.C. A calorimetric determination of the standard enthalpy and heat capacity changes that accompany micelle formation for four long chain alkyldimethylphosphine oxides in H2O and D2O solution from 15 to 79°C. J. Am. Chem. Soc. 1998;120:10964–10969. [Google Scholar]
- 43.Aniansson E.A.G., Wall S.N., Tondre C. Theory of the kinetics of micellar equilibria and quantitative interpretation of chemical relaxation studies of micellar solutions of ionic surfactants. J. Phys. Chem. 1976;80:905–922. [Google Scholar]
- 44.Nichols J.W. Thermodynamics and kinetics of phospholipid monomer-vesicle interaction. Biochemistry. 1985;24:6390–6398. doi: 10.1021/bi00344a011. [DOI] [PubMed] [Google Scholar]
- 45.Petrache H.I., Tristram-Nagle S., Parsegian V.A. Swelling of phospholipids by monovalent salt. J. Lipid Res. 2006;47:302–309. doi: 10.1194/jlr.M500401-JLR200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Marsh D. Molecular volumes of phospholipids and glycolipids in membranes. Chem. Phys. Lipids. 2010;163:667–677. doi: 10.1016/j.chemphyslip.2010.06.005. [DOI] [PubMed] [Google Scholar]