Diffusion of Bacterial Cells in Porous Media

Abstract

The chemotaxis signal transduction network regulates the biased random walk of many bacteria in favorable directions and away from harmful ones through modulating the frequency of directional reorientations. In mutants of diverse bacteria lacking the chemotaxis response, migration in classic motility agar, which constitutes a fluid-filled porous medium, is compromised; straight-swimming cells unable to tumble become trapped within the agar matrix. Spontaneous mutations that restore spreading have been previously observed in the enteric bacterium Escherichia coli, and recent work in other bacterial species has isolated and quantified different classes of nonchemotacting mutants exhibiting the same spreading phenotype. We present a theoretical description of bacterial diffusion in a porous medium—the natural habitat for many cell types—which elucidates how diverse modifications of the motility apparatus resulting in a nonzero tumbling frequency allows for unjamming of otherwise straight-swimming cells at internal boundaries and leads to net migration. A unique result of our analysis is increasing diffusive spread with increasing tumbling frequency in the small pore limit, consistent with earlier experimental observations but not captured by previous models. Our theoretical results, combined with a simple model of bacterial diffusion and growth in agar, are compared with our experimental measurements of swim ring expansion as a function of time, demonstrating good quantitative agreement. Our results suggest that the details of the cellular tumbling process may be adapted to enable bacteria to propagate efficiently through complex environments. For engineered, self-propelled microswimmers that navigate via alternating straight runs and changes in direction, these results suggest an optimal reorientation strategy for efficient migration in a porous environment with a given microarchitecture.

Introduction

Fluid-filled porous media—environments such as soil, tissue, or a biofilm matrix—constitute the natural habitat for many bacterial cell types. Flagella are used by more than 80% of bacteria to swim through fluid media (1). In many cases, the strategy used by motile bacteria to explore their local environment consists of relatively straight-swimming intervals punctuated by random changes in direction, described by a random walk. Even when moving in a preferred direction in response to chemical environmental stimuli, there is a random component to the bacterial trajectory. The frequency of random directional changes is suppressed along favorable directions by a chemosensory network, resulting in a biased random walk. These changes in direction, governed by flagellar dynamics, play a crucial role in bacterial migration in porous media, allowing cells to clear obstacles. It is conceivable that details of bacterial sensing and motility determining the biased random walk trajectory can be adapted to the microarchitecture of a given environment to enhance spreading, with relevance to the evolution of these mechanisms in microorganisms (2, 3) as well as their application to artificial microswimmers (4).

In this work, we present a theoretical description of bacterial diffusion in a porous environment, elucidating its dependence on details of bacterial motility, through the frequency and degree of directional reorientations, and the mean pore size of the medium. The presentation is organized as follows. In the context of flagellar motility, bacterial chemosensing, and diffusion, first we describe the experimental motivation for our analysis, namely the emergence of spontaneous motility mutations that allow diffusive expansion of bacterial colonies in porous agar by restoring reorientations in straight-swimming parent strains (5, 6). We describe how incorporating bacterial idling at internal boundaries leads to a new microscopic description, to our knowledge, of bacterial diffusion in a porous medium. Our theoretical results are consistent with previous experimental observations in soft agar of the nonspreading phenotype of straight-swimming mutants, and the perhaps counterintuitive trend that the diffusive spread of cells increases with increasing tumbling frequency, both features not captured by previous models. We make a connection between the spontaneous motility mutations that restore diffusive migration and existing computational results on flagellar dynamics governing swimming and reorientations. We compare our theoretical results with fits with our measurement of the diffusive spread of mutants in motility agar assays, and we conclude with implications for optimization of the swimming strategy of microswimmers in porous habitats.

Flagellar motility, bacterial chemotaxis, and diffusion

In multiflagellated cells, straight-swimming motion and directional reorientations are governed by collective flagellar dynamics, through flagellar bundling and unbundling, respectively. Flagella are helical extracellular filaments connected via a flexible curved segment, called the hook, to the basal body and powered by a rotary motor complex (7, 8). The best-studied motility paradigm, shared by other well-studied bacteria, is that of Escherichia coli (E. coli), where multiple-rotating flagella form a bundle that acts as a propeller to drive the cell forward. In E. coli, counterclockwise (CCW) flagellar rotation promotes bundle formation, leading to intervals of straight swimming, called runs. Clockwise (CW) rotation of one or more flagella leads to bundle disruption and results in reorientation of the cell’s motion, known as tumbles. In other bacterial species with unidirectional motors, unbundling occurs when one or more flagella slow or stop their rate of rotation (9, 10, 11). The dynamics of unbundling determine the extent to which the cell is reoriented during a tumble. The biophysical mechanisms underlying bundling, unbundling, and reorientation, which necessarily depend on properties of both intracellular and extracellular components of the motility apparatus, are the subject of ongoing experimental and computational studies (12, 13, 14, 15, 16, 17, 18).

Rotation of the flagellar motor is modulated by the output of the chemotaxis network, the phosphorylated form of the intracellular response regulator, CheY (CheY-P). In this sensory network, consisting of multiple (Che) proteins, the binding of a chemical signal to receptor clusters in the cytoplasmic membrane triggers a complex internal signaling pathway (19), culminating in a change in the concentration of CheY-P. In turn, the binding of CheY-P to the FliM protein in the FIiM-FliG-FliN flagellar motor switch complex induces tumbling, which in the E. coli motility paradigm is achieved through increasing the CW rotational bias. Recent work has highlighted the fact that the flagellar motor assembly itself is a dynamic structure, with protein components exchanging between the working motor and cytoplasmic pools in response to intra- and extracellular signals (20, 21, 22, 23, 24).

These chemical kinetic events and resulting conformational changes of the motor complex are subject to noise, and as such, the generation of tumbles is an inherently stochastic process. In the absence of an external gradient, the trajectory of a cell is characterized by a random walk of alternating runs and tumbles (19, 25), namely diffusion. The chemotaxis signaling network, through changes in CheY-P concentration in response to external gradients, serves to bias this random walk toward (away from) favorable (harmful) directions.

Diffusion of bacterial cells as active particles is fundamentally different from that (because of the thermal energy) of inanimate gaseous particles. In the latter case, particle-particle or particle-boundary collisions randomize the trajectory, whereas for bacteria, tumbles are generated intrinsically by each cell’s motility apparatus. Furthermore, bacteria encountering an internal or external boundary are not reflected as in the collision of a hard sphere with a hard boundary; rather, a cell idles at a boundary until the next tumble reorients it. The main result of this study is that in porous media, especially in the small pore regime, this distinction becomes central; consequently, the diffusion constant characterizing the random motion of a bacterial cell is different from that obtained in analogy with a gas particle.

Pseudotaxis

An important assay medium for studying swimming motility over the past few decades has been semi-solid agar, which is a low concentration, high-porosity fluid-filled random network of agarose polymers (26, 27, 28, 29). Bacteria are inoculated at a single point and the radial spread of the population, known as the swim ring or disc, is measured over time. As bacteria metabolize nutrients locally, a chemical gradient is established, and in addition to bacterial diffusion, chemotaxis enhances the outward radial migration of cells toward higher nutrient concentrations. A wide variety of chemotaxis mutants have been identified and assayed in motility agar. For example, tumbling frequency is significantly decreased in cheA mutants (disabled for the kinase that phosphorylates the CheY response regulator) with respect to wild-type, leading to relatively straight, uninterrupted runs. Consequently, these mutants do not advance appreciably, becoming trapped in the agar network. Likewise, in cheB mutants (disabled for a methyltransferase enzyme involved in the adaptation phenomenon) with increased tumbling, advancement of the swim ring is also diminished with respect to wild-type as these cells change direction so frequently that their net movement is compromised. In both cases, decoupling the mean runtime from Che control abolishes the ability to bias movement in response to gradients (30, 31, 32, 33, 34).

Wolfe and Berg (5) showed that in motility agar assays of E. coli che deletion strains, spontaneous mutations arose that restored the radial expansion of the population, appearing to overcome the chemotaxis deficiency. These mutants were found to have point mutations in the fliM and fliG genes that encode components of the flagellar switch complex, leading to flagellar rotation reversals in contrast with the straight-swimming parent strain. However, although the chemotaxis network normally modulates the frequency of motor reversals in response to external chemical queues (30, 35, 36), in these mutants the switching is random. The resulting effective migration of nonchemotactic mutants in porous agar, termed pseudotaxis by others (36, 37), is therefore a purely diffusive spread of motile bacteria that are not able to respond to chemical gradients. (The migration of these spontaneous mutants in agar as a result of regaining the ability to generate tumbles via various motility defects is not to be confused with pseudochemotaxis. Pseudochemotaxis, proposed by Lapidus (38), refers to apparent chemotaxis, or motion in the direction of increasing chemoattractant concentration, when the diffusion constant is itself a function of the chemoattractant concentration.) Also of relevance, Stock et al. (39) reported the spreading of cheR cheB double mutants in agar assays, incorrectly inferring that the migration of these transferase-esterase double mutants, which exhibit both runs and tumbles, was because of chemotaxis. Wolfe and Berg (5) showed that their migration rate increases with tumbling frequency, and Berg and Turner (40) demonstrated definitively in capillary assays that this strain was in fact nonchemotactic.

Related work (41) on mutants of the plant pathogen Agrobacterium tumefaciens (A. tumefaciens), in which the cheA chemotaxis regulator or the entire che gene cluster was deleted, led to the isolation of chemotaxis mutation suppressor (cms) mutants that were similarly able to rescue the decreased migration of the straight-swimming phenotype parent strain. It was shown that these cms mutants were indeed able to tumble in suspension.

In A. tumefaciens, up to six flagella are organized as a polar tuft (42). In contrast to E. coli and as with other related members of the Rhizobiaceae family, it is believed that A. tumefaciens is propelled forward during runs by CW flagellar rotation resulting in bundle formation (10, 43, 44). The slowing of the CW rotation rate of the flagellar motor, rather than the reversal of the direction of rotation, is thought to initiate tumbles (11, 45), presumably causing disruption of the flagellar bundle. The mechanistic differences in the generation of tumbles suggested that cms mutations resulting in pseudotaxis in A. tumefaciens might be different from those observed in E. coli.

Indeed, recent work quantifying a collection of A. tumefaciens cms mutants using whole genome resequencing to map their mutations has identified novel mutations that affect the structure of the flagellum and the process by which its rotation is powered (6). Three classes of mutations were discovered. Class I mutations were mapped to the (D1 domain of the) flagellar hook protein, FlgE. Class II mutations were found to extend the fliK coding sequence and are predicted to produce a longer FliK protein; while motile, these mutants produced coiled and polyhook filaments, consistent with the role of FliK as the flagellar hook length regulator (46). Class III mutations corresponded to the flagellar motor protein MotA involved in torque generation (11). Single-cell tracking studies have directly confirmed that these mutations restore changes in direction in the straight-swimming trajectories of the parent strain.

Motivated by these experimental observations, we have developed a theoretical description of bacterial diffusion in porous media. Our analysis unifies the phenomenology of diverse mutations in the motility apparatus of various bacterial species that compromise flagellar bundling in different ways. It quantifies how effective tumbling, or directional change, leads to diffusive migration in porous agar in an otherwise straight-swimming background strain. The emergence of these spontaneous mutations in a chemotaxis deletion background provides a unique setting in which to separate the chemotaxis response from the purely diffusive spread of bacterial cells in motility agar assays. At the heart of our analysis is the fact that bacterial diffusion arises from the inherently stochastic generation of tumbles by individual cells, in contrast with gaseous diffusion where reorientations result from particle-particle and particle-boundary collisions. Indeed, as directly observed in Wolfe and Berg’s work (5), and depicted schematically in Fig. 1, cells idle at internal boundaries until reoriented by a new tumble. Absent these unique mutant classes, previous theoretical works quantifying bacterial migration in agar and other porous media have necessarily also addressed chemotaxis, making this distinction less apparent.

Figure 1.

Idealized schematic model of migration through the motility agar matrix. Although straight-swimming cells can be trapped in the agar matrix and idle, tumbles generated via a variety of mechanisms that alter flagellar bundling enable the unjamming of cells at internal boundaries and net migration through the porous medium. In wild-type cells, tumbles are under the control of the chemotaxis sensory network, whereas in the cms mutants lacking the chemotactic response, erratic swimming motion and random directional changes are caused by mutations in the motility apparatus. The panels schematically illustrate how a straight-swimming cell (A) can encounter an agar matrix barrier and idle (B), until a tumble occurs (C) causing reorientation (D), and allowing the cell to become unjammed and swim away (E). The arrows denote the run direction.

Material and Methods

For motility assays in swim agar fresh colonies of bacteria were streaked out and used to inoculate the plates. Expansion of the swim ring was measured as a function of incubation time. The strains used were the wild-type A. tumefaciens, the parent mutant $\Delta che$, and one representative mutant from each class of cms mutants: class I (flgE), class II (fliK), and class III (motA). A. tumefaciens (AT) is typically grown in AT minimal medium (47) supplemented with 0.5% (wt/vol) glucose and 15 mM ammonium sulfate (ATGN). Microbiological media were obtained from Fisher Scientific (Pittsburg, PA) and Sigma-Aldrich (St. Louis, MO). For the preparation of ATGN motility agar plates (agar concentration, C = 0.25%), 100 mm petri dishes with 20 ml of Bacto agar (BD, Sparks, MD) were used. A toothpick was used to inoculate colonies by stabbing them into the agar at the center of the plate. Following inoculation, the plates were incubated at 28°C for up to 7 days, with swim ring diameters measured daily.

Results

Below, we first derive the diffusion constant for a bacterial cell as a function of the properties of the cell—cell speed, steady-state tumbling frequency, and tumble angle distribution—and that of the porous medium, characterized by the average pore size. Given the importance of tumbling, we then make connection between previous computational results on the biophysical mechanisms underlying flagellar bundling and unbundling and the experimentally identified mutations in the motility apparatus of strains exhibiting pseudotaxis. Finally, we compare the theoretical results for diffusion in agar with experimental measurements of the expansion of the swim disc for various mutant classes. In the subsequent sections, we summarize our results and comment on their broader implications for optimizing the propagation of self-propelled particles in porous habitats.

Bacterial random walk in porous media

For a particle diffusing isotropically in three dimensions, the mean square displacement 〈r²(t)〉 traveled in a time t is the following:

$$\langle r^2\left(t\right)\rangle \simeq 6Dt,$$ (1)

where D is the diffusion coefficient. Lovely and Dahlquist provided a framework for formulating statistical measures of bacterial motility in terms of a random walk model of a polymer chain (48), with each run representing a bond and each tumble a vertex at which a bond angle between successive bonds (runs) can be defined. We assume that tumbles are described as a homogeneous Poisson process; hence, the distribution of run-times, τ, is exponential with a characteristic tumbling frequency (rate at which tumbles occur), ω, as in the following:

$$R\left(\tau \right)=\omega \text{exp}\left(-\omega \tau \right).$$ (2)

Assuming variable uncorrelated bond lengths, ℓ = vτ, and bond angles, θ, it can be shown that

$$D=\frac{\langle {\ell }^2\rangle }{6T\left(1-\alpha \right)}\left[1+\left(2\frac{{\langle \ell \rangle }^2}{\langle {\ell }^2\rangle }-1\right)\alpha \right],$$ (3)

where 〈ℓ〉 and 〈ℓ²〉, are the mean run length and mean-squared run length, respectively, T = 〈τ〉 = 1/ω is the mean run-time, and α = 〈cosθ〉 is the mean projection of adjacent bonds. This is achieved by equating the mean-squared displacement of a cell in its random walk trajectory to the mean end-to-end distance of an N-link polymer chain with variable uncorrelated bond lengths and angles, and interpreting N as t / 〈τ〉 (48, 49).

Extending this framework to diffusion in a homogeneous porous medium, characterized by an average pore size, a, we consider how the statistics of runs and tumbles are modified with respect to that in bulk. First, we note that the tumbling frequency, ω, remains unchanged. Indeed, collisions with the pore walls do not result in increased tumbling frequency; unlike gaseous particles in a confined geometry, bacteria do not reflect off of boundaries. This frequency is a property of the active particle and is determined by the parameters of the intracellular chemotaxis network and motor response, independent of the geometry of the external medium. Rather, we assume that a running bacterium that encounters a boundary wall remains trapped, idling until a tumble reorients it, as directly observed by Wolfe and Berg (5) in studying the motion of individual cells in agar. In this way, the mean run length is modified, according to the following:

$$\langle \ell \rangle ={\int }_0^{\infty }R\left(\tau \right)\left[v\tau u\left(a-v\tau \right)+au\left(v\tau -a\right)\right]d\tau ,$$ (4)

where the unit step function u(t) is defined as u(t) = 0 for t < 0 and u(t) = 1 for t ≥ 0. We find that

$$\langle \ell \rangle =\frac{v}{\omega }\left(1-e^{-x}\right),$$ (5)

and

$$\langle {\ell }^2\rangle =\frac{2v^2}{{\omega }^2}\left[1-\left(1+x\right)e^{-x}\right],$$ (6)

with the dimensionless parameter, x = ωa/v. Hence, the diffusion coefficient becomes the following:

$$D=\frac{va}{3\left(1-\alpha \right)}\frac{1}{x}\left[1-\left(1+x\right)e^{-x}+\alpha e^{-x}\left(e^{-x}-1+x\right)\right].$$ (7)

Previous works on diffusion of bacterial cells in confined spaces (50, 51, 52, 53, 54) have adopted a kinetic gas approach, assuming bacteria behave as diffusing gaseous particles, and collisions with boundary walls are equivalent to hard particle-particle collisions. Of direct relevance, work on migration of chemotactic bacteria in soft agar (55) has addressed the role of gel concentration on the chemotactic sensitivity and diffusivity of cells, also treating the tumbling rate as being enhanced because of collisions with the agar matrix. Other related works (56, 57) consider general strategies for chemotaxis as a biased random walk, highlighting the fact that different assumptions about the microscopic details of the random walk process give rise to distinct diffusion equations.

For a gas diffusing in a capillary tube, Pollard and Present (58) derive a rigorous solution, which in the low pressure limit is in agreement with the Knudsen result (59), where momentum transfer takes place predominantly in collisions with the tube walls. The high pressure limit of their result yields the expected self-diffusion coefficient from kinetic theory. Their result is consistent with the analysis from Bosanquet (58), where the random walk trajectory of a molecule in a tube is terminated either by collisions with other molecules or with the tube wall, and the frequencies of the two types of collisions are taken to be additive. In terms of the mean free paths associated with particle-particle and particle-wall collisions, 〈ℓ_g〉 and 〈ℓ_w〉, respectively, the frequencies are related as follows:

$$v/\langle \ell \rangle =v/\langle {\ell }_g\rangle +v/\langle {\ell }_w\rangle .$$ (8)

The diffusion constants associated with each of these steps are assumed to be proportional to v times the mean step size as follows:

$$1/D=1/D_g+1/D_w,$$ (9)

where D_g = 〈ℓ_g〉v/3 and D_w = 〈ℓ_w〉v/3 = av/3; a is the capillary diameter; and D_g and D_w correspond to the high and low pressure limits, respectively. An important distinction between our analysis and previous work on bacterial motion in porous media based on this description is that cell-boundary interactions are not treated as hard sphere-hard wall collisions; rather, a running cell idles at an obstacle until the next tumble reorients it.

To highlight this distinction, it is informative to consider limiting cases of our general result (Eq. 7). In the limit of large pore size (a≫v/ω), we find that the diffusion constant approaches the value in the bulk is the following:

$$D=\frac{1}{3\left(1-\alpha \right)}\frac{v^2}{\omega }=\frac{1}{3\left(1-\alpha \right)}v\langle \ell \rangle .$$ (10)

In the limit of small pore size (a≪v/ω), it becomes the following:

$$D=\frac{1}{6}\frac{\left(1+\alpha \right)}{1-\alpha }\omega a^2,$$ (11)

which differs from the Knudsen limit, D_K = av/3 for a kinetic gas at low pressure (52). For a bacterium, the mean squared displacement in this limit, a², occurs during a time 1/ω, rather than a / v (≪1/ω), because it remains idling at the boundary until a new tumble. We note that because the Knudsen limit is independent of tumbling frequency, it does not capture the response of the Δche strain in agar assays. Were it a correct description of bacterial diffusion in confined geometries, straight-swimming strains would spread in agar assays with D∼10−50 μm²s⁻¹ for a∼1−5μm and v∼30μm/s. On the contrary, for chemotaxis gutted mutants of various bacterial species, there is very little expansion of the swim ring with time, because straight swimmers unable to tumble remain obstructed in pores.

This linearly increasing functional dependence of the diffusion constant on the tumbling frequency in the small pore limit (with other dependences, namely the tumble angle distribution and directional persistence, held fixed) is a unique prediction of our model, not captured by other theoretical descriptions of bacterial diffusion in porous media. (Of direct relevance, in Croze et al. (55), the diffusion constant in agar is inversely proportional to the effective tumbling frequency, ω_eff, which is taken to be a product of the intrinsic tumbling frequency, ω, and a phenomenologically imposed function of the agar gel concentration, C, given by ω_eff = ω(1+f(C)), where by ansatz, f(C) = exp[(C−C₁)/C₀], and C₁, C₀ are constants. This result has the correct limiting behavior for the nonspreading phenotype of hypertumbling mutants with large intrinsic tumbling frequency, and captures the divergence of the diffusion constant in bulk for chemotaxis-deficient cells with zero intrinsic tumbling frequency. However, it also diverges for straight-swimming cells in the porous environment of agar assays, where in fact there is no diffusive spread. Correspondingly, the trend predicted in agar assays with increasing intrinsic tumbling frequency would be that of decreasing migration rate, in contrast with the observed trend for small tumbling frequencies (5).)

Our theoretical result is qualitatively supported by Wolfe and Berg’s (5) observation of increasing migration rate with increasing isopropyl-beta-D-thiogalactopyranoside concentration in the chemotaxis gutted strain with CheY expression under control of the lactose promoter. Wolfe and Berg showed that the fraction of time tethered cells of this strain spun clockwise increased with increasing isopropyl-beta-D-thiogalactopyranoside concentration, as did the fraction of time that cells tumbled, and thereby concluded that the migration rate increased with increasing tumbling frequency. Although below we make connection between the small pore limit of our theoretical result and diffusion constants inferred from measurements of swim ring expansion rates of cms mutants, similar experiments to those of Wolfe and Berg probing diffusion of bacterial cells in agar assays at successively increasing tumbling frequencies are required to quantitatively establish the linear dependence predicted by Eq. 11.

Considering limits of our general result in terms of the tumbling frequency, the hypertumbling phenotype is obtained for x = ωa/v≫1, given by Eq. 10, leading to D→0 as ω→∞; this limit is satisfied by incessantly tumbling cells (ω→∞) for finite pore size, a, as well as in bulk where a→∞. The smooth-swimming phenotype is described separately in the large pore limit by Eq. 10 (x = ωv/a≫1, obtained by requiring a→∞ faster than v/ω→∞ as ω→0), and in the small pore size limit by Eq. 11 (x = ωv/a≪1 obtained for ω≪v/a). Hence, in the large pore or bulk limit, for smooth-swimming cells D→∞ as ω→0, as expected for cells that do not tumble in bulk, whereas in the small pore limit, D→0 as ω→0, also as expected for cells trapped in agar.

With the direction of cell movement given by $+\hat{z}$, we introduce the tumble angle distribution W(θ) where θ is the polar angle. For E. coli it has been measured in bulk fluid (60) and is well approximated by W(θ) = $(1/2)$(1+cosθ) (61), giving the following:

$$\alpha =\langle \text{cos}\theta \rangle ={\int }_0^{\pi }W\left(\theta \right)\text{sin}\theta \text{cos}\theta d\theta =1/3.$$ (12)

As measured for Pseudomonas putida, W(θ) = $(1/16)$(3 + 15cos²θ), giving α = 0 (53). For concreteness, we use these values obtained from measured distributions in bulk to examine the dependence of D on other governing physical parameters, given by a, v, and ω. However, we note that in confined geometries, interference of the bacterial turning mechanism with geometrical constraints could give rise to a different tumble angle distribution with respect to that in bulk, and steric inhibition at internal obstacles may further modify the directional persistence, α, with respect to its bulk value. In the Supporting Material, we discuss the dependence of D on α and refinements to the derivation of the diffusion constant, accounting for steric inhibition at collisions are presented.

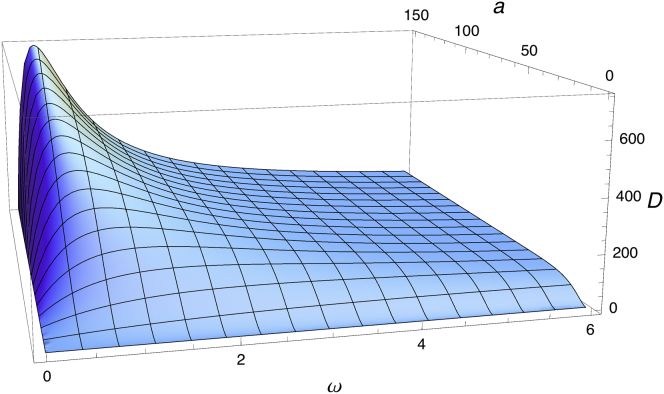
In Fig. 2, the dependence of D on ω and a is plotted for v = 30 μms⁻¹ and α = 1/3. This figure shows a maximum in the diffusion coefficient, realized when the bacterium runs until almost reaching a boundary, but tumbles before idling, corresponding to x = ωa/v∼1. As discussed above, as ω→0, D vanishes as expected given the nonexpanding phenotype of straight-swimming strains trapped in pores, and as ω→∞, D approaches zero as expected for hypertumbly cells that also do not advance appreciably. Finally, D approaches the value in bulk fluid (which depends on ω) as a increases. In the Supporting Material, we plot a similar dependence of D on ω and v at fixed a.

Figure 2.

The diffusion coefficient D (in units of μm²s⁻¹), as given by Eq. 7, as a function of ω (in units of s⁻¹) and a (in units of μm) for fixed v = 30 μms⁻¹ and α = 1/3. For free diffusion in bulk fluid, bacterial diffusion constants are ∼200 to 1900 μm²s⁻¹ (25, 52).

Connection between diffusion, tumbling, and motility defects in A. tumefaciens cms mutants

Our theoretical model of bacterial diffusion in a porous environment demonstrates how spontaneous mutations that restore tumbling in otherwise straight-swimming parent strains lead to diffusive spread in agar assays. Indeed, in Fig. 3, A–E, we show results of single-cell, two-dimensional tracking studies of A. tumefaciens in bulk fluid for wild-type, chemotaxis deficient (Δche), class I (FlgE mutation), class II (FliK mutation), and class III (MotA mutation) cell types, directly demonstrating that class I to III mutations restore reorientations (see Mohari et al. (6), for details of tracking analysis). Given that the motility paradigm shared by A. tumefaciens and related species is less well characterized than that of E. coli, the biophysical basis of how the motility defects genetically characterized by Mohari et al. (6) generate effective tumbles remains unknown. Therefore, in this section, we make connection between previous computational results on flagellar bundling and unbundling and the generation of tumbles by the class I to III cms mutants in A. tumefaciens, central to their migration in agar assays.

Figure 3.

Single-cell tracking of A. tumefaciens strains. Two-dimensional swimming trajectories in fluid for the different strains are shown. (A) Δche, (B) wild-type, (C) class I (flgE), (D) class II (fliK), and (E) class III (motA). The starts and ends of tracks are denoted by arrows and dots, respectively. The duration of each track is shown. See also Mohari et al. (6) for other representative trajectories. To see this figure in color, go online.

Reigh et al. (14) computationally investigated the stability of a flagellar bundle (consisting of three polar flagella) using a hybrid approach that combines molecular dynamics simulations of bacterial flagellar filaments, using Rhizobium lupini structural parameters and a mesoscale hydrodynamics simulation method for the fluid. We note that Rhizobium lupini has been renamed as Agrobacterium sp. H13-3, and is highly related to Agrobacterium tumefaciens (62). They determined hydrodynamic interactions between flagella, short-range volume exclusion and flagellar flexibility to be key physical factors governing their synchronization and bundling. For small differences in adjacent motor torques, they find bundle formation to be robust. As the torque difference increases, a phase lag in flagellar rotations occurs, followed by intermittent slippage and finally unbundling. In earlier work, they showed that synchronization starts at the fixed ends of the flagella and propagates to the tips (17). At higher torques the bundles were found to be tighter, leading to marginally higher swimming efficiency (14). In the slippage and unbundled states, the force and torque balances on the cell body determine its new orientation (17).

Relating these simulation results and the class I and II pseudotaxis mutants identified in Mohari et al. (6), the flexibility and length of the flagellar hook are likely to be important physical parameters affecting the hydrodynamic interactions between flagella. For bacteria such as A. tumefaciens possessing complex flagellar filaments that are more rigid than homogeneous filaments such as for enteric bacteria, the physical properties of the hook may be especially important in driving flagellar bundling and unbundling. We speculate that for these mutant classes, the degree to which the flagella are able to synchronize and form a bundle is affected, as are the resulting forces and torques on the cell body that determine its reorientation angle when a bundle is disrupted.

For the class III mutant involving MotA, it has been shown that electrostatic interactions between this stator protein and the rotor protein FliG are important for bacterial flagellar motor torque generation (7, 63, 64, 65, 66). Given that rotational slowing is the proposed mechanism for tumbling in members of the family Rhizobiaceae with unidirectional (CW-only) motors, it is possible that in class III mutants, the speed of rotation of flagellar motors is altered in such a way that bundling is disrupted, leading to a nonzero tumbling frequency and hence the pseudotaxis phenotype. We note that in a class III mutant, the cell speed is also diminished with respect to wild-type, consistent with the role of MotA in powering the flagellar motor (6).

These computational results suggest how the observed, spontaneous motility defects influencing flagellar bundling and unbundling may give rise to effective tumbles in A. tumefaciens cms mutants, and hence the pseudotaxis phenotype. They also point to how details of the flagellar unbundling process determining the degree of directional reorientation at a tumble may differ among the mutant classes, giving rise to differential diffusive spreading. Further experimental studies are needed to quantify the effects of the identified motility defects in the tumbling process through measurements of individual flagellar rotation and unbundling dynamics of multiple flagella. These studies on cms mutants will also serve to better characterize the biophysical mechanisms underlying the motility paradigm in A. tumefaciens and related species.

Analysis of swim ring assays

To make connection with motility agar assays, in addition to diffusion, we must account for bacterial growth. In the absence of chemotaxis, we take the bacterial density, ρ(r,t), to satisfy the following:

$$\frac{\partial \rho }{\partial t}=D{\nabla }^2\rho +\lambda \rho ,$$ (13)

where λ is the growth rate. Recent work has investigated patterns of growth and gene expression of chemotactic bacterial populations in space and time, using as a model system expanding populations of E. coli on soft agar plates with galactose as a nutrient source (67). Here, we neglect the spatial dependence of the growth rate in the expanding disc of cms mutants, assuming λ to be uniform and constant (i.e., not limited by nutrient). Similar future assays can be used to establish the spatiotemporal dependence of growth in cms mutants, where comparison with the chemotactic strains will help elucidate how bacteria evolve to balance growth, chemotaxis, diffusion, and survival.

By considering the simplified model of growth coupled to diffusion given by Eq. 13, we are able to write an analytical solution for ρ(r,t). For N₀ bacteria inoculated at the origin at time t = 0, we obtain the following:

$$\rho \left(r,t\right)=\frac{N_0}{4\pi Dt}\text{exp}\left(-\frac{r^2}{4Dt}\right)\text{exp}\left(\lambda t\right).$$ (14)

Assuming the designation of the swim ring boundary, $\mathcal{R}\left(t\right)$, is made on the basis of an absolute threshold of cell density, ρ_th (as visually determined by the experimenter), and solving $\rho \left(\mathcal{R},t\right)$ = ρ_th, we find the following:

$${\mathcal{R}}^2\left(t\right)=4D\lambda t^2-4Dt\text{ln}\left(4\pi {\rho }_{0}Dt\right),$$ (15)

where ρ₀ = ρ_th/N₀. Note that the leading behavior for $\mathcal{R}\left(t\right)$ is linear in t, in agreement with the observed linear expansion of the swim ring radius in time. As commented by Wolfe and Berg (5), this dependence deviates from the expected diffusive spread with t^1/2 time dependence as a result of cell division.

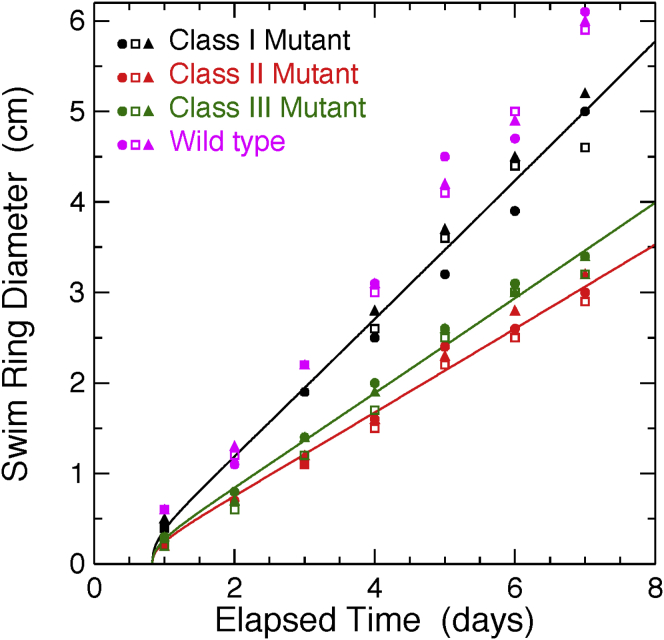
For A. tumefaciens, the growth rate in minimal media is given by λ ≈ ln2/3 h = 6.4×10⁻⁵ s^–1. Using this value, in Fig. 4, we show the swim ring data (for C = 0.25% motility agar) and fits according to Eq. 15. The fitted values of diffusion constants for class I to III mutants are D_I = (7.9 ± 0.2)μm²/s, D_II = (2.9 ± 0.1)μm²/s, and D_III = (3.7 ± 0.1)μm²/s. We note that the fit results for the diffusion constants, D_I−III, are insensitive to the fit value for ρ₀.

Figure 4.

Fits to swim ring expansion as a function of time for the three classes of mutants, according to Eq. 15. We find D_I = (7.9 ± 0.2)μm²/s, D_II = (2.9 ± 0.1)μm²/s, D_III = (3.7 ± 0.1)μm²/s, and ρ₀ = (1.1 ± 1.0) × 10⁻³μm⁻², where ρ₀ is constrained to be the same for all three fits. For comparison, the swim ring expansion for wild-type is also included, showing that the cms mutants perform comparably with the chemotacting wild-type in agar (to within factors of ∼0.5 to 0.8 at 1 week). Three trials are plotted for each mutant class.

To compare fit values with our theoretical result for diffusion in the small pore limit (Eq. 11), we use the mean values of the tumbling frequencies determined by Mohari et al. (6) in the free-swimming tracking assays. The mean pore size, 〈a〉, is estimated from previous work on atomic force microscopy analysis of agarose gels (68, 69) at higher concentrations. Agarose gel is characterized as a complex, heterogeneous fibrous matrix with a wide pore size distribution that broadens with decreasing gel concentration. We estimate the mean pore size to be in the range 740 nm < 〈a〉 < 4800 nm for C = 0.25% (see the Supporting Material). We note that this range is consistent with observations by Wolfe and Berg (5) of the mean run lengths in 0.20 to 0.35% agar, ranging from less than one to several micrometers in length. In Table 1, we give the predicted ranges for values of D_1−III for turn angle distributions previously measured in bulk, giving α = 0 (for P. putida) and α = 1/3 (for E. coli), as previously discussed. The relative error on the theoretical value of the diffusion constant (σ_D/D) given the statistical uncertainty on the measured tumbling frequencies from Mohari et al. (6) is also shown.

Table 1.

Diffusion Constants for Class I to III A. tumefaciens Mutant Strains

Class	ω (s−1)	Predicted Range (α = 0) (μm2 / s−1)	Predicted Range (α = 1/3) (μm2 / s−1)	σD/D	Fit Result (μm2 / s−1)
I	(0.8 ± 0.1)	(0.07 < DI < 3.1)	(0.15 < DI < 6.2)	0.12	7.9 ± 0.2
II	(1.0 ± 0.1)	(0.09 < DII < 3.9)	(0.18 < DII < 7.6)	0.10	2.9 ± 0.1
III	(0.6 ± 0.1)	(0.05 < DIII < 2.3)	(0.11 < DIII < 4.6)	0.17	3.7 ± 0.1

We note that the values of D obtained from fits to the agar assays are generally consistent with the theoretical ranges. For class I, the fit result is slightly greater than the predicted values. The agreement is improved for larger values of tumbling frequency and pore size, both of which possess broad distributions. Also, because D is a monotonically increasing function of α, greater directional persistence in the tumble angle distribution of class I mutants in agar would lead to a larger theoretical value for the diffusion constant, further improving this agreement. We also note that although class II mutants have a higher mean tumbling frequency, D_II is smaller than D_I and D_III, suggesting that in agar, class II mutants have less directional persistence than the other two mutant classes. Indeed, as discussed above, details of the flagellar unbundling process determining the tumble angle distribution could be different for each mutant class.

An open question that emerges is how the values of the governing biophysical parameters in a porous environment differ from those in bulk fluid used in our fits. In the Supporting Material, we discuss how steric inhibition may modify the tumbling frequency and directional persistence. Furthermore, the tumble angle distribution itself may differ for cells swimming in bulk fluid relative to that in a porous environment where the scale of confinement is comparable to the cell size and smaller than the flagellar length. For intermediate and large pore sizes, where D also depends on the cell speed, measurement of v in the porous medium is required as input into the theoretical result for the diffusion constant. Therefore, to fully corroborate the agreement between experiment and theory, the comparison in Table 1 must be carried out using parameters obtained for a given porous medium, informed by experimental approaches such as those quantifying the motility of bacterial cells in microfabricated channel arrays (70) and in polymer solutions (71) using high-throughput microscopy methods (72, 73), as well as theoretical and computational studies of flagellated motility in confined geometries (74, 75, 76). For motion of bacteria in porous media filled with biological or environmental fluids containing proteins and other polymers, viscoelastic effects on motility parameters must also be considered (71, 77, 78, 79, 80, 81, 82).

Discussion

Our theoretical analysis of the random walk of bacterial cells in a homogeneous porous medium quantifies the dependence of the diffusion constant on the governing physical and biophysical parameters. The average pore size, tumbling frequency, cell speed, and directional persistence arising from the tumble angle distribution. As such, it unifies the phenomenology of pseudotaxis achieved via different classes of mutations in the motility apparatus of various bacterial species identified experimentally in earlier studies (5, 6, 35, 36, 41). Importantly, our model is based on the cell’s intrinsic tumbling mechanism as the biophysical process giving rise to directional reorientation, in contrast with previous treatments based on kinetic gas theory in porous media, whereby the random walk trajectories of diffusing particles are governed by collisions of hard ballistic particles with each other and boundaries. Indeed, as directly observed by Wolfe and Berg (5), a cell encountering internal agar walls is not deflected, but rather idles until a subsequent tumble reorients it. Incorporating idling at pore walls constitutes a fundamentally new microscopic mechanism of bacterial diffusion in porous media, to our knowledge, and the resulting theoretical model offers an understanding of existing experimental observations, not captured by previous models, as well as suggestions for future experiments.

Although we show that values of the diffusion constant obtained from fits to the swim ring expansion in agar assays of A. tumefaciens cms mutants are generally consistent with our theoretical result in the small pore limit, we note that the diffusion constant is a coarse discriminant of the agreement between experiment and theory. Further experimental studies of single-cell motility in porous media are required to quantify the cell’s motion in environments where the spatial scale of confinement is comparable to the size of the cell and the flagellar bundle. Explicit measurement of biophysical parameters (tumbling frequency, directional persistence, cell speed) that reflect the presence of steric constraints in a given porous medium as input into the theoretical result for the diffusion constant will allow for more direct corroboration.

Our findings suggest that details of the tumbling process can be adapted for effective migration through a given microenvironment with characteristic pore size. Indeed, we find that with other motility and environmental parameters held fixed, the diffusion constant is maximal at a given tumbling frequency. Supporting this, recent work has highlighted the difference in the chemotactic response of bacterial cells in liquid media versus agar from the standpoint of optimal concentrations of chemotaxis proteins ([CheR, CheB]) that determine the adaptation rate and tumbling frequency (83).

Our results have direct relevance to biomimetic engineering of microrobots emulating bacteria, for controlled navigation and cargo delivery in applications such as medical diagnosis, drug delivery, and bioremediation (84, 85, 86, 87). In many cases, these engineered active swimmers utilize flagellar-based motility for swimming in the fluid-filled porous environments that constitute human tissues, biofilm exopolymeric matrix and soil. Our work suggests that details of the run-and-tumble dynamics, through the tumbling frequency and tumble angle distribution, can be tuned to the microarchitecture of the environment to optimize the spread of biologically inspired synthetic swimmers in various habitats.

Author Contributions

N.L., B.M., C.F., and S.S. designed the research, performed the research, and wrote the article.

Editor: Charles Wolgemuth

Supporting Citations

References (88, 89, 90, 91, 92, 93, 94, 95, 96, 97) appear in the Supporting Material.