Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2016 Jan 5;110(1):147–156. doi: 10.1016/j.bpj.2015.11.030

Shock Wave-Induced Damage of a Protein by Void Collapse

Edmond Y Lau 1,∗, Max L Berkowitz 2, Eric Schwegler 1
PMCID: PMC4806186  PMID: 26745418

Abstract

In this study, we report on a series of molecular dynamics simulations that were used to examine the effects of shock waves on a membrane-bound ion channel. A planar shock wave was found to compress the ion channel upon impact, but the protein geometry resembles the crystal structure as soon as the solvent density begins to dissipate. When a void was placed in close proximity to the membrane, the shock wave proved to be more destructive to the protein due to formation of a nanojet that results from the asymmetric collapse of the void. The nanojet was able to cause significant structural changes to the protein even at low piston velocities that are not able to directly cause poration of the membrane.

Introduction

Blast-induced mild traumatic brain injury (mBTI) from improvised explosive devices is the most frequent wound occurring from the conflicts in Afghanistan and Iraq (1). It has been estimated that more than 200,000 veterans have had at least one traumatic brain injury (2). Clinical reports and in vivo studies show exposure to a blast can cause mBTI, although how the energy is transmitted to the brain is not well understood (3). Many of our war fighters have reported cognitive problems such as memory loss, difficulty thinking, attention deficits, and mood swings long after the initial injury (4). When a body is exposed to a blast, shock waves are produced resulting in shear forces within the cranium (5). In skull models, cavitation was observed due to shock-bubble interactions and proposed as an injury mechanism (6). Experiments and molecular simulations of bubble-shock interactions have shown that the force generated by bubble collapse is great enough to cause membrane poration (7, 8, 9, 10). Blast-induced poration of the membrane undoubtedly leads to injury and ultimately neuronal death but it does not account for the observed axonal retraction (11). The rapid stretching of axons cause unregulated fluxes in ion concentrations, including an efflux in potassium and influx of sodium from and into the axon that, in turn, cause increased calcium levels (12, 13). The increased calcium levels trigger proteolysis of cytoskeletal proteins and irreversible damage (14). Ionic imbalances likely play an important role in the cellular damage incurred from mBTI. Unfortunately, finding the possible causes of damage to cellular tissue can be difficult and is likely to require a wide variety of techniques to elucidate the underlying mechanism.

Studying the damage caused by poration with experiment can be very difficult, especially below the micron scale. In general, molecular dynamics (MD) with empirical force fields is an approach that allows the simulation of millions of atoms for timescales up to microseconds. MD simulations are routinely used to study atomic-level interactions in exquisite detail (15) and have proven to be an effective tool for aiding in the interpretation of experimental measurements. In particular, MD simulations have been previously used to study the effects of shock waves on membranes (9, 10, 16, 17, 18, 19, 20, 21, 22). Many recent simulations (9, 10, 18) used the momentum-reflecting mirror method (see below) to imitate the motion of a piston to produce shock waves in the system under study. In one of the recent studies, when the piston moved with a velocity above 3900 m/s, the resulting shock wave severely damaged the membrane but reversible damage occurred when piston velocities were below 3000 m/s (18). More recently, MD simulations using all-atom and coarse-grained (several atoms are merged into a single bead) force fields have been used to study the effects of shock wave-induced void collapse on membranes (9, 10). These studies showed impact of a shock wave against one side of the void caused rapid collapse and formation of a nanojet due to the solvent traveling through a low density medium (void). At much lower piston velocities (700 to 1000 m/s), the nanojet was able to readily cause poration of the membrane. These results could have significant consequences, because unregulated or faulty ions exchange between the cell and the environment can lead to cellular disease and death (23). In this regard, molecular simulation can play an important role in elucidating the mechanism of cellular damage by shock waves.

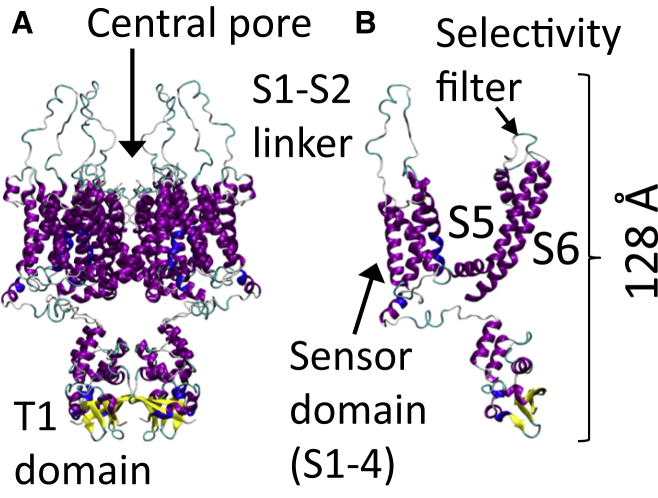
This study focuses on the effects of shock waves on a membrane bound protein. Cell walls are composed mainly of lipids but contain a large number of proteinaceous material that is vital for the normal function of the cell (24). We have performed all-atom MD simulations on shock wave-induced void collapse to determine its impact on an axonal membrane bound protein (voltage-gated potassium ion channel, Kv1.2) (25). Although we are using a Kv ion channel for this study, the results should be applicable to many voltage-gated ion channels because they share similar overall structures (26). Voltage-gated ion channels sense the change in voltage across the cell membrane and respond by allowing specific ions in or out of the cell (27). Among ion channels, the voltage-gated potassium channels (Kv) are the most well-studied members (28). Kv channels allow intracellular potassium ions to leave the cell to return the membrane potential to the polarized state. Failure to release cellular potassium can result in overexcitability of neuron cells and disease. The Kv channels are homotetramers that contain four voltage sensors and a central pore domain. Each monomer contains four transmembrane helices (S1, S2, S3, and S4) that form the voltage sensor domain and two transmembrane helices (S5 and S6) that help form the central pore of this channel (Fig. 1). Additionally, an intracellular soluble domain (T1) is important for proper assembly of the channel and a docking site for the β subunit. Potassium ion channels play an important role in regulating cardiac repolarization, insulin release, and smooth muscle relaxation (28). Additionally, they are associated with diseases such as diabetes, epilepsy, and long QT syndrome.

Figure 1.

Figure 1

Open in a new tab

(A) Structure of the homotetrameric Kv1.2 potassium ion channel (A). (B) Single subunit of Kv1.2, helices S5 and S6 form the central pore of the ion channel. To see this figure in color, go online.

Materials and Methods

All MD simulations were performed using the program GROMACS (version 4.5.5) (29) with the all-atom CHARMM force field (version 36) (30, 31). The voltage-gated potassium ion channel Kv1.2 (Protein Data Bank (PDB): 3LUT) (32) was embedded into the center of a preequilibrated 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC) lipid membrane that has a surface area of ∼320 × 320 Å2. The membrane-protein system was solvated on the extracellular side of the membrane with a TIP3P (33) water box 320 × 320 × 550 Å3 and with a 320 × 320 × 450 Å3 water box on the intracellular side of the membrane using the program PACKMOL (34). Counterions (NaCl) were added to the solution to neutralize the system and to bring the ion concentration to 0.150 M. The final system size was ∼320 × 320 × 1000 Å3 and consisted of 3055 DPPC lipids, 3,290,641 water molecules, 8809 sodium cations, and 8765 chloride anions (10,311,891 total atoms).

The system was energy minimized using the steepest descent algorithm and positional restraints were placed on nonhydrogen atoms of the protein and lipid (Kr = 1000 kJ/mol ⋅ nm2) to prevent large deviations. MD (200 ps run) was performed on the energy minimized system initially using the NVT ensemble with positional restraints. The system was coupled to a thermostat (323 K) using the Berendsen method (35) with a coupling constant of 0.1 ps. The short-range interaction was cut off with a switching function between 8 and 10 Å (36) and the electrostatic interactions were treated with the particle mesh Ewald method using a grid spacing of 1.6 Å (37). A 2 fs time step was used and bonds containing hydrogens were constrained using LINCS (38). The MD simulations were continued using the NPT ensemble with the Nose-Hoover method (39, 40) for temperature coupling (323 K and 0.5 ps) and the Parrinello-Rahman method (41) for pressure coupling (5 ps) at 1 atm. All other parameters were the same as in the NVT simulation. The positional restraints were gradually removed during the dynamics and the system was equilibrated for 4.2 ns.

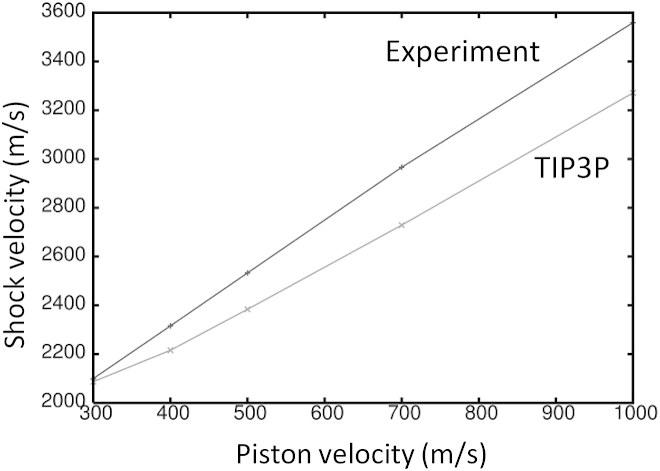
To determine the suitability of the TIP3P water model for shock wave simulations, a rectangular box of water 110 × 110 × 430 Å3 in size was tested. NPT dynamics was performed on the water using the same parameters as in the previous protein-membrane simulation. The final coordinates from the NPT dynamics was used for the shock wave simulation. All shock wave simulations were performed in the NVE ensemble without constraints. The system was periodic only in the XY direction and a time step of 1 fs was used in the simulations to conserve energy. The nonperiodic system required the electrostatics interactions to be treated with a reaction field (42) (reaction-field-zero as implemented in GROMACS 4.5.4 (43)) to better conserve energy. A twin-range cutoff of 10/12 Å was used for the short-range and Coulomb interactions, respectively. The short-range and long-range neighbor lists were cut off at 15 and 20 Å, respectively. Simulating a shock wave propagating through the system was achieved by colliding the system with a solid wall consisting of carbon atoms with a density of 25 atoms/nm3 placed at Z = 0 and spanned the XY plane. The Lennard-Jones interaction between the wall and all other atoms were treated with a 9-3 potential (44). Initially, all atoms were translated +20 Å along the Z axis to create a gap between the water and solvent to avoid unfavorable interactions. All atoms in the system were given an additional (piston) velocity in the –Z direction causing the system to collide with the wall (reflecting the momentum) and generated a shock wave traveling in the opposite direction (+Z). This procedure is equivalent to having a massive piston pushing the system along the –Z direction. This method is relatively simple and similar to experiments that use a high-speed impactor on a stationary target (45). A different method for generating a shock wave was used by Koshiyama et al. to study water penetration through a membrane (16). In their study, a segment (slab) of water was given an excess velocity resulting in a shock impulse. This method requires a large number of atoms to produce a shock wave. We observed that the calculated shock wave velocities of TIP3P water are in reasonable agreement with experiment (46) for piston velocities ranging from 300 to 1000 m/s (Fig. 2). The deviation between the simulated and experimental shock wave velocities was <10% for all piston velocities tested.

Figure 2.

Figure 2

Open in a new tab

Shock wave velocity of TIP3P water and experiment as a function of piston velocity.

To study the effects of a shock wave on the protein-membrane system, the coordinates from the equilibrium NPT dynamics were used as the starting coordinates for the shock wave simulations. Five shock wave simulations were performed using the coordinates from the equilibrium dynamics at 3.8, 3.9, 4.0, 4.1, and 4.2 ns. The same protocol used previously to generate a shock wave was used for the protein-membrane system. A piston velocity of 1000 m/s was added to all the atoms to produce the shock wave.

The effect of shock wave-induced void collapse on the protein-membrane system was studied by creating a 100 Å radius void by the membrane. Removing a 100 Å radius sphere of water from the system reduced the amount of water by ∼4% (∼140,850 water molecules were removed). The edge of the void was within 20 Å of the membrane. The same protocol used to generate a shock wave in water was used for the protein-membrane system. Piston velocities of 1000, 500, 400, and 300 m/s were added to all atoms to produce the shock wave. To determine the reproducibility of the results, five simulations at each piston velocity (500, 400, and 300 m/s) were performed. The initial coordinates for these simulations were taken from the equilibrium dynamics at times 3.8, 3.9, 4.0, 4.1, and 4.2 ns. We observed that the results from five repeated simulations were very similar in each case when repeated simulations were performed; therefore, we report here results from one of the simulations.

A recent study showed that void collapse (without a shock wave) in close proximity to a membrane causes severe deformation to the lipid bilayer (47). To investigate if damage to the protein could occur by this mechanism, we continued the equilibrium NPT dynamics without a shock wave but containing the 100 Å radius void. The system was periodic in all directions and all parameters used for the NPT dynamics were also used for this simulation. This simulation was performed for a total of 2 ns.

The α-helix content of the protein was monitored with the program STRIDE (48) that uses a hydrogen bond criteria and dihedral angle potential to determine the secondary structure. The pore radius of the ion channel was determined with the program HOLE (49). This program finds the channel cavity from a user-defined point and vector (direction) by moving the point on a plane normal to the vector to find the largest sphere that can be accommodated without overlap with the van der Waals surface of any atom. The shape parameter (S) was used to determine the overall shape of the protein (50). The shape parameter measures the deviation from a spherical geometry and ranges in value from −0.25 to 2. Negative values refer to oblate structures and positive values correspond to prolate structures. The root mean-squared deviations (RMSDs) were performed with VMD (51) and the density profiles and distance matrices were calculated and rendered with programs within GROMACS.

Results and Discussion

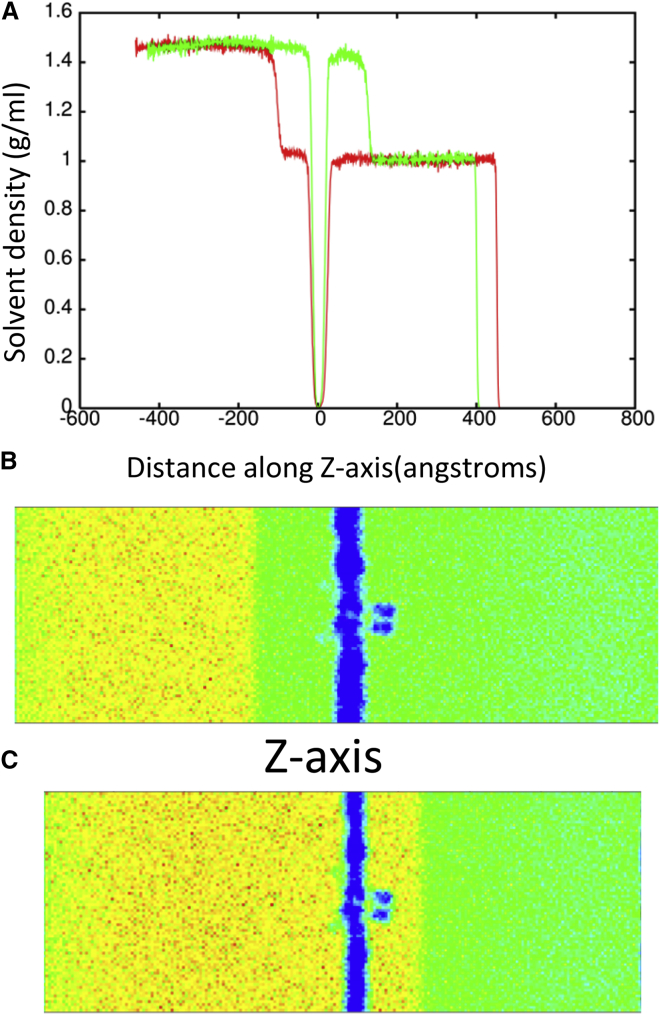
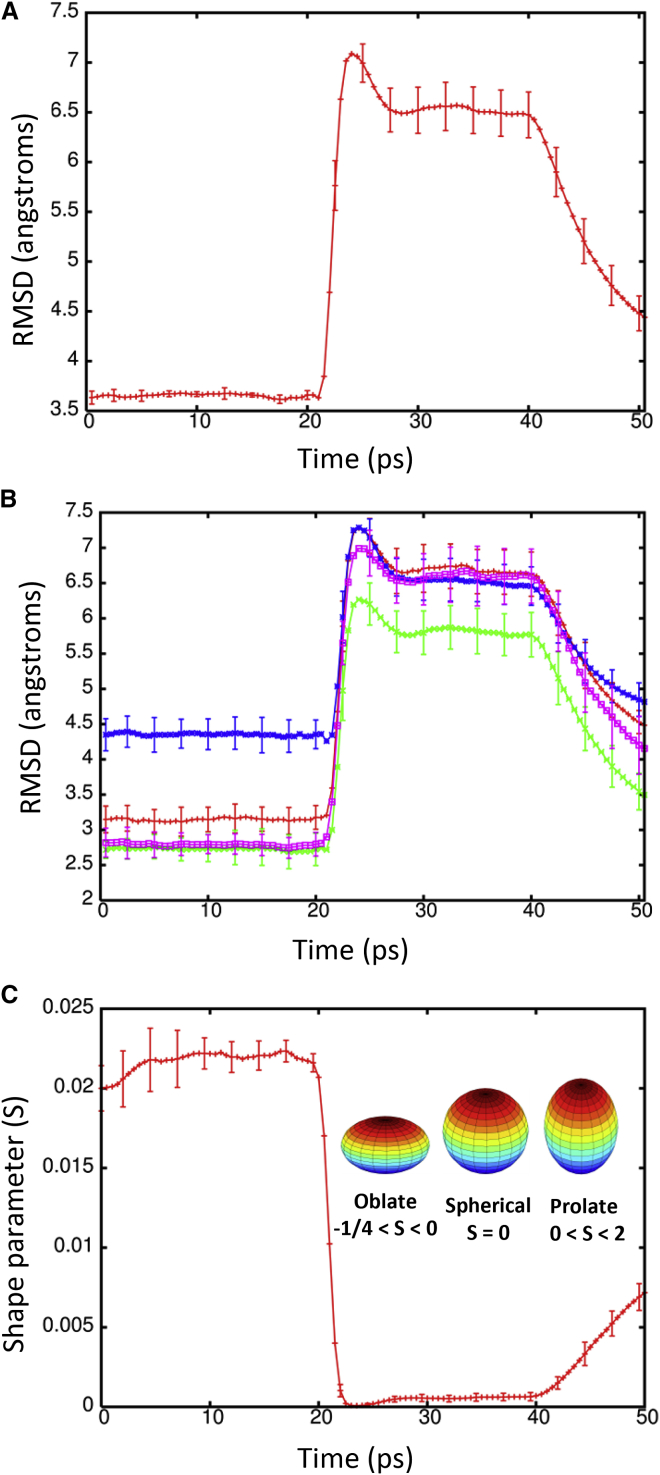
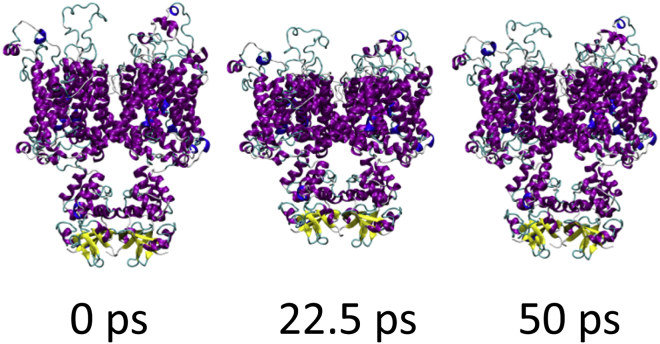
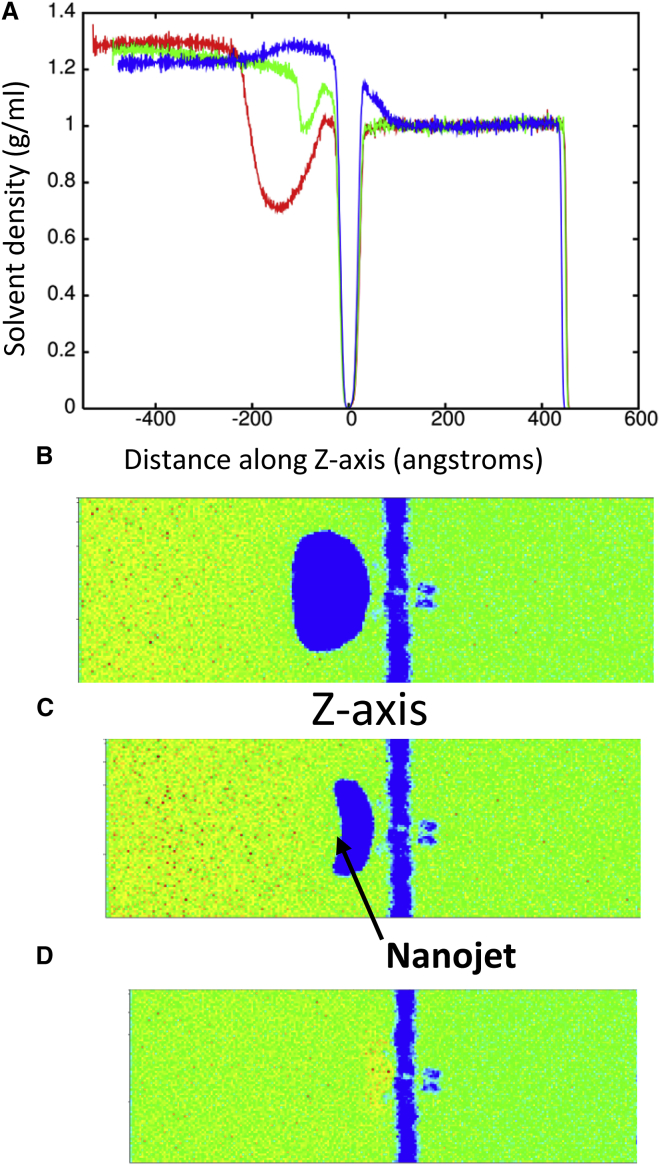
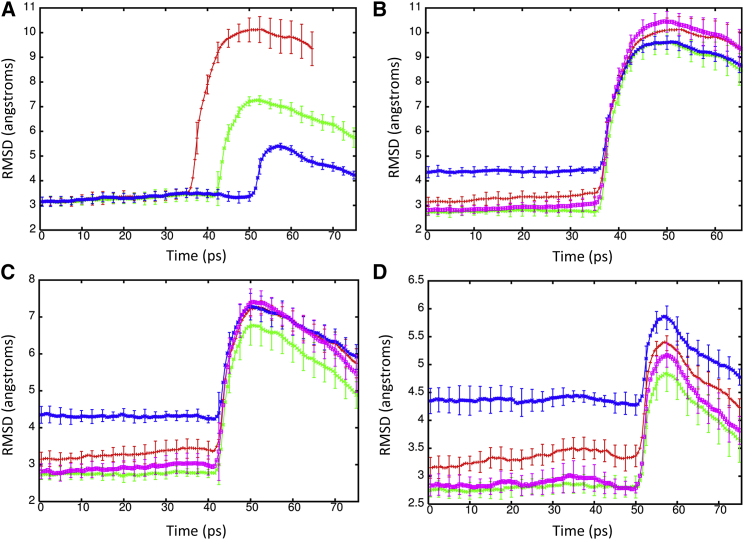
To determine the effect of a shock wave on the structure of the Kv1.2 ion channel, the system was moved at a piston velocity of 1000 m/s into a solid wall to produce the planar shock wave. When the shock wave passes through the protein-membrane system, it caused temporary compression of these entities as the solvent density jumps from 1 g/ml to ∼1.45 g/ml (Fig. 3). The average phosphorous to phosphorous distance between the inner and outer leaflets of the DPPC membrane is 40.4 Å before the shock wave. The initial helical content of Kv1.2 is 58.5% (912 out of 1560 residues). The RMSD of the backbone atoms (N, C, and CA) relative to the crystal structure (PDB: 3LUT) is most affected when the shock wave initially impacts the structure at ∼20 ps (Fig. 4 A). The RMSD of the protein backbone jumps from 3.6 Å to almost 7 Å during impact. Residues 184 to 219 (S1–S2 linker) in each subunit were excluded from the RMSD calculation because this is a long loop region that is highly flexible and normally absent in most crystal structures of Kv1.2 (52). The individual subunits of Kv1.2 react in the same manner to shock waves as the complex (Fig. 4 B). Chain C of the ion channel has a higher RMSD relative to the other subunits due to having the first turn of helix S4 unwind and having the S3–S4 linker change position (see Fig. S1 in the Supporting Material). If these residues (270 to 290) are excluded from the fitting, the RMSD for chain C is reduced by ∼0.5 Å. The average phosphorous to phosphorous distance of the membrane contracts to 31.6 Å and the helical content of Kv1.2 reduces slightly to 57.8 ± 0.6% at 25 ps. Interestingly, as the shock wave progresses through the system and the solvent density decreases, the protein structure begins to resemble the crystal structure again.

Figure 3.

Figure 3

Open in a new tab

(A) Shows the solvent density during shock wave simulation (piston velocity 1000 m/s) at 17 ps (red) and 25 ps (green). (B) and (C) Show the progression of the shock wave in the system before (17 ps) and after (25 ps) impact with the membrane shown in blue. The blue regions show an absence of solvent density (membrane and T1 domain). The Z axis is perpendicular to the membrane. To see this figure in color, go online.

Figure 4.

Figure 4

Open in a new tab

(A) RMSD of the backbone atoms (N, C, and CA) of Kv1.2 during the shock wave simulation (1000 m/s) relative to the crystal structure PDB: 3LUT. (B) RMSD for the individual subunits A (red), B (green), C (blue), and D (violet) of Kv1.2. (C) Shape parameter (S) for the protein complex during the shock wave simulation. To see this figure in color, go online.

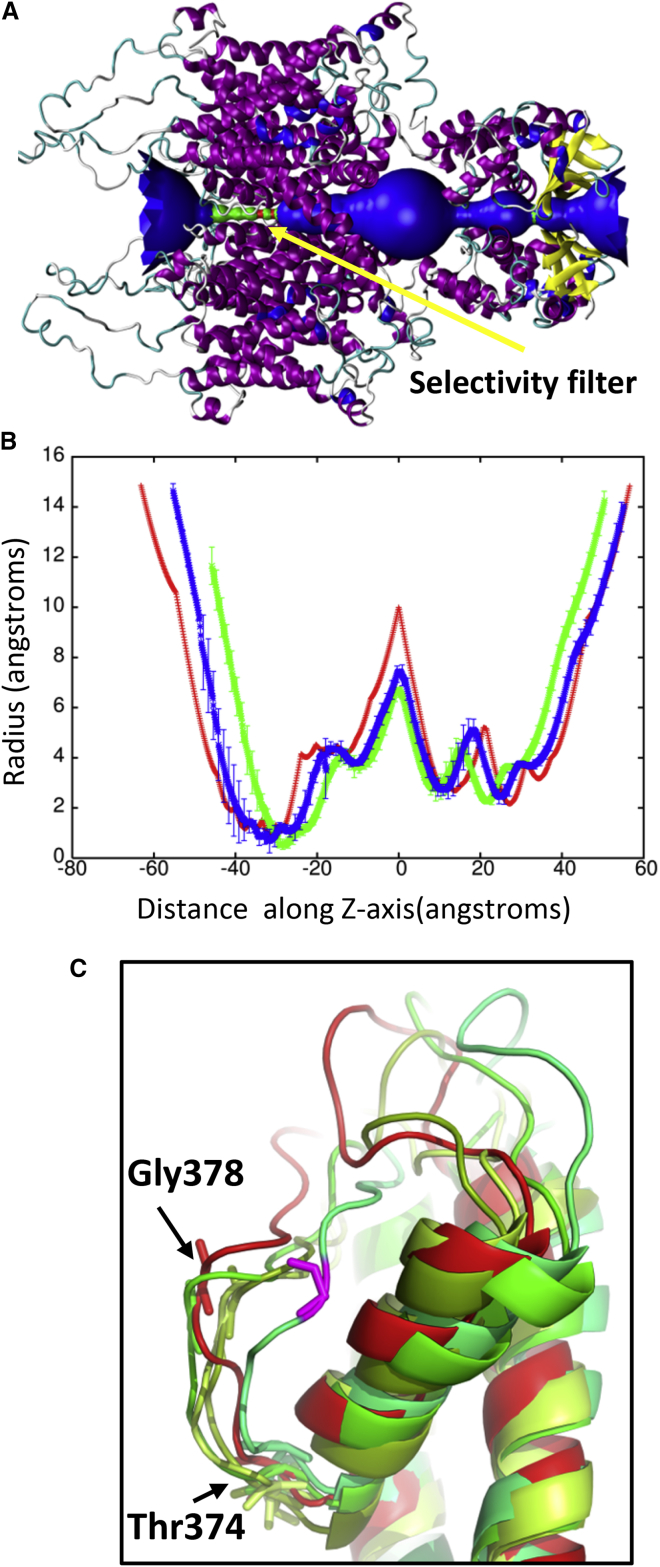
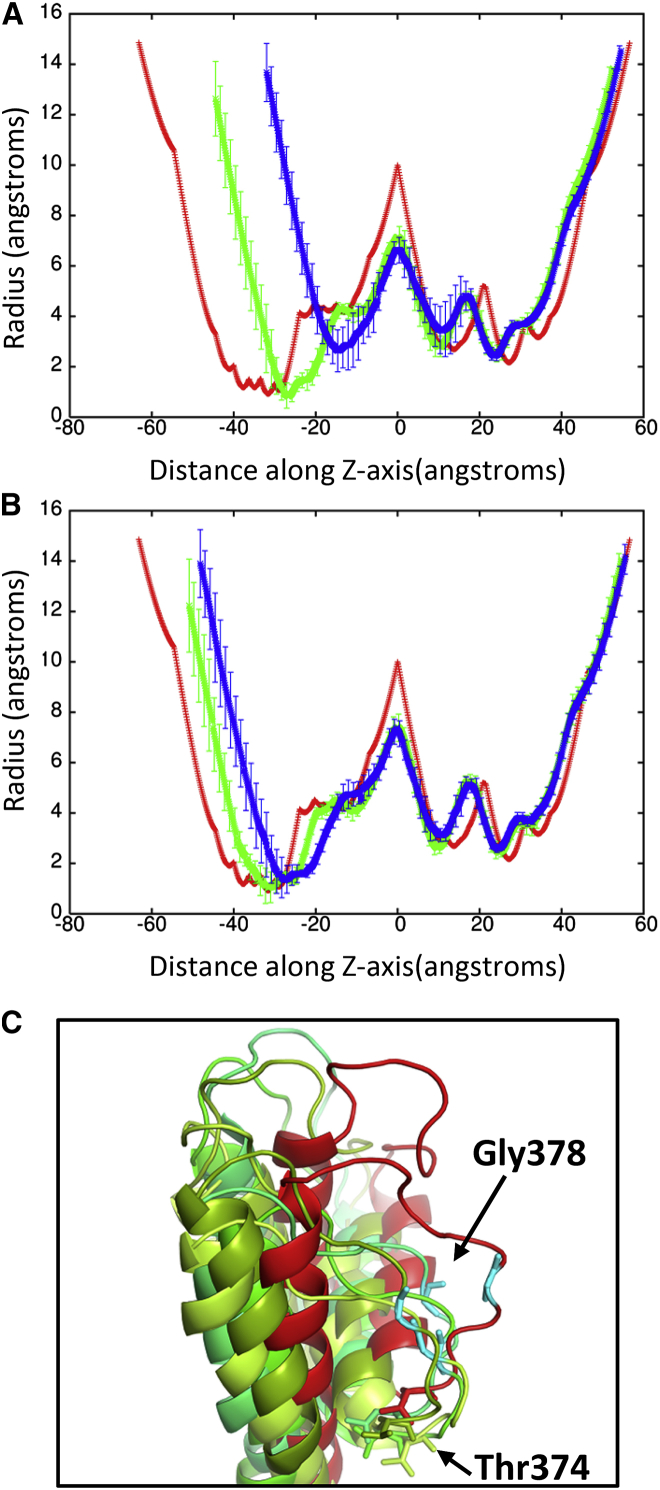
The RMSD lowers to ∼4.5 Å relative to the crystal structure at 50 ps. The application of high pressures is known to cause proteins to denature and is a common method for studying protein folding and stability (53). Because the shock wave passes through the system quickly (the wavefront leaves the system at 33 ps), the change in pressure does not significantly affect the protein structure (Fig. 5). The protein begins to approach its previous ternary structure as the solvent density decreases after 40 ps. The helical content of the ion channel is 57.5 ± 1.1% at 50 ps and is almost identical to the starting structure. The shape parameter (S) measures the deviation from a spherical geometry (Fig. 4 C). A plot of S for the protein shows the compression of the protein at ∼20 ps into a spherical shape but after 43 ps, the shape parameter steady approaches its previous value. Calculation of the alpha-carbon distance matrices for Kv1.2 at times 22.5 and 50 ps show that the protein initially compresses (22.5 ps) as many of the CA-CA separations >100 Å disappears but does not drastically change the overall structure (Fig. S2). At 50 ps, Kv1.2 elongates and begins to resemble the crystal structure (PDB: 3LUT). The channel along the central pore of the protein contracts during the initial impact of the shock wave but the channel widens as the simulation progresses (see Fig. 6 B). The shock wave causes the channel of the central pore to close off at 25 ps. After 50 ps, the central pore has not returned to its original dimension, thus producing changes in the selectivity filter. The selectivity filter is the narrowest portion of the central pore and consists of the highly conserved residues 374–378 (TVGYG). The backbone carbonyl groups of these five residues form the selectivity filter and reside in the P-loop. After passage of the shock wave, these loops in Kv1.2 are displaced and end up closing off the central pore (Fig. 6 C). Typically, one or two of the loops cause closure of the central pore. No water molecules were able to cross the membrane in these shock wave simulations. The shock wave does not appear to cause significant damage to either the membrane or the associated voltage-gated ion channel. These results are consistent with high-pressure experiments of ion channels in squid giant axon (54). The resistance and capacitance across the membrane were not affected over a range of pressures up to 62 MPa (54, 55). The predominant effect of pressure was to slow the overall kinetics of the voltage clamp currents. Both the early (sodium) and delay (potassium) currents were slowed down by the same factor.

Figure 5.

Figure 5

Open in a new tab

Snapshots of Kv1.2 during the shock wave simulation with piston velocity 1000 m/s and no void. To see this figure in color, go online.

Figure 6.

Figure 6

Open in a new tab

(A) Shows a schematic of the pore radius along the crystal structure of Kv1.2. The selectivity filter is shown in green and found between −40 and −25 along the Z axis. (B) Shows the pore radius along the Z axis for the protein at time points 25 ps (green) and 50 ps (blue). The pore radius of the crystal structure (PDB: 3LUT) is shown in red. These plots are centered on the largest radius along the Z axis. (C) Shows an overlay of the selectivity filter from the individual subunits (shades of green) at 50 ps with the crystal structure (red). Gly-378 in the displaced loop that blocks the pore is shown in violet. Typically one or two loops cause the closure of the pore. To see this figure in color, go online.

MD simulations of shock wave-induced void collapse have shown that a nanojet forms (Fig. 7) due to the shock wave impinging on the side of the void opposite the membrane. This causes the void to collapse more rapidly on one side and water is able to move faster through the void than in solution to form a nanojet (Fig. S3). Jet formation from shock-induced bubble collapse is a well-known phenomena (56) and commonly used to destroy kidney stones (57). Previous simulations showed that nanoject can cause poration of a membrane at relatively mild velocities (10), likely leading to unregulated exchange of ions and molecules across the membrane. Present shock wave simulations of the protein-membrane system in the presence of a void showed that the result of void collapse can be detrimental to the cell. Fig. 8 shows that poration of the DPPC membrane occurred when the piston velocity was 1000 m/s. A pore of ∼65 Å in radius was created in the membrane at 33 ps. The force of the nanojet is great enough that Kv1.2 is forced out of the membrane and denaturation of the ion channel occurs. The Kv1.2 channel has a RMSD of over 30 Å relative to the crystal structure and only retains 11.9% helical content at 50 ps. The shape parameter for the channel at 50 ps indicates the protein is spherical (−0.004). All S5 and S6 helices that formed the central pore in this ion channel are completely denatured and the voltage sensor domain lacks most of its helical structure. The force of the nanojet was also great enough to cause separation of the T1 domain of the subunits and 27,341 water molecules were able to pass through the membrane by 50 ps.

Figure 7.

Figure 7

Open in a new tab

(A) Shows the solvent density during shock wave simulation (piston velocity 500 m/s) with a 100 Å radius void at 24 ps (red), 28.5 ps (green), and 33 ps (blue). The blue areas show an absence of solvent density. (B)–(D) Show progression of the shock wave comes in contact with the void (B), creation of the nanojet (C), and impact with the membrane (D). To see this figure in color, go online.

Figure 8.

Figure 8

Open in a new tab

(A) Snapshot showing the effects of poration on the membrane and protein at 50 ps in shock wave simulation with piston velocity of 1000 m/s with void. (B) Rotated side view of the membrane. To see this figure in color, go online.

We next studied the impact of shock wave-induced void collapse at piston velocities that are known to cause minimal to no damage to the membrane (10). A piston velocity of 500 m/s was able to create a nanojet with enough force to cause deformation of the lipid bilayer without poration of the membrane and was not able to dislodge the protein before the shock wave left the system. The solvent density reaches ∼1.30 g/ml during creation of the shock wave (Fig. 7 A). The RMSD for the protein rises to 10.0 Å at 50 ps and only decreases slightly during the remainder of the simulation (Fig. 9 A). Although the protein does not denature during the simulation, the impact of the nanojet causes the overall topology of the channel to change drastically. Similar to the planar shock wave, the protein is compressed, but because of the nanojet, the protein also expands outward. Both the sensor domain and the central pore are severely impacted, although the T1 domain is not greatly affected. Analysis of the pore radius shows the protein length is drastically shortened and does not recover during the simulation (Fig. 10 A). The narrowest region of the central pore no longer exists and the transmembrane portion of the central channel is only 10 Å in length. The shape parameter shows the deformation the protein undergoes is more severe when the void is present and that the protein becomes more oblate (−0.005 ± 0.001). Additionally, the helical content of the protein drops to 51.1 ± 1.9% after impact of the nanojet and dips to 45.9 ± 1.1% during the remainder of the simulation.

Figure 9.

Figure 9

Open in a new tab

(A) RMSD of the backbone atoms (N, C, and CA) for Kv1.2 relative to crystal structure (PDB: 3LUT excluding residues 184–219 in each monomer) during shock wave simulations at piston velocities of 500 (red), 400 (green), and 300 (blue) m/s. (B)–(D) Show the RMSD for the individual subunits A (red), B (green), C (blue), and D (violet) of Kv1.2 at piston velocities 500 (B), 400 (C), and 300 (D) m/s. To see this figure in color, go online.

Figure 10.

Figure 10

Open in a new tab

(A) Pore radius along the Z axis for Kv1.2 in the crystal structure (red, PDB: 3LUT) and at time 37 ps (green) and 50 ps (blue) for shock wave simulation at 500 m/s piston velocity. (B) Pore radius for the Kv1.2 crystal structure (red) and for the 300 (green) and 400 (blue) m/s piston velocity shock wave simulations at 75 ps. In both plots, the pore radius of the crystal structure is shown in red. (C) Shows an overlay of the selectivity filter of the individual subunits (in shades of green) at 50 ps (300 m/s) with the crystal structure (red). To see this figure in color, go online.

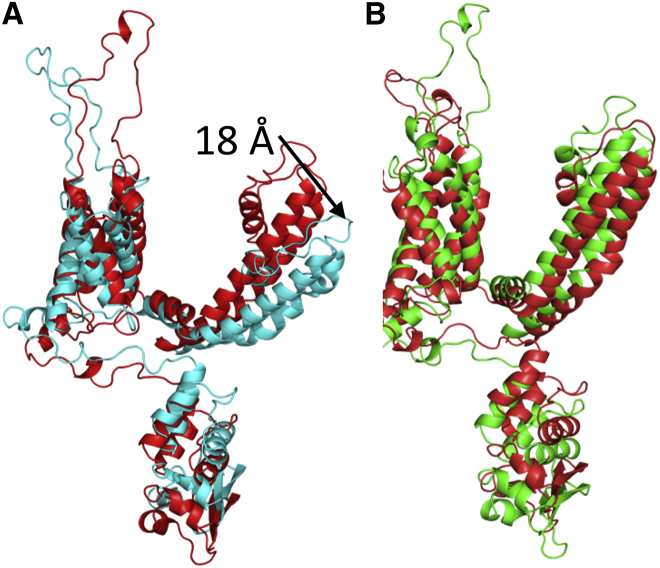
Although nanojets created with piston velocities of 400 and 300 m/s do not deform the lipid bilayer, the nanojet damages the protein when the piston velocity is 400 m/s. The RMSD for the protein is above 7 Å at 42 ps and slowly decreases as the simulation proceeds (Fig. 9 A). The radius of the central pore region shows the deformation of the protein is not as severe as seen at 500 m/s but still undergoes significant changes (Fig. 10 B). In particular, the transmembrane portion of the central pore is drastically reduced. An overlay of the crystal structure with the subunit at 50 ps shows that S5 and S6 are displaced ∼18 Å (Fig. 11 A) but are able to retain their secondary structure. All four subunits of Kv1.2 have the S5 and S6 displaced. Previous MD simulations of Kv1.2 have shown that the pore lining helices are very rigid relative to the rest of the protein (58). The sensor and T1 domains are not significantly affected by the nanojet and retain their overall structure. The helical content of the protein is 54.6 ± 1.8% at 50 ps. The shape factor of the protein is spherical (0.001) after impact of the shock wave and remains spherical for the duration of the simulation. When a nanojet was created by the shock wave due to the motion of the piston with a velocity of 300 m/s, only modest changes in the structure of the protein occurred. The RMSD only reaches ∼5 Å relative to the crystal structure during the impact of the nanojet and slowly decreases. The density of the solution only reaches ∼1.20 g/ml at this piston velocity. The helical content of the protein is 57.2 ± 0.6% at 75 ps. An overlay of the crystal structure with the protein at 75 ps after the shock wave shows most of the secondary structure has remained intact and in the same relative positions (Fig. 11 B). Most of the change in structure is due to movement of the flexible loops connecting the helices. The transmembrane portion of the central pore, although shorter than the crystal structure, still retains most of the general features (Fig. 10 B). The selectivity filter in the central pore is affected by the nanojet (Fig. 10 C). An overlay of the subunits shows that the extracellular portion of the loops have shifted and are further away from each other. Gly-378 has shifted ∼7–8 Å from its position in the crystal structure after the shock wave. Only Thr-374 remains close to its original position in the crystal structure. The modest changes to the overall structure of the ion channel at this piston velocity should enable the protein to rapidly recover activity. Although there is only modest changes to the protein at slower shock wave speeds, the impact of these slower shock waves with larger voids would likely cause greater damage to the ion channel. Santo and Berkowitz have shown that far more damage to a membrane can occur at lower shock speed when it causes the collapse of large voids (10).

Figure 11.

Figure 11

Open in a new tab

(A) Overlay of the Kv1.2 crystal structure (red) subunit with subunit (cyan) taken at 50 ps from the 400 m/s piston velocity shock wave simulation. Although only subunit A is shown relative to the crystal structure for clarity, the other three subunits show the same positional change in helices S5–S6. (B) Shows an overlay of the crystal structure (red) with a subunit of Kv1.2 at 75 ps from the 300 m/s piston velocity shock wave simulation (green). To see this figure in color, go online.

A recent study by Fu et al. showed that void collapse can damage a membrane without a shock wave impact (47). The violent collapse of the void in close proximity to the membrane caused large-scale distortion of the lipid bilayer. We performed a single simulation to explore the effects of void collapse on the structure of the ion channel when no shock wave was present. The void was able to persist in the system for almost 1.6 ns (Fig. 12). The void causes deformation of the membrane and the embedded protein. Interestingly, the deformation of the protein is localized within the linker region that connects the transmembrane domain to the T1 domain. Collapse of the void causes the separation of the T1 domain from the transmembrane domain. The helical transmembrane domain within the lipid bilayer is relatively unchanged (Fig. S4) and the helical content of the protein is 56.3%. The RMSD of the transmembrane domain was 3.72 Å relative to the crystal structure PDB: 3LUT (calculated without the contributions of the T1 domain, S1–S2 linker, and S3–S4 linker). The individual RMSD of the subunits of Kv1.2 were 3.35 Å (A), 2.67 Å (B), 4.90 Å (C), and 2.78 Å (D). The nanoscale void collapse caused large deformation to the membrane, but the structural domains of the ion channel were resistant to major damage, although much larger voids are likely more destructive.

Figure 12.

Figure 12

Open in a new tab

(A) Void collapse simulation without a shock wave at 400 ps. (B) The void has reduced to a radius of 85 Å. At 1000 ps, the void has reduced to 65 Å in radius and deformation of the membrane is substantial. (C) The void collapses by 1600 ps. To see this figure in color, go online.

Conclusion

The effects of mTBI are of great concern and will require a great deal of study to pinpoint the underlying causes. It has been previously shown that shock wave-induced void collapse at moderate velocities can lead to significant damage to lipid bilayers. The resulting poration of the membrane likely leads to unregulated exchange of ions and molecules that can have adverse effects on an organism. For example, ion channel dysfunction in humans is known to be a factor in diseases such as cystic fibrosis, long QT syndrome, and epilepsy (59). Molecular simulations have shown that membranes can self-heal from nanometer size pores in tens of nanoseconds (9, 10). In this study, we have shown that shock waves alone do not significantly damage membrane bound proteins (ion channel). In fact, the RMSD of the ion channel after the solvent density reduces is no greater than seen for a standard MD simulation for a protein of this size. But, shock wave-induced void collapse can have adverse effects on a membrane bound ion channel even at piston velocities that are too slow to affect the membrane. The damage to the organism from faulty ion regulation can be severe since, unlike a membrane, ion channels may not self-heal as rapidly (60, 61). Voltage-gated potassium channels fold without assistance in suitable membranes. Injection of proteoliposomes containing in vitro synthesized Shaker potassium channel from fruit flies into Xenopus laevis oocytes will show activity after 4 h (61). Additionally, 15% of denatured KvAP, a thermophilic voltage-gated potassium channel, in a liposome will refold after 2 h at room temperature, although elevating the temperature will significantly increase the refolding rate (73% after 10 min at 80°C) for this channel (60). For the protein damage seen in our simulations, Kv1.2 will repair itself rapidly over time. Protein dysfunction from shock wave-induced void collapse could contribute to ionic imbalances and initials symptoms of mTBI such as headaches and seizures (62), but it is unknown if this could contribute to longer term problems.

Author Contributions

E.Y.L. performed the simulations. E.Y.L., M.L.B., and E.S. analyzed the data. E.Y.L., M.L.B., and E.S. wrote the article.

Acknowledgments

This work was funded by a grant from the Office of Naval Research (N00014151P00020) and was performed under the auspices of the U.S. Department of Energy by Lawrence Livermore National Laboratory under contract DE-AC52-07NA27344. Computing support for this work came from the Lawrence Livermore National Laboratory (LLNL) Institutional Computing Grand Challenge program.

Editor: Scott Feller.

Footnotes

Supporting Material

Document S1. Figs. S1–S4
mmc1.pdf (1.5MB, pdf)
Document S2. Article plus Supporting Material
mmc2.pdf (5.9MB, pdf)

References

  • 1.Warden D. Military TBI during the Iraq and Afghanistan wars. J. Head Trauma Rehabil. 2006;21:398–402. doi: 10.1097/00001199-200609000-00004. [DOI] [PubMed] [Google Scholar]
  • 2.Tanielian T., Jaycox L.H. RAND; Santa Monica, CA: 2008. Invisible Wounds of War. [Google Scholar]
  • 3.Rosenfeld J.V., McFarlane A.C., Ling G.S. Blast-related traumatic brain injury. Lancet Neurol. 2013;12:882–893. doi: 10.1016/S1474-4422(13)70161-3. [DOI] [PubMed] [Google Scholar]
  • 4.Peskind E.R., Petrie E.C., Minoshima S. Cerebrocerebellar hypometabolism associated with repetitive blast exposure mild traumatic brain injury in 12 Iraq war Veterans with persistent post-concussive symptoms. Neuroimage. 2011;54(Suppl 1):S76–S82. doi: 10.1016/j.neuroimage.2010.04.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Ravin R., Blank P.S., Zimmerberg J. Shear forces during blast, not abrupt changes in pressure alone, generate calcium activity in human brain cells. PLoS One. 2012;7:e39421. doi: 10.1371/journal.pone.0039421. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Goeller J., Wardlaw A., Weiss G. Investigation of cavitation as a possible damage mechanism in blast-induced traumatic brain injury. J. Neurotrauma. 2012;29:1970–1981. doi: 10.1089/neu.2011.2224. [DOI] [PubMed] [Google Scholar]
  • 7.Prentice P., Cuschieri A., Campbell P. Membrane disruption by optically controlled microbubble cavitation. Nat. Phys. 2005;1:107–110. [Google Scholar]
  • 8.Zhou Y., Yang K., Deng C.X. Controlled permeation of cell membrane by single bubble acoustic cavitation. J. Control. Release. 2012;157:103–111. doi: 10.1016/j.jconrel.2011.09.068. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Choubey A., Vedadi M., Vashishta P. Poration of lipid bilayers by shock-induced nanobubble collapse. Appl. Phys. Lett. 2011;98:023701-1–023701-3. [Google Scholar]
  • 10.Santo K.P., Berkowitz M.L. Shock wave interaction with a phospholipid membrane: coarse-grained computer simulations. J. Chem. Phys. 2014;140:054906. doi: 10.1063/1.4862987. [DOI] [PubMed] [Google Scholar]
  • 11.Hemphill M.A., Dabiri B.E., Parker K.K. A possible role for integrin signaling in diffuse axonal injury. PLoS One. 2011;6:e22899. doi: 10.1371/journal.pone.0022899. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Johnson V.E., Stewart W., Smith D.H. Axonal pathology in traumatic brain injury. Exp. Neurol. 2013;246:35–43. doi: 10.1016/j.expneurol.2012.01.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Wolf J.A., Stys P.K., Smith D.H. Traumatic axonal injury induces calcium influx modulated by tetrodotoxin-sensitive sodium channels. J. Neurosci. 2001;21:1923–1930. doi: 10.1523/JNEUROSCI.21-06-01923.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Saatman K.E., Creed J., Raghupathi R. Calpain as a therapeutic target in traumatic brain injury. Neurotherapeutics. 2010;7:31–42. doi: 10.1016/j.nurt.2009.11.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Adcock S.A., McCammon J.A. Molecular dynamics: survey of methods for simulating the activity of proteins. Chem. Rev. 2006;106:1589–1615. doi: 10.1021/cr040426m. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Koshiyama K., Kodama T., Fujikawa S. Structural change in lipid bilayers and water penetration induced by shock waves: molecular dynamics simulations. Biophys. J. 2006;91:2198–2205. doi: 10.1529/biophysj.105.077677. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Koshiyama K., Kodama T., Fujikawa S. Molecular dynamics simulation of structural changes of lipid bilayers induced by shock waves: effects of incident angles. Biochim. Biophys. Acta. 2008;1778:1423–1428. doi: 10.1016/j.bbamem.2008.03.010. [DOI] [PubMed] [Google Scholar]
  • 18.Ganzenmuller G.C., Hiermaier S., Steinhauser M.O. Shock-wave induced damage in lipid bilayers: a dissipative particle dynamics simulation study. Soft Matter. 2011;7:4307–4317. [Google Scholar]
  • 19.Ganzenmüller G.C., Hiermaier S., Steinhauser M.O. Consistent temperature coupling with thermal fluctuations of smooth particle hydrodynamics and molecular dynamics. PLoS One. 2012;7:e51989. doi: 10.1371/journal.pone.0051989. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Steinhauser M.O., Schmidt M. Destruction of cancer cells by laser-induced shock waves: recent developments in experimental treatments and multiscale computer simulations. Soft Matter. 2014;10:4778–4788. doi: 10.1039/c4sm00407h. [DOI] [PubMed] [Google Scholar]
  • 21.Schmidt M., Kahlert U., Steinhauser M.O. Characterization of a setup to test the impact of high-amplitude pressure waves on living cells. Sci. Rep. 2014;4:3849. doi: 10.1038/srep03849. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Espinosa S., Asproulis N., Drikakis D. Chemotherapy efficiency increase via shock wave interaction with biological membranes: a molecular dynamics study. Microfluidic Nanofluidics. 2014;16:613–622. [Google Scholar]
  • 23.Jentsch T.J., Hübner C.A., Fuhrmann J.C. Ion channels: function unravelled by dysfunction. Nat. Cell Biol. 2004;6:1039–1047. doi: 10.1038/ncb1104-1039. [DOI] [PubMed] [Google Scholar]
  • 24.Karp G. Wiley; New York: 2013. Cell and Molecular Biology: Concepts and Experiments; pp. 121–181. [Google Scholar]
  • 25.Lai H.C., Jan L.Y. The distribution and targeting of neuronal voltage-gated ion channels. Nat. Rev. Neurosci. 2006;7:548–562. doi: 10.1038/nrn1938. [DOI] [PubMed] [Google Scholar]
  • 26.Payandeh J., Scheuer T., Catterall W.A. The crystal structure of a voltage-gated sodium channel. Nature. 2011;475:353–358. doi: 10.1038/nature10238. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.Catterall W.A. Structure and function of voltage-gated ion channels. Annu. Rev. Biochem. 1995;64:493–531. doi: 10.1146/annurev.bi.64.070195.002425. [DOI] [PubMed] [Google Scholar]
  • 28.Shieh C.-C., Coghlan M., Gopalakrishnan M. Potassium channels: molecular defects, diseases, and therapeutic opportunities. Pharmacol. Rev. 2000;52:557–594. [PubMed] [Google Scholar]
  • 29.Hess B., Kutzner C., Lindahl E. GROMACS 4: algorithms for highly efficient, load-balanced, and scalable molecular simulation. J. Chem. Theory Comput. 2008;4:435–447. doi: 10.1021/ct700301q. [DOI] [PubMed] [Google Scholar]
  • 30.Klauda J.B., Venable R.M., Pastor R.W. Update of the CHARMM all-atom additive force field for lipids: validation on six lipid types. J. Phys. Chem. B. 2010;114:7830–7843. doi: 10.1021/jp101759q. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Best R.B., Zhu X., Mackerell A.D., Jr. Optimization of the additive CHARMM all-atom protein force field targeting improved sampling of the backbone φ, ψ and side-chain χ(1) and χ(2) dihedral angles. J. Chem. Theory Comput. 2012;8:3257–3273. doi: 10.1021/ct300400x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Chen X., Wang Q., Ma J. Structure of the full-length Shaker potassium channel Kv1.2 by normal-mode-based X-ray crystallographic refinement. Proc. Natl. Acad. Sci. USA. 2010;107:11352–11357. doi: 10.1073/pnas.1000142107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Neria E., Fischer S., Karplus M. Simulation of activation free energies in molecular systems. J. Chem. Phys. 1996;105:1902–1921. [Google Scholar]
  • 34.Martínez L., Andrade R., Martínez J.M. PACKMOL: a package for building initial configurations for molecular dynamics simulations. J. Comput. Chem. 2009;30:2157–2164. doi: 10.1002/jcc.21224. [DOI] [PubMed] [Google Scholar]
  • 35.Berendsen H.J.C., Postma J.P.M., Haak J.R. Molecular-dynamics with coupling to an external bath. J. Chem. Phys. 1984;81:3684–3690. [Google Scholar]
  • 36.Piggot T.J., Pineiro A., Khalid S. Molecular dynamics simulations of phosphatidylcholine membrane: a comparative force field study. J. Chem. Theory Comput. 2012;8:4593–4609. doi: 10.1021/ct3003157. [DOI] [PubMed] [Google Scholar]
  • 37.Darden T., York D., Pedersen L. Particle mesh Ewald: an N∗log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993;98:10089–10092. [Google Scholar]
  • 38.Hess B., Bekker H., Fraaije J.G.E.M. LINCS: a linear constraint solver for molecular simulations. J. Comput. Chem. 1997;18:1463–1472. [Google Scholar]
  • 39.Nose S. A unified formulation of the constant temperature molecular-dynamics methods. J. Chem. Phys. 1984;81:511–519. [Google Scholar]
  • 40.Hoover W.G. Canonical dynamics: equilibrium phase-space distributions. Phys. Rev. A. 1985;31:1695–1697. doi: 10.1103/physreva.31.1695. [DOI] [PubMed] [Google Scholar]
  • 41.Parrinello M., Rahman A. Polymorphic transitions in single crystals: a new molecular dynamics method. J. Appl. Phys. 1981;52:7182–7190. [Google Scholar]
  • 42.Tironi I., Sperb R., Van Gunsteren W. A generalized reaction field method for molecular-dynamics simulations. J. Phys. Chem. 1995;102:5451–5459. [Google Scholar]
  • 43.Van Der Spoel, D., E. Lindahl, …, K. A. Feenstra. 2010. Gromacs User Manual Version 4.5.4.
  • 44.Abraham F.F., Singh Y. The structure of a hard-sphere fluid in contact with a soft repulsive wall. J. Chem. Phys. 1977;67:2384–2385. [Google Scholar]
  • 45.Schiffer A., Tagarielli V.L. The response of rigid plates to blast in deep water: fluid-structure interaction experiments. Proc. R. Soc. A. 2012;468:2807–2828. [Google Scholar]
  • 46.Rybakov A.P., Rybakov I.A. Polymorphism of shocked water. Eur. J. Mech. B, Fluids. 1995;14:323–332. [Google Scholar]
  • 47.Fu H., Comer J., Chipot C. Sonoporation at small and large length scales: effect of cavitation bubble collapse on membranes. J. Phys. Chem. Lett. 2015;6:413–418. doi: 10.1021/jz502513w. [DOI] [PubMed] [Google Scholar]
  • 48.Andersen C.A., Palmer A.G., Rost B. Continuum secondary structure captures protein flexibility. Structure. 2002;10:175–184. doi: 10.1016/s0969-2126(02)00700-1. [DOI] [PubMed] [Google Scholar]
  • 49.Smart O.S., Goodfellow J.M., Wallace B.A. The pore dimensions of gramicidin A. Biophys. J. 1993;65:2455–2460. doi: 10.1016/S0006-3495(93)81293-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 50.Dima R., Thirumalai D. Asymmetry in the shapes of folded and denatured states of proteins. J. Phys. Chem. B. 2004;108:6564–6570. [Google Scholar]
  • 51.Humphrey W., Dalke A., Schulten K. VMD: visual molecular dynamics. J. Mol. Graph. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. 27–28. [DOI] [PubMed] [Google Scholar]
  • 52.Long S.B., Campbell E.B., Mackinnon R. Crystal structure of a mammalian voltage-dependent Shaker family K+ channel. Science. 2005;309:897–903. doi: 10.1126/science.1116269. [DOI] [PubMed] [Google Scholar]
  • 53.Kamatari Y.O., Kitahara R., Akasaka K. High-pressure NMR spectroscopy for characterizing folding intermediates and denatured states of proteins. Methods. 2004;34:133–143. doi: 10.1016/j.ymeth.2004.03.010. [DOI] [PubMed] [Google Scholar]
  • 54.Conti F., Fioravanti R., Stühmer W. Pressure dependence of the sodium currents of squid giant axon. J. Membr. Biol. 1982;69:23–34. doi: 10.1007/BF01871238. [DOI] [PubMed] [Google Scholar]
  • 55.Heinemann S.H., Conti F., Neher E. Effects of hydrostatic pressure on membrane processes. Sodium channels, calcium channels, and exocytosis. J. Gen. Physiol. 1987;90:765–778. doi: 10.1085/jgp.90.6.765. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 56.Brujan E.A., Ikeda T., Matsumoto Y. Jet formation and shock wave emission during collapse of ultrasound-induced cavitation bubbles and their role in the therapeutic applications of high-intensity focused ultrasound. Phys. Med. Biol. 2005;50:4797–4809. doi: 10.1088/0031-9155/50/20/004. [DOI] [PubMed] [Google Scholar]
  • 57.McAteer J.A., Evan A.P. The acute and long-term adverse effects of shock wave lithotripsy. Semin. Nephrol. 2008;28:200–213. doi: 10.1016/j.semnephrol.2008.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 58.Bjelkmar P., Niemelä P.S., Lindahl E. Conformational changes and slow dynamics through microsecond polarized atomistic molecular simulation of an integral Kv1.2 ion channel. PLOS Comput. Biol. 2009;5:e1000289. doi: 10.1371/journal.pcbi.1000289. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 59.Lehmann-Horn F., Jurkat-Rott K. Voltage-gated ion channels and hereditary disease. Physiol. Rev. 1999;79:1317–1372. doi: 10.1152/physrev.1999.79.4.1317. [DOI] [PubMed] [Google Scholar]
  • 60.Devaraneni P.K., Devereaux J.J., Valiyaveetil F.I. In vitro folding of KvAP, a voltage-gated K+ channel. Biochemistry. 2011;50:10442–10450. doi: 10.1021/bi2012965. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 61.Jarecki B.W., Makino S., Chanda B. Function of Shaker potassium channels produced by cell-free translation upon injection into Xenopus oocytes. Sci. Rep. 2013;3:1040. doi: 10.1038/srep01040. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 62.Cooper E.C., Jan L.Y. Ion channel genes and human neurological disease: recent progress, prospects, and challenges. Proc. Natl. Acad. Sci. USA. 1999;96:4759–4766. doi: 10.1073/pnas.96.9.4759. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Document S1. Figs. S1–S4
mmc1.pdf (1.5MB, pdf)
Document S2. Article plus Supporting Material
mmc2.pdf (5.9MB, pdf)

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES