Segmentation of Infant Hippocampus Using Common Feature Representations Learned for Multimodal Longitudinal Data

Abstract

Aberrant development of the human brain during the first year after birth is known to cause critical implications in later stages of life. In particular, neuropsychiatric disorders, such as attention deficit hyperactivity disorder (ADHD), have been linked with abnormal early development of the hippocampus. Despite its known importance, studying the hippocampus in infant subjects is very challenging due to the significantly smaller brain size, dynamically varying image contrast, and large across-subject variation. In this paper, we present a novel method for effective hippocampus segmentation by using a multi-atlas approach that integrates the complementary multimodal information from longitudinal T1 and T2 MR images. In particular, considering the highly heterogeneous nature of the longitudinal data, we propose to learn their common feature representations by using hierarchical multi-set kernel canonical correlation analysis (CCA). Specifically, we will learn (1) within-time-point common features by projecting different modality features of each time point to its own modality-free common space, and (2) across-time-point common features by mapping all time-point-specific common features to a global common space for all time points. These final features are then employed in patch matching across different modalities and time points for hippocampus segmentation, via label propagation and fusion. Experimental results demonstrate the improved performance of our method over the state-of-the-art methods.

1 Introduction

Effective automated segmentation of the hippocampus is highly desirable, as neuroscientists are actively seeking hippocampal imaging biomarkers for early detection of neurodevelopment disorders, such as autism and attention deficit hyperactivity disorder (ADHD) [1, 2]. Due to rapid maturation and myelination of brain tissues in the first year of life [3], the contrast between gray and white matter on T1 and T2 images undergo drastic changes, which poses great challenges to hippocampus segmentation.

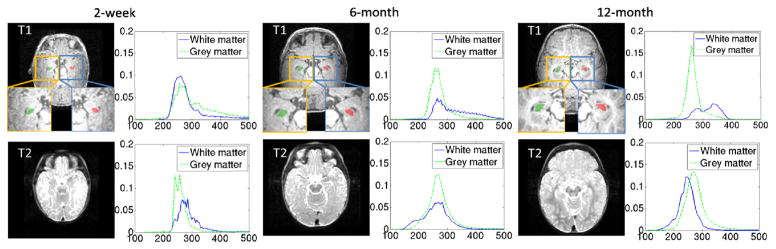
Multi-atlas approaches with patch-based label fusion have demonstrated effective performance for medical image segmentation [4–8]. This is mainly due to their ability to account for inter-subject anatomical variation during segmentation. However, infant brain segmentation introduces new challenges that need extra consideration before multi-atlas segmentation can be applied. First, using either T1 or T2 images alone is insufficient to provide an effective tissue contrast for segmentation throughout the first year. As shown in Fig. 1, the T1 image has very poor tissue contrast between white matter (WM) and gray matter (GM) in the first three months (such as the 2-week image shown in the left panel), as WM and GM become distinguishable only after the first year (such as the 12-month image shown in the right panel). However, the T2 image has better WM/GM contrast than the T1 image in the first few months. Second, some time periods (around the 6-month age as shown in the middle panel of Fig. 1) are more challenging to decipher because of very similar WM and GM intensity ranges (as shown by green and blue curves in Fig. 1) as partial myelination occurs.

Fig. 1.

Typical T1 (top) and T2 (bottom) brain MR images acquired from an infant at the 2 weeks, 6 months and 12 months, with the zoom-in views of local regions of hippocampi (green and red areas) shown at the bottom of T1 images. The WM and GM intensity distributions of T1 and T2 images on these local regions are also given to the right of each image.

Since the infant brain undergoes drastic changes in the first year of life, across-time-point feature learning is significant to help normalize cross-distribution differences and to borrow information between subjects at different time points for effective segmentation. Therefore, we propose to combine information from multiple modalities (T1 and T2) and different time points together via a patch matching mechanism to improve the label propagation in tissue segmentation. Specifically, to overcome the issue of significant tissue contrast change across different time points, we propose a hierarchical approach to learn a common feature representation. First, we learn the common features for the T1 and T2 images at each time point by using the classic kernel CCA [9, 10] to estimate the highly nonlinear feature mapping between the two modalities. Then, we further map all these within-time-point common features to a global common space to all different time points by applying the multi-set kernel CCA [11, 12]. Finally, we utilize the learned common features for guiding patch matching and propagating atlas labels to the target image (at each time point) for hippocampus segmentation, via a sparse patch-based labeling [13]. Qualitative and quantitative experimental results of our method on multimodal infant MR images acquired from 2-week-old to 6-month-old infants confirm more accurate hippocampus segmentation.

2 Method

2.1 Hierarchical Learning of Common Feature Representations

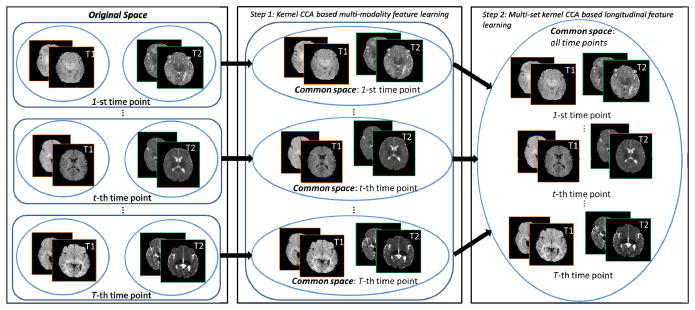
Suppose our training set consists of the longitudinal data including S subjects, each with T time points and two modalities (1: T1; 2: T2), denoted as $\mathit{A}=\left\{(I_{s,t}^{(1)},I_{s,t}^{(2)})\mid s=1,\dots ,S,t=1,\dots ,T\right\}$. I_s,t denotes the intensity image for subject s at time point t. We first register each training image $I_{s,t}^{(m)}(m=\{1,2\})$ to a template image by deformable registration [14]¹, thus producing a registered image ${\stackrel{\sim }{I}}_{s,t}^{(m)}$. We then gather the images into 2 × T groups, one for each modality m and time point t, consisting of S registered images ${\stackrel{\sim }{\mathit{I}}}_t^{(m)}=\left\{{\stackrel{\sim }{I}}_{s,t}^{(m)}\mid s=1,\dots ,S\right\}$, as shown in the left panel of Fig. 2. The patches from Q randomly sampled locations V = {v_q|q = 1, …, Q} in the template domain are similarly organized into 2 × T image patch groups $\mathit{P}=\left\{{\mathit{P}}_t^{(m)}\mid t=1,\mathrm{..},T;m=1,2\right\}$, where ${\mathit{P}}_t^{(m)}=[{\mathit{p}}_{1,t}^{(m)}(v_1),\dots ,{\mathit{p}}_{s,t}^{(m)}(v_q),\dots ,{\mathit{p}}_{s,t}^{(m)}(v_Q)]$ is a matrix for each patch group with N = Q × S columns of patches sampled from ${\stackrel{\sim }{\mathit{I}}}_{.,t}^{(m)}$. Each patch ${\mathit{p}}_{s,t}^{(m)}(v_q)$ is rearranged as a column vector in ${\mathit{P}}_t^{(m)}$. For simplicity, we omit the location v and denote the i-th column of ${\mathit{P}}_t^{(m)}$ as ${\mathit{P}}_t^{(m)}(i)$, i = 1, …, N. In the following, we describe the hie erarchical feature learning in two steps as illustrated in Fig. 2.

Fig. 2.

Schematic diagram of the proposed hierarchical feature learning method.

Step 1: Learning Within-Time-Point Common Features

Learning a common feature representation for all patch groups P simultaneously is challenging, since features vary significantly across groups. To overcome this problem, we first determine the common feature representation across modalities by employing the kernel CCA to learn the non-linear mappings of ${\mathit{P}}_t^{(1)}$ and ${\mathit{P}}_t^{(2)}$ for each time point t.

Specifically, we apply the Gaussian kernel ϕ(·,·) to measure similarity of any pair of image patches in ${\mathit{P}}_t^{(1)}$ and obtain a N × N kernel matrix ${\mathit{K}}_t^{(1)}={[\varphi ({\mathit{P}}_t^{(1)}(i),{\mathit{P}}_t^{(1)}(j))]}_{N\times N}(i,j=1,\dots ,N)$. Similarly, we can obtain a N × N kernel matrix ${\mathit{K}}_t^{(2)}$ for group ${\mathit{P}}_t^{(2)}$. Then, kernel CCA aims to find two sets of linear transforms $\left\{{\mathit{W}}_t^{(m)}={[{\mathit{w}}_t^{(m)}(1),\dots ,{\mathit{w}}_t^{(m)}(r),\dots ,{\mathit{w}}_t^{(m)}(R)]}_{N\times R}\mid m=1,2\right\}$ for ${\mathit{P}}_t^{(1)}$ and ${\mathit{P}}_t^{(2)}$, respectively, such that the correlation between mapped features ${({\mathit{w}}_t^{(1)}(r))}^T{\mathit{K}}_t^{(1)}$ and mapped features ${({\mathit{w}}_t^{(2)}(r))}^T{\mathit{K}}_t^{(2)}$ is maximized in the common space:

$${\text{argmax}}_{{\mathit{w}}_t^{(1)}(r),{\mathit{w}}_t^{(2)}(r)}\frac{{\left({\mathit{w}}_t^{(1)}(r)\right)}^T{\mathit{K}}_t^{(1)}{\left({\left({\mathit{w}}_t^{(2)}(r)\right)}^T{\mathit{K}}_t^{(2)}\right)}^T}{\left[{\left({\mathit{w}}_t^{(1)}(r)\right)}^T{\mathit{K}}_t^{(1)}{\left({\left({\mathit{w}}_t^{(1)}(r)\right)}^T{\mathit{K}}_t^{(1)}\right)}^T\right]\left[{\left({\mathit{w}}_t^{(2)}(r)\right)}^T{\mathit{K}}_t^{(2)}{\left({\left({\mathit{w}}_t^{(2)}(r)\right)}^T{\mathit{K}}_t^{(2)}\right)}^T\right]}$$ (1)

where $R=min(\mathit{rank}({\mathit{K}}_t^{(1)}),\mathit{rank}({\mathit{K}}_t^{(2)}))$. The denominator of Eq. (1) requires that the distribution of the mapped features should be as compact as possible within each group. Partial Gram-Schmidt orthogonalization method [9] can be sequentially used to find the optimal ${\mathit{w}}_t^{(1)}(r)$ and ${\mathit{w}}_t^{(2)}(r)$ in Eq. (1), where the r^th pair of ${\mathit{w}}_t^{(1)}(r)$ and ${\mathit{w}}_t^{(2)}(r)$ are orthogonal to all previous pairs and also maximize Eq. (1). By transforming ${\mathit{P}}_t^{(1)}$ and ${\mathit{P}}_t^{(2)}$ with ${\mathit{W}}_t^{(1)}$ and ${\mathit{W}}_t^{(2)}$, respectively, we obtain a common-space feature representation at time point t as ${\widehat{\mathit{F}}}_t^{(1)}={({\mathit{W}}_t^{(1)})}^T{\mathit{K}}_t^{(1)}$ and ${\widehat{\mathit{F}}}_t^{(2)}={({\mathit{W}}_t^{(2)})}^T{\mathit{K}}_t^{(2)}$.

Step 2: Learning Across-Time-Point Common Features

After concatenating the features obtained in Step 1 as ${\widehat{\mathit{F}}}_t={\left[{\left[{\widehat{\mathit{F}}}_t^{(1)}\right]}^T,{\left[{\widehat{\mathit{F}}}_t^{(2)}\right]}^T\right]}_{2R\times N}^T$, the N × N kernel matrix K̂_t can be computed for each F̂_t. We then estimate the feature transformations Z_t = [z_t(1), … z_t(g), …, z_t(G)]_N×G for each F̂_t, which maximize the correlations of all the transformed features in a global common space with G = min_t rank(K̂_t). This can be solved using the multi-set kernel CCA [11, 12], which maximizes the correlations of multiple transformed features between each pair of time points t and t′:

$$\begin{array}{c}{\text{argmax}}_{{\mathit{z}}_t(g){\mid }_{t=1}^T}{\sum }_{t=1}^T{\sum }_{t^{\prime }=1,t^{\prime }\ne t}^T\left[{({\mathit{z}}_t(g))}^T{\widehat{\mathit{K}}}_t{\left({({\mathit{z}}_{t^{\prime }}(g))}^T{\widehat{\mathit{K}}}_{t^{\prime }}\right)}^T\right]\\ s.t.,\forall t,{\left({\mathit{z}}_t(g)\right)}^T{\widehat{\mathit{K}}}_t{\left({({\mathit{z}}_t(g))}^T{\widehat{\mathit{K}}}_t\right)}^T=1\end{array}$$ (2)

By transforming F̂_t with Z_t, we can obtain a common-space feature representation across different time points as D̂_t = (Z_t)^TK̂_t.

2.2 Patch-Based Label Fusion for Hippocampus Segmentation

Hierarchical Feature Representation

Before adopting the segmentation algorithm, each original intensity patch from both target images and atlas images is mapped into an across-time-point common space by our proposed hierarchical feature learning method in Section 2.1. Specifically, for segmenting a target subject $\left\{I_{0,t}^{(m)},m=1,2\right\}$ at time point t, where we use “0” for representing the current target subject, we first align its T1 image with T2 image and then linearly register H atlas subjects $\left\{\left(I_{h,t}^{(m)},L_{h,t}\right),m=1,2;t=1,\dots ,T;h=1,\dots H\right\}$ to them. Here, L_h,t indicates the respective hippocampus mask. Instead of simply using the original T1 and T2 intensity patches $\left\{{\mathit{p}}_{h,t}^{(m)}(v),m=1,2\right\}$ as the features at location v in the target image (h = 0) or atlas images (h =1, …, H), we apply the following steps to map all these original image patches to the across-time-point common space: (1) obtain the within-time-point features by ${\widehat{\mathit{f}}}_{h,t}^{(m)}(v)={({\mathit{W}}_t^{(m)})}^T\varphi ({\mathit{p}}_{h,t}^{(m)}(v),{\mathit{P}}_t^{(m)})$, m = 1,2, where Gaussian kernel ϕ(·,·) measures the similarity between ${\mathit{p}}_{h,t}^{(m)}(v)$ and all patches in ${\mathit{P}}_t^{(m)}$ (defined in Section 2.1); (2) concatenate ${\widehat{\mathit{f}}}_{h,t}^{(1)}(v)$ and ${\widehat{\mathit{f}}}_{h,t}^{(2)}(v)$ to form a within-time-point feature f̂_h,t(v); and (3) obtain the feature in the across-time-point common space by d̂_h,t(v) = (Z_t)^T(f̂_h,t(v), F̂_t), where d̂_h,t(v) is the final learned feature vector for target image (h = 0) or atlas images (h =1, …, H) at location v.

Patch-Based Label Fusion

To determine the label l_0,t(u) at each target image point u, we collect a set of candidate multi-modality patches along with their corresponding bels $\left\{\left({\mathit{p}}_{h,t}^{(m)}(v),l_{h,t}(v)\right),m=1,2;t=1,\dots ,T;h=1,\dots ,H;v\in \mathrm{\Omega }(u)\right\}$ in a certain search neighborhood Ω(u) from H aligned atlases. After mapping all candidate atlas image patches for obtaining the common feature representations {d̂_h,t(v), t = 1, …, T; h =1, …, H; v ∈ Ω(u)} across H atlas subjects at different time t, we can construct a dictionary matrix 𝓓 (u) by arranging {d̂_h,t(v)} column by column. Since each atlas patch bears the anatomical label (“1” for hippocampus and “−1” for non-hippocampus), we can also construct a label vector l(u) from the labels of candidate atlas patches {l_h,t(v), t = 1, …, T; h =1, …, H; v ∈ Ω(u)} by following the same order of 𝓓 (u), where each element l_h,t(v) is the atlas label at v ∈ Ω(u). Then, the label fusion can be formulated as a sparse representation problem as:

$${\text{argmin}}_{\mathit{\xi }(u)}\left\{{\Vert {\widehat{\mathit{d}}}_{0,t}(u)-\mathcal{D}(u)\mathit{\xi }(u)\Vert }_2^2+\lambda {\Vert \mathit{\xi }(u)\Vert }_1\right\},$$ (3)

where λ controls the strength of sparsity constraint. ξ is the weighting vector where each element is associated with one atlas patch in the dictionary and a larger value in ξ indicates the high similarity between the target image patch and the associated atlas patch. SLEP [15] is used to solve the above sparse representation problem. Finally, the label at the target image point u can be determined by l_0,t(u) = sign(ξ^T(u)l(u)).

3 Experimental Results

We evaluate the proposed method on infant MR brain images of twenty subjects, where each subject has both T1 and T2 MR images acquired at 2 weeks, 3 months, and 6 months of age. Standard image pre-processing steps, including resampling, skull stripping, bias-field correction and histogram matching, are applied to each MR images. We fix the patch size to 9 × 9 × 9 and the weight λ in Eq. (3) to 0.002. FLIRT in the FSL software package [16] with 12 DOF and correlation as the similarity metric is used to linearly align all atlas images to the target image. The twenty subjects are divided into two groups for training and testing, respectively.

Discriminative Power of Learned Common Features

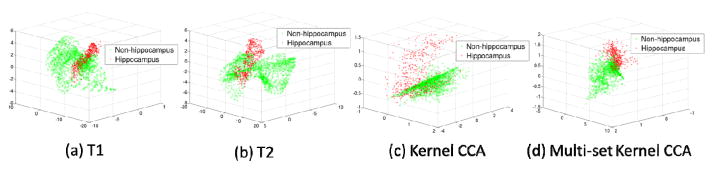
Fig. 3 compares the sample distribution represented by the four different features: T1 intensities, T2 intensities, within-time-point features given by kernel CCA features, and across-time-point features by multi-set kernel CCA features. Based on the projected feature distribution (reduced to three dimensions for visualization) shown in Fig. 3, kernel CCA and multi-set kernel CCA can better separate hippocampus from non-hippocampus samples.

Fig. 3.

Distributions of voxel samples with four types of features, respectively. Red crosses and green circles denote hippocampus and non-hippocampus voxel samples, respectively.

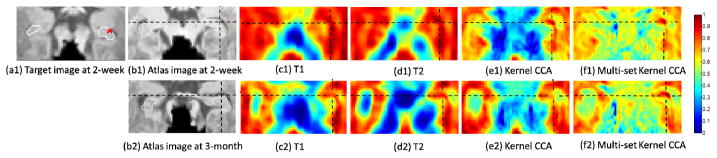
In Fig. 4, we further show the similarity maps resulting from different feature matching between a key point (red cross) on the boundary of the hippocampus (white contours) in the target image (a1) and all points in each of the two atlas images (b1 & b2), respectively. Four feature representation methods: T1 (c1 & c2), T2 (d1 & d2), kernel CCA (e1 & e2), and multi-set kernel CCA (f1 & f2) are compared. For the first row, the target and atlas images are from the same time point. The results demonstrate the effectiveness of the within-time-point common features. For the second row, the target and atlas images are from different time points. The results demonstrate the effectiveness of the across-time-point common features.

Fig. 4.

Comparison of similarity maps for four different feature representations between a key point (red cross) in the target image (a1) and all points in the two atlas images (b1 & b2). (b1) An atlas from the same time point as (a1); (b2) An atlas from a different time point as (a1).

Quantitative Evaluation on Hippocampus Segmentation

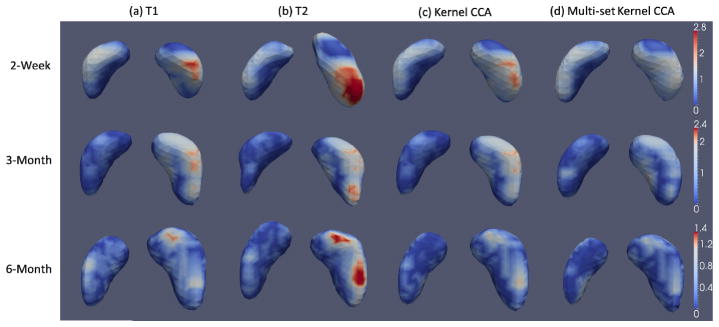
The mean and standard deviation of the Dice ratios and the average symmetric surface distance (ASSD) of the segmentation results based on the four feature representations are listed in Table 1. The best results are marked in bold. Our feature learning method based on multi-set kernel CCA achieves significant improvement over all other methods in terms of overall Dice ratio (paired t-test, p<0.014) and ASSD (paired t-test, p<0.049). It is worth noting that, although segmenting the 6-month images seems to be the most challenging among all time points, all comparison methods achieve their longitudinally highest segmentation accuracy at 6 months. This is partially due to the large increase of hippocampus volume during early brain development (i.e., average around 20% growth rate of hippocampus volume from 2-week-old to 6-month-old infants), making large hippocampus volumes in the 6-month-olds relatively easy to segment. Besides, the Dice ratios for combined T1 and T2 are 59.3%, 67.2%, and 70.2%, respectively, for 2-week, 3-month, and 6-month images, which are 5.9%, 3.1%, and 2.4% lower than our proposed method. To test consistency in hippocampal volume measured by different raters, an overall inter-rater reliability ICC (intra-class correlation coefficient) between segmentation techniques for each rater is calculated for hippocampal volumes. The inter-rater ICC is 79.4% for the manual segmentations. Fig. 5 further shows some typical results of surface distances between automatic segmentations and manual segmentations by the four feature representation methods. Our proposed hierarchical feature learning achieves the best performance.

Table 1.

Mean and standard deviation of Dice ratio (Dice, in %) and average symmetric surface distance (ASSD, in mm) for the segmenations obtained by four feature representation methods.

	Age	T1	T2	Kernel CCA	Multi-set kernel CCA
Dice (%)	2-Week	60.3±14.5	50.7±13.8	63.1±12.1	65.2±10.1
	3-Month	66.7±11.9	59.5± 8.8	69.2±4.9	70.3±5.3
	6-Month	69.6±10.1	66.9±8.3	71.5±7.9	72.6±7.0
	Average	65.5±12.5	59.0±12.4	67.9±9.3	69.3±8.2
ASSD (mm)	2-Week	0.96±0.49	1.20±0.39	0.89±0.37	0.88±0.33
	3-Month	0.79±0.33	0.97±0.21	0.78±0.14	0.76±0.17
	6-Month	0.79±0.31	0.84±0.24	0.75±0.25	0.72±0.22
	Average	0.85±0.38	1.00±0.32	0.81±0.27	0.79±0.25

Fig. 5.

Visualization of surface distance (in mm) for hippocampus segmentation results.

4 Conclusion

In this paper, we proposed a multi-atlas patch-based label propagation and fusion method for the hippocampus segmentation of infant brain MR images acquired from the first year of life. To deal with dynamic change in tissue contrast, we proposed a hierarchical feature learning approach to obtain common feature representations for multi-modal and longitudinal imaging data. These features resulted in better patch matching, which allowed for better hippocampus segmentation accuracy. In the future, we will evaluate the proposed method using more time points from infant data.