Abstract
Quantitative trait locus (QTL) mapping is often conducted in line-crossing experiments where a sample of individuals is randomly selected from a pool of all potential progeny. QTLs detected from such an experiment are important for us to understand the genetic mechanisms governing a complex trait, but may not be directly relevant to plant breeding if they are not detected from the breeding population where selection is targeting for. QTLs segregating in one population may not necessarily segregate in another population. To facilitate marker-assisted selection, QTLs must be detected from the very population which the selection is targeting. However, selected breeding populations often have depleted genetic variation with small population sizes, resulting in low power in detecting useful QTLs. On the other hand, if selection is effective, loci controlling the selected trait will deviate from the expected Mendelian segregation ratio. In this study, we proposed to detect QTLs in selected breeding populations via the detection of marker segregation distortion in either a single population or multiple populations using the same selection scheme. Simulation studies showed that QTL can be detected in strong selected populations with selected population sizes as small as 25 plants. We applied the new method to detect QTLs in two breeding populations of rice selected for high grain yield. Seven QTLs were identified, four of which have been validated in advanced generations in a follow-up study. Cloned genes in the vicinity of the four QTLs were also reported in the literatures. This mapping-by-selection approach provides a new avenue for breeders to improve breeding progress. The new method can be applied to breeding programs not only in rice but also in other agricultural species including crops, trees and animals.
Introduction
Over a century of breeding efforts has produced numerous varieties of domestic plants and animals to provide ample food resources for human. The great successes in plant and animal breeding have largely been achieved by exploiting within-species genetic variation for traits of interest through phenotypic selection. Although appropriate phenotypic selection is effective to exploit useful genetic variation of complex traits in breeding populations, the rich sources of naturally occurring genetic variation in plants and animals are largely hidden at the phenotypic levels and remain uncharacterized at the genomic and molecular levels. As a result, they are very much under-utilized in the past breeding programs. Meanwhile, the past decades have witnessed tremendous progress in genetic dissections of complex traits in plants and animals using DNA markers and genomic technologies (Francia et al., 2005; Collard and Mackill, 2008; Miah et al., 2013). During this period of time, thousands of quantitative trait locus (QTL) affecting a wide range of complex traits have been identified in different plant and animal species. These QTLs have greatly deepened our understanding on the genetic basis of complex traits. Unfortunately, results of QTL mapping have not yet changed much of today's activities of breeding because past efforts on QTL mapping almost exclusively used randomly selected populations that were not directly relevant to breeding. The phenotypic effects of target QTLs are largely unpredictable when they are transferred into different genetic backgrounds or tested in different environments using marker-assisted selection (Wang et al., 2012).
It is well known that genetic study of quantitative traits largely depends on the amount of genetic variation of the traits in the target populations (Falconer and Mackay, 1996; Lynch and Walsh, 1998). In terms of QTL mapping, the greater the genetic variation, the higher the statistical power of QTL detection. Therefore, geneticists often use line-crossing populations with large genetic variation for QTL mapping. Selective genotyping by keeping the two extreme distributions of the phenotype in mapping populations is a mean of artificially increasing genetic variation and reducing sample sizes (Darvasi and Soller, 1992). The detected QTLs can help us understand the genetic mechanisms of the traits under study but are not necessarily relevant to breeding programs because the QTLs detected in populations of crossing experiments may not segregate in breeding populations. Breeders, on the other hand, try to improve agricultural production by eliminating undesired individuals from the populations (one-tailed directional selection), resulting in reduced genetic variation and very small population sizes. Keeping undesired individuals in breeding populations as controls represents substantial additional cost and is not a common practice in many breeding programs. To facilitate breeding via marker-assisted selection, QTLs are better detected in the very population which the selection is targeting. However, depleted genetic variation of traits under selection in the small group of surviving individuals will reduce the statistical power of QTL detection. The more effective the selection, the lower the statistical power of QTL detection. Therefore, QTL mapping in selected breeding populations is not practical owing to reduced genetic variation and small population sizes based on the conventional marker–trait association models (Lander and Botstein, 1989). The small group of selected progeny actually contains the most important genetic information regarding specific target traits of interest to breeders and we must take advantage of such information to optimize our breeding strategy.
In many cases of plant breeding, selection for abiotic stress tolerances is simply based on survival or death. If selection is effective, frequencies of genes controlling the selected traits will shift in the selected population compared with the unselected base population (Hermisson and Wagner, 2004). Markers linked to the actual genes will show shifted frequencies accordingly. What we observe in the selected populations are distorted genotypic frequencies of markers from the frequencies in the base population. If the base population is a line-crossing population, the allele and genotypic frequencies are theoretically known, and they are called Mendelian segregation ratios. Distorted markers in selected populations are presumably linked to QTLs of the target traits. Therefore, mapping segregation distortion locus (SDL) is an alternative but more powerful approach to QTL mapping. One assumption of the QTL mapping-by-selection approach is that segregation distortion of markers is purely caused by artificial selection. Other evolutionary forces, for example, gametic and zygotic selections, may also cause segregation distortion. These loci are confounded with QTL, but the distorted loci themselves are interesting in their own rights.
We propose to perform QTL mapping in selected breeding populations via mapping SDL. The conventional QTL mapping via marker–trait association usually requires hundreds of genotyped individuals. Such a QTL mapping study provides information on genetic architecture of complex traits, albeit some of the QTL may not be useful for breeding purposes. Segregation distortion analysis, however, only requires a few dozens of genotyped individuals (Luo et al., 2005). The detected SDLs provide information on the loci that are targeted by phenotypic selection. This information is useful for breeding purposes, for example, by operating selection before the phenotype is measurable.
Chi-square tests are commonly used to test segregation distortion, but more advanced methods should be taken. Fu and Ritland (1994) and Lorieux et al. (1995) developed maximum likelihood methods to map SDLs. Vogl and Xu (2000) used a Bayesian method to detect multiple SDLs in a simultaneous manner. These methods are quite different from the usual QTL mapping procedures. Luo and Xu (2003) first developed an EM (expectation and maximization) algorithm for mapping viability selection loci (the same as SDLs). Luo et al. (2005) further developed a quantitative genetic model to map these loci. The above authors postulated a hidden underlying liability for each individual. The liability is an unobserved quantitative trait and selection acts on the liability. The method of Luo et al. (2005) actually maps loci controlling the hidden liability (an unobserved quantitative trait). Therefore, methods of QTL mapping and SDL mapping have been unified into the same framework of interval mapping. Most recently, Zhan and Xu (2011) extended the liability model for SDL mapping by incorporating into a prior variance to the effect of each SDL and such a method is called generalized linear mixed model (GLMM) (McGilchrist, 1994).
The GLMM approach to detecting segregation distortion (Zhan and Xu, 2011) provides a mechanism to handle missing genotypes. With proper modification, the GLMM method is able to combine different populations for joint analysis. The rice-breeding program in the Chinese Academy of Agricultural Science (CAAS) produced many small breeding populations, all under the same scheme of selection. We show that the combined analysis has increased the statistical power of QTL detection.
Materials and methods
Detecting segregation distortion in single selected population
We first dealt with a single selected population with no missing markers. We then combined several selected populations to perform a joint mapping. Because the populations are subject to selection, if a locus is linked to QTL controlling for a selected trait, for example, drought tolerance, this locus will show a segregation distorted from the expected Mendelian ratio. Although the method can be extended to any populations with known Mendelian ratios, we focus our study to the BC2F2 population, which happens to be the type of populations produced by the rice-breeding team lead by one of the corresponding authors. First, we conducted two generations of backcrosses of a donor parent to a recurrent parent (RP), obtaining a population called BC2F1. The BC2F1 progeny were then subject to one generation of selfing, resulting in a population called BC2F2. Let A1 be the allele of the RP and A2 be the allele of the donor parent. The three genotypes in the BC2F2 population have an expected Mendelian ratio of 13/16, 2/16 and 1/16 for the three genotypes, A1A1, A1A2 and A2A2, respectively. For a single population, testing segregation distortion can be performed using the Chi-square test with two degrees of freedom. However, the simple Chi-square test is hard to be extended to multiple populations. Furthermore, the Chi-square test cannot handle missing genotypes. Therefore, we adopted the generalized linear mixed model approach to test segregation distortion (Zhan and Xu, 2011).
We now focus on a single population. Let φ11=13/16, φ11=2/16 and φ22=1/16 be the expected Mendelian frequencies for the three genotypes. Let us propose an underlying quantitative trait yj for individual j of the BC2F2 population. This underlying quantitative trait is called the liability, which can be described by the following linear model, yj=Zja+ɛj, where Zj =1 for A1A1, Zj=0 for A1A2 and Zj =−1 for A2A2. The genetic effect of the locus on the liability is denoted by a. The residual error is assumed to be ɛj~N(0,1). Assume that all individuals observed are selected based on the yj>0 criterion. The surviving probability is Pr(yj>0)= Φ(Zja), where Φ(.) is the standardized cumulative normal distribution function. The surviving probability of each individual depends on the genotype and the effect of the locus (a) on the liability. Although all individuals observed have survived the selection, they can have different probabilities because they may have different genotypes. Using the Bayes' theorem, we formulated the following posterior probability of survival for each genotype, 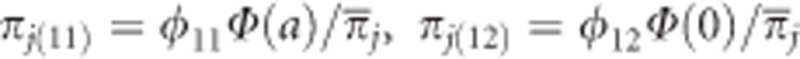 or
or 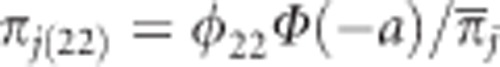 , where
, where 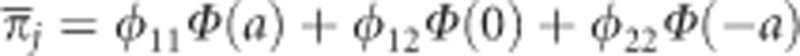 is a normalization factor (mean fitness). These posterior probabilities facilitate a mechanism for us to estimate the genetic parameter a. Note that when a=0, the three posterior probabilities would be identical to the Mendelian frequencies for all individuals and we will not be able to detect segregation distortion. If a≠0, then the posterior probabilities of genotypes will deviate from the expected Mendelian segregation ratios. Therefore, testing segregation distortion and testing the genetic effect of the liability are equivalent. This is the basis of our generalized linear model. We further placed a prior distribution on the genetic parameter, say normal prior, so that
is a normalization factor (mean fitness). These posterior probabilities facilitate a mechanism for us to estimate the genetic parameter a. Note that when a=0, the three posterior probabilities would be identical to the Mendelian frequencies for all individuals and we will not be able to detect segregation distortion. If a≠0, then the posterior probabilities of genotypes will deviate from the expected Mendelian segregation ratios. Therefore, testing segregation distortion and testing the genetic effect of the liability are equivalent. This is the basis of our generalized linear model. We further placed a prior distribution on the genetic parameter, say normal prior, so that 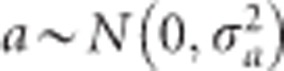 , which makes the problem as a Bayesian parameter estimation problem.
, which makes the problem as a Bayesian parameter estimation problem.
Under the Bayesian framework, we present a Bayesian posterior mode estimate of the genetic effect. The log likelihood function combined with the log prior gives the log posterior of the genetic parameter. Let us define the data using wj(11)=1 for A1A1, wj(12)=1 for A1A2, and wj(22)=1 for A2A2. Each individual is represented by values of three variables, one for each genotype. One of the three variables takes a value 1 if that variable happens to indicate the actual genotype of the individual and the other two variables must take values of zero. For example, if individual j has a genotype A1A1, then wj(11)=1 and wj(12)=wj(22)=0. With this notation, the observed count for genotype A1A1 in the population is 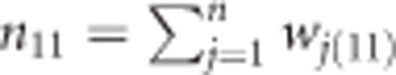 , where n is the total sample size. The log likelihood function is formulated as
, where n is the total sample size. The log likelihood function is formulated as
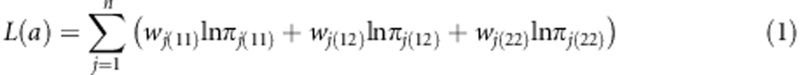 |
The logarithm of the prior normal density is
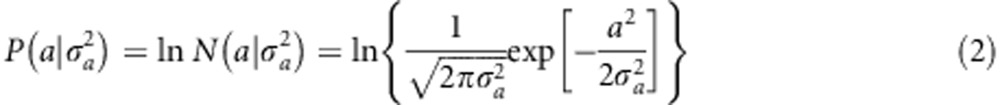 |
Ignoring a constant term (not a function of the parameter), we have the following simplified log prior,
 |
Therefore, the log posterior is 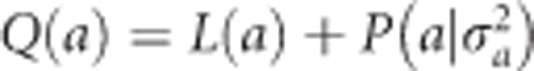 , which is the sum of the log likelihood and the log prior. The posterior modes of a and
, which is the sum of the log likelihood and the log prior. The posterior modes of a and 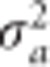 are obtained numerically by maximizing Q(a). We adopted an EM algorithm (Dempster et al., 1977) to estimate the parameters. Starting with
are obtained numerically by maximizing Q(a). We adopted an EM algorithm (Dempster et al., 1977) to estimate the parameters. Starting with 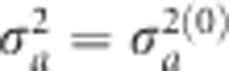 , the conditional posterior mode of a is obtained by maximizing Q(a). Let a(0) be the solution that maximizes Q(a) and the variance of a(0) is approximated by
, the conditional posterior mode of a is obtained by maximizing Q(a). Let a(0) be the solution that maximizes Q(a) and the variance of a(0) is approximated by 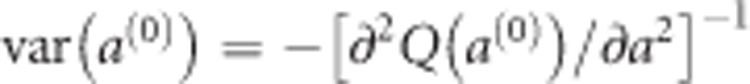 . Given a(0), we then update
. Given a(0), we then update 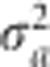 using
using
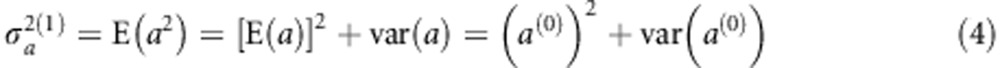 |
The updated 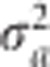 then replaces the original
then replaces the original 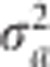 in the log posterior, which is maximized again to obtain a(1) and var(a(1)). In general, the EM iteration is described by
in the log posterior, which is maximized again to obtain a(1) and var(a(1)). In general, the EM iteration is described by 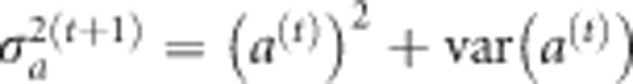 . When the iteration process converges, we get both estimates of a and
. When the iteration process converges, we get both estimates of a and 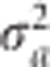 . We used the Wald test statistic,
. We used the Wald test statistic, 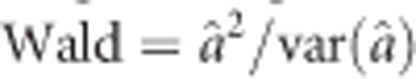 , to test the hypothesis H0:a=0. Such a Wald test is applied to every locus of the genome for detecting segregation distortion loci.
, to test the hypothesis H0:a=0. Such a Wald test is applied to every locus of the genome for detecting segregation distortion loci.
Detecting segregation distortion in multiple selected populations
Because breeding populations after selection often have small sample sizes, particularly when selection intensity is high, the power of SDL detection can be low from a single selected population. This is very important in plant breeding today when introgression (backcross) breeding with a few elite recipients is increasingly used. To increase the statistical power, we proposed to combine several populations together and perform a joint analysis for SDL in multiple populations. The GLMM method of Zhan and Xu (2011) does not have an option to perform such a joint analysis. One problem of the multiple population analysis is that different populations often involve different markers. We need to generate a consensus map, in which markers not genotyped in any single population are treated as missing markers in that population. Genotypes of missing markers are inferred from the multipoint method (Jiang and Zeng, 1997). The multipoint analysis requires transition matrix from one marker to the next marker. Let A1A1, A1A2 and A2A2 be the three genotypes for marker A and B1B1, B1B2 and B2B2 be the three genotypes for marker B. The transition matrix from A to B is given in Table 1 (derivation is complicated and thus not given) and denoted by matrix TAB, where r is the recombination fraction between the two loci. For example, if the genotype of locus A is A1A2, the probability of a individual taking genotype B1B1 is  , which is the element of the second row and the first column of matrix TAB. Given the transition matrix and the marginal frequencies of the three genotypes, the multipoint method of Jiang and Zeng (1997) directly applies for the BC2F2 population.
, which is the element of the second row and the first column of matrix TAB. Given the transition matrix and the marginal frequencies of the three genotypes, the multipoint method of Jiang and Zeng (1997) directly applies for the BC2F2 population.
Table 1. The transition matrix for two linked loci, A and B, with a recombination fraction of r in a BC2F2 populationa.
Let 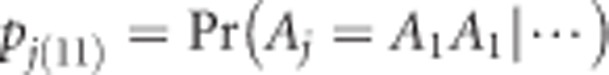 be the multipoint calculated probability of individual j taking genotype A1A1 for the locus of interest. Recall that we used wj(11) to denote the indicator of genotype A1A1. The log likelihood function for individual j is defined as
be the multipoint calculated probability of individual j taking genotype A1A1 for the locus of interest. Recall that we used wj(11) to denote the indicator of genotype A1A1. The log likelihood function for individual j is defined as
When the genotype is missing, we simply replace wj(11) by pj(11) so that
Suppose that we have p donor parents and all cross with one common RP. Let ai be the genetic effect of donor i for i = 1,...,p. The corresponding πj(11) and pj(11) in population i are denoted by 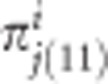 and
and 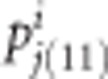 , respectively. Let us also assume that
, respectively. Let us also assume that 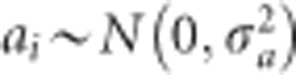 for all i = 1,...,p. The common prior variance
for all i = 1,...,p. The common prior variance 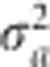 links all the populations together and provides a mechanism to increase power compared with the single population analysis. Let a = {a1,...,ap} be a vector of genetic effects, one for each population. The log likelihood function combining all populations is
links all the populations together and provides a mechanism to increase power compared with the single population analysis. Let a = {a1,...,ap} be a vector of genetic effects, one for each population. The log likelihood function combining all populations is
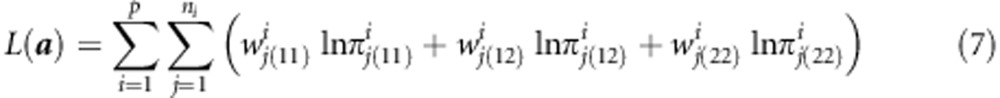 |
The log prior is 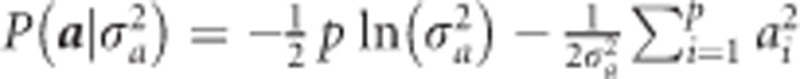 . Therefore, the log posterior is
. Therefore, the log posterior is 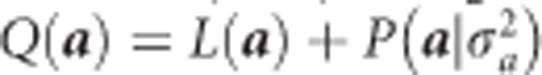 . The EM algorithm for estimating
. The EM algorithm for estimating 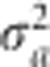 is a simple extension of the algorithm in the single population situation,
is a simple extension of the algorithm in the single population situation,
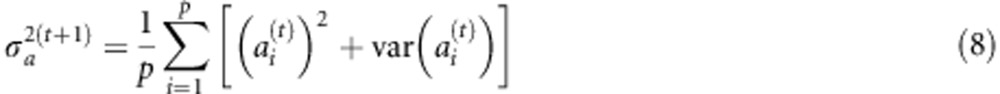 |
The corresponding Wald test for multiple populations is 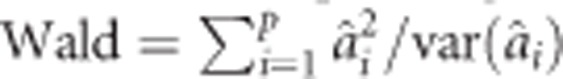 . It appears that the multiple populations Wald test simply takes the sum of the Wald test of each individual population. The gain by combining the populations comes from the common variance
. It appears that the multiple populations Wald test simply takes the sum of the Wald test of each individual population. The gain by combining the populations comes from the common variance 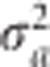 shared by all the p populations.
shared by all the p populations.
Design of simulation experiments
The new method was validated using simulated data. Twelve chromosomes were simulated with a total genome length of 1500 cM. The genome was evenly covered by 300 markers. The type of population was BC2F2, mimicking the breeding populations produced in the CAAS rice-breeding program. Two selection schemes were implemented in the experiment. One scheme was the ‘additive' fitness model where the fitness of the heterozygote was the average of the fitness of the two homozygotes. The other scheme was the ‘dominance' fitness model in which the heterozygote had the same fitness as one of the two homozygotes. Within each selection scheme, there were two levels of selection intensity: strong selection and weak selection (see Table 2). For example, in the strong additive selection, the survival probability of A1A1 genotype (RP) was only 0.05 while that of A2A2 genotype (donor parent) was 0.90. The survival probability of the heterozygote was (0.05 + 0.90)/2=0.475. We also performed a simulation experiment for two-locus joint selection. The fitness (survival probability) of the nine two-locus joint genotypes took the product of the fitness of individual loci and these fitness are given in Table 3. When the additive model and strong selection in Table 3, for example, is taken, the marginal fitness of genotype A2A2 is 0.90 and the marginal fitness for genotype B1B2 is 0.475, leading to a fitness of 0.9 × 0.475=0.4275 for the joint genotype A2A2B1B2.
Table 2. Assigned fitness values of the three genotypes at a single locus, A, under two schemes of selection used in the simulation study: additive and dominance.
| Selection scheme | Strength of selection |
Genotype |
||
|---|---|---|---|---|
| A1A1 | A1A2 | A2A2 | ||
| Additive | Strong | 0.050 | 0.475 | 0.900 |
| Weak | 0.200 | 0.400 | 0.600 | |
| Dominance | Strong | 0.050 | 0.900 | 0.900 |
| Weak | 0.200 | 0.600 | 0.600 | |
Table 3. Fitness values of the nine two-locus joint genotypes used in the simulation study.
| Selection intensity | Genotype |
Additive model |
Dominance model |
||||
|---|---|---|---|---|---|---|---|
| A1A1 | A1A2 | A2A2 | A1A1 | A1A2 | A2A2 | ||
| Strong | B1B1 | 0.0025 | 0.02375 | 0.045 | 0.0025 | 0.045 | 0.045 |
| B1B2 | 0.02375 | 0.225625 | 0.4275 | 0.045 | 0.81 | 0.81 | |
| B2B2 | 0.045 | 0.4275 | 0.81 | 0.045 | 0.81 | 0.81 | |
| Weak | B1B1 | 0.04 | 0.08 | 0.12 | 0.04 | 0.12 | 0.12 |
| B1B2 | 0.08 | 0.16 | 0.24 | 0.12 | 0.36 | 0.36 | |
| B2B2 | 0.12 | 0.24 | 0.36 | 0.12 | 0.36 | 0.36 | |
The simulation experiments were performed as described below. First, we used a Markov model to simulate 300 markers on 12 chromosomes for a BC2F2 individual under Mendelian segregation (13:2:1 ratio). Depending on the genotype of the target locus (or loci), this individual might be selected (survival) or eliminated (death). If the individual was selected, we added this individual to the sample; otherwise, it was eliminated. The simulation was repeated until n=10, 25 or 50 individuals were cumulated in the sample. For the single locus selection experiment, the locus at position 50 cM on chromosome 6 was the target locus for selection. For the two-locus joint selection experiment, one locus at position 50 cM on chromosome 6 and the other locus at position 45 cM on chromosome 10 were the target loci for selection. Under each scenario, the simulation was replicated 100 times to facilitate power analyses.
Plant materials
Two selected populations of rice were used as the materials for testing the methods described above. A superior high yield japonica variety from Northeast China, Ji-Geng88 (JG88), was used as the RP of the introgression populations. Two other varieties, Sheng-Nong265 (SN265) and MR77, were used as the donor parents. SN265 is a japonica variety from Northeast China and MR77 is an indica variety from Malaysia. The RP was crossed with each of the two donors to generate F1 progeny, which were backcrossed with the RP for two generations to produce BC2F1 lines. The selfed seeds of all BC2F1 plants from each cross were bulk-harvested to produce a BC2F2 population. In the summer of 2011, we planted 800 individuals from each population under normal irrigated field conditions on the farm of the Ningxia Academy of Agricultural Science (NAAS) of Northwest China. At maturity, we visually selected 68 BC2F2 plants, which had ideal plant type and high yield compared with the RP parents, plus 120 random BC2F2 plants from the two populations in the field. These included 98 BC2F2 introgression lines (ILs) (38 from selected population and 60 from random population) from the JG88/SN265 cross and 90 ILs (30 from selected population and 60 from random population) from the JG88/MR77 cross. On May 5 of 2012, seeds of all BC2F2 ILs sown on the seedling nursery and 25-day seedlings of each IL were transplanted into a two-row plot of 20 plants on the experimental farm of the Institute of Crop Sciences, Chinese Academy of Agricultural Sciences (CAAS) in Beijing. In the field layout, one RP plot was inserted in every 10 plots as the checks. The field was managed with regular irrigation and the standard crop management practices. At maturity, five typical plants in each plot were harvested and placed in a plastic net bag. All harvested plants were dried in drying ovens under 80 °C for 3 days. The dried plant samples were then measured for grain yield (GY) per plant. In the summer of 2013, the 188 BC2F4 lines were progeny-tested for GY under the same conditions on the CAAS experimental farm in Beijing. The 98 BC2F2 ILs from the JG88/MR77 population were genotyped with 120 polymorphic SSR markers and the 90 BC2F2 ILs from the JG88/SN265 population were genotyped with 38 polymorphic SSR markers. On the basis of the 2-year phenotypic data, 21 ILs from the JG88/MR77 population showed consistently higher yield than the RP parent (JG88), while 26 ILs of the JG88/SN265 population had significantly higher yield than the JG88 parent.
Results
Simulation studies
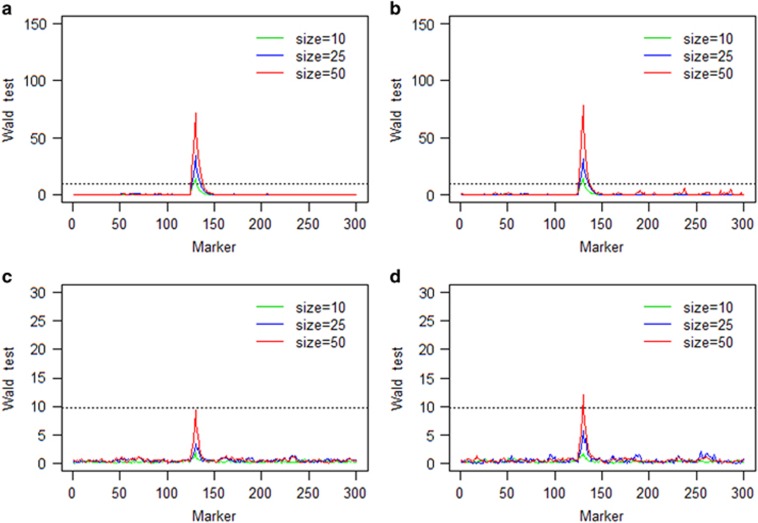
The average Wald test statistics of 100 repeated simulations of the single locus selection experiment using one population are presented in Figure 1. Under the strong selection scenario (both additive and dominance), the target locus was successfully detected in all three different population sizes using 9.85 as the critical value of the Wald test statistics (drawn from 1000 repeated simulations under the null model). Under the weak selection, however, the target locus was detected only in the dominance selection scenario with sample size 50. Under all population sizes, the Wald test statistic was higher in the dominance selection model than that in the additive selection model.
Figure 1.
Wald test statistics of the single locus selection simulation experiment using one population: (a) strong additive fitness selection; (b) strong dominance fitness selection; (c) weak additive fitness selection; and (d) weak dominance fitness selection. The horizontal broken line on each panel is the 9.85 threshold in Wald test statistic drawn from 1000 repeated simulations of the null model. Note that 10, 25 and 50 are the numbers of selected plants and are defined as the population sizes.
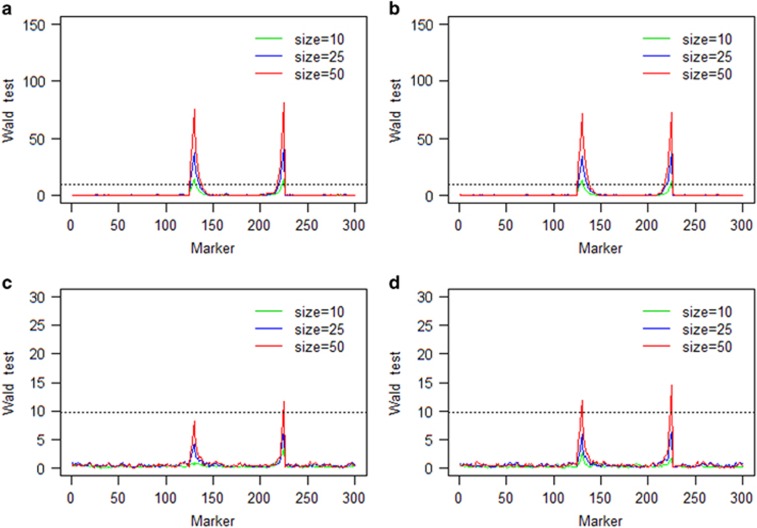
When two genetically independent target loci were involved in the selection, the target loci were detected only in three scenarios with population size 50, but not under other cases (Figure 2). Larger sample size and stronger selection had greater powers in detecting the target loci with higher test statistics. Again, under the same scenarios of selection and sample size, the Wald test statistic was higher for the dominance fitness model than the additive fitness model.
Figure 2.
Wald test statistics of the two-locus selection simulation experiment using one population: (a) strong additive fitness selection; (b) strong dominance fitness selection; (c) weak additive fitness selection; and (d) weak dominance fitness selection. The horizontal broken line on each panel is the 9.85 threshold in Wald test statistics drawn from 1000 repeated simulations under the null model.
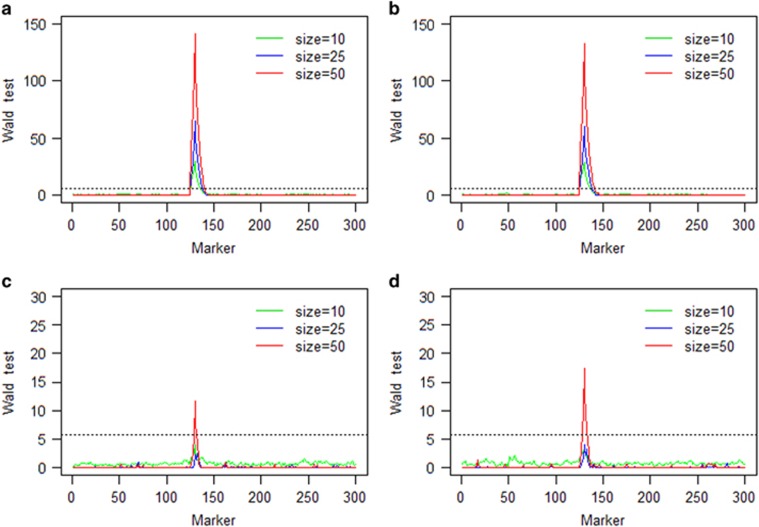
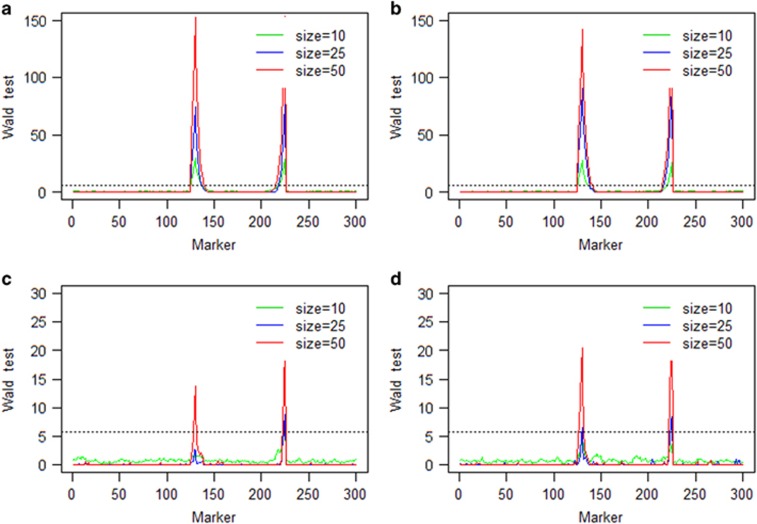
The average Wald test statistics over 100 repeated simulations of the single locus selection experiment using two combined populations are given in Figure 3. Under strong selection, the target locus was detected successfully in all scenarios using a critical value of 5.83 of the Wald test statistics (drawn from 1000 repeated simulations under the null model). For weak selection, the target locus was detected only when the sample size was 50. Figure 4 presents the average Wald test statistics for the two locus selection experiment using two combined populations. The target loci were detected successfully in all scenarios under strong selection. Under the additive fitness model with weak selection, the target loci were also detected in all scenarios except for the additive model with population size 10. Comparing the results of Figures 3 and 4, we found that the Wald test statistics were much greater for the two populations combined analysis than those for the single population analysis.
Figure 3.
Wald test statistics of the single locus selection simulation experiment using two combined populations: (a) strong additive fitness selection; (b) strong dominance fitness selection; (c) weak additive fitness selection; and (d) weak dominance fitness selection. The horizontal broken line on each panel is the 5.83 threshold in Wald test statistics drawn from 1000 repeated simulations under the null model.
Figure 4.
Wald test statistics of the two-locus selection simulation experiment using two combined populations: (a) strong additive fitness selection; (b) strong dominance fitness selection; (c) weak additive fitness selection; and (d) weak dominance fitness selection. The horizontal broken line on each panel is the 5.83 threshold in Wald test statistics drawn from 1000 repeated simulations under the null model.
Tables 4 and 5 show the average statistical powers from the 100 repeated simulation experiments. Under strong selection, the power of detecting segregation distortion was very high and the combined analysis of multiple populations had further increased the power. Under weak selection, the power was low, particularly when the sample size was smaller than 25.
Table 4. Statistical powers in detecting segregation distortion obtained from 100 replicated simulation experiments of a single population analysis.
| Selection intensity | Sample size |
One locus |
Two loci |
||
|---|---|---|---|---|---|
| Additive | Dominance | Additive | Dominance | ||
| Strong | 10 | 75% | 88% | 73% | 71.5% |
| 25 | 100% | 100% | 100% | 100% | |
| 50 | 100% | 100% | 100% | 100% | |
| Weak | 10 | 0% | 2% | 0% | 0% |
| 25 | 12% | 6% | 6% | 9% | |
| 50 | 44% | 60% | 28% | 48% | |
Table 5. Statistical powers in detecting segregation distortion for two loci obtained from 100 replicated simulation experiments using two population combined analysis.
| Selection intensity | Sample size |
One locus |
Two loci |
||
|---|---|---|---|---|---|
| Additive | Dominance | Additive | Dominance | ||
| Strong | 10 | 100% | 100% | 96% | 100% |
| 25 | 100% | 100% | 100% | 100% | |
| 50 | 100% | 100% | 100% | 100% | |
| Weak | 10 | 30% | 20% | 4% | 10% |
| 25 | 20% | 18% | 8% | 18% | |
| 50 | 76% | 92% | 48% | 78% | |
Real data analysis
Table 6 shows the summary statistics for GY of the selected and unselected (random) populations from the two introgression populations. In 2012, the mean GY of the 30 selected BC2F3 lines from cross JG88/MR77 and the 38 selected BC2F3 lines from cross JG88/SN265 were 12.2% and 16.5%, respectively, higher than that of the RP JG88. These two selected populations had variances of GY reduced by 50.2% and 46.5%, respectively, compared with the random populations. The 21 confirmed high yield BC2F3 lines of cross JG88/MR77 and the 26 confirmed high yield BC2F3 lines of cross JG88/SN265 had means of GY 18.9% and 24.5% higher than that of the JG88 parent, respectively. These lines had GY variances reduced by 71.8% and 65.1%, respectively, compared with the random populations. In 2013, the mean GY of the 30 selected BC2F4 lines from cross JG88/MR77 was the same as that of the JG88 parent, while the mean GY of the 38 selected BC2F4 lines from cross JG88/SN265 was 12.2% higher than that of the JG88 parent. The two selected introgression populations had variances of GY reduced by 38.3% and 31.5%, respectively, compared with the random populations. The 21 confirmed high yield BC2F4 lines of cross JG88/MR77 and the 26 confirmed high yield BC2F4 lines of cross JG88/SN265 had means of GY 7.8% and 15.9% higher than that of the JG88 parent, respectively. The variances in GY were reduced by 61.6% and 56.2%, respectively, for the two populations compared with the random populations.
Table 6. Summary statistics of selected and unselected populations for grain yield from two introgression populations of rice.
|
Population |
Grain yield (g/plant) in year 2012 |
Grain yield (g/plant) in year 2013 |
|||||
|---|---|---|---|---|---|---|---|
| Cross | Size (N) | Mean | Variance | Range | Mean | Variance | Range |
| JG88/MR77 | 60a | 21.3 | 25.9 | 9.7~33.4 | 24.6 | 22.2 | 14.4~32.8 |
| 30b | 23.8 | 12.9 | 15.6~30.4 | 24.8 | 13.7 | 17.5~32.1 | |
| 21c | 25.2 | 7.3 | 20.6~30.4 | 26.4 | 8.5 | 22.2~32.1 | |
| JG88/SN265 | 60a | 23.1 | 31.8 | 10.4~39.1 | 27.8 | 25.1 | 16.1~35.4 |
| 38b | 24.7 | 17.0 | 15.1~34.4 | 27.5 | 17.2 | 16.5~37.2 | |
| 26c | 26.4 | 11.1 | 20.4~34.4 | 28.4 | 11.0 | 22.5~37.2 | |
| JG88 (CK) | 10 | 21.2 | 5.4 | 18.2~26.4 | 24.5 | 8.1 | 20.2~29.6 |
Population size: the number of BC2F4 lines from the random (unselected) population.
Population size: the number of BC2F3 lines selected for high yield.
Population size: the number of BC2F4 lines with higher yield than the JG88 parent based on progeny testing.
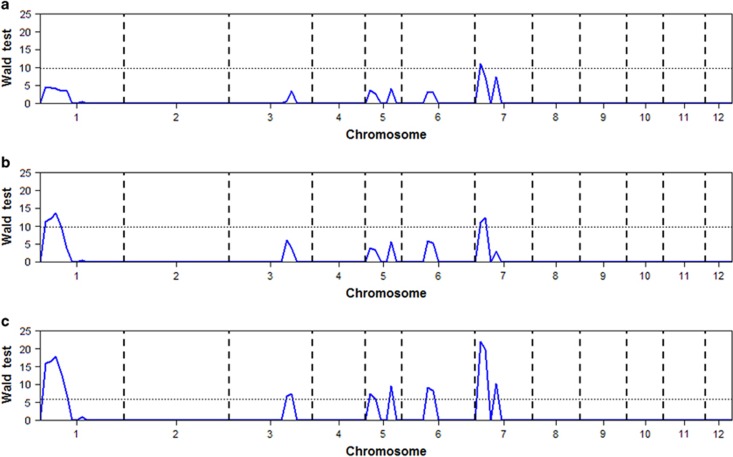
When using a single population and the 9.85 threshold in Wald test statistics (drawn from 1000 permutations under the null model), the segregation distortion approach based on 120 markers for population JG88/MR77 detected one QTL for yield and the same approach based on 38 markers for population JG88/SN265 detected two QTLs, with one common QTL near RM481 on chromosome 7 detected in both populations (see Figures 5a and b). When the two populations were combined using a consensus linkage map with a total of 133 markers (including imputed missing markers), we detected seven QTLs for yield on rice chromosomes 1, 3, 5, 6 and 7, based on the 5.83 threshold drawn from multiple permuted samples under the null model (Figure 5c, see also Table 7). Four out of the seven QTLs (qGY1.2, qGY5.2, qGY7.1, qGY7.4) were detected in the combined two populations (see Table 7). Results of the real data analysis are consistent with those of the simulation studies in that the combined analysis detected more QTLs than the single population analysis.
Figure 5.
Wald test statistic profiles for segregation distortion in individual populations and combined population selected for high yield: (a) population JG88/MR77; (b) population JG88/SN265; and (c) combined two populations. The horizontal broken lines on panels (a) and (b) are the 9.85 threshold in Wald test statistics and the corresponding line in panel (c) is the 5.83 threshold in Wald test statistics drawn from 1000 permuted samples under the null model.
Table 7. Quantitative trait loci for grain yield (GY) detected via segregation distortion in two selected breeding populations of rice using two population joint analysis.
| QTL | Marker |
BC2F2
single plant selection |
BC2F3
and BC2F4
progeny testing |
||
|---|---|---|---|---|---|
| Wald test | P-value | Wald test | P-value | ||
| qGY1.2 | RM220 | 15.86 | 0.0004 | 9.36 | 0.0092 |
| qGY3.10 | RM186 | 7.32 | 0.0258 | ||
| qGY5.2 | RM413 | 7.47 | 0.0239 | 6.76 | 0.0339 |
| qGY5.5 | RM430 | 9.60 | 0.0082 | ||
| qGY6.3 | RM217 | 8.35 | 0.0154 | ||
| qGY7.1 | RM481 | 19.73 | <0.0001 | 24.22 | 5.5E-06 |
| qGY7.4 | RM542 | 10.29 | 0.0058 | 10.28 | 0.0059 |
To validate the mapping results, data from the random (unselected) populations of 60 BC2F3/BC2F4 lines from each cross were used to validate the QTL near marker RM481 on chromosome 7, qGY7.1. This locus had the largest effect on GY among all other QTLs. The random ILs with the donor genotype (BB) had 3.2 g higher GY per plant, 13% higher than the recipient genotype (AA). The difference was statistically significant in both populations and both years, except for the JG88/MR77 population in 2013 (see Table 8).
Table 8. Validation via t-test for association of grain yield (g/plant) with marker RM481 (qGY7.1) in random BC2F3 (2012) and BC2F4 (2013) populations from crosses JG88/SN265 and JG88/MR77.
| Population | Year |
Genotype |
Additive effect | P-value | |
|---|---|---|---|---|---|
| AA | BB | ||||
| JG88/MR77 | 2012 | 20.7±3.9 | 23.9±2.8 | 1.6 | 0.031 |
| 2013 | 24.3±4.9 | 24.7+2.2 | 0.2 | 0.785 | |
| JG88/SN265 | 2012 | 22.7±4.2 | 25.8±2.4 | 1.6 | 0.021 |
| 2013 | 27.3±3.4 | 30.4±1.8 | 1.6 | 0.008 | |
Discussion
In modern plant and animal breeding, directional phenotypic selection remains the most powerful way for genetic improvement of productivity in agricultural crops and animals. A unique characteristic of these breeding programs is that breeders are handling large numbers of progenies derived from dozens or even hundreds of crosses between a few key backbone (elite) parents and a diverse set of donors with a relatively small number of progenies from each cross. These breeding progenies normally have been selected for different combinations of target traits and thus contain important genetic information regarding the target traits of selection. These progeny are also segregating for some non-target traits as a result of genetic hitchhiking (Zhang et al., 2013). Therefore, advanced lines from breeding populations can be useful materials for identifying and mapping loci associated with traits interesting to breeders. However, mapping QTL in selected populations is challenging because of the reduced variance of traits in the selected populations and the small population sizes after selection. The reduced trait variance may cause substantial power loss in QTL detection, even under moderate selection intensity. The small populations after selection are too small to be utilized for QTL mapping using a conventional marker–trait association model. Nevertheless, efforts have recently been made to map QTL in single selected populations by detecting segregation distortion loci using simple Chi-square tests (Li et al., 2005; Venuprasad et al., 2009; Zhang et al., 2011, 2014). Obviously, the simple Chi-square tests are not the optimal methods because they cannot take advantage of the unique feature of large number of small advanced breeding progenies to perform a joint analysis in most plant and animal breeding programs. In this respect, the method developed in this study provided a powerful strategy for detecting QTL in selected breeding populations of plants and animals.
Our results indicated that mapping QTL by detecting segregation distortion is effective in detecting QTL affecting complex traits in selected populations. If the small population sizes are due to strong selection, the new method actually enjoys small populations because they mean strong selection had happened and thus high degrees of segregation distortion are expected. Results of our study were consistent with several recent studies where large numbers of loci responsive to strong directional selection for abiotic stress tolerances and heritable quantitative traits were detected and mapped (Zhang et al., 2014; Wang et al., 2015).
Compared with a previously developed method of multiple SDL mapping in single populations (Zhan and Xu, 2011), our approach of joint mapping using multiple small and related breeding populations by testing segregation distortion was more powerful in detecting QTL affecting traits with low heritability. Therefore, our new method has solved two major problems in mapping QTL in selected populations, that is, the extremely small population sizes and low genome coverage by DNA markers in single selected breeding populations. This was clearly demonstrated by identifying and mapping seven QTLs for GY in the two small selected populations of rice. We noted that among the seven QTLs identified for GY, four (qGY1.2, qGY5.2, qGY7.1 and qGY7.4) were consistently identified with data from single selected BC2F2 plants and their corresponding BC2F3 progeny (Table 7). Interestingly, qGY7.1 had the largest phenotypic effect and was verified in the random populations of both crosses (Table 8). qGY1.2 was mapped to the close vicinity of Gn1a, a cloned gene that increases grain number per panicle and grain weight by reducing the expression of OsCKX2 that leads to accumulation of cytokinins in inflorescence meristems (Ashikari et al., 2005). The qGY7.4 overlaps with Ghd7, another cloned gene that regulates yield by modulating panicle branching (Weng et al., 2014). qGY5.2 is also in the vicinity of a previously cloned gene, GW5, which improves GY by regulating cell division during seed development (Weng et al., 2008). These four newly detected QTLs were less likely to be false positives.
The new method of QTL mapping developed in this study will have a huge potential to be applied to real plant and animal breeding programs, as most breeding materials consist of advanced lines or families selected for one or more target traits from related segregating populations. As the high throughput and cost-effective SNP genotyping technology has become increasingly feasible in many important crops and domestic animals, identification and mapping of QTL associated with both target and non-target traits from breeding materials will provide extremely valuable genetic information for breeders, which is expected to be a routine practice in the post-genomic era plant and animal breeding programs (Li and Zhang, 2013).
Our method of combined QTL analysis by detecting segregation distortion in multiple breeding populations remains a one-dimensional approach for genome-wide scan of loci affecting target traits responsive to directional selection. Efficient and powerful statistical methods for characterizing high dimensional non-random associations (epistasis) between or among alleles at unlinked loci resulting from selection are needed (Zhang et al., 2014) but are hard to address under the current models. Extension to pairwise interaction involving two loci at a time may be possible with some modification of the one-dimensional scan to two-dimensional scan. Such an extension is a future project of this research team.
Implementation of the new method for QTL mapping via segregation distortion is straightforward. It requires marker genotype imputation for non-overlapping markers in the multiple population joint analysis. If all markers are aligned perfectly among all populations to be combined, this step can be escaped. An R code called multiple imputation is available from authors as request for marker genotype imputation. Users are required to provide the expected Mendelian segregation ratios and the transition matrix that are determined by the type of introgression population. Once the genotypes of all markers are imputed, the second step is to call an R function named SDL method to perform the joint multiple population analysis using the GLMM method described in the text. These R codes along with a BC2F2 sample data which includes two breeding populations as a package named SDL BC2F2 method have been uploaded to our CAAS rice-breeding website (www.rmbreeding.cn).
Data archiving
Data available from the Dryad Digital Repository: http://dx.doi.org/10.5061/dryad.f6rr4.
Acknowledgments
The project was supported by the United States Department of Agriculture National Institute of Food and Agriculture Grant 2007-02784 to SX, The National Natural Science Foundation of China-Consultative Group on International Agriculture Research (NSFC-CGIAR #31261140369) to ZL, The 863 GSR grants (2014AA10A601) and Shenzhen Peacock Plan and BMGF grants (GD1393) to ZL. Yanru Cui was supported by the Beachell-Borlaug International Student Fellowship from Monsanto.
The authors declare no conflict of interest.
References
- Ashikari M, Sakakibara H, Lin S, Yamamoto T, Takashi T, Nishimura A. (2005). Cytokinin oxidase regulates rice grain production. Science 309: 741–745. [DOI] [PubMed] [Google Scholar]
- Collard BC, Mackill DJ. (2008). Marker-assisted selection: an approach for precision plant breeding in the twenty-first century. Phil Trans R Soc Lond B Biol Sci 363: 557–572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Darvasi A, Soller M. (1992). Selective genotyping for determination of linkage between a marker locus and a quantitative trait locus. Theor Appl Genet 85: 353–359. [DOI] [PubMed] [Google Scholar]
- Dempster AP, Laird NM, Rubin DB. (1977). Maximum likelihood from incomplete data via the EM algorithm. J R Stat Soc B 39: 1–38. [Google Scholar]
- Falconer DS, Mackay TFC. (1996) Introduction to Quantitative Genetics. Addison Wesley Longman: Harlow, Essex, UK. [Google Scholar]
- Francia E, Tacconi G, Crosatti C, Barabaschi D, Bulgarelli D, Dall'Aglio E, Valè G. (2005). Marker assisted selection in crop plants. Plant Cell Tissue Organ Cult 82: 317–342. [Google Scholar]
- Fu YB, Ritland K. (1994). On estimating the linkage of marker genes to viability genes-controlling inbreeding depression. Theor Appl Genet 88: 925–932. [DOI] [PubMed] [Google Scholar]
- Hermisson J, Wagner GP. (2004). The population genetic theory of hidden variation and genetic robustness. Genetics 168: 2271–2284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang C, Zeng ZB. (1997). Mapping quantitative trait loci with dominant and missing markers in various crosses from two inbred lines. Genetica 101: 47–58. [DOI] [PubMed] [Google Scholar]
- Lander ES, Botstein D. (1989). Mapping Mendelian factors underlying quantitative traits using RFLP linkage maps. Genetics 121: 185–199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li ZK, Fu BY, Gao YM, Xu JL, Ali J, Lafitte HR et al. (2005). Genome-wide introgression lines and their use in genetic and molecular dissection of complex phenotypes in rice (Oryza sativa L.). Plant Mol Biol 59: 33–52. [DOI] [PubMed] [Google Scholar]
- Li Z, Zhang F. (2013). Rice breeding in the post-genomics era: from concept to a practice. Curr Opin Plant Biol 16: 261–269. [DOI] [PubMed] [Google Scholar]
- Lorieux M, Goffinet B, Perrier X, León DG, Lanaud C. (1995). Maximum-likelihood models for mapping genetic markers showing segregation distortion. 1. Backcross populations. Theor Appl Genet 90: 73–80. [DOI] [PubMed] [Google Scholar]
- Luo L, Xu S. (2003). Mapping viability loci using molecular markers. Heredity 90: 459–467. [DOI] [PubMed] [Google Scholar]
- Luo L, Zhang YM, Xu S. (2005). A quantitative genetics model for viability selection. Heredity 94: 347–355. [DOI] [PubMed] [Google Scholar]
- Lynch M, Walsh B. (1998) Genetics and Analysis of Quantitative Traits. Sinauer Associates, Inc.: Sunderland, MA. [Google Scholar]
- McGilchrist CA. (1994). Estimation in generalized mixed models. J R Stat Soc B 56: 61–69. [Google Scholar]
- Miah G, Rafii MY, Ismail MR, Puteh AB, Rahim HA, Islam Kh N, Latif MA. (2013). A review of microsatellite markers and their applications in rice breeding programs to improve blast disease resistance. Int J Mol Sci 14: 22499–22528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vogl C, Xu SZ. (2000). Multipoint mapping of viability and segregation distorting loci using molecular markers. Genetics 155: 1439–1447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Venuprasad R, Bool ME, Dalid CO, Bernier J, Kumar A, Atlin GN. (2009). Genetic loci responding to two cycles of divergent selection for grain yield under drought stress in a rice breeding population. Euphytica 167: 261–269. [Google Scholar]
- Wang Z, Cheng J, Chen Z, Huang J, Bao Y, Wang J, Zhang H. (2012). Identification of QTLs with main, epistatic and QTL x environment interaction effects for salt tolerance in rice seedlings under different salinity conditions. Theor Appl Genet 125: 807–815. [DOI] [PubMed] [Google Scholar]
- Weng J, Gu S, Wan X, Gao H, Guo T, Su N et al. (2008). Isolation and initial characterization of GW5, a major QTL associated with rice grain width and weight. Cell Res 18: 1199–1209. [DOI] [PubMed] [Google Scholar]
- Weng X, Wang L, Wang J, Hu Y, Du H, Xu C et al. (2014). Grain number, plant height, and heading date7 is a central regulator of growth, development, and stress response. Plant Physiol 164: 735–747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhan H, Xu S. (2011). Generalized linear mixed model for segregation distortion analysis. BMC Genet 12: 97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang H, Wang H, Qian Y, Xia J, Li Z, Shi Y et al. (2013). Simultaneous improvement and genetic dissection of grain yield and its related traits in a backbone parent of hybrid rice (Oryza sativa L.) using selective introgression. Mol Breed 31: 181–194. [Google Scholar]
- Zhang F, Zhai H, Paterson A, Xu J, Gao Y, Zheng T et al. (2011). Dissecting genetic network underlying complex phenotypes: the theoretical framework. PloS One 6: e14541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang F, Ma X, Gao Y, Hao X, Li Z. (2014). Genome-wide response to selection and genetic basis of cold tolerance in rice (Oryza sativa L.). BMC Genet 15: 55. [DOI] [PMC free article] [PubMed] [Google Scholar]