A comparison of genomic selection models across time in interior spruce (Picea engelmannii × glauca) using unordered SNP imputation methods

Abstract

Genomic selection (GS) potentially offers an unparalleled advantage over traditional pedigree-based selection (TS) methods by reducing the time commitment required to carry out a single cycle of tree improvement. This quality is particularly appealing to tree breeders, where lengthy improvement cycles are the norm. We explored the prospect of implementing GS for interior spruce (Picea engelmannii × glauca) utilizing a genotyped population of 769 trees belonging to 25 open-pollinated families. A series of repeated tree height measurements through ages 3–40 years permitted the testing of GS methods temporally. The genotyping-by-sequencing (GBS) platform was used for single nucleotide polymorphism (SNP) discovery in conjunction with three unordered imputation methods applied to a data set with 60% missing information. Further, three diverse GS models were evaluated based on predictive accuracy (PA), and their marker effects. Moderate levels of PA (0.31–0.55) were observed and were of sufficient capacity to deliver improved selection response over TS. Additionally, PA varied substantially through time accordingly with spatial competition among trees. As expected, temporal PA was well correlated with age-age genetic correlation (r=0.99), and decreased substantially with increasing difference in age between the training and validation populations (0.04–0.47). Moreover, our imputation comparisons indicate that k-nearest neighbor and singular value decomposition yielded a greater number of SNPs and gave higher predictive accuracies than imputing with the mean. Furthermore, the ridge regression (rrBLUP) and BayesCπ (BCπ) models both yielded equal, and better PA than the generalized ridge regression heteroscedastic effect model for the traits evaluated.

Introduction

The principal limitation in most tree-improvement programs is the time required for the completion of one cycle of breeding, testing and selection. In some programs, it can take up to 30 years to complete a single cycle of breeding, specifically for traits with late expression patterns. Strategies to maximize genetic gain per unit time should then be the primary focus to rationalize the enormous spatial and economic requirements associated with forest tree-improvement practices (White et al., 2007). The concept of genomic selection (GS) (Meuwissen et al., 2001) has promised to reduce the time associated with breeding cycles, and has since established itself as a paradigm in animal (Hayes et al., 2009) and plant (Heffner et al., 2009) breeding systems. Though this movement has yet to occur within a forest tree species context.

The novel GS approach combines phenotypes and genotypes of a training population (TP) to develop a prediction model that estimates genomic breeding values (GEBV) for selection candidates, requiring only their genotypic information (Meuwissen et al., 2001). This method may circumvent the need for the long testing phase that forest trees require to attain accurate phenotypic data for traditional pedigree-based estimation of breeding values, and offers a unique opportunity to substantially increase the response to selection through increasing the number of selection candidates. Previously, marker-assisted early selection (MAES) has been considered as a selection strategy for forest tree breeding to exploit the linkage disequilibrium (LD) between quantitative trait loci (QTL) and genetic markers (White et al., 2007). However, MAES has not been rewarding in forest tree breeding programs owing to its severe limitations (Strauss et al., 1992).

The primary constraint that has withheld MAES from use in forest trees is the low proportion of the phenotypic variance accounted for by the relatively low number of statistically significant markers used in the analysis (White et al., 2007). This limitation results primarily from the infinitesimal genetic architecture of most complex growth-related traits (Hill et al., 2008). Further limitations to MAES in forest trees include low levels of LD (Neale and Savolainen, 2004) and strong QTL-environment and QTL-lineage interactions due to overestimation of the QTL effects (Beavis, 1998). GS is fundamentally different from MAES through its simultaneous use of phenotypes and dense set of markers (thousands), which are implemented without a prior assumption concerning marker significance. GS is thus thought to capture more variation in traits with complex inheritance because it is assumed that at least some of the many fitted markers will be in LD with some of the QTL of the desired trait (Meuwissen et al., 2001).

The GS method has been enabled via current generation sequencing technologies, their low per-sample cost and the use high density single nucleotide polymorphism (SNP) genotyping platforms such as genotyping-by-sequencing (GBS) (Elshire et al., 2011). The GBS method is characterized by its use of methylation-sensitive restriction enzymes to reduce genome complexity, and high levels of multiplexing, which efficiently obtain genome-wide SNP markers. The GBS pipeline thus does not require prior genomic information, making it suitable for non-model species such as forest trees owing to their current lack of high-quality reference genomes (Elshire et al., 2011). Recently, Chen et al. (2013) successfully demonstrated the suitability of GBS for SNP discovery in two economically important forest tree species, white spruce (Picea glauca (Moench) Voss) and lodgepole pine (Pinus contorta Dougl. ex. Loud.). The density of SNP markers obtained by GBS can be increased substantially by tolerating high levels of missing data and use of marker imputation (Crossa et al., 2013). However, the benefit of using imputation and the optimal imputation method have not yet been completely validated in GS studies that utilize GBS (Rutkoski et al., 2013).

The potential for use of GS in forest trees was first explored by Grattapaglia and Resende (2011) through the use of deterministic simulation studies. More recently, empirical studies have all produced promising results in regards to acceleration of the breeding cycle for three tree species; namely, eucalypts (Eucalyptus spp.) (Resende et al., 2012a), loblolly pine (Pinus taeda L.) (Zapata-Valenzuela et al., 2012; Resende et al., 2012b, c) and white spruce (Beaulieu et al., 2014a, b). This study represents a novel approach over the preceding studies through the application of the non-model GBS SNP discovery pipeline, in addition to high missing data ratio imputation methods to produce GS prediction models.

In the present study, we randomly selected 769 40-year-old interior spruce (Picea engelmannii × glauca) trees from 25 elite open-pollinated families grown on two progeny test sites near Prince George, BC. Height at ages 3, 6, 10, 15, 30 and 40 were used to obtain estimates of pedigree-based breeding values (EBV), narrow-sense heritability, age-age genetic correlations, and in combination with SNP marker data, GS prediction models and associated GEBV. The prediction models were developed using three statistical approaches: ridge regression BLUP (rrBLUP), generalized ridge regression (GRR) and BayesCπ (BCπ). Further, we used the GBS pipeline for discovery of SNP markers for each of the 769 interior spruce trees. Three unordered high-density SNP imputation methods (K-Nearest Neighbor (KNN); Singular Value Decomposition (SVD); Mean Imputation (M60)) were used on a 60% missing data set to produce the SNP table, and used to explore the effect of imputation method.

The objectives of this study are to: (i) Assess the predictive accuracy (PA) of GS at different ages for the complex trait, tree height, in interior spruce, (ii) evaluate the temporal PA of GS models for purposes of model retraining, (iii) explore variation of PA in the previous two objectives using combinations of three GS statistical approaches and three imputation methods, (iv) consider the suitability of SNPs discovered through a GBS pipeline in conjunction with unordered high-density imputation, for GS in interior spruce, and (v) assess the relative efficiency of GS to traditional pedigree-based BLUP selection.

Materials and Methods

Genetic material

Fresh foliage was obtained post flush in spring 2013 from two 40 year-old interior spruce progeny trial sites, Quesnel and PGTIS, located within the Prince George Seed Planning Zone (SPZ) of North-central British Columbia, Canada (http://www2.gov.bc.ca/gov/topic.page?id=E06AB7FFB0AA49B8814483B1ADC1F5F8). Tissues were sampled, separated, sealed and placed on ice prior to being stored at −80 °C until DNA extraction. Briefly, the two sites, PGTIS (Lat. 53.771639 N, Long. 122.718778 W, Elev. 610 m) and Quesnel (Lat. 52.990889 N, Long. 122.2085 W, Elev. 915 m), contain a total of 32 940 trees initially planted with 2-year-old container nursery stock in a randomized complete block design. The two sites are represented by the same 174 open-pollinated families each planted in 10-tree-row plots within 10 replicate blocks and 2.5 by 2.5 mm spacing. This study concerns 769 randomly selected trees from within a subset of 25 elite families based on breeding value for tree volume.

Phenotypic data and MBLUP analysis

Tree height (m) at ages 3, 6, 10, 15, 30 and 40 year were used in this study. Mature tree heights were obtained using an ultrasonic clinometer Vertex III (Haglöf, Långsele, Sweden). The full data set consisting of a maximum of 29 475 trees from 174 open-pollinated families were used for estimation of variance components, EBVs, age-age genetic correlations (r_ij), narrow-sense individual tree heritabilities 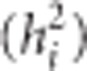and their respective standard errors. The following pedigree-based, multivariate polygenic model (MBLUP) (Mrode, 2014) was implemented using ASReml v. 3.0 software (VSN International, Hemel Hempstead, UK; Gilmour et al., 2009):

where Y_i is the vector of phenotypes for height at the i^th year, and X_i and Z_i are the incidence matrices relating observations of height at the i^th year to the vector of fixed site effect (β_i), and vectors of random additive genetic effect (a_i), block effect (b_i), additive genetic by site effect (ae_i), and residual effect (e_i). Assuming, 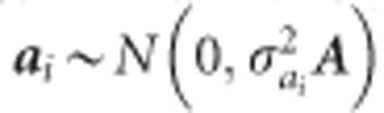is the additive genetic variance for the i^th trait and A is the average numerator relationship matrix; 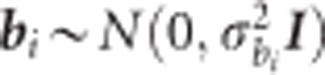, where 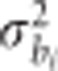is the block variance for i^th trait, and I is the identity matrix; 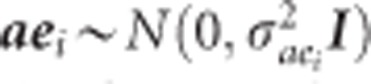, where 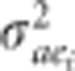is the additive genetic by site interaction variance for the i^th trait; and 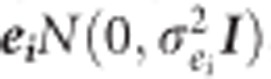, where 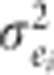is the residual variance for the i^th trait. The covariance matrix of the additive genetic term was modeled with a heterogeneous general correlation structure (‘CORGH') in ASReml to directly obtain age-age genetic correlations (Gilmour et al., 2009).

Estimates of individual tree narrow-sense heritability, 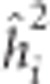, for trait i were calculated as the ratio of estimated additive variance 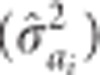to total phenotypic variance 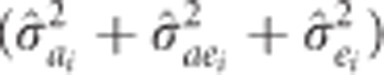from equation (1). Accuracy of individual EBVs for height at age i obtained from the MBLUP model were estimated following Dutkowski et al. (2002):

where PEV is the individual tree prediction error variance (square of standard error), and 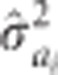is the estimated additive genetic variance component of the i^th trait from equation (1).

SNP genotyping and missing data imputation

SNP markers were discovered utilizing a GBS pipeline for non-model species; see Chen et al. (2013) for details. Additionally, the three SNP imputation methods evaluated in this study for SNP tables with 60% missing data were: mean imputation (M60), KNN with special family weighting (KNN) and SVD. The KNN and SVD imputation methods are described in detail by Gamal El-Dien et al. (2015). Mean imputation was carried out using the ‘A.mat' function provided in the ‘rrBLUP' R package, and refers to imputation using the mean for each marker (Endelman, 2011).

Genomic selection

Three GS analytical approaches were assessed: a common shrinkage model, rrBLUP (Whittaker et al., 2000) and two variable selection models, GRR (Shen et al., 2013), and BayesCπ (BCπ) (Habier et al., 2011). Further, rrBLUP and BCπ are both homoscedastic effects models using common marker variances for shrinkage, whereas GRR is a heteroscedastic effects model (that is, marker-specific variances are used). SNP tables were coded as: aa=−1, Aa=0, AA=1, where a is the reference allele, and A is the alternative allele. All analyses were completed using R software (R-Core-Team, 2014). The following base model was implemented (Moser et al., 2009):

where y_i is the EBV of individual i obtained from equation (1), 1 is an incidence matrix of ones, μ is the overall mean, x_i is a 1 × p vector of SNP genotypes for individual, g(x_i) is a function to estimate the GEBV as the combined effect of p SNP markers on the EBV of individual i, and e_i is the residual error.

Ridge regression BLUP (rrBLUP)

rrBLUP estimates of GEBV were obtained using the R package ‘rrBLUP' (Endelman, 2011). The model for rrBLUP follows:

where x_ik is the genotype of individual i for SNP marker k, and u_k is the additive effect of SNP marker k. The BLUP solution for marker effects, 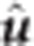, is obtained using Henderson's methods for mixed model equations (MME) (Henderson, 1953):

where Z is an incidence matrix relating SNP markers to individuals, I is an identity matrix, y is the vector of EBV and 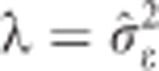assuming 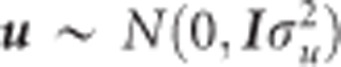. The SNP shrinkage parameter expressed as the ratio between the residual and common marker variances, 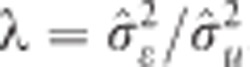. This method shrinks all marker effects equally, where the shrinkage is dependent on the marker allele frequency.

Generalized ridge regression (GRR)

GRR is a two-step variable selection process, and was carried out using the R package ‘bigRR' (Shen et al., 2013). In the first step, initial estimates of 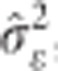, , 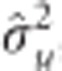and 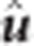were obtained through the same MME as in rrBLUP. However, the BLUP estimate, 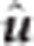, is modified to accommodate a SNP-specific shrinkage parameter:

where Z and y are the same as in equation (5) and λ is a vector of p shrinkage parameters with 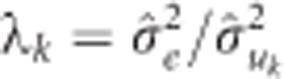as the shrinkage parameter for SNP k, and 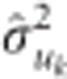is the variance component for SNP k computed as: 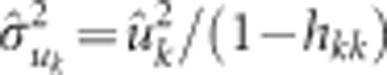, where 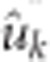is the marker effect BLUP for SNP k obtained in equation (5) and h_kk is the (n+k)^th diagonal of the hat matrix, H=T(TT)⁻¹T′, where

BayesCπ (BCπ)

BayesCπ was developed by (Habier et al., 2011) as an extension to the Bayesian GS methods developed by (Meuwissen et al., 2001). The statistical model for BCπ follows:

where x_ik and u_k are the same as in equation (4) and δ_k is an additional dummy variable that reflects the effect of SNP marker k in the model being equal to zero with probability π.

The proportion of markers with null effect in the model, π, is inferred from the data using a uniform prior distribution (0,1). BCπ assumes a common SNP effect variance, with a scaled inverse chi-square prior, v_u degrees of freedom and scale parameter, 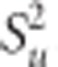. The proportion (1–π) markers included in the model have effects following a mixture of multivariate Student's t-distributions 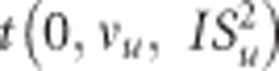, as described in (Habier et al., 2011).

The R package ‘BGLR' (Perez and de los Campos, 2014) was used to implement the BCπ algorithm. Gibbs sampling was used to generate the Monte Carlo Markov Chain using 100 000 iterations thinned at a rate of 100, with the first 20 000 discarded for burn-in. The ‘BGLR' package default estimate for the scale parameter, 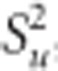, and degrees of freedom, v_u=5, was used. Trace plots were visually checked for model convergence.

Cross validation, PA and relative efficiency of GS

To assess GS prediction accuracy we used 10 replications in a 10-fold random cross-validation scheme. Under this scenario, 90% of available data are selected randomly as the TP while the remaining 10% is designated as the validation population (VP). Here, we define prediction accuracy of GS as the mean Pearson product-moment correlation between EBV from the MBLUP model [1] and GEBV from the GS models, for the VP from the 10 replications, that is, r(GEBV, EBV). The temporal PA (TPA) is then r(GEBV_j, EBV_k), where k is age 40 and j is an age less than 40.

To explore the relative efficiency of GS to TS, we obtained estimates of PA from model [1] using raw phenotypes of the genotyped individuals as training data, and applying the same cross-validation method previously stated. Breeding value estimates were then obtained under two scenarios. The first scenario utilized the pedigree-based average numerator relationship matrix, A (EBV_TS). The second replaced A with the realized relationship matrix, G (GEBV_GS) (Habier et al., 2007; VanRaden, 2008). The latter method is known colloquially as GBLUP and is equivalent to rrBLUP (Mrode, 2014). We used the SVD marker data to compute G as:

where Z=M–P with M as the genotype matrix and P as vector of 2(p_j–0.5), and p is the frequency of the alternative allele of the SNP at the j^th locus. The relative efficiency of GS to TS, assuming selection response is inversely proportional to the length of the breeding cycle is:

where EBV is the estimated breeding value using the full data from model [1], and t_TS and t_GS are the length of time to complete a breeding cycle under TS and GS, respectively (Grattapaglia and Resende, 2011).

Results

Phenotypic and MBLUP analysis

Variation in measures of height among trees within the two sites was relatively stable across years (range: CV=25.09% (HT40)—34.44% (HT6) (Table 1). Narrow-sense individual tree heritability estimates from the MBLUP analysis ranged from low (0.25, HT10) to moderate (0.64, HT30) (Table 2). As expected, the age-age genetic correlation between juvenile and mature height (HT40) increased with increasing juvenile age (Table 2). Mean individual accuracy of breeding values estimated with the MBLUP method were consistent across years of measurement and ranged from 0.74 to 0.76 (Table 2).

Table 1. Sample size (n) and descriptive statistics for interior spruce height (m) used in the pedigree based analysis.

Age	n	Mean	s.d.	CV (%)	Min	Max
3	29 475	0.36	0.11	30.56	0.04	1.05
6	29 184	0.90	0.31	34.44	0.10	2.51
10	28 696	1.54	0.50	32.47	0.18	4.47
15	27 922	2.69	0.90	33.46	0.30	7.19
30	27 466	7.15	2.27	31.75	0.62	14.98
40	26 808	11.32	2.84	25.09	0.70	20.80

Abbreviations: CV, coefficient of variation; s.d., standard deviation.

Table 2. Pedigree-based estimates of variance components for interior spruce height (m) at ages 3, 6, 10, 15 and 30 (years), and the estimated narrow-sense individual tree heritabilities 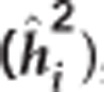, age-age genetic correlations with age 40 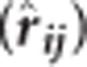, mean estimated individual breeding value accuracies (r _(EBV,TBV)).

Age		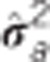		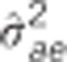		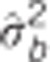	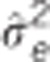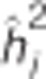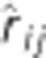r(EBV,TBV)
3	2.95E-03 (3.80E-04)	6.89E-04 (1.02E-04)	4.17E-05 (2.05E-05)	2.55E-03 (2.88E-04)	0.48 (0.05)	0.63 (0.06)	0.74
6	1.74E-02 (2.55E-03)	7.64E-03 (1.13E-03)	2.16E-03 (1.03E-03)	3.65E-02 (1.97E-03)	0.28 (0.04)	0.75 (0.04)	0.74
10	7.56E-03 (1.16E-03)	3.73E-03 (5.70E-04)	1.25E-03 (5.94E-04)	1.94E-02 (9.03E-04)	0.25 (0.04)	0.84 (0.03)	0.74
15	7.82E-01 (4.01E-02)	7.68E-03 (1.19E-03)	2.33E-03 (1.11E-03)	3.54E-02 (2.32E-03)	0.33 (0.04)	0.93 (0.02)	0.75
30	3.09 (3.87E-01)	6.00E-01 (9.00E-02)	1.60E-01 (7.59E-02)	1.12 (2.32E-01)	0.64 (0.06)	1.00(0.00)	0.76
40	4.53 (5.67E-01)	8.56E-01 (1.33E-01)	4.26E-01 (2.02E-01)	2.14 (4.29E-01)	0.61 (0.07)	1.00(0.00)	0.76

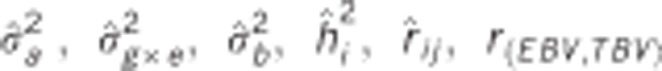are the estimated additive genetic, additive genetic by site, block, residual, narrow-sense individual heritability, age-age genetic correlation and mean estimated individual breeding value accuracy.

Standard errors in parentheses.

Prediction accuracy

Imputation method and statistical approach

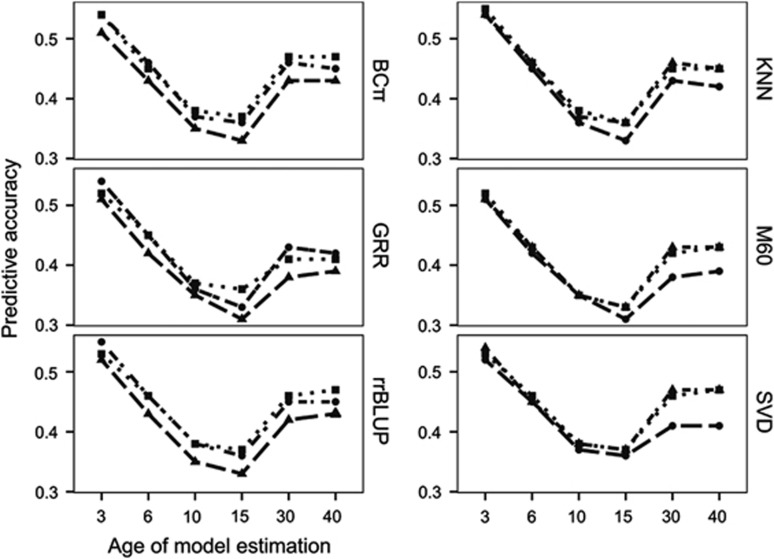
The number of SNP markers retained after filtering for minimum minor allele frequency (0.05), averaged from the cross-validation scenarios was 34 570 (M60), 39 915 (KNN) and 50 803 (SVD). On average, SVD, followed by the novel KNN family-based imputation approach both surpassed the PA of M60 imputation in all GS analysis methods, with the observed differences being comparatively minor between SVD and KNN (Figure 1, left; Table 3). The increase in PA relative to the baseline M60 imputation method, averaged across statistical approaches and ages, was greatest for SVD (7.9%), followed by KNN (6.6%). The average increase in PA of SVD relative to KNN was 1.2%. The former result produced a trend of diminishing return when comparing the number of markers used in GS analyses.

Figure 1.

GS prediction accuracies from models trained using interior spruce height data at ages 3, 6, 10, 15, 30 and 40 years and validated against EBV at the training age. Shape and pattern in left panels represent imputation methods for 60% missing genomic data (M60, triangle/dash; KNN, circle/dash-dot; SVD, square/dot). Shape and pattern in right panels represent genomic prediction methods (GRR, circle/dash; BCπ, square/dash-dot; rrBLUP, triangle/dot).

Table 3. Genomic prediction accuracy obtained from rrBLUP, GRR and BCπ analytical approaches for SVD, KNN and M60 imputation methods for interior spruce tree height at ages 3, 6, 10, 15, 30 and 40 (years).

Age	rrBLUP			GRR			BCπ
	SVD	KNN	M60	SVD	KNN	M60	SVD	KNN	M60
3	0.53 (0.003)	0.55 (0.001)	0.52 (0.002)	0.52 (0.003)	0.54 (0.004)	0.51 (0.003)	0.54 (0.002)	0.54 (0.002)	0.51 (0.002)
6	0.46 (0.002)	0.46 (0.002)	0.43 (0.003)	0.45 (0.002)	0.45 (0.002)	0.42 (0.006)	0.45 (0.001)	0.46 (0.003)	0.43 (0.002)
10	0.38 (0.002)	0.38 (0.002)	0.35 (0.002)	0.37 (0.002)	0.36 (0.002)	0.35 (0.004)	0.38 (0.004)	0.37 (0.003)	0.35 (0.004)
15	0.37 (0.005)	0.36 (0.003)	0.33 (0.003)	0.36 (0.005)	0.33 (0.005)	0.31 (0.005)	0.37 (0.002)	0.36 (0.003)	0.33 (0.003)
30	0.46 (0.003)	0.45 (0.003)	0.42 (0.002)	0.41 (0.003)	0.43 (0.003)	0.38 (0.006)	0.47 (0.002)	0.46 (0.001)	0.43 (0.002)
40	0.47 (0.003)	0.45 (0.002)	0.43 (0.002)	0.41 (0.004)	0.42 (0.002)	0.39 (0.005)	0.47 (0.002)	0.45 (0.002)	0.43 (0.003)

Abbreviations: BCπ, BayesCπ GRR, generalized ridge regression; KNN, k nearest neighbor; M60, mean 60% rrBLUP, ridge regression BLUP; SVD, singular value decomposition.

Standard errors in parentheses.

On average, variation in the relative difference between GS analytical approaches was less than that among imputation methods and number of markers (Figure 1, right; Table 3). PA was, on average, equal between the rrBLUP and BCπ methods and both performed better than GRR, with differences being largest at ages 15, 30 and 40 years. The relative increase in PA, averaged across imputation methods and ages, indicated that rrBLUP and BCπ both performed equally well over GRR (4.3%). Pairwise groupings of statistical approach and imputation method scenarios indicated that rrBLUP or BCπ in combination with SVD produced the greatest PA, on average, across all ages. Standard errors of the predictions computed from the 10 replicates were low, ranging from 0.001 to 0.006 (Table 3).

Predictive accuracy across time

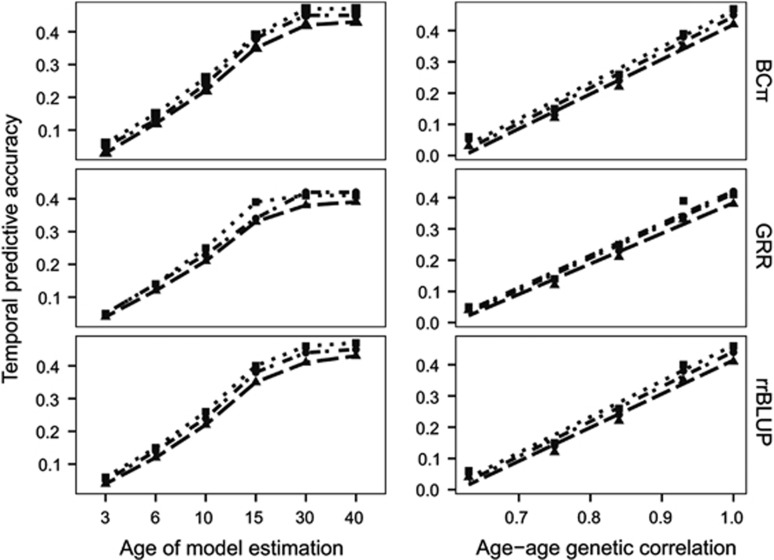
The GS PA was inconsistent across ages (Table 3; Figure 1). The greatest PA occurred for HT3, and while a reduction occurred for all other ages, it was largest for HT10 and HT15 across all imputation and GS analytical approach combinations. As expected, the TPA decreased with increasing difference between the training and VP age of height measurement (Table 4; Figure 2, right). Differences in TPA mirrored the results from imputation comparisons, with SVD and KNN producing the greatest average relative increases over M60 by 22.2% and 12.6%, respectively. Diversity in TPA between analytical approaches was lower than that between imputation procedures with average relative increases of rrBLUP and BCπ at 5.5% and 2.6% over GRR, respectively. Age-age genetic correlations from the MBLUP model were plotted with TPA of GS models (Figure 2, left). As anticipated, the Pearson product-moment correlation between the two was, on average, near perfect (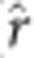=0.99, not tabulated), with the TPA and age-age genetic correlation both decreasing with difference in years. Interestingly, the TPA of GS models based on 30-year data was often equivalent to those based on 40-year data.

Table 4. Age 40 temporal genomic prediction accuracy obtained from rrBLUP, GRR and BCπ analytical approaches for SVD, KNN and M60 imputation methods for interior spruce tree height at ages 3, 6, 10, 15 and 30 (years).

Age	rrBLUP			GRR			BCπ
	SVD	KNN	M60	SVD	KNN	M60	SVD	KNN	M60
3	0.06 (0.003)	0.05 (0.002)	0.04 (0.002)	0.05 (0.003)	0.05 (0.003)	0.04 (0.002)	0.06 (0.002)	0.05 (0.002)	0.03 (0.002)
6	0.15 (0.003)	0.14 (0.002)	0.12 (0.002)	0.14 (0.003)	0.14 (0.002)	0.12 (0.004)	0.15 (0.001)	0.13 (0.003)	0.12 (0.002)
10	0.26 (0.003)	0.24 (0.002)	0.22 (0.002)	0.25 (0.003)	0.23 (0.003)	0.21 (0.004)	0.26 (0.003)	0.24 (0.002)	0.22 (0.003)
15	0.40 (0.005)	0.38 (0.005)	0.35 (0.003)	0.39 (0.005)	0.34 (0.004)	0.33 (0.005)	0.39 (0.003)	0.38 (0.004)	0.35 (0.002)
30	0.46 (0.003)	0.44 (0.004)	0.41 (0.001)	0.41 (0.003)	0.42 (0.003)	0.38 (0.005)	0.47 (0.002)	0.45 (0.001)	0.42 (0.003)

Abbreviations: BCπ, BayesCπ GRR, generalized ridge regression; KNN, k nearest neighbor; M60, mean 60% rrBLUP, ridge regression BLUP; SVD, singular value decomposition.

Standard errors in parentheses.

Figure 2.

Left panels: Temporal GS prediction accuracy for three models (rrBLUP, GRR, BCπ) trained using interior spruce height data at ages 3, 6, 10, 15, 30 and 40 years and validated against EBV at age 40 year. Right panels: Relationship between age-age genetic correlations from the MBLUP model and temporal GS prediction accuracy from the three GS models (rrBLUP, GRR, BCπ). Shape and patterns in both panels represent imputation methods for 60% missing genomic data (M60, triangle/dash; KNN, circle/dash-dot; SVD, square/dot).

Distribution of SNP effects

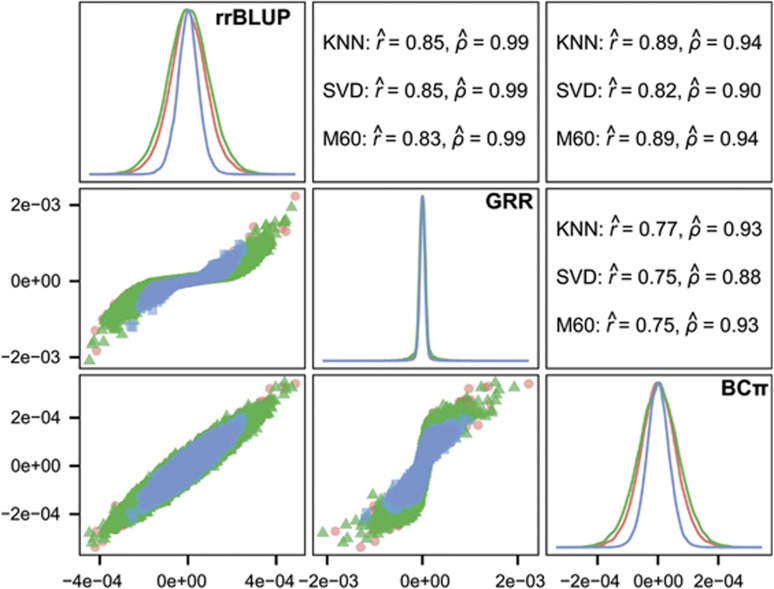
The scatter plots, histograms and correlations of estimated marker effects from the three GS analytical methods suggested greatest similarity between the rrBLUP and BCπ methods, and least similarity between GRR and BCπ (Figure 3, Supplementary Figures 1–5). Evident in the plots is the relative tendency of GRR to apply intense shrinkage to the minor effect SNPs while allowing SNPs with large effect to persist. The latter result contrasts with rrBLUP and BCπ where they tended to distribute marker effects more widely owing to the common shrinkage parameter. The posterior mean of the π parameter (that is, probability of null effect) for BCπ was relatively constant across ages and with estimates ranging from 0.03 to 0.04 (not tabulated), accounting for some of the similarity between the rrBLUP and BCπ methods. The intensity of shrinkage due to marker quantity is also apparent when comparing the SVD to KNN and M60 marker effects plot. Pearson product-moment correlation was used to assess the linear relationship between the absolute value of marker effects in the three analytical approaches (Figure 3, Supplementary Figures 1–5; upper triangles). Pearson product-moment correlation, averaged across imputation methods and ages (not tabulated), was greatest between rrBLUP-BCπ (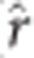=0.88), followed by rrBLUP-GRR (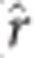=0.86) and BCπ-GRR (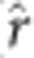=0.86). Spearman rank-correlation, averaged across imputation methods and ages (not tabulated), of marker effects yielded nearly identical ranking between rrBLUP-GRR (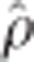=0.99), as expected because the rrBLUP procedure precedes GRR. Lower rank correlations were observed between rrBLUP-BCπ (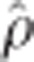=0.93) and BCπ-GRR (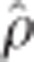=0.90). Additional marker effect plots for the remaining height measurement years are available in the supplement.

Figure 3.

Comparison of SNP marker effects by kernel density plots (diagonal), scatter plots (lower triangle), and Pearson (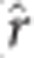) and Spearman (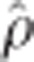) correlations (upper triangle) for three imputation methods (KNN, red; SVD, blue; M60, green) and three analytical approaches (rrBLUP, top; GRR, middle; BCπ, right) estimated for tree height at age 15 years in interior spruce.

Relative efficiency

PA from rrBLUP and the SVD marker data (GS) was compared with those using TS (Table 5). Under the early selection scenario (10 and 15 years), the TPA using GS was greater than that of TS resulting in 112% and 106% increase in selection response, respectively. GS PA for mature tree height (30 and 40 years) of the same age as model estimation was lower (HT30) or equal (HT40) to their TS counterparts, however, assuming a 25% reduction in breeding cycle length resulted in increases of selection response by 137 and 139% for both ages separately. Additionally, a high (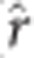=0.85, not tabulated) Pearson correlation between PA and proportion of additive genetic variance explained by the GS model (that is, narrow-sense genomic heritability) was observed in this study. A lower correlation (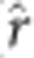=0.75, not tabulated) was also observed between TS narrow-sense heritability and TS PA.

Table 5. Predictive accuracy and relative efficiency from cross-validated models using realized (GEBV _GS ) and average (EBV _TS ) relationship matrices for early (10 and 15 years) and mature (30 and 40 years) interior spruce tree height.

Age	r(EBVTS,EBV)	r(GEBVGS,EBV)	Efficiency	Increase (%)
10	0.20a (0.003)	0.22a (0.004)	1.12	112
15	0.29a (0.002)	0.31a (0.002)	1.06	106
30	0.45 (0.003)	0.43 (0.003)	1.29b	129
40	0.43 (0.004)	0.43 (0.003)	1.33b	133

Abbreviations: EBV, estimated breeding values; GEBV, genomic breeding values. Standard errors in parentheses.

^aRepresents the temporal predictive accuracy.

^bAssumes a 25% reduction in breeding cycle length attributed to genomic selection.

Discussion

Accuracy of GS prediction through time

In this study, repeated measures of tree height over time permitted the testing of GS models' accuracy (PA) at different ages (Figure 1,Table 3). PA reported in this study varied substantially throughout time (Figure 1, Table 3). This may reflect the capacity of the SNP markers to account for differential gene expression due to physiological or G × E interaction over time. Interestingly, the large drop in PA at age 10 and 15 years seems to coincide with a period of intense competitive exclusion between trees at this age, perhaps exacerbated by the relatively narrow tree spacing (2.5 × 2.5 m). The observed extent of PA for tree height was comparable with that reported in other studies using clonal eucalypts (Resende et al., 2012a) and 1–6-year tree height in loblolly pine (Resende et al., 2012b, c; Zapata-Valenzuela et al., 2012). More recently, Beaulieu et al. (2014a) tested GS in a half-sib population of white spruce and reported PA for 22-year tree height that were similar to those described here.

Next, we trained GS models with EBV of tree height at ages 3, 6, 10, 15 and 30 year and validated the GEBV against EBV from 40-year measurements (Figure 2, Table 4). This scenario is of interest because the PA is expected to decline after each breeding cycle owing to the decay of SNP-QTL LD as a result of recombination in the offspring (Habier et al., 2013). Thus, the TPA of GS methods is an important consideration for retraining said models as it offers potential to further accelerate the breeding cycle if target phenotypes can be selected earlier. TPA in this study decreased as the difference in age of training and VP increased. Interestingly, the TPA of GS models based on 30-year height was nearly equivalent to those based on 40-year despite the 10 years difference in measurements, suggesting consistency between the EBVs and SNP effects at both ages. This analysis is in agreement with that of Resende et al. (2012b), who tested TPA for ages 1–6 years in clonal loblolly pine and concluded that model retraining will likely require phenotypic data from mid-rotation age or later to accurately reflect mature growth trait performance (White et al., 2007). These results are not unexpected as conifers typically have weak age-age genetic correlations (Namkoong et al., 1988) attributed to their long life spans and exposure to a wide range of environmental contingencies over time. Currently, selection based on growth attributes is carried out at the age 15 years in interior spruce.

Model comparison

We tested the PA of rrBLUP, GRR and BCπ statistical approaches for a time series of tree height measurements in interior spruce (Figure 1,Table 3). The rrBLUP and BCπ models both performed consistently well, producing the highest PA across all ages. These two models can be considered equivalent when the posterior mean of π in the BCπ model approaches zero value. The π parameter posterior mean estimate ranged from 0.03 to 0.04 in this study, accounting for some of the models' observed similarity. The marker effect plots (Figure 3, Supplementary Figures 1–5) illustrate the likeness of the number of markers fitted, marker effect distributions and shrinkage for both methods. Similarly, Resende et al. (2012b) found no difference in PA between rrBLUP and BCπ for 6-year height in loblolly pine, although they did find that BCπ outperformed rrBLUP for an oligogenic disease resistance trait. This demonstrates the flexibility of the BCπ algorithm, where the π parameter allows the model to behave like rrBLUP when traits follow the Fisher's infinitesimal model (Fisher, 1918). This concept gives BCπ the possibility to be useful in prediction of traits with unknown genetic basis at the cost of additional computational time (BCπ took upwards of five times longer than both rrBLUP and GRR combined). rrBLUP has often been suggested as a baseline model to which comparisons should be made because it has been shown to yield high and stable PA across a wide variety of species and traits with low computational time investment (Heslot et al., 2012). Indeed, this result has been found to be true in the present as well as other studies involving forest trees (Resende et al., 2012c; Beaulieu et al., 2014b).

As anticipated, the GRR model did not offer improved PA over rrBLUP or BCπ for mature tree height under this study's conditions. Tree height is widely regarded as having a complex inheritance pattern under the Fisher's infinitesimal model (Fisher, 1918). In theory, the statistical approach used in GS can lead to variation in PA, depending on the genetic architecture of the trait (Daetwyler et al., 2010). Hence, variable selection methods are generally expected to perform optimally for traits with simple genetic architecture (that is, few loci with large effect), because SNPs of low effect are strongly shrunk toward zero, while those of large effect persist. Beaulieu et al. (2014b) and Resende et al. (2012c) evaluated BayesA and Bayesian LASSO, approaches similar to GRR, where the improvement in PA of growth related traits was found to be null. The GRR model did, however, offer PA comparable with rrBLUP and BCπ at juvenile ages (3, 6 and 10 years). As observed in the distributions of marker effects at these juvenile ages, the GRR model appeared to shrink all markers equally because of an apparent absence of those with large effect compared with mature ages (Figure 3, Supplementary Figures 1). However, in mature ages where large marker effects were perceived to exist by the GRR model, the intense shrinkage applied to markers of low effect led to an obvious impairment of PA. This is expected because of the complex genetic nature of tree height, guiding the decision that these large effect markers in mature tree height were likely false positives. Further, the increase in PA by rrBLUP and BCπ over GRR at later ages may be accounted for by the knowledge that when markers are shrunk equally, the kinship component of PA is more effectively captured, when compared with heteroscedastic models (Heslot et al., 2012). GS models should, however, ideally be based on the LD between SNP-QTL rather than kinship, because the SNP-QTL LD component of PA is expected to persevere in subsequent generations following breeding (Habier et al., 2007).

GBS and marker imputation

The use of GBS, in combination with several imputation methods, was successful in supplying a dense genome-wide marker data set, and further, enabled moderate levels of PA to be captured for tree height in interior spruce. This study represents the first use of GBS data as a base for genomic prediction in a forest tree species. We report that both SVD and novel KNN imputation methods offered increases in PA over mean imputation (M60) (Figure 1, left). However, it is unclear whether this result is the product of the number of markers retained by the imputation method or the imputation method itself. Although the initial marker matrix with 60% missing information was used for the three imputation methods, variation in the number of retained markers should be expected as some marker loci may be non-imputable with certain algorithms and differences will occur because of filtering of minor allele frequency. Thus, the imputation method should be wholly evaluated based on both its marker yield and PA, because restricting the markers to a common set would lend unintentional penalization to methods that yield greater numbers of markers. Similarly, Rutkoski et al. (2013) noted comparable increases in PA over mean imputation while using both SVD and KNN imputation on GBS-derived markers for wheat (Triticum aestivum L.). Further, we found that on average, the SVD imputation method yielded only slightly better PA than KNN. The former result alludes to diminishing returns given the average difference in available markers after filtering the TP SNP tables for a minimum minor allele frequency of 0.05. This result corresponds well to the asymptotic relationship between marker density and PA derived by Grattapaglia and Resende (2011) who used simulated data and deterministic formulae.

Foundationally, the GBS method produces a large number of missing data due to low read depth and possible mutation at restriction sites in some individuals (Elshire et al., 2011), thus, it relies heavily on accurate imputation methods to derive dense marker data. With the availability of a complete reference genome assembly of white spruce, it may be possible to increase the accuracy of imputation through use of methods designed for ordered data and constructed haplotypes (Rutkoski et al., 2013). In the interim, scaffolds of the draft genome assembly for white spruce published by Birol et al. (2013) may suffice to aid in aligning the unordered genomic data produced in this study, and additionally assist in discovering additional markers that can be used for GS. This would be greatly beneficial because the genome size and complexity of conifers demand a large number of markers to sufficiently saturate the genome and provide high PA. Marker density is also particularly important in determining PA for forest tree populations where the effective size (N_e) is commonly large (Grattapaglia and Resende, 2011).

Relative efficiency

The observed GS prediction accuracies (PA) in the present study are adequate to produce greater genetic gain over TS (Table 5). The relative efficiency results are compatible with those described by other studies involving white spruce and loblolly pine (Resende et al., 2012b; Beaulieu et al., 2014a). However, we chose to limit the reduction in time of breeding cycle to a conservative value of 25%, as opposed to 50% in other studies, because the reliability of the PA produced from the present study has not been validated in a progeny generation. The theoretical increase in genetic gain produced by GS hinges on the capacity of the prediction models to remain relevant in the next generation. For this to occur, PA must ideally be based on SNP-QTL LD rather than kinship (Habier et al., 2013). Recently, the source of the relationship between marker and QTL described by GS models has been decomposed by Habier et al. (2013) into factors involving both kinship and pure marker-QTL LD, generating questions about the validity of such models in subsequent generations.

The origin of PA produced by the GS models in this study is currently unknown, and further testing via a progeny VP, or the partitioning of families in a restricted cross-validation scheme as demonstrated by Beaulieu et al. (2014a), will be required in the future. Optimally, the PA of the models was produced via LD between markers and QTL. Sub-optimally, PA was derived through kinship information between individuals in the training and VPs. GS PA can be composed of a combination of the two factors, leading to inflated estimates of PA to occur without proper validation because the kinship component is anticipated to decay more rapidly than marker-QTL LD in the progeny generations (Habier et al., 2007, 2010, 2013). In a study of a large population of white spruce open-pollinated families, Beaulieu et al. (2014a) observed that PA decreased significantly when kinship between the training and VPs was restricted. This is not unexpected in forest trees, where decay in LD is typically fast (Neale and Savolainen, 2004). Thus, it may be necessary in the future to create ‘designer' breeding populations through intense management to maximize marker-QTL LD. Alternatively, selective within-family genotyping of phenotypically extreme individuals (that is, best and worst) could be used to train accurate GS models based on haplotype blocks (Odegard and Meuwissen, 2014).

In the open-pollinated testing used in the present study, GS models were trained using traditional pedigree-based EBVs that incorporate expected additive genetic relationships between individuals into the matrix, A, to estimate genetic parameters (Lynch and Walsh, 1998). Mixed model theory assumes that covariance matrices are error-free (that is, ideally reflecting the segregation of only QTLs), thus, the accuracy of information contained in A is critical in obtaining unbiased and accurate estimates of genetic parameters and breeding values (Mrode, 2014). Ideally, data fitted to train GS models should be analogous to the true additive genetic merit of each individual in the TP (Garrick et al., 2009). Earlier studies have fitted de-regressed EBV in GS models to improve prediction accuracy (Garrick et al., 2009). However, there are empirical results in animal breeding to suggest EBV to be superior in some cases (Guo et al., 2010). Kinship explained by marker data can be used to overcome this limitation and has been used in the past to correct pedigree errors (Munoz et al., 2014), and produce increased accuracy of EBV (El-Kassaby and Lstiburek, 2009; El-Kassaby et al., 2011). Munoz et al. (2014) applied this concept to GS and noted improved PA by correcting pedigree errors prior to estimating EBVs of the training data.

It appears that in the short-term, single step methods such as those incorporating the realized (G) (VanRaden, 2008) or augmented (H) (Legarra et al., 2009; Christensen and Lund, 2010) genomic relationship matrix may be better suited for tree-breeding programs with simple mating structures and shallow pedigrees because EBV accuracy suffers from the insufficiencies produced by the simplified mating design. At present, selection with increased accuracy could be made over traditional BLUP methods with the benefit of accumulating genotypic information that can be used in the long term when deep pedigrees and ‘designer' TPs have been established. This concept is most relevant to young breeding programs with open-pollinated mating structure such as the one studied here.

Data Archiving

Data available from the Dryad Digital Repository: http://dx.doi.org/10.5061/dryad.m4vh4.

The authors declare no conflict of interest.