The Goldilocks Effect in Infant Auditory Attention

Abstract

Infants must learn about many cognitive domains (e.g., language, music) from auditory statistics, yet capacity-limited cognitive resources restrict the quantity that they can encode. While we know infants can attend to only a subset of available acoustic input, few previous studies have directly examined infant auditory attention—and none have directly tested theorized mechanisms of attentional selection based on stimulus complexity. Using model-based behavioral methods that were recently developed to examine visual attention in infants (e.g., Kidd, Piantadosi, & Aslin, 2012), we demonstrate that 7- to 8-month-old infants selectively attend to non-social auditory stimuli that are intermediately predictable/complex with respect to their current implicit beliefs and expectations. Our results provide evidence of a broad principle of infant attention across modalities and suggest that sound-to-sound transitional statistics heavily influence the allocation of auditory attention in human infants.

Infants are remarkably sensitive to their auditory environment, showing the ability to learn from their mother’s speech even before birth (DeCasper & Fifer, 1980). This process of learning from the auditory environment continues during the first postnatal year, as infants discover phonetic categories (Kuhl, 2004) and learn the sequences of speech that will form the words of their native language (Saffran, Aslin & Newport, 1996). These auditory milestones must be based on gathering input from the natural environment, where a myriad of novel sounds and sound-sequences (e.g., speech syllables, musical notes) unfold rapidly over time. A learner with an infinite information processing capacity could theoretically encode all available auditory input as it arrives at the ear. A human infant, however, possesses only finite, capacity-limited cognitive resources (e.g., attention, memory, processing capacity). These cognitive constraints impose severe limits on the kind and quantity of auditory input an infant can encode in real time. Infants’ learning is thus limited by constraints such as the temporal rate at which they can access sequential inputs (e.g., Conway & Christiansen, 2009), the number of elements they can hold in working memory (e.g., Ross-Sheehy, Oakes & Luck, 2003), and the depth to which they can ultimately encode the novel stimulus (e.g., Sokolov, 1969).

Even a single auditory stream (e.g., a mother speaking to her child in an otherwise silent room) expresses a complex composition and arrangement of acoustic variables (e.g., intensity, pitch, timbre) that additionally encode hierarchical levels of structure (e.g., sounds, syllables, phrases) and semantic meaning (e.g., salience, emotion, category, identity). Additionally, previous work with adults suggests that human auditory processing is likely inferior to visual processing in terms of resolution and capacity (e.g., Cohen, Horowitz, & Wolfe, 2009). Thus, the infant must pick and choose both which auditory inputs to attend and on which aspects of a single auditory stream to focus. Locating and tracking the relevant statistics from within the continuous surge of incoming auditory data is then crucial for infants to solve the many auditory learning tasks they face.

One reasonable strategy infants might employ in the natural environment is to allocate attention on an “as available” basis; that is, they might attempt to encode all auditory inputs, and effectively ignore stimuli that exceed their information processing capacity. However, such an undirected learning strategy would be inefficient at best, and futile at worst. Imagine, for example, attempting to complete an open-book exam on an unfamiliar subject in a vast library by drawing books from the shelves at random. An alternative strategy would be to make attention dependent upon relevant properties of the stimulus itself, perhaps actively allocating attention to auditory material that is most useful for learning. This latter strategy might be particularly advantageous for language learning, where the inventory of inputs is quite large (e.g., 40 phonemes, 1,000 syllables, 50,000 words) and combined in a huge variety of sequences.

A substantial amount of previous work on infant attention theorized that such a strategy might help infants focus on learning material that is sufficiently novel from—but also sufficiently related to—the infants’ existing knowledge (e.g., Kinney & Kagan, 1976; Jeffrey & Cohen, 1971, Friedlander, 1970; Horowitz, 1972; Melson & McCall, 1970), Zelazo & Komer, 1971). Kinney and Kagan (1976) suggested that preferring stimuli that are moderately novel would prevent infants from wasting time on material that is already known. They further suggested that preferring stimuli that are somewhat related to existing knowledge might help infants focus on completing partially built cognitive representations. These partial representations could then facilitate more efficient construction of newer, bigger or more elaborate cognitive constructs later on in learning. This formulation of the “discrepancy hypothesis” thus suggests that the complexity of a stimulus can be conceptualized as relating to the infant’s current knowledge state. A “simple” stimulus would be one with little or no new information for the infant to learn. A “complex” stimulus would be one that contains almost entirely new information, distinct from nearly everything in the infant’s current conceptual inventory. Further, these theories hold that infants should exhibit a U-shaped attentional pattern with respect to stimulus complexity: infants should more readily terminate attention to events that are either too simple (predictable) or too complex (surprising).

Our previous work (Kidd, Piantadosi, & Aslin, 2010; 2012) demonstrated that infants’ visual attention was influenced by the complexity (or information content) of the visual stimulus. We used an idealized learning model in order to quantify the complexity of particular visual events in a sequence. We then measured at what point in a visual sequence an infant terminated their attention to the sequence. In these studies, infants looked away at visual events of either very low complexity (very predictable) or very high complexity (very surprising), even controlling for other temporal factors known to influence attentional selection. Additional work demonstrated that this U-shaped pattern of preference for visual events of intermediate complexity occurred not only across a population of infants, but also within individual infants (Piantadosi, Kidd, & Aslin, in press). In the present study, we asked whether such an active strategy of attentional allocation extends from the visual modality to the auditory modality.

As suggested by the discrepancy hypothesis of infant auditory attention discussed earlier, the potential utility of such a strategy is substantial. In contrast to the large quantity of work examining auditory learning in infants (e.g., the literature on language learning and music cognition), few previous studies have directly examined infant auditory attention—and none to our knowledge have employed computationally well-defined stimuli varying in complexity. Although there are limits on selective auditory attention infants, including stimulus discriminability and working memory (see Werner, 2002), we chose highly discriminable stimuli and a rate of presentation that fell well within the working-memory capacity of 7- to 8-month-olds (as documented by many previous statistical learning experiments; see Aslin & Newport, 2012). Thus, we focused on infants’ implicit preferences for maintaining attention to auditory stimuli that were easily accessible, yet varied in their information “value” as determined by a quantitative model.

It is important to note that the general idea of a U-shaped function along a dimension of stimulus complexity is not new. In fact, several recent studies of infants (Gerken, Balcomb & Minton, 2011; Spence, 1996) have reported similar effects. What is new about our approach is to make a specific prediction about the U-shaped function based on a quantitative metric of complexity. Previous studies have either defined complexity after obtaining a U-shaped function or have contrasted learnable versus unlearnable information rather than exploring the space of complexity in a continuous manner. Moreover, it is important to determine whether the same general principles of attention allocation apply in the auditory modality as well as in the visual modality, especially given modality differences in the temporal and spatial statistics typically used to process natural stimuli in each domain.

Experiment and Modeling Approach

In the present experiment with 7- and 8-month-olds, we measured infants’ visual attention to sequential sounds that varied in complexity, as determined by an idealized learning model. We examined the influence of complexity, while simultaneously controlling for other factors known to influence infants’ attention (e.g., trial number, repeat events). Both the experiment and modeling approach were based on our earlier studies on visual attention (Kidd, Piantadosi, & Aslin, 2010; Kidd, Piantadosi, & Aslin, 2012; Piantadosi, Kidd, & Aslin, in press). The behavioral experiment measured the point, in a sequence of auditory events, when an infant terminated their attention to the sequence. The auditory stimuli were easily captured by a simple statistical model.

Each trial consisted of one of 32 possible sound sequences. The within-sequence events and the sequences themselves were designed to vary in terms of their information-theoretic properties. For example, some events in a sequence were highly predictable (e.g., sound A occurs after 20 successive occurrences of sound A), and others were less predictable (e.g., sound B occurs after 21 successive occurrences of sound A). Likewise, some sequences contained many more highly predictable events (e.g., AAAAAAAAAAAAAAAA...), while others contained fewer (e.g., AAACCBAABBCABACACCC...). For each trial, a script randomly selected a new available sequence from the pool of 32. The script also randomly selected three different non-social sounds from a pool of 96 possible sounds. (See Materials and Methods for more details.)

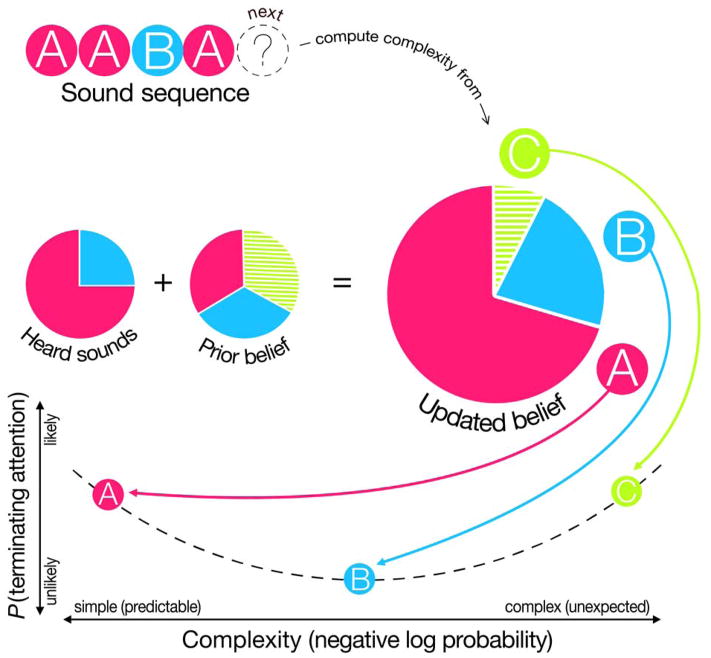
Fig. 1 illustrates the logic of the experiment and our analysis approach. In this simplified example trial, the observer has heard a sequence composed of three A sounds and one B sound, and the key question is whether the infant terminates the trial upon hearing the next sound in the sequence. The heard sounds (AAAB...) comprise the observed data, which are combined with the prior—essentially a smoothing term to avoid zero probabilities—to form an updated (posterior) belief. In this example, the updated belief leads to an expectation that the next event has a high probability of being sound A, a moderate probability of it being sound B, and a low (but nonzero) probability of it being sound C. The complexity of the next sound is quantified by an information theoretic metric—negative log probability— which represents the amount of “surprise” an idealized learner would have on hearing the next event, or, equivalently, the amount of information processing such a learner would be required to do (Shannon 1948). Thus, if the next sound is A—a sound that is highly likely according to the model’s updated belief—the complexity of that event would be low (i.e., the sound would be highly predictable according to the model). The “Goldilocks” hypothesis thus holds that infants would be more likely to terminate their attention at this sound. Conversely, if the next sound is C—a sound that is highly unlikely according to the model’s updated belief—the complexity of that event would be high (i.e., the sound would be highly surprising according to the model). The “Goldilocks” hypothesis holds that infants should also terminate their attention to the sound sequence at this type of event. However, if the next sound is B—a sound that is moderately probable according to the model’s updated belief—the complexity of that event would fall in the intermediate “Goldilocks” range, thus leading infants to be less likely to terminate their attention to the sound sequence. If attention was not terminated at a given sound, the sequence continued until a sound resulted in termination of the trial (or 60 sec. elapsed). Once terminated, the next trial consisted of a new set of three sounds in a sequence whose complexity was unique among all 32 trials presented to each infant.

Figure 1.

Schematic showing an example sound sequence and how the idealized learning model combines heard sounds with a simple prior to form expectations about upcoming sound events (the “updated belief” above). The next sound then conveys some amount of complexity according to these probabilistic expectations of the updated belief. The “Goldilocks” hypothesis holds that infants will be most likely to terminate their attention to the sequence at sounds that are either overly simple (predictable) or that are overly complex (unexpected), according to the model. Thus, sounds to which the updated belief assigns either a very high probability (e.g., sound A) or a very low probability (e.g., sound C) would be expected to be more likely to generate attentional termination (look-aways) than those to which it assigns an intermediate probability (e.g., sound B).

The example shown in Fig. 1 treats each event as statistically independent (a non-transitional model). However, our previous work also indicated that a model that tracked the bigram probabilities of events (a transitional model) out-performed the non-transitional model. In the present experiment, therefore, we also constructed and tested a transitional model of the auditory stimuli, which captured how likely each sound was to follow each other sound in computing complexity. Note that for either model, if an infant continued to attend to the sound sequence, the predictions of the model would be updated for the next sound in the sequence. Thus, although infants may terminate their attention at different points in different sound sequences, we hypothesize that these attentional terminations (as measured by look-aways) will occur predictably during events with both very high and very low complexity values, as estimated by the two models.

We note that this modeling approach and analysis contrast with those employed by most infant studies. Previous infant research typically tested for differences in overall mean looking times. Here, we predicted a binary outcome (whether an infant terminates attention) at each individual auditory event in a sequence. This is a more precise prediction based on probabilities computed on-line.

Method

Participants

Thirty-four infants (mean = 7.7 months, range = 7.1 – 8.9) were tested and all were included in the analysis. All infants were born full-term and had no known health conditions, hearing loss, or visual deficits according to parental report.

Stimuli

We presented each infant with 32 trials consisting of sequences composed by up to three unique sounds, with trials presented in a random order across infants. These sequences were constructed to vary in their information-theoretic properties (e.g., entropy, surprisal). Thus, some sound sequences contained many highly predictable events (e.g., AAAAAAAAA...) and others contained many less predictable ones (e.g., BBACAACAB...).

Each of the sound sequences presented up to three non-social sounds (e.g., door closing, flute note, train whistle). These sounds were selected randomly for each infant and the three sounds in each sequence were unique, such that each infant heard up to 96 sounds across all 32 trials. (Infants could have heard fewer than 3 sounds within a trial, for example, if they terminated the sequence before each of the 3 possible sounds had occurred.) The sounds were chosen to be both reasonably familiar, but also maximally memorable and distinct from one another. Each sound sequence was presented while infants viewed a unique scene on each of the 32 trials, generated by a Matlab script. Each scene consisted of a single, uniquely patterned and colored box concealing a single, unique toy at the center of the screen (see Fig. 2 and Video S1). The box was animated to open (1 sec.), thus revealing its contents, then immediately close (1 sec.), so that each reveal lasted 2 sec. Each reveal was accompanied by one sound from the sound sequence. The box continued to open and close continuously, revealing the same toy on that particular trial and each time accompanied by the next sound in the sound sequence—until the infant looked away continuously for 1 sec., or until the sequence timed out at 60 sec (see Video S2). The toy was present to maintain infants’ visual fixation, and did not change within a sequence, but was randomized across trials and infants; thus, there were no differences in the visual displays across sounds in a sequence, and look-aways could only be attributed to the auditory portion of the stimulus presentation.

Figure 2.

Example of display used in the experiment. A novel toy object (e.g., a little teardrop-shaped figure) in the box was revealed by up-down animation of an occluder (e.g., a yellow-striped box). Each reveal was accompanied by the next sound in the sequence associated with the trial. The animation and sound sequence continued until the infant looked away continuously for 1 sec. Also see Video S1 for examples of animated displays and Video S2 for an example of an infant watching and terminating a trial.

Neither the boxes nor the objects were repeated across the 32 trials, rendering each object-box pair independent and unique. Thus, there were 32 visual stimuli, one for each sound sequence, and each sound sequence was associated with a different, randomized box-object pairing across infants. This design ensured that differences in attentional termination across sound sequences were not driven by differences in visual materials or particular sounds.

Procedure

Each infant was seated on his or her parent’s lap in front of a table-mounted Tobii 1750 eye-tracker. The infant was positioned such that his or her eyes were approximately 23 inches from the monitor, the recommended distance for accurate eye-tracking. At this viewing distance, the 17-inch LCD screen subtended 24 × 32 degrees of visual angle. The box at the center of the screen was 3 × 3 inches. To prevent parental influence on the infants’ behavior, the parents were asked to wear headphones playing music, lower their eyes, and abstain from interacting with their infants throughout the experiment.

Each of the 32 trials was preceded by an animation designed to attract the infant’s attention to the center of the screen—a laughing and cooing baby. Once the infant looked at the attention-getter, an experimenter who was observing remotely via a wide-angle video camera pushed a button to start the trial. Every infant heard all 32 sound-sequence trials.

For each trial, an animated scene (box opening and closing) for that sound sequence was played. The animated sequence of events—single instances of one of three sounds accompanied by a box opening and closing—continued until the infant looked away continuously for 1 sec., or until the sequence timed out at 60 sec. The Tobii eye-tracking software automatically determined the 1-sec. look-away criterion for trial termination. If the trial was terminated before the infant actually looked away, as determined after the experiment by a wide-angle video-recording of the infant’s face, the trial was labeled by an experimenter as a “false stop” and discarded before the analysis. False stops occurred as a result of the Tobii software being unable to detect the child’s eyes continuously for 1 sec., usually due to infants inadvertently moving out-of-range or inadvertently blocking their own eyes from detection (14.7% of trials). If the infant looked continuously for the entire 60-sec. sequence, the trial was automatically labeled as a “time out” and also discarded (4.4% of trials). Finally, trials in which the infant looked for fewer than four events were also discarded, since we judged such limited observations are likely insufficient for establishing expectations about the distribution of events (40.9% of trials). These stringent inclusion criteria imply that infants terminated many trials before they could compute a reliable estimate of information complexity, suggesting that infants have a strong bias to seek other (e.g., off-screen) sources of information. We note that changing the minimum-attention criterion to include more data (e.g., discarding only trials in which the infant looked for fewer than three events instead of four) does not affect the general qualitative or quantitative pattern of results. We report data here based on the less-than-four minimum-attention criterion in order to more closely match those of Kidd, Piantadosi, & Aslin (2012). This resulted in the final analysis including a mean of 11.5 +/− 5.5 sequences from each infant.

The dependent measure for the subsequent computational modeling was the sound at which the infant looked away in each trial (e.g., the specific point in each sequence where the infant looked away from the display for more than 1 consecutive second).

Analysis

Analysis of the behavioral data followed the approach used in Kidd, Piantadosi, & Aslin (2012) and Piantadosi, Kidd, & Aslin (in press). A Markov Dirichlet-multinomial model first quantified an idealized learner’s expectation that each of the three sounds would occur next, at each point in the sequence. This rational model essentially combines a “smoothing” term—or prior expectation of sound likelihood—with counts of how often each sound has been heard previously in the sequence to predict each sound’s probability of occurring next. The model’s estimated negative log probability for each sound quantifies the sound’s complexity on a scale corresponding to how many bits of information an idealized learner would require to remember or process each sound. We also applied the MDM model to the data under an assumption of event-order dependence. That is, instead of treating every sound as independent, we examined whether look-aways were predicted by the immediately preceding sound (i.e., a transitional model).

We note that the models imperfectly assume that infants know how many sounds are possible on each display. This simplification keeps the analysis in line with Kidd, Piantadosi, & Aslin (2012) and Piantadosi, Kidd, & Aslin (in press); further, and more importantly, it is the most reasonable of several possible imperfect analysis options. It is likely that infants would learn that only three sounds occur per sequence within the first few trials. Other analyses that model uncertainty in the number of sounds per trial (e.g. a Chinese restaurant process) lead to implausible assumptions, such as that the first sound always has probability of 1 (meaning no other sound was possible).

In the analysis that relates model-measured complexity to behavior, standard linear or logistic regressions are inappropriate because infants cannot provide additional data on a trial once they have terminated their attention, thus violating the independence assumption required for these analyses. Thus, the obtained complexity measure was then entered as a quadratic term in a stepwise Cox regression of the behavioral data, as employed in Kidd, Piantadosi, & Aslin (2012). The Cox regression is a type of survival analysis that measures the log linear influence of predictors on infants’ probability of terminating attention, but respects the fact that infants cannot provide additional trial data once they terminate attention (Hosmer, Lemeshow, & May, 2008; Klein & Moeschberger, 2003). Importantly, the Cox regression allows the significance of a quadratic complexity term (an underlying U-shape) to be tested while controlling for a baseline distribution of look-aways and other factors known to influence infant attention, including generalized boredom, trial number, sequence position, whether the current sound was its first occurrence, the number of unheard sounds, and whether the sound was an immediate sequential repeat.

Results

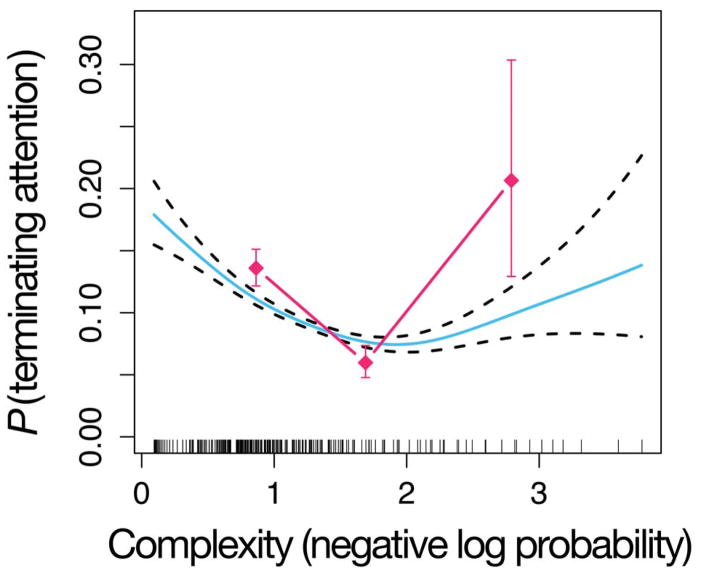
Fig. 3 shows infants’ probability of terminating attention, as a function of the negative log probability of a sound according to the non-transitional model. The plot collapses across infants, sequences, and sequence positions. The diamonds represent the raw probability of terminating attention with complexity divided into 3 discrete bins. The smooth curve represents the fit of a Generalized Additive Model (Hastie & Tibshirani, 1990) with logistic linking function, which fits a continuous relationship between complexity and probability of terminating attention. The figure shows a U-shaped relationship between infants’ probability of attentional termination and the model-based estimate of sound event complexity. This indicates that infants were more likely to terminate attention at a sound in the sequences with either very low or very high complexity (i.e., ones that are very predictable or very surprising, according to the model). There is a “Goldilocks” value of complexity around 2 bits, corresponding to infants’ preferred rate of information in this task. However, the Cox regression analysis revealed that this U-shaped trend was not significant controlling for the baseline look-away distribution (β= 0.008, z = 0.325, p > 0.7), suggesting that other factors contributed to the U-shape.

Figure 3.

U-shaped curve for the non-transitional model. The blue solid curve represents the fit of a Generalized Additive Model (GAM) (Hastie & Tibshirani, 1990) with binomial link function, relating complexity according to the MDM model (x-axis) to infants’ probability of terminating attention (y-axis). The dashed curves show standard errors according to the GAM. The GAM fits include the effect of complexity (negative log probability) and the effect of position in the sequence. Note, the error bars and GAM errors do not take into account subject effects. Vertical spikes along the x-axis represent data points collected at each complexity value. The fuchsia diamonds represent the raw probabilities of terminating attention binned along the x-axis.

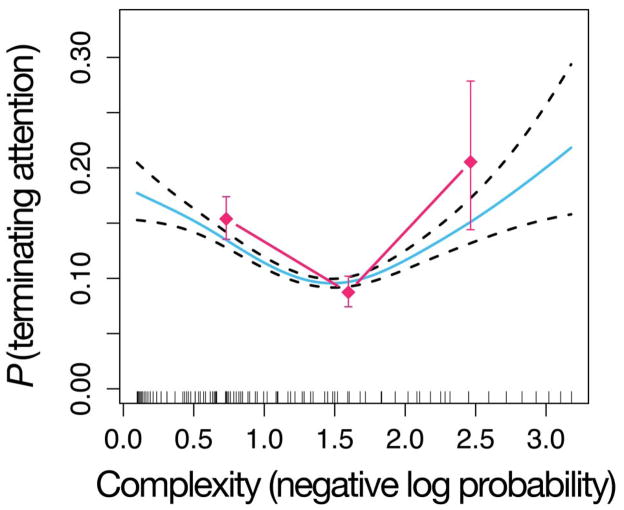
Fig. 4 shows the outcome of the same analysis, but now applied to successive pairs of events. This transitional model also yields a U-shaped function. The complexity measure—along with a number of control covariates that could plausibly influence infant attentional termination—were entered into the Cox regression using a stepwise procedure that only added variables that improved model fit. The control variables included trial number, whether or not the sound had occurred before in the sequence, and whether or not the sound was the same as the last one that had played in the sequence (Table 1). This stepwise procedure revealed a highly significant effect for squared complexity (β = 0.136, z = 2.91, p < 0.01). This indicates that the U-shape observed in Fig. 4 is statistically significant, even after controlling for an overall baseline look-away distribution and the other potentially confounding variables.

Figure 4.

U-shaped curve for the transitional model. The blue solid curve represents the fit of a GAM, relating complexity as measured by the transitional MDM (x-axis) to probability of terminating attention (y-axis). Dashed curves show GAM standard errors. The GAM fits include the effect of complexity (negative log probability) and the effect of position in the sequence. Note, the error bars and GAM errors do not take into account subject effects. Vertical spikes along the x-axis represent data points collected at each complexity value. The fuchsia diamonds represent the raw probabilities of terminating attention binned along the x-axis.

Table 1.

Cox Regression Coefficients (Transitional model)

Covariate	Coefficient	exp(coefficient)	Standard error	Z-statistic	P-value
Squared complexity	0.136	1.15	0.047	2.91	0.004 **
Trial number	0.031	1.03	0.005	5.76	8.61e–09 ***
First occurrence	0.523	1.69	0.235	2.23	0.026 *

All transitional-model variables added by the stepwise procedure, which only added variables that improved model fit according to the Akaike information criterion (Akaike, 1974). These results reveal significant quadratic effects of complexity. Both the complexity and squared complexity variables were shifted and scaled to have a mean of 0 and standard deviation of 1 before they were entered into the regression.

The magnitude of this effect can be understood by exponentiating the coefficient for squared complexity (e^0.136 = 1.15). This number quantifies how much more likely infants are to terminate attention at events that are one standard deviation from the experiment’s overall mean complexity. In this case, infants are 1.15 times more likely to terminate attention at such high- or low-complexity sounds. This effect is relatively small, though statistically reliable. This analysis also revealed an effect of trial number (β = 0.031, z = 5.76, p < 0.001) and first occurrence of a sound (β = 0.523, z = 2.23, p < 0.05), suggesting an overall tendency to look away at earlier sounds during later trials and on sounds which are occurring for the first time in the sequence.

Discussion

Our results from the transitional MDM model suggest that infants seek to maintain intermediate rates of complexity when allocating their auditory attention to sequential sounds. This is consistent with the hypothesis that infants employ an implicit strategy of attentional allocation in the auditory modality that is very similar to attention in the visual modality. As hypothesized in Kidd, Piantadosi, & Aslin (2012), the existence of this effect for auditory stimuli indicates that the Goldilocks effect may be a general way for children to handle James’ “blooming, buzzing confusion” by providing a rational mechanism to direct attention to the most important aspects of the world. Of course, future work will be required to understand the intricacies of this attentional strategy—in particular, how it interacts with social factors (e.g., pedagogy and reward) and with overall stimulus familiarity (e.g., mom’s face or a favorite toy). Together with our earlier work on infant visual attention, which also used “arbitrary” stimuli rather than highly familiar or positive-valence stimuli, the results demonstrate that predictability plays an important role in influencing infant attention—but it is by no means the only relevant factor. In typical looking-time paradigms, it is the overall duration of looking, prior to meeting a criterion for a look-away, that serves as the dependent measure of attention. In contrast, our paradigm used briefly presented sequential stimuli because it afforded us a quantitative metric of information complexity. It remains to be seen whether attention to briefly presented stimuli and to static images (e.g., of a scene) can be captured by a similar model. Finally, in real-world learning situations, multiple complex factors likely compete to influence learners’ attention. Examining the complexities of these dynamics and understanding how they interact with the effects reported here will be a major topic of future work.

Interestingly, the results from the non-transitional model for auditory stimuli were not significant—in contrast to the robust results of the non-transitional model reported for visual stimuli in Kidd, Piantadosi, and Aslin (2012). Dissimilarly, the transitional model for auditory stimuli showed robust evidence of the U-shaped function, even after controlling for a number of other factors, including a baseline look-away distribution. This notable difference across models could indicate that effects of non-transitional learning are weak or non-existent for auditory stimuli. In other words, attention to auditory stimuli could rely more heavily on temporal order information than does attention to visual stimuli. If so, this would have interesting implications for potential cross-modality differences in infants’ attentional systems and learning. For example, though children certainly show sensitivity to frequency differences for auditory stimuli, this apparent sensitivity could arise as the result of learning about transitional statistics (e.g., children’s learning about the transitional probabilities between words could yield apparent phrase-frequency sensitivity as in Bannard & Matthews, 2008). It could be that the transient nature of auditory stimuli leads attention to be directed more to successive differences rather than to raw frequencies of occurrence, something that may be less relevant in the visual modality. Alternatively, tracking of the transitional probabilities of auditory stimuli may either be easier or more crucial for developing useful expectations about the auditory world. This is arguably true in language learning, where the meanings of words are composed not of single events but rather sequences of sounds, and the meanings of utterances tend to be composed not of single words, but of sequences of words. If this were the case, it could be relevant to determine whether this is an innate bias of humans to process auditory stimuli in this way, or whether this attentional pattern might develop over time as infants begin to acquire language. It may also be the case that the non-transitional model regression was insignificant because the effects of non-transitional complexity were too highly correlated with the baseline looking distribution. In this case, we might not have had enough power to find an effect of non-transitional sound event complexity while controlling for the baseline distribution.

Our results provide quantitative evidence that infants possess an attentional selection mechanism that operates over the predictability of the stimulus. However, understanding the precise nature of the mechanism will require further work. Previous theories hypothesized that infants would exhibit a U-shaped pattern of preference over stimulus complexity because of a gradually learned, experience-dependent selection mechanism that allocated attention with respect to encoding/learning efficiency. However, it is equally possible that our pattern of results could fall out of a far more automatic, low-level selection mechanism designed to filter out noise inherent in human perceptual systems. In other words, infants’ behavior may instead result from an attentional mechanism designed to select the most informative, trustworthy observations—and discard those that are uninformative (overly predictable) or unreliable (so surprising that they are implausible). In-progress and planned work will test these two competing theories by longitudinally examining patterns of selection within individuals, in other species, and across different timescales.

Conclusions

We hypothesized that infants’ probability of terminating their auditory attention would be greatest on sounds whose complexity (negative log probability), according to an idealized learning model, was either very low or very high. We found evidence that this was true for the transitional version of the model, but the trend in the non-transitional version was not significant after controlling for other factors. This may indicate that transitional statistics are more readily tracked by infants in the auditory modality. In general, our results are further evidence for a principle of infant attention that may have broad applicability: infants implicitly seek to maintain intermediate rates of information absorption and avoid wasting cognitive resources on overly simple or overly complex events—in both visual and auditory modalities.

Appendix 1.

Auditory sequences Sequences were randomized across infants, and each sequence continued until the infant looked away continuously for 1 sec. or until the sequence timed out (at 60 sec.).

	Sequence Position
		1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30
Sequence ID	1.	B	A	B	B	B	A	C	C	C	A	C	A	A	B	B	A	A	A	B	C	B	B	A	B	A	A	A	C	B	B
	2.	C	C	C	C	A	C	C	A	C	C	C	B	C	C	C	A	A	A	C	C	A	C	A	B	A	A	A	B	B	B
	3.	A	A	A	A	A	A	A	C	C	C	B	B	A	B	C	C	C	B	B	A	B	B	C	A	A	B	C	A	A	B
	4.	C	B	A	B	B	A	B	A	A	C	B	B	A	A	B	B	B	A	A	A	B	A	A	A	B	B	A	B	B	B
	5.	C	A	C	C	C	C	C	C	C	B	B	C	A	C	C	B	B	B	A	C	B	C	A	C	C	A	B	C	B	C
	6.	A	A	A	A	A	A	A	A	B	B	B	A	B	C	C	A	B	B	A	B	C	B	C	C	B	B	A	C	C	A
	7.	B	A	A	B	A	A	C	C	A	B	A	A	B	B	A	B	B	B	B	B	B	A	A	B	B	B	B	B	B	A
	8.	A	A	A	A	A	C	A	A	B	C	C	A	A	A	C	A	A	A	B	C	B	A	C	C	B	B	C	B	B	B
	9.	A	C	A	A	C	A	C	B	A	C	C	A	B	A	A	A	A	A	C	C	B	A	A	A	A	A	B	A	A	B
	10.	B	A	A	C	B	C	C	B	A	C	B	C	C	A	A	A	A	C	A	C	A	A	C	C	C	A	C	C	A	C
	11.	A	A	C	B	A	B	B	C	C	B	A	A	B	B	A	B	A	A	C	B	A	A	A	B	B	A	B	A	B	A
	12.	A	B	A	B	C	A	B	B	C	A	B	A	B	C	B	B	B	B	B	A	A	C	C	C	B	C	C	A	C	B
	13.	C	C	B	C	A	B	B	A	A	B	C	C	C	C	B	A	A	B	C	C	C	B	A	A	A	B	A	B	A	B
	14.	C	B	B	C	C	B	B	B	C	C	B	C	C	B	B	C	C	B	C	B	B	B	C	B	C	C	A	A	A	C
	15.	B	C	A	B	A	A	B	A	A	B	B	A	C	B	B	A	B	A	B	A	B	C	B	A	A	C	A	A	C	C
	16.	B	B	B	B	B	A	B	B	A	B	A	A	B	A	A	A	A	B	C	B	B	B	B	C	C	C	A	C	C	A
	17.	A	B	C	A	B	C	C	A	B	C	B	C	A	B	B	B	C	A	C	C	A	B	B	C	A	C	A	A	C	B
	18.	B	A	B	A	A	B	A	A	A	A	C	B	B	B	B	B	C	B	A	B	B	B	C	B	C	A	B	C	C	B
	19.	B	C	C	A	B	B	B	B	C	C	B	C	C	C	B	B	B	B	B	B	B	B	C	B	C	C	B	B	B	C
	20.	A	C	C	A	C	C	B	B	A	B	B	C	B	B	C	A	A	B	B	C	A	A	B	B	C	B	A	B	B	B
	21.	C	A	A	A	A	C	A	C	C	C	A	C	C	A	C	C	A	C	A	A	C	A	B	B	C	B	A	A	B	C
	22.	B	A	B	B	A	C	A	B	B	B	B	A	C	B	B	B	B	B	A	C	B	B	B	A	C	B	A	B	A	C
	23.	C	B	A	C	B	A	A	C	A	B	C	B	A	A	B	A	B	A	A	A	A	B	A	A	A	B	A	A	B	B
	24	B	A	A	A	C	C	A	C	A	A	C	C	C	A	C	C	A	C	B	A	A	B	B	C	A	B	A	A	B	B
	25	C	B	A	C	A	C	B	B	A	C	A	C	A	B	C	A	A	C	C	B	C	B	A	C	C	C	C	B	A	B
	26.	C	C	C	C	C	C	C	B	B	A	B	A	B	A	A	A	B	C	A	A	C	A	C	A	B	A	C	C	B	B
	27	B	B	A	B	C	A	A	C	B	B	C	C	B	B	C	A	A	C	A	C	A	A	C	A	A	A	A	A	C	B
	28	B	C	A	C	C	A	A	A	B	B	C	C	A	C	C	A	B	B	C	B	B	C	C	B	A	B	A	C	C	B
	29	A	A	A	A	A	A	A	A	A	A	A	A	A	A	A	A	A	A	A	A	A	A	A	A	A	A	A	A	A	A
	30	A	B	A	B	A	B	A	B	A	B	A	B	A	B	A	B	A	B	A	B	A	B	A	B	A	B	A	B	A	B
	31	A	B	C	A	B	C	A	B	C	A	B	C	A	B	C	A	B	C	A	B	C	A	B	C	A	B	C	A	B	C
	32	A	B	A	B	A	B	A	B	A	B	A	B	C	A	B	A	B	C	C	C	C	C	C	C	C	C	C	C	C	C