The Transient Dermal Exposure II: Post-Exposure Absorption and Evaporation of Volatile Compounds

Abstract

The transient dermal exposure is one where the skin is exposed to chemical for a finite duration, after which the chemical is removed and no residue remains on the skin’s surface. Chemical within the skin at the end of the exposure period can still enter the systemic circulation. If it has some volatility, a portion of it will evaporate from the surface before it has a chance to be absorbed by the body. The fate of this post-exposure “skin depot” is the focus of this theoretical study. Laplace domain solutions for concentration distribution, flux, and cumulative mass absorption and evaporation are presented, and time domain results are obtained through numerical inversion. The Final Value Theorem is applied to obtain the analytical solutions for the total fractional absorption by the body and evaporation from skin at infinite time following a transient exposure. The solutions depend on two dimensionless variables: χ, the ratio of evaporation rate to steady-state dermal permeation rate; and the ratio of exposure time to membrane lag time. Simple closed form algebraic equations are presented that closely approximate the complete analytical solutions. Applications of the theory to the dermal risk assessment of pharmaceutical, occupational, and environmental exposures are presented for four example chemicals.

INTRODUCTION

Recent analyses have advanced our understanding of the absorption of chemicals in contact with skin from finite dose^1–5 and transient exposures.^6,7 The former is characterized as an exposure to a small (finite) dose (mass/area) of chemical, the disposition of which has been shown to depend on the relative rates of evaporation and permeation as well as the initial load. The finite dose is a good model for splash-type exposures in the workplace and also for pharmaceutical and cosmetic product applications. The transient exposure is one where the skin is exposed to chemical for a finite duration, after which the chemical is removed and no residue remains atop the surface. Chemical within the skin at the end of the exposure period can still enter the systemic circulation. If it has some volatility, a portion of it will evaporate from the skin surface before it has a chance to be absorbed by the body. As an example that is relevant to dermal risk assessment, consider bathing or showering with contaminated water. Dermal absorption proceeds for the duration of the exposure, but once the bath or shower has ended, contaminant residing within the skin may still be absorbed by the body while some may evaporate into the surrounding air. The fate of this post-exposure “skin depot” is the focus of this theoretical study.

Frasch and Barbero⁷ provided analytical solutions for total mass absorbed by the body (exposure duration plus post-exposure) for the extreme cases of non-volatile and infinitely volatile chemicals. N’Dri-Stempfer and Bunge⁶ presented finite difference post-transient exposure solutions for chemicals of varying volatility. Based on the numerical results, they derived a four-parameter empirical equation to predict post-exposure evaporation expressed as a fraction of the mass residing within the membrane at the conclusion of the exposure time. Herein, we derive the complete analytical solutions for fractional absorption by the body and evaporation from skin for variable volatility. In this study, as in previous ones, the skin is considered to be a single pseudo-homogeneous membrane.

THEORY

It is assumed here that the skin is transiently exposed to a (possibly) volatile chemical. At the end of the exposure period, the skin is efficiently decontaminated such that zero residual chemical remains on the surface. We wish to determine the disposition of chemical residing within the skin following this exposure.

With the exception of highly lipophilic chemicals, the main barrier property of the skin is imparted by the stratum corneum (SC). In its simplest form, the SC may be considered to be a uniform effective medium of thickness h, occupying the space between x = 0 (the skin surface) and x = h (bottom of tissue). The permeant has an effective diffusivity D that does not vary with position or time. This implies that neither the permeant nor its vehicle alter the SC permeability. The SC, initially free of chemical, is exposed to a constant concentration in vehicle C_v for a specified duration t_exp. It is assumed that the chemical does not bind to the SC and that the dermal vasculature acts as a perfect sink at the bottom of the tissue.

With these stipulations, post-exposure (t ≥ t_exp) permeant transport is governed by the one-dimensional diffusion equation:

$$\frac{\partial C}{\partial t}=D\frac{{\partial }^{2}C}{\partial x^2}0\le x\le h,$$ (1)

with the initial condition:

$$\begin{array}{l}C(x,0)=C_0(x)\\ =K_{\text{mv}}{C}_{\mathrm{v}}\left[1-\frac{x}{h}-\frac{2}{\mathrm{\pi }}\sum _{n=1}^{\infty }\frac{1}{n}sin\left(\frac{n\mathrm{\pi }x}{h}\right)\text{exp}\left(\frac{-n^2{\mathrm{\pi }}^2}{6}\frac{t_{exp}}{t_{\text{lag}}}\right)\right],\end{array}$$ (2)

where K_mv is the membrane–vehicle partition coefficient and the lag time $t_{\text{lag}}=\frac{h^2}{6D}$. The boundary conditions are:

$$\begin{array}{l}C(h,t)=0\\ {D\frac{\partial C}{\partial x}|}_{x=0}=\mathrm{\gamma }C(0,t),\end{array}$$ (3)

where

$$\mathrm{\gamma }=\mathrm{\chi }\frac{D}{h}.$$ (4)

The parameter χ is the dimensionless ratio of the evaporation rate to the steady-state dermal absorption rate of the permeant, and is discussed in detail elsewhere.^2,6 Physically, χ describes the post-exposure conditions at the skin surface and its value, depending on the situation, can vary from zero, representing zero flux from the skin surface, to infinity, which corresponds to zero concentration (sink conditions) on the skin surface. In addition to representing chemicals that evaporate rapidly from the skin surface, χ → ∞ mathematically describes a situation in which a chemical is removed from the skin with a continuous rinse or solvent immersion. In instances where chemical volatility is equated with χ in this manuscript, it is understood that volatility is relative to the dermal absorption rate. Any two chemicals may have similar evaporation rates, but χ will differ if the dermal absorption rates differ.

The initial concentration distribution specified by Eq. (2) is given by Crank.⁸ Note that the initial mass (per unit area) within the SC, that is, the total mass at the end of the exposure time, is:

$$\begin{array}{l}{m}_0=\underset{0}{\overset{h}{\int }}{C}_0(x)dx\\ =3k_{\mathrm{p}}{C}_{\mathrm{v}}{t}_{\text{lag}}\left[1-\frac{8}{{\mathrm{\pi }}^2}\sum _{n=0}^{\infty }\frac{1}{{(2n+1)}^2}\text{exp}\left(\frac{-{(2n+1)}^2{\mathrm{\pi }}^2}{6}\frac{t_{exp}}{t_{\text{lag}}}\right)\right],\end{array}$$ (5)

where the permeability coefficient k_p = K_mvD/h.

METHODS

The solution of Eq. (1) with associated initial and boundary conditions was undertaken using the method of Laplace transforms. Solutions for concentration distribution, flux, and cumulative mass absorption and evaporation are presented. Time domain solutions were obtained through numerical inversion of the Laplace domain equations using Scientist (MicroMath Scientific Software, St. Louis, Missouri). The Final Value Theorem was applied to obtain total cumulative mass absorption and evaporation at infinite time postexposure, expressed as fractions of the total mass within the skin at the end of the exposure time. Simple closed form algebraic equations are presented that closely approximate the complete analytical solutions. For practical applications, the time it takes for the body to absorb 90% of the total infinite-time amount was estimated.

RESULTS

The Laplace transform of Eq. (1) is:

$$\frac{d^2\widehat{C}(x,s)}{{dx}^2}-{\mathrm{\lambda }}^2\widehat{C}(x,s)=\frac{-C_0(x)}{D},$$ (6)

with the hat (ˆ) indicating a function of the Laplace variable s, and $\mathrm{\lambda }=\sqrt{s/D}$. The Laplace transform of Eq. (3) is:

$$\begin{array}{l}\widehat{C}(h,s)=0\\ \mathrm{\gamma }\widehat{C}(0,s)-{D\frac{d\widehat{C}(x,s)}{dx}|}_{x=0}=0.\end{array}$$ (7)

The solution of Eq. (6) with specified initial (Eq. (2)) and boundary (Eq. (7)) conditions is:

$$\widehat{C}(x,s)=\frac{{\widehat{R}}_0(s)\text{sinh}[\mathrm{\lambda }(h-x)]}{-\mathrm{\lambda }D\text{cosh}(\mathrm{\lambda }h)-\mathrm{\gamma }\text{sinh}(\mathrm{\lambda }h)}+{\widehat{C}}_{\mathrm{p}}(x,s),$$ (8)

with

$${\widehat{C}}_{\mathrm{p}}(x,s)=\frac{K_{\text{mv}}{C}_{\mathrm{v}}}{D}\left[\frac{1}{{\mathrm{\lambda }}^2}-\frac{x}{{\mathrm{\lambda }}^{2}h}-\frac{2}{\mathrm{\pi }}\sum _{n=1}^{\infty }\frac{sin(k_{n}x)}{n(k_n^2+{\mathrm{\lambda }}^2)}\text{exp}\left(\frac{-n^2{\mathrm{\pi }}^2}{6}\frac{t_{exp}}{t_{\text{lag}}}\right)\right],$$ (9)

where k_n = nπ/h, and

$$\begin{array}{l}{\widehat{R}}_0(s)=\mathrm{\gamma }{\widehat{C}}_{\mathrm{p}}(0,s)-D\frac{d{\widehat{C}}_{\mathrm{p}}(0,s)}{dx}\\ =K_{\text{mv}}{C}_{\mathrm{v}}\left[\frac{\mathrm{\gamma }}{{\mathrm{\lambda }}^{2}D}+\frac{1}{{\mathrm{\lambda }}^{2}h}+\frac{2}{h}\sum _{n=1}^{\infty }\frac{1}{(k_n^2+{\mathrm{\lambda }}^2)}\text{exp}\left(\frac{-n^2{\mathrm{\pi }}^2}{6}\frac{t_{exp}}{t_{\text{lag}}}\right)\right].\end{array}$$ (10)

Ĉ_p (x, s) is the particular solution to Eq. (6). Its value depends on the specific form taken by the nonhomogeneous terms (here, −C₀(x)/D). Tables of solutions are available in a number of sources (e.g., the CRC Standard Mathematical Tables⁹).

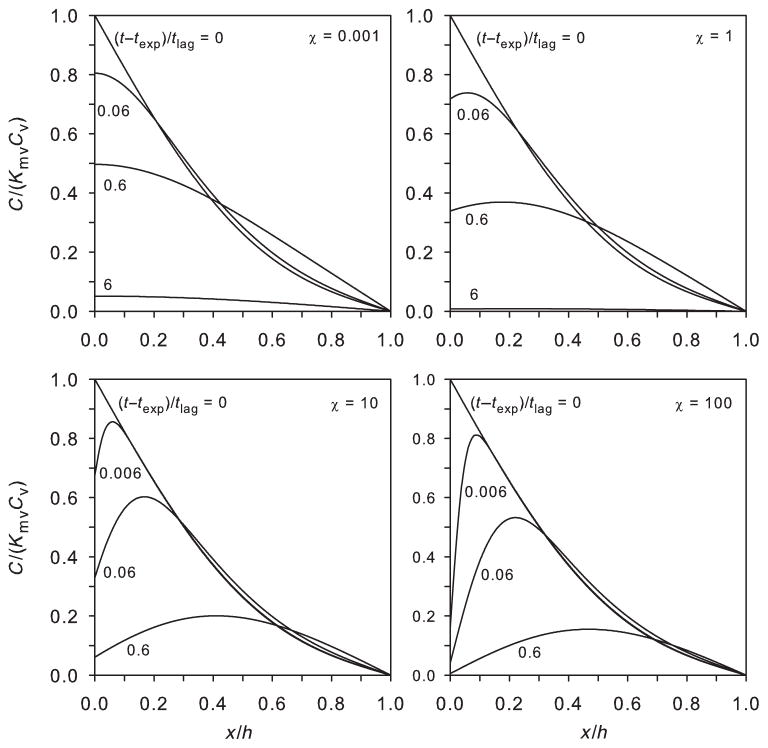
Figure 1 shows plots of C(x, t) within the membrane for various values of χ. The plots represent inverse Laplace transforms of Eq. (8). For small χ, there is little evaporation and the chemical concentration is greatest at the skin surface. The time to clear chemical from the SC is relatively long. For large χ, most of the chemical within the skin at the end of the exposure evaporates. Chemical concentration is greatest in the mid to upper portions of the skin, and the clearance time is relatively short.

Figure 1.

Dimensionless concentration distributions at relative positions within the membrane for varying times after an exposure of t_exp/t_lag = 0.6. Different values of χ are shown, representing non-volatile (χ = 0.001), semivolatile (χ = 1, 10), and highly volatile (χ = 100) compounds. Plots represent inverse Laplace transforms of Eq. (8).

In the Laplace domain, the flux is given by:

$$\begin{array}{l}\widehat{F}(x,s)=-D\frac{d\widehat{C}(x,s)}{dx}\\ =\frac{-\mathrm{\lambda }D{\widehat{R}}_0(s)cosh[\mathrm{\lambda }(h-x)]}{\mathrm{\lambda }D\text{cosh}(\mathrm{\lambda }h)+\mathrm{\gamma }\text{sinh}(\mathrm{\lambda }h)}-D\frac{d{\widehat{C}}_{\mathrm{p}}(x,s)}{dx},\end{array}$$ (11)

with

$$\frac{d{\widehat{C}}_{\mathrm{p}}(x,s)}{dx}=-\frac{K_{\text{mv}}{C}_{\mathrm{v}}}{Dh}\left[\frac{1}{{\mathrm{\lambda }}^2}+2\sum _{n=1}^{\infty }\frac{cos(k_{n}x)}{(k_n^2+{\mathrm{\lambda }}^2)}\text{exp}\left(\frac{-n^2{\mathrm{\pi }}^2}{6}\frac{t_{exp}}{t_{\text{lag}}}\right)\right].$$ (12)

The cumulative mass absorption by the body (mass/area) is given by:

$${\widehat{M}}_{\text{abs}}(s)=\frac{\widehat{F}(h,s)}{s},$$ (13)

and the cumulative mass evaporation from the skin surface is given by:

$${\widehat{M}}_{\text{evap}}(s)=-\frac{\widehat{F}(0,s)}{s}.$$ (14)

The convention that the x axis points into the skin necessitates the minus sign in Eq. (14) because efflux from the skin by evaporation corresponds to transport in the −x direction.

Figure 2 shows plots of normalized absorption by the body over time (m_abs(t)/ m₀) and evaporation from the surface (m_evap (t) /m₀) for several values of χ when t_exp/t_lag = 0.6. Plots were obtained from the inverse Laplace transforms of Eqs. (13) and (14), both divided by Eq. (5). For a poorly volatile permeant (small χ), nearly all of the chemical within the skin at the end of the exposure time is eventually absorbed by the body. For highly volatile compounds (large χ), evaporation is substantial and under the exposure conditions shown in Figure 2, only about 27% of the initial skin amount is absorbed. Compared with a small χ permeant, the time to completely distribute the chemical from the SC is shorter.

Figure 2.

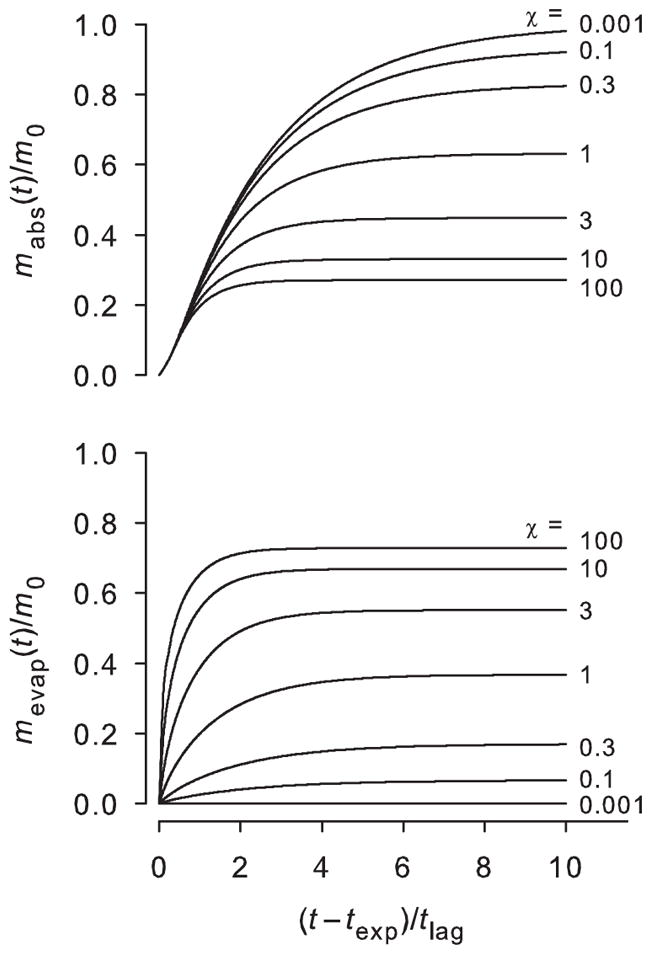
Mass absorption into the body (top) and mass evaporation from the skin surface (bottom) over time following an exposure of t_exp/t_lag = 0.6 for various values of χ. Plots represent inverse Laplace transforms of Eqs. (13) and (14), normalized by Eq. (5).

The total amount absorbed by the body (per area), after infinite time may be calculated from the Final Value Theorem:

$$m_{\text{abs}}(\infty )=\underset{s\to 0}{lim}s{\widehat{M}}_{\text{abs}}(s)=\underset{s\to 0}{lim}\widehat{F}(h,s).$$ (15)

The result is given here as the fraction of the initial amount present in the membrane at the end of the exposure duration (Eq. (5)) that absorbs into the body:

$$\begin{array}{l}{F}_{\text{abs}}=\frac{m_{\text{abs}}(\infty )}{m_0}\\ =\frac{3+\mathrm{\chi }\left[\frac{1+\frac{12}{{\mathrm{\pi }}^2}{\displaystyle \sum _{n=1}^{\infty }}\frac{{(-1)}^n}{n^2}\text{exp}\left(\frac{-n^2{\mathrm{\pi }}^2}{6}\frac{t_{exp}}{t_{\text{lag}}}\right)}{1-\frac{8}{{\mathrm{\pi }}^2}{\displaystyle \sum _{n=0}^{\infty }}\frac{1}{{(2n+1)}^2}\text{exp}\left(\frac{-{(2n+1)}^2{\mathrm{\pi }}^2}{6}\frac{t_{exp}}{t_{\text{lag}}}\right)}\right]}{3(1+\mathrm{\chi })}.\end{array}$$ (16)

At infinite time, all permeant has either been absorbed or evaporated. Therefore, the fraction that evaporates is:

$$\begin{array}{l}{F}_{\text{evap}}=1-F_{\text{abs}}\\ =\frac{2\mathrm{\chi }\left[\frac{1-\frac{6}{{\mathrm{\pi }}^2}{\displaystyle \sum _{n=1}^{\infty }}\frac{1}{n^2}\text{exp}\left(\frac{-n^2{\mathrm{\pi }}^2}{6}\frac{t_{exp}}{t_{\text{lag}}}\right)}{1-\frac{8}{{\mathrm{\pi }}^2}{\displaystyle \sum _{n=0}^{\infty }}\frac{1}{{(2n+1)}^2}\text{exp}\left(\frac{-{(2n+1)}^2{\mathrm{\pi }}^2}{6}\frac{t_{exp}}{t_{\text{lag}}}\right)}\right]}{3(1+\mathrm{\chi })}.\end{array}$$ (17)

Detailed solutions are available as Supplementary Materials (Part 1). Note that the limits for long exposure times (t_exp ≫ t_lag) are:

$$F_{\text{abs}}=\frac{3+\mathrm{\chi }}{3(1+\mathrm{\chi })}$$ (18)

$$F_{\text{evap}}=\frac{2\mathrm{\chi }}{3(1+\mathrm{\chi })}.$$ (19)

Thus, the fraction of what is in the skin following a long exposure that absorbs into the body is between 1/3, for a highly volatile chemical, and one, for a non-volatile chemical.

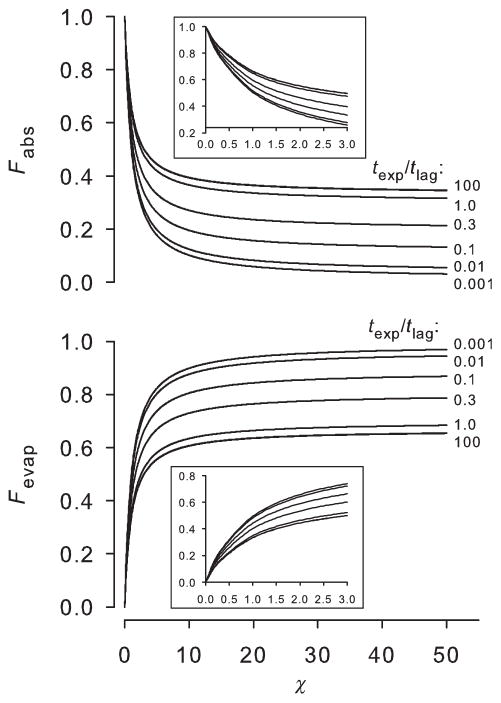
Figure 3 shows the solutions to Eqs. (16) and (17) for the first 100 terms in the series, for which the quantities are independent of the number of terms to at least six significant figures for t_exp/t_lag ≥ 0.001. For a poorly volatile permeant (small χ), nearly all of the chemical within the skin at the end of the exposure time is eventually absorbed by the body; this outcome is independent of exposure time. For χ < 0.1, less than 10% of the amount in the skin evaporates. As χ increases, evaporation becomes important and for highly volatile chemicals, at least 2/3 of the chemical in the skin at the end of the exposure evaporates. For highly volatile compounds, the total absorbed and evaporated fractions depend on the exposure time: F_abs varies from zero for small values of t_exp/t_lag to a maximum of one-third for large values of t_exp/t_lag.

Figure 3.

The fractions of chemical in the skin at the end of exposure that will be absorbed (F_abs) and evaporated (F_evap). Plots represent 100 terms of Eqs. (16) and (17). Insets: F_abs and F_evap for smaller values of χ.

Equations (16) and (17) are somewhat cumbersome, although they may readily be approximated to a finite number of terms using commercially available mathematical software packages (e.g., Mathcad or even Excel). The presence of infinite series in the equations is a consequence of the initial concentration distribution of permeant (Eq. (2)). Because of the complexity of these equations, simple algebraic approximations were sought empirically. The following one-parameter equations were explored:

$$F_{\text{abs}}=\frac{3+\mathrm{\chi }\left[1-\text{exp}\left(-a_1\frac{t_{exp}}{t_{\text{lag}}}\right)\right]}{3(1+\mathrm{\chi })}$$ (20)

$$F_{\text{evap}}=\frac{2\mathrm{\chi }\left[1+\frac{1}{2}\text{exp}\left(-{\mathrm{\alpha }}_1\frac{t_{exp}}{t_{\text{lag}}}\right)\right]}{3(1+\mathrm{\chi })}.$$ (21)

Nonlinear regression with the 100-term series solutions yielded a value of 2.906 for a₁. The correlation coefficient R² > 0.98, but the differences are largest for small t_exp/t_lag. Numerical comparisons were made to investigate errors of using the simple F_abs equation. The estimate for F_abs provided by the Eq. (20) approximation should be within 10% of the exact value if:

$$\begin{array}{ll}\frac{t_{exp}}{t_{\text{lag}}}>0.001\hfill & \text{for}\mathrm{\chi }<3.5\hfill \\ \frac{t_{exp}}{t_{\text{lag}}}>0.039+\frac{0.149(\mathrm{\chi }-3.5)}{2.693+(\mathrm{\chi }-3.5)}\hfill & \text{for}\mathrm{\chi }>\mathrm{3.5.}\hfill \end{array}$$ (22)

Consequently, Eqs. (20) and (21) (with a₁ as specified) may be used with confidence in lieu of the full series solutions, with the proviso implied by Eq. (22). Additional information on the numerical comparisons leading to Eq. (22) is presented in Supplementary Materials (Part 2).

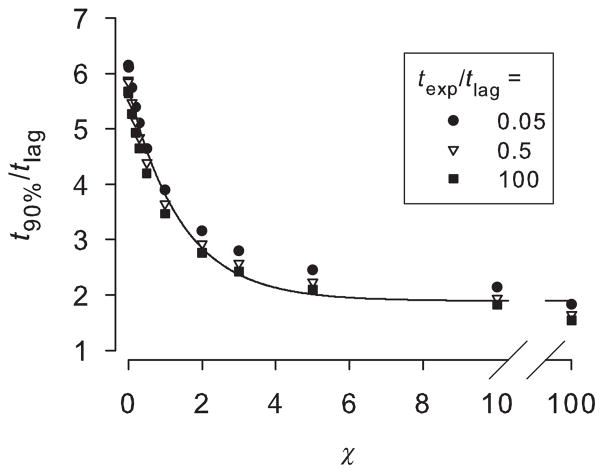
In any realistic setting, infinite time is of course an abstraction. A practical application may require an estimate of the time it takes for the body to absorb most of the final quantity. Figure 4 shows the time after the exposure ends to reach 90% of the final quantity absorbed by the body (t_90%). There is a weak dependence on t_exp/t_lag: all intermediate values fell within the displayed values of 0.05 and 100. The time it takes for nearly complete absorption ranges from about 6 × t_lag for poorly volatile compounds to about 2 × t_lag for highly volatile ones. The pooled data were fitted to the following three-parameter decay curve:

$$\frac{t_{90\%}}{t_{\text{lag}}}=a_2+b_2\text{exp}(-c_2\mathrm{\chi }).$$ (23)

Figure 4.

Time after the exposure ends to reach 90% of the final quantity absorbed by the body (t_90%). Solid line is a three-parameter exponential decay curve with parameter values, listed in the text, fitted to the pooled data.

Parameter values for the solid curve displayed in Figure 4 are: a₂ = 1.895, b₂ = 3.856, c₂ = 0.698; the global R² > 0.97.

The figure confirms and quantifies what is shown in Figure 2: for large χ, the time to distribute almost all of the chemical from the SC is shorter than that for small χ. For a poorly volatile chemical, surface evaporation is insignificant and most chemical within the skin must diffuse inward into the body. The chemical is concentrated at the skin surface (Fig. 1) and so the overall time to complete absorption is relatively longer. For large χ, most of the chemical within the skin at the end of the exposure evaporates. Chemical concentration is greatest in the mid to upper portions of the skin (Fig. 1). Rapid evaporation clears this permeant and the overall time to complete dermal absorption is shorter.

DISCUSSION

The solutions presented here for F_abs and F_evap refer to the post-exposure absorbed and evaporated fractions of the amount of permeant present in the membrane at the end of the exposure time (t = t_exp). In many instances, it would be desirable to estimate the total amount of permeant that has been absorbed into the body from the entire transient exposure. For example, dermal risk assessments of exposures to occupational chemicals, environmental contaminants, cosmetic and consumer products, as well as pharmaceutical compound applications, require such estimates.

The total mass absorbed (m_T, mass/area) is given by:

$$m_{\mathrm{T}}=m_{\text{abs}}(t_{exp})+F_{\text{abs}}{m}_0,$$ (24)

where m_abs(t_exp) is the mass that has been absorbed into the body at t = t_exp¹⁰:

$$m_{\text{abs}}(t_{exp})=k_{\mathrm{p}}{C}_{\mathrm{v}}{t}_{\text{lag}}\left[\frac{t_{exp}}{t_{\text{lag}}}-1-\frac{12}{{\mathrm{\pi }}^2}\sum _{n=1}^{\infty }\frac{{(-1)}^n}{n^2}\text{exp}\left(-\frac{n^2{\mathrm{\pi }}^2}{6}\frac{t_{exp}}{t_{\text{lag}}}\right)\right].$$ (25)

F_abs is given by Eq. (16), and m₀ by Eq. (5). Frasch and Barbero⁷ derived solutions for m_T (m_∞ in their terminology) for the special cases of χ = ∞ (their Case 1) and χ = 0 (Case 2). Note that m_T may be estimated with quantities commonly measured from standard in vitro diffusion cell experiments, specifically k_p and t_lag. Other required parameters are chemical concentration, exposure duration and χ. Kasting and Miller² provide equations to estimate χ based on known or measurable chemical properties including vapor pressure, molecular weight, octanol–water partition coefficient, and water solubility. Alternatively, χ may be measured directly under controlled conditions. Gajjar et al.¹¹ provide data on the evaporation rates of 21 volatile organic compounds from films of neat liquid on human skin, which may be combined with measured or estimated steady-state dermal flux of the compounds from a solution at unit activity (i.e., either neat or in a saturated solution) to obtain χ.

A strategy such as outlined in this paper could be used to identify chemical and exposure situations for which chemical in the SC is or is not likely to be systemically absorbed. Current practices vary on whether chemical in skin at the end of an exposure should or should not be included in estimates of the systemically absorbed.¹² For example, risk assessment guidance documents from the USEPA,¹³ OECD,^14–16 and ECETOC¹⁷ identify chemical left after washing the exposed skin, including the entire SC, as absorbable but not absorbed. In contrast, the European Commission¹⁸ and USEPA in the final test rule for in vitro dermal penetration rate testing issued in 2004¹⁹ consider chemical in the SC and deeper skin layers as absorbed. European guidance for cosmetics and consumer products exclude chemical in the SC from estimates of the absorbed dose,^20–24 whereas the EFSA²⁵ specifies that chemical in all but the first two tape strips should be classified as absorbed unless it can be shown that remaining chemical is not bioavailable or that >75% of the material in the receptor solution (or systemically absorbed in an in vivo study) occurred within half of the duration of the sampling time.

In Tables 1 and 2, we illustrate the use of the method by calculating F_abs, m₀, m_T, and the fraction of m_T that is absorbed postexposure (F_abs × m₀/m_T). Table 1 contains the chemical and skin permeation properties for four example chemicals, and Table 2 contains calculated values for skin exposures of 5 min, 1 h, and much longer than t_lag. The chosen chemicals are important components in dermatological, cosmetic, and consumer products (ethanol, diphenylamine), produced and used in large quantities in the United States (p-nitrophenol and diphenylamine), and a commonly used plasticizer (benzylbutylphthalate). They illustrate a range of evaporation and skin penetration rates, giving small and large estimates for χ. Disposition of chemical in the SC at the end of the exposure was calculated assuming the skin was either left open to the air or immersed in a liquid solution with a large saturation concentration for the chemical. Washout into a liquid solution corresponds to χ approaching infinity, which was approximated with χ = 1000. The absorption fraction (Eq. (16)) and absorbed masses (Eq. (24)) have been calculated using the first 20 terms of the series, which were sufficient for the solutions to be independent of the number of terms to three significant digits. Fractional absorption was also calculated using the simple approximation represented by Eq. (20). The quantities differ most for small values of F_abs, but overall the agreement is excellent. The absorbed masses were calculated assuming an exposed area of 180 cm², equivalent to the area of the palm of one hand,²⁶ and a vehicle concentration equal to the chemical’s aqueous saturation value; that is, the calculations were made using estimates of maximum flux conditions. The time for 90% of the ultimate absorption of chemical within the skin at the end of exposure (Eq. (23)) is also listed. An Excel spreadsheet was developed to perform these calculations; it is available for use in Supplementary Materials (Part 4).

Table 1.

Chemical and Skin Permeation Properties for Four Example Compounds^*

Compound	CAS No.	MW	Log Kow	Pvap	Sw	tlag	kp	χ
Ethanol	64–17–5	46.1	−0.31	59.3	789	0.29	0.0008	155
Diphenylamine	122–39–4	169.2	3.5	0.00067	0.0636	1.34	0.0077	5.3
Benzylbutyl-phthalate	85–68–7	312.4	4.73	8.25 × 10−6	0.00269	8.86	0.037	0.48
p-Nitroaniline	100–01–6	138.1	1.39	0.0001	0.728	1.29	0.00844	0.060

^*

Definitions (in alphabetical order): k_p, permeability coefficient for chemical transport through the SC from an aqueous vehicle (cm/h); K_ow, octanol–water partition coefficient (unitless); MW, molecular weight (mol/g = mmol/mg); P_vap, vapor pressure of the chemical (Torr); S_w, water saturation (mg/mL); t_lag, lag time for chemical transport through the SC (h); χ, ratio of the evaporation rate from the SC surface to the dermal absorption rate through the SC (unitless) calculated using the following equation described by Kasting and Miller ² and N’Dri Stempfer and Bunge ⁶:

$$\mathrm{\chi }=(k_{\mathrm{g}}{P}_{\text{vap}}MW/(RT))/(k_{\mathrm{p}}{S}_{\mathrm{w}})$$

in which T is absolute temperature (K) assumed to be 298 K, R is the real gas constant in consistent units (62.37 mL Torr/K-mmol), and k_g = gas phase mass transfer coefficient (cm/h) calculated from the following equation for laminar flow of air past a flat plate [derived as described in the Supplementary Materials (Part 3)], from the expression, Sh = 0.664 Re^1/2Sc^1/3 where Sh = k_gL/D, Re = uL (ρ/μ) and Sc = (μ/ρ)/D, available in Liu et al.²⁷ and many engineering textbooks (e.g., Geankoplis²⁸):

$$k_{\mathrm{g}}=3260D^{2/3}\sqrt{u/L}$$

In this equation, the factor of 3260 includes the ratio of the viscosity to the density for air (μ/ρ) at 25°C and atmospheric pressure (0.1558 cm²/s; Wolfram|Alpha ²⁹); L, characteristic length (cm) calculated from the square-root of the exposed skin area; D, diffusivity of the compound (cm²/s) calculated using the Fuller, Schettler, and Giddings relation (described in many references including Cussler³⁰ and Perry et al.³¹ at 25°C and one atmosphere pressure, and u = air velocity (cm/s), which is typically between 5 and 25 cm/s for indoor air with values to 50 cm/s (Girman³²; Evans³³; Knudsen et al.³⁴; VENT-AXIA³⁵). In the calculations above, u = 10 cm/s, which is recommended as the standard residential room condition (Girman³², and L = 13.4 cm, which is the square-root of the area of the palm of one hand (180 cm² from NIOSH²⁶). Additional details are provided in Supplementary Materials (Part 3), including the calculations of D and an explanation of why the equation chosen for estimating k_g is different from the equation suggested previously by Kasting and Miller² and N’Dri-Stempfer and Bunge.⁶

Data sources: Unless specified otherwise, values for MW, log K_ow, P_vap, and S_w are from the Syracuse Research PhysProp database and reported at 25°C. When experimental values were not available, estimates for k_p and t_lag were calculated using the following equations from US EPA Risk Assessment Guidance for Superfund, part E (US EPA (2004) assuming the parameter B was small:

$$\begin{array}{l}log{k}_{\mathrm{p}}=-2.80+0.66log{K}_{\text{ow}}-0.0056\text{MW}\\ t_{\text{lag}}=h/(6D/h)\text{where}D\text{is}\text{the}\text{effective}\text{diffusion}\text{coefficient}\text{for}\mathrm{a}\text{chemical}\text{in}\text{the}\text{SC}\text{and}h\text{is}\text{the}\text{SC}\text{thickness}(\text{assumed}\text{to}\text{be}15\mathrm{\mu }\mathrm{m}),\text{and}\\ D/h={10}^{(-2.80-0.0056\text{MW})}\end{array}$$

Chemical specific notes (listed in alphabetical order): Benzylbutylphthalate: Consistent with the calculations in this analysis, which ignore resistance from the viable epidermis or dermis, the calculation assumed the B-parameter described in Risk Assessment Guidance for Superfund (US EPA (2004)) was small. The estimated value for B is 0.25, which would have an effect, although small. Diphenylamine: S_w (at unspecified temperature), k_p, and t_lag are from Chemtura³⁶. Ethanol: S_w is the density of neat ethanol; experimental k_p is from Scheuplein and Blank³⁷. p-Nitroaniline: S_w is at 30°C; experimental values for k_p and t_lag were calculated from the slope and intercept of cumulative mass that penetrated through the skin between 4 and 12 h in the 24-h experiment taken from Aceto Corporation³⁸.

Table 2.

Estimates of the Disposition of Chemical for Skin Exposed to Air or Liquid with a High Saturation Limit at the End of the Exposure for Four Example Compounds at Three Different Exposure Durations and at Maximum Activity (i.e., Saturated in an Aqueous Vehicle)^*

Compound		χ	texp	texp/tlag	Fabs	Fabs (alt)	m0	mT	Fabs × m0/mT	t90%/tlag	t90%
Ethanol	Air	155	5 min	0.29	0.20	0.19	48.8	9.71	1.00	1.9	0.6
			1 h	3.4	0.34	0.34	98.6	114	0.29
			10 × tlag	10	0.34	0.34	98.8	330	0.10
	Liquid	1000	5 min	0.29	0.19	0.19	48.8	9.51	1.00	1.9	0.6
			1 h	3.4	0.33	0.33	98.6	114	0.29
			10 × tlag	10	0.33	0.33	98.8	330	0.10
Diphenylamine	Air	5.3	5 min	0.062	0.24	0.21	0.081	0.019	1.00	2.0	2.7
			1 h	0.75	0.40	0.41	0.270	0.119	0.90
			10 × tlag	10	0.44	0.44	0.354	1.22	0.13
	Liquid	1000	5 min	0.062	0.091	0.056	0.081	0.007	1.00	1.9	2.5
			1 h	0.75	0.28	0.30	0.270	0.088	0.87
			10 × tlag	10	0.33	0.33	0.354	1.18	0.10
Benzylbutyl-phthalate	Air	0.48	5 min	0.0094	0.69	0.68	0.043	0.029	1.00	4.7	41
			1 h	0.11	0.72	0.71	0.147	0.105	1.00
			10 × tlag	10	0.78	0.78	0.476	1.80	0.21
	Liquid	1000	5 min	0.0094	0.036	0.010	0.043	0.002	1.00	1.9	17
			1 h	0.11	0.12	0.094	0.147	0.018	1.00
			10 × tlag	10	0.33	0.33	0.476	1.59	0.10
p-Nitroaniline	Air	0.060	5 min	0.065	0.95	0.95	1.00	0.95	1.00	5.6	7.2
			1 h	0.78	0.96	0.96	3.31	3.34	0.95
			10 × tlag	10	0.96	0.96	4.28	17.0	0.24
	Liquid	1000	5 min	0.065	0.093	0.058	1.00	0.093	1.00	1.9	2.5
			1 h	0.78	0.29	0.30	3.31	1.11	0.85
			10 × tlag	10	0.33	0.33	4.28	14.3	0.10

^*Definitions (in alphabetical order): F_abs, fraction of chemical in the SC at end of the chemical exposure that is predicted to absorb systemically (unitless). Calculated with 1st 20 terms of Eq. (16); F_abs (alt), alternate form of F_abs calculated from Eq. (20); m₀, initial mass in membrane at the end of the exposure duration (mg), assuming an exposed area of 180 cm² and a vehicle concentration equal to the water saturation value; m_T, total mass absorbed into the body from the entire transient exposure (mg), both during and after the exposure, assuming the same exposure area and vehicle concentration, t_90%, estimated time to 90% of F_abs (h); t_lag, lag time for chemical transport through the SC (h), taken from Table 1; t_exp, length of time that skin is exposed to the chemical; χ, ratio of the evaporation rate from the SC surface to the dermal absorption rate through the SC (unitless), calculated for air exposure as described in Table 1.

The absorption fraction is smallest for volatile chemicals with short exposure times relative to the lag time. Thus, although ethanol is much more volatile than diphenylamine, almost the same fraction of diphenylamine and ethanol absorbs after a 5 min exposure because the ratio of exposure time to lag time is smaller for diphenylamine. However, because its lag time is larger than ethanol’s, 90% absorption of diphenylamine takes four times longer than ethanol (2.7 compared with 0.6 h). Evaporation of compounds with low vapor pressure can occur if the skin permeation rate is slow. Benzylbutylphthalate is a low vapor pressure example in which the estimate for χ = 0.48 and 21% is predicted to evaporate, although 41 h are required.

For the chemicals listed in Table 2, at least 85% of the total absorbed mass is absorbed after the exposure for exposure durations up to 0.78 × t_lag. Thus, m_T will depend strongly on F_abs (and hence χ). For skin exposed to air following a 5 min exposure to p-nitroaniline, (small χ, large F_abs), nearly all of the skin depot (m₀) is eventually absorbed. If the skin is exposed to liquid (large χ, small F_abs), m_T is only about 10% that of the air-exposed skin but in both cases, nearly all of the absorption occurs postexposure. As t_exp/t_lag increases, a greater proportion of m_T occurs within the exposure duration. For a 1 h ethanol exposure, about 30% of the total absorption occurs postexposure; this percentage would increase for a chemical with less volatility. Even for exposures of 10 × t_lag, at least 10% of the total absorption occurs postexposure, and this post-exposure amount may exceed the total absorbed amount for shorter exposures. These results support the consideration of skin depot amounts in estimates of the systemically absorbed amount. Theoretically, two-thirds or more of all the chemicals could be washed out of the skin with a suitable solvent, although, except for ethanol, the time required would be unrealistically large (2.4 or more hours).

Strong chemical binding to skin components and desquamation of the skin would also prevent systemic absorption of chemical from the SC and skin. Because turnover of the SC occurs over many days, it is only important for chemicals that are strongly bound or slowly permeating as shown by diffusion modeling similar to that described here for evaporation.^39,40 Based on these model results, the USEPA risk assessment guidance for dermal absorption considers the effect of desquamation.⁴¹

This manuscript provides a theoretical framework for transient dermal exposures to volatile chemicals that do not bind to the membrane or substantially impact skin permeability. With the results presented here, combined with previous studies, substantial progress has been made in our understanding of the disposition of chemicals from both finite and transient dose dermal exposures. Analytical expressions for fractional absorption and evaporation have previously been presented for the finite dose case.⁵ The current work provides corresponding expressions for the transient exposure. A logical next step might be the inclusion of binding of compounds to skin components.^42,43 The theory should be tested by controlled in vitro experiments using skin or artificial membranes.⁷