Generation of micro-sized PDMS particles by a flow focusing technique for biomicrofluidics applications

Abstract

Polydimethylsiloxane (PDMS), due to its remarkable properties, is one of the most widely used polymers in many industrial and medical applications. In this work, a technique based on a flow focusing technique is used to produce PDMS spherical particles with sizes of a few microns. PDMS precursor is injected through a hypodermic needle to form a film/reservoir over the needle's outer surface. This film flows towards the needle tip until a liquid ligament is steadily ejected thanks to the action of a coflowing viscous liquid stream. The outcome is a capillary jet which breaks up into PDMS precursor droplets due to the growth of capillary waves producing a micrometer emulsion. The PDMS liquid droplets in the solution are thermally cured into solid microparticles. The size distribution of the particles is analyzed before and after curing, showing an acceptable degree of monodispersity. The PDMS liquid droplets suffer shrinkage while curing. These microparticles can be used in very varied technological fields, such as biomedicine, biotechnology, pharmacy, and industrial engineering.

I. INTRODUCTION

Polydimethylsiloxane (PDMS) is a useful polymer in many industrial and medical applications due to its remarkable properties, such as good optical transparency, flexibility, non-toxicity, chemical inertness, thermal stability, biocompatibility, and permeability to gases.^1,2 It is widely used to fabricate microfluidic devices to perform blood cells separation^3–6 and deformability analysis,^7,8 to culture endothelial cells,^9–11 and to investigate several flow phenomena happening in microvessels.^12–14

In the last years, the production of monodisperse particles with this inert elastomer has stimulated great interest of researchers because of their potential applications, especially in biomedicine.¹⁵ Microfluidics, particularly flow focusing principle, has proven to be an extraordinary working platform to produce fluid microentities. A co-flowing method was used to generate amphiphilic PDMS particles with hundreds of microns in size by Zhao et al.¹⁶ Jiang et al.¹⁵ have proposed a flow-focusing technique where a PDMS precursor was dispersed into microdroplets within an aqueous continuous phase. By using this method, they were able to produce PDMS microbeads with an average dimension of 80 μm to use them as discrete oxygen sensors. However, in many applications it is essential to have PDMS microparticles with dimensions below 10 μm. For example, to develop blood analogue fluids, PDMS microparticles must have dimensions closer to the red blood cells (RBCs), which are the most abundant cells in blood, with a contribution of around 45% by volume.¹⁴

The study of the blood flow behaviour through microchannels is crucial to improve our understanding about phenomena happening in the human microcirculatory system. However, the difficulties associated with the use of in vitro blood, such as coagulation and sample storage, have promoted the increasing interest to develop fluids with rheological properties similar to real blood.¹⁷ The most typical blood analogues used in experimental flow studies are either Newtonian using a mixture of glycerine and water or non-Newtonian aqueous solutions based on xanthan gum and polyacrylamide.^17–19 However, blood analogue solutions taking into account only the rheological behaviour is not enough to ensure an accurate representation of several blood physiological phenomena happening in microcirculation. For this reason, the development of more reliable blood analogues is of great importance and still lacking. Ideally, particulate solutions having particles that mimic key structural attributes of RBCs including size, shape, and mechanical properties would be an excellent candidate to reproduce multiphase effects of blood. A very recent study, rigid polymethylmethacrylate microparticles were suspended in Newtonian and non-Newtonian solutions to mimic both rheological properties of blood and the cell free layer (CFL) that frequently happens in microcirculation.²⁰ However, by using rigid microparticles the CFL was only formed downstream of a hyperbolic contraction, whereas no CFL was observed at the upstream region. Hence, this work shows evidence for the need to develop flexible microparticles such as the PDMS microparticles generated by the flow focusing technique reported here.

The flow focusing technique is very attractive because it uses purely hydrodynamic means to produce monodisperse collections of micrometer drops at a continuous high rate.^21,22 In flow focusing,²¹ an outer coflowing stream accelerates and steadily ejects a liquid injected through a feeding capillary. Both the liquid jet and the outer stream cross an orifice located in front of the capillary and whose diameter is much larger than that of the microjet. If the outer stream is a high-speed gas current,²¹ the outcome is a capillary jet which breaks up into droplets due to the Rayleigh instability.²³ When the focusing effect is caused by a viscous liquid current, emulsions consisting of micrometer droplets are produced.²² In this case, both the inner and outer liquids coflow downstream with almost the same speed until the interface pinches due to the growth of capillary waves too. Drops significantly larger than those predicted by the inviscid Rayleigh's theory²³ can be obtained due to the disparity between the two viscosities involved.²⁴

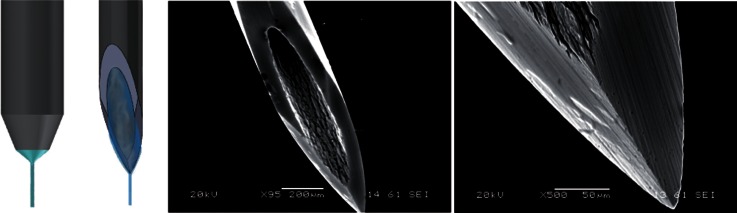
A new flow focusing technique²⁵ has recently been proposed for producing jets, droplets, and emulsions with sizes ranging from tens of microns down to the submicrometer scale. The cylindrical capillary used in the classical flow focusing.^21,22,26,27 is replaced with a (common) hypodermic needle of a similar dimension (see Fig. 1). The needle ends in a sharp tip over which the injected liquid flows dragged by the outer current. In this way, the tapering meniscus of the standard flow focusing configuration is substituted by a Couette-type flow directed towards the needle tip. A liquid ligament is ejected from the very tip of the needle, which is only a few microns in size. This constitutes a fundamental change in the flow focusing method because it alters completely the dynamics and, therefore, the stability of the liquid source.

FIG. 1.

(Left) Standard capillary and needle, and (right) SEM images of the needle tip (not chemically attacked) used in the technique proposed by Acero et al.²⁵

In this work, a technique based on that proposed by Acero et al.²⁵ is used to produce PDMS microparticles below 10 μm. It must be pointed out that such small particles are produced with orifices of about 200 μm in diameter, thereby avoiding the clogging of the injection system. Additionally, our technique is able to produce particles with an acceptable monodispersity.

The paper is organized as follows. The materials and experimental technique used in this work is presented in Sec. II. This includes describing the considered experimental apparatus and working fluids (Sec. II A), and the experimental procedure (Sec. II B). In Sec. III, we present the results of the generated primary and satellite droplets diameter followed by solid particles diameter after curing. The paper closes with the main conclusions in Sec. IV.

II. EXPERIMENTAL METHOD

A. Experimental apparatus

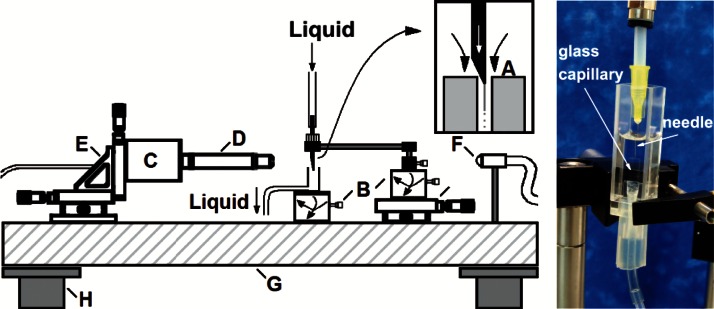
The experimental setup is sketched in Fig. 2. We used a hypodermic needle (Becton Dickinson Microlance 3 30G 1/2) with an inner (outer) diameter of about 160 (300) μm, and with an outer hydraulic radius r_t of a few microns in the tip (around 3 μm). The needle tip was not subjected to any kind of treatment. The needle was placed inside a glass cylindrical capillary (A), with 200 μm in diameter and 1 cm in length, by using high-precision orientation-translation systems (B). We used a common PDMS elastomer kit (Dow Corning Sylgard 186 Silicone Elastomer Kit) consisting of two parts: a base of vinyl-terminated siloxane oligomers (Part A) and a curing agent of siloxane oligomers and catalyst (Part B). The proportion Part A:Part B of the mixture was 6:4, whose viscosity was around 827 cSt,¹⁵ in order to decrease the viscosity of the PDMS precursor making its focusing easier. The mixture was injected through the needle at a constant flow rate, e.g., 0.1 ml/h, by means of a syringe pump connected to a stepping motor. Thanks to it, a film/reservoir was formed around the tip of the needle before starting production and was fed to maintain the ejection during the production. The needle and the glass cylindrical capillary were immersed in a bath of a mixture (9:1) of glycerol qp (Panreac) and surfactant Brij[textregistered] L4 (Sigma-Aldrich) to avoid the coalescence of the droplets downstream. This solution is immiscible with the PDMS precursor. The outer bath was suctioned across the glass cylindrical capillary at a constant flow rate Q = 2 ml/h with another syringe pump to produce the focusing effect. Both mixtures were prepared carefully by agitation at very low speeds, by using a magnetic stirrer (Agimatic-E, P-Selecta) in the case of the glycerol and surfactant mixture. Experiments were conducted at 24 ± 2 °C.

FIG. 2.

(Left) Experimental apparatus consisting of the following elements: needle located inside a glass cylindrical capillary (A), high-precision orientation-translation systems (B), digital camera (C), optical lenses (D), triaxial translation stage (E), optical fiber (F), optical table (G), and pneumatic anti-vibration isolation system (H). (Right) Details of the experimental cell (A): needle, glass cylindrical capillary, and bath in a glass optical cell. The connections between the components were made by using flexible tubes (under pressure).

Digital images of the fluid configuration were acquired using an ultra-high-speed CMOS camera (Photron, Fastcam SA5) (C) which allowed us to take images with an exposure time from 50 μs down to 340 ns. The camera was equipped with a set of optical lenses (D). The optical lenses were selected depending on the size of the imaged object, with a magnification ranging from 0.076 to 0.52 μm/pixel. This parameter was calculated for each optical system by measuring the diameter of a calibration rod located in the field of view. In this way, the optical distortion caused by the glass capillary was checked to be negligible. The camera could be displaced both horizontally and vertically using a triaxial translation stage (E) to focus the jet. The fluid configuration was illuminated from the back side with the cool white light provided by an optical fiber light source (F). We also acquired images of the needle by using an auxiliary CCD camera (not shown in Fig. 2) assembled in an optical axis perpendicular to that of the CMOS camera. The use of the two cameras allowed us to check that the needle was correctly positioned. All these elements were mounted on an optical table (G) with a pneumatic anti-vibration isolation system (H) to damp the vibrations coming from the building. By way of illustration, Fig. 3 shows three images acquired in the course of the experiments along the stream of fluids: (a) emitted jet of PDMS precursor attached to the needle tip, (b) PDMS droplets about 7 μm in diameter formed after the jet breakage travelling through the glass cylindrical capillary, and (c) stream of these droplets downstream the glass capillary.

FIG. 3.

Images acquired in the course of the experiments along the stream of fluids: (a) emitted jet of PDMS precursor attached to the needle tip, (b) PDMS droplets about 7 μm in diameter formed after the jet breakage travelling through the glass cylindrical capillary, and (c) stream of these droplets downstream the glass capillary.

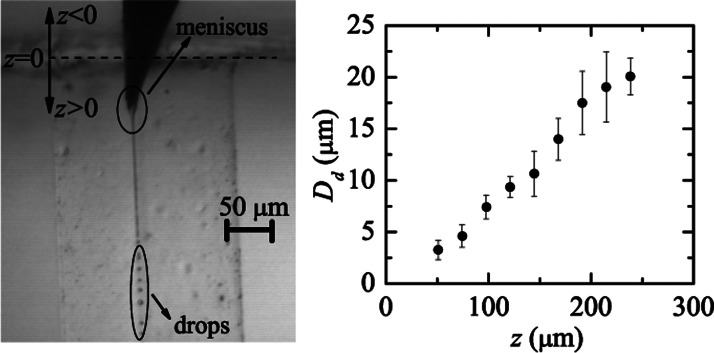
The production of the liquid microjet entails the stretching of a tiny meniscus hanging on the needle tip (see image of Fig. 5). That stretching takes place due to the combination of both extensional viscous stresses associated with the outer flow acceleration and the drag force due to the difference between the continuous and disperse phase velocities. In this sense, the phenomenon should be regarded as flow focusing rather than as a co-flow of two liquid streams.²⁸ As it will be shown in Fig. 5, the fact that the jet diameter depends significantly on the needle tip position in the glass cylindrical capillary confirms that the focusing effect is relevant in the present phenomenon.

FIG. 5.

Diameter D_d of the produced droplets by focusing PDMS precursor with the mixture of glycerol and surfactant Brij L4 and its dependence on z position.

B. Experimental procedure

The size of the liquid droplets and solid particles (just after curing) was measured systematically by processing the images to determine their dependence on the control parameters of the problem. So we could compare the results before and after curing for the production of several samples of different droplet sizes.

Figure 4 gives a general outline of the steps followed in each experimental realization, consisting of:

• (1)The experimental configuration described above was used to produce liquid droplets of PDMS precursor by purely hydrodynamic means. A film is formed on the outer surface of a hypodermic needle by injecting PDMS precursor at a constant flow rate. The coflowing fluid stream drags the film to the very tip of the needle and provides it with the momentum necessary to overcome the surface tension forming a small jet. The proposed method benefits from the remarkable stability of the fluidic structure from which the jets originate.²⁵ During the production time (around 2 h), images were recorded to measure the size distribution of the droplets.
• (2)When the production system was halted, the emulsion obtained (around 4 ml) was deposited in a glass optical cell. This container was heated up at 70 °C for 14 h by using the heater of a common magnetic stirrer in order to conduct crosslinking and cure the PDMS droplets in the solution.
• (3)Then, when the solution cooled down to the room temperature, the PDMS solid particles were visualized to measure the size distribution of the particles after curing by using our optical imaging method. The optical cell was scanned carefully to find, focus, and measure the size of the solidified particles of PDMS within the glycerol-surfactant bath.

FIG. 4.

Scheme of the experimental procedure to produce and analyse the PDMS liquid droplets and the subsequent solid particles: (1) production of PDMS liquid droplets by using our flow focusing technique, and measurement of the droplets size in liquid phase, (2) curing process at 70 °C by using the heater of a common magnetic stirrer, and (3) visualization of the samples through a glass optical cell to measure the size distribution of the particles after curing by using our optical imaging method (most of the blurred points in the image correspond to unfocused particles).

It must be noted that the film of PDMS precursor around the needle was much larger than the size of the jet eventually ejected from the needle tip, and it was growing very slowly during our experiments. It means that this film worked as a reservoir from which the system suctioned the flow rate necessary to form a stable jet, depending on the position of the needle tip inside the cylindrical glass capillary and the dragging flow rate Q. Therefore, for a fixed Q, the system established a natural flow rate for each position of the needle, which was the real flow rate of the jet emitted. This natural flow rate Q_n can be estimated from the videos/images of our experiments recorded at 28 000 frames/s with an exposure time of 35 μs, just by counting the number of primary spherical droplets produced over time and multiplying this value by the mean volume of the primary droplet.

III. RESULTS

During the experiments, we checked that the present technique is very sensitive to the position (in the three directions of space) of the needle tip in the glass capillary. In fact, when one fixes it in the center of the orifice, the size of droplets produced can be precisely controlled by shifting the needle tip along the axis of the cylindrical glass capillary without varying the flow rates. Figure 5 shows the diameter D_d of the liquid droplets plotted as a function of the distance z between the needle tip and the entrance to the capillary. D_d increases as z grows, i.e., as the needle is moved downstream inside the glass capillary. Eventually the jet is destabilized and breaks up into droplets.²⁹ It was verified that the jet's breakage gave rise to a quasi-monodisperse collection of primary drops whose diameter D_d was roughly twice the jet's diameter D_j. It must be noted that Rayleigh's dispersion relation does not apply to our experimental configuration due to the high viscosities of both the inner and outer streams, but using Tomotika's dispersion relation for the Stokes regime,²⁴ one gets $D_d\simeq 2.01D_j$, which approximately coincides with our experimental results.

The PDMS precursor jet breakup results in the formation of primary and satellite droplets (see Fig. 6, right). The size and formation of satellite droplets are directly linked with the dynamic of the rupture of the neck (between two primary drops). In the linear regime, the thread cross-section of maximum liquid depletion is that equidistant between the two primary drops, but that section can shift towards the vicinities of those drops in the non-linear phase. As a consequence, a liquid ligament forms and inflates between the primary drops, which generates a satellite droplet. It is well-known that the formation of satellite drops for non-viscous liquids is driven by inertia.³⁰ Due to the high viscosity of the liquids involved in the present technique, the Stokes regime was reached in our experiments, and so inertia can be neglected. In this viscous case, a highly nonlinear phenomenon produces the appearance of those satellite droplets,³¹ nonlinearity comes from the surface tension force.

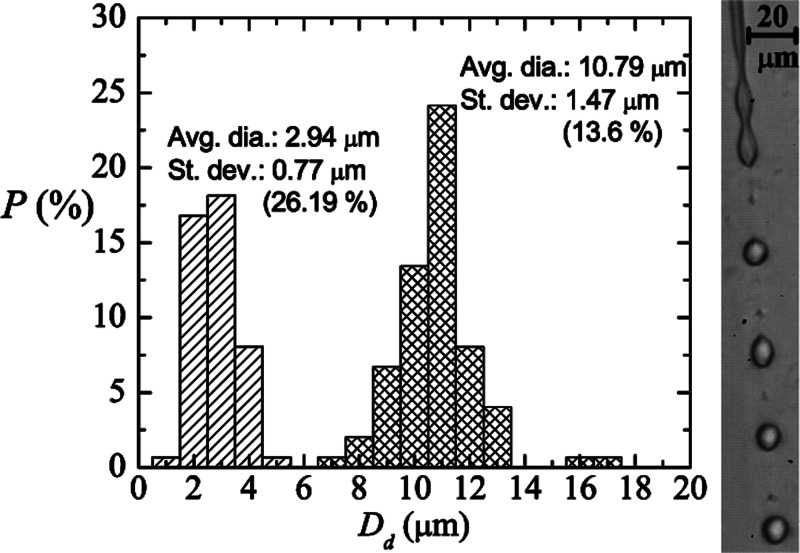
FIG. 6.

Probability distribution $\mathcal{P}(D_d)$ for the droplet diameter D_d produced with our technique for z = 144 μm, $Q_n\simeq 10$ μl/h, and Q = 2 ml/h. The meshed and striped bars correspond to the results obtained for primary and satellite droplets, respectively, resulting from the breakup of a liquid PDMS precursor jet. The image on the right shows the primary and satellite droplets coming from the breakup of the jet.

The size of the satellite drops depends on the viscosity ratio between continuous and dispersed phases.³² For each experimental run, we observed the formation of satellite droplets to be almost constant in size. In all the cases, the satellite droplet size ranged from around 4 μm in diameter down to values hardly observable with standard microscopy. The formation and size of the satellite droplets in our configuration could be quantitatively influenced by the use of surfactant in the outer stream. The presence of surfactants can greatly dampen and suppress surface waves. Zhang and Basaran³³ found that the volume of satellite drops grew with increasing surfactant concentration. The accumulation of surfactants on the drop surface helps to stabilize the rapidly stretching thread during drop breakup and thereby increases the volume of the liquid thread and ultimately that of the satellite. On the other hand, the complex chemical composition of PDMS precursor could lead to a rheological behavior on the jet breakup participating in the production of such satellite droplets too. Figure 6 shows the probability distribution $\mathcal{P}(D_d)$ obtained for both primary and satellite droplets produced for z = 144 μm, $Q_n\simeq 10$ μl/h, and Q = 2 ml/h. The average diameter $\overline{D_d}$ was determined to be 10.79 (2.94) μm and the standard deviation σ was 1.47 (0.77) μm for primary (satellite) droplets. The coefficient of variance C_v, $C_v=\frac{\sigma }{\overline{D_d}}100$, for primary and satellite drops was 13.6% and 26.19%, respectively. As can be observed, these two collections of drops exhibit a relatively high degree of monodispersity. The number of satellite drops represented around 50% of the complete sample. The polydispersity can be partially explained by the observed fluctuations of the wavelength responsible for the jet pinch-off.

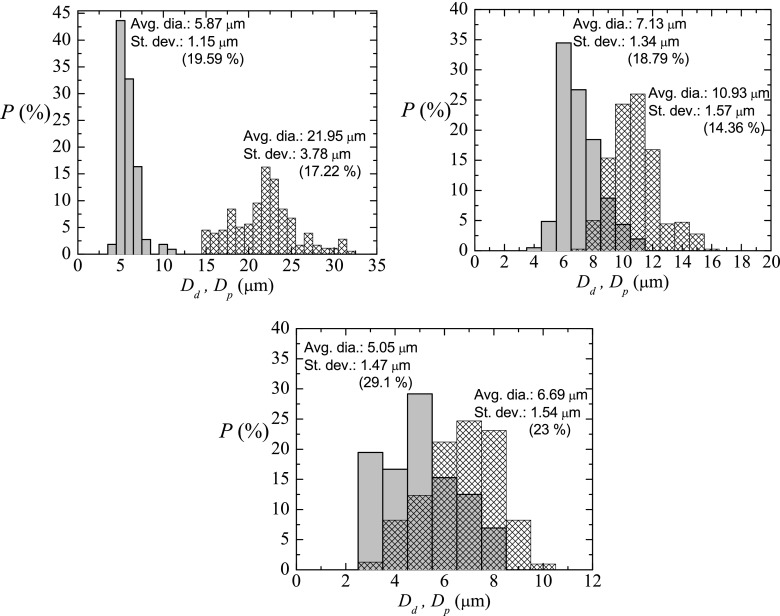
In order to characterize appropriately the technique here depicted, experiments were conducted to measure the size of liquid primary droplets and subsequent solid particles (just after curing) for several cases. For this purpose, the emulsion obtained was heated up to cure the PDMS droplets, and the subsequent PDMS solid particles were afterwards visualized by scanning the optical glass cell containing the solution with optical microscopy. Figure 7 shows the probability distribution $\mathcal{P}(D_d)$ for the primary liquid droplet diameter D_d and $\mathcal{P}(D_p)$ for the solid particle diameter after curing D_p, for three samples with different size of the primary droplets. In all the cases, before and after curing, the coefficient of variance C_v is around 20%, and it can be considered as a relatively high degree of monodispersity, taking into account the smallness of the samples of droplets/particles. Interestingly, it was always found a pronounced shrinkage of the liquid droplets after turning into solid particles, that is, $\overline{D_p}<\overline{D_d}$.

FIG. 7.

Probability distribution $\mathcal{P}(D_d)$ for the primary liquid droplet diameter D_d (meshed bars) and $\mathcal{P}(D_p)$ for the solid particle diameter after curing D_p (gray bars). The parameters characterizing the production were (a) z = 240 μm, $Q_n\simeq 50$ μl/h, and Q = 2 ml/h; (b) z = 144 μm, $Q_n\simeq 10$ μl/h, and Q = 2 ml/h; (c) z = 90 μm, $Q_n\simeq 1$ μl/h, and Q = 2 ml/h. Note that the results of (b) came from a different experimental realization from that of Fig. 6, for the same parameters characterizing the production. It shows that the results are reproducible for primary liquid droplets.

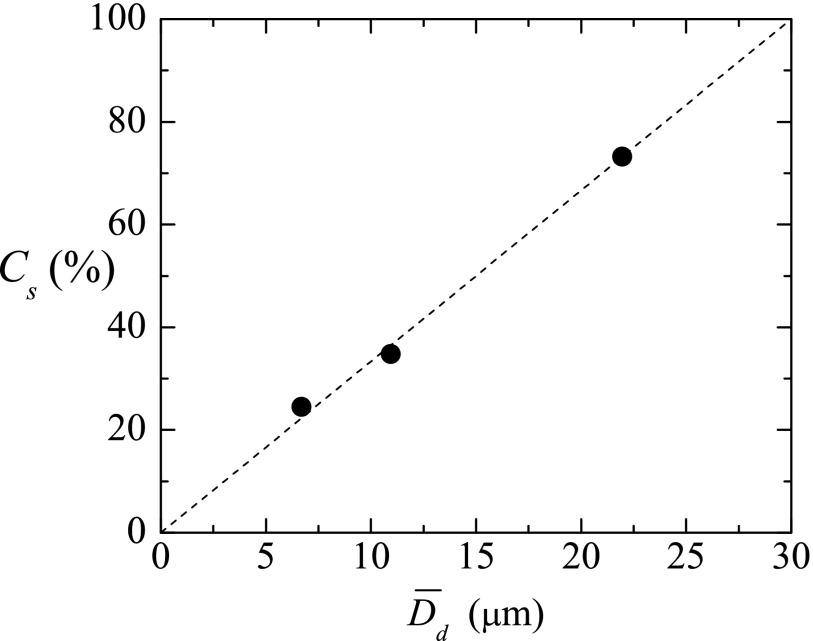
PDMS shrinkage is highly variable as many parameters are involved, especially when working in a multi-user environment without tightly controlled fabrication conditions.³⁴ Typically, it is characterized on a case-by-case basis and individual calibration or alignment methods are needed for each design. For further analysis of the shrinkage produced by curing in our experiments, we calculated a curing shrinkage coefficient C_s as $C_s=\frac{\overline{D_d}-\overline{D_p}}{\overline{D_d}}100$. Figure 8 depicts the values for the samples in Fig. 7, for liquid droplet diameters approximately comprised between 5 and 25 μm, the range of diameters the present technique is designed for. C_s increased considerably with the average liquid droplet diameter $\overline{D_d}$, and interestingly, linear dependency of C_s with respect to $\overline{D_d}$ can be found within that relatively small range. The equation $C_s\simeq \frac{10}{3}\overline{D_d}$ could predict approximately this shrinkage. For much higher droplet diameters, surface effects can be neglected, and one expects the shrinkage of the droplet to be proportional to its volume, i.e., $D_p\simeq \alpha D_d$ ($\alpha <1$). In this case, C_s becomes a constant. This behavior is not observed in our experiments due to the relatively large droplet surface-to-volume ratio. Because of C_s is not constant in our range, one also could conclude that the cured PDMS particles of each sample have different density. To the best of the authors' knowledge, it is the first time that such shrinkage is reported for PDMS spherical microparticles. Lee and Lee³⁵ observed PDMS shrinkage to increase with growing curing temperature, layer thickness and width, and mixing ratio of dilutant and curing agent, for theirs 2D PDMS structure. Jeong and Konishi³⁶ found PDMS molds/stamps shrinkage to be size-dependent, being greater for increasing dimensions, as occurred in our experiments. They also showed the temperature-dependence. Shrinkage is also dependent on the ambient during curing, different shrinkage velocities were found when the PDMS surface was exposed to air or not.³⁷ In our experiments, the unusually high amount of curing agent could have pronounced the shrinkage of the samples.

FIG. 8.

Curing shrinkage coefficient C_s of the PDMS liquid droplets after curing as a function of the original diameter in liquid phase $\overline{D_d}$. The dashed line indicates a possible fit line to predict this shrinkage, $C_s\simeq \frac{10}{3}\overline{D_d}$.

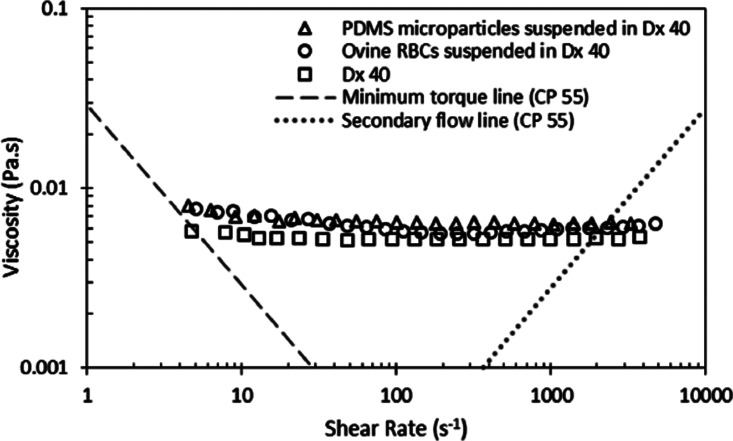
The PDMS microparticles produced by our technique can be either stored in the glycerol and surfactant solution or centrifuged, rinsed, and dried under vacuum to a powder. Dried particles can be re-dispersed in various media depending on the application (see Fig. 9). To investigate whether the produced cured PDMS microparticles have flow properties similar to in vitro experiments,^{2,4–8,12–14} rheological measurements were performed for a fluid containing cured PDMS particles and Dextran 40 (Dx40). The sample containing cured PDMS microparticles, with an average diameter of 5.87 μm, was dried and suspended in Dx40. Moreover, rheological measurements were also performed for two additional working fluids, i.e., a solution containing only Dx40 and another containing ovine RBCs suspended in Dx40 at 5% by volume. More detailed information regarding the preparation of the in vitro blood sample can be found at Ref. 38. The rheological characterization of the working fluids was carried out by means of a stress controlled rheometer (Bohlin CVO, Malvern, Worcestershire, UK) using a cone-plate geometry with 55 mm of diameter and an angle of 1°, where all measurements were carried out at 20 °C. The flow behavior of the samples under steady state experiments is shown in Fig. 10. Two tendencies in their viscosity curves are clearly distinguished. On one hand, the sample containing only Dx40 presents a clear Newtonian flow behavior, with a constant viscosity. On the other hand, both samples containing cured PDMS microparticles and ovine RBCs, at low shear rates present a smooth shear thinning behavior and a constant viscosity at high shear rates. It is also clear from these results that the sample containing PDMS microparticles shows a good agreement with the rheological properties of the in vitro blood sample.

FIG. 9.

Image, obtained by using an inverted microscope, of the cured PDMS particles (corresponding to the sample of Fig. 7(b)) re-dispersed in Dextran 40.

FIG. 10.

Steady shear viscosity curves of Dx40, around 1% by volume of PDMS cured microparticles in Dx40, and 5% by volume of ovine RBCs in the Dx40. The minimum torque line represents the limit of accuracy of the rheometer.

IV. CONCLUSIONS

In this work, we have applied a flow focusing technique to produce PDMS microparticles with diameters below 10 μm, and relatively high degree of monodispersity. One of the features of the present technique is that the variation of the needle position in the glass capillary enables one to select the size of the resulting PDMS precursor droplets, which confers both flexibility and robustness on the method. It was found a shrinkage of these droplets while curing.

The degree of monodispersity could be improved by controlling precisely the wavelength of the breakage of the jet, e.g., by using a piezoelectric mechanism. The ability to control the size and other mechanical properties of such microparticles will enable the production of innovative and versatile delivery vehicles suitable for different biomedical applications. For instance, the proposed microparticles have great potential to mimic the structural and functional properties of blood cells and consequently to develop a blood analogue fluid with rheological properties similar to real blood.