Reproducibility and Inter-Observer Variability of Systolic Blood Flow Velocity and 3D Wall Shear Stress Derived From 4D flow MRI in the Healthy Aorta

Abstract

Purpose

To investigate the reproducibility and inter-observer variability of 3D aortic velocity vector fields and wall shear stress (WSS) averaged over five systolic timeframes derived from non-contrast 4D-flow-MRI.

Methods

Fourteen controls underwent test-retest 4D-flow-MRI examinations separated by 16±3 days (resolution=3.0–3.6×2.3–2.6×2.5–2.7mm³; TE/TR/FA=2.5ms/4.9ms/7°; Venc=150cm/s). Two observers was segmented the aorta, and WSS was calculated for both series of scans and both segmentations. Test-retest and inter-observer velocity and WSS vectors were compared on a voxel-by-voxel basis in the aorta and on a regional basis by subdividing the aortas in six segments.

Results

Test-retest: voxel-by-voxel Bland-Altman analysis revealed small differences (−0.03/−0.02 m/s/Pa), limits of agreement of 0.25 m/s/0.29 Pa and coefficients of variation (CV) of 20% for velocity/WSS. Voxel-by-voxel orthogonal regression analysis showed moderate agreement (Slope: 1.14/1.16, Intraclass Correlation Coefficient (ICC): 0.76/0.67 for velocity/WSS). The regional analysis revealed a CV of 9%/8% and ICC of 0.9/0.9 for velocity/WSS. Inter-observer: voxel-by-voxel difference for WSS was 0, LOA: 0.17/0.19 Pa, CV: 12/13%, slope: 1.01/1.09, ICC: 0.87/0.85 for test/retest. The CV/ICC for WSS in the regional analysis was 4%/1.0 for test and 3%/1.0 for retest.

Conclusions

Systolic velocity and WSS derived from 4D flow MRI are reproducible between consecutive visits, with low inter-observer variability in healthy volunteers.

INTRODUCTION

4D flow MRI (time resolved 3D phase contrast MRI with three-directional velocity encoding) is a tool to assess changes in 3D blood flow associated with cardiovascular disease. Recent studies have demonstrated the potential of 4D flow MRI for the evaluation of changes in hemodynamics associated with aortic disease such as bicuspid aortic valve (1), aortic aneurysms (2), or coarctation (3). In addition to the 3D visualization of aortic blood flow patterns, the volumetric velocity vector fields measured with 4D flow MRI allow for derivation of hemodynamic parameters such as wall shear stress (WSS)(4). There is evidence that changes in WSS can alter and regulate endothelial cell function (5–7). WSS may thus be an important parameter to assess individual risk for aortic complication such as progressive dilatation or dissection.

The most widely adopted method used for 2D phase contrast flow measurements (8), is to calculate WSS from 4D flow MRI data based on manually placing 2D planes at specific landmarks (8,9) (10). This approach has been successfully applied in studies investigating changes in WSS in aortic, carotid and intracranial pathologies (11–14). However, the manual placement of 2D planes can be laborious, is subject to observer variability, and can miss important regional variations in WSS.

Recently, methods have been introduced that permit the 4D flow MRI based calculations of 3D WSS along the entire lumen surface (2,15–18). Pilot studies have shown good qualitative agreement, albeit with underestimated absolute WSS values, with CFD in in-vitro and in-vivo intracranial aneurysms (19) and carotid arteries (20). Furthermore, 3D WSS estimation has been successfully applied to investigate differences in wall shear forces between healthy controls and patients with aortic pathologies (21,22).

However, variability of the 3D segmentation process as well as inter-scan differences in the 4D flow MRI data are not well characterized. This is especially true when regarding the impact on the reproducibility of 3D WSS estimation. Bieging et al. investigated 3D WSS in healthy and dilated aortas, but did not perform reproducibility measurements (17). Markl et al. investigated reproducibility of aortic WSS in healthy volunteers, but calculated WSS in 2D cross-sectional cut-planes rather than the full 3D aorta (23). The aim of this study was therefore to investigate the systolic test-retest reproducibility and inter-observer variability of 4D flow derived 3D velocity fields and 3D WSS in the thoracic aorta.

METHODS

Study populations

Fourteen healthy control subjects (10 men, 4 women ranging in age from 19–74 years, mean: 49 ± 17 years) with no history of cardiovascular disease, normal valve function and normal thoracic aorta geometry were prospectively enrolled in the study. Each subject underwent two separate MRI examinations, using the same scan protocol (difference between first and second scan = 14–25 days, mean: 16 ± 3 days). Exams were scheduled in the morning at the same time and subjects were instructed to avoid caffeine intake before the exam. The study was approved by the local Institutional Review Board (IRB) and informed consent was obtained from all subjects. The heart rate and blood pressure were measured before and after the 4D flow MRI scan.

MR Imaging

All 4D flow MRI exams were performed in a sagittal oblique volume covering the entire thoracic aorta with prospective ECG gating and respiratory navigator gating with 80% scan efficiency (24). All exams were performed on a 1.5 T MAGNETOM Aera system (Siemens Medical Systems, Erlangen, Germany). Pulse sequence parameters for all scans were: spatial resolution = 3.0–3.6 × 2.3–2.6 × 2.5–2.7 mm³; field of view = 360–420 × 270–341 × 60–81 mm³; temporal resolution = 39.2 ms (13–30 time frames); TE/TR/FA = 2.5 ms/4.9 ms/7°; Venc = 150 cm/s in all three velocity encoding directions. All scans were acquired using standard parallel imaging (GRAPPA) with an acceleration factor of R=2 and 24 reference lines, resulting in a net acceleration factor of 1.7.

Data analysis

Pre-processing and 3D segmentation

All 4D flow MRI data were corrected for eddy currents, Maxwell terms and velocity aliasing using in-house built software in Matlab (Natick, The Mathworks, USA) (25). 3D Phase contrast (PC) magnetic resonance angiography (MRA) images were created by voxel-wise multiplication of the magnitude data with absolute velocities averaged over all cardiac time frames (25). The thoracic aorta was semi-automatically segmented (Mimics, Materialise, Leuven, Belgium) by two observers (PvO and ALP with three months and 1 month, respectively, of experience with the segmentation software) blinded to each other's results. First, a threshold was visually chosen to mask the aorta in the PC-MRA images. By verification with a watershed algorithm, attached features such as the right pulmonary artery and vena cava were manually disconnected from the aorta. If present, holes were manually filled and attached noise pixels deselected. Finally, the mask was exported for later use. The segmentations created by PvO were used for the reproducibility analyses.

Peak systole was defined as the time frame with the highest absolute velocity averaged over the segmentation of the first observer. The peak velocity in the aortic segmentation in the proximal aorta (start aorta to mid-ascending aorta) was extracted from a maximum intensity projection image of the absolute velocity at peak systole.

WSS estimation

For WSS calculation, all segmentations were smoothed using a Laplacian filter (26) to obtain a smooth surface of the aortic wall. 3D WSS along the aortic lumen surface was calculated as described previously by Potters et al. (18). Briefly, for each time frame within the cardiac cycle WSS estimation was based on the shear stress tensor

$$\overline{\tau }=2\eta \stackrel{.}{\epsilon }·\overrightarrow{n}$$ [1]

with η the dynamic viscosity (Newtonian: 3.2•10⁻³ Pa•s), ε̇ the rate of deformation tensor and n⃗ the normal vector orthogonal to the vessel wall. This equation can be simplified by rotating the aorta such that the z-axis (0,0,1) is aligned with the normal vector of the aortic wall: n⃗ = (0,0,1). Assuming that no flow occurred through the aortic wall, n⃗ • v⃗ = 0 at the wall), the inner product of the rate of deformation tensor and the normal vector is reduced to:

$$2\stackrel{.}{\epsilon }·\overrightarrow{n}=(\frac{\partial {v_x}^{\prime }}{\partial z^{\prime }},\frac{\partial {v_y}^{\prime }}{\partial z^{\prime }},0)$$ [2]

with $\frac{\partial {v_x}^{\prime }}{\partial z^{\prime }}$ and $\frac{\partial {v_y}^{\prime }}{\partial z^{\prime }}$ the shear rates or spatial velocity derivatives at the wall in the rotated coordinate system. The rotated WSS vector τ⃗′ was then defined as:

$${\overrightarrow{\tau }}_x^{\prime }=\eta \frac{\partial {v_x}^{\prime }}{\partial z^{\prime }},{\overrightarrow{\tau }}_y^{\prime }=\eta \frac{\partial {v_y}^{\prime }}{\partial z^{\prime }},{\overrightarrow{\tau }}_z^{\prime }=0)$$ [3]

and the shear rates were derived from 1D smoothing splines (27) fitted through the rotated x- and y-velocity values along the inward normal vector. Subsequently, the WSS vector was transformed to the original coordinate system by inverse rotation. Systolic 3D WSS vectors were then calculated by averaging WSS vectors for five time frames centred on peak systole (defined as the cardiac time frame with the highest average velocity in the aorta segmentation).

Voxel-by-voxel comparison of the systolic velocity field and 3D WSS

To calculate test-retest variability on a voxel-by-voxel basis, the retest aorta segmentation of each individual subject was rigidly registered to the test aorta segmentation using FLIRT (FMRIB’s Linear Image Registration Tool (28)). The systolic 3D velocity fields and systolic 3D WSS of the retest (or observer 2) segmentation were subsequently interpolated to the test (or observer 1) geometry. Based on the registered data, voxel-by-voxel test-retest as well as inter-observer differences for systolic velocity magnitude and WSS magnitude were calculated. In addition, voxel-by-voxel differences in velocity and WSS direction were assessed by calculating the angle between test and retest for the velocity and WSS vectors. The angles were plotted in a distribution between 0 and 180° and the median of this velocity and WSS angle distribution was used to quantify the directional difference. Regions corresponding to the left ventricle, supra-aortic arteries and distal descending aorta were manually removed from the systolic velocity and 3D WSS analyses (see figure 1). Furthermore, to calculate the inter-observer difference between segmentations, FLIRT was used for each individual subject to register the segmentation of observer 2 to the segmentation of observer 1. The difference in segmentations between observers was expressed as the number of voxels not overlapping as a percentage of the mean number of voxels of both segmentations:

$$\mathit{segmentation}\mathit{difference}=\frac{\left|N_{{\mathit{segmentation}}_1}^{\mathit{voxels}}-N_{{\mathit{segmentation}}_2}^{\mathit{voxels}}\right|}{(N_{{\mathit{segmentation}}_1}^{\mathit{voxels}}+N_{{\mathit{segmentation}}_2}^{\mathit{voxels}})/2}$$ [4]

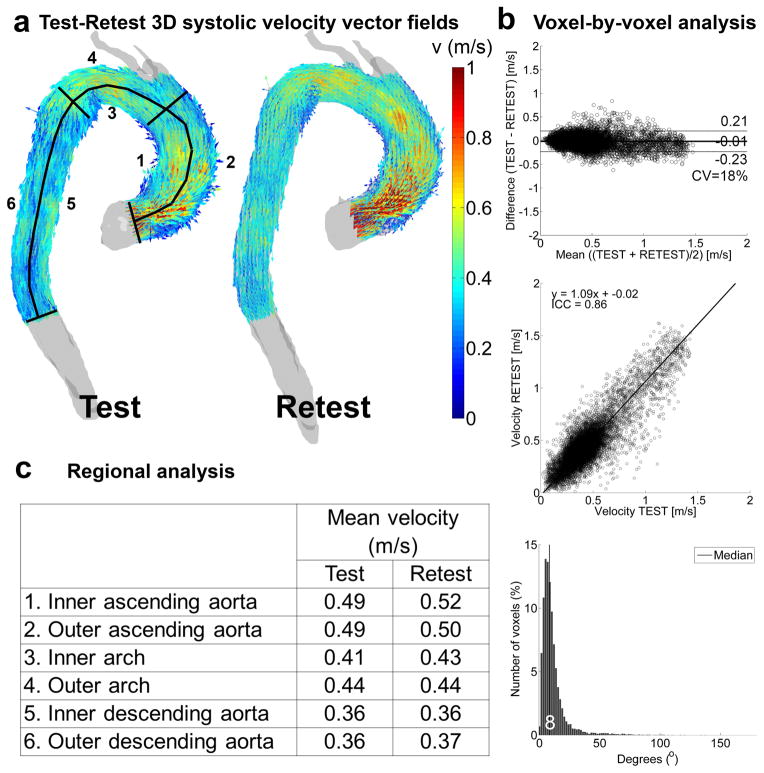
Figure 1.

Test-retest velocity analysis in one volunteer. a) The full 3D velocity vector field used for the voxel-by-voxel analysis with the delineation of the regions of interest for the regional analysis. b) Voxel-by-voxel analysis: Bland-Altman comparison (top), orthogonal regression (center) and histogram of the angle difference distribution (bottom, with median angle difference in white). c) Regional analysis: mean velocity values for test and retest in the six regions displayed in (a).

Region of Interest comparisons of systolic velocities and 3D WSS

To compare regional systolic velocity and WSS for each individual subject, the aorta geometries were manually subdivided in six aortic segments as shown in figures 1 and 2: 1) the inner ascending aorta (AAo), 2) the outer AAo, 3) the inner aortic arch, 4) the outer arch, 5) the inner descending aorta (DAo) and 6) the outer DAo (see figure 1). For each region mean systolic absolute velocities and mean WSS magnitude were calculated. Furthermore, for each region, velocity and WSS variability was expressed as the difference between test and retest velocity and WSS divided by the mean test and retest velocity and WSS.

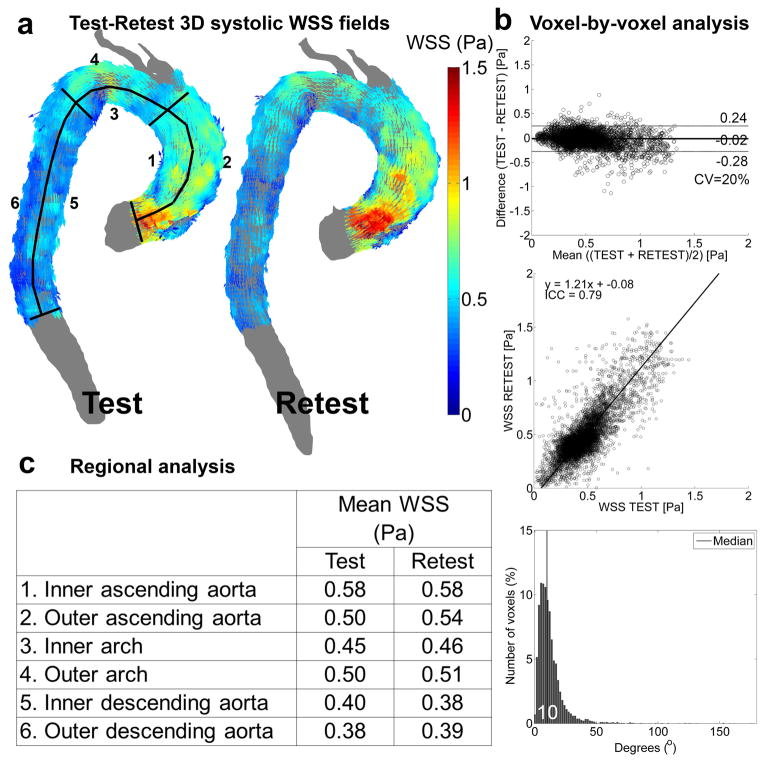
Figure 2.

Test-retest WSS analysis in one volunteer. a) The full 3D WSS vector field used for the voxel-by-voxel analysis with the delineation of the regions of interest for the regional analysis. b) Voxel-by-voxel analysis: Bland-Altman comparison (top), orthogonal regression (center) and histogram of angle difference distribution (bottom, with median angle difference in white). c) Regional analysis: mean WSS values for test and retest in the six regions displayed in (a).

Comparisons of cohort-averaged systolic velocity fields and 3D WSS

Cohort-averaged systolic 3D velocity fields and 3D WSS maps for test and retest cohorts were generated and compared by: 1) creation of a shared aorta geometry by rigid co-registration of all aortas scanned in the test or retest session and determination of the maximum overlap of all aortas, as previously described (21). 2) Affine registration of each individual aorta to the shared geometry followed by nearest neighbour interpolation of all systolic 3D absolute velocity and WSS values to the shared geometry. Subsequently, the interpolated absolute velocity and WSS values were averaged over the cohort in a voxel-wise manner. The influence of affine registration and nearest neighbour interpolation in step 2) was investigated by reporting the difference in velocity or WSS before and after this process according to:

$$\mathit{interpolation}\mathit{difference}=\frac{\mid v/{\tau }_{\mathit{before}}-v/{\tau }_{\mathit{after}}\mid }{(v/{\tau }_{\mathit{before}}+v/{\tau }_{\mathit{after}})/2}$$ [5]

The interpolation difference was calculated in the six regions and subsequently averaged.

Analysis for the averaged systolic time frames and for peak systole

To be able to investigate test-retest changes and segmentation influences, measurement noise effects were mitigated by averaging velocity vectors for five time frames centred on peak systole, as has been reported previously (11,21,22). In addition, an identical analysis for the peak systolic time frame with measurement noise was performed to understand if the averaging over 5 time frames is necessary to reduce noise.

Statistical Analysis

All continuous parameters are expressed as mean ± SD. The difference in peak velocity between the test and retest scans was tested with a Wilcoxon rank sum test. P<0.05 was considered significant. For the voxel-by-voxel analysis for velocity and WSS, the mean difference and limits of agreement (LOA) were established by Bland-Altman analysis. Orthogonal regression was used to calculate the slope and intercept of the agreement between the test and retest velocity and WSS values. For the regional analysis, the difference in mean velocity and mean WSS in the 6 regions of interest was tested with a Wilcoxon rank sum test. P<0.05 was considered statistically significant. The Intraclass Correlation Coefficient (ICC) and the coefficient of variation (CV) were calculated for peak velocity, the voxel-by-voxel and the regional analysis.

Furthermore, velocity and WSS of the test and retest scans were tested on voxel-by-voxel basis by using P-value maps (21) . For the creation of the P-value maps, both the test and retest velocity and WSS values were interpolated to the idealized geometry of the test scan, followed by a Wilcoxon rank sum test comparing velocity and WSS in every voxel. P<0.05 was considered statistically significant.

RESULTS

Heart rate and blood pressure

The average age of the volunteer subjects was 49±17 years. Heart rate and blood pressure taken before and after the 4D flow MRI scan were similar (Heart Rate: P = 0.89, systolic blood pressure: P = 0.43, diastolic blood pressure: P = 0.55, Wilcoxon rank sum test) for the test (heart rate = 66 ± 14 bpm; blood pressure = 123 ± 19 / 78 ± 15 mmHg) and the retest scan (heart rate = 64 ± 11 bpm; blood pressure = 117 ± 20 / 74 ± 17 mmHg).

Test-Retest

Peak velocity

The peak velocity for the test scans averaged over all volunteers was 1.7±0.3 m/s. For the retest scans, the peak velocity was 1.8±0.3 m/s. The difference was not significant (P=0.45), the ICC was 0.67 and the CV was 3%.

Voxel-by-voxel comparison of the systolic velocity field and 3D WSS

Figures 1a–b and 2a–b illustrate the results of the test-retest voxel-by-voxel analysis for the systolic velocity field and 3D WSS for one representative subject. The gray shaded geometries (figures 1a and 2a) depict the 3D test and retest segmentations of the aorta, whereas the colored arrows show the velocity field or 3D WSS that were used for the voxel-by-voxel comparison. It can be seen that both the velocity and WSS of the test and retest scans are higher in the ascending aorta than in the arch and descending aorta. In figure 1b and 2b the results of the Bland-Altman (top) analyses, orthogonal regression analyses (center) and the distribution of the angle deviation (bottom) are shown. The mean differences are close to 0 for both velocity and WSS, but slightly negative since the values for the retest scan were slightly higher than for the test scan. This is also illustrated by the 9 and 21% deviation from unity for the slope of the orthogonal regression line for higher retest velocity and WSS, respectively, compared to the test scan. The CV, ICC and the median angle differences were respectively lower, higher and lower for velocity compared to WSS. Except for the CV, which was identical for velocity and WSS, this example illustrates the general findings for all volunteers, as summarized in table 1.

Table 1.

Test-Retest voxel-by-voxel analysis: Mean difference, limits of agreement, Coefficient of Variation, slope, intercept, Intraclass Correlation Coefficient and the angle difference for systolic velocity fields and 3D WSS averaged over all subjects

	Bland-Altman			Orthogonal Regression			Angle difference
	Mean difference (m/s or Pa)	LOA (m/s or Pa)	CV (%)	Slope (−)	Intercept (m/s or Pa)	ICC (−)	Median (°)
Velocity	−0.03 ± 0.06	0.25 ± 0.05	20 ± 4	1.14 ± 0.16	−0.05 ± 0.07	0.76 ± 0.09	7 ± 2
WSS	−0.02 ± 0.05	0.29 ± 0.06	20 ± 4	1.16 ± 0.15	−0.07 ± 0.06	0.67 ± 0.11	9 ± 1

Region of Interest comparisons of systolic velocities and 3D WSS

As illustrated in figures 1c and 1c, the differences in regional systolic velocities were minimal (<0.03 m/s in the inner descending aorta), whereas WSS demonstrated greater variability (up to 0.04 Pa for the outer ascending aorta). The results of the regional analyses for all subjects are summarized in table 2. No significant differences in systolic absolute velocity or WSS magnitude between test and retest in all six regions were found. The CV was 9% for velocity and 8% for WSS. The ICC was 0.9 for both velocity and WSS.

Table 2.

Test-Retest region of interest analysis: absolute velocity and WSS magnitude averaged over all subjects

	Inner AAo			Outer AAo			Inner arch			Outer arch			Inner DAo			Outer DAo
	Test	Retest	P	Test	Retest	P	Test	Retest	P	Test	Retest	P	Test	Retest	P	Test	Retest	P
Mean velocity (m/s)	0.52 ± 0.13	0.55 ± 0.12	0.48	0.50 ± 0.11	0.51 ± 0.12	1	0.49 ± 0.14	0.50 ± 0.13	0.95	0.45 ± 0.14	0.46 ± 0.13	0.95	0.51 ± 0.17	0.53 ± 0.19	0.87	0.50 ± 0.17	0.52 ± 0.19	1
CV velocity (%)	8			8			8			8			10			10
ICC velocity (−)	0.9			0.9			0.9			0.9			0.9			0.9
Mean WSS (Pa)	0.60 ± 0.17	0.62 ± 0.15	0.84	0.55 ± 0.14	0.56 ± 0.14	0.98	0.58 ± 0.19	0.61 ± 0.18	0.87	0.51 ± 0.17	0.53 ± 0.17	0.84	0.58 ± 0.20	0.62 ± 0.25	0.80	0.60 ± 0.22	0.63 ± 0.27	0.91
CV WSS (%)	8			6			7			7			10			10
ICC WSS (−)	0.9			0.9			0.9			1.0			0.9			0.9

Comparisons of test-retest cohort-averaged systolic velocity fields and 3D WSS

Voxel-by-voxel analysis

For the creation of the cohort-averaged velocity and WSS maps, the interpolation difference for the test velocity and WSS map was 9% and 4%, respectively. For the retest velocity and WSS, the interpolation difference was 8% and 3%, respectively. Figures 3a and 4a depict cohort-averaged systolic velocity and 3D WSS maps. The individual maps represent the distribution of systolic velocity magnitude and 3D WSS magnitude, mapped onto a co-registered aortic geometry and averaged over all 14 subjects for the test and the retest cohort.

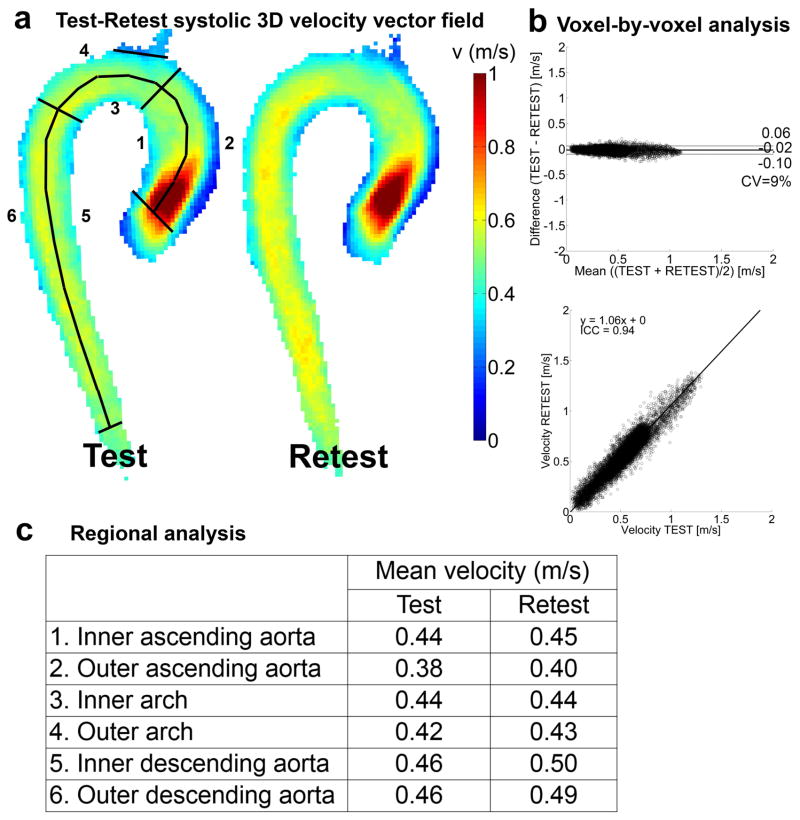
Figure 3.

The results for the test-retest analysis for the cohort-averaged velocity map. a) A maximum intensity projection for the voxel-by-voxel analysis with the delineation of the regions of interest for the regional analysis. b) Voxel-by-voxel analysis: Bland-Altman plot (top), orthogonal regression (center) and angle distribution (bottom). c) Regional analysis: mean velocity values and variability for test and retest in the six regions displayed in (a).

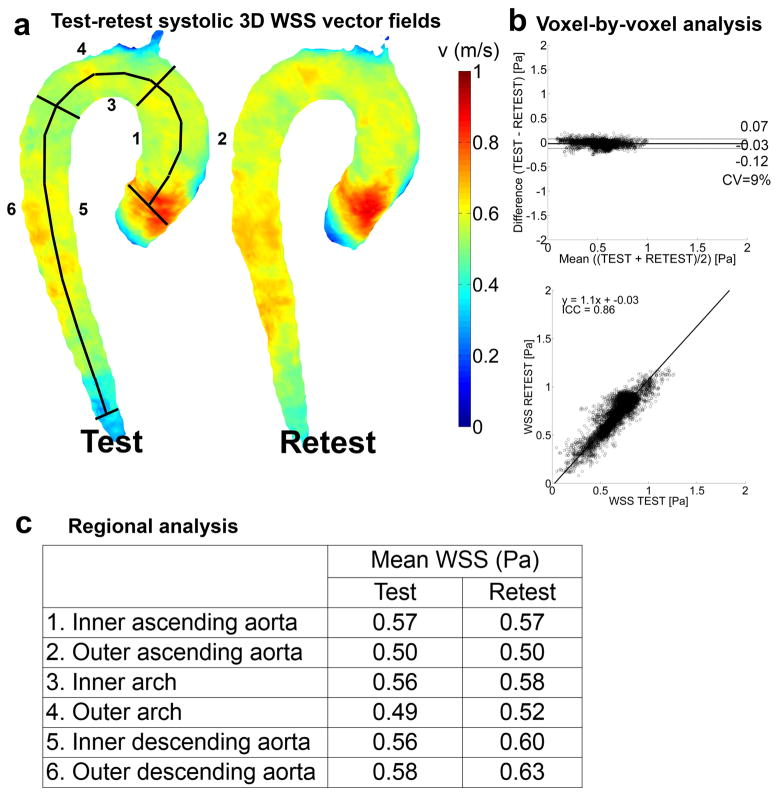
Figure 4.

The results for the test-retest analysis for the cohort-averaged WSS map. a) Full 3D rendering of the WSS magnitude field used for the voxel-by-voxel analysis with the delineation of the regions of interest for the regional analysis. b) Voxel-by-voxel analysis: Bland-Altman plot (top), orthogonal regression (center) and angle distribution (bottom). c) Regional analysis: mean WSS values and variability for test and retest in the six regions displayed in (a).

The mean difference, LOA, CV, slope, intercept and ICC for the Bland-Altman and regression analyses of the cohort-averaged velocity and WSS maps are given in figure 3b and 4b, respectively. The mean differences are close to 0 for both velocity and WSS. The 6 and 10% deviation from unity for the slope of the orthogonal regression line illustrate the higher retest velocity and WSS, respectively, compared to the test scans. The ICC was lower for WSS compared to velocity.

Regional analysis

In figures 3c and 4c, the mean velocity and mean WSS of the regional analysis are given. Velocity and WSS were slightly higher for retest than test scans (maximum of 0.04 m/s and 0.06 Pa in the inner descending aorta).

P-value analysis

In figure 5, the P-value maps for velocity and WSS are displayed. No significant differences between test and retest was found for velocity and WSS on the entire aorta.

Figure 5.

a) Right-Anterior view of the test-retest P-value maps for velocity at the averaged systolic time frames. The region where retest velocity is significantly higher/lower than test velocity would have been shown in red/blue. However, no significant differences were found. b) Right-Anterior view of the test-retest P-value maps for WSS at the systolic time frames. The region where retest WSS is significantly higher/lower than test WSS is shown in red/blue. c) Left-posterior view of the test-retest P-value maps for WSS at the systolic time frames. Regions without significant differences are shown in grey.

Inter-observer analysis

The mean segmentation errors between observers for the test and retest scans were 6±2% and 6±3%, respectively.

Voxel-by-voxel analysis

In table 3, the results of the voxel-by-voxel analysis for inter-observer systolic WSS are given. The mean differences are close to 0. The 1% deviation from unity for the slope of the orthogonal regression line illustrate that WSS are very similar for both segmentations for the test scans. For the retest scans the variability was higher, illustrated by the 9% deviation from unity for the slope. The CV (12 and 13%), ICC (0.87 and 0.85) and the median angle difference (6 and 5°) were very similar for both the test and retest segmentations.

Table 3.

Inter-observer voxel-by-voxel analysis: Mean difference, limits of agreement, Coefficient of Variation, slope, intercept, Intraclass Correlation Coefficient and the angle difference for systolic 3D WSS averaged over all subjects

	Bland-Altman			Orthogonal Regression			Angle distribution
	Mean difference (Pa)	LOA (Pa)	CV (%)	Slope (−)	Intercept (Pa)	ICC (−)	Median (°)
Test	0.00 ± 0.01	0.17 ± 0.04	12 ± 5	1.01 ± 0.09	−0.00 ± 0.03	0.87 ± 0.08	6 ± 2
Retest	−0.00 ± 0.02	0.19 ± 0.06	13 ± 7	1.09 ± 0.27	−0.02 ± 0.09	0.85 ± 0.12	5 ± 3

Regional analysis

In table 4, the results of the regional analysis for inter-observer systolic velocity and WSS magnitude. The differences were minimal (maximum 0.03 m/s in the descending aorta for velocity and 0.01 Pa in multiple regions for WSS). No significant differences in WSS between observers in all six regions were found for both the test and retest scans. The CV was ~3% between observers for the test and retest velocity and WSS. All ICCs were 1, except for the retest WSS in the inner AAo and outer AAo (0.9).

Table 4.

Inter-observer region of interest analysis: Mean velocity and mean WSS for the test scans and the retest scans averaged over all subjects

			Inner AAo			Outer AAo			Inner arch			Outer arch			Inner DAo			Outer DAo
			Observer 1	Observer 2	P	Observer 1	Observer 2	P	Observer 1	Observer 2	P	Observer 1	Observer 2	P	Observer 1	Observer 2	P	Observer 1	Observer 2	P
Velocity	Test	Mean velocity (m/s)	0.52 ± 0.13	0.52 ± 0.13	0.91	0.50 ± 0.11	0.49 ± 0.11	0.95	0.49 ± 0.14	0.47 ± 0.13	0.54	0.45 ± 0.14	0.44 ± 0.13	0.63	0.51 ± 0.17	0.48 ± 0.16	0.54	0.50 ± 0.17	0.48 ± 0.16	0.54
		CV Velocity (%)	3			3			3			3			4			4
		ICC Velocity (−)	1.0			1.0			1.0			1.0			1.0			1.0
	Retest	Mean velocity (m/s)	0.55 ± 0.12	0.54 ± 0.14	0.77	0.51 ± 0.12	0.51 ± 0.13	0.95	0.50 ± 0.13	0.49 ±0.13	0.84	0.46 ± 0.13	0.45 ± 0.13	0.84	0.53 ± 0.19	0.51 ± 0.19	0.70	0.52 ± 0.19	0.50 ± 0.19	0.63
		CV Velocity (%)	5			4			2			2			2			2
		ICC Velocity (−)	1.0			1.0			1.0			1.0			1.0			1.0
WSS	Test	Mean WSS (Pa)	0.60 ± 0.17	0.60 ± 0.16	0.80	0.55 ± 0.14	0.54 ± 0.14	0.80	0.58 ± 0.19	0.57 ± 0.18	0.80	0.51 ± 0.17	0.50 ± 0.17	0.84	0.58 ± 0.20	0.58 ± 0.19	0.91	0.60 ± 0.22	0.60 ± 0.21	0.98
		CV WSS(%)	5			4			3			2			4			4
		ICC WSS (−)	1.0			1.0			1.0			1.0			1.0			1.0
	Retest	Mean WSS (Pa)	0.62 ± 0.15	0.61 ± 0.15	0.73	0.56 ± 0.14	0.57 ± 0.15	0.98	0.61 ± 0.18	0.61 ± 0.19	0.91	0.53 ± 0.17	0.53 ± 0.17	1	0.62 ± 0.25	0.61 ± 0.24	0.98	0.63 ± 0.27	0.63 ± 0.26	0.91
		CV WSS (%)	6			7			1			1			2			3
		ICC WSS (−)	0.9			0.9			1.0			1.0			1.0			1.0

Analyses for peak systole

For the peak systolic test-retest voxel-by-voxel analysis, similar mean differences (−0.04 vs −0.03 m/s and −0.04 vs −0.02 Pa), higher LOA (0.38 vs 0.25 m/s and 0.43 vs. 0.29 Pa), higher CV’s (23 vs. 20% for both velocity and WSS), similar slopes (1.16 vs. 1.14 m/s and 1.15 vs. 1.16 Pa), similar intercepts (−0.06 vs −0.05 m/s and −0.08 vs. −0.07 Pa), lower ICCs (0.69 vs 0.77 and 0.59 vs 0.67) and similar median angle differences (10 vs. 7° and 11 vs 9°) for velocity and WSS, respectively were found. The test-retest CV and ICC in the regional analysis was similar (peak systole: ~10% and ~0.8 vs systolic time frames: ~8% and ~0.9 for both velocity and WSS). The P-value maps showed no significant differences at peak systole. For the inter-observer analysis, the results between peak systole and the systolic time frames was very similar as well, except for the LOA (~0.26 m/s / Pa vs. ~0.18 m/s / Pa for both velocity and WSS at peak systole vs. the systolic time frames). No significant differences between observers was found for both velocity and WSS in the peak systolic regional analysis. Peak systolic test and retest inter-observer CV and ICC were ~3% and ~1.0 for both velocity and WSS.

DISCUSSION

Test-retest and inter-observer reproducibility for flow and WSS have been investigated for both 2D PC-MRI (29,30) and 4D flow techniques (30,31); however, few have looked in detail at WSS in the context of retest and inter-observer error with 4D flow (17,23). To our knowledge, this is the only study to have investigated the retest and observer variability of a volumetric 3D WSS computational algorithm, as presented here. Retest and user variability for the technique must be understood in order to justify further prospective studies which assess flow and WSS as a prognostic for disease development. Since the measurement of flow (a spatial integration of the velocity field) has already been shown to be reproducible (23), we chose to investigate the reproducibility of the velocity field and measurement of WSS in a 3D volume.

While the use of contrast agents have been shown to improve velocity SNR, we chose a ‘worst-case’ situation in which no contrast was used in order to understand the robustness of the measurements for all potential subjects, including those who are intolerant to contrast administration. The results presented in this study show that the voxel-by-voxel, regional and cohort-averaged analyses of the 3D velocity fields and 3D WSS of non-contrast test-retest subjects are reproducible.

Bieging et al. (17) assessed the inter-observer variability of their in-house developed volumetric 3D WSS algorithm for contrast-enhanced 4D flow MRI and found an 8% variability for time-averaged WSS. The choice to focus on the high SNR portion of the cardiac cycle, i.e. systole, was a potential reason for the lower variability found here.

Despite the finding of no significant differences in blood pressure and heart rate, the mean difference and slope of the regression in the voxel-by-voxel analysis indicate that the velocity and WSS values for the retest scan were generally higher than the test scan. Since measurement bias was minimized by performing the exact same scan protocol at the same time of day, with ensuring no caffeine intake, and with identical post-processing techniques for the retest scan as for the test scan, this may simply be due to physiologic variation. A deviation from unity in the ICCs can be attributed to measurement noise and the fact that no contrast was used for the 4D flow MRI acquisitions. The decrease in ICC for WSS as compared to velocity in the test-retest voxel-by-voxel analysis is expected, given that WSS is a derivative of the velocity field and noise effects will be propagated. However, the CV, slope and median angle difference were similar for velocity and WSS. This illustrates that the measurement of WSS is similar in robustness to the velocity measurements. Note that test-retest differences are not a consequence of registration and interpolation processes needed for the voxel-by-voxel analysis. Due to the similarity of the segmentations for test and retest scans, differences in mean velocity and WSS before and after interpolation were minimal.

The analysis investigating the test-averaged and retest-averaged 3D velocity and WSS maps further indicates that the differences between the test and retest cohort-averaged maps are small. The lower CVs and ICCs for the cohort-averaged analysis follows from the notion that noise is mitigated when averaging velocity and WSS over multiple subjects.

The P-value maps indicated that the higher velocity and WSS for the retest scans compared to the test scans found in the voxel-by-voxel, regional and cohort-averaged analyses was not significant. This is an important finding given that reliable cohort-averaged maps are an important tool to detect disease-related changes in large patient populations (21). In addition, if WSS is found predictive for disease progression, it is important to be able to detect abnormal WSS on a case by case basis in individual patients (22).

Numerical simulations have shown that the delineation of the aortic wall can influence the accuracy of WSS estimations (18,32). The results presented here indicate that a carefully executed, well-defined segmentation protocol (and the use of the algorithm presented here), can produce low variability in 3D segmentation and thus in the estimation of WSS (due to choice of wall position).

Various methods exist to report WSS over the time domain. For example, time-averaged WSS has been used in a number of studies, especially those investigating the atherosclerosis hypothesis (13,33) . The measurement of time-averaged WSS is less noisy; however, it requires a robust time resolved segmentation, given the movement of the ascending aorta. Time-resolved 3D segmentation is difficult to achieve, especially when segmenting vessel regions with limited diastolic signal. Additionally, in cases investigating valve disease, it has been found that important time-dependent events, such as systolic ejection, are diluted over hemodynamically inactive portions of the cardiac cycle (such as in diastole) (34). Thus, the protocol for this study focused on velocity and WSS measurements weighted over 5 systolic phases of the cardiac cycle, which has been reported to be less susceptible to the noise when reporting a single time point measurement (34). Given the improvements to the WSS calculation algorithms since these initial reports (18), it is unclear whether this approach is less noisy than a single time point measurement. As a result, an additional, identical analysis was carried out which examined the sole peak systolic time frame of the cardiac cycle. It was found that differences with the analysis for the averaged systolic time frames were small. These results are informative, as they indicate that, using the WSS computation approach presented here, noise is not a problem when measuring a single-time point at systole. It can be surmised with these results that future studies can investigate single time point events without problems with reproducibility.

A previous study employed a study design similar to that here, but used a measurement method which manually placed 2D analysis planes at pre-defined anatomical landmarks (23). Subjects were rescanned at an average interval of one year and found limits of agreement and peak systolic WSS variability identical to those reported here (LOA=0.43 and variability<6% for the 3D approach). The inter-observer limits of agreement were lower for the 3D than the 2D WSS calculation approaches (LOA at peak systole = 0.26 in (23)). While the variability was similar, it is important to note that the study is fundamentally different in the WSS computational approach, as 2D planes and spatially averaged WSS over the aorta lumen was used. In our approach, we projected the 3D velocities and WSS of the retest scan onto the inner surface of the test geometry and reported spatially resolved WSS in the Bland-Altman analysis.

The advantage of the 3D approach is that no manual placement of 2D planes is needed, which can be time-consuming. Moreover, the entire thoracic aorta is included in the 3D approach and measurements can be regionally benchmarked to control references. 4D flow MRI velocity data has been compared to simulations employing computational fluid dynamics (CFD)(35).

4D flow is advantageous in that it does not require assumptions about boundary conditions, which can influence the results heavily (mean WSS difference of 3.5 Pa between generalized boundary conditions and measured with 2D phase contrast MRI in (36)) or long computation times (on the order of hours). However, 4D flow MRI can require long scan times which necessitate compromises in terms of spatiotemporal resolution and signal-to-noise ratio. The lower spatial resolution used in 4D flow MRI compared to CFD generally leads to lower WSS (19,20). Furthermore, the accuracy of WSS depends on the fitting method and the segmentation of the vessel of interest (32). Nevertheless, taking into account these potential sources of error, estimates of relative WSS from 4D flow MRI remains useful for investigation of differences in healthy controls and patients with cardiovascular disease, if scanned with similar scan parameters.

A limitation of the study is that no patients were included in the study. It might be possible that physiological changes of aortic flow over time may be greater than those found in healthy volunteers. Therefore, the reproducibility of velocity and WSS may be lower than as presented in this study. The investigation of reproducibility of velocity and WSS derived from 4D flow MRI in patients is part of ongoing work.

Additionally, it is difficult to perform a time-resolved 3D segmentation in vasculature known to have significant movement over the cardiac cycle, especially given the SNR provided by the PC-MRA approach. Thus, we chose to perform a 3D segmentation weighted for the systolic phases of the cardiac cycle. While this approach has been shown to detect WSS differences in the aorta of subjects with valve disease (34), the approach may not be appropriate for all applications.

The threshold used to mask the aorta in the PC-MRA images was manually chosen such that the voxels adjacent to the aorta lumen were included. Since the PC-MRA images were created from a weighted composite of the velocity and magnitude images, the PC-MRA values corresponding to the lumen area varied for each subject. This variation in threshold selection, however, should be reflected in the WSS values computed between both observers and did not lead to large errors.

Furthermore, the limited experience of the observers with the segmentation software (less than three months) may have increased the potential for obtaining a ‘worst case’ number for inter-observer agreement. One may expect those with more experience to produce better observer agreement.

In this study, anisotropic voxels of different sizes for different subjects were used, which could have led to inter-subject differences in accuracy of the WSS estimations. For example, Stalder et al. and Potters et al. showed that differences in WSS for voxel lengths of between 2–4 mm were in the order of 0.05 Pa (or about 10% of the cohort averaged WSS value, Figure 4) (10,18). In a worst case scenario, anisotropic voxels and inter-subject inaccuracy may cause a 10% error. In addition, the reproducibility should be relatively unaffected by a difference in voxel size as long as the test and retest scans use similar resolutions. The values reported in this paper are comparable to other studies involving WSS derived from 4D flow MRI. The clinical utility of WSS estimations such as those presented here have yet to be demonstrated and remain a preclinical research endeavor.

To assess true velocity and WSS reproducibility, only one MR system with one set of scan parameters was used. Variability in velocity and WSS due to different scanners and scan parameters is certain to exist. Furthermore, the reproducibility of recent novel techniques such as 3D WSS heat maps (22) remain to be investigated. Future work will include these analyses.

In conclusion, we have demonstrated that voxel-by-voxel velocity and 3D WSS derived from 4D flow MRI are reproducible quantities in this cohort of healthy volunteers for both the peak systolic time frame and five averaged systolic time frames.