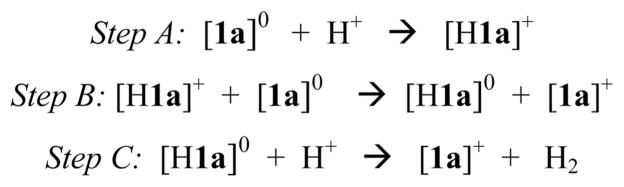Models of the Ni-L and Ni-SI_a States of the [NiFe]-Hydrogenase Active Site

Abstract

A new class of synthetic models for the active site of [NiFe]-hydrogenases are described. The Ni^I/II(SCys)₂ and Fe^II(CN)₂CO sites are represented with (RC₅H₄)Ni^I/II and Fe^II(diphos)(CO) modules, where diphos = 1,2-C₂H₄(PPh₂)₂(dppe) or cis-1,2-C₂H₂(PPh₂)₂(dppv). The two bridging thiolate ligands are represented by CH₂(CH₂S)₂²⁻ (pdt²⁻), Me₂C(CH₂S)₂²⁻ (Me₂pdt²⁻), and (C₆H₅S)₂²⁻. The reaction of Fe(pdt)(CO)₂(dppe) and [(C₅H₅)₃Ni₂]BF₄ affords [(C₅H₅)Ni(pdt)Fe(dppe)-(CO)]BF₄ ([1a]BF₄). Monocarbonyl [1a]BF₄ features an S = 0 Ni^IIFe^II center with five-coordinated iron, as proposed for the Ni-SI_a state of the enzyme. One-electron reduction of [1a]⁺ affords the S = ¹/₂ derivative [1a]⁰, which, according to density functional theory (DFT) calculations and electron paramagnetic resonance and Mössbauer spectroscopies, is best described as a Ni^IFe^II compound. The Ni^IFe^II assignment matches that for the Ni-L state in [NiFe]-hydrogenase, unlike recently reported Ni^IIFe^I-based models. Compound [1a]⁰ reacts with strong acids to liberate 0.5 equiv of H₂ and regenerate [1a]⁺, indicating that H₂ evolution is catalyzed by [1a]⁰. DFT calculations were used to investigate the pathway for H₂ evolution and revealed that the mechanism can proceed through two isomers of [1a]⁰ that differ in the stereochemistry of the Fe(dppe)CO center. Calculations suggest that protonation of [1a]⁰ (both isomers) affords Ni^III–H–Fe^II intermediates, which represent mimics of the Ni-C state of the enzyme.

Graphical abstract

INTRODUCTION

Hydrogenases are enzymes that catalyze the oxidation of hydrogen and reduction of protons at high rates and low overpotentials, reactions that are potentially useful for clean energy applications.^1–4 Hydrogenases are classified into three main families according to the metals in their active site: [Fe]-, [FeFe]-, and [NiFe]-hydrogenases.^5,6 These enzymes are oxygen-sensitive but the [NiFe]-hydrogenases can recover from oxygen poisoning.^8,9 Model compounds have been useful in elucidating catalytic mechanisms or atom identity, notably with [FeFe]-hydrogenases.^7,10 [FeFe]-hydrogenase models are fairly advanced and have strong resemblance and relevance to the enzymatic system.^3,4,11 In contrast, models of the oxygentolerant [NiFe]-hydrogenases are less mature, and comparisons to the enzymatic system are sometimes less applicative.^3,4,12,13

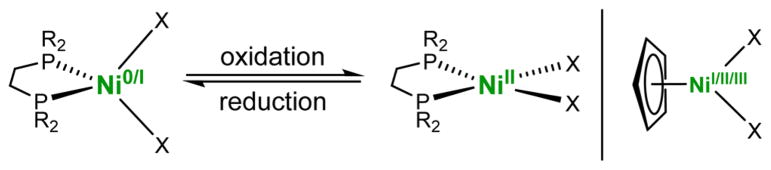
The [NiFe]-hydrogenase active site features a [Ni(SCys)₄]^z center linked through two thiolate bridges to an Fe(CN)₂(CO) center (Figure 1). In the absence of a third bridging ligand, the geometry at nickel resembles that of SF₄, while iron is square-pyramidal. The active states of the enzyme differ in three ways: (i) the oxidation state of the Ni center, (ii) the presence/absence of a hydride ligand bridging the two metals, and (iii) the state of protonation of at least one terminal cysteinyl thiolate. In contrast to the fluctuating oxidation states at the nickel center, iron appears to remain low-spin Fe^II throughout all of the known states of the enzyme active site.

Figure 1.

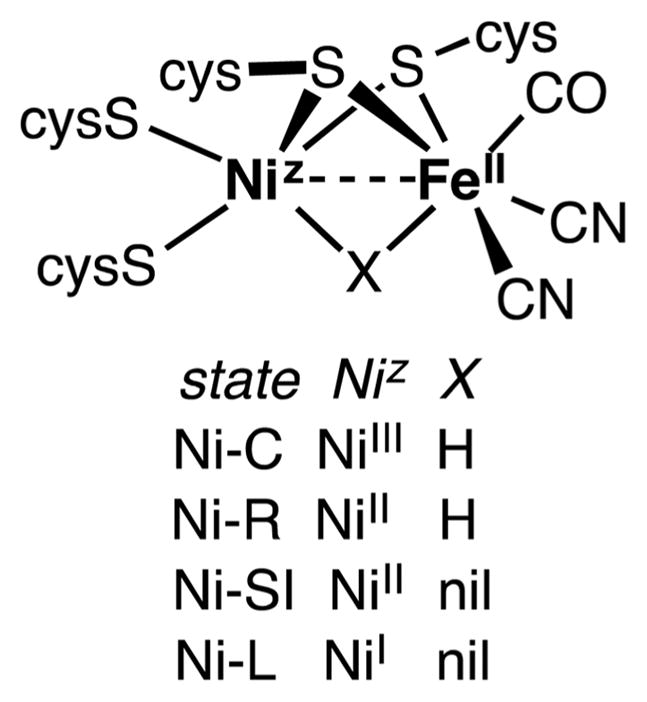
States of the active site of the [NiFe]-hydrogenases.

Beyond complementing our understanding of the enzyme, synthetic models could underpin the development of new catalysts for the processing of H₂.^1,2 The possibility of connecting synthetic complexes to enzyme states was established with [(dppe)Ni(pdt)(μ-H)Fe(CO)₃]^+.14,21 A related nickel–iron hydride [(amine)₂Ni(SR)₂(μ-H)FeL₃]⁺ catalyzes the reduction of redox dyes by H₂, a characteristic assay for the hydrogenases.¹⁵ With a Ni^II–H–Fe^II core, these synthetic complexes represent early models for the Ni-R state of the protein, despite discrepancies (Table 1).¹⁶

Table 1.

Summary of Models for the Active States of the [NiFe]-Hydrogenase^a

state	core description	state of the art models	comment
Ni-R	NiII–H–FeII	[(diphos)Ni(pdt)(μ-H)Fe(CO)2L]+14 [(amine)2Ni(SR)2(μ-H)FeL3]+ 15	models: dFe–H < dNi–H enzyme: dFe–H > dNi–H16
Ni-SI	NiII–_–FeII	[(diphos)Ni(SR)2Fe(CO)2L2]+ 17	model: six-coordinated iron enzyme: five-coordinated iron18
Ni-C	NiIII–H–FeII 19	none	no progress
Ni-L	NiI–_–FeII	[(diphos)Ni(pdt)Fe(CO)2L]+ 20	model: NiIIFeI vs enzyme: NiIFeII 16

^adiphos = R₂PCH₂CH₂PR₂; (amine)₂(SR)₂ = tetradentate diaminodithiolate;¹⁵ L = PR₃ or P(OR)₃; pdt²⁻ = CH₂(CH₂S⁻)₂.

Concurrent with the development of these diamagnetic models,^21,22 efforts have been made to replicate the paramagnetic states of the enzyme. The two most prominent paramagnetic states are Ni-C and Ni-L. Invoked in all catalytic mechanisms is Ni-C,^6,7,23–25 which features a hydride bridging the Ni^III and Fe^II centers. No synthetic analogues of this nickel(III) hydride have been detected, but this paper provides a first glimpse of a synthetic model. With a Ni^IFe^II core, Ni-L is typically generated by low-temperature photolysis of Ni-C, and recent evidence points to its role in catalysis.^26,27 These S = ¹/₂ states deviate most strongly from the conventional chemistry of dimetal systems and therefore offer the greatest opportunity for the discovery of fundamentally new reactivity. The first reported S = ¹/₂ NiFe complex was [(diphos)Ni(pdt)Fe-(CO)₂L]⁺. Spectroscopic, crystallographic, and computational analyses show, however, that these cations are described as Ni^IIFe^I derivatives,^20,28 not Ni^IFe^II as assigned to the Ni-L state of the enzyme.¹⁶ The lapse is a consequence of the Fe(CO)₂L center, which stabilizes Fe^I. In the present report, the Fe(CO)₂L center is replaced by the Fe(diphos)(CO) module, which more strongly stabilizes Fe^II.22

One of the weaknesses in the first generation of active-site model is a high reorganization energy upon oxidation at nickel.²¹ This work addresses this weakness. Redox at the nickel centers typically induces changes in the coordination geometry, such that Ni^I species (cf. Ni-L) are tetrahedral and Ni^II/III species (cf. Ni-SI_a, Ni-R, Ni-C) are square-planar (Figure 2). In contrast, the NiFe active site changes only subtly as it converts among catalytic states.^16,27 To minimize reorganizational barriers, the [Ni(diphos)]^z site is replaced by [(C₅H₅)Ni]^z. The [(C₅H₅)Ni(SR)₂]^z center has the advantage that its geometry is relatively insensitive to redox, in contrast to Ni(dppe)(SR)₂-based models (Figure 2). Not only does the hapticity of C₅H₅ not change, but crystallographic studies^29–31 show that the Ni-C₅H₅ distances are relatively invariant (<0.12 Å) for Ni^I, Ni^II, and Ni^III(C₅H₅) compounds.

Figure 2.

Nickel diphosphine complexes changing geometry upon the oxidation of tetrahedral Ni^0/I. The Ni(C₅H₅) center is structurally invariant over three oxidation states.

RESULTS AND DISCUSSION

Models for Ni-SI: Synthesis and Structure

The reaction of Fe(pdt)(CO)₂(dppe) and [(C₅H₅)₃Ni₂]BF₄ in nitromethane affords [(C₅H₅)Ni(pdt)Fe(dppe)(CO)]BF₄ ([1a]BF₄; eq 1) as a dark-red powder. The derivatives [(C₅H₅)Ni(pdt)Fe(dppv)-(CO)]BF₄ ([1b]BF₄), [(C₅H₅)Ni(Me₂pdt)Fe(dppe)(CO)]-BF₄ ([1c]BF₄), and [(CH₃C₅H₄)Ni(pdt)Fe(dppe)(CO)]BF₄ ([1d]BF₄), where dppv = cis-1,2-C₂H₂(PPh₂)₂ and Me₂pdt²⁻ = Me₂C(CH₂S⁻)₂, were also prepared using the appropriate nickel and iron precursors. These salts are similar to [1a]BF₄ in terms of their reactivity and spectroscopic properties. The reaction of Fe(pdt)(CO)₂(dppe) and [(C₅H₅)₃Ni₂]BF₄ proceeds via an intermediate with ν̃_CO = 1980 cm⁻¹ that converts to [1a]⁺. We assign this intermediate band to the dicarbonyl complex trans-[(C₅H₅)Ni(pdt)Fe(dppe)(CO)₂]-BF₄. The disappearance of the intermediate band follows first-order decay (Figures S45 and S46). When the reaction progress is monitored by ³¹P NMR spectroscopy, the iron precursor is consumed within ca. 5 min and two new singlet resonances are observed, one of which corresponds to the product [1a]⁺. Additionally, electrospray ionization mass spectrometry (ESI-MS) of the reaction mixture indicates the presence of the molecular cation [(C₅H₅)Ni(pdt)Fe(dppe)-(CO)₂]⁺. These observations are consistent with the rapid attachment of “(C₅H₅)Ni⁺” to the two isomers of the iron dithiolate. The cis-carbonyl derivative appears to release CO rapidly, whereas the isomer with trans-CO ligands is somewhat persistent.

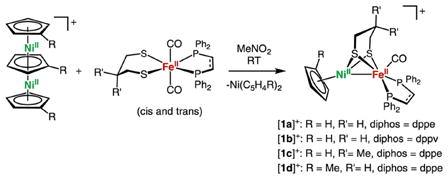(1)

Purified compounds [1a–1d]BF₄ display a single ν̃_CO band in the range of 1940–1951 cm⁻¹, consistent with the presence of one isomer. These values are similar to those observed in Ni-SI_a, which range from 1927 to 1947 cm⁻¹ (Table 2).⁶

Table 2.

IR Data for Compounds [1a–1d]BF₄ and [2b]BF₄ in a CH₂Cl₂ Solution and the Ni-SI_a State in Selected Organisms

compound	ν̃CO (cm−1)
	expt	calca
[(C5H5)Ni(pdt)Fe(dppe)(CO)]BF4 ([1a]BF4)	1943	1948/1946
[(C5H5)Ni(pdt)Fe(dppv)(CO)]BF4 ([1b]BF4)	1951	1951/1949
[(C5H5)Ni(Me2pdt)Fe(dppe)(CO)]BF4 ([1c]BF4)	1940	1937/1935
[(CH3C5H4)Ni(pdt)Fe(dppe)(CO)]BF4 ([1d]BF4)	1943	1947/1945
[(C5H5)Ni(SPh)2Fe(dppv)(CO)]BF4 ([2b]BF4)	1956	1959
Ni-SIa (Synechocytis SH)6	1947	n/a
Ni-SIa (D. vulgaris Miyazaki F)32	1943	n/a
Ni-SIa (D. gigas)32	1934	n/a
Ni-SIa (A. aeolicus)6	1927	n/a
Ni-SIa (Allochromatium vinosum)32	1931	n/a

^aThe first value corresponds to the conformer in which the central CH₂ of the Fe(pdt)Ni core is oriented toward iron, and the second value corresponds to the conformer in which the same CH₂ is oriented toward nickel. The calculations were performed in the absence of BF₄⁻.

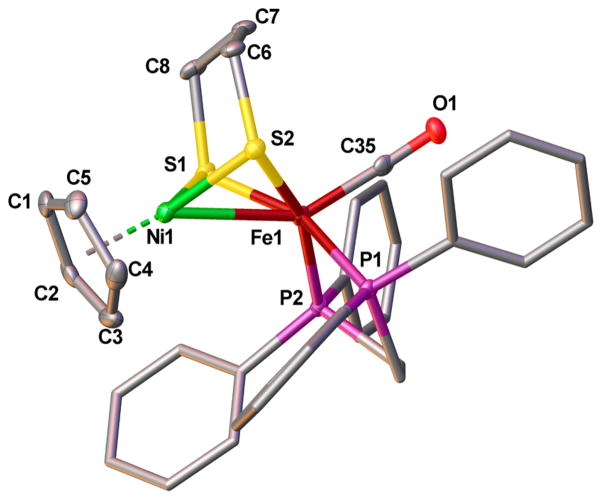
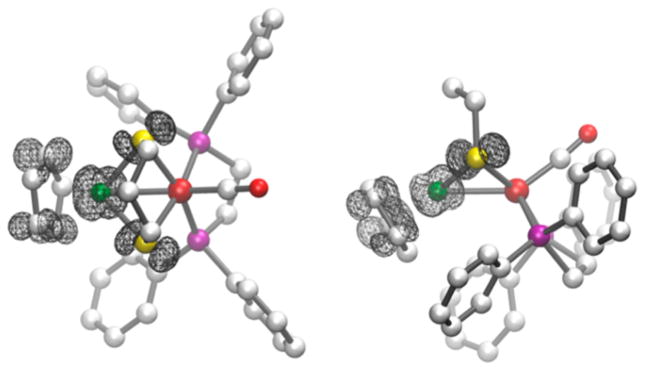
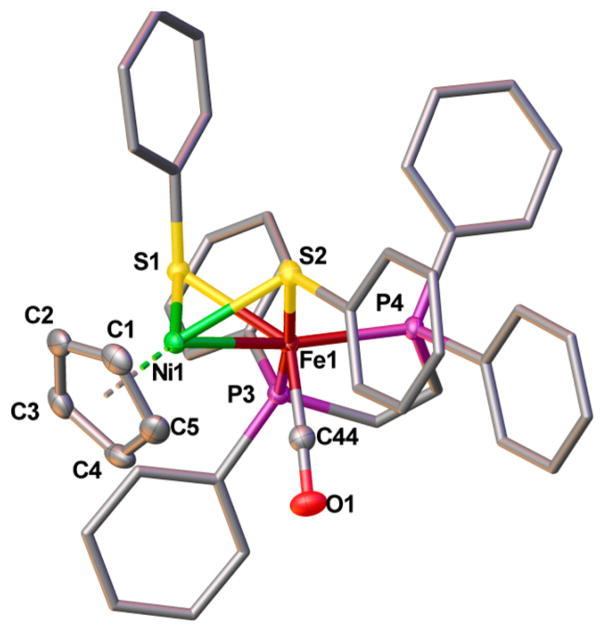
The structure of [1a]⁺ was confirmed by X-ray crystallography. The Ni–Fe distance is 2.5145(4) Å (Figure 3). Although the enzyme in the SI_a state has not been characterized crystallographically, it is generally assumed that the Ni–Fe distance is ~2.6 Å in all active states.⁶ The stereochemistry of the FeL₂(CO) site is biomimetic in the sense that CO occupies an apical site, and the two Lewis basic phosphine ligands are approximately trans to the sulfur centers of the thiolates.

Figure 3.

Solid-state structure of [1a]BF₄ shown at the 50% probability level. Hydrogen atoms, counterions, and solvent have been omitted for clarity. Selected bond distances (Å): Ni1–Fe1, 2.5145(4); Ni1–centroid, 1.722(3); Ni1–S_avg, 2.1645(7); Fe1–S_avg, 2.2208(7); Fe1–C35, 1.757(2); C35–O1, 1.147(2).

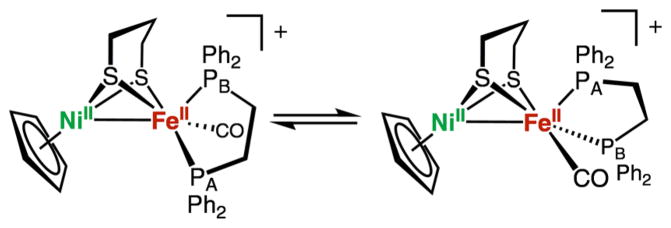
The ³¹P NMR spectra of complexes [1a–1d]BF₄ are simple, exhibiting only a single resonance, indicating chemically equivalent phosphorus centers or a dynamic process. The diphosphine in complexes [1a–1d]BF₄ is only observed in the dibasal arrangement, whereas other Fe(dithiolate)-(diphosphine)CO compounds have been shown to adopt both a dibasal and an apical–basal arrangement.³³ The phosphorus centers remain NMR-equivalent at −90 °C, suggesting either an exceptionally low barrier for isomerization or the presence of a single isomer. In the IR spectrum, only a single isomer is observed, which, like the enzyme’s active site, has both donor ligands in basal positions.

The reaction of cis,cis-Fe(SPh)₂(CO)₂(dppv) and [(C₅H₅)₃Ni₂]BF₄ gave the dicarbonyl [(C₅H₅)Ni(SPh)₂Fe-(dppv)(CO)₂]BF₄ ([2bCO]BF₄), isolated as dark, almost black, microcrystals. Its ¹H NMR spectrum exhibits only one (C₅H₅) signal, and an AB quartet pattern in the ³¹P NMR spectrum, indicating low symmetry. The structure was confirmed crystallographically (Figure S53). The Ni–Fe distance is 3.308(1) Å, indicating a noncovalent interaction. The stereochemistry at iron is identical with the precursor, wherein all ligands are cis. The μ-SPh groups are diaxial.

Upon treatment with Me₃NO, the dicarbonyl readily decarbonylated to give [2b]BF₄, isolated as a black solid. The IR spectrum of [2b]⁺ in a CH₂Cl₂ solution displays a single ν̃_CO band at 1956 cm⁻¹, versus 2042 and 2002 cm⁻¹ observed for the precursor. The monocarbonyl cation, [2b]⁺, decomposes gradually in a CH₂Cl₂ solution. However, the complex is stable in MeCN, and the ν̃_CO band shifts 22 cm⁻¹ to higher energies, suggesting the formation of an adduct. The ³¹P NMR spectrum of [2b]⁺ exhibits a singlet at δ 78.8. Under 1 atm of CO, MeCN solutions of [2b]⁺ partially convert back to [2bCO]⁺. In contrast, [1a]⁺ is not reactive toward CO.

Electrochemistry

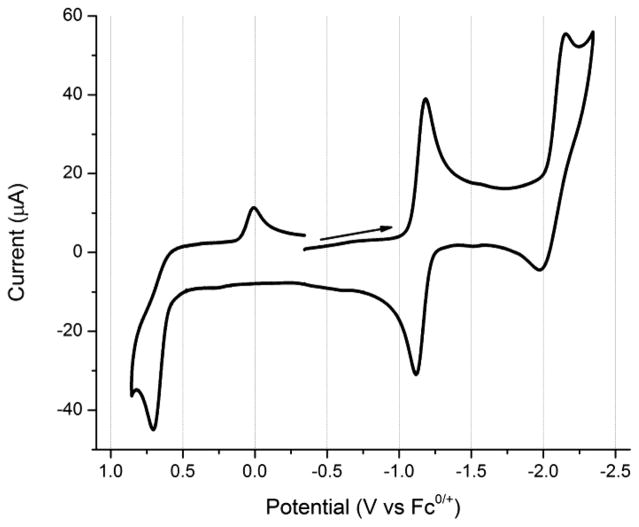
The cyclic voltammetry of [1a]BF₄ in dichloromethane (CH₂Cl₂) is very rich (Figure 4). Compounds [1b–1d]⁺ produce similar voltammograms (Table 3). Compounds [1a–1d]⁺ exhibit an irreversible oxidation near +0.65 V and a reversible one-electron reduction near −1.20 V, all versus Fc^0/+. Additionally, a quasi-reversible reduction is observed near −2.15 V, which becomes fully reversible when in tetrahydrofuran (THF) with [Bu₄N]B(C₆H₃-3,5-(CF₃)₂)₄ as the electrolyte. An irreversible reduction wave is generated at ca. 0.0 V versus Fc^0/+ following the irreversible oxidation.

Figure 4.

Cyclic voltammogram of [1a]BF₄ at 500 mV s⁻¹. Conditions: ~1 mM in CH₂Cl₂; 100 mM [NBu₄]PF₆; glassy carbon electrode (d = 3 mm); silver wire as the pseudoreference with an internal Fc standard at 0 V; platinum as the counter electrode.

Table 3.

Electrochemical Properties of Compounds [1a–1d]⁺ (V vs Fc^+/0 in CH₂Cl₂)^a

compound	Ep,ox(NiIIFeII/NiIIIFeII)	calcb,c	E1/2(NiIIFeII/NiIFeII)	calcb,c	Ep,redd(NiIFeII/NiIFeI)	calcb,c,d
[1a]BF4	0.70	0.70	−1.16	−1.16	−2.15	−2.15
[1b]BF4	0.72	0.73	−1.15	−1.12	−2.18	−2.05
[1c]BF4	0.67	0.76	−1.09	−1.16	−2.15	−2.12
[1d]BF4	0.62	0.66	−1.21	−1.23	−2.17	−2.18

^aFor the calculated values, the central CH₂ of the Fe(pdt)Ni core is oriented toward iron and assumed to remain in this orientation upon reduction or oxidation. Additional calculated values corresponding to the same CH₂ being oriented toward nickel, or flipping from iron to nickel, are available in Tables S1 and S2. In all cases, the conformation of the Fe(pdt)Ni core does not affect the potential.

^b[1a]BF₄ was used as the reference so the experimental and calculated values agree by construction.

^cThe calculations were performed on the positively charged species in the absence of BF₄⁻.

^dThis wave is assigned to a Ni^IFe^II/Ni^IFe^I couple, where the Ni^IFe^I state is an open-shell singlet.

The redox couples in the different derivatives are relatively similar. The reversible couple is most affected by Me₂pdt substitution. With Δν̃_CO = 3 cm⁻¹ (Table 1), the donor properties of pdt²⁻ and Me₂pdt²⁻ are similar in this system, and the difference in the potential of the Ni^IIFe^II/Ni^IFe^II redox couple may be due to the steric effects of the methyl groups. The reversible reduction in complexes [1a–1d]⁺ shifts to more positive potentials by 50 mV upon replacement of (C₅H₅) for CH₃C₅H₄. This effect suggests that the reduction is nickel-centered, generating a Ni^IFe^II species. CH₃C₅H₄ substitution most affected the oxidation observed at ≈0.75 V, shifting this couple by −80 mV, whereas other substitutions only generate a 20–30 mV effect. This observation suggests that oxidation is nickel-centered. The reduction near −2 V is negligibly affected by the nickel-based ligands and is proposed to be an iron-centered reduction, generating a Ni^IFe^I species.

Density functional theory (DFT) was used to calculate the potentials associated with the couples [1a–1d]^2+/+, [1a–1d]^+/0, and [1a–1d]^0/−. The potentials were calculated relative to [1a]BF₄ and are provided in Table 3. The experimental trends are well reproduced by the calculations. The BF₄⁻ ions were not included in the calculations, which may cause deviations between the calculated and experimental values. The reduction potentials were also calculated for an alternative geometry optimization scheme, as well as using different functionals, and these results are provided in Tables S1 and S2.

Models for Ni-L: Synthesis and Structure

The reduced species [1a–1d]⁰ and [2b]⁰ were produced on a preparative scale by treatment with (C₅H₅)₂Co (E⁰ = −1.23 V; eq 2).

$$[({\mathrm{C}}_5{\mathrm{H}}_5)\text{Ni}{(\text{SR})}_2\text{Fe}(\text{diphos})(\text{CO})]{\text{BF}}_4+{({\mathrm{C}}_5{\mathrm{H}}_5)}_2\text{Co}\to ({\mathrm{C}}_5{\mathrm{H}}_5)\text{Ni}{(\text{SR})}_2\text{Fe}(\text{diphos})(\text{CO})+[{({\mathrm{C}}_5{\mathrm{H}}_5)}_2\text{Co}]{\text{BF}}_4$$ (2)

Purified samples [1a–1d]⁰ and [2b]⁰ were isolated as black, air-sensitive solids. Reduction of [1a–1d]⁺ and [2b]⁺, a Ni^IIFe^II/Ni^IFe^II couple, shifts ν̃_CO by ca. 40 cm⁻¹ to around 1900 cm⁻¹. A similar change is observed for the reduction of [(dppe)Ni(pdt)Fe(CO)₃]⁺, a Ni^IIFe^I/Ni^IFe^I couple (Δν̃_CO ≈ 35 cm⁻¹ for this tricarbonyl).²⁰ Oxidation state changes centered at iron typically shift ν̃_CO by ca. 100 cm⁻¹ as observed for [(dppe)Pt(pdt)Fe(CO)₃]^+/0, a Pt^IIFe^I/Pt^IIFe⁰ couple.²¹ For the Ni-L state of the [NiFe]-hydrogenases, the values of ν̃_CO range from 1911 (Desulfovibrio vulgaris Miyazaki F)³⁴ to 1862 cm⁻¹ (Aquifex aeolicus) (Table 4).^26,35

Table 4.

IR Data for ν̃_CO in Compounds [1a–1d]⁰ and [2b]⁰ in a CH₂Cl₂ Solution

compound	ν̃CO (cm−1)
	expt	calca
[1a]0	1901	1901/1901
[1b]0	1903	1909/1906
[1c]0	1897	1898/1899
[1d]0	1898	1900/1900
[2b]0	1915	1911

^aThe first value corresponds to the isomer in which the central CH₂ of the Fe(pdt)Ni core is oriented toward iron, and the second value corresponds to the isomer in which the same CH₂ is oriented toward nickel.

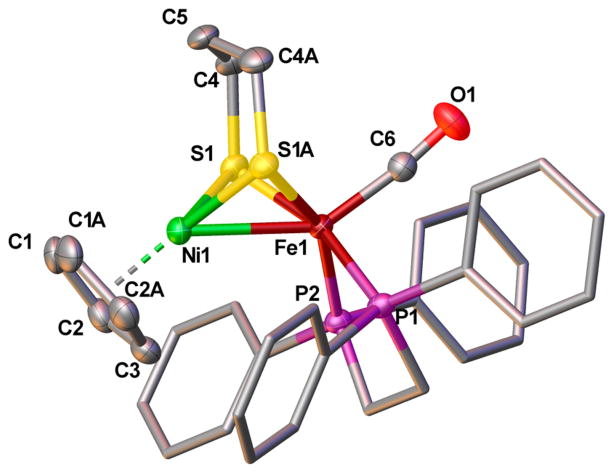
X-ray crystallographic analysis confirmed that the solid-state structures of [1a]⁰ (Figure 5) and [1a]⁺ (Figure 3) are very similar. The principal changes in these structures are in the coordination sphere of nickel, which suggests that the couple [1a]^+/0 involves a nickel-centered reduction. The Ni-C₅H₅ and Ni–S bonds elongate by about 5%, while the Fe–ligand bond lengths remain virtually unchanged. The Ni–Fe distance shortens by ~0.1 Å to 2.4593(5) Å, which is well within the sum of the atomic radii [2.56(6) Å], indicating the presence of metal–metal bonding. Although there are no crystallographic data on the metal–metal-bonded Ni-L state of the enzyme, DFT calculations predict this distance to be 2.56 Å.³⁶ The observed structural changes are consistent with reduction at the nickel center in the transformation of [1a]⁺ to [1a]⁰. The DFT-optimized structures of [1a]⁺ and [1a]⁰ were in excellent agreement with the crystal structures (Table 5).

Figure 5.

Solid-state structure of [1a]⁰ shown at the 50% probability level. Hydrogen atoms and solvent have been omitted for clarity. Selected bond distances (Å): Ni1–Fe1, 2.4593(6); Ni1–centroid, 1.795(3); Ni1–S_avg, 2.2772(5); Fe1–S_avg, 2.2544(5); Fe1–C6, 1.745(3); C6–O1, 1.159(3).

Table 5.

Key Bond Distances (Å) in [1a]BF₄ and [1a]⁰ and the Differences from the Crystal Structures and DFT Calculations

bond	[1a]BF4	calc	[1a]0	calc	experimental difference	DFT difference
Ni–Fe	2.5145(4)	2.566	2.4593(5)	2.508	−0.055	−0.058
Ni–centroid	1.722(3)	1.739	1.795(3)	1.814	+0.073	+0.075
Ni–Savg	2.1645(7)	2.168	2.2772(5)	2.259	+0.113	+0.091
Fe–Savg	2.2208(7)	2.236	2.2544(5)	2.252	+0.034	+0.016
Fe–Pavg	2.2256(7)	2.249	2.235(8)	2.236	+0.009	−0.013
Fe–C	1.757(2)	1.721	1.745(3)	1.727	−0.012	+0.006
C–O	1.147(2)	1.171	1.159(3)	1.174	+0.012	+0.003

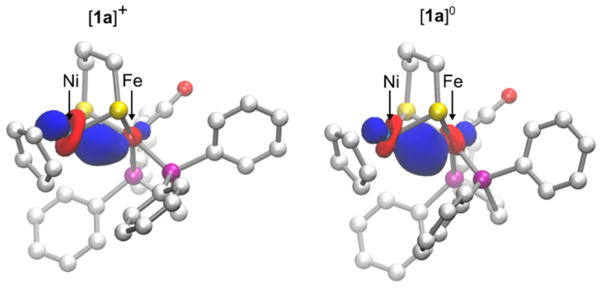
DFT analysis of the spin density was used to determine the site of reduction of [1a–1d]⁺. The plot of the spin density for [1a]⁰ (Figure 6) reveals that the unpaired electron resides primarily on the nickel center, with some delocalization on the pdt²⁻ and (C₅H₅)⁻ ligands but no significant delocalization on the iron. This result is consistent with the Ni^IFe^II assignment and the experimentally observed elongation of the Ni–ligand bonds upon reduction of [1a]⁺.

Figure 6.

Views of the isocontour plot of the positive spin density for [1a]⁰ from two perspectives. The spin density is localized about the nickel coordination sphere. Color scheme: green, nickel; maroon, iron; yellow, sulfur; purple, phosphorus; red, oxygen; white, carbon. The hydrogen atoms have been removed for clarity.

The spin densities for the reduced species [1a–1d]⁰ and [2b]⁰ are given in Table 6 and consistently indicate a nickel-based reduction across all species. As observed for related nickel–iron dithiolate complexes,^20,21 the spin densities are not significantly affected by the conformation of the pdt ligand. Furthermore, the calculations also predict that an iron-based reduction would require potentials of 0.2–0.4 V more negative than the experimentally observed nickel-based reduction potentials (Table S1).

Table 6.

Calculated Spin Densities in Mixed-Valence Species [1a–1d]⁰ and [2b]^{0 a}

compound	Ni	Fe	2S	C5H5
[1a]0	0.71	−0.17	0.24	0.24
	0.71	−0.19	0.23	0.25
[1b]0	0.69	−0.16	0.22	0.25
	0.69	−0.17	0.22	0.25
[1c]0	0.69	−0.15	0.22	0.24
	0.71	−0.20	0.24	0.25
[1d]0	0.69	−0.17	0.23	0.25b
	0.70	−0.19	0.23	0.26b
[2b]0	0.72	−0.20	0.20	0.26

^aFor each complex, the first entry corresponds to the isomer in which the central CH₂ of the Fe(pdt)Ni core is oriented toward the Fe center, and the second entry corresponds to the isomer in which the same CH₂ is oriented toward the Ni center.

^bFor [1d]⁰, this is the spin density over the CH₃C₅H₄ ligand.

Crystallographic analysis revealed that the structure of [2b]⁰ differs strongly from that of [1a]⁰ (Figure 7). Specifically, the iron center is inverted such that the CO ligand is poised between the iron and nickel centers (eq 3). The CO ligand is not bridging, as indicated by the long Ni–CO distance of 2.878 Å. The DFT-optimized geometry of [2b]⁰ is in good agreement with the crystal structure (Table S8), and the Ni–CO distance is calculated to be 2.916 Å. Furthermore, ν̃_CO for [2b]⁰ is calculated to be 1911 cm⁻¹ for the rotated structure, close to the observed value of 1915 cm⁻¹. A small shoulder at approximately 1900 cm⁻¹ is also observed in the spectrum and may result from the presence of a second rotamer. For [2b]⁰, the isomer in which the CO ligand is apical, as in the structure of [2b]⁺, is calculated to be higher in free energy by 3.70 kcal mol⁻¹ compared to the isomer in which the CO ligand is poised between the iron and nickel centers. This free energy difference is consistent with the crystal structure of [2b]⁰ featuring an inverted iron center.

Figure 7.

Solid-state structure of [2b]⁰ shown at the 50% probability level. Hydrogen atoms and solvent have been omitted for clarity. Selected bond distances (Å): Ni1–Fe1, 2.4594(3); Ni1–centroid, 1.817(2); Ni1–S_avg, 2.3067(5); Fe1–S_avg, 2.2868(5); Fe1–P_avg, 2.1934(5); Fe1–C44, 1.738(2); C44–O1, 1.162(2).

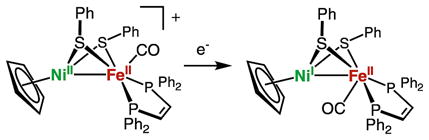(3)

Models for Ni-L: Spectroscopy

The X-band continuous-wave electron paramagnetic resonance (CW-EPR) spectrum of [1a]⁰ is rhombic with g values of 1.991, 2.042, and 2.138. No hyperfine coupling was detected (Figure 8). Spectra of [1b–1d]⁰ are very similar to that of [1a]⁰ (Table 7). The absence of significant ³¹P hyperfine coupling is consistent with a nickel-centered radical, indicating that these compounds feature (C₅H₅)Ni^I centers. Large ³¹P hyperfine coupling was observed in related mixed-valence compounds containing iron(I) phosphine centers, e.g., [(CO)₂(PR₃)Fe(pdt)Ni-(diphosphine)]^+.20,28

Figure 8.

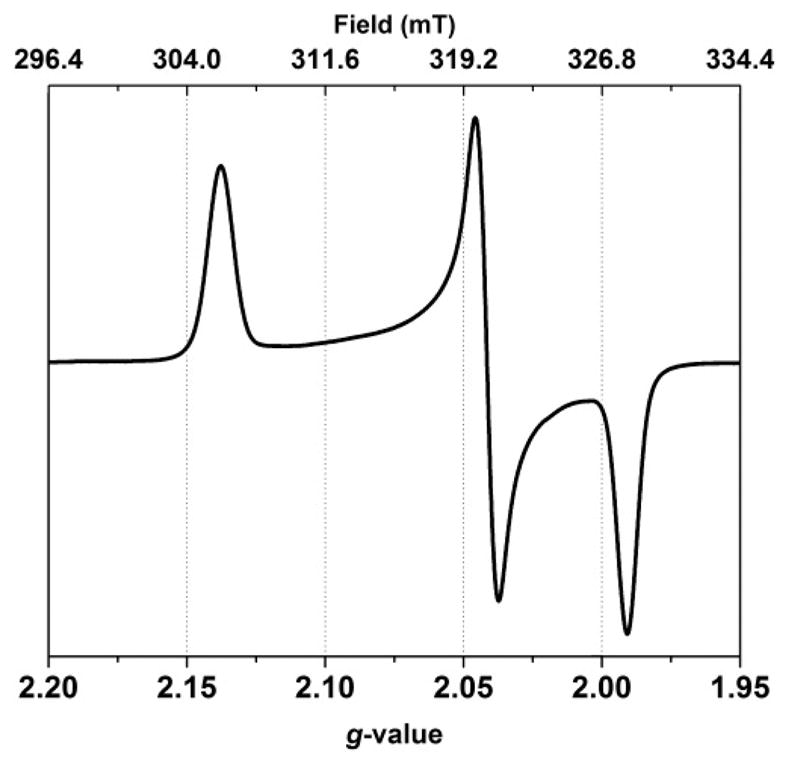
X-band CW-EPR spectrum of a ~2 mM frozen solution of [1a]⁰ in 1:1 CH₂Cl₂/THF (110 K).

Table 7.

EPR Parameters for Compounds [1a–1d]⁰ and [2b]⁰ (Frozen CH₂Cl₂/Toluene Solution at 110 K) and the Ni-L State in Desulfovibrio vulgaris Miyazaki F⁶

compound	g1, g2, g3
[1a]0	1.991, 2.042, 2.138
[1b]0	1.987, 2.042, 2.134
[1c]0	1.997, 2.044, 2.138
[1d]0	1.987, 2.039, 2.130
[2b]0	1.984, 2.039, 2.143
Ni-L1 (D. vulgaris)	2.046, 2.118, 2.296

Q-band ENDOR experiments were conducted to probe the spin distribution in the mixed-valence state. Consistent with the absence of any hyperfine splitting in the EPR spectrum, the ³¹P hyperfine couplings were found to be very small (~11 MHz; Table 8 and Figure S10). Several proton hyperfine contributions were detected using ENDOR spectroscopy with hyperfine splittings ranging from 4 to 11 MHz (Figure S9). The variant of complex [1a]⁰ carrying C₅D₅ ([1a-d₅]⁰) in place of C₅H₅ afforded a greatly simplified ¹H ENDOR pattern with the largest proton coupling (~11 MHz) being absent (Figure S8), indicating that the spin density is localized on the nickel and its immediate coordination sphere. The weaker ¹H couplings observed for [1a-d₅]⁰ are assigned to two equivalent methylene protons of pdt²⁻. These observations are consistent with DFT analysis, which shows that the spin density in [1a]⁰ and [2b]⁰ is primarily localized on the (C₅H₅)Ni(pdt) center (Figure 6 and Table 6). Despite the different stereochemistry at iron, at least in the solid state, and the presence of SPh⁻ versus R₂pdt²⁻, the EPR spectra of all mixed-valence compounds are similar.

Table 8.

Hyperfine Couplings in [1a]⁰ from Q-Band ENDOR and Applied Field Mössbauer Measurements

nucleus	HFI expt (MHz)
	A1	A2	A3
C51H5	−4.86	+3.25	−11.25
CH2(C1H2S)2	7.3	4.4	4.36
31P	11.1	11.3	12.7
57Fe	−3.8	−0.73	−0.9

The [1a-d₅]⁰ orientation-selective ENDOR patterns (Figure S8) could be simulated with one proton hyperfine interaction (originating from two equivalent pdt²⁻ methylene protons). Although, in principle, up to eleven protons [C₅H₅ + CH₂(CH₂S)₂] could contribute to the ¹H ENDOR spectra of [1a]⁰, only one additional contribution, assigned to the (C₅H₅) ligand, could be distinguished and evaluated (see Figure S9). It can be assumed that the proton(s) with their hyperfine tensors approximately aligned with the g-tensor axes lead to the strongest contributions along these axes in the orientation-selective ENDOR spectra. The hyperfine tensors of the C₅H₅ protons that are not aligned with the g-tensor axes give rise to additional weaker features in the ENDOR spectra (Figure S9), which have not been simulated. The simulation parameters of the C₅H₅⁻ and pdt²⁻ (CH₂S) contributions are given in Table 8.

The measured Mössbauer spectra of [1a–1c]⁰ and the corresponding cations are quite similar (see Figures S1–S6). All exhibit low isomer shifts of δ = 0.11–0.14 mm s⁻¹ and small quadrupole splittings of ΔE_q = 0.72–1.15 mm s⁻¹ (Table 9). The Mössbauer data are in agreement with a low-spin iron in all complexes. Consistent with other data in this paper, the spectra support the oxidation-state assignments of Ni^IIFe^II for compounds [1a–1c]BF₄ and Ni^IFe^II for compounds [1a–1c]⁰. The isomer shifts observed in the Ni^IFe^II compounds [1a–1c]₀ are larger than the shift observed for the Ni^IIFe^I compound [(dppe)Ni(pdt)Fe(CO)₃]BF₄ (δ = 0.04 mm s⁻¹), while the quadrupole splittings are comparable (ΔE_q = 0.57).²⁰ Mössbauer data for the [NiFe]-hydrogenases are sparse and suffer from difficulties in identifying and correcting for the dominating subspectra of the accessory FeS clusters.^37,38 Isomer shifts in the range of 0.05–0.15 mm s⁻¹ have been assigned to the iron center of the [NiFe] center.³⁹

Table 9.

Mössbauer Parameters for Compounds [1a–1c]BF₄, [1a–1c]⁰, and Ni-SI_a in Regulatory Hydrogenase (RH) from Ralstonia eutropha

compound	δ (mm s−1)	ΔEqa (mm s−1)	η
[1a]BF4	0.11	1.15	0.13
[1b]BF4	0.11	1.10
[1c]BF4	0.12	0.87
[1a]0	0.14	−0.73
[1b]0	0.13	−0.72
[1c]0	0.13	−0.76
Ni-SIa RH (R. eutropha)86	0.10	1.60

^aΔE_q signs for [1a–1c]⁰ are obtained from magnetic Mössbauer spectra.

The Mössbauer spectrum of [1a]⁰ was further examined at high magnetic fields. This spectrum shows a very weak internal field contribution with an isotropic ⁵⁷Fe hyperfine coupling of 2 MHz (Table 8 and Figure S7). For comparison, magnetic Mössbauer spectra of the Fe^I center in the H_ox state of the [FeFe]-hydrogenase indicate ⁵⁷Fe hyperfine couplings in the range of 10–20 MHz.^40,41 The weak coupling is consistent with the spin being localized on the nickel center.

Electronic Structure Analysis

The geometries of the various species were optimized using DFT/BP86 and compared to the available experimental data to further probe the electronic structures of [1a–1d]⁺ and [1a–1d]⁰. The optimized geometries are in good agreement with the X-ray crystal structures. Relevant bond lengths for [1a]⁺ and [1a]⁰ are compared in Table 5. The BF₄⁻ counterions were not included in the geometry optimizations, which may introduce minor discrepancies between the X-ray crystal and DFT-optimized structures. Comparisons between the DFT and X-ray crystal structures for species [1b–1d]⁺ and [2b]⁰, as well as structural and energetic information for all systems studied, are provided in Tables S4–S8. Moreover, the CO stretching frequencies (ν̃_CO) calculated with DFT are also in good agreement with the experimental data (Tables 2 and 4).

The short Ni–Fe distances in both [1a]⁺ and [1a]⁰ suggest the presence of metal–metal bonding interactions. According to previous analyses, such Ni–Fe bonds typically arise from overlap of the d_z² orbitals.^21,42,43 Interestingly, however, the nature of the Ni–Fe bonding is quite different between [1a]⁺ and [1a]⁰, as revealed by analysis of the bonding molecular orbitals (MOs) localized using the Pipek–Mezey criteria.⁴⁴ For [1a]⁺, the bonding orbital (Figure 9, left) reveals a dative Ni → Fe two-center, two-electron bond, which resembles a Lewis acid–base-type interaction between the d⁸ Ni^II and d⁶ Fe^II centers. In contrast, for [1a]⁰, a more covalent two-center, two-electron bond is present (Figure 9, right), in which the Ni and Fe d_z² orbitals contribute equally to the bonding orbital. An alternative bonding analysis using natural bond orbitals (NBOs)⁴⁵ is provided in the Supporting Information (pp S38–S40). The formation of a stronger σ bond in [1a]⁰ is consistent with the experimentally observed contraction of the Ni–Fe bond distance from 2.51 Å in [1a]⁺ to 2.46 Å in [1a]⁰. This Ni–Fe bond-length contraction is also found in the DFT-optimized structures (Table 5). These chemical bonding patterns are similar for [2b]⁺ and [2b]⁰ (Figure S58), indicating that the stereochemistry at iron and the presence of SPh⁻ or R₂pdt²⁻ does not disrupt the Ni–Fe bond.

Figure 9.

Pipek–Mezey localized MOs showing the Ni–Fe σ bonds in [1a]⁺ and [1a]⁰. The composition of the MO in [1a]⁺ is 85% nickel and 15% iron, and the composition of the MO in [1a]⁰ is 53% nickel and 47% iron. Only the α orbital is shown for [1a]⁰; however, the β orbital is similar.

Protonation of Ni-L Model

Upon treatment with ≥1 equiv of acid, solutions of [1a]⁰ liberate H₂ and afford the formation of [1a]⁺ (eq 4).

$$\underset{{[\mathbf{1}\mathbf{a}]}^0}{[({\mathrm{C}}_5{\mathrm{H}}_5)\text{Ni}(\text{pdt})\text{Fe}(\text{CO})(\text{dppe})]}+{\mathrm{H}}^{+}\to \underset{{[\mathbf{1}\mathbf{a}]}^{+}}{{[({\mathrm{C}}_5{\mathrm{H}}_5)\text{Ni}(\text{pdt})\text{Fe}(\text{CO})(\text{dppe})]}^{+}}+\frac{1}{2}{\mathrm{H}}_2$$ (4)

H₂ evolution was observed for HBF₄, p-toluenesulfonic acid (pK_a^MeCN = 8.01), and [pyridinium]BF₄ (pK_a^MeCN = 12.33) but not for [NH₄]PF₆ (pK_a^MeCN = 14.46). With HBF₄, the yield of H₂ was 0.44 equiv, as assayed by gas chromatography. With [1a]⁰ functioning as a one-electron reductant, 0.5 equiv would be predicted.

Protonolysis of [1a]⁰ to give [1a]⁺ entails the conversion of an S = ¹/₂ precursor to an S = 0 product, which implicates a multistep process involving electron transfer. We anticipated that protonation of [1a]⁰ would afford [(C₅H₅)Ni(pdt)HFe-(CO)(dppe)]⁺ ([H1a]⁺), a Ni^III–Fe^II species (see the DFT section below). However, hydrides were not obtained experimentally; rather, only [1a]⁺ was obtained. To explain this result, [H1a]⁺ is proposed to undergo reduction by its conjugate base [1a]⁰, giving [H1a]⁰, which, in turn, undergoes protonolysis to give [1a]⁺. Similarly, we found that protonation of [2b]⁰ afforded [2b]⁺. The proposed sequence of reactions is summarized in Scheme 1.

Scheme 1.

Proposed H₂ Evolution Mechanism

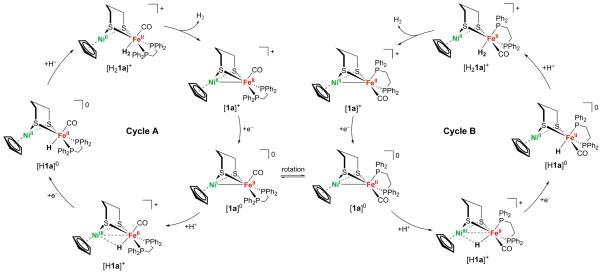
In the presence of excess acid, [1a]^0/+ is a formal, albeit slow, electrocatalyst for H₂ evolution. Using trifluoroacetic acid, the catalytic current is observed at −1.16 V, corresponding to the [1a]^+/0 couple, with an acid-independent rate⁴⁶ of ca. 4 s⁻¹ (Figure S32). Because the hydride intermediates could not be characterized, they were analyzed with DFT in the context of the mechanism for H₂ evolution. Additionally, the exclusive observation of the dibasal intermediate prompted theoretical investigation of an apical–basal isomer. These calculations provide insight into the structure and bonding of the nickel(III) hydride intermediate and also predict the occurrence of two parallel catalytic cycles involving isomers of [1a]⁰. Similar bimetallic hydrides have been known to adopt different isomers.^22,47 Furthermore, recent work suggests that the protonation of (dppe)Ni(pdt)-Fe(CO)₃ proceeds via an unobserved isomer.²¹

According to the calculations, the dibasal and apical–basal isomers of [1a]⁰ are nearly isoergic (ΔG° = +0.48 kcal mol⁻¹) and interconvert via a relatively low free energy barrier, ΔG^ǂ = 11.76 kcal mol⁻¹ (Table 11); however, all other protonation and oxidation states have a much higher barrier for isomerization (ΔG > 20 kcal mol⁻¹). This result prompted the investigation of two parallel pathways for H₂ evolution, labeled A and B in Figure 10.

Table 11.

Calculated Reaction Free Energies and Free Energy Barriers (kcal mol⁻¹) for Isomerization of Dibasal to Apical–Basal Isomers for [1a]⁰ and Its Derivatives in the Proposed Catalytic Cycle^a,^b,^c

compound	ΔG°	ΔGǂ
[1a]0	0.48	11.76
[H1a]+	2.21	20.84
[H1a]0	5.18	25.64
[H21a]+	9.86	30.03
[1a]+	2.03	21.54

^aSee Figure 10 for structures of all species.

^bFor the isomerization considered here, the central CH₂ of the Fe(pdt)Ni core is oriented toward the nickel center. The calculated values corresponding to the cases where the same CH₂ is oriented toward the iron center are provided in Table S9.

^cThe potential energy surface was found to be relatively flat along the isomerization pathway, leading to relatively small imaginary frequencies for the TSs.

Figure 10.

Proposed mechanism for H₂ production proceeding through two isomers. Cycle A, on the left, proceeds through structures in which the dppe ligand is in the dibasal position. Cycle B, on the right, proceeds through structures in which the dppe ligand spans apical–basal positions. Isomerization of [1a]⁰, which has the lowest free energy barrier, could lead to a transition between cycles A and B.

These pathways are initiated by protonation of isomers of [1a]⁰ that differ in terms of the stereochemistry of the (pdt)Fe(dppe)(CO) site. The adoption of the apical–basal isomer does not disrupt the Ni–Fe σ bond (Figure S56) or the localization of the unpaired spin density (Table 10 and Figure S57). The isomerization from the dibasal to the apical–basal configuration is expected to occur only for the [1a]⁰ species because the calculated ΔG^ǂ values for the analogous isomerization for all other intermediates in the catalytic cycle shown in Figure 10 are greater than 20 kcal mol⁻¹ (Table 11). DFT analysis revealed that the transition state (TS) for this isomerization disrupts the metal–metal bonding (Supporting Information, p S41). For [1a]⁰, the TS is best described as Ni^IIFe^I, while the TS is Ni^IIFe^II in [1a]⁺. The lower isomerization barrier for [1a]⁰ is attributed to the greater stability of five-coordinated Fe^I compared to five-coordinated Fe^II.

Table 10.

Spin Densities and Bond Lengths (Å) of [1a]⁰, [H1a]⁺, and [H1a]^{0 a}

	[1a]0		[H1a]+		[H1a]0
	isomer A	isomer B	isomer A	isomer B	isomer A	isomer B
ρ(Ni)	0.71	0.70	0.45	0.42	0.00	0.00
ρ(Fe)	−0.19	−0.16	0.24	0.29	0.00	0.00
ρ(2S)	0.23	0.23	0.12	0.09	0.00	0.00
ρ(C5H5)	0.25	0.23	0.18	0.16	0.00	0.00
d(Ni–Fe)	2.53	2.47	2.60	2.59	3.01	2.85
d(Ni–H)	n/a	n/a	1.80	1.79	2.44	2.05
d(Fe–H)	n/a	n/a	1.61	1.58	1.54	1.53

^aFor these calculations, the central CH₂ of the Fe(pdt)Ni core is oriented toward the nickel center. An analogous table for the cases where the same CH₂ is oriented toward the iron center is provided in the Table S10.

The first step in the catalytic cycle produces isomers of [H1a]⁺. In both isomers, the unpaired electron is localized mainly in the nickel coordination sphere (Table 10), indicating that these species are best described as Ni^IIIHFe^II, analogous to the Ni-C state in the enzyme. Moreover, the DFT-optimized structure of [H1a]⁺ reveals that the hydride is more closely bound to iron than to nickel.

Subsequent to its formation, [H1a]⁺ is reduced by a second 1 equiv of [1a]⁰ to form [1a]⁺ and the nickel(II)–iron(II) hydride [H1a]⁰. This electron transfer is proposed to occur spontaneously on the basis of the calculated reduction potential of [H1a]⁺, which is less negative than the calculated reduction potential of [1a]⁺ by 0.16 (cycle A) and 0.03 V (cycle B) versus Fc^+/0 in CH₂Cl₂. Reduction to form [H1a]⁰ mainly affects the nickel center and results in significant elongation of the Ni–H distance by 0.64 and 0.26 Å for the A and B isomers, respectively. Thus, [H1a]⁰, which would be analogous to the Ni-R state of the enzyme, is more accurately described as a semiterminal iron(II) hydride than a bridging hydride.

The catalytic cycle closes with the protonation of [H1a]⁰ to produce the H₂-adduct intermediate, [H₂1a]⁺, followed by the release of H₂ from [H₂1a]⁺ to generate [1a]⁺. Although the two cycles are very similar energetically, the calculations predict that this protonation is thermodynamically less favorable for the apical–basal isomer [H1a^B]⁰ than for the dibasal isomer [H1a^A]⁰ by ~5 kcal mol⁻¹.

In light of these computational results, additional experiments were performed to probe for the presence of two isomers in the catalytic cycle. The calculated ν̃_CO values for [1a^A]⁰ and [1a^B]⁰ are 1901 and 1904 cm⁻¹, respectively, and the calculated ν̃_CO values for [1a^A]⁺ and [1a^B]⁺ are 1946 and 1949 cm⁻¹, respectively. The calculated ν̃_CO values for all intermediates in the catalytic cycles are provided in Table S11. These small calculated ν̃_CO differences between the isomers are within the numerical accuracy of DFT. As previously mentioned, solutions of [1a]⁺, which were synthesized directly, were confirmed crystallographically and spectroscopically to exist only in the dibasal geometry. However, the preparation of [1a]⁺ by the addition of excess acid to [1a]⁰, presumably going through the catalytic cycle(s) to generate H₂, produced a solution containing both isomers of [1a]⁺. The ³¹P NMR spectrum of the [1a]⁺ solution obtained after presumably proceeding through the catalytic cycle(s) displayed two ³¹P NMR signals, one assigned to the dibasal isomer (cycle A), in which the two ³¹P centers are equivalent, and the other assigned to the apical–basal isomer (cycle B), in which the two ³¹P centers are equilibrated by the rocking motion shown in Figure 11. The free energy barrier to this rocking motion is calculated to be relatively low, ΔG^ǂ = 9.5 kcal mol⁻¹, and the ³¹P NMR spectrum of the isomer mixture was unchanged when recorded at −100 °C, consistent with a relatively low free energy barrier. These analyses support the proposal that H₂ evolution can proceed via either cycle A or cycle B shown in Figure 10, thereby producing both isomers of [1a]⁺.

Figure 11.

Representation of the iron-centered rocking motion in [1a^B]⁺.

CONCLUSIONS

Experiment and theory indicate that the new complexes reported in this paper replicate aspects of the following enzyme states: Ni-SI_a, Ni-L, Ni-C, and Ni-R. Two of these species, the Ni^IIFe^II and Ni^IFe^II derivatives, were crystallized and fully characterized. The other two species are implicated in a H₂ evolution experiment and characterized computationally.

The Ni-SI_a state is distinguished by the Ni^IIFe^II bimetallic core and the absence of a third bridging ligand, features that are replicated in compounds [1a–1d]BF₄. The Ni-L state is distinguished by the formal Ni^IFe^II oxidation states, a feature that is replicated in [1a–1d]⁰. The oxidation state assignments are supported by EPR and Mössbauer spectroscopic data, crystallographic results, voltammetric measurements, and DFT calculations.

The previous attempts to model states with Ni^IIFe^II cores suffered from the presence of six-coordinated iron centers.^17,48 The Ni^IIFe^II models reported in this paper, in fact, arise via such FeL₄(μ-SR)₂-containing intermediates, which undergo decarbonylation. DFT analysis of the bonding suggests that decarbonylation is driven by formation of the Ni–Fe bond. Although [1a–1d]⁺ and [2b]⁺ are reasonable spectroscopic models for the Ni-SI_a state of the enzyme, challenges remain. In the Ni-SI_a state, the nickel center binds CO to give Ni-SI_a^CO.6,49 In contrast, [1a–1d]⁺ exhibit no detectable affinity for CO. Substitution of the dithiolate bridge with bridging monothiolates, as in [2b]⁺, facilitates the binding of CO at iron. In contrast, the enzyme binds CO at nickel. This difference is understandable because the (C₅H₅)Ni(μ-SR)₂ site has a higher electron count than the (RS)₂Ni(μ-SR)₂ site found in the enzyme. Replicating terminal thiolate ligation at nickel remains one of the central challenges in this area.⁵⁰

The first attempts to model the mixed-valence active site of the Ni-L state focused on [(CO)₂LFe(pdt)Ni-(diphosphine)]^+.20,28 These cations are described as Ni^IIFe^I, which is reversed from the Ni^IFe^II states assigned in Ni-L. More recently, we have characterized complexes with the configuration Ni^IRu^II, wherein the Ru^II center is redox-inactive.⁵¹ In this work, the Fe(CO)₂(PR₃) center in previous Fe–Ni models was replaced by a Fe(CO)(PR₃)₂ center, which stabilizes the Fe^II state, as illustrated by [1a–1d]⁰ and [2b]⁰.

Because they are substrates, hydrogenic ligands are a major focus in research concerning the hydrogenases and their models.^52,53 The DFT-optimized analysis of the nickel(III)–iron(II) hydride [H1a]⁺ reveals that the unpaired electron is localized mainly in the nickel coordination sphere, as seen for Ni-C. In the model, the hydride ligand is more closely bound to iron than to nickel [Δ(M–H) ~ 0.2 Å]. This report is the first suggestion of the accessibility of such a state in [NiFe]-hydrogenase model complexes. In the enzyme, proton-transfer reactions are coupled to electron-transfer reactions,¹⁶ and a similar effect is seen in the reduction of [H1a]⁺ by [1a]⁰. The resulting nickel(II)–iron(II) hydride [H1a]⁰, analogous to the Ni-R state of the enzyme, reacts with proton sources to liberate H₂. Although thwarting efforts to isolate this hydride, this facile protonolysis is analogous to the behavior of the Ni-R/Ni-SI pair.¹⁶ According to our calculations, the nickel(II)–iron(II) hydride is more accurately described as a terminal iron(II) hydride than a bridging hydride. In contrast, high-resolution X-ray crystallographic analysis of Ni-R from D. vulgaris reveals Ni–H and Fe–H distances of 1.58 and 1.78 Å (error 0.08 Å), respectively; i.e., the hydride is more closely associated with nickel.¹⁶ The structural difference between the model complex and the protein may reflect the influence of terminal thiolate ligands on nickel.⁵⁰

EXPERIMENTAL SECTION

Reactions and manipulations were performed using standard Schlenk techniques at room temperature or in a nitrogen atmosphere glovebox. Solvents were HPLC-grade and dried by filtration through activated alumina or distilled under nitrogen over an appropriate drying agent. Bu₄NPF₆ (GFS Chemicals, Columbus, OH) was recrystallized multiple times from a CH₂Cl₂ solution by the addition of hexane. Chromatography was performed using Siliflash P60 from Silicycle (230–400 mesh). ESI-MS data for compounds were acquired using a Waters Micromass Quattro II spectrometer. ¹H NMR spectra (500 MHz) were referenced to residual solvent relative to tetramethylsilane. ³¹P{¹H} NMR spectra (202 MHz) were referenced to external 85% H₃PO₄. Fourier transform infrared (FT-IR) spectra were recorded on a PerkinElmer 100 FT-IR spectrometer. Crystallographic data for compounds [1a]⁰, [1c]⁰, [2b]⁰, and [2b]BF₄ were collected using a Siemens SMART diffractometer equipped with a Mo Kα source (λ = 0.71073 Å), and crystallographic data for compounds [1a]BF₄ and [1d]BF₄ were collected using a Bruker D8 Venture diffractometer equipped with a Mo Kα microfocus source and a Photon 100 detector. X-band EPR spectra were recorded on a Varian E-line 12″ Century Series X-band continuous-wave spectrometer. Q-band ENDOR spectra were recorded on a Bruker Elexsys E580 Q-band pulse EPR spectrometer using a home-built pulse Q-band ENDOR resonator⁵⁴ and an ENI 300L RF amplifier. Cryogenic temperatures were achieved using a Cryogenic Ltd. closed-cycle cryostat. ENDOR simulations and spectral fits were performed using EasySpin (“salt”)⁵⁵ and home-written scripts in Matlab. Mössbauer spectra were recorded on an alternating constant-acceleration spectrometer. The minimum experimental line width was 0.24 mm s⁻¹ (full width at half-maximum). The sample temperature was maintained constant in either an Oxford Variox or an Oxford Mössbauer-Spectromag cryostat. The latter is a split-pair conducting magnet system for applying fields of up to 8 T to the samples that can be kept at temperatures in the range 1.5–250 K. The field at the sample is perpendicular to the γ-ray beam. Isomer shifts are quoted relative to metallic iron at 300 K. Mössbauer spectra were simulated with a home-written spin-Hamiltonian program based on the usual nuclear Hamiltonian formalism.³⁷

[(C₅H₅)₃Ni₂]BF₄, [(MeC₅H₄)₃Ni₂]BF₄, and [(C₅D₅)₃Ni₂]BF₄

In a modification of Werner’s procedure,⁵⁶ a solution of nickelocene (2.08 g, 11.0 mmol) in Et₂O (150 mL) was treated dropwise with an excess of HBF₄·Et₂O (2 mL, 13.8 mol). Over the course of several minutes, a purple solid precipitated from a pale yellow solution. The solid was collected by filtration and washed thoroughly with ether. Yield: 2.07 g (95%). ¹H NMR (nitromethane-d₃): δ 5.48 (10H, s), 4.80 (5H, s). ¹³C{¹H} NMR (nitromethane-d₃): δ 87.8, 56.6.

[(C₅H₅)Ni(pdt)Fe(dppe)(CO)]BF₄ ([1a]BF₄)

To a solution of [(C₅H₅)₃Ni₂]BF₄ (498 mg, 1.24 mmol) in CH₃NO₂ (50 mL) was added a solution of Fe(pdt)(dppe)(CO)₂²² (771 mg, 1.25 mmol) in CH₃NO₂ (25 mL). After 30 min, the slurry converted to a dark-red solution. Solvent was removed under reduced pressure, and the residue was washed several times with pentane until the filtrate was colorless. The residue was extracted into a minimal volume of CH₂Cl₂ and subjected to column chromatography. Byproducts elute with 100% CH₂Cl₂. The product eluted with 90:10 CH₂Cl₂/THF as a dark-red band. The solvent was removed under reduced pressure to yield a dark-red solid. Yield: 841 mg (85%). ¹H NMR (acetone-d₆): 8.01 (m, 4H), 7.5 (m, 16H), 4.75 (s, 5H, C₅H₅), 3.83 (m, 2H, PCH₂CH₂P), 3.62 (m, 2H, PCH₂CH₂P), 2.83 (m, 3H), 2.43 (m, 2H), 1.66 (m, 1H, S₂CH₂CH₂CH₂S₂). ³¹P{¹H} NMR (acetone-d₆): δ 77.1. ESI-MS: m/z 711 ([M]⁺), 683 ([M – CO]⁺). IR (CH₂Cl₂): ν̃_CO 1943 cm⁻¹ (THF). Anal. Calcd for C₃₅H₃₅FeNiOP₂S₂ (found): C, 52.61 (52.67); H, 4.42 (4.70). Single crystals of [1a]BF₄ were obtained by vapor diffusion of pentane into THF solutions.

[(C₅H₅)Ni(pdt)Fe(dppv)(CO)]BF₄ ([1b]BF₄)

Compound [1b]BF₄ was prepared in a fashion similar to that of [1a]BF₄ using Fe(pdt)(dppv)(CO)₂²² as the iron reagent. Yield: 66%, dark-red powder. ¹H NMR (CH₂Cl₂): δ 8.44 (m, 2H, PCHCHP), 7.91 (br, 4H), 7.54 (s, br, 4H), 7.45 (s, br 12H), 4.31 (s, 5H, C₅H₅), 2.77 (m, 3H) 2.36 (m, 2H), 1.69 (m, 1H, S₂CH₂CH₂CH₂S₂). ³¹P{¹H} NMR (CH₂Cl₂): δ 83.8. ESI-MS: m/z 709 ([M]⁺), 681 ([M – CO]⁺). IR (CH₂Cl₂): ν̃_CO 1951 cm⁻¹.

[(C₅H₅)Ni(Me₂pdt)Fe(dppe)(CO)]BF₄ ([1c]BF₄)

Compound [1c]BF₄ was prepared in a fashion similar to that of [1a]BF₄ using Fe(Me₂pdt)(dppe)(CO)₂²² as the iron source. Yield: 77%, dark-red powder. ¹H NMR (CH₂Cl₂): δ 7.77 (m, 4H), 7.46 (m, 16), 4.46 (s, 5H, C₅H₅), 3.65 (m, 2H, PCH₂CH₂P), 3.11 (m, 2H PCH₂CH₂P), 2.71 (m, 2H, S₂CH₂CMe₂CH₂S₂), 2.17 (m, 2H, S₂CH₂CMe₂CH₂S₂), 1.50 (s, 3H, S₂CH₂CMe₂CH₂S₂), 1.19 (s, S₂CH₂CMe₂CH₂S₂). ³¹P{¹H} NMR (CD₂Cl₂): δ 75.1. ESI-MS: m/z 739 ([M]⁺), 711 ([M – CO]⁺). IR (CH₂Cl₂): ν̃_CO 1940 cm⁻¹. Single crystals of [1c]BF₄ were obtained by evaporation of concentrated THF solutions.

[(CH₃C₅H₄)Ni(pdt)Fe(dppe)(CO)]BF₄ ([1d]BF₄)

Compound [1d]BF₄ was prepared in a similar fashion to [1a]BF₄ using the [(CH₃C₅H₄)₃Ni₂]BF₄ as the nickel source and Fe(pdt)(dppe)(CO)₂ as the iron source. Yield: 81%, dark-red powder. ¹H NMR (CH₂Cl₂): δ 7.80 (br, 4H) 7.52 (br, 4H) 7.43(br, 12H), 4.67 (br, 1H) 3.91 (br, 1H), 3.82 (s, 3H), 3.43 (m, 2H, PCH₂CH₂P), 3.05 (m, 2H, PCH₂CH₂P), 3.05 (m, 3H), 2.31 (m, 2H), 1.89 (br, 2H), 1.75 (m, 1H, S₂CH₂CH₂CH₂S₂). ³¹P{¹H} NMR (CD₂Cl₂): δ 79.2. ESI-MS: m/z 725 ([M]⁺), 697 ([M – CO]⁺). IR (CH₂Cl₂): ν̃_CO 1943 cm⁻¹.

[(C₅D₅)Ni(pdt)Fe(dppe)(CO)]BF₄ ([1a]BF₄-d₅)

Compound [1a]BF₄-d₅ was prepared in a fashion similar to that of [1a]BF₄ using [(C₅D₅)₃Ni₂]BF₄ as the nickel source. The product was characterized by ESI-MS, which indicated >95% deuteration (see the Supporting Information).

Fe(SPh)₂(CO)₂(dppv)

This compound was synthesized in a fashion similar to that of the published procedure.⁵⁷ To a mixture of FeSO₄·7H₂O (1.112g, 4.0 mmol) and dppv (1.584 g, 4.0 mmol) in MeOH (80 mL) was added dropwise a solution of PhSNa (1.056 g, 8.0 mmol) in MeOH (20 mL) with stirring under the presence of CO. After stirring for 6 h at room temperature, the solvent was removed under reduced pressure. The residue was extracted with CH₂Cl₂ (40 mL). After filtration to remove Na₂SO₄, the extract was concentrated (15 mL) and diluted with hexane (50 mL). Cooling this mixture at −20 °C for 12 h gave a red solid. Yield: 2.23 g (77%). ¹H NMR (CD₂Cl₂): δ 6.85–8.03 (32H, m). ³¹P{¹H} NMR (CD₂Cl₂): δ 81.9 (d, J = 55 Hz), 61.1 (d, J = 55 Hz). IR (CH₂Cl₂): ν̃_CO 2023, 1978 cm⁻¹.

[(C₅H₅)Ni(SPh)₂Fe(dppv)(CO)₂]BF₄ ([2bCO]BF₄)

To a solution of [(C₅H₅)₃Ni₂]BF₄ (200 mg, 0.5 mmol) in CH₃NO₂ (15 mL) was added a solution of Fe(SPh)₂(dppv)(CO)₂ (364 mg, 0.5 mmol) in CH₃NO₂ (10 mL). After 30 min, the slurry converted to a dark-red solution. Solvent was removed under reduced pressure, and the residue was washed with pentane until the filtrate was colorless. The residue was extracted into a minimal volume of CH₂Cl₂ and subjected to column chromatography. After eluting impurities with 100% CH₂Cl₂, the product eluted with 90:10 CH₂Cl₂/THF as a dark-red band. The solvent was removed under reduced pressure to yield a dark-red solid. Yield: 380 mg (81%). ¹H NMR (CD₂Cl₂): δ 6.85–8.57 (32H, m), δ 4.46 (5H, s). ³¹P{¹H} NMR (CD₂Cl₂): δ 75.9 (d, J = 45 Hz), 64.2 (d, J = 45 Hz). ESI-MS: m/z 849 ([M]⁺), 821 ([M – CO]⁺), 793 ([M – 2CO]⁺). IR (CH₂Cl₂): ν̃_CO 2042, 2002 cm⁻¹. Anal. Calcd for C₄₅H₃₇BF₄FeNiO₂P₂S₂·CH₂Cl₂ (found): C, 54.05 (53.69); H, 3.85 (3.72). Single crystals of [2bCO]BF₄ were obtained by solvent diffusion of pentane into CH₂Cl₂ solutions.

[(C₅H₅)Ni(SPh)₂Fe(dppv)(CO)]BF₄ ([2b]BF₄)

To a solution of [2bCO]BF₄ (280 mg, 0.3 mmol) in CH₂Cl₂ (30 mL) was added Me₃NO·2H₂O (34 mg, 0.3 mmol). After 1 h, the solvent was removed under reduced pressure, and the residue was washed several times with pentane. The residue was extracted into a minimal volume of CH₂Cl₂ (5 mL), pentane (30 mL) was added, and the mixture was cooled to −20 °C. The product was collected as a black powder. Yield: 200 mg (74%). ³¹P{¹H} NMR (CD₂Cl₂): δ 78.8. ESI-MS: m/z 821 ([M]⁺), 793 ([M – CO]⁺). IR (CH₂Cl₂): ν̃_CO 1956 cm⁻¹. Anal. Calcd for C₄₄H₃₇BF₄FeNiOP₂S₂·0.5CH₂Cl₂ (found): C, 56.16 (56.08); H, 4.02 (4.19).

(C₅H₅)Ni(pdt)Fe(dppe)(CO) ([1a]⁰)

To a stirred solution of [1a]BF₄ (21.2 mg, 26.5 μmol) in THF (3 mL) was added cobaltocene (5.8 mg, 30.7 μmol) in THF (3 mL). The solution immediately darkened, and solid [(C₅H₅)₂Co]BF₄ precipitated. The solvent is removed under reduced pressure, and the product was extracted into toluene (2 mL). The slurry was filtered through diatomaceous earth to yield a homogeneous, brown-black solution. The product is crystallized upon the addition of pentane (15 mL). Yield: 17.0 mg (90%), black powder. Single crystals were obtained by vapor diffusion of pentane into concentrated toluene solutions. IR (CH₂Cl₂): ν̃_CO 1901 cm⁻¹. Anal. Calcd for C₃₅H₃₅FeNiOP₂S₂ (found): C, 59.02 (58.72); H, 4.95 (4.65).

(C₅H₅)Ni(pdt)Fe(dppv)(CO) ([1b]⁰)

Compound [1b]⁰ was prepared in a fashion similar to that of [1a]⁰. Yield: 86%, black powder. IR (CH₂Cl₂): ν̃_CO 1903 cm⁻¹.

(C₅H₅)Ni(Me₂pdt)Fe(dppe)(CO) ([1c]⁰)

Compound [1c]⁰ was prepared in a fashion similar to that of [1a]⁰. Yield: 87%, black powder. IR (CH₂Cl₂): ν̃_CO 1897 cm⁻¹.

(CH₃C₅H₄)Ni(pdt)Fe(dppe)(CO) ([1d]⁰)

Compound [1d]⁰ was prepared in a fashion similar to that of [1a]⁰. Yield: 80%, black powder. IR (CH₂Cl₂): ν̃_CO 1898 cm⁻¹.

(C₅D₅)Ni(pdt)Fe(dppe)(CO) ([1a-d₅]⁰)

Compound [1a-d₅]⁰ was prepared in a fashion similar to that of [1a]⁰.

(C₅H₅)Ni(SPh)₂Fe(dppv)(CO) ([2b]⁰)

Compound [2b]⁰ was prepared in a fashion similar to that of [1a]⁰. Yield: 61%, black powder. IR (CH₂Cl₂): ν̃_CO 1915 cm⁻¹. Single crystals of [2b]⁰ were obtained by vapor diffusion of pentane into concentrated toluene solutions.

COMPUTATIONAL METHODS

DFT results reported herein were performed using the BP86 density functional.^58,59 Additional benchmarking was performed using the B3P86,^58,60 BP86-D2,^58,59,61 M06-L,⁶² and ωB97XD^61,63–65 functionals and is presented in Tables S1–S7. The DFT calculations were performed with the Stuttgart pseudopotential and associated basis set of Preuss and co-workers (SDD)⁶⁶ for the nickel and iron centers, the 6-31G** basis set⁶⁷ for the μ-hydrogen ligand, and the 6-31G* basis set^68,69 for all other atoms. The starting geometries for [1a–1d]⁺, [1a]⁰, and [2b]⁰ were obtained from their respective crystal structures. The starting coordinates for species without crystal structures were obtained by manual alteration of the most closely related crystal structure. Solvation free energies were calculated in CH₂Cl₂ using the conductor-like polarizable continuum model (C-PCM)^70,71 with the Bondi atomic radii⁷² and including the nonelectrostatic contributions of dispersion,^73,74 repulsion,^73,74 and cavitation energies.⁷⁵

For the results presented in the main paper, geometry optimizations were performed in the gas phase. However, geometry optimizations were also performed in solution and were found to be consistent with the gas-phase optimizations. A comparison of the structures optimized in the gas and solution phases is provided in Tables S4–S7. In all cases, the minimum-energy structures were confirmed to have no imaginary frequencies. The ν̃_CO frequencies were calculated within the harmonic model. Typically, DFT is more reliable for calculating changes in the frequencies than the absolute frequencies, and often scaling factors dependent on the functional are used.⁷⁶ Herein, however, the absolute ν̃_CO values are reported because the BP86 functional gives excellent agreement with the experimental values without the application of scaling factors. Nonetheless, Δν̃_CO values calculated using different functionals are provided in Table S3. The TSs for isomerization of the Fe(dppe)(CO) subunit were identified using the synchronous transit-guided quasi-Newton method,^77,78 and the TSs were confirmed to have only one imaginary frequency. Each TS was verified to lead to the relevant dibasal or apical–basal isomers by following the intrinsic reaction coordinate using the local quadratic approximation^79,80 for 5–10 steps in the forward and reverse directions and subsequently optimizing the geometries.

Thermochemical data were calculated at T = 298.15 K. All calculated free energies included zero-point energy, entropic contributions, and solvation effects. The reaction free energies (ΔG°) and free energy barriers (ΔG^ǂ) associated with isomerization of the Fe(dppe)(CO) subunit in solution were calculated from the optimized geometries and TSs. The relative reduction potentials were calculated from the corresponding reaction free energies using a methodology described elsewhere.^81–84 Chemical bonding analysis was performed using the Pipek–Mezey localization criteria,⁴⁴ using keyword IOp(4/9=20212), and NBOs.⁴⁵ All calculations were performed using the Gaussian 09 electronic structure program.⁸⁵ Structures and energies of the systems studied herein are provided in Tables S12–S73.