Millimeter-scale epileptiform spike propagation patterns and their relationship to seizures

Abstract

Objective

Current mapping of epileptic networks in patients prior to epilepsy surgery utilizes electrode arrays with sparse spatial sampling (∼1.0 cm inter-electrode spacing). Recent research demonstrates that sub-millimeter, cortical-column-scale domains have a role in seizure generation that may be clinically significant. We use high-resolution, active, flexible surface electrode arrays with 500 μm inter-electrode spacing to explore epileptiform local field potential spike propagation patterns in two dimensions recorded from subdural micro-electrocorticographic signals in vivo in cat. In this study, we aimed to develop methods to quantitatively characterize the spatiotemporal dynamics of epileptiform activity at high-resolution.

Approach

We topically administered a GABA-antagonist, picrotoxin, to induce acute neocortical epileptiform activity leading up to discrete electrographic seizures. We extracted features from local field potential spikes to characterize spatiotemporal patterns in these events. We then tested the hypothesis that two dimensional spike patterns during seizures were different from those between seizures.

Main results

We showed that spatially correlated events can be used to distinguish ictal versus interictal spikes.

Significance

We conclude that sub-millimeter-scale spatiotemporal spike patterns reveal network dynamics that are invisible to standard clinical recordings and contain information related to seizure-state.

1. Introduction

Epilepsy is a disorder characterized by the occurrence of seizures, globally synchronous electrical activity in the brain which disrupts its normal functioning (Fisher et al 2005, Raol and Brooks-Kayal 2012). Clinically, 68% of patients with epilepsy respond well to anti-epileptic drugs, resulting in 32% who are medically refractory and must seek surgery to treat their symptoms (Brodie et al 2012). Surgery is successful in reducing the occurrence of seizures in 44% of medically refractory patients (Schmidt and Stavem 2009). However, surgery is not an option for many patients because either their epileptic network cannot be localized, or consists of multiple wide-spread regions, or because a patient is at high risk for incurring unacceptable neurological or neuropsychological damage (Bien et al 2006). Even when epilepsy surgery is a viable option, the risk of incurring cognitive or psychiatric deficits deters some patients from these irreversible procedures. These facts call for an aggressive push towards advancing our understanding of seizure generation and progression in order to improve surgical techniques and generate alternative therapies (Fisher 1989, Raol and Brooks-Kayal 2012).

The mainstay of research into mechanisms of seizure generation is the use of animal models (Raol and Brooks-Kayal 2012). These models employ chemical convulsants, electrical stimulation, genetic manipulation, induced aberrations of development (febrile seizures, hypoxic-ischemia, etc.), or trauma to produce seizures and epilepsy. Each model targets a specific type of human epilepsy or addresses a specific type of underlying disease mechanism, such as seizure generation, spread, termination, progression, or comorbidities (e.g cognitive dysfunction) (Raol and Brooks-Kayal 2012). Models can be classified as acute, where single or multiple seizures are studied in a single session, to chronic, in which manipulations generate repeated seizures that arise spontaneously over time, often after a latent period. Many of these models generate seizures over hours, repetitively, enabling investigators to carefully study the ictal process and interventions to disrupt it. Topical application of chemoconvulsants, such as picrotoxin on cat neocortex, simulates acute simple partial seizures in intact brains of mammals (Fisher 1989), enabling investigators to study the propagation patterns of local field potential (LFP) spikes leading up to ictal events.

Electroencephalography (EEG) is commonly used to evaluate seizure activity in patients and animal models of epilepsy. EEG voltages result from summed synchronous synaptic activity in the cortical regions under the surface of intracranial recording electrodes and provide insight in the location and classification of seizure activity (Engel et al 2007, Fisher 1989). Prior to epilepsy surgery, clinicians implant intracranial electrocorticography (ECoG) electrodes in order to map the “seizure onset zone,” the “epileptogenic zone” and/or the “seizure focus.” Currently, electrode arrays with a sparse spatial density (0.5-1.0 cm spacing; 0.2-0.4 cm in diameter) are used for these implants (Engel et al 2007). However, as a result of only modest successes when studying non-lesional epilepsies, clinical investigators have begun to question the wide-spread use of EEG and ECoG as the best scale for mapping epileptic networks and their dynamics. Advances in neural electrode technology are enabling brain recordings with increasingly fine spatial resolution. Recent studies have found that sampling at higher spatial resolution reveals seizure-like phenomena not visible with standard clinical arrays and conclude that the optimal electrophysiological scale to observe epileptic networks might require sampling on the sub-millimeter-scale (Stead et al 2010). A number of these studies utilize the Utah array (covering an area of 4 mm × 4 mm) (Campbell et al 1991, Truccolo et al 2011), which records multi-unit activity (MUA) from 100 penetrating microelectrodes spaced 400 μm apart, while others employ standard research subdural grids (covering an area of 3.4 cm × 5.4 cm) that contain up to 112 40-micron diameter microwires in groups of 4 or 16 with 1.0 mm spacing, interspersed between 16-24 macro-electrodes (1.0 cm spacing, 0.4 cm in diameter) to record neuronal spikes and LFP activity (Van Gompel et al 2008). These studies suggest that seizures are generated from dispersed microdomains on the scale of distinct cortical columns (500 μm diameter; comprised of 1,000-10,000 neurons) (Stead et al 2010) or neuronal ensembles of an even smaller scale (∼40 neurons comprising a functional group exhibiting similar peri-ictal activity) (Bower and Buckmaster 2008, Schevon et al 2012, Truccolo et al 2011). Despite this work, a clear picture of a global ictal network process has not emerged. We propose that this is perhaps because sampling is too spatially constrained in multi-unit recordings and too sparse in current LFP studies using conventional ECoG grids.

Our experiments used novel, high-spatial density subdural, non-penetrating, surface active electrode arrays of 360 channels covering an area of 10 mm × 9 mm to measure LFP-scale electrical signals (Viventi et al 2010). The size of each electrode is 300 μm × 300 μm and the interelectrode distance is 500 μm. These electrode arrays provide high spatial and temporal sampling that is lacking in traditional ECoG arrays, and their multiplexed design eliminates the requirement that each contact is individually wired to data recording circuitry. The ability to record LFPs and MUA at these spatial and temporal resolutions provides new opportunities to understand neural dynamics within and among closely spaced areas on the cortical surface of the brain. Modern data analysis techniques, such as feature extraction, dimensionality reduction and clustering, are arguably well suited to augment traditional data-analysis methods, with the goal of obtaining additional information from extremely large data sets and presenting results in an easily interpretable way (Bishop 2006, Mitchell 1997). These techniques include extracting spatiotemporal (ST) features, reducing the dimensionality of feature vectors, and employing unsupervised learning to reveal patterns in large data sets that might otherwise escape detection.

In this study, we leverage the high spatial and temporal resolution in our electrophysiological recordings from an acute in vivo model of epilepsy to interpret the ictal process using modern data analysis techniques. Preliminary results from a small subset of data from Cat 1 (∼14 minutes containing approximately 30% of the detected spikes and two seizures from that data set) have been previously reported by our group (Viventi et al 2011) as one of several demonstrations of the novel array technology presented in that paper. This paper expands our data set, extends our data analysis and provides a detailed description of our algorithm.

2. Methods

This section describes three major areas: (1) an acute in vivo feline model of seizures, (2) data collection and pre-processing with an active, flexible, high-resolution electrode array covering 1.0 cm² of neocortex, and (3) interpretation of the data using feature extraction, dimensionality reduction and clustering algorithms to identify and track two dimensional (2-D) spatiotemporal (ST) patterns associated with epileptiform activity recorded by the array. All experiments were conducted in accordance with the ethical guidelines of the National Institutes of Health and with the approval of the Institutional Animal Care and Use Committee of the University of Pennsylvania.

2.1 Surgical procedures and induction of seizures

Three adult cats were anesthetized with an intraperitoneal injection of nembutal (25-30 mg/kg) and supplemental isoflurane (2-5% in 70% N₂0 and 30% O₂) for 15 minutes while placing an intravenous cannula. Subsequently, the animal was paralyzed with gallamine triethiodide (Flaxedil) and artificially ventilated (end tidal CO₂ held at 3.8-4.0%). A stereotaxic frame was used to stabilize the head of the animal and a craniotomy and durotomy were performed to expose at least a 2 × 3 cm region of cortex. During surgery, the cat received additional nembutal as needed in approximately 5 mg boluses to maintain a stable depth of anesthesia. Following the surgery and for the remainder of the experiment (8-12 h), anesthesia was maintained by continuous infusion of intravenous thiopental or nembutal (3-15 mg/kg-hr). Rate of infusion was adjusted to maintain a surgical plane of anesthesia as defined by assessing the following continuously monitored parameters: a macroscopic EEG recorded from a bone screw inserted in the contralateral hemisphere, heart rate, blood pressure, and pCO₂ (partial pressure of carbon dioxide). Rectal temperature was maintained at 37-38°C.

Picrotoxin, a GABA-A receptor antagonist that blocks inhibition, was applied topically adjacent to the electrode array to induce focal neocortical seizures, as described by Raol and Fisher, to study mechanisms of seizure generation and spread (Fisher 1989, Raol and Brooks-Kayal 2012). Cortical activity was monitored continuously before and after picrotoxin administration. No abnormal electrical spikes were observed prior to picrotoxin administration. Picrotoxin dosage was increased gradually until epileptiform activity (abnormal electrical spikes and seizures from the cortical region covered by the array) was observed. During the Cat 3 experiment, we collected data from two different but overlapping locations on the neocortex yielding two separate data sets from one experiment. Table 1 describes data sets collected for the above experiments. Each experiment spanned 8-12 hours and induced repeated seizures.

Table 1.

Collected data summary.

	Post-Trim File Length (h:m:s)	Number of Spikes	Number of Seizures	Individual Seizure Length (seconds)	Total Time in Seizure (h:m:s (%file length))	Sampling Frequency (Hz)	Array Channel Yield (working/total (% working))
Cat 1	0:53:37	2894	7	5-42	0:02:00 (3.73%)	277.78	295/360 (81.9%)
Cat 2	3:15:30	255	17	16-53	0:08:31 (4.35%)	555.56	318/360 (88.3%)
Cat 3a	4:24:15	14,528	76	6-65	0:39:06 (14.8%)	925.93	294/360 (81.6%)
Cat 3b	0:37:49	8,654	23	7-70	0:15:50 (41.9%)	925.93	294/360 (81.6%)
Total	9:11:11	26,331	123	n/a	1:05:27 (11.9%)	n/a	n/a

Post-Trim File Length is the length of the file after segments of noise were clipped. Seizures were marked by a board-certified epileptologist and were defined to be at least 5 seconds in length. Spikes were detected via a threshold detector. Sampling Frequency is per channel. Array Channel Yield gives the number and percentage of working electrodes on an array. Data for the non-functioning channels were interpolated from surrounding electrodes using a 2-D averaging spatial filter of window size 3 × 3 channels.

2.2 Data acquisition

A high-density flexible active electrode array was placed on the exposed cortex using a micro-manipulator prior to the administration of picrotoxin. The arrays, first described in Viventi et al (2011), use active multiplexing circuitry at the electrode interface to provide very high spatial and temporal resolution for our electrophysiological recordings (Viventi et al 2011). The 300 μm² platinum electrodes recorded micro-electrocorticographic (μECoG) data continuously from 360 independent channels arranged in 20 columns and 18 rows, spaced 500 μm apart. Buffering and multiplexing was accomplished on the electrode array by two high-performance, flexible silicon transistors for each electrode on the array (Viventi et al 2011). The total array size was 10 mm × 9 mm, which approximates the area of one standard clinical ECoG electrode (Van Gompel et al 2008). Signals were recorded with an effective sampling rate of 277.7, 555.6 or 925.9 Hz per channel (see Table 1) depending on the experiment. Figure S1a depicts the average trace over 360 channels of approximately the first 38 minutes of data from the Cat 1 data set. The selected sample of data includes three marked seizures. Additionally, figure S1b depicts a zoomed-in view of figure S1a with markers identifying detected epileptiform LFP spikes retained in the data analysis.

Custom hardware and software (LabVIEW) was developed based around a National Instruments PXI system (National Instruments Corporation, Austin, TX) (Bink et al 2013) to facilitate recording with the active electrode array. The software was used to de-multiplex, visualize and store recorded signals. A schematic of the experimental set-up is depicted in Figure 1a. Figure 1b displays a photograph of the 360 channel, high-density neural electrode array used in the experiments.

Figure 1.

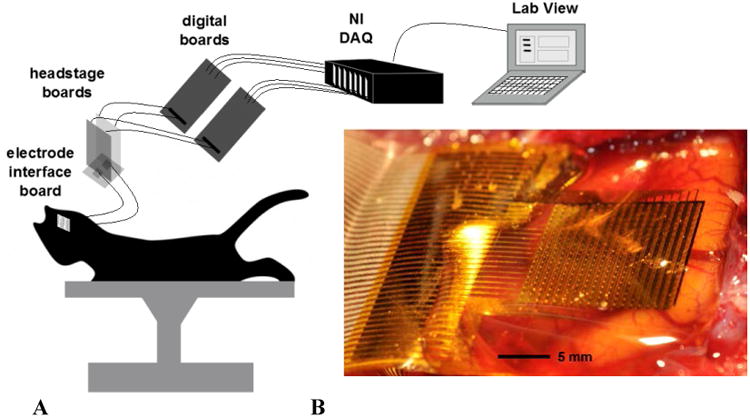
a. A schematic of the experimental set-up. The flexible array was connected via anisotropic conductive film (ACF) ribbon to a custom electrode interface board (EIB). The EIB connected to two headstage boards which provided signal amplification and high pass filtering (Bink et al 2013). The outputs of the headstage boards were connected to custom digital boards which generated the row-select-timing signals. The outputs of the digital boards were connected to standard National Instruments (NI) digital acquisition (DAQ) PXI systems. Data were acquired and de-multiplexed in real time using custom open source LabVIEW software (Bink et al 2013). 1b. Photograph of a 360-channel, high density neural electrode array used in a feline model of epilepsy. The electrode array is placed on the cortical surface. The electrode size and spacing are 300 μm × 300 μm and 500 μm, respectively.

2.3 Data analysis

We developed algorithms to visualize and classify spatiotemporal (ST) patterns of local field potential (LFP) spikes. These algorithms detect epileptiform LFP spikes on each channel of the array and extract time-delay and power-based features from their temporal signals. Subsequently, Principal Component Analysis (PCA) was used to reduce the data (retaining 99% of its variance), after which we performed clustering to group spikes by their pattern of propagation and distribution of power across the array. Data analysis was performed using custom developed MATLAB (MathWorks, Natick, MA) scripts. More detailed descriptions of our algorithms follow.

All recorded data were band-pass filtered between 1 and 50 Hz using a bidirectional 6th-order Butterworth filter to achieve zero-phase filtering. Due to the experimental design of the electrodes, some electrodes failed to capture data (< 20% in each experiment; see Table 1). This was handled by employing a 2-D averaging spatial filter of window size 3 × 3 channels which interpolated the small amount of missing data from surrounding electrodes. Noisy epochs of data (i.e. extremely high-amplitude signals recorded across all channels) were identified by visual inspection and excluded prior to conducting any further analysis.

We used an amplitude threshold to detect spikes from recorded signals; the threshold was set manually by visual inspection following the data acquisition but prior to further analysis. On detection of a spike on any individual channel, a 50 ms data segment from all channels (2 ms prior to the crossing and 48 ms post-crossing) was stored for further analysis. The window size (50 ms) was chosen to minimize the detection of multiple epileptiform spikes within the detection window (few LFP spikes were detected at a frequency greater than 20 Hz). Consecutive 50 ms windows of recorded data were intentionally non-overlapping (i.e. infrequent detections subsequent to the triggering spike within a given window were not collected). All further analysis of the data was performed on these segments. Table 1 shows the number of spikes detected in each data set.

We extracted “delay features” to characterize the direction and speed of spike propagation and “power features” to represent the strength of the spike in each of the array's 360 channels. These features were visualized as ‘maps,’ preserving the geographic location of each channel. Figures 2-4 visually depict the detection of a spike on 360 electrodes of the array using three different representations. Figure 2 depicts the 360 individual voltage traces from a single detected spike, during a non-seizure epoch, overlaid on a single plot. Figure 3 depicts the 360 individual voltage traces in 360 individual subplots using a geographic layout corresponding to the location of each electrode channel on the μECoG array. And figure 4 depicts the extracted delay and power features maps generated from the same single spike detection. The “spike-delay” feature was calculated by identifying the relative time of the maximum amplitude of the signal in the segment captured on each channel with respect to the time of the maximum amplitude on the channel with the earliest identifiable spike peak in the entire electrode group. This method allowed us to numerically capture the velocity of the spike propagation across the array in the 360 elements of the delay feature vector. We calculated root mean square (RMS) values on each channel after subtracting the window mean to represent the average power of each spike within a window. Each set of maps (delay and power) was then independently normalized via feature scaling to bring values into the range [0,1] across all spikes in a data set for further analysis. Subsequently, we concatenated the two sets of features (360 delay values, 360 power values), yielding 720 features per detected spike.

Figure 2.

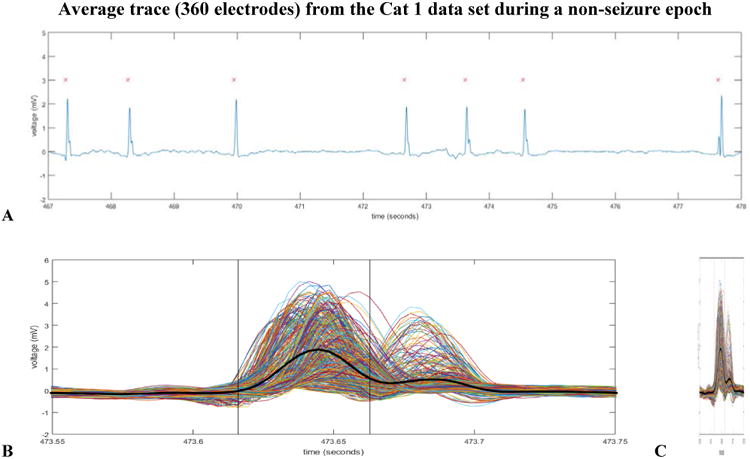
a. Displayed in this figure is the average voltage trace (from 360 channels on the array) during a non-seizure epoch where there were a total of seven detected spikes. The 5^th detected LFP spike in the above window from the Cat 1 data set was later determined to be the spike closest to the centroid for Cluster 8. 2b. All 360 voltage waveforms for the 5^th spike detection in 2a are overlaid on one axis to emphasize differences in voltage amplitude (captured by the power features map of our algorithm) and spike peak time (captured by the delay features map of our algorithm). The heavy black voltage waveform is of the average trace and the black vertical lines depict the width of the analysis window (50 msec). The various colors of the traces are random. 2c. This figure is identical to figure 2b. It has been horizontally compressed for an easier comparison of the average voltage trace waveform shape (heavy black line) to the average voltage trace waveform shape of the 5^th detected spike in figure 2a.

Figure 4.

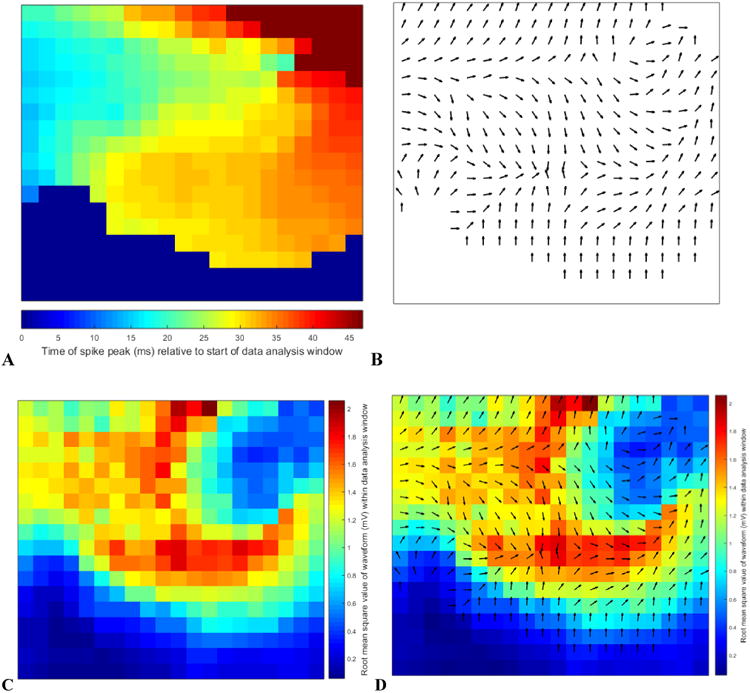
The above four subplots depict the intermediate stages of our feature extraction algorithm. We extracted a delay and power value for each channel on the 2-dimensional array obtaining a total of 720 features comprising a 720-dimension vector from each spike detection. We chose to generate these vectors to characterize the spatiotemporal patterns that we later used as the basis for our clustering algorithm. All four subplots originate from the same detected spike depicted in figures 2 and 3 and labeled as the spike closest to the centroid of Cluster 8 in figure 5. 4a. Color-coded delay map. Blue represents spike peak time early within the data analysis window and red is late. 4b. The quiver plot generated from the color-coded delay map in 4a. In the figure, the quivers only depict direction (for simplicity of display); however the feature vector data retain direction and speed. 4c. Color-coded RMS (root means square) value map to represent power features. 4d. Combined delay and power map created by overlaying figures 4b and 4c to simultaneously display the 720 extracted features from each spike detection. During subsequent stages of the data analysis, this spike was determined to be the spike closest to the centroid for Cluster 8.

Figure 3.

The voltage traces from the 360 channel array for the spike depicted in figure 2. The above traces are identical to the traces in figure 2b and 2c but are here displayed according to array channel location as opposed to superimposed on one axis. The scale of the y-axis of each channel is -5 to 5 mV. The scale of the x-axis of each channel from -70 ms to 175 ms relative to the spike detection at 0 ms. (The 50 ms data analysis window is from 0 ms to 50 ms in the above figure). The data analysis window for this spike is more clearly depicted in figure 2b.

We used Principal Component Analysis (PCA) to reduce the dimensionality of this comprehensive feature set and retained only the number of dimensions necessary to account for 99% of the variance within the data (Bishop 2006). The number of dimensions retained varied across data sets (Cat 1 data set – 251 dimensions; Cat 2 – 155; Cat 3a – 281; Cat 3b – 316). Figures S2-5 in the supplementary material provide scatter plots of the data onto the first two principal components obtained from each data set. The first two principal components capture 52%, 39%, 41% and 42% of the variance in the Cat 1, Cat 2, Cat 3a and Cat 3b data sets respectively. Figures S6-9 in the supplementary material provide a visual representation of the loading coefficients for the 1^st and 2^nd principal components obtained by the application of the PCA algorithm to each of the four data sets.

K-medians clustering (k=10) of the spike feature set was performed to group spikes with similar features into separate clusters. This algorithm is an adaptation of the widely used k-means algorithm but employs the L1 (city block) rather than L2 (Euclidean) norm as its distance metric and computes cluster prototypes as medians rather than means (MacQueen 1967). Although computationally more expensive, k-medians is more robust to the presence of outliers in the data. We chose to seed the k-medians clustering algorithm heuristically with ten clusters (k=10) to aid comparison between experiments. We expand upon this decision in the discussion section.

The k-medians algorithm was initialized by randomly selecting the coordinates of ten spikes within the entire data set of a given experiment as cluster centers. Next, numerical optimization was used to converge towards optimal cluster centers (at least locally) by minimizing the sum, over all clusters, of L1 distances between each data point and its assigned cluster center. The iterative descent algorithm used a two-phase scheme. The first phase used batch updates to assign points to their nearest cluster center, followed by recalculating all cluster centers. The second phase used online updates, where points were individually reassigned in an attempt to further reduce the sum of distances to cluster centers, which were recomputed after each reassignment. The iterations stopped when the algorithm either converged to a local minimum or reached a maximum number of iterations, which we set at 750. In order to increase the chances of finding the global minimum, we ran the algorithm 30 times and used the clustering for which the computed value of the optimization metric was smallest.

We tested whether 2-D ST spike patterns occurring during seizures (ictal spike patterns) could be differentiated from those occurring between seizures (interictal spike patterns). More specifically, we hypothesized that ST patterns of certain clusters occurred preferentially during seizure epochs. (As noted in the caption to Table 1, seizures were marked by a board-certified epileptologist and were defined to be at least 5 seconds in length). With a null hypothesis that the proportion of spikes occurring during seizures is equal across clusters, we employed a permutation test (n=1,000,000), holding the cluster membership of each ST spike pattern fixed while randomly permuting the seizure/non-seizure labels for one million permutations. For every permutation we recorded the proportion of ST patterns with a seizure label within each cluster to obtain the null distribution. We then compared the observed proportions to this null distribution.

Finally, to augment the clustering and permutation test, we performed a supervised analysis that utilized the interictal and ictal spike labels to directly assess the predictive power of our combined 2-D delay and power features. We trained a Quadratic Discriminant Analysis (QDA) classifier on the data from Cat 1 (first 23 principal components of the concatenated delay-power feature set described above, accounting for 90.02% of the data variance; n = 2894 spikes: 2498 interictal and 396 ictal) and assessed its generalization performance using 10-fold cross-validation and the F1 measure. To account for the heavy class-imbalance we arbitrarily set the cost associated with misclassifying interictal observations to be fifty times that associated with misclassifying ictal observations. The classifier was trained to minimize expected classification cost. To compare the QDA classifier's performance to that of a chance classifier, we performed a permutation test in which we randomly permuted the ictal-interictal labels 1000 times, each time training a QDA classifier with cost parameters identical to those used in classifying the real data and computing the resulting 10-fold cross-validated F1 measure. This procedure allowed us to estimate the p-value associated with our observed F1 value. Analogous QDA classifiers were trained and tested in the same fashion on the Cat 2, Cat 3a and Cat 3b data sets.

3. Results

3.1 Data clusters

The data consisted of 9 hours of μECoG recordings (∼70 Gigabytes), 26,331 detected spikes and 123 seizures. All seizures were defined to be 5 seconds or longer in duration. Figures 5-8 depict clustering results from the Cat 1-3b data sets, respectively. Every cluster is comprised of a mix of ictal and interictal spikes, though the percentages of ictal labels varied between clusters in each cat. The specifics of the ictal composition of clusters are discussed in more detail in Section 3.2 below. For figures 5-8, each window depicts a representative spike event for the associated cluster and shows both the power and direction of the spike waveform. The figures show these features for each of the 360 electrodes in the same layout as the grid electrode configuration. The colors in the figures represent the power detected within the extracted spike window. The directions of the arrows represent the direction of wave propagation of the detected spike. For example, cluster 3 in figure 5 shows a spike waveform that originates near the center of the grid and increases in power while moving to the top right of the grid, and cluster 8 starts on the left and has a bifurcation near the center of the grid. Note that most detected spikes do not cover the entire surface area of the array. This provides some evidence that high density arrays can capture LFP epileptiform spike patterns which may not be detectable with traditional large ECoG electrodes, which average LFPs over a larger volume. A local field potential spike that affects a smaller volume of cortex may not reach the detection threshold and consequently may be overlooked during data analysis.

Figure 5.

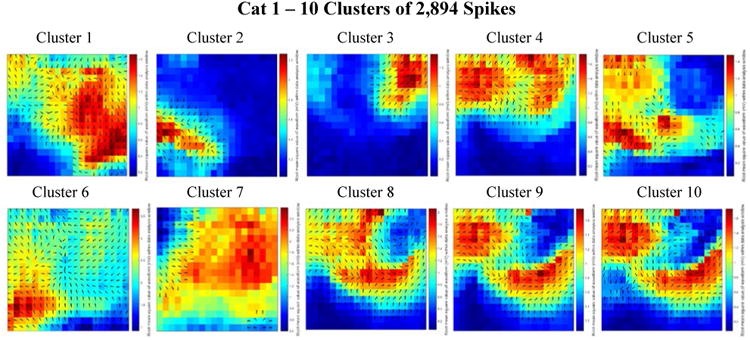
Combined delay and power maps of the spike closest to each of the ten cluster centers in the Cat 1 data set. These maps were obtained following the implementation of k-medians clustering (k=10) of the spike feature set (one delay and one power feature for each of the 360 channels) to group spikes with similar features into separate clusters. Prior to clustering we employed Principal Component Analysis (PCA) to reduce the dimensionality of this feature set and retained only the number of dimensions necessary to account for 99% of the variance within the data. 251 dimensions were retained in the Cat 1 data set. The colors represent the relative amount of power recorded from each electrode within the 50 ms spike detection window. Blue is relatively low power; red is relatively high power. The black arrows on each plot depict the direction of spike wave propagation (the arrows are not scaled by speed). The speed of wave propagation varied between spikes with the wave from Cluster 1 traveling the fastest, crossing the width and length of the array in 50 ms and the wave from Cluster 7 traveling the slowest, only traveling across 25% of the array width in the 50 ms data analysis window. Every cluster is comprised of a mix of ictal and interictal spikes; the percentages of ictal labels varied between clusters.

Figure 8.

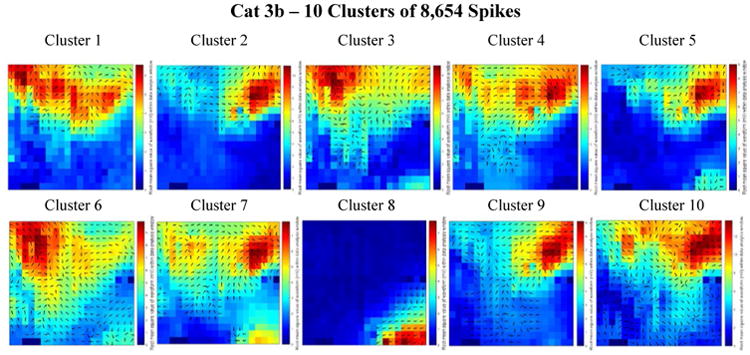
Combined delay and power maps of the spike closest to each of the ten cluster centers in the Cat 3b data set. These maps were obtained following the implementation of k-medians clustering (k=10) of the spike feature set (one delay and one power feature for each of the 360 channels) to group spikes with similar features into separate clusters. Prior to clustering we employed Principal Component Analysis (PCA) to reduce the dimensionality of this feature set and retained only the number of dimensions necessary to account for 99% of the variance within the data. 316 dimensions were retained in the Cat 3b data set. The colors represent the relative amount of power recorded from each electrode within the 50 ms spike detection window. Blue is relatively low power; red is relatively high power. The black arrows on each plot depict the direction of spike wave propagation (the arrows are not scaled by speed). The speed of wave propagation varied between spikes with the wave from Cluster 6 traveling the fastest, crossing diagonally upward from the bottom right of the array in 16 ms and the wave from Cluster 8 traveling the slowest, crossing 40% of the width of the array in 26 ms. Every cluster is comprised of a mix of ictal and interictal spikes; the percentages of ictal labels varied between clusters.

Also note that patterns of LFP spike wave propagation appear to be quite different across cats. This is expected given what we know about the differences in protocol between experiments, such as the exact placement of the electrode array over the cortex, the amount of anesthesia administered, the overall duration of the experiment, and the amount and location of picrotoxin employed to induce seizures. Therefore we did not combine the data across all four data sets when conducting statistical tests.

The three bottom-right cluster centroids for Cat 1 appear to illustrate a case in which over-splitting of clusters has occurred. From figures 5-8, we conclude it is possible, in heuristically seeding the k-medians algorithm with the number of clusters equal to 10, that our algorithm resulted in over-splitting some clusters (e.g., figure 5 clusters 8-10; figure 6 clusters 3-4 and 6-7; figure 7 clusters 5-6).

Figure 6.

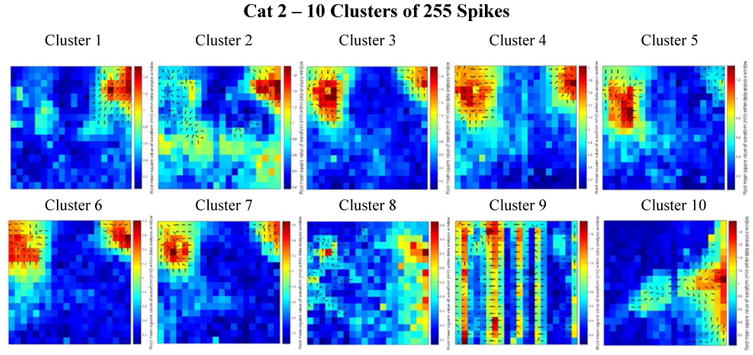
Combined delay and power maps of the spike closest to each of the ten cluster centers in the Cat 2 data set. These maps were obtained following the implementation of k-medians clustering (k=10) of the spike feature set (one delay and one power feature for each of the 360 channels) to group spikes with similar features into separate clusters. Prior to clustering we employed Principal Component Analysis (PCA) to reduce the dimensionality of this feature set and retained only the number of dimensions necessary to account for 99% of the variance within the data. 155 dimensions were retained in the Cat 2 data set. The colors represent the relative amount of power recorded from each electrode within the 50 ms spike detection window. Blue is relatively low power; red is relatively high power. The black arrows on each plot depict the direction of spike wave propagation (the arrows are not scaled by speed). The speed of wave propagation varied between spikes with the wave from Cluster 4 traveling the fastest, crossing 33% of the length of the array (along the left side) in 4 ms and the wave from Cluster 1 traveling the slowest, crossing only 25% diagonally across the array in 17 ms. Every cluster is comprised of a mix of ictal and interictal spikes; the percentages of ictal labels varied between clusters.

Figure 7.

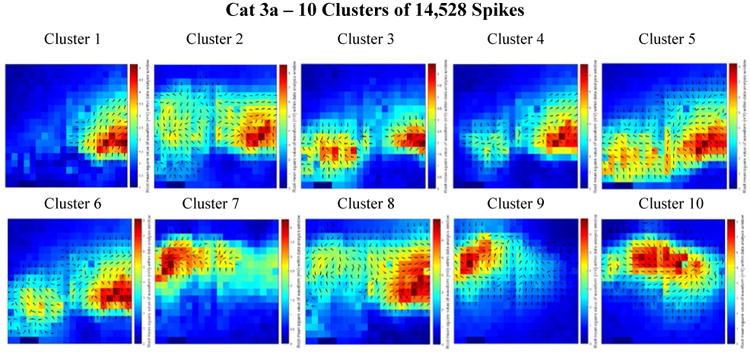
Combined delay and power maps of the spike closest to each of the ten cluster centers in the Cat 3a data set. These maps were obtained following the implementation of k-medians clustering (k=10) of the spike feature set (one delay and one power feature for each of the 360 channels) to group spikes with similar features into separate clusters. Prior to clustering we employed Principal Component Analysis (PCA) to reduce the dimensionality of this feature set and retained only the number of dimensions necessary to account for 99% of the variance within the data. 281 dimensions were retained in the Cat 3a data set. The colors represent the relative amount of power recorded from each electrode within the 50 ms spike detection window. Blue is relatively low power; red is relatively high power. The black arrows on each plot depict the direction of spike wave propagation (the arrows are not scaled by speed). The speed of wave propagation varied between spikes with the wave from Cluster 8 traveling the fastest, crossing 75% of the width of the array in 16 ms and the wave from Cluster 3 traveling the slowest, crossing 50% of the width of the array in 29 ms. Every cluster is comprised of a mix of ictal and interictal spikes; the percentages of ictal labels varied between clusters.

Figure 6 shows some unique differences present only in the Cat 2 data set. It appears that smaller areas of high power (as compared to the size of the areas of high power in the remaining data sets) are present in each of the detected spike windows and that virtually none of the detections cover the entire array. Additionally, it appears that cluster 9 resulted from an aggregate of noise artefacts. We speculate that these differences from the other three data sets is due to a reduced amount of picrotoxin application during this experiment resulting in reduced spike activity and strength (relative to background activity and noise).

In figure 7 (Cat 3a), most of the wave propagation patterns appear to lie along a mid-horizontal band across the array. We compare this to the majority of cluster center patterns in figure 8 (Cat 3b), in which horizontal bands appear closer to the top of the array. We believe this observation is a consequence of repositioning the array with a vertical downward shift in the middle of the Cat 3 experiment.

Figure 9 illustrates the homogeneity of the ST spike patterns for the 25 detected spikes closest (in L1 distance) to their respective cluster centers (medians), for three different clusters from the Cat 1 data set. In this figure, the colors represent the relative delay of the spike peak for each detected spike with an amplitude large enough to cross the detection threshold. Blue indicates an electrode with an early detection and red indicates an electrode with a late detection. The background color (dark blue) represents the electrodes whose spike amplitudes were not large enough to cross the voltage threshold. The power detected within the extracted spike window by each of the electrodes is not depicted. It is clear that the spikes within a cluster are very homogenous and that the pattern is robust over time. This validates the notion that spikes travel across the high density electrodes in consistent identifiable patterns.

Figure 9.

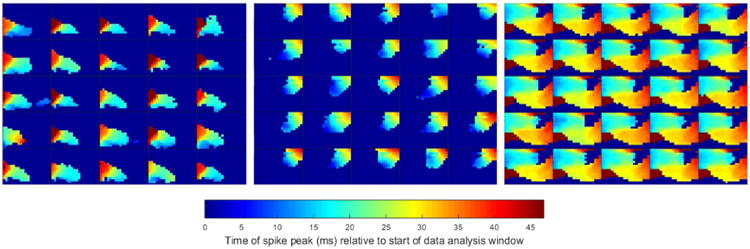
Cluster homogeneity of delay maps from Cat 1. Delay maps from 25 detected spikes closest to their respective cluster centers (L1 distance) are depicted for three different clusters within the Cat 1 data set. The colors represent the relative delay of the spike peak for each detected spike with voltage amplitudes large enough to cross the detection threshold. Blue indicates an electrode with an early detection and red indicates an electrode with a late detection. The deep blue of the background represents the electrodes whose voltage spike amplitudes were not large enough to cross the voltage threshold.

In figure 10, we observe cases in which the high density array distinguishes disparate spike patterns that do not appear to be easily separable on emulated standard intra-cranial ECoG. Figure 10a shows 16 different delay maps of various spikes detected in the data. Blue indicates electrodes with an early delay value and red indicates electrodes with a late delay value. In figure 10b, these same spikes are represented as they might appear on a standard 1.0 cm clinical electrode. (To generate the waveforms in figure 10b, we averaged the spike traces detected across all 360 electrodes of our array.) Spikes that have very different wave propagation patterns in figure 10a appear to have closely related morphologies on a clinical electrode (figure 10b: spike waveform pair 9-13 and 11-15). Comparing figure 10a and 10b side-by-side, we see how much additional detail is provided by the high-density array that is not captured by current clinical electrodes.

Figure 10.

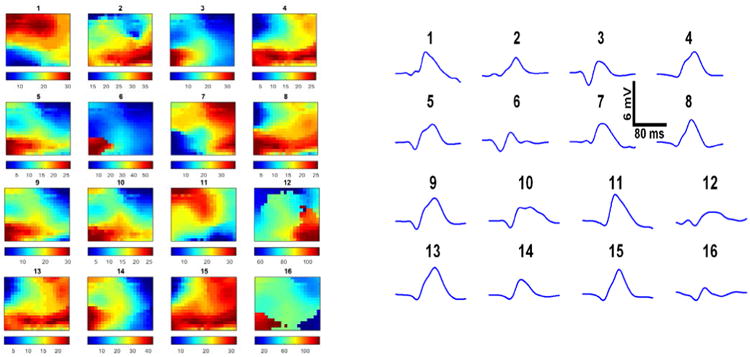
a. Delay maps for 16 various detected spikes. Color shading represents relative timing of peak voltage detected by individual channels in each spike window. Color bars in figure 10a are in milliseconds. Blue represents the earliest time to peak of each waveform and red represents the latest relative peak time of the detected spike; colors do not correspond to the same delay values across images. The delay map for spike 1 displays a ST spike pattern of propagation across the array of a spike that enters on the bottom left and proceeds in a sweeping arc until it exits the array in the top left. The corresponding power maps of these 16 spikes are not depicted. 10b. The same 16 various detected spikes from figure 10a. are represented as they might appear had they been detected by a 1.0 cm clinical electrode. To generate the waveforms in figure 10b, we averaged the spike traces detected across all 360 electrodes of our array. Spike detection windows utilized to generate this figure are 160 ms in length; we intentionally chose spikes which occurred at a lower frequency than the majority of detected spikes to more clearly present our observation of the enhanced ability of the high-density array to provide additional spatiotemporal detail that is not captured by current clinical electrodes.

3.2 Statistical testing

Statistical analysis confirmed that some spatiotemporal (ST) patterns of LFP spike activity recorded on a millimeter-scale are unique to seizures and others to interictal epochs. The remainder of clusters has a mixed representation, containing ST patterns of spikes occurring both ictally and interictally. Figure 11 captures the results of our statistical analysis. The number of interictal spikes was chosen for the comparison of ratios in the top two data sets because the number of interictal spikes in the Cat 1 and 2 data sets (86.3% and 94.1% of total spikes detected, respectively) greatly exceeded the number of ictal spikes. The converse reasoning was chosen for the Cat 3a and 3b (bottom two) data sets where a larger percentage of detected spikes occurred ictally (81.4% and 78.1% of total spikes detected, respectively). We suspect that the cat in experiment 3 quickly entered status epilepticus, a state of continual and prolonged seizing without returning to normal EEG activity between seizures.

Figure 11.

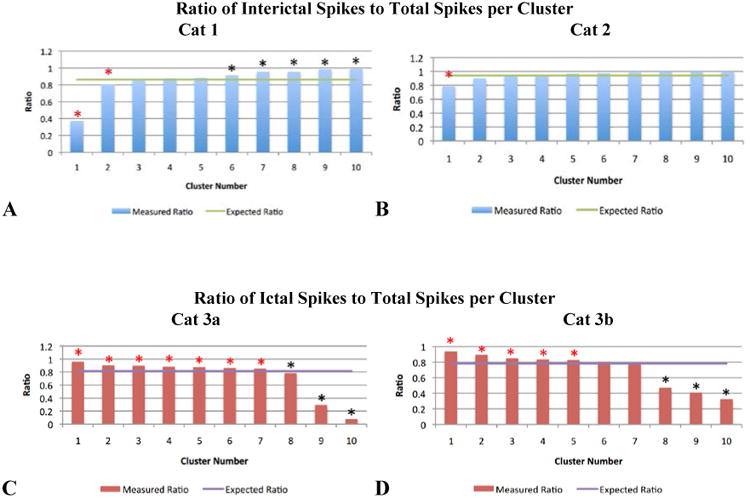
Ratios of interictal or ictal spikes to total spikes, by cluster. In 11a and 11b (the Cat 1 and 2 data sets), the majority of spikes detected occurred interictally (86.3% and 94.1% respectively, represented by the green horizontal lines). The blue bars depict the observed ratio of interictal spikes to total spikes within a given cluster. In 11c and 11d (the Cat 3a and 3b data sets), the majority of spikes detected occurred ictally (81.4% and 78.1% respectively, represented by the purple horizontal lines). The red bars depict the observed ratio of ictal spikes to total spikes within a given cluster. In all bar graphs, a red asterisk identifies the clusters that showed a statistically significant (p<0.007) preference for containing LFP spikes that occurred during seizure (ictal epochs); a black asterisk identifies the clusters that showed a statistically significant (p<0.001) preference for containing LFP spikes that occurred between seizures (interictal epochs).

The four bar charts correspond to the four data sets from three experiments. In the top two charts, the blue bars quantify the ratio of interictal spikes to total spikes detected for a given cluster. The horizontal green line is the ratio of interictal spikes to total spikes in the data set. In the bottom two charts, the red bars quantify the ratio of ictal spikes to total spikes detected for a given cluster. And the purple line is the ratio of ictal spikes to total spikes in the data set. In each data set, we found a strong relationship between ST pattern and seizure state. We rejected the null hypothesis that the proportion of spikes occurring during seizure in each of the 10 clusters was the same. For every bar in figure 11 that has a red asterisk above it, we found the proportion of within-seizure spikes contained in the corresponding cluster was significantly higher than would be expected by chance (permutation test, p<0.007). For every bar in figure 11 that has a black asterisk above it, we found the proportion of interictal spikes within the corresponding cluster was significantly higher than would be expected by chance (permutation test, p<0.001). The graphs in figure 11 were generated from the data contained in Tables S1-S4 in the supplemental material.

Our supervised analysis confirmed the clustering-based conclusion that 2-D power-delay features contain information about the interictal-ictal labels of spikes. The Cat 1 QDA classifier achieved an overall accuracy of 90.6% with a positive predictive value for detecting ictal spikes of 73.4% and a sensitivity of 48.7%; and a negative predictive value for detecting interictal spikes of 92.3% and a specificity of 97.3%. The QDA classifier's F1 measure of 0.59 was significantly greater than that of a chance QDA classifier trained to learn random interictal-ictal spike labels (permutation test, p < 0.001). Classifier performance on the other three data sets was in one case weaker (Cat 2: F1 = 0.40) and in two cases much stronger (Cat 3a: F1 = 0.90; Cat 3b: F1 = 0.91) than for Cat 1, but significantly better than that of a chance QDA classifier (permutation test, p < 0.001 in all cases).

4. Discussion

In this study, we aimed to develop methods to quantitatively characterize the spatiotemporal dynamics of epileptiform activity at high-resolution to determine the relationship between interictal electrophysiologic patterns on the cortical surface of the brain and seizures in a focal acute animal model of epilepsy. The long-term goals of this work are two-fold: 1) to better understand mechanisms of seizure generation, and 2) to determine if changes in these patterns might provide opportunity for therapeutic intervention to arrest seizures.

This paper highlights the initial steps we have made toward these goals. Prior to developing our algorithm, we observed that within each data set the trajectory, speed and amplitude of epileptiform LFP spike waveforms evolved as they propagated across the array. Based on the results of our analysis, we conclude that we are able to identify differences between clusters of spikes because these propagation pattern and amplitude differences are well captured via the delay and power features. We show that spatially correlated events differ statistically between seizures and non-seizures. We also show that traditional centimeter scale electrodes, technology dating back to the work of Penfield and Jasper in the 1950s (Penfield and Jasper 1954) may not be sufficient to map cortical activity at the resolution required to provide an understanding of underlying epileptic networks.

In our methods, the number of clusters was chosen arbitrarily to explore whether any 2-D spatiotemporal patterns identified by the clustering algorithm were more prevalent during rather than outside of seizures or vice versa. A negative answer to this question would have left open the possibility that increasing the number of clusters would change the result. However, our findings indicate that there are indeed 2-D spatiotemporal spike patterns that occur preferentially during or outside of seizures, sufficiently answering this question with the selection of only 10 clusters. This result is meaningful, especially in light of the findings shown in figure 10, because it suggests that there are differences between seizure and non-seizure spike dynamics that occur on a spatial scale not measured by traditional clinical electrodes. This in turn is important because it implies network mechanisms for seizure generation that produce spikes not only with specific large-scale amplitude, rate, and/or burst characteristics, for instance, but also with specific, smaller-scale morphologies of the type that we show in our clustering images. We believe pursuing analysis to more exactly identify what number of clusters are intrinsically present in the data will be most valuable in future experiments where precise neuroanatomical correlation, down to the cortical column, cellular and axonal level is obtained in order to mechanistically explore the neurophysiological drivers behind various prevalent patterns.

The work presented in this paper shows that novel recording hardware combined with modern data analysis techniques, provides useful information about interictal and ictal LFP spikes that is not apparent using traditional electrode arrays and data analysis techniques. We hypothesized that some ST patterns occur preferentially during seizures (ictally), and that these patterns are different from other ST patterns that occur preferentially between seizures (interictally). Our main findings confirmed this hypothesis. However, another result of our experiments is that we did not find any unifying pattern of spike waveform propagation that was common to all animals. We attribute this to variability in our experimental preparations and the animal models used in this study. Despite controlling for the amount of picrotoxin used in each experiment and its anatomical placement, there was considerable variability in spikes, seizures and spatiotemporal spread of these waveforms in each animal. This is the norm in human epilepsy, even in the expression of genetic seizure disorders in identical twins. Differences in functional anatomy and dynamic changes in cortical architecture from neuroplasticity resulting from unique experiences might account for such variability. What we did observe is that certain μECoG spike patterns were more common in seizures. Additionally, these findings held despite the observation that the morphology of ictal and interictal patterns differed across animals. We conclude that there is a need for high-resolution local field potential recordings to understand both the temporal and spatial characteristics of neocortical seizures in ways not possible with multi-unit or clinical ECoG recordings.

One question raised by our analysis, with basic science implications, is whether the differences between spike patterns were driven by power or delay differences, or both. We found that the answer to this question depends on the data set. For the Cat 1 data set the first principal component (PC1) accounts for 42% of the variance in the data and was found to heavily weight the delay features across the entire array with the exception of the top right corner (figure S6a,c); while the second principal component (PC2) (accounting for the next 10% of data variance) approximately equally weights the delay and power features localized to the upper right quadrant of the array (figure S6b,d). For the Cat 2 data set PC1 accounts for 25% of the variance in the data and was found to heavily weight the delay and power features localized to the upper left quadrant of the array, with the delay features having slightly higher loading coefficients than the power features in that area (figure S7a,c); while PC2 (accounting for the next 14% of data variance) more heavily weighted the delay features along the left half of the array (figure S7b,d). For the Cat 3a data set PC1 accounts for 22% of the variance in the data and was found to heavily weight the delay features across the central horizontal band of the array (figure S8a,c); and PC2 (accounting for the next 18% of data variance) also heavily weighted the delay features across a central horizontal band of the array. This band is closer to the top of the array than the band favored in PC1 (figure S8b,d). Finally, for the Cat 3b data set PC1 accounts for 27% of the variance in the data and was found to heavily weight the delay features along a diagonal band from the top left corner down toward the center of the array (figure S9a,c) and PC2 (accounting for the next 15% of data variance) more heavily weighted the delay features localized to the upper right corner of the array (figure S9b,d). These findings suggest that differences in spike patterns and propagation may relate to underlying mechanisms that differentially synchronize neuronal firing, for example changes in gap junctions, increasing the discriminating power in our measures. Other possible causes of these differences could be the presence of anatomical abnormalities, lesions or aberrant cellular structures due to abnormalities of cortical development.

Our results add to the body of evidence that reports the presence of LFP spike propagation waves in cortex. Prechtl et al (1997) described finding waves of electrical activity in turtle visual cortex induced by visual stimuli (Prechtl et al 1997). Using voltage-sensitive dyes (VSDs), Prechtl et al (1997) found different types of waves of activity including plane waves, spiral waves and more complex patterns. More recently, Huang et al (2010) demonstrated in a murine model the use of VSD imaging for the observation and analysis of unique patterns of brain activity in induced sleep states (Huang et al 2010). They postulated that the patterns point toward underlying cortical mechanisms. Spiral waves detected in this study were thought to explain mechanisms occurring on the mesoscopic scale. They proposed that patterns which modify cortical activity via disruptions in frequency, spatial coherence and modulation of LFP amplitude result in local organization, impacting small networks. Similar to our results, they were able to detect a variety of propagating wave patterns. A highly excitable medium is required to propagate various ST waves and in the case of Huang et al (2004), this was achieved using a Bicuculline model of epilepsy. Bicuculline is a GABA-A receptor antagonist that blocks inhibition similar to picrotoxin. Our results validate the published data by Huang et al (2004) where spiral, plane, ring and irregular waves of LFP activity were observed occurring spontaneously in vitro in an acute model of cortical dis-inhibition.

We acknowledge that in large quantities, the topical application of picrotoxin can quickly lead to status epilepticus (Fisher 1989). We believe this is what occurred in Cat 3 and explains why the overwhelming majority of spikes (90%) in this animal occurred ictally in contrast to the data collected in Cats 1 and 2. In the first two animals, roughly 10% (13.7% and 5.9%) of detected spikes occurred during seizures, suggesting that there are specific network elements activated during seizures that can be separated from the rest of the cortical network.

In our algorithm all detected spikes were assumed to be epileptiform LFP spikes and no consideration was given to the fact that some of the LFP spikes could have been normal sharp discharges, which can be present in animal models under anesthesia (Fisher 1989). We contend that combining both types of spikes was not detrimental to the results of our study since it is possible, even likely that the onset of a seizure is disruptive to both abnormal and normal spikes.

We conclude that large area high-density cortical arrays provide a window into ST activity that was previously unobservable via current clinical or research technologies. It is our opinion that the continued development of these arrays along with the employment of modern data analysis techniques, such as those employed in our algorithm, shows great potential for continued understanding of the mechanisms underlying the differentiation of local field potential spikes from one another. We believe LFP patterns may hold information about the evolution of abnormal electrical activity as seizures develop and progress.

The main contributions of this paper, as an extension of findings presented by Viventi et al (2011), are methods we have developed to quantitatively characterize the spatiotemporal dynamics of epileptiform activity at high resolution in brain. These tools provide a quantitative framework for analyzing, localizing and mapping network activity at high resolution that may be important to basic science investigation of the mechanisms underlying these phenomena. They will contribute to practical tools, similar to those used in cardiac electrophysiology, that might be used to pinpoint and locally treat seizure generating regions in the clinical arena, should this approach be validated. Our findings that there may be subject-specific preferred spatiotemporal patterns involved in generating or sustaining seizures might enable clinical trials of creative therapies, such as localized thermal or electrical ablation of these preferred ictal pathways, similar to the way that electrical cardiac ablations are conducted.

While we believe that our analytic methods and observations of differences in spatiotemporal patterns between seizures and interictal states are important, the relationship of our findings to underlying neural mechanisms is unclear. We could speculate that modulation of propagation patterns during seizures may result from changes in inhibitory tone, accumulation of synaptic noise in abnormally connected regions, or other phenomena felt to be ictogenic, however a better understanding of these phenomena will require more detailed experiments at the cellular network level to address these questions. We are hopeful that the tools and observations we present will help advance these investigations.

There is still much more to be understood concerning the dynamics of neuronal network processing, both in response to external input and when associated with pathological states of the brain, such as seizures. High-resolution recordings of this nature have yet to be performed in humans, but it is clear that these could provide insight about epileptic networks with a resolution that is unprecedented. The technology required to utilize these new arrays in humans is rapidly advancing. At this time it is not known to what extent the spike patterns we have observed apply to spontaneous human seizures, but some human ictal events look quite similar, at least at a macroscopic level, to the acute seizures recorded in our work.

Recordings at this spatial scale may be important to clinical patient care and evaluation for epilepsy surgery. We anticipate that this new electrode technology, combined with novel methods for analyzing the large, high-resolution data sets arising from it, will lead to a better understanding of mechanisms underlying local circuit activity leading to spike discharges and seizure development. Ultimately, we hope this technology will provide a novel opportunity for therapeutic intervention at the micro-scale to treat epilepsy for the more than 33% of epilepsy patients who remain medically refractory.

Supplementary Material

Figure S1. Average trace from all 360 electrodes on the array. 1a. The first 2265 seconds (37 minutes, 45 seconds) of data from the Cat 1 data set is depicted. Three seizures are annotated with black vertical lines (blue vertical lines were the result of spurious noise in the recording yielding voltage amplitudes exceed the limits of the plot). Seizures were marked by a board-certified neurologist and were defined to be at least 5 seconds in length. S1b. A zoomed-in view (horizontal only) of the trace in figure S1a. Again the black vertical lines show the bounding times of marked seizures (only two in this view). Additionally the red ‘x’s above individual LFP spikes mark several of the detected spikes retained in our data analysis.

Figure S2. S2a. Scatter plot of 1^st two principal components from the Cat 1 data set containing 2894 detected spikes. Together PC1 and PC2 capture 52% of the variance in the data. S2b. The same scatter plot as in S2a with each data point colored by its ictal or interictal label (i.e. within seizure vs. outside of seizure; seizures were marked by a board certified neurologist). S2c. The same scatter plot as in S2a with each data point colored by its cluster membership. S2d. The same scatter plot as in S2a with each data point colored by its membership to: a cluster with a statistically significant proportion of ictal spikes (Clusters 1 and 2, colored in red), a cluster with a statistically significant proportion of interictal spikes (Clusters 6-10, colored in black) or clusters with a mix of ictal and interictal spikes matching the overall population proportion of ictal and interictal spikes (Clusters 3-5, colored in blue). See figure 11a and table S1.

Figure S3. S3a. Scatter plot of 1^st two principal components from the Cat 2 data set containing 255 detected spikes. Together PC1 and PC2 capture 39% of the variance in the data. S3b. The same scatter plot as in S3a with each data point colored by its ictal or interictal label (i.e. within seizure vs. outside of seizure; seizures were marked by a board certified neurologist). S3c. The same scatter plot as in S3a with each data point colored by its cluster membership. S3d. The same scatter plot as in S3a with each data point colored by its membership to: a cluster with a statistically significant proportion of ictal spikes (Cluster 1, colored in red), or clusters with a mix of ictal and interictal spikes matching the overall population proportion of ictal and interictal spikes (Clusters 2-10, colored in blue). See figure 11b and table S2.

Figure S4. S4a. Scatter plot of 1^st two principal components from the Cat 3a data set containing 14,528 detected spikes. Together PC1 and PC2 capture 41% of the variance in the data. S4b. The same scatter plot as in S4a with each data point colored by its ictal or interictal label (i.e. within seizure vs. outside of seizure; seizures were marked by a board certified neurologist). S4c. The same scatter plot as in S4a with each data point colored by its cluster membership. S4d. The same scatter plot as in S4a with each data point colored by its membership to: a cluster with a statistically significant proportion of ictal spikes (Clusters 1-7, colored in red), or a cluster with a statistically significant proportion of interictal spikes (Clusters 8-10, colored in black). See figure 11c and table S3.

Figure S5. S5a. Scatter plot of 1^st two principal components from the Cat 1 data set containing 8654 detected spikes. Together PC1 and PC2 capture 42% of the variance in the data. S5b. The same scatter plot as in S5a with each data point colored by its ictal or interictal label (i.e. within seizure vs. outside of seizure; seizures were marked by a board certified neurologist). S5c. The same scatter plot as in S5a with each data point colored by its cluster membership. S5d. The same scatter plot as in S5a with each data point colored by its membership to: a cluster with a statistically significant proportion of ictal spikes (Clusters 1-5, colored in red), a cluster with a statistically significant proportion of interictal spikes (Clusters 8-10, colored in black) or clusters with a mix of ictal and interictal spikes matching the overall population proportion of ictal and interictal spikes (Clusters 6 and 7, colored in blue). See figure 11d and table S4.

Figure S6. S6a and S6c provide a visual representation of the loading coefficients for the 1^st principal component obtained by the PCA algorithm to the 2894 720-dimension feature vectors of the Cat 1 data set. S6a and S6c use the same color bar in order to reveal which features were most heavily weighted when projecting the feature vector data onto the 1^st principal component. For the Cat 1 data set PC1 accounts for 42% of the variance in the data and appears to heavily weight the delay features across entire array with the exception of the top right corner. S6b and S6d provide a similar representation as S6a and S6c but for the 2^nd principal component which accounts for the next 10% of variance in the data. S6b and S6d use the same color bar. PC2 appears to equally weight the delay and power features localized to the upper right quadrant of the array.

Figure S7. S7a and S7c provide a visual representation of the loading coefficients for the 1^st principal component obtained by the PCA algorithm to the 255 720-dimension feature vectors of the Cat 2 data set. S7a and S7c use the same color bar in order to reveal which features were most heavily weighted when projecting the feature vector data onto the 1^st principal component. For the Cat 2 data set PC1 accounts for 25% of the variance in the data and appears to heavily weight the delay and power features localized to the upper left quadrant of the array, with the delay features having slightly higher loading coefficients than the power features in that area. S7b and S7d provide a similar representation as S7a and S7c but for the 2^nd principal component which accounts for the next 14% of variance in the data. S7b and S7d use the same color bar. PC2 appears to more heavily weight the delay features along the left half of the array.

Figure S8. S8a and S8c provide a visual representation of the loading coefficients for the 1^st principal component obtained by the PCA algorithm to the 14,528 720-dimension feature vectors of the Cat 3a data set. S8a and S8c use the same color bar in order to reveal which features were most heavily weighted when projecting the feature vector data onto the 1^st principal component. For the Cat 3a data set PC1 accounts for 22% of the variance in the data and appears to heavily weight the delay features across the central horizontal band of the array. S8b and S8d provide a similar representation as S8a and S8c but for the 2^nd principal component which accounts for the next 18% of variance in the data. S8b and S8d use the same color bar. PC2 appears to also heavily weight the delay features across a central horizontal band of the array. This band is closer to the top of the array than the band favored in PC1.

Figure S9. S9a and S9c provide a visual representation of the loading coefficients for the 1^st principal component obtained by the PCA algorithm to the 8654 720-dimension feature vectors of the Cat 3b data set. S9a and S9c use the same color bar in order to reveal which features were most heavily weighted when projecting the feature vector data onto the 1^st principal component. For the Cat 3b data set PC1 accounts for 27% of the variance in the data and appears to heavily weight the delay features along a diagonal band from the top left corner down toward the center of the array. S9b and S9d provide a similar representation as S9a and S9c but for the 2^nd principal component which accounts for the next 15% of variance in the data. S9b and S9d use the same color bar. PC2 appears to heavily weight the delay features localized to the upper right corner of the array.

Table S1. Cat 1, permutation test results. (n=1,000,000)

Table S2. Cat 2, permutation test results. (n=1,000,000)

Table S3. Cat 3a, permutation test results. (n=1,000,000)

Table S4. Cat 3b, permutation test results. (n=1,000,000)