3D microwave tomography of the breast using prior anatomical information

Abstract

Purpose:

The authors have developed a new 3D breast image reconstruction technique that utilizes the soft tissue spatial resolution of magnetic resonance imaging (MRI) and integrates the dielectric property differentiation from microwave imaging to produce a dual modality approach with the goal of augmenting the specificity of MR imaging, possibly without the need for nonspecific contrast agents. The integration is performed through the application of a soft prior regularization which imports segmented geometric meshes generated from MR exams and uses it to constrain the microwave tomography algorithm to recover nearly uniform property distributions within segmented regions with sharp delineation between these internal subzones.

Methods:

Previous investigations have demonstrated that this approach is effective in 2D simulation and phantom experiments and also in clinical exams. The current study extends the algorithm to 3D and provides a thorough analysis of the sensitivity and robustness to misalignment errors in size and location between the spatial prior information and the actual data.

Results:

Image results in 3D were not strongly dependent on reconstruction mesh density, and the changes of less than 30% in recovered property values arose from variations of more than 125% in target region size—an outcome which was more robust than in 2D. Similarly, changes of less than 13% occurred in the 3D image results from variations in target location of nearly 90% of the inclusion size. Permittivity and conductivity errors were about 5 times and 2 times smaller, respectively, with the 3D spatial prior algorithm in actual phantom experiments than those which occurred without priors.

Conclusions:

The presented study confirms that the incorporation of structural information in the form of a soft constraint can considerably improve the accuracy of the property estimates in predefined regions of interest. These findings are encouraging and establish a strong foundation for using the soft prior technique in clinical studies, where their microwave imaging system and MRI can simultaneously collect breast exam data in patients.

1. INTRODUCTION

Magnetic resonance imaging (MRI) is widely applied in challenging breast imaging cases, for example, in women with dense breasts and those at high risk for breast cancer, especially women with genetic predispositions.^1–6 In addition, it is routinely used prior to surgery because of its ability to reveal multifocal and extent of disease which provides spatial context for planning the interventional procedures. In terms of performance, breast MR suffers from a high false positive rate which can reach 19% and poses an important clinical challenge because multiple false positives can occur within a single breast.^7,8 MRI also depends on the use of gadolinium as a contrast agent, lowering its effectiveness in the imaging of recurrences^9,10 and causing health risks to patients with compromised kidney function.¹¹ Breast MR’s combination of strengths and weaknesses represents opportunities to add value to the examination, especially if achieved through minimal changes in clinical workflow. With the advent of emerging vector network analyzers (VNAs) on-a-chip technology, microwave imaging (MI) could become a cost effective alternative to contrast enhanced interventions.

MI is emerging as a potential alternative and/or adjunct to conventional modalities such as MRI that may be able to exploit meaningful contrast between the dielectric properties (namely, the permittivity and conductivity) of malignant and normal breast tissue. A number of reports have demonstrated that the microwave properties of cancerous tissue are high due to the increased water content associated with rapidly proliferating cells and their concomitant angiogenic vasculature^12–14 relative to lower water content normal breast tissue comprised mainly of adipose and fibroglandular constituents.¹⁵ In fact, recent clinical studies involving microwave tomography^16,17 and radar methods¹⁸ for breast diagnosis and tumor margin assessment¹⁹ suggest that these properties distinguish cancer from normal tissue at statistically significant levels. While radar techniques have demonstrated promise in terms of detecting breast tumors, these methods appear to offer less specificity.^18,20,21 Notwithstanding, some studies²² have presented data showing that the contrast between tumors and naturally occurring fibroglandular tissue may not be especially high because both have relatively elevated water content. However, analyses of the experimental methodology used in those measurements indicate that the lack of contrast observed may not reflect the contrast that would be imaged.²³ In fact, data from a recent report by Sugitani et al.²⁴ appear to contradict some conclusions in Lazebnik et al.²² One mechanism for the apparent contrast^{12–14,16,17} may be the link between dielectric properties and bound and free water effects,^25–27 which have been shown to play a significant role in both MRI²⁸ and diffuse optical tomography (DOT),^29,30 and would be expected to influence tissue dielectric properties at low microwave frequencies.

Microwave tomography operates similarly to x-ray CT in which the breast is surrounded by an array of antennas which individually illuminate the tissue of interest from all directions and receive the scattered fields. The system developed by Meaney et al.^31–36 operates in a frequency range from 500 MHz to 2 GHz and incorporates monopole antennas submerged in a liquid that are positioned closely around the breast. A nonlinear imaging algorithm reconstructs dielectric property maps of the breast from these measurements. Since the problem is ill-posed, some form of regularization is required to stabilize the process. Previously, we have successfully employed variations on Tikhonov and Levenberg–Marquardt (LM) schemes;^37,38 however, loss of spatial resolution of internal features occurs from the smoothing effects caused by the regularization. Alternatively, when spatial information about the target is known, we have applied a soft prior regularization which smoothens the estimated properties within homogeneous, segmented regions but allows near stepwise variation at interfaces between zones.³⁹ The technique has dramatically improved the property recovery in a range of simulation and phantom studies and even in a patient exam.^40,41 The major impediment to implementing the approach is obtaining spatial information that accurately aligns with the breast geometry at the time of microwave data acquisition. Interestingly, a coregistration technique has recently been reported whereby the breast is held in position using a thermoplastic mesh during separate MR and microwave examinations.⁴² While the approach is attractive, opportunities exist for alignment errors because the breast will likely deform during transition from one exam to the other. Additionally, the breast is buoyant in most coupling liquids, which would further exacerbate the registration problem.

To translate this technique clinically, we recently reported the first implementation of a microwave tomography system operating within an MR scanner.⁴¹ The integration was challenging on a number of levels because of (a) space limitations, (b) signal interference, (c) metal-induced image artifacts, and (d) multipath signal corruption. Fortunately, our monopole antenna configuration contained little metal and minimized imaging tank size relative to other approaches.^21,43,44 The system yielded the first clinical microwave breast images with MRI as the modality providing spatial information. The implications are substantial: by reconstructing microwave images spatially encoded with MR, dielectric property differentiation can increase the specificity of breast MRI. This multimodality breast exam has the potential to add value to MRI without using invasive contrast agents such as gadolinium and without substantial alterations to existing MRI systems.

Multiple factors will ultimately impact the value of this approach. For instance, the degree of accuracy of the prior anatomical information extracted from the MR images depends on several factors including the spatial resolution of the actual MR images, type of MR sequence, and tissue segmentation techniques (manual, semiautomatic, or automatic), which could involve interoperator and intraoperator variability. Therefore, evaluation of the sensitivity of the 3D soft prior technique to imperfect prior information is important. While all sources of variability have not been evaluated, the potential errors in the priors considered in this study are likely to be the biggest contributors to exams in the microwave property recovery. It is important to note that the microwave examination is performed simultaneously with MRI which does minimize coregistration and associated segmentation errors between the microwave and MR exams related to performing the two exams sequentially.

While we have demonstrated the capability with 2D MI, the approach benefits substantially by expanding the technology to 3D. As an important step toward clinical translation, this study introduces the 3D soft prior regularization and assesses its performance in a controlled manner. First, the image reconstruction algorithm including both soft and hard prior techniques is outlined. Then, a series of simulation studies evaluating the algorithms’ sensitivity and robustness are presented, along with results from breast phantom experiments. Finally, an error analysis is described. The study sets the stage for full 3D implementation with a more advanced microwave data acquisition system.

2. METHODS

2.A. Image reconstruction

MI is based on determining the distribution of constitutive parameters within tissue where the dielectric properties are embedded in the squared complex-valued wave number, $k^2\left(r\right)={\omega }^2{\mu }_0\epsilon \left(r\right)-j\omega {\mu }_0\sigma \left(r\right)$, where r is the 3D position vector within the imaging domain, ω is the angular frequency, j is the imaginary unit, μ₀ is the free-space permeability, ε is the permittivity, and σ is the conductivity.⁴⁵ During the reconstruction process, the field problem is initially solved by computing the 3D scattering from Maxwell’s equations using a finite difference time domain (FDTD) algorithm.⁴⁶ The next step estimates the dielectric properties of the interrogated tissue by minimizing the difference between computed and measured scattered electric fields. Since the inverse electromagnetic problem is nonlinear, we use an iterative LM technique with a variance stabilizing transformation in which the 3D measured electric field vector (E^m) is compared with the calculated vector using the forward model (E^c(k²)) for a given distribution of the constitutive parameters stored in the 3D vector, k².^47,48 Other approaches to solve inverse problems, such as genetic algorithms and stochastic processes, are also possible and have been applied successfully to MI as well.^49–51

Tikhonov regularization³⁷ imposes additional constraints to stabilize the reconstruction procedure. In our algorithm, the objective function is as follows:

$${\displaystyle \mathrm{\Omega }={‖{\mathrm{\Gamma }}^m-{\mathrm{\Gamma }}^c\left(k^2\right)‖}_2^2+{‖{\mathrm{\Phi }}^m-{\mathrm{\Phi }}^c\left(k^2\right)‖}_2^2+\lambda {‖L(k^2-k_0^2)‖}_2^2,}$$ (1)

where Γ^m and Γ^c are the log magnitudes, and Φ^m and Φ^c are the phases of the measured and computed field values, respectively,^33,47,48 λ is the weighting coefficient, also known as the Tikhonov regularization parameter, and L is a positive definite, dimensionless regularization matrix, and $k_0^2$ is a prior estimate of k². The objective function in (1) can be solved for the iterative property update, $k_{\eta }^2$,

$${\displaystyle \mathrm{\Delta }{k}_{\eta }^2={\left[J^{T}J+\lambda L^{T}L\right]}^{-1}\left(J^T\left[\begin{array}{c}\hfill {\mathrm{\Gamma }}^m-{\mathrm{\Gamma }}^c\left(k_{\eta }^2\right)\hfill \\ \hfill {\mathrm{\Phi }}^m-{\mathrm{\Phi }}^c\left(k_{\eta }^2\right)\hfill \end{array}\right]-L^{T}L\left(k_{\eta }^2-k_0^2\right)\right),}$$ (2)

where J is the Jacobian matrix, which has dimensions 2M × 2N and consists of derivatives of the log magnitude and phases of the computed field values (M is the number of measurements) with respect to the property values at each of the N nodes in the 3D reconstruction mesh. $k_{\eta }^2$ is the vector k² at iteration η and is updated as $\mathrm{\Delta }{k}_{\eta }^2=k_{\eta +1}^2-k_{\eta }^2$. We use a dual-mesh approach where the forward solution is computed on a uniform rectangular parallelepiped FDTD grid, while the electromagnetic property parameters are reconstructed on a tetrahedral element mesh, placed concentrically within the antenna array.³⁵ As was reported earlier,³⁴ the FDTD approach is significantly less computationally expensive in 3D situations than for finite element approaches and is, therefore, better suited to the iterative imaging techniques.

In the absence of prior structural information, also referred to as the “no prior” case, L in (2) is set to the identity matrix, which applies a homogeneously distributed smoothing effect to the property distribution within the imaging domain. However, when structural information from MRI is available, the relative spatial location of different regions of interest is applied to achieve a heterogeneously distributed smoothing effect to the property estimates.^39,40 More specifically, the segmented MR images yield a volumetric mesh with different assigned regions of interest, which in turn becomes the reconstruction mesh. Incorporating the relative locations of the reconstruction parameters and their associated regions into the reconstruction algorithm is achieved through the regularization matrix, L. Given two nodes i and j in the 3D reconstruction mesh, the corresponding entry in the matrix is 1 if i = j, 0 if the nodes are located in different regions, and −1/N_R if they belong to the same region, R, containing N_R + 1 nodes.^39,40 This technique is called “soft prior” regularization: the spatial prior is considered “soft” because it does not force the property estimates inside an identified region to be constant. Instead, the known spatial locations of different regions adjust the regularization weights to favor uniformity within regions that are assumed to have similar dielectric properties. In addition, when two different regions share the same boundary, the smoothing across their common interface is penalized, i.e., not allowed to vary substantially.

The prior structural information can also be incorporated in the reconstruction algorithm through a different approach called “hard prior.” This technique is based on reducing the number of the reconstruction parameters by assuming complete homogeneity within each region.⁵² Therefore, given R distinct regions, only R values of permittivity and conductivity are estimated. The region identification process is identical to the soft prior case; however, the parameter reduction is implemented during the property update by defining a new Jacobian matrix: $\tilde{J}=J\tilde{K}$, where $\tilde{K}=\left[\begin{array}{c}\hfill K\hfill \\ \hfill K\hfill \end{array}\right]$, and the a priori parameter reduction matrix K is defined as

$${\displaystyle k_{ij}=\left\{\begin{array}{l}1\text{if}\text{node}\left(i\right)\in R_j\hfill \\ 0\text{if}\text{node}\left(i\right)\notin R_j\hfill \end{array},\right.}$$ (3)

where node(i) is the ith node in the reconstruction parameter mesh, and R_j is the jth region identified from the prior structural information. The dimensions of K are the number of nodes by the number of regions (N × R), and therefore, $\tilde{K}$ has the dimensions of 2N × R. As long as R < M, no regularization is required during the image reconstruction, and the property update equation in Eq. (2) can be simplified to

$${\displaystyle \mathrm{\Delta }{k}_{\eta }^2={\left[{\tilde{J}}^T\tilde{J}\right]}^{-1}{\tilde{J}}^T\left[\begin{array}{c}\hfill {\mathrm{\Gamma }}^m-{\mathrm{\Gamma }}^c\left(k_{\eta }^2\right)\hfill \\ \hfill {\mathrm{\Phi }}^m-{\mathrm{\Phi }}^c\left(k_{\eta }^2\right)\hfill \end{array}\right].}$$ (4)

The focus of this paper is to evaluate the performance of the soft prior technique in 3D. However, for comparison purposes, the hard prior approach is also evaluated in one set of simulation experiments.

2.B. Simulation experiments

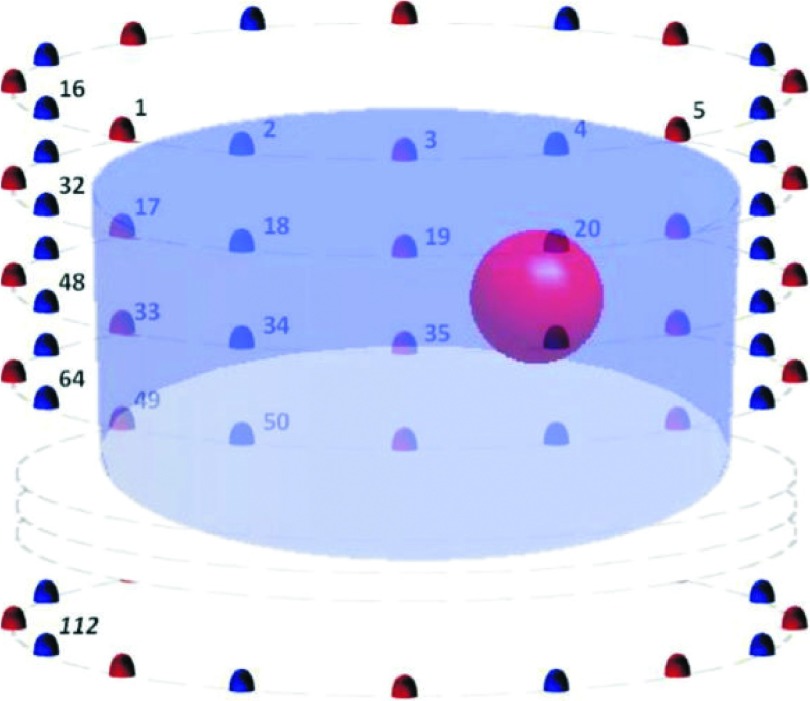
Simulated measurements were generated by our FDTD forward solver with a generalized perfectly matched layer (G-PML) as the absorbing boundary condition, for different shaped and different sized target inclusions. To account for measurement effects, −100 dBm synthetic noise was introduced into the data. In practice, the noise floor of our system is closer to −135 dBm, and therefore, we generally have very large signal-to-noise ratios (SNRs) even for the weakest signals transmitted from the furthest antennas.³¹ In order to avoid the so-called “inverse crime,” i.e., when the discretization in the numerical simulation is the same as the one used in the inversion, different meshes were used for the forward and inverse solvers.⁵³ Generally, the finite difference grid used for generating the simulated data was at least 50% denser than the one used for reconstruction. Figure 1 shows a schematic of the simulation experiments evaluated in this paper. In seven evenly spaced 15.2 cm diameter circles with 1 cm vertical separation, 112 monopole antennas were configured. A spherical inclusion of 1.5 cm radius with dielectric properties of ε_r,Inc = 40.0 and σ_Inc = 2.0 S/m at 1300 MHz (a representative value within the frequency range of the imaging system) was centered at (x, y, z) = (3, 0, 0) cm, where the origin (0, 0, 0) is the center on the imaging tank. The imaging tank was filled with a background medium of ε_r,Bk = 22.4 and σ_Bk = 1.23 S/m at 1300 MHz, which are typical properties of the glycerin/water mixture used in clinical studies. The glycerin/water mixtures generally provide properties reasonably consistent with our clinical results.^34,54

FIG. 1.

Schematic of the imaging domains evaluated: the background diameter was 14 cm (antennas are positioned on a 15.2 cm diameter). The spherical inclusion of 1.5 cm radius was centered at (3, 0, 0) cm.

In order to compare the no prior and soft prior regularizations in 3D and study the effects of factors such as the reconstruction mesh density, imperfect and false spatial priors, and the size and shape of target inclusions, a set of 3D simulation experiments was performed.

2.B.1. No prior versus soft prior regularization

The synthetic data were reconstructed using both the soft prior and our original Tikhonov (no prior) regularizations. The 3D soft prior mesh was composed of 3083 nodes and 16 257 tetrahedral elements, whereas for the no prior case, a cylindrical mesh of 7 cm radius, 6 cm height, composed of 3594 nodes and 15 095 tetrahedral elements, was used. For quantitative comparison, the corresponding errors [see Sec. 2.D—Eq. (5)] were calculated, accordingly. Past experience has demonstrated that mesh size differences on this order have no appreciable effect on the final results.

2.B.2. Number of the reconstruction nodes

While higher density meshes may provide better spatial resolution,⁵⁴ they can considerably increase overall computational time. Thus, knowing how the number of nodes in the reconstruction mesh influences the soft prior recovered dielectric properties is important. To study the question, a set of meshes with varying node densities was used to reconstruct the synthetic data using the soft prior regularization. A list of these meshes (including the number of nodes and elements) is summarized in Table I. All other factors were kept constant to isolate the effects of mesh density.

TABLE I.

Reconstruction meshes used in the soft prior regularization simulation experiment.

Case	Number of nodes	Number of elements
(a)	2180	11 033
(b)	3083	16 257
(c)	4509	21 330
(d)	7972	40 686

2.B.3. Sensitivity to imperfect spatial priors

Obtaining perfect prior structural information of the tissue being imaged may not be possible in practice. Therefore, evaluating the sensitivity of the soft prior technique to imperfect priors is critical. We studied the performance of the 3D soft prior algorithm in the presence of two types of imperfections: size and location of an inclusion.

2.B.3.a. Imperfect prior size of a target inclusion.

In these meshes, the prior location of the inclusion was exact, while the inclusion prior sizes ranged from 0.7 to 2.5 cm (actual inclusion radius was 1.5 cm). For comparison purposes, the total number of nodes as well as the number of nodes in the inclusion region was kept within the same order of magnitude. To compare the recovered dielectric properties with the actual values, the reconstructed permittivity and conductivity values of the background and the target inclusion were extracted at the center of each region.

2.B.3.b. Imperfect prior location of a target inclusion.

In this case, the inclusion prior size was exact, while the inclusion prior location was centered from 0 to 4.2 cm along the x-axis (actual center of the inclusion was 3 cm along the x-axis). Again, the total number of nodes as well as the number of nodes in the inclusion region was kept approximately the same. To evaluate the recovered dielectric properties relative to the actual values, the reconstructed permittivity and conductivity of the background and the target inclusion were extracted at the center of each region.

2.B.4. Sensitivity to a false region of interest

During segmentation of MR images, false regions of interest may be detected, i.e., when regions are assumed to be different from their surroundings, but in reality, they have similar dielectric properties. For the false region of interest study, synthetic data with only one spherical inclusion [1.5 cm radius centered at (3, 0, 0) cm] were used. However, as a part of the prior information, an additional false region of interest at a randomly different location (same size) was delineated in the soft prior reconstruction mesh. The actual and recovered dielectric properties were extracted at the center of the true and false inclusions.

2.B.5. Size and shape of the target

Incorporating structural information into MI can improve the accuracy of the reconstructed dielectric properties. However, improvements may vary for different sizes and shapes of objects being imaged. In order to study the effects of the size and shape of the target inclusion on the recovered dielectric properties, we modified the simulation geometry shown in Fig. 1: 48 monopole antennas were configured in three evenly spaced circles with a 15.2 cm diameter and a 0.5 cm vertical separation. Five different sized spherical and cylindrical shaped inclusions [0.25, 0.5, 0.75, 1.0, and 1.25 cm radius, centered at (3, 0, 0) cm] were embedded in a homogeneous background medium. The corresponding dielectric properties were the same as in the other simulation experiments.

The synthetic 3D measurement data were reconstructed both in 2D and 3D using the original Tikhonov (no priors) as well as the soft and hard prior regularizations. For 3D reconstructions, full-data sets consisting of in-plane and cross-plane measurements were used, whereas for 2D reconstructions, only the middle in-plane data were selected. The no prior 2D images were reconstructed on a circular mesh of 7 cm radius, composed of 559 uniformly distributed nodes and 1044 triangular elements, whereas the no prior 3D images were reconstructed on a cylindrical mesh of 7 cm radius, 6 cm height, comprised of 4608 uniformly distributed nodes and 22 184 tetrahedral elements. The soft and hard prior images, on the other hand, were reconstructed on the 2D and 3D meshes summarized in Table II. Note that because the hard prior approach only recovers a single value for each zone, the images are less informative than for the soft prior case and are easily summarized by tabulated results. In each case, the recovered dielectric properties were evaluated at the center of the inclusion.

TABLE II.

Characteristics of the 2D and 3D meshes used for the simulation experiments with different sized and shaped target inclusions.

Inclusion shape	Inclusion size radius (cm)	2D/3D mesh	Number of nodes	Number of elements
Cylinder	0.25	2D	803	1 537
		3D	3000	13 863
	0.5	2D	512	962
		3D	2160	9 220
	0.75	2D	421	788
		3D	1891	7 850
	1.0	2D	418	780
		3D	1726	7 029
	1.25	2D	429	800
		3D	1628	6 562
Sphere	0.25	2D	803	1 537
		3D	6382	35 131
	0.5	2D	512	962
		3D	3493	18 534
	0.75	2D	421	788
		3D	1990	9 846
	1.0	2D	418	780
		3D	1556	7 428
	1.25	2D	429	800
		3D	1175	5 305

2.C. Breast phantom experiment

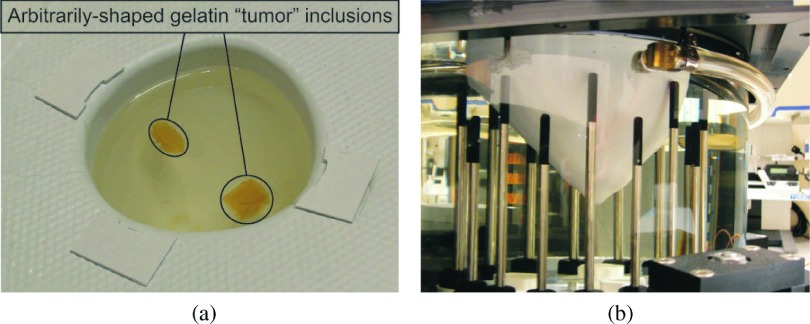
In order to study the robustness of the 3D soft prior technique in more complex shapes and to evaluate the accuracy of dielectric property distributions reconstructed from actual measured data, phantom experiments were performed. Specifically, MR scans of a real breast of cup size B (425 ml) were used to create a breast mold which was then fabricated into a rapid-prototyped thin plastic breast model. Two arbitrarily shaped gelatin “tumor” inclusions were placed inside the breast model, as shown in Fig. 2(a). The mold was filled with a 88:12 glycerin:water mixture (ε_r and σ values reported in Table III, mimicking the dielectric properties of a breast with scattered radiographic density—average ε_r ≈ 14 and σ ≈ 0.3–0.4 S/m).³⁴ The complete model was suspended in the imaging tank filled with a matching liquid of 86:14 mixture of glycerin:water, as illustrated in Fig. 2(b). For quantitative analysis, the dielectric properties of the coupling medium, breast model, and two tumor inclusions were independently measured with an Agilent 85070E Dielectric Probe Kit at 1100 MHz (data in Table III). During the 3D microwave data acquisition, the antenna array transmitted and received the signal at 11 equally spaced (1 cm) vertical positions, at which 16 (transmitters) × 15 (receivers) measurements were collected in each plane. During image reconstruction, only data from the receivers in the closest three planes were used for each transmitter.

FIG. 2.

Breast-shaped phantom experiment: (a) two arbitrary shaped gelatin tumor inclusions suspended in the plastic breast model, (b) rapid-prototyped plastic breast model submerged in the microwave imaging tank.

TABLE III.

Independently measured dielectric properties of the background medium (Bk), breast model (Br), and the tumor inclusions (Inc1 and Inc2) at 1100 MHz.

Bk		Br		Inc1		Inc2
εr	σ	εr	σ	εr	σ	εr	σ
12.2	0.71	14.2	0.77	35.0	1.17	35.0	1.17

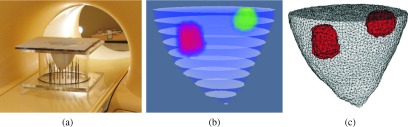
In order to obtain structural priors, the phantom was imaged with MRI. For coregistration, the breast model and tumor inclusions were placed in the identical location in an empty tank with an equivalent antenna array, as shown in Fig. 3(a). Once the MR images were acquired, they were postprocessed and segmented. Figure 3(b) shows a stack of binary-segmented images used to create the corresponding 3D soft prior mesh in Fig. 3(c), which contained 7540 nodes and 34 591 tetrahedral elements. While this mesh was used to reconstruct microwave images with spatial priors, the no prior images were recovered on a 6.9 cm radius, 11 cm height cylindrical mesh composed of 5720 uniformly distributed nodes and 25 800 tetrahedral elements.

FIG. 3.

(a) Photograph of the phantom placed in an empty MI tank inside the MR bore, (b) stack of binary-segmented MR images of the breast phantom experiment, and (c) corresponding 3D soft prior mesh composed of 7540 nodes and 34 591 tetrahedral elements. Elements associated with the segmented inclusions are colored in red (see color online version).

2.D. Error analysis

In order to compare quantitatively the dielectric property measurements recovered with and without spatial priors, the relative root mean square error (RRMSE) in the inclusion was calculated as

$${\displaystyle \text{RRMSE}=\sqrt{\sum _{n=1}^N{\left(\frac{\underset{n}{\overset{\text{recon}}{V}}-\underset{n}{\overset{\text{exact}}{V}}}{V_n^{\text{exact}}}\right)}^2/N},}$$ (5)

where N is the total number of nodes in the inclusion region, $V_n^{\text{recon}}$ is the reconstructed dielectric property value (either permittivity or conductivity) at node n (in the reconstruction mesh), and $V_n^{\text{exact}}$ is the true value of the selected dielectric property at that location. The permittivity and conductivity RRMSE associated with the inclusion region was calculated and summarized accordingly.

To evaluate how the prior structural information improved contrast between the inclusions and the background breast region in the phantom experiment, the percentage of contrast enhancement (CE) was calculated as

$${\displaystyle {\text{CE}}_{t_i}=\frac{-100\times \left(C_{t_i}^{NP}-C_{t_i}^{SP}\right)}{C_{t_i}^{NP}},}$$ (6)

where $C_{t_i}^{NP}$ and $C_{t_i}^{SP}$ are the no prior and soft prior contrasts of the ith inclusion with respect to the true properties of the breast region, respectively, and calculated as

$${\displaystyle C_{t_i}^{NP}=\frac{\sum _{n=1}^{N_{NP}}{V}_n^{NP}/N}{V^{\text{ExactBR}}},C_{t_i}^{SP}=\frac{\sum _{n=1}^{N_{SP}}{V}_n^{SP}/N}{V^{\text{ExactBR}}},}$$ (7)

where $V_n^{NP}$ and $V_n^{SP}$ are the no prior and soft prior reconstructed dielectric property values (either permittivity or conductivity) at node n (in the corresponding reconstruction meshes with N_NP and N_SP nodes), respectively, whereas V^ExactBR is the true dielectric property value of the breast region.

3. RESULTS

In the simulation experiments, we compared no prior with soft prior regularization in 3D, and studied how different factors such as the reconstruction mesh density, imperfect and false spatial priors, and size and shape of target inclusions affect the performance of the soft prior technique. We also performed a comparison of reconstructed 3D images from a realistic breast phantom experiment at 1100 MHz using prior spatial information from MRI.

3.A. Simulation experiments

3.A.1. No prior versus soft prior regularization

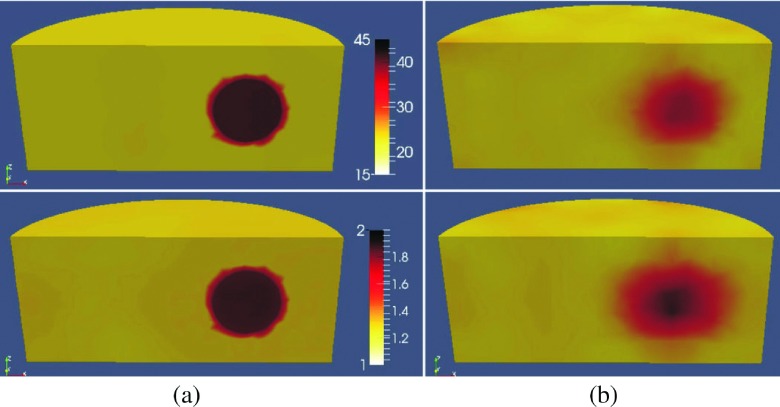
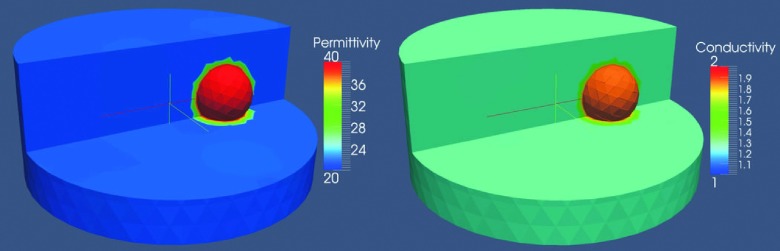
Figures 4(a) and 4(b) show 3D reconstructed images with and without spatial priors, respectively. For visualization purposes, horizontal slices normal to the XY plane at z = 0 along with isosurfaces of the target inclusion are presented. While the target inclusion is successfully detected in both cases, the soft prior reconstructed dielectric properties are much closer to the actual values in both permittivity and conductivity images. Moreover, the level of background artifacts is notably reduced in the images when structural information was incorporated. The permittivity and conductivity RRMSE associated with the inclusion region were 0.8% and 8% for the soft prior, and 22% and 18% for the no prior cases, respectively.

FIG. 4.

3D reconstructed permittivity (top) and conductivity (bottom) images from a simulation experiment at 1300 MHz using (a) soft prior regularization and (b) no prior spatial information.

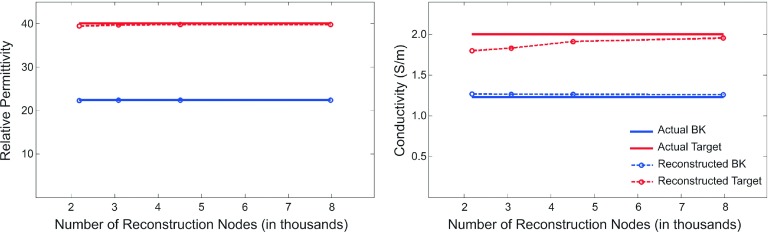
3.A.2. Number of the reconstruction nodes

Figure 5 shows the reconstructed dielectric property values extracted at the center of the inclusion [(3, 0, 0) cm] and at the center of the imaging domain [(0, 0, 0) cm], compared to the actual property values, as a function of the number of reconstruction nodes in Table I. It should be noted that only the centroid values are reported here, mainly due to the fact that the reconstructed properties within the regions evaluated had minor variations (variations which are penalized, and therefore, suppressed by the soft prior regularization technique). For instance, for the results presented in Fig. 4(a), the difference between the reconstructed permittivity values using the average values over the inclusion region vs the center node value was only about 0.004%, whereas the conductivity counterpart was 1.6%. Examination of other cases has provided consistent results. In all cases, both permittivity and conductivity profiles of the target inclusion were effectively characterized. Interestingly, the recovered dielectric property values were similar for different reconstruction meshes spanning a wide range of node numbers. The recovered permittivity values are nearly independent of the number of reconstruction nodes, while the target region conductivity values improved by approximately 10% when a denser reconstruction mesh was used (2180 vs 7972 nodes).

FIG. 5.

3D recovered permittivity (left) and conductivity (right) profiles compared to the exact property values as a function of number of nodes in the 3D soft prior reconstruction mesh.

3.A.3. Sensitivity to imperfect spatial priors

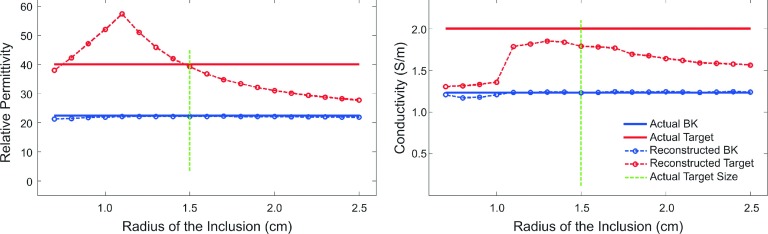
3.A.3.a. Imperfect prior size of the target inclusion.

The dielectric property values at the center of each region were plotted in Fig. 6 as a function of the spatial inclusion radius in the reconstruction mesh. The exact size of the target inclusion is marked by a green vertical line, which indicates where the exact prior information was used. As the radius of the inclusion in the reconstruction mesh increased from below the exact prior, both reconstructed permittivity and conductivity values of the target inclusion approached those of the background medium (Bk). At the other end, as the prior size of the inclusion decreased, the reconstructed conductivity values also approached those of the background medium, while their permittivity counterparts first increased and then decreased, toward the background values.

FIG. 6.

Soft prior recovered permittivity (left) and conductivity (right) values at the center of each region compared to the exact property distributions, using different inclusion-sized meshes as prior information.

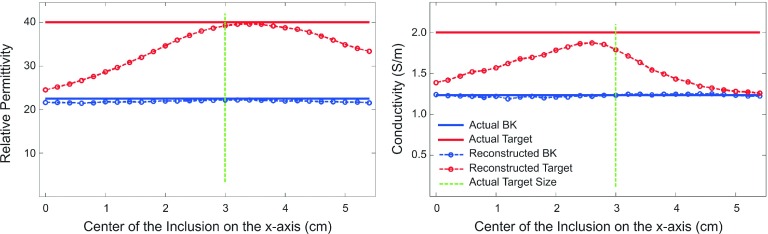
3.A.3.b. Imperfect prior location of the target inclusion.

The dielectric property values at the center of each region are plotted in Fig. 7 as a function of position along the X-coordinates of the prior spherical inclusion center where the exact location is marked with a green vertical line. Overall, the imperfect prior location of the target had a similar effect (hill-shaped curve) on both recovered permittivity and conductivity profiles. When the prior and actual target locations matched, the reconstructed permittivity and conductivity values of the inclusion approached their exact profiles. However, the most accurate values for each property were not recovered when the mismatch was zero, but rather when the prior inclusion was slightly offset. The offset for the permittivity and conductivity profiles is in opposite directions making the recovered values at the actual target location (green vertical line), the most accurate solution for both permittivity and conductivity. When the partial overlap between the actual and prior target volumes decreased, the recovered property distributions of the inclusion approached those of the background.

FIG. 7.

Soft prior 3D recovered permittivity (left) and conductivity (right) values at the center of each region compared to the exact property distributions, using different inclusion-located meshes as prior information.

3.A.4. Sensitivity to a false region of interest

Figure 8 shows 3D reconstructed images from a soft prior mesh with a false region of interest. For illustration purposes, the reconstructed images are sliced so that both the true and false inclusion regions are exposed. Moreover, isosurface thresholds of ε_r = 39 and σ = 1.85 S/m (target inclusion) are applied to the reconstructed permittivity and conductivity images, respectively.

FIG. 8.

3D reconstructed permittivity (left) and conductivity (right) images obtained from the corresponding soft prior meshes with a false region of interest. Isosurface thresholds of ε_r = 39 and σ = 1.85 S/m are applied to visualize the reconstructed volume of the target inclusion.

The false region of interest presents a subtle variation from the background properties. The recovered properties and calculated errors indicate that the false region appears as a very small increase (less than 0.5%) in the permittivity image, but a slightly larger increase (3%) in the conductivity image. In the true inclusion region, the permittivity error is only 1%, while the conductivity error is somewhat larger, but still only 5%.

3.A.5. Size and shape of the target

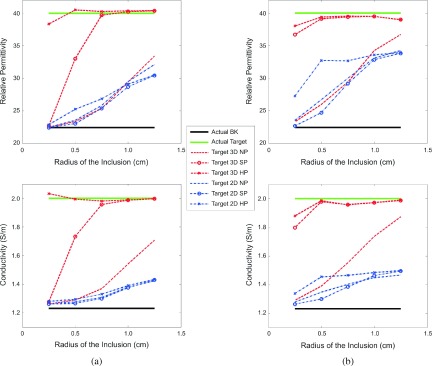
The dielectric property values at the center of each region are plotted as a function of inclusion radius using different reconstruction algorithms, including 2D and 3D with no priors, 3D soft priors, and 3D hard priors, respectively. Figures 9(a) and 9(b) show the reconstructed values of the spherical and cylindrical inclusions, respectively.

FIG. 9.

Recovered permittivity (top) and conductivity (bottom) values at the center of the (a) spherical and (b) cylindrical inclusions as a function of the inclusion radius using different reconstruction approaches (2D and 3D with no prior, 3D soft prior, and 3D hard prior, respectively) (see color online version).

Overall, as the size of the inclusion decreased, the recovered dielectric properties were less accurate. In addition, the properties of the cylindrical inclusion were generally more accurate than those of the spherical inclusion, especially for the smaller size targets. This improvement was even more prominent when prior structural information was incorporated into the reconstruction algorithm. Results for the spherical case are more indicative of the expected clinical performance; although, the outcomes from the cylindrical geometry provide information that is more directly related to previous 2D results. The no prior 3D reconstructed permittivity values (red dotted lines in the upper portion of Fig. 9) were similar to those recovered in 2D with and without prior information (all blue lines). However, the corresponding conductivity values (the bottom graphs in Fig. 9) were considerably more accurate when the radius of the inclusion was greater than 0.5 cm, indicating that the 3D reconstruction algorithm had a more substantial impact on the conductivity profiles.

Comparisons between the two regularization methods (i.e., hard priors and soft priors) show that the hard prior properties are slightly superior to those reconstructed with the soft prior regularization. This effect is more pronounced for the 3D reconstructed profiles (red dotted lines) of smaller sized spherical inclusions in Fig. 9(a) and may be due to the fact that with the hard priors, the number of unknowns—i.e., the number of reconstruction parameters—is drastically reduced from 418 to 803 in 2D and 1175 to 3000 in 3D to only two parameters for each of the two identified regions (Bk and Target), and as a result, no extra regularization is required during the reconstruction (λ = 0). On the other hand, in the soft prior technique, the number of unknowns (i.e., the number of nodes in the customized reconstruction mesh) is considerably greater than the number of measurements and requires additional regularization (λ > 0) to stabilize the image reconstruction.

3.B. Phantom experiments

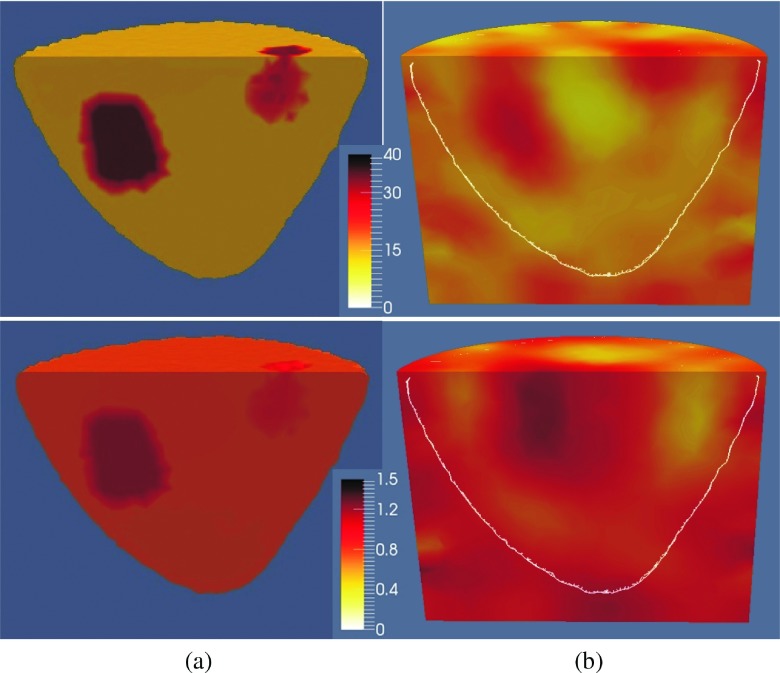
The 1100 MHz reconstructed permittivity (top) and conductivity (bottom) images with and without spatial priors are presented in Figs. 10(a) and 10(b), respectively. To visualize the recovered profiles of the regions of interest, the reconstructed volumes are sliced vertically through the breast region.

FIG. 10.

A vertical slice through the (a) soft prior and (b) no prior reconstructed permittivity (top) and conductivity (bottom) images of a breast phantom with two inclusions at 1100 MHz. The white line on the no prior image shows the actual outline of the breast.

When the soft prior regularization is used, inclusions are successfully characterized in both permittivity and conductivity, although they appear weaker in the conductivity image. For the no prior algorithm, the inclusions are successfully detected only in the permittivity images. For the corresponding conductivity images, only the lower inclusion (Inc2) appears to be detected. In addition, its size was larger and its location was shifted from the actual position. In all cases, the recovered property distributions of the breast were closely matched to the exact values. The soft prior and no prior RRMSE are summarized in Table IV.

TABLE IV.

Soft prior and no prior RRMSE of the recovered properties in each region of the breast phantom with two inclusions.

	Br		Inc1		Inc2		All regions
RRMSE	εr	σ	εr	σ	εr	σ	εr	σ
Soft priors	0.06	0.11	0.09	0.28	0.09	0.11	0.06	0.12
No priors	0.29	0.25	0.44	0.44	0.35	0.23	0.30	0.25

4. DISCUSSION

The results presented in this paper confirm that the recovered soft prior dielectric properties are more accurate than those estimated with no priors. In addition, they are somewhat insensitive to the 3D reconstruction mesh density. While the reconstructed permittivity profiles were accurate, the conductivity values improved as the reconstruction mesh density increased from 2000 to over 4000 nodes, suggesting that for a breast of this size, a reconstruction mesh composed of 3000–4000 nodes is sufficient.

In terms of the sensitivity of the algorithm to the imperfect prior size of the target, changes of 30% and 15% occurred in the recovered permittivity and conductivity values, respectively, when more than 125% variation was applied to the target region volume (changing inclusion radius from 1.3 to 1.7 cm). A comparison of these results with those reported in Golnabi et al.⁴⁰ reveals that the soft prior algorithm is less sensitive to imperfect prior size of the target in 3D than that it is in 2D.

In the presence of imperfect prior location data, minor variations were observed in the recovered dielectric properties. In fact, the most accurate values were obtained at the exact prior location of the inclusion. In terms of the sensitivity of the algorithm to imperfect prior location of the target, changes of 4% and 15% in the recovered permittivity and conductivity values occurred, respectively, when the prior target region was shifted by 87% of its radius (i.e., shifting the center of the inclusion from 2.6 to 3.4 cm).

We also showed that the 3D soft prior algorithm was able to manage situations where a false region of interest was identified as a part of the prior structural information. Under these conditions, the false region of interest showed minimal variations (<5%) around the background properties.

Finally, the soft prior regularization considerably improved the recovered dielectric property distributions in a realistic breast phantom. In fact, the permittivity RRMSE was about 5 times smaller than the no prior case when the soft prior regularization was applied. The improvement was less pronounced in the conductivity profiles, as the soft prior RRMSE was only about 2 times smaller than those in the no prior case. When the soft prior regularization was applied, contrast in both inclusions was enhanced relative to the background breast region. More specifically, the contrast enhancement in the upper inclusion (Inc1) was 44% and 25% for permittivity and conductivity, respectively, whereas the lower inclusion (Inc2) had a smaller improvement in contrast enhancement of 29% for permittivity and 8% for conductivity.

5. CONCLUSIONS

We have extended our soft prior regularization technique from 2D to 3D and evaluated its performance in tomographic microwave imaging. The soft prior technique is based on encoding prior spatial information into the image reconstruction algorithm. Results from 3D simulation and phantom experiments confirm that the incorporation of structural information in the form of a soft constraint can considerably improve the accuracy of the property estimates in predefined regions of interest. The presence of false priors (i.e., predefined regions without actual contrast) was well tolerated, as were inaccuracies in the size and spatial location of the region of interest. These findings are encouraging and establish a strong foundation for using the soft prior technique in clinical studies, where our microwave imaging system and MRI can simultaneously collect breast exam data in patients.