Abstract
Recent anatomical and functional characterization of cortical inhibitory interneurons has highlighted the diverse computations supported by different subtypes of interneurons. However, most theoretical models of cortex do not feature multiple classes of interneurons and rather assume a single homogeneous population. We study the dynamics of recurrent excitatory-inhibitory model cortical networks with parvalbumin (PV)-, somatostatin (SOM)-, and vasointestinal peptide-expressing (VIP) interneurons, with connectivity properties motivated by experimental recordings from mouse primary visual cortex. Our theory describes conditions under which the activity of such networks is stable and how perturbations of distinct neuronal subtypes recruit changes in activity through recurrent synaptic projections. We apply these conclusions to study the roles of each interneuron subtype in disinhibition, surround suppression, and subtractive or divisive modulation of orientation tuning curves. Our calculations and simulations determine the architectural and stimulus tuning conditions under which cortical activity consistent with experiment is possible. They also lead to novel predictions concerning connectivity and network dynamics that can be tested via optogenetic manipulations. Our work demonstrates that recurrent inhibitory dynamics must be taken into account to fully understand many properties of cortical dynamics observed in experiments.
Keywords: inhibition, V1, modeling
the role of inhibitory neurons in visual processing has been extensively studied, playing a role in, for example, orientation selectivity (Shapley et al. 2003), surround suppression (Ozeki et al. 2009), and expansion of dynamic range (Liu et al. 2011). Mechanistic computational models of visual processing have also frequently incorporated an inhibitory neuronal subpopulation (Somers et al. 1995; Ben-Yishai et al. 1995; Ozeki et al. 2009; Hansel and van Vreeswijk 2012). Few models have incorporated different subtypes of interneuron (Wang et al. 2004; Vierling-Claassen et al. 2010), with most studies assuming that inhibitory neurons can be grouped into a single population with homogeneous functional and anatomical properties (Vogels et al. 2005).
However, recent work in mouse V1 has revealed substantial heterogeneity in the connectivity, function, and dynamics of different inhibitory neuron subtypes. In mouse cortex, three major interneuron subtypes, parvalbumin-expressing (PV), somatostatin-expressing (SOM), and vasointestinal peptide-expressing (VIP) neurons comprise 80–90% of inhibitory neurons (Markram et al. 2004; Rudy et al. 2011). Connectivity between these subtypes follows stereotyped rules: for example, SOM neurons are strongly inhibited only by VIP neurons and VIP neurons strongly inhibit only SOM neurons (Pfeffer et al. 2013). Furthermore, these neurons perform distinct computational roles: in layer 2/3, VIP neurons disinhibit the excitatory pyramidal neuron (E) population during locomotion via suppression of SOM neurons (Fu et al. 2014), while activation of PV or SOM neurons divides or subtracts, respectively, E neuron responses to oriented bars (Wilson et al. 2012; Atallah et al. 2012).
Given these observations, mechanistic models of visual processing must be extended to include heterogeneous interneuron subtypes. The need for consistent models is especially important given ongoing debates on the role of recurrent V1 inhibitory circuitry in visual processing in mouse. It has been argued that a critical role of inhibition is to stabilize the intrinsically unstable dynamics of recurrent excitation (Murphy and Miller 2009), consistent with the dynamics of surround suppression in cat V1 (Ozeki et al. 2009) and a recent model of orientation selectivity in mouse V1 (Hansel and van Vreeswijk 2012). However, experimental reports suggest that recurrent excitation is weak in layer 2/3 of mouse V1 (Atallah et al. 2012), questioning the need for inhibition to stabilize cortical dynamics. The mechanism of surround suppression in this region is also debated (Ozeki et al. 2009; Adesnik et al. 2012), with the contributions of SOM and PV interneurons remaining unclear (Adesnik et al. 2012; Ayaz et al. 2013). Finally, the effects of activation of different subtypes of inhibitory interneuron on excitatory neuron tuning curves have also been the subject of recent discussion (Wilson et al. 2012; Atallah et al. 2012; Lee et al. 2012; Seybold et al. 2015). So far, a consistent theoretical framework in which to investigate the circuit mechanisms underlying these observations has been lacking.
We study the impact of heterogeneous inhibitory subpopulations using a recurrent network model of mouse V1 with connectivity constrained by previous experimental observations (Pfeffer et al. 2013). Our analysis generalizes the notion of inhibition stabilized networks (Tsodyks et al. 1997; Ozeki et al. 2009) to architectures with multiple, distinct inhibitory subpopulations. Using this framework, we first investigate the dynamics of surround suppression (Adesnik et al. 2012) and disinhibition (Fu et al. 2014) based on recent experimental observations. Next, we evaluate different hypotheses concerning the mechanisms of the subtractive and divisive shifts observed experimentally during optogenetic activation of SOM and PV neurons (Wilson et al. 2012; Atallah et al. 2012; Lee et al. 2012; Seybold et al. 2015) and propose a testable model for how these shifts can occur. Given that many features of interneuron organization and function in V1 are conserved in other cortical areas (Avermann et al. 2012; Hamilton et al. 2013; Kvitsiani et al. 2013; Pi et al. 2013), many of our results may be applicable to neural circuit dynamics beyond mouse visual cortex.
MATERIALS AND METHODS
Paradoxical effects of inhibitory neuron modulation.
We consider a firing rate network with M populations obeying the Wilson-Cowan equations (Wilson and Cowan 1972):
| (1) |
where rA denotes the average firing rate of neurons in population A = 1 ․ ․ ․ M, JAB is the connection strength from population B to A, μA is the bias current to population A, τA is its time constant, and fA(u) is its firing rate response function to an input current u. We assume that the network has some equilibrium r0 = (r1 ․ ․ ․ rM)T, near which the dynamics of Eq. 1 can be approximated by the linear system:
| (2) |
Here Δr = r − r0 and T is a diagonal matrix whose Ath diagonal element is τA. Letting GA = represent the gain of population A at equilibrium, WAB = GAJAB represents the effective interaction from population B to A, and bA = GAΔμA represents the effect of a perturbation to the bias current μA. We note that this effective interaction depends both on the transfer of presynaptic firing rate to synaptic current and synaptic current to postsynaptic firing rate, evaluated at equilibrium. Thus WAB will be reduced or increased by, for example, synaptic depression and facilitation, respectively.
Suppose that population 1 is excitatory and 2 ․ ․ ․ M are inhibitory. Consider a small perturbation b = (0, b2, b3, ․ ․ ․, bM)T that does not target the excitatory population. The steady-state change in firing rates Δs = limt→∞Δr is obtained by setting Eq. 2 to zero: (I − W)Δs = b. Letting e1 = (1, 0, 0, ․ ․ ․ , 0)T, we therefore have e1T (I − W)Δs = e1Tb = 0. Hence,
| (3) |
| (4) |
Note that the sign of 1 − W11 determines the stability of the excitatory subnetwork: it is stable when W11 < 1 [noninhibition-stabilized network (non-ISN) regime] and unstable when W11 > 1 (ISN regime) (Murphy and Miller 2009). Also note that W1BΔsB represents the summed change in inhibitory current onto the excitatory population due to the perturbation. As long as the gain GB is positive, we have the following two cases:
1) If the excitatory subnetwork is stable (non-ISN), then the sign of the change in the firing rate of the excitatory population and of the change in the total inhibitory current are opposite.
2) If the excitatory subnetwork is unstable (ISN), then the sign of the change in the firing rate of the excitatory population and the sign of the change in the total inhibitory current are the same.
Modulation of inhibitory subpopulations.
We consider the dynamics of the linearized system in Eq. 2 with Δr = (rE, rP, rS, rV)T representing the changes in the excitatory (E), PV (P), SOM (S), and VIP (V) populations. The coupling matrix is given by:
| (5) |
The steady-state change in firing rates is given by Δs = (I − W)−1b. We consider a modulation that targets VIP neurons: b = (0, 0, 0,ϵ)T. In this case:
| (6) |
Note that det(I − W) > 0 if the system described by Eq. 2 is stable. We do not explicitly write the expression for ΔsV due to its length.
Linear firing rate model.
For the linear firing rate model of mouse V1,
| (7) |
WEE was set to either 0.8 (non-ISN) or 1.2 (ISN). Firing rates evolved according to Eq. 2, with τA = 20 ms. The firing rates were given by r = r0+Δr, where r0 = (4, 9, 5, 3)T Hz. The modulation was given by b = (0, 0, 0, 5)T
For the spatial model of surround suppression, firing rates depended on the spatial position x:
| (8) |
.
Δr(x) was discretized into 200 points with x (−10, 10). The coupling matrix K(x − y) was given by KAB(x − y) = , where the normalization constant Z ensured the integral of KAB equaled WAB. For all connections except the excitatory to SOM neuron connections, λAB → 0 (only local connectivity). Otherwise, λSE = 1. The input bA(x) was equal to aAe−x2/σ2, with aE = 5, aP = 5/2, and aS = aV = 0. σ Ranged from 1 to 3.
Spiking neuron dynamics.
The voltage of neuron i in population A, ViA, was modeled as an adaptive exponential integrate- and-fire neuron (Brette and Gerstner 2005):
| (9) |
Parameters were chosen based on reported electrophysiological measurements from mouse V1 and S1 where V1 data could not be found. Where available, the reference used to determine the relevant parameter is included. The membrane capacitance was Cm = 180 pF for E neurons and Cm = 80 pF for I neurons (Zhou and Roper 2011). All neurons had a rest voltage of EL = −60 mV (Gentet et al. 2010). gL = 6.25 nS for E neurons and 5 nS for I neurons (Avermann et al. 2012). The reversal potential Esyn was 0 mV for excitatory synapses and −67 mV for inhibitory synapses (Pfeffer et al. 2013). The exponential integrate-and-fire slope parameter ΔT was 0.25 mV for PV neurons and 1 mV otherwise (Brette and Gerstner 2005). The threshold voltage VT,i was chosen from a Gaussian distribution, with a mean of −40 mV for E and PV neurons and −45 mV for SOM and VIP neurons, and a standard deviation of 3 mV (Avermann et al. 2012; Gentet et al. 2010; Zhou and Roper 2011).
When ViA diverged, the neuron spiked and the voltage was reset to Vre = −60 mV (Gentet et al. 2010) for an absolute refractory period of 2 ms. The adaptation current followed:
| (10) |
with a = 4 nS and τw = 150 ms (Brette and Gerstner 2005). For PV neurons, the adaptation current was set to zero consistent with the weak adaptation of these neurons (Pfeffer et al. 2013). wiA was incremented by an amount b = 8 pA whenever the corresponding neuron spiked (Brette and Gerstner 2005).
The conductance due to input from population B was given by:
| (11) |
where * denotes convolution. The synaptic kernel was given by a difference of exponentials: . Rise times were 0.5 ms for synapses from E and PV and 1 ms for SOM and VIP neurons. Decay times were 2 ms for synapses from E neurons, 3 ms for PV neurons, and 4 ms for SOM and VIP neurons. yjB(t) = FjB(t)DjB(t)δ(t − tj,kB) represented the instantaneous neurotransmitter release of neuron j in population B and followed a standard Tsodyks-Markram model of short-term synaptic plasticity (Tsodyks and Markram 1997) with facilitation F and depression D. E ← E and PV ← E exhibited depression with UD = 0.75, and all connections from PV neurons exhibited depression with UD = 0.9. The depression time constant was 800 ms. Only SOM E connections exhibited facilitation, with UF = 0.5, Fmax = 2, and a time constant of 200 ms. These parameters were chosen to produce short-term synaptic plasticity dynamics consistent with reported measurements (Ma et al. 2012; Reyes et al. 1998).
For two-compartment simulations, E neurons were characterized by a somatic voltage Vi,sE and a dendritic voltage Vi,dE, with a coupling conductance of gsd = 18.75 nS. The ratio of somatic to total surface area was κ = 0.3. The current due to the dendritic compartment's effect on the soma was , while the soma's effect on the dendrite was . E and SOM connections targeted the passive dendritic compartment, while PV connections targeted the somatic compartment. The synaptic conductances were chosen so that unitary postsynaptic potentials were the same magnitude as in the single compartment model.
Spiking neuron connectivity.
The network consisted of 400 E, 50 PV, 25 SOM, and 25 VIP neurons with orientation preference arranged uniformly on (−π/2, π/2). For tuned connections, connection probabilities were given by pijAB = p0AB[1 + p2ABcos(θiA − θjB)], where θiA is the orientation preference of neuron i in population A. E ← E connections had baseline probability p0EE = 0.1, SOM ← VIP had p0SV = 0.4, and all other probabilities had a baseline of 0.6, if they existed (Pfeffer et al. 2013). p2 Was nonzero only for connections involving E and PV neurons, with p2EE = 0.8 and p2PE = 0.1. For the network with tuned PV inhibition, p2EE = 0.8 and p2PE = 0.1.
External input was provided by background excitatory Poisson inputs with rates These rates were (r0E, r0P, r0S, r0V) = (2.4, 0.4, 0.8, 0.3) Hz. This input was tuned only for E neurons with r0E = 0.2 and, for the tuned PV network, r2P= 0.2. To mimic optogenetic activation, Ii was increased by 25 and 45 pA for PV and SOM neurons, respectively (55 and 25 pA for the 2 compartment simulation).
Finally, if a connection existed, the synaptic conductance was given by gi,synAB = GAB, with
| (12) |
leading to inhibitory postsynaptic current sizes consistent with reported data (Pfeffer et al. 2013).
Simulations were done with a time step of 0.1 ms and a maximum voltage of 20 mV before spike reset.
RESULTS
Inhibitory stabilization of excitatory activity.
We begin by reviewing the dynamics of a simple network with one excitatory and one inhibitory population (Wilson and Cowan 1972; Grossberg 1973; Ermentrout and Cowan 1979). Such networks have been extensively analyzed, and their dynamics can be broadly classified into two regimes. In the first regime, the recurrent excitatory coupling strength WEE is weak, such that the network activity remains stable even in the absence of inhibitory feedback. In the second, WEE is strong enough that, if feedback inhibition were not present, excitatory activity would be unstable and increase to saturation. A network satisfying the latter condition is known as an ISN (Murphy and Miller 2009).
ISNs and non-ISNs have distinct response properties. A striking difference is the shift in firing rates due to perturbations of the inhibitory population. In non-ISNs, a depolarizing perturbation applied to inhibitory neurons causes an increase in their firing rate and corresponding decrease in excitatory firing (Fig. 1A). The same perturbation applied to inhibitory neurons within an ISN leads to an initial increase in inhibitory firing rates, which then leads to suppression of excitatory neurons, as expected. However, in contrast to non-ISNs, after this initial transient, inhibitory firing rates begin to decrease due to the loss of recurrent excitation, eventually reaching a steady state below their initial value (Fig. 1B). Hence, depolarizating current applied to inhibitory neurons surprisingly reduces their firing rate in the steady state. This “paradoxical effect” of inhibitory neuron activation has been observed in rat CA1 (Tsodyks et al. 1997) and has been used to explain the dynamics of surround suppression in cat V1 (Ozeki et al. 2009).
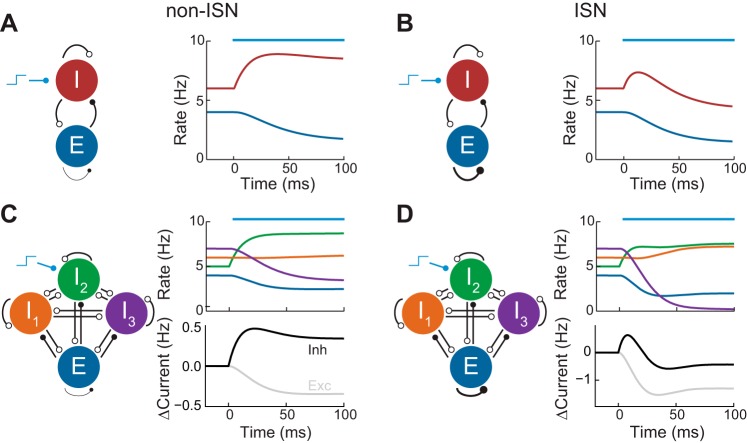
Fig. 1.
Inhibition stabilized networks (ISNs) and non-ISNs. A, left: schematic of non-ISN with excitatory (E) and inhibitory (I) populations. Open circles represent inhibitory synapses while closed circles represent excitatory synapses. Right: E and I population firing rates in response to a stimulus applied to the I population (blue bar). B: same as A but for an ISN in which the EE connection is strong. C, left: schematic of non-ISN with 3 inhibitory populations. Right: population firing rates and change in magnitude of the total excitatory and inhibitory currents received by the excitatory population in response to a stimulus applied to population I2 (blue bar). D: same as C but for an ISN.
We begin by generalizing the “paradoxical effect” of inhibitory neuron modulation to networks with multiple inhibitory neuron subtypes. We consider any network in which neurons of a given subtype can be treated homogeneously, synaptic currents are additive, and perturbations are sufficiently weak. Calculations based upon these assumptions (see materials and methods) yield the following result: if depolarizing current is injected to an arbitrary subset of inhibitory neuron subpopulations and consequently decreases excitatory firing rates, then 1) if the network is non-ISN, the total inhibitory current recorded within excitatory neurons should be enhanced, or 2) if the network is ISN, the total inhibitory current recorded within excitatory neurons should, paradoxically, be reduced in the steady state. The same holds in reverse: if excitatory firing rates increase, then non-ISNs will show reduced inhibitory current, while ISNs will show increased inhibitory current.
To illustrate this result, we considered a network with three inhibitory subpopulations (I1, I2, and I3) and coupling between all populations. A static depolarizing bias input was applied to I2, leading to a complex transient response in all populations. After the network reached steady state, the excitatory firing rates were reduced. When excitatory coupling was weak, this reduction was accompanied by an increase in the inhibitory recurrent recorded onto the excitatory population (Fig. 1C). However, when the excitatory coupling was increased so that the network was ISN, the inhibitory current was reduced in the steady state (Fig. 1D). This reduction was not immediately visible in the firing rates of the inhibitory populations, some of which increased and some of which decreased. In particular, for the chosen parameters, the stimulated population increased its rate, unlike the two-population case (Fig. 1B).
In summary, the relationship between steady states of excitatory firing rate and inhibitory-to-excitatory current determines whether the system is in the ISN regime. ISNs exhibit the “paradoxical effect” that a decrease in inhibitory current co-occurs with a decrease in excitatory firing rates, while the opposite relationship occurs in non-ISNs. In networks with only a single inhibitory subpopulation, the monotonic relationship between inhibitory firing rate and inhibitory-to-excitatory current means that recordings of inhibitory neuron firing rates can be used as a proxy for this current. When multiple inhibitory subpopulations are present, recurrent interactions dissociate the firing rate of any particular subpopulation with the total inhibition excitatory neurons receive. Hence, firing rates in response to a perturbation alone are insufficient to characterize the net effect of inhibition.
Recurrent dynamics in mouse V1.
In recent years there has been significant characterization of the circuitry of layer 2/3 and 5 of mouse V1 (Pfeffer et al. 2013). Specifically, paired recordings have established that pyramidal neurons are inhibited primarily by PV and SOM neurons, SOM neurons are primarily inhibited by VIP neurons, and PV neurons are inhibited by both PV and SOM neurons (Fig. 2A). Nonetheless, prior models of layer 2/3 of mouse V1 differ with respect to the ISN operating regime. Hansel and van Vreeswijk (2012) developed a balanced network model with strong recurrence, placing the network in the ISN regime. In contrast, other models have assumed that recurrent excitation is weak, placing the network in a non-ISN regime (Atallah et al. 2012). We apply the analysis of the previous section to a model network of layer 2/3 of mouse V1 with PV, SOM, and VIP interneurons (see materials and methods) and discuss how the existing literature may support a non-ISN regime.
Fig. 2.
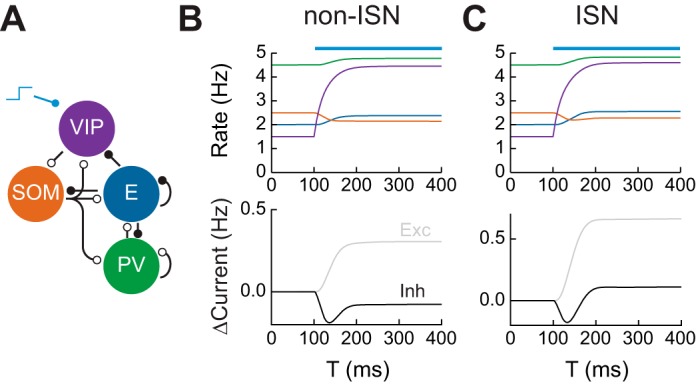
Connectivity in mouse V1 and disinhibition. A: connectivity between neuronal subtypes in mouse V1. Open circles represent inhibitory synapses while closed circles represent excitatory synapses. SOM, somatostatin; PV, parvalbumin. B, top: firing rates of neuronal subpopulations in a non-ISN in response to activation of vasointestinal peptide (VIP)-expressing interneurons at T = 100 ms. Bottom: change in magnitude of total excitatory and inhibitory currents received by the excitatory subpopulation. C: same as B for an ISN.
We begin by examining the response of the network to activation of VIP interneurons. VIP activation increases the gain of E neurons in layer 2/3 of visual cortex during locomotion via disinhibition (Fu et al. 2014) and performs similar roles in somatosensory, auditory, and prefrontal cortex (Lee et al. 2013; Pi et al. 2013). We simulated the firing rate network and applied a depolarizing current to the VIP subpopulation. In both non-ISN and ISNs, this led to suppression of SOM neurons and activation of E neurons (Fig. 2, B and C). Consistent with the predictions of the previous section, this activation was accompanied by reduced inhibition onto E neurons in the non-ISN case (Fig. 2B) but increased inhibition in the ISN case (Fig. 2C).
To investigate what controls the magnitude of VIP-mediated disinhibition, we can use our knowledge of network connectivity to derive expressions for the response to the perturbation. Let WAB ≥ 0 represent the effective strength of connections from population B to population A. Denote the E, PV, SOM, and VIP populations by E, P, S, and V, respectively. Then, the steady-state change in E firing rate can be written as ΔsE ∝ WSV[WES(1 + WPP) − WEPWPS]. Similar expressions can be obtained for different forms of perturbation (see materials and methods). This equation has two terms: the first is proportional to WES, representing SOM inhibition of E neurons, while the second is proportional to WEPWPS, the strength of the E⃖PV⃖SOM pathway. For the net effect of VIP activation to be disinhibitory, the first term must be larger than the second, a requirement that is true in layer 2/3 of mouse V1 (Adesnik et al. 2012).
Does mouse visual cortex operate in the ISN or non-ISN regime? In layer 2/3 of anesthetized mice, optogenetic suppression of PV neurons leads to increased E neuron firing accompanied by reduced total inhibitory current recorded in E neurons (Atallah et al. 2012). This argues that layer 2/3 of anesthetized mouse V1 is a non-ISN, calling into question whether standard balanced network models can account for its dynamics (Hansel and van Vreeswijk 2012). On the other hand, other layers of V1 such as layer 4 receive more intralaminar excitation than layer 2/3 (Lien and Scanziani 2013). Future experiments will determine whether these other layers lie in the ISN regime.
Mechanisms of surround suppression.
We next study the effects of surround suppression in a spatially extended network. Lateral E projections in layer 2/3 preferentially target SOM neurons, which increase their firing rate during surround stimulation unlike PV neurons (Adesnik et al. 2012). This appears to be in contrast to previous models of surround suppression motivated by cat V1, in which an ISN exhibits decreased excitatory and inhibitory activity during surround suppression (Ozeki et al. 2009).
We extended the model of the previous section by modeling E, PV, SOM, and VIP populations at each point in a one-dimensional space. Networks at different spatial locations interacted via long-range excitatory projections that targeted SOM neurons with a Gaussian profile (see materials and methods). Stimuli were modeled as Gaussian depolarizing current applied to E and PV neurons. Stimuli evoked spatially localized activity whose width increased as the stimulus size was increased from center-only (Fig. 3B) to center + surround (Fig. 3C).
Fig. 3.
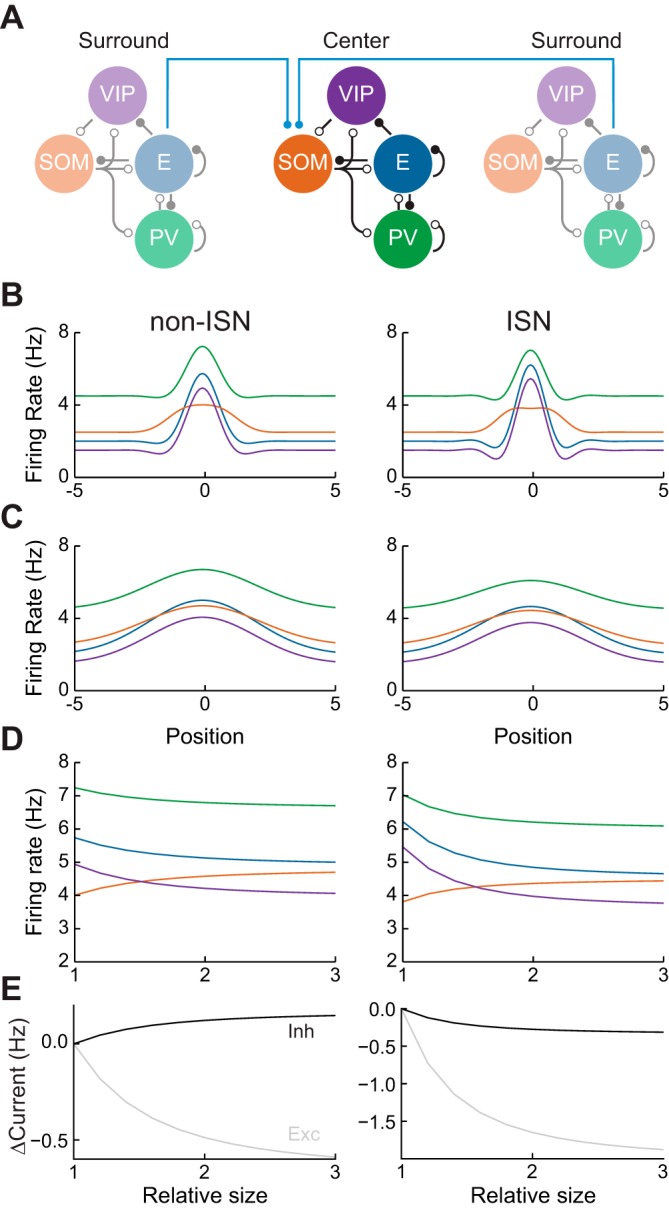
Dynamics of surround suppression. A: surround suppression circuit. Local networks as in Fig. 2 interact via long-range projections from excitatory subpopulations to SOM subpopulations (blue lines). B: firing rates of each subpopulation as a function of distance from stimulus center, when a center stimulus is presented. C: same as B for a center + surround stimulus. D: firing rates of each neuronal subtype at the stimulus center, as a function of relative stimulus size. E: change in magnitude of total excitatory and inhibitory currents received by excitatory neurons at the stimulus center.
To examine surround suppression, we measured the firing rate of neurons at position zero (center of the stimulus-evoked depolarization) as a function of the stimulus width. All neuron subtypes exhibited surround suppression, except for SOM neurons, which exhibited facilitation (Fig. 3D). This was true for both ISN and non-ISNs. Hence, the presence of surround facilitation in SOM neurons (Adesnik et al. 2012) is compatible with the network being in the ISN regime.
This observation can be understood using our perturbative framework, examining the response of an isolated population in response to surround input to the SOM population. In this case, the change in SOM firing rate can be written as ΔsS ∝ (1 + WPP)(1 − WEE) + WEPWPE. Since ISNs have WEE > 1, then the sign of the first term in this expression depends on whether the network is ISN or not: if it is ISN, the term is negative, otherwise it is positive. The second term represents the strength of the EPV loop. If the network is not ISN, both terms are positive and ΔsS > 0 always. On the other hand, if the network is ISN, ΔsS may be positive or negative. Without strong EPV recurrence, the first term will dominate and ΔsS will be negative. On the other hand, strong EPV recurrence can shift ΔsS toward positive values. As connections between E and PV neurons are strong in mouse V1 (Pfeffer et al. 2013), it is likely that this term is indeed large, and therefore the surround facilitation of SOM neurons is not sufficient to alone determine whether mouse V1 is in the ISN or non-ISN regime.
As before, however, the change in total inhibitory current onto E neurons during surround suppression does differentiate between non-ISN and ISNs. In non-ISNs, surround suppression is accompanied by increased inhibition, while for ISNs it is accompanied by decreased inhibition (Fig. 3E). We note that the above conclusion is strictly true only when the total amount of excitation received by E neurons at the stimulus center is unchanged when the surround stimulus is presented.
Recordings in layer 2/3 of mouse V1 suggest that optogenetic activation of increasing area recruits increasing inhibitory current onto pyramidal neurons at the center of the activated area (Adesnik et al. 2012). This appears in contrast to studies in cat V1 (Ozeki et al. 2009), in which surround stimuli led to reduced inhibitory current at the stimulus center. However, because the excitatory current at the stimulation center was not controlled, it is possible that the optogenetic experiments in mouse V1 are not representative of surround suppression dynamics.
Mechanisms of division and subtraction in recurrent circuits.
Above, we neglected orientation tuning of neurons, focusing only on stimuli that uniformly activate neurons in a particular spatial location. On the other hand, if neurons are tuned to specific stimulus features, then evoked states will involve differential activation of neurons within a local network depending on their stimulus preferences. Recent studies have shown that weak to moderate perturbations of PV and SOM circuits in layer 2/3 of mouse V1 have differential effects on E neuron orientation tuning. Specifically, activation of PV neurons divisively modulates E neuron responses, while activation of SOM neurons subtractively modulates E neuron responses (Atallah et al. 2012; Wilson et al. 2012; but see Lee et al. 2012). The circuit mechanisms underlying these computations remain unclear.
To address how inhibition either divides or subtracts neuron responses, we consider a simplified model of E neuron activity within a local network. In our model, the steady-state firing rate of an E neuron tuned to orientation θ is given by sE(θ) = fE[IE(θ)], where fE(·) is the input current to firing rate transfer function and IE(θ) is the subthreshold input, a sum of excitatory and inhibitory components (Fig. 4A). For now, we consider mechanisms that modulate total inhibition, but not excitation, consistent with the weak recurrent excitation in mouse layer 2/3 (Atallah et al. 2012).
Fig. 4.
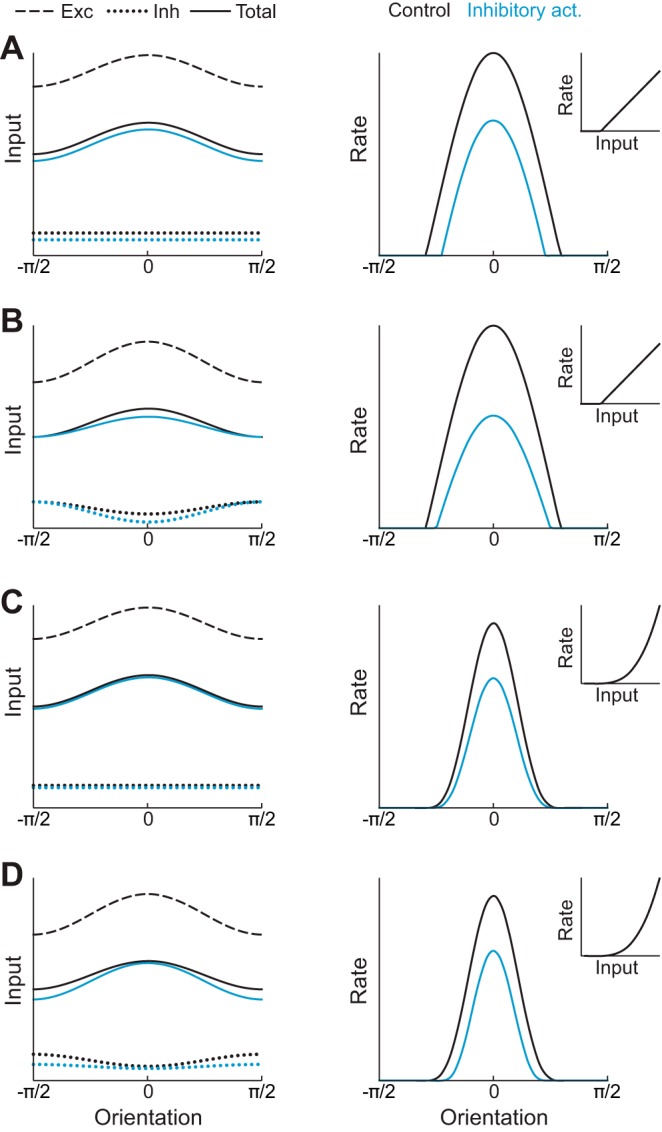
Possible mechanisms of division and subtraction. A, left: schematic of excitatory (dashed) and inhibitory (dotted) inputs to an E neuron and their sum (solid) as a function of orientation. Activation of inhibitory neurons increases untuned inhibition, reducing the total input (blue curves). Right: E neuron tuning curve, calculated by applying a threshold-linear function (inset) to the total input on the left. Activation of inhibitory neurons leads to subtraction of the tuning curve (blue line). B: similar to A, but with a power-law transfer function, leading to approximate division of the tuning curve. C: similar to A, but with inhibition whose tuning increases during activation, leading to approximate division of the tuning curve. D: similar to A, but with a power-law transfer function and inhibition whose tuning is reduced during activation. The total subthreshold input is both reduced and sharpened, leading to approximate subtraction of the tuning curve.
Assuming fE is linear and the only orientation-tuned input arises from external sources, then any increase of recurrent inhibition will have a purely subtractive effect on E responses (Fig. 4A, right). This is because the tuned component of the input remains unchanged. For a modulation of inhibitory inputs to cause division when fE is linear, the tuned component of the input must be suppressed, which can be accomplished by enhancing tuned inhibition (Fig. 4B).
We next consider the case of nonlinear fE. It has been argued that the responses of visual cortical neurons are best described by an expansive power-law nonlinearity (Hansel and Van Vreeswijk 2002; Fourcaud-Trocmé et al. 2003; Murphy and Miller 2003), with support from in vivo whole cell recordings in cat V1 (Priebe et al. 2004). In this case, a uniform decrease in the subthreshold input to the system nonetheless results in approximate division (Fig. 4C). This is because the slope of fE is higher for preferred stimuli than nonpreferred stimuli (Hansel and Van Vreeswijk 2002; Murphy and Miller 2003). However, for subtractive effects to occur in this nonlinear case, the subthreshold input must be sharpened. This sharpening is only consistent with a withdrawal of tuned inhibition (Fig. 4D). We conclude that the implementation of realistic power-law nonlinearities makes division more robust (Hansel and Van Vreeswijk 2002; Murphy and Miller 2003) but makes the mechanisms necessary to support subtraction more complex. We next investigate how these computations may be performed in a realistic V1 circuit model with distinct inhibitory subpopulations.
Division and subtraction with tuned inhibition.
To investigate the insights about subtraction and division from the phenomenological model (Fig. 4), we constructed a spiking neuron model network of layer 2/3 mouse V1 constrained by biological data. The network contained E, PV, SOM, and VIP neurons following, at the population level, the same connectivity rules as before (Fig. 3A). However, to fully specify the network architecture, the specific connectivity between similarly or dissimilarly tuned neurons must be prescribed. Anatomical studies have shown that similarly tuned E neurons in layer 2/3 are more likely to be connected (Yoshimura et al. 2005; Ko et al. 2011) but that the strength of these connections is weak relative to feedforward input (Hofer et al. 2011; Atallah et al. 2012). Specific connectivity may also exist for PV but not SOM neurons (Yoshimura and Callaway 2005; Wilson et al. 2012), although the extent to which inhibitory neurons exhibit tuning is controversial (Kerlin et al. 2010; Bock et al. 2011). Inhibitory currents recorded in E neurons exhibit orientation tuning (Tan et al. 2011), although it is weaker than that of excitatory currents (Liu et al. 2011; Atallah et al. 2012), suggesting that at least some specificity in inhibitory to excitatory connections exists. We aimed to determine the extent to which such specific connectivity was necessary to obtain the divisive and subtractive effects reported in the literature. We therefore studied a network in which PV neurons exhibited tuning and then contrasted its behavior to networks in which they did not.
The network consisted of 500 neurons with realistic connectivity strengths, cellular and synaptic parameters, and short-term plasticity dynamics (Fig. 5A). We examined the network's response to an oriented stimulus in three states: the control state, the PV activation state in which PV neurons received depolarizing current mimicking the effects of optogenetic activation of PV neurons, and the SOM activation state (Fig. 5B).
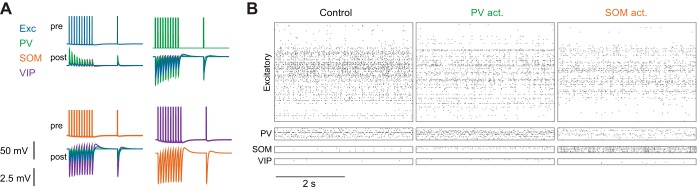
Fig. 5.
Large-scale network model of mouse V1. A: excitatory postsynaptic potentials (EPSPs) and inhibitory postsynaptic potentials (IPSPs) (bottom traces) in neuronal subtypes that are connected to a presynaptic neuron in which spikes are evoked (top traces). B: spike rasters in response to visual stimulation, in control conditions (left), with PV neuron activation (middle), and with SOM neuron activation (right).
PV activation has been shown to act divisively (Atallah et al. 2012; Wilson et al. 2012; Lee et al. 2014). In our network, consistent with this observation, activation of PV neurons led to approximately divisive shifts in orientation tuning (Fig. 6A, compare black and green curves). These shifts arose from two effects. First, the magnitude of the tuned inhibition provided by PV neurons increased, preferentially suppressing responses to stimuli at the peak of the tuning curve (Fig. 6B). Second, the firing rate nonlinearity also preferentially suppressed responses at the peak of the tuning curve, since the slope of fE was greater for such stimuli (Murphy and Miller 2003). Hence, tuned inhibition and/or a firing rate nonlinearity can account for division by PV neurons, as suggested previously (Atallah et al. 2012; Wilson et al. 2012).
Fig. 6.
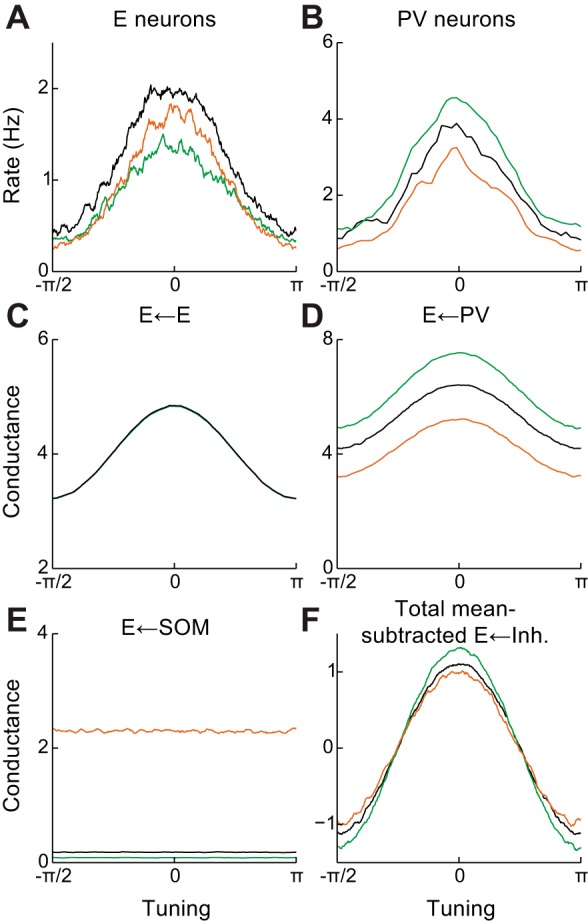
Modulation of pyramidal neuron tuning curves by inhibitory activation in a network with tuned PV neurons. A: excitatory neuron tuning curves in control and PV/SOM-activated states. B: same as A for PV neurons. C: tuning of excitatory conductance onto excitatory neurons. D: same as C but for PV neuron conductance. E: same as C but for SOM neuron conductance. F: tuning of total inhibitory conductance onto excitatory neurons, showing decreased tuning of inhibition during SOM activation. Green, PV neuron activation; orange, SOM neuron activation.
We next considered activation of SOM neurons, which has been shown to subtractively shape E neuron tuning curves, sharpening orientation selectivity (Wilson et al. 2012). Since tuned excitation does not increase during SOM activation, the only way for the total input to be sharpened is a withdrawal of tuned inhibition (Fig. 4D). Since SOM neurons do not appear to provide direct tuned inhibition (Wilson et al. 2012) and any they did would likely be enhanced during activation, this may only be accomplished through recurrent interactions within the local interneuron network. Notably, suppression of PV neurons by SOM neurons (Fig. 3A) is consistent with such a withdrawal. Indeed, in our model, SOM activation led to approximately subtractive shifts on E neuron tuning (Fig. 6A, compare black and orange curves), due to a decrease in tuned inhibition driven by suppression of PV input (Fig. 6, B–F). Hence, SOM-induced suppression of tuned PV neurons is one mechanism that can lead to sharpening of subthreshold input and consequently subtractive shifts in excitatory tuning curves.
Alternative mechanisms for division and subtraction.
In the previous section, in order to obtain subtractive shifts in excitatory tuning curves, it was necessary to assume that subthreshold input was sharpened by withdrawal of tuned inhibition. Assuming inhibition from PV neurons was tuned while that from SOM neurons was not then led to PV-mediated division and SOM-mediated subtraction. This effect could be quantified as an increase in the orientation selectivity index (OSI) of E neuron tuning curves during SOM activation (Fig. 7A). A network without tuned inhibition was unable to produce this effect, with manipulations of both PV and SOM neurons leading to division (Fig. 7B).
Fig. 7.
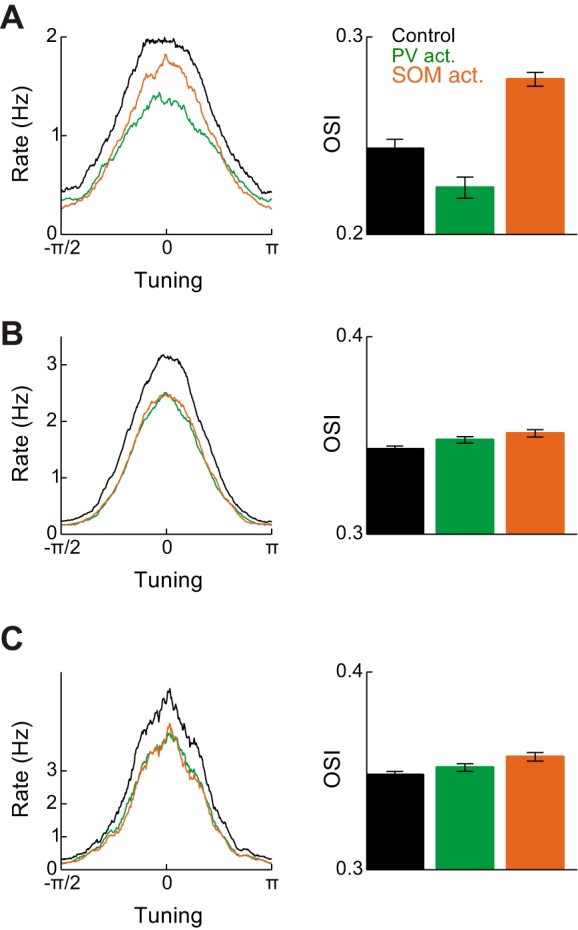
Orientation selectivity in different networks. A, left: excitatory neuron tuning curves in control, PV neuron activation, and SOM neuron activation conditions, for the network in Fig. 6. Right: orientation selectivity index (OSI) in the 3 conditions. B: same as A for a network without tuned PV neurons. C: Same as B for a network in which excitatory neurons were modeled with 2 compartments.
However, an additional potential explanation for these differential effects of PV and SOM activation is that these neurons target different compartments of pyramidal neurons: PV and SOM neurons, respectively, tend to contact proximal to the soma or distally on the dendritic tree (Markram et al. 2004). We therefore investigated whether this difference alone could lead to both divisive and subtractive effects of activating each population, even in the absence of tuned inhibitory connectivity. We modified the pyramidal neurons in our spiking network so that they had both a somatic and passive dendritic component. Parameters were modified so that PV, SOM, and VIP neuron spiking again led to integrated inhibitory postsynaptic potential sizes consistent with experimental measurements (Pfeffer et al. 2013). In such a network, the effect of PV or SOM neuron activation had identical effects on pyramidal neuron tuning curves, as in the single-compartment case (Fig. 7C). Hence, passive dendritic integration is unlikely to support both subtraction and division on the same target neuron.
In summary, tuning curve division by PV neurons may be mediated by either a reduction of tuned input or firing rate nonlinearities, and both of these are likely to occur in vivo. Tuning curve subtraction by SOM neuron activation is less straightforward and may be mediated by at least three distinct mechanisms. If excitatory f-I curves are linear, untuned inhibition could lead to subtraction (Fig. 8A). In this case, no change in inhibitory tuning would be present during SOM activation. If excitatory f-I curves are nonlinear, suppression of tuned PV input by SOM activation could mediate subtraction (Fig. 8B). In this case, a reduction in tuned inhibition onto neurons would be recorded intracellularly. Alternatively, a sharpening of tuned excitation by some previously undescribed mechanism could also support subtraction (Fig. 8C). If this occurred, the tuning of excitatory, but not inhibitory, currents recorded at the soma would increase during SOM activation. Hence, these three mechanisms can be differentiated by their effects on the tuning of excitatory and inhibitory currents during SOM activation. We further note that assuming strong, tuned excitatory recurrence can help explain tuning curve division (Ben-Yishai et al. 1995) but not subtraction by SOM neuron activation. This is because SOM-mediated suppression of E neurons will lead to a reduction in the sharpness of subthreshold tuning and hence division, rather than subtraction.
Fig. 8.
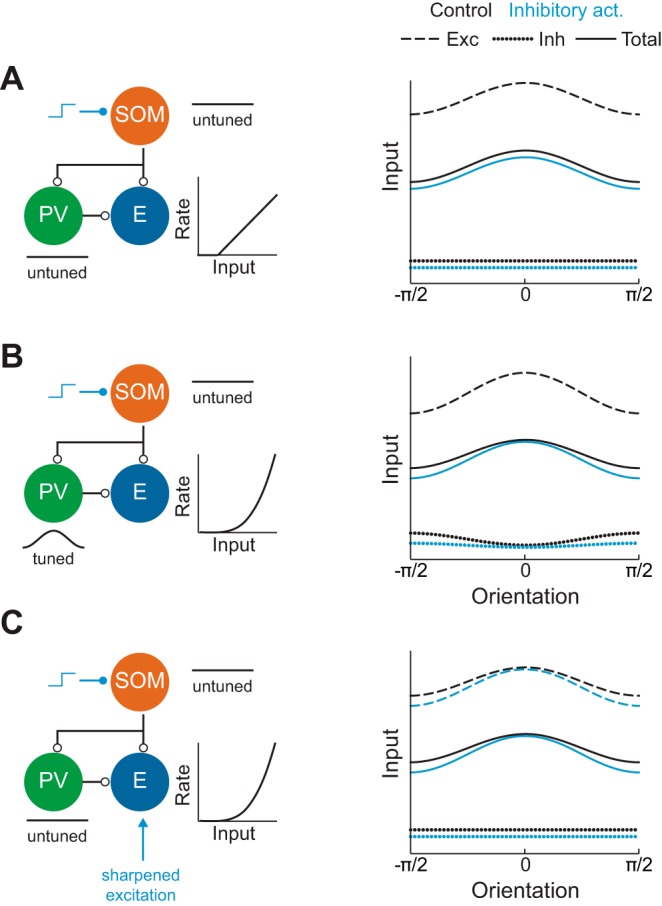
Three hypotheses for the mechanism of subtraction. A: untuned inhibition leads to subtraction if excitatory f-I curves are linear. B: withdrawal of tuned PV inhibition leads to sharpening of subthreshold input and approximate subtraction if excitatory f-I curves are nonlinear. C: nonlinear dendritic integration allows untuned SOM inhibition to sharpen tuned excitatory input, leading to subtraction if excitatory f-I curves are nonlinear.
DISCUSSION
Inhibitory stabilization and E/I balance in mouse V1.
We have outlined a theory for the dynamics of recurrent E/I networks with multiple inhibitory neuron subtypes. A key element of this theory is whether the network is in the ISN regime or not. In mouse V1, evidence for this is equivocal. Our theory demonstrates that recording total inhibitory current while activating inhibitory neurons can unambiguously differentiate the ISN and non-ISN regimes.
Current evidence in favor of the non-ISN regime for layer 2/3 includes the dynamics of SOM neurons during surround suppression (Adesnik et al. 2012), the reduction in inhibitory input during PV neuron inactivation (Atallah et al. 2012), and the apparently weak excitatory connectivity in this region (Jiang et al. 2015). Evidence in favor of the ISN regime includes reports that surround suppression occurs in all inhibitory neurons, including SOM neurons (Ayaz et al. 2013; Pecka et al. 2014). It is also possible that the dynamical regime of the network may be modulated by other factors, such as locomotion (Fu et al. 2014).
If layer 2/3 of mouse V1 is a non-ISN, theoretical models of this area must be modified to account for this fact. Non-ISNs rule out standard “balanced” network models with strong recurrent excitation and inhibition (van Vreeswijk and Sompolinsky 1998; Hansel and van Vreeswijk 2012; Pehlevan and Sompolinsky 2014) and argue against mechanisms of orientation selectivity that rely on strong recurrent excitation (Ben-Yishai et al. 1995). However, it should be noted that the “balanced” state can also exist when strong feedforward excitation is balanced by strong recurrent inhibition, without recurrent excitation (Zillmer et al. 2009). It has been argued that strong recurrent inhibition decorrelates the inputs to different neurons in recurrent networks, leading to sparse and irregular firing (Renart et al. 2010; Tetzlaff et al. 2012; Ly et al. 2012; Middleton et al. 2012). This could explain the origin of asynchronous firing without requiring strong recurrent excitation as in standard balanced networks (van Vreeswijk and Sompolinsky 1998).
Conclusions for layer 2/3 of mouse V1 may not generalize to other cortical regions or layers or analogous regions in different species. Indeed, recurrent excitation in layer 4 of mouse V1 has been shown to be large relative to feedforward input (Lien and Scanziani 2013), and cat V1 has been convincingly argued to be ISN (Ozeki et al. 2009). Our theory provides a framework in which to determine the extent to which the dynamical regime of V1 depends on species, layer, or both.
Surround suppression and locomotion.
The lack of surround suppression in SOM neurons has been observed in running animals (Adesnik et al. 2012). Other studies have argued that all neurons exhibit surround suppression (Pecka et al. 2014) and that this effect is reduced by locomotion (Ayaz et al. 2013). Surround suppression in all neuron types, including inhibitory neurons, would result in a reduction in inhibition during surround suppression, consistent with cat V1 in the ISN regime (Ozeki et al. 2009). However, it is possible that some of the effects reported in these experiments may be due to surround suppression occurring earlier in the visual processing hierarchy. Further experiments are needed to determine the circuit mechanisms that contribute to surround suppression and how each are affected by locomotion.
Our work shows that a lack of surround suppression in SOM neurons can be consistent with either ISN or non-ISN regimes. Measuring the total inhibitory current during surround stimulation (Ozeki et al. 2009) would differentiate between these two possibilities.
Mechanisms of subtraction and division.
The effects of PV and SOM neurons on E tuning have been the subject of debate. Atallah et al. (2012) showed that activation of PV neurons leads to division of E tuning, corroborated by Wilson et al. (2012), who also showed SOM neurons act subtractively. Lee et al. (2012), in contrast, obtained the opposite result, with PV and SOM neurons performing subtraction and division, respectively. Subsequent experiments in Lee et al. (2014) suggested that this difference may have been be due to the stronger stimuli used in the original experiments. Seybold et al. (2015) showed that in auditory cortex there is a large heterogeneity across pyramidal cells in the degree of subtractive and divisive modulation recruited by activation of both PV and SOM population. The authors conclude that the underlying mechanisms for division and subtraction are likely complex and simple subtractive/divisive labeling is perhaps oversimplified.
A recent study argued that distinctions between subtraction and division may be due to the temporal overlap between excitatory and inhibitory neuron activation (El-Boustani and Sur 2014). In this framework, concurrent activation of excitatory and inhibitory neurons results in inhibition whose magnitude depends on the current excitatory firing rate, while activation of inhibitory neurons without excitatory activation results in inhibition with a fixed magnitude. If PV neurons are activated by stimuli in tandem with E neurons, while SOM neurons are activated at later latencies, this could result in divisive and subtractive, respectively, effects on E neuron f-I curves. However, it is unclear how this mechanism would explain divisive and subtractive shifts in orientation tuning curves without tuned inhibition. Such shifts require the feedback inhibition to be specifically modulated by the firing rate of neurons with similar orientation preference, which cannot occur if excitatory and inhibitory neurons are connected randomly.
We have provided three possible mechanisms for division and subtraction of tuning curves mediated by PV and SOM neurons, respectively. When f-I curves are nonlinear, subtraction requires sharpening of subthreshold input, and identifying the mechanism behind this sharpening becomes the key objective. One mechanism assumes tuned PV inhibition mediates this effect (Fig. 8A). The tuning of PV neurons has been the subject of debate, and further experiments are needed to determine whether tuning of inhibitory inputs contributes substantially to visual processing in mouse V1 (Runyan et al. 2010; Runyan and Sur 2013; Kerlin et al. 2010; Bock et al. 2011). If inhibition is completely untuned and f-I curves are nonlinear, this sharpening must come from a modulation of excitatory input (Fig. 8C). We found that a two-compartment model with a passive dendrite did not yield the necessary effect without tuned inhibition. Standard models of nonlinear dendritic integration assume that dendritic inhibition provides multiplicative gain control (Mehaffey et al. 2005; Murayama et al. 2009; Jadi et al. 2012), also inconsistent with the sharpening of excitatory input required for subtractive modulation. It is also possible that f-I curves are linear in layer 2/3 pyramidal neurons, so that subtraction does not require sharpening of subthreshold input (Fig. 8B). This would require a substantial rethinking of pyramidal neuron response properties, which have been argued to be best described by a power law nonlinearity (Hansel and Van Vreeswijk 2002; Fourcaud-Trocmé et al. 2003; Priebe et al. 2004).
Our theory demonstrates that these possibilities can be tested by determining whether changes in the tuning of excitatory and inhibitory conductances, or neither, accompany interneuron activation that causes subtractive tuning curve modulations (Fig. 8). Future experiments in mouse V1 should be guided by circuit models that incorporate recurrent interactions between different inhibitory subpopulations, and the present study represents a first step in this direction.
GRANTS
The work was supported by an National Institutes of Health Postdoctoral Fellowship 1F32-DC-014387 (to A. Litwin-Kumar); National Science Foundation Grants DMS-1313225 (to B. Doiron), DMS-1517082 (to B. Doiron), DMS-1517828 (to R. Rosenbaum), and Collaborative Research in Computational Neuroscience (CRCNS) R01-DC-015139-01ZRG1 (to B. Doiron); and a grant from the Simons Foundation Collaboration on the Global Brain (to B. Doiron).
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the author(s).
AUTHOR CONTRIBUTIONS
Author contributions: A.L.-K., R.R., and B.D. conception and design of research; A.L.-K. and R.R. performed experiments; A.L.-K. and R.R. analyzed data; A.L.-K., R.R., and B.D. interpreted results of experiments; A.L.-K. prepared figures; A.L.-K. and B.D. drafted manuscript; A.L.-K., R.R., and B.D. edited and revised manuscript; A.L.-K., R.R., and B.D. approved final version of manuscript.
ACKNOWLEDGMENTS
We are grateful to Kenneth Miller for helpful discussions.
REFERENCES
- Adesnik H, Bruns W, Taniguchi H, Huang ZJ, Scanziani M. A neural circuit for spatial summation in visual cortex. Nature 490: 226–231, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atallah B, Bruns W, Carandini M, Scanziani M. Parvalbumin-expressing interneurons linearly transform cortical responses to visual stimuli. Neuron 73: 159–170, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Avermann M, Tomm C, Mateo C, Gerstner W, Petersen CC. Microcircuits of excitatory and inhibitory neurons in layer 2/3 of mouse barrel cortex. J Neurophysiol 107: 3116–3134, 2012. [DOI] [PubMed] [Google Scholar]
- Ayaz A, Saleem A, Schölvinck M, Carandini M. Locomotion controls spatial integration in mouse visual cortex. Curr Biol 23: 890–894, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ben-Yishai R, Bar-Or RL, Sompolinsky H. Theory of orientation tuning in visual cortex. Proc Natl Acad Sci USA 92: 3844–3848, 1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bock DD, Lee WC, Kerlin AM, Andermann ML, Hood G, Wetzel AW, Yurgenson S, Soucy ER, Kim HS, Reid RC. Network anatomy and in vivo physiology of visual cortical neurons. Nature 471: 177–182, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brette R, Gerstner W. Adaptive exponential integrate-and-fire model as an effective description of neuronal activity. J Neurophysiol 94: 3637–3642, 2005. [DOI] [PubMed] [Google Scholar]
- El-Boustani S, Sur M. Response-dependent dynamics of cell-specific inhibition in cortical networks in vivo. Nat Commun 5: 5689, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ermentrout G, Cowan JD. Temporal oscillations in neuronal nets. J Math Biol 7: 265–280, 1979. [DOI] [PubMed] [Google Scholar]
- Fourcaud-Trocmé N, Hansel D, van Vreeswijk C, Brunel N. How spike generation mechanisms determine the neuronal response to fluctuating inputs. J Neurosci 23: 11628–11640, 2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fu Y, Tucciarone JM, Espinosa JS, Sheng N, Darcy DP, Nicoll RA, Huang ZJ, Stryker MP. A cortical circuit for gain control by behavioral state. Cell 156: 1139–1152, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gentet LJ, Avermann M, Matyas F, Staiger JF, Petersen CC. Membrane potential dynamics of GABAergic neurons in the barrel cortex of behaving mice. Neuron 65: 422–435, 2010. [DOI] [PubMed] [Google Scholar]
- Grossberg S. Contour Enhancement, Short Term Memory, and Constancies in Reverberating Neural Networks. New York: Springer, 1973. [Google Scholar]
- Hamilton LS, Sohl-Dickstein J, Huth AG, Carels VM, Deisseroth K, Bao S. Optogenetic activation of an inhibitory network enhances feedforward functional connectivity in auditory cortex. Neuron 80: 1066–1076, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansel D, Van Vreeswijk C. How noise contributes to contrast invariance of orientation tuning in cat visual cortex. J Neurosci 22: 5118–5128, 2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansel D, van Vreeswijk C. The mechanism of orientation selectivity in primary visual cortex without a functional map. J Neurosci 32: 4049–4064, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hofer SB, Ko H, Pichler B, Vogelstein J, Ros H, Zeng H, Lein E, Lesica NA, Mrsic-Flogel TD. Differential connectivity and response dynamics of excitatory and inhibitory neurons in visual cortex. Nat Neurosci 14: 1045–1052, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jadi M, Polsky A, Schiller J, Mel BW. Location-dependent effects of inhibition on local spiking in pyramidal neuron dendrites. PLoS Comput Biol 8: e1002550, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang X, Shen S, Cadwell CR, Berens P, Sinz F, Ecker AS, Patel S, Tolias AS. Principles of connectivity among morphologically defined cell types in adult neocortex. Science 350: aac9462, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kerlin AM, Andermann ML, Berezovskii VK, Reid RC. Broadly tuned response properties of diverse inhibitory neuron subtypes in mouse visual cortex. Neuron 67: 858–871, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ko H, Hofer SB, Pichler B, Buchanan KA, Sjöström PJ, Mrsic-Flogel TD. Functional specificity of local synaptic connections in neocortical networks. Nature 473: 87–91, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kvitsiani D, Ranade S, Hangya B, Taniguchi H, Huang JZ, Kepecs A. Distinct behavioural and network correlates of two interneuron types in prefrontal cortex. Nature 498: 363–366, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee S, Kruglikov I, Huang ZJ, Fishell G, Rudy B. A disinhibitory circuit mediates motor integration in the somatosensory cortex. Nat Neurosci 16: 1662–1670, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee SH, Kwan AC, Dan Y. Interneuron subtypes and orientation tuning. Nature 508: E1–E2, 2014. [DOI] [PubMed] [Google Scholar]
- Lee SH, Kwan AC, Zhang S, Phoumthipphavong V, Flannery JG, Masmanidis SC, Taniguchi H, Huang ZJ, Zhang F, Boyden ES, Deisseroth K, Dan Y. Activation of specific interneurons improves V1 feature selectivity and visual perception. Nature 488: 379–383, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lien AD, Scanziani M. Tuned thalamic excitation is amplified by visual cortical circuits. Nat Neurosci 16: 1315–1323, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu HB, Li YT, Ma WP, Pan CJ, Zhang LI, Tao HW. Broad inhibition sharpens orientation selectivity by expanding input dynamic range in mouse simple cells. Neuron 71: 542–554, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ly C, Middleton JW, Doiron B. Cellular and circuit mechanisms maintain low spike co-variability and enhance population coding in somatosensory cortex. Front Comput Neurosci 6: 7, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma Y, Hu H, Agmon A. Short-term plasticity of unitary inhibitory-to-inhibitory synapses depends on the presynaptic interneuron subtype. J Neurosci 32: 983–988, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markram H, Toledo-Rodriguez M, Wang Y, Gupta A, Silberberg G, Wu C. Interneurons of the neocortical inhibitory system. Nat Rev Neurosci 5: 793–807, 2004. [DOI] [PubMed] [Google Scholar]
- Mehaffey WH, Doiron B, Maler L, Turner RW. Deterministic multiplicative gain control with active dendrites. J Neurosci 25: 9968–9977, 2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Middleton JW, Omar C, Doiron B, Simons DJ. Neural correlation is stimulus modulated by feedforward inhibitory circuitry. J Neurosci 32: 506–518, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murayama M, Pérez-Garci E, Nevian T, Bock T, Senn W, Larkum ME. Dendritic encoding of sensory stimuli controlled by deep cortical interneurons. Nature 457: 1137–1141, 2009. [DOI] [PubMed] [Google Scholar]
- Murphy BK, Miller KD. Multiplicative gain changes are induced by excitation or inhibition alone. J Neurosci 23: 10040–10051, 2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murphy BK, Miller KD. Balanced amplification: a new mechanism of selective amplification of neural activity patterns. Neuron 61: 635–648, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ozeki H, Finn IM, Schaffer ES, Miller KD, Ferster D. Inhibitory stabilization of the cortical network underlies visual surround suppression. Neuron 62: 578–592, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pecka M, Han Y, Sader E, Mrsic-Flogel T. Experience-dependent specialization of receptive field surround for selective coding of natural scenes. Neuron 84: 457–469, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pehlevan C, Sompolinsky H. Selectivity and sparseness in randomly connected balanced networks. PLoS One 9: e89992, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pfeffer CK, Xue M, He M, Huang ZJ, Scanziani M. Inhibition of inhibition in visual cortex: the logic of connections between molecularly distinct interneurons. Nat Neurosci 16: 1068–1076, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pi HJ, Hangya B, Kvitsiani D, Sanders JI, Huang ZJ, Kepecs A. Cortical interneurons that specialize in disinhibitory control. Nature 503: 521–524, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Priebe NJ, Mechler F, Carandini M, Ferster D. The contribution of spike threshold to the dichotomy of cortical simple and complex cells. Nat Neurosci 7: 1113–1122, 2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Renart A, de la Rocha J, Bartho P, Hollender L, Parga N, Reyes A, Harris KD. The asynchronous state in cortical circuits. Science 327: 587–590, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reyes A, Lujan R, Rozov A, Burnashev N, Somogyi P, Sakmann B. Target-cell-specific facilitation and depression in neocortical circuits. Nat Neurosci 1: 279–285, 1998. [DOI] [PubMed] [Google Scholar]
- Rudy B, Fishell G, Lee S, Hjerling-Leffler J. Three groups of interneurons account for nearly 100% of neocortical GABAergic neurons. Dev Neurobiol 71: 45–61, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Runyan CA, Sur M. Response selectivity is correlated to dendritic structure in parvalbumin-expressing inhibitory neurons in visual cortex. J Neurosci 33: 11724–11733, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Runyan CA, Schummers J, Van Wart A, Kuhlman SJ, Wilson NR, Huang ZJ, Sur M. Response features of parvalbumin-expressing interneurons suggest precise roles for subtypes of inhibition in visual cortex. Neuron 67: 847–857, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seybold BA, Phillips EA, Schreiner CE, Hasenstaub AR. Inhibitory actions unified by network integration. Neuron 87: 1181–1192, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shapley R, Hawken M, Ringach DL. Dynamics of orientation selectivity in the primary visual cortex and the importance of cortical inhibition. Neuron 38: 689–699, 2003. [DOI] [PubMed] [Google Scholar]
- Somers DC, Nelson SB, Sur M. An emergent model of orientation selectivity in cat visual cortical simple cells. J Neurosci 15: 5448–5465, 1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tan AY, Brown BD, Scholl B, Mohanty D, Priebe NJ. Orientation selectivity of synaptic input to neurons in mouse and cat primary visual cortex. J Neurosci 31: 12339–12350, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tetzlaff T, Helias M, Einevoll GT, Diesmann M. Decorrelation of neural-network activity by inhibitory feedback. PLoS Comput Biol 8: e1002596, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsodyks MV, Markram H. The neural code between neocortical pyramidal neurons depends on neurotransmitter release probability. Proc Natl Acad Sci USA 94: 719–723, 1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsodyks MV, Skaggs WE, Sejnowski TJ, McNaughton BL. Paradoxical effects of external modulation of inhibitory interneurons. J Neurosci 17: 4382–4388, 1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Vreeswijk C, Sompolinsky H. Chaotic balanced state in a model of cortical circuits. Neural Comput 10: 1321–1371, 1998. [DOI] [PubMed] [Google Scholar]
- Vierling-Claassen D, Cardin J, Moore CI, Jones SR. Computational modeling of distinct neocortical oscillations driven by cell-type selective optogenetic drive: separable resonant circuits controlled by low-threshold spiking and fast-spiking interneurons. Front Human Neurosci 4: 198, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vogels TP, Rajan K, Abbott L. Neural network dynamics. Ann Rev Neurosci 28: 357–376, 2005. [DOI] [PubMed] [Google Scholar]
- Wang XJ, Tegnér J, Constantinidis C, Goldman-Rakic PS. Division of labor among distinct subtypes of inhibitory neurons in a cortical microcircuit of working memory. Proc Natl Acad Sci USA 101: 1368–1373, 2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson HR, Cowan JD. Excitatory and inhibitory interactions in localized populations of model neurons. Biophys J 12: 1–24, 1972. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson NR, Runyan CA, Wang FL, Sur M. Division and subtraction by distinct cortical inhibitory networks in vivo. Nature 488: 343–348, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yoshimura Y, Callaway EM. Fine-scale specificity of cortical networks depends on inhibitory cell type and connectivity. Nat Neurosci 8: 1552–1559, 2005. [DOI] [PubMed] [Google Scholar]
- Yoshimura Y, Dantzker JL, Callaway EM. Excitatory cortical neurons form finescale functional networks. Nature 433: 868–873, 2005. [DOI] [PubMed] [Google Scholar]
- Zhou FW, Roper SN. Altered firing rates and patterns in interneurons in experimental cortical dysplasia. Cereb Cortex 21: 1645–1658, 2011. [DOI] [PubMed] [Google Scholar]
- Zillmer R, Brunel N, Hansel D. Very long transients, irregular firing, and chaotic dynamics in networks of randomly connected inhibitory integrate-and-fire neurons. Phys Rev E Stat Nonlin Soft Matter Phys 79: 031909, 2009. [DOI] [PubMed] [Google Scholar]