Delayed feedback during sensorimotor learning selectively disrupts adaptation but not strategy use

Abstract

In sensorimotor adaptation tasks, feedback delays can cause significant reductions in the rate of learning. This constraint is puzzling given that many skilled behaviors have inherently long delays (e.g., hitting a golf ball). One difference in these task domains is that adaptation is primarily driven by error-based feedback, whereas skilled performance may also rely to a large extent on outcome-based feedback. This difference suggests that error- and outcome-based feedback may engage different learning processes, and these processes may be associated with different temporal constraints. We tested this hypothesis in a visuomotor adaptation task. Error feedback was indicated by the terminal position of a cursor, while outcome feedback was indicated by points. In separate groups of participants, the two feedback signals were presented immediately at the end of the movement, after a delay, or with just the error feedback delayed. Participants learned to counter the rotation in a similar manner regardless of feedback delay. However, the aftereffect, an indicator of implicit motor adaptation, was attenuated with delayed error feedback, consistent with the hypothesis that a different learning process supports performance under delay. We tested this by employing a task that dissociates the contribution of explicit strategies and implicit adaptation. We find that explicit aiming strategies contribute to the majority of the learning curve, regardless of delay; however, implicit learning, measured over the course of learning and by aftereffects, was significantly attenuated with delayed error-based feedback. These experiments offer new insight into the temporal constraints associated with different motor learning processes.

learning to link actions with their respective outcomes is necessary for successfully interacting with the world. Feedback delays can present a significant problem in learning action-outcome associations, yet such delays are ubiquitous in motor control. Feedback from proprioception and vision are inherently delayed because of neural transmission and integration time. Even if these delays are relatively short, the control system faces a significant problem due to potentially destabilizing effects arising from body and environmental dynamics.

One prominent solution for handling delayed feedback in the sensorimotor learning literature centers on the idea of an adaptive forward model, a representation that allows the system to anticipate or predict the sensory consequences of an action through sensory-prediction errors (Wolpert and Miall 1996). However, various lines of evidence indicate that this solution is subject to severe temporal constraints. Modest additional delays in feedback can significantly slow or attenuate motor learning (Held et al. 1966; Held and Durlach 1989; Honda et al. 2012; Kitazawa et al. 1995; Kitazawa and Yin 2002). For example, Kitazawa et al. (1995) estimated that, during prism adaptation, a 50-ms delay of the visual feedback results in a 50% reduction in the learning rate. This is rather surprising given that delivery of common types of feedback (e.g., knowledge of results or end-point feedback of position) in a sensorimotor adaptation task is inherently delayed to some extent since the action has to occur before feedback is delivered and processed by the individual.

The impact of feedback delay is also important to consider given that many motor skills entail substantial delays between the action and feedback. In golf, for example, there is a considerable delay between the moment at which the ball is struck and the time at which the golfer is able to evaluate the quality of the shot (at least for the novice who may not have a good sense of the “feel” of a good shot). A similar problem holds in a range of skills such as dart throwing, bowling, and baseball pitching.

How is learning accomplished in motor tasks with significant feedback delays? One possibility is that learning reflects the operation of multiple processes that operate on different sources of feedback, and these sources may be subject to different temporal constraints. Task success, or outcome-based feedback, is known to play an important role in many motor learning tasks, and the literature suggests that this type of information is subject to a much softer temporal constraint than error-based feedback (Bilodeau 1956, 1966; Salmoni et al. 1984). For example, Bilodeau and colleagues delivered feedback in an intermittent fashion, frequently with several intervening trials between the action and feedback about its specific outcome. Not only was learning possible under such conditions, but retention and transfer were greater compared with when the feedback was provided on every trial (Anderson et al. 2005; Guay et al. 1992; Salmoni et al. 1984).

Task outcome information is central to reinforcement learning. In reinforcement learning, reward-prediction errors are used to learn a value function so that an actor can select an action to maximize expected reward (Sutton and Barto 1998). This outcome-based information stands in contrast to the error-based information (i.e., sensory-prediction errors) thought to be essential for the adaptation of an internal model (Izawa and Shadmehr 2011; Mazzoni and Krakauer 2006; Schlerf et al. 2012). Whereas the former is emphasized in learning models of action selection, the latter is central in learning models of action execution.

Recent work has highlighted how processes such as reinforcement learning can influence performance in sensorimotor adaptation tasks (Galea et al. 2015; Huang et al. 2011; Izawa and Shadmehr 2011; Nikooyan and Ahmed 2015; Shmuelof et al. 2012). Izawa and Shadmehr (2011) showed that learning to compensate for a visuomotor perturbation can be supported by either outcome-based or error-based feedback. Interestingly, forward model adaptation, measured by shifts in perceived hand position and generalization, only occurred in the latter condition. Similarly, outcome feedback, in the form of graded points, appears to speed the rate of learning in a visuomotor rotation task and affects the degree of retention (Galea et al. 2015; Shmuelof et al. 2012). However, this form of feedback does not appear to influence forward model adaptation (Izawa and Shadmehr 2011; Nikooyan and Ahmed 2015).

The preceding discussion suggests that outcome-based feedback may not influence motor adaptation directly but, rather, influences other learning processes that operate during sensorimotor adaptation tasks such as operant conditioning (Shmuelof et al. 2012) and explicit strategic aiming (Bond and Taylor 2015; McDougle et al. 2015; Taylor et al. 2014; Taylor and Ivry 2011). Moreover, these other processes may have temporal constraints different from that associated with adaptation, allowing learning to occur under conditions with significant feedback delays. However, previous studies of delayed feedback have always manipulated outcome- and error-based feedback in a confounded manner. That is, participants are not informed of either the success or the failure of their action until the time they receive information about the sensory consequences of the movement (e.g., cursor position). Dissociating these variables provides a novel opportunity to examine whether outcome- and error-based feedback are subject to different temporal constraints.

Here we conducted three visuomotor rotation experiments in which we provided error- and outcome-based feedback. In experiments 1 and 2, error-based feedback was based on the presentation of a cursor, indicating hand position. Outcome-based feedback was binary, signaled by the accrual of points when an unseen cursor terminated within a target region. For different groups of participants, the two types of feedback were presented with no delay, with a 5-s delay, or in a hybrid condition in which the outcome feedback was available with no delay but the error feedback was delayed by 5 s. In contrast to previously reported findings, we find that learning was supported in all conditions regardless of the form of feedback. However, the size of the aftereffect, the signature measure of motor adaptation, differed between conditions, suggesting that learning with delayed feedback may have been supported by other learning processes. We tested this idea in experiment 3, using a task designed to dissociate adaptation and explicit aiming (Taylor et al. 2014). Explicit aiming, a form of strategy use, accounted for a considerable amount of the learning regardless of delay, while implicit learning was attenuated with delayed error-based feedback.

METHODS

Participants

One hundred and thirty participants (76 women, 54 men; ages 18–34 yr) were recruited in exchange for course credit or payment from the human research participation pool maintained by the Department of Psychology at Princeton University. All participants were right hand dominant, verified by the Edinburgh Handedness Inventory (Oldfield 1971), and had normal or corrected-to-normal vision. All of the participants provided informed consent prior to the experiment under a protocol approved by the Princeton University Internal Review Board.

Experiment 1 (n = 30)

Apparatus.

Participants made reaching movements to visually displayed targets by moving the handle of a two-link robotic manipulandum (Kinarm, Bkin Technologies, Kingston, ON, Canada). The manipulandum recorded hand position data at 2,000 Hz for online processing and 1,000 Hz for off-line analyses. Stimuli, including the position of the starting location, target location, and hand position (real or perturbed), appeared on a horizontal mirror positioned 25 cm above the plane of the manipulandum (approximate chest height, occluding vision of the hand). This mirror was located 25 cm below an overhead LCD monitor (LG, Englewood Cliffs, NJ). This created an illusion such that the visual display appeared to be in the plane of the movement.

The high sampling rate of the robotic device and software system allowed us to control feedback timing with considerable precision. Using an LCD camera (GoPro HD Hero2, San Mateo, CA), we determined that the lag between the sampling time of the handle and the time at which the position of that sample could be displayed on the computer monitor was ∼8.3 ms.

Procedure.

At the start of each trial, the robotic manipulandum gently moved the participant's hand to the start position, a gray annulus (1.2 cm in diameter) that appeared at the center of the workspace. When the hand entered the starting position, the annulus brightened and a white cursor (0.74 cm in diameter) appeared, representing the current position of the hand. The participants had to maintain the feedback cursor within 0.25 cm of the start position for 0.5 s. Once this criterion was achieved, a blue target (1 cm in diameter) appeared on screen. The target could appear at one of eight possible positions separated by 45° along an invisible ring (22.5°, 67.5°, 112.5°, 157.5°, 202.5°, 247.5°, 292.5°, 337.5°) with a radius of 10 cm from the starting position. The sequence of target locations was pseudorandomly selected, such that a particular target location never repeated on consecutive trials. The sequence of locations was randomized across participants.

The participant was instructed to make a fast reaching movement to the target, “slicing” through the target. Once the movement exceeded 5 cm/s, visual feedback of the cursor position was removed. The participant was instructed to remain at the terminal position of the movement until the end of the feedback display (which differed between groups depending on the imposed delay, see below). There were two types of feedback on all trials, end-point feedback and outcome feedback. For end-point feedback, the feedback cursor reappeared at a position along the invisible ring (e.g., when the movement amplitude had reached 10 cm). This position was either at the location where the hand intersected the ring (no perturbation trials) or offset in the clockwise direction from the hand position (rotation trials, see below). For outcome feedback, the target turned green if the feedback cursor overlapped any part of the target region; otherwise the target turned red. In addition, on “hit” trials, the display indicated that the participant had received one point.

We imposed two temporal criteria on the participants' behavior. First, the 10-cm reach had to be completed within 3.5 s of the onset of the target (reaction time plus movement time). If this criterion was exceeded, the trial was immediately aborted and the error message “TOO SLOW!” was displayed on the screen. Second, if the participant moved his/her hand after completion of the movement, regardless of the imposed delay in feedback (see below), the trial was aborted and the error message “HOLD STILL” was displayed. A running tally of points earned was displayed between the trials.

The experiment was divided into three blocks: Baseline, Rotation, and Washout, with the form of feedback held constant within each group for all three blocks (see below). To familiarize participants with the task, veridical feedback was presented during a 64-trial Baseline block. For the next 160 trials (Rotation block), a 30° counterclockwise rotation was imposed between the end-point position of the hand and the position of the feedback cursor. The session concluded with a 64-trial Washout block in which the rotation was suddenly removed and cursor feedback was again veridical. Participants were not informed of the transition from rotated to veridical feedback.

Experimental conditions.

Participants were randomly assigned to create three groups of 10 that differed with respect to the timing of the error- and outcome-based feedback. For two groups, the two feedback signals were presented synchronously. Participants in the No-Delay group received outcome feedback and error feedback as soon as movement amplitude reached 10 cm (Fig. 1A). Participants in the Both-Delay group received error and outcome feedback 5 s after movement amplitude reached 10 cm (Fig. 1B). For both of these groups, the two types of feedback signals were visible for 2 s. For the Cursor-Delay group, the two feedback signals were asynchronous: Outcome feedback was delivered with no delay and remained visible for 7 s, whereas error feedback was delayed by 5 s (presented at a location based on when movement amplitude reached 10 cm) and remained visible for 2 s (Fig. 1C). For all groups, the screen blanked at the end of the feedback interval and the robot moved the hand back to the start position. The overall rate of the experiment was kept constant across groups by imposing a fixed duration of 10 s from the start of one trial to the start of the next trial. Thus the time from the end of the feedback period to the start of the next trial was longer for the No-Delay group compared with the other two groups. For example, if the movement was completed 1 s after target onset, participants in the No-Delay group would have to wait 9 s before the start of the next trial (2 s with immediate feedback, 7-s wait period). Participants in the other two groups would have to first wait 5 s to receive feedback (delayed only for error feedback in the Cursor-Delay group and for cursor and outcome in the Both-Delay group), have 2 s to process the feedback, and then wait an additional 2 s before the start of the trial. This confound—longer delay from feedback onset to start of next trial for the No-Delay group compared with delay groups—is unavoidable in tasks that manipulate delay (see Salmoni et al. 1984). Note that we did not include a “Reward-Delay” group since outcome information (hit/miss) can be inferred from the error feedback.

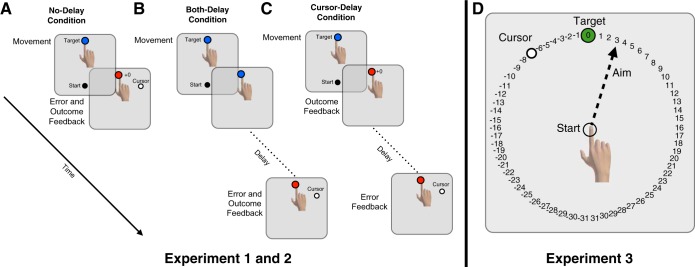
Fig. 1.

Experimental conditions. A: No-Delay condition: Participants were provided with outcome and error feedback as soon as movement amplitude reached 10 cm radial from the start location. The former was indicated by a color change at the target location (green = hit; red = miss), as well as a +1 point increment on hit trials. The latter was provided by displaying a cursor to indicate hand position. In the example shown, the cursor is rotated clockwise by 30° (e.g., start of rotation block). B: Both-Delay condition: Outcome and error feedback were delayed by 5 s. C: Cursor-Delay condition: Outcome feedback was provided immediately, while error feedback was delayed by 5 s. D: experiment 3 task workspace. Participants were instructed to verbally report the number corresponding to where they planned to aim to get their cursor on the target. The numbers always flanked each side of the target and rotated along with the target such that 1 and −1 were always adjacent to the target.

Experiment 2 (n = 60)

The apparatus and experimental conditions were the same as in experiment 1. We increased the sample size such that 60 participants were randomly assigned to one of three equal-sized groups, No-Delay, Cursor-Delay, and Both-Delay.

The Baseline and Rotation blocks were unchanged. After the Rotation block, we included a No-Feedback block during which error and outcome feedback were withheld for 40 trials. This block of trials was preceded by a message on the screen that read, “On the next set of trials, please aim directly for the target. You won't receive feedback on your performance and you won't be scoring points. The target will change color only to indicate that you've reached far enough.” The experimenter verbally instructed the participants to stop using any “aiming” strategy they may have adopted and reach until the target color changed from blue to purple, which occurred when the movement amplitude reached 10 cm. The cumulative score and percentage score were also withheld during these 40 trials. This No-Feedback block provides an assay of the size of the aftereffect while minimizing two possible sources of contamination (see Taylor et al. 2014). First, the instructions should minimize any persistent use of an aiming strategy, should the participants have spontaneously adopted one. Second, the aftereffect is measured in the absence of unlearning since the visual feedback is removed.

After the No-Feedback block, feedback was restored for the final 24 trials and presented in a format identical to that used in the original Baseline block for each group (Washout block). Participants were not provided with any additional instructions for the Washout block.

Experiment 3 (n = 20)

Apparatus.

Participants made reaching movements to visually displayed targets by moving their hand across a digitizing tablet while holding onto a digitizing pen (Intuous Pro, Wacom, Vancouver, WA). The tablet recorded hand position at 100 Hz. The visual workspace appeared on a 17-in., 1,024 × 768-pixel-resolution LCD computer monitor with a refresh rate of 60 Hz (Dell, Dallas, TX). The monitor was horizontally mounted 25.4 cm above the tablet. With this arrangement, vision of the hand was occluded by the monitor. The visual display and task were controlled by custom software written in Python (https://python.org). Using an LCD camera (GoPro HD Hero2), we measured the lag between the sampling time of the tablet and the time at which the position of that sample was displayed on the computer monitor. This lag, ∼70 ms, was considerably longer than the lag associated with the robotic manipulandum setup. Despite this additional lag, we chose to use the tablet setup, as opposed to the robotic manipulandum, because our prior work employing verbally reported aiming strategies was implemented with this equipment.

Procedure.

At the start of each trial, participants positioned their hand within a start position (0.41-cm-radius gray circle) located at the center of the visual workspace and tablet. Participants were guided to the start position by a circle whose diameter changed as a function of the distance between the participant's hand and the start position. In this way, participants were provided with radial, but not angular, information about the location of their hand. Once the hand was within 0.5 cm of the start position, the ring was replaced by a white cursor (0.31-cm-radius circle) that appeared at the center of the start position. Participants were instructed that this cursor represented the position of their hand. However, the cursor position did not change once the participant entered the start circle, even if there were slight movements of the hand. We did this to eliminate information about the visuomotor rotation at the start circle. If participants moved their hand outside of the start position, the guiding circle reappeared and participants were required to find the start position again. After participants held their hand within the start position for 1 s, a green target (0.60-cm-radius circle) was presented at one of eight locations (0°, 45°, 90°, 135°, 180°, 225°, 270°, 315°). The distance to the targets was reduced to 7 cm to fit within the limits of the drawing tablet.

Participants made fast reaching movements, attempting to “slice” through the target. If participants failed to reach 7 cm within 400 ms after leaving the start position, they were provided with an auditory warning, “too slow.” Note that, in contrast to experiments 1 and 2, participants received feedback (cursor or points) on trials in which the movements were too slow. End-point feedback was similar to that used in experiments 1 and 2, a static, small red circle at the angular position of the hand when the movement amplitude reached 7 cm. Outcome feedback was modified in experiment 3 such that the amount of points earned on a trial corresponded to the angular error, the absolute value of the difference between the cursor and target location. This point-based feedback was calculated based on the equation (similar to Nikooyan and Ahmed 2015)

$$R=100\left(\frac{90°-\left|{\theta }_{\text{error}}\right|}{90°}\right)\mathrm{.}$$

The point score was displayed midway between the start position and target for 0.5 s after the hand crossed 7 cm. In addition, when the cursor overlapped with the target a pleasant “ding” sound was played; otherwise, an unpleasant “buzz” sound was played. The total of points accumulated during each block was displayed every 40 trials and at the end of each block. Before the start of the experimental task, the experimenter used a diagram to explain the point system to the participants.

To assess the use of aiming strategies, we employed an aiming report task (see Bond and Taylor 2015; McDougle et al. 2015; Taylor et al. 2014). The visual display included numbered landmarks presented on the virtual ring (Fig. 1D). Participants were required to report their aiming location before initiating the reaching movement. Visual instructions were presented on the screen every 40 trials to remind the participants that the goal of the task was to get the red cursor on the green target and that aiming directly at the target might not be effective. If the participant failed to report a number before moving, the experimenter provided a reminder before the next trial. These trials were excluded from the analyses and, overall, occurred on 1.3% of trials.

Note that with the tablet setup participants must actively find the start position for each trial, rather than be passively moved to this location by the robotic manipulandum. In addition, the aiming report task required a verbal report on each trial. Because of these two changes, we did not employ a fixed intertrial time. Rather, the interval was dictated by the time required for the participant to reach the start location, plus the 500-ms hold period within this position prior to the onset of the target.

There were seven blocks of the experiment. The experiment started with two short blocks to familiarize the participants with the experimental apparatus. The first block was composed of reaches with veridical online cursor feedback, and the second was composed of reaches with veridical end-point cursor feedback. In the third block (Baseline block), both groups continued to receive end-point feedback for 32 more trials. The aiming report task was introduced in the fourth block (Baseline-Report block), composed of eight trials in which the participants reported the aiming target (usually the target location since there was no perturbation). In the fifth block (Rotation block), a 45° counterclockwise rotation was imposed for 320 trials. Participants were instructed to continue to report their aiming location before each reach. In the sixth block (No-Feedback block), the numbered landmarks, the rotation, and all feedback were removed. In addition, participants were instructed to aim directly for the target. In the final, seventh block (Washout block), feedback was restored, with the type of feedback for each group the same as that used in the Baseline block.

Experimental conditions (n = 20).

Twenty participants were equally divided into two groups, No-Delay and Delay. Cursor feedback and points were provided as soon as the movement amplitude reached 7 cm (subject to the apparatus delay) in the No-Delay group. The points and the cursor feedback were delayed by 1 s in the Delay group. We chose to impose only a 1-s delay so that we could obtain sufficient trials within the experimental session to fully characterize the implicit and explicit learning curves (see Taylor et al. 2014).

Analysis

Kinematic and statistical analyses were performed with MATLAB (MathWorks, Natick, MA). To assess task performance, we focused on the initial heading angle of the hand, defining this angle with respect to the target location. Each movement trajectory, regardless of the actual target location, was rotated to a common reference axis with the target location set at 0°. A line was drawn between two referent points along the observed trajectory, one positioned 1 cm from the start position and one positioned 3 cm from the start position. The angular difference between this line and a line between the start position and the target defined the heading angle. Positive angles indicate a clockwise deviation from the target, and negative angles indicate a counterclockwise deviation from the target.

To quantify effects of delay, we focused on the early and late performance in the Rotation block and Washout/No-Feedback block. Early and late performance in the Rotation block were defined as the average heading angle of the hand over the first and last eight trials (epicycle) in the Rotation block, respectively. To account for individual reach biases in baseline performance, we subtracted the average hand heading angle over the last epicycle in the Baseline block for each measure. These baseline-corrected measures serve as a proxy to quantify the rate and extent of learning. An alternative approach would be to fit functions (e.g., exponential) to the learning curves, but this procedure tends to be highly variable when applied to individual data (Taylor et al. 2014), often providing poor and potentially misleading fits (Gallistel et al. 2004). Early and late aftereffects were similarly quantified in the Washout block, averaging the first and last epicycle of the Washout block and subtracting the average hand heading angle of the last epicycle of the Baseline block. The early and late corrected heading angle scores were submitted to a mixed factorial ANOVA with Delay as a between-subjects factor and Time (early vs. late) as a within-subjects factor. Separate ANOVAs were conducted on the data from the Rotation and Washout blocks.

In experiment 2, early and late performance in the Rotation block were calculated in the same manner as for experiment 1. For the No-Feedback block, we restricted the analysis to just the first epicycle (again, subtracting the last epicycle of the Baseline block) since our interest was in the size of the initial aftereffect and not in unlearning. We performed a two-step analysis on these data. We first used one-sample t-tests to determine whether aftereffects were present for each group individually. We then used a one-way ANOVA to test whether the aftereffects were different between groups. When appropriate, pairwise comparisons were computed by separate t-tests using a Bonferroni correction based on the number of comparisons. To report the correction, we multiplied the uncorrected P value by the number of comparisons to maintain the customary 0.05 level of significance. We report both the uncorrected and corrected values.

In experiment 3, early and late performance in the Rotation block were calculated in the same manner as for experiments 1 and 2. The aiming report data and estimates of implicit learning were also binned in the same manner. To baseline correct the aiming reports, we subtracted the average aiming angles over the last epicycle of the Baseline-Report block. The aftereffect data were analyzed in the same manner as in experiment 2, again limited to the first epicycle of the No-Feedback block.

To evaluate consistency across participants during the Rotation block in experiments 1 and 2, we examined the variance between participants. For this analysis, movements in the Rotation block were binned into eight-trial epicycles and then averaged within a bin for each participant. The variance of these epicycles was then computed across participants.

We also computed target error, reaction time, movement time, and peak movement speed during the baseline block of 32 trials. Target error was defined as the angular difference between the position of the hand at 10 cm (experiments 1 and 2) or 7 cm (experiment 3) and the target location. Reaction time was defined as the interval between target appearance and the time when hand velocity exceeded 5 cm/s. Movement time was defined as the interval between when hand velocity exceeded 5 cm/s and movement amplitude reached the radial distance of the target. Peak velocity was defined by deriving a continuous measure of movement velocity with a fourth-order Savitsky-Golay filter, a method that introduces less noise than basic differentiation (Savitzky and Golay 1964). To compare these dependent variables between groups, the values were submitted to one-way ANOVAs for experiments 1 and 2 and two-sample t-tests for experiment 3.

In experiment 1, we determined minimum sample sizes for sufficient power based on the change in learning observed in the Kitazawa et al. (1995) study of feedback delays. We estimated the power for an independent-samples t-test using a one-tailed α of 0.05. Based upon the correction rates from Kitazawa et al. (1995), the effect size is approximately d = 1.57 (based on estimated group means and standard deviations), requiring a sample size of at least 10 participants. For experiment 2, we estimated power for an independent-samples t-test using a one-tailed α of 0.05 based on the size of the aftereffect over the first eight trials of the Washout block observed in experiment 1. The effect size is d = 1.09 (based on group means and standard deviations), requiring a sample size of at least 20 participants. For experiment 3, we estimated power for an independent-samples t-test using a one-tailed α of 0.05 based on the size of the aftereffect over the first eight trials of the No-Feedback block observed in experiment 2. The effect size is d = 1.6 (based on group means and standard deviations), requiring a sample size of ∼10 participants.

For all dependent measures, we report the median and the 95% confidence interval.

RESULTS

Experiment 1

The different delay conditions did not have an appreciable effect on kinematic features of the movements (Table 1). We analyzed the various measures using the data from the last epicycle of the Baseline block. None of the measures showed significant differences between groups, although there was a marginal effect for slower reaction times for groups with delayed feedback (F_2,27 = 3.02, P = 0.065). Importantly, there were no differences between hand heading angles in the Baseline block (F_2,27 = 0.15, P = 0.86).

Table 1.

Kinematic features of movements for each group during Baseline block

	Heading Angle, °	Target Error, °	Peak Speed, cm/s	Reaction Time, ms	Movement Time, ms
Experiment 1
No-Delay	1.66 ± 0.58	1.17 ± 0.55	81.9 ± 3.9	473 ± 55	317 ± 51
Cursor-Delay	1.68 ± 0.65	1.20 ± 1.21	84.1 ± 5.6	494 ± 48	314 ± 46
Both-Delay	2.25 ± 1.24	1.90 ± 0.93	84.3 ± 5.6	593 ± 109	352 ± 53
Experiment 2
No-Delay	1.61 ± 0.63	1.56 ± 0.96	67.4 ± 3.9	611 ± 56	350 ± 81
Cursor-Delay	1.45 ± 1.08	1.26 ± 1.43	70.6 ± 5.0	697 ± 90	344 ± 61
Both-Delay	1.28 ± 0.76	0.97 ± 0.86	70.9 ± 3.9	740 ± 76	400 ± 61
Experiment 3
No-Delay	1.16 ± 2.73	1.13 ± 2.43	34.4 ± 4.34	1,382 ± 1,080	276 ± 47
Delay	2.10 ± 1.22	1.81 ± 1.19	36.6 ± 2.42	678 ± 445	270 ± 23

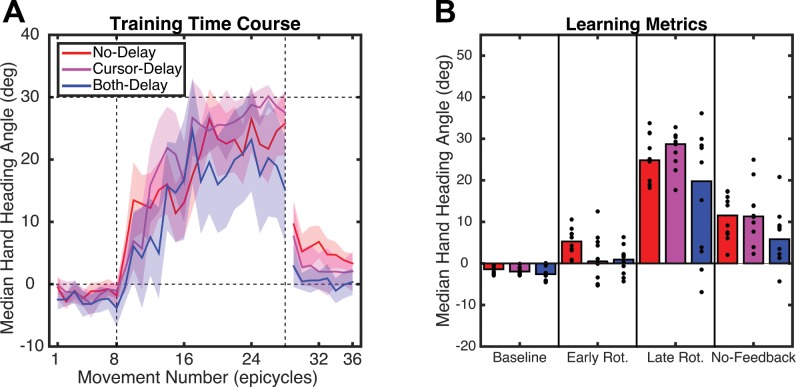
During the 160-trial Rotation block, the participants in all three groups modified their behavior in a task-appropriate manner, moving in a direction opposite to the counterclockwise rotation (Fig. 2A). The baseline-corrected heading angle data during the first and last epicycles were submitted to a mixed factorial ANOVA with the between factor Group and repeated measure Time (Fig. 2B). All three groups significantly changed their heading angle during the Rotation block (Time: F_1,27 = 89.8, P < 0.001) such that the feedback cursor ended up much closer to the target location by the end of the Rotation block. There was also a significant Group effect (F_2,27 = 3.48, P = 0.038), while the interaction term was only marginally significant (F_1,27 = 2.82, P = 0.069).

Fig. 2.

A: hand heading angle over the course of experiment 1. Hand angles were binned into trials of 8 (epicycle) for each participant and then combined across participants. Median (solid line) and 95% confidence interval for the No-Delay, Cursor-Delay, and Both-Delay conditions are shown. The rotation was present between the 2 vertical dashed lines. B: hand heading angle during the baseline, early, and late phases of the Rotation block and the first epicycle of the Washout block. Bar graphs indicate median values and dots individual participants. Colors as in A.

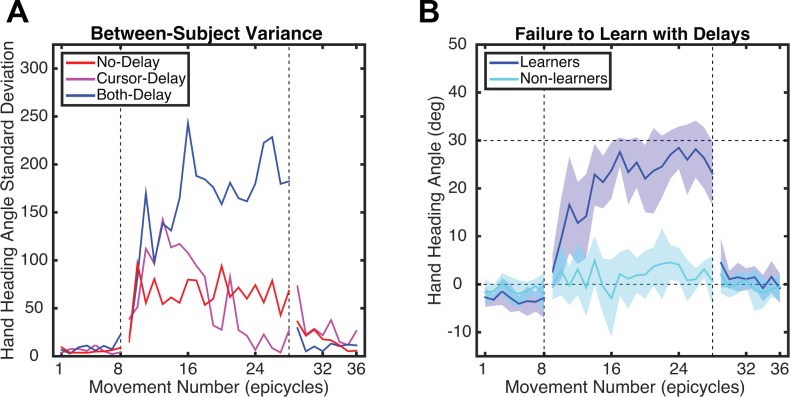
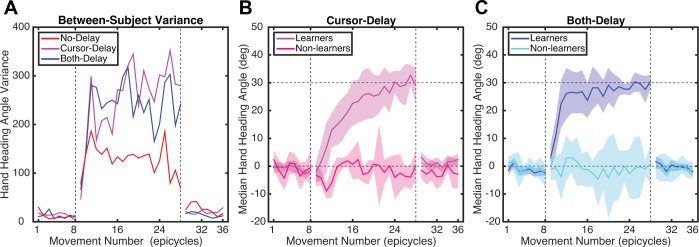
The Group effect is likely due to smaller changes in hand angle for the Both-Delay group compared with the other two groups. However, this effect should be qualified. As can be seen from the confidence intervals in Fig. 2A, as well as dispersion of individual data points for the late rotation data in Fig. 2B, there is considerable variability between participants in the Both-Delay group. Variance, calculated on an individual basis, initially increased for all groups at the start of the Rotation block but only remained elevated throughout the Rotation block for the Both-Delay group (Fig. 3A). The large between-participant variability for this group reflects the fact that some of the participants exhibited minimal changes in their behavior in response to the rotation. To objectively distinguish between participants who learned and those who did not, we computed a one-sample t-test on individual data sets, comparing the hand heading angles between the last epicycle of the Baseline block and the last epicycle of the Rotation block. Based on this measure, 4 of 10 participants in the Both-Delay group were considered nonlearners, as they failed to show a significant change in the hand heading angle over the course of the rotation block (P > 0.1). In contrast, the other six participants in this group showed a significant change in hand heading angle (P < 0.05), and, in fact, their performance looks similar to that of the other groups (compare Fig. 3B and Fig. 2A). Indeed, when the basic ANOVA is restricted to just those participants who learned, we find only a main effect of Time (F_1,23 = 147, P < 0.001) and no effect of Group (F_2,23 = 0.01, P = 0.99) or interaction (F_1,23 = 0.77, P = 0.47).

Fig. 3.

A: variability in hand angle over the course of experiment 1 for the 3 groups. B: performance functions for participants in the Both-Delay group after division into 2 subgroups, “learners” (n = 6) and “nonlearners” (n = 4).

After the Rotation block, the rotation was abruptly removed. All groups exhibited significant aftereffects, measured as the difference between the first epicycle of the Washout block and the last epicycle of the Baseline block (Fig. 2B; P < 0.03). Using the baseline-corrected heading angle data from the first and last epicycles in the Washout block, there was a main effect of Time (F_1,27 = 13.0, P < 0.001) and a marginal effect of Group (F_2,27 = 3.07, P = 0.055). The interaction was not significant (F_1,27 = 0.31, P = 0.74). When this analysis was repeated but, for the Both-Delay group, restricted to the six participants who showed significant learning, there was an effect of Time (F_1,23 = 11.0, P = 0.002) but no effect of Group (F_2,23 = 1.37, P = 0.26) or interaction (F_1,23 = 0.09, P = 0.92).

Performance changes during the Rotation block and the size of the aftereffect are generally assumed to provide two measures of adaptation. We evaluated this in the present experiment by computing the correlation between the heading angle data from the late epoch in the Rotation block and the early epoch in the Washout block. Surprisingly, the correlation was modest (r = 0.11, P = 0.08), and likely inflated by the inclusion of the four participants in the Both-Delay group who showed minimal learning (Fig. 4). When these four participants are excluded, the correlation drops to 0.04, suggesting that performance changes during the Rotation and Washout blocks may reflect different learning processes (note that the correlations are low when calculated within each group, an issue we address in discussion). However, our measure of the aftereffect is problematic since feedback was present, allowing participants to unlearn the rotation during the first epicycle. We addressed this issue in experiment 2.

Fig. 4.

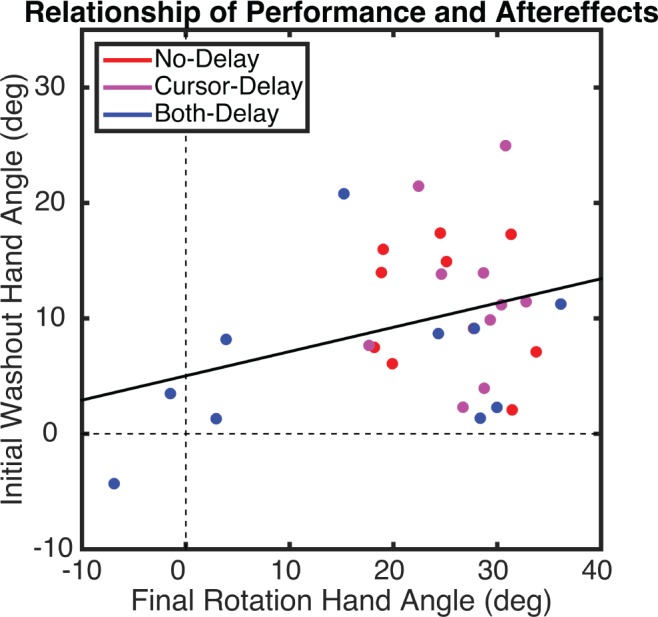
Experiment 1: relationship between mean hand angle during final epicycle in the Rotation block and first epicycle of the Washout block (i.e., aftereffect), calculated across all participants. Dots represent individual participants, with colors indicating group membership, and the solid line represents the regression.

Experiment 2

Experiment 2 was identical to experiment 1 with two exceptions. First, there were 20 participants in each group, providing increased power. Second, we included a No-Feedback block immediately after the Rotation block. This block provides a stronger assessment of the size of the aftereffect since error-based unlearning is precluded by the absence of visual feedback (Kitago et al. 2013). During this block, the participants were asked to aim directly to the target, and to refrain from using an aiming strategy they may have developed during the Rotation block (Taylor et al. 2014; Taylor and Ivry 2011).

Similar to experiment 1, movement kinematics at the end of the Baseline block were similar across the three groups (Table 1), with the exception that movement time was longer for the Both-Delay group (F_2,57 = 3.23, P = 0.047). There were no differences between hand heading angles in the Baseline block (F_2,57 = 0.69, P = 0.50).

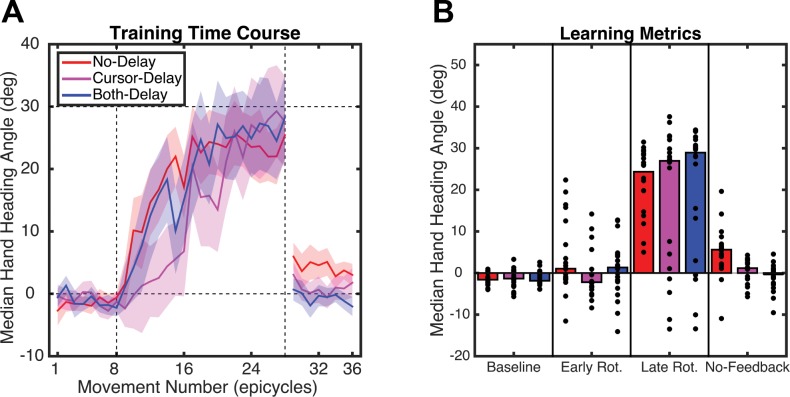
All groups learned to counter the rotation over the course of the Rotation block (Fig. 5A). Using the same analysis as in experiment 1, we first analyzed the baseline-corrected heading angle data for the early and late phases of rotation. The main effect of Time was significant (F_1,57 = 75.11, P < 0.001), but the effect of Group was not (F_2,57 = 0.79, P = 0.45), nor did the two factors interact (F_1,19 = 0.04, P = 0.97). Thus the three groups changed performance in response to the rotation to a similar degree and at a similar rate.

Fig. 5.

A: hand heading angle over the course of experiment 2. B: hand heading angle during the baseline, early, and late phases of the Rotation block and the first epicycle of the No-Feedback block.

Similar to experiment 1, there was considerable variability between participants, and this was now evident for the Cursor-Delay group as well as the Both-Delay group (Fig. 6A). We again classified participants as “learners” and “nonlearners” by determining whether the participant showed a significant change in hand heading angle between the last epicycle of the Rotation block compared with the Baseline block. This analysis revealed that 5 of the 20 participants in the Cursor-Delay group (Fig. 6B) and 6 of the 20 participants in the Both-Delay group (Fig. 6C) failed to show a significant change in performance over the Rotation block (P > 0.1; Fig. 6, B and C).

Fig. 6.

A: variability in hand angle over the course of experiment 2 for the 3 groups. B and C: performance functions in 2 subgroups of “learners” (n = 15) and “nonlearners” (n = 5) for the Cursor-Delay group (B) and “learners” (n = 14) and “nonlearners” (n = 6) for the Both-Delay group (C).

The first epicycle of the No-Feedback block provides the cleanest measure of adaptation, since visual feedback was absent and participants were instructed to aim directly at the target location. We first tested for the presence of aftereffects for each group separately, using one-sample t-tests of the difference between the first epicycle of the No-Feedback block and the last epicycle of the Baseline block. A significant aftereffect was observed for the No-Delay (t₁₉ = 7.15, P < 0.001) and Cursor-Delay (t₁₉ = 3.81, P = 0.001) groups. The effect was only marginally significant for the Both-Delay group (t₁₉ = 2.07, P = 0.052). As can be seen in Fig. 5B, the size of the aftereffect was quite small in either group with delayed feedback.

Next, we used a one-way ANOVA to compare the size of the aftereffects between groups. There was a main effect of Group (F_2,57 = 5.0, P = 0.01). Post-hoc t-tests revealed that aftereffects were greater in the No-Delay group compared with the Both-Delay group (t₁₈ = 4.2, P = 0.002 uncorrected, P = 0.007 corrected). None of the other contrasts was significant (P > 0.1). Since the delay groups included a mixture of learners and nonlearners, we repeated this analysis but restricted the data to the learners. Here, there remained a main effect of Group (F_2,43 = 5.85, P = 0.006). While participants in the delay groups showed sizable changes in performance during the Rotation block, these groups showed minimal aftereffects. Moreover, as observed in experiment 1, the correlation between the degree of final learning in the Rotation block and the aftereffect was modest (r = 0.17; P = 0.19; Fig. 7), providing further evidence that the degree of learning during the Rotation block may not reflect “true” motor adaptation.

Fig. 7.

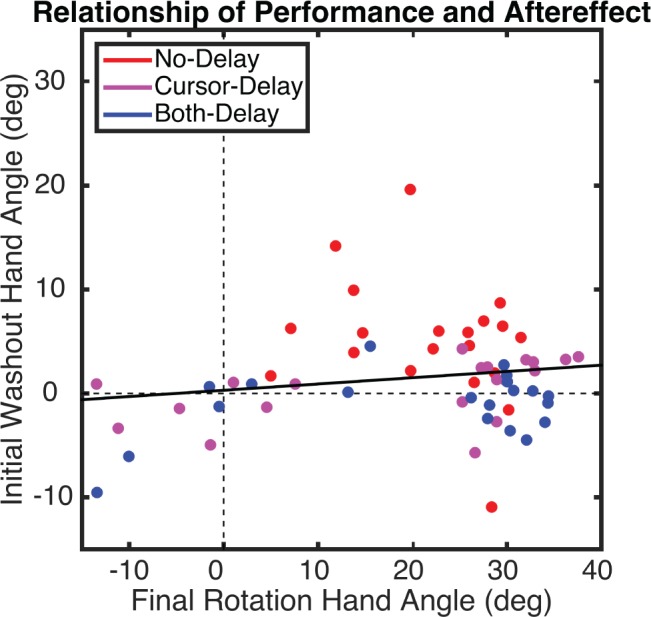
Experiment 2: relationship between mean hand angle during final epicycle in Rotation block and first epicycle of the No-Feedback block (i.e., aftereffect), calculated across all participants. Dots represent individual participants, with colors indicating group. The solid line is the regression line, calculated across all participants.

Experiment 3

The results of experiments 1 and 2 demonstrate that learning was possible when there were significant delays in error-based feedback, regardless of when outcome-based feedback was available. However, the size of the aftereffect—the standard marker for implicit motor adaptation—was reduced in experiment 2 when error feedback was delayed. This suggests that learning with delayed error feedback may not be the result of implicit motor adaptation but rather reflects the operation of a different learning process or learning processes. We designed experiment 3 to examine one such process, an explicit aiming strategy. To this end, we employed an aiming report task that allows for the continuous assessment of how participants modify their aim when faced with a visuomotor perturbation and, by inference, allows a continuous estimate of implicit adaptation (Bond and Taylor 2015; McDougle et al. 2015; Taylor et al. 2014). Since the timing of outcome-based feedback did not produce marked effects on the various measures of learning in experiments 1 and 2, we only tested participants in the No-Delay and Delay conditions.

Before introduction of the rotation, participants in the two groups practiced reaching to each target location with veridical feedback while reporting where they were aiming. For both groups, participants reported aiming directly at the target for the majority of the time (80% of trials). On the remaining trials, the aiming angle was almost always toward a neighboring location (∼5° from the target). Reaching accuracy, measured in terms of heading angle, was not affected by the delay (t₁₈ = 1.25, P = 0.26). There were no appreciable differences in reaction time, movement time, or peak speed between groups, although we note that we did not put constraints on these dependent variables (Table 1; P > 0.1).

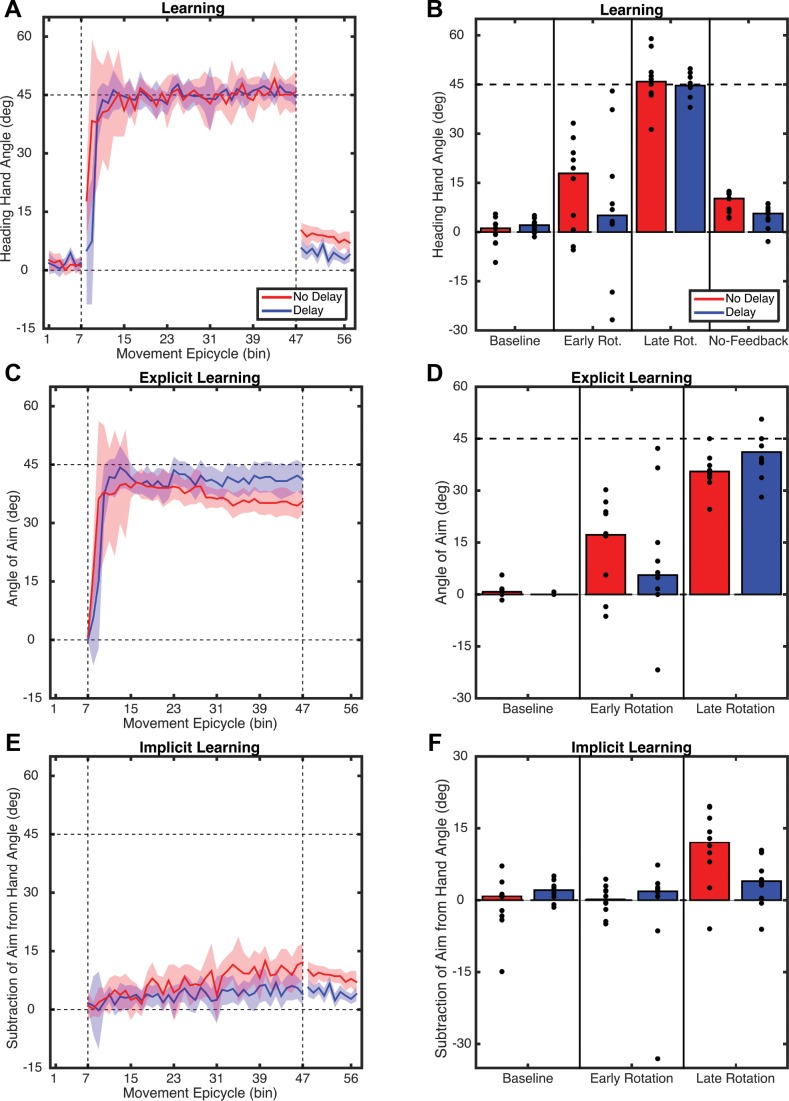
Both groups learned to counter the rotation during the 320-trial Rotation block, moving their hand ∼45° in the clockwise direction from the target location (Fig. 8A). To determine whether the groups differed in the rate or final degree of learning, we submitted the baseline-corrected heading angle data for the first and last epicycles of the Rotation block to a two-way ANOVA with factors of Time and Delay (Fig. 8B). There was a main effect of Time (F_1,18 = 62, P = < 0.001) but no effect of Delay (F_1,18 = 1.78, P = 0.19) or interaction (F_1,18 = 0.29, P = 0.60). Thus, despite the differences in the conditions, participants learned to counter the rotation at a similar speed and to a similar degree.

Fig. 8.

A: hand heading angle over the course of experiment 3 for the No-Delay and Delay conditions. B: average hand heading angles for the last epicycle of the Baseline block and the first and last epicycles of the Rotation block and the aftereffect measured during the first epicycle of the No-Feedback block. C and D: explicit aiming: angle of aiming location, relative to target location (C) and average aiming angle for the Baseline-Report and first and last epicycle of the Rotation block (D). E and F: implicit learning: adaptation as estimated by subtracting aiming direction from hand heading angle (E) along with average values for the Baseline-Report block and first and last epicycles of the Rotation block (F). Bars represent the group mean of each 8-trial bin (epicycle), and dots represent individual participants.

After the Rotation block, participants performed a No-Feedback block. The numbered landmarks were no longer visible, and participants were explicitly instructed to aim directly at the target. Based on one-sample t-tests of the difference between the first epicycle of the No-Feedback block and the last epicycle of the Baseline block, both groups displayed significant aftereffects (No-Delay: t₉ = 4.40, P = 0.002; Both-Delay: t₉ = 3.03, P = 0.014). However, a two-sample t-test revealed that the No-Delay group exhibited a larger aftereffect than the Both-Delay group, even when corrected for multiple comparisons (t₁₈ = 2.70, P = 0.014 uncorrected, P = 0.03 corrected).

The aiming report task allowed us to monitor how participants adjusted their aim after the introduction of the perturbation. Participants in both groups rapidly adjusted their aiming strategy to offset the rotation. Moreover, the use of an aiming strategy persisted throughout the Rotation block (Fig. 8, C and D). The mixed-factor ANOVA of these data revealed a main effect of Time (F_1,18 = 45.5, P < 0.001). Interestingly, neither the effect of Delay (F_1,18 = 0.1, P = 0.76) nor the interaction (F_1,18 = 1.5, P = 0.22) was significant. Note that while the mean data show a marked increase in the aiming angle from the early rotation to the last rotation epicycles (main effect of Time), the rise is actually quite early and falls off slightly over the course of the Rotation block (Fig. 8C). Thus, by the end of the Rotation block, much of the change in performance for both groups is due to changes in aiming.

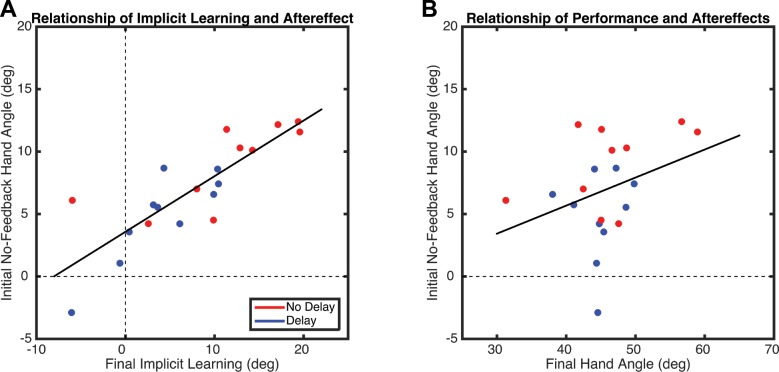
Subtraction of the explicit aiming strategies from the time series of hand angles provides an indirect estimate of implicit motor adaptation (Taylor et al. 2014). This procedure revealed a gentle increase in the estimate of implicit learning over the course of the Rotation block (Fig. 8E). There was a main effect of Time (F_1,18 = 9.84, P = 0.003) and Delay (F_1,18 = 696, P = 0.012) but no interaction (F_1,18 = 84, P = 0.36). Thus delaying error feedback led to less implicit learning, which is consistent with the aftereffect data. Indeed, there was a strong correlation (r = 0.83, P < 0.0001) between the degree of implicit learning and the size of the aftereffect (Fig. 9A). This correlation is not observed between overall performance gains and the aftereffect (r = 0.33, P = 0.15; Fig. 9B).

Fig. 9.

A: experiment 3: relationship between estimate of implicit learning during the final epicycle in the Rotation block and first epicycle of the No-Feedback block (i.e., the aftereffect), calculated across all participants. B: relationship between hand heading angle (i.e., performance) during the final epicycle in the Rotation block and the first epicycle of the No-Feedback block. Dots represent individual participants, with colors indicating group membership. The solid lines are the regression lines, calculated across all participants.

DISCUSSION

Summary

Delayed feedback has been shown to be disruptive to sensorimotor learning. In previous studies, the effect of delaying error and outcome information has been confounded. In the present study, we separated these two sources of information by including a condition in which participants received immediate feedback concerning whether they hit or missed the target (outcome information) but delayed feedback concerning the actual end point of the movement (error information). We found that learning to counter the rotation was possible when error and outcome feedback were delayed, as well as when only error feedback was delayed. However, learning was more variable between participants in the delay conditions. Indeed, a number of participants in these groups showed minimal evidence of learning, suggesting that learning with delayed feedback was not obligatory. Moreover, when the aftereffect was tested in the absence of feedback (experiment 2), the groups with delayed error feedback showed minimal aftereffects. Similar performance gains with different aftereffects suggest that learning may be supported by different processes when feedback is delayed or based on outcome feedback.

To explore this hypothesis, we employed a task in experiment 3 that allowed us to continuously measure participants' use of aiming strategies and, by inference, adaptation. A change in aim accounted for the lion's share of learning in all conditions. Overall, the estimates of implicit learning increased over the course of the Rotation block, although this increase was only significant for the No-Delay group. In addition, while both groups showed significant aftereffects, the aftereffect was smaller when the feedback was delayed. Thus the results of experiment 3 provide further evidence that learning with delayed feedback is especially disruptive to adaptation.

Learning vs. Adaptation

The results of these experiments underscore the importance in distinguishing between motor learning and motor adaptation, terms that are frequently used interchangeably. Overall, performance improved during the Rotation block for all groups in the three experiments, with participants adjusting their hand direction to counter the direction of the rotation. However, the groups with delayed error feedback showed substantially smaller aftereffects. Aftereffects have been considered the hallmark signature of motor adaptation, reflecting changes to an internal model based on sensory prediction errors from cursor feedback (Krakauer and Mazzoni 2011). By this definition, participants with delayed outcome and error feedback were capable of learning but did so without significant adaptation. The results are more ambiguous when outcome feedback was presented immediately and only the error feedback was delayed. In experiment 1, this group exhibited an aftereffect. However, the more sensitive probe used in experiment 2 showed only minimal adaptation with delayed error feedback, even when participants were immediately informed of the outcome. Small, or negligible, aftereffects were also observed in experiment 3 when cursor feedback was delayed or withheld.

We believe the small aftereffects observed in experiment 1 for the groups with delayed feedback were a product of the task design and not adaptation per se. Experiment 1 is similar to most studies of motor adaptation, with the Washout block initiated by simply turning the rotation off unexpectedly. Under such conditions, participants would be expected to continue to reach in the same manner as on the previous trial of the rotation phase, making the initial heading angle similar to that at the end of the Rotation block. In addition, providing feedback during the Washout block allows learning processes to continue to operate. As such, the aftereffect measures in experiment 1 conflate different processes. In experiment 2, we removed the visual feedback and instructed the participants to aim directly toward the target. Here, we found that aftereffects were minimal for groups with delayed feedback, consistent with the hypothesis that the performance changes during the Rotation block for these groups were not due to adaptation. The time course of implicit adaptation, as estimated in experiment 3, showed minimal change over the course of the Rotation block when feedback was delayed, and the aftereffect, while significant, was small and considerably less compared with when feedback was not delayed. Finally, the estimate of implicit adaptation correlated strongly with the size of the aftereffect but did not correlate with overall performance, further underscoring the difference between multiple learning processes.

It should be noted that in all experiments the size of the aftereffect for the No-Delay group was substantially less than the performance change observed during the Rotation block. Indeed, in experiments 2 and 3, participants showed less than a 10° aftereffect. Recent work from our lab, using the same method as in experiment 3, has shown that implicit motor adaptation appears to plateau at a level of ∼15–20° under conditions of end-point feedback, regardless of the size of the rotation (Bond and Taylor 2015). This result, consistent with those found in the present study, suggests that visuomotor adaptation may operate over a limited extent. When the perturbation exceeds this range, other learning processes may need to be recruited in order to improve performance (at least within a single session of training).

Alternatively, implicit motor adaptation may have failed to fully compensate for the full extent of the rotation in the present experiments because we used end-point feedback. This feedback is inherently delayed in that it occurs after the movement has ended. In contrast, online, continuous feedback of cursor position during the movement is, by definition, less delayed. It is possible that online feedback may allow implicit motor adaptation to fully compensate for the rotation, or at least compensate for the rotation to a greater extent than that observed with end-point feedback. In a previous study, we found that while online feedback led to stronger learning than end-point feedback, it still remained incomplete by the end of training (Taylor et al. 2014). It remains unclear whether additional training would have led to full adaptation. Finally, Honda and colleagues (2012) found that participants could fully recalibrate to expect delayed feedback when it was delivered in a continuous fashion. Thus the limited extent of implicit motor adaptation observed in the present studies could be due to the inherent delay that occurs with end-point feedback.

Temporal Constraints on Different Processes for Motor Learning

The motor system is inherently challenged to handle delayed information when incorporating visual and proprioceptive feedback into ongoing motor commands. This problem has motivated the idea that the motor system employs forward models to anticipate the sensory consequences of actions (Wolpert and Miall 1996). The cerebellum has been hypothesized to play a critical role in this process, both for the control of movement and for sensorimotor learning (Schlerf et al. 2013; Taylor et al. 2010; Tseng et al. 2007).

The strong temporal constraints on sensorimotor learning are consistent with the idea that the cerebellum is essential for representing temporal relationships (Ivry 1997; Ivry and Keele 1989). Indeed, studies of cerebellum-dependent learning have suggested a strong constraint with respect to the timing of stimulus information. The rate of acquisition in cerebellum-dependent eyeblink conditioning is significantly decreased when the time interval between the conditioned stimulus (CS) and the unconditioned stimulus (US) increases beyond a half second (Schneiderman and Gormezano 1964). For longer CS-US intervals, learning becomes dependent on extracerebellar inputs such as the hippocampus (Moyer et al. 1990; Solomon et al. 1986), prefrontal cortex (Kronforst-Collins and Disterhoft 1998), and medial prefrontal cortex (McLaughlin et al. 2002; Powell et al. 2001). In fact, recent studies suggest that the cerebellum requires nearly coincident inputs to learn the conditioned response when extracerebellar regions are lesioned (Kalmbach et al. 2009).

Similar results have been obtained in various sensorimotor learning tasks (see, e.g, Howard et al. 2012) that appear to be cerebellum dependent (Baizer and Glickstein 1974; Martin et al. 1996; Smith and Shadmehr 2005; Weiner et al. 1983). The rate of prism adaptation decreases as the time interval between termination of a reaching movement and resultant visual feedback is delayed. In monkeys, learning is nearly fully abolished if the delay exceeds 0.5 s (Kitazawa and Yin 2002). Humans can tolerate longer delays but also show a reduction in adaptation with increasing delay (Kitazawa et al. 1995). The reduced susceptibility to delays in humans may be the result of the operation of learning processes that are less temporally constrained. For example, assuming that explicit aiming strategies are less sensitive to delays and can remain relatively stable over time (Morehead et al. 2015), they may be sufficient to support the required changes in performance to sustain goal-oriented behavior. Alternatively, extracerebellar systems may be able to modulate error-based learning in the cerebellum, perhaps by sustaining the memory or error trace (Gerwig et al. 2008; Kalmbach et al. 2009). Thus the temporal extent of an error-based learning system might be extended, albeit in compromised form.

To date, little work has compared temporal constraints on other learning processes linked to motor learning. Despite the reduction observed in adaptation with delayed error feedback, the participants were still able to modify their performance to substantially reduce error introduced by the perturbation. Thus a delay of 5 s was not sufficient to affect performance gains in experiments 1 and 2. Moreover, the delay appeared to have no impact on participants' ability to use an aiming strategy, with aiming measures similar for delayed and immediate feedback. Previously, we have shown that target error, rather than a sensory prediction error, is the critical source of information for adjusting aiming strategies (Taylor et al. 2014; Taylor and Ivry 2011). This suggests that abstract forms of feedback, even with delay, can be utilized by participants to adjust an aiming strategy, even though it is not sufficient to drive implicit motor adaptation.

Given that we only tested two delays (5 s in experiments 1 and 2, 1 s in experiment 3), our design is limited for specifying in detail how the variation in feedback timing impacts different learning processes engaged during motor learning. A more fine-grained analysis such as that employed by Kitazawa and colleagues (1995) would be required to plot out the costs of error and outcome feedback delays. Such studies will also add to current efforts to dissociate changes in task performance from true motor adaptation.

Manipulations of delayed feedback have also been employed in studies of category learning (Ashby et al. 1998), another task domain in which performance has been shown to reflect the operation of multiple learning processes. Interestingly, delayed feedback on such tasks is also selectively disruptive to implicit forms of learning in which categorization is based on the development of stimulus-response associations. In contrast, explicit, rule-based learning has been shown to be minimally affected by feedback delays (Maddox et al. 2003). Taken together with the present results, the category learning work further suggests that delayed feedback may present a useful tool for dissociating multiple learning processes across task domains.

The present results raise interesting questions concerning the utility of error-based learning for skills in which the feedback is delayed. For example, in golf, feedback may be delayed by several seconds as the player awaits seeing where the ball lands (or, for beginners, even succeeds in tracking the shot). Of course, proprioceptive information is immediately available and the player may catch the early trajectory of the ball (although lifting the head would be ill-advised), but these sources of information would still have to be associated with a delayed task outcome. Thus it is unlikely that these sources of error feedback could entirely support learning. However, participants can accurately predict the outcome when observing the actions of another person (Aglioti et al. 2008; Jalali et al. 2015; Knoblich and Flach 2001). It is currently unclear whether this is truly the result of a skilled motor system predicting the outcome (Aglioti et al. 2008) or some form of perceptual learning system (Jalali et al. 2015).

We also recognize that sensorimotor adaptation tasks, which appear to be heavily dependent on error-based feedback, may not be an appropriate model task for understanding skill acquisition. Indeed, recent work has revealed that learning to compensate for complex perturbations requires processes that are quite distinct from those used to learn visuomotor rotations (Gutierrez-Garralda et al. 2013; Kasuga et al. 2015; Telgen et al. 2014). For example, learning a mirror reversal is much slower, accompanied by large changes in reaction time, exhibits significant off-line improvements, and, most importantly, results in a shift in the speed-accuracy trade-off curve (Telgen et al. 2014). These features may reflect the development of new strategies (Taylor et al. 2014) and control policies (Telgen et al. 2014), processes that are essential for skill acquisition and are, as suggested here, tolerant to temporal delays.

GRANTS

This work was supported by National Institute of Neurological Disorders and Stroke Grants NS-084948 (J. A. Taylor), NS-092079 (R. B. Ivry), and NS-074917 (R. B. Ivry).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: S.N.B., R.B.I., and J.A.T. conception and design of research; S.N.B., N.K., and D.G. performed experiments; S.N.B., D.G., and J.A.T. analyzed data; S.N.B., N.K., D.G., R.B.I., and J.A.T. interpreted results of experiments; S.N.B. and J.A.T. prepared figures; S.N.B., R.B.I., and J.A.T. drafted manuscript; S.N.B., N.K., D.G., R.B.I., and J.A.T. edited and revised manuscript; S.N.B., N.K., D.G., R.B.I., and J.A.T. approved final version of manuscript.