Adaptation of multijoint coordination during standing balance in healthy young and healthy old individuals

Abstract

Standing balance requires multijoint coordination between the ankles and hips. We investigated how humans adapt their multijoint coordination to adjust to various conditions and whether the adaptation differed between healthy young participants and healthy elderly. Balance was disturbed by push/pull rods, applying two continuous and independent force disturbances at the level of the hip and between the shoulder blades. In addition, external force fields were applied, represented by an external stiffness at the hip, either stabilizing or destabilizing the participants' balance. Multivariate closed-loop system-identification techniques were used to describe the neuromuscular control mechanisms by quantifying the corrective joint torques as a response to body sway, represented by frequency response functions (FRFs). Model fits on the FRFs resulted in an estimation of time delays, intrinsic stiffness, reflexive stiffness, and reflexive damping of both the ankle and hip joint. The elderly generated similar corrective joint torques but had reduced body sway compared with the young participants, corresponding to the increased FRF magnitude with age. When a stabilizing or destabilizing external force field was applied at the hip, both young and elderly participants adapted their multijoint coordination by lowering or respectively increasing their neuromuscular control actions around the ankles, expressed in a change of FRF magnitude. However, the elderly adapted less compared with the young participants. Model fits on the FRFs showed that elderly had higher intrinsic and reflexive stiffness of the ankle, together with higher time delays of the hip. Furthermore, the elderly adapted their reflexive stiffness around the ankle joint less compared with young participants. These results imply that elderly were stiffer and were less able to adapt to external force fields.

aging is associated with impaired balance and falls (Muir et al. 2010; Pasma et al. 2014b; Rubenstein 2006). To maintain balance, several underlying systems work together. One of the mechanisms to maintain balance is to alter the coordination of postural responses, i.e., multijoint coordination, which is often explored by analyzing ankle strategies and hip strategies (Horak and Nashner 1986), describing the movement in these joints. Coordination of movements around the ankle and hip joints depends on the amount of external disturbances, such as gravity and pushes having impact on the body, and on the support surface conditions (Creath et al. 2005; Fujisawa et al. 2005; Horak and Nashner 1986). Adaptability of multijoint coordination is an essential feature of standing balance control to adjust to various conditions.

Previous studies showed that the elderly tend to have altered multijoint coordination to maintain standing balance compared with young individuals. The elderly exhibited higher cross-correlation between the upper and lower body in quiet stance, indicating that the displacements of the two body segments were less independent (Accornero et al. 1997; Gariépy et al. 2008). In addition, the elderly had a less-flexible joint coordination pattern to compensate for externally applied balance disturbances (Hsu et al. 2013). This possibly indicates that the elderly used less hip strategy and behaved more rigidly.

Various underlying mechanisms have been put forth as contributing factors of altered multijoint coordination in the elderly. Some studies indicated that the elderly increase their reflexive stiffness around the ankle joint when they are exposed to altered sensory information (Amiridis et al. 2003; Benjuya et al. 2004), whereas other studies found altered intrinsic properties of muscles and tendons having impact on stiffness in the elderly (Cenciarini 2010; Ishida et al. 2008; Kearney et al. 1997).

The detection of the underlying mechanisms of altered multijoint coordination in standing balance is complex, as there exists substantial redundancy at the joint, muscle, and neural levels (Hsu et al. 2013). Multiple sensory systems contribute to balance control, i.e., the proprioceptive, visual, and vestibular system. The sensory signals are integrated and processed by the central nervous system and are then used to generate corrective joint torques by precise muscle-activation patterns. Due to this redundancy, cause and effect remain unclear; increased stiffness can be due to altered intrinsic muscle properties or increased reflex activity, or it might be a compensation strategy and a result of the fact that the elderly change their dynamic behavior to maintain stability. Multivariate closed-loop system-identification techniques (CLSIT) (Boonstra et al. 2013; Engelhart et al. 2014) are required to unravel cause and effects. The application of multiple and specifically designed external disturbances on the human body allows the study of multijoint coordination in standing balance. Multijoint coordination is expressed in the generation of corrective joint torques as a response to body movement, i.e., the dynamic behavior of the neuromuscular controller.

With system-identification techniques, we investigated the underlying mechanisms of multijoint coordination in standing balance in healthy young and healthy elderly. Furthermore, we investigated the adaptation to externally applied force fields. Studies in the upper and lower extremities showed that postural responses adapted when external force fields were applied (Burdet et al. 2001; Franklin et al. 2003; Shadmehr and Mussa-Ivaldi 1994; van Asseldonk et al. 2009). In standing balance studies, it was shown that the elderly possess the ability to adapt to external disturbances, although to a lesser degree than the young (Pavol et al. 2002; Van Ooteghem et al. 2009). Therefore, we hypothesize that a stabilizing force field will down scale the postural responses and that this effect is more pronounced in the young than the elderly, indicating that the elderly are less adaptive. In addition to existing studies, identification of the underlying factors that change multijoint coordination with age could provide insight into mechanisms influencing the risk of falling in the elderly (Engelhart et al. 2014). Adequate treatment of balance disorders requires unraveling the underlying primary causes and applied (adaptive) strategies.

METHODS

Participants

Fifteen healthy young (age range 20–30 yr) and 14 healthy elderly (age range 70–79 yr) individuals participated in the study (Table 1). Participants were excluded when they experienced the following: 1) were in a dependent living situation; 2) were unable to walk a distance of 250 m; 3) presented comorbidity (dementia, neurologic disorders, metabolic diseases, rheumatic diseases, heart failure, severe chronic obstructive pulmonary disease); 4) used medication with an influence on balance control (immunosuppressive drugs, insulin, anticoagulation); 5) were immobilized for 1 wk during the last 3 mo; or 6) had orthopedic surgery during the last 2 yr with unresolved pain or functional limitation.

Table 1.

Participant characteristics

	Young, n = 15	Elderly, n = 14
General characteristics
Age, yr	25.9 (2.8)	74.4 (3.5)
Women, n (%)	8 (53)	6 (43)
Weight, kg	71.7 (10.4)	78.7 (10.6)
Height, m	1.80 (0.09)	1.72 (0.08)
Health characteristics
Number of medication, median (IQR)	0 (0–0)	2 (0–3)
MMSE, points; median (IQR)	30 (30–30)	29 (28–30)
Physical functioning
Handgrip strength, kg	50.8 (16.75)	36.7 (7.8)
Gait speed, m/s	1.07 (0.16)	1.07 (0.15)
SPPB score, points; median (IQR)	12 (12–12)	12 (11–12)

All parameters are presented as means with SD (in parentheses) unless indicated otherwise. IQR, interquartile range; MMSE, Mini-Mental State Examination; SPPB, Short Physical Performance Battery.

To illustrate the state of health of the study population, several outcome parameters were measured. Cognition was assessed using the Mini-Mental State Examination (MMSE) (Folstein et al. 1975), and participants with a score lower than 26 points were not included. Physical functioning was assessed by handgrip strength and the Short Physical Performance Battery (SPPB) (Guralnik et al. 1994). Walking speed was obtained from the 4-m walking test of the SPPB. The total amount of medication was obtained by questioning the participants.

The study was performed according to the principles of the Declaration of Helsinki and was approved by the Medical Ethics Committee of Medisch Spectrum Twente (Enschede, The Netherlands). All participants gave written, informed consent before participating in the study.

Apparatus

Multijoint coordination was investigated using a custom-made device (Motekforce Link, Culemborg, The Netherlands)—the double-inverted pendulum perturbator (DIPP) (Engelhart et al. 2015)—which consists of two manipulators and applies forces using push/pull rods at hip and shoulder level (Fig. 1). Both manipulators were adjustable in height to align the rods to the participant's hip and shoulder level. The manipulators were force controlled, such that force disturbances and force fields could be applied simultaneously. Force disturbances are pushes and pulls on the human body, required for identification of the neuromuscular controller. Force fields were applied at hip level to evoke adaptation of multijoint coordination. Participants experienced the force fields as if they were attached to a spring with varying stiffness, pushing or pulling them back to an equilibrium position. During the experiments, participants wore a safety harness to prevent falling. The harness did not constrain movements or provide support in any way.

Fig. 1.

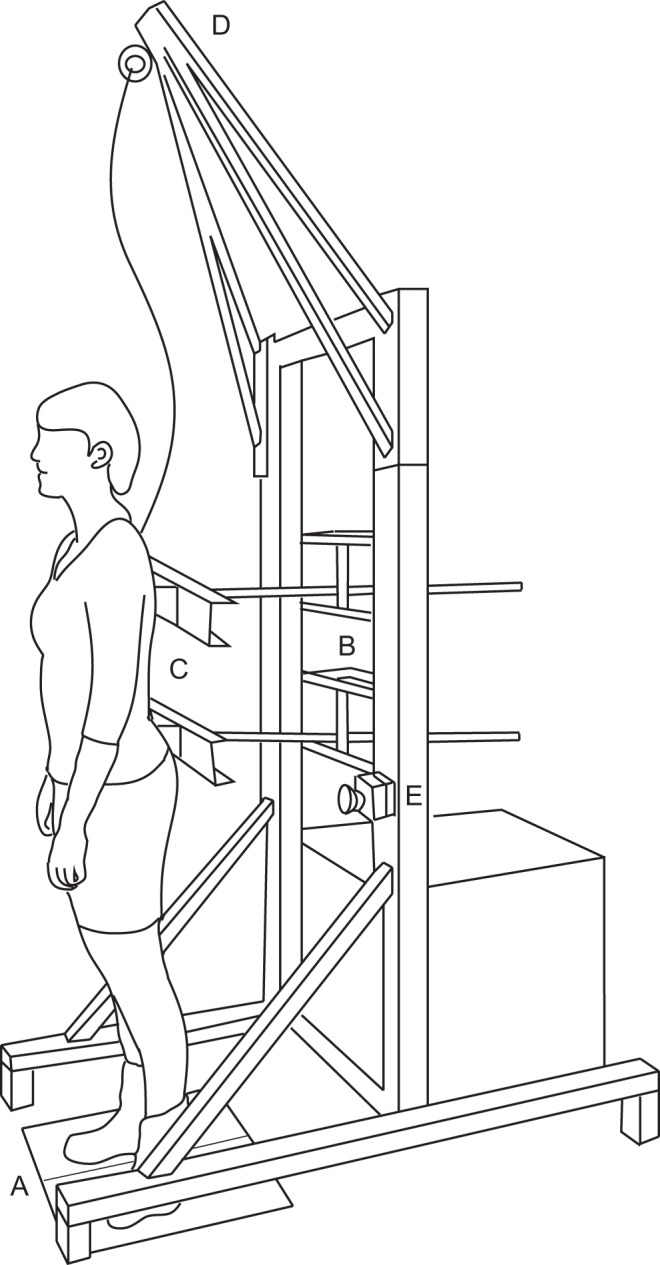
Double-inverted pendulum perturbator with a subject standing on a force plate (A) and attached to 2 manipulators at shoulder and hip level (B). Both manipulators are adjustable in height and driven by an electromotor, pushing and pulling the subject. Body kinematics are measured by potentiometers attached to the rod (C). A safety harness is attached to the pyramidal construction (D), and an emergency button is mounted on the frame (E).

Disturbance Signals

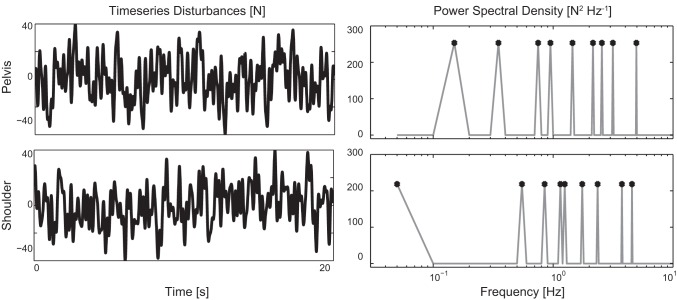
The force disturbances were unpredictable and continuous multisine signals in a range from 0.05 to 5 Hz (Fig. 2). The shoulder and pelvis disturbances were the zippered multisine (Pintelon and Schoukens 2012), such that each disturbance contained nine excited frequencies at an interleaved frequency grid. Both multisine signals had a period of 20 s and were repeated nine times over a time course of 3 min. Disturbances had a peak-to-peak amplitude of 80 N.

Fig. 2.

Time series of the applied force disturbances at the pelvis and between the shoulder blades, with the corresponding power spectral density. The force disturbances are zippered multisine, as the excited frequencies (indicated with circles) are independent.

Procedures

Participants were attached to the DIPP and stood with eyes open, without shoes, and their arms folded across their chest. Participants were instructed to maintain a normal, upright stance position. Force disturbances at the hip and shoulder were applied simultaneously. External force fields were applied only at the level of the hip. The (spring) stiffness of the force field was set such that it compensated partially for the gravitational stiffness around the participant's ankle joint and was normalized to mgl [where m is the mass of the participant, g the gravitational acceleration (9.81 m/s²), and l the height of the center of mass (CoM), estimated by 0.575 × height of the participant].

Within the five experimental trials, a fixed stiffness level was set, expressed in a percentage of full compensation. One baseline trial was recorded without force field (0%). Three force fields were stabilizing the human body (20, 50, and 80%), and one force field destabilized the human body (−20%). All trials were randomized, and participants were allowed to rest between trials according to their needs. Before the experiments, participants were allowed to get familiarized with the disturbances according to their individual needs. In the case of the five force-field trials, participants were allowed to familiarize ∼10 s before recording the data. This familiarization reduced any transient effects in the responses.

Recordings

Body kinematics were measured using two draw-wire potentiometers (Celesco SP2-25; Celesco Transducer Products, Chatsworth, CA), which were attached to the end of the push/pull rods and measured the displacement of the participant's upper and lower body segments. A dual-force plate (Advanced Mechanical Technology, Watertown, MA) measured the ground reaction forces and torques in 6° of freedom under each foot. All signals were recorded with a sample frequency of 1,000 Hz and processed in Matlab (The MathWorks, Natick, MA).

Data Analysis

To study the age-related changes in adaptation of multijoint coordination, different data analysis methods were used. In various studies (Creath et al. 2005; Horak and Nashner 1986), multijoint postural control is described by the ankle and hip strategy, which is defined as movements around the ankle and hip joints. Therefore, sway and torque responses of young and elderly participants were compared, expressed by the root mean square (RMS), which gives an indication of the effective amplitude instead of a maximum, yielding a representative value for the response amplitudes. Secondly, covariance descriptors (Kuo et al. 1998) resulted from a kinematic analysis, which included postural coordination between the ankle and hip joints. To include multisegmental influences in postural control (Boonstra et al. 2013), system-identification techniques were used, which resulted in frequency response functions (FRFs), which describe the relationship between the torques and the angles as a response to the disturbances only; i.e., intersegmental coordination of the neuromuscular controller is identified. Finally, to find physiologically relevant parameters that describe the underlying mechanisms of multijoint coordination, a model was fit to the FRF. This resulted in an estimate of time delays and parameters describing intrinsic and reflexive feedback properties.

Preprocessing.

All signals were filtered with a phase-preserving, fourth-order Butterworth filter, with a cutoff frequency of 10 Hz. The ankle and hip angle was calculated with goniometric rules from the recorded upper- and lower-body displacements and the participant's dimensions. The ankle angle was described as the angle of the lower body with respect to the foot (and thus the horizontal, as the support surface was fixed). The hip angle was described as the angle of the upper body with respect to the longitudinal axis of the upper leg. From the force plate data, the total ankle and hip torques were calculated with inverse dynamics (van der Linde and Schwab 1998; Winter 1990). Data were segmented in 20-s periods of the disturbance signals, yielding 9 data blocks/trial. From each data block, the mean and trends were removed. The responses were averaged over the nine data blocks for each condition and participant and used for further analysis.

RMS and covariance descriptor.

A description of the response amplitude of the ankle and hip angle and the ankle and hip torque was given by the RMS.

To represent the upper- and lower-body movement and their coupling, the two-by-two covariance matrix of the ankle and hip angle was used (Kuo et al. 1998)

$$Q=cov\left(\theta \right)=\frac{1}{n-1}{\displaystyle \sum _{i=1}^n}\left({\theta }_i-\overline{\theta }\right){\left({\theta }_i-\overline{\theta }\right)}^T$$ (1)

in which θ_i is the i^th time sample of the vector containing the ankle and hip angles. The diagonal terms of the covariance matrix represent the variances of the ankle and hip angle. The off-diagonal terms represent the intersegmental coupling between the ankle and hip.

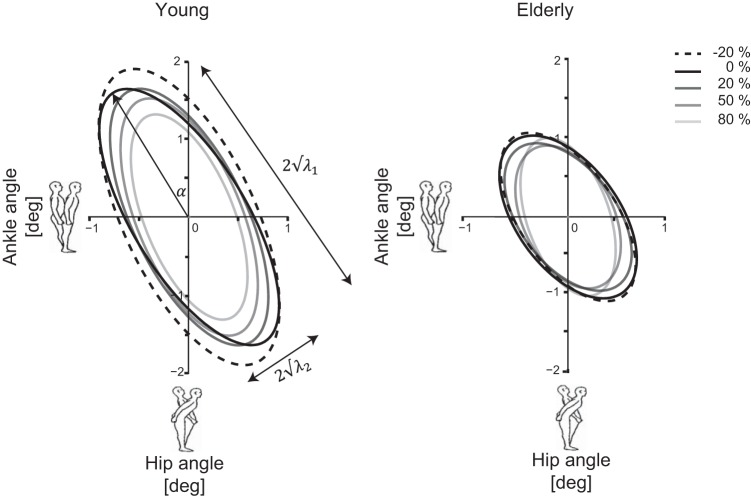
The covariance matrix may be described by an ellipse (Kuo et al. 1998; Speers et al. 2002). The extent of the ellipse along the horizontal and vertical axes is proportional to the RMS motion of the ankle and hip, respectively. The eigenvalues of the covariance matrix, λ₁ and λ₂, describe the squared lengths of the major and minor ellipse axes, respectively. The long axis of the ellipse (λ₁) represents the amount of hip strategy used by the participant, whereas the minor axis of the ellipse (λ₂) is an approximate indicator of the amount of CoM movement. The eigenvector with the largest eigenvalue was used to calculate the orientation angle (α) of the ellipse. The angle quantifies the direction of the relationship between the ankle and hip angles.

Frequency response functions.

The dynamical properties of the neuromuscular controller were quantified in the frequency domain by FRFs, which consist of two parts: a magnitude and a phase, describing the relationship between disturbances and the responses in terms of magnitude and time, respectively. With the use of CLSITs (Engelhart et al. 2015; van der Kooij et al. 2005), the FRFs of the neuromuscular controller (H_c) are computed from the experimental data, according to

$$H_c=-S_{dT}{\left(S_{d\theta }\right)}^{-1}$$ (2)

in which S_dT and S_dθ are the cross-spectral density matrices between the external disturbances (d) and the corrective ankle and hip torques (T) and the ankle and hip angles (θ), respectively, resulting in a two-by-two FRF matrix (H_c). The inverse of the S_dθ matrix and multiplication of it with the S_dT matrix requires that the matrix components are known at all excited frequencies, which is untrue for the zippered multisine, as both disturbance signals contain different frequencies. Therefore, the complex numbers of the cross-spectral densities were interpolated in terms of magnitude and phase to obtain all matrix components for the full range of excited frequencies in the zippered multisine. The FRFs were only evaluated at the frequencies where the disturbance signals contained power. The FRFs were normalized for the gravitational stiffness (mgl) to compensate for differences in the participants' mass and pendulum height, which influence the FRFs.

H_c consists of two direct terms covering the FRFs from ankle angle to ankle torque (H_c,θank2Tank) and from hip angle to hip torque (H_c,θhip2Thip). These direct terms quantify the ankle and hip contributions to balance control. Furthermore, there are two indirect terms, which cover the FRFs from ankle angle to hip torque (H_c,θank2Thip) and from hip angle to ankle torque (H_c,θhip2Tank) and reflect the intersegmental coupling (Boonstra et al. 2013).

Model description.

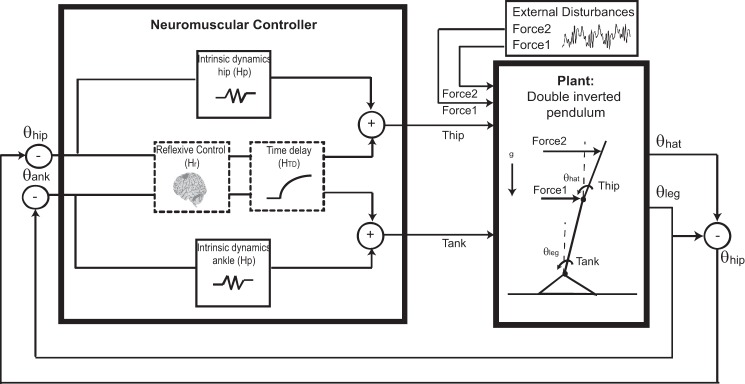
An FRF describes the behavior of the system, but it does not reveal which physiological mechanisms are underlying the system. To relate the changes in behavior to the changes in the underlying physiology, a model of the neuromuscular controller was fit to the non-normalized FRFs (Fig. 3).

Fig. 3.

Schematics of the human balance control system. The human body was represented as a double-inverted pendulum, with disturbances acting at the hip and shoulder level. The model of the neuromuscular controller was used for parameter estimation. The inputs were the ankle and hip angle (θ_ank, θ_hip) and the outputs, the corrective joint torques (T_ank, T_hip). Intrinsic dynamics were modeled as a spring and were different for the ankle and hip joints. Reflexive control and time-delay dynamics were multiple-input, multiple-output transfer functions (shown as dotted boxes), in which interaction existed between the ankle and hip-joint signals. Hp, intrinsic feedback; Hr, reflexive feedback; Htd, feedback of time delay; θhat, segment angle of the head-arms-trunk segment; θleg, segment angle of the leg.

The neuromuscular controller stabilizes the human body by generation of joint torques. The corrective joint torques around the ankles and hips result from intrinsic feedback, together with delayed neural feedback. Each system in the neuromuscular controller was described by a mathematical formula (i.e., transfer function), with parameters describing the physiology. This resulted in a model for the four terms of the neuromuscular controller

$$H_{c,{\theta }_{ank}2T_{ank}}=H_p^{ank}+H_r^{ank2T_{ank}}{H}_{TD}^{ank}$$

$$H_{c,{\theta }_{hip}2T_{ank}}=H_r^{hip2T_{ank}}{H}_{TD}^{ankhip}$$

$$H_{c,{\theta }_{ank}2T_{hip}}=H_r^{ank2T_{hip}}{H}_{TD}^{ankhip}$$

$$H_{c,{\theta }_{hip}2T_{hip}}=H_p^{hip}+H_r^{hip2T_{hip}}{H}_{TD}^{hip}$$ (3)

The transfer function of intrinsic feedback (H_p) describes the muscle and tendon dynamics together with the soft tissue properties. Intrinsic feedback is described for each joint by only stiffness (H_p = K_p). Intrinsic dynamics only exists directly at joint level, i.e., the direct terms of the neuromuscular controller, with different values for the ankle and hips (H_p^ank, H_p^hip).

In the transfer function of the lumped time delay (H_TD = e^−τ_ds), τ_d represents the sum of neural conduction time (transport delay), an electromechanical delay (to activate the muscles), and the processing time of sensory information. A separate lumped delay was introduced for each path length that the sensory information travels; e.g., the direct terms of the neuromuscular controller had separate delays (H_TD^ank, H_TD^hip), and the indirect terms of the FRF had equal delays (H_TD^ankhip).

The transfer function of reflexive feedback (H_r) was represented by a matrix with stiffness and damping terms, relating the joint torques to the ankle and hip angles and angular velocities. This resulted in four transfer functions

$$H_r^{ank2T_{ank}}=K_{ank2T_{ank}}+D_{ank2T_{ank}}s$$

$$H_r^{hip2T_{ank}}=K_{hip2T_{ank}}+D_{hip2T_{ank}}s$$

$$H_r^{ank2T_{hip}}=K_{ank2T_{hip}}+D_{ank2T_{hip}}s$$ (4)

$$H_r^{hip2T_{hip}}=K_{hip2T_{hip}}+D_{hip2T_{hip}}s$$

The model had a total of 13 physiologically interpretable parameters. Table 2 shows the model parameters and how they are estimated, as is outlined next.

Table 2.

Overview of the parameters as used in the model fits

	Parameter	Unit	Varied over Conditions
Time delay
Ankle	τdank	s	No
Hip	τdhip	s	No
Ankle-hip and vice versa	τdank hip	s
Intrinsic feedback
Stiffness ankle	Kpank	Nm/rad	No
Stiffness hip	Kphip	Nm/rad	No
Reflexive feedback
Stiffness Ank2Tank	Kank 2Tank	Nm/rad	Yes
Stiffness Hip2Tank	Khip2Tank	Nm/rad	Yes
Stiffness Ank2Thip	Kank 2Thip	Nm/rad	Yes
Stiffness Hip2Thip	Khip2Thip	Nm/rad	Yes
Damping Ank2Tank	Dank 2Tank	Nms/rad	Yes
Damping Hip2Tank	Dhip2Tank	Nms/rad	Yes
Damping Ank2Thip	Dank 2Thip	Nms/rad	Yes
Damping Hip2Thip	Dhip2Thip	Nms/rad	Yes

The parameters were fit to the 5 force-field conditions simultaneously and for each subject individually. Time delay and intrinsic feedback parameters were kept constant over the 5 conditions, whereas the values for the reflexive feedback parameters varied over the conditions. The time delay for ankle-hip and vice versa was calculated as the average of the time-delay ankle and time-delay hip.

Model fitting.

The transfer functions from the model were fitted to the experimental, non-normalized FRFs using a nonlinear least-squares optimization algorithm. The algorithm searches for a parameter set that minimizes the objective function (J_i,fk)

$$J_{i,f_k}=\sqrt{\frac{1}{1+f_k}}\left|ln\left(H_{c,i}\left(f_k,p\right)\right)-ln\left({\widehat{H}}_{c,i}\left(f_k\right)\right)\right|$$ (5)

$$SSE={\displaystyle \sum _{i=1}^4}{\displaystyle \sum _{k=1}^{18}}{J}_{i,f_k}$$

The logarithmic difference between the FRF (H_c) based on the calculated parameter vector (p) and the estimated FRF (Ĥ_c) obtained from experimental data was summed over the frequencies (f_k, k = 1:18) and the different terms of the FRFs (H_i, i = 1:4), resulting in a sum squared error (SSE). The objective function is chosen, such that there is more emphasis on the low frequencies, $\left(\frac{1}{1+f_k}\right)$, where stiffness typically manifests. In addition, a relative error is calculated for all frequencies on a logarithmic scale.

The optimization algorithm was run 20 times with random initial conditions to assure that a global minimum was found. The best parameter set was obtained from the fit with the lowest SSE value. In addition, the goodness of fit (GOF) describes how well the data compare with the estimation with the parameter set and is expressed as

$$GO{F}_i=1-\frac{{\displaystyle \sum {\left|H_{c,i}\left(f_k,p\right)-{\widehat{H}}_{c,i}\left(f_k\right)\right|}^2}}{{\displaystyle \sum {\left|{\widehat{H}}_{c,i}\left(f_k\right)\right|}^2}}\ast 100\%$$ (6)

The models were fitted for each participant on all five experimental trials simultaneously. To limit the number of parameter combinations in the fit, lumped time delays and intrinsic stiffness were constant over trials in which force-field levels were varied. The lumped time delays of the indirect terms were calculated as the averages of the direct terms. Reflexive feedback was variable over trials, as it was assumed that subjects alter their control action when they are exposed to a force field. After the model-fitting procedures, the passive stiffness and the reflexive stiffness and damping values were normalized for the gravitational stiffness of each participant to correct for the differences in mass and height between participants.

Statistical Analysis

The characteristics of the participants were represented by means and SD in the case of a Gaussian distribution. Else, median, and interquartile range or number and percentage were presented. To test significant differences between groups, an independent, two-sided t-test was performed. In the case of the non-normal distributed values, a Mann-Whitney U-test was performed.

To test significant differences in RMS and covariance descriptors between age and force-field levels, linear mixed models were used. Age and force-field level were fixed effects. To account for the repeated measurements, participant intercept was included as a random effect. In addition, interaction effects between age and force-field levels were studied.

For statistical analysis of the FRFs, the magnitude of each FRF was logarithmically transformed to make the data normally distributed. Subsequently, the magnitudes were averaged within three frequency bands (<1, 1–2.5, and 2.6–5 Hz). The lowest frequencies generally describe the stiffness properties of the system, whereas the magnitude at middle and high frequencies is shaped by damping and mass (inertia), respectively. Linear mixed models were used to test significant differences in FRFs between age and force-field levels for each frequency band. Age group, force-field level, and frequency band were fixed effects, and participant intercept was a random effect. In addition, interaction effects between age group and force-field level were studied.

To test significant differences of the estimated model parameters that were constant over trials, an independent, two-sided t-test was performed, as there can only be an effect of age and not of force-field level. To test significant differences between age and different force-field levels in the estimated model parameters that were allowed to vary over trials, linear mixed models were used. Age group and force-field level were fixed effects, and participant intercept was a random effect. In addition, interaction effects between age and force-field level were studied.

For all tests, the significance level (α) was set at 0.05. All analyses were performed with SPSS version 22.0 (SPSS, Chicago, IL).

RESULTS

Characteristics of the group of healthy young and healthy old participants are presented in Table 1 to illustrate the health of the study population. The elderly used more medication (P = 0.001) and had a lower MMSE score (P = 0.023) and lower handgrip strength (P = 0.014) compared with the young participants (Table 1). All subjects were able to maintain balance during the disturbances and the force-field trials.

Root Mean Square

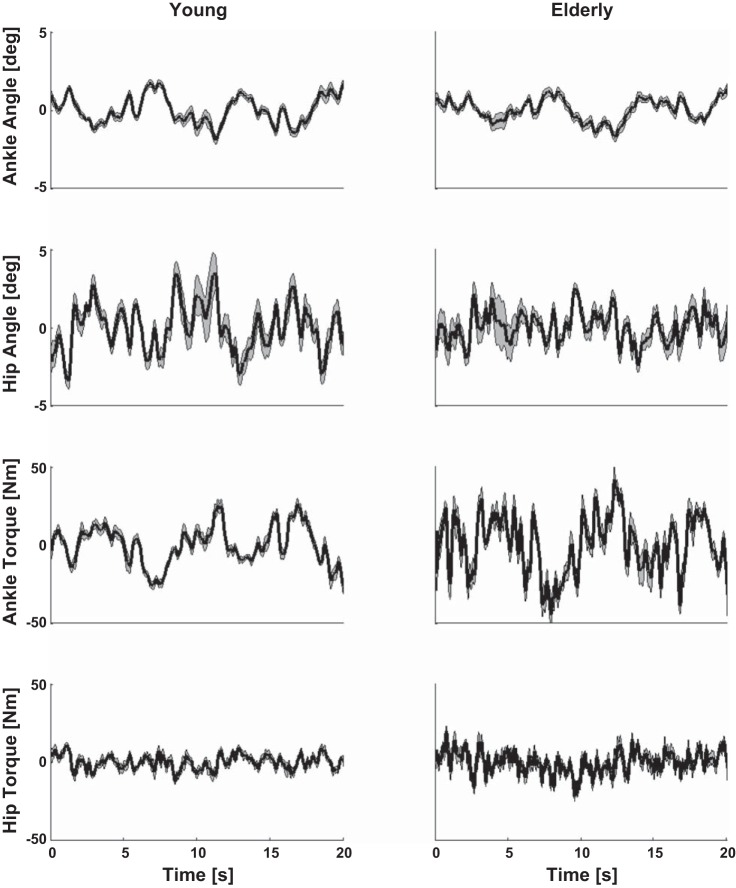
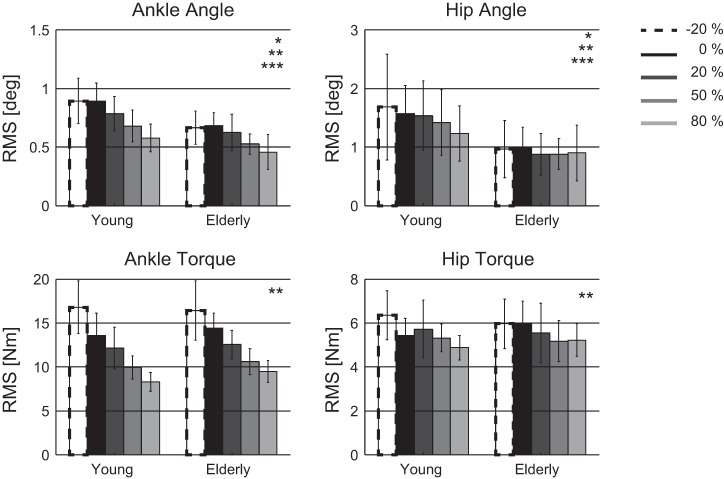
Figure 4 shows the joint angles and torques as a response to the force disturbances for a representative young and elderly participant (without application of a force field). Figure 5 shows the RMS of the ankle and hip angle and the ankle and hip torque. The elderly had smaller ankle (P = 0.001) and hip (P = 0.003) angles than the young participants. The exerted ankle and hip torques were not found to be significantly different between the two groups.

Fig. 4.

Joint angles and joint torques in response to the applied disturbances of a representative young (left) and elderly (right) participant in the baseline trial without force field (0%). The average over the 9 disturbance cycles is indicated with the black line; the gray area represents the SD.

Fig. 5.

Root mean square (RMS) values of the joint angles and torques for young and elderly participants per force-field level represented by means and SD. Significant differences with *age, **force field, or ***interaction between age and force field.

For every 10% increase in external force field, the averaged postural responses decreased, namely, the ankle angle with −0.02° (P < 0.001), the hip angle with −0.03° (P < 0.001), the ankle torque with −0.7 Nm (P < 0.001), and the hip torque with −0.07 Nm (P < 0.001).

An interaction effect was found between age and force-field level; with increasing force-field level, the decrease in ankle (P = 0.007) and hip (P = 0.004) angle was less in the elderly than the observed decrease in young participants. No interaction effect was found between age and force-field level for the ankle and hip torque. The elderly and the young participants showed comparable adaptation of their joint torques with different force-field levels.

Covariance Descriptor

Figure 6 shows the covariance descriptor for the young and elderly participants for the different force-field levels. The length of the ellipse major axis was lower in the elderly compared with the young participants (P = 0.013). No differences were found for the minor axis or the orientation of the ellipse between the young and elderly.

Fig. 6.

Covariance descriptor of the young and elderly participants per force-field level. λ₁ and λ₂, squared lengths of the major and minor ellipse axes, respectively; α, orientation of the ellipse.

With the application of a stiffer force field, the orientation angle of the ellipse increased, and the covariance descriptors decreased. For every 10% increase in force field, the values (averaged over the repetitions of the disturbance signals) altered: λ₁ (−0.013, P < 0.001), λ₂ (−0.001, P < 0.001), and α (0.002 rad, P < 0.001).

An interaction effect between age and force-field level was found; the decrease of λ₁ was less in the elderly compared with the young (P = 0.01). No interaction effect was found between age and force-field level for the λ₂ and α; the elderly adjusted these values compared with the young participants.

Frequency Response Functions

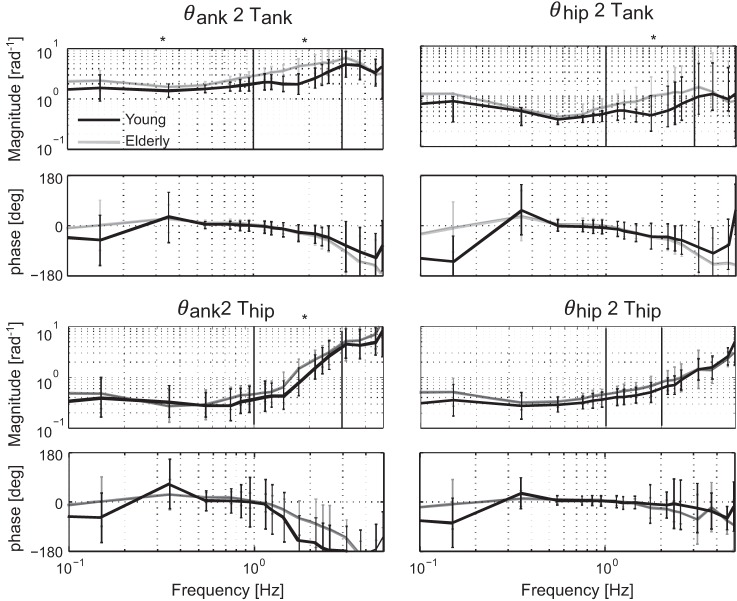
Figure 7 shows the neuromuscular controller FRF (Ĥ_c) of the young and elderly in the baseline trial when only disturbances were applied without external stiffness (0%).

Fig. 7.

Baseline differences in normalized frequency response function (FRF) between young (black lines) and elderly (gray lines) participants, where only the 2 disturbances were applied without additional force fields (0%), represented by means and SD. The FRF consists of 4 terms: 2 direct terms from ankle angle to ankle torque (θ_ank2T_ank) and from hip angle to hip torque (θ_hip2T_hip) and 2 indirect terms from hip angle to ankle torque (θ_hip2T_ank) and from ankle angle to hip torque (θ_ank2T_hip). *Frequency bins in which there is a significant difference with age.

There was a main effect of age, as the magnitude of H_c,θank2Tank was higher in the elderly for the lowest (P = 0.002) and mid-range (P < 0.001) frequencies. For the other terms, the magnitude was higher in the elderly in the mid-range frequencies of H_c,θhip2Tank (P = 0.001) and H_c,θank2Thip (P = 0.006). No significant differences with age were found in any of the frequency bands for H_c,θhip2Thip, and no differences were found for the high-frequency range of the neuromuscular controller.

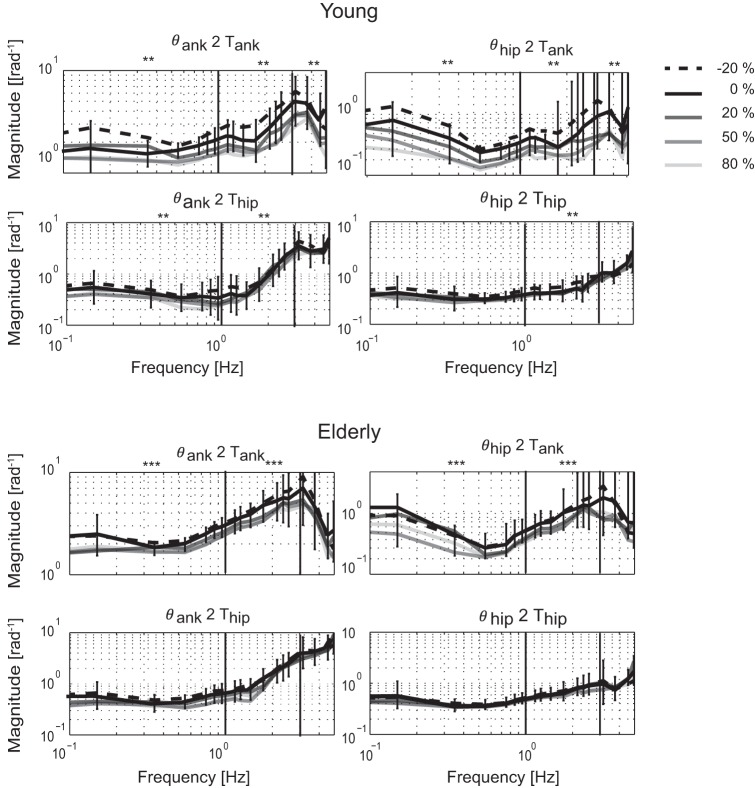
With the application of a force field, the FRF magnitude changed (Fig. 8). With increasing force field, the FRF magnitudes became lower for the entire frequency range in H_c,θank2Tank (P < 0.001 for all frequency bands) and H_c,θhip2Tank (P < 0.001 for all frequency bands). A significant decrease of FRF magnitude was also found for the lowest and mid-range frequencies in H_c,θank2Thip (P < 0.005 for both frequency bands) and the mid-range frequencies of H_c,θhip2Thip (P < 0.016).

Fig. 8.

Adaptation of normalized FRF magnitude in the young (top) and elderly (bottom) participants. For each force-field level, the mean is shown. For displaying reasons only, the SD was shown for the baseline trial. SDs of the other force-field levels were compared with the baseline trials. Frequency bins in which there are **significant differences with force field or the ***interaction between age and force field.

An interaction effect between age and force-field level was found for the low and mid-range frequencies in H_c,θank2Tank (P = 0.027 and P = 0.008) and H_c,θhip2Tank (P = 0.026 and P = 0.002). Elderly participants reduced the FRF magnitude around the ankle less compared with young participants. The FRF magnitude adjustment around the hips was comparable in both groups. For example, the magnitude of H_c,θank2Tank for the lowest frequencies in young participants was decreased by 21% for the stiffest force field (80%), whereas for the elderly, it was decreased by 14%. For the destabilizing force field (−20%), postural responses increased 28% in young, whereas for the elderly, they were only increased by 8%.

Model Parameters

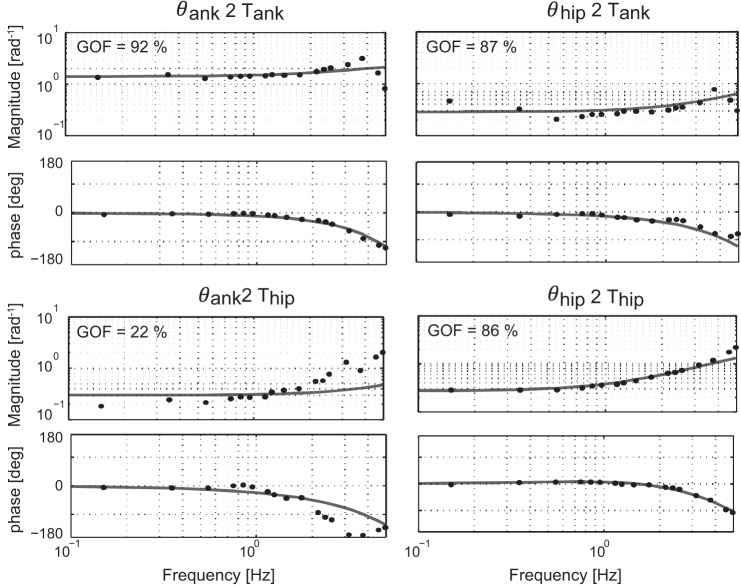
The GOF values were averaged (±SD) over force-field levels and participants, resulting in a GOF value for each FRF term (H_c,θank2Tank, H_c,θhip2Tank, H_c,θank2Thip, and H_c,θhip2Thip). The average GOF values for the young participants were 81 ± 14%, 70 ± 18%, 50 ± 23%, and 75 ± 17% and for the elderly were 75 ± 13%, 70 ± 13%, 63 ± 20%, and 82 ± 14%. Similar GOF values were obtained for the young and elderly. Different GOF values were found among conditions; e.g., some of the conditions had higher GOF values and thereby, were fit better than others. Furthermore, the GOF values of the direct FRF terms were higher than those of the indirect terms, and the GOF values of H_c,θank2Thip were lowest. The GOF is also displayed in Fig. 9, which shows the estimated FRFs together with the model fit for a representative participant.

Fig. 9.

Normalized FRFs based on measured data (black dots) and model fits (gray lines) of a representative healthy young subject for the baseline trial (0%). The goodness of fit (GOF) values are shown for each term in the FRF.

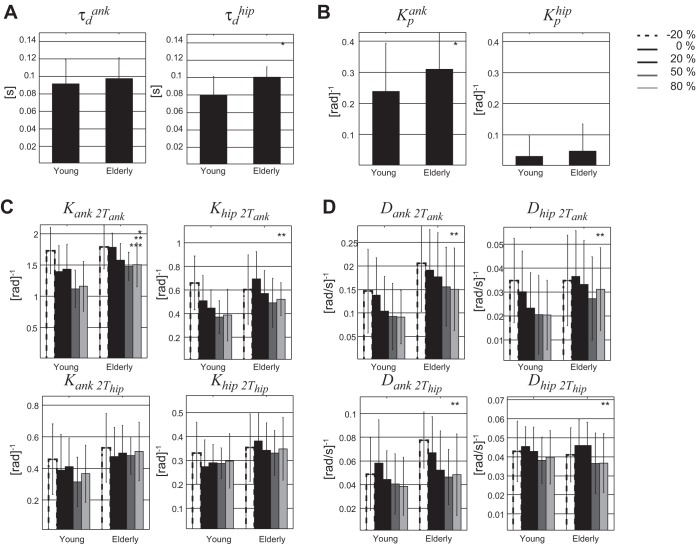
Figure 10 shows the estimated parameters for the young and elderly participants. The elderly had larger lumped time delays for the hips (P < 0.001) compared with the young participants. The lumped time delays of the ankle were not found to be significantly different between age groups. Furthermore, the intrinsic ankle stiffness (P = 0.007) was higher in elderly, but no significant differences were found for the intrinsic hip stiffness. The reflexive stiffness K_ank2Tank was significantly higher in elderly than in young participants (P = 0.036). None of the other reflexive stiffness and damping terms were found significantly different between the young and elderly.

Fig. 10.

Estimated parameters represented by means and SD (error bars) for young and old participants per force-field level. Stiffness and damping are normalized to the gravitational stiffness (mass × gravitation × center of mass height) for each subject. A: estimated time delays (τ_d); B: intrinsic properties (K_p); C: reflexive stiffness (K_ank2Tank, K_hip2Tank, K_ank2Thip, K_hip2Thip); D: reflexive damping (D_ank2Tank, D_hip2Tank, D_ank2Thip, D_hip2Thip). Significant differences with *age, **force field, or ***interaction between age and force field.

When increasing the force-field level in both groups, all reflex stiffness and damping values decreased (P < 0.04), except for the reflexive stiffness around the hip, K_ank2Thip and K_hip2Thip. An interaction effect was found between age and force-field level only for K_ank2Tank (P = 0.04). The elderly reduced their reflexive stiffness around the ankle joint less for increasing force fields compared with the young.

DISCUSSION

The results of this study show age-related differences in multijoint coordination. The elderly swayed less than the young participants, and the elderly showed a reduced hip strategy. As the corrective joint torques were not significantly different between age groups, the FRF magnitude was higher in the elderly. The ratio of the corrective joint torques and the body sway was increased; i.e., the elderly exhibit a higher stiffness. Parameter estimation showed that the elderly have higher intrinsic stiffness and reflexive stiffness around the ankle joint. When an external force field was applied, both age groups lowered their postural responses, expressed as lower FRF magnitude around the ankle. However, the elderly adapted their postural responses less compared with the young participants.

Participant Characteristics

Based on the inclusion criteria, all young and elderly participants were characterized as healthy. None of the young participants were taking medication. The elderly used medication, but none of the medication had a known influence on balance control. Comparison between young and elderly participants showed a significantly lower MMSE score in the elderly. It is known that cognitive processing has an influence on the control of balance (Ambrose et al. 2013; Doumas et al. 2009; Stijntjes et al. 2015; Teasdale and Simoneau 2001); e.g., low cognitive function increases the risk of imbalance. Although all of the elderly were characterized as healthy with normal cognitive function, the lower MMSE score might have influenced the results. None of the participants reported fear of falling or fatigue during the experiment.

RMS and Covariance Descriptor

Results show that the elderly swayed less when being disturbed by forces at the hip and shoulder compared with the young participants. These results were in contrast with multiple studies of quiet stance, showing that body sway increased with age (Abrahamová and Hlavačka 2008; Demura et al. 2008; Pasma et al. 2014a). In our study, the balance control system was externally disturbed. Humans altered their feedback gains to correct for these disturbances; i.e., the amount of joint torque relative to the amount of joint motion was adjusted. To be more specific, with increasing stabilizing force-field level, the feedback gains were reduced. In quiet stance, the balance control system is mainly influenced by internal disturbances, such as sensory and motor noise, which cannot be corrected. The alteration of feedback gains during quiet stance would amplify the internal disturbances, which increases body sway (Speers et al. 2002). This could explain why in quiet stance, the elderly sway more and that it is possible that in perturbed stance, the elderly sway less.

Covariance descriptors were used to describe not only whether the application of force fields resulted in changes of sway but also in postural coordination. Eigenvectors and eigenvalues were used to describe independent combinations of joint movements, defined by principle component analysis (Alexandrov et al. 2001; Hsu et al. 2007; Kuo et al. 1998). From the covariance matrix of the ankle and hip angle, the first component λ₁ may be interpreted as double-inverted pendulum behavior and quantifies the amount of hip strategy. Our results show that λ₁ is smaller in the elderly, indicating that they have less hip strategy and behave more like a single inverted pendulum. The second component λ₂ was not found to be significantly different between age groups, indicating that the control of the CoM was similar. In a previous study (Hsu et al. 2013), where external disturbances (platform translations) were applied, the elderly exhibited a less-flexible stance and a decreased covariance between the joints, whereas the CoM excursion was not significantly different between the groups. This is in accordance with our findings.

When a stabilizing force field was applied, a decrease of both λ₁ and λ₂ was found, as maintaining standing balance became easier. A decrease in λ₁ indicates that the combination of opposing ankle and hip motion was reduced; i.e., hip strategy became less with increasing force field. A decreased λ₂ value indicates that a reduction was found in the combination of movements, dominated more by the ankle angle. The negative relation remained; a positive ankle angle was accompanied with negative hip angle. There was an interaction effect between age and force-field level. The elderly adapted their hip strategy less than young participants. This might be explained by the fact that the λ₁ was lower in the elderly at baseline. The elderly adapted their control of CoM similar to the young.

Frequency Response Functions

Measured joint angles contain not only a sway response due to the disturbances but also contain the subject's own spontaneous body sway [remnant sway due to, e.g., motor and sensory noise (van der Kooij and Peterka 2011)]. As both RMS measures and covariance descriptors are based directly on these measured joint angles, they do not distinguish between the responses due to the disturbances and spontaneous sway. Therefore, in this study, we used system-identification techniques to identify solely the neuromuscular control mechanisms from the closed-loop feedback system, i.e., the corrective joint torques as a response to body movement around the joints. The neuromuscular controller dynamics and the coordination between joints have frequency-specific effects, which were shown in FRFs. Compared with RMS values and covariance descriptors, the FRF is potentially a more informative measure. The FRF describes only the part of the angles and corresponding corrective joint torques as a response to the disturbances, i.e., changes in the neuromuscular controller only.

In the elderly, the RMS values of the joint angles were lower, and the joint torques were compared with young adults. These results were also seen in higher FRF magnitude of the elderly at the lowest frequencies of the direct ankle term. Stiffness is assumed to dominate the magnitude of the FRFs in the low-frequency range, indicating that the elderly have higher ankle-joint stiffness. When the pull of gravity is compensated for by an external force field, the elderly adapted their FRF magnitudes around the ankle less compared with young. These age-related differences in adaptation to force-field levels were also found in the RMS outcomes and the covariance descriptors.

In addition to the adaptation at the lowest frequency range, in the mid-range frequencies, significant differences were found between force-field conditions. The mid-range frequencies are mostly affected by damping properties. The increase of damping reduces oscillations in the response to external disturbances (Cenciarini 2010). No significant differences were found between force-field conditions at high frequencies, because the FRF magnitude at high frequencies is generally shaped by the mass properties of the participants, which were not significantly different between young and elderly (Table 1).

Model Parameters

The estimation of model parameters on the FRF reveals the underlying factors of the neuromuscular controller. The elderly exhibit a larger intrinsic stiffness and reflexive stiffness of the ankle compared with the young, which is in concordance with our expectations following the results of the FRFs. When the force-field level was increased, both the young and elderly reduced their reflexive stiffness and damping. However, the reflexive feedback gains around the ankle joint were reduced less in elderly compared with young participants.

The body is mostly represented as an inverted pendulum, based on body rotation around the ankle joint. Our study includes a hip joint, which might result in different values of the estimated parameters compared with other studies. Kiemel et al. (2008) estimated intrinsic joint parameters of both the ankles and hips using system-identification techniques based on electromyography (EMG) signals and joint angles when healthy young subjects were faced with visual scene disturbances. The intrinsic stiffness of the ankle and hips was found to be 293 Nm/rad and 95 Nm/rad, respectively. Cenciarini (2010) found intrinsic ankle stiffness of 157 and 99 Nm/rad for the young and elderly, respectively, when exposed to support surface tilts. The estimated stiffness values (i.e., the non-normalized values) in this study are in the same range as the other two studies; however, in our study, the elderly exhibit larger intrinsic ankle stiffness compared with the young.

Estimated reflexive stiffness and damping of the ankle in the current study are within the ranges found earlier in the literature, varying from 898 to 1,500 Nm/rad and from 288 to 480 Nms/rad (Cenciarini 2010; Davidson et al. 2011; Mahboobin et al. 2005; Peterka 2002). Furthermore, others found a comparable reflexive stiffness between young and elderly, which is in accordance with our results (Ho and Bendrups 2002). Upper-body stiffness and damping between 100 and 300 Nm/rad and 20 and 60 Nms/rad were found in healthy young subjects (Goodworth and Peterka 2012), similar to our results.

The time delays as estimated in this study consisted of processing time, electromechanical delay, and neural conduction time. Previous studies, in which the human body was represented as an inverted pendulum, found a time delay of ∼172 ms, which was not significantly different between the young and elderly (Cenciarini 2010). Other studies found time delays in the range of 100–200 ms (Davidson et al. 2011; Mahboobin 2007; Peterka 2002), and the elderly exhibited significantly higher delays compared with the young (Davidson et al. 2011). This compares with our results.

Underlying Mechanisms

In this study, we used system-identification techniques to quantify age-related differences in adaptation of multijoint coordination. With current clinical balance tests, the subsystem that is responsible for the observed behavior remains largely unknown (Pasma et al. 2014b; Visser et al. 2008). With system-identification techniques and parameter estimation, the contribution of the underlying subsystems can be unraveled, as the balance-control mechanism is expressed in physiologically relevant parameters (Engelhart et al. 2014). Identification of the factors that contribute to altered postural responses in the elderly may provide insight into the mechanisms resulting in impaired balance and finally, falling. More insight into these factors and mechanisms might help to develop and test targeted interventions to reduce the risk of falling. For example, a higher joint stiffness is found, which can increase the risk of falling in the elderly (Ishida et al. 2008). Although it is currently unclear what causes the increased stiffness, it could result from, e.g., altered muscle properties, or could indicate compensatory co-contraction for increased noise.

This study showed a higher intrinsic stiffness of the ankle in the elderly compared with the young, which could be explained by age-related changes in fiber elasticity in type I and IIa muscle fibers. This change in elasticity will result in a higher stiffness of the muscle (Ochala et al. 2007). On the other hand, a higher stiffness could be a way to compensate for the deterioration of sensory systems. Previous studies showed that the proprioceptive information from the distal joints (i.e., the ankle) was insufficient to maintain standing balance due to peripheral neuropathy (Horak et al. 1990). A higher intrinsic stiffness, for example, generated by co-contraction (Benjuya et al. 2004), would increase the response of the proprioception and therefore, will enhance the proprioceptive input from the ankle (Accornero et al. 1997).

Furthermore, we found significant differences in reflexive stiffness around the ankle joint between the young and elderly. Besides, the elderly adapt their reflexive stiffness around the ankle less compared with the young when the force field at the hip level was increased, resulting in a more stable ankle joint. This difference might be due to the loss of flexibility to control multiple joints (Hsu 2013; Ooteghem 2009). It could be that age-related changes, both in muscles (e.g., intrinsic stiffness and muscle strength) and sensory systems (e.g., peripheral sensory loss and afferent and efferent conduction impairment), result in less options to control balance.

Last, the time delays of the hip were higher in the elderly compared with the young. The time delays estimated in this study were comprised of processing time, electromechanical delay, and neural conduction time. Therefore, a higher time delay might be due to the slowing down of the nerve conduction speed in afferent and efferent pathways with age, due to a decrease in the number of neurons and loss of myelination and other neural changes (Barin and Dodson 2011; Sturnieks et al. 2008). On the other hand, a higher time delay with age can be due to deficits in stimulus encoding, central processing, and response initiation (Horak et al. 1989).

Strengths and Limitations

In contrast with current RMS values and covariance descriptors, system-identification techniques make it possible to derive parameters of the neuromuscular controller in multisegmental balance control. Nevertheless, the results might be influenced by various factors. First, the control scheme of the neuromuscular controller may not be an adequate representation of actual postural control, and it may not describe all age-related changes in standing balance. We assumed that the states of the human body (joint angles and angular velocities) were fully known, and the sensory information was “perfect.” However, with age, the sensory systems might become impaired (Sturnieks et al. 2008). Furthermore, we did not model the integration of sensory information, i.e., the process of sensory reweighting (Mahboobin et al. 2009; Peterka and Loughlin 2004). Therefore, age-related changes in the quality of sensory information and sensory reweighting capacities were not studied.

Second, estimation of model parameters based on experimental data is a constant trade-off between a good model fit and the least amount of parameters. The increase in the number of parameters improves the fit; however, the physiological interpretation becomes difficult. Two aspects are important when interpreting a parameter set obtained from a model fit on experimental data. The first is independency; i.e., when two parameters give similar contributions to the FRF, redundancy exists, which hampers the physiological interpretation. The second is identifiability, meaning that a parameter has to contribute to the FRF within the excited frequency band to assure that the influence of that parameter can be detected. The goal of model fitting is to find the most compact model with parameters that are both independent and identifiable.

During the process of model fitting, various combinations of parameter sets were estimated and validated, based on previously used models in literature (Goodworth and Peterka 2012; Kiemel et al. 2008). In our fitting procedure, the intrinsic damping properties and the activation dynamics (mapping of EMG signals to joint torques) were found unidentifiable. Muscle-activation dynamics did not influence the magnitude of the FRF in the frequency range in which the data were obtained (0.05–5 Hz). However, the FRF phase was affected. Interaction existed with the lumped delays, which also shaped the FRF phase, resulting in poorly interpretable values. Therefore, we decided not to include the muscle-activation dynamics in the model, and we attributed all phase changes to the lumped delays (which represent the sum of transport delay, the processing time of sensory information, and an electromechanical delay). Interaction also existed in the direct terms of the FRF (H_c,θank2Tank and H_c,θhip2Thip) among the intrinsic stiffness, the reflexive stiffness, and the lumped delay. The FRF magnitude displayed the sum of the stiffness values. The identified FRF phase was somewhere between the phase of zero (due to the intrinsic stiffness) and the phase due to the lumped delay. The result is that only the product of reflexive stiffness and time delay was identifiable. To solve the redundancy among the three parameters, we assumed two of the three interacting parameters to remain constant over the five experimental conditions. The changes in intrinsic properties and lumped delays were expected to be much smaller than the changes in reflexive properties (Cenciarini 2010; Peterka 2002). Therefore, the intrinsic properties and lumped delays were averaged over conditions, and the reflexive stiffness was left to vary over conditions.

However, the assumption of average intrinsic stiffness over the experimental conditions might have influenced our results. Intrinsic stiffness scales with the contraction level of the muscles, which is influenced by co-contraction or other external factors (such as a force field) (Ludvig et al. 2011). With increasing force-field levels, the pull of gravity on the participants' CoM was reduced, and this possibly also reduced the activation level of the muscles as control of balance became easier. With decreased muscle activation, the intrinsic stiffness will also decrease. Due to our assumption, variations in intrinsic stiffness were now captured in the reflexive stiffness values.

As mentioned before, the lumped delay in the model was estimated from the FRF phase, which resulted from the contribution of intrinsic stiffness (which acts without a delay and has a phase shift of 0) and reflexive stiffness (which acts with a delay and induced a negative-phase shift). If there were an increased contribution of corrective torque due to intrinsic properties compared with reflexive feedback, then the estimated lumped delay might appear to decrease (Peterka 2002). Therefore, the lumped delay parameter in the model can be better thought of as an “effective delay” rather than as a parameter representing actual delays in neural processing, transmission, and muscle activation. With an interest in the separate contribution of the transport delay, the electromechanical delay, and the processing time in the lumped delay, EMG measures can be of additional value.

Conclusion

In this study, we used novel system-identification techniques to derive a description of the neuromuscular control mechanisms in multijoint balance control by applying force disturbances at the level of the hip and between the shoulder blades. Adaptation of multijoint coordination was induced by external force fields, represented as virtual springs at the pelvis with various stiffness levels. Our results demonstrate that humans adapt to force fields by altering their postural responses, i.e., reflexive stiffness and damping. However, the elderly adapted their reflexive stiffness around the ankle less compared with young participants. In addition to higher reflexive ankle stiffness, the elderly had higher intrinsic ankle stiffness and larger lumped time delays of the hip. Insight in the factors that alter multijoint coordination with age could provide insight into the mechanisms that influence fall risk. Adaptability of multijoint coordination is an essential feature of standing balance control to adjust to various conditions. A reduced ability to adapt may underlie an increased risk of falls with aging.

GRANTS

Support for this research was provided by the Dutch Technology Foundation STW (NeuroSIPE #10737 BalRoom), which is part of the Netherlands Organisation for Scientific Research (NWO) and is partly funded by the Ministry of Economic Affairs.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

Author contributions: D.E., J.H.P., A.C.S., R.G.K.M.A., C.G.M.M., A.B.M., and H.v.d.K. conception and design of research; D.E. performed experiments; D.E. and J.H.P. analyzed data; D.E., J.H.P., A.C.S., R.G.K.M.A., and H.v.d.K. interpreted results of experiments; D.E. prepared figures; D.E. drafted manuscript; D.E., J.H.P., A.C.S., R.G.K.M.A., C.G.M.M., and H.v.d.K. edited and revised manuscript; D.E., J.H.P., A.C.S., R.G.K.M.A., C.G.M.M., A.B.M., and H.v.d.K. approved final version of manuscript.