Abstract
We introduce an initial implementation of the LICHEM software package. LICHEM can interface with Gaussian, PSI4, NWChem, TINKER, and TINKER–HP to enable QM/MM calculations using multipolar/polarizable force fields. LICHEM extracts forces and energies from unmodified QM and MM software packages to perform geometry optimizations, single–point energy calculations, or Monte Carlo simulations. When the QM and MM regions are connected by covalent bonds, the pseudo-bond approach is employed to smoothly transition between the QM region and the polarizable force field. A series of water clusters and small peptides have been employed to test our initial implementation. The results obtained from these test systems show the capabilities of the new software and highlight the importance of including explicit polarization.
I. INTRODUCTION
Our quantum mechanical/molecular mechanical (QM/MM) interface (LICHEM) for polarizable models can calculate energies, optimize geometries, and perform Monte Carlo (MC) simulations via wrappers to quantum mechanics (QM) and molecular mechanics (MM) software packages. QM/MM calculations, where part of the system is treated quantum mechanically and the rest of the system is treated classically, is a popular technique in computational chemistry and biology [1–26]. QM/MM calculations have been quite successful in the past several decades, primarily due to the efficiency of simulating most of the system with a classical model. In fact, these techniques are essentially required to model large enzyme catalyzed reactions.
Most QM/MM simulations are performed with simple point–charge based force fields; however, the electrostatic field is known to have a strong effect on excited states and reaction barriers [27–32]. Several research groups have improved the description of the MM environment by including point–multipoles, induced dipoles, and/or diffuse charge densities in QM/MM simulations [1, 2, 5, 21, 33–47]. These polarizable QM/MM simulations are promising steps toward efficient high–accuracy simulations of chemical reactions.
Multipolar and polarizable force fields can help ameliorate some errors associated with QM/MM simulations by providing a more accurate representation of the charge density of the environment. The improved MM description reduces the over–polarization of the QM wavefunction due to large point–charges in the MM subsystem, as well as providing in a more accurate description of the MM–MM interactions [1, 2, 21, 39, 44, 46, 48–51]. A more advanced approach for modeling the electrostatic field and polarization involves polarizable electron density on atomic centers [5, 27–30, 37, 52, 53]. These electron density models, such as the Gaussian Electrostatic Model (GEM), reduce errors even further [30, 32, 37, 52, 54].
There are several approaches for including polarization in the MM environment [18, 30, 55–57]. One approach is to allow charge to flow from one MM atom to another [40–42, 55, 58–61]. These charge equilibration force fields introduce polarization, while only requiring standard point–charge interactions between the QM and MM regions, which is appealing for QM/MM implementations. However, these models are still limited by the inherent lack of accuracy of point–charge based models [30]. An alternative approach is to add polarizable sites or Drude oscillators to the MM atoms [1, 33–36, 38, 43–45, 47, 62, 63]. This enhances the description of the electric field by introducing induced dipole moments on top of the point–charge based models. These polarizable force fields can be further extended by placing both polarizable sites and multipole moments on each atom [44, 49, 64], which enhances both the static and polarized parts of the field.
Most QM and MM packages have some form of QM/MM functionality or are being actively developed to introduce such functionality. A smaller number of software packages allow atomic multipoles, polarizabilties, and/or diffuse charges to be added to the MM potential [21, 22, 44, 65–68]. Often, introducing these electrostatic models requires modifying the self–consistent field (SCF) routines in the QM software packages. Thus, implementing polarizable QM/MM capabilities can be quite difficult.
We have designed the LICHEM interface to perform a wide variety of QM/MM simulations. Our software enables the use of advanced potentials for the MM environment. QM/MM simulations are often performed within a MM (QM) package, which may call a wrapper for the QM (MM) part of the calculations. However, this procedure can severely limit the available approximations. By creating a separate open source interface, new approximations and wrappers can easily be implemented without modifying key components of the QM or MM software.
In this work we present a novel QM/MM software package, named LICHEM (Layered Interacting CHEmical Models). LICHEM is tested by performing QM/MM calculations including single–point energies, geometry optimizations, and Monte Carlo simulations for a series of systems with both polarizable and point–charge force fields. Our results highlight the current capabilities of LICHEM and stress the importance of using multipolar/polarizable force fields to provide an accurate description of the MM environment.
The remainder of the manuscript is organized as follows. The Methods section presents a brief background of QM/MM theory, including treatment of QM/MM interactions and covalent bonds which cross the QM/MM boundary in LICHEM. This is followed by a description of a method to transform Cartesian point–multipoles to a set of point–charges and the treatment of polarization in QM/MM calculations within LICHEM. Subsequently, we present results for single–point energies, geometry optimizations, and Monte Carlo simulations for several water clusters and peptides. Finally, the Development and Conclusion sections summarize the capabilities of LICHEM.
II. METHODS
This section presents a description of the QM/MM methods currently implemented in LICHEM, including how the point–multipoles and polarization of the MM environment are included in the QM subsystem and QM/MM boundaries.
A. QM/MM methods
QM/MM calculations divide the system into several different regions to enable accurate simulations with a large number of atoms. This allows for the use of accurate quantum mechanical methods on a small subset of the atoms while approximating the remainder of the system with efficient classical models. The Hamiltonian of the QM/MM system, Ĥ, can be written as
| (1) |
where ĤQM is the Hamiltonian for the nuclei and electrons in the quantum region, V̂MM is the potential for the atoms in the classical region, and V̂QMMM is the potential for the interaction between the QM and MM (QM–MM) atoms. The QM–MM interaction potential contains the electrostatic, van der Waals (vdW), and bonding potentials from the MM force field, which constitute the external field for the QM nuclei and electrons. The MM and QM–MM energies resulting from these potentials are given by
| (2) |
and
| (3) |
where Eij,bnd is the energy arising from the bond, angle, and dihedral interactions, Eij,vdw is the energy due to the empirical exchange and dispersion interactions, and Eij,chg is the energy due to the electrostatic interactions. The summations are over the sets of atoms treated classically ({MM}) or quantum mechanically ({QM}). For simplicity, the notation in Eqs. 2 and 3 assumes that the MM energies are pairwise additive.
Since EMM and EQMMM are written in terms of relatively simple and often pairwise potential energy functions, calculating the total energy for the full QM/MM system is straightforward. The total system energy may be written as:
| (4) |
where
| (5) |
In our implementation, the QM wavefunction is explicitly polarized by the MM environment by adding the MM point–charges to the effective QM Hamiltonian. In addition, when polarizable force fields, such as AMOEBA, are employed, the MM environment is polarized by the QM wavefunction as explained in subsection II C.
The electrostatic coupling between the QM and MM subsystems gives rise to complications in calculations of the forces [26, 69]. However, accurate geometry optimizations with the QM/MM Hamiltonian may be performed with an iterative procedure [15, 26], where the QM and MM atoms are optimized separately. During the MM optimization, point–charges are placed on the QM atoms to match the electrostatic potential due to the electron density and nuclei. Once the MM geometry has been sufficiently relaxed, the QM coordinates are optimized by minimizing ETot. The optimization algorithm continues to alternate between relaxing the MM and QM regions until the entire system satisfies the convergence criteria.
B. QM–MM interactions
When the QM and MM regions are not connected by covalent bonds, the QM–MM interactions are straightforward. The electrostatic interaction between the MM subsystem and the QM region is calculated by including the MM electrostatic field (point–charges or point–multipoles) in the effective QM Hamiltonian. The electrostatic embedding allows the wavefunction to polarize in response to the external field. The remaining exchange and dispersion interactions are included (approximately) through the MM vdW potentials from the force field.
For a single–point energy calculation in LICHEM, the QM+charges calculation is performed with the QM wrapper, while the MM wrapper calculates the MM energy with no charges or bonded potentials on any of the QM atoms. These two energies are then added together to get the total energy. This approach divides EQMMM between the MM calculation (E′MM) and the QM calculation (E′QM). Eq. 4 can now be rewritten as:
| (6) |
where
| (7) |
and
| (8) |
Here V̂QMMM,chg is the electrostatic potential from the MM field interacting with the electron density and atomic nuclei of the QM region.
C. Multipolar/Polarizable models
Point–charges are often inadequate for representing the electrostatic field around a molecule [31]. The external MM field can be improved by assigning point–multipoles, generally up to the quadrupole moments, and polarizable sites to the MM atoms. These force fields are more computationally expensive than point–charge models since multipole–multipole interactions involve a larger number of operations per site; however, the results can be significantly more accurate [5, 31, 37]. The point–multipoles provide a better description of the charge distribution of the molecular fragment, which results in a more accurate representation of the charge anisotropy [70]. Many force fields currently in use do not take into account how the charge distribution changes due to an external field. This effect may be included in several ways such as fluctuating charges [40–42, 61], electronegativity equalization [58–60], or inducible point–dipoles [33–36, 38, 43, 45, 47, 49]. In this initial implementation of LICHEM, MM polarization is included via inducible dipoles from polarizable force fields, such as the AMOEBA model [49, 64].
Multipolar models add an additional complication to the calculations in that the multipole potentials are aspherical. To address this, a local frame of reference is defined for each atom using 1–3 neighboring atoms [70] and the local frame multipoles are rotated to the global frame on–the–fly during the evaluation of the potential. Unfortunately, few QM packages can perform calculations with atomic multipoles. In order to include point–multipoles in the external potential, either QM packages must be modified or the multipoles must be approximated. In our implementation, we have chosen to approximate the multipoles as an octahedral set of point–charges [71, 72].
A set of Cartesian multipoles in the global frame of reference can be simplified by converting to a spherical harmonic (SH) representation [70]. The SH representation removes a redundant degree of freedom from the traceless quadrupole tensor. The first step in the conversion is to diagonalize the quadrupole tensor,
| (9) |
where R is the set of eigenvectors which define a quadrupole frame of reference and Θ′ is the set of eigenvalues. The Cartesian multipoles through the quadrupole moments can then be converted to SH multipoles, Q, in the quadrupole frame [70],
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
and
| (15) |
were is the eigenvector in the i direction. The SH multipole moments can then be further simplified to a set of six point–charges [71, 72] in an octahedral arrangement,
| (16) |
| (17) |
and
| (18) |
where q±i are the charges in the direction, and d is the displacement from the atomic center in atomic units. We chose to follow the recommendations of Devereux et al. [71] and Gao et al. [72] and set d = 0.25 a.u. Before the electrostatic interactions can be calculated, the point–charges must be rotated from the quadrupole frame of reference back to the global frame, although in practice this amounts to a vector projection of the coordinates onto the global axes [71].
Representing the multipoles as a set of point–charges reduces the accuracy of the electrostatic field. However, the approximation of point–multipoles by point–charges for the calculation of intermolecular Coulomb interactions at hydrogen bonding and longer distances is sufficiently accurate (see supporting information). Moreover, most QM packages can easily add additional point–charges to the potential. Thus, employing a multipole to point–charge conversion avoids the need to modify existing software packages.
While treating the static field in QM/MM is straightforward, the polarization energy needs to be calculated self–consistently. To avoid modifying the SCF routines in the QM packages, the polarization energy can be approximated using the MM force field and the QM electrostatic field. In LICHEM, the QM calculations are performed within the static field from the MM multipoles, which allows the QM region (Eq. 7) to capture a large portion of the polarization energy [73]. Two MM calculations are required to accurately calculate the polarization energy for the MM region. The first calculation is performed with only the static MM field and without charges on the QM atoms (Eq. 8), which captures the non–polarizable portions of the potential. The second MM calculation evaluates the polarization energy, EMM,pol, of the QM/MM system when point–charges are placed on the QM atoms. The energies from the three calculations can then be added together to determine the total QM/MM energy. For polarizable models, Eq. 6 becomes
| (19) |
where EMM,pol includes the interactions of the MM induced dipoles with the MM field and the static (polarized) QM charges.
Eq. 19 captures most of the polarization energy, and it is instructive to examine which electrostatic interactions are included in the QM and MM calculations. The QM regions interact with only the static MM field, and the QM calculation produces a set of point–charges on the QM atoms, which effectively include the induced dipole moments of the QM field. The MM polarization is calculated self–consistently in the QM/MM field. Thus, the (induced dipole)–(induced dipole) QM–MM interactions are present in EMM,pol. While the QM region only responds to the static MM field, it has been shown that approximately 80% of the polarization energy is recovered in the first iteration of the self–consistent polarization calculation [73].
In essence, the procedure described above captures more than 80% of the polarization energy in the QM region, and effectively all the polarization energy of the MM region. While Eqs. 16–19 produce approximate multipolar/polarizable interactions, these approximations are only required for QM packages without native functionality for multipolar/polarizable external fields. We will explore these approximations further in a future publication.
D. QM/MM boundaries and the pseudo–bond method
QM/MM calculations are more difficult when there are covalent bonds between the QM and MM regions. Several methods have been developed to smoothly transition between the QM region and the MM region. One of the most common approaches is the link atom method [74, 75], which involves adding extra hydrogen atoms to saturate the severed bonds. Unfortunately, these extra bonds do not always accurately reproduce the original environment [74, 76]. Other approaches involve creating a set of localized orbitals at the edge of the QM region where the bonds have been severed [76–80]. A simpler approach involves adding pseudopotentials at the edge of the QM region [16, 81–85]. These pseudopotentials are parametrized such that the carbon and nitrogen atoms at the edge of the QM region form reasonable bonds with the QM atoms (termed pseudo–bonds).
The treatment of covalent bonds in LICHEM requires two additional classes of atoms in the QM/MM system, the atoms with the pseudo–bond potentials (PB), and boundary atoms (BA), which balance the electrostatic interactions near the pseudo–bonds. A PB atom is created by adding a pseudopotential to a fluorine atom, which allows it to mimic the behavior of a sp3 (sp2) hybridized carbon (nitrogen) atom [16]. Boundary atoms account for two additional deficiencies in the calculations: 1) point–charges near the QM region can cause the electron density to over–polarize [18, 30] and 2) the obvious restriction that the QM region must have an integer number of electrons. Both of these complications can be mitigated by absorbing the point–charges on the MM atoms bonded to the PB atoms into the QM region during the QM parts of the calculations. This procedure produces a BA region with zero charge between the QM and MM regions. Since the pseudo–bond potentials are parametrized for specific environments and MM force fields do not always have convenient regions that sum to a whole number, selecting appropriate PB and BA regions is one of the most difficult tasks in the calculations.
In order to avoid double counting the bonding interactions, only bonding terms with at least one atom in the MM or BA regions are included in the QM–MM interaction energy [16, 26, 84, 85]. The full treatment of different interaction types are given in Table I for single–point energy calculations.
TABLE I.
The treatment of interactions in the MM and QM wrappers during single–point energy calculations.
| Interaction | Wrapper calculation | |
|---|---|---|
| MM | QM | |
| MM–MM | FF | Zero |
| QM–QM | Zero | ρ el |
| PB–PB | Zero | PP+ρel |
| BA–BA | FF-{q}QM | Zero |
| QM–MM | FF-{q}QM | ρel+{q}MM |
| QM–PB | Bonds | PP+ρel |
| QM–BA | FF-{q}QM | Zero |
| MM–PB | FF-{q}QM | PP+ρel+{q}MM |
| MM–BA | FF-{q}QM | Zero |
| PB–BA | FF-{q}QM | Zero |
Interaction types were abbreviated as follows: force field (FF), electron density (ρel), pseudopotential (PP), no interaction (Zero), {QM,PB,BA} point–charges ({q}QM), MM bond/angle/dihedral potentials (Bonds), and MM point–charges ({q}MM). A “-” sign is used if the interaction is removed instead of added (i.e. FF-{q}QM denotes the force field with no charges on the {QM,PB,BA} atoms).
During the polarization energy calculations and MM minimization steps, the BA regions have their charges restored and the total charge is balanced by subtracting the BA charges from the charge on the corresponding PB atom. Thus, the BA region also introduces a buffer zone between the MM and the modified charges on the QM atoms.
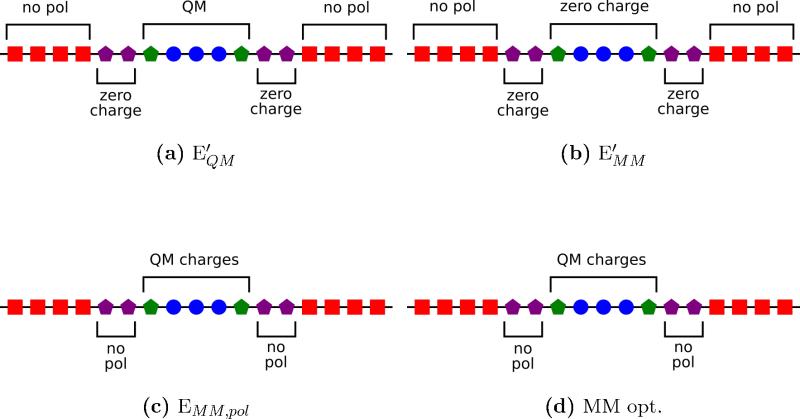
The pseudo–bond treatment of the multipole moments is essentially the same as the point–charges in the original pseudo–bond method, except that the all of the BA multipole moments are absorbed into the QM region. However, the use of polarizable models complicates the pseudo–bond method, since large charges on the QM atoms can over–polarize the MM region. To address this, the polarizable sites on the BA region are removed from both the QM and the MM parts of the calculation. By removing the polarizable sites on the BA regions, the over–polarization of the MM region is avoided. Additionally, polarizable sites on multipole–free BA atoms would produce unphysical forces on the QM atoms. Figure 1 shows 1D schematics of the multipolar and polarizable interactions during different parts of the QM and MM calculations.
FIG. 1.
One dimensional schematics of the modifications to the force field in the QM (blue circles), PB (green pentagons), BA (purple pentagons), and MM (red squares) regions. A QM/MM optimization requires four different calculations. (a) QM in the MM static field, (b) MM without charges on the QM and BA regions, (c) MM polarization with point–charges from the QM calculation, and (d) MM optimizations with non–polarizable QM, PB, and BA regions. Unmarked regions have no modifications to the MM force field.
E. Interface to packages
LICHEM calls QM and MM packages through a series of wrappers. While employing wrappers can be less efficient than linking to the packages directly, the vast majority of the computer time is spent on the QM calculations. Since the QM and MM packages are unmodified, the efficiency of the simulations is effectively limited by the speed of the QM packages. Additionally, restart and checkpoint files are preserved between calls to the wrappers to reduce the computational overhead and increase the efficiency of the methods.
Currently, LICHEM can perform calculations with Gaussian [86], NWChem [87], PSI4 [88], TINKER [89], and TINKER-HP [90, 91]. Additional interfaces to LAMMPS [92] and AMBER [93] are under development. Adding new wrappers to LICHEM can be accomplished by creating routines which write input files for the desired software package and then read the output to gather energies, forces, and charges.
For QM and QM/MM geometry optimizations, LICHEM can either use the forces for steepest descent (SD) [94] and DavidonFletcherPowell (DFP) [94] optimizations or employ the native optimizer in the QM packages. Currently, native QM optimizations are only an option for the trivial case where all the atoms are in the QM region or for QM/MM calculations with Gaussian (via the GauExternal interface [86]). The SD and DFP routines optimize the positions of the QM atoms in Cartesian coordinates and are useful for interfacing with QM packages which cannot read MM forces into their native optimization routines. Since the positions and charges of the QM atoms can be fixed during the MM optimizations, there is no need for separate MM optimizers in LICHEM.
One advantage of using wrappers is that LICHEM can use essentially any force field or method implemented in the QM or MM packages. For instance, LICHEM can easily take advantage of any polarizable and non-polarizable force fields implemented in TINKER. An additional advantage of employing wrappers (and the point–charge representation of the multipoles) is that multipolar/polarizable QM/MM calculations can be performed with essentially any QM package.
III. RESULTS
Several sets of calculations were chosen to highlight the capabilities of LICHEM, the importance of the MM polarization in QM/MM simulations, and the potential pitfalls of QM/MM simulations. Simulations were performed with the Gaussian/TINKER interface and employed with the AMOEBA [48, 64], TIP3P [95], and AMBER99 [96] potentials. For consistency, all QM and QM/MM geometry optimizations were performed with the LICHEM DFP optimizer.
A. Water clusters
Small water clusters have been well studied in the literature [97–99], and hence, they are useful test systems for software development. QM/MM interaction energies were determined for a selection of ten water dimers [52, 99] and two water trimer isomers [52]. The first trimer has all three free OH bonds pointed in the same direction (uuu) and the second trimer has two pointing up and one pointing down (uud). The binding energies were calculated for all possible subsets of QM/MM systems. For instance, all possible trimer QM/MM subsets with 2 QM water molecules and all subsets with 2 MM water molecules were employed in the trimer calculations. This procedure results in a total of 20 dimer and 12 trimer QM/MM systems.
The mean absolute error of the water dimer and trimer binding energies are reported in Tables II and III. Since the energies are for the binding of the QM subsystem to the MM subsystem, these calculations highlight the errors in the interactions between the QM and MM regions. It is clear from these results that the interactions between the QM and MM regions contain errors comparable to, and sometimes larger than, the pure MM calculations. This is not surprising since exchange, dispersion, and polarization between the two regions are determined from the parameters in the MM potential.
TABLE II.
Mean absolute error of the binding energy from the ten water dimers compared with BSSE corrected binding energies from PBE0/aug-cc-pVTZ (PBE0/6-311++G(d,p)).
| QM | MM | MAE, Ebind |
|
|---|---|---|---|
| meV | kcal/mol | ||
| PBE0 | AMOEBA | 19.02 (25.54) | 0.4385 (0.5889) |
| PBE0 | TIP3P | 32.89 (27.75) | 0.7584 (0.6398) |
| – | AMOEBA | 9.26 (36.62) | 0.2136 (0.8446) |
| – | TIP3P | 44.84 (27.19) | 1.0340 (0.6270) |
These calculations are effectively measuring the error in the QM/MM interactions.
TABLE III.
Mean absolute error of the binding energy from the 6 water trimers compared with BSSE corrected binding energies from PBE0/aug-cc-pVTZ (PBE0/6-311++G(d,p)).
| QM | MM | MAE, Ebind |
|
|---|---|---|---|
| meV | kcal/mol | ||
| PBE0 | AMOEBA | 76.80 (68.88) | 1.7711 (1.5885) |
| PBE0 | TIP3P | 9.92 (1.54) | 0.2287 (0.0355) |
| – | AMOEBA | 5.46 (39.36) | 0.1259 (0.9076) |
| – | TIP3P | 63.84 (97.74) | 1.4724 (2.2540) |
These calculations are effectively measuring the error in the QM/MM interactions.
Small systems, such as water dimers and trimers, are a worst case scenario for QM/MM methods due to the lack of electrostatic screening. Several examples of the effect of the QM subsystem size have been reported in the literature previously [100, 101]. Most QM/MM calculations are performed on large systems where the MM potential is screened by the outer edges of the QM region and the force field only needs to give a reasonable description of the external field near the center of the QM region.
To test LICHEM on a system that is closer to a conventional QM/MM calculation, solvation energies were determined for a (H2O)21 cluster (see Figure 2). The initial structure was constructed from a (H2O)20 dodecahedron with an additional water added at the center of the cluster. The (H2O)21 system was then allowed to relax using the AMOEBA potential and the collapsed cluster was used as a starting point for the QM/MM calculations. The QM region was chosen to consist of the central water molecule and the 4 water molecules hydrogen bonded to the central water molecule.
FIG. 2.
The cluster of 21 water molecules used in the QM/MM calculations. Five of the central water molecules (blue and green) were treated quantum mechanically, while the remaining molecules were modeled with classical potentials. The solvation energy (Eq. 20) of the central water molecule (blue) is used as a test of the accuracy of the polarization approximations.
The solvation energy, Esolv, of the central water molecule is approximately given by
| (20) |
where En,m is the QM/MM energy for the subsystem with n QM waters and m MM waters. The (H2O)21 cluster is large enough to completely surround the QM region with an external field when using the QM/MM approximation, while still being small enough to easily calculate the energy with all atoms in the QM region.
As seen in Table IV, the errors relative to the QM results (DFT and MP2) can be as much as 5 times larger for TIP3P than for AMOEBA. When the AMOEBA calculations are repeated without polarizable sites on the MM atoms, the results are nearly identical to those calculated with the TIP3P model. Additionally, all of the non-polarizable calculations are under–bound. Thus, our results show that providing a better description of the MM environment by adding higher order multipoles is not sufficient to provide the correct QM/MM interactions. The polarization of the MM environment due to the QM region is equally as important as the polarization of the QM region due to the static field. Furthermore, when all polarizable sites are removed during pure AMOEBA calculations, it can be seen that ~67% of the solvation energy is due to polarization.
TABLE IV.
QM/MM solvation energy for the (H2O)5(H2O)16 → (H2O)+(H2O)4(H2O)16 system shown in Figure 2.
| QM | MM | Esolv (eV) | Error (%) | |
|---|---|---|---|---|
| B97D | – | −1.5239 | 0.00 | (3.12) |
| B97D | AMOEBA | −1.4663 | 3.78 | (6.78) |
| B97D | TIP3P | −1.2817 | 15.89 | (18.52) |
| B97D | AMOEBA† | −1.2387 | 18.71 | (21.25) |
| B3LYP | – | −1.3901 | 0.00 | (11.63) |
| B3LYP | AMOEBA | −1.4835 | 6.72 | (5.69) |
| B3LYP | TIP3P | −1.2977 | 6.65 | (17.50) |
| B3LYP | AMOEBA† | −1.2560 | 9.65 | (20.15) |
| PBE0 | – | −1.5156 | 0.00 | (3.65) |
| PBE0 | AMOEBA | −1.5814 | 4.34 | (0.53) |
| PBE0 | TIP3P | −1.3999 | 7.64 | (11.00) |
| PBE0 | AMOEBA† | −1.3575 | 10.43 | (13.70) |
| MP2 | – | −1.5730 | – | – |
| – | AMOEBA | −1.5419 | – | – |
| – | AMOEBA† | −0.5091 | – | – |
Without MM polarization
Errors relative to MP2 are given in parentheses. The calculations were performed with the AMOEBA optimized structure, the 6-311++G(d,p) basis set, and do not include BSSE corrections.
These calculations suggest that the inclusion of atomic multipole moments only results in a marginal improvement and underscore the need for the inclusion of the MM polarization to accurately model the interactions of the QM and MM regions, in agreement with our previous work [5, 37]. Using Eq. 19, the polarizable calculations already out–perform the point–charge based models; however, the errors could be further reduced by calculating the polarization energy self–consistently.
While the QM/MM interaction and solvation energies of the water clusters do not always match the results from pure QM calculations, it is clear from the energies reported in Tables II–IV that the effects of polarization are non–negligible in QM/MM calculations.
B. Geometry optimizations
To test the effects of polarization on the molecular structure, geometry optimizations were performed on the uud and uuu water trimers and two peptide sequences. The following calculations were performed to ensure that the approximations described above are sufficiently accurate for calculating forces and optimizing geometries.
1. Water Trimers
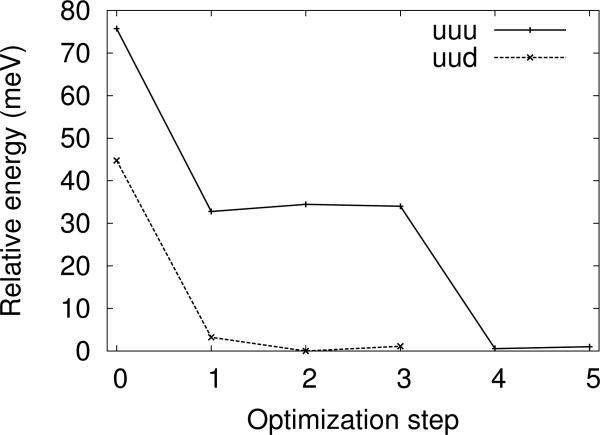
In the QM/MM optimizations of the water trimer, two water molecules were included in the QM region while the third molecule was modeled with the AMOEBA or TIP3P potentials (see Figure 3). In many of the optimizations, the uuu starting structures optimized to the lower energy uud isomer. This is partially an artifact of the asymmetry of the QM/MM potential during the iterative optimization procedure. The QM atoms move in the full QM/MM potential, while the MM atoms move in a modified MM potential. The discrepancies between the two potential energy surfaces allows for a conversion between the two isomers during the MM optimization step (see Figure 4). Despite the instability of the uuu isomer, a local minimum can be found by first optimizing the structure with pure QM, then reoptimizing with QM/MM simulations.
FIG. 3.
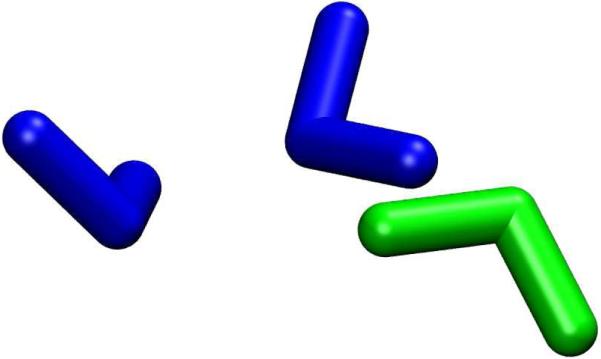
Water trimer (uud) optimized at the ωB97xD/6-311++G(d,p)/AMOEBA level of theory. The blue water molecules were treated quantum mechanically while the green water was modeled with a classical potential.
FIG. 4.
QM/MM energies of the water trimers plotted against the number of QM/MM optimization steps. Each optimization step includes the full relaxation of the QM and the MM regions. A transition between the uuu and uud isomers can be seen between the 3rd and 4th iterations. Energies are given relative to the lowest energy structure found in the geometry optimizations.
An extreme example of the asymmetry of the QM/MM potential comes from the calculations performed with the TIP3P model. Pure MM optimizations of the water trimer with the TIP3P model result in a planar geometry. Since the MM atoms in a QM/MM simulation are moving in an external field due to a modified MM potential, the QM part of ωB97xD/6-311++G(d,p)/TIP3P geometry optimizations start from a geometry with the MM free OH in the plane of the oxygen atoms, which is the predicted minimum of the modified TIP3P force field. Thus, the flaws in the MM optimization influence the iterative QM/MM procedure and present an opportunity for the uuu isomer to rapidly convert to the uud isomer. It is also clear from these calculations that the order in which the QM and MM optimizations are performed has a strong influence on the results. However, by optimizing the QM after the MM has relaxed, the QM calculation has a larger influence on the final structure.
Table VI reports the oxygen–oxygen distances and hydrogen bond lengths of the optimized uud trimer. The optimized structures are in good agreement with the HF/POL calculations of Aida et al. [1] which also deviated from the pure QM calculations by approximately 0.1 Å. In addition to the optimized geometries, the energy difference between the two trimer isomers was determined at the ωB97xD/6-311++G(d,p)/AMOEBA level of theory. The energy difference predicted by the pure AMOEBA model is smaller than the difference predicted by pure QM calculations. Two different values of the QM/MM energy difference are given in Table V, corresponding to different QM and MM subsystems in the uud isomer. The first energy difference corresponds to the uud isomer given in Figure 3, where the MM free OH is in the down position. However, it is energetically favorable to flip the arrangement of the hydrogens so that a QM free OH is in the down position. When this change is introduced, the energy difference between the isomers is in better agreement with the pure QM calculations.
TABLE VI.
Optimized oxygen–oxygen and hydrogen bond distances (Å) for the water trimer shown in Figure 3.
| ωB97xD† | ωB97xD†/AMOEBA | AMOEBA | ωB97xD†/TIP3P | TIP3P | |
|---|---|---|---|---|---|
| O–O | 2.78 | 2.81 | 2.80 | 2.82 | 2.74 |
| H–O | 1.91 | 1.96 | 1.91 | 1.97 | 1.81 |
| O–O* | 2.77 | 2.88 | 2.79 | 2.76 | 2.74 |
| H–O* | 1.88 | 1.98 | 1.89 | 1.85 | 1.81 |
| O*–O | 2.77 | 2.87 | 2.79 | 2.64 | 2.74 |
| H*–O | 1.88 | 1.99 | 1.89 | 1.70 | 1.81 |
6-311++G(d,p)
MM atom in Figure 3
TABLE V.
Relative energies of the optimized uuu and uud water trimer isomers determined from QM, MM, and QM/MM calculations.
| QM | MM | ΔE |
|
|---|---|---|---|
| meV | kcal/mol | ||
| ωB97xD† | – | 40.74 | 0.9394 |
| ωB97xD† | AMOEBA | 33.02 | 0.7560 |
| ωB97xD† | AMOEBA | 44.36* | 1.0231* |
| – | AMOEBA | 33.74 | 0.7781 |
6-311++G(d,p)
QM free OH is down
The QM/MM geometries were found by re–optimizing the ωB97xD optimized structures. Two different uud isomers were used in the QM/MM calculations, as described in the text.
QM/MM calculations on these small systems are performed to investigate the role of point–multipoles and polarization in the MM environment. Thus, while the optimizations of floppy QM/MM clusters in the gas phase can be problematic, it is unlikely that the MM environment will have such a large range of motion in systems such as proteins.
2. Monte Carlo
The iterative QM/MM optimization procedure [26] decouples the motions of the QM and MM atoms, which may introduce artifacts during the optimizations. This is a known issue, since the QM and MM forces are calculated with slightly different approximations [69, 102]. An example of the artifacts can be seen in Figure 4, where the QM/MM energy increases slightly after some of the iterations. Effectively, the QM and MM regions move along slightly different potential energy surfaces during the optimizations. In very rare cases, this mismatch may prevent the iterative procedure from finding a minimum of ETot.
However, geometries can also be optimized using a Metropolis Monte Carlo (MC) algorithm [103], which avoids the iterative QM/MM optimization. Low temperature MC simulations produce structures very similar to those reported in Table VI; however, the MC algorithm consistently finds the lower energy uud minimum where one QM free OH is up, one QM free OH is down, and the MM free OH is up. This is a different arrangement of the hydrogens; however, the oxygen–oxygen distances and hydrogen bond lengths are nearly identical to those obtained from the optimization reported in Table VI. The similarity between the structures determined from MC and geometry optimizations strongly suggests that only minimal errors are introduced by the iterative optimization procedure.
3. Optimizations with pseudo–bonds
In order to evaluate the accuracy of the pseudo–bond approach for polarizable QM/MM simulations, geometry optimizations were performed on two oligo–peptide chains in the gas phase. The first peptide sequence was a capped deca–alanine (DA), (NHCH3)-(A)10-(COCH3), chain in a helical arrangement. The second sequence comprises the dodeca–peptide (DP), (NHCH3)-AWWAFYYFAWWA-(COCH3), in a helical arrangement. While neither of these peptides have biological significance, the optimizations provide useful tests of the pseudo–bond approximations in two different environments. The DA helix essentially offers a non-polarizable peptide chain, while the DP helix has relatively large polarizable side chains.
Optimizations were performed at the B97D/6-31++G(d,p)/AMOEBA level of theory. The four central amino acids in each sequence were placed in the QM region, and the QM–MM boundaries were chosen to lay in alanine residues (Cα → PB). The remaining amino acids and the capping groups were modeled with the AMOEBA potential. Table VII reports the root mean square deviation (RMSD) of the QM, MM, and QM–MM boundary regions from structures optimized with B97D/6-31++G(d,p) and AMOEBA. The QM/MM optimized geometries are within 0.2 Å of the AMOEBA optimized structures. For DA, the deviation of the MM region from the QM optimized geometry is ~0.3 Å; however, most of the deviation occurs in the capping groups. When the larger DP chain was optimized, large deviations from the QM optimized structure were not observed. These calculations suggest that, even in the gas phase, the pseudo–bond method does not significantly perturb the optimized geometries.
TABLE VII.
RMS deviations of the B97D/6-31++G(d,p)/AMOEBA optimized peptide chains compared to structures optimized at the B97D/6-31++G(d,p) or AMOEBA level of theory.
| Chain | region | num. atoms | RMSD QM (Å) | RMSD MM (Å) |
|---|---|---|---|---|
| DA | {QM,PB,BA,MM} | 112 | 0.206 | 0.144 |
| {QM} | 44 | 0.110 | 0.114 | |
| {PB,BA} | 16 | 0.125 | 0.076 | |
| {MM} | 52 | 0.277 | 0.178 | |
| DP | {QM,PB,BA,MM} | 230 | 0.110 | 0.110 |
| {QM} | 86 | 0.079 | 0.109 | |
| {PB,BA} | 16 | 0.114 | 0.078 | |
| {MM} | 128 | 0.125 | 0.115 | |
Additional non-polarizable QM/MM geometry optimizations were performed on reactant and product structures of a nucleotide addition reaction catalyzed by the human DNA polymerase λ enzyme. The ωB97xD/6-31++G(d,p)/AMBER99 optimizations produced structures in good agreement with the crystal structures and our previous results [3, 6, 104]. The non-polarizable optimizations further confirm the accuracy of our pseudo–bond implementation. Additional details can be found in the supporting information.
IV. DEVELOPMENT
The results presented above provide a sample of the current capabilities in LICHEM. LICHEM can also perform optimizations with several different algorithms, perform pure QM (or MM) calculations, and interconvert chemical file formats. In addition, functionality exists for more complicated simulations. The MC routines can perform NVT, NPT, and/or path–integral simulations. The source code is freely available at https://github.com/kratman/LICHEM_QMMM.
LICHEM is in continuous development to add new features. An implementation of the climbing image nudged elastic band [105, 106], and inclusion of GEM for the MM environment [5, 27–29, 32, 37, 52] are currently under development. In addition, we are in the process of introducing fully self–consistent induced dipoles, the COSMO solvation model [107], molecular dynamics, and our recently developed method to include long–range electrostatic corrections for QM/MM simulations [108], which is ideally suited to the current LICHEM implementation for multipoles. The implementation and testing of these features will be discussed in future publications.
V. CONCLUSION
We have presented an interface for performing multipolar/polarizable QM/MM calculations via wrappers to unmodified simulation packages. Test calculations on small peptides and clusters confirm that LICHEM can accurately perform QM/MM calculations with point–charge, multipole, and/or polarizable force fields. In particular, our implementation of the pseudo–bond method smoothly transitions between the QM region and the polarizable MM region. Furthermore, the calculations highlight the importance of allowing the MM environment to polarize during QM/MM simulations. LICHEM is under active development, and additional functionality is being added for reaction pathways, the GEM force field, molecular dynamics simulations, AMBER, and LAMMPS.
Supplementary Material
ACKNOWLEDGEMENTS
Calculations were carried out using computers in the Wayne State University's high performance computing grid. This work was partly supported by the National Institutes of Health grant R01GM108583 to GAC. Jean-Philip Piquemal is grateful for support by the Direction Générale de l'Armement (DGA) – Maitrise NRBC of the French Ministry of Defense. Filippo Lipparini gratefully acknowledges financial support from the Alexander von Humboldt Foundation. LICHEM is available free of charge from https://github.com/kratman/LICHEM_QMMM.
Footnotes
SUPPORTING INFORMATION AVAILABLE
Supporting information with DNA polymerase λ optimizations, molecular structures, and additional tables of QM/MM interaction energies is available online.
References
- 1.Aida M, Yamataka H, Dupuis M. Int. J. Quantum Chem. 2000;77:199. [Google Scholar]
- 2.Caprasecca S, Jurinovich S, Viani L, Curutchet C, Mennucci B. J. Chem. Theory Comput. 2014;10:1588. doi: 10.1021/ct500021d. [DOI] [PubMed] [Google Scholar]
- 3.Chaudret R, Piquemal J-P, Cisneros G. Andres. Phys. Chem. Chem. Phys. 2011;13:11239. doi: 10.1039/c0cp02550j. [DOI] [PubMed] [Google Scholar]
- 4.Cisneros GA, Liu H, Lu Z, Yang W. J. Chem. Phys. 2005;122:114502. doi: 10.1063/1.1860560. [DOI] [PubMed] [Google Scholar]
- 5.Cisneros GA, Piquemal J-P, Darden TA. J. Phys. Chem. B. 2006;110:13682. doi: 10.1021/jp062768x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Cisneros GA, Perera L, García-Díaz M, Bebenek K, Kunkel TA, Pedersen LG. DNA Repair. 2008;7:1824. doi: 10.1016/j.dnarep.2008.07.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Cui F, Li H. J. Chem. Phys. 2013;138:174114. doi: 10.1063/1.4803143. [DOI] [PubMed] [Google Scholar]
- 8.Banik S. Dutta, Chandra A. J. Phys. Chem. B. 2014;118:11077. doi: 10.1021/jp506196m. [DOI] [PubMed] [Google Scholar]
- 9.Fang D, Chaudret R, Piquemal J-P, Cisneros GA. J. Chem. Theory Comput. 2013;9:2156. doi: 10.1021/ct400130b. [DOI] [PubMed] [Google Scholar]
- 10.Fang D, Lord RL, Cisneros GA. J. Phys. Chem. B. 2013;117:6410. doi: 10.1021/jp403116e. [DOI] [PubMed] [Google Scholar]
- 11.Haynes PD, Mostof AA, Skylaris C-K, Payne MC. J. Phys. Conf. Series. 2006;26:143. [Google Scholar]
- 12.Hu H, Lu Z, Yang W. J. Chem. Theory Comput. 2007;3:390. doi: 10.1021/ct600240y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Hu H, Lu Z, Parks JM, Burger SK, Yang W. J. Chem. Phys. 2008;128:034105. doi: 10.1063/1.2816557. [DOI] [PubMed] [Google Scholar]
- 14.Janowski T, Wolinski K, Pulay P. Chem. Phys. Lett. 2012;530:1. [Google Scholar]
- 15.Liu H, Lu Z, Cisneros GA, Yang W. J. Chem. Phys. 2004;121:697. doi: 10.1063/1.1759318. [DOI] [PubMed] [Google Scholar]
- 16.Parks JM, Hu H, Cohen AJ, Yang W. J. Chem. Phys. 2008;129:154106. doi: 10.1063/1.2994288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Riccardi D, Li G, Cui Q. J. Phys. Chem. B. 2004;108:6467. doi: 10.1021/jp037992q. [DOI] [PubMed] [Google Scholar]
- 18.Senn HM, Thiel W. Angew. Chem. Int. Ed. 2009;48:1198. doi: 10.1002/anie.200802019. [DOI] [PubMed] [Google Scholar]
- 19.Sharir-Ivry A, Varatharaj R, Shurki A. J. Chem. Theory Comput. 2015;11:293. doi: 10.1021/ct500751f. [DOI] [PubMed] [Google Scholar]
- 20.Sodt AJ, Mei Y, Knig G, Tao P, Steele RP, Brooks BR, Shao Y. J. Phys. Chem. A. 2015;119:1511. doi: 10.1021/jp5072296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Thellamurege NM, Si D, Cui F, Zhu H, Lai R, Li H. J. Comput. Chem. 2013;34:2816. doi: 10.1002/jcc.23435. [DOI] [PubMed] [Google Scholar]
- 22.Thompson MA, Schenter GK. J. Phys. Chem. 1995;99:6374. [Google Scholar]
- 23.Várnai C, Bernstein N, Mones L, Csányi G. J. Phys. Chem. B. 2013;117:12202. doi: 10.1021/jp405974b. [DOI] [PubMed] [Google Scholar]
- 24.Woodcock HL, Miller BT, Hodoscek M, Okur A, Larkin JD, Ponder JW, Brooks BR. Journal of Chemical Theory and Computation, J. Chem. Theory Comput. 2011;7:1208. doi: 10.1021/ct100738h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Xie W, Gao J. J. Chem. Theory Comput. 2007;3:1890. doi: 10.1021/ct700167b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Zhang Y, Liu H, Yang W. J. Chem. Phys. 2000;112:3483. [Google Scholar]
- 27.Cisneros GA, Piquemal J-P, Darden TA. J. Chem. Phys. 2005;123:044109. doi: 10.1063/1.1947192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Cisneros GA, Piquemal J-P, Darden TA. J. Chem. Phys. 2006;125:184101. doi: 10.1063/1.2363374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Cisneros GA. J. Chem. Theory Comput. 2012;8:5072. doi: 10.1021/ct300630u. [DOI] [PubMed] [Google Scholar]
- 30.Cisneros GA, Karttunen M, Ren P, Sagui C. Chem. Rev. 2014;114:779. doi: 10.1021/cr300461d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Kramer C, Spinn A, Liedl KR. J. Chem. Theory Comput. 2014;10:4488. doi: 10.1021/ct5005565. [DOI] [PubMed] [Google Scholar]
- 32.Piquemal J-P, Cisneros GA, Reinhardt P, Gresh N, Darden TA. J. Chem. Phys. 2006;124:104101. doi: 10.1063/1.2173256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Boulanger E, Thiel W. J. Chem. Theory Comput. 2012;8:4527. doi: 10.1021/ct300722e. [DOI] [PubMed] [Google Scholar]
- 34.Boulanger E, Thiel W. J. Chem. Theory Comput. 2014;10:1795. doi: 10.1021/ct401095k. [DOI] [PubMed] [Google Scholar]
- 35.Caprasecca S, Curutchet C, Mennucci B. J. Chem. Theory Comput. 2012;8:4462. doi: 10.1021/ct300620w. [DOI] [PubMed] [Google Scholar]
- 36.Caprasecca S, Jurinovich S, Lagardère L, Stamm B, Lipparini F. J. Chem. Theory Comput. 2015;11:694. doi: 10.1021/ct501087m. [DOI] [PubMed] [Google Scholar]
- 37.Chaudret R, Gresh N, Narth C, Lagardère L, Darden TA, Cisneros GA, Piquemal J-P. J. Phys. Chem. A. 2014;118:7598. doi: 10.1021/jp5051657. [DOI] [PubMed] [Google Scholar]
- 38.Curutchet C, Losa A. Muñoz, Monti S, Kongsted J, Scholes GD, Mennucci B. J. Chem. Theory Comput. 2009;5:1838. doi: 10.1021/ct9001366. [DOI] [PubMed] [Google Scholar]
- 39.Li H. J. Phys. Chem. A. 2011;115:11824. doi: 10.1021/jp206425z. [DOI] [PubMed] [Google Scholar]
- 40.Lipparini F, Cappelli C, Barone V. J. Chem. Theory Comput. 2012;8:4153. doi: 10.1021/ct3005062. [DOI] [PubMed] [Google Scholar]
- 41.Lipparini F, Cappelli C, Scalmani G, De Mitri N, Barone V. J. Chem. Theory Comput. 2012;8:4270. doi: 10.1021/ct300635c. [DOI] [PubMed] [Google Scholar]
- 42.Lipparini F, Cappelli C, Barone V. J. Chem. Phys. 2013;138:234108. doi: 10.1063/1.4811113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Nielsen CB, Christiansen O, Mikkelsen KV, Kongsted J. J. Chem. Phys. 2007;126:154112. doi: 10.1063/1.2711182. [DOI] [PubMed] [Google Scholar]
- 44.Olsen JM, Aidas K, Kongsted J. J. Chem. Theory Comput. 2010;6:3721. doi: 10.1021/ct900502s. [DOI] [PubMed] [Google Scholar]
- 45.Schwabe T, Olsen JMH, Sneskov K, Kongsted J, Christiansen O. J. Chem. Theory Comput. 2011;7:2209. doi: 10.1021/ct200258g. [DOI] [PubMed] [Google Scholar]
- 46.Si D, Li H. J. Chem. Phys. 2011;135:144107. doi: 10.1063/1.3649947. [DOI] [PubMed] [Google Scholar]
- 47.Steindal AH, Ruud K, Frediani L, Aidas K, Kongsted J. J. Phys. Chem. B. 2011;115:3027. doi: 10.1021/jp1101913. [DOI] [PubMed] [Google Scholar]
- 48.Ren P, Ponder JW. J. Phys. Chem. B. 2003;107:5933. [Google Scholar]
- 49.Shi Y, Xia Z, Zhang J, Best R, Wu C, Ponder JW, Ren P. J. Chem. Theory Comput. 2013;9:4046. doi: 10.1021/ct4003702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Wu JC, Piquemal J-P, Chaudret R, Reinhardt P, Ren P. J. Chem. Theory Comput. 2010;6:2059. doi: 10.1021/ct100091j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Xiang JY, Ponder JW. J. Comput. Chem. 2013;34:739. doi: 10.1002/jcc.23190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Duke RE, Starovoytov ON, Piquemal J-P, Cisneros GA. J. Chem. Theory Comput. 2014;10:1361. doi: 10.1021/ct500050p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Hodak M, Lu W, Bernholc J. J. Chem. Phys. 2008;128:014101. doi: 10.1063/1.2814165. [DOI] [PubMed] [Google Scholar]
- 54.Cisneros GA, Elking D, Piquemal J-P, Darden TA. J. Phys. Chem. A. 2007;111:12049. doi: 10.1021/jp074817r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Field MJ. Mol. Phys. 1997;91:835. [Google Scholar]
- 56.Dykstra CE. Chem. Rev. 1993;93:2339. [Google Scholar]
- 57.Mackerell AD. J. Comput. Chem. 2004;25:1584. doi: 10.1002/jcc.20082. [DOI] [PubMed] [Google Scholar]
- 58.van Duin ACT, Dasgupta S, Lorant F, Goddard WA. J. Phys. Chem. A. 2001;105:9396. [Google Scholar]
- 59.Verstraelen T, Bultinck P, Van Speybroeck V, Ayers PW, Van Neck D, Waroquier M. J. Chem. Theory Comput. 2011;7:1750. doi: 10.1021/ct200006e. [DOI] [PubMed] [Google Scholar]
- 60.York DM, Yang W. J. Chem. Phys. 1996;104:159. [Google Scholar]
- 61.Zhao D-X, Liu C, Wang F-F, Yu C-Y, Gong L-D, Liu S-B, Yang Z-Z. J. Chem. Theory Comput. 2010;6:795. doi: 10.1021/ct9006647. [DOI] [PubMed] [Google Scholar]
- 62.Kumar R, Wang F-F, Jenness GR, Jordan KD. J. Chem. Phys. 2010;132:014309. doi: 10.1063/1.3276460. [DOI] [PubMed] [Google Scholar]
- 63.Lamoureux G, Roux B. J. Chem. Phys. 2003;119:3025. [Google Scholar]
- 64.Laury ML, Wang L-P, Pande VS, Head-Gordon T, Ponder JW. J. Phys. Chem. B. 2015;119:9423. doi: 10.1021/jp510896n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Gascon JA, Leung SSF, Batista ER, Batista VS. J. Chem. Theory Comput. 2006;2:175. doi: 10.1021/ct050218h. [DOI] [PubMed] [Google Scholar]
- 66.Gordon MS, Freitag MA, Bandyopadhyay P, Jensen JH, Kairys V, Stevens WJ. J. Phys. Chem. A. 2001;105:293. [Google Scholar]
- 67.Thompson MA. J. Phys. Chem. 1996;100:14492. [Google Scholar]
- 68.Shao Y, Gan Z, Epifanovsky E, Gilbert AT, Wormit M, Kussmann J, Lange AW, Behn A, Deng J. Mol. Phys. 2014;113:184. Others. [Google Scholar]
- 69.Vreven T, Morokuma K, Farkas O, Schlegel HB, Frisch MJ. J. Comput. Chem. 2003;24:760. doi: 10.1002/jcc.10156. [DOI] [PubMed] [Google Scholar]
- 70.Stone AJ. The Theory of Intermolecular Forces. Oxford University Press; 2013. [Google Scholar]
- 71.Devereux M, Raghunathan S, Fedorov DG, Meuwly M. J. Chem. Theory Comput. 2014;10:4229. doi: 10.1021/ct500511t. [DOI] [PubMed] [Google Scholar]
- 72.Gao Q, Yokojima S, Fedorov DG, Kitaura K, Sakurai M, Nakamura S. Chem. Phys. Lett. 2014;593:165. doi: 10.1063/1.4870261. [DOI] [PubMed] [Google Scholar]
- 73.Wang L-P, Head-Gordon T, Ponder JW, Ren P, Chodera JD, Eastman PK, Martinez TJ, Pande VS. J. Phys. Chem. B. 2013;117:9956. doi: 10.1021/jp403802c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Das D, Eurenius KP, Billings EM, Sherwood P, Chatfield DC, Hodoscek M, Brooks BR. J. Chem. Phys. 2002;117:10534. [Google Scholar]
- 75.Singh UC, Kollman PA. J. Comput. Chem. 1986;7:718. [Google Scholar]
- 76.König PH, Hoffmann M, Frauenheim T, Cui Q. J. Phys. Chem. B. 2005;109:9082. doi: 10.1021/jp0442347. [DOI] [PubMed] [Google Scholar]
- 77.Jung J, Choi CH, Sugita Y, Ten-no S. J. Chem. Phys. 2007;127:204102. [Google Scholar]
- 78.Kairys V, Jensen JH. J. Phys. Chem. A. 2000;104:6656. [Google Scholar]
- 79.Pu J, Gao J, Truhlar DG. J. Phys. Chem. A. 2004;108:632. [Google Scholar]
- 80.Wang Y, Gao J. J. Phys. Chem. B. 2015;119:1213. doi: 10.1021/jp507983u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.DiLabio GA, Hurley MM, Christiansen PA. J. Chem. Phys. 2002;116:9578. [Google Scholar]
- 82.von Lilienfeld OA, Tavernelli I, Rothlisberger U, Sebastiani D. J. Chem. Phys. 2005;122:014113. doi: 10.1063/1.1829051. [DOI] [PubMed] [Google Scholar]
- 83.Slavícek P, Martínez TJ. J. Chem. Phys. 2006;124:084107. doi: 10.1063/1.2173992. [DOI] [PubMed] [Google Scholar]
- 84.Zhang Y, Lee T-S, Yang W. J. Chem. Phys. 1999;110:46. [Google Scholar]
- 85.Zhang Y. J. Chem. Phys. 2005;122:024114. doi: 10.1063/1.1834899. [DOI] [PubMed] [Google Scholar]
- 86.Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Scalmani G, Barone V, Mennucci B. Gaussian 09 rev. d.01. 2009 Others. [Google Scholar]
- 87.Valiev M, Bylaska E, Govind N, Kowalski K, Straatsma T, Van Dam H, Wang D, Nieplocha J, Apra E, Windus T, de Jong W. Comput. Phys. Comm. 2010;181:1477. [Google Scholar]
- 88.Turney JM, Simmonett AC, Parrish RM, Hohenstein EG, Evangelista FA, Fermann JT, Mintz BJ, Burns LA, Wilke JJ. WIREs Comput. Mol. Sci. 2012;2:556. Others. [Google Scholar]
- 89.Ponder JW. Tinker, software tools for molecular design, version 7.0. Washington University; St. Louis, MO: 2015. [Google Scholar]
- 90.Lagardère L, Lipparini F, Polack E, Stamm B, Cancès E, Schnieders M, Ren P, Maday Y, Piquemal J-P. J. Chem. Theory Comput. 2015;11:2589. doi: 10.1021/acs.jctc.5b00171. [DOI] [PubMed] [Google Scholar]
- 91.Lipparini F, Lagardère L, Stamm B, Cancès E, Schnieders M, Ren P, Maday Y, Piquemal J-P. J. Chem. Theory Comput. 2014;10:1638. doi: 10.1021/ct401096t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Plimpton S. J. Comp. Phys. 1995;117:1. [Google Scholar]
- 93.Case D, Berryman J, Betz R, Cerutti D, Cheatham TI, Darden T, Duke R, Giese T, Gohlke H. Amber 2015. University of California; San Francisco: 2015. Others. [Google Scholar]
- 94.Press WH, Teukolsky SA, Vetterling WT, Flannery BP. Numerical Recipes. 3rd ed. Cambridge University Press; 2007. [Google Scholar]
- 95.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. J. Chem. Phys. 1983;79:926. [Google Scholar]
- 96.Wang J, Cieplak P, Kollman PA. J. Comput. Chem. 2000;21:1049. [Google Scholar]
- 97.Cui J, Liu H, Jordan KD. J. Phys. Chem. B. 2006;110:18872. doi: 10.1021/jp056416m. [DOI] [PubMed] [Google Scholar]
- 98.Temelso B, Archer KA, Shields GC. J. Phys. Chem. A. 2011;115:12034. doi: 10.1021/jp2069489. [DOI] [PubMed] [Google Scholar]
- 99.Tschumper GS, Leininger ML, Hoffman BC, Valeev EF, Schaefer HF, Quack M. J. Chem. Phys. 2002;116:690. [Google Scholar]
- 100.Kulik HJ, Zhang J, Klinman JP, Martinez TJ. arXiv:1505.05730. 2015 [Google Scholar]
- 101.Meier K, Thiel W, van Gunsteren WF. J. Comput. Chem. 2012;33:363. doi: 10.1002/jcc.21962. [DOI] [PubMed] [Google Scholar]
- 102.Marx D, Hutter J. Ab Initio Molecular Dynamics. Cambridge University Press; 2009. [Google Scholar]
- 103.Metropolis N, Rosenbluth AW, Rosenbluth MN, Teller AH, Teller E. J. Chem. Phys. 1953;21:1087. [Google Scholar]
- 104.Garcia-Diaz M, Bebenek K, Krahn JM, Pedersen LC, Kunkel TA. DNA Repair. 2007;6:1333. doi: 10.1016/j.dnarep.2007.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.Henkelman G, Jónsson H. J. Chem. Phys. 2000;113:9978. [Google Scholar]
- 106.Henkelman G, Uberuaga BP, Jónsson H. J. Chem. Phys. 2000;113:9901. [Google Scholar]
- 107.Lipparini F, Lagardère L, Raynaud C, Stamm B, Cancès E, Mennucci B, Schnieders M, Ren P, Maday Y, Piquemal J-P. Journal of Chemical Theory and Computation, J. Chem. Theory Comput. 2015;11:623. doi: 10.1021/ct500998q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Fang D, Duke RE, Cisneros GA. J. Chem. Phys. 2015 doi: 10.1063/1.4926652. (Accepted) [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.