Abstract
Simulated annealing (SA) algorithm is a popular intelligent optimization algorithm which has been successfully applied in many fields. Parameters' setting is a key factor for its performance, but it is also a tedious work. To simplify parameters setting, we present a list-based simulated annealing (LBSA) algorithm to solve traveling salesman problem (TSP). LBSA algorithm uses a novel list-based cooling schedule to control the decrease of temperature. Specifically, a list of temperatures is created first, and then the maximum temperature in list is used by Metropolis acceptance criterion to decide whether to accept a candidate solution. The temperature list is adapted iteratively according to the topology of the solution space of the problem. The effectiveness and the parameter sensitivity of the list-based cooling schedule are illustrated through benchmark TSP problems. The LBSA algorithm, whose performance is robust on a wide range of parameter values, shows competitive performance compared with some other state-of-the-art algorithms.
1. Introduction
Simulated annealing (SA) algorithm, which was first independently presented as a search algorithm for combinatorial optimization problems in [1, 2], is a popular iterative metaheuristic algorithm widely used to address discrete and continuous optimization problems. The key feature of SA algorithm lies in means to escape from local optima by allowing hill-climbing moves to find a global optimum. One of the major shortages of SA is that it has several parameters to be tuned, and its performance is sensitive to the values of those control parameters. There are two special strategies for parameter tuning: the online parameter tuning and the off-line parameter tuning. In the online approach, the parameters are controlled and updated dynamically or adaptively throughout the execution of the SA algorithm [3–7], whereas in the off-line approach, the values of different parameters are tuned before the execution of the SA algorithm and are fixed during its execution. Fine-tuning parameter values is not trivial, and those parameters are quite often very poorly made by trial and error. So, SA algorithm, which has less parameter or is less sensitive to parameter setting, is very attractive for practical users.
Recently, a metaheuristic algorithm called the list-based threshold-accepting (LBTA) algorithm has been developed and has shown significant performance for combinatorial optimization problems that are NP-complete. The advantage of LBTA over the majority of other neighbourhood search-based metaheuristic methods is that it has fewer controlling parameters that have to be tuned in order to produce satisfactory solutions. Since its appearance, LBTA has been successfully applied to many combinatorial optimization problems [8–14].
In this work we are motivated by the success of LBTA in simplifying parameter tuning to study how list-based parameter control strategy can be applied to SA algorithm. Towards by this goal, our paper presents a novel list-based cooling schedule for SA algorithm to solve travelling salesman problem (TSP), and we call our proposed algorithm as list-based simulated annealing (LBSA) algorithm. In list-based cooling schedule, all temperatures are stored in a list which is organized as a priority queue. A higher temperature has higher priority. In LBSA, a list of temperatures is created first, and then, in each generation, the maximum value in the list is used as current temperature to calculate acceptance probability for candidate solution. The temperature list is updated adaptively according to the topology of the solution space of the problem. Using the list-based cooling schedule, SA algorithm has good performance on a wide range of parameter values; and it also has competitive performance compared with some other state-of-the-art algorithms. The parameter robustness of list-based cooling schedule can greatly simplify the design and implementation of LBSA algorithm for practical applications.
The remainder of this paper is organized as follows: Section 2 provides a short description of TSP problem and SA algorithm. Section 3 presents our proposed list-based SA algorithm. Section 4 gives the experimental approach and results of experiments carried out on benchmark TSP problems. Finally, in Section 5 we summarize our study.
2. Preliminaries
2.1. Traveling Salesman Problem
TSP problem is one of the most famous hard combinatorial optimization problems. It belongs to the class of NP-hard optimization problems. This means that no polynomial time algorithm is known to guarantee its global optimal solution. Consider a salesman who has to visit n cities. The TSP problem consists of finding the shortest tour through all the cities such that no city is visited twice and the salesman returns back to the starting city at the end of the tour. It can be defined as follows. For n cites problem, we can use a distance matrix D = (d i,j)n×n to store distances between all the pair of cites, where each element d i,j of matrix D represents the distance between cities v i and v j. And we use a set of permutations π of the integers from 1 to n, which contains all the possible tours of the problem. The goal is to find a permutation π = (π(1), π(2),…, π(n)) that minimizes
| (1) |
TSP problem may be symmetric or asymmetric. In the symmetric TSP, the distance between two cities is the same in each opposite direction, forming an undirected graph. This symmetry halves the number of possible solutions. In the asymmetric TSP, paths may not exist in both directions or the distances might be different, forming a directed graph. Traffic collisions, one-way streets, and airfares for cities with different departure and arrival fees are examples of how this symmetry could break down.
2.2. Simulated Annealing Algorithm
SA algorithm is commonly said to be the oldest among the metaheuristics and surely one of the few algorithms that have explicit strategies to avoid local minima. The origins of SA are in statistical mechanics and it was first presented for combinatorial optimization problems. The fundamental idea is to accept moves resulting in solutions of worse quality than the current solution in order to escape from local minima. The probability of accepting such a move is decreased during the search through parameter temperature. SA algorithm starts with an initial solution x, and candidate solution y is then generated (either randomly or using some prespecified rule) from the neighbourhood of x. The Metropolis acceptance criterion [15], which models how a thermodynamic system moves from one state to another state in which the energy is being minimized, is used to decide whether to accept y or not. The candidate solution y is accepted as the current solution x based on the acceptance probability:
| (2) |
where t is the parameter temperature. The SA algorithm can be described by Figure 1.
Figure 1.
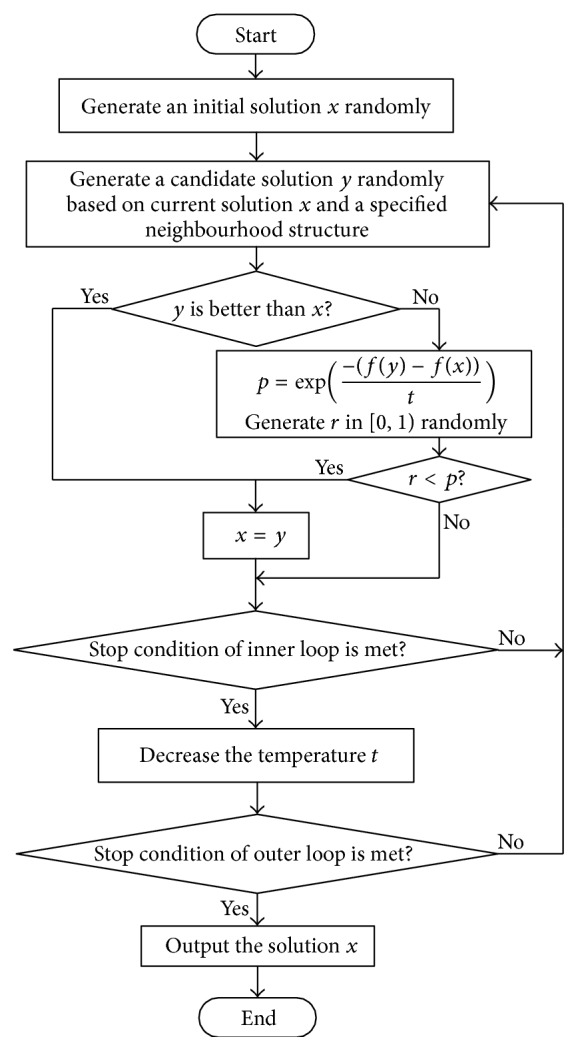
Flowchart of simulated annealing algorithm.
In order to apply the SA algorithm to a specific problem, one must specify the neighbourhood structure and cooling schedule. These choices and their corresponding parameter setting can have a significant impact on the SA's performance. Unfortunately, there are no choices of these strategies that will be good for all problems, and there is no general easy way to find the optimal parameter sets for a given problem. A cooling schedule should consist of starting temperature, temperature decrement function, Markov chain length, and termination condition. Geometric cooling schedule, which can be described by the temperature-update formula t k+1 = at k, is probably the most commonly used in the SA literature and acts as a base line for comparison with other more elaborate schemes [16]. Typical values of a for moderately slow cooling rates are 0.8 through 0.99.
For practical application where computation complexity of objective function is high, SA algorithm may run with constant Markov chain length and use fixed iteration times as termination condition. As a result, initial temperature and cooling coefficient a are the two key parameters that impact the performance of SA algorithm. Even in this simple situation, it is not an easy task to find optimal values for those two parameters, because SA's performance is sensitive to those parameters. One way to tackle the parameter setting problem of SA algorithm is to use adaptive cooling strategy [3–7]. Adaptive cooling strategy is definitely efficient and it makes SA algorithm less sensitive to user defined parameters than canonical SA, but it also makes SA algorithm lose the feature of simplicity. Another way to tackle this problem is to find new cooling schedule which has fewer parameters or the parameters are more robust.
2.3. Simulated Annealing Algorithm for TSP Problems
In order to use SA algorithm for TSP problem, we can represent solution x as a permutation π. Then, a large set of operators, such as the famous 2-Opt, 3-Opt, inverse, insert, and swap operators, can be used to generate candidate solution y. Since its appearance, SA algorithm has been widely and deeply studied on TSP problems [17–21]. Many cooling schedules, such as geometric, exponential, logarithmic, and arithmetic ones and their variants, have been used in literature.
The theory convergence conditions of SA make it very time consuming in most cases [22]. Wang et al. [23] proposed a two-stage SA algorithm which was tested on 23 TSP benchmark instances with scale from 51 to 783. The numerical results show that it is difficult for SA algorithm to solve TSP benchmark instances with scale exceeding 1000 cities based on time complexity. Geng et al. [24] proposed an adaptive simulated annealing algorithm with greedy search (ASA-GS), where greedy search technique is used to speed up the convergence rate. The ASA-GS achieves a reasonable trade-off among computation time, solution quality, and complexity of implementation. It has good scalability and has good performance even for TSP benchmark instances with scale exceeding 1000 cities. Wang et al. [25] proposed a multiagent SA algorithm with instance-based sampling (MSA-IBS) by exploiting learning ability of instance-based search algorithm. The learning-based sampling can effectively improve the SA's sampling efficiency. Simulation results showed that the performance of MSA-IBS is far better than ASA-GS in terms of solution accuracy and CPU time. In this paper, MSA-IBS is used as basis to use list-based cooling schedule.
3. List-Based Simulated Annealing Algorithm
3.1. The Neighbourhood Structure
In this paper, we use the greedy hybrid operator proposed by Wang et al. [25] to produce candidate solution. This is a kind of multiple move operators, which select the best one from three neighbours. Specifically, after two positions i and j are selected, it uses inverse operator, insert operator, and swap operator to produce three neighbour solutions. And the best one is used as the candidate solution. The inverse, insert, and swap operators can be defined as follows.
Define 1 (inverse operator inverse(π, i, j)). —
It means to inverse the cities between positions i and j. The inverse(π, i, j) will generate a new solution π′ such that π′(i) = π(j), π′(i + 1) = π(j − 1),…, π′(j) = π(i), where 1 ≤ i, j ≤ n∧1 ≤ j − i < n − 1; in addition, if j − i = n − 1, it means i = 1 and j = n, and then π′(i) = π(j) and π′(j) = π(i). Two edges will be replaced by inverse operator for symmetric TSP problems.
Define 2 (insert operator insert(π, i, j)). —
It means to move the city in position j to position i. The insert(π, i, j) operator will generate a new solution π′ such that π′(i) = π(j), π′(i + 1) = π(i),…, π′(j) = π(j − 1), in the case of i < j, or π′(j) = π′(j + 1),…, π′(i − 1) = π(i), π′(i) = π(j), in the case of i > j. In general, three edges will be replaced by insert operator.
Define 3 (swap operator swap(π, i, j)). —
It means to swap the city in position j and city in position i. The swap(π, i, j) operator will generate a new solution π′ such that π′(i) = π(j) and π′(j) = π(i). In general, four edges will be replaced by swap operator.
Using the above three operators, the used hybrid greedy operator can be defined as follows:
| (3) |
where min returns the best one among its parameters.
3.2. Produce Initial Temperature List
As in LBTA algorithms [8–14], list-based parameter controlling strategy needs to produce an initial list of parameters. Because temperature in SA is used to calculate acceptance probability of candidate solution, we use initial acceptance probability p 0 to produce temperature t as follows. Suppose x is current solution and y is candidate solution which is randomly selected from x's neighbours. Their objective function values are f(x) and f(y), respectively. If y is worse than x, then the acceptance probability p of y can be calculated using formula (2). Conversely, if we know the acceptance probability p 0, then we can calculate the corresponding temperature t as follows:
| (4) |
Figure 2 is the flowchart of producing initial temperature list. In Figure 2, after a feasible solution x is produced, a candidate solution y is randomly selected from x's neighbours. If y is better than x, then x is replaced by y. And using formula (4), the absolute value of f(y) − f(x) is used to calculate an initial temperature value t. Then t will be inserted into initial temperature list. The temperature list is a priority list, where higher temperature has higher priority. The same procedure is repeated until the list of temperature values is filled.
Figure 2.
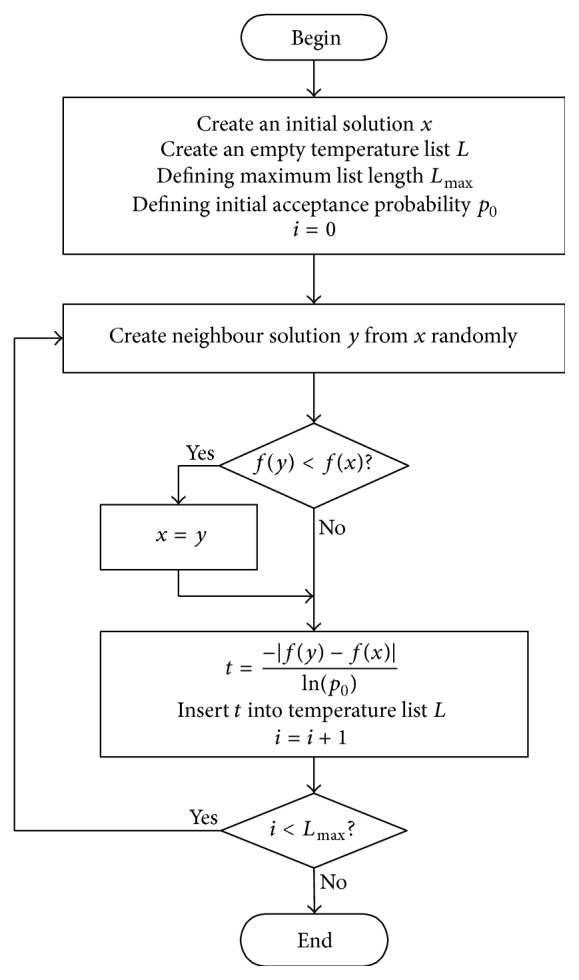
Flowchart of producing initial temperature list.
3.3. Temperature Controlling Procedure
In each iteration k, the maximum temperature in list is used as current temperature t max. If Markov chain length is M, then t max may be used at best M times for the calculation of acceptance probability of candidate solution. Suppose there are n times that bad solution is accepted as current solution; we use d i and p i to represent the difference of objective function values and acceptance probability, respectively, where i = 1 ⋯ n, and the relation between d i and p i can be described as the following equation:
| (5) |
According to the Metropolis acceptance criterion, for each time a bad candidate solution is met, a random number r is created. If r is less than the acceptance probability, then the bad candidate solution will be accepted. So, for each pair of d i and p i, there is a random number r i and r i is less than p i. We use d i and r i to calculate a new temperature t i as the following formula described:
| (6) |
We use the average of t i to update the temperature list. Specifically, t max will be removed from list, and average of t i will be inserted into list. Because t i is always less than t max, the average of t i is less than t max also. In this way, the temperature decreases always as the search proceeds.
3.4. Description of LBSA Algorithm
Because the main purpose of this paper is to study the effectiveness of list-based cooling schedule, we use a simple SA framework which uses fixed iteration times for outer loop and fixed Markov chain length in each temperature. The detailed flowchart of the main optimization procedure is shown in Figure 3. Besides the creation of initial temperature list, the main difference between the flowchart of LBSA and the flowchart of canonical SA is about the temperature control strategy. In canonical SA, the temperature controlling procedure is independent of the topology of solution space of the problem. Conversely, the temperature controlling procedure of LBSA is adaptive according to the topology of solution space of the problem. In Figure 3, K is maximum iteration times of outer loop, which is termination condition of LBSA. M is Markov chain length, which is termination condition of inner loop. Counter k is used to record the current iteration times of outer loop, m is used to record current sampling times of inner loop, and c is used to record how many times bad solution is accepted in each temperature. Variable t is used to store the total temperature calculated by formula (6), and the average temperature t/c will be used to update the temperature list. We can use a maximum heap to implement the temperature list. As the time complexity of storage and retrieval from heap is logarithmic, the use of temperature list will not increase the time complexity of SA algorithm.
Figure 3.

Flowchart of list-based SA algorithm.
4. Simulation Results
In order to observe and analyse the effect of list-based cooling schedule and the performance of LBSA algorithm, five kinds of experiments were carried out on benchmark TSP problems. The first kind of experiments was used to analyse the effectiveness of the list-based cooling schedule. The second kind was carried out to analyse the parameter sensitivity of LBSA algorithm. The third kind was carried out to compare the performance of different ways to update the temperature list. The fourth kind was carried out to compare the performance of different neighbourhood structures. And the fifth kind was carried out to compare LBSA's performance with some of the state-of-the-art algorithms.
4.1. The Effectiveness of List-Based Cooling Schedule
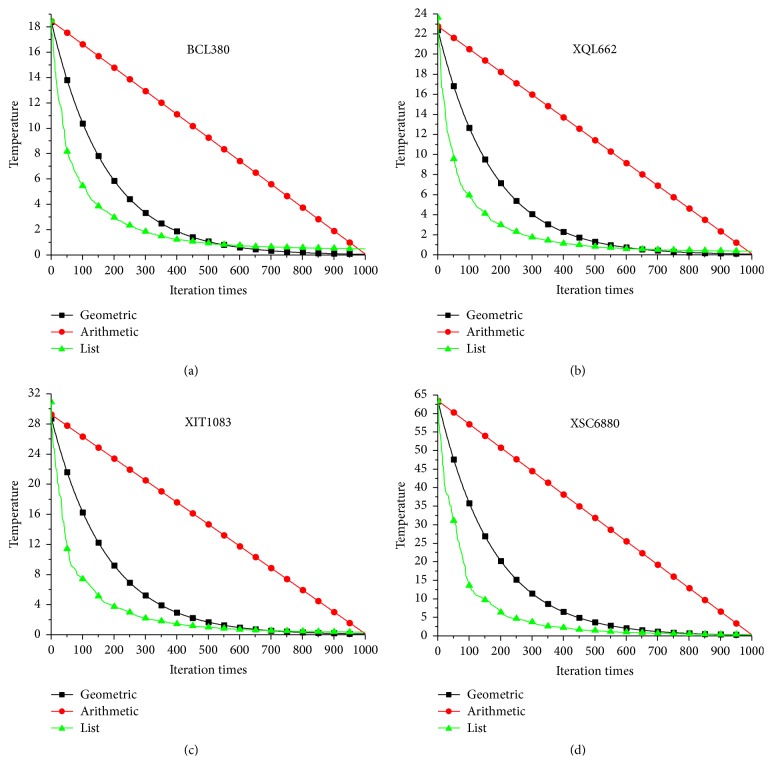
To illustrate the effectiveness of list-based cooling schedule, we compare the temperature varying process and search process of LBSA algorithm with SA algorithms based on the classical geometric cooling schedule and arithmetic cooling schedule. Those experiments were carried out on BCL380, XQL662, XIT1083, and XSC6880 problems from VLSI data sets. The best known integer solutions of those problems are 1621, 2513, 3558, and 21537, respectively. The iteration times of outer loop are 1000, and the Markov chain length in each temperature is the city number of the problem, which is 380, 662, 1083, and 6880, respectively.
Figure 4 compares the temperature varying process of different cooling schedules on the four benchmark problems. List-based cooling schedule can be viewed as a kind of geometric cooling schedule with variable cooling coefficient. Compared with the temperature varying of geometric cooling schedule, temperature of list-based cooling schedule decreases quicker in the early stage, but slower in the later stage. As indicated by Abramson et al. [16], geometric cooling schedule always uses constant cooling coefficient regardless of the stages of search. However, at high temperatures almost all candidate solutions are accepted, even though many of them could be nonproductive. To use variable cooling coefficients, which depend on the stages, would allow SA algorithm to spend less time in the high temperature stages. Consequently, more time would be spent in the low temperature stages, thus reducing the total amount of time required to solve the problem.
Figure 4.
Compare the temperature varying process of different cooling schedule.
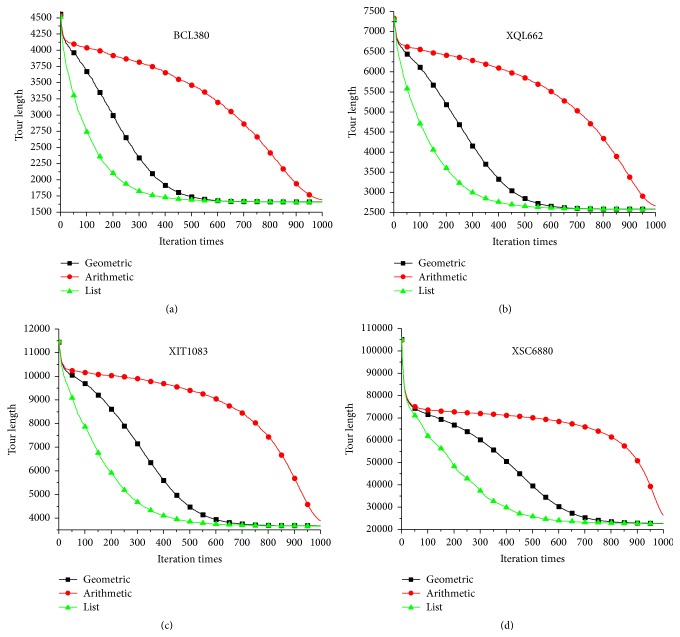
Figure 5 compares the search process of different cooling schedules on the four benchmark problems. Compared with geometric cooling schedule and arithmetic cooling schedule, list-based cooling schedule has quicker convergence speed and has good long-term behaviour also. This good performance may be due to the variable cooling coefficient feature of list-based cooling schedule. The temperature is updated adaptively according to the topology of solution space of the problem. As a result, LBSA algorithm can spend more time to search on promising area finely.
Figure 5.
Compare the search process of different cooling schedule.
4.2. Sensitivity Analysis of Temperature List Length and Initial Temperature Values
We observe the sensitivity of list length on BCL380, XQL662, XIT1083, and XSC6880 problems. For each problem, we test 30 different list lengths from 10 to 300 with a step 10. For each list length, we run LBSA algorithm 50 times and calculate the average tour length and the percentage error of the mean tour length to the best known tour length. Figure 6 is the relation between percentage error and list length. It shows the following: (1) for all the problems, there is a wide range of list length for LBSA to have similar promising performance; (2) list length is more robust on small problems than on large problems; (3) list length should not be too big for large problems. For big problems, the used Markov chain length, which is the city number of the problem, is not big enough for LBSA to reach equilibrium on each temperature. Big list length means the temperature decreases more slowly, so the algorithm will spend too much time on high temperature and accept too much nonproductive solutions. As a result, a big list length will dramatically deteriorate LBSA's performance for large problems. Because of the robust temperature list length, we use fixed temperature list length in the following simulations, which is 120 for all instances.
Figure 6.
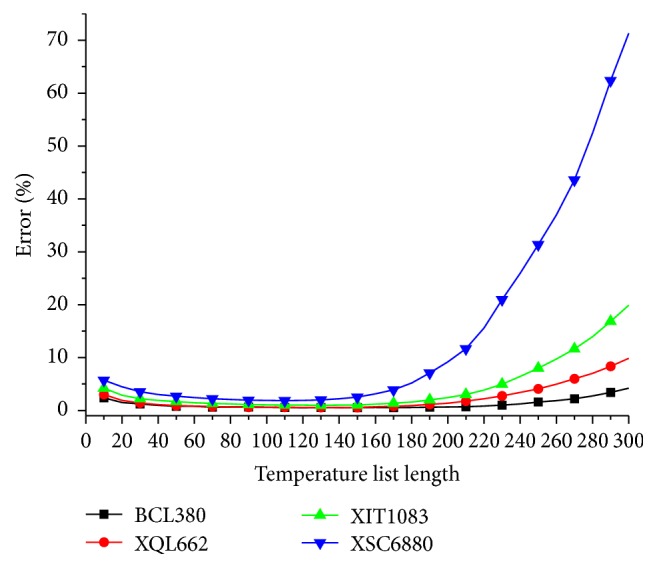
Sensitivity of parameter temperature list length.
In order to observe the sensitivity of initial temperature values, we carried out experiments with different initial temperature values on BCL380, XQL662, XIT1083, and XSC6880 problems. Because the initial temperature values are produced according to initial acceptance probability p 0, we use 30 different p 0, which range from 10−20 to 0.9, to create initial temperature values. Specifically, the set of p 0 is the union of geometric sequence from 10−20 to 10−2 with common ratio 10 and arithmetic sequence from 0.1 to 0.9 with common difference 0.1. For each initial acceptance probability, we run LBSA algorithm 50 times and calculate the average tour length and the percentage error of the mean tour length to the best known tour length. Figure 7 is the relation between percentage error and index of initial acceptance probability. It shows the following: (1) the performance of LBSA is not sensitive to the initial temperature values; (2) there is a different varying direction among different problems. For small problems, the initial temperature should not be too low, but for big problems, the initial temperature should not be too high. This difference is due to the limited computation resource used and the nonlinear computation complexity of TSP problem. The LBSA algorithm can have similar promising performance on a wide range of initial temperature values; this high robustness of initial temperature is due to the adaptive nature of list-based cooling schedule.
Figure 7.
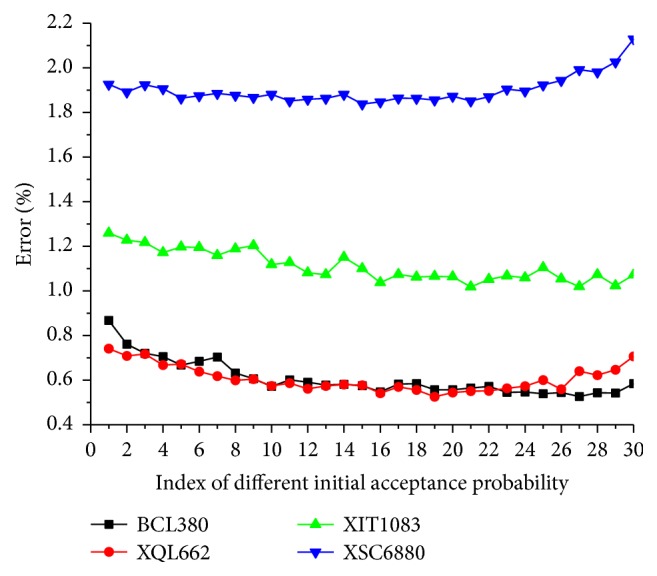
Sensitivity of parameter initial temperature values.
4.3. Comparing Different Temperature Updating Schemes
In our algorithm described in Section 3.4, we use the average of temperature t i to update temperature list. There are several variants, such as using maximum t i or minimum t i. To show the advantage of using average of t i, we compare the results and the decreasing process of temperature using those three updating schemes. Table 1 is the simulation results; it is clear that using average temperature to update temperature list has far better performance than the other methods. The temperature decreasing process of different strategies on BCL380, which is showed in Figure 8, can explain why using average temperature is the best option. If we use maximum temperature to update the temperature list, the temperature will decrease very slowly. As a result, the acceptation probability of bad solution is always high, and SA algorithm will search randomly in the solution space. Conversely, if we use minimum temperature to update the temperature list, the temperature will decrease sharply. As a result, the SA algorithm will be trapped into local minimum quickly and lose the advantage of escaping from local minimum by using Metropolis acceptance criterion.
Table 1.
Comparison of different temperature list updating schemes.
| Instance | OPT | Average | Maximum | Minimum |
|---|---|---|---|---|
| BCL380 | 1621 | 1630.2 | 2357.4 | 1651.9 |
| XQL662 | 2513 | 2527.2 | 4117.8 | 2565.8 |
| XIT1083 | 3558 | 3592.9 | 6663.0 | 3674.6 |
| XSC6880 | 21537 | 21920.0 | 63472.2 | 22649.8 |
Figure 8.
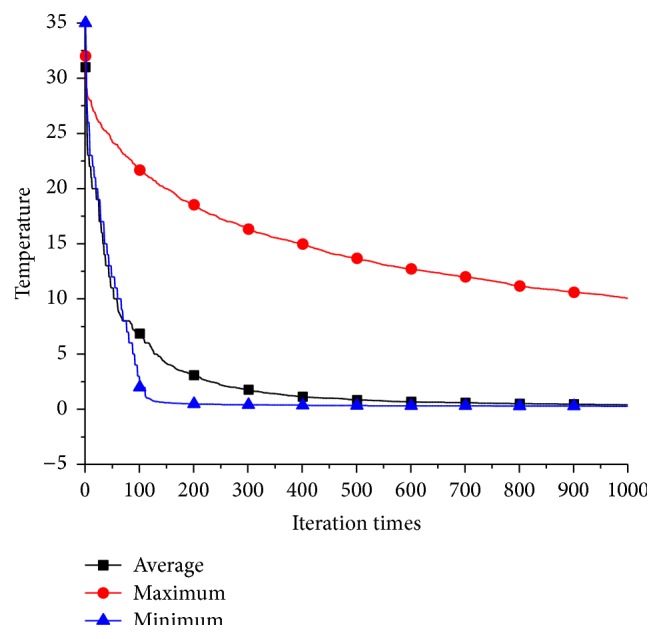
Temperature decreasing process of different temperature list updating schemes on instance BCL380.
4.4. Comparing Different Neighbourhood Structures
In our algorithm, we use a greedy hybrid neighbour operator proposed by Wang et al. [25] to produce candidate solution. This hybrid operator uses the best one produced by inverse, insert, and swap operators. To show its advantage, we compare the results produced by inverse, insert, swap, and hybrid operators. And we compare the percentage of inverse, insert, and swap operators accepted when we use hybrid operator. Table 2 is the simulation results; it is clear that hybrid operator has the best performance. Among the three basic operators, inverse is the best. If we compare the percentages of different basic operators accepted when we use hybrid operator, we found that inverse operator is accepted most. Figure 9 is the percentages of different operators accepted on instance BCL380. The percentages of inverse, insert, and swap operators are 65%, 31%, and 4%, respectively. The relative percentages of the three operators accepted are similar on other instances as on BCL380. The good performance of inverse operator is due to its ability to produce more fine-grained neighbourhood structure, because it changes two edges only. The hybrid operator, which uses inverse, insert, and swap operators at the same time, has a bigger neighbourhood structure. So it has higher probability to find promising solutions.
Table 2.
Comparison of different neighbourhood structures.
| Instance | Inverse | Insert | Swap | Hybrid |
|---|---|---|---|---|
| BCL380 | 1631.96 | 1776.24 | 2666.44 | 1630.84 |
| XQL662 | 2535.2 | 2836.52 | 4437.2 | 2527.2 |
| XIT1083 | 3603.48 | 4118.72 | 6760.84 | 3592.08 |
| XSC6880 | 22115.6 | 29048 | 64263.4 | 21930.6 |
Figure 9.
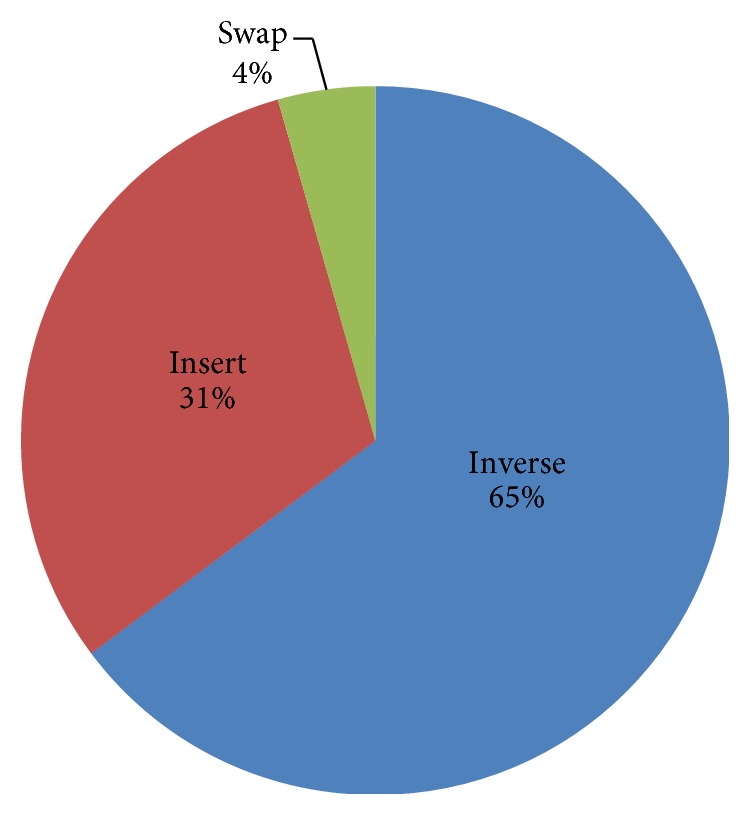
Percentage of inverse, insert, and swap operators accepted in hybrid operator on instance BCL380.
4.5. Competitiveness of LBSA Algorithm
We compare LBSA algorithm with genetic simulated annealing ant colony system (GSAACS) [26] and MSA-IBS on 24 benchmark instances with cities from 51 to 1655. The GSAACS is a hybrid algorithm which uses the ant colony system (ACS) to generate the initial solutions of the genetic algorithms. Then, it uses genetic algorithm (GA), which uses SA as mutation operator, to generate offspring solutions based on the initial solutions. If the solutions searched by GA are better than the initial solutions, GSAACS will use these better solutions to update the pheromone for the ACS. After a predefined number of generations, GSAACS uses particle swarm optimization (PSO) to exchange the pheromone information between groups.
The results of GSAACS are from [26]. GSAACS uses 120 ants and 1000 generations. In each generation of GSAACS, GA runs 100 generations. In MSA-IBS and LBSA algorithm, we set the population size to 30 and the iteration times of outer loop to 1000, and the Markov chain length in each temperature is two times the number of cities. The end condition is that either it finds the optimal solution or the iteration times of outer loop reach 1000. The algorithm was executed 25 times on each TSP problem, and the results are listed in Table 3.
Table 3.
Compare LBSA with GSAACS and MSA-IBS on 24 benchmark instances from TSPLIB.
| Number | Instance | OPT | GSAACS | MSA-IBS | LBSA | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Best | Mean | PEav | Best | Mean | PEav | Best | Mean | PEav | |||
| 1 | eil51 | 426 | 427 | 427.27 | 0.30 | 426 | 426 | 0 | 426 | 426 | 0 |
| 2 | eil76 | 538 | 538 | 540.20 | 0.41 | 538 | 538 | 0 | 538 | 538 | 0 |
| 3 | eil101 | 629 | 630 | 635.23 | 0.99 | 629 | 629 | 0 | 629 | 629 | 0 |
| 4 | berlin52 | 7542 | 7542 | 7542.00 | 0 | 7542 | 7542 | 0 | 7542 | 7542 | 0 |
| 5 | bier127 | 118282 | 118282 | 119421.83 | 0.96 | 118282 | 118291.2 | 0.01 | 118282 | 118282 | 0 |
| 6 | ch130 | 6110 | 6141 | 6205.63 | 1.57 | 6110 | 6110 | 0 | 6110 | 6110.6 | 0.01 |
| 7 | ch150 | 6528 | 6528 | 6563.70 | 0.55 | 6528 | 6544.4 | 0.25 | 6528 | 6537.5 | 0.15 |
| 8 | rd100 | 7910 | 7910 | 7987.57 | 0.98 | 7910 | 7910 | 0 | 7910 | 7910.1 | 0 |
| 9 | lin105 | 14379 | 14379 | 14406.37 | 0.19 | 14379 | 14379 | 0 | 14379 | 14379 | 0 |
| 10 | lin318 | 42029 | 42487 | 43002.90 | 2.32 | 42040 | 42170.9 | 0.34 | 42029 | 42138.55 | 0.26 |
| 11 | kroA100 | 21282 | 21282 | 21370.47 | 0.42 | 21282 | 21282 | 0 | 21282 | 21284.15 | 0.01 |
| 12 | kroA150 | 26524 | 26524 | 26899.20 | 1.41 | 26524 | 26524.15 | 0 | 26524 | 26524.05 | 0 |
| 13 | kroA200 | 29368 | 29383 | 29738.73 | 1.26 | 29368 | 29383.45 | 0.05 | 29368 | 29371.9 | 0.01 |
| 14 | kroB100 | 22141 | 22141 | 22282.87 | 0.64 | 22141 | 22174.2 | 0.15 | 22141 | 22184.2 | 0.2 |
| 15 | kroB150 | 26130 | 26130 | 26448.33 | 1.22 | 26130 | 26134.05 | 0.02 | 26130 | 26137.9 | 0.03 |
| 16 | kroB200 | 29437 | 29541 | 30035.23 | 2.03 | 29438 | 29439.4 | 0.01 | 29437 | 29438.65 | 0.01 |
| 17 | kroC100 | 20749 | 20749 | 20878.97 | 0.63 | 20749 | 20749 | 0 | 20749 | 20749 | 0 |
| 18 | kroD100 | 21294 | 21309 | 21620.47 | 1.53 | 21294 | 21342.75 | 0.23 | 21294 | 21294.55 | 0 |
| 19 | kroE100 | 22068 | 22068 | 22183.47 | 0.52 | 22068 | 22114.4 | 0.21 | 22068 | 22092.6 | 0.11 |
| 20 | rat575 | 6773 | 6891 | 6933.87 | 2.38 | 6813 | 6824.65 | 0.76 | 6789 | 6815.55 | 0.63 |
| 21 | rat783 | 8806 | 8988 | 9079.23 | 3.10 | 8845 | 8869.7 | 0.72 | 8846 | 8866.6 | 0.69 |
| 22 | rl1323 | 270199 | 277642 | 280181.47 | 3.69 | 270893 | 271972.3 | 0.66 | 270475 | 271415 | 0.45 |
| 23 | fl1400 | 20127 | 20593 | 21349.63 | 6.07 | 20299 | 20392.4 | 1.32 | 20140 | 20182.2 | 0.27 |
| 24 | d1655 | 62128 | 64151 | 65621.13 | 5.62 | 62786 | 62966.3 | 1.35 | 62454 | 62610.1 | 0.78 |
| Average | 1.62 | 0.25 | 0.15 | ||||||||
In Table 3, the columns Instance, OPT, Best, Mean, and PEav denote the name of the TSP problem, the optimal tour length from TSPLIB, the shortest tour length found, the average tour length among the 25 trials, and the percentage error of the mean tour length to the OPT, respectively. As can be seen in Table 3, both MSA-IBS and LBSA have better performance than GSAACS on all 24 instances. LBSA is a little better than MSA-IBS in terms of average percentage error.
We compare LBSA algorithm with GA-PSO-ACO [27] and MSA-IBS on 35 benchmark instances with cities from 48 to 33810. GA-PSO-ACO combines the evolution ideas of the genetic algorithms, particle swarm optimization, and ant colony optimization. In the GA-PSO-ACO algorithm, the whole process is divided into two stages. In the first stage, GA and PSO are used to obtain a series of suboptimal solutions to adjust the initial allocation of pheromone for ACO. In the second stage, ACO is used to search the optimal solution. The results of GA-PSO-ACO are from [27]. GA-PSO-ACO uses 100 individuals and 1000 generations. In LBSA and MSA-IBS algorithm, we set the number of population size to 10 and the iteration times of outer loop to 1000, and the Markov chain length in each temperature is the number of cities. The end condition of LBSA is that either it finds the optimal solution or the iteration times of outer loop reach 1000. Like GA-PSO-ACO and MSA-IBS, LBSA was executed 20 times on each TSP instance, and the results are listed in Table 4.
Table 4.
Compare LBSA with GA-PSO-ACO and MSA-IBS on 35 benchmark instances from TSPLIB.
| Instance | OPT | GA-PSO-ACO | MSA-IBS | LBSA | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Best | Mean | PEav | Best | Mean | PE | Best | Mean | PEav | ||
| Att48 | 33522 | 33524 | 33662 | 0.42 | 33522 | 33554.64 | 0.10 | 33522 | 33536.6 | 0.04 |
| Eil51 | 426 | 426 | 431.84 | 1.37 | 426 | 426.48 | 0.11 | 426 | 426.5 | 0.12 |
| Berlin52 | 7542 | 7544.37 | 7544.37 | 0.03 | 7542 | 7542 | 0 | 7542 | 7542 | 0 |
| St70 | 675 | 679.60 | 694.60 | 2.90 | 675 | 677.16 | 0.32 | 675 | 675.55 | 0.08 |
| Eil76 | 538 | 545.39 | 550.16 | 2.26 | 538 | 538.2 | 0.04 | 538 | 538 | 0 |
| Pr76 | 108159 | 109206 | 110023 | 1.72 | 108159 | 108288 | 0.12 | 108159 | 108268.3 | 0.10 |
| Rat99 | 1211 | 1218 | 1275 | 5.28 | 1211 | 1211.04 | 0.00 | 1211 | 1211.1 | 0.01 |
| Rad100 | 7910 | 7936 | 8039 | 1.63 | 7910 | 7914.56 | 0.06 | 7910 | 7914.7 | 0.06 |
| KroD100 | 21294 | 21394 | 21484 | 0.89 | 21294 | 21340.64 | 0.22 | 21294 | 21314.2 | 0.09 |
| Eil101 | 629 | 633.07 | 637.93 | 1.42 | 629 | 629.6 | 0.10 | 629 | 629 | 0 |
| Lin105 | 14379 | 14397 | 14521 | 0.99 | 14379 | 14380.48 | 0.01 | 14379 | 14379 | 0 |
| Pr107 | 44303 | 44316 | 44589 | 0.65 | 44303 | 44379.88 | 0.17 | 44303 | 44392.25 | 0.20 |
| Pr124 | 59030 | 59051 | 60157 | 1.91 | 59030 | 59032.88 | 0.00 | 59030 | 59031.8 | 0.00 |
| Bier127 | 118282 | 118476 | 120301 | 1.71 | 118282 | 118334.6 | 0.04 | 118282 | 118351.2 | 0.06 |
| Ch130 | 6110 | 6121.15 | 6203.47 | 1.53 | 6110 | 6121.96 | 0.20 | 6110 | 6127.95 | 0.29 |
| Pr144 | 58537 | 58595 | 58662 | 0.21 | 58537 | 58549.72 | 0.02 | 58537 | 58570.15 | 0.06 |
| KroA150 | 26524 | 26676 | 26803 | 1.05 | 26524 | 26538.2 | 0.05 | 26524 | 26542.6 | 0.07 |
| Pr152 | 73682 | 73861 | 73989 | 0.42 | 73682 | 73727.96 | 0.06 | 73682 | 73688.8 | 0.01 |
| U159 | 42080 | 42395 | 42506 | 1.01 | 42080 | 42182.32 | 0.24 | 42080 | 42198.85 | 0.28 |
| Rat195 | 2323 | 2341 | 2362 | 1.68 | 2328 | 2334.2 | 0.48 | 2328 | 2331 | 0.34 |
| RroA200 | 29368 | 29731 | 31015 | 5.61 | 29368 | 29422.64 | 0.19 | 29368 | 29405.35 | 0.13 |
| Gil262 | 2378 | 2399 | 2439 | 2.57 | 2379 | 2383.56 | 0.23 | 2379 | 2382.45 | 0.19 |
| Pr299 | 48191 | 48662 | 48763 | 1.19 | 48192 | 48263.08 | 0.15 | 48191 | 48250 | 0.12 |
| Lin318 | 42029 | 42633 | 42771 | 1.77 | 42076 | 42292.04 | 0.63 | 42070 | 42264.35 | 0.56 |
| Rd400 | 15281 | 15464 | 15503 | 1.45 | 15324 | 15377.56 | 0.63 | 15311 | 15373.75 | 0.61 |
| Pcb442 | 50778 | 51414 | 51494 | 1.41 | 50879 | 51050.12 | 0.54 | 50832 | 51041.7 | 0.52 |
| Rat575 | 6773 | 6912 | 6952 | 2.64 | 6819 | 6854.64 | 1.21 | 6829 | 6847.95 | 1.11 |
| U724 | 41910 | 42657 | 42713 | 1.92 | 42150 | 42302.12 | 0.94 | 42205 | 42357.8 | 1.07 |
| Rat783 | 8806 | 9030 | 9126 | 3.63 | 8897 | 8918.28 | 1.28 | 8887 | 8913.25 | 1.22 |
| Pr1002 | 259045 | 265987 | 266774 | 2.98 | 261463 | 262211.7 | 1.22 | 261490 | 262202.5 | 1.22 |
| D1291 | 50801 | 52378 | 52443 | 3.23 | 51098 | 51340.84 | 1.06 | 51032 | 51358.7 | 1.10 |
| D1655 | 62128 | 64401 | 65241 | 5.01 | 62784 | 63011.96 | 1.42 | 62779 | 62994.65 | 1.39 |
| Nl4461 | 182566 | 18933 | 192574 | 5.48 | 185377 | 185631.1 | 1.68 | 185290 | 185501.7 | 1.61 |
| Brd14051 | 469385 | 490432 | 503560 | 7.28 | 478040 | 478618.8 | 1.97 | 477226 | 477612.7 | 1.75 |
| Pla33810 | 66048945 | 70299195 | 72420147 | 9.65 | 67868250 | 68038833.1 | 3.01 | 67754877 | 67848535.1 | 2.72 |
| Average | 2.43 | 0.53 | 0.49 | |||||||
As can be seen in Table 4, both MSA-IBS and LBSA have better performance than GA-PSO-ACO on all 35 instances. LBSA is a little bit better than MSA-IBS in terms of average percentage error.
We compare LBSA algorithm with ASA-GS [24] and MSA-IBS algorithm on 40 benchmark instances with cities from 151 to 85900. The experiments were run on a 2.8 GHz PC, and the ASA-GS was run on a 2.83 GHz PC. For all instances, we set the iteration times of outer loop to 1000 and set the Markov chain length in each temperature to the number of cities. As in MSA-IBS algorithm, a suitable population size is selected for each instance such that the CPU time of LBSA is less than that of ASA-GS. The end condition of LBSA and MSA-IBS is either when it finds the optimal solution or when the iteration times of outer loop reach 1000. The algorithm is executed 25 trials on each instance, and the results are listed in Table 5.
Table 5.
Compare LBSA with ASA-GS and MSA-IBS on 40 benchmark instances from TSPLIB.
| Number | Instance | OPT | ASA-GS | MSA-IBS | LBSA | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | PEav | Time | Mean | PEav | Time | Mean | PEav | Time | |||
| 1 | Ch150 | 6528 | 6539.8 | 0.16 | 10.91 | 6529 | 0.02 | 0.86 | 6529.8 | 0.03 | 1.29 |
| 2 | Kroa150 | 26524 | 26538.6 | 0.05 | 10.9 | 26524 | 0 | 0.82 | 26524 | 0 | 0.98 |
| 3 | Krob150 | 26130 | 26178.1 | 0.18 | 10.9 | 26135 | 0.02 | 1.51 | 26137 | 0.03 | 1.65 |
| 4 | Pr152 | 73682 | 73694.7 | 0.01 | 10.85 | 73682 | 0 | 0.84 | 73682 | 0 | 0.87 |
| 5 | U159 | 42080 | 42398.9 | 0.75 | 11.49 | 42080 | 0 | 0.79 | 42080 | 0 | 0.91 |
| 6 | Rat195 | 2323 | 2348.05 | 1.07 | 14.37 | 2330.2 | 0.31 | 1.86 | 2328 | 0.22 | 1.93 |
| 7 | D198 | 15780 | 15845.4 | 0.41 | 14.6 | 15780 | 0 | 1.39 | 15780 | 0 | 1.53 |
| 8 | Kroa200 | 29368 | 29438.4 | 0.23 | 14.26 | 29378 | 0.03 | 1.74 | 29373.8 | 0.02 | 1.67 |
| 9 | Krob200 | 29437 | 29513.1 | 0.25 | 14.24 | 29439.8 | 0.01 | 1.95 | 29442.2 | 0.02 | 2.1 |
| 10 | Ts225 | 126643 | 126646 | 0.00 | 16.05 | 126643 | 0 | 1.3 | 126643 | 0 | 1.54 |
| 11 | Pr226 | 80369 | 80687.4 | 0.39 | 16.7 | 80369 | 0 | 1.93 | 80369.8 | 0.00 | 2.16 |
| 12 | Gil262 | 2378 | 2398.61 | 0.86 | 19.43 | 2378.8 | 0.03 | 2.39 | 2379.2 | 0.05 | 2.72 |
| 13 | Pr264 | 49135 | 49138.9 | 0.00 | 19.09 | 49135 | 0 | 1.43 | 49135 | 0 | 1.49 |
| 14 | Pr299 | 48191 | 48326.4 | 0.28 | 21.94 | 48226.4 | 0.07 | 2.67 | 48221.2 | 0.06 | 2.93 |
| 15 | Lin318 | 42029 | 42383.7 | 0.84 | 23.35 | 42184.4 | 0.37 | 2.4 | 42195.6 | 0.40 | 2.58 |
| 16 | Rd400 | 15281 | 15429.8 | 0.97 | 30.4 | 15347.2 | 0.43 | 3.2 | 15350.4 | 0.45 | 3.46 |
| 17 | Fl417 | 11861 | 12043.8 | 1.54 | 32.02 | 11875.6 | 0.12 | 3.72 | 11867.8 | 0.06 | 4.01 |
| 18 | Pr439 | 107217 | 110226 | 2.80 | 34.92 | 107407.2 | 0.18 | 3.6 | 107465.2 | 0.23 | 3.95 |
| 19 | Pcb442 | 50778 | 51269.2 | 0.96 | 35.75 | 50970 | 0.38 | 3.68 | 50877 | 0.19 | 4.31 |
| 20 | U574 | 36905 | 37369.8 | 1.25 | 48.47 | 37155.8 | 0.68 | 5.21 | 37164.6 | 0.70 | 6.13 |
| 21 | Rat575 | 6773 | 6904.82 | 1.94 | 52.1 | 6839.8 | 0.99 | 5.27 | 6837.4 | 0.95 | 5.99 |
| 22 | U724 | 41910 | 42470.4 | 1.33 | 66.83 | 42212.2 | 0.72 | 8.11 | 42252 | 0.82 | 8.34 |
| 23 | Rat783 | 8806 | 8982.19 | 2.00 | 78.9 | 8893.4 | 0.99 | 8.99 | 8888.2 | 0.93 | 8.9 |
| 24 | Pr1002 | 259045 | 264274 | 2.01 | 164.42 | 261481.8 | 0.94 | 12.71 | 261805.2 | 1.07 | 12.96 |
| 25 | Pcb1173 | 56892 | 57820.5 | 1.63 | 193.08 | 57561.6 | 1.18 | 8.9 | 57431.8 | 0.95 | 9.61 |
| 26 | D1291 | 50801 | 52252.3 | 2.85 | 214.64 | 51343.8 | 1.07 | 10.59 | 51198.8 | 0.78 | 11.77 |
| 27 | Rl1323 | 270199 | 273444 | 1.20 | 210.16 | 271818.4 | 0.6 | 11.53 | 271714.4 | 0.56 | 12.64 |
| 28 | Fl1400 | 20127 | 20782.2 | 3.25 | 232.02 | 20374.8 | 1.23 | 17.72 | 20249.4 | 0.61 | 15.43 |
| 29 | D1655 | 62128 | 64155.9 | 3.26 | 281.88 | 62893 | 1.23 | 16.18 | 63001.4 | 1.41 | 16.45 |
| 30 | Vm1748 | 336556 | 343911 | 2.18 | 276.98 | 339617.8 | 0.91 | 19.7 | 339710.8 | 0.94 | 19.05 |
| 31 | U2319 | 234256 | 236744 | 1.06 | 410.97 | 235236 | 0.42 | 17.02 | 235975 | 0.73 | 18.94 |
| 32 | Pcb3038 | 137694 | 141242 | 2.57 | 554.28 | 139706.2 | 1.46 | 27.64 | 139635.2 | 1.41 | 29.05 |
| 33 | Fnl4461 | 182566 | 187409 | 2.65 | 830.9 | 185535.4 | 1.63 | 30.43 | 185509.4 | 1.61 | 29.67 |
| 34 | Rl5934 | 556045 | 575437 | 3.48 | 1043.95 | 566166.8 | 1.82 | 50.76 | 566053 | 1.80 | 52.5 |
| 35 | Pla7397 | 23260728 | 24166453 | 3.89 | 1245.22 | 2.38E+07 | 2.48 | 100.69 | 2.38E+07 | 2.24 | 89.61 |
| 36 | Usa13509 | 19982859 | 20811106 | 4.14 | 2016.05 | 2.04E+07 | 2.06 | 365.12 | 2.04E+07 | 1.89 | 326.76 |
| 37 | Brd14051 | 469385 | 486197 | 3.58 | 2080.5 | 478609.6 | 1.97 | 375.28 | 478010 | 1.84 | 369.86 |
| 38 | D18512 | 645238 | 669445 | 3.75 | 2593.97 | 658149.2 | 2.00 | 654.85 | 657457.2 | 1.89 | 629.14 |
| 39 | Pla33810 | 66048945 | 69533166 | 5.27 | 4199.88 | 68075607 | 3.07 | 1959.68 | 68029226.4 | 3.00 | 1998.19 |
| 40 | Pla85900 | 142382641 | 156083025 | 9.63 | 8855.13 | 146495515.6 | 2.89 | 7596.18 | 145526542.6 | 2.21 | 7586.6 |
| Average | 1.87 | 650.31 | 0.81 | 283.52 | 0.75 | 282.49 | |||||
As can be seen in Table 5, the average PEav of LBSA for all instances is 0.75, which is better than 1.87 of ASA-GS, and the average CPU time of LBSA for all instances is 282.49, which is far less than 650.31 of ASA-GS. LBSA is a little bit better than MSA-IBS in terms of average PEav.
5. Conclusion
This paper presents a list-based SA algorithm for TSP problems. The LBSA algorithm uses novel list-based cooling schedule to control the decrease of temperature parameter. The list-based cooling schedule can be viewed as a special geometric cooling schedule with variable cooling coefficient. The variance of cooling coefficient is adaptive according to the topology of solution space, which may be more robust to problems at hand. Simulated results show that this novel cooling schedule is insensitive to the parameter values and the proposed LBSA algorithm is very effective, simple, and easy to implement. The advantage of insensitive parameter is very attractive, allowing LBSA algorithm to be applied in diverse problems without much effort on tuning parameters to produce promising results.
Acknowledgment
This work was supported by Nature Science Foundation of Fujian Province of China (no. 2014J01219, no. 2013J01216).
Conflict of Interests
The authors declare that there is no conflict of interests regarding the publication of this paper.
References
- 1.Černý V. Thermodynamical approach to the traveling salesman problem: an efficient simulation algorithm. Journal of Optimization Theory and Applications. 1985;45(1):41–51. doi: 10.1007/bf00940812. [DOI] [Google Scholar]
- 2.Kirkpatrick S., Gelatt C. D., Vecchi M. P. Optimization by simulated annealing. Science. 1983;220(4598):671–680. doi: 10.1126/science.220.4598.671. [DOI] [PubMed] [Google Scholar]
- 3.Ingber L. Adaptive simulated annealing. Lester Ingber. 1993;52(5):491–500. [Google Scholar]
- 4.Ingber L. Adaptive simulated annealing (ASA): lessons learned. Control and Cybernetics. 1996;25(1):32–54. [Google Scholar]
- 5.Jeong S.-J., Kim K.-S., Lee Y.-H. The efficient search method of simulated annealing using fuzzy logic controller. Expert Systems with Applications. 2009;36(3):7099–7103. doi: 10.1016/j.eswa.2008.08.020. [DOI] [Google Scholar]
- 6.E Oliveira H. A., Jr., Petraglia A. Solving nonlinear systems of functional equations with fuzzy adaptive simulated annealing. Applied Soft Computing Journal. 2013;13(11):4349–4357. doi: 10.1016/j.asoc.2013.06.018. [DOI] [Google Scholar]
- 7.Oliveira H., Jr., Petraglia A. Establishing nash equilibria of strategic games: a multistart fuzzy adaptive simulated annealing approach. Applied Soft Computing Journal. 2014;19:188–197. doi: 10.1016/j.asoc.2014.02.013. [DOI] [Google Scholar]
- 8.Tarantilis C. D., Kiranoudis C. T. A list-based threshold accepting method for job shop scheduling problems. International Journal of Production Economics. 2002;77(2):159–171. doi: 10.1016/S0925-5273(01)00231-6. [DOI] [Google Scholar]
- 9.Tarantilis C. D., Kiranoudis C. T., Vassiliadis V. S. A list based threshold accepting algorithm for the capacitated vehicle routing problem. International Journal of Computer Mathematics. 2002;79(5):537–553. doi: 10.1080/00207160210948. [DOI] [Google Scholar]
- 10.Tarantilis C. D., Kiranoudis C. T., Vassiliadis V. S. A list based threshold accepting metaheuristic for the heterogeneous fixed fleet vehicle routing problem. Journal of the Operational Research Society. 2003;54(1):65–71. doi: 10.1057/palgrave.jors.2601443. [DOI] [Google Scholar]
- 11.Tarantilis C. D., Ioannou G., Kiranoudis C. T., Prastacos G. P. Solving the open vehicle routeing problem via a single parameter metaheuristic algorithm. Journal of the Operational Research Society. 2005;56(5):588–596. doi: 10.1057/palgrave.jors.2601848. [DOI] [Google Scholar]
- 12.Lee D. S., Vassiliadis V. S., Park J. M. List-based threshold-accepting algorithm for zero-wait scheduling of multiproduct batch plants. Industrial & Engineering Chemistry Research. 2002;41(25):6579–6588. doi: 10.1021/ie010570n. [DOI] [Google Scholar]
- 13.Lee D. S., Vassiliadis V. S., Park J. M. A novel threshold accepting meta-heuristic for the job-shop scheduling problem. Computers & Operations Research. 2004;31(13):2199–2213. doi: 10.1016/s0305-0548(03)00172-2. [DOI] [Google Scholar]
- 14.Nikolakopoulos A., Sarimveis H. A threshold accepting heuristic with intense local search for the solution of special instances of the traveling salesman problem. European Journal of Operational Research. 2007;177(3):1911–1929. doi: 10.1016/j.ejor.2005.12.010. [DOI] [Google Scholar]
- 15.Metropolis N., Rosenbluth A. W., Rosenbluth M. N., Teller A. H., Teller E. Equation of state calculations by fast computing machines. The Journal of Chemical Physics. 1953;21(6):1087–1092. doi: 10.1063/1.1699114. [DOI] [Google Scholar]
- 16.Abramson D., Krishnamoorthy M., Dang H. Simulated annealing cooling schedules for the school timetabling problem. Asia-Pacific Journal of Operational Research. 1999;16(1):1–22. [Google Scholar]
- 17.Aarts E. H., Korst J. H., van Laarhoven P. J. A quantitative analysis of the simulated annealing algorithm: a case study for the traveling salesman problem. Journal of Statistical Physics. 1988;50(1-2):187–206. doi: 10.1007/BF01022991. [DOI] [Google Scholar]
- 18.Allwright J. R. A., Carpenter D. B. A distributed implementation of simulated annealing for the travelling salesman problem. Parallel Computing. 1989;10(3):335–338. doi: 10.1016/0167-8191(89)90106-3. [DOI] [Google Scholar]
- 19.Jeong C.-S., Kim M.-H. Fast parallel simulated annealing for traveling salesman problem on SIMD machines with linear interconnections. Parallel Computing. 1991;17(2-3):221–228. doi: 10.1016/s0167-8191(05)80107-3. [DOI] [Google Scholar]
- 20.Hasegawa M. Verification and rectification of the physical analogy of simulated annealing for the solution of the traveling salesman problem. Physical Review E. 2011;83 doi: 10.1103/physreve.83.036708.036708 [DOI] [PubMed] [Google Scholar]
- 21.Tian P., Yang Z. An improved simulated annealing algorithm with genetic characteristics and the traveling salesman problem. Journal of Information and Optimization Sciences. 1993;14(3):241–255. doi: 10.1080/02522667.1993.10699153. [DOI] [Google Scholar]
- 22.Sadati N., Amraee T., Ranjbar A. M. A global Particle Swarm-Based-Simulated Annealing Optimization technique for under-voltage load shedding problem. Applied Soft Computing Journal. 2009;9(2):652–657. doi: 10.1016/j.asoc.2008.09.005. [DOI] [Google Scholar]
- 23.Wang Z. C., Geng X. T., Shao Z. H. An effective simulated annealing algorithm for solving the traveling salesman problem. Journal of Computational and Theoretical Nanoscience. 2009;6(7):1680–1686. doi: 10.1166/jctn.2009.1230. [DOI] [Google Scholar]
- 24.Geng X. T., Chen Z. H., Yang W., Shi D. Q., Zhao K. Solving the traveling salesman problem based on an adaptive simulated annealing algorithm with greedy search. Applied Soft Computing Journal. 2011;11(4):3680–3689. doi: 10.1016/j.asoc.2011.01.039. [DOI] [Google Scholar]
- 25.Wang C. Y., Lin M., Zhong Y. W., Zhang H. Solving travelling salesman problem using multiagent simulated annealing algorithm with instance-based sampling. International Journal of Computing Science and Mathematics. 2015;6(4):336–353. doi: 10.1504/ijcsm.2015.071818. [DOI] [Google Scholar]
- 26.Chen S.-M., Chien C.-Y. Solving the traveling salesman problem based on the genetic simulated annealing ant colony system with particle swarm optimization techniques. Expert Systems with Applications. 2011;38(12):14439–14450. doi: 10.1016/j.eswa.2011.04.163. [DOI] [Google Scholar]
- 27.Deng W., Chen R., He B., Liu Y., Yin L., Guo J. A novel two-stage hybrid swarm intelligence optimization algorithm and application. Soft Computing. 2012;16(10):1707–1722. doi: 10.1007/s00500-012-0855-z. [DOI] [Google Scholar]