Abstract
Screening cytosine-phosphate-guanine dinucleotide (CpG) DNA methylation sites in association with some covariate(s) is desired due to high dimensionality. We incorporate surrogate variable analyses (SVAs) into (ordinary or robust) linear regressions and utilize training and testing samples for nested validation to screen CpG sites. SVA is to account for variations in the methylation not explained by the specified covariate(s) and adjust for confounding effects. To make it easier to users, this screening method is built into a user-friendly R package, ttScreening, with efficient algorithms implemented. Various simulations were implemented to examine the robustness and sensitivity of the method compared to the classical approaches controlling for multiple testing: the false discovery rates-based (FDR-based) and the Bonferroni-based methods. The proposed approach in general performs better and has the potential to control both types I and II errors. We applied ttScreening to 383,998 CpG sites in association with maternal smoking, one of the leading factors for cancer risk.
1. Background
Due to its high throughput, accuracy, small sample requirement, and acceptable cost, the Illumina Infinium HumanMethylation450 BeadChip has been widely used to analyze deoxyribonucleic acid (DNA) methylation profiles in epigenetic studies that target various types of cancer. In particular, the illumina infinium assay utilizes a pair of probes (a methylated probe and an unmethylated probe) to measure the intensities of methylated and unmethylated alleles at the interrogated cytosine-phosphate-guanine dinucleotide (CpG) sites [1]. Two measures of DNA methylation are usually used: beta-values and M-values. A beta-value is the ratio of signal from the methylated probe relative to the sum of both methylated and unmethylated probes. Beta-values are in the range of (0,1) with 0 being completely unmethylated and 1 being fully methylated. M-values are log2 ratio of intensities for methylated and unmethylated probes and range from (−∞, +∞) [2, 3]. M-values are used more often in appreciation of its wide data range and variance homogeneity compared to beta-values.
Given the feature of high dimensionality of high-throughput methylation data, when performing designed and possibly complicated statistical analyses, it is wise to target potentially important CpG sites, for instance, CpG sites potentially associated with single-nucleotide polymorphisms (SNPs) and/or other covariate(s) of interest. Otherwise, the statistical power will be substantially lost. There is evidence that methylation is affected by genetic and some known factors such as smoking [4, 5]. Screening CpG sites have become overwhelmingly important across multiple health fields of study such as cancer research, genetic diseases, and epigenetic research.
Common methods for screening CpG sites assume some relationship of the M-values in association with SNPs or some other genetic or environmental factors conditional on the assumption of linearity with some post hoc adjustment for multiple comparisons. The advantage to this method is the flexibility of incorporating additional covariates and their interactions. The primary limitation lies in controlling for multiple testing. Two popular adjustment methods are the Bonferroni-based method [6, 7] and the Benjamini-Hochberg method for controlling the false discovery rate (FDR) [8, 9]. These methods alter the p-value or critical value to control for type I error. Bonferroni correction is the most conservative by dividing the linear regression p-value, respective of the regression term of interest, by the total number of comparisons (m) or CpG sites in this case such that those adjusted p-values above the significance level are rejected. The FDR method first orders the p-values, P(k) for k ∈ 1 ⋯ m, such that lower ordered p-values that are less than or equal to k/m × α are rejected [9]. It follows that the conservative Bonferroni-based method cannot control for type II error while the FDR-based method cannot control for type I error.
There are other potential issues that arise when dealing with DNA methylation. It is possible that the variation in methylation cannot be fully explained by the known covariates and there exist latent factors that confound with these known covariates [5]. To improve the screening quality, it is thus important to account for variations introduced by other unknown factors. Furthermore, CpG sites screened from one data set may not be consistent with those from another data set which directly affects the type I error rate and leads to a loss of power. It is thus equally important to improve the reproducibility of the selected CpG sites.
In this paper, we propose a novel collaboration of existing statistical techniques to screen genome-wide methylation. It takes unknown factor effects into account and achieves better reproducibility. The method has the ability to control for both types I and II error while adjusting for covariates as well as latent variables. The proposed screening method incorporates surrogate variable analysis [5], which identifies unknown latent variables, in conjunction with a training and testing approach [10] across CpG methylation sites linearly associated with covariates of interest, including the identified surrogate variables. Independently, each method is well established for different purposes. We mingle these methods and form, compared to existing methods, an improved and more efficient process to screen (filter) informative DNA methylation sites. In addition, this proposed method has been built into an efficient and user-friendly R package. In the following sections, further description and details of the proposed method can be found in Section 2, simulation studies and a real data application are included in Section 3, and we summarize the approach in Section 4.
2. Materials and Methods
The proposed screening procedure is built for analyzing the associations between methylation data (M-values), or some high-dimensional data, and covariates of interest and their potential interactions. It consists of two consecutive components and surrogate variable analysis followed by a series of regressions while controlling for multiple testing. Surrogate variable analysis (SVA) aims to identify and estimate latent factors or surrogate variables (SVs) that potentially affect the association between known factors and the response variable, for example, SNPs (known factor) and DNA methylation (response variable) [5]. Including the estimated surrogate variables into the screening process has the potential to reduce unexplained variations, adjust for confounding effects, and consequently improve the accuracy of screening in terms of important variable identification [5]. In the context of DNA methylation, inclusion of the surrogate variables explains the variation in DNA methylation not explained by the covariates currently under consideration. This implies that the identified surrogate variables can be further used to identify important factors (markers) showing large contribution to the variation in the response variable explained by the surrogate variables [11]. These surrogate variables along with other variable(s) of interest can be included in regression analysis as independent variables. After SVA, we then begin the screening process with regressions and adjust for multiple comparisons.
As mentioned in the introduction, several methods exist to adjust for multiple testing but lack the ability to control for both types I and II errors. We have elected to implement a method that will control for both while simultaneously helping the issue of reproducibility. We let randomly chosen training and testing samples estimate and test the effects of the primary covariate(s), termed the TT method. General ideas of this approach are discussed in Dobbin and Simon and Faraggi and Simon [10, 12]. This method follows the concept of cross-validation. It has been shown that the implementation of the training and testing technique can provide a better control of type I error rate [10, 12]. In the next two subsections, we provide detailed steps and options available to both the surrogate variable analysis component and the TT method.
2.1. Identifying Surrogate Variables
Surrogate variables are inferred prior to screening using an algorithmic method developed by Leek and Storey (2007) called surrogate variable analysis [5]. Following the descriptions in Leek and Storey (2007), these SVs are developed by removing the amount of methylation or signal due to the variable(s) of interest and then decomposing the remaining residuals to identify an orthogonal basis of singular vectors that can be reproduced. These vectors are further examined for significant variation to form surrogate variables. Leek and Storey built an R package to perform the surrogate variable analyses (SVAs). The first step in SVA is to identify the number of surrogate variables based on the data using one of two methods, “be” or “leek” as noted in the package. The “be” method, being the default choice according Leek and Storey's R package, is based on a permutation procedure originally proposed by Buja and Eyuboglu in 1992 [13], while the “leek” method provides an interface to the asymptotic approach proposed by Leek in 2011 [14]. Once the number of surrogate variables is calculated, they are then estimated using one of three algorithms, the iteratively reweighted (“irw”), supervised (“supervised”), and the two-step (“two-step”) method. Iteratively reweighted method is for empirical estimation of control probes, supervised method is for when control probes are known, and the two-step method is for general estimation of surrogate variables [15]. We elected to implement the “two-step” method following Leek and Storey [5]. Conditional on the data, a number of latent unknown variables have been identified, estimated, and will now be incorporated into the regression in association with DNA methylation as additional covariates.
2.2. The Training and Testing (TT) Screening Method
After surrogate variable analysis is complete, the TT screening method then begins as an iterative process of randomly sampling the training and testing data by a specified proportion. By default, 2/3 of the data will be included in the training data set, which is suggested in Dobbin and Simon [10] to maximize statistical power. Linear regressions are first applied to the training data to calculate the p values for the association between the CpG site and the covariates, including SVs, using either ordinary least squares (this is a default choice in our R package) or robust regression. Robust regression is a type of linear regression that allows for more relaxed assumptions about normality and presence of outliers in the data. A CpG site is included as a candidate if the covariate(s) of interest is statistically significant according to a prespecified significance level, for example, 0.05. In our designed R package, we give user the flexibility to define which term (covariate) is used to decide the selection of CpG sites. For example, suppose the defined right-hand side of the regression is x 1 + x 2 + x 1 × x 2, where x 1 × x 2 denotes the interaction of x 1 and x 2. If the decision of selecting a CpG site is based on one single term, for example, the significance of the interaction effect, the p value for the interaction term would be used to test statistical significance against the prespecified significance level of 0.05.
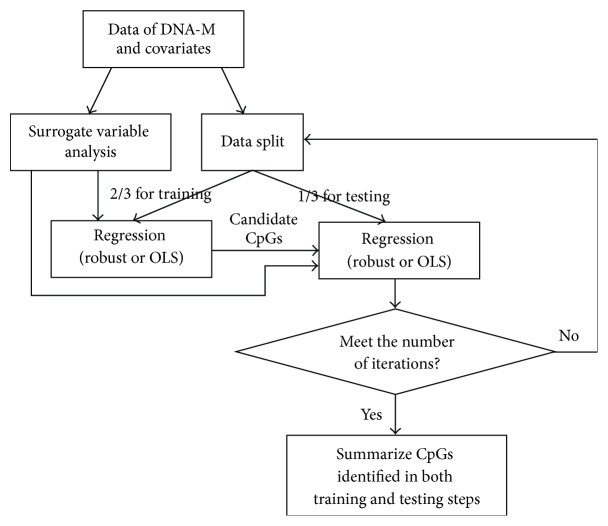
The process continues with these candidate CpG sites being further tested using the remaining subjects (testing data set) with linear regressions. For one pair of training and testing data sets, a candidate CpG site is deemed as being important if the significance still holds in the testing data. The significance level for the testing data by default is set at the same level as for the training data, 0.05. This screening process will be repeated i times (i.e., iterations); at each iteration, a training and testing data set will be randomly selected. After one iteration, a pool of candidate CpG sites will be selected. This process is continued for total i iterations. We summarize this screening process in Figure 1. Across all i iterations, CpG sites selected in at least m iterations will be included in the final pool of potentially important CpG sites; that is, the cutoff percentage of selection is m/i × 100%. Final estimates of the associations and statistical significance for the selected CpG sites are inferred by use of the complete data via the same analytical methods (i.e., linear regression including surrogate variables previously estimated from complete data) as in the training and testing process. A cutoff percentage of 50 (m = 50 across 100 total iterations (i = 100)) was used to determine the final pool of potentially important CpG sites. Suggestions on the determination of this predefined value, m, are discussed later in Section 3.1.
Figure 1.
A conceptual representation of the training and testing algorithm.
The user-friendly R package, ttScreening, is available from the Comprehensive R Archive Network (CRAN) at https://cran.r-project.org/web/packages/ttScreening/index.html, which implements the proposed screening procedure discussed above. This ttScreening package also provides access to other screening methods: FDR and Bonferroni methods. Various options, such as type of linear regression and surrogate variable estimation method, are available for the user to specify while other options are data specific and will need to be defined by the user. However, the package does provide acceptable defaults values for those options that are not data specific. A list of package options along with descriptions are available in the package manual at https://cran.r-project.org/web/packages/ttScreening/ttScreening.pdf.
3. Results and Discussion
Simulations are used to demonstrate and assess the TT screening method in comparison with the FDR- and Bonferroni-based methods using the ttScreening R package. These are followed up by an application to a data set of 383,998 CpG sites and their association with maternal smoking.
3.1. Simulations
Simulation Scenarios. In total, 2,000 CpG sites across n = 600 subjects were simulated. In these 2,000 CpG sites, k sites were assumed to be important. Different settings of k were considered, k = 10, 100, 200, and 400. Among the k important sites, DNA methylation at 90% of the k CpG sites was associated with two variables x 1 and x 2, their interaction, and 5 unobservable independent uncorrelated variables, and the remaining 10% of the k sites were associated with x 1, the interaction of x 1 and x 2, and the 5 unobservable independent uncorrelated variables. Variable x 1 is generated from normal distribution with mean 1 and variance 1, and x 2 is a four-level categorical variable generated from multinomial with parameters n and π = {0.15,0.25,0.25,0.35}. The remaining CpG sites (2000 − k) were only associated with the 5 unobservable variables and were deemed as unimportant ones. Linear regressions were applied to simulate the data. To assess the robustness of each method (TT screening and FDR- and Bonferroni-based methods), we considered two types of random error in the regressions, one following normal distribution with mean 0 and variance σ 2 = 1.5 and the other χ 2 distribution with a degree freedom of 1. Combining the choices on k and the distributions of random error, in total, we have 8 settings. For each setting, we generated 100 Monte Carlo (MC) replicates. The results presented below include means of the number of incorrect selections (rounded to the nearest integer), estimates of sensitivity, and estimates of specificity across the 100 MC replicates. The number of incorrect selections refers to the number of CpG sites misidentified (refers to both false positive and false negative CpG sites) out of the 2,000 CpG sites.
3.2. Results
Variables x 1 or x 2 would be selected if their interaction effect was statistically significant. All package options were chosen as the default values with training and testing significance levels both set to 0.05. The screening results (Table 1) indicate that, in general, the sensitivity from the FDR-based method is comparable to that from the TT screening method but its specificity is lower when the number of important variables is not sparse; for example, k = 200. Compared to the Bonferroni-based method, the TT method in general gave better sensitivity and comparable specificity. These were as expected, as the Bonferroni-based method lacks the ability to control type II error while the FDR-based method cannot control well type I error [16]. The TT screening method, on the other hand, has the potential to control both types I and II errors. This is reflected by the results that the TT screening method overall produced the smallest number of incorrectly identified variables, a statistic incorporating information from both sensitivity and specificity. We also performed the screening using robust regressions and similar results were obtained (not shown). These findings are invariant to the distribution pattern of random errors, normally, or skew distributed.
Table 1.
Simulation results for selecting k important variables among 2,000 candidates with surrogate variables included.
| Statistics | Bon | FDR | TT | Bon | FDR | TT |
|---|---|---|---|---|---|---|
| Random error normally distributed | ||||||
|
| ||||||
| k = 10 | k = 100 | |||||
| # incorrect | 0 | 1 | 1 | 3 | 8 | 2 |
| Sensitivity | 0.981 | 0.991 | 0.994 | 0.968 | 0.999 | 0.991 |
| Specificity | 1 | 1 | 1 | 1 | 0.996 | 1 |
|
| ||||||
| k = 200 | k = 400 | |||||
| # incorrect | 13 | 32 | 7 | 78 | 213 | 46 |
| Sensitivity | 0.936 | 0.998 | 0.982 | 0.814 | 0.996 | 0.931 |
| Specificity | 1 | 0.982 | 0.998 | 0.998 | 0.868 | 0.989 |
|
| ||||||
| Random error χ 2 distributed (df = 1) | ||||||
|
| ||||||
| k = 10 | k = 100 | |||||
| # incorrect | 1 | 1 | 1 | 16 | 9 | 7 |
| Sensitivity | 0.892 | 0.958 | 0.963 | 0.837 | 0.982 | 0.941 |
| Specificity | 1 | 1 | 1 | 1 | 0.996 | 1 |
|
| ||||||
| k = 200 | k = 400 | |||||
| # incorrect | 46 | 29 | 21 | 169 | 158 | 95 |
| Sensitivity | 0.771 | 0.981 | 0.906 | 0.582 | 0.969 | 0.790 |
| Specificity | 1 | 0.986 | 0.999 | 0.999 | 0.909 | 0.993 |
Bon: Bonferroni, FDR: false discovery rate, and TT: training and testing.
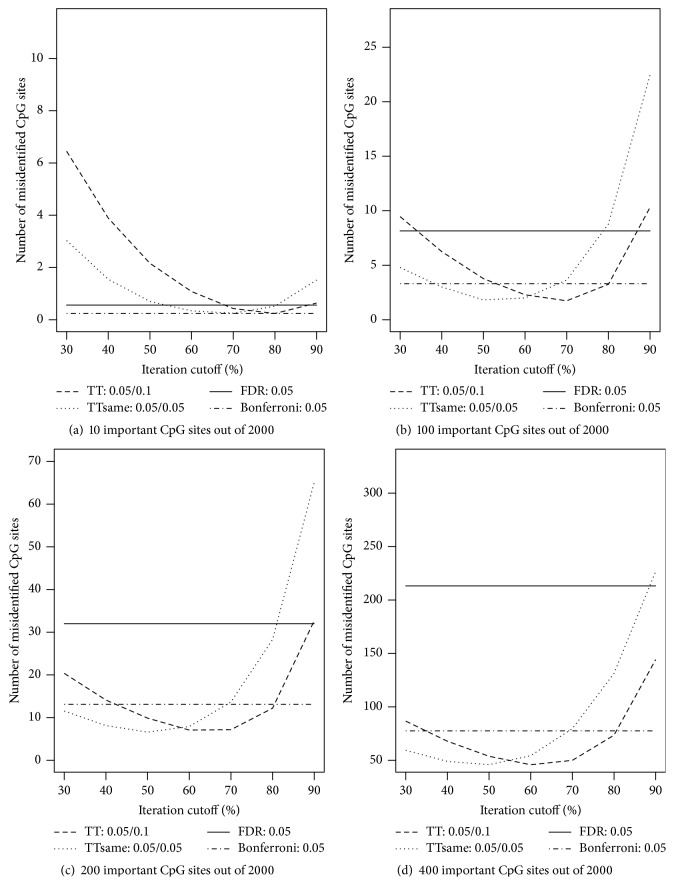
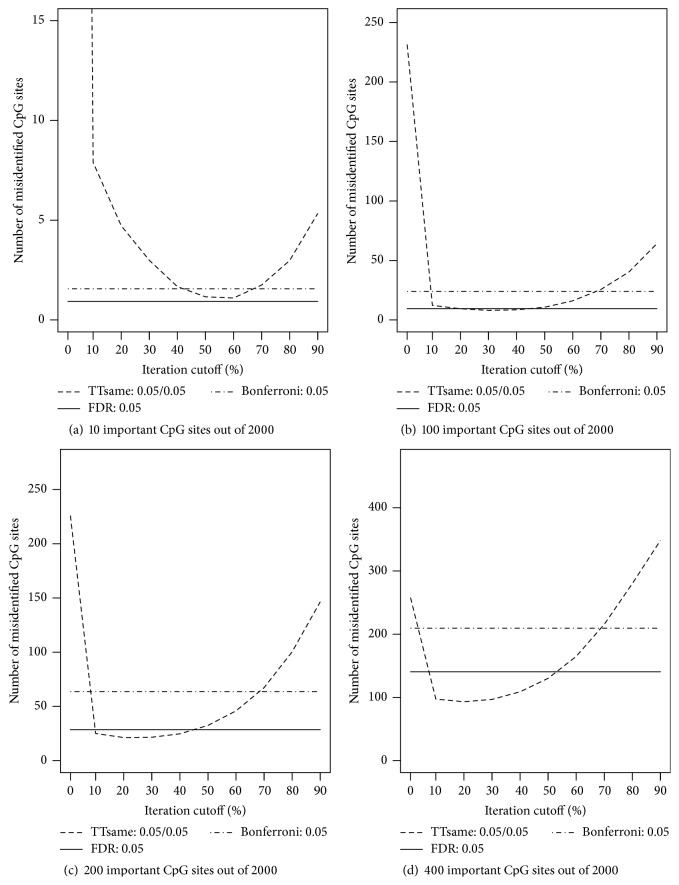
Recall that the default value of the cutoff percentage required for a CpG site to be treated as an informative site across all iterations was 50%, and the significance levels for both the training and testing data set were at 0.05. To further evaluate how the choices of this cutoff percentage and the significance levels in the training and testing steps influence the screening results, we chose a set of the cutoff percentage values ranging from 30 to 90 and set the training significance level to 0.1 instead of default value 0.05. All other settings were kept the same. As seen in Figure 2, across the different number of important CpG sites and sample sizes, overall taking the cutoff percentage close to 50% works the best with significance level of 0.05 for both the training and testing steps. If a higher significance level is chosen in the testing step, then a higher value for cutoff percentage should be used.
Figure 2.
Numbers of misidentified CpG sites versus cutoff frequency for a CpG site being potentially important (based on ordinary least squares regressions). The true numbers of important CpG sites are (a) 10, (b) 100, (c) 200, and (d) 400 out of 2,000 CpG sites. For the TT screening method, two sets of significance levels are considered: (1) 0.05 for training data and 0.1 for testing data; (2) 0.05 for both training and testing data. For the FDR-based and Bonferroni methods, the level was set at 0.05.
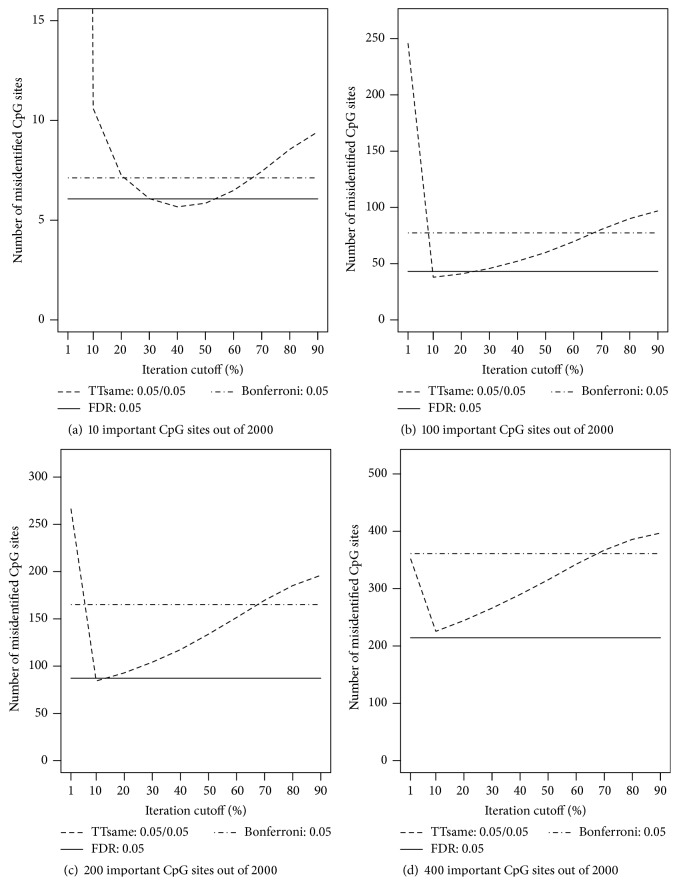
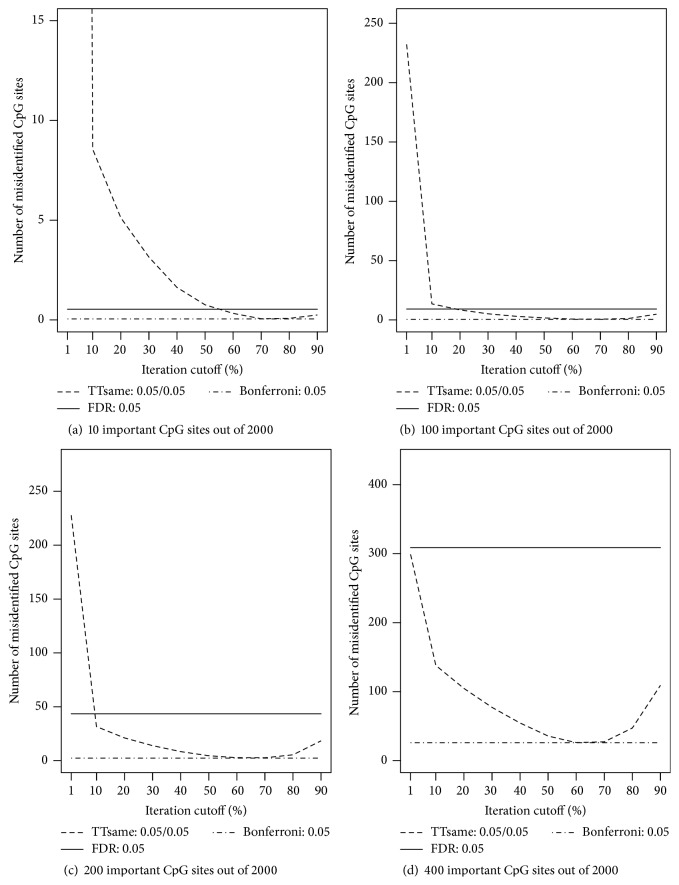
The above examination on cutoff percentage is with sample size n = 600. To assess whether and how sample size influences the choice of cutoff percentage, we repeated the above analyses for different sample sizes (and for each sample size, 100 MC replicates were generated), n = 200, 400, and 800 with all options in ttScreening() set at default values except for cutoff percentage. The results (Figures 3–5) indicated that if the number of important variables is expected to be sparse (e.g., 0.5% of the total number variables), the default cutoff value (50%) is a reasonable choice regardless of the sample size. On the other hand, if important variables are not sparse, for example, at least 5% of the total number of variables, then the cutoff value tends to be influenced by the sample size only if sample size is not large, for example, ≤400. In this case, the smaller the sample size is, the lower the cutoff percentage should be taken. This is as expected; when the sample size is smaller, the probability of true positives will be lower. We thus do not expect a higher proportion of correct selection and consequently a lower cutoff percentage is desired. From our simulations, we recommend 20% cutoff if both the following two conditions are not satisfied: (1) important variables are not expected to be sparse (which rarely happens in high-throughput and high-dimensional data) and (2) we have small samples compared to the number of candidate CpG sites. However, if sample size is large, the default cutoff 50% is still recommended. The selection results for sample sizes n = 200, 400, and 800 following these recommendations are included in the appendix (Tables 3, 4, and 5).
Figure 3.
Numbers of misidentified CpG sites versus cutoff frequency for a CpG site being potentially important (based on ordinary least squares regressions). The true numbers of important CpG sites are (a) 10, (b) 100, (c) 200, and (d) 400 out of 2,000 CpG sites across 200 subjects. For the TT screening method, significance levels considered are 0.05 for both training and testing data. For the FDR-based and Bonferroni methods, the level was set at 0.05.
Figure 5.
Numbers of misidentified CpG sites versus cutoff frequency for a CpG site being potentially important (based on ordinary least squares regressions). The true numbers of important CpG sites are (a) 10, (b) 100, (c) 200, and (d) 400 out of 2,000 CpG sites across 800 subjects. For the TT screening method, significance levels considered are 0.05 for both training and testing data. For the FDR-based and Bonferroni methods, the level was set at 0.05.
Table 3.
Simulation results for selecting k important variables among 2,000 candidates including surrogate variables across 200 subjects.
| Statistics | Bon | FDR | TT | Bon | FDR | TT |
|---|---|---|---|---|---|---|
| Random error normally distributed | ||||||
|
| ||||||
| k = 10 | k = 100† | |||||
| # incorrect | 7 | 6 | 6 | 77 | 43 | 41 |
| Sensitivity | 0.292 | 0.423 | 0.475 | 0.227 | 0.605 | 0.641 |
| Specificity | 1 | 1 | 1 | 1 | 0.998 | 0.997 |
|
| ||||||
| k = 200† | k = 400† | |||||
| # incorrect | 165 | 87 | 93 | 361 | 214 | 244 |
| Sensitivity | 0.175 | 0.616 | 0.571 | 0.099 | 0.565 | 0.432 |
| Specificity | 1 | 0.994 | 0.996 | 1 | 0.975 | 0.989 |
|
| ||||||
| Random error χ 2 distributed (df = 1) | ||||||
|
| ||||||
| k = 10 | k = 100† | |||||
| # incorrect | 9 | 8 | 7 | 88 | 62 | 55 |
| Sensitivity | 0.126 | 0.193 | 0.307 | 0.124 | 0.408 | 0.498 |
| Specificity | 1 | 1 | 1 | 1 | 0.998 | 0.997 |
|
| ||||||
| k = 200† | k = 400† | |||||
| # incorrect | 182 | 123 | 119 | 380 | 274 | 288 |
| Sensitivity | 0.093 | 0.422 | 0.435 | 0.051 | 0.377 | 0.314 |
| Specificity | 1 | 0.996 | 0.997 | 1 | 0.985 | 0.992 |
Bon: Bonferroni, FDR: false discovery rate, and TT: training and testing. †Cutoff percentage of 20%.
Table 4.
Simulation results for selecting k important variables among 2,000 candidates including surrogate variables across 400 subjects.
| Statistics | Bon | FDR | TT | Bon | FDR | TT |
|---|---|---|---|---|---|---|
| Random error normally distributed | ||||||
|
| ||||||
| k = 10 | k = 100† | |||||
| # incorrect | 2 | 1 | 1 | 24 | 10 | 9 |
| Sensitivity | 0.851 | 0.949 | 0.941 | 0.761 | 0.968 | 0.965 |
| Specificity | 1 | 1 | 1 | 1 | 0.997 | 0.997 |
|
| ||||||
| k = 200† | k = 400† | |||||
| # incorrect | 64 | 29 | 21 | 210 | 141 | 93 |
| Sensitivity | 0.682 | 0.968 | 0.947 | 0.479 | 0.948 | 0.864 |
| Specificity | 1 | 0.988 | 0.994 | 0.999 | 0.925 | 0.976 |
|
| ||||||
| Random error χ 2 distributed (df = 1) | ||||||
|
| ||||||
| k = 10 | k = 100† | |||||
| # incorrect | 4 | 3 | 3 | 47 | 19 | 18 |
| Sensitivity | 0.612 | 0.767 | 0.786 | 0.531 | 0.878 | 0.883 |
| Specificity | 1 | 1 | 1 | 1 | 0.997 | 0.997 |
|
| ||||||
| k = 200† | k = 400† | |||||
| # incorrect | 111 | 42 | 42 | 289 | 146 | 141 |
| Sensitivity | 0.445 | 0.88 | 0.837 | 0.281 | 0.841 | 0.717 |
| Specificity | 1 | 0.99 | 0.995 | 0.999 | 0.949 | 0.983 |
Bon: Bonferroni, FDR: false discovery rate, and TT: training and testing. †Cutoff percentage of 20%.
Table 5.
Simulation results for selecting k important variables among 2,000 candidates including surrogate variables across 800 subjects.
| Statistics | Bon | FDR | TT | Bon | FDR | TT |
|---|---|---|---|---|---|---|
| Random error normally distributed | ||||||
|
| ||||||
| k = 10 | k = 100 | |||||
| # incorrect | 2 | 44 | 5 | 26 | 309 | 36 |
| Sensitivity | 0.991 | 1 | 0.998 | 0.949 | 1 | 0.988 |
| Specificity | 1 | 0.976 | 0.998 | 0.996 | 0.807 | 0.981 |
|
| ||||||
| k = 200 | k = 400 | |||||
| # incorrect | 64 | 29 | 32 | 210 | 141 | 130 |
| Sensitivity | 0.682 | 0.968 | 0.847 | 0.479 | 0.948 | 0.696 |
| Specificity | 1 | 0.988 | 0.999 | 0.999 | 0.925 | 0.995 |
|
| ||||||
| Random error χ 2 distributed (df = 1) | ||||||
|
| ||||||
| k = 10 | k = 100 | |||||
| # incorrect | 0 | 1 | 1 | 4 | 9 | 2 |
| Sensitivity | 0.975 | 0.994 | 0.993 | 0.961 | 0.998 | 0.99 |
| Specificity | 1 | 1 | 1 | 1 | 0.995 | 0.999 |
|
| ||||||
| k = 200 | k = 400 | |||||
| # incorrect | 15 | 34 | 7 | 82 | 214 | 50 |
| Sensitivity | 0.928 | 0.998 | 0.98 | 0.803 | 0.994 | 0.924 |
| Specificity | 1 | 0.981 | 0.998 | 0.998 | 0.868 | 0.988 |
Bon: Bonferroni, FDR: false discovery rate, and TT: training and testing.
To demonstrate the benefit of using the identified surrogate variables in screening, we reanalyzed the simulated data (for n = 600) but with the surrogate variable analysis excluded (this option is available in the package). The relative patterns of statistics between different methods were intact compared to the results when surrogate variables were included in the screening process. However, when surrogate variables were not considered, a drastic drop in the mean sensitivity was observed across all the settings (Table 2). The sensitivity measures across all the 100 replicates ranged from 0 to 30%, implying that all methods had trouble deciphering CpG sites that are truly important. However, instead of completely excluding surrogate variables, what if we include a set of surrogate variables with each surrogate variable explaining quite a small portion of variation (i.e., less informative)? To examine this, we extracted surrogate variables that are less informative and reanalyzed the data. Similar findings as shown in Table 2 were concluded (Table 6), indicating the importance of including informative surrogate variables in order to substantially improve the quality of selection.
Table 2.
Simulation results for selecting k important variables among 2,000 candidates with surrogate variables excluded.
| Statistics | Bon | FDR | TT | Bon | FDR | TT |
|---|---|---|---|---|---|---|
| Random error normally distributed | ||||||
|
| ||||||
| k = 10 | k = 100 | |||||
| # incorrect | 10 | 51 | 9 | 99 | 114 | 90 |
| Sensitivity | 0.011 | 0.054 | 0.100 | 0.014 | 0.167 | 0.102 |
| Specificity | 1 | 0.979 | 1 | 1 | 0.984 | 1 |
|
| ||||||
| k = 200 | k = 400 | |||||
| # incorrect | 197 | 182 | 180 | 394 | 310 | 359 |
| Sensitivity | 0.015 | 0.232 | 0.102 | 0.015 | 0.288 | 0.104 |
| Specificity | 1 | 0.984 | 1 | 1 | 0.984 | 1 |
|
| ||||||
| Random error χ 2 distributed (df = 1) | ||||||
|
| ||||||
| k = 10 | k = 100 | |||||
| # incorrect | 10 | 38 | 9 | 98 | 103 | 91 |
| Sensitivity | 0.018 | 0.053 | 0.095 | 0.015 | 0.158 | 0.096 |
| Specificity | 1 | 0.986 | 1 | 1 | 0.99 | 1 |
|
| ||||||
| k = 200 | k = 400 | |||||
| # incorrect | 197 | 176 | 181 | 394 | 314 | 363 |
| Sensitivity | 0.014 | 0.217 | 0.094 | 0.014 | 0.273 | 0.095 |
| Specificity | 1 | 0.989 | 1 | 1 | 0.986 | 1 |
Bon: Bonferroni, FDR: false discovery rate, and TT: training and testing.
Table 6.
Simulation results for selecting k important variables among 2,000 candidates including the most and least important surrogate variables across 600 subjects.
| Bonferroni | FDR | TT | |||||||
|---|---|---|---|---|---|---|---|---|---|
| n.sv = 5 | n.sv = 10 | n.sv = 15 | n.sv = 5 | n.sv = 10 | n.sv = 15 | n.sv = 5 | n.sv = 10 | n.sv = 15 | |
| Most important surrogate variables included | |||||||||
|
| |||||||||
| # incorrect | |||||||||
| k = 10 | 0 | 0 | 0 | 6 | 6 | 6 | 5 | 4 | 3 |
| k = 100 | 2 | 3 | 2 | 19 | 19 | 19 | 7 | 5 | 5 |
| k = 200 | 6 | 6 | 5 | 26 | 29 | 29 | 6 | 6 | 4 |
| k = 400 | 12 | 11 | 11 | 40 | 38 | 39 | 7 | 7 | 7 |
|
| |||||||||
| Sensitivity | |||||||||
| k = 10 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| k = 100 | 0.98 | 0.97 | 0.98 | 1 | 1 | 1 | 0.98 | 0.98 | 0.98 |
| k = 200 | 0.97 | 0.97 | 0.975 | 0.995 | 0.995 | 0.995 | 0.985 | 0.985 | 0.985 |
| k = 400 | 0.97 | 0.973 | 0.973 | 1 | 1 | 1 | 0.988 | 0.988 | 0.985 |
|
| |||||||||
| Specificity | |||||||||
| k = 10 | 1 | 1 | 1 | 0.997 | 0.997 | 0.997 | 0.997 | 0.998 | 0.998 |
| k = 100 | 1 | 1 | 1 | 0.99 | 0.99 | 0.99 | 0.997 | 0.998 | 0.998 |
| k = 200 | 1 | 1 | 1 | 0.986 | 0.984 | 0.984 | 0.998 | 0.998 | 0.999 |
| k = 400 | 1 | 1 | 1 | 0.975 | 0.976 | 0.976 | 0.999 | 0.999 | 0.999 |
|
| |||||||||
| Most important surrogate variables not included | |||||||||
|
| |||||||||
| # incorrect | |||||||||
| k = 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 |
| k = 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| k = 200 | 200 | 200 | 200 | 200 | 200 | 200 | 200 | 200 | 200 |
| k = 400 | 400 | 400 | 400 | 400 | 400 | 400 | 400 | 400 | 400 |
|
| |||||||||
| Sensitivity | |||||||||
| k = 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| k = 100 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| k = 200 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| k = 400 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
|
| |||||||||
| Specificity | |||||||||
| k = 10 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| k = 100 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| k = 200 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| k = 400 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
FDR: false discovery rate, TT: training and testing, n.sv = number of surrogate variables, and k: the number of truly important CpG sites out of 2,000.
We further examined confounding effect of surrogate variables. To achieve this, we followed the same simulation scenarios noted earlier but, instead of assuming independence between all the (observed and unobserved) independent variables, we allow the 5 unobserved variables to be correlated with observed variable x 1 with a correlation of 0.7|i − j| where i, j ∈ L and L = (0,1, 2,3, 4,5) represents an arbitrary locations of the variables. For example, the observed variable is identified at location 0 and the 5 unobserved variables are locations (1,2, 3,4, 5). Then we generated 100 Monte Carlo replicates based on normal distributions with a sample size of n = 600. In the simulations, we considered the impact of including and excluding identified surrogate variables. The screening results (results not shown) are consistent with the previous findings when no correlations between unobserved and observed variables were assumed (Tables 1 and 2); that is, including the identified surrogate variable substantially improves the screening statistics (number of incorrectness, sensitivity, and specificity).
Based on the simulations, it is advised that users follow default setting for the TT screening method: 2/3 of the data for training, “two-step” for SVA analysis as described in the published literature [5], 100 iterations for the total number of TT screenings, 50% as the cutoff proportion of those 100 iterations, and 0.05 significance level for the training and testing data. We recommend 100 iterations as a balance between computing efficiency and adequate resampling of the subjects to decipher true associations. We recommend 50% as the default because in general informative CpGs are sparse compared to the number of candidate CpG sites, in which case, as seen in simulations the 50% cutoff percentage is suitable for small and large sample sizes.
3.3. Real Data Analysis
We applied the ttScreening package to 383,998 CpG sites with DNA methylation available for 245 subjects. The data were collected from a study cohort of 18-year-old females on the Isle of Wight (IOW) in the United Kingdom [17]. We examined a single factor that may be potentially associated with DNA methylation, maternal smoking status during pregnancy (0/1). It is thought that maternal smoking in utero increases chances of asthma and wheezing in children and modifies defensive mechanisms such as xenobiotic detoxification systems, antioxidant responses, and damage repair mechanisms [18]. Certain modifications to such systems have been known to increase risk of lung cancer [18].
We applied the TT, FDR-based, and Bonferroni-based methods to identify potentially important CpG sites. In the TT method, 2/3 of the samples were used for training and the remaining for testing. The number of iterations was set at 100 with relative frequency of 50% as the cutoff and the significance level in both training and testing steps was set at 0.05. The significance level for FDR-based and Bonferroni-based methods was set to 0.05. OLS regression was used to estimate associations and p values. Other settings were chosen as the default.
FDR- and Bonferroni-based methods, respectively, identified ten and five CpG sites associated with maternal smoking status. The five CpG sites identified by the Bonferroni-based method were also included in the ten CpG sites identified by FDR. The TT screening method identified 91 CpG sites potentially linked to maternal smoking status. The 10 CpG sites collectively identified by Bonferroni and FDR were included in the 91 identified by TT. Significant CpG site locations and annotated genes identified are included in Table 7 in Figure 6.
Table 7.
Information for CpG sites associated with maternal smoking identified by the training and testing screening method.
| Model 2: maternal smoking only | ||||
|---|---|---|---|---|
| CpG site | Chromosome: map | Gene | Promoter region | CpG island |
| name | information | name | and exon | location |
| cg20464068 | chr1: 14026054 | PRDM2 | TSS1500 | 14026481–14027200 |
| cg07951355 | chr1: 40123717 | |||
| cg14179389 | chr1: 92947961 | GFI1 | Body | 92945907–92952609 |
| cg00909806 | chr1: 212688762 | 212688031–212688448 | ||
| cg26143053 | chr2: 3718125 | ALLC | 5′UTR | |
| cg03690080 | chr2: 39188006 | LOC100271715, LOC375196 | Body, TSS1500 | 39186777–39187968 |
| cg19243656 | chr2: 73340094 | RAB11FIP5 | 5′UTR, 1stExon | 73339292–73340733 |
| cg18703066‡ | chr2: 105363536 | |||
| cg07516970 | chr2: 157181359 | NR4A2 | 3′UTR | 157184389–157184632 |
| cg19273101 | chr2: 191734576 | |||
| cg14075934 | chr2: 200137014 | SATB2 | Body | |
| cg03158780 | chr3: 577964 | |||
| cg10663973 | chr4: 6642559 | MRFAP1 | 1stExon, 5′UTR | 6642194–6643322 |
| cg10364374 | chr4: 125857940 | |||
| cg23743778 | chr4: 140357491 | 140357362–140357610 | ||
| cg21401642 | chr4: 174421114 | 174421347–174421559 | ||
| cg17924476† | chr5: 323794 | AHRR | Body | 320788–323010 |
| cg05575921 | chr5: 373378 | AHRR | Body | 373842–374426 |
| cg21161138 | chr5: 399360 | AHRR | Body | |
| cg12287936 | chr5: 1800606 | NDUFS6, MRPL36 | TSS1500 | 1799461–1801905 |
| cg16244648 | chr5: 141555043 | |||
| cg18349863 | chr6: 29912713 | HLA-A | Body | 29910202–29911367 |
| cg11492288 | chr6: 30290596 | HCG18 | Body | 30294169–30295071 |
| cg04325960 | chr6: 147124986 | LOC729176, C6orf103 | TSS200, Body | |
| cg00004963 | chr6: 147124996 | LOC729176, C6orf103 | TSS200, Body | |
| cg11881038 | chr6: 154408701 | OPRM1 | Body, 1stExon, 5′UTR | |
| cg20418529 | chr6: 166260012 | |||
| cg00794911 | chr6: 166260532 | |||
| cg18132363† | chr6: 166260572 | |||
| cg08634229 | chr6: 169326603 | |||
| cg06769202 | chr7: 27142535 | HOXA2 | TSS200 | 27143181–27143479 |
| cg23206851 | chr7: 27143046 | HOXA2 | TSS1500 | 27143181–27143479 |
| cg02225599 | chr7: 27143252 | HOXA2 | TSS1500 | 27143181–27143479 |
| cg10319053 | chr7: 27143370 | HOXA2 | TSS1500 | 27143181–27143479 |
| cg00445443 | chr7: 27143478 | HOXA2 | TSS1500 | 27143181–27143479 |
| cg06401979 | chr7: 27143717 | HOXA2 | TSS1500 | 27143181–27143479 |
| cg11986226 | chr7: 40026390 | CDK13 | Body | |
| cg19089201‡ | chr7: 45002287 | MYO1G | 3′UTR | 45002111–45002845 |
| cg04180046‡ | chr7: 45002736 | MYO1G | Body | 45002111–45002845 |
| cg12803068‡ | chr7: 45002919 | MYO1G | Body | 45002111–45002845 |
| cg25949550‡ | chr7: 145814306 | CNTNAP2 | Body | 145813030–145814084 |
| cg11207515 | chr7: 146904205 | CNTNAP2 | Body | |
| cg21015808 | chr7: 149809179 | |||
| cg21330896 | chr7: 28205705 | ZNF395 | 3′UTR | |
| cg17199018 | chr7: 28206278 | ZNF395 | Body | |
| cg04690729 | chr8: 133494328 | KCNQ3 | TSS1500 | 133492398–133493586 |
| cg15707110 | chr8: 144311102 | 144311708–144311985 | ||
| cg08126560 | chr9: 92291523 | LOC100129066 | Body | 92291268–92291524 |
| cg13393408 | chr9: 132874232 | GPR107 | Body | |
| cg11813497 | chr10: 14372879 | FRMD4A | TSS200 | |
| cg12490835 | chr10: 22623821 | 22623350–22625875 | ||
| cg26520012 | chr10: 42672589 | 42672509–42673432 | ||
| cg05329352 | chr10: 112838983 | ADRA2A | 1stExon | 112835990–112839303 |
| cg18424850 | chr10: 132945786 | TCERG1L | Body | |
| cg19494188 | chr11: 1466780 | BRSK2 | Body | 1466304–1467210 |
| cg26204383 | chr11: 2435667 | TRPM5 | Body | 2435295–2436651 |
| cg14436038 | chr11: 6494706 | TRIM3 | 5′UTR | 6494725–6495453 |
| cg15627089 | chr11: 16625751 | 16626053–16629180 | ||
| cg25160605 | chr11: 21087846 | NELL1 | Body | |
| cg17517598 | chr11: 61659090 | FADS3 | TSS200 | 61658569–61659592 |
| cg10788371 | chr11: 76381040 | LRRC32 | 5′UTR, 1stExon | 76381449–76382295 |
| cg11395306 | chr11: 98939366 | CNTN5 | 5′UTR | |
| cg01186919 | chr11: 111742365 | ALG9 | TSS1500, TSS200 | 111741953–111742292 |
| cg02820646 | chr11: 115398838 | |||
| cg05730269 | chr11: 118477055 | PHLDB1 | TSS200, TSS1500 | 118478235–118481896 |
| cg18493761 | chr11: 125386885 | |||
| cg09932758 | chr12: 58022542 | B4GALNT1 | Body | 58021294–58022037 |
| cg09644707 | chr12: 114885161 | 114885105–114885418 | ||
| cg27103591 | chr12: 124809023 | NCOR2 | 3′UTR | 124808972–124809176 |
| cg02032696 | chr14: 67982198 | TMEM229B | TSS200 | 67981514–67982380 |
| cg21511816 | chr14: 76597824 | 76597648–76597911 | ||
| cg24874277 | chr15: 33211107 | FMN1 | Body | |
| cg03643241 | chr15: 44487910 | FRMD5 | TSS1500 | 44486741–44487860 |
| cg20596162 | chr15: 45408861 | DUOXA2 | Body | 45408573–45409528 |
| cg16754378 | chr15: 57179394 | LOC145783 | Body | 57179277–57179838 |
| cg06899985 | chr15: 65689298 | IGDCC4 | Body | 65689142–65689362 |
| cg05549655† | chr15: 75019143 | CYP1A1 | TSS1500 | 75018186–75019336 |
| cg17852385 | chr15: 75019188 | CYP1A1 | TSS1500 | 75018186–75019336 |
| cg11924019† | chr15: 75019283 | CYP1A1 | TSS1500 | 75018186–75019336 |
| cg18092474† | chr15: 75019302 | CYP1A1 | TSS1500 | 75018186–75019336 |
| cg01060282 | chr16: 17033575 | |||
| cg07675285 | chr16: 27121267 | 27121011–27121241 | ||
| cg11705699 | chr16: 87742845 | KLHDC4 | Body | 87742556–87743109 |
| cg09554007 | chr16: 89627174 | RPL13, SNORD68 | 5′UTR, 1stExon, TSS1500 | 89626644–89627869 |
| cg16483033 | chr17: 1090441 | ABR | 1stExon, 5′UTR | |
| cg08682866 | chr17: 13818946 | |||
| cg17624073 | chr17: 79393583 | BAHCC1 | Body | 79393341–79393742 |
| cg13723693 | chr17: 80656731 | RAB40B | TSS200 | 80655335–80657183 |
| cg18495341 | chr17: 80909836 | B3GNTL1 | Body | |
| cg18449879 | chr19: 16045054 | CYP4F11 | 1stExon, Body | |
| cg02543506 | chr20: 33876594 | FAM83C | Body | 33879904–33880215 |
CpG: cytosine-phosphate-guanine dinucleotide, chr: chromosome, locations of each CpG are for v37 of the human genome, †CpG sites identified by false discovery rate, and ‡CpG sites identified by false discovery rate and Bonferroni-based methods.
Figure 6.
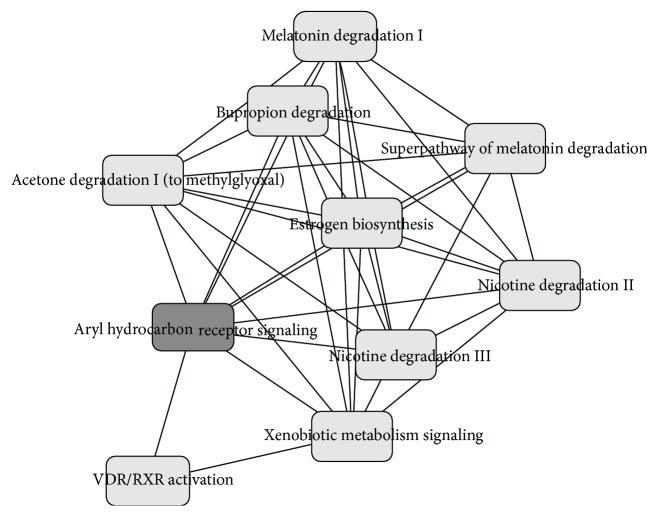
Top pathways enriched among genes identified by training and testing method from the Isle of Wight data include aryl hydrocarbon receptor signaling and xenobiotic metabolism signaling, which overlap with other pathways including the nicotine degradation II and nicotine degradation III pathways, as well as pathways for the metabolism of cigarette smoke components and producing known effects of smoke exposure.
To understand the biological meaning of the identified sets of CpGs, pathway analysis was used. The genes annotated to each significant CpG site were extracted from the 450 K array manifest file (v1.2; available: http://support.illumina.com/downloads/humanmethylation450_15017482_v1-2_product_files.html). Where a CpG site was annotated to more than one gene, all annotated genes were included. The resulting gene lists were analyzed with Ingenuity Pathway Analysis tool (IPA; Qiagen). Statistical significance for each pathway is reported by IPA using p values. The set of 91 CpGs differentially methylated with maternal smoking identified by TT (includes the 5 and 10 CpG sites identified by Bonferroni and FDR, resp.) were mapped to 54 unique genes.
The 91 CpGs differentially methylated with maternal smoking included 18 previously identified top maternal smoking-associated CpG sites in AHRR, CYP1A1, GFI1, MYO1G, CNTNAP2 [4, 19–21], FRMD4A [4, 21], LRRC32, and intergenic CpGs near LOC284998 and PDE10A-SDIM1 [21]. Bonferroni identified five maternal smoking-associated CpGs and FDR identified ten (including all five identified by Bonferroni), all of which have been previously published in association with maternal smoking. However, the TT method identified many more CpGs that have been previously identified as statistically significant in other cohorts, suggesting that these are not simply false positive results, and represent additional truly maternal smoking associated genes worthy of future investigation and validation. Our observation of differential methylation at age 18 in response to maternal smoking during pregnancy also agrees with previous observations that these epigenetic responses are preserved at least into adolescence [20]. The top pathways enriched among genes containing the 91 CpG sites included aryl hydrocarbon receptor signaling (p = 0.005) and xenobiotic metabolism signaling (p = 0.030), which support a long-lasting effect of maternal smoking on metabolic pathways controlling responses to smoke exposure. Furthermore, these pathways overlap with other pathways including the nicotine degradation II and nicotine degradation III pathways, as well as pathways for the metabolism of cigarette smoke components, and producing known effects of smoke exposure (Figure 6), such as melatonin degradation [22]. The TT method also identified six differentially methylated CpG sites in HOXA2, whose mutation causes cleft palate [23], the risk of which is known to be affected by maternal smoking [21].
In conclusion, the CpGs detected by TT in association with maternal smoking were enriched among pathways related to the known biology of those processes. Disruption or modification of some of these pathways results in greater risk of lung cancer [18]. TT also identified CpGs located in genes not previously identified which indicates potentially new findings.
4. Conclusions
We developed a unique screening procedure built into an R package for the purpose of screening important variables. It includes the developed method that involves training and testing steps (the TT screening method), along with another two existing methods, the method controlling for FDR and the other controlling overall significance level through the Bonferroni method. Simulations are used to demonstrate and assess the TT screening method.
Overall, the TT screening method produced comparable sensitivity results to that of FDR-based method and comparable specificity results of Bonferroni-based methods. However, the number of misidentified CpG sites from the TT method is in general smaller than those from the other two approaches. The findings on sensitivity and specificity were as expected, because the Bonferroni-based method lacks the ability to control type II error while the FDR-based method cannot control well type I error [16]. The TT screening method, on the other hand, has the potential to control both the types I and II errors, which was supported by the smaller numbers of incorrect detections. It was also noticed that, by incorporating surrogate variable analysis, all three methods produced higher sensitivity measures. In the real data application, the TT method identified a larger number of CpGs compared to the other two methods. The subsequent pathway analyses further support the practical strength of the proposed method. It is worth noting that since the screening process is to identify the CpG sites, to properly assess the functionality of these sites, it is critical to evaluate them jointly, for example, using pathway analyses.
An important contribution of the developed process is its computing efficiency. Although we combined three methods into one package, the computing is not burdensome. The computing time for screening 383,998 CpG sites (the real data analysis) with the ttScreening() function using default options only takes 82 minutes on a personal computer with a central processing unit (CPU) of 2.0 gigahertz (GHz) and memory of 4.0 gigabytes (GB) of random-access memory (RAM). The ttScreening() function always automatically adjusts for multiple testing using three methods, FDR, Bonferroni, and the training and testing method.
Lastly, the versatility of the proposed screening method allows it to be applied to a variety of scientific fields in which large data or high dimensionality is a computational problem. DNA methylation is of growing interest in all aspects of public health, in cancer and genetics/epigenetics specifically. TT reduces dimensionality in a timely manner while controlling for types I and II errors and adjusting unknown latent variables estimated using the surrogate variable analysis. Finally, the package incorporates a variety of options which allows the user to create very specific settings while maintaining convenient usability.
Acknowledgments
Many thanks to Dr. Nelis Soto-Ramirez for her effort in assisting the authors with the testing of the package. This work is supported by NIH Grant nos. R01AI091905 (Principal Investigator (PI): Karmaus) and R21AI099367 (PI: Zhang).
Appendix
See Tables 3, 4, 5, 6, and 7 and Figures 3, 4, 5, and 6.
Figure 4.
Numbers of misidentified CpG sites versus cutoff frequency for a CpG site being potentially important (based on ordinary least squares regressions). The true numbers of important CpG sites are (a) 10, (b) 100, (c) 200, and (d) 400 out of 2,000 CpG sites across 400 subjects. For the TT screening method, significance levels considered are 0.05 for both training and testing data. For the FDR-based and Bonferroni methods, the level was set at 0.05.
Conflict of Interests
The authors declare that there is no conflict of interests regarding the publication of this paper.
References
- 1.Weisenberger D., Van Den Berg D., Berg F., Berman B., Laird P. Comprehensive DNA Methylation Analysis on the Illumina Infinium Assay Platform. San Diego, Calif, USA: Illumina; 2008. [Google Scholar]
- 2.Irizarry R. A., Ladd-Acosta C., Wen B., et al. The human colon cancer methylome shows similar hypo- and hypermethylation at conserved tissue-specific CpG island shores. Nature Genetics. 2009;41(2):178–186. doi: 10.1038/ng.298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Du P., Zhang X., Huang C.-C., et al. Comparison of Beta-value and M-value methods for quantifying methylation levels by microarray analysis. BMC Bioinformatics. 2010;11, article 587 doi: 10.1186/1471-2105-11-587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Joubert B. R., Håberg S. E., Nilsen R. M., et al. 450K epigenome-wide scan identifies differential DNA methylation in newborns related to maternal smoking during pregnancy. Environmental Health Perspectives. 2012;120(10):1425–1431. doi: 10.1289/ehp.1205412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Leek J. T., Storey J. D. Capturing heterogeneity in gene expression studies by surrogate variable analysis. PLoS Genetics. 2007;3(9, article e161) doi: 10.1371/journal.pgen.0030161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Dunn O. J. Estimation of the medians for dependent variables. The Annals of Mathematical Statistics. 1959;30:192–197. doi: 10.1214/aoms/1177706374. [DOI] [Google Scholar]
- 7.Dunn O. J. Multiple comparisons among means. Journal of the American Statistical Association. 1961;56(293):52–64. doi: 10.1080/01621459.1961.10482090. [DOI] [Google Scholar]
- 8.Hochberg Y., Benjamini Y. More powerful procedures for multiple significance testing. Statistics in Medicine. 1990;9(7):811–818. doi: 10.1002/sim.4780090710. [DOI] [PubMed] [Google Scholar]
- 9.Benjamini Y., Hochberg Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. Journal of the Royal Statistical Society—Series B: Methodological. 1995;57(1):289–300. [Google Scholar]
- 10.Dobbin K. K., Simon R. M. Optimally splitting cases for training and testing high dimensional classifiers. BMC Medical Genomics. 2011;4(1, article 31) doi: 10.1186/1755-8794-4-31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Ren X., Wang Y., Chen L., Zhang X.-S., Jin Q. ellipsoidFN: a tool for identifying a heterogeneous set of cancer biomarkers based on gene expressions. Nucleic Acids Research. 2013;41(4, article e53) doi: 10.1093/nar/gks1288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Faraggi D., Simon R. A simulation study of cross-validation for selecting an optimal cutpoint in univariate survival analysis. Statistics in Medicine. 1996;15(20):2203–2213. doi: 10.1002/(SICI)1097-0258(19961030)15:20<2203::AID-SIM357>3.0.CO;2-G. [DOI] [PubMed] [Google Scholar]
- 13.Buja A., Eyuboglu N. Remarks on parallel analysis. Multivariate Behavioral Research. 1992;27(4):509–540. doi: 10.1207/s15327906mbr2704_2. [DOI] [PubMed] [Google Scholar]
- 14.Leek J. T. Asymptotic conditional singular value decomposition for high-dimensional genomic data. Biometrics. 2011;67(2):344–352. doi: 10.1111/j.1541-0420.2010.01455.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Leek J. T., Johnson W. E., Parker H. S., Jaffe A. E., Storey J. D. sva: Surrogate Variable Analysis. 2014. (Package Version 3.8.0). [Google Scholar]
- 16.Storey J. D. The positive false discovery rate: a bayesian interpretation and the q-value. The Annals of Statistics. 2003;31(6):2013–2035. doi: 10.1214/aos/1074290335. [DOI] [Google Scholar]
- 17.Ziyab A. H., Karmaus W., Holloway J. W., Zhang H., Ewart S., Arshad S. H. DNA methylation of the filaggrin gene adds to the risk of eczema associated with loss-of-function variants. Journal of the European Academy of Dermatology and Venereology. 2013;27(3):e420–e423. doi: 10.1111/jdv.12000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Gilliland F. D., Li Y.-F., Dubeau L., et al. Effects of glutathione S-transferase M1, maternal smoking during pregnancy, and environmental tobacco smoke on asthma and wheezing in children. American Journal of Respiratory and Critical Care Medicine. 2002;166(4):457–463. doi: 10.1164/rccm.2112064. [DOI] [PubMed] [Google Scholar]
- 19.Lee K. W. K., Richmond R., Hu P., et al. Prenatal exposure to maternal cigarette smoking and DNA methylation: epigenome-wide association in a discovery sample of adolescents and replication in an independent cohort at birth through 17 years of age. Environmental Health Perspectives. 2015;123(2):193–199. doi: 10.1289/ehp.1408614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Richmond R. C., Simpkin A. J., Woodward G., et al. Prenatal exposure to maternal smoking and offspring DNA methylation across the lifecourse: findings from the Avon Longitudinal Study of Parents and Children (ALSPAC) Human Molecular Genetics. 2015;24(8):2201–2217. doi: 10.1093/hmg/ddu739.ddu739 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Markunas C. A., Xu Z., Harlid S., et al. Identification of DNA methylation changes in newborns related to maternal smoking during pregnancy. Environmental Health Perspectives. 2014;122(10):1147–1153. doi: 10.1289/ehp.1307892.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Ozguner F., Koyu A., Cesur G. Active smoking causes oxidative stress and decreases blood melatonin levels. Toxicology and Industrial Health. 2005;21(10):21–26. doi: 10.1191/0748233705th211oa. [DOI] [PubMed] [Google Scholar]
- 23.Gendron-Maguire M., Mallo M., Zhang M., Gridley T. Hoxa-2 mutant mice exhibit homeotic transformation of skeletal elements derived from cranial neural crest. Cell. 1993;75(7):1317–1331. doi: 10.1016/0092-8674(93)90619-2. [DOI] [PubMed] [Google Scholar]