Collimator optimization and collimator-detector response compensation in myocardial perfusion SPECT using the ideal observer with and without model mismatch and an anthropomorphic model observer

Abstract

The collimator is the primary factor that determines the spatial resolution and noise tradeoff in myocardial perfusion SPECT images. In this paper, the goal was to find the collimator that optimizes the image quality in terms of a perfusion defect detection task. Since the optimal collimator could depend on the level of approximation of the collimator-detector response (CDR) compensation modeled in reconstruction, we performed this optimization for the cases of modeling the full CDR (including geometric, septal penetration and septal scatter responses), the geometric CDR, or no model of the CDR. We evaluated the performance on the detection task using three model observers. Two observers operated on data in the projection domain: the Ideal Observer (IO) and IO with Model-Mismatch (IO-MM). The third observer was an anthropomorphic Channelized Hotelling Observer (CHO), which operated on reconstructed images. The projection-domain observers have the advantage that they are computationally less intensive. The IO has perfect knowledge of the image formation process, i.e. it has a perfect model of the CDR. The IO-MM takes into account the mismatch between the true (complete and accurate) model and an approximate model, e.g. one that might be used in reconstruction. We evaluated the utility of these projection domain observers in optimizing instrumentation parameters. We investigated a family of 8 parallel-hole collimators, spanning a wide range of resolution and sensitivity tradeoffs, using a population of simulated projection (for the IO and IO-MM) and reconstructed (for the CHO) images that included background variability. We simulated anterolateral and inferior perfusion defects with variable extents and severities. The area under the ROC curve was estimated from the IO, IO-MM, and CHO test statistics and served as the figure-of-merit. The optimal collimator for the IO had a resolution of 9–11 mm FWHM at 10 cm, which is poorer resolution than typical collimators used for MPS. When the IO-MM and CHO used a geometric or no model of the CDR, the optimal collimator shifted toward higher resolution than that obtained using the IO and the CHO with full CDR modeling. With the optimal collimator, the IO-MM and CHO using geometric modeling gave similar performance to full CDR modeling. Collimators with poorer resolution were optimal when CDR modeling was used. The agreement of rankings between the IO-MM and CHO confirmed that the IO-MM is useful for optimization tasks when model mismatch is present due to its substantially reduced computational burden compared to the CHO.

1. Introduction

In SPECT imaging, reconstructed image quality is affected by a host of physical, instrumentation, and patient-related degrading factors. Accordingly, compensating for these factors typically results in improved quantification and better performance on a variety of tasks. The collimator-detector response (CDR) including the geometric, septal penetration and scatter, and the detector intrinsic resolution components, is the primary factor that determines the spatial resolution of SPECT images. The design of the collimator is the primary factor determining the resolution-noise tradeoff in the image data and thus is an important determinant of image quality.

The CDR function (CDRF) describes the probability that photons emitted from a point in space will be detected at each point in the detection plane. The CDRF can be decomposed into 4 components that affect the quality of SPECT images. The intrinsic response function (IRF) describes the response of the detector to a perfectly collimated point source; its integral represents the efficiency of the detector. The IRF is determined by the uncertainty in position estimation, which, for a scintillation camera, is due to the statistical variation of the estimated interaction position in the crystal. For such cameras the intrinsic resolution can be well modeled as a Gaussian function and is typically assumed to be invariant across the detector surface.

The other 3 components of the CDRF depend on the collimator characteristics and the photon energy. This includes the geometric (GRF), septal penetration (SPRF) and septal scatter (SSRF) response functions that describe the probabilities that photons emitted from a point are detected after passing through the collimator holes, penetrating the septa, or scattering in the septa, respectively. All of these components are spatially varying. The GRF can be modeled analytically by calculating a distance dependent response function that is typically averaged in the direction parallel to the detector surface. The CDR can be modeled in an iterative reconstruction algorithm (Metz et al 1980, Tsui et al 1988, Zeng and Gullberg 1992). Reconstruction-based compensation has been shown to provide accurate quantitation (Pretorius et al 1998) and improved lesion detection in the context of thoracic Ga-67 citrate SPECT (Gifford et al 2000b). The SPRF and SSRF are difficult to treat analytically and must be modeled using Monte Carlo (MC) simulation techniques. The relative importance of these components largely depends on the collimator parameters and the energy of the incident photons. For example, for a collimator with a relatively small aspect ratio, defined as the ratio of hole length to the hole size, septal scatter and penetration are non-negligible factors and potentially important.

The major goal of this work was to find the optimal combination of collimator and CDR modeling that optimized the tradeoff between efficiency and resolution in the context of myocardial perfusion SPECT. We investigated a family of collimators that spanned a wide range of sensitivity and resolution tradeoffs. We compared three different CDR compensation schemes: modeling the full CDR including the geometric, septal penetration, and septal scatter responses; the geometric response only; and the case when no CDR model was used, i.e. modeling the acquisition as the sum through the activity distributions of strips perpendicular to the detection plane and with widths defined by the projection bin size. For all the cases, other effects such as attenuation, scatter, and energy resolution were modeled. Investigating various levels of CDR compensation is of interest because increasing levels of realism in CDR modeling require additional computational costs. So, clinically, images are often reconstructed with geometric or no CDR compensation. Full CDR compensation is not, to our knowledge, implemented commercially. It is thus interesting to know if the optimal collimator is different depending on the level of approximation in the CDR modeling.

It is important to optimize the resolution-sensitivity tradeoff and compare the different compensation methods for a given imaging task, such as estimation, i.e. quantifying parameters of interest using the given image data (Lau et al 2001, Inoue et al 2004, Moore et al 2005), or classification, i.e. deciding to which class a patient belongs based on an image (Tsui 1978, Tsui et al 1983, Myers et al 1990, Moore et al 1995, 2005, Narayanan et al 2002, Zeng and Gullberg 2002, Gross et al 2003, Zhou and Gindi 2009). In this work, we focused on a binary defect detection task in which an observer was asked to classify a given image as either containing or not containing a defect. Ideally, human observers would be used to evaluate imaging systems. However, they are slow and expensive. To overcome these limitations, model observers have been proposed to optimize imaging systems (Barrett et al 1993). Model observers are mathematical operators, either linear or non-linear, that act on an image to extract some information and return a test statistic or decision variable that is then compared with a decision threshold to decide whether the signal is present or absent. A receiver operating characteristic (ROC) curve is then constructed by calculating the true positive fraction (TPF) and false positive fraction (FPF) pair for each decision threshold. The performance of a specific observer can be characterized by the ROC curve and the area under that curve (AUC) (Metz 1978). We used 2 classes of model observers: the Ideal Observer (IO) and its extension, the Ideal Observer with Model Mismatch (IO-MM) (Ghaly et al 2012, 2013, 2015) operating on projection images, and an anthropomorphic model observer, the Channelized Hotelling Observer (CHO) (Myers and Barrett 1987), to assess the performance of the human observers on reconstructed images.

The IO is a model observer that outperforms all other observers and sets an upper limit on task performance (Barrett and Myers 2004). Because the IO requires full knowledge of the data statistics, it is extremely difficult in practice to apply to reconstructed images. A further limitation of the IO is that, since it has perfect knowledge of the image formation process, including all physical processes and factors that degrade image quality (e.g. finite energy resolution, scatter, attenuation, CDR, etc), its performance reflects the best achievable with perfect compensation. When human observers interpret SPECT images that are reconstructed with imperfect or even no CDR compensation, as is often the case clinically, the optimum reconstruction parameters and ultimate performance may thus differ from those identified by the IO. The IO-MM is an observer that takes into account the mismatch between the true (complete and accurate) model and that used in reconstruction, and it allows optimization of acquisition and instrumentation parameters in the absence or presence of non-ideal compensation methods in the IO framework (Rong et al 2013, Ghaly et al 2015). The CHO (Myers and Barrett 1987) is a model observer that has shown good agreement with human observers in a variety of clinical application and tasks (Yao and Barrett 1992, Wollenweber et al 1999, Gifford et al 2000a, 2005, Frey et al 2002, Farncombe et al 2004, He et al 2004, Oldan et al 2004, Gilland et al 2006). The CHO is typically applied to reconstructed images, and thus, for a fair comparison, requires optimization of reconstruction and regularization parameters (e.g. iteration number and cutoff frequency of post-reconstruction smoothing filters). Thus, optimizing imaging systems in the projection domain using the IO and IO-MM is appealing in part because it avoids the need to select and optimize the reconstruction algorithm and associated compensation methods.

In this work, we evaluated the performance of the IO (which had a perfect model of CDR) and IO-MM (which had either no model or a model of the geometric CDR only). We investigated and compared the optimal collimator for each compensation method. We also compared the performance of the IO and IO-MM to an anthropomorphic model observer (CHO) applied to Ordered-Subset Expectation-Maximization (OS-EM) reconstructed images for the same compensation methods. This was done to validate the utility of the IO and IO-MM for optimizing instrumentation in the projection domain.

2. Methods

2.1. Phantom population and projection data

In this study, we were interested in the task of detecting a fixed signal in a realistic and randomly varying background. To model background variability, including anatomical and tracer uptake variations, we used a realistic digital phantom population, based on the 3D Extended CArdiac Torso (XCAT) phantom, and the corresponding Tc-99m projection database. A full description of the phantom database is given in (Ghaly et al 2014). The population consists of 54 phantoms, including anatomical models for both genders and 3 (small, medium and large) body habitus, subcutaneous adipose tissue thicknesses, and heart sizes.

We simulated anterolateral and inferior perfusion defects with variable extents and severities, as shown in table 1. The extent and severity were defined as the fraction of the left ventricular myocardial volume and reduction of uptake in the perfusion defect relative to the normal myocardium, respectively. The extent and severity of the defect were chosen to be challenging and clinically relevant, and their product was kept constant to model constant reduction of the activity in the myocardium. Figure 1 shows short axis images of hearts with defects in either the anterolateral or inferior wall.

Table 1.

Parameters of the simulated defects.

Defect	Location	Extent (%)	Severity (%)
dI,1	Inferior	5	50
dA,1	Anterolateral	5	50
dI,2	Inferior	10	25
dA,2	Anterolateral	10	25
dI,3	Inferior	25	10
dA,3	Anterolateral	25	10

Figure 1.

Sample short axis images showing hearts with defects present in the anterolateral (top) and inferior (bottom) myocardium with extents of 5%, 10% and 25% from left to right. For illustrative purposes, defects shown have 100% severity.

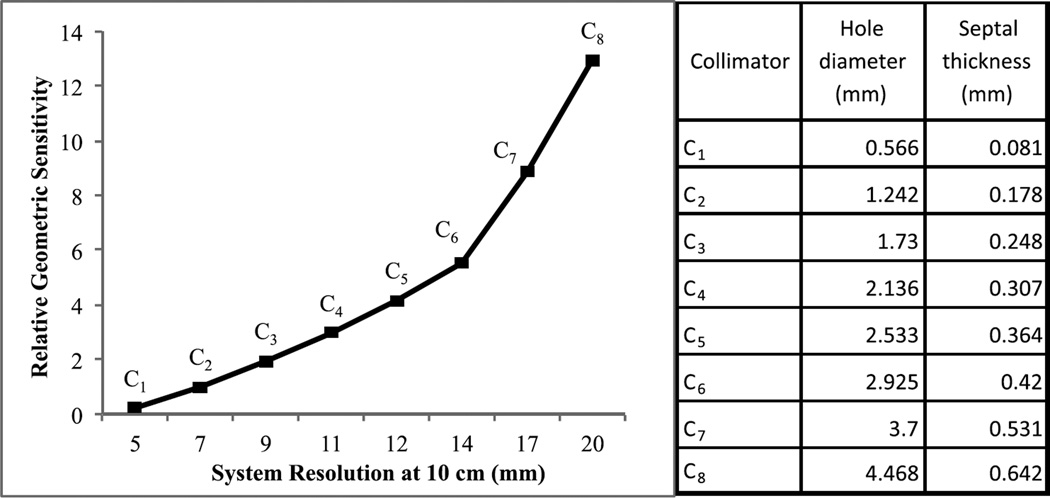
We investigated a family of eight parallel hole collimators, labeled C₁ to C₈, spanning a wide range of sensitivity and resolution tradeoffs, as shown in figure 2. The parameters of collimator C₂ were chosen to match the resolution and sensitivity of the GE-LEHR collimator, a standard collimator commonly used in clinic for MPS imaging. We calculated the collimator parameters for each given resolution using standard formulas (Beck and Redtung 1985, Moore et al 2005). The hole-length was 32 mm for all collimators, which was the hole-length that maximized the sensitivity for a septal penetration criterion of 0.3% at 140 keV. The hole diameter and the septal thickness of the different collimators are reported in figure 2. Figure 3 shows sample noise-free and noisy projection images for the different collimators.

Figure 2.

Plot of the resolution-sensitivity tradeoff for the collimators investigated in this study. The resolution is the total system (geometric + intrinsic) FWHM resolution at 10 cm from the collimator face and the geometric sensitivity is relative to that of the GE-LEHR collimator (C₂). On the right, the corresponding hole diameter and the septal thickness of the different collimators are reported.

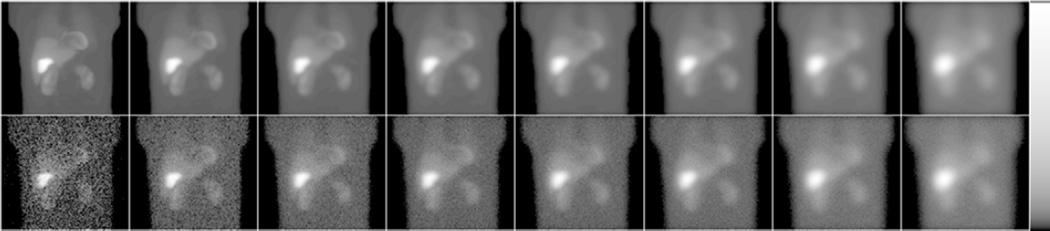
Figure 3.

Noise-free (top) and noisy (bottom) projection images obtained using collimators C₁ to C₈ (from left to right). From left-to-right note the decreasing noise and sharpness of the images, as expected. Images were displayed using a logarithmic map to better show the low activity organs.

To compare the different CDR compensation methods, for each collimator, projections of the phantom population were simulated using an analytical projector that modeled attenuation (A), scatter (S) and the three CDR models. The three models studied were (1) F (full CDR including geometric, septal penetration and septal scatter response components) using pre-calculated CDRF tables obtained from MC simulations (Frey and Tsui 2006, Song et al 2011), (2) G (geometric response) using distant-dependent Gaussian functions and (3) N (no model). We modeled a GE Infinia dual-head SPECT system with a 9.5 mm thick NaI(Tl) crystal and a Gaussian intrinsic resolution with a FWHM of 4.0 mm. We simulated non-circular body-contouring orbits and projections acquired at 60 equispaced angles over a 180° acquisition arc extending from 45° right anterior oblique to 45° left posterior oblique. Projection images were binned in a 128 × 114 matrix with a pixel size of 0.442 cm.

We separately generated noise-free Tc-99m projection data for the heart, liver, and body (including all other organs) for each phantom. This enabled us to separately scale the individual projection images of the different organs using random scale factors obtained from distributions that were based on data from a set of 34 patients who underwent MPS. We could then sum the scaled projections before simulating Poisson noise to generate an uptake realization. In this study, we modeled an injected activity of 10mCi of Tc-99m sestamibi and a total acquisition time of 13 min using a 2-camera system. Figure 4 shows noise-free projection images for the different collimators and the various CDR modeling methods.

Figure 4.

Sample noise-free projection images using the collimators C₁ to C₈ (from left to right) when modeling the full CDR (top), the GRF only (middle) and no CDR modeling (bottom). Images were displayed using a logarithmic map to better show the low activity organs.

2.2. Ideal observer (IO) and ideal observer with model mismatch (IO-MM)

In SPECT, given an object, f, the projection data, g, can be represented by:

$$\mathbf{g}=p_t(\mathbf{f})+\mathbf{n},$$ (1)

where p_t(․) is a projection operator that maps the object f to the projection space and n is the Poisson measurement noise.

For a binary detection task, the two hypotheses to be tested can be written as:

$$H_0:\mathbf{g}={\mathbf{b}}_t+\mathbf{n},$$ (2)

$$H_1:\mathbf{g}={\mathbf{b}}_t+{\mathbf{s}}_t+\mathbf{n},$$ (3)

where H₀ and H₁ are the hypotheses that a signal (i.e. perfusion defect) is absent or present, respectively, and b_t and s_t are the projection images of the background, f_b, and signal, f_s, generated using the operator p_t(․), respectively.

For the IO-MM and a binary decision task, the two hypotheses to be tested can be represented mathematically by:

$${H_0}^{*}:\mathbf{g}={\mathbf{b}}_m+\mathbf{n},$$ (4)

$${H_1}^{*}:\mathbf{g}={\mathbf{b}}_m+{\mathbf{s}}_m+\mathbf{n},$$ (5)

where g was the input projection image generated using (1), and the background and signal projection images, b_m and s_m respectively, were generated using the approximate model, p_m(․).

The IO and IO-MM use the likelihood ratio (LR) of defect-present versus defect-absent as the test statistic. In the standard IO, we tested the hypothesis (H₀ versus H₁) that a signal (i.e. perfusion defect) is absent or present in a random background, where both the signal and the background images were generated using the true model (p_t(․)) of the image formation process. For the IO-MM, we tested the hypothesis ($H_0^{*}$ versus $H_1^{*}$), where the signal and the background images provided to the observer were generated using an approximate model p_m(․). Thus the IO-MM is analogous to reconstruction using an approximate model of the imaging physics.

For each collimator, we computed IO and IO-MM test statistics. The IO had, by definition, a model of all image-degrading factors, so we denoted it as IO-ASF (A and S stand for the inclusion of attenuation and scatter modeling, respectively). The IO-MM had either no model of the CDR (IO-MM-ASN) or a GRF model only (IO-MM-ASG). Following the methodologies adopted in (Kupinski et al 2003, He et al 2008, Ghaly et al 2015), we computed the test statistics using a Markov Chain Monte Carlo (MCMC) method for an ensemble of 6480 pairs of defect-present and defect-absent projection images modeling different anatomical and uptake variations. The projection data were contained within a 64 × 24 pixel region of interest centered over the heart centroid in each of the 60 projection views. This ensured that the whole heart was included inside the volume-of-interest. For each collimator, the IO and IO-MM test statistics were used as inputs to the ROCkit code (Metz et al 1998), which fits a binormal ROC curve to the input data to estimate the AUC value.

2.3. Application of the channelized hotelling observer

We used an anthropomorphic CHO as a surrogate for human observer performance, and compared performance for the various collimators and CDR compensation methods to those obtained from the IO and IO-MM. We performed CHO studies on images reconstructed using the Ordered-Subsets Expectation-Maximization (OS-EM) algorithm for three combinations of compensations: (1) attenuation, scatter and full CDR modeling (CHO-ASF); (2) attenuation, scatter and spatially varying geometric response modeling (CHO-ASG); and (3) attenuation, scatter and no CDR modeling (CHO-ASN). For the CHO-ASF and CHO-ASG compensation methods, images for the first 10 iterations were saved for collimators C₁ to C₅, images for the first 20 iterations were saved for C₆, and images for the first 30 iterations were saved for collimators C₇ and C₈. Higher iterations with methods that included modeling of either the full CDR or the GRF only and lower resolution collimators were saved due to the fact that these reconstructions tend to converge more slowly. For CHO-ASN, we saved the first 10 iterations for all collimators since convergence was rapid. We used twelve subsets with five projections/subset in the OS-EM algorithm. Figure 5 shows sample transaxial slices from images reconstructed using the different CDR compensation methods.

Figure 5.

Sample transaxial images containing the center of mass of the heart centroid for different phantoms and the corresponding attenuation maps (rows 1 and 2). Rows 3 to 5 show the corresponding reconstructed image slices using collimator C₂ and ASF, ASG and ASN compensation methods after 36 updates.

For each collimator and the compensation methods ASG and ASN, we simulated 20 pairs of input projection images per defect per phantom, leading to a total of 6480 pairs of defect-present and defect-absent images. For the ASF compensation method, we limited the number of input projection images to 5 pairs per defect per phantom, leading to a total of 1620 pairs. We chose a smaller number of pairs because of the computational cost associated with incorporating the full CDR model into the reconstruction. For each final number of iterations, images were filtered using a low pass Butterworth filter with order 8 and cutoff frequencies of 0.08, 0.1, 0.12, 0.14, 0.16, 0.2 and 0.24 pixel⁻¹. We then extracted the short axis image containing the center of the defect and applied the CHO. In this study, we used four non-overlapping difference-of-mesa frequency channels (Myers and Barrett 1987, Burgess et al 1997) with successively doubling widths and a starting frequency of 0.5 pixel⁻¹. We used a leave-one-out technique to estimate the test statistics, where the CHO was trained using all images but one and tested using the left-out image, one-by-one for all images. These test statistics were used as inputs to the ROCkit code to estimate the AUC (Metz et al 1998). For each collimator and compensation method, the iteration and cutoff frequency giving the highest AUC were selected as optimal.

3. Results and discussion

3.1. IO and IO-MM studies

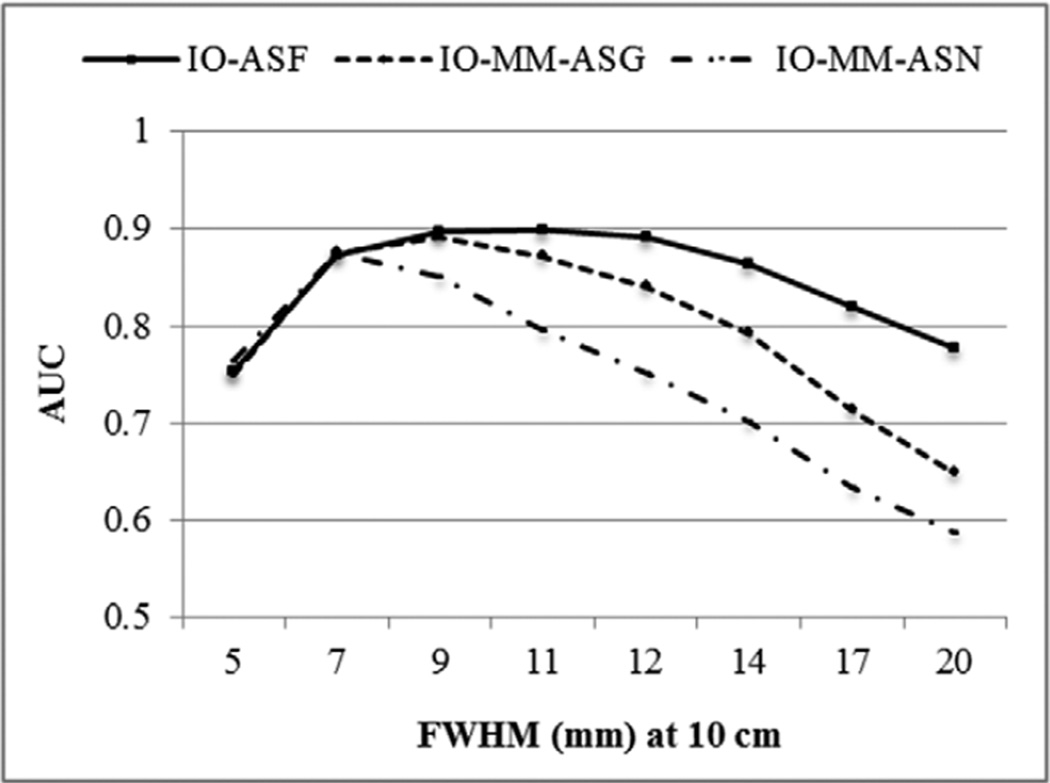
Figure 6 shows a plot of the AUC values for the different collimators of the IO (i.e. the case where the observer used the full CDR model) and the IO-MM, for the cases where CDR was modeled using the GRF only and no model. Note that the error bars were very small (~0.005). The IO, which included the full CDR, suggested that a collimator with a full-width at half-maximum (FWHM) of 9–11 mm (C₃–C₄) at 10 cm was optimal. Collimators with FWHM of 9 mm (C₃) and 7 mm (C₂) were optimal when the observer incorporated an approximate model (GRF only) or when it did not include a model for the CDR, respectively. We also noted that IO-MM observer performance degraded more for higher sensitivity/poorer resolution collimators, due to the progressively increased mismatch between the models incorporated in the IO-MM and the true full CDR model.

Figure 6.

Performances of the IO and IO-MM observers as represented by the AUC for the different collimators and CDR modeling methods.

These results suggest that the closer the model used by the observer to the true model, the higher the observer performance, and the more the optimal collimator shifts toward poorer resolution. This result indicates the primary importance of statistical noise in a detection task. It may be tempting to argue that resolution compensation makes up for poorer resolution more effectively than filtering makes up for poorer sensitivity, but resolution compensation still requires the presence of some signal at high spatial frequencies, so the result is not necessarily intuitively obvious.

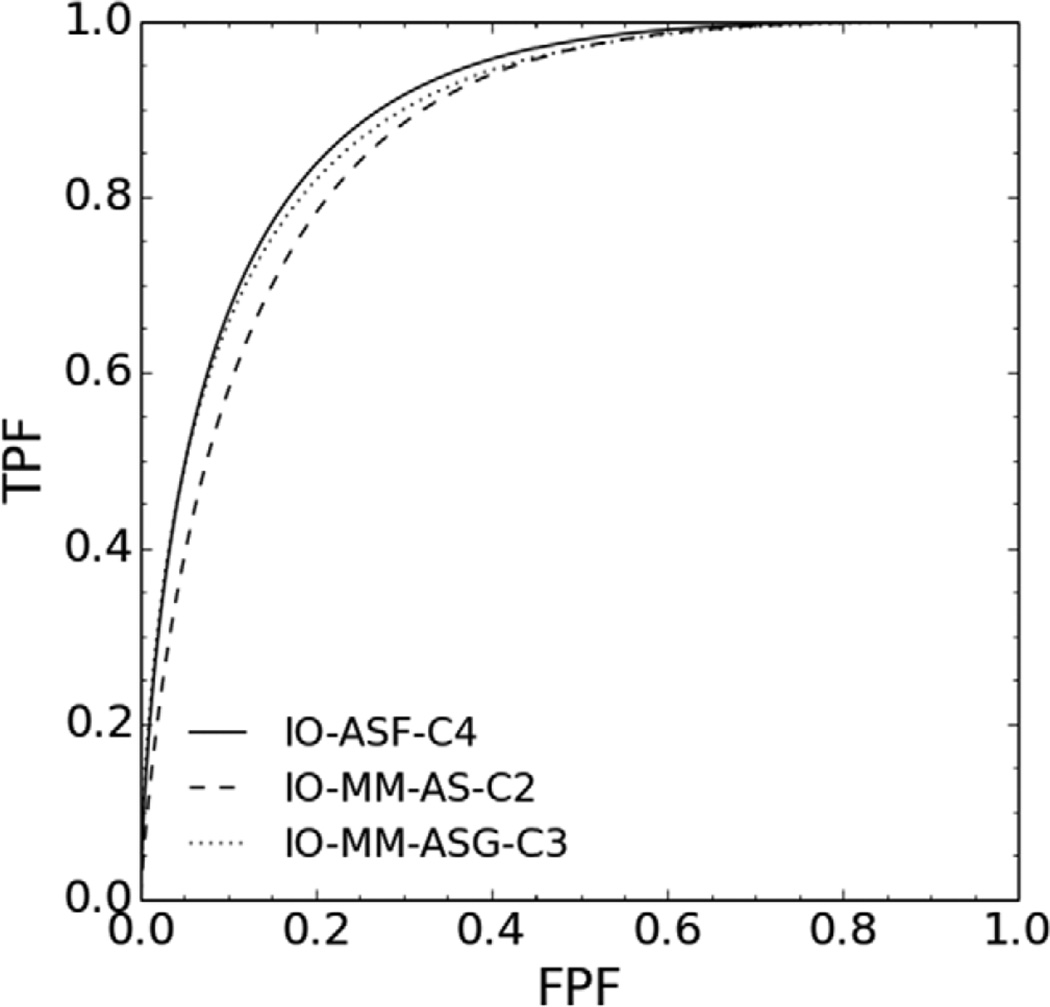
Our results also suggest that it is important to take into account the effects to be modeled (compensated for) in the reconstruction when optimizing the collimator. In other words, these data suggest that simultaneous optimization of the reconstruction/compensation methods and instrumentation produces optimal results. In this regard, we tested the statistical significance of the differences between the AUC value of the IO-ASF, at the optimal collimator (C₄), and the AUC values of the IO-MM-ASG and IO-MM-ASN at the corresponding optimal collimators, C₃ and C₂, respectively, using a 2-sided t-test. The tests indicated that the differences between the AUC values when using the full and the geometric responses were not statistically significant, at a 95% confidence level, with a p-value of 0.34. However, the differences between the AUC values when using full and no CDR modeling were statistically significant, with a p-value less than 10⁻¹⁰. ROC curves for the optimal collimators and the three CDR modeling methods are shown in figure 7. These data suggest that, when using a good model of the CDR, poorer resolution/higher sensitivity collimators than the GE-LEHR collimator were optimal for MPS. This agrees with previous results as reported in (Zhou and Gindi 2009, Zeng and Gullberg 2002, He et al 2008) for different clinical tasks.

Figure 7.

ROC curves for the optimal collimators for three different CDR modeling methods.

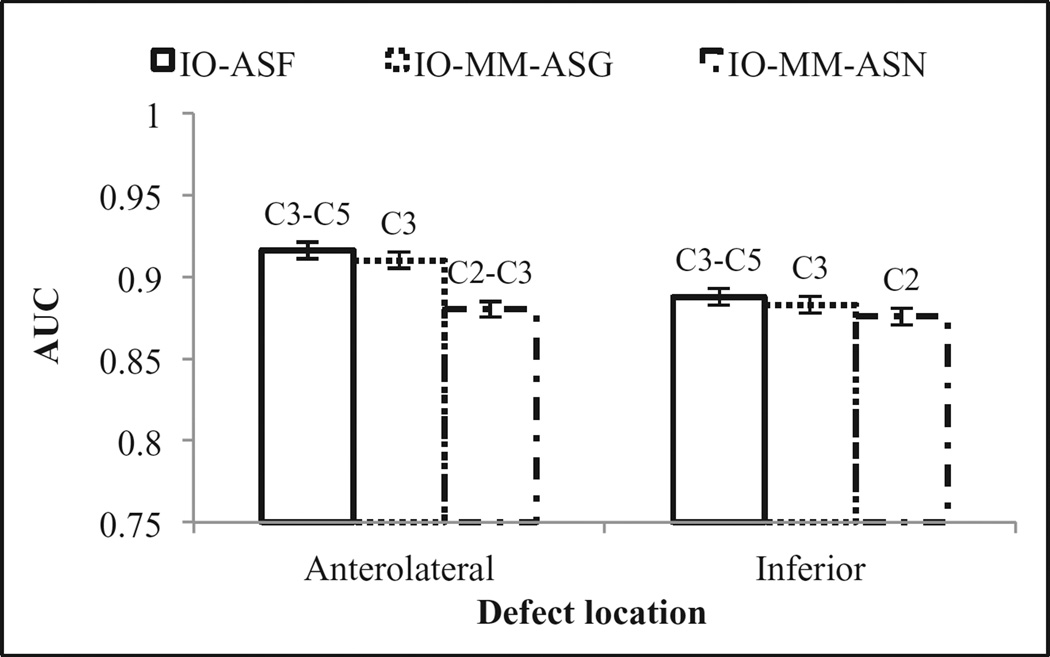
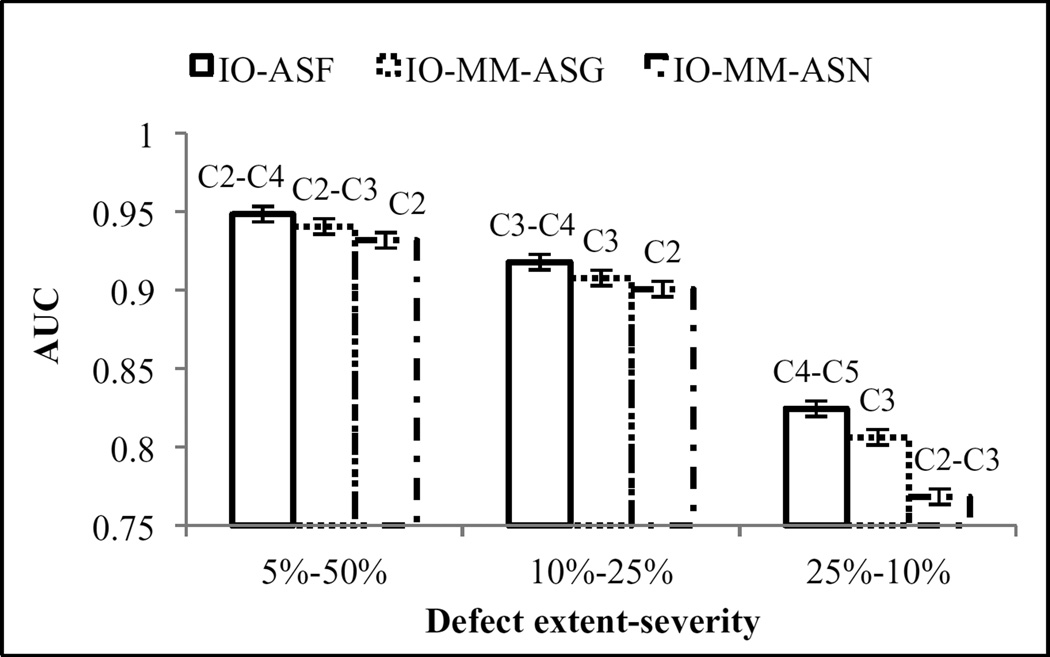
We analyzed observer performance as a function of defect location (figure 8) and extent and severity (figure 9). The observers performed better on detecting the anterolateral defects than on defects located at the inferior wall of the myocardium. This is likely because of the effect of high uptake in the liver, which reduced the visibility of inferior wall defects due to partial volume effects, or greater photon attenuation, resulting in higher noise in the inferior wall. The optimal collimators using the various CDR modeling methods did not change for the different locations. Figure 9, shows that the observers’ performances degraded when the defect severity decreased. We also observed dependence of the optimal collimator on defect size: the optimal collimator shifted toward poorer resolution as the defect size increased. This result is again consistent with an overall finding that noise is a primary factor in detection performance.

Figure 8.

Observers’ performances for the different defect locations.

Figure 9.

Observers’ performances for the different defect extent-severity combinations.

3.2. CHO study

3.2.1. Optimization of reconstruction parameters

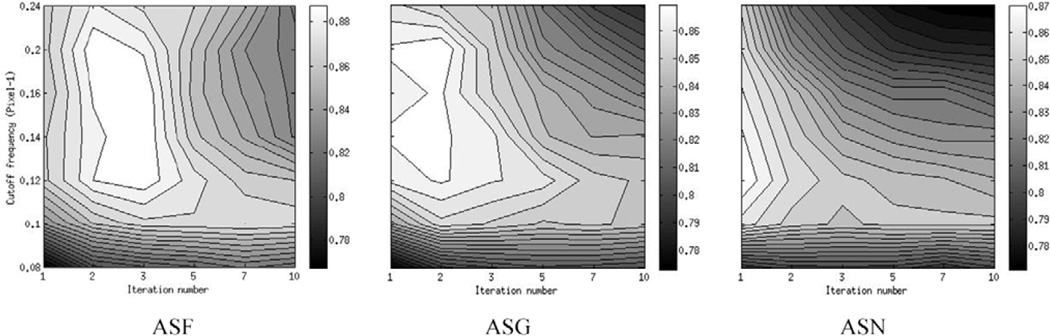
Figure 10 shows 2D contour plots of the AUC values as a function of the iteration number and the Butterworth post-reconstruction filter cutoff frequency for the different compensation methods. The plots correspond to collimators with FWHM of 11 (C₄), 9 (C₃) and 7 mm (C₂) at 10 cm for compensation methods ASF, ASG and ASN, respectively; as will be shown below, these collimators were optimal for each of these methods. Table 2 shows the optimal cutoff frequency and iteration for each collimator and compensation method. Figure 11 shows short axis images reconstructed using the different compensation methods and optimal reconstruction parameters. From the data in table 2, more iterations were required for compensation methods that incorporated CDR compensation. The optimal number of iterations also increased for poorer resolution collimators. We observed that there was a relatively large region of near-optimal cutoff frequencies. This may be due to the fact that there was a range of defect sizes and a different cutoff frequency was optimal for each defect size.

Figure 10.

2D contour plots of the AUC values as a function of the iteration number and the Butterworth filter cutoff frequency for the different compensation methods using the optimal collimators.

Table 2.

Optimal reconstruction parameters for each compensation method.

System FWHM (mm)	ASF		ASG		ASN
	Iteration	Cutoff	Iteration	Cutoff	Iteration	Cutoff
5	1	0.1	1	0.1–0.12	1	0.1
7	1–2	0.12–0.24	1	0.12–0.24	1	0.12–0.14
9	2–3	0.12–0.2	1–2	0.12–0.24	1	0.14–0.16
11	3–5	0.24	2–3	0.14–0.24	1	0.14–0.16
12	7	0.2	2–5	0.14–0.24	1	0.14–0.16
14	12	0.24	3–10	0.12–0.24	1–3	0.14–0.2
17	24–30	0.12–0.24	7–22	0.1–0.24	1–2	0.14–0.2
20	24–30	0.1–0.24	10–30	0.08–0.24	1	0.14–0.24

Figure 11.

Sample short axis of defect-free images corresponding to the optimal reconstruction parameters for collimators C₁ to C₈ (from left to right) reconstructed using compensation methods ASF (top), ASG (middle) and ASN (bottom).

3.2.2. Comparison of compensation methods

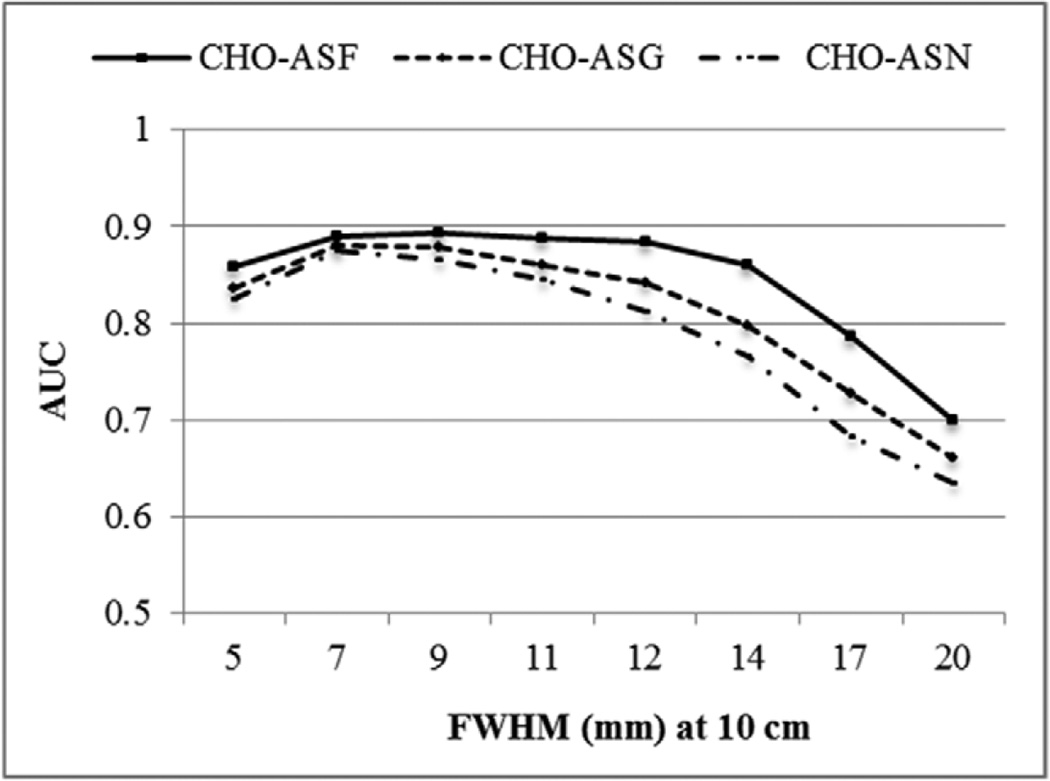
A plot of the AUC for the different collimators and compensation methods is shown in figure 12. Again, as was the case with the IO, the error bars were very small (~0.004). CHO performance for the various compensation methods was very similar to the performance of the IO and IO-MM. The optimal collimator when compensating for the full CDR had a FWHM of 7–11 mm at a distance of 10 cm (C₂–C₄), and the differences between the AUC values of the three collimators were statistically indistinguishable when tested using a 2-sided t-test (i.e. had a p-value > 0.05). As was observed with the IO and IO-MM, approximating the CDR by the GRF or when no model was used, the optimal collimator shifted toward higher resolution.

Figure 12.

Plot of AUC values for the different collimators and CDR compensation methods using optimal reconstruction parameters.

We compared the optimal collimators obtained when using the IO and IO-MM versus the CHO to evaluate the different compensation methods, as shown in table 3. We found that the IO and IO-MM well predicted the optimal resolution range indicated by the CHO for the different compensation methods. However, estimating the IO and IO-MM performance on projection images was faster by factors of ~28, 8 and 2 than estimating the CHO operating on reconstructed images using ASF, ASG and ASN compensations, respectively. The results also suggested that compensating for the geometric response component of the CDR yielded similar performance as full CDR compensation, and there was little benefit from computationally expensive full CDR compensation.

Table 3.

Optimal collimators for the IO, IO-MM and CHO.

	ASF		ASG		ASN
	AUC	Optimal FWHM (mm)	AUC	Optimal FWHM (mm)	AUC	Optimal FWHM (mm)
IO	0.899	9–11	N/A		N/A
IO-MM	N/A		0.892	9	0.875	7
CHO	0.893	7–11	0.886	7–9	0.875	7

4. Conclusions

In this work, we sought the collimator that optimizes the tradeoff between efficiency and resolution and compared various levels of realism of CDR compensation in terms of performance on a defect detection task. The study was performed in the context of myocardial perfusion SPECT using Tc-99m labeled agents using a realistic simulated phantom population with anatomical and uptake variability. We used 2 classes of model observers: the IO and its extension, the IO-MM, operating on projection images, and an anthropomorphic CHO, to assess the performance of the human observers on reconstructed images.

The optimal collimator for the IO, had an FWHM system resolution of 9–11 mm at 10 cm from the collimator face, which is poorer resolution than typical collimators used for MPS and was very similar to the optimal resolution range for the CHO when operating on images reconstructed using full CDR compensation. For projection and image domain observers, the more realistic the CDR modeling incorporated, the poorer the resolution of the optimal collimator. The IO-MM and CHO had the same rankings and gave similar optimal collimators for the different compensation methods. The results also suggested that compensating for the geometric response component of the CDR yielded similar performance as full CDR compensation, and there was little benefit from computationally expensive full CDR compensation.

Finally, based on these results, the IO provides a powerful tool for optimizing instrumentation in the projection domain in cases where good models (i.e. having small mismatch with the true model) of the true image formation process are incorporated into the reconstruction algorithm. The results also indicate that the IO-MM is useful as a surrogate for optimizing acquisition and instrumentation in cases where there is significant model mismatch in the reconstruction methods used to generate images for human observer MPS defect detection.