Neuropsychological Test Selection for Cognitive Impairment Classification: A Machine Learning Approach

Abstract

Introduction

Reducing the amount of testing required to accurately detect cognitive impairment is clinically relevant. The aim of this research was to determine the fewest number of clinical measures required to accurately classify participants as healthy older adult, mild cognitive impairment (MCI) or dementia using a suite of classification techniques.

Methods

Two variable selection machine learning models (i.e., naive Bayes, decision tree), a logistic regression, and two participant datasets (i.e., clinical diagnosis, clinical dementia rating; CDR) were explored. Participants classified using clinical diagnosis criteria included 52 individuals with dementia, 97 with MCI, and 161 cognitively healthy older adults. Participants classified using CDR included 154 individuals CDR = 0, 93 individuals with CDR = 0.5, and 25 individuals with CDR = 1.0+. Twenty-seven demographic, psychological, and neuropsychological variables were available for variable selection.

Results

No significant difference was observed between naive Bayes, decision tree, and logistic regression models for classification of both clinical diagnosis and CDR datasets. Participant classification (70.0 – 99.1%), geometric mean (60.9 – 98.1%), sensitivity (44.2 – 100%), and specificity (52.7 – 100%) were generally satisfactory. Unsurprisingly, the MCI/CDR = 0.5 participant group was the most challenging to classify. Through variable selection only 2 – 9 variables were required for classification and varied between datasets in a clinically meaningful way.

Conclusions

The current study results reveal that machine learning techniques can accurately classifying cognitive impairment and reduce the number of measures required for diagnosis.

Introduction

Classification of cognitive impairment is challenging. This challenge is particularly true at the early, mild cognitive impairment (MCI) stage. Early detection of cognitive impairment is clinically valuable as treatment interventions are most beneficial when started prior to significant decline (Gauthier, 2002). Diagnosis of cognitive impairment is time intensive, requires evaluation of multiple pieces of information (e.g., neuropsychological and laboratory test results, neuroimaging, collateral report, and historical data), and accuracy and efficiency are governed by level of practitioner expertise. The present study explores the utility of employing a suite of classification techniques, including machine learning (e.g., naive Bayes, decision tree) and traditional statistical (logistic regression) applications, to reduce the number of measures required to correctly classify degree of cognitive impairment in older adult populations.

Machine learning models were originally designed to analyze large, complex medical datasets (Kononenko, 2001). Machine learning algorithms have been used to detect coronary artery disease (Kukar, Kononenko, & Groselj, 2011), classify liver malfunctioning (Breiman, 2001), and select genes for cancer detection (Cho & Won, 2003; Wang et al., 2005). It has been argued that machine learning algorithms can produce reliable information about the relationships between input and response variables in ways that are unique, but not necessarily superior, to traditional statistical approaches (Breiman, 2001). For example, while traditional statistics relies on a stochastic system, machine learning algorithms presume that the underlying mechanism(s) of data generation are either unknown or inconsequential (Breiman, 2001). Because few assumptions are made about the data, algorithms carefully learn the relationships between input variables (e.g., test scores) and response variables (e.g., clinical diagnosis). Once pertinent relationships have been learned, and an algorithm established, the algorithm is applied to an independent set of participant scores. A prediction of how to classify the individual can then be derived based on their test scores.

After classification predictions have been made, cross validation can be used to determine the validity and generalizability of the learned model to a new, but similar in terms of selection criteria, sample of data. This approach is similar to the goodness-of-fit tests, significance testing of model parameters, and residual examination for model assessment under a traditional statistical framework. Because the machine learning model optimizes the model parameters to fit the training data, it is important that an independent sample is used to validate the model. If the model fits the training data better than the independent sample the model is considered to be overfit, and generalization to similar, new sample data is unlikely. Model overfit is particularly likely to occur if the training data set is small, or there are too many model variables.

All statistical and modeling techniques have advantages and disadvantages based on their capabilities, the dataset in question, and purpose of analysis (Caruana & Niculescu-Mizil, 2006 & Entezari-Maleki, Rezaei, & Minaei-Bidgolo, 2009). For example, traditional statistical models require more manual user input, whereas machine learning models take a black-box approach with limited user interface. As a result, traditional statistical methods are flexible, easily used, and lend themselves to clinically meaningful interpretations to a greater extent than machine learning approaches (Cox & Snell, 1989). Although user input can be incredibly valuable, automaticity provided by machine learning models also holds great benefits. For example, machine learning methods can automatically apply variable scaling (Lemsky et al., 1996). If impairment on one cognitive measure carries more weight in favor of a particular diagnosis relative to another measure, the model will automatically adjust the algorithm to account for this relationship without any user manipulation. This automatic adjustment is useful when the magnitude or direction of the relationship is unknown or challenging to estimate. Machine learning models can also manage data in its raw form, unlike traditional statistic methods that require removal of outlying data and imputation of missing data (Magoulas & Prentz, 2001).

Machine learning approaches have been utilized in dementia research (e.g., Datta, Shankle, & Pazzani, 1996; Lemsky, Smith, Malec, & Ivnik, 1996; Magnin et al., 2009; Shankle, Mani, Dick, & Pazzani, 1998). For example, Shankle and colleagues (1998) evaluated the relative accuracy of two machine learning models for classification of Clinical Dementia Rating (CDR; Morris, 1993) scores using variables from demographic and neuropsychological data. The interrater reliability of the CDR is approximately 80.0% (80.0%, Burke et al., 1988; 75.0%, McCulla et al., 1989; 83.0%, Morris, 1997). Results from the Shankle et al. study showed that the models correctly classified CDR scores with 69.0 – 76.0% accuracy. Additional studies have classified cognitively healthy controls and MCI or dementia as separate learning problems. For example, Datta and colleagues (1996) correctly differentiated individuals with dementia from healthy older adults on neuropsychological test scores with 84.0% accuracy. In a related study, MCI and cognitively healthy groups were correctly identified with 83.0 – 88.0% accuracy using scores from a functional ability questionnaire (Shankle, Mani, Pazzani, & Smyth, 1997).

Unlike traditional statistical approaches, machine learning models generally do not produce a simple and understandable picture of the relationship between input and response variables (Breiman, 2001). Furthermore, as data becomes more complex, the algorithms become more cumbersome and time intensive. One approach that balances dimensionality with interpretability is variable selection (or elimination). According to Saeys, Inza, and Larranaga (2007), there are four advantages to variable selection: avoid data over-fit, improve classification accuracy, provide faster and more cost-effective models, and gain deeper insight into the underlying processes that generate the data. Variable reduction is also of clinical relevance. More specifically, reduction of evaluation cost and time may be realized if a few select variables of known diagnostic importance can be reliably identified. Automated wrapper-based algorithms are commonly used in tandem with machine learning models for variable selection. Because the wrapper approach interacts with the classification model, all variable subsets can be explored until an optimal subset is discovered, taking relationships and dependencies between variables into account (see Saeys et al., 2007 for a review of variable selection techniques). As a result, only the most important variables required for classification are isolated and balance between model complexity and interpretability is realized. An improvement in classification accuracy over a model that uses all variables is also generally realized (Zadeh, 1973). Unlike other reduction techniques (e.g., principal components analysis; Abdi & Williams, 2010), variable selection does not alter the original representation of the input variables. It simply selects a subset of the original input variables; thus, offering the advantage of interpretation by variable domain (Saeys et al., 2007).

Variable reduction can also be applied to traditional statistical approaches, and is generally applied manually, resulting in both advantages and disadvantages. More specifically, manual selection allows the researcher to include/exclude variables based on clinical relevance and importance. Therefore, the researcher, not the classification algorithm, is ultimately responsible for the evolution and evaluation of the model. This manual process, however, is time intensive and may fail to be fully exhaustive, potentially excluding important relationships. Mechanical stepwise forward selection and backward elimination approaches are also available in most statistical packages; however, they have received much criticism because they often yield irrelevant or noise variables (Flack & Chang, 1987; Griffiths & Pope, 1987).

In this paper, we compare multiple classification models to determine the fewest number of clinical measures (i.e., input variables) required to accurately diagnose participants according to degree of cognitive impairment. Classification models are among the strongest techniques for this type of problem. Therefore, two machine learning algorithms that mimic diagnostic decision making (i.e., decision tree, naive Bayes) and a traditional statistical technique (i.e., logistic regression) with variable selection are utilized to determine the best and smallest combination of neuropsychological, psychiatric, functional, and demographic data necessary to classify cognitive impairment with a high degree of accuracy.

In the machine learning/computer science literature, it is common practice to evaluate multiple classification techniques simultaneously. Validity can be improved when overlapping results occur from independent algorithms, especially when little prior knowledge of data relationships is known. In addition to evaluating multiple machine learning techniques, we also include a more traditional statistical comparison to assist the reader in understanding and evaluating alternative approaches. It should be noted that the goal of this paper is not to determine the best classification measure. Rather, the goal is to provide credence across approaches regarding the accuracy and validity of reported results. Including multiple methods also provides a backdrop to discuss relative strengths and weaknesses across the models.

In a similar vein to utilizing multiple classification approaches, two datasets with identical input variables are used to determine the degree of variable selection and model accuracy convergence. The “clinical diagnosis” dataset is comprised of participants falling within one of three diagnostic classes: neurologically healthy, MCI, and dementia. Because some of the data provided as input variables to the machine learning models were used (along with collateral information) for clinical diagnosis, analogous CDR scores (i.e., CDR = 0, 0.5, 1+) are used to independently classify individuals according to degree of cognitive impairment. Including two data sets will allow us to make judgments regarding the strength of the algorithms independent of a priori knowledge. Given this relationship, clinical diagnosis models are expected to have higher accuracy rates than CDR models. The most challenging class to identify is hypothesized to be MCI as it lays on a spectrum between healthy aging and dementia. To learn more about the variables that are important in defining each participant group, separate binary variable selection models (e.g., CDR = 0 vs. 0.5; 0.5 vs. 1+) are closely examined. Significant differences are not expected to occur between the machine learning and statistical models. Rather, they are expected to provide converging results with similar levels of accuracy. A secondary goal of the paper is to showcase the functionality of machine learning to assess problems unique to neuropsychology.

Method

Participants

Participants classified using clinical diagnosic criteria were 52 individuals with possible or probable dementia (22 female, 30 male), 97 individuals with MCI (54 female, 43 male) and 161 cognitively healthy older adult participants (119 female, 42 male). Descriptive data are presented in Table 1.

Table 1.

Clinical diagnosis sample demographics

	Control (n = 161)		MCI (n = 97)		Dementia (n = 53)		p
Variable or test	Mean	SD	Mean	SD	Mean	SD
Age (years)	71.14	8.47	71.96	9.43	75.73ab	8.33	.005
Education (years)	16.28	2.83	15.52	2.93	15.31	3.01	.036
% Female	74	-	57		45	-	<.001
TICS	34.85	2.25	32.46a	2.94	24.38ab	5.88	<.001

Note: Scores are raw scores unless otherwise listed. AD = Alzheimer's disease; MCI = mild cognitive impairment; TICS = Telephone Interview for Cognitive Status.

^adiffered significantly from control group;

^bdiffered significantly from MCI group.

Participants classified using CDR were 154 individuals (109 females, 45 males) receiving a CDR of 0 (no dementia), 93 individuals (54 females, 39 males) had a CDR of 0.5 (very mild dementia), and 25 individuals (8 females, 17 males) had a CDR of 1 (mild dementia) or 2 (moderate dementia). Descriptive data are presented in Table 2. CDRs of 1 and 2 were combined as only 8 participants fell within the CDR = 2 category. This group is referred to as CDR = 1+. Furthermore, we are more interested in defining a lack of cognitive impairment, impairment lying between healthy aging and dementia, and impairment meeting the threshold of dementia than the degree of dementia severity.

Table 2.

Clinical Dementia Rating sample demographics

	CDR = 0 (n = 154)		CDR = 0.5 (n = 93)		CDR = 1+ (n = 25)		p
Variable or test	Mean	SD	Mean	SD	Mean	SD
Age (years)	70.06	9.39	71.84	9.40	74.04	7.97	.084
Education (years)	16.13	2.86	15.52	2.79	16.12	2.89	.251
% Female	71	-	58		32	-	<.001
TICS	34.66	2.38	32.40a	3.36	23.92ab	4.84	<.001

Note: Scores are raw scores unless otherwise listed; CDR = Clinical Dementia Rating scale; TICS = Telephone Interview for Cognitive Status.

^adiffered significantly from CDR = 0 group;

^bdiffered significantly from CDR = 0.5 group.

All participants were tested voluntarily as part of two larger studies at Washington State University (see Schmitter-Edgecombe, Woo, & Greeley, 2009; Schmitter-Edgecombe, Parsey, & Cook, 2011). Both studies were reviewed and approved by Washington State University Institutional Review Board. Participants were recruited through advertisements, community health and wellness fairs, physician and agency referrals, and from past studies. Initial screening of potential participants was conducted over the phone. Participant exclusion criteria included history of significant head trauma, current or recent (past year) psychoactive substance abuse, history of cerebrovascular accidents, and known medical, neurological, or psychiatric causes of cognitive dysfunction. Participants who met initial screening criteria completed a 3 hour battery of standardized and experimental neuropsychological tests. Each participant appointed a knowledgeable informant (e.g., spouse, adult child) who, along with the participant, completed a CDR, which was administered by a CDR certified examiner. All participants were given a report reviewing their performance on the neuropsychological tests as compensation for their time.

Interview, testing, and collateral medical information were carefully evaluated by two neuropsychologists to determine clinical criteria for MCI or dementia. Inclusion criteria for MCI were consistent with the diagnostic criteria defined by Petersen and colleagues (Petersen et al., 2001; Petersen & Morris, 2005) and by the National Institute on Aging-Alzheimer's Association workgroup (Albert et al., 2011) and included the following: (a) self or knowledgeable informant report of subjective memory impairment for at least 6 months; (b) objective evidence of impairment (< 1.5 standard deviations below appropriate norms) in one or more cognitive domains; (c) preserved general cognitive functions as confirmed by a score of 27 or above on the Telephone Interview of Cognitive Status (TICS; Brandt & Folstein, 2003); (d) no significant impact of cognitive deficits on the participant's daily activities, as confirmed, in most cases, by a total CDR score of no greater than 0.5; (e) non-fulfillment of the Diagnostic and Statistical Manual of Mental Disorders, Fourth Edition, Text Revision(DSM-IV-TR) criteria for dementia (American Psychiatric Association, 2000); and (f) absence of severe depression as confirmed by a score ≤ 10 on the 15 item Geriatric Depression Scale (GDS; Yesavage et al., 1983). Participants were considered to have dementia if they met research criteria of the National Institute of Neurological and Communicative Disorders and Stroke and the Alzheimer's disease and Related Disorders Association (NINCDS–ADRDA; McKhann et al., 1984) and were free of severe depression. Participants classified as cognitively healthy older adults met the following criteria: (a) no self or informant reported history of cognitive changes; (b) a CDR of 0; (c) score on the TICS within normal limits; and (d) absence of severe depression.

Datasets

Two independent dataset were used. The clinical diagnosis dataset included control, MCI, and dementia as response variables. The CDR dataset included class labels of 0 (no dementia; proxy for control), 0.5 (very mild dementia; proxy for MCI), and 1+ (mild-moderate dementia; proxy for dementia). The same variables detailed below were used with both datasets.

Variables

Prior to variable selection, 27 variables were available to the models (see Table 3). Variables were limited by the assessment battery as well as test overlap between the two research studies. Different functional ability and memory measures were used in the two studies. Therefore, these scores were converted to standard scores to facilitate cross-study comparisons. Variables fell within the following domains: demographics (age, education, gender), psychological functioning as measured by level of depression (GDS), global cognitive status (TICS), attention and speeded processing (Symbol Digit Modalities Test, oral and written subtests; Smith, 1991; Trail Making Test, Part A; Reitan, 1958), verbal learning and memory (Rey Auditory Verbal Learning Test; Schmidt, 1996; or the Memory Assessment Scales; Williams, 1991), visual learning and memory (7/24; Barbizet & Cany, 1968; or the Brief Visual Memory Test; Benedict, 1997), executive functioning (Trail Making Test, Part B; Reitan, 1958, Clox 1; Royall, Cordes, & Polk, 1998; Design Fluency subtest of Delis-Kaplan Executive Functioning System [D-KEFS]; Delis, Kaplan, & Kramer, 2001), working memory (WAIS-III Letter-Number Span and Sequencing; Wechsler, 1997), language (D-KEFS Verbal Fluency subtest; Delis et al., 2001), object naming (Boston Naming Test; Kaplan, Goodglass, & Weintraub, 1983), word knowledge (Shipley Institute of Living Scale; Zachary, 1991), visuospatial/constructional ability (Clox 2; Royall et al., 1998), and functional ability (Instrumental Activities of Daily Living - Compensatory Aids; Schmitter-Edgecombe, Parsey, & Lamb 2014; Lawton IADL; Lawton & Brody, 1969).

Table 3.

Full variable list

Cognitive Domains	Neuropsychological Test
Global Cognitive Status	Telephone Interview for Cognitive Status (TICS)
Language	Boston Naming Test (BNT)
	Shipley Vocabulary Test
	Category Fluency
Executive Functioning	Letter Fluency
	Category Switching
	Design Fluency – Solid Dots
	Design Fluency – Open Dots
	Design Fluency – Switching
	Clox 1
	Trails B
Memory	Verbal Memory – Immediate
	Verbal Memory – Short Delay
	Verbal Memory – Long Delay
	Visual Memory – Long Delay
	Visual Memory – Total Score
Attention	Symbol Digit Modality – Written
	Symbol Digit Modality – Oral
	Trails A
Working Memory	Letter-Number Sequencing
	Letter-Number Span
Visuospatial/Constructional Ability	Clox 2
Demographic Factors	Age
	Education
	Gender
Functional Ability	Instrumental Activities of Daily Living (IADL)
Depression	Geriatric Depression Scale (GDS)

Variable values were missing with a frequency of 2 – 4% across the datasets. Missing variable values were not imputed.

Machine Learning Models

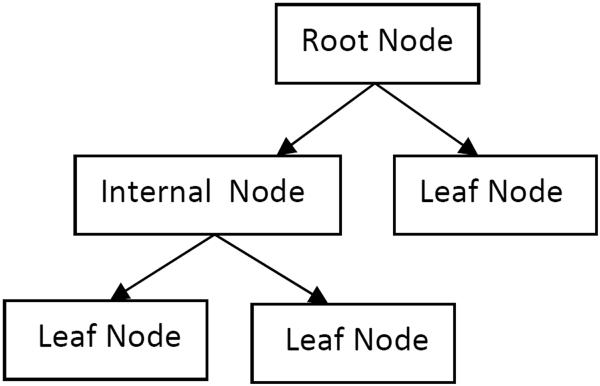
Machine learning algorithms were implemented in Python using Orange (Curk et al., 2005). Discretization was performed to transform continuous data to discrete data. A C4.5 algorithm (Quinlan, 1993) was used to generate a decision tree. This decision tree utilizes if/then rules to successively partition input variables into branch-like segments until predefined stopping criteria are met. These segments form an inverted tree that originates with a root node at the top of the tree (see Figure 1). Once an input variable is defined as the root node, it is split on some boundary (e.g., age > 60) and two branch segments are defined below it. The new segments may either be additional internal (decision) or leaf (terminal) nodes based on the if/then condition. A new input variable is called, defining the internal node that is furtherer split into two additional branch segments. A leaf node represents the outcome or response variable (e.g., dementia). Branching and splitting of internal nodes continue recursively until only leaf nodes remain. To validate a decision tree developed from training data, a new set of data is provided and the participants classified based on how they are segmented within the tree. In comparison to logistic regressions, decision tree models have previously been found to achieve comparable predictive accuracy (Lemon, Roy, Clark, Friedmann, & Rakowski, 2003; Salmon et al., 2002; Tsien, Fraser, Long, & Kennedy, 1998).

Figure 1.

Decision Tree Example

To establish credibility of machine learning operations a second model, naive Bayes, was employed. Naive Bayes is a probabilistic classifier relying on Bayes theorem which can account for prior knowledge of class affiliation and further assumptions about the data to lead to accurate classifications. It also presumes that each input variable independently contributes to the probability of observing a given response variable (hence the moniker “Naive”). Naive Bayes is used across many disciplines, even in cases where the assumption of conditional independence is known to be violated, given that it often performs with high accuracy regardless of this assumption (Fraser et al., 2014). The naive Bayes classifier is trained by first estimating two quantities known as the prior and likelihood. The prior defines the probability that a given response variable (i.e., 0, 0.5, 1+) occurs in the population. The likelihood defines the probability of observing the input variables given that a participant belongs to a particular diagnostic class. Training samples are used by naive Bayes to determine the relationship between input variables and diagnostic class (and is embedded in the likelihood probabilities). Determining the class of a new participant involves plugging the scores of the new participant into the likelihood function and multiplying this by the prior probabilities. The resulting products are known as posterior probabilities. The new participant is assigned to the class (e.g., 1+) showing the largest posterior probability.

In addition to reducing the dimensionality of the learning problem, variable selection can play a valuable role in determining which measures are the most critical to a classification decision. A “wrapper-based” variable selection approach was utilized. In this approach the variable subset search is “wrapped around” the learning algorithm (i.e., decision tree, naive Bayes; Gütlein, Frank, Hall, & Karwath, 2009), allowing it to exam all variable subsets until an optimal subset is found. Our wrapper method proceeded as follows: a variable subset size is defined and all combinations of variables of that subset size are generated. For example, a subset size fixed at four variables requires that 17,550 combinations of variables are evaluated given 27 available total variables. Models are next evaluated using each combination and their relative performance (accuracy) assessed. The model showing the highest accuracy is retained as the global optimum. To reduce the size of the wrapper's search domain, the subset size was incrementally increased from 2 variables until only a 2% improvement in accuracy over the accuracy of the best model in the previous subset size was no longer realized. This cut-off rule for variable subset size was selected as it balances clinical time (i.e., number of tests needed to administer) with model precision.

Models were evaluated using all 3 classification groups (e.g., CDR = 0, 0.5, 1+) in addition to two-group only (binary) classifications (e.g., CDR = 0/1+, 0/0.5, 0/1+). Breaking the ternary problem down into a binary problem allows us to determine how well the models can classify each participant group in comparison to the other two. A comparative continuous regression approach was also utilized to assess the feasibility of using machine learning to assess cognition on a continuum.

Model Validation

For each model, 80.0% of participant data was used to train the model. Participant classification (validation) was representative of the full (trained) model. For example, there was an equal representation of participants in each diagnostic class (e.g., CDR score) in the training sample (80% total participants) as in the testing sample (20% total participants). During the training phase, the models learned to associate input variables with provided response variable targets (i.e., clinical diagnosis, CDR). Five-fold cross-validation was performed to validate and strengthen the model. In five-fold cross-validation, the original 80% sample was partitioned into five equal size subsamples with proportional participant representation (Geisser, 1993). During the training phase a subsample was held out as the validation data for testing the model. The cross-validation process was then repeated 4 more times, each time with a different subsample held out. The results from each training and validation procedure were then averaged to create one model of the data. Cross-validation was followed by an independent test with the remaining 20% of participant data that was not used during the training phase. During the testing phase, the trained models are blind to the response variable for each data point and forced to predict the target response variable based on assumptions made during the training phase.

Model performance was assessed based on four primary criteria: (1) accuracy, (2) sensitivity, (3) specificity, and (4) geometric-mean. The accuracy of each model defines the percentage of participants correctly classified during the final 20% testing phase. Although the purpose of this paper is not to determine whether one machine learning model outperforms the other, 95% confidence intervals around accuracy are presented as a means for comparison and a measure of reliability. Sensitivity is the true positive rate defined as the proportion of true positives to true positives and false negatives. Specificity is the true negative rate defined as the proportion of true negatives to false negatives and true negatives. Geometric mean is the square root of the product of sensitivity and specificity. Geometric mean balances classification performance when the sample includes more participants in one group than another. For example, if 90 out of 100 participants had no cognitive impairment, 5 had MCI, and 5 had dementia, an accuracy of 90.0% could be reached by only classifying participants without cognitive impairment correctly. Although imbalance naturally occurs between individuals with a disorder and those without it, imbalance amongst participant groups in research studies may not readily reflect reality. As a result, algorithmic imbalance may lead to artificially inflated results and results that do not directly generalize to populations with differing prevalence rates. When group imbalance may be an issue, geometric mean can be used to achieve a more equitable view of the available data by giving equal weight to both false positives and false negatives; thereby, deriving a more balanced view of model performance (Kubat & Matwin, 1997). The geometric mean, of course, does not preclude the potential for false negatives or false positives, and should be carefully examined in combination with sensitivity and specificity and understood within the context of data that is not available to the models.

Inter-rater reliability of the CDR is approximately 80.0% (Burke et al., 1988; McCulla et al., 1989; Morris, 1997), therefore, model accuracy that is 80.0% or above is considered to be an adequate comparison. Geometric mean will be considered satisfactory if it is also above 80.0%. For clinical diagnosis, sensitivity is 80.9% – 90.0% and specificity is 44.0% –98.0% (Cahn et al., 1995; Swearer, O'Donnell, Kane, Hoople, & Lavoie, 1998; Wilder et al., 1995). Thus, performance of the models will show clinical relevance if sensitivity and specificity are within these ranges. Because the control/CDR = 0 groups are composed of more participants than the other groups it is expected that participants will be more frequently placed in the control group based on size alone (Provost & Fawcett, 2013). Note, that this relationship was only true for decision tree given that naive Bayes incorporates group size directly in the estimation of prior probabilities. A majority vote classifier is often used as a baseline, in which every individual is assigned to the class that has the most participants in the training set (Provost & Fawcett, 2013). The models are also anticipated to perform above random chance. For our data the calculated majority prediction was 51.8% and 56.6% for clinical diagnosis and CDR, respectively. If decision tree models perform above these estimates they are considered to be performing above chance.

Statistical Analysis

Multi and binomial logistic regression was performed in Statistical Package for Social Sciences version 21 (SPSS; IBM, 2012). Logistic regression attempts to model the boundary between continuous valued functions and estimates the posterior probability of some event occurring as a linear function (Entezari-Maleki at al., 2009; Fraser, 2014). Because the SPSS implementation of logistic regressions cannot handle missing values, the mean variable values for each diagnostic/CDR group were manually imputed prior to analysis. Participants with outlier performance 3 standard deviations above or below the mean were removed. For the clinical diagnosis dataset 16 dementia, 6 MCI, and 6 older adult participants were removed, leaving 37 dementia, 91 MCI, and 155 older adult participants for analysis. For the CDR dataset 9 participants with CDR = 1+, 7 with CDR = 0.5, and 8 with a CDR = 0 were removed, leaving 16 participants with CDR =1+, 86 with CDR = 0.5, and 145 CDR = 0 participants for analysis.

Good model fit criteria for the multinomial logistic regressions was defined as a non-significant (p > .05) goodness of fit Pearson chi-square and a significant (p < .05) likelihood ratio test. A non-significant (p > .05) Hosmer and Lemeshow chi-square test of goodness of fit and a significant (p < .05) Omnibus test of model coefficients were used to test the overall fit of the binary logistic regressions. A significance level of p = .05 and standard errors below 2.0 were set for the model's regression coefficients.

Manual variable selection was followed as outlined by Homesmer and Lemeshow (2000) with additional measures taken to ensure model stability and fit. Variable selection began with a careful analysis of each variable. More specifically, a univariate logistic regression model was fit to obtain the estimated coefficient, estimated standard error, likelihood ratio test, and univariable Wald statistic. Any variable whose univariable test resulted in p < .25 was added to the multivariate model, along with variables of known clinical importance (e.g., memory measures). Significance level was set to p < .25 for this step based on previous work suggesting that the traditional level (p < .05) often fails to identify variables of known importance (Mickey & Greenland, 1989). Following the fit of the multivariable model, the importance of each variable was examined to determine if it should be retained. Variables with non-significant (p < .05) Wald statistics and likelihood ratio tests were removed and the model re-ran. Variables were then reduced one at a time until a 2% improvement in accuracy over the previous model was no longer achieved. Any variable of known importance that was previously deleted was added back into the model to verify that all essential variables were either included or ruled out. Once the preliminary working model was established multicolinearity was examined to determine if any variables were highly correlated (r ≥ .70). Multicolinearity was not found to be an issue. Preliminary models were further validated by means of non-parametric bootstrapping. Two thousand bootstrap samples produced percentile based confidence intervals for each regression coefficient in the model. A large deviation from the normal, standard confidence interval estimates would suggest that the model included excessive noise and, therefore, made the regression coefficients unreliable and ungeneralizable (Tierney, Yao, Kiss, & McDowell, 2005). These variables were removed and the model and bootstrap process repeated until only variables significantly and reliably contributing to a well fit model were included.

Results

Learning Curve

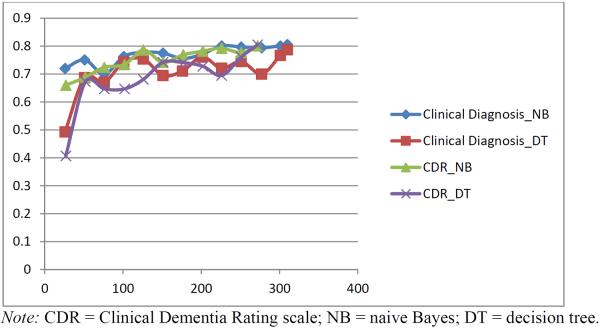
A learning curve was performed to verify that a sufficient number of participants were available to run the models. To develop the learning curve, participants were sampled in increments of 25 (e.g., 25, 50, 75). To keep data partitioning consistent, each subset had the same participant distribution as the original sample. For example, if the participant breakdown of the original sample is 55% cognitively healthy older adults, 30% MCI, and 15% dementia, the reduced sample size of 25 participants would have 14 health older adults, 8 MCI, and 4 dementia participants. To maintain the ratio of each participant group reflected in the full model, participants were rounded up, resulting in numbers slightly over the desired curve spot. Results from our learning curve showed that both CDR and clinical diagnosis naive Bayes models plateau at approximately 200 participants (See Figure 2). The results suggest that our sample of 272 and 311 participants, respectively, is sufficient to achieve model stability. Decision tree models, on the other hand, still exhibited performance fluctuations at this level, suggesting that additional participants might result in a leveling out or improvement in model performance.

Figure 2.

Learning Curve

Model Performance

Prior to variable selection, all 27 variables were used to classify participants to determine base accuracy levels. Accuracy ranged from 66.2 – 79.7% and sensitivity and specificity ranged from 46.5 – 88.8% and 69.8 – 96.1%, respectively, for the machine learning models. Logistic regression models with all 27 variables resulted in an unstable over fit of the data and are, therefore, not reported.

Clinical Diagnosis

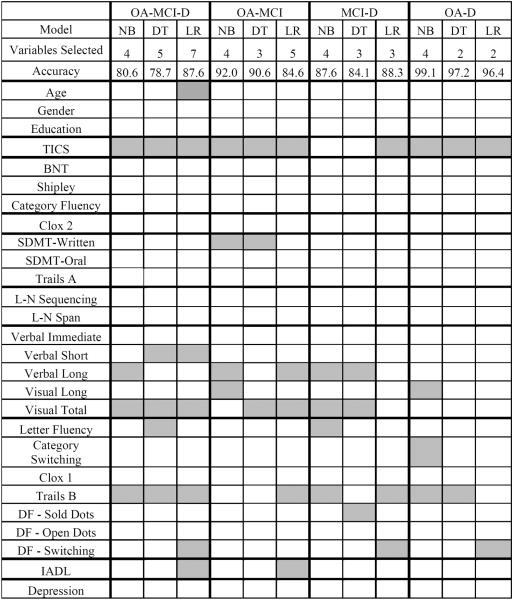
Table 4 presents the classification accuracy, confidence interval, geometric mean, sensitivity, and specificity for clinical diagnosis variable selection models. Using all three diagnostic categories (i.e., neurologically normal older adult, MCI, dementia) accuracy was 80.6% for naive Bayes, 78.7% for decision tree, and 87.6% for logistic regression. The confidence intervals suggest that the logistic regression classifies slightly better than decision tree. Overlapping confidence intervals indicate no statistical differences between naive Bayes and decision tree and logistic regression models. Slight variation between models is not uncommon given noise and model differences (Roderick & Rubin, 2002).

Table 4.

Clinical diagnosis machine learningmodel performance

Naive Bayes	OA	MCI	D	OA	MCI	MCI	D	OA	D
Accuracy	80.6%			92.0%		87.6%		99.1%
CI	76.2 – 85.0%			89.0 – 95.0%		73.9 – 91.3%		97.9 – 100%
G-mean	90.0%	79.3%	87.2%	88.9%	88.9%	85.4%	85.4%	98.1%	98.1%
Sensitivity	85.3%	60.7%	91.3%	80.8%	97.9%	78.4%	93.2%	96.2%	100.0%
Specificity	96.5%	90.1%	79.8%	97.9%	80.8%	93.2%	78.4%	100.0%	96.2%
Decision Tree	OA	MCI	D	OA	MCI	MCI	D	OA	D
Accuracy	78.7%			90.6%		84.1%		97.2%
CI	74.1 – 83.26%			87.1 – 94.1%		76.6 – 85.37%		94.1 – 98.33
G-mean	88.6%	72.6%	82.3%	86.2%	86.2%	81.5%	81.5%	95.5%	95.5%
Sensitivity	80.8%	58.8%	90.1%	75.0%	99.0%	73.2%	90.7%	92.3%	98.8%
Specificity	97.3%	89.7%	75.2%	99.0%	75.0%	90.7%	73.2%	98.8%	92.3%
Logistic Regression	OA	MCI	D	OA	MCI	MCI	D	OA	D
Accuracy	87.6%			84.6%		88.3%		96.4%
CI	83.9 – 90.7%			80.6 – 88.6%		84.7 – 91.9%		94.3 – 98.5%
G-mean	90.7%	82.9%	95.4%	81.8%	81.8%	83.9%	83.9%	93.5%	93.5%
Sensitivity	93.5%	80.2%	93.5%	91.0%	73.6%	93.4%	75.7%	98.1%	89.2%
Specificity	88.0%	92.1%	97.3%	73.6%	91.0%	75.7%	93.4%	89.2%	98.1%

Note: OA = older adult; MCI = mild cognitive impairment; D = dementia; CI = confidence interval; G-mean = geometric mean.

The geometric mean is at an acceptable level for classifying neurologically normal older adults and individuals with dementia (82.3 – 95.4%). As predicted, classification of MCI participants was the most challenging for the models. Although specificity for MCI was satisfactory (89.7 – 97.3%), sensitivity was below the acceptable rate (58.8 – 60.7%) for naive Bayes and decision tree, but was adequate for logistic regression (80.2%). The ternary classification problem was divided into three binary models to determine which groups are most challenging to differentiate between. Accuracy above 80.0% was realized for all binary problems. Differentiation of MCI and the other participant groups, again, appeared be the most challenging based on accuracy and geometric mean between the models (see Table 4). Expectedly, neurologically normal adults and dementia participants were the easiest binary group to classify with accuracy, geometric mean, sensitivity, and specificity all above 89.2%. Overlapping confidence intervals were observed for all models.

CDR

Table 5 presents the classification accuracy, confidence interval, geometric mean, sensitivity, and specificity for CDR models. Using all three diagnostic categories (i.e., neurologically normal older adult, MCI, dementia) accuracy was above 80.0% for both machine learning models. Accuracy for logistic regression, however, was 70.0%. This finding is in contrast to the logistic regression performance with clinical diagnosis, where it was found to have the highest level of accuracy. This finding may reflect the smaller and more group imbalanced CDR sample, with the CDR = 1+ group comprised of only 16 participants. Given a larger and/or more balanced sample we would likely expect to see similar results to the clinical diagnosis regression analysis.

Table 5.

CDR machine learning model performance

Naive Bayes	0	0.5	1+	0	0.5	0.5	1+	0	1+
Accuracy	80.1%			81.8%		94.0%		98.3%
CI	75.36 – 84.84%			77.2 – 86.4%		91.2 – 96.8%		96.8 – 99.8%
G-mean	81.5%	74.2%	74.2%	77.1%	77.1%	84.9%	84.9%	93.8%	93.8%
Sensitivity	92.2%	61.3%	76.0%	92.2%	64.5%	100.0%	72.0%	100%	88.0%
Specificity	72.0%	89.9%	98.8%	64.5%	92.2%	72.0%	100%	88.0%	100%
Decision Tree	0	0.5	1+	0	0.5	0.5	1+	0	1+
Accuracy	80.5%			81.0%		94.1%		97.7%
CI	75.79 – 85.2%			76.3 – 85.7%		91.3–96.9%		95.9– 99.5%
G-Mean	79.9%	73.4%	89.1%	75.8%	75.8%	94.1%	94.1%	95.6%	95.6%
Sensitivity	94.2%	58.1%	80.0%	92.2%	62.4%	94.6%	92.0%	100%	84.0%
Specificity	67.8%	92.7%	99.2%	62.4%	92.2%	92.0%	94.6%	84.0%	100%
Logistic Regression	0	0.5	1+	0	0.5	0.5	1+	0	1+
Accuracy	70.0%			71.9%		91.2%		98.8%
CI	64.6 – 75.5%			66.6 – 77.2%		87.8 – 94.6%		97.5 – 100.0%
G-Mean	67.1%	60.9%	81.9%	65.6%	65.6%	81.2%	81.2%	96.5%	96.5%
Sensitivity	85.5%	44.2%	68.8%	84.1%	51.2%	95.8%	68.8%	99.3%	93.8%
Specificity	52.7%	83.9%	97.6%	51.2%	84.1%	68.8%	95.8%	93.8%	99.3%

Note: CI = confidence interval; G-mean = geometric mean.

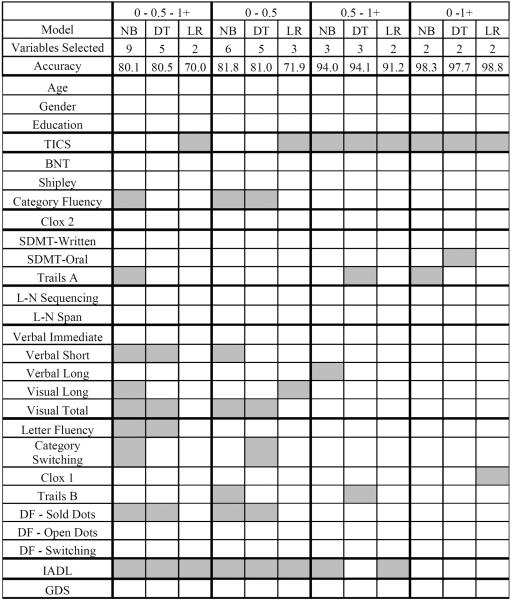
Overlapping confidence intervals indicate there is no significant difference between the models, with the exception of logistic regression and decision tree models. The geometric mean ranged from (67.1 – 89.1%). Although naive Bayes classified CDR = 0 with the highest geometric mean, decision tree and logistic regression were better able to classify CDR = 1+. Accuracy for distinguishing between binary groups was above 80.0% in all instances, with the exception of differentiation of CDR = 0 - 0.5 with logistic regression (71.9%). Geometric mean was within an acceptable range (81.2–96.5%) for CDR = 0.5 - 1+ and CDR = 0 – 1+, but lower for CDR = 0 - 0.5 (65.6 – 75.8%).

Similar to difficulty classifying MCI with clinical diagnosis models, the poorest classification was for CDR = 0.5. However, unlike clinical diagnosis models, which generally found MCI and dementia to be the most challenging binary problem, CDR models showed poorer accuracy distinguishing CDR = 0 from CDR = 0.5 (81.0 – 81.8%). This finding may be due to differences in participant presentation at the point of distinction between these categories in particular. More specifically, CDR = 0.5 is defined as “questionable dementia.” Participants falling within this category are varied; some may continue on a path toward dementia, while others may develop a different disorder or revert back to normal. On the other hand, the clinical diagnosis of MCI is on a continuum with dementia. Given the difficulty in defining the dividing line between categories it is not surprising that the models had more difficulty differentiating between no dementia (CDR = 0) and questionable dementia (CDR = 0.5) for the CDR dataset and MCI and dementia for the clinical diagnosis dataset.

Clinically, individuals with cognitive impairment are diagnosed as meeting criteria for a particular disorder (e.g., MCI, dementia). However, cognitive impairment truly exists along a continuum, rather than distinct and mutually exclusive states. When cognitive impairment was examined on a continuum using a regression tree similar results were generally found (accuracy between 72.8 – 80.5%; geometric mean between 60.8 – 89.1%).

Variable Selection

Clinical Diagnosis

When all three diagnostic categories (cognitively normal, MCI, dementia) were taken into consideration, models required between four and seven variables to classify participants with a high degree of accuracy (see Table 6). Selected variables fell within three cognitive domains: global cognitive status, memory, and executive functioning. The logistic regression also drew upon functional ability and age to make classification decisions. Given the challenge of classifying MCI it is of interest to determine whether selected cognitive domains differ between binary classification groups. Between two and five variables were used to identify binary participant groups. Cognitive domains selected as important for classifying neurologically normal older adults and dementia and for classifying MCI and dementia were similar to the ternary model: global cognitive status, memory, and executive functioning. Classification of neurologically normal older adults and MCI, however, did not rely as heavily on executive functioning tasks and incorporated attentional abilities.

Table 6.

Clinical DiagnosisVariable Selection

Note:OA = older adult; MCI = mild cognitive impairment; D = dementia;NB = naive Bayes; DT = decision tree; LR = logistic regression; TICS = Telephone Interview for Cognitive Status; BNT = Boston Naming Test; SDMT = Symbol Digit Modality Test; L-N = letter-number; DF = Design Fluency; IADL = instrumental activities of daily living.

CDR

When variables were selected to classify all three CDR groups, between two and nine variables were chosen. Selected variables fell broadly within domains representing language, attention, memory, executive functioning, and functional ability. These domains closely represent the five categories assessed on the CDR: memory, orientation, judgment/problem solving, community affairs, home/hobbies, and personal care. Classification of CDR = 0 and 0.5 required between three and six variables from the following cognitive domains: language, memory, executive functioning, daily functioning, and global cognitive status. Classification of CDR = 0.5 and 1+ utilized two to three variables and spanned similar cognitive domains, with the exception of language. Just two variables comprising global cognitive status and attention/executive functioning were necessary to correctly classify CDR 0 and 1+.

Discussion

Classification techniques offer opportunities to assist and enhance the work of clinical experts. Improved efficiency and quality of care are the expected results of adopting a more diverse set of tools in understanding neuropsychological and medical data. The present research illustrates one application of classification methods that can be used as an example for future work in this area. In this study, naive Bayes, decision tree, and logistic regression algorithms were selected to classify participants as having no cognitive impairment, mild impairment, or dementia based on their resemblance to clinically-based diagnostic decision-making. We examined two datasets: clinical diagnosis (no cognitive impairment, MCI, dementia) and CDR scores (0, 0.5, 1+).

Machine learning and statistical models were tasked with determining the fewest of 27 variables required to predict, with a high degree of accuracy, which diagnostic category/CDR score the participant belonged to given their performance on a subset of selected variables. Results suggest that naive Bayes and decision tree models are successful, and comparable to a logistic regression, at classifying participants with accuracy greatly exceeding chance occurrence. Sensitivity, specificity, and geometric mean were generally satisfactory, with the exception of participant groups representing mild impairment (i.e., MCI, CDR = 0.5). Prior studies have also shown that classifying MCI is challenging given that it lies on a continuum between healthy aging and dementia (e.g., Nasreddine et al., 2005). In comparison to the ternary classification problem, binary classification, unsurprisingly, resulted in improved accuracy across all comparisons.

Overall, variable selection resulted in an improvement in classification accuracy over machine learning models that used all 27 variables to classify participants. This finding suggests that machine learning models can benefit from variable reduction, which is also useful clinically. The improvement in model performance was likely due to the removal of noisy and/or redundant variables and lessening the likelihood of model overfit. Of note, the logistic regression model was found to be unstable when all of the variables were entered. The recommended number of participants required per participant ranges from 10 (Hosmer & Lemeshow; Peduzzi et al., 1996) to 30 (Pedhazur, 1997). Our small sample size in the dementia/CDR = 1+ participant group may have contributed to this imbalance.

Marginal (0.3 – 0.6 points) or no significant difference was observed between the three models for both clinical diagnosis and CDR data sets based on 95% confidence intervals for accuracy. This information provides credence to each models' ability to learn and make associations within and between the data despite utilizing distinct approaches. Within the computer science/machine learning literature it is common to examine more than one learning approach. If similar results are found between methods, the reliability and generalizability of the findings to a new, similar dataset are enhanced. This approach is comparable to the method of converging operations utilized within neuropsychology (Banich & Compton, 2010). The findings support the notion that the models complement each other and no claims of superiority of one method over the other are to be made. Based on the results it appears that logistic regression does well with a large sample size (> 250) and a minority class (e.g., dementia) that is greater than 10% of the overall sample. Strengths of this method include prediction of MCI participants with adequate sensitivity and specificity. Therefore, it may be particularly useful for ternary problems when there is a large sample size with adequate group distribution.

Similar to other traditional statistical approaches, logistic regression requires a complete data set with no missing data and careful examination and removal of outlying cases. Removal of incomplete data may become particularly problematic when a limited sample size already exists, as was our case. A relative strength of machine learning techniques is that they do not require complete datasets and examination of outlying cases is not necessary. In our prior work, we found that some models even performed better when values are missing compared to when they are imputed (Williams, Weakley, Cook, Schmitter-Edgecombe, 2013). The ability of machine learning models to provide diagnostic information in the presence of missing values may be of particular benefit in clinical settings as it is not uncommon to have missing data (e.g., unable to return for testing, invalid administration, too impaired to complete). Examining missing data alone or using the quantity or character of the missing values as an input variable itself is an intriguing area of future study.

One drawback to machine learning models is that they tend to rely on a black-box approach, with limited researcher input. An interesting future study would be a comparison between automated variable selection and clinician's hand selected measures based on clinical relevance, literature, and experience. Assessing variables selected by cognitive domain provides interpretable information regarding how models learn variable associations when making classification decisions. Overlapping cognitive domains selected by the models suggest that variables tapping a given cognitive ability are important to distinguishing between diagnostic classes. For example, when models were tasked with differentiating between all three clinical diagnoses (no cognitive impairment, MCI, dementia) all ternary machine learning models selected variables from global cognitive status, memory, and executive functioning domains. This finding suggests that measures representing these cognitive constructs may be most important for detecting cognitive decline. Neurologically normal older adults were defined from individuals with dementia using these same three cognitive domains. However, distinctions between MCI and no cognitive impairment revealed that variables measuring global cognitive impairment, memory, and attention were required to achieve prediction accuracy above 85.0%. Executive functioning and memory were the primary cognitive domains needed to differentiate MCI from dementia, suggesting that declines in executive functioning may become more prominent with advancing cognitive impairment, a finding that is common within the literature (Farias, Mungas, Reed, Harvey, & DeCarli, 2009; Grundman et al., 2004).

Variables selected for the ternary CDR model (i.e., CDR = 0, 0.5, 1+) largely reflect the subscores that comprise the CDR: personal care (daily functioning), home and hobbies (daily functioning), community affairs (language), judgment and problem solving (executive functioning), orientation (attention), and memory (memory). The same domains were largely involved in separating CDR = 0 and CDR = 0.5. Distinguishing CDR = 0.5 from CDR = 1+ predominately depended on global cognitive status and functional ability; though attention, memory, and executive functioning may also be valuable differentiation measures. CDR = 0 vs.CDR = 1+ predominately required global cognitive status and attention domains. Similar to clinical diagnosis models, CDR models did not rely on age, education, gender, or depression to classify cognitive impairment. This finding suggests that performance on neuropsychological tasks is paramount for classifying level of cognitive impairment and not greatly influenced by demographic or psychological factors. In addition, neither the clinical diagnosis nor CDR models relied on the visuospatial or working memory cognitive domains.

In comparison to the variable reduction approach utilized with logistic regression, machine learning variable selection is automated. Although both are time intensive, the machine learning approach can run in the background on its own, while the logistic regression requires manual manipulation which may become problematic when dealing with more than thirty variables. There is also the risk of missing clinically relevant combinations of variables with the manual approach, whereas, the machine learning approach considers and reports each possible combination. Of note, mechanical stepwise forward selection and backward elimination were explored with logistic regression. Unexpectedly, no variables were eliminated, even though the regression clearly overfit the results based on examination of coefficient standard error scores greater than two. These results support the notion that stepwise methods are not adequate variable selection techniques. Best subsets approach, which operates similarly to the wrapper-based approach, is an automated alternative that may also be employed in the future.

While the machine learning methods we utilized are driven by the data and do not ascribe directly to a clinical rationale for selecting variables. This data-driven approach is quite significant considering that the machine learning algorithms identified clinically relevant predictor variables. Furthermore, they did so without any collateral information that is generally available to clinicians (e.g., age, education, family history, medical history, lab/scan results). This result provides validation not only for the use of machine learning models to inform diagnostic decisions but also for our clinical knowledge. Given that similar results were found across three different classification techniques, two datasets with three groups each, and with clinically relevant measures we can confidently say that the models are consistent and clinically reliable. However, the results found here may not directly generalize to different populations (e.g., inpatient settings, specialist referral centers). Future research may focus on important populations and variables of known significance. If the best subset of variables from a broader dataset made up of neuropsychological assessment scores, imaging results, knowledgeable informant report, medical history, behavioral observations and other information generally available to clinicians could be examined the implication of classification techniques may be tremendous.

It is well known that neuropsychological tasks are not process pure. Just one task can tap executive functioning, attention, and processing speed abilities. In this study we grouped tasks into cognitive domains based on the literature (Spreen & Strauss, 1998). To determine if the measures selected underscore particular cognitive constructs, prospective research utilizing a variable selection technique might explore proxy or substitute variables. For example, if a model selects Trails B, an assessment of executive functioning, will another executive functioning measure be selected if Trails B is removed from the dataset? This is an exciting question for future research and can be taken in a number of novel directions.

Classification of diagnostic status is just one example of how machine learning techniques can benefit the field of clinical neuropsychology. More recently, researchers are beginning to utilize machine learning to differentiate between older adults with neurodegenerative disorders using extracted narrative speech (Fraser et al., 2014; Orimaye, Wong, and Golden, 2014). Our group has also utilized machine learning techniques and sensor technology to assess everyday functional ability and cognitive health of older adults (Cook & Schmitter-Edgecombe, 2009; Dawadi, Cook, Schmitter-Edgecombe, & Parsey, 2013; Rashidi, Cook, Holder, & Schmitter-Edgecombe, 2011).

One of the most notable drawbacks of some machine learning techniques is the requirement for large sample sizes. In the current example, naive Bayes required as few as 225 participants in our sample (according to a learning curve); but our decision tree may have benefitted from additional participants. When extreme class imbalance is present, machine learning models may experience difficulty successfully learning the smallest class resulting in fewer accurate classifications. Sampling techniques to improve model optimization may be of interest to manage class imbalance issues. Having a large number of variables for the models to explore is also important. Our example was limited by tests that were available to serve as variables. Including additional variables such as collateral information (e.g., knowledgeable information report, lab results) into the model is of relevance and could result in an improvement of model performance.

Machine learning algorithms applied to clinical data is not a new line of inquiry. Yet, few studies have explored the use of automated learning methods within the neuropsychological literature. The current study results revealed that machine learning techniques can accurately classifying cognitive impairment and complement traditional statistical techniques. CDR classification reproduced clinical diagnosis model results, indicating that these results are likely generalizable to other, similar datasets. Furthermore, our machine learning models yielded strong accuracy even with missing values. This finding has significant clinical implications given how commonplace it is for individuals to have incomplete assessment data, especially when substantial cognitive impairment is present and longitudinal data is being collected. The study also highlights the prudence of reducing the full array of variables to those showing relevance to the classification problem. Not only can this method enhance diagnostic differentiation of cognitive impairment, it can also reduce the cost and time required for accurate diagnosis.

With more information becoming available in digital format, clinicians have the unique opportunity to take advantage of automated classification techniques. Clinical experts may not definitively know how to formulate methods to solve certain complex problems, especially those involving large data sets. Evaluation of stored data through machine learning techniques has the potential of unearthing hidden trends and patterns thereby enhancing our understanding of disease detection, progression, prognosis, and management. In the future, clinicians may be able to rapidly screen clients suspected of cognitive impairment. Rapid screening may improve the detection rate relative to current methods of diagnosis that are both time and cost intensive. We hope this primer and illustrative example of machine learning in clinical neuropsychological practice has sparked interest in this method of research.

Table 7.

CDR Variable Selection

Note: NB = naive Bayes; DT = decision tree; LR = logistic regression; TICS = Telephone Interview for Cognitive Status; BNT = Boston Naming Test; SDMT = Symbol Digit Modality Test; L-N = letter-number; DF = Design Fluency; IADL = instrumental activities of daily living; GDS = Geriatric Depression Scale.