Bayesian Group Sequential Clinical Trial Design using Total Toxicity Burden and Progression-Free Survival

Abstract

Delivering radiation to eradicate a solid tumor while minimizing damage to nearby critical organs remains a challenge. For esophageal cancer, radiation therapy may damage the heart or lungs, and several qualitatively different, possibly recurrent toxicities associated with chemoradiation or surgery may occur, each at two or more possible grades. In this article, we describe a Bayesian group sequential clinical trial design, based on total toxicity burden (TTB) and progression-free survival duration, for comparing two radiation therapy modalities for esophageal cancer. Each patient’s toxicities are modeled as a multivariate doubly stochastic Poisson point process, with marks identifying toxicity grades. Each grade of each type of toxicity is assigned a severity weight, elicited from clinical oncologists familiar with the disease and treatments. TTB is defined as a severity-weighted sum over the different toxicities that may occur up to 12 months from the start of treatment. Latent frailties are used to formulate a multivariate model for all outcomes. Group sequential decision rules are based on posterior mean TTB and progression-free survival time. The proposed design is shown to provide both larger power and smaller mean sample size when compared to a conventional bivariate group sequential design.

1 Introduction

Esophageal cancer affects over 17,000 people per year in the United States, with five-year survival rates between 20% and 35%. Standard of care is neoadjuvant chemoradiation, consisting of radiation therapy (RT) and concurrent chemotherapy, possibly followed by surgery. The decision of whether surgery may be performed is made adaptively based on early chemoradiation outcomes. Since the esophagus is nestled between critical organs, dosimetric RT planning is challenging. An ideal RT plan delivers sufficient dose to the tumor while minimizing or avoiding radiation exposure to the heart anteriorly, the spinal cord posteriorly, and the lungs on either side.

One recently developed X-ray modality, intensity modulated radiation therapy (IMRT), uses a computer-controlled multi-leaf collimator to partially block the paths of five beams of charged high energy photons. The approach enables flexibility for controlling the extent of radiation intensity over the irradiated volume, and thereby has the potential to effectively irradiate the targeted tumor volume, while limiting radiation exposure to critical organs surrounding the tumor. However, because X-ray beams deposit energy along a path that passes through the targeted volume and beyond, IMRT is incapable of sparing healthy tissues located directly behind the tumor. Another modality, proton beam therapy (PBT), delivers radiation using a beam of charged protons that have been accelerated through a cyclotron to high energy levels. Unlike photons, protons have a limited range and can be modulated to deposit their maximum intensity at the tumor site, thus sparing the surrounding organs. For example, Zhang et al. (2008) have demonstrated that PBT results in better sparing of the lung compared to IMRT.

In this article, we describe a design that is being used to conduct a randomized, group sequential clinical trial for comparing radiation modalities for stage II-III esophageal cancer (The University of Texas MD Anderson Cancer Center, 2015). The purpose of this trial is to determine whether PBT’s dosimetric advantages over IMRT translate into meaningful improvements in clinical outcomes, primarily reduced toxicity and prolonged progression-free survival (PFS), defined as the time to disease progression or recurrence, or death, from the start of RT. Patients with esophageal cancer undergoing this regime, called “trimodality therapy,” are at risk of several qualitatively different toxicities. These may occur at random times and at varying levels of severity, and some may occur more than once. Toxicities not only impact the patient’s quality of life, but also may decrease the patient’s ability to undergo surgery and thus increase the risk of disease recurrence. The surgeon’s decison of whether a patient may undergo surgery includes consideration of toxicities that have occurred with the chemoradiation. Patients who do receive surgery are at risk of postoperative complications (POCs), which may be exacerbated by earlier toxicities from the chemoradiation. Although each particular toxicity is unlikely, all are potentially life threatening, necessitating a design with rules that terminate the trial early if the interim data show that the trimodality regime is safer with one RT modality versus the other. Moreover, while the risk of toxicity often dominates thinking about RT modalities, delaying disease recurrence/progression and thereby prolonging survival remains the therapeutic goal.

The main statistical challenge in designing a trial to compare RT modalities used with the chemoradiation ± surgery trimodality regime is that the clinical outcomes are very complex. To measure the combined impact of the diverse array of possible toxicities, we define a statistic, total toxicity burden (TTB), which provides a continuous measure of the combined effect of all toxicities experienced by the patient over the course of follow up. To construct this statistic, numerical weights of each possible grade of each toxicity that quantify their relative severities first must be elicited from the physicians planning the trial. TTB is defined as a severity-weighted sum over the different toxicities that may occur. Since some toxicities may occur up to 12 months from the start of treatment, each patient’s observed TTB is a process that may change over time.

Our trial design treats TTB and PFS as co-primary endpoints. It relies on a multivariate Bayesian model that accounts for the incidence and severity of each type of toxicity, and accounts for dependence between the toxicity vector, an indicator of whether surgery is performed, and PFS. A key feature of the model is that it provides an analytically tractable expression for mean TTB. The two RT modalities are compared using two group sequential rules, based on the posterior distributions of mean TTB and PFS log hazard ratio, respectively.

Including a vector of qualitatively different toxicities via TTB in this way is very different from most randomized oncology trials, which are based on PFS or survival, while including toxicities as secondary outcomes. In most trials, toxicity is monitored informally. When formal decision rules based on toxicity are used, they are defined by first reducing the vector of toxicities to a binary indicator of the worst toxicity of any type occurring at or above a given grade, ignoring recurrences entirely. As a basis for comparison, we consider a trial with two sets of conventional group sequential rules with O’Brien-Fleming (O’Brien and Fleming, 1979) boundaries, one based on PFS and the other based on an indicator of any toxicity occurring within one year of follow up. Our simulations, given in Section 5, show that our design yields as much as a 66% increase in power and 18% reduction in mean sample size when compared to this conventional design.

The general problem of designing clinical trials to compare multiple endpoints has been considered by many authors, predominately using frequentist approaches for testing composite hypotheses, and relying on large-sample normal approximations. O’Brien (1984) considered a generalized linear least squares statistic for composite alternatives that characterizes treatment differences among multiple endpoints using a common multiplier. Tang et al. (1989a) proposed an approximate likelihood ratio test for multiple treatment effects over all possible directions, with application to group sequential design (Tang et al., 1989b). Tang et al. (1993) provided group sequential critical values for designs based on several types of frequentist multiple hypothesis testing procedures. Other authors have considered two-stage and multi-stage designs for monitoring toxicity and response rates in single-arm trials where both endpoints are binary and observed shortly after treatment (Bryant and Day, 1995; Conaway and Petroni, 1995). Quality-adjusted time without symptoms and toxicity (Q-TWiST) methods were developed to incorporate health-related quality of life measures into analysis of time-to-failure endpoints (Gelber et al., 1995). Kosorok et al. (2004) provided a group sequential design for multiple primary endpoints with multiple decision rules that control overall type I error and probabilities of concluding incorrect alternatives. O’Neill (2008) discussed challenges in evaluating the risk versus benefit of new therapies in clinical trial design and analysis.

The ideas in this article are presented in the following sequence. In Section 2, we define TTB for the esophageal RT trial. The group sequential design is presented in Section 3. In Section 4, we present the probability model, derive mean TTB, and discuss prior specification and elicitation. In Section 5, we present results of a simulation study. Section 6 describes our process and rationale in constructing the model and design for this study, and provides general guidelines for practitioners who may wish to use TTB.

2 Total Toxicity Burden

Table 1 presents the 11 toxicities monitored in the RT trial. Each toxicity is either possibly recurrent at random times over the patient’s follow up period, or is a POC evaluated once, approximately one week after surgery. Radiation-induced pulmonary and cardiovascular toxicities may occur up to 12 months following RT, and thus require long-term follow-up (Abid et al., 2001; Rancati et al., 2003; Yusuf et al., 2011). Each of the first three possibly recurrent toxicities, pericardial effusion, pleural effusion, and pneumonitis, and the POC anastomotic leak, is ordinal with three severity levels. Each of the remaining seven toxicities has one severity level. The set of severity weights used in the trial are given in Table 1, with a higher weight corresponding to greater severity. The numerical value of each severity weight reflects the relative extent of harm that is associated with experiencing the toxicity at the given level of severity in relation to the other severity levels of the same toxicity and other toxicities monitored in the trial. These were elicited from the clinical oncologists planning the trial, and represent the group’s consensus. For example, pericardial effusion requiring medical but not surgical intervention, and the occurrence of a pulmonary embolism, both have elicited weight 60, and thus are considered equally harmful. Weights were elicited in the range 0 to 100 for convenience, since the oncologists were comfortable with this domain. However, any finite positive domain would work in practice. In our study, w = 0 implies no harm to the patient, while w = 100 represents an extent of harm that is imminently life threatening. We describe the manner in which we elicited the severity weights as well as provide justification for the numerical values in Section 6 and in Section A of the supplementary material.

Table 1.

Toxicities and elicited severity weights for the 11 toxicities that are monitored in the esophageal cancer trial. Medical rationale to justify the numerical values is provided in Section A of the supplemental material.

Recurrent Toxicities	Severity Level	Elicited Weight
	non-symptomatic	10
Pericardial Effusion (PEF)	medical intervention	60
	surgical intervention	90
	non-symptomatic	10
Pleural Effusion (PLE)	medical intervention	30
	surgical intervention	60
	grade 1-2	20
Radiation Pneumonitis (RP)	grade 3	60
	grade 4-5	90
Pneumonia (PNA)	occurrence	40
Atrial Fibrillation (AFIB)	occurrence	30
Myocardial Infarction (MI)	occurrence	70
Postoperative Complications	Severity Level	Elicited Weight
	radiographic only	30
Anastomotic Leak (AL)	medical intervention	60
	surgical intervention	90
Acute Respiratory Distress Syndrome (ARDS)	occurrence	90
Pulmonary Embolism (PEM)	occurrence	60
Reintubation (RI)	occurrence	70
Stroke (ST)	occurrence	90

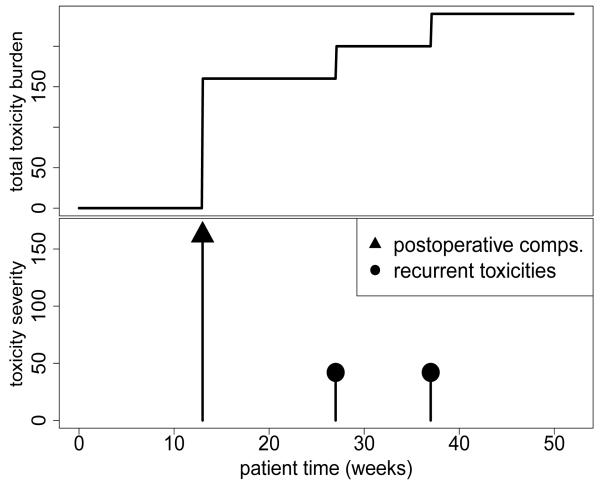
Figure 1 illustrates TTB for a hypothetical patient, computed using each of the four sets of weights. Each spike in the bottom graph indicates either a single toxicity or a collection of POCs. The heights of the spikes correspond to the weights, and thus illustrate severities. The top graph plots the patient’s TTB over time for each of the four sets of weights. The hypothetical patient’s TTB was zero until postoperative reintubation and stroke in week 13, then successive onsets of pneumonia at weeks 27 and 37. Using the elicited weights, these toxicities contributed severity scores 70+90=160 at week 13 and 40 at each of weeks 27 and 37.

Figure 1.

Example of toxicity severity scores (lower graph) and their sum, the total toxicity burden, (upper graph) for a single patient.

The following notation expresses TTB as a function of elicited severity weights and event indicators arising from two multivariate marked point processes, one characterizing recurrent toxicity, the other POCs following surgery. Indexing the toxicities in Table 1 by k = 1, … , 11, we denote the vectors of elicited ordinal toxicity severity weights by w₁, … , w₁₁. For example, w₁ = (w_1,1, w_1,2, w_1,3) = (10, 60, 90) for the three levels of pericardial effusion, w₄ = w_4,1 = 30 if atrial fibrillation occurs, and so on (Table 1). Without loss of generality, we represent patient follow-up as a proportion of the maximum follow-up duration (52 weeks) required to account for late-onset radiation-induced toxicity, t ∈ (0, 1]. Let N(t) = {N₁(t), … , N₆(t)} denote the multivariate counting process characterizing the numbers of toxicities occurring by time t for the 6 recurrent toxicities. The 1 × M_k vector Z_k,j(t) = {Z_k,j,1(t), … , Z_k,j,Mk(t)} denotes the multinomial point process that marks the severity of the j^th occurrence of toxicity type k. Each Z_k,j,m(t) is a simple point process with Z_k,j,m(t*) = 1, for all t* > t if the jth incidence of the kth toxicity occurs at the mth severity level prior to time t. If the jth event has not occurred by time t, then Z_k,j,m(t*) = 0, for all m = 1, …, M_k.

We use the elicited weights, w_k, the observed occurrence processes, N_k(t), and the mark processes, Z_k(t), to define the toxicity burden for the kth recurrent toxicity at follow-up time t,

$$B_k^{\mathit{REC}}\left(t\right)=\sum _{j=1}^{N_k\left(t\right)}{\mathit{w}}_k^{\prime }{\mathit{Z}}_{k,j}\left(t\right)=\sum _{j=1}^{N_k\left(t\right)}\sum _{m=1}^{M_k}{w}_{k,m}{Z}_{k,j,m}\left(t\right).$$ (1)

The j^th occurrence of recurrent toxicity type k produces a jump of size ${\mathit{w}}_k^{\prime }{\mathit{Z}}_{k,j}\left(t\right)$ in the $B_k^{\mathit{REC}}\left(t\right)$ process at the event time. We define the total toxicity burden contributed by the 6 recurrent toxicities at follow-up time t as the sum,

$$B^{\mathit{REC}}\left(t\right)=\sum _{k=1}^6{B}_k^{\mathit{REC}}\left(t\right).$$

For the subset of patients who undergo surgery, there are five possible POCs in the RT trial. These consist of one ordinal-valued toxicity, anastomotic leak, indexed by k = 7, with M₇ = 3 levels, and four binary-valued toxicities for which M_k ≡ 1, indexed by k = 8, … , 11. The POCs are assessed only once, approximately one week following surgery. Let {S(t) = 0, 1 : 0 < t < 1} denote an event process with at most a single jump discontinuity of size +1 at the time surgery is performed. Matching indices for recurrent events (k, j, m) = (toxicity type, recurrence number, severity level), we use Z₇(t) = {Z_7,1,1(t), Z_7,1,2(t), Z_7,1,3(t)} to denote the vector of severity level indicators for the ordinal-valued POC. The occurrence indicators for the four remaining POCs are denoted by Z_k,1,1(t), k = 8, … , 11. We define the toxicity burden contributed by POCs at follow-up time t as

$$B^{\mathit{POC}}\left(t\right)=S\left(t\right)\left\{\sum _{m=1}^3{w}_{7,m}{Z}_{7,1,m}\left(t\right)+\sum _{k=8}^{11}{w}_{k,1}{Z}_{k,1,1}\left(t\right)\right\}.$$

We can now define each patient’s TTB at follow-up time t as the sum of these two components,

$$B\left(t\right)=B^{\mathit{REC}}\left(t\right)+B^{\mathit{POC}}\left(t\right).$$ (2)

Because we account for occurrence over time and possible recurrences, this definition generalizes that used for Bayesian phase I dose-finding by Bekele and Thall (2004).

3 Group Sequential Bivariate Trial Design

Because toxicities induced by RT are rare but serious, our trial must include interim monitoring based on TTB. In planning the radiation therapy trial, the participating oncologists were unwilling to continue randomizing if the data showed strong evidence of a difference between PBT and IMRT for either TTB and PFS. Consequently, these are co-primary endpoints, and the group sequential design stops the trial early if one modality is superior with respect to TTB, PFS, or both. The trial’s decision scheme thus is complex. For each interim decision, there are three possibilities for each of the two outcomes, namely that PBT is superior, IMRT is superior, or neither is superior. This yields nine possible joint decisions.

At any trial time, patients will have different follow up times t₁, … , t_n, and some will have undergone surgery while others will not, so in general their TTBs will not be comparable. E.g., B^REC(0.5) and B^REC(1) correspond to different follow up periods. Thus, we will conduct the trial by specifying a joint model for the multivariate patient outcome, deriving the resulting expectation of TTB, E{B(1)}, and formulating group sequential decision rules for comparing safety using the inter-modality difference in mean TTB. Importantly, E{B(1)}, is the function of severity weights and model parameters (we’ll use θ to denote model parameters) that characterizes the extent of total toxicity burden experienced by a patient on average over the course of the entire at risk duration for one modality. Our trial’s decision rules are based on the resulting posteriors of the difference in mean TTB, Δ(θ, w) = E{B(1) ∣ IMRT} − E{B(1) ∣ PBT}, and the PFS log hazard ratio, δ^ξ. Model specification and derivation of Δ(θ, w) is given in Section 4.

Let $\mathcal{D}\left(\tau \right)$ denote the observed data for all patients enrolled by trial time τ. Let ε^TTB denote a small value of Δ(θ, w) and ε^PFS a small value of δ^ξ that are considered clinically insignificant. At interim analysis time τ, the safety comparison is based on posterior probabilities that difference in mean TTB of one modality compared to the other exceeds ε^TTB,

$$\begin{array}{cc}\hfill {\phi }^{\mathit{PB}}({\epsilon }^{\mathit{TTB}},\tau )& =\mathit{Pr}\left\{\Delta \right(\theta ,w)>{\epsilon }^{\mathit{TTB}}\mid \mathcal{D}(\tau \left)\right\}\text{in favor of PBT, and}\hfill \\ \hfill {\phi }^{\mathit{IM}}({\epsilon }^{\mathit{TTB}},\tau )& =\mathit{Pr}\{-\Delta (\theta ,w)>{\epsilon }^{\mathit{TTB}}\mid \mathcal{D}(\tau \left)\right\}\text{in favor of IMRT}.\hfill \end{array}$$

Similarly, the PFS comparison is based on the posterior probability that the PFS log hazard ratio exceeds ε^PFS in favor of one modality compared to the other,

$$\begin{array}{cc}\hfill {\chi }^{\mathit{PB}}({\epsilon }^{\mathit{PFS}},\tau )& =\mathit{Pr}\left\{{\delta }^{\xi }>{\epsilon }^{\mathit{PFS}}\mid \mathcal{D}\left(\tau \right)\right\}\text{in favor of PBT, and}\hfill \\ \hfill {\chi }^{\mathit{IM}}({\epsilon }^{\mathit{PFS}},\tau )& =\mathit{Pr}\left\{-{\delta }^{\xi }>{\epsilon }^{\mathit{PFS}}\mid \mathcal{D}\left(\tau \right)\right\}\text{in favor of IMRT}.\hfill \end{array}$$

The model, which is described in Section 4, is formulated such that larger values of φ^PB(ε^TTB, τ) represent stronger a posteriori evidence that PBT is the safer modality, while larger values of χ^PB(ε^PFS, τ) correspond to PBT being more effective for delaying recurrence/progression and prolonging survival. Similarly, larger φ^IM(ε^TTB, τ) or χ^IM(ε^PFS, τ) correspond to superior safety or effectiveness of IMRT.

Numerical values of ε^TTB and ε^PFS must be specified in the context of possible values of Δ(θ, w) and δ^ξ. While the hazard ratio δ^ξ is readily interpretable, the magnitude of clinical relevance for Δ(θ, w) may be less obvious. For the RT trial, any improvement in mean TTB or PFS was considered clinically relevant by the participating oncologists, therefore posterior probabilities were computed using ε^TTB = ε^PFS = 0. The resulting decision rules are structurally similar to the multiple hypothesis test-based method of Kosorok et al. (2004) using “vague” alternative hypotheses.

In order to conduct a trial with the group sequential comparisons, one must determine both the “timing” and minimal extent of “evidence” that is required to confer each decision at each analysis time. For our trial, we defined posterior thresholds on φ and χ, referred to hereafter as “decision boundaries,” to which the posterior probabilities will be compared to make decisions during the trial as functions of information statistics. The information statistics characterize the proportion of total information, $\mathcal{I}\left(\tau \right)\in [0,1]$, that has been observed at the time of analysis in relation to the maximum possible information that could be observed in the trial. Using accumulated information, rather than calendar time or sample size, to decide when to perform the interim comparisons provides robustness to mis-specification of the assumed enrollment rate, which is a common practical issue in group sequential trials.

Let n(τ) denote the number of patients enrolled by τ. We used the cumulative follow-up duration at $\tau ,{\mathcal{I}}^{\mathit{TTB}}\left(\tau \right)={\sum }_{i=1}^{n\left(\tau \right)}{t}_i∕N$, to define an information statistic for TTB. Because t_i denotes the ith patient’s proportion of total follow-up out of 52 weeks, ${\mathcal{I}}^{\mathit{TTB}}$, represents the cumulative follow-up for toxicity as a proportion of total follow-up that would be observed if all N patients were monitored for toxicity for the entire post-RT toxicity at-risk period of 52 weeks. The appropriate information statistic for PFS is the proportion of events by τ, ${\mathcal{I}}^{\mathit{PFS}}\left(\tau \right)={\sum }_{i=1}^{n\left(\tau \right)}(1-C_i)∕N$. To use φ and χ for decision making, we defined boundaries on the posterior probability domain using the function

$$c^y\left(\tau \right)=1-{\beta }^y{\left\{{\mathcal{I}}^y\right\}}^{{\alpha }^y}\left(\tau \right),\text{for}y=\text{TTB}\text{or}\text{PFS}$$ (3)

at trial time τ. The exponents, α^TTB, α^PFS > 0, and scaling parameters, 0 < β^TTB, β^PFS < 1, must be calibrated to obtain a design that satisfies pre-specified size, power, and optimality criteria. The approach is similar to the boundary functions proposed by Wathen and Thall (2008). The boundaries (3) are consistent with conventional group sequential designs (O’Brien and Fleming, 1979; Lan and DeMets, 1983; DeMets and Lan, 1994) in the sense that early stopping requires a smaller numerical difference as more information accrues during the trial.

The nine joint decision rules are given in Table 2. Decisions 1, 2, or 4 each would lead to the conclusion that PBT is superior, since it is superior to IMRT for either both endpoints or at least one endpoint without evidence of a clinically significant difference for the other. Similarly, Decisions 6, 8, or 9 would lead to the conclusion that IMRT is superior. Decision 5 corresponds to the absence of evidence for a meaningful difference between PBT and IMRT for either endpoint. Decision 5 may be achieved at the end of the trial, in this case it might be described as failing to reject the global null hypothesis. Decisions 3 and 7 both conclude that, with either modality, it is inferior for one outcome and superior for the other. These conclusions are not made by conventional hypothesis tests, but easily could arise in any clinical setting where treatments have both harmful and beneficial effects. At the extremes, Decisions 1 and 9 might be called “win-win” decisions, and represent extremely optimistic scenarios that are rarely obtained in practice. For this treatment regime and disease, it is considered unethical to continue randomizing patients if one modality is determined to be inferior for either endpoint. Thus, the only case where the trial is continued interimly is under Decision 5, since it reflects clinical equipoise, or indifference for both PFS and TTB.

Table 2.

Joint decision rules for monitoring TTB and PFS at trial time τ. For brevity, we denote the posterior probabilities φ^PB = φ^PB(ε^TTB, τ), φ^IM = φ^IM(ε^TTB, τ), χ^PB = χ^PB(ε^PFS, τ), and χ^IM = χ^IM(ε^PFS, τ) and the monitoring boundaries c^TTB = c^TTB(τ) and c^PFS = c^PFS(τ). We denote ind. to abbreviate indeterminate and u ∨ v = maximum {u, v}.

		TTB Rule
		φPB > cTTB	φPB ∨ φIM < cTTB	φIM > cTTB
PFS Rule	χPB > cPFS	1. PBT safer and more effective	2. PBT more effective with ind. safety	3. IMRT safer and less effective
	χPB ∨ χIM < cPFS	4. PBT safer with ind. efficacy	5. continue enrolling patients	6. IMRT safer with ind. efficacy
	χIM > cPFS	7. PBT safer and less effective	8. IMRT more effective with ind. safety	9. IMRT safer and more effective

For trial conduct, the decision rules are applied at three interim analyses when 33%, 50%, and 67%, of the expected total information has accrued, and utilized at the final analysis one year after the patient enrollment period ends. Patients are expected to be enrolled at a rate of 4 per month, requiring a total of 3.75 years to reach the targeted maximum enrollment of N = 180, and 4.75 years to complete patient follow-up.

4 Probability Model

We expect associations among the toxicities, surgery, and PFS. Thus, we formulated our model to induce a dependence structure that we believed was qualitatively consistent with the clinical context, for which we assumed the following. Radiation delivered to the thoracic cavity may adversely affect critical organs and thus has the potential to reduce survival. Additionally, a patient with early RT-induced toxicity is less likely to undergo surgery, hence experiencing both a higher risk of disease progression and a lower risk of POCs. To reflect these assumptions, we used the following frailty model. Indexing patients by i = 1, … , n, let {U_i, i = 1, … , n} denote i.i.d. random patient frailties with E(U_i) = 1 and var(U_i) = ϕ. To induce positive correlation among the counts of the recurrent toxicities, we employed the common device of assuming that the k^th recurrent toxicity process N_i,k(t) of patient i in treatment arm x is Poisson with conditional intensity U_iψk(x). This is presented in Section 4.1. We used an exponential model for time-to-surgery (presented in Section 4.2) with hazard rate multiplied by $U_i^{-1}$. The conditional distribution of PFS Y_i given U_i, presented below in Section 4.3, is assumed to follow a piecewise exponential distribution with the baseline hazard on each time subinterval multiplied by U_i. Details are given in Section B of the supplemental material. Averaging over the distribution of U_i, these assumptions give a model with (1) association among the recurrent toxicity counts N_i,1(t), … , N_i,6(t), (2) each N_i,k(t) negatively correlated with Y_i, so that increased toxicity is associated with shorter PFS, and (3) negative association between surgery and the incidence of each recurrent toxicity, and positive association between surgery and PFS.

Moreover, the model must also yield analytical tractability for expressing the difference in mean TTB between treatment modalities as a function of model parameters and severity weights, since its posterior along with the posterior distribution for the PFS hazard ratio are used in the group sequential procedure. We assumed that the frailties follow an inverse gamma distribution, $U_i~{\Gamma }^{-1}(\frac{1}{\varphi }+2,\frac{1}{\varphi }+1)$. This gives a multivariate model that yields an analytically tractable expression for the mean TTB difference. We considered other parametric and non-parametric models, but did not use them because they required numerical integration to compute mean TTB, which complicated computation of the design’s operating characteristics.

Our model represents just one possible set of assumptions. Moreover, alternative methods could have been used to account for interdependence among toxicities, surgery, and PFS. For example, instead of using recurrent event processes, one could assume that a transformation, g(), applied to the TTB statistic and perhaps scaled per follow up duration (i.e. g{B(t)/t} ) is Gaussian. Then one could conceivably proceed by specifying a multivariate normal model for the transformed TTB statistic in conjunction with transformations of the time-to-surgery and time-to-PFS endpoints. A perhaps more appealing, but less tractable solution might use copulas to describe the dependence among toxicities, surgery, and PFS.

4.1 Recurrent Toxicity Processes

Initially, we considered a model with toxicity-specific marked point processes for severities and treatment effects for both event recurrence and severity probabilities. For the 6 recurrent toxicities, this requires a minimum of 18 model parameters. Similarly, assuming POC-specific marked point processes with a modality effect for the rate of surgery and separate modality effects for the severity probabilities for each of the 5 POCs requires a minimum of 12 model parameters. We found this model too complex to use as a practical basis for trial design.

To further simplify the model and reduce its dimension, we now exploit the fact that treatment comparisons based on TTB need only consider the incidence of each possible total toxicity severity. Together, the recurrent toxicities in the RT trial may have one of seven unique severities, w* = (10, 20, 30, 40, 60, 70, 90). Thus, with a slight abuse of notation, hereafter we formulate the model in terms of the counting processes N_i,1(t) for all toxicities of any type giving total severity 10, N_i,2(t) for all toxicities of any type with total severity 20, and so on. Hereafter, the toxicity index is k = 1, … , 7 rather than 1, … , 11. This reduces the number of model parameters from 30 to 18. However, to assess robustness in the simulation studies described in Section 5, we will use a saturated 11-dimensional marked point process model to generate the data.

We assume that each patient’s risk of radiation-induced toxicity depends on the type of irradiation that is delivered (at the group-level) as well as the anatomic location of the tumor (at the patient-level). The latter impacts the dosimetric plan and thereby determines the extent of irradiation that is delivered to healthy tissues in neighboring regions. To accommodate intra-patient dependence, we used doubly stochastic Poisson (Cox) processes to induce association among recurrent toxicity severities (Cox, 1955; Snyder and Miller, 1991; Jacobsen, 2006; Cook and Lawless, 2007).

We’ll denote treatment by x = −0.5 for IMRT and x = +0.5 for PBT. Let ${\psi }_k\left(x\right)={\lambda }_k\text{exp}(-x{\delta }_k^{\psi })$ denote the mean rate of recurrent toxicity severity k for a patient in treatment arm x. Thus, λ_k > 0 is the baseline rate and ${\delta }_k^{\psi }$ is the real-valued PBT-versus-IMRT RT modality effect on the log mean rate. We assume that, given U_i and x_i, the k^th recurrent severity process {N_i,k(t), t ≥ 0 ∣ U_i, x_i} for patient i is a Poisson process with conditional intensity U_iψk(x_i). The random frailty, U_i, acts as a common scalar of the mean rates of N_i,1(t), …, N_i,7(t) inducing positive association among the event processes. Since E(U_i) = 1, after averaging over the distribution of U_i, N_i,k(t) has unconditional mean tψ_k(x_i), variance tψ(x_i) + ϕ t²ψ_k(x_i)², and covariance cov {N_i,r(t), N_i,l(t) ∣ x_i} = ϕ t²ψ_r(x_i)ψl(x_i). The frailty variance, ϕ, determines the degree of association between counts over disjoint intervals within each event process as well as the degree of association between different event processes (Cox and Isham, 1980; Breslow, 1984; Lawless, 1987a,b).

A likelihood is necessary to conduct posterior inference. Section B.1 of the supplemental material provides the likelihood contribution for the toxicity count vector N_i(t). Our model is parameterized so that larger treatment effects, denoted by δ with appropriate subscripts and superscripts, correspond to superiority of PBT over IMRT. For example, a larger positive value of ${\delta }_k^{\psi }$ corresponds to a smaller occurrence rate of recurrent severity k with PBT versus IMRT.

4.2 Surgery Process and Postoperative Complications

Because TTB is the sum B(t) = B^REC(t) + B^POC(t), treatment comparison based on E{B(t)} is influenced by the probability of undergoing surgery following chemoradiation, and thus becoming at risk of POCs. We assumed that a patient experiencing a severe toxicity with chemoradiation is less likely to undergo surgery, while surgery reduces the risk of disease recurrence and thus is positively associated with PFS. To reflect these relationships, given frailty U_i and treatment arm x_i, we assume that the time-to-surgery distribution is exponential, with conditional hazard rate $\tilde{\lambda }\text{exp}\left(x_i\tilde{\delta }\right)∕U_i$, inducing dependence with N_i(t) and PFS as per our assumptions when ϕ > 0. Thus, $\tilde{\lambda }$ is the baseline rate and $\tilde{\delta }$ is the real-valued PBT-versus-IMRT RT modality effect, with $\tilde{\delta }$ > 0 corresponding to increased relative rate of surgery in favor of PBT. Section B.2 of the supplemental material provides the likelihood contribution. However, as described in Section 5.1, we evaluate our design’s operating characteristics by generating surgery times with an approximation of the baseline hazard function that we expect to observe in the trial using a piecewise constant model.

The POCs that are monitored in this trial are serious, rare events. A major motivation for the trial is whether the relative incidences or severities of these POCs may differ between the two RT modalities, since chemoradiation may impact the extent to which a patient tolerates surgery. Because all five POCs are assessed at a single time point following surgery, we use a multinomial model for the aggregate severity of the POCs. There are 24 possible values of the total POC severity (computed from Table 1) which we denote in order from least to most severe by $\tilde{w}=(0,30,\cdots ,400)$. Let Z_i(t) = {Z_i,1(t), … , Z_i,24(t)} denote the vector of aggregate severity level indicators for patient i, whereby ${\sum }_{m=1}^{24}{Z}_{i,m}\left(t\right)=1$ if S(t) > 0, and Z_i,m(t) = 0, for all m otherwise. We assume [Z_i(t) ∣ x_i] ~ Multinomial{π(x_i)}, with RT-specific probability vector π(x_i) = {π₁(x_i), … , π₂₄(x_i)}, where ${\sum }_{m=1}^{24}{\pi }_m\left(x_i\right)=1$. Section B.3 of the supplemental material provides the likelihood contribution for POC severity.

4.3 Progression-Free Survival and Mixture Model

Our trial uses a piecewise constant hazard formulation for PFS (e.g. Ibrahim et al., 2001, section 3.1). This model facilitates between-modality comparisons under the typical proportion hazards assumption that are robust to the actual shape of the underlying baseline hazard. Given the frailty, U_i, we assume that the hazard for PFS is piecewise constant over the time axis partition (0, s₁], (s₁, s₂], …, (s_G−1, s_G], (s_G, ∞), where 0 < s₁ < s₂ < … < s_G < ∞. For [Y_i ∣ U_i] in the interval (s_g−1, s_g], g = 1, …, G, the constant baseline hazard is ξ_g(x_i, U_i) = U_iγg exp {−x_iδ^ξ}, where γ_g > 0, and we denote γ = (γ₁, …, γ_G). This model can approximate any underlying smooth baseline hazard function, providing a robust relative comparison between modalities. We selected the set of hazard discontinuities, (s₁, …, s_G), adaptively using the interim data to obtain a time axis partition that is AIC-optimal among sets of all equidistant quantiles so that each interval contains at least 10 observed events. Positive values of δ^ξ correspond to longer median PFS for PBT versus IMRT. Section B.4 of the supplemental material provides the likelihood contribution for PFS. Additionally, multiplying each interval hazard γ_g exp {−x_iδ^ξ} by the frailty U_i provides subject-specific perturbations of the baseline hazard function inducing positive (negative) correlation with surgery (toxicity).

Collecting terms, the i^th patient’s observable outcome vector is ${\mathcal{D}}_i=({\mathit{N}}_i,S_i,{\mathit{Z}}_i,Y_i,C_i),i=1,\dots ,n$, and the overall joint likelihood contribution is obtained by averaging the product of conditional likelihoods of the observables. Since these are assumed to be conditionally independent given U_i, this is

$${\mathcal{L}}_i(\theta \mid {\mathcal{D}}_i)={\mathcal{L}}_{{\mathit{Z}}_i}{\int }_{u=0}^{\infty }{\mathcal{L}}_{{\mathit{N}}_i}\left(u\right){\mathcal{L}}_{{\mathit{S}}_i}\left(u\right){\mathcal{L}}_{{\mathit{Y}}_i}\left(u\right)\mathrm{d}{\Gamma }^{-1}(u\mid \frac{1}{\varphi }+2,\frac{1}{\varphi }+1).$$ (4)

The model parameter vector is $\theta =(\lambda ,\tilde{\lambda },\pi ,\gamma ,\varphi ,{\delta }^{\psi },\tilde{\delta },{\delta }^{\xi })$, and we denote the data for n patients by $\mathcal{D}={\cup }_{i=1}^n{\mathcal{D}}_i$.

4.4 Mean Total Toxicity Burden

Having specified a model for the multivariate patient outcome, we can now derive the expectation of (2) as well as the inter-modality difference in mean TTB, Δ(θ, w) = E{B(1) ∣ IMRT} − E{B(1) ∣ PBT}, which provides the basis for comparing safety in our trial. The marginal expected toxicity burden of N_k(t) for a patient assigned to treatment x is

$${\mu }_k^{\mathit{REC}}(t,x,\theta )=t{\psi }_k\left(x\right)w_k^{\ast },k=1,\dots ,7.$$ (5)

The expected severity from POCs over the follow-up period [0, t) for a patient assigned to treatment x is a tractable function of π(x), the surgery rate $\tilde{\lambda }\text{exp}\left(x\tilde{\delta }\right)$, and frailty variance ϕ, given by

$${\mu }^{\mathit{POC}}(t,x,\theta )={\tilde{w}}^{\prime }\pi \left(x\right)\left\{1-{\left(\frac{\varphi t\tilde{\lambda }\text{exp}\left(x\tilde{\delta }\right)}{\varphi +1}+1\right)}^{-(1∕\varphi +2)}\right\}.$$ (6)

Details of the derivation are provided in Appendix A. In the absence of frailty dispersion (ϕ = 0), the mean TTB from POCs would be the multinomial mean ${\mu }^{\mathit{POC}}(t,x,\theta )={\tilde{\mathit{w}}}^{\prime }\pi \left(x\right)$. Equation (6) shows that the frailties reduce ${\tilde{\mathit{w}}}^{\prime }\pi \left(x\right)$ by a multiplicative factor that depends on $(\varphi ,\tilde{\lambda },\tilde{\delta },x)$ and takes values between 0 and 1. As the frailty dispersion increases, there is a decrease in the probability of undergoing surgery after experiencing recurrent toxicity, thereby attenuating the influence of POCs. The multiplicative term approaches the lower limit $1-{\left(t\tilde{\lambda }\text{exp}\right(x\tilde{\delta })+1)}^{-2}$, as ϕ → ∞, which is the largest multiplicative amount by which frailty dispersion may reduce ${\tilde{\mathit{w}}}^{\prime }\pi \left(x\right)$.

The μ’s given by (5) and (6) quantify risk-severity trade-offs, and their sum,

$$\mu (t,x,\theta )=\sum _{r=1}^7{\mu }_r^{\mathit{REC}}(t,x,\theta )+{\mu }^{\mathit{POC}}(t,x,\theta ),$$ (7)

is the mean TTB for a patient assigned to modality x. Recalling that x = −0.5 for IMRT and x = 0.5 for PBT, the design uses the 52 week (t = 1) mean difference as the basis for IMRT-versus-PBT safety comparison, denoted by Δ(θ, w) = μ(−0.5, θ) − μ(0.5, θ). Positive values of Δ(θ, w) correspond to superior safety for PBT compared to IMRT.

4.5 Establishing Priors

To specify priors, we selected distributions to satisfy model constraints or exploit analytical properties of conditional conjugacy. Let $\delta =({\delta }^{\psi },\tilde{\delta },{\delta }^{\xi })$ characterize the respective modality differences for recurrent toxicity, surgery, and PFS. The remaining parameters in θ characterize baseline features of the recurrent toxicity severity or surgery processes, severity probabilities from POCs, or the frailty dispersion.

Given that one modality effectuates a safer plan, we expect reductions in the event rates of each of the radiation-induced toxicities monitored in the trial. Under this assumption, parameters that characterize the corresponding “group-level” treatment effects should be positively associated. To effectuate this, we used a hierarchical prior to induce shrinkage among exchangeable treatment effects : ${\delta }_k^{\psi }~N({\delta }^{\psi },{\omega }^2),k=1,\cdots ,7$. A non-informative prior was assumed for the hierarchical mean, δ^ψ ~ N(0, 100). Following the recommendations of Gelman (2006), the hierarchical standard deviation, ω, was assumed to be uniform over (0, 10]. For the treatment effects for surgery, $\tilde{\delta }$, and PFS, δ^ξ, we assumed N(0, 100) priors. We assumed weakly informative priors for the non-treatment effect parameters, including conditionally conjugate gamma distributions for the λ’s, and for the piecewise constant PFS hazard parameters, γ, and Dirichlet priors for the POC severity probabilities, π(x). In the absence of prior knowledge about the extent of interdependence among the observables, we assumed a weakly informative uniform prior distribution over the interval (0, 10] for the frailty variance.

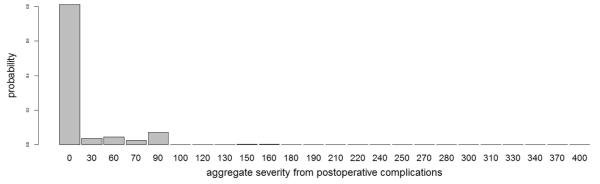
Prior hyperparameters for baseline means were estimated from historical data and/or elicited from the team of oncologists. Each hazard component for PFS was centered at the estimated hazard rate derived from a parametric exponential fit to a cohort of 246 patients with stage II-III esophageal cancer who underwent the trimodality regime at MD Anderson with IMRT. Table 3 summarizes elicited information characterizing the non-occurrence rate and severity probability of each toxicity. Prior means of baseline event rates of recurrent toxicities were derived by combining event rates and severity probabilities among toxicity-grades having identical severity weights, assuming independence. For example, the occurrence of an atrial fibrillation or a pleural effusion requiring medical intervention both have severity weight $w_3^{\ast }=30$. The corresponding elicited baseline event rate was obtained by mapping the induced probability that both toxicities are absent after 52-weeks of follow-up onto the domain of λ. The prior mean baseline event rate for surgery followed similarly from the expectation that 65% of patients would undergo surgery. For each treatment arm, the mean probability of each POC severity level, depicted in Figure 2, was calibrated using the elicited POC-specific severity probabilities in Table 3 under the assumption of independence.

Table 3.

Elicited prior information based on experience treating patients with photon radiation therapy. For each recurrent toxicity, the probability that a patient will not experience the toxicity over 52 weeks was elicited. Binomial/multinomial severity probabilities were elicited for POCs and recurrent toxicities with ordinal severities. Elicited values for toxicities with identical severity weights were combined to establish prior distributions for baseline model parameters.

Recurrent Toxicity Event Processes
Toxicity	52-week Absence Probability
Pericardial Effusion (PEF)	0.96
Pleural Effusion (PLE)	0.95
Radiation Pneumonitis (RP)	0.90
Pneumonia (PNA)	0.85
Atrial Fibrillation (AFIB)	0.75
Myocardial Infarction (MI)	0.95

Recurrent Ordinal Toxicity Severities
Toxicity	Severity Level	Severity Probability Given Occurrence
	non-symptomatic	0.50
Pericardial Effusion	medical intervention	0.30
	surgical intervention	0.20
	non-symptomatic	0.60
Pleural Effusion	medical intervention	0.20
	surgical intervention	0.20
	grade 1-2	0.80
Radiation Pneumonitis	grade 3	0.10
	grade 4	0.10
Postoperative Complications
Toxicity	Severity Level	Severity Occurrence Probability
	absence	0.87
Anastomotic Leak (AL)	radiographic only	0.08
	medical intervention	0.03
	surgical intervention	0.02
Acute respiratory distress syndrome (ARDS)	absence	0.97
Pulmonary Embolism (PEM)	absence	0.97
Reintubation (RI)	absence	0.95
Stroke (ST)	absence	0.98

Figure 2.

Elicited Dirichlet prior mean for aggregate POC severity used for posterior inference with prior effective sample size set at 1. The domain of numerical scores, which represents the 24 unique values that result from all possible combinations of the ordinal-valued POC severities, is slightly irregular.

Prior variances for toxicity severity and surgery were specified using prior effective sample size (ESS) (Morita et al., 2008, 2012) to characterize prior informativeness relative to the amount of information contributed by the likelihood based on the trial’s maximum sample size of N = 180. The concentration hyperparameters for probability of aggregate POC severity were scaled to sum to 1, inducing a Dirichlet prior with ESS = 1. We set the gamma rate hyperparameter for each conjugate time-homogeneous Poisson process to 5. Thus, conditional on the frailty, the induced prior distribution for each baseline intensity contained information equivalent to 5 patients.

Given the frailty variance, priors for the unconditional intensities, Uλ_k∗s and $U^{-1}\tilde{\lambda }$, are proportional to an intractable mixture of Meijer G-functions (Springer and Thompson, 1970). Therefore, unconditional prior ESS values were derived using least squares gamma approximations. Among the recurrent toxicity severities, the resulting ESS values ranged from a minimum of 0.68 for severity weight w∗₂ = 20 (RP of grade< 3) to a maximum of 1.8 for w∗₇ = 90 (surgical PEF or RP of grade 4). The unconditional event rate for surgery had prior ESS= 0.74.

5 Simulation Study

5.1 Simulation Design

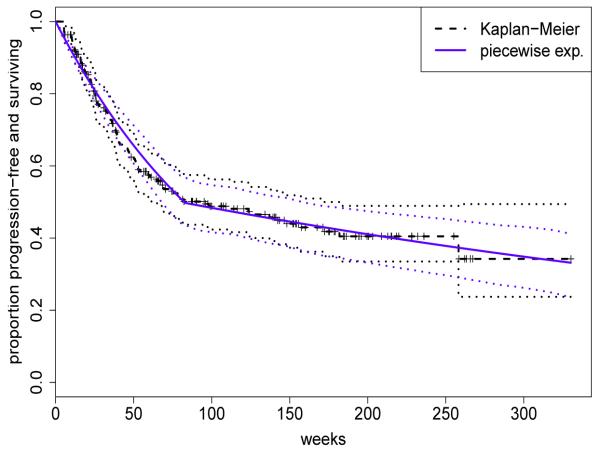
We used simulation as a tool to calibrate the boundary function parameters in order to obtain a design with desirable operating characteristics, including acceptable overall frequentist size and power. Proper evaluation of the design’s frequentist properties required simulation of observables under a reasonable set of true distributions. To ensure robustness, these must include distributions substantially different from those in the model used to construct the design. We thus simulated the toxicities using a saturated multivariate marked point process with toxicity-specific parameters for event intensities and severities. Baseline model parameters for PFS were fixed at estimates derived from analysis of a cohort of 246 historical patients treated with IMRT by the participating oncologists. Posterior inference used the model and approach for selecting the time-axis partition described in Section 4.3, which resulted in an AIC-optimal partition with two intervals [0, 83], (83, ∞) and a median of 81.6 weeks. Figure 3 provides the Kaplan-Meier curve, with 95% log-transformed (Klein and Moeschberger, 2003) pointwise confidence intervals, and fitted survival curve derived from analysis using the piecewise constant hazard formulation (in blue). The corresponding piecewise constant baseline hazard parameters were used to generate random PFS durations in the simulations.

Figure 3.

Progression-free survival for a cohort of 246 patients with stage II-III esophageal cancer who underwent the trimodality regime with IMRT: Kaplan-Meier curve (dashed), fitted piecewise constant curve (blue) with 95% pointwise confidence intervals (dotted).

Surgery event times were generated using the hazard function that we expect to observe in the trial, which is well approximated by a step function. For example, it is expected that 65% of enrolled patients will undergo surgery following RT, with none undergoing surgery within 4 weeks following RT (therefore within the first 9 weeks of follow-up). For most patients who do undergo surgery it is expected to take place before week 15. Specifically, surgery times were generated using a piecewise constant baseline hazard with cumulative distribution probabilities 0.065, 0.49, 0.55, 0.65 at follow-up durations 10.33, 14.67, 19, 52, respectively. Both the time axis partition and cumulative event probabilities were elicited from the surgeon performing the procedure in the trial. The baseline POC severity probability vector was fixed at the elicited prior mean used for analysis (Figure 2). After exploring a range of numerical values, the frailty variance was set equal to 0.20 in the simulations to induce moderate correlation among counts of recurrent events, surgery, and PFS.

The top portion of Table 4 provides the baseline mean burden for each toxicity separately, and their sum or TTB. The participating oncologists expect that a typical patient in the trial will experience a TTB score of 33.67, and they believe that atrial fibrillation will contribute the largest component of TTB, followed by pneumonia and anastomotic leak.

Table 4.

Simulation scenarios. a) Baseline mean burden for individual toxicities, identified by the acronyms in Tables 1 and 2, and for TTB, obtained from the elicited values in Tables 1-2. b) Each Scenario (Sc) is characterized by percent reductions in mean TTB and hazard ratio (HR) of PFS, for IMRT versus PBT. Scenarios 1-12 were obtained by randomly perturbing toxicity incidences and severity probabilities to give a 50% reduction in mean TTB for PBT, while fixing HR=1. Scenarios 13-16 were obtained by increasing the IMRT versus PBT HR for PFS, while fixing mean TTB difference = 0. Scenario 17 combines Scenarios 6 and 16 to yield a “win-win” scenario for PBT, with a 50% reduction in mean TTB for PBT and 2-fold increase in PFS hazard for IMRT. Scenario 18 combines Scenario 6 with a 2-fold decrease in IMRT-versus-PBT HR for PFS, to yield a “win-lose” scenario for PBT.

a)Baseline Mean Toxicity Burden by toxicity
	Recurrent Toxicities						Postoperative Complications
	PEF	PLE	RP	PNA	AFIB	MI	AL	ARDS	PEM	RI	ST	Total
μ	1.67	1.23	3.27	6.5	8.63	3.59	4.88	1.17	0.78	1.37	0.59	33.67

b) Simulation Scenarios combining effects for Mean TTB and PFS Hazard Ratio Percent Reduction in Mean Toxicity Burden for PBT vs IMRT by Toxicity													PFS HR
Sc	PEF	PLE	RP	PNA	AFIB	MI	AL	ARDS	PEM	RI	ST	Total
0	0	0	0	0	0	0	0	0	0	0	0	0	1
1	75	50	87	4	34	76	26	70	70	34	3	50	1
2	69	56	32	81	34	8	4	22	70	81	82	50	1
3	67	81	29	7	81	19	6	32	3	67	52	50	1
4	70	48	83	11	14	69	62	71	15	78	50	50	1
5	45	63	7	72	13	71	73	14	17	35	38	50	1
6	56	52	83	64	13	69	40	23	9	1	79	50	1
7	57	50	78	55	14	2	75	74	70	28	58	50	1
8	63	85	57	52	9	79	26	5	79	78	74	50	1
9	59	71	79	39	6	53	75	69	71	6	44	50	1
10	65	24	29	17	64	83	22	25	26	74	70	50	1
11	62	73	75	7	78	45	0	0	0	0	0	50	1
12	60	59	60	41	78	32	0	0	0	0	0	50	1
13	0	0	0	0	0	0	0	0	0	0	0	0	1.35
14	0	0	0	0	0	0	0	0	0	0	0	0	1.6
15	0	0	0	0	0	0	0	0	0	0	0	0	1.8
16	0	0	0	0	0	0	0	0	0	0	0	0	2
17	56	52	83	64	13	69	40	23	9	1	79	50	2
18	56	52	83	64	13	69	40	23	9	1	79	50	0.5

A total of 19 scenarios, given in Table 4, were simulated to evaluate the design’s operating characteristics. Modality effects were induced by adjusting the relative baseline toxicity event rates, recurrent and POC severity probabilities, and difference in PFS hazards. For each scenario, Table 4 provides the percentage change from baseline in mean toxicity burden for each toxicity, and the IMRT-versus-PBT hazard ratio (HR) for PFS. Scenario 0 is the global null, where the modalities have identical mean TTB and the PFS HR= 1. Scenarios 1-12 characterize alternatives chosen randomly to yield a 50% reduction in mean TTB for PBT versus IMRT, with PFS HR ≡ 1. For example, Scenario 12 achieves 50% reduction in mean TTB for PBT by adjusting the relative event occurrence rates and severity probabilities for recurrent toxicities only to induce 60% reduction for PBT versus IMRT in mean toxicity burden for pericardial effusion, 59% reduction for pleural effusion, as well as 60%, 41%, 78% and 32% reductions for radiation pneumonitis, pneumonia, atrial fibrillation, and myocardial infarction, respectively, in combination with no difference in mean toxicity burden contributed by POCs and equivalent PFS hazard.

For PFS, we evaluated sensitivity to four different time-invariant hazard ratios, while constraining mean TTB difference Δ(θ, w) ≡ 0 in Scenarios 13-16. Two additional scenarios were used to evaluate the design’s sensitivity to detecting modality effects for both endpoints. Scenario 17 combines Scenarios 6 and 16 to yield a “win-win” scenario consisting of a 50% reduction in mean TTB for PBT and 2-fold increase in PFS hazard for IMRT. Scenario 18 combines Scenario 6 with a 2-fold decrease in PFS hazard for IMRT, yielding a “win-lose” scenario for PBT. Posterior probabilities for the TTB and PFS modality comparisons were calculated using Markov chain Monte Carlo (MCMC), details of which are given in Section C of the supplemental material.

As a comparator, we used a conventional frequentist bivariate group sequential design based on PFS and a binary indicator Y_T of any toxicity occurring at any severity level by 52 weeks (τ = 1). For each patient, Y_T was scored as 1 at the time of toxicity, or as 0 at τ = 1 if no toxicity occurred. A group sequential log-rank test (see e.g. Klein and Moeschberger, 2003) was used for PFS, and a normal approximation for a two-sample binomial test for toxicity, both with O’Brien-Fleming monitoring boundaries (O’Brien and Fleming, 1979; Jennison and Turnbull, 2000). Although the information times for the binomial data were not identical to ${\mathcal{I}}^{\mathit{TTB}}\left(\tau \right)$ used for TTB, we formulated the monitoring schedule for toxicity in the conventional design to be as close as possible to that of TTB in the Bayesian design. Additionally, the conventional design was calibrated so that its familywise type I error rate was 0.07 to match that of the Bayesian design. Appendix B describes the process for selecting optimal monitoring boundaries for our design, and presents the corresponding optimal group sequential critical values that were used to implement the conventional design.

5.2 Operating Characteristics

In this section we present operating characteristics (OCs) for the RT trial when implemented using our group sequential design based on TTB and PFS, and for the conventional design. Table 5 presents the marginal decision probabilities for scenarios that characterize true treatment effects for only one endpoint. Corresponding values for the conventional design are given in parentheses. In Scenarios 1 - 12, all of which have true PFS HR = 1, our design provides probability 0.83 to 0.95 of detecting a 50% reduction in mean TTB, while controlling the false positive rate for TTB at < 0.02. The TTB design has early stopping probabilities 0.56 to 0.72, resulting in a trial with mean sample size 140 to 153 in these scenarios. In contrast, the conventional design provides probability 0.50 to 0.81, and in each scenario it is far less likely than the Bayesian design to correctly conclude that PBT is the safer modality, far less likely to stop early, and has a larger mean sample size. These large differences may be attributed, in large part, to the conventional practice of combining many toxicities into one binary variable and ignoring their severities.

Table 5.

Marginal probabilities of final comparative decisions and early stopping. a) considers decisions for TTB under scenarios 0-12. b) considers decisions for PFS under the null (Scenario= 0) and Scenarios 13-16. Operating characteristics for conventional bivariate sequential design using O’Brien Fleming monitoring boundaries are provided in parentheses, ().

a) Total Toxicity Burden with identical PFS hazard
	Final Decision for TTB			Early Stopping Probability	Mean Sample Size
Scenario	PBT	Indeterminate	IMRT
0	0.01 (0.01)	0.98 (0.98)	0.01 (0.01)	0.04 (0.01)	178 (180)
1	0.83 (0.50)	0.17 (0.50)	0.00 (0.00)	0.56 (0.18)	153 (173)
2	0.89 (0.66)	0.11 (0.34)	0.00 (0.00)	0.66 (0.28)	145 (168)
3	0.93 (0.80)	0.07 (0.20)	0.00 (0.00)	0.70 (0.38)	143 (163)
4	0.85 (0.54)	0.15 (0.46)	0.00 (0.00)	0.58 (0.22)	150 (172)
5	0.89 (0.62)	0.11 (0.38)	0.00 (0.00)	0.64 (0.25)	149 (170)
6	0.90 (0.67)	0.10 (0.33)	0.00 (0.00)	0.68 (0.30)	144 (167)
7	0.87 (0.61)	0.13 (0.39)	0.00 (0.00)	0.60 (0.27)	150 (169)
8	0.86 (0.53)	0.14 (0.47)	0.00 (0.00)	0.59 (0.19)	151 (172)
9	0.87 (0.61)	0.13 (0.39)	0.00 (0.00)	0.61 (0.27)	149 (170)
10	0.90 (0.67)	0.10 (0.33)	0.00 (0.00)	0.65 (0.27)	148 (169)
11	0.93 (0.79)	0.07 (0.21)	0.00 (0.00)	0.71 (0.41)	143 (164)
12	0.95 (0.81)	0.05 (0.19)	0.00 (0.00)	0.72 (0.40)	140 (162)

b) Progression-free Survival with identical mean TTB
	Final Decision for PFS			Early Stopping Probability	Mean Sample Size
Scenario	PBT	Indeterminate	IMRT
0	0.02 (0.02)	0.96 (0.96)	0.02 (0.02)	0.04 (0.01)	178 (180)
13	0.26 (0.27)	0.74 (0.73)	0.00 (0.00)	0.17 (0.08)	169 (177)
14	0.56 (0.57)	0.44 (0.43)	0.00 (0.00)	0.33 (0.25)	162 (172)
15	0.76 (0.80)	0.24 (0.20)	0.00 (0.00)	0.52 (0.41)	149 (167)
16	0.89 (0.89)	0.11 (0.11)	0.00 (0.00)	0.66 (0.52)	139 (160)

In Scenario 16, where the true difference in mean TTB is Δ(θ, w) ≡ 0, both designs result in identical probability of 0.89 to detect a 2–fold increase in PFS hazard, while controlling the false positive rate for PFS at ≤ 4%. However, the Bayesian design is far more likely to stop early and offers smaller mean sample size when compared to the conventional design. That is, the Bayesian design detects the difference in PFS with the same reliability but offers a shorter trial, with mean sample size 139 versus 160 for the conventional design.

Table 6 provides the joint probabilities for each of the nine decisions under Scenarios 0, 6, 17, and 18. In the null Scenario 0, both designs have familywise false positive rate ≤ 0.07. Moreover, the four corner decisions have probability of approximately 0.00, so it is very unlikely that either design results in a trial that yields a false positive for both endpoints. Recall that Scenario 6 corresponds to a 50% reduction in mean TTB with PBT when the PFS HR = 1. The TTB design provides much higher probability for concluding that PBT is superior for TTB and indeterminate PFS when compared to the conventional design, 0.88 versus 0.66. For Scenario 17, the “win-win” case for PBT, the probability that both of the Bayesian design’s tests, for TTB and for PFS, correctly conclude that PBT is superior is 0.20. However, since PBT will be chosen as the superior modality for any of the three decisions 1, 2, or 4 in Table 3, the design provides probability equal to 0.20 + 0.42 + 0.37 = 0.99 to detect an improvement for at least one endpoint. Moreover, the Bayesian design has probability 0.89 of terminating early and mean sample size 125, when compared to 0.65 and 152 for the conventional design, respectively. The 0.01 false negative probability is confined only to the global null decision. In Scenario 18, the “win-lose” case for PBT, the Bayesian design has probability 0.21 of making the correct “win-lose” conclusion, probability 0.33 of concluding that PBT is superior for TTB and indeterminate for PFS, and probability 0.45 of concluding that IMRT is superior for PFS and indeterminate for TTB. Again, the 0.01 false negative probability is confined only to the global null decision and, similarly to Scenario 17, the design has probability 0.88 of terminating early.

Table 6.

Joint probabilities of final decisions for TTB and PFS for Scenarios 0, 6, 17, and 18 using three interim analyses. Operating characteristics for conventional bivariate sequential design using O’Brien Fleming monitoring boundaries are provided in parentheses, ().

Scenario 0: Identical mean TTB and PFS hazard (global null)
			TTB Decision
		PBT Better	Indeterminate	IMRT Better
	PBT Better	0.00 (0.00)	0.02 (0.02)	0.00 (0.00)
PFS Decision	Indeterminate	0.01 (0.01)	0.93 (0.93)	0.01 (0.01)
	IMRT Better	0.00 (0.00)	0.02 (0.02)	0.00 (0.00)
Early Stopping Probability = 0.04 (0.01);		Mean Sample Size = 178 (180)
Scenario 6: 50% reduction in mean TTB for PBT and PFS HR= 1 (null case)
			TTB Decision
		PBT Better	Indeterminate	IMRT Better
	PBT Better	0.01 (0.005)	0.01 (0.01)	0.00 (0.00)
PFS Decision	Indeterminate	0.88 (0.66)	0.07 (0.31)	0.00 (0.00)
	IMRT Better	0.01 (0.005)	0.02 (0.01)	0.00 (0.00)
Early Stopping Probability = 0.68 (0.30);		Mean Sample Size = 144 (167)
Scenario 17: 50% reduction in mean TTB for PBT and PFS HR= 2 (in favor of PBT)
			TTB Decision
		PBT Better	Indeterminate	IMRT Better
	PBT Better	0.20 (0.16)	0.42 (0.65)	0.00 (0.00)
PFS Decision	Indeterminate	0.37 (0.15)	0.01 (0.04)	0.00 (0.00)
	IMRT Better	0.00 (0.00)	0.00 (0.00)	0.00 (0.00)
Early Stopping Probability = 0.89 (0.65);		Mean Sample Size = 125 (152)
Scenario 18: 50% reduction in mean TTB for PBT and PFS HR= 0.5 (in favor of IMRT)
			TTB Decision
		PBT Better	Indeterminate	IMRT Better
	PBT Better	0.00 (0.00)	0.00 (0.00)	0.00 (0.00)
PFS Decision	Indeterminate	0.33 (0.35)	0.01 (0.02)	0.00 (0.00)
	IMRT Better	0.21 (0.29)	0.45 (0.34)	0.00 (0.00)
Early Stopping Probability = 0.88 (0.73);		Mean Sample Size = 126 (147)

6 Guidelines for Constructing a Design with TTB

When patients are at risk of multiple, qualitatively different toxicities, a Bayesian design based on TTB and PFS may offer a powerful tool for comparing safety and effectiveness between competing treatments. However, many decisions must be made when choosing the set of toxicities, features of the Bayesian model, and sequential decision rules. These decision are inherently subjective, and require close collaboration between the statisticians and physicians. In this section, we briefly explain the process for constructing a design and evaluating its operating characteristics.

6.1 Eliciting toxicities and severity weights

The two essential components of the TTB statistic are the toxicities and severity weights. The toxicities, and when each may occur in the treatment regime, are identified by the physicians. In essence, there are three fundamental types of toxicities: toxicities that occur at random times 1) with and 2) without the possibility of recurrence and 3) toxicities that are observed only at prespecified evaluation times, such as POCs following surgery. The next step is to ask the physicians to define the ordinal categories of each toxicity that matter clinically, e.g. the three groups grade 1-2, 3, and 4-5 for radiation pneumonitis, or simply whether pneumonia occurs, in Table 1. Once this structure is established, the numerical severity weights must be elicited.

Section A of the supplementary material describes the process that we used to elicit the severity weights in Table 1 as well as provides the medical rationale put forth by the participating oncologists to justify the resultant numerical values. Our approach should be considered informal in the sense that we didn’t use an established method (e.g. Hunink et al., 2014), which would have been preferable. For example, a structured communication technique known as the “Delphi method” (Dalkey and Helmer, 1963; Dalkey, 1969; Brook et al., 1986) could have been used to quantify the relative severity of each possible grade of each toxicity. Additional techniques for elicitation, characterization, and use of expert opinion were examined systematically by Cooke (1991). A few authors have effectuated implementations of such utility-based approaches to clinical cancer studies in recent years. Swinburn et al. (2010) conducted in-depth interviews with clinical experts to establish the relative burden of a variety of toxicities commonly encountered from first-line therapies for metastatic renal cell carcinoma (RCC) when each is experienced in conjunction with stable versus progressive disease. Wong et al. (2012) conducted sequential semi-structured interviews with cancer patients to attempt to establish patient priorities for weighing prolonged PFS versus inflated risk of multiple types of toxicities that may occur from second-line therapy for RCC.

6.2 Modeling decisions

The model should provide a reasonable representation of the process of treatment and outcome observation, but must be tractable. One must decide whether the toxicities and other outcomes are positively associated, negatively associated, or independent. We characterized toxicity incidence using a multivariate Poisson process and formulated a joint model for the toxicities, surgery, and PFS duration using i.i.d. patient frailties. A simple device is to invert the patient frailty, i.e. use 1/U, to accommodate negative association, or omit it for independence. In the RT trial, radiation-induced toxicities were assumed to be influenced by the RT modality (at the group-level) and the anatomic location of each patient’s tumor (at the patient-level). Because the tumor’s location within the esophagus influences how a dosimetric plan is formulated and implemented, incidences of all radiation-induced toxicities were assumed to be positively associated. Because radiation-induced toxicities may decrease survival, and PFS includes death as an event, toxicity incidence was assumed to be negatively associated with PFS.

To specify prior hyperparameters, a general approach that works well in practice is to use elicited values to establish means and then calibrate the variances using ESS. One should avoid priors that are either excessively informative or unrealistically dispersed. Taking this approach, we specified priors that characterized the expected incidence of each toxicity, and marginally contained the amount of information that would be contributed by 1 or 2 patients. One also must decide whether treatment effects that determine the relative incidences of each toxicity severity are independent or a priori dependent for the therapeutic regimes. We decided that it was appropriate to assume that the treatment effects for the radiation-induced toxicities were exchangeable, and thus used hyperpriors to induce shrinkage for the esophageal RT trial. Finally, the model requires specification of a prior for the frailty variance in relation to an assumed degree of association between the endpoints on the scale of the Poisson intensity domain. We used an uniform prior with lower bound at 0 (independence) and selected the upper bound, 10, to restrict the prior to an interval that excluded an unrealistically high probability of toxicity recurrence.

6.3 Design considerations

Several design features must be considered when planning a TTB-based trial. One first must determine the maximum follow-up duration for which a patient will be monitored for toxicity following treatment. The design requires a schedule for the group sequential tests, based on the information statistics that determine the number and “timing” of the interim analyses. The schedule should be specified in relation to the trial’s expected enrollment rate and the assumed event rates. In addition, the investigators must fix ε to reflect a difference in mean TTB that should be considered too small to be clinically relevant.

We next describe the process of using simulation to calibrate tuning parameters to obtain targeted operating characteristics. To construct alternative simulation scenarios from combinations of the treatment effects, δ, one first must ascertain a “baseline” value for mean TTB, hereafter denoted by μ₀, (e.g. Table 4a) that reflects the expected TTB for a typical patient receiving the control therapy. This can be achieved by accounting for or neglecting prior uncertainty for the model parameters, depending on investigator preference. The former approach requires Monte Carlo simulation, whereby one generates model parameters from the priors for the baseline model parameters (treatment effects omitted), obtains a prior distribution for mean TTB, and fixes μ₀ at the resulting mean. The latter, more practical approach simply fixes the model parameters at their respective prior means and uses (7) to determine μ₀ where δ = 0.

When considering simulation scenarios, one uses μ₀ to identify targeted “effect sizes” for the power computations by considering scenarios that induce varying degrees of relative difference in true mean TTB between treatments. For example, μ₀ was determined to be 33.67 for the control modality, IMRT, in the esophageal trial. The sample size was selected to target a 50% reduction in mean TTB for PBT, which we denote by %Δ*. Thereafter, one can identify alternative simulation scenarios (e.g. Scenarios 1 – 12, 17, 18 in Table 4b) through computation by selecting treatment effect vectors at random, δ = δ*, that achieve the target $\%{\Delta }^{\ast }=100({\mu }^{\ast }∕{\mu }_0^{\ast }-1)$, where μ* and ${\mu }_0^{\ast }$ denote true values of mean TTB determined by δ* for treatment and control, respectively. Note for our model ${\mu }_0^{\ast }$ attains the baseline value, ${\mu }_0^{\ast }={\mu }_0$, when δ* = 0.

After establishing the alternative scenarios, one must simulate trials under each alternative and the null, δ* = 0, storing the resulting posterior probabilities obtained for each sequential interim analysis. After determining the design’s false positive rate, optimal monitoring boundaries can be selected using the process described in Appendix B. In the presence of co-primary endpoints, an objective function characterizing the relative importance of power for each endpoint must be defined with respect to at least one alternative scenario before selecting an optimal design (note that Appendix B uses equal costs). Finally, operating characteristics can be obtained through post-processing of the replicate trials using the optimal monitoring boundaries. The entire simulation process may be repeated multiple times to determine a minimal sample size that detects %Δ* with acceptable power for all alternative scenarios.

7 Discussion

We have proposed a Bayesian design for a randomized clinical trial with group sequential treatment comparisons based on posterior mean TTB and PFS. The complexity of the underlying probability model reflects the complexity of the disease and therapeutic outcomes. TTB, constructed from subjective severity weights, provides a practical continuous statistic for measuring the extent to which a patient tolerates a therapeutic intervention. The statistical model and corresponding trial design offer powerful tools for sequential safety monitoring in settings wherein patients are at risk of many types of toxicities that may result from each single treatment or stem from the combined impacts of multiple types of therapy when used concurrently or administered over a sequence of intervention periods. The trial design reflects the fact that, for many diseases and therapeutic regimes, it is essential to account for both toxicity and efficacy in treatment evaluation.

The problem of handling multiple co-primary endpoints is quite general, and does not pertain specifically to whether Bayesian or conventional frequentist decision rules are used. There is an extensive literature on testing for multiple endpoints. Some useful references are O’Brien (1984), Cook and Farewell (1996), Wassmer et al. (1999), and Jennison and Turnbull (2000). For our comparator in the simulation study, we assumed that PFS and the indicator of toxicity were independent. Alternative approaches that account for association between multiple endpoints have been proposed. Pocock et al. (1987) extended the multiple endpoint testing methods of O’Brien (1984) to address the bivariate problem of combining survival and binary endpoints using linear combinations of asymptotically multivariate normal test statistics. Chang et al. (1997) considered sequential analysis of paired survival endpoints using multivariate counting processes arising from a time-dependent frailty model. Murray (2000) discussed a method for two-sample sequential monitoring of paired censored survival endpoints based on weighted log-rank statistics. The latter two methods could have been used as the comparator in our simulation study by replacing the toxicity indicator with a time-to-event endpoint. Application of any of the three methods aforementioned may have yielded a more powerful comparator.

An important aspect of our decision rules is that they allow the conclusion that one modality is superior in terms of TTB but yields shorter PFS. Such scenarios are not unlikely in many oncology settings, where qualitatively different or more aggressive treatments may improve PFS or survival, but at the cost of increased severity or incidence of adverse events. The model and joint decision rule used in our sequentially adaptive design provide a formal method for treatment comparison based on both safety and efficacy.

Appendix. A Mean Total Toxicity Burden Derivation

Here we provide additional details pertaining to the derivation of mean TTB in Section 4.4. Denoting v = 1/u and

$$c={\left\{\Gamma (1∕\varphi +2){\left(\frac{\varphi }{\varphi +1}\right)}^{(1∕\varphi +2)}\right\}}^{-1},$$

by iterated expectation,

$$\begin{array}{cc}\hfill {\mu }^{\mathit{POC}}(t,x,\theta )& ={\tilde{w}}^{\prime }\pi \left(x\right)E_U\left[\mathit{Pr}\left\{S\right(t)>0\mid u,x,\tilde{\lambda },\tilde{\delta }\}\mid \varphi \right],\hfill \\ \hfill & ={\tilde{w}}^{\prime }\pi \left(x\right){\int }_0^{\infty }\mathit{Pr}\left\{S\right(t)>0\mid u,x,\tilde{\lambda },\tilde{\delta }\}d{\Gamma }^{-1}(u\mid \frac{1}{\varphi }+2,\frac{1}{\varphi }+1),\hfill \\ \hfill & ={\tilde{w}}^{\prime }\pi \left(x\right){\int }_0^{\infty }\{1-\text{exp}(-\mathit{tv}\tilde{\lambda }\text{exp}\left(x\tilde{\delta }\right)\left)\right\}{v}^{(1∕\varphi +1)}\text{exp}\{-v(\varphi +1)∕\varphi \}\mathit{dv},\hfill \\ \hfill & ={\tilde{w}}^{\prime }\pi \left(x\right)\left[1-c{\int }_0^{\infty }{v}^{(1∕\varphi +1)}\text{exp}\left\{-v\left(t\tilde{\lambda }\text{exp}\left(x\tilde{\delta }\right)+\frac{\varphi +1}{\varphi }\right)\right\}\mathit{dv}\right],\hfill \\ \hfill & ={\tilde{w}}^{\prime }\pi \left(x\right)\left\{1-{\left(\frac{\varphi t\tilde{\lambda }\text{exp}\left(x\tilde{\delta }\right)}{\varphi +1}+1\right)}^{-(1∕\varphi +2)}\right\}.\hfill \end{array}$$ (A.1)

B Selecting Optimal Sequential Monitoring Boundaries

A set of optimal sequential monitoring boundaries was selected using the following process. Initially, we simulated 3000 replications for each of scenarios 0, 6 and 16. For each simulated sequential trial, g = 1, …, 3000, we saved the set of posterior probabilities corresponding to each of the four sequential analyses, τ₁, …, τ₄ :

$$\begin{array}{cc}\hfill & \left\{{\phi }^{\mathit{PB}}\right({\epsilon }^{\mathit{TTB}},{\tau }_1),{\phi }^{\mathit{IM}}({\epsilon }^{\mathit{TTB}},{\tau }_1),{\chi }^{\mathit{PB}}({\epsilon }^{\mathit{PFS}},{\tau }_1),{\chi }^{\mathit{IM}}({\epsilon }^{\mathit{PFS}},{\tau }_1),\dots ,\hfill \\ \hfill & {{\phi }^{\mathit{PB}}({\epsilon }^{\mathit{TTB}},{\tau }_4),{\phi }^{\mathit{IM}}({\epsilon }^{\mathit{TTB}},{\tau }_4),{\chi }^{\mathit{PB}}({\epsilon }^{\mathit{PFS}},{\tau }_4),{\chi }^{\mathit{IM}}({\epsilon }^{\mathit{PFS}},{\tau }_4)\}}^{\left(g\right)}.\hfill \end{array}$$

Any improvement in mean TTB or PFS was considered clinically relevant by the participating oncologists, therefore posterior probabilities were computed using ε^TTB = ε^PFS = 0.

A gradient optimization method was implemented to select the set of values for the posterior boundary parameters, α^TTB, α^PFS, β^TTB, β^PFS, that yielded maximum total power for Scenarios 1 and 16 among all choices that controlled the familywise type I error at ≤ 0.07 under Scenario 0. We defined the total power to be the sum of the marginal probability that the sequential procedure concluded that PBT was superior to IMRT for TTB in Scenario 1 plus the marginal probability that the sequential procedure concluded that PBT was superior to IMRT for PFS in Scenario 16. The final design used α^TTB = 3.92, β^TTB = 0.030 and α^PFS = 0.965, β^PFS = 0.028, which produced the OCs provided in Tables 5-6.

In contrast, the conventional design used O’Brien-Fleming boundaries for both group sequential rules. The OCs in Tables 5-6 were computed using the following critical values for comparing toxicity rates between modalities using sequential z-tests for a difference in proportions: (3.60563, 3.08866, 2.74145, 2.13505). The sequential log-rank testing procedure used the following critical values for z-tests for a difference in PFS corresponding to each of the four analyses: (3.675, 3.217, 2.529, 2.167). The O’Brien-Fleming group sequential critical values were obtained through a two-step process that involved generating a set of candidate boundaries using statistical software PASS version 11 using the closest approximation of the actual interim monitoring schedule, then simulating the TTB design under each candidate boundary and selecting the one that yielded the largest total power among those that controlled familywise type I error rate at ≤ 0.07.