A Proportional Hazards Regression Model for the Sub-distribution with Covariates Adjusted Censoring Weight for Competing Risks Data

Abstract

With competing risks data, one often needs to assess the treatment and covariate effects on the cumulative incidence function. Fine and Gray proposed a proportional hazards regression model for the subdistribution of a competing risk with the assumption that the censoring distribution and the covariates are independent. Covariate-dependent censoring sometimes occurs in medical studies. In this paper, we study the proportional hazards regression model for the subdistribution of a competing risk with proper adjustments for covariate-dependent censoring. We consider a covariate-adjusted weight function by fitting the Cox model for the censoring distribution and using the predictive probability for each individual. Our simulation study shows that the covariate-adjusted weight estimator is basically unbiased when the censoring time depends on the covariates, and the covariate-adjusted weight approach works well for the variance estimator as well. We illustrate our methods with bone marrow transplant data from the Center for International Blood and Marrow Transplant Research (CIBMTR). Here cancer relapse and death in complete remission are two competing risks.

1 Introduction

Biomedical research often involves competing risks in which each subject is at risk of failure from K different causes. For competing risks data, one only observes the first event to occur and this precludes the occurrence of another event. Also, one often wishes to estimate and model the cumulative incidence function (CIF), which is the marginal probability of failure of a specific cause. The standard approach of modeling CIF is to model the cause-specific hazard functions for all causes. Let λ_k(t; Z) be the kth conditional cause-specific hazard (k = 1, 2 for simplicity), where Z is given set of covariates. The CIF of cause 1 given by Z is

$$F_1(t;Z)=P(\tilde{T}\le t,∊=1\mid Z)={\int }_0^t{\lambda }_1(s;Z)\exp \left[-{\int }_0^{s^{-}}\left\{{\lambda }_1\right(u;Z)+{\lambda }_2(u;Z\left)\right\}du\right]ds,$$

where $\tilde{T}$ is the failure time and ∊ indicates the type of failure. Here, all cause-specific hazards need to be modeled adequately and correctly. Note that the cumulative incidence function F₁(t; Z) is a subdistribution function since F₁(∞; Z) < 1. Prentice et al. (1978) and Cheng et al. (1998) proposed using Cox (1972) proportional hazards model for all causes. Alternatively, Shen and Cheng (1999) considered a special additive model, and Scheike and Zhang (2002, 2003) proposed and studied a flexible Cox-Aalen model, which allows some of the covariates to have time-varying effects. Since the cumulative incidence function of a specific cause is a function of cause-specific hazards for all causes, it is difficult to summarize the covariate effect (Zhang and Fine, 2008) and to identify the covariate effect on the cumulative incidence function. However, regression methods have been developed to directly model the cumulative incidence function. Fine and Gray (1999) (FG) developed a regression method to directly model the CIF by modeling the subdistribution hazard function through a Cox type regression model, ${\lambda }_k^{\ast }(t,\mathit{Z})=-d\log \{1-F_k(t;\mathit{Z}\left)\right\}∕dt={\lambda }_{k0}^{\ast }\left(t\right)\exp \left({\beta }_k^{⊺}\mathit{Z}\right)$ based on early work by Gray (1988) and Pepe (1991). FG proposed using an inverse probability of the censoring weighting (IPCW) technique to estimate the regression parameter β_k and cumulative baseline subdistribution hazard function ${\Lambda }_{k0}^{\ast }\left(t\right)={\int }_0^t{\lambda }_{k0}^{\ast }\left(s\right)ds$. This approach has been implemented in an R-package, cmprsk. FG's model has been considered and used extensively in cancer studies, epidemiological studies, and many other biomedical studies (Scrucca et al., 2007; Wolbers et al., 2009; Kim, 2007; Lau et al., 2009). Let $r\left(t\right)=I\{C\ge (\tilde{T}\wedge t\left)\right\}$ and G_C(t) = P(C > t), where C is the censoring time. Fine and Gray's approach is based on the fact that $E\left[r\right(t)∕G_{\mathrm{C}}\{(\tilde{T}\wedge C)\wedge t\}\mid \mathit{Data}]=1$ provided that censoring time is independent of the covariates, and FG proposed using the Kaplan-Meier estimator to estimate the unknown censoring distribution G_C. However, in biomedical research studies, the censoring time may depend on some of the covariates and the treatment group. In a clinical trial, patients may be more likely to drop out with some specific value of covariate characteristics, and one treatment group may have a higher dropout rate than the others (Mai, 2008). DiRienzo and Lagakos (2001a,b) showed that when the distribution of censoring depends on both the treatment group and the covariates, in general the null asymptotic distribution of the score test is not centered at zero when the model is misspecified, the tests of treatment group effect can be severely biased. Heinze et al. (2003) showed that if the censoring distributions are not similar in the two comparison groups, the log-rank test and fitting a regression model, such as fitting a proportional hazards model, may not be valid. For the competing risks data, one can show that $E\left[r\right(t)∕G_{\mathrm{C}}\{(\tilde{T}\wedge C)\wedge t\mid \mathit{Data}\}\mid \mathit{Data}]=1$, where $G_{\mathrm{C}}\left\{\right(\tilde{T}\wedge C)\wedge t\mid \mathit{Data}\}$ is the conditional censoring distribution given by Data. Thus, parameter estimates using the inverse probability of censoring weighting approach with the Kaplan-Meier estimator may be biased when the censoring distribution depends on some of the covariates. To adjust the IPCW when censoring distribution depends on some of the covariates, Fine and Gray (1999) suggested using a stratified Kaplan-Meier estimator for the discrete covariates and assuming the Cox model for the continuous covariates. In this study, we considered a regression model for the censoring distribution, such as a Cox proportional hazards model, and using the predicted censoring probability for each individual subject for the weight function. With the Cox model adjusted weight, we derived an efficient variance estimator which includes variation contributed from estimated censoring distribution, and we performed a simulation study to examine the bias that would arise without adjusting covariates for estimating the censoring distribution, potential bias reduction and robustness of using the Cox model for the censoring distribution. Furthermore, Fine and Gray proposed using a stabilized factor ${\widehat{G}}_{\mathrm{C}}\left(t\right)$ with inverse weight $r\left(t\right){\widehat{G}}_{\mathrm{C}}\left(t\right)∕{\widehat{G}}_{\mathrm{C}}\left\{\right(\tilde{T}\wedge C)\wedge t\}$. Our simulation indicates that this stabilized weight improves the efficiency and reduces the bias, but not enough. With the Cox model adjusted weight function, we also considered using a stabilized weight $r\left(t\right){\widehat{G}}_{\mathrm{C}}(t\mid \mathit{X}=x)∕{\widehat{G}}_{\mathrm{C}}\left\{\right(\tilde{T}\wedge C)\wedge t\mid \mathit{X}=x\}$ to improve efficiency and to reduce bias, where X is the covariates, which is associated with the censoring distribution and could be a subset covariates of Z.

The outline of the remainder of the paper is as follows. In Section 2 we describe the competing risks data structure. We introduce a regression-adjusted inverse weighted estimation for the proportional subdistribution hazards model and present the asymptotic results that can be used for inference. Simulation studies are provided in Section 3. In Section 4 we analyze two real data sets, which were originally studied by Kumar et al. (2012) and by Ringdén et al. (2012) using data from the Center for International Blood and Marrow Transplant Research (CIBMTR). Concluding remarks are provided in Section 5. The proof of the main asymptotic result and the simulation procedure are given in Appendix A and B, respectively.

2 Data and covariate adjusted censoring weight

Let ${\tilde{T}}_i$ and C_i be the event time and right censoring time for ith individual, respectively. ∊_i ∈ {1,…,K} indicates the cause of failure. For simplicity, we assume K = 2 in this study. Let $T_i=\min ({\tilde{T}}_i,C_i)$ and ${\Delta }_i=\mathcal{I}({\tilde{T}}_i\le C_i)$. We observe n independent and identically distributed (i.i.d.) data {T_i, Δ_i, Δ_i∊_i, Z_i} for i = 1, …, n, where Z_i = (Z_i1,…, Z_iq)^T are associated covariates. We assume that (${\tilde{T}}_i,{∊}_i$) are independent of C_i given covariates of Z_i. We are interested in modeling the cumulative incidence function of cause 1, F₁(t; Z). Based on Gray (1988) subdistribution hazard technique, Fine and Gray (1999) proposed a proportional subdistribution hazards model

$${\lambda }_1^{\ast }(t;Z)=\frac{-d\log \{1-F_1(t;Z\left)\right\}}{dt}={\lambda }_{10}^{\ast }\left(t\right)\exp \left\{{\beta }_0^{⊺}Z\right\}.$$ (2.1)

There is a direct relationship between the CIF and subdistribution hazard function:

$$F_1(t;Z)=1-\exp \left\{-\left({\int }_0^t{\lambda }_{10}^{\ast }\left(u\right)du\right)e^{{\beta }_0^{⊺}\mathit{Z}}\right\}.$$

Let $N_i^1\left(t\right)=I({\tilde{T}}_i\le t,{∊}_i=1)$ be the underlying counting process associated with cause 1. For right censored competing risks data, $N_i^1\left(t\right)$ and $Y_i^1\left(t\right)=1-N_i^1\left(t^{-}\right)$ are not fully observed. For a censored individual, they are only observed up to the censoring time C_i. Define $r_i\left(t\right)=I\{C_i\ge ({\tilde{T}}_i\wedge t\left)\right\}$. Then $r_i\left(t\right)N_i^1\left(t\right)$ and $r_i\left(t\right)Y_i^1\left(t\right)$ are computable for all times t. Let G_C(t; Z) = P (C ≥ t|Z) be the conditional censoring distribution. Based on the assumption that given covariates Z the event time and censoring time are independent and the models are formulated as standard regression models conditional on Z, it then follows that given Z

$$\begin{array}{cc}\hfill E\left\{\phantom{\mid }\frac{r\left(t\right)N^1\left(t\right)}{G_{\mathrm{C}}(T\wedge t;\mathit{Z})}\mid \mathit{Z}\right\}& =E\left[E\phantom{\mid }\left\{\phantom{\mid }\frac{r\left(t\right)N^1\left(t\right)}{G_{\mathrm{C}}(T\wedge t;\mathit{Z})}\mid T,∊,\mathit{Z}\right\}\mid \mathit{Z}\right]\hfill \\ \hfill & =E\left[\phantom{\mid }E\left\{N^1\right(t)\mid T,∊,\mathit{Z}\}\frac{E\left\{r\right(t)\mid T,∊,\mathit{Z}\}}{G_{\mathrm{C}}(T\wedge t;\mathit{Z})}\mid \mathit{Z}\right]\hfill \\ \hfill & =F_1(t;\mathit{Z}).\hfill \end{array}$$

FG proposed using an inverse probability of the censoring weighting (IPCW) approach to fit the model (2.1) and proposed an IPCW weight function ${\widehat{w}}_i^{\mathrm{KM}}\left(t\right)=r_i\left(t\right){\widehat{G}}_{\mathrm{C}}^{\mathrm{KM}}\left(t\right)∕{\widehat{G}}_{\mathrm{C}}^{\mathrm{KM}}(T_i\wedge t)$, where ${\widehat{G}}_{\mathrm{C}}^{\mathrm{KM}}\left(t\right)$ is the Kaplan-Meier estimator for the unknown censoring distribution. FG proposed estimating the unknown regression coefficient β by solving the score equation

$${\mathit{U}}_{\mathrm{KM}}\left(\beta \right)=\sum _i{\int }_0^{\tau }\left\{{\mathit{Z}}_i-\frac{{\Sigma }_j{w}_j^{\mathrm{KM}}\left(u\right)Y_j^1\left(u\right){\mathit{Z}}_j\exp \left\{{\beta }^{⊺}{\mathit{Z}}_j\right\}}{{\Sigma }_j{w}_j^{\mathrm{KM}}\left(u\right)Y_j^1\left(u\right)\exp \left\{{\beta }^{⊺}{\mathit{Z}}_j\right\}}\right\}{w}_i^{\mathrm{KM}}\left(u\right)d{N}_i^1\left(u\right)=0,$$

where τ is is end of the study time point, and denote the estimate as ${\widehat{\beta }}_{\mathrm{KM}}$. FG showed that under regularity conditions and the condition that the censoring distribution is independent of covariates, ${\widehat{\beta }}_{\mathrm{KM}}$ is consistent for β₀ and derived large sample properties for $\sqrt{n}\left({\widehat{\beta }}_{\mathrm{KM}}-{\beta }_0\right)$ and $\sqrt{n}\left\{{\widehat{\Lambda }}_{10}^{\mathrm{KM}}\left(t\right)-{\Lambda }_{10}^{\ast }\left(t\right)\right\}$, where the cumulative baseline subdistribution hazard ${\Lambda }_{10}^{\ast }\left(t\right)={\int }_0^t{\lambda }_{10}^{\ast }\left(u\right)$ is estimated by

$${\widehat{\Lambda }}_{10}^{\mathrm{KM}}\left(t\right)=\sum _i{\int }_0^t\frac{w_i^{\mathrm{KM}}\left(u\right)d{N}_i^1\left(u\right)}{{\Sigma }_j{w}_j^{\mathrm{KM}}\left(u\right)Y_j^1\left(u\right)\exp \left\{{\widehat{\beta }}_{\mathrm{KM}}^{⊺}{\mathit{Z}}_j\right\}}.$$

It has been shown that in biomedical research studies the censoring time may depend on some of the covariates and the treatment group. To make asymptotically unbiased inference, we needed to model the censoring distribution and to estimate the censoring survival probability, G_C(T ∧ t; Z_i), for each individual. In this study, as suggested by Fine and Gray (1999), we considered the commonly used Cox proportional hazards model for the censoring distribution,

$${\lambda }_{\mathrm{C}}(t;{\mathit{X}}_i)={\lambda }_{\mathrm{C}0}\left(t\right)\exp \left\{{\gamma }_0^{⊺}{\mathit{X}}_i\right\},$$

where X_i is the covariates associated with the censoring distribution and can be a function or subset of Z_i. In practice one can use the standard model checking procedure to check the Cox model assumption for the censoring distribution and use the standard model building procedure to identify the risk factors which are associated with the censoring time. Let x_i be the fixed observed value for the ith individual's covariates, we estimate the predicted censoring survival probability $G_{\text{COX}}^{\mathrm{C}}(t;{\mathit{x}}_i)=P(C>t\mid {\mathit{X}}_i={\mathit{x}}_i)=\exp \{-{\Lambda }_{\mathrm{C}0}(t\left)\exp \right({\gamma }_0^{⊺}{\mathit{x}}_i\left)\right\}$ by

$${\widehat{G}}_{\mathrm{C}}^{\text{COX}}(t;{\mathit{x}}_i)=\exp \{-{\widehat{\Lambda }}_{\mathrm{C}0}(t\left)\exp \right({\widehat{\gamma }}^{⊺}{\mathit{x}}_i\left)\right\},$$ (2.2)

where $\widehat{\gamma }$ is a maximum partial likelihood estimate for γ₀ and ${\widehat{\Lambda }}_{\mathrm{C}0}\left(t\right)$ is the standard Breslow estimator for the cumulative baseline censoring hazard ${\Lambda }_{\mathrm{C}0}\left(t\right)={\int }_0^t{\lambda }_{\mathrm{C}0}\left(u\right)du$. Note that, any administrative censoring events at time τ are not considered as events in the regression estimation. In this study, we considered a covariate-adjusted IPCW weight function

$${\widehat{w}}_i^{\text{COX}}\left(t\right)=r_i\left(t\right){\widehat{G}}_{\mathrm{C}}^{\text{COX}}(t;{\mathit{x}}_i)∕{\widehat{G}}_{\mathrm{C}}^{\text{COX}}(T_i\wedge t;{\mathit{x}}_i).$$

We estimated β in model (2.1) by solving the score equation

$${\mathit{U}}_{\text{COX}}\left(\beta \right)=\sum _i{\int }_0^{\tau }\left\{{\mathit{Z}}_i-\frac{{\Sigma }_j{\widehat{w}}_j^{\text{COX}}\left(u\right)Y_j^1\left(u\right){\mathit{Z}}_j\exp \left\{{\beta }^{⊺}{\mathit{Z}}_j\right\}}{{\Sigma }_j{\widehat{w}}_j^{\text{COX}}\left(u\right)Y_j^1\left(u\right)\exp \left\{{\beta }^{⊺}{\mathit{Z}}_j\right\}}\right\}{\widehat{w}}_i^{\text{COX}}\left(u\right)d{N}_i^1\left(u\right)=0,$$ (2.3)

and denoted the estimate as ${\widehat{\beta }}_{\text{COX}}$. Then we estimated ${\Lambda }_{10}^{\ast }\left(t\right)$ by

$${\widehat{\Lambda }}_{10}^{\text{COX}}\left(t\right)=\sum _i{\int }_0^t\frac{{\widehat{w}}_i^{\text{COX}}\left(u\right)d{N}_i^1\left(u\right)}{{\Sigma }_j{\widehat{w}}_j^{\text{COX}}\left(u\right)Y_j^1\left(u\right)\exp \left\{{\widehat{\beta }}_{\text{COX}}^{⊺}{\mathit{Z}}_j\right\}}.$$

Under regularity conditions (given in Section 6.1)), it can be shown that (see (6.6))

$$\sqrt{n}({\widehat{\beta }}_{\text{COX}}-{\beta }_0)={\Omega }^{-1}\left\{\frac{1}{\sqrt{n}}{\mathit{U}}_{\text{COX}}\left({\beta }_0\right)\right\}+o_P\left(1\right),$$

where Ω = lim_n→∞ n⁻¹I_COX(β₀), I_COX(β) = −∂{U_COX(β)}/∂β, and Ω can be estimated by $\widehat{\Omega }=n^{-1}{\mathit{I}}_{\text{COX}}\left(\widehat{\beta }\right)$ Furthermore (see(6.4)), $n^{-1∕2}{\mathit{U}}_{\text{COX}}\left({\beta }_0\right)=n^{-1∕2}{\sum }_i({\xi }_i^{\text{COX}}+{\psi }_i^{\text{COX}})+o_P\left(1\right)$, where explicit expressions for ${\xi }_i^{\text{COX}}$ and ${\psi }_i^{\text{COX}}$ are given in the Appendix A. The quantities can be estimated by plug-in estimators denoted by ${\xi }_i^{\text{COX}}$ and ${\psi }_i^{\text{COX}}$, respectively. It follows that $\sqrt{n}\left({\widehat{\beta }}_{\text{COX}}-{\beta }_0\right)$ converges in distribution to a mean zero Gaussian distribution with an asymptotic variance that can be estimated by

$${\widehat{\Sigma }}_{\beta }^{\text{COX}}=n\sum _i{\left({\widehat{W}}_{\beta ,i}^{\text{COX}}\right)}^{\otimes 2}=n{\left\{{\mathit{I}}_{\text{COX}}\right({\widehat{\beta }}_{\text{COX}}\left)\right\}}^{-1}\left\{\sum _i{({\widehat{\xi }}_i^{\text{COX}}+{\widehat{\psi }}_i^{\text{COX}})}^{\otimes 2}\right\}{\left\{{\mathit{I}}_{\text{COX}}\right({\widehat{\beta }}_{\text{COX}}\left)\right\}}^{-1},$$

where a^⊗2 = aa^⊺ for a column vector a.

Similarly (see (6.10)), $\sqrt{n}\left\{{\widehat{\Lambda }}_{10}^{\text{COX}}\left(t\right)-{\Lambda }_{10}^{\ast }\left(t\right)\right\}=n^{-1∕2}{\sum }_i{W}_{\Lambda ,i}^{\text{COX}}\left(t\right)+o_P\left(1\right)$, which converges weakly to a mean zero Gaussian process with asymptotic variances, which can be estimated by

$${\widehat{\Sigma }}_{{\Lambda }_{10}}^{\text{COX}}\left(t\right)=\frac{1}{n}\sum _i{\left\{{\widehat{W}}_{\Lambda ,i}^{\text{COX}}\right(t\left)\right\}}^2.$$

Explicit expressions for $W_{\Lambda ,i}^{\text{COX}}\left(t\right)$ and ${\widehat{W}}_{\Lambda ,i}^{\text{COX}}\left(t\right)$ can be found in the Appendix A.

For a given set value of covariates, z₀, the predicted CIF of cause 1 can be estimated by ${\widehat{F}}_1^{\mathrm{KM}}(t;{\mathit{z}}_0)=1-\exp \left\{-{\widehat{\Lambda }}_{10}^{\mathrm{KM}}\left(t\right)\exp \left({\widehat{\beta }}_{\mathrm{KM}}^{⊺}{\mathit{z}}_0\right)\right\}$ or ${\widehat{F}}_1^{\text{COX}}(t;{\mathit{z}}_0)=1-\exp \left\{-{\widehat{\Lambda }}_{10}^{\text{COX}}\left(t\right)\exp \left({\widehat{\beta }}_{\text{COX}}^{⊺}{\mathit{z}}_0\right)\right\}$ respectively. Fine and Gray (1999) derived the large sample property for $\sqrt{n}\left\{{\widehat{F}}_1^{\mathrm{KM}}(t;{\mathit{z}}_0)-F_1(t;{\mathit{z}}_0)\right\}$ when the censoring distribution is independent of the covariates. When the censoring distribution depends on the covariates through a Cox model, by the functional Delta method it follows that $\sqrt{n}\left\{{\widehat{F}}_1^{\text{COX}}(t;{\mathit{z}}_0)-F_1(t;{\mathit{z}}_0)\right\}$ converges in distribution to a Gaussian process with mean zero and asymptotic variances, which can be estimated by

$$n{\{1-{\widehat{F}}_1^{\text{COX}}(t;z_0\left)\right\}}^2\sum _i{\left\{{\widehat{W}}_{F_1,i}^{\text{COX}}\right(t;z_0\left)\right\}}^2,$$

where

$${\widehat{W}}_{F_{1,i}}^{\text{COX}}(t;z_0)=\exp \left({\widehat{\beta }}_{\text{COX}}^{⊺}{z}_0\right)\left\{{\widehat{\Lambda }}_{10}^{\text{COX}}\right(t){\left({\widehat{W}}_{\beta ,i}^{\text{COX}}\right)}^{⊺}{z}_0+{\widehat{W}}_{\Lambda ,i}^{\text{COX}}(t\left)\right\}.$$

Resampling techniques can be used to construct confidence bands for ${\Lambda }_{10}^{\ast }\left(t\right)$ and F₁(t;z₀) (Lin et al., 1994; Scheike et al., 2008).

3 Simulations

We compared the finite-sample performance of the estimator using the covariate-adjusted censoring weight to the unadjusted estimator using the Kaplan-Meier estimator for the censoring distribution. Two simulation studies were considered to examine the potential bias reduction with the covariate-adjusted censoring weight estimator. For the first study, we had one binary covariate. For the second study, we considered one binary covariate and one continuous covariate. In both studies, we compared the performance of estimators using two weights, ${\widehat{w}}_i^{\mathrm{KM}}\left(t\right)$ and ${\widehat{w}}_i^{\text{COX}}\left(t\right)$, respectively.

3.1 Study 1

The regression model below has one binary covariate Z. Given Z, the cumulative incidence functions are given by

$$F_1(t;Z)=1-{\{1-p(1-e^{-t}\left)\right\}}^{\exp \left(\beta Z\right)}$$

and

$$F_2(t;Z)={(1-p)}^{\exp \left(\beta Z\right)}\{1-e^{-t\exp \left(\beta Z\right)}\},$$

where p = F₁(∞|Z = 0). We let p = 0.66 and Z be a Bernoulli random variable, with value 1 for half of the sample and 0 for the other half. For each setting, we simulated 10,000 replicates with sample size of n = 100 and 300, respectively (detailed simulating procedure is given in Appendix B). We set β = 1 and considered the following three simulation scenarios.

Scenario 1	Censoring times are independent of Z:
	Generate censoring times from an exponential distribution ~ exp(λC)
	Set λC = 0.556 for 30% censoring, λC = 1.342 for 50% censoring
Scenario 2	Censoring times depend on Z by a Cox model:
	Generate censoring times from a Cox model, λC(t|Z) = λC exp(βCZ)
	Set βC = 2.5 and λC = 0.137 for 30% censoring
	Set βC = 2.5 and λC = 0.391 for 50% censoring
Scenario 3	Censoring times depend on Z, not by a Cox model:
	C ~ U(0.25, 4.00), if Z = 0, C ~ U(0.07, 1.12), if Z = 1 for 30% censoring
	C ~ U(0.25, 2.00), if Z = 0, C ~ U(0.06, 0.46), if Z = 1 for 50% censoring

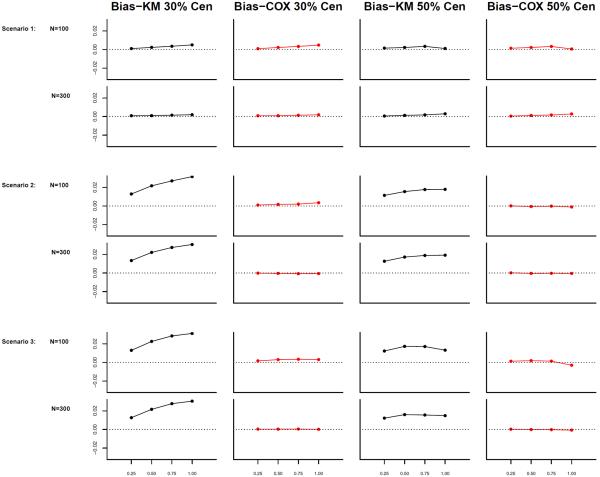
The regression coefficient β was estimated by the methods described in Section 2. We report the average of bias (Bias), the sample standard deviation of $\widehat{\beta }$ (SD), the average of estimated standard error $\left(\overline{\widehat{\sigma }}\right)$ using formula given in Appendix A, average of standardized bias ($\text{Std-B}=E\{\mid \widehat{\beta }-\beta \mid ∕\widehat{\sigma }$), the coverage probability of β, and the mean squared error (MSE). Table 1 shows the simulation results. We also examined the potential bias of estimating the cumulative baseline subdistribution hazard, ${\Lambda }_{10}^{\ast }\left(t\right)$, using both weights at a set of time points, t = (0.25, 0.5, 0.75, 1.00)^⊺. Figure 1 shows the simulation results.

Table 1.

Simulation results for bias reduction with a single binary covariate (β = 1).

				Unadjusted weight				Cox model adjusted weight
Scenario	N	Cens.	β	Bias (Std-B)	$\overline{\widehat{\sigma }}$(SD)	Coverage	MSE	Bias (Std-B)	$\overline{\widehat{\sigma }}$(SD)	Coverage	MSE
1	100	30%	β	0.0081 (0.0291)	0.2759 (0.2798)	0.9494	0.0783	0.0089 (0.0319)	0.2757 (0.2797)	0.9495	0.0783
		50%	β	0.0145 (0.0430)	0.3329 (0.3384)	0.9488	0.1147	0.0153 (0.0450)	0.3331 (0.3387)	0.9489	0.1149
	300	30%	β	0.0010 (0.0061)	0.1584 (0.1586)	0.9499	0.0252	0.0013 (0.0079)	0.1580 (0.1583)	0.9512	0.0251
		50%	β	0.0030 (0.0155)	0.1899 (0.1909)	0.9498	0.0365	0.0033 (0.0174)	0.1898 (0.1908)	0.9503	0.0364
2	100	30%	β	−.1119 (0.3592)	0.3041 (0.3116)	0.9278	0.1096	0.0050 (0.0160)	0.3080 (0.3123)	0.9487	0.0976
		50%	β	−.1162 (0.2719)	0.4075 (0.4271)	0.9359	0.1959	0.0175 (0.0398)	0.4217 (0.4388)	0.9501	0.1929
	300	30%	β	−.1244 (0.7109)	0.1741 (0.1750)	0.8865	0.0461	0.0042 (0.0236)	0.1765 (0.1762)	0.9503	0.0311
		50%	β	−.1336 (0.5596)	0.2306 (0.2346)	0.9063	0.0729	0.0055 (0.0226)	0.2393 (0.2409)	0.9511	0.0581
3	100	30%	β	−.1020 (0.3383)	0.2937 (0.3016)	0.9312	0.1013	0.0045 (0.0145)	0.3036 (0.3096)	0.9503	0.0958
		50%	β	−.0988 (0.2507)	0.3797 (0.3941)	0.9350	0.1650	0.0168 (0.0401)	0.4057 (0.4198)	0.9487	0.1765
	300	30%	β	−.1099 (0.6491)	0.1685 (0.1692)	0.8927	0.0407	0.0026 (0.0147)	0.1748 (0.1749)	0.9535	0.0306
		50%	β	−.1088 (0.5009)	0.2152 (0.2173)	0.9152	0.0591	0.0072 (0.0310)	0.2309 (0.2332)	0.9508	0.0544

Bias=Average of bias of $\widehat{\beta }$; SD=Sample standard deviation of $\widehat{\beta }$; $\overline{\widehat{\sigma }}$=Average of estimated standard error; Std-B = $E\{\mid \widehat{\beta }-\beta \mid ∕\widehat{\sigma }\}$; MSE=Mean squared error.

Figure 1.

Simulation results (1 covariate) for biases of cumulative baseline subdistribution hazards at t = (0.25, 0.5, 0.75, 1)^T with 30% and 50% censoring, respectively.

The simulation results show that when the censoring time depends on the covariate (scenario 2 and 3), the unadjusted estimator produces significantly biased results, and the estimator using the covariate-adjusted censoring weight provides satisfactory results where the biases are all close to zero. Both estimators give satisfactory variance estimates and have almost identical sample standard deviations (see scenario 2 and 3 in Table 1). Regarding the cumulative subdistribution hazard estimators, estimates using the Cox model adjusted weights have smaller biases compared to those using the unadjusted Kaplan-Meier weight at almost all time points (see Figure 1). Simulation results also indicated that the estimator using the Cox model adjusted weight provides satisfactory results when the Cox model is not the true model for the censoring distribution (see scenario 3 in Table 1 and Figure 1). In scenario 1, where the censoring distribution is independent of the covariate Z, both estimators provide satisfactory results in estimating the covariate effect and cumulative baseline subdistribution hazard function. Both estimators also have almost identical sample standard deviation and similar MSE, which indicate that the potential efficiency losses from modeling the censoring distribution are minimal when using covariate-adjusted censoring weights.

3.2 Study 2

The regression models below have one binary covariate Z₁ and one continuous covariate Z₂. Given Z₁ and Z₂, the cumulative incidence functions are given by

$$F_1(t;Z_1;Z_2)=1-{\{1-p(1-e^{-t}\left)\right\}}^{\exp ({\beta }_1{Z}_1+{\beta }_2{Z}_2)}$$

and

$$F_2(t;Z_1,Z_2)={(1-p)}^{\exp ({\beta }_1{Z}_1+{\beta }_2{Z}_2)}\{1-e^{-t\exp ({\beta }_1{Z}_1+{\beta }_2{Z}_2)}\}.$$

We let p = 0.66, and Z₁ is a Bernoulli random variable, with a value 1 for half of the sample and 0 for the other half. Z₂ is a N(0,1) random variable. We set β₁ = 1, β₂ = 0.5 and considered the following four scenarios.

Scenario 1	Censoring times are independent of Z1 and Z2
	Generate censoring times from an exponential distribution ~ exp(λC)
	Set λC = 0.547 for 30% censoring, λC = 1.352 for 50% censoring
Scenario 2	Censoring times depend on Z1 by a Cox model
	Generate censoring times from λC(t|Z) = λC exp(βC1Z1)
	Set βC1 = 2.5. Set λC = 0.137 for 30% censoring,
	λC = 0.397 for 50% censoring
Scenario 3	Censoring times depend on Z1 and Z2 by a Cox model
	Generate censoring times from λC(t|Z) = λC exp(βC1Z1 + βC2Z2)
	Set βC1 = 2.5, βC2 = 2.5. Set λC = 0.082 for 30% censoring,
	λC = 0.389 for 50% censoring
Scenario 4	Censoring times depend on Z1, not by a Cox model
	C ~ U(0.25, 4.00), if Z1 = 0, C ~ U(0.07, 1.14), if Z1 = 1 for 30% censoring
	C ~ U(0.25, 2.00), if Z1 = 0, C ~ U(0.06, 0.438), if Z1 = 1 for 50% censoring

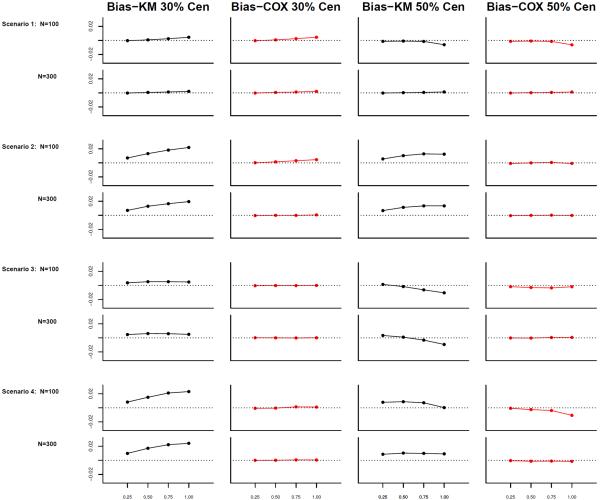
For each setting, we simulated 10,000 replicates with n = 100 and 300. The regression coefficients β₁ and β₂ were estimated by the methods described in Section 2. Table 2 shows the simulation results. We also examined the potential bias of estimating the cumulative baseline subdistribution hazard, ${\Lambda }_{10}^{\ast }\left(t\right)$, using both weights at a set of time points t = (0.25, 0.5, 0.75, 1.00)^T for selected scenarios. Figure 2 shows the simulation results.

Table 2.

Simulation results for biases using 1 binary and 1 continuous covariate (β₁ = 1, β₂ = 0.5).

				Unadjusted weight				Cox model adjusted weight
Scenario	N	Cens.	β	Bias (Std-B)	$\widehat{\sigma }$(SD)	Coverage	MSE	Bias (Std-B)	$\widehat{\sigma }$(SD)	Coverage	MSE
1	100	30%	β 1	0.0148 (0.0521)	0.2793 (0.2849)	0.9462	0.0814	0.0154 (0.0542)	0.2793 (0.2847)	0.9463	0.0813
			β 2	0.0130 (0.0873)	0.1424 (0.1483)	0.9381	0.0222	0.0130 (0.0876)	0.1424 (0.1482)	0.9394	0.0221
		50%	β 1	0.0293 (0.0847)	0.3353 (0.3463)	0.9474	0.1207	0.0299 (0.0863)	0.3355 (0.3464)	0.9468	0.1209
			β 2	0.0143 (0.0812)	0.1676 (0.1763)	0.9362	0.0313	0.0146 (0.0827)	0.1676 (0.1764)	0.9362	0.0313
	300	30%	β 1	0.0039 (0.0242)	0.1595 (0.1608)	0.9498	0.0259	0.0041 (0.0254)	0.1592 (0.1602)	0.9495	0.0257
			β 2	0.0042 (0.0521)	0.0807 (0.0813)	0.9494	0.0066	0.0043 (0.0535)	0.0806 (0.0811)	0.9485	0.0066
		5%0	β 1	0.0062 (0.0327)	0.1898 (0.1883)	0.9525	0.0355	0.0063 (0.0333)	0.1897 (0.1881)	0.9529	0.0354
			β 2	0.0063 (0.0661)	0.0941 (0.0958)	0.9448	0.0092	0.0065 (0.0674)	0.0941 (0.0957)	0.9438	0.0092
2	100	30%	β 1	−.0938 (0.2949)	0.3036 (0.3180)	0.9243	0.1099	0.0119 (0.0370)	0.3101 (0.3220)	0.9421	0.1038
			β 2	0.0273 (0.1778)	0.1462 (0.1536)	0.9355	0.0243	0.0160 (0.1037)	0.1468 (0.1540)	0.9357	0.0240
		50%	β 1	−.0955 (0.2241)	0.4031 (0.4262)	0.9325	0.1908	0.0179 (0.0409)	0.4181 (0.4385)	0.9414	0.1926
			β 2	0.0247 (0.1349)	0.1740 (0.1831)	0.9333	0.0341	0.0142 (0.0771)	0.1748 (0.1839)	0.9354	0.0340
	300	30%	β 1	−.1089 (0.6286)	0.1734 (0.1733)	0.9002	0.0419	0.0049 (0.0277)	0.1771 (0.1769)	0.9514	0.0313
			β 2	0.0174 (0.2056)	0.0827 (0.0845)	0.9409	0.0074	0.0050 (0.0589)	0.0831 (0.0848)	0.9428	0.0072
		50%	β 1	−.1136 (0.4956)	0.2271 (0.2291)	0.9153	0.0654	0.0049 (0.0205)	0.2363 (0.2380)	0.9516	0.0566
			β 2	0.0142 (0.1418)	0.0979 (0.1002)	0.9407	0.0102	0.0027 (0.0273)	0.0984 (0.1004)	0.9434	0.0101
3	100	30%	β 1	−.0299 (0.0945)	0.3061 (0.3168)	0.9418	0.1012	0.0145 (0.0459)	0.3070 (0.3149)	0.9466	0.0994
			β 2	−.0527 (0.2665)	0.1898 (0.1979)	0.9224	0.0419	0.0014 (0.0069)	0.1934 (0.1992)	0.9422	0.0397
		50%	β 1	−.0692 (0.1711)	0.3872 (0.4042)	0.9366	0.1682	0.0163 (0.0398)	0.3935 (0.4090)	0.9441	0.1676
			β 2	−.0963 (0.3695)	0.2501 (0.2605)	0.9087	0.0771	−.0007 (0.0025)	0.2630 (0.2728)	0.9380	0.0744
	300	30%	β 1	−.0473 (0.2687)	0.1750 (0.1762)	0.9363	0.0333	0.0018 (0.0102)	0.1749 (0.1758)	0.9486	0.0309
			β 2	−.0631 (0.5767)	0.1079 (0.1094)	0.8987	0.0159	−.0016 (0.0148)	0.1097 (0.1101)	0.9494	0.0121
		50%	β 1	−.0874 (0.3920)	0.2196 (0.2231)	0.9266	0.0574	0.0046 (0.0206)	0.2230 (0.2251)	0.9489	0.0507
			β 2	−.1035 (0.7300)	0.1404 (0.1418)	0.8698	0.0308	0.0022 (0.0146)	0.1488 (0.1504)	0.9451	0.0226
4	100	30%	β 1	−.0773 (0.2578)	0.2934 (0.2999)	0.9358	0.0959	0.0149 (0.0481)	0.3035 (0.3089)	0.9476	0.0956
			β 2	0.0251 (0.1642)	0.1441 (0.1526)	0.9346	0.0239	0.0146 (0.0952)	0.1444 (0.1529)	0.9361	0.0236
		50%	β 1	−.0731 (0.1868)	0.3799 (0.3913)	0.9402	0.1584	0.0265 (0.0636)	0.4040 (0.4163)	0.9494	0.1740
			β 2	0.0248 (0.1390)	0.1708 (0.1783)	0.9361	0.0324	0.0150 (0.0840)	0.1713 (0.1787)	0.9366	0.0322
	300	30%	β 1	−.0924 (0.5450)	0.1672 (0.1695)	0.9076	0.0372	0.0055 (0.0314)	0.1735 (0.1750)	0.9485	0.0306
			β 2	0.0142 (0.1703)	0.0816 (0.0833)	0.9439	0.0071	0.0028 (0.0330)	0.0818 (0.0834)	0.9462	0.0070
		50%	β 1	−.0877 (0.4128)	0.2149 (0.2124)	0.9327	0.0528	0.0101 (0.0446)	0.2290 (0.2269)	0.9544	0.0516
			β 2	0.0123 (0.1255)	0.0960 (0.0977)	0.9434	0.0097	0.0023 (0.0232)	0.0963 (0.0982)	0.9455	0.0096

Bias=Average of bias of $\widehat{\beta }$; SD=Sample standard deviation of $\widehat{\beta }$; $\overline{\widehat{\sigma }}$=Average of estimated standard error; Std-B = $E\{\mid \widehat{\beta }-\beta \mid ∕\widehat{\sigma }\}$; MSE=Mean squared error.

Figure 2.

Simulation results (2 covariates) for biases of cumulative baseline subdistribution hazards at t = (0.25, 0.5, 0.75, 1.00)^T with 30% and 50% censoring, respectively.

This simulation study shows similar results as in study 1. The unadjusted estimator produces biased results when the censoring distribution depends on the covariates (scenario 2 to 4), and the estimator using the Cox model adjusted weight provides a good bias reduction. Both estimators give satisfactory variance estimates for both parameters. Regarding the cumulative baseline subdistribution hazard estimates, estimates using the Cox-adjusted weight have smaller biases at almost all points (see Figure 2).

Both simulation studies show that the unadjusted estimator produces significant biased results when the censoring time depends on the covariates and the proposed estimator using covariate adjusted weight works well in bias reduction.

4 Real data examples

4.1 Example 1

We considered data from multiple myeloma patients treated with allogeneic stem cell transplantation from the Center for International Blood and Marrow Transplantat Research (CIBMTR) (Kumar et al., 2012). The CIBMTR is comprised of clinical and basic scientists who share data on their blood and bone marrow transplant patients with the CIBMTR Data Collection Center located at the Medical College of Wisconsin. The CIBMTR has a repository of information regarding the results of transplants at more than 450 transplant centers worldwide. The data used in this paper consist of patients transplanted from 1995 to 2005, and we compared the outcomes between transplant periods: 2001-2005 (N=488) versus 1995-2000 (N=375) (Kumar et al., 2012). Two competing events are multiple myeloma relapse and treatment-related mortality (TRM) defined as death without relapse. The CIBMTR study (Kumar et al., 2012) identified that donor type and prior autologous transplantation were associated with relapse or TRM. The variables considered in this example are transplant time period (GP (main interest of the study): 1 for transplanted in 2001-2005 versus 0 for transplanted in 1995-2000), donor type (DNR: 1 for Unrelated or other related donor (N=280) versus 0 for HLA-identical sibling (N=584)), and prior autologous transplant (PREAUTO: 1 for Auto+Allo transplant (N=399) versus 0 for allogeneic transplant alone (N=465)).

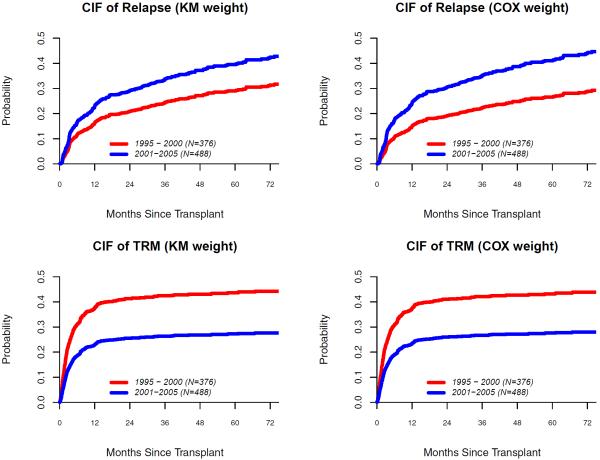
First, we fit a Cox model for the censoring distribution where relapsed or dead individuals are considered as censoring subjects. The hazard ratios (HR) are: HR(GP)=6.42 (P < 0.0001); HR(DNR)=0.48 (p = 0.0018); HR(PREAUTO)=1.73 (p = 0.0013). These results indicate that the censoring distribution depends on the transplant time period, donor type and prior autologous transplantation. Next, we fit a proportional subdistribution hazards model (2.1) with the Kaplan-Meier estimated unadjusted weight and the Cox model adjusted weight, and we computed the predicted cumulative incidence probability for a patient who received an HLA-identical sibling donor allogeneic transplantation in 1995-2000 or in 2001-2005 (see results in Table 3–4 and Figure 3). Both weights give similar estimates for TRM. However, for cancer relapse, the regression estimate of the main treatment effect are $\widehat{\beta }=0.38$ and $\widehat{\beta }=0.54$ by unadjusted weight and Cox model adjusted weight, respectively. At three years after transplant, the differences in cumulative incidence of relapse between late and early transplant (TX) patients are 0.09 (CIF=0.34 for the late TX versus CIF=0.25 for the early TX) and 0.13 (CIF=0.35 for the late TX versus CIF=0.22 for the early TX) by unadjusted weight and Cox model adjusted weight, respectively. The unadjusted weight underestimates the effect size of CIF of relapse by 4% compared to the point estimate using the Cox model adjusted weight (Table 4). Underestimated effect size counts about 14% (0.04/((0.22+0.35)/2)) of estimated average CIF, which leads to quite a large relative bias.

Table 3.

Fit a proportional subdistribution hazards model.

	Unadjusted weight	Cox model adjusted weight
Variable	$\widehat{\beta }$; exp(β) (95% CI); P	$\widehat{\beta }$; exp(β) (95% CI); P
RELAPSE
GP	0.38; 1.47(1.16–1.86); 0.0017	0.54; 1.71(1.34–2.20); < 0.0001
DNR	0.39; 1.48(1.18–1.86); 0.0007	0.35; 1.42(1.13–1.78); 0.0027
PREAUTO	0.41; 1.51(1.19–1.91); 0.0007	0.42; 1.53(1.21–1.93); 0.0004
TRM
GP	−0.59; 0.55(0.42–0.73); < 0.0001	−0.56; 0.57(0.43–0.75); < 0.0001
DNR	0.57; 1.76(1.38–2.25); < 0.0001	0.55; 1.73(1.35–2.20); < 0.0001
PREAUTO	−0.38; 0.68(0.51–0.91); 0.0099	−0.37; 0.69(0.52–0.92); 0.0117

Table 4.

Predicted CIF of relapse and TRM for a patient who received an HLA-identical sibling donor and allogeneic along transplantation

	Unadjusted Weight			Cox model adjusted Weight
	1995–2000	2001–2005		1995–2000	2001–2005
Time	${\widehat{F}}_1$ (95% CI)	${\widehat{F}}_2$ (95% CI)	$\mid {\widehat{F}}_1-{\widehat{F}}_2\mid$	${\widehat{F}}_1$ (95% CI)	${\widehat{F}}_2$ (95% CI)	$\mid {\widehat{F}}_1-{\widehat{F}}_2\mid$
RELAPSE
1 Year	0.16 (0.13–0.19)	0.23 (0.18–0.27)	0.07	0.15 (0.13–0.17)	0.24 (0.18–0.30)	0.09
3 Year	0.25 (0.20–0.29)	0.34 (0.28–0.40)	0.09	0.22 (0.20–0.25)	0.35 (0.28–0.42)	0.13
5 Year	0.29 (0.24–0.34)	0.40 (0.33–0.46)	0.11	0.26 (0.24–0.30)	0.41 (0.33–0.49)	0.15
TRM
1 Year	0.38 (0.32–0.43)	0.23 (0.18–0.28)	0.15	0.37 (0.34–0.41)	0.23 (0.17–0.29)	0.14
3 Year	0.42 (0.37–0.48)	0.26 (0.20–0.32)	0.16	0.42 (0.38–0.46)	0.27 (0.20–0.33)	0.15
5 Year	0.44 (0.38–0.49)	0.27 (0.21–0.33)	0.17	0.43 (0.39–0.47)	0.27 (0.21–0.34)	0.16

Figure 3.

Predicted cumulative incidence probability of relapse and TRM for a patient who received an HLA-identical sibling donor allogeneic transplantation.

4.2 Example 2

We considered another CIBMTR study data set (Ringdén et al., 2012) that consists of 177 myeloma patients who received a reduced-intensity conditioning allogeneic transplantation. Cancer relapse and TRM were two competing risks in this study. 105 patients received prior autologous transplant, and 72 patients received allogeneic transplant alone. We were interested in transplant type effect on relapse and TRM. Let PREAUTO be the indicator of transplant type (1 for Auto+Allo transplant versus 0 for Allogeneic transplant alone). Here the censoring distribution depends on the transplant type (p = 0.0047). We fit a proportional subdistribution hazards model (2.1) for PREAUTO with unadjusted weight and Cox model adjusted weight, respectively. For relapse, we have ${\widehat{\beta }}_{\text{cox}}=-0.34(\widehat{\sigma }=0.25)$; $\exp \left({\widehat{\beta }}_{\text{cox}}\right)=0.71$ and ${\widehat{\beta }}_{\mathrm{KM}}=-0.41(\widehat{\sigma }=0.25)$; $\exp \left({\widehat{\beta }}_{\mathrm{KM}}\right)=0.66$. Here the Cox model adjusted weight reduces a relative bias of 21% ((0.41 − 0.34)/0.34).

5 Concluding remarks

We have shown that the competing risks regression based on IPCW techniques may be biased when the censoring distribution depends on the covariates and the biases could be significant for fixed sample sizes. We considered a regression model for the censoring distribution, and used the Cox proportional hazards model to predict the censoring weight for each individual.

Clearly, using the Cox model to estimate the censoring weights rely on this model fitting well. Our methodology may be adapted to deal with other regression models for the censoring distribution, for example additive hazards models that are more flexible. Efficient variance estimator, which includes variation contributed from estimated censoring distribution, needs to be derived for any alternative model-based weight function, and a computing package needs to be further developed as well.

The censoring time could depend on a time-dependent covariate, but in this case the predictions given the fixed covariates of the competing risks regression model may be hard to get, and this is generally not directly feasible. As Kalbfleisch and Prentice (2002) pointed out that the predicted survival probability is no longer feasible for a random (internal) time-dependent covariate. Further study will be needed.

Recently, the inverse probability of censoring weighting (IPCW) technique (Robins and Rotnitzky, 1992) has been used extensively for right-censored survival data and, specifically, for completing risks data. It has been shown that regression modeling of the censoring distribution can be used to improve the efficiency of the IPCW technique (Bickel et al., 1993; Van der Laan and Robins, 2003; Scheike et al., 2008) even if the censoring distribution is independent of the covariates. In this study, we showed that the covariate-adjusted IPCW technique can be used to reduce bias for modeling the subdistribution hazard function when censoring depends on the covariates. In general, the covariate-adjusted IPCW technique should be considered to improve efficiency and reduce bias.

We have developed an R-package, wtcrsk, which is available on CRAN.

6 Appendix A

Here we present regularity conditions and give detailed proofs for the asymptotic properties of ${\widehat{\beta }}_{\mathit{COX}}$ and ${\widehat{\Lambda }}_{10}^{\text{COX}}\left(t\right)$. Similar arguments can been seen in Ghosh and Lin (2002). First, assuming the censoring distribution depends on covariates X through a Cox proportional hazards model where X could be a subset covariates of Z,

$${\lambda }_{\mathrm{C}}(t;\mathit{X})={\lambda }_{\mathrm{C}0}\left(t\right)\exp \left\{{\gamma }_0^{⊺}\mathit{X}\right\}.$$

Let $N_i^{\mathrm{C}}\left(t\right)=I(T_i\le t;{\Delta }_i=0)$, Y_i(t) = I(T_i ≥ t), U_C(γ) be the partial likelihood for the censoring time, and

$${\mathit{S}}_{\mathrm{C}}^{\left(k\right)}(\gamma ,t)=\frac{1}{n}\sum _i{Y}_i\left(t\right){\mathit{X}}_i^{\otimes k}\exp \left\{{\gamma }^{⊺}{\mathit{X}}_i\right\},\text{for}k=0,1,2$$

$$s_{\mathrm{C}}^{\left(k\right)}(\gamma ,t)=E\left\{Y_1\right(t\left){\mathit{X}}_1^{\otimes k}{e}^{{\gamma }^{⊺}{\mathit{X}}_1}\right\},\text{for}k=0,1,2.$$

Further, let

$${\mathit{S}}_{\text{COX}}^{\left(k\right)}(\beta ,t)=\frac{1}{n}\sum _i{\widehat{w}}_i^{\text{COX}}\left(t\right)Y_i^1\left(t\right){\mathit{Z}}_i^{\otimes k}\exp \left\{{\beta }^{⊺}{\mathit{Z}}_i\right\},\text{for}k=0,1,2.$$

$${\mathit{s}}_{\text{COX}}^{\left(k\right)}(\beta ,t)=E\left\{Y_1^1\right(t\left)G_{\mathrm{C}}^{\text{COX}}\right(t;{\mathbf{X}}_1\left){\mathit{Z}}_1^{\otimes k}{e}^{{\beta }^{⊺}{\mathit{Z}}_1}\right\},\text{for}k=0,1,2,$$

where $G_{\mathrm{C}}^{\text{COX}}(t;\mathit{X})=\exp \{-{\Lambda }_{\mathrm{C}0}(t\left)\exp \right({\gamma }_0^{⊺}\mathit{X}\left)\right\}$ and ${\Lambda }_{\mathrm{C}0}\left(t\right)={\int }_0^t{\lambda }_{\mathrm{CO}}\left(u\right)du$.

We assume the following regularity conditions to be hold throughout the appendix.

6.1 Assumptions

• (A1){${\tilde{T}}_i$, X_i, Z_i, $Y_i^1$, Δ_i, ε_i}, i = 1, …, n, are i.i.d. instances of {$\tilde{T}$, X, Z, Y¹, Δ, ε}.
• (A2)$\tilde{T}$ and C are independent conditional on X, Z.
• (A3)There is a maximum follow-up time τ < ∞ such that P(T > τ) > 0.
• (B1)The hazard for the right-censoring times is ${\lambda }_{\ma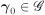thrm{C}}(t;\mathit{X})={\lambda }_{\mathrm{C}0}\left(t\right)\exp \left\{{\gamma }_0^{⊺}\mathit{X}\right\}$, where ${\int }_0^{\tau }{\lambda }_{\mathrm{C}0}\left(t\right)dt<\infty$ and , for a compact .
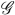• (B2)The covariates X are bounded almost surely.
• (B3)
  The matrix

  $${\Omega }_{\mathrm{C}}={\int }_0^{\tau }\left[\frac{{\mathit{s}}_{\mathrm{C}}^{\left(2\right)}({\gamma }_0,t)}{s_{\mathrm{C}}^{\left(0\right)}({\gamma }_0,t)}-{\left\{\frac{{\mathit{s}}_{\mathrm{C}}^{\left(1\right)}({\gamma }_0,t)}{s_{\mathrm{C}}^{\left(0\right)}({\gamma }_0,t)}\right\}}^{\otimes 2}\right]s_{\mathrm{C}}^{\left(0\right)}({\gamma }_0,t){\lambda }_{\mathrm{C}0}\left(t\right)dt$$

  is positive definite.
• (C1)The subdistribution hazards for cause one is ${\lambda }_1^{\a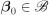st }(t\mid \mathit{Z})={\lambda }_{10}^{\ast }\left(t\right)\exp \left({\beta }_0^{⊺}\mathit{Z}\right)$, where ${\int }_0^{\tau }{\lambda }_{10}^{\ast }\left(t\right)dt<\infty$ and , for a compact .
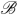• (C2)The covariates Z are bounded almost surely.
• (C3)
  The matrix

  $$\Omega ={\int }_0^{\tau }\left[\frac{{\mathit{s}}_{\text{COX}}^{\left(2\right)}({\beta }_0,t)}{s_{\text{COX}}^{\left(0\right)}({\beta }_0,t)}-\left\{\frac{{\mathit{s}}_{\text{COX}}^{\left(1\right)}({\beta }_0,t)}{s_{\text{COX}}^{\left(0\right)}({\beta }_0,t)}\right\}{}^{\otimes 2}\right]s_{\text{COX}}^{\left(0\right)}({\beta }_0,t){\lambda }_{10}^{\ast }\left(t\right)dt$$

  is positive definite.

6.2 Preliminaries

To estimate the censoring distribution we use Cox regression with the roles of $\tilde{T}$ and C exchanged. Any administrative censoring events at time τ are not considered as events in the regression estimation. From assumption (B1) the censoring process N^C(t), for 0 ≤ t < τ, has intensity on the Cox model form. For this process, conditions (A1), (A2), (A3), (B1), (B2), and (B3), are sufficient to fulfill the conditions for the large sample results on the Cox model of Andersen and Gill (1982) (see their Theorem 4.1).

Let $\widehat{\gamma }$ and ${\widehat{\Lambda }}_{\mathrm{C}0}$ be the Cox estimates of γ₀ and Λ_C0, and let

$${\widehat{G}}_{\mathrm{C}}^{\text{COX}}(t;{\mathit{X}}_i)=\exp \left\{-{\widehat{\Lambda }}_{\mathrm{C}0}\left(t\right)\exp \left({\widehat{\gamma }}^{⊺}{\mathit{X}}_i\right)\right\}$$

By the arguments given by Andersen and Gill (1982), see also Equation (2.1) of Lin et al. (1994), we have

$${\widehat{G}}_{\mathrm{C}}^{\text{COX}}(t;{\mathit{X}}_i)-G_{\mathrm{C}}^{\text{COX}}(t;{\mathit{X}}_i)=-\frac{G_{\mathrm{C}}^{\text{COX}}(t;{\mathit{X}}_i)}{n}\sum _{j=1}^n{\int }_{u=0}^{\tau }\left[{\mathit{h}}^{⊺}(t,0,{\mathit{X}}_i){\Omega }_{\mathrm{C}}^{-1}\left\{{\mathit{X}}_j-\frac{{\mathit{s}}_{\mathrm{C}}^{\left(1\right)}({\gamma }_0,u)}{s_{\mathrm{C}}^{\left(0\right)}({\gamma }_0,u)}\right\}+\frac{e^{\left({\gamma }_0^{⊺}{\mathit{X}}_i\right)}I(u\le t)}{{\mathit{s}}_{\mathrm{C}}^0({\gamma }_0,u)}\right]d{M}_{\text{COX},j}^{\mathrm{C}}\left(u\right)+o_P\left(n^{-1∕2}\right),$$ (6.1)

where Ω_C was defined in (B3), and

$$\mathit{h}(t,u,\mathit{X})=e^{\left({\gamma }_0^{⊺}\mathit{X}\right)}{\int }_{v=u}^t\left\{\mathit{X}-\frac{{\mathit{s}}_{\mathrm{C}}^{\left(1\right)}({\gamma }_0,v)}{s_{\mathrm{C}}^{\left(0\right)}({\gamma }_0,v)}\right\}d{\Lambda }_{\mathrm{C}0}\left(v\right),$$

and

$$M_{\text{COX},i}^{\mathrm{C}}\left(t\right)=N_i^{\mathrm{C}}\left(t\right)-{\int }_0^t{Y}_i\left(u\right)\exp \left\{{\gamma }_0^{⊺}{\mathit{X}}_i\right\}d{\Lambda }_{\mathrm{C}0}\left(u\right),$$

is a martingale with respect to the censoring filtration. Note that by (6.1),

$$\begin{array}{cc}\hfill & \frac{{\widehat{G}}_{\mathrm{C}}^{\text{COX}}(t;{\mathit{X}}_i)}{{\widehat{G}}_{\mathrm{C}}^{\text{COX}}(T_i\wedge t;{\mathit{X}}_i)}-\frac{G_{\mathrm{C}}^{\text{COX}}(t;{\mathit{X}}_i)}{G_{\mathrm{C}}^{\text{COX}}(T_i\wedge t;{\mathit{X}}_i)}\hfill \\ \hfill & =I(T_i<t)\frac{G_{\mathrm{C}}^{\text{COX}}(T_i;{\mathit{X}}_i)\left\{{\widehat{G}}_{\mathrm{C}}^{\text{COX}}\right(t;{\mathit{X}}_i)-G_{\mathrm{C}}^{\text{COX}}(t;{\mathit{X}}_i\left)\right\}-G_{\mathrm{C}}^{\text{COX}}(t;{\mathit{X}}_i)\left\{{\widehat{G}}_{\mathrm{C}}^{\text{COX}}\right(T_i;{\mathit{X}}_i)-G_{\mathrm{C}}^{\text{COX}}(T_i;{\mathit{X}}_i\left)\right\}}{{\widehat{G}}_{\mathrm{C}}^{\text{COX}}(T_i;{\mathit{X}}_i)G_{\mathrm{C}}^{\text{COX}}(T_i;{\mathit{X}}_i)}\hfill \\ \hfill & =-I(T_i<t)\frac{G_{\mathrm{C}}^{\text{COX}}(t;{\mathit{X}}_i)}{G_{\mathrm{C}}^{\text{COX}}(T_i;{\mathit{X}}_i)}\hfill \\ \hfill & \times \frac{1}{n}\sum _{j=1}^n{\int }_{u=0}^{\tau }\left[{\mathit{h}}^{⊺}(t,T_i,{\mathit{X}}_i){\Omega }_{\mathrm{C}}^{-1}\left\{{\mathit{X}}_j-\frac{{\mathit{s}}_{\mathrm{C}}^{\left(1\right)}({\gamma }_0,u)}{s_{\mathrm{C}}^{\left(0\right)}({\gamma }_0,u)}\right\}+\frac{e^{{\gamma }_0^{⊺}{\mathit{X}}_i}I(T_i<u\le t)}{s_{\mathrm{C}}^{\left(0\right)}({\gamma }_0,u)}\right]d{M}_{\text{COX},j}^{\mathrm{C}}\left(u\right)\hfill \\ \hfill & +o_P\left(n^{-1∕2}\right).\hfill \end{array}$$ (6.2)

Let $w_i^{\text{COX}}\left(t\right)=r_i\left(t\right)G_{\mathrm{C}}^{\text{COX}}(t;{\mathit{X}}_i)∕G_{\mathrm{C}}^{\text{COX}}(T_i\Lambda t;{\mathit{X}}_i)$. From the i.i.d. assumption (A1) and the boundedness implied by (A3), (B1), (B2), (C1) and (C2)

$${\mathit{S}}_{\text{COX}}^{\left(k\right)}(\beta ,t)=\frac{1}{n}\sum _{i=1}^n{Y}_i^1\left(t\right)w_i^{\text{COX}}\left(t\right){\mathit{Z}}_i^{\otimes k}{e}^{{\beta }^{⊺}{\mathit{Z}}_i}+\frac{1}{n}\sum _{i=1}^n{Y}_i^1\left(t\right)r_i\left(t\right)\left\{\frac{{\widehat{G}}_{\mathrm{C}}^{\text{COX}}(t;{\mathit{X}}_i)}{{\widehat{G}}_{\mathrm{C}}^{\text{COX}}(T_i\wedge t;{\mathit{X}}_i)}-\frac{G_{\mathrm{C}}^{\text{COX}}(t;{\mathit{X}}_i)}{G_{\mathrm{C}}^{\text{COX}}(T_i\wedge t;{\mathit{X}}_i)}\right\}{\mathit{Z}}_i^{\otimes k}{e}^{{\beta }^{⊺}{\mathit{Z}}_i}\underrightarrow{P}{s}_{\text{COX}}^{\left(k\right)}(\beta ,t),$$

uniformly in t ∊ [0, τ] and $\beta \in \mathcal{B}$, by (6.2) and the uniform weak law of large numbers. Also note that, by the same assumptions, the limit is bounded from above and bounded away from zero, and we may take derivatives by differentiating under the integral sign.

6.3 Asymptotic normality of n^−1/2U_COX(β₀)

The IPCW score function (2.3) for β evaluated at β₀ is

$$\begin{array}{cc}\hfill U_{\text{COX}}\left({\beta }_0\right)& =\sum _{i=1}^n{\int }_0^{\tau }\left\{{\mathit{Z}}_i-\frac{{\mathit{S}}_{\text{COX}}^{\left(1\right)}({\beta }_0,t)}{S_{\text{COX}}^{\left(0\right)}({\beta }_0,t)}\right\}{\widehat{w}}_i^{\text{COX}}\left(t\right)d{M}_i^1\left(t\right)\hfill \\ \hfill & =\sum _{i=1}^n{\int }_0^{\tau }\left\{{\mathit{Z}}_i-\frac{{\mathit{s}}_{\text{COX}}^{\left(1\right)}({\beta }_0,t)}{s_{\text{COX}}^{\left(0\right)}({\beta }_0,t)}\right\}{w}_i^{\text{COX}}\left(t\right)d{M}_i^1\left(t\right)\hfill \\ \hfill & +\sum _{i=1}^n{\int }_0^{\tau }\left\{{\mathit{Z}}_i-\frac{{\mathit{S}}_{\text{COX}}^{\left(1\right)}({\beta }_0,t)}{S_{\text{COX}}^{\left(0\right)}({\beta }_0,t)}\right\}\left\{{\widehat{w}}_i^{\text{COX}}\right(t)-w_i^{\text{COX}}(t\left)\right\}d{M}_i^1\left(t\right)+o_P\left(n^{1∕2}\right).\hfill \end{array}$$

The first term on the right-hand side above is a sum of mean zero i.i.d. random variables. From (6.2), the second term on the right-hand side is

$$\sum _{i=1}^n{\int }_0^{\tau }\left\{{\mathbf{Z}}_i-\frac{{\mathit{S}}_{\text{COX}}^{\left(1\right)}({\beta }_0,t)}{S_{\text{COX}}^{\left(0\right)}({\beta }_0,t)}\right\}{r}_i\left(t\right)\left\{\frac{{\widehat{G}}_{\mathrm{C}}^{\text{COX}}(t;{\mathit{X}}_i)}{{\widehat{G}}_{\mathrm{C}}^{\text{COX}}(T_i;{\mathit{X}}_i)}-\frac{G_{\mathrm{C}}^{\text{COX}}(t;{\mathit{X}}_i)}{G_{\mathrm{C}}^{\text{COX}}(T_i;{\mathit{X}}_i)}\right\}d{M}_i^1\left(t\right)=\sum _{i=1}^n{\int }_{u=0}^{\tau }{\mathit{q}}_i^{\left(1\right)}\left(u\right)d{M}_{\text{COX},i}^{\mathrm{C}}\left(u\right)+o_P\left(n^{1∕2}\right),$$ (6.3)

where

$${\mathit{q}}_i^{\left(1\right)}\left(u\right)=-\underset{n\to \infty }{\text{lim}}\frac{1}{n}\sum _{i=1}^n{\int }_{t=T_j}^{\tau }\left\{{\mathbf{Z}}_j-\frac{{\mathit{s}}_{\text{COX}}^{\left(1\right)}({\beta }_0,t)}{s_{\text{COX}}^{\left(0\right)}({\beta }_0,t)}\right\}{w}_j^{\text{COX}}\left(t\right)\times \left[{\mathit{h}}^{⊺}(t,T_j,{\mathbf{X}}_j){\Omega }_{\mathrm{C}}^{-1}\left\{{\mathit{X}}_i-\frac{{\mathit{s}}_{\mathrm{C}}^{\left(1\right)}({\gamma }_0,u)}{s_{\mathrm{C}}^{\left(0\right)}({\gamma }_0,u)}\right\}+\frac{e^{\left({\gamma }_0^{⊺}{\mathit{X}}_j\right)}I(u\le t)}{s_{\mathrm{C}}^{\left(0\right)}({\gamma }_0,u)}\right]d{M}_j^1\left(t\right).$$

Thus,

$$\frac{1}{\sqrt{n}}{\mathit{U}}_{\text{COX}}\left({\beta }_0\right)=\frac{1}{\sqrt{n}}\sum _{i=1}^n({\eta }_i^{\text{COX}}+{\psi }_i^{\text{COX}})+o_P\left(1\right),$$ (6.4)

where

$${\eta }_i^{\text{COX}}={\int }_0^{\tau }\left\{{\mathit{Z}}_i-\frac{{\mathit{s}}_{\text{COX}}^{\left(1\right)}({\beta }_0,t)}{s_{\text{COX}}^{\left(0\right)}({\beta }_0,t)}\right\}{w}_i^{\text{COX}}\left(t\right)d{M}_i^1\left(t\right),$$

$${\psi }_i^{\text{COX}}={\int }_0^{\tau }{\mathit{q}}_i^{\left(1\right)}\left(t\right)d{M}_{\text{COX},i}^C\left(t\right).$$

and $({\eta }_i^{\text{COX}}+{\psi }_i^{\text{COX}})$ are independent and identically distributed zero-mean variables.

6.4 Consistency and asymptotic normality ${\widehat{\beta }}_{\text{COX}}$

Consider the derivative of U_COX(β) with respect to β. Let

$${\mathit{I}}_{\text{COX}}\left(\tilde{\beta }\right)={\phantom{\mid }-\frac{\partial }{\partial \beta }{\mathit{U}}_{\text{COX}}\left(\beta \right)\mid }_{\beta =\tilde{\beta }}={\int }_0^{\tau }\left[\frac{{\mathit{S}}_{\text{COX}}^{\left(2\right)}(\tilde{\beta },t)}{S_{\text{COX}}^{\left(0\right)}(\tilde{\beta },t)}-{\left\{\frac{{\mathit{S}}_{\text{COX}}^{\left(1\right)}(\tilde{\beta },t)}{S_{\text{COX}}^{\left(0\right)}(\tilde{\beta },t)}\right\}}^{\otimes 2}\right]\sum _{i=1}^n{\widehat{w}}_i^{\text{COX}}\left(t\right)d{N}_i^1\left(t\right).$$

By the same boundedness arguments as used in connection with (6.2), n⁻I(β) converges in probability uniformly in β to a continuous limit such that lim_n→∞ n⁻¹I_COX(β₀ = Ω). From Assumption (C3), Ω is positive definite, and from the previous section we know that n⁻¹U_COX(β₀) = o_P(1). Thus, by the argument in the proof of Theorem 2 of Foutz (1977), ${\widehat{\beta }}_{\text{COX}}$ converges in probability to β₀.

Because $U_{\text{COX}}\left({\widehat{\beta }}_{\text{COX}}\right)=0$, it follows that

$$\begin{array}{cc}\hfill 0& =\frac{1}{\sqrt{n}}{\mathit{U}}_{\text{COX}}\left({\widehat{\beta }}_{\text{COX}}\right)\hfill \\ \hfill & =\frac{1}{\sqrt{n}}{\mathit{U}}_{\text{COX}}\left({\beta }_0\right)-\frac{1}{n}{\int }_0^1{\mathit{I}}_{\text{COX}}\{{\beta }_0+v({\widehat{\beta }}_{\text{COX}}-{\beta }_0\left)\right\}dv\sqrt{n}({\widehat{\beta }}_{\text{COX}}-{\beta }_0),\hfill \end{array}$$ (6.5)

Then by the consistency of ${\widehat{\beta }}_{\text{COX}},n^{-1}{\int }_0^1{\mathit{I}}_{\text{COX}}\left\{{\beta }_0+v\left({\widehat{\beta }}_{\text{COX}}-{\beta }_0\right)\right\}dv\stackrel{P}{\to }\Omega$. By (C3), Ω is invertible and (6.5) gives that

$$\begin{array}{cc}\hfill \sqrt{n}({\widehat{\beta }}_{\text{COX}}-{\beta }_0)& ={\Omega }^{-1}\left\{\frac{1}{\sqrt{n}}{\mathit{U}}_{\text{COX}}\left({\beta }_0\right)\right\}+0_P\left(1\right)\hfill \\ \hfill & ={\Omega }^{-1}\left\{\frac{1}{\sqrt{n}}\sum _{i=1}^n({\eta }_i^{\text{COX}}+{\psi }_i^{\text{COX}})\right\}+0_P\left(1\right),\hfill \end{array}$$ (6.6)

which is essentially a sum of bounded independent and identically distributed variables and thus by the central limit theorem it is asymptotically normally distributed with mean zero and variance matrix

$${\Sigma }_{\beta }^{\text{COX}}={\Omega }^{-1}E\left\{\right({\xi }_1^{\text{COX}}+{\psi }_1^{\text{COX}}\left){({\xi }_1^{\text{COX}}+{\psi }_1^{\text{COX}})}^{⊺}\right\}{\Omega }^{-1}.$$

The variance matrix ${\sum }_{\beta }^{\text{COX}}$ can be estimated by a plug-in estimator

$${\widehat{\Sigma }}_{\beta }^{\text{COX}}=n\sum _i{\left({\widehat{\mathit{W}}}_{\beta ,i}^{\text{COX}}\right)}^{\otimes 2}=n{\left\{{\mathit{I}}_{\text{COX}}\right({\widehat{\beta }}_{\text{COX}}\left)\right\}}^{-1}\left\{\sum _i{({\widehat{\xi }}_i^{\text{COX}}+{\widehat{\psi }}_i^{\text{COX}})}^{\otimes 2}\right\}{\left\{{\mathit{I}}_{\text{COX}}\right({\widehat{\beta }}_{\text{COX}}\left)\right\}}^{-1},$$

where

$${\widehat{\xi }}_i^{\text{COX}}={\int }_0^{\tau }\left\{{\mathit{Z}}_i-\frac{{\mathit{S}}_{\text{COX}}^{\left(1\right)}({\widehat{\beta }}_{\text{COX}},t)}{S_{\text{COX}}^{\left(0\right)}({\widehat{\beta }}_{\text{COX}},t)}\right\}{\widehat{w}}_i^{\text{COX}}\left(t\right)d{\widehat{M}}_{\text{COX},i}^1\left(t\right)$$

$${\widehat{\psi }}_i^{\text{COX}}={\int }_{u=0}^{\tau }{\widehat{\mathit{q}}}_i^{\left(1\right)}\left(u\right)d{\widehat{M}}_{\text{COX},i}^{\mathrm{C}}\left(u\right)$$

$${\widehat{q}}_i^{\left(1\right)}\left(u\right)=-\sum _{j=1}^n{\int }_{t=T_j}^{\tau }\left\{{\mathit{Z}}_j-\frac{{\mathit{S}}_{\text{COX}}^{\left(1\right)}({\beta }_{\text{COX}},t)}{S_{\text{COX}}^{\left(0\right)}({\widehat{\beta }}_{\text{COX}},t)}\right\}{\widehat{w}}_j^{\text{COX}}\left(t\right)\times \left[{\widehat{\mathit{h}}}^{⊺}(t,T_j,{\mathit{X}}_j){\left\{{\mathit{I}}_{\mathrm{C}}\right(\widehat{\gamma }\left)\right\}}^{-1}\left\{{\mathit{X}}_i-\frac{{\mathit{S}}_{\mathrm{C}}^{\left(1\right)}(\widehat{\gamma },u)}{S_{\mathrm{C}}^{\left(0\right)}(\widehat{\gamma },u)}\right\}+\frac{e^{\left({\widehat{\gamma }}^{⊺}{\mathit{X}}_j\right)}I(u\le t)}{S_{\mathrm{C}}^{\left(0\right)}(\widehat{\gamma },u)}\right]d{\widehat{M}}_{\text{COX},j}^1\left(t\right)$$

$$\widehat{\mathit{h}}(t,T_i,{\mathit{X}}_i)=e^{\left({\widehat{\gamma }}^{⊺}{\mathit{X}}_i\right)}{\int }_{u=T_i}^t\left\{{\mathit{X}}_i-\frac{{\mathit{S}}_{\mathrm{C}}^{\left(1\right)}(\widehat{\gamma },u)}{S_{\mathrm{C}}^{\left(0\right)}(\widehat{\gamma },u)}\right\}d{\widehat{\Lambda }}_{\mathrm{C}0}\left(u\right)$$

$${\mathit{I}}_{\mathrm{C}}\left(\gamma \right)=-\frac{\partial {\mathit{U}}_{\mathrm{C}}\left(\gamma \right)}{\partial \gamma }=\sum _i{\int }_0^{\tau }\left\{\frac{{\mathit{S}}_{\mathrm{C}}^{\left(2\right)}(\gamma ,t)}{S_{\mathrm{C}}^{\left(0\right)}(\gamma ,t)}-{\left(\frac{{\mathit{S}}_{\mathrm{C}}^{\left(2\right)}(\gamma ,t)}{S_{\mathrm{C}}^{\left(0\right)}(\gamma ,t)}\right)}^{\otimes 2}\right\}d{N}_i^{\mathrm{C}}\left(t\right)$$

$${\widehat{w}}_i^{\text{COX}}\left(t\right)d{\widehat{M}}_{\text{COX},i}^t\left(t\right)={\widehat{w}}_i^{\text{COX}}\left(t\right)d{N}_i^1\left(t\right)-{\widehat{w}}_i^{\text{COX}}\left(t\right)Y_i^1\left(t\right)\exp \left({\widehat{\beta }}_{\text{COX}}^{⊺}{\mathit{Z}}_i\right)d{\widehat{\Lambda }}_{10}^{\text{COX}}\left(t\right)$$

$$d{\widehat{M}}_{\text{COX},i}^{\mathrm{C}}\left(t\right)=d{N}_i^{\mathrm{C}}\left(t\right)-Y_i\left(t\right)\exp \left({\widehat{\gamma }}^{⊺}{\mathit{X}}_i\right)d{\widehat{\Lambda }}_{\mathrm{C}0}\left(t\right).$$

6.5 Consistency and weak convergence of ${\widehat{\Lambda }}_{10}^{\mathbf{COX}}$

We first note that ${\widehat{\Lambda }}_{10}^{\text{COX}}\left(t\right)$ is uniformly consistent for ${\Lambda }_{10}^{\ast }\left(t\right)={\int }_0^t{\lambda }^{10}\left(u\right)du$. To see this, write

$${\widehat{\Lambda }}_{10}^{\text{COX}}\left(t\right)-{\Lambda }_{10}^{\ast }\left(t\right)=\frac{1}{n}\sum _{i=1}^n{\int }_0^t\frac{{\widehat{w}}_i^{\text{COX}}\left(u\right)d{M}_i^1\left(u\right)}{S_{\text{COX}}^{\left(0\right)}({\beta }_0,u)}+\frac{1}{n}\sum _{i=1}^n{\int }_0^t\left\{\frac{1}{S_{\text{COX}}^{\left(0\right)}({\widehat{\beta }}_{\text{COX}},u)}-\frac{1}{S_{\text{COX}}^{\left(0\right)}({\beta }_0,u)}\right\}{\widehat{w}}_i^{\text{COX}}\left(u\right)d{N}_i^1\left(u\right).$$ (6.7)

By the arguments in Section 6.2, the consistency of ${\widehat{\beta }}_{\text{COX}}$ and the boundedness away from zero and smoothness of $S_{\text{COX}}^{\left(0\right)}$, the right-hand side of (6.7) converges to zero in probability, uniformly in t ∊ [0, τ].

Consider the first term on the right-hand side of (6.7). By the same argument as used for establishing (6.3),

$$\begin{array}{cc}\hfill \frac{1}{n}\sum _{i=1}^n{\int }_0^t\frac{{\widehat{w}}_i^{\text{COX}}\left(u\right)d{M}_i^1\left(u\right)}{S_{\text{COX}}^{\left(0\right)}({\beta }_0,u)}& =\frac{1}{n}\sum _{i=1}^n{\int }_0^t\frac{w_i^{\text{COX}}\left(u\right)d{M}_i^1\left(u\right)}{S_{\text{COX}}^{\left(0\right)}({\beta }_0,u)}+\frac{1}{n}\sum _{i=1}^n{\int }_0^t\frac{{\widehat{w}}_i^{\text{COX}}\left(u\right)-w_i^{\text{COX}}\left(u\right)}{S_{\text{COX}}^{\left(0\right)}({\beta }_0,u)}d{M}_i^1\left(s\right)\hfill \\ \hfill & =\frac{1}{n}\sum _{i=1}^n{\int }_0^t\frac{w_i^{\text{COX}}\left(s\right)s{M}_i^1\left(s\right)}{s_{\text{COX}}^{\left(0\right)}({\beta }_0,u)}+\frac{1}{n}\sum _{i=1}^n{\int }_0^t{q}_i^{\left(2\right)}(u,t)d{M}_{\text{COX},i}^{\mathrm{C}}\left(u\right)+o_P\left(n^{-1∕2}\right),\hfill \end{array}$$ (6.8)

where

$$q_i^{\left(2\right)}(u,t)=-\underset{n\to \infty }{\lim }\frac{1}{n}\sum _{j=1}^n{\int }_{v=T_j}^t\frac{1}{s_{\text{COX}}^{\left(0\right)}({\beta }_0,v)}\times \left[{\mathit{h}}^{⊺}(v,T_j,{\mathit{X}}_j){\Omega }_{\mathrm{C}}^{-1}\left\{{\mathit{X}}_i-\frac{{\mathit{s}}_{\mathrm{C}}^{\left(1\right)}({\gamma }_0,u)}{{\mathit{s}}_{\mathrm{C}}^{\left(0\right)}({\gamma }_0,u)}\right\}+\frac{e^{\left({\gamma }_0^{⊺}{\mathit{X}}_j\right)}\mathit{I}(u\le v)}{{\mathit{s}}_{\mathrm{C}}^{\left(0\right)}({\gamma }_0,u)}\right]w_j^{\text{COX}}\left(v\right)d{M}_j^1\left(v\right).$$

Similar to (6.5), by a first-order expansion, the last term on the right-hand side of (6.7), is

$$\begin{array}{cc}\hfill & -{\int }_0^t{\left\{\frac{{\mathit{S}}_{\text{COX}}^{\left(1\right)}({\beta }_0,u)}{S_{\text{COX}}^{\left(0\right)}({\beta }_0,u)}\right\}}^{⊺}\frac{n^{-1}{\Sigma }_{i=1}^n{\widehat{w}}_i^{\text{COX}}\left(u\right)d{N}_i^1\left(u\right)}{S_{\text{COX}}^{\left(0\right)}({\beta }_0,u)}({\widehat{\beta }}_{\text{COX}}-{\beta }_0)+o_P\left(n^{-1∕2}\right)\hfill \\ \hfill & ={\mathit{h}}_{\Lambda }^{⊺}\left(t\right){\Omega }^{-1}\frac{1}{n}\sum _{i=1}^n({\eta }_i^{\text{COX}}+{\psi }_i^{\text{COX}})+o_P\left(n^{-1∕2}\right),\hfill \end{array}$$ (6.9)

where

$${\mathit{h}}_{\Lambda }\left(t\right)=-{\int }_0^t\frac{{\mathit{s}}_{\text{COX}}^{\left(1\right)}({\beta }_0,u)}{{\mathit{s}}_{\text{COX}}^{\left(0\right)}({\beta }_0,u)}{\lambda }_{10}^{\ast }\left(u\right)du.$$

Combining (6.5), (6.8) and (6.9),

$$\sqrt{n}\left\{{\widehat{\Lambda }}_{10}^{\text{COX}}\right(t)-{\Lambda }_{10}^{\ast }(t\left)\right\}=\frac{1}{\sqrt{n}}\sum _{i=1}^n{W}_{\Lambda ,i}^{\text{COX}}\left(t\right)+o_P\left(1\right),$$ (6.10)

where

$$W_{\Lambda ,i}^{\text{COX}}\left(t\right)={\int }_0^t\frac{w_i^{\text{COX}}\left(u\right)d{M}_i^1\left(u\right)}{s_{\text{COX}}^{\left(0\right)}({\beta }_0,u)}+{\int }_0^t{q}_i^{\left(2\right)}(u,t)d{M}_{\text{COX},i}^{\mathrm{C}}\left(u\right)+{\mathit{h}}_{\Lambda }^{⊺}\left(t\right){\Omega }^{-1}({\eta }_i^{\text{COX}}+{\psi }_i^{\text{COX}}).$$

The $W_{\Lambda ,i}^{\text{COX}}\left(t\right)$ terms are i.i.d. stochastic processes forming a Donsker class indexed by t. To see this, note that $M_i^1$, $M_{\text{COX},i}^{\mathrm{C}}$ and $w_i^{\text{COX}}$ are of bounded variation and thus Donsker and that sums of bounded Donsker classes are Donsker (van der Vaart, 1998, Example 19.20, Example 19.11). Thus, $\sqrt{n}\left\{{\widehat{\Lambda }}_{10}^{\text{COX}}\left(t\right)-{\Lambda }_{10}^{\ast }\left(t\right)\right\}$ converges weakly to a mean-zero Gaussian process with variance ${\Sigma }_{{\Lambda }_{10}}^{\text{COX}}\left(t\right)=E\left\{W_{\Lambda ,i}^{\text{COX}}\left(t\right)\right\}$. The variance can be estimated by a plug in estimator, ${\widehat{\Sigma }}_{{\Lambda }_{10}}^{\text{COX}}\left(t\right)=n^{-1}{\sum }_i{\left\{{\widehat{W}}_{\Lambda ,i}^{\text{COX}}\left(t\right)\right\}}^2$, where

$${\widehat{W}}_{\Lambda ,i}^{\text{COX}}\left(t\right)={\int }_0^t\frac{{\widehat{w}}_i^{\text{COX}}\left(u\right)d{\widehat{M}}_i^1\left(u\right)}{S_{\text{COX}}^{\left(0\right)}({\widehat{\beta }}_{\text{COX}},u)}+{\int }_0^{\tau }{\widehat{q}}_i^{\left(2\right)}(u,t)d{\widehat{M}}_{\text{COX},i}^{\mathrm{C}}\left(u\right)+{\widehat{\mathit{h}}}_{\Lambda }^{⊺}\left(t\right){\widehat{\Omega }}^{-1}({\widehat{\eta }}_i^{\text{COX}}+{\widehat{\psi }}_i^{\text{COX}})$$

$${\widehat{q}}_i^{\left(2\right)}(u,t)=-\frac{1}{n}\sum _{j=1}^n{\int }_{j=1}^t\frac{1}{S_{\text{COX}}^{\left(0\right)}({\widehat{\beta }}_{\text{COX}},v)}\times \left[\widehat{\mathit{h}}(v,T_j,{\mathit{X}}_j){\widehat{\Omega }}_{\mathrm{C}}^{-1}\left\{{\mathit{X}}_i-\frac{{\mathit{S}}_{\mathrm{C}}^{\left(1\right)}(\widehat{\gamma },u)}{S_{\mathrm{C}}^{\left(0\right)}(\widehat{\gamma },u)}\right\}+\frac{e^{\left(\widehat{\gamma }{\mathit{X}}_j\right)}\mathit{I}(u\le v)}{S_{\mathrm{C}}^{\left(0\right)}(\widehat{\gamma },u)}\right]{\widehat{w}}_j^{\text{COX}}\left(v\right)d{\widehat{M}}_j^1\left(v\right)$$

$${\widehat{\mathit{h}}}_{\Lambda }\left(t\right)=-\frac{1}{n}\sum _{i=1}^n{\int }_0^t\frac{{\mathit{S}}_{\text{COX}}^{\left(1\right)}({\widehat{\beta }}_{\text{COX}},u)}{{\left\{S_{\text{COX}}^{\left(0\right)}\right({\widehat{\beta }}_{\text{COX}},u\left)\right\}}^2}{\widehat{w}}_i^{\text{COX}}\left(u\right)d{N}_i^1\left(u\right).$$

7 Appendix B

Cumulative incidence functions for cause 1 and 2 are generated from

$$F_1\left(t\right)=1-{\{1-p(1-e^{-1}\left)\right\}}^{\exp \left(betaZ\right)}$$

$$F_2\left(t\right)={(1-p)}^{\exp \left(\beta Z\right)}\{1-e^{-t\exp \left(\beta Z\right)}\}$$

where 0 < p < 1. Generating data step (need to set parameters p and β first):

1. Generate covariate Z

2. Based on p, β and Z, compute P₁ and P₂ (probability of type 1 and type 2 failures): P₁ = F₁(∞) = 1 – (1 – p)^exp(βZ) and P₂ = F₂(∞) = (1 – p)^exp(βZ)

3. Generate an uniform r.v. U₁ ~ U(0, 1). Generate cause of death indicator, δ, by

   $$\delta =\{\begin{array}{cc}1,\hfill & \text{if}{U}_1\le P_1\hfill \\ 2,\hfill & \text{Otherwise}\hfill \end{array}\phantom{\}}$$
4. Based on δ = k, k = 1,2, compute the conditional probability

   $${\tilde{F}}_k\left(t\right)=P(T_k\le t\mid \delta =k)=\frac{F_k\left(t\right)}{P(\delta =k)}=\frac{F_k\left(t\right)}{F_k\left(\infty \right)}=\frac{F_k\left(t\right)}{P_k}$$

5. Generate second uniform r.v. U₂ ~ U(0,1). Then use inverse distribution method to generate T_k based on ${\tilde{F}}_k\left(t\right)$.