Abstract
Children (n=747; 6.5 years) were assessed on domain-general processes and mathematics and reading-related competencies (start of 1st grade); addition retrieval (end of 2nd grade); and calculations and word reading (end of 3rd grade). Attentive behavior, reasoning, visuospatial memory, and rapid automatized naming (RAN) indirectly contributed to both outcomes, via retrieval. However, there was no overlap in domain-general direct effects on calculations (attentive behavior, reasoning, working memory) versus word reading (language, phonological memory, RAN). Results suggest ease of forming associative relations and abilities engaged during the formation of these long-term memories are common to both outcomes and can be indexed by addition fact retrieval, but further growth in calculations and word reading is driven by different constellations of domain-general abilities.
Keywords: calculations, word reading, retrieval, pathways of development, associative memory, domain-general abilities
Mathematics achievement, reading achievement, and their co-occurrence are strong predictors of quality of life, financial security, and life expectancy (Batty et al., 2010). It is therefore alarming that children’s developmental trajectories in mathematics (Duncan et al., 2007) and reading (Shaywitz, 1998) are established early and remain stable over time. Additionally, the relation between mathematics and reading achievement is substantial (Davis et al., 2014). So it is not surprising that concurrent difficulty across mathematics and reading is common (Mann-Koepke & Miller, 2013) and that comorbidity is associated with poorer mathematics and reading outcomes than is difficulty in one domain (Willcutt et al., 2013).
Designing effective interventions to meet the needs of such students is therefore essential, and such design would be enhanced by insights into which child-level variables contribute to development across both domains and which are unique to each domain. To gain such insight, the dominant approach is applying achievement-test cut-points to classify children with difficulty in one or the other or both domains and then identifying variables that distinguish among the three groups. Because results vary with the stringency of cut-points, Branum-Martin et al. (2013) argued for an approach that treats mathematics and reading performance continuously.
Only a handful of studies have taken this approach to examine whether sources of individual differences in development of calculation versus word-reading skill are more alike or different, and among existing studies, findings are inconsistent. We followed this approach in a longitudinal study of a large representative sample to assess the effects of start-of-first-grade cognitive, linguistic, and early numerical and reading-related competencies on end-of-third-grade calculation and word-reading skill. We focused on calculations because it is foundational to higher-level mathematics (Cowan et al., 2011), while word reading is foundational to text comprehension (Catts et al., 2005).
Previous Studies
Hecht, Torgesen, Wagner, and Rashotte (2001) found that second-grade phonological processing predicted different forms of mathematics and reading at fifth grade, controlling for vocabulary knowledge. Koponen, Aunola, Ahonen, and Nurmi (2007) included a broader set of predictors at an earlier start point: predicting fourth-grade arithmetic fluency, computation accuracy, and text reading fluency using kindergarten cognitive ability, listening comprehension, processing speed, conceptual number knowledge, letter naming accuracy, mother’s education and fourth-grade RAN. Flexible use of counting and RAN uniquely predicted single-digit arithmetic fluency; concepts and education uniquely predicted procedural calculations accuracy. Across a factor score of fluency on arithmetic and text reading, counting and RAN uniquely accounted for variance, but only arithmetic uniquely predicted a factor score across procedural calculation accuracy and text reading fluency. The implication is that counting and RAN are important across mathematics and reading, when fluent performance is predicted, but predictors of reading were not reported.
In their 2013 study, Koponen, Salmi, Ekland, and Aro provided corroborating evidence for the importance of RAN and flexible counting in fluency with procedural calculations and text reading, controlling for phonological awareness and verbal short-term memory. They attributed RAN’s unique contribution to the importance of ease in accessing information from long-term memory, a central process in calculations and word reading. Yet, the effects of other potentially important predictors were not controlled and a focus on fluency outcomes may heighten the role of RAN and counting.
Geary’s (2011) study in grades 1–5 included the most comprehensive set of potential predictors. Central executive and addition-fact retrieval predicted school-entry word reading and growth in calculations. Phonological memory and speed of letter retrieval were unique to word reading; visuospatial memory, speed of numeral retrieval, and several early numerical competencies were unique to calculations. Counting knowledge was not a unique predictor of the start point or growth for either outcome. One possible reason for this divergent finding relative to Koponen et al. (2013) is that although understanding of counting concepts (Geary’s measure) is important in learning simple calculations, more complex relations between number words and numerals (Koponen’s measures) are relevant for learning complex calculations. Another possibility is that Geary’s calculation and word-reading outcomes indexed performance accuracy, whereas Kopenen et al. indexed fluency.
Present Study Purpose
We extended earlier investigations in five ways. As in Geary (2011), we administered an extensive battery of predictors: early mathematics and reading-related competencies plus eight domain-general variables identified in the four studies or in studies focused on one but not the other outcome. We extended Geary’s battery to include attentive behavior; consider effects of reasoning and language separately; and determine if previous results are due to fluency of retrieving information from long-term memory or to general processing speed. Second, to clarify the role of counting, we operationalized counting as in Geary (addressing early competence), while indexing other early numerical competencies separately to capture the number knowledge likely supporting skill on Koponen’s (2007, 2013) counting measures. Third, to more fully examine relations between the domains, we assessed effects of early mathematics on the word-reading outcome and effects of early reading-related competencies on the calculations outcome. Fourth, our sample was nearly as large as the four prior studies combined, providing power to detect subtle effects.
Finally, we focused on Geary’s (2011) finding that addition retrieval was associated with school-entry word-reading skill, suggesting overlap in mechanisms that support addition fact and word retrieval, but was not a significant predictor of word-reading growth. Moreover, addition retrieval explained growth in calculations across grades but not at school entry. We therefore assessed retrieval at end of second grade, when it may differentiate skill development more effectively. This also allowed us to investigate whether effects of first-grade predictors on third-grade outcomes occur indirectly via second-grade retrieval.
Development of Calculation and Word-Reading Skill and Study Hypotheses
Over the primary school grades, the typical developmental course for calculations (Geary, 1994) and word reading (Ehri, 2008) proceeds as follows. Children enter first grade with rudimentary understanding of number, insights into basic addition-subtraction concepts, and skill in counting objects to solve single-digit problems. In word reading, they understand letters represent sounds and have established some associations, but word reading is driven largely by visual and semantic-contextual connections.
In both domains, a period of discovery ensues. Children achieve a reliable, full set of associations among visual, phonological, and semantic representations of numerals, as addition-subtraction concepts and skilled use of counting for problem solving improve. Alphabetic insight is achieved, with a full set of reliable associations between letters-sounds, as word-level knowledge continues to grow via grapho-semantic connections. Children then develop efficient strategies based on counting to solve simple arithmetic problems and on decoding to link whole written words with phonological representations, enhancing memory for sight words. These procedural strategies produce repeated correct associations to secure representations of arithmetic problems and words in long-term memory, likely through the same underlying brain and cognitive mechanisms (Qin et al., 2014).
This increasingly permits direct retrieval instead of reliance on procedural strategies, as children progress to a phase that reflects greater differentiation between the domains. For multi-digit calculations, children develop understanding of place value and knowledge of procedural steps that vary in complexity according to place value-operation. Because the sequence of steps differs by problem type, deliberate decision making is required, constrained by understanding of the numeration system (Fuchs et al., 2014). Also, close monitoring of the strings of procedural actions is needed. In this timeframe, alphabetic knowledge is consolidated, with new words added to the lexicon using letter-blends, morphemes, and syllables. This increases the pace of word learning, and students develop automaticity in recognizing pronunciations and meanings of written words, without strong demands on attention or working memory.
Based on similarities in earlier phases and distinctions in later development, we hypothesized the following. We expected early knowledge of counting principles to predict later calculation skill, but indirectly via addition retrieval, because early competence with counting is associated with its skilled counting for solving addition problems, resulting in formation of long-term memories of facts (Geary et al., 1992). Fact retrieval supports more complex calculations (Fuchs et al., 2006).
Less is known about how knowledge of counting principles contributes to word reading, as in Koponen et al. (2007, 2103). Assuming the predictor and outcome may be related to a third variable – an underlying ability to form and retrieve from memory arbitrary associations between visual symbolic and phonological forms, we did not expect counting knowledge to contribute to word reading indirectly via retrieval once phonological memory, visuospatial memory, and RAN were controlled. We did expect these three abilities to affect calculation and word-reading outcomes indirectly via retrieval. Moreover, based on the previous four studies and because RAN (Norton & Wolf, 2012) and phonological processing (Lambrecht et al., 2008) are core deficits in reading disability, we anticipated direct effects for RAN and phonological memory on third-grade word reading. Because reliance on the visual form dominates the process through which new words are added to the lexicon in early but less so later phases of word reading, we expected the effect of visuospatial memory to be entirely indirect, through retrieval. With counting, phonological memory, RAN, and visuospatial memory in the model, we did not expect effects for general processing speed. (We indexed phonological memory rather than awareness because early reading instruction improves phonological awareness [Fuchs et al., 2001], complicating interpretation of its role as a predictor of word reading or calculations [with reading in the model]. Temporary storage of the phonological form of novel words [phonological memory] supports long-term specification of words: The better the short-term trace, the fewer exposures needed to learn words [Gathercole et al., 1997].)
In terms of complex calculations, we anticipated direct effects of attentive behavior, reasoning, central executive, and visuospatial memory on third-grade calculations (Geary, 2011; Li & Geary, 2013; Fuchs et al. 2006). Attentive behavior, reasoning, and central executive likely support complex (end of third grade) calculations, which require close monitoring of procedural actions and understanding of the rationale for each step (Fuchs et al., 2014). Visuospatial memory may be invoked to keep track of place value and trading across columns, as in the reciprocal effect between numeration and multi-digit calculations (Fuchs et al., 2014).
By contrast, on the word-reading outcome, we expected direct effects for attentive behavior, which seems required through much of primary-grade development until automaticity has been achieved, and we expected language comprehension to be uniquely and directly associated with word reading, given that the semantic grasp of words facilitates the association between a word’s orthographic and phonological form in memory (Ouellette, 2006). We assumed that reasoning and the central executive are uniquely associated with calculations.
In terms of effects of early academic skill, given stability in the rate of development in these domains over the primary grades, we expected early numerical competencies to predict later calculation skill and early reading-related competencies to predict later word-reading skill. For reciprocal effects, we had no basis to specify a hypothesis. Although Duncan et al. (2007) found that early math predicts reading but early reading does not predict math, their outcomes were broader than calculations and word reading.
Method
Readers should consult the supplementary file (LINK) for complete information on method and results. Data were collected at start of grade 1 and end of grades 2 and 3. The sample comprised 747 children from 228 first-grade classrooms in 37 schools. At start of first grade, mean age (49% girls) was 6.52 years (SD = 0.37 months); 76% received subsidized lunch; 8% received English language services; 42% came from single-parent homes; 60% were African American, 30% non-Hispanic white, 8% Hispanic white, 2% other. Mean IQ (2-subtest Wechsler Abbreviated Scale of Intelligence; WASI; Wechsler, 1999) was 93.65 (SD = 12.28). First grade scores on Wide Range Achievement Test (WRAT; Wilkinson, 1993)-Arithmetic and Reading averaged 97.93 (SD = 14.34) and 99.98 (SD = 14.96).
First-grade predictors were attentive behavior (Strengths and Weaknesses of ADHD [Swanson et al., 2004]); reasoning (WASI-Matrix Reasoning [Wechsler, 1999]); listening comprehension (Woodcock Diagnostic Reading Battery-Listening Comprehension [Woodcock, 1997]); central executive working memory (Working Memory Test Battery for Children [WMTB-C; Pickering & Gathercole, 2001]-Counting Recall); phonological short-term memory (WMTB-C Nonword List Recall); visuospatial short-term memory (WMTB-C-Mazes Memory); processing speed (WJ-III Visual Matching [Woodcock, McGrew, & Mather, 2001]); RAN (Denkla & Rudel, 1976); counting knowledge (Geary, 2011); early numerical competencies (WRAT-Arithmetic [Wilkinson, 1993]-oral and written components); early reading-related competencies (WRAT-Reading). Second-grade addition retrieval was Addition Strategy Assessment (Geary et al., 2007). Third-grade outcomes were WRAT-Arithmetic (written component) and Reading.
Results and Discussion
Table 1 shows path coefficients. Figure 1 shows significant effects. Results support three general conclusions. First, both types of third-grade outcomes depend on a combination of cognitive and linguistic processes and early domain-specific skill. Second, the effect of early domain-specific competencies on later achievement is, arguably, substantial: Over almost three years, every 1 SD increase in early math was associated with an increase of .23 SD unit in later mathematics; each of 1 SD increase in early word reading was associated with an increase of .50 SD unit in later word reading. This corroborates previous work showing that academic trajectories are established early (Duncan et al., 2007; Shaywitz, 1998). This finding is notable given the control of eight domain-general processes and early skill in another academic domain. The final general conclusion is that child-level pathways in developing calculation and word-reading skill include interesting commonalities but major distinctions.
Table 1.
Effects of First-Grade Predictors on Third-Grade Calculations and Word Reading, with Second-Grade Retrieval in the Model (n=747)
| Outcome/Predictor | Total Effect on Outcome Path c(SE) | Direct Effect on Outcome Path c’(SE) | Effect on Retrieval Path a(SE) | Effect of Retrieval on Outcome Path b(SE) | Indirect Effect on Outcome Path (CI) |
|---|---|---|---|---|---|
| Calculations | .20(.03)c | ||||
| Attentive Behavior | .20(.04)c | .18(.04)c | .11(.04)c | .02(.043 .005) | |
| Reasoning | .08(.04)a | .06(.03)a | .12(.04)a | .02(.007 .043) | |
| Central Executive | .11(.03)b | .10(.04)b | .06(.04) | .01(−.030 .004) | |
| Language | .03(.03) | .03(.03) | −.01(.04) | .00(−.019 .015) | |
| Phono Mem | .02(.03) | .01(.03) | .01(.04) | .00(−.014 .019) | |
| Visuospa Mem | .03(.03) | .03(.03) | .09(.04)a | .02(.030 .035) | |
| Processing Speed | .03(.03) | .02(.03) | .02(.04) | .00(−.012 .021) | |
| RAN | .05(.03) | .04(.03) | .10(.04)a | .02(.037 .003) | |
| Counting | .01(.03) | .02(.03) | −.02(.04) | −.00(−.019 .010) | |
| Early Math | .23(.04)c | .18(.04)c | .23(.05)c | .05(.004 .073) | |
| Early Reading | .16(.04)c | .14(.04)c | .12(.05)a | .02(.004 .045) | |
| Word Reading | .06(.03)a | ||||
| Attentive Behavior | .05(.03) | .04(.03) | .11(.04)c | .01(.020 .0004) | |
| Reasoning | .04(.03) | .04(.03) | .12(.04)a | .01(.001 .017) | |
| Working Memory | .04(.03) | .04(.03) | .06(.04) | −.00(−.012 .001) | |
| Language | .10(.03)b | .10(.03)b | −.01(.04) | −.00(−.007 .005) | |
| Phono Mem | .08(.03)b | .08(.03)b | .01(.04) | .00(−.005 .007) | |
| Visuospa Mem | −.02(.03) | −.02(.03) | .09(.04)a | .01(.0002 .010) | |
| Processing Speed | −.02(.03) | −.02(.03) | .02(.04) | .00(−.004 .008) | |
| RAN | .17(.03)c | .16(.03)c | .10(.04)a | .01(.010 .0002) | |
| Counting | .05(.03) | .05(.03) | −.02(.04) | −.00(−.007 .004) | |
| Early Math | .02(.04) | .00(.04) | .23(.05)c | .01(.0003 .018) | |
| Early Reading | .50(.04)c | .49(.04)c | .12(.05)a | .01(.002 .030) |
p<.05;
p<.01;
p<.001.
Bolded coefficients are statistically significant.
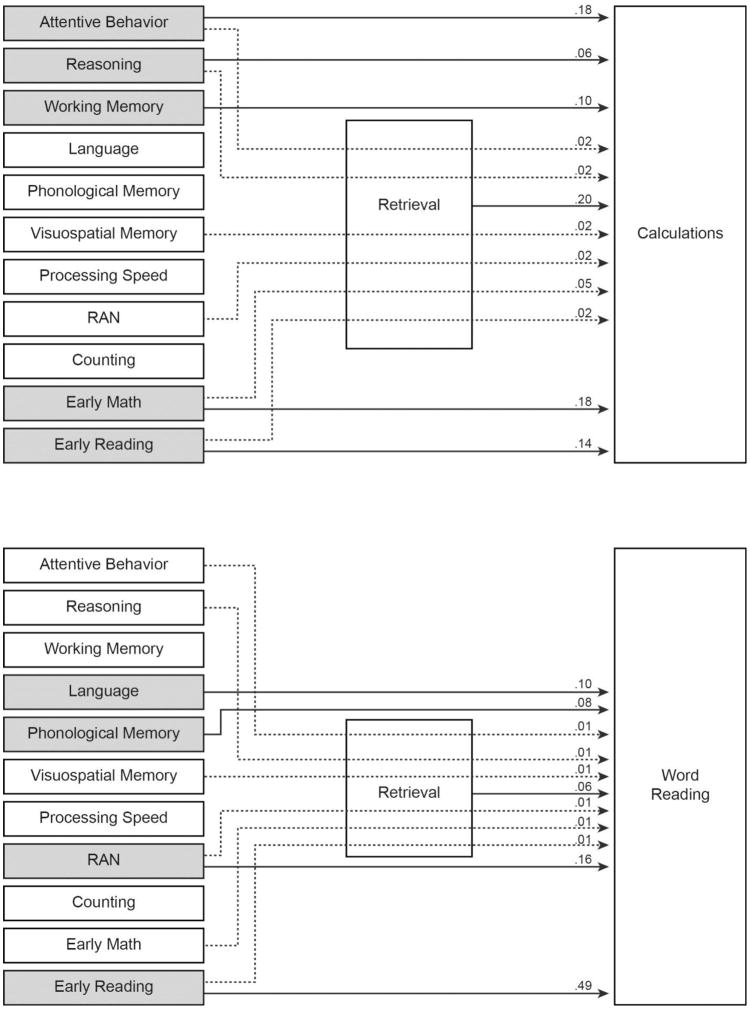
Figure 1.
Direct effects (solid arrows) and indirect effects (dotted arrows) on calculations (top panel) and word reading (bottom panel). Shading indicates total (direct+indirect) effects.
In terms of commonalities, results revealed sizeable effects for early reading skill, in the form of identifying letters and simple high-frequency words, not only on word reading but also calculations. This included direct and indirect effects via retrieval, and retrieval was supported by a broad set of domain-general abilities (attentive behavior, reasoning, visuospatial memory, RAN) that resulted in significant indirect effects of these domain-general processes on both outcomes. This suggests that competent third-grade calculation and word-reading performance both rely on the ability to form and fluently retrieve from memory arbitrary associations between the visual symbolic and phonological forms – in keeping with Koponen et al.’s (2013) suggestion as to why their counting measures predicted calculation and reading fluency.
These relations may reflect the functional integrity of the hippocampal-dependent memory system, which during the early phases of learning engages prefrontal, parietal, and medial temporal areas. The system is important for early phases of learning arithmetic facts (Qin et al., 2014) and written words (Cherodath & Singh, 2015), which at this stage would be correlated with domain-general processes. In this view, relations between early reading skills, retrieval, and calculation reflect, in part, individual differences in the ease of learning associative relations (Supekar et al., 2013).
As in previous work, we found such effects for visuospatial memory (Li & Geary, 2013) and RAN (Hecht et al., 2001; Koponen et al., 2007, 2013). We also found a shared indirect effect for attentive behavior, as hypothesized for both domains (Fuchs et al., 2012; Miller et al., 2014), and for reasoning, which was unexpected. Results suggest attentive behavior and reasoning increase children’s capacity to produce correct responses required to form associations in long-term memory and support addition-fact retrieval. This is consistent with Geary et al.’s (2012) finding that first-grade retrieval use is related to attentive behavior and working memory and across-grade retrieval improvement is related to reasoning and attentive behavior. Findings are consistent with effortful engagement of prefrontal systems during learning of associative relations (Qin et al., 2014). A final commonality was the unexpected lack of significance for phonological memory’s indirect effect via retrieval on both outcomes, possibly due to inclusion of multiple other correlated domain-general measures. We did, however, find the anticipated direct effect of phonological memory on word reading, which brings us to distinctions between the pathways.
Although results indicate extensive overlap in the indirect effects of first-grade general cognitive abilities on both third-grade outcomes, these effects manifested in different ways. On word reading, indirect effects were due more to the magnitude of effects of these abilities on second-grade retrieval (paths a, identical for both outcomes, ranging from .09 to .12) than on the effect of retrieval on later word reading (.06). By contrast, on calculations, the indirect effect of retrieval was due more to the effect of retrieval on later calculations (.20). This difference in retrieval’s direct effects on the two outcomes produced indirect effects via retrieval for each cognitive ability that were twice as large on the calculation than word-reading outcome. Although each indirect effect was small, they summed to .15 for calculations; less than half that, .06, for word reading.
As noted, reliance on retrieval at second grade may be an indicator of the ability to form and fluently retrieve associations from long-term memory, which facilitates early word and arithmetic-fact learning (Qin et al., 2014). But the measure also captures domain-specific knowledge: fluency in retrieving addition facts, which directly facilitates computation (Cowan et al., 2011), by freeing attentional and working memory resources that can be used to execute multi-digit computations. This may account for the additional direct effects on third-grade calculations of attentive behavior, reasoning, and the central executive (Fuchs et al., 2012; Geary, 2011). It is notable that these direct effects were specific to third-grade calculations (not involved in third-grade word reading), consistent with Geary and the greater novelty and complexity of third-grade calculations relative to third-grade word reading.
In fact, a major difference in sources of individual differences in development of calculation versus word-reading skill was the nature of domain-general processes that exerted direct effects. While direct effects were significant for attentive behavior, reasoning, and the central executive on calculations, direct effects were significant for language comprehension, phonological memory, and RAN on word reading. Although major roles for these processes have been identified in the individual differences literature for mathematics (Fuchs et al., 2012; Geary, 2011; Geary et al., 2012) and reading (Lambrecht et al., 2008; Norton & Wolf, 2012; Ouellette, 2006), studies that simultaneously focused on both outcomes have identified shared direct effects for RAN (Hecht et al., 2001) or counting and RAN (Koponen et al., 2007, 2013).
Inconsistency in previous and present findings may occur because Hecht et al. (2001) considered a limited set of predictors (vocabulary knowledge, phonological processing), and in Koponen (2007, 2013), counting and RAN were significant only when outcomes were indexed as fluency. Yet, in rectifying differences in the counting findings, we note distinctions between the measures. Ours assessed counting knowledge; Koponen et al.’s indexed verbal counting skill based on understanding of number relations. As they noted, their method may have proved more salient for predicting calculations and word reading because it better taps the ability to form and access associative relations. In this way, our results support Koponen et al.’s finding for the role of counting (as an index of number knowledge associations) in calculations and word reading, even as it suggests an important source of consistency between Koponen et al. and present results.
Our findings are, however, more similar to Geary (2011), for whom domain-general predictors were distinct for growth in calculations versus word reading, perhaps because Geary and the present study included a broad set of predictors while focusing on performance accuracy for both outcomes. The present study extends Geary by including in-class attention, a significant predictor of calculations (direct and indirect effects) and word reading (indirect effects), and by treating IQ components separately, revealing a significant direct effect for reasoning on calculations but a significant direct effect for language comprehension on word reading.
Another major distinction was the proportion of total effects due to domain-general processes versus early domain-specific skill. For third-grade calculations, the total path coefficients for domain-general processes summed to .50; the sum for early numerical competencies was .23 (ratio of ~2:1). This is consistent with Bailey et al. (2014), in which domain-general effects were greater than domain-specific effects on across-year gains in mathematics. By contrast, for the third-grade word-reading outcome, the distribution of effects was nearly equal: Coefficients summed to .56 for domain-general processes; .50 for early reading skill. So, in the primary grades, domain-general processes exercise relatively greater influence in development of calculation than word-reading skill. The engagement of domain-general processes follows from the greater novelty and complexity in third-grade calculation problems compared to early mathematics skills.
Finally, although early reading competency predicted calculations, the reverse was less true. The total effect of early reading on later calculation skill (.16) was sizeable and significant; the total effect of early numerical competencies on later word reading (.02) was neither. Duncan et al. (2007) found that while early mathematics predicted later reading achievement, the reverse was not true, but they synthesized effects across broader measures of achievement. Additional work examining the reciprocity of effects is warranted.
In considering the question posed in this paper’s title, we conclude that pathways to calculation and word-reading outcomes are more different than alike. First, although results indicate extensive overlap in indirect effects of first-grade general cognitive and linguistic abilities on outcomes, these indirect effects accrued in different ways, reflecting different processes. Second, the direct effects of general cognitive and linguistic processes were non-overlapping for calculations versus word reading. Third, the proportion of total effects due to domain-general processes was larger for calculations than word reading (with early reading competencies accounting for substantially more variance in word reading than early numerical competencies explained in calculations). Finally, although word reading had a direct effect on calculations, the reverse was not found.
Finding commonalities but major distinction in pathways to calculation and word-reading competence brings us back to the topic of comorbid mathematics and reading difficulty, for which Willcutt et al. (2013) discussed four competing explanations. The alternate forms model indicates mathematics and reading are different manifestations of the same disorder. With the phenocopy model, one disorder creates difficulty in the other. Both models suggest entirely or largely common pathways, which the present study does not support. The third and fourth models, by contrast, involve distinctive pathways. The three independent disorders model proposes that weaknesses involved in mathematics versus reading difficulty are entirely distinct; the correlated liabilities model argues for shared as well as distinct pathways. Our findings seem most concordant with the last perspective and are in line with twin studies, suggesting such comorbidity involves common genetic influences, as well as separate genetic and environmental influences (Kovas et al., 2007; Willcutt, Pennington, et al., 2010).
Even so, a different phenomenon for comorbidity emerges in prior longitudinal studies that focus on higher-order mathematics and reading outcomes, even when they treat mathematics and reading performance continuously and focus on accuracy. For example, Fuchs et al. (in press) found that predictors of word-problem solving and text comprehension operated in a highly similar manner for both outcomes. This suggests need for unified study of a comprehensive set of domain-general processes and domain-specific competencies on mathematics and reading outcomes, involving foundational skills and higher-order performance.
Supplementary Material
Acknowledgments
This research was supported by R01 HD053714, R24 HD075443, and Core Grant #HD15052 from the Eunice Kennedy Shriver National Institute of Child Health & Human Development to Vanderbilt University. The content is solely the responsibility of the authors and does not necessarily represent the official views of the Eunice Kennedy Shriver National Institute of Child Health & Human Development or the National Institutes of Health. Geary also thanks the Institute of Advanced Study, Durham University, for its support during preparation of portions of this manuscript.
References
- Bailey DH, Watts, Littlefield AK, Geary DC. State and trait effects on individual differences in children’s mathematical development. Psychological Science. 2014;25:2017–2026. doi: 10.1177/0956797614547539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Batty GD, Kivimaki M, Deary IJ. Intelligence, education, and mortality. British Medical Journal. 2010;340:c563. doi: 10.1136/bmj.c654. [DOI] [PubMed] [Google Scholar]
- Branum-Martin L, Fletcher JM, Stuebing KK. Classification and identification of reading and math disabilities: The special case of comorbidity. Journal of Learning Disabilities. 2013;46:490–499. doi: 10.1177/0022219412468767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Catts HW, Hogan TP, Adolf SM. Developmental changes in reading and reading disabilities. In: Catts HW, Kamhi AG, editors. The connections between language and reading disabilities. Mahwah, NJ: Erlbaum; 2005. pp. 25–40. [Google Scholar]
- Cherodath S, Singh NC. The influence of orthographic depth on reading networks in simultaneous biliterate children. Brain and Language. 2015;143:42–51. doi: 10.1016/j.bandl.2015.02.001. [DOI] [PubMed] [Google Scholar]
- Cowan R, Cowan Donlan C, Shepherd D, Cole-Fletcher R, Saxton M, Hurry J, et al. Basic calculation proficiency and mathematics achievement in elementary school children. Journal of Educational Psychology. 2011;103:786–803. doi: 10.1037/a0024556. [DOI] [Google Scholar]
- Davis OSP, Band G, Pirinen M, Haworth CMS, Meaburn EL, Kovas Y, Spencer CCA. The correlation between reading and mathematics ability at age twelve has a substantial genetic component. Nature Communications. 2014;5:4204. doi: 10.1038/ncomms5204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Denkla MB, Rudell R. Rapid automatized naming (RAN): Dyslexia differentiated from other learning disabilities. Neuropsychologia. 1976;14:471–479. doi: 10.1016/0028-3932(76)90075-0. [DOI] [PubMed] [Google Scholar]
- Duncan GJ, Dowsett CJ, Classens A, et al. School readiness and later achievement. Developmental Psychology. 2007;43:1428–1446. doi: 10.1037/0012-1649.43.6.1428. [DOI] [PubMed] [Google Scholar]
- Ehri LC. Development of sight word reading: Phases and findings. In: Snowling MJ, Hulme C, editors. The science of reading: A handbook. Oxford: Blackwell; 2008. pp. 135–154. [DOI] [Google Scholar]
- Fuchs D, Fuchs LS, Thompson A, Al Otaiba S, Yen L, Yang N, Braun M, O’Connor R. Is reading important in reading-readiness programs? A randomized field trial with teachers as program implementers. Journal of Educational Psychology. 2001;93:251–267. doi: 10.1037//0022-0663.93.2.251. [DOI] [Google Scholar]
- Fuchs LS, Compton DL, Fuchs D, Powell SR, Schumacher RF, Hamlett CL, Namkung JM, Vukovic RK. Contributions of domain-general cognitive resources and different forms of arithmetic development to pre-algebraic knowledge. Developmental Psychology. 2012;48:1315–1326. doi: 10.1037/a0027475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fuchs LS, Fuchs D, Compton DL, Hamlett CL, Wang A. Is word-problem solving a form of text comprehension? Scientific Studies of Reading. doi: 10.1080/10888438.2015.1005745. in press. Published online February 23, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fuchs LS, Fuchs D, Compton DL, Powell SR, Seethaler PM, Capizzi AM, Schatschneider C, Fletcher JM. The cognitive correlates of third-grade skill in arithmetic, algorithmic computation, and arithmetic word problems. Journal of Educational Psychology. 2006;98:29–43. doi: 10.1037/0022-0663.98.1.29. [DOI] [Google Scholar]
- Fuchs LS, Geary DC, Fuchs D, Compton DL, Hamlett CL. Sources of individual differences in emerging competence with numeration understanding versus multidigit calculation skill. Journal of Educational Psychology. 2014;106:482–498. doi: 10.1037/a0034444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gathercole SE, Hitch GJ, Service E, Martin AJ. Phonological short-term memory and new word learning in children. Developmental Psychology. 1997;33:966–979. doi: 10.1037/0012-1649.33.6.966. [DOI] [PubMed] [Google Scholar]
- Geary DC. Children’s mathematical development: Research and practical applications. Washington, DC: American Psychological Association; 1994. [Google Scholar]
- Geary DC. Cognitive predictors of achievement growth in mathematics: A 5-year longitudinal study. Developmental Psychology. 2011;47:1539–1552. doi: 10.137/a0025510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geary DC, Bow-Thomas CC, Yao Y. Counting knowledge and skill in cognitive addition: A comparison of normal and mathematically disabled children. Journal of Experimental Child Psychology. 1992;54:372–391. doi: 10.1016/0022-0965(92)90026-3. [DOI] [PubMed] [Google Scholar]
- Geary DC, Hoard MK, Byrd-Craven J, Nugent L, Numtee C. Cognitive mechanisms underlying achievement deficits in children with mathematical learning disability. Child Development. 2007;78:1343–1459. doi: 10.1111/j.1467-8624.2007.01069.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geary DC, Hoard MK, Nugent L. Independent contributions of the central executive, intelligence, and in-class attentive behavior to developmental change in the strategies used to solve addition problems. Journal of Experimental Child Psychology. 2012;113:49–65. doi: 10.1016/j.jecp.2012.03.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hecht SA, Torgesen JK, Wagner RK, Rashotte CA. The relations between phonological processing abilities and emerging individual differences in mathematical computation skills: A longitudinal study from second to fifth grades. Journal of Experimental Child Psychology. 2001;79:192–227. doi: 10.1006/jecp.2000.2586. [DOI] [PubMed] [Google Scholar]
- Koponen T, Aunola K, Ahonen T, Nurmi J. Cognitive predictors of single-digit and procedural calculation skills and their covariation with reading skill. Journal of Experimental Child Psychology. 2007;97:220–241. doi: 10.1016/j.jecp.2007.03.001. [DOI] [PubMed] [Google Scholar]
- Koponen T, Salmi P, Ekland K, Aro T. Counting and RAN: Predictors of arithmetic calculation and reading fluency. Journal of Educational Psychology. 2013;105:162–175. doi: 10.1037/a0029285. [DOI] [Google Scholar]
- Kovas Y, Haworth CM, Harlaar N, Petriall SA, Plomin R. ‘Generalist genes’ and mathematics in 7-year-old twins. Intelligence. 2007;33:473–489. doi: 10.1016/j.intell.2005.05.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lambrecht S, Scott KA, Roberts J, Locke JL. Disabled readers’ performance on tasks of phonological processing, rapid naming, and letter knowledge before and after kindergarten. Learning Disabilities Research & Practice. 2008;2008:23, 113. doi: 10.1111/j.1540-5826.2008.00269.x. [DOI] [Google Scholar]
- Li Y, Geary DC. Developmental gains in visuospatial memory predict gains in mathematics achievement? PLoS ONE. 2013;8(7):e70160. doi: 10.1371/journal.pone.0070160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mann Koepke K, Miller B. At the intersection of math and reading disabilities: Introduction to special issue. Journal of Learning Disabilities. 2013;46:483–489. doi: 10.1177/0022219413498200. [DOI] [PubMed] [Google Scholar]
- Miller AC, Fuchs D, Fuchs LS, Compton DL, Kearns D, Kirchner D. Behavioral attention: A longitudinal study of whether and how it influences the development of word reading and reading comprehension among at-risk readers. Journal of Research in Educational Effectiveness. 2014;7:232–249. doi: 10.1080/19345747.2014.906691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Norton ES, Wolf M. Rapid automatized naming (RAN) and reading fluency: Implications for understanding and treatment of reading disabilities. Annual Review of Psychology. 2012;63:427–52. doi: 10.1146/annurev-psych-120710-100431. [DOI] [PubMed] [Google Scholar]
- Ouellette GP. What’s meaning got to do with it: The role of vocabulary in word reading and reading comprehension. Journal of Educational Psychology. 2006;98:54–566. doi: 10.1037/0022-0663.98.3.554. [DOI] [Google Scholar]
- Pickering S, Gathercole S. Working Memory Test Battery for Children. London: The Psychological Corporation; 2001. [Google Scholar]
- Qin S, Cho S, Chen T, Rosenberg-Lee M, Geary DC, Menon V. Hippocampal-neocortical functional reorganization underlies children’s cognitive development. Nature Neuroscience. 2014;17:1263–1269. doi: 10.1038/nn.3788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shaywitz S. Current concepts: Dyslexia. New England Journal of Medicine. 1998;338:307–312. doi: 10.1056/NEJM199801293380507. [DOI] [PubMed] [Google Scholar]
- Supekar K, Swigart AG, Tenison C, Jolles DD, Rosenberg-Lee M, Fuchs L, Menon V. Neural predictors of individual differences in response to math tutoring in primary-grade school children. Proceedings of the National Academy of Sciences. 2013;110:8230–8235. doi: 10.1073/pnas.1222154110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swanson J, et al. [12/20/2004];Categorical and dimensional definitions and evaluations of symptoms of ADHD: The SNAP and the SWAN rating scales. 2004 Downloaded from www.adhd.net. [PMC free article] [PubMed]
- Wechsler D. Wechsler Abbreviated Scale of Intelligence. San Antonio, TX: Psychological Corporation; 1999. [Google Scholar]
- Wilkinson GS. Wide Range Achievement Test 3. Wilmington: Wide Range; 1993. [Google Scholar]
- Willcutt EG, Pennington BF, Duncan L, Smith SD, Keenan JM, Wadsworth SJ, Defries JC. Understanding the complex etiology of developmental disorders: Behavioral and molecular genetic approach. Journal of Developmental and Behavioral Pediatrics. 2010;31:533–544. doi: 10.1097/DBP.0b013e3181ef42a1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Willcutt EG, Petrill SA, Wu S, Boada R, Defries JC, Olson RK, Pennington BF. Comorbidity between reading disability and math disability: concurrent psychopathology, functional impairment, and neuropsychological functioning. Journal of Learning Disabilities. 2013;46:500–516. doi: 10.1177/0022219413477476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woodcock RW. Woodcock Diagnostic Reading Battery. Itasca, IL: Riverside; 1997. [Google Scholar]
- Woodcock RW, McGrew KS, Mather N. Woodcock-Johnson III. Itasca, IL: Riverside; 2001. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.