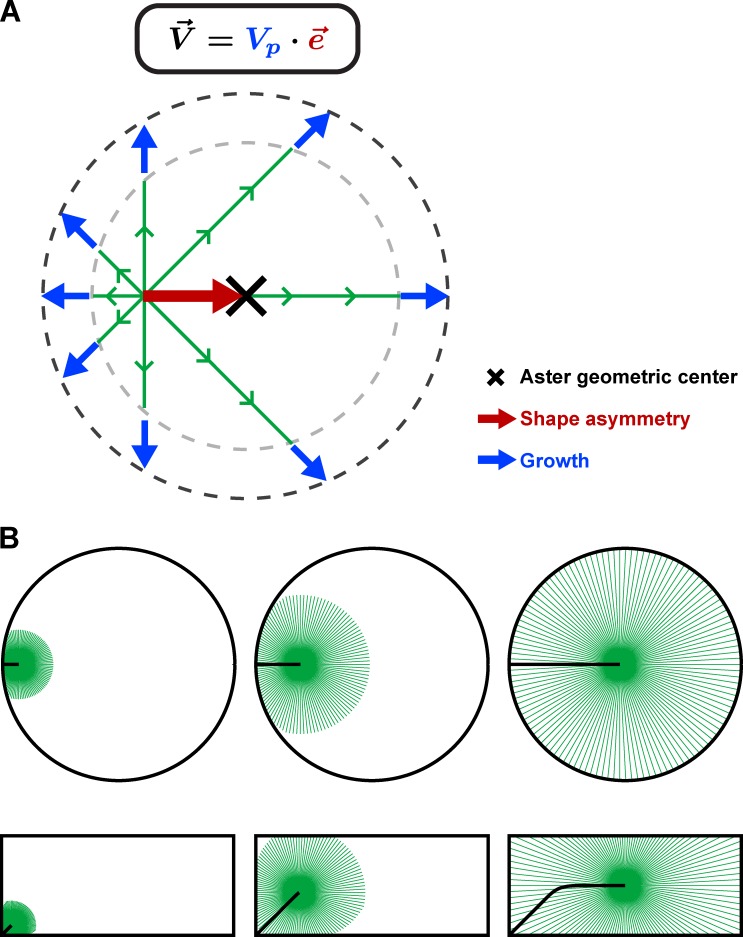
To faithfully target the center of large eggs, microtubule asters translate their shape into directed motion through length-dependent microtubule forces mediated by dynein in the cytoplasm. Their speed is independent of aster shape but determined by their growth rate.
Abstract
Although mechanisms that contribute to microtubule (MT) aster positioning have been extensively studied, still little is known on how asters move inside cells to faithfully target a cellular location. Here, we study sperm aster centration in sea urchin eggs, as a stereotypical large-scale aster movement with extreme constraints on centering speed and precision. By tracking three-dimensional aster centration dynamics in eggs with manipulated shapes, we show that aster geometry resulting from MT growth and interaction with cell boundaries dictates aster instantaneous directionality, yielding cell shape–dependent centering trajectories. Aster laser surgery and modeling suggest that dynein-dependent MT cytoplasmic pulling forces that scale to MT length function to convert aster geometry into directionality. In contrast, aster speed remains largely independent of aster size, shape, or absolute dynein activity, which suggests it may be predominantly determined by aster growth rate rather than MT force amplitude. These studies begin to define the geometrical principles that control aster movements.
Introduction
Microtubule (MT) asters are animal cells’ organizational units made of MTs radiating from a centrosome. They orchestrate fundamental processes such as cell polarity, division, and embryogenesis (Gilbert, 2010). Asters can grow, shrink, and interact with cytoplasmic and surface elements to produce forces that move them to defined cellular locations. Aster forces are exerted at the level of individual MTs and integrated at the aster scale. Single MTs may generate pushing forces by polymerizing against the cell surface (Tran et al., 2001; Brito et al., 2005; Zhu et al., 2010; Laan et al., 2012; Pavin et al., 2012; Zhao et al., 2012) or exert pulling forces from the movement of minus-end–directed motors such as dynein bound to cortical or cytoplasmic anchors (Gönczy et al., 1999; Wühr et al., 2010; Zhu et al., 2010; Kimura and Kimura, 2011a; Laan et al., 2012; Pavin et al., 2012). Although much has been learned on the biology and biophysics of aster positioning problems (Minc and Piel, 2012; McNally, 2013; Kiyomitsu, 2015), little is known about how asters move inside cells.
The centration of sperm asters represents a ubiquitous and stereotypical aster long-range movement. Sperm asters are nucleated around sperm centrioles attached to the male pronucleus, brought inside eggs at fertilization. These asters assemble from the side of the egg and continuously grow in size while moving to the cell center (Mitchison et al., 2012). Given the atypical large size of eggs and the short timescale of early embryonic cell cycles, sperm asters must migrate at high speeds on the order of several micrometers per minute and target the cell center with unusual precision. In general, how aster speed and directionality are established is not well understood.
Here, we use quantitative 3D imaging, aster laser surgery, cell manipulation, and modeling to understand how sperm aster motion characteristics are determined in sea urchin embryos. We provide direct evidence that aster centration is driven by MT-length–dependent pulling forces mediated by dynein in the cytoplasm. Our data suggest that aster directionality is determined by aster shape asymmetries and that its speed is set by its growth rate.
Results and discussion
Sperm asters move persistently to the egg center with a constant velocity
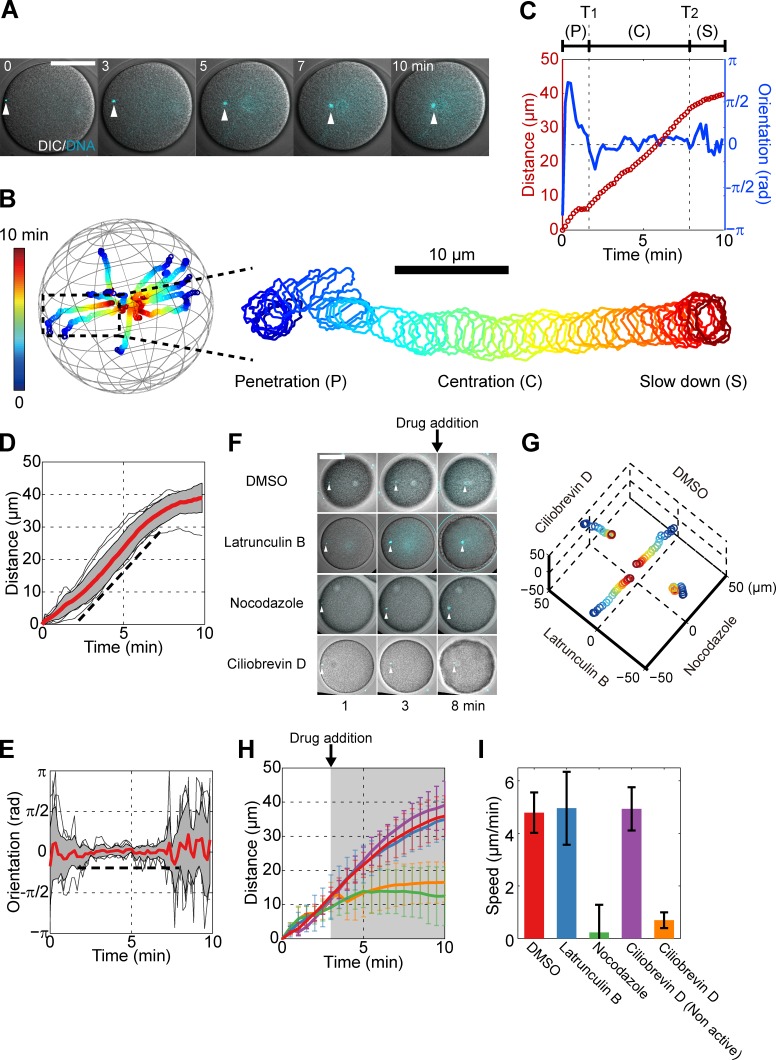
To investigate the centration dynamics of sperm asters in sea urchin eggs, we tracked sperm pronuclei, which mark aster centers, in 3D with a short time interval of 10 s over full centration periods typically 15–20 min long. This analysis revealed the existence of three main phases of motion: (1) a short, 2-min-long initial phase after sperm penetration with slow speed and no preferential direction; (2) a centration phase, ∼6 min long, that accounted for ∼80% of the traveled distance and during which the aster migrated with persistent orientation toward the egg center and with a constant speed V = 5.3 ± 1.2 µm/min (n = 17 eggs); and (3) a slowing-down phase when the aster neared the center (Fig. 1, A–E; Fig. S1, A–E; and Video 1). Thus, sperm asters move in a highly persistent manner with near constant speed and orientation during most of their centration period.
Figure 1.
Sperm asters move to the egg center with persistent directionality and constant speed, in a MT- and dynein-dependent manner. (A) Time-lapse confocal images superimposed with differential interference contrast (DIC) of a male pronucleus (white arrowhead) at the center of a sperm MT aster. (B) 3D trajectories of 10 individual asters and enlarged trajectory of an aster that migrates mostly in-plane. Time is color-coded. The centration is subdivided into three phases: an initial penetration phase (P), a rapid centration phase with straight path and constant speed (C), and a final slowing-down phase (S). (C) Aster traveling distance and orientation toward the cell center as a function of time, for the sample enlarged in B. T1 and T2 denote the beginning and end of the rapid centration phase. (D and E) Distance and orientation time plots for 10 individual asters. Red line, mean; gray section, SD. The broken line is a guide for the eyes. (F) Time-lapse images of eggs treated with different inhibitors 3 min after sperm entry. (G) 3D trajectories corresponding to the eggs and conditions from F. Time is color-coded as in B. (H) Mean aster traveling distance as a function of time in the presence of inhibitors. The gray region indicates the period during which inhibitors are present. Red, DMSO (n = 5); blue, 20 µM latrunculin B (n = 5); green, 20 µM nocodazole (n = 7); purple, 50 µM ciliobrevin D nonactive analog (n = 6); and orange, 50 µM ciliobrevin D (n = 6). (I) Aster speed computed using the distance–time curve between 5 and 7 min. Error bars represent SD. Bars, 50 µm.
Aster centration involves dynein-dependent MT pulling forces exerted in the cytoplasm
As in other systems (Gönczy et al., 1999; Kimura and Onami, 2005; Wühr et al., 2010; Kimura and Kimura, 2011a), aster movement depended on MTs and dynein. Depolymerization of MTs with 20 µM nocodazole stopped aster migration within 1 min of drug addition. In contrast, depolymerization of F-actin did not affect centration. Inhibition of dynein with 50 µM ciliobrevin D had similar effects as nocodazole (Fig. 1, F–I; Fig. S1, E–G; and Video 2). Ciliobrevin D halted minus-end–directed lysosome trafficking and affected spindle bipolarity at metaphase but did not grossly influence MT organization in the aster, suggesting a specific effect of this drug in this system (Fig. S1 H; Fig. S2, A–F; and Videos 3 and 4).
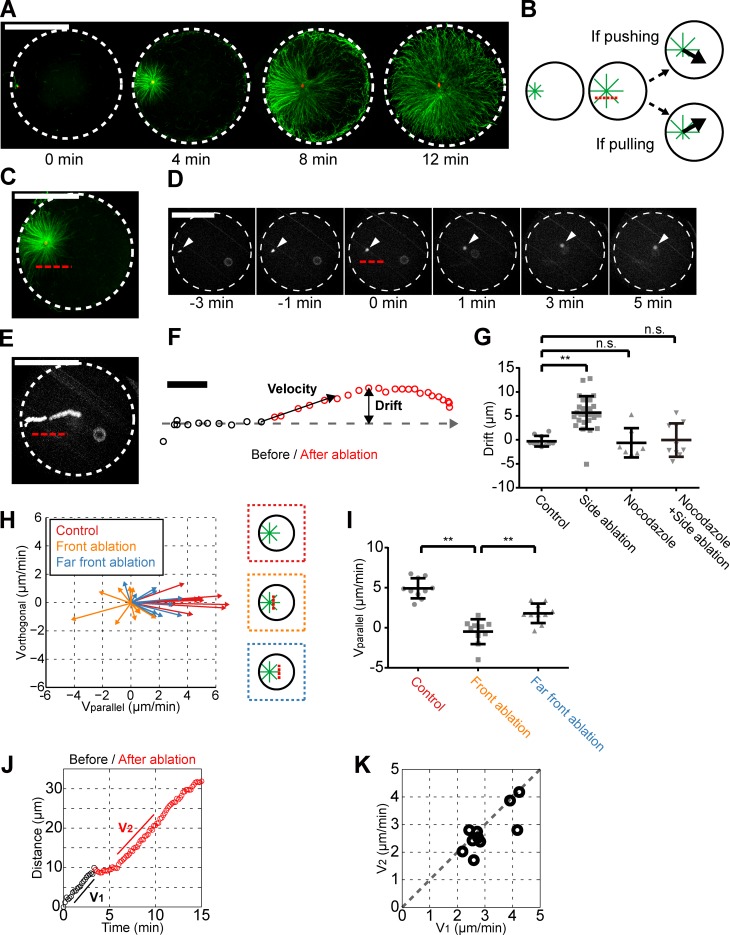
Dynein may generate pulling forces on MTs. However, aster MT staining revealed a consistent increased MT density at the aster rear close to the cortex, which could be more in agreement with a pushing-based mechanism (Figs. 2 A and S2 G). To test this directly, we set up an ablation assay to cut a portion of sperm asters and assess the impact on aster movements. We first ablated asters on the side parallel to their centration direction. Strikingly, 96% of ablated asters (n = 28) drifted away from the ablation line with a drift amplitude varying from 2 to 15 µm. The same assay performed in nocodazole-treated eggs did not yield any significant drift, suggesting this effect is caused by MTs (Fig. 2, B–G; and Video 5). Ablation of MTs at the aster front caused asters to move backward in 50% of cases (n = 10) or to exhibit a transient stop in the other cases, both followed by a rapid recovery to a normal centration motion (Fig. 2, H–K; and Video 6). Together, these results suggest that MTs generate pulling forces in all directions and that the imbalance of these forces around asters may determine aster directionality.
Figure 2.
Aster centration is driven by MT-pulling forces in the cytoplasm. (A) Time-dependent immunostaining of centering MT asters (MT, green; DNA, red). The indicated time is taken in reference with sperm entry by accounting for a mean 3-min delay between sperm addition and entry. (B) Centering MT asters are ablated parallel to the centration trajectory. A drift in the trajectory toward (away from) the ablation line suggests that MTs are pushing (pulling). (C) In situ MT aster immunostaining performed immediately after laser ablation along the red broken line. (D and E) Time-lapse (D) and time projection (E) of a centering aster ablated as indicated. Time 0 is the time of ablation. White arrowhead, male pronucleus. (F) Definition of aster velocity and drift after ablation. (G) Aster drift in the indicated conditions (n = 10 for control; n = 28 for side ablation; n = 7 for nocodazole; n = 10 for nocodazole + side ablation). Bar, 10 μm. (H) Aster velocity vectors after ablation at the indicated locations. (I) Aster speed along the centration path after ablation in the indicated conditions. (J) Distance–time plot of a front-ablated aster. (K) Aster velocity along the centration path after ablation (V2) as a function of the velocity before (V1). n.s., nonsignificant; **, P < 10−4 (Student’s t test). Error bars represent SD. Bars, 50 µm.
Next, we investigated if MTs and dynein may pull from the cortex (Grill and Hyman, 2005; Kozlowski et al., 2007) or the cytoplasm (Kimura and Onami, 2005; Wühr et al., 2010; Kimura and Kimura, 2011a) with time-dependent immunostaining. In 96% of stained embryos (n = 60) at timings inferior to 7 min postfertilization, when asters are already moving at maximum speed, we did not observe any MTs touching the opposite cortex, suggesting that interactions between MTs and the cortex are not required for centration. At timings between 7 and 10 min, when asters begin to slow down, some MTs started to contact the opposite cortex, and after 10–15 min, asters had finished centration and filled the whole cytoplasm (Figs. 2 A and S2 G; and Video 7). Given that dynein has been reported to locate homogeneously in the cytoplasm in fertilizing sea urchins (Mohri et al., 1976), we conclude that sperm aster centration may be driven by pulling forces mediated by MTs and dynein in the cytoplasm.
Length-dependent forces convert aster geometry into aster directionality
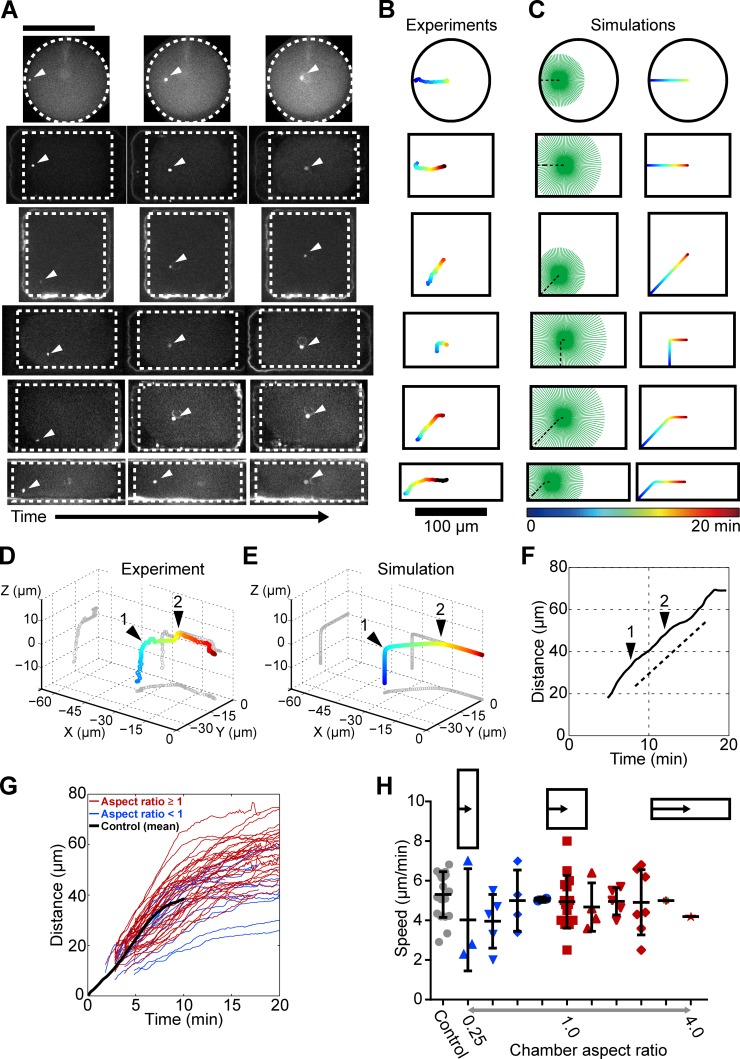
Dynein forces generated in the cytoplasm may be consistent with a length-dependent pulling hypothesis, which posits that the amplitude of pulling force on each MT scales to its length (Hamaguchi and Hiramoto, 1986). This model has been used to account for sperm aster centration: MTs at the aster front are longer than at the back and pull more, allowing them to propel the aster forward until length equilibrium is reached at the cell center. Accordingly, a simple 3D simulation, which assumes that (a) MT pulling forces positively depend on MT length and (b) MT growth rates are constant in the cytoplasm and null at the cell cortex, recapitulates aster centration in normal spherical eggs (Fig. 3, A–C; and Video 9; Kimura and Onami, 2005; Longoria and Shubeita, 2013).
Figure 3.
Aster geometry determines aster directionality. (A) Time lapses of aster centration in shape-manipulated eggs. (B) Centering trajectories for the time lapses presented in A. (C) Corresponding numerical simulations. (D) 3D centering trajectory of a sperm aster exhibiting two subsequent turning points (black arrowheads). The plot volume corresponds to a cell quarter with X = Y = Z = 0 marking the cell center. (E) Numerical simulation corresponding to D. (F) Distance–time plot for the centration trajectory presented in D, with black arrowheads marking the turning points. (G) Distance–time curves for 35 centering asters in various cell geometries. Shape aspect ratio: red, ≥1; blue, <1. The black line is an averaged distance–time curve for normal spherical cells. (H) Aster speed in different cell geometries. Error bars represent ±SD. Bars, 100 µm.
To systematically test this hypothesis, we monitored aster centration in defined cell shapes by rapidly pushing freshly fertilized eggs into microfabricated wells (Minc et al., 2011). Asters were still able to find the center of shaped eggs, but they consistently followed a trajectory that highly depended on cell shape and sperm entry point. In axisymmetric situations such as in cases of sperm entrance halfway from the side of a rectangle or from the corner of a square, asters migrated straight, as expected. However, when sperms entered off-center, asters first migrated perpendicular to the rectangle side and then exhibited a sharp turn toward a novel direction pointing to the cell center. Similarly, sperm entry close to the corner of elongated rectangular cells also yielded a concave trajectory, with the position of the turning point depending on shape aspect ratio (Fig. 3, A and B; and Video 8). When sperm entry occurred away from the midplane, asters exhibited multiple turning points in 3D (Fig. 3 D). Importantly, by altering the boundary conditions in our 3D simulation, we could quantitatively reproduce all observed aster trajectories including 3D multiple rotations, with no adjusted parameter besides cell shape (Fig. 3, C and E; and Video 9). Thus, these results directly suggest that asters may interconvert local cell-shape sensing into instantaneous directionality through length-dependent MT pulling forces.
Speed determination in growing asters
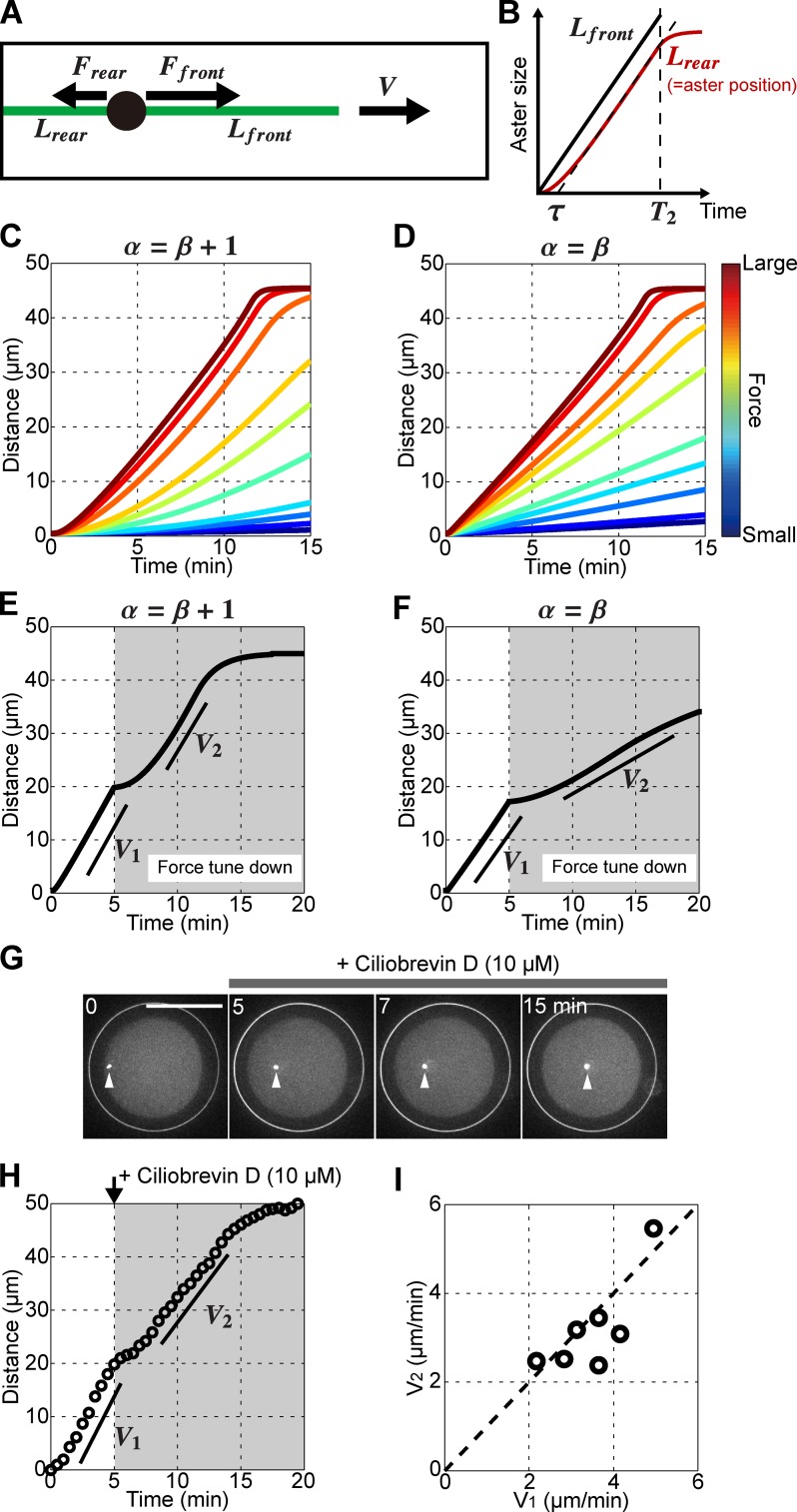
Although cell shape had a strong influence on aster trajectories, it did not affect aster speed. In all cell shapes assessed, asters migrated with constant speed even when exhibiting turning points in the centration path (Fig. 3 F). Aster speed in shape-manipulated cells was close to the speed measured in round control cells and did not vary significantly with the length or duration of the centration phase (Fig. 3, G and H). This speed was a little superior but close to the aster growth rate Vp = 3.8 µm/min estimated from time-dependent immunostaining (Fig. S2 H). In addition, the aster front radius was 5 to 10 µm larger than the rear radius independent of absolute aster size, further indicating that asters may move with a speed similar to their front growth rate (Fig. S2 I). Aster speed also completely recovered in frontal MT ablation assays (Fig. 2, J and K). Together, these results suggest that aster constant speed is close to aster growth rate and independent of aster size, geometry, or fine-tuned cell-cycle regulation. This finding is unexpected given that aster size increases by almost 20-fold during centration (Fig. 2 A). Indeed, a constant centration speed close to aster growth rate has been suggested to be a signature of MT pushing, rather than pulling (Chambers, 1939; Hamaguchi and Hiramoto, 1980). In what follows, we propose a simple model that explains how length-dependent pulling forces may yield constant aster speed, and we exploit this analysis to dissect the generic mechanisms of aster speed determination.
To understand how aster speed is determined, we analyzed a simple 1D model consisting of one MT at the front and one at the rear with respective lengths Lfront and Lrear (Fig. 4 A). Both MTs polymerize with a constant rate Vp in the cytosol and stop polymerization at the cell surface. Size-dependence of MT pulling force F and drag η are represented by a general scaling form: F = aLα and η = bLβ, where a and b are length-independent constants representing dynein density/activity and aster drag, respectively, and α and β are scaling exponents that reflect how forces and drag may scale to MT length (Hays et al., 1982; Minc et al., 2011). Aster speed V is determined by the force balance between MT forces and viscous friction so that
| (1) |
By analyzing Eq. 1, we found that a constant speed may arise from either one of the two conditions linking scaling exponents: α = β + 1 or α = β (Materials and methods). This analysis, confirmed by 3D simulation, suggested that in the first condition α = β + 1, aster speed is determined by, and is an increasing function of, the length difference Lfront − Lrear (Eq. 12 and Fig. S3). Initially V < Vp, so that front MTs grow faster than at the rear. As a consequence both Lfront − Lrear and V continuously increase. When V reaches Vp, front and rear MTs grow at the same rate Vp and thus Lfront − Lrear and V become constant, which can be pictured as a treadmilling in MT front–rear length differences. Importantly, in this condition, the parameter a/b negatively influences the time τ needed to reach constant speed but only has a minor impact on the constant speed value (Fig. 4, B and C; and Fig. S3). In other words, MT/dynein force amplitude does not affect stationary aster speed, which is determined by aster growth rate. The speed determination in the second condition, α = β, is conceptually different. Aster speed is now determined by the length ratio Lfront/Lrear, and the constant speed positively depends on a/b and may take any value between 0 and Vp (Eq. 15 and Figs. 4 D and S3). Both conditions give similar centration dynamics in the high force limit: a short acceleration phase and a speed close to aster growth rate, as observed in the experiments. Thus, this analysis suggests that the forces driving aster centration in this system may be relatively high.
Figure 4.
Speed determination in growing asters. (A) 1D model of a centering aster. Each MT exerts a pulling force F that scales to its length L. The aster moves with a speed V. (B) Time evolution of MT lengths in the model. Note that Lrear is equal to aster position in the model. τ and T2 correspond to the time needed to reach constant speed and to the time at which the front MT contacts the opposite cortex. (C and D) 3D simulations for various force parameter values and for the two scaling conditions linking α and β. (E and F) Simulations assessing the impact of abruptly reducing the force amplitude in the two different scaling conditions. The force parameter was decreased by a factor 20 in the simulation at 5 min (G) Confocal time lapse of a centering aster treated with a low dose of 10 µM ciliobrevin D at 5 min after sperm entry. (H and I) Aster speed before (V1) and after (V2) ciliobrevin D treatment. (I) V2 plotted as a function of V1 for seven individual eggs. Broken line marks V1 = V2. Bars, 50 µm.
Aster speed is largely independent of absolute dynein activity
These two scaling conditions give different centration dynamics for smaller MT/dynein forces. In simulations, a reduction of the force amplitude after asters have reached constant speed V = Vp yielded a transient aster slowdown followed by a complete speed recovery in the condition α = β + 1 (Fig. 4 E). In contrast, in the condition α = β, aster speed remained smaller and did not recover to Vp (Fig. 4 F). To test these predictions experimentally, we rapidly rinsed eggs 5 min after sperm entry with different doses of ciliobrevin D (Fig. S3 E). We found that a concentration of 10 µM consistently caused asters to stop transiently for a period of ∼2 min, after which they recovered their initial speed (Fig. 4, G–I; and Video 10). This behavior was observed in 92% of the eggs treated with ciliobrevin D but only in 13% of eggs rinsed with DMSO. This suggests that aster speed determination in this system may satisfy the condition α = β + 1 and is mostly determined by aster growth rate and weakly influenced by the absolute amplitude of MT pulling forces.
Conclusions
In sum, we here systematically test and validate a quantitative model based on length-dependent MT pulling forces as a pure geometrical mechanism determining centering trajectories and speeds of sperm asters. Inhibitor assays, laser ablation, and time-lapse immunostaining all provide novel additional evidence supporting aster centration driven by dynein pulling directly in the cytoplasm, not at the cortex. Our data on centration trajectories in shape-manipulated eggs disentangle aster motion from the polarity set by sperm entry and demonstrates that asters are able to probe their local geometrical environment to faithfully target the cell center (Fig. 5).
Figure 5.
Aster shape–motion relationships. (A) Proposed model for how centering MT asters may determine their speed and directionality. Each MT exerts a pulling force on the centrosome that scales to MT length. Aster shape asymmetry, which corresponds to the difference between centrosome position and aster geometrical center, is characterized by a unit vector corresponding to aster directionality. Asters migrate with a constant speed determined by the growth rate Vp. Therefore, the aster velocity vector can be simply represented as . (B) These shape–motion relationships enable asters to probe local cell geometry to faithfully find the center in any cell shape.
We suggest that sperm asters in sea urchin migrate in a high-force regime. Signatures of this regime are a near symmetric aster shape and a constant speed. Sperm asters in Xenopus laevis are also mostly symmetric and move with constant speed (Stewart-Savage and Grey, 1982; Wühr et al., 2009, 2010). In contrast, asters in Caenorhabditis elegans exhibit a large asymmetry and long acceleration/deceleration phases, likely reflecting a relatively low-force regime (Kimura and Onami, 2005). Thus, we expect our analysis to be valuable in unifying qualitatively different aster dynamics in various systems.
Our results further constrain the functional form of aster force-size and drag-size dependencies. The relationship α = β + 1 implies that aster force grows faster than aster drag with size. In addition, aster trajectories appear to be influenced by the centripetal movement of female pronuclei on the aster only when the aster is very small (Fig. S2, L and M; Chambers, 1939; Hamaguchi and Hiramoto, 1980). This suggests that the drag of small asters may be smaller than the drag of large asters, so that β > 0 and hence α > 1, consistent with a previous study suggesting nonlinearity in length-dependent pulling forces with α ∼3–5 (Minc et al., 2011). A tentative speculation would be to assume that astral MT forces scale to a local volume around MTs (Minc et al., 2011; Kimura and Kimura, 2011b), so that α = 3 and β = 2. This would imply that aster drag may scale to a local cone-like surface surrounding MTs. Interactions of endomembrane elements such as the ER and other vesicles all along astral MTs could account for such nonlinear MT–cytoplasm frictional interactions (Terasaki and Jaffe, 1991). Future work analyzing the relationships between force, motion and geometry of asters in vivo will be instrumental to understand further the core spatial organization principles of cells and embryos.
Materials and methods
Sea urchin eggs
Purple sea urchins (Paracentrotus lividus) were obtained from L’Oursine de Ré or the Roscoff Marine station and maintained in a large aquarium for several weeks. The aquariums were filled with artificial sea water (ASW; Instant Ocean; Reef Crystals) and kept at 16°C, with constant oxygenation and water filtering. The ASW was filtered using an 80-µm Nitex mesh (Sefar) and used for all experiments. Gametes were collected by intracoelomic injection of 0.5 M KCl. Sperms were kept at 4°C and used within 1 wk. Eggs were rinsed twice, kept at 16°C, and used on the day of collection. For live imaging, except for shape manipulation assays, the jelly coat of unfertilized eggs was removed by passing them three times through an 80-µm Nitex mesh to facilitate egg adhesion on glass dishes.
Microscopy
Live imaging and laser ablation were performed on a spinning-disk confocal fluorescent microscope (Ti-Eclipse [Nikon] combined with a spinning-head [CSU-X1; Yokogawa] and an EM-CCD camera [Hamamatsu]) equipped with a 40× oil-immersion objective (Plan Fluor, NA 1.3; Nikon). The microscope and motorized stage were operated by MetaMorph (Molecular Devices). The microscopy room was air conditioned and kept at 15–17°C. Microtubule immunostaining images were acquired with a scanning confocal microscope (LSM 780; ZEISS). Either coverslips (24 × 50 mm, thickness no. 1; VWR) or glass-bottom dish (50-mm glass-bottom dish, thickness no. 1.5; MatTek Corporation) were used for microscopy.
Aster 3D tracking
The male pronucleus at the aster center was stained with Hoechst 33342 (Sigma-Aldrich) at a final concentration of 1 µg/ml. The dye was added before fertilization and left in the sea water throughout the experiment. Aster 3D centration was monitored by taking time-lapse confocal stacks (Fig. S1 A). The acquisition was started just after sperm-head penetration (distance between cell cortex and sperm-head center <5 µm) for the experiments presented in Figs. 1, 2, and 4, and at ∼4 min after fertilization for the cell-shape manipulation experiments presented in Fig. 3. The tracking period was at least 15 min long to ensure that asters finished centration. Both illumination intensity and exposure time were adjusted to minimize phototoxicity. 15 images with a slice interval of 3 µm were taken at each time point. The z stack covered one hemisphere of the eggs and was thus sufficient to monitor the whole centration. Each z stack took ∼8 s of acquisition and were spaced with an interval of 10 or 30 s. All image analyses were done with a custom code written in MATLAB (MathWorks). Aster position in Z was determined by detecting the plane in which the male pronucleus was in focus. The XY position in the selected image was then automatically detected. The XY precision was calibrated with immobile sperm heads stuck on coverslip surface and was close to 1 µm. The Z precision was set by the spacing between Z slices and was ∼3 µm. This Z resolution was sufficient to confirm that aster centration trajectory was straight not only in XY but also in XZ and YZ (Fig. S1 B). Aster Z position was smoothened using a cubic spline method. In a subset of cases, small movements of the observation chamber and/or eggs were observed and were subtracted from the aster motion. Centration dynamics were not affected by the imaging, and in general, the first division timing of imaged eggs was <10% different than nonimaged control eggs from the same batch.
Data analysis
Aster traveling distance at time t was defined as , where is the aster 3D position at time t and is the initial position. For asters with multiple rotations, the trajectory was split into linear paths between rotations, and the traveling distance was defined as the sum of the passed paths and the distance from the last rotating position. For chamber assays, the time delay between fertilization and beginning of the time-lapse was measured for each experiments, and the onset of the traveling distance was defined as the aster speed multiplied by the time delay. The uniform motion phase (phase 2) was manually defined as the linear region in the distance–time curve, and aster constant speed (referred simply as aster speed) was determined by a linear fitting of the curve. Aster instantaneous velocity was defined as , where τ0 was set to 30 s and τ0 to 1 min for quantifications of laser ablation experiments and where the induced transient effect has a timescale of ∼2 min. Time average of aster velocity in phase 2 gave a similar aster constant speed as determined with the distance–time curve. In plane orientation of asters was defined as the angle formed by aster in-plane velocity vector and the in-plane line connecting aster initial position and the cell center. The mean squared displacement (MSD) was defined as , where denotes time average. Data of 7-min length were used for MSD analyses, and time 0 was set to be t = 0 for controls and 2 min after drug addition for inhibitor assays (Fig. S1 E).
Laser ablation
Aster local laser ablation was conducted using a high-power pulsed 355-nm UV laser system (iPulse; Roper Technologies) and a 40× 1.3 NA Plan-Fluor oil objective. The system was operated by iLas2 software (Roper Technologies). Different ablation conditions were assayed to optimize the laser irradiation protocol. The ablated asters were immediately fixed in situ and the results were judged based on MT immunostaining. The protocol described hereafter was found to be sufficient to significantly reduce both length and density of astral MTs at the ablation line, without damaging the egg (Fig. 2 C). Asters migrating in the equatorial plane were selected, and a 25-µm line region situated at 15 µm away from the aster center was irradiated. The irradiated line was parallel to the previous migrating direction for side-ablation assays and perpendicular for front-ablation assays. The line consisted of three 350-nm beam lines spaced by an interval of 1 µm. Each single laser irradiation took 7 ms and was iterated 400 times. The ablation was done at three different heights: at the aster center and 5 µm above and below. The total time needed to complete ablation was ∼10 s. For ablation assays, asters migrating mostly in plane were selected and only in plane motion was analyzed.
Pharmacological inhibitors
Inhibitor assays were performed in small glass chambers that allowed a rapid exchange of solutions. The chamber was composed of two clean coverslips and a spacer of 100–150 µm thickness. Using a fluorescence solution, we confirmed that solution exchange was completed within seconds in this chamber. The bottom coverslip was coated with 1% protamine (Sigma-Aldrich) and rinsed and dried before chamber assembly. Unfertilized eggs were introduced in chambers and fertilized in situ by introducing a diluted sperm solution. Inhibitors were applied at 3 min after sperm entry in the experiments presented in Fig. 1 (F–I) and at 5 min in the experiments presented in Fig. 4 (G–I). All inhibitors were prepared in 100× stock aliquots in DMSO. Latrunculin B (Sigma-Aldrich) was used at a final concentration of 20 µM, and nocodazole (Sigma-Aldrich) was used at a final concentration of 20 µM. Ciliobrevin D (EMD Millipore) was used at various final concentrations. Ciliobrevin D inactive analogue (a gift from T.M. Kapoor [Rockefeller University, New York, NY] and J.K. Chen [Stanford University School of Medicine, Stanford, CA) was used at a final concentration of 50 µM.
Polydimethylsiloxane (PDMS) chamber and operation
Two types of PDMS systems were used in this study: (1) slabs containing egg-sized microwells for cell-shape manipulation and (2) flat and wide perfusion channel for immunostaining assays. General procedures for soft-lithography and PDMS molding are described elsewhere (Chang et al., 2014). The PDMS slab used for cell shape manipulation contained typically thousands of rectangular microwells with various aspect ratios. The depth of the microwells was ∼55 µm, and the aspect ratio varied to keep the microwell volume roughly equal to the egg volume. The aspect ratio varied from 1:1 (91 × 91 µm) to 4:1 (182 × 45 µm). PDMS slabs were activated with plasma cleaner (PDC-002; Harrick) a few minutes before use and covered with ASW. Eggs were fertilized in a falcon tube, 40 µl dense egg solution was placed on a clean coverslip, and the PDMS slab was gently applied from the top. The slab was moved down further by removing excess ASW between the coverslip and the PDMS. This procedure took ∼3–5 min from sperm addition to the beginning of image acquisitions. The eggs shaped by this method developed through multiple cell divisions in the microwells. For in situ immunostaining of eggs in chambers, the PDMS slab was first pierced with a hole at the center to allow for fluid exchange, in a similar manner as described before (Minc et al., 2011). To flatten eggs in a reproducible manner and force sperm aster centration to occur in 2D in round eggs, we used other custom-made PDMS channels. The channel height was ∼70–75 µm, ∼10% smaller than the egg diameter. The channel dimension was 25 mm × 8 mm. The two extremities of the channels were pierced with holes. Both PDMS slab and coverslip were washed with acetone, isopropanol, and water and subsequently air-dried. A drop of 25 µl unfertilized egg solution was placed on the PDMS channel and covered with a large coverslip. Edges of the coverslip were pushed onto the PDMS to seal the channel. Eggs were then fertilized in situ by introducing the sperm solution from the reservoir hole and fixed and stained through liquid exchange when relevant.
Immunostaining
Immunostaining was performed using similar procedures as described previously (Foe and von Dassow, 2008; Minc et al., 2011). The fixation was performed in bulk (Figs. 2 A and S1 F), in the flat PDMS perfusion chamber (Figs. 2 C and S2 G), or in microwells (Fig. S2 J). Fixations in chamber or microwells were done under the microscope to ensure that eggs do not move or change shape during liquid exchange. All experiments involved similar protocols. Eggs were first fixed for 70 min in 100 mM Hepes, pH 6.9, 50 mM EGTA, 10 mM MgSO4, 2% formaldehyde, 0.2% glutaraldehyde, 0.2% Triton X-100, and 400 mM glucose. Eggs were then rinsed three times for 10 min in PBS plus Tween 20 (PBT) and one time in PBS and placed in 0.1% NaBH4 in PBS made fresh for 30 min. Eggs were rinsed again with PBS and PBT and blocked in PBT plus 5% goat serum and 0.1% BSA for 30 min. For MT staining, cells were incubated for 48 h with a primary anti–α-tubulin antibody, clone DM 1A (Sigma-Aldrich) at 1/8,000, rinsed twice in PBS, and then incubated for 4 h with fluorophore-conjugated anti-mouse secondary antibody (Sigma-Aldrich) at 1/750. Aster staining after laser ablation was done in a PDMS flow chamber, and the fixative was introduced 10 s after ablation.
Analysis of aster shape
Aster shape was analyzed based on tubulin immunostaining images obtained by confocal microscopy. Live imaging of fluorescently labeled MTs provided qualitatively similar results (Video 7). The immunostaining was performed in flat flow chambers (described in the PDMS chamber and operation section) to force asters to move in the equatorial plane. Aster centration was monitored live, and eggs were fixed in situ. Samples in which aster center was largely deviating from the cell equator were discarded from the analysis. Stained eggs were imaged with a point confocal with a slice interval of 0.5 µm and 10 to 15 images around the aster center and projected to obtain the images presented throughout the manuscript. Aster rear radius was defined as the distance between the male pronucleus and the closest cell cortex, and the front radius was defined as the mean MT length at the aster front. More than 10 MTs were analyzed for each aster.
Injection
For the experiments involving live imaging of labeled MTs, HiLyte 488–conjugated tubulin (Cytoskeleton, Inc.) was microinjected into unfertilized eggs at a final concentration of 1 mg/ml, following previous injection protocols (Strickland et al., 2005).
Vesicle tracking
To visualize moving lysosomes, LysoTracker (Molecular Probes) was added at final concentration of 1/10,000, 10 min before fertilization. The time-lapse images were analyzed using the ImageJ plugin Particle Tracker.
Theoretical analysis of the 1D model for aster centration
1D model for MT aster migration
We consider a 1D microtubule aster with one MT at the front and one at the back (Fig. 4 A). The two MTs polymerize with a constant rate Vp in the cytoplasm and stop polymerizing when touching the cell cortex. Length dependencies of each MT force F and drag η are phenomenologically modeled with a general scaling form, so that F = aLα and η = bLβ, where L denotes MT length and a and b are coefficients corresponding to dynein density/activity and MT hydrodynamic friction, respectively. α is a scaling exponent that may represent the nature of dynein–MT interaction (Minc et al., 2011; Kimura and Kimura, 2011b). For instance, a homogeneous distribution of dynein motors along MTs would be represented by α = 1, whereas a diffusion-limited dynein–MT interaction in the cytoplasm with limited amount of dynein may correspond to α = 3. β is a scaling exponent that characterizes the frictional interaction between aster components and their surrounding environment. For instance, if the main contribution to aster drag comes from elements with fixed size such as pronuclei, the aster drag is not expected to depend on aster size (or MT length), so that β = 0 (Kimura and Onami, 2005, 2007; Shinar et al., 2011). If the drag of each MTs has a dominant contribution to the overall aster drag, then β may be close to 1 (Longoria and Shubeita, 2013).
Given the polarity of MTs, the net force Fnet and net resistance ηnet can be written as and . Dynein–MT forces must be balanced by the frictional force experienced by the aster, and thus aster speed V is determined by its instantaneous shape:
| (2) |
Necessary conditions for aster motion at constant speed
We consider an aster migrating with a constant speed V = VC. Because we assume that free MTs polymerize with a constant rate Vp, the length of the front MT Lfront is proportional to the time t (aster starts growing at t = 0), so that
| (3) |
The rear MT can freely polymerize with a rate Vp if ; however, its growth is hindered by the cell boundary if VC < Vp. Therefore, the length of the rear MT Lrear is given by
| (4) |
with L0 being the rear MT length when the aster begins to move at a constant speed. From Eq. 4, VC and Vp must then satisfy one of these two relationships:
| (5) |
with δL = L0 − VpT0; or
| (6) |
with δL = L0 − VCT0. For sufficiently large times, Eqs. 5 and 6 become
| (7) |
and
| (8) |
Therefore, an aster constant speed motion may be accounted for by either one of these two necessary conditions: α = β + 1 or α = β. The first condition encompasses a simplified version of a previous stochastic model, with α = 1 (mean force proportional to MT length) and β = 0 (constant aster drag; Kimura and Onami, 2005, 2007). A particular case of the second condition is close to another proposed model incorporating a linear scalable drag so that α = β = 1 (Longoria and Shubeita, 2013). In the following paragraph, we separately analyze these two conditions to see if they are indeed sufficient to account for constant speed and to understand how speed is influenced by different parameters.
Analysis 1: α = β + 1
A simple analytical solution of the 1D model satisfying the scaling condition α = β + 1 can be obtained in the simplest situation: (α,β) = (1,0) (force proportional to MT length, constant drag coefficient). As we will see hereafter, the aster speed is bounded by the growth rate Vp, so that the aster position X is equal to Lrear. Putting Eq. 3 into Eq. 2, the time evolution of aster position is given by
| (9) |
which yields
| (10) |
and
| (11) |
with . These equations show that aster speed approaches to its growth rate in an exponential manner. An interesting outcome from this result is that the final constant aster speed is determined only by the aster growth rate and is independent on the force and drag coefficients a and b. These mechanical parameters, however, determine the timescale τ needed to reach constant speed.
Simple analytical solution are not available for higher values of the exponents; however, for sufficient time, the leading term from Eq. 2, with α = β + 1, is
| (12) |
This indicates that past a sufficient time, aster speed in this condition is solely determined by the front–rear length difference Lfront − Lrear. Initially both aster speed and the length difference are close to 0. Lfront − Lrear increases in time, whereas aster speed V is smaller than Vp. Because aster speed is a positive function of the length difference, the aster accelerates until the speed reaches Vp. After aster speed has reached Vp, the length difference remains constant (a process similar to a length difference treadmilling), and consequently, the speed keeps the same value. Therefore, in this condition, the aster constant speed VC is always equal to Vp.
Analysis 2: α = β
Next, we investigate the second condition, α = β. Taking the leading terms in Eq. 6 for large t, we obtain
| (13) |
where VC < Vp. For α = β = 1, Eq. 13 can be solved and yields
| (14) |
Eq. 14 indicates that VC can take any value between 0 and Vp and depends strongly on a/b. VC is a positive function of a/b and increases linearly with a/b for small a/b and then gradually approaches Vp for large a/b.
Speed determination in higher values of the exponents may be qualitatively understood as follows. Eq. 13 can be rewritten as
| (15) |
In addition, , and for large t, . Therefore, in this condition, aster speed is determined by the length ratio between front and rear MTs
| (16) |
This analysis highlights the conceptual difference in aster constant speed determination in the two scaling conditions. If α = β + 1, aster speed is determined by the length difference, Lfront − Lrear, and by the length ratio, Lfront/Lrear, in the condition α = β. When speed is determined by the length difference, the final constant speed is always Vp. However, when it is determined by the length ratio, this speed may reach any value between 0 and Vp. The initial aster speed is small, and Lfront/Lrear = ∼1. The aster then continues accelerating, and Lfront/Lrear increases until aster speed reaches VC determined by Eq. 15. After the aster speed has reached VC, front MTs polymerize with Vp, whereas the rear MT polymerizes with VC; thus, the length ratio Lfront/Lrear = Vp/VC remains constant. Therefore, aster constant speed in this condition can take any value between 0 and Vp and is strongly influenced by the force parameters a and b.
Numerical 3D simulation for aster centration
We performed 3D numerical simulations to confirm the conclusions from the 1D model analysis. In the simulations, astral MTs are nucleated from a single point centrosome and evenly distributed around the centrosome with a constant angle difference. The number of total MTs did not influence the simulation results and was set to be 10,000. Initial MT length was set to 0. MTs grew with a constant rate Vp and stopped growing when touching the cell cortex. The contributions of individual MTs to aster force and drag are assumed to be additive. Therefore, the aster velocity must satisfy the force balance as
| (17) |
where i is an index corresponding to each MTs and is a unit vector pointing in the direction of MT plus end from the centrosome.
The simulation has four input parameters: MT growth rate Vp, the ratio between force and drag coefficients a/b, and scaling exponents α and β. We fixed Vp at 4 µm/min (similar to the aster growth rate determined from time-lapse staining of 3.8 µm/min) and varied other parameters. For the simulations in Fig. 3, we used (α,β) = (1,0), and the force parameter was determined so that the timescale of aster acceleration is the same as the typical duration of T1 (∼2 min; Fig. 1 C). The aster shape and position were updated every 0.1 s based on the aster growth rule and Eq. 17. Several time steps for the simulations were tested and did not influence the results. Simulations were performed using MATLAB.
As inputs, the simulation requires a defined cell geometry and an initial centrosome position. To simulate the centration in normal round eggs, we modeled the egg as a sphere of 90 µm diameter. To simulate cell shape manipulation experiments, the chamber shape was used as a good approximation of actual egg shape and the initial centrosome position was set to be 0.5 µm inside the egg at the site of sperm entry. The height of the chamber was taken as 55 µm as in the experiments, and the initial Z position of the centrosome was the midplane, except for analyses like in Fig. 3 G, in which the centrosome started from the bottom surface.
We first performed 3D simulations to test the general condition α = β + 1, for (α,β) = (1,0) for which analytical solutions are available (Eqs.10 and 11) and systematically changed the force parameter a/b. The simulations were done for normal spherical cell geometries. The results fully agreed with the outcome of the 1D analytical solution (Fig. S3 A). The aster speed in this simulation approached to Vp in an exponential manner. The time required to establish the final constant speed was negatively correlated with the force amplitudes. We however noted that aster speed slightly exceeded Vp for very high forces, plausibly because of 3D effects. Very similar results were obtained for higher values of the exponents (α,β) = (2,1) and (3,2) (Fig. S3 A).
Similar validations of the 1D analysis from 3D simulation were also obtained for the general conditions α = β. Asters exhibited a constant speed motion with speeds that depended on the force amplitude, a/b. The constant speed was an increasing function of a/b, and was bounded by Vp for high forces. Aster speed also slightly exceeded Vp for very high forces in this scaling condition (Fig. S3 B).
To confirm the conceptual difference in speed determinants between the two scaling conditions, we computed aster instantaneous speed at each step of the simulation and plotted it against Lfront − Lrear or Lfront/Lrear for one single simulation run and represented the result using a density color plots (Fig. S4, C and D). Lfront was here defined as the length of the longest MT and Lrear as the shortest one. For α = β + 1, aster speed linearly depended on Lfront − Lrear, as expected (Fig. S3 C, left). In contrast aster speed was not uniquely determined by Lfront − Lrear for α = β (Fig. S3 D, left). In contrast, in the condition α = β, speed was independent of Lfront − Lrear but exhibited a single localized peak in the density plot of aster speed against Lfront/Lrear, indicating that aster speed is primarily determined by Lfront/Lrear in this condition (Fig. S3 D, right).
Finally, we performed all the aforementioned simulations in a 3D rectangular geometry, which yielded similar conclusions (Fig. S3, E–H).
Online supplemental material
Fig. S1 shows 3D imaging methods and provides additional quantification of aster centration dynamics, and control experiments of all inhibitor assays presented in Fig. 1. Fig. S2 shows control experiments of ciliobrevin D, additional time-lapse images of MT aster growth and quantification, and dose-dependent effects of ciliobrevin D on aster centration speed, as well as experiments on the influence of female pronucleus movements on aster motion. Fig. S3 includes extended 3D simulation results for general scaling exponents and cell geometry. Video 1 is a time lapse of MT aster centration in normal conditions (corresponding to Fig. 1 A). Video 2 is a time lapse of aster centration in the presence of various inhibitors (Fig. 1, F and G). Videos 3 and 4 are lysosome live imaging in 1% DMSO and 50 µM ciliobrevin D, respectively (Fig. S1, G–J). Videos 5 and 6 are time lapses of the motions of laser ablated MT asters (side ablation and front ablation, respectively; Fig. 2, D and E; and Fig. 2 J). Video 7 is a live imaging of a centering MT aster visualized by injecting fluorescent tubulin. Video 8 is a time lapse of aster centration in a rectangular-shaped egg (Fig. 3 A, fifth row). Video 9 is a 3D simulation of aster centration in normal spherical cell geometry and in a rectangular cell geometry. Video 10 is a time lapse of aster centration in the presence of low-dose ciliobrevin D (Fig. 4, G and H). Online supplemental material is available at http://www.jcb.org/cgi/content/full/jcb.201510064/DC1. Additional data are available in the JCB DataViewer at http://dx.doi.org/10.1083/jcb.201510064.dv.
Supplementary Material
Acknowledgments
We thank members of the Minc laboratory, Drs. Miyoshi and Hamaguchi for technical help and discussions, and Drs. Kapoor and Chen for sharing active and inactive forms of ciliobrevin D. We thank K. Labland for carefully reading the manuscript. A. Kimura visited the Minc laboratory through the SOKENDAI Young Faculty Overseas Visit Program.
This work is supported by the Centre National de la Recherche Scientifique and grants from the “Mairie de Paris emergence” program, the Fondation pour la Recherche Médical “amorçage” AJE20130426890, and the European Research Council (Consolidator Grants Forcaster 647073).
The authors declare no competing financial interests.
Footnotes
Abbreviations used in this paper:
- ASW
- artificial sea water
- MSD
- mean square displacement
- MT
- microtubule, PDMS, polydimethylsiloxane
References
- Brito D.A., Strauss J., Magidson V., Tikhonenko I., Khodjakov A., and Koonce M.P.. 2005. Pushing forces drive the comet-like motility of microtubule arrays in Dictyostelium. Mol. Biol. Cell. 16:3334–3340. 10.1091/mbc.E05-01-0057 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chambers E.L. 1939. The movement of the egg nucleus in relation to the sperm aster in the echinoderm egg. J. Exp. Biol. 16:409–424. [Google Scholar]
- Chang F., Atilgan E., Burgess D., and Minc N.. 2014. Manipulating cell shape by placing cells into micro-fabricated chambers. Methods Mol. Biol. 1136:281–290. 10.1007/978-1-4939-0329-0_13 [DOI] [PubMed] [Google Scholar]
- Foe V.E., and von Dassow G.. 2008. Stable and dynamic microtubules coordinately shape the myosin activation zone during cytokinetic furrow formation. J. Cell Biol. 183:457–470. 10.1083/jcb.200807128 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilbert S. 2010. Developmental Biology. Ninth edition Sinauer Associates, Sunderland, MA: 711 pp. [Google Scholar]
- Gönczy P., Pichler S., Kirkham M., and Hyman A.A.. 1999. Cytoplasmic dynein is required for distinct aspects of MTOC positioning, including centrosome separation, in the one cell stage Caenorhabditis elegans embryo. J. Cell Biol. 147:135–150. 10.1083/jcb.147.1.135 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grill S.W., and Hyman A.A.. 2005. Spindle positioning by cortical pulling forces. Dev. Cell. 8:461–465. 10.1016/j.devcel.2005.03.014 [DOI] [PubMed] [Google Scholar]
- Hamaguchi M., and Hiramoto Y.. 1980. Fertilization process in the heart urchin, Clypeaster Japonicus observed with a differential interference microscope. Dev. Growth Differ. 22:517–530. 10.1111/j.1440-169X.1980.00517.x [DOI] [PubMed] [Google Scholar]
- Hamaguchi M.S., and Hiramoto Y.. 1986. Analysis of the role of astral rays in pronuclear migration in sand dollar eggs by the Colcemid-UV method. Dev. Growth Differ. 28:143–156. 10.1111/j.1440-169X.1986.00143.x [DOI] [PubMed] [Google Scholar]
- Hays T.S., Wise D., and Salmon E.D.. 1982. Traction force on a kinetochore at metaphase acts as a linear function of kinetochore fiber length. J. Cell Biol. 93:374–389. 10.1083/jcb.93.2.374 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura A., and Onami S.. 2005. Computer simulations and image processing reveal length-dependent pulling force as the primary mechanism for C. elegans male pronuclear migration. Dev. Cell. 8:765–775. 10.1016/j.devcel.2005.03.007 [DOI] [PubMed] [Google Scholar]
- Kimura A., and Onami S.. 2007. Local cortical pulling-force repression switches centrosomal centration and posterior displacement in C. elegans. J. Cell Biol. 179:1347–1354. 10.1083/jcb.200706005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura K., and Kimura A.. 2011a Intracellular organelles mediate cytoplasmic pulling force for centrosome centration in the Caenorhabditis elegans early embryo. Proc. Natl. Acad. Sci. USA. 108:137–142. 10.1073/pnas.1013275108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura K., and Kimura A.. 2011b A novel mechanism of microtubule length-dependent force to pull centrosomes toward the cell center. BioArchitecture. 1:74–79. 10.4161/bioa.1.2.15549 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiyomitsu T. 2015. Mechanisms of daughter cell-size control during cell division. Trends Cell Biol. 25:286–295. 10.1016/j.tcb.2014.12.003 [DOI] [PubMed] [Google Scholar]
- Kozlowski C., Srayko M., and Nedelec F.. 2007. Cortical microtubule contacts position the spindle in C. elegans embryos. Cell. 129:499–510. 10.1016/j.cell.2007.03.027 [DOI] [PubMed] [Google Scholar]
- Laan L., Pavin N., Husson J., Romet-Lemonne G., van Duijn M., López M.P., Vale R.D., Jülicher F., Reck-Peterson S.L., and Dogterom M.. 2012. Cortical dynein controls microtubule dynamics to generate pulling forces that position microtubule asters. Cell. 148:502–514. 10.1016/j.cell.2012.01.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Longoria R.A., and Shubeita G.T.. 2013. Cargo transport by cytoplasmic Dynein can center embryonic centrosomes. PLoS One. 8:e67710 10.1371/journal.pone.0067710 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McNally F.J. 2013. Mechanisms of spindle positioning. J. Cell Biol. 200:131–140. 10.1083/jcb.201210007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Minc N., and Piel M.. 2012. Predicting division plane position and orientation. Trends Cell Biol. 22:193–200. 10.1016/j.tcb.2012.01.003 [DOI] [PubMed] [Google Scholar]
- Minc N., Burgess D., and Chang F.. 2011. Influence of cell geometry on division-plane positioning. Cell. 144:414–426. 10.1016/j.cell.2011.01.016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitchison T., Wühr M., Nguyen P., Ishihara K., Groen A., and Field C.M.. 2012. Growth, interaction, and positioning of microtubule asters in extremely large vertebrate embryo cells. Cytoskeleton (Hoboken). 69:738–750. 10.1002/cm.21050 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mohri H., Mohri T., Mabuchi I., Yazaki I., Sakai H., and Ogawa K.. 1976. Localization of dynein in sea urchin eggs during cleavage. Dev. Growth Differ. 18:391–398. 10.1111/j.1440-169X.1976.00391.x [DOI] [PubMed] [Google Scholar]
- Pavin N., Laan L., Ma R., Dogterom M., and Jülicher F.. 2012. Positioning of microtubule organizing centers by cortical pushing and pulling forces. New J. Phys. 14:105025 10.1088/1367-2630/14/10/105025 [DOI] [Google Scholar]
- Shinar T., Mana M., Piano F., and Shelley M.J.. 2011. A model of cytoplasmically driven microtubule-based motion in the single-celled Caenorhabditis elegans embryo. Proc. Natl. Acad. Sci. USA. 108:10508–10513. 10.1073/pnas.1017369108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stewart-Savage J., and Grey R.. 1982. The temporal and spatial relationships between cortical contraction, sperm trail formation, and pronuclear migration in fertilized Xenopus eggs. Rouxs Arch. Dev. Biol. 191:241–245. [DOI] [PubMed] [Google Scholar]
- Strickland L.I., Donnelly E.J., and Burgess D.R.. 2005. Induction of cytokinesis is independent of precisely regulated microtubule dynamics. Mol. Biol. Cell. 16:4485–4494. 10.1091/mbc.E05-04-0305 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Terasaki M., and Jaffe L.A.. 1991. Organization of the sea urchin egg endoplasmic reticulum and its reorganization at fertilization. J. Cell Biol. 114:929–940. 10.1083/jcb.114.5.929 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tran P.T., Marsh L., Doye V., Inoué S., and Chang F.. 2001. A mechanism for nuclear positioning in fission yeast based on microtubule pushing. J. Cell Biol. 153:397–411. 10.1083/jcb.153.2.397 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wühr M., Dumont S., Groen A.C., Needleman D.J., and Mitchison T.J.. 2009. How does a millimeter-sized cell find its center? Cell Cycle. 8:1115–1121. 10.4161/cc.8.8.8150 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wühr M., Tan E.S., Parker S.K., Detrich H.W. III, and Mitchison T.J.. 2010. A model for cleavage plane determination in early amphibian and fish embryos. Curr. Biol. 20:2040–2045. 10.1016/j.cub.2010.10.024 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao T., Graham O.S., Raposo A., and St Johnston D.. 2012. Growing microtubules push the oocyte nucleus to polarize the Drosophila dorsal-ventral axis. Science. 336:999–1003. 10.1126/science.1219147 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu J., Burakov A., Rodionov V., and Mogilner A.. 2010. Finding the cell center by a balance of dynein and myosin pulling and microtubule pushing: a computational study. Mol. Biol. Cell. 21:4418–4427. 10.1091/mbc.E10-07-0627 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.