Assessment of future changes in water availability and aridity

Abstract

Substantial changes in the hydrological cycle are projected for the 21st century, but these projections are subject to major uncertainties. In this context, the “dry gets drier, wet gets wetter” (DDWW) paradigm is often used as a simplifying summary. However, recent studies cast doubt on the validity of the paradigm and also on applying the widely used P − E (precipitation − evapotranspiration) metric over global land surfaces. Here we show in a comprehensive CMIP5‐based assessment that projected changes in mean annual P − E are generally not significant, except for high‐latitude regions showing wetting conditions until the end of the 21st century. Significant increases in aridity do occur in many subtropical and also adjacent humid regions. However, combining both metrics still shows that approximately 70% of all land area will not experience significant changes. Based on these findings, we conclude that the DDWW paradigm is generally not confirmed for projected changes in most land areas.

Key Points

• Future changes in water availability and aridity are assessed

• Underlying uncertainties are explicitly taken into account

• The “dry gets drier, wet gets wetter” paradigm is challenged

1. Introduction

Changes in dryness and water availability are projected to be large in many regions, with major impacts on a wide range of socioeconomic sectors. However, major uncertainties regarding both past and especially future drought assessments [Sheffield et al., 2012; Seneviratne et al., 2012; Orlowsky and Seneviratne, 2013] hinder a straightforward communication of projected changes to the public and policymakers.

A commonly used simplifying summary of projected changes in the global water cycle is that “dry regions become drier, and wet regions become wetter,” yet over land this is not applicable to changes in hydroclimatological conditions relevant to water availability for human society [e.g., Sun et al., 2012; Roderick et al., 2014; Greve et al., 2014, hereafter G14].

One first issue, as highlighted by G14 and Roderick et al. [2014], is a deficiency of the widely used P − E metric [e.g., Held and Soden, 2006; Dai, 2013; Liu and Allan, 2013] to assess climatic regimes over land. Following the notation of Held and Soden [2006], P − E > 0 implies a “wet regime” and P − E < 0 a “dry regime” at climatological time scales. However, over land E is limited by the amount of water supplied through P. Consequently, all land area is defined as wet (P − E > 0) according to this metric, which is certainly misleading. Held and Soden [2006] mentioned and discussed these issues in their study, and the zonally averaged P − E signal pointing toward a DDWW response is clearly ocean‐dominated (see Figure 1) since changes in P − E over land are generally not significant. This issue was also recently highlighted for historical trends in G14 and pointed out for future assessments by Roderick et al. [2014].

Figure 1.

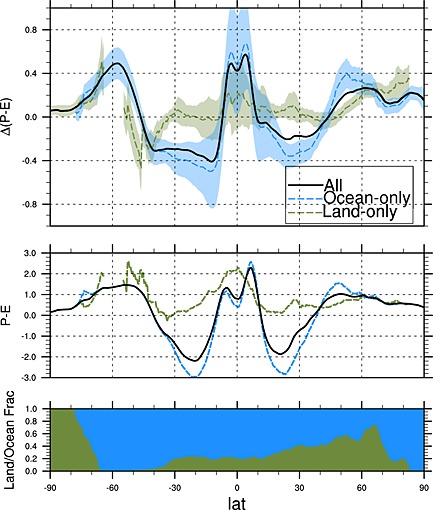
The zonal mean Δ(P − E) (1980–99 vs 2080–99, top panel) and P − E of the present climate(1980–99, middle panel) from the ensemble mean of 35 CMIP5 model runs (black), for ocean grid points only (blue) and for land grid points only(green). The shading denotes the ensemble standard deviation. The overall result (black line) corresponds very well to the finding of Held and Soden [2006]. However, the distinction between land and ocean grid points reveals fundamental differences. Over land the zonal mean drying trends are, if any, very small and not significant in subtropical regions. The figure clearly shows that the overall signal[Held and Soden, 2006] is dominated by the ocean signal (which makes sense regarding the unequal distribution of zonal land area vs. ocean area, bottom panel). The figure further shows that P − E > 0 over land and thus technically all land regions are wet (middle panel). (Figure taken from G14, supporting information.)

Although observations‐based data sets do not suggest that the DDWW holds for the historical time period (e.g., G14), it has not yet been investigated whether it holds for the future when considering suitable hydrological regimes definition over land. Hence, a careful reevaluation of the DDWW paradigm for climate projections over land is required. We note that we focus here on annual changes in the water cycle and not on contrasting changes in wet and dry season precipitation [e.g., Liu and Allan, 2013; Chou et al., 2013]. This study aims to assess future projected changes in water availability and aridity within the physically based framework of G14.

2. Data and Methods

Changes in hydroclimatological conditions are examined using P, E, and net radiation R _n estimates of an ensemble of 30 models from the Coupled Model Intercomparison Project Phase 5 (CMIP5). All data are bilinearly regridded to a unified 2.5 × 2.5^∘ grid, and climatological means are computed for the 1980–1999 (using historical data) and 2080–2099 (using data estimated under the RCP8.5 scenario) time periods. Here we use net radiation to define the energy constraint on E, usually referred to as potential evapotranspiration E _p, unlike in G14 where E _p formulations were used for the historical assessments. Thus, we assume E _p=R _n/λ (with λ denoting latent heat of vaporization). We chose this definition of E _p for two reasons: (i) In contrast to R _n, E _p itself is not part of the standard output in CMIP5; and (ii) we expect other (especially temperature‐based) approaches to estimate E _p to be less robust under substantially different climatic conditions occurring under strong climate change [Milly, 1992; Shaw and Riha, 2011; Milly and Dunne, 2011]. An analysis performed using the Priestley‐Taylor method [Priestley and Taylor, 1972] to estimate E _p is provided in the supporting information .

3. Trends in P − E

Considering 20year climatologies, the partitioning of annually averaged P into E and runoff Q over land follows the simplified water balance P = E + Q since the time derivative of the storage term is considered to be negligibly small in comparison. Hence, the assessed metric P − E is equal to Q and is basically a measure of water availability when examined from a land hydrological viewpoint. However, P − E is an incomplete metric to define present conditions of dryness at the land surface for several reasons. First, negative P − E values are impossible on land because E is constrained by the available P. Consequently—as highlighted in section 1—although a definition of “dryness” through P − E holds over the oceans (to the extent that ocean areas can be considered as being “dry”), it is questionable in a land‐based hydrological framework. We note that accumulated changes in soil moisture storage are also relevant, although the year‐to‐year changes are negligible in comparison to P, E, and Q. Indeed, if mean soil moisture storage is decreased below a threshold at which it constrains plant transpiration, net effects on vegetation and agriculture could be relevant. Correspondingly, long‐term changes in soil moisture storage have also been considered in previous studies [Wang, 2005; Orlowsky and Seneviratne, 2011, 2013], as well as in Intergovernmental Panel on Climate Change reports [Meehl et al., 2007; Seneviratne et al., 2012], although we only focus on fluxes in the present study. It was further found by, e.g., Boening et al. [2012] that year‐to‐year changes in local water storage in the context of sea level rise can be significant, which locally might influence the computation of 20year climatologies.

Any change in water availability could have major impacts on agriculture, logistics, power production, and various other socioeconomic sectors. Figure 2 displays mean ensemble changes in P − E comparing the 1980–1999 and the 2080–2099 time periods. Significance at the 95% level is assigned by computing the Mahalanobis distance using the covariance matrix between the ensemble data cloud within the (P,E) space and the identity line (indicating the line of no change). This methodology accounts for the uncertainty in both P and E simultaneously. Further details are provided in G14.

Figure 2.

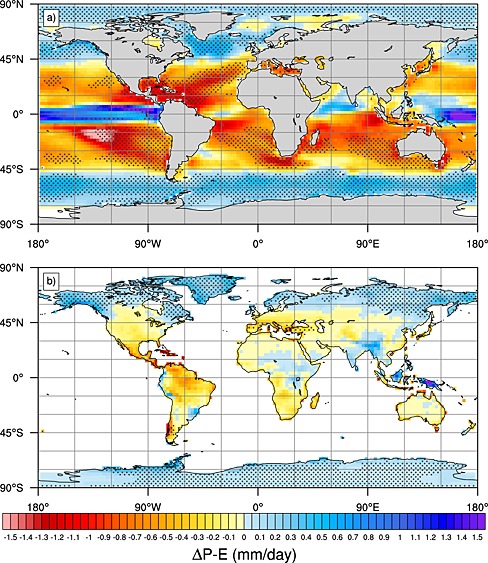
Changes in P − E comparing present‐day (1980–2000) and future climate (2080–2100) following the RCP8.5 pathway for (a) ocean‐only and (b) land‐only areas. Stippling denotes regions where the change is significant at the 95% level.

Over ocean surfaces, the total area experiencing robust changes in P − E comprises 38.7% of all ocean area, with a significant change toward less P − E in approximately 20.7% of all ocean area versus 18.0% with significant increase in P − E (see Figure 2). Thus, a significant surplus in P − E in some regions is basically balanced by a decline in other areas. Significant decreases in P − E (indicating suppressed freshwater fluxes) are basically found in all subtropical ocean basins. A significant increase in P − E (indicating enhanced freshwater fluxes) are found in midlatitude to Arctic ocean regions, whereas positive trends primarily found in the equatorial Pacific Ocean are just partly significant. Signals in the equatorial Atlantic and Indian Ocean are smaller and not significant. Overall, these results basically support the findings of Held and Soden [2006] obtained for zonally averaged estimates and also support the results of Roderick et al. [2014], stating that the DDWW does not necessarily hold at local (gridbox) scales. These tendencies (for projected changes) are further consistent with the findings of Durack et al. [2012] for historical changes, which showed increases in salinity for subtropical and decreases in salinity for equatorial and midlatitude ocean areas (which can be summarized as “fresh gets fresher, and salty gets saltier”).

Over land surfaces, changes in P − E are found to be significant for 22.8% of all land area. In summary, the results with respect to changes in P − E show barely any significant drying signal over land with a significant change toward drier conditions in only 3.3% of all land area. These minor drying regions are mainly located in the Mediterranean and parts of Patagonia, which, however, are located close to ocean areas exhibiting strong decreases in P − E. On the contrary, significant wetting signals are found for 19.5% of all land area, located entirely in the high latitudes. It is further important to note that no regions with robust signals are located in the tropics.

4. Aridity Changes

The P − E metric alone is insufficient to assess changes toward drying which are not reflected within the water balance, since the limitation of E through soil water is not taken into account [Held and Soden, 2006, G14]. To incorporate the specific hydroclimatological characteristics of the land surface into the analysis, the aridity index provides a more meaningful measure of dryness. The aridity index is usually defined as the ratio of P and E _p (here R _n/λ) [Budyko, 1974] and thus conceptually represents the complex interplay of water supply and demand.

Analyzing changes in R _n and P − R _n/λ (following the same method as applied to P − E) provides estimates of changes in aridity shown in Figure 3. Since R _n/λ is increasing globally due to stronger longwave emissions from the warmer and generally moister atmosphere [Stephens and Ellis, 2008; Allan, 2009; Roderick et al., 2014], a significant shift toward more humid conditions is experienced in regions with a stronger increase in P, being the case for only 6.7% of all land area and primarily located in the northern high latitudes. On the contrary, regions with a change in R _n/λ exceeding the change in P, thus leading to a significant change toward more arid conditions, are found for 16.4% of all land area. These changes are basically found in central North America, Central America, Amazonia, southern and northern Africa, southern Europe, the Middle East, and central Asia, as well as southern Australia, from which some are potentially related to a poleward expansion of model subtropical dry zones [Scheff and Frierson, 2012; Alessandri et al., 2014]. In summary, for a total of 23.1% of all land area a significant shift with respect to the model ensemble spread (toward either more arid or humid conditions) in aridity is projected.

Figure 3.

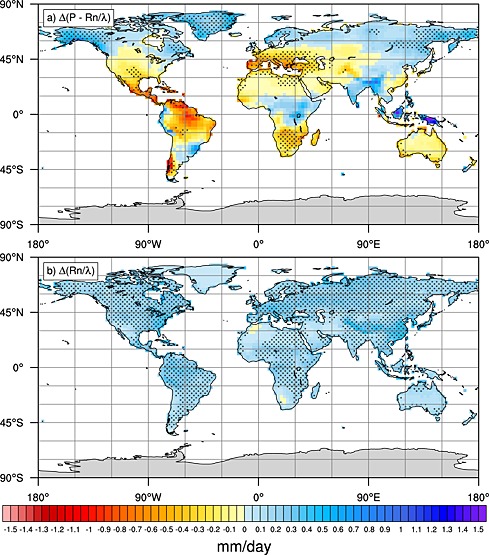
Aridity changes within the 21st century. (a) Changes in P − R _n/λ comparing present‐day (1980–2000) and future climate (2080–2100) following the RCP8.5 pathway and (b) changes in R _n/λ. Stippling denotes regions where the change is significant at the 95% level.

An analysis of aridity changes based on E _p estimated via the Priestley‐Taylor method reveals a similar picture; however, a much larger fraction of land area shows significant changes (45.4%). Especially regions experiencing changes toward more aridity are larger and extend even further into adjacent transitional and humid areas (more information is provided in the supporting information ).

5. Future DDWW: Summary and Conclusions

Combining both metrics in a merged framework as introduced in G14 provides a new perspective on changes in hydroclimatological conditions for the land surface. Within the framework we are able to establish that drying or wetting hydroclimatological conditions, due to either changing water availability or atmospheric demand, are significant for approximately 30.6% of all land area. However, it is important to note that significance is assigned with respect to the model ensemble spread and not with respect to internal variability, which might lead to an overestimation of the actual area with change [see, e.g., Power et al., 2011]. The spatial distribution of trends summarizing the results shown in Figures 2 and 3 is illustrated in Figure 4a. Changes in water availability are found to be significant mainly in high and middle latitudes, whereas changes in the atmospheric demand are significant in subtropical regions. Thus, a shift toward wetter conditions in the high latitudes is primarily due to P increasing faster than E (and partly also faster than R _n/λ). A shift toward drier conditions in subtropical regions is induced by an increase in R _n/λ versus a decrease (or a weaker increase) in P. Close to the Mediterranean Sea this also results in a significant decrease in E (not shown).

Figure 4.

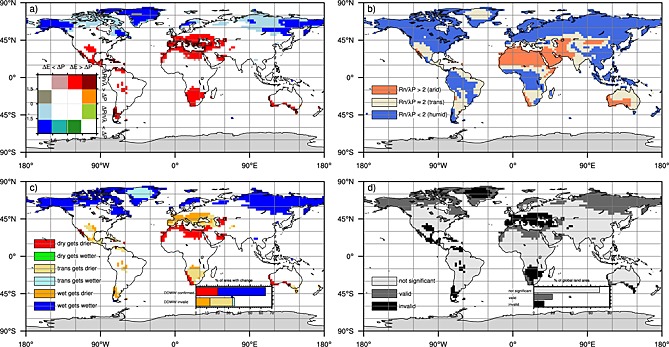
Investigating the DDWW paradigm. (a) Significant drying/wetting trends computed at the grid box level. Dark red (dark blue) denotes a significant change toward drier (wetter) conditions regarding both the land water balance and hydrological regime shifts. Red/orange shows a shift toward more arid conditions. Drying due to changes in the land water balance only is depicted by green/pink color. (b) Distribution of arid (orange) to humid (blue) areas within the period from 1980 to 2000. Beige colors denote transitional areas where no significant attribution is possible. (c) Comparing the changes in Figure 4a with the hydrological conditions in Figure 4b yields an evaluation of the “dry gets drier, wet gets wetter” paradigm. Red/dark blue colors indicate regions where the paradigm is found to be valid. Humid areas getting drier (orange) are widely found. (d) Conceptual evaluation of the DDWW, with areas confirming (dark grey) and invalidating (black) the paradigm compared to areas showing no robust trend. Note that Antarctica is not accounted for in the subplots.

Contrary to P − E, the aridity index also provides a reliable estimate of the distribution of arid/humid areas (see Figure 4b). Regions with significant R _n/λ P > 2 (R _n/λ P < 2) are classified as arid (humid) [Middleton et al., 1997]. Regions with no significant classification are defined as transitional. The methodology to assign significance is analogous to the method applied above and explained in more detail in G14. The obtained world map (see Figure 4b) is further in good correspondence to the Köppen‐Geiger climate classification [Peel et al., 2007]. We note that the spatial distribution of arid/humid areas is strongly sensitive to the threshold used to define these areas (see supporting information ).

Determining recent (1980–2000) aridity conditions (displayed in Figure 4b) allows us to compare end of twentieth century conditions with projected dryness changes until the end of the 21st century (displayed in Figure 4a) and thus to evaluate the DDWW as shown in 4c.

We identify that the paradigm is confirmed for humid areas projected to experience a significant increase in water availability in the high latitudes. Further, the combination of decreasing P and increasing atmospheric demand R _n/λ leading to a significant increase in aridity in many subtropical areas confirms the paradigm for dry desert regions in Africa and western Asia.

However, the DDWW paradigm is invalidated for the relatively large fraction of affected neighboring areas which are currently in a humid or transitional climate regime. These areas include large parts of southern and central Europe and parts southern Africa and North America. Drying conditions are further found in parts of humid tropical Amazonia. Changes toward more arid conditions (despite not being significant regarding the applied test metric) are also found in humid tropical Africa, Indonesia, and coastal regions of South America.

Thus, despite the above mentioned notable exceptions in large areas of the high latitudes and subtropics, we conclude that the “dry gets drier, wet gets wetter” paradigm is generally not confirmed for projected changes in most land areas (i) because of a lack of robustness of the projected changes in some regions (tropics) and (ii) because many humid to transitional regions are projected to shift toward drier conditions, i.e., not following the paradigm.

In summary, we found that uncertainties regarding projected changes in water availability and aridity are large and do not permit reliable predictions for 69.4% of all land area (see Figure 4d). Robust signals showing an increase in water availability are found for high‐latitude regions of the Northern Hemisphere. Significant increases in aridity are found for some subtropical regions (such as, e.g., the Mediterranean region) and also in adjacent humid regions, supporting previous findings of dryland expansion [Feng and Fu, 2013; Chou et al., 2013; Cook et al., 2014; Alessandri et al., 2014] and dynamically induced poleward expansion of subtropical dry zones [Cherchi et al., 2010; Scheff and Frierson, 2012; Allan, 2014; Alessandri et al., 2014]. Based on these results, the DDWW paradigm is confirmed for only approximately 19.5% of all land area in climate projections, whereas it is invalidated for another approximately 11.1%. Hence, we do not find substantial support for the DDWW paradigm in projections.

Supporting information

Readme

Figure S1

Figure S2

Figure S3

Figure S4

Figure S5

Greve, P. , and Seneviratne S. I. (2015), Assessment of future changes in water availability and aridity, Geophys. Res. Lett., 42, 5493–5499, doi:10.1002/2015GL064127.