Secondary Structure Bias in Generalized Born Solvent Models: Comparison of Conformational Ensembles and Free Energy of Solvent Polarization from Explicit and Implicit Solvation

Abstract

The effects of the use of three generalized Born (GB) implicit solvent models on the thermodynamics of a simple polyalanine peptide are studied via comparing several hundred ns of well-converged replica exchange molecular dynamics (REMD) simulations using explicit TIP3P solvent to REMD simulations with the GB solvent models. It is found that when compared to REMD simulations using TIP3P, the GB REMD simulations contain significant differences in secondary structure populations; most notably an over-abundance of α-helical secondary structure. This discrepancy is explored via comparison of the differences in the electrostatic component of the free energy of solvation (ΔΔG_Pol) between TIP3P (via Thermodynamic Integration calculations), the GB models, and an implicit solvent model based on the Poisson Equation (PE). The electrostatic component of the solvation free energies are calculated using each solvent model for four representative conformations of Ala10. Since PE is found to have the best performance with respect to reproducing TIP3P ΔΔG_Pol values, effective Born radii from the GB models are compared to effective Born radii calculated with PE (so-called perfect radii), and significant and numerous deviations in GB radii from perfect radii are found in all GB models. The effect of these deviations on the solvation free energy is discussed, and it is shown that even when perfect radii are used the agreement of GB with TIP3P ΔΔG_Pol values does not improve. This suggests a limit to the optimization of the effective Born radius calculation, and that future efforts to improve the accuracy of GB must extend beyond such optimizations.

Introduction

In order to correctly model protein behavior in an aqueous environment it is given that an accurate representation of solvent is necessary. In computational simulations of proteins it is common to either represent the solvent atoms explicitly or to estimate the solute response to bulk solvent using a dielectric continuum model, which is generally referred to as implicit solvation¹. Although explicit solvent models are more realistic and physically rigorous², implicit solvent models have several features that make their use attractive. Not having to include solvent atoms can considerably reduce the size of a system, which can result in a significant decrease in the computational cost of a simulation. In addition, conformational sampling is increased from the lack of explicit solvent molecules in two ways: 1) there is no need to average over the extremely large number of solvent configurations in a simulation, 2) the lack of friction from solvent molecules effectively removes the viscosity of the solvent environment, accelerating molecular motions³.

In an implicit solvent model, the overall free energy cost of solvating a solute molecule is typically decomposed into a non-polar component (ΔG_Nonpol) and a polar component (ΔG_Pol)⁴. ΔG_Nonpol is the free energy cost of rearranging the solvent to accommodate an uncharged solute molecule of arbitrary shape, and ΔG_Pol is the free energy cost of solvent polarization due to solute charges. The most accurate method for calculating ΔG_Pol in a continuum dielectric environment (neglecting salt effects) is solving the Poisson Equation (PE)⁵. However, this method is not easily incorporated into molecular dynamics (MD) simulations due to computational expense. Despite the recent advances that have been made in using implicit solvent models based on PE in MD simulations^6–8, this calculation remains highly computationally demanding⁹. In light of this, another method of calculating ΔG_Pol is often used: the generalized Born (GB) implicit solvent model¹⁰. GB is based on PE but contains several approximations which increase the speed of the calculation. As a result, the GB model has become quite popular in computational simulations¹¹.

However, this increase in speed comes at the cost of accuracy. Although the GB model has been shown to give solvation free energies in agreement with experiment for small molecules^10,12, there has been some question as to the performance of this model for simulations of larger biomolecules. Grycuk has shown that significant errors arise in GB calculations due to the Coulomb-field approximation¹³. Several studies^14–18 have also shown that GB models tend to over-stabilize ion pair interactions, which can lead to the trapping of molecules in (and thus over-population of) non-native states. There have been several reports suggesting that certain GB models tend to over-stabilize α-helical conformations^14,19–21, although the exact cause for this remains unclear. In addition, it has been shown for several biological macromolecules that accuracy of GB often results from widespread cancellation of errors^22,23.

Due to these issues it is desirable to quantitatively compare ensemble properties from simulations with implicit and explicit solvent models. However, this kind of direct comparison can be difficult since explicit solvent simulations require a greater length of time to converge than implicit solvent simulations due to considerably slower conformational sampling for flexible solutes. Recently, the development of enhanced sampling techniques such as Parallel Tempering²⁴ or Replica Exchange Molecular Dynamics (REMD)²⁵ have provided a means to bridge the sampling gap between implicit and explicit solvent simulations.

In this study we assess the performance of three GB implicit solvent models implemented in Amber²⁶ as compared to the TIP3P explicit solvent model and the PE implicit solvent model. Our test peptide is alanine decapeptide (Ala10, Ace-A₁₀-NH₂). We chose this model system to compare explicit and implicit solvent models as there are no potential salt bridges, eliminating formation of these as an issue. Ala10 is also long enough to form more than one or more repeats of basic secondary structure types found in larger proteins, such as helices and β-hairpins.

We compare ensembles of structures from well-converged REMD simulations of Ala10 using either the TIP3P explicit solvent or three variations of the GB implicit solvent model implemented in Amber²⁶. It is shown that in simulations of Ala10 with the TIP3P solvent model, residues predominantly adopt a polyproline II (PP2) conformation, in agreement with various experimental observations of short Alanine-rich peptides (see discussion in Ref. 31). However, it is then shown that the conformational preferences of Ala10 are altered in simulations with GB solvent models; in particular, certain GB models appear to strongly foster the formation of α-helical conformations. The results suggest that these models may have serious limitations when one wants to quantitatively investigate the conformational preferences of peptides and proteins.

To explain these observed differences between explicit and implicit simulations, we first directly compare explicit solvent ΔG_Pol values obtained from Thermodynamic Integration (TI) calculations to ΔG_Pol values from PE and GB implicit solvent models for four basic secondary structure types: right-handed α-helix, left-handed α-helix, β-hairpin, and polyproline II helix. In particular, we focus on comparing the difference in the electrostatic component of the solvation free energy between these conformations (ΔΔG_Pol), and how this relates to the ensembles of structures observed in the REMD simulations. In particular, we show that the observed α-helical bias in certain GB models results from overestimation of ΔΔG_Pol for α-helical structures. We also show that in terms of reproducing TIP3P ΔΔG_Pol values, the PE implicit solvent model has the best performance overall.

Given that the PE implicit model has the best performance, we then compare effective Born radii calculated with GB to ‘perfect’ effective Born radii calculated with PE, and show that there are large discrepancies, especially for backbone atoms. It is shown that use of ‘Perfect’ effect Born radii improves the accuracy of the Self and Interaction terms of the GB energy calculation with respect to PE results (as has been reported previously²²). However, it is also shown that in terms of reproducing TIP3P ΔΔG_Pol values, a GB model with ‘Perfect’ effect Born radii does not approach the performance of the PE model, and indeed does not provide an appreciable improvement over any of the other GB models studied here. This suggests that there is a limit to how far radii optimization alone can improve the GB solvent model.

Methods

REMD Simulation Details

The peptide simulated is Ala10 (Ace-A₁₀-NH₂) in both TIP3P²⁷ and several variations of the GB implicit solvent model; GBHCT²⁸, GBOBC²⁹, and GBNeck³⁰ (igb = 1, 5, and 7 respectively in Amber 9). A variant of GBOBC with different α, β, and γ parameters (discussed below) was also used (igb=2 in Amber9). In the text, GBOBC will be used to refer to results with igb=5 and results from GBOBC with igb=2 parameters will be specifically noted using the igb value. For TIP3P REMD simulations, Ala10 is solvated in a truncated octahedral box with 983 solvent molecules. Amber 9²⁶ was used with the ff99SB force field³¹ for all REMD simulations. For consistency, MBondi2 radii²⁹ were used in both the GB REMD simulations and subsequent GB and PE energy calculations described below.

For each solvent model, two separate REMD simulations of Ala10 were run starting from different initial conformations: an extended conformation and a collapsed conformation. The distribution of temperatures was chosen to ensure good overlap of potential energy between replicas and to achieve an exchange acceptance ratio of 0.20. The TIP3P REMD simulations involved 40 replicas at temperatures ranging from 266.9 to 571.2 K. Since the GB REMD simulations had far fewer degrees of freedom, only 8 replicas were required at temperatures ranging from 269.5 to 570.9 K. All data analysis was performed on REMD structure ensembles at 300.0 K. The high degree of convergence of these ensembles has been demonstrated in a previously published study²¹.

Bonds to hydrogen atoms were constrained with the SHAKE³² algorithm using a geometrical tolerance of 0.000001 Å. The non-bonded interaction cutoff was 7.0 Å for the TIP3P simulations, and 99.0 Å (effectively infinite) for the GB simulations. The TIP3P simulations were run in the nVT ensemble, long range electrostatic interactions were calculated using periodic boundary conditions via the particle mesh Ewald (PME) summation³³, and the non-bonded list was updated every 20 steps. Simulations were run with a time-step of 2 fs, with exchange attempts occurring every 1 ps. Both explicit and implicit solvent simulations employed a weak temperature coupling algorithm³⁴ with a time constant of 0.1 ps.

Solvent Model Details

Each GB model used in this study has the same basic formulation. For a given solute (neglecting salt effects), the GB model calculates the electrostatic contribution to the solvation free energy between all atoms in the solute as

$$\mathrm{\Delta }{\mathrm{G}}_{\text{Pol}}=\frac{1}{2}({\epsilon }_{\mathit{\text{in}}}^{-1}-{\epsilon }_{\mathit{\text{out}}}^{-1})\sum _{i,j}\frac{q_i{q}_j}{{\mathrm{f}}_{\mathrm{G}\mathrm{B}}},$$ (1)

Where ε_in and ε_out are the dielectric constants inside and outside the solute respectively, q_i and q_j are partial atomic charges on atoms i and j, and f_GB is a function that modifies the strength of the charge interaction based on the screening of the charges by other atoms and the solvent. It is common (although other forms have been used^22,35) to calculate f_GB using the formula

$${\mathrm{f}}_{\mathrm{G}\mathrm{B}}=\sqrt{{r_{ij}}^2+R_i{R}_j\text{exp}\left(\frac{-r_{ij}^2}{4R_i{R}_j}\right)},$$ (2)

where r_ij is the distance between atoms i and j, and R_i and R_j are the effective Born radii of atoms i and j¹⁰. The effective Born radius (hereafter referred to as R_GB) of an atom reflects the effect of solvent dielectric on the atom charge; the more surrounded an atom is by high-dielectric solvent, the more its charge is screened and the smaller its R_GB becomes.

The main difference in the three GB models studied here is in the calculation of R_GB. The GBHCT model calculates R_GB for each atom as

$$R_i^{-1}={\rho }_i^{-1}-I,$$ (3)

where ρ_i is the intrinsic Born radius of atom i, and

$$I=\frac{1}{4\pi }\underset{VDW}{\int }\theta (|\overrightarrow{r}|-{\rho }_i)\frac{1}{r^4}{d}^3\overrightarrow{r},$$ (4)

which modifies the intrinsic radius of the atom based on the amount of screening from all other atoms²⁹; for a single ion R_GB is equal to the intrinsic radius. The integral is calculated over the Van der waals (VDW) radii of those atoms, essentially defining the dielectric boundary as a VDW surface (as opposed to the molecular surface used in solutions to PE³⁶). As it is implemented in Amber, the above integral is solved in an analytical and pair-wise way, the exact form of which is given by Hawkins et al.²⁸. Another functionally identical solution to this integral has been given by Schaeffer & Froemmel³⁷.

It was shown that the above formulation would give R_GB values that were too small for deeply buried atoms^23,38 due to regions of high dielectric created when the VDW radii of spheres do not overlap inside a molecule, even if the region is inaccessible to solvent. To correct for this, the GBOBC model introduced a correction to the R_GB calculation,

$$R_i^{-1}={\rho }_i^{-1}-{\rho }_i^{-1}\text{ tan}\mathrm{h}(\alpha \mathrm{\Psi }-\beta {\mathrm{\Psi }}^2+\gamma {\mathrm{\Psi }}^3),$$ (5)

where Ψ = Iρ_i, and α, β, and γ are adjustable empirical parameters²⁹. This was designed to increase R_GB for buried atoms, while leaving R_GB for atoms near the surface relatively unchanged.

Although the GBOBC model compensated for the underestimation of R_GB for buried atoms, there remained the possibility that because of the VDW surface representation, regions of high dielectric (or ‘Neck’ regions) that should be inaccessible to water could develop between surface atoms, such as atoms in a hydrogen-bonding pair. The GBNeck model was designed to correct for these ‘Neck’ regions, and in doing so bring the VDW surface calculated in Equation 4 more in line with the molecular surface used in PE calculations. This correction is in addition to the one in Equation 5, and is applied during the calculation of the integral in Equation 4.

In order to obtain effective Born radii from the PE model, a method similar to one used by Onufriev et al.²² is used. Equation 1, the generalized Born equation, can be separated into Self (i=j) and Interaction (i≠j) terms. From Equations 1 and 2 the Self solvation free energy for atom i, ΔG_i, becomes

$$\mathrm{\Delta }{\mathrm{G}}_{\mathrm{i}}=\frac{1}{2}({\epsilon }_{\mathit{\text{in}}}^{-1}-{\epsilon }_{\mathit{\text{out}}}^{-1})\frac{q_i^2}{R_i},$$ (6)

By setting all atomic charges to zero except the charge on atom i, ΔG_i can be solved using PE, from which R_i is easily obtained. Effective Born radii obtained in this fashion will be referred to hereafter as R_PE.

All PE calculations were performed with DelPhi version 2.0³⁶ using a grid spacing of 0.25 Å and an internal relative dielectric of 1.0. The grid spacing of 0.25 Å was found to provide the best balance of speed and accuracy, as smaller grid spacings did not result in significant improvement in calculated energies. Calculations of structures used an external relative dielectric of 78.5 to be consistent with Amber GB models. Calculations of effective Born radii with PE used an external relative dielectric of 1000.0 (effectively infinite) for consistency with standard GB effective radii calculations, as suggested by Sigalov et al.³⁹. A percent fill value of 80% was used.

Thermodynamic Integration Calculations

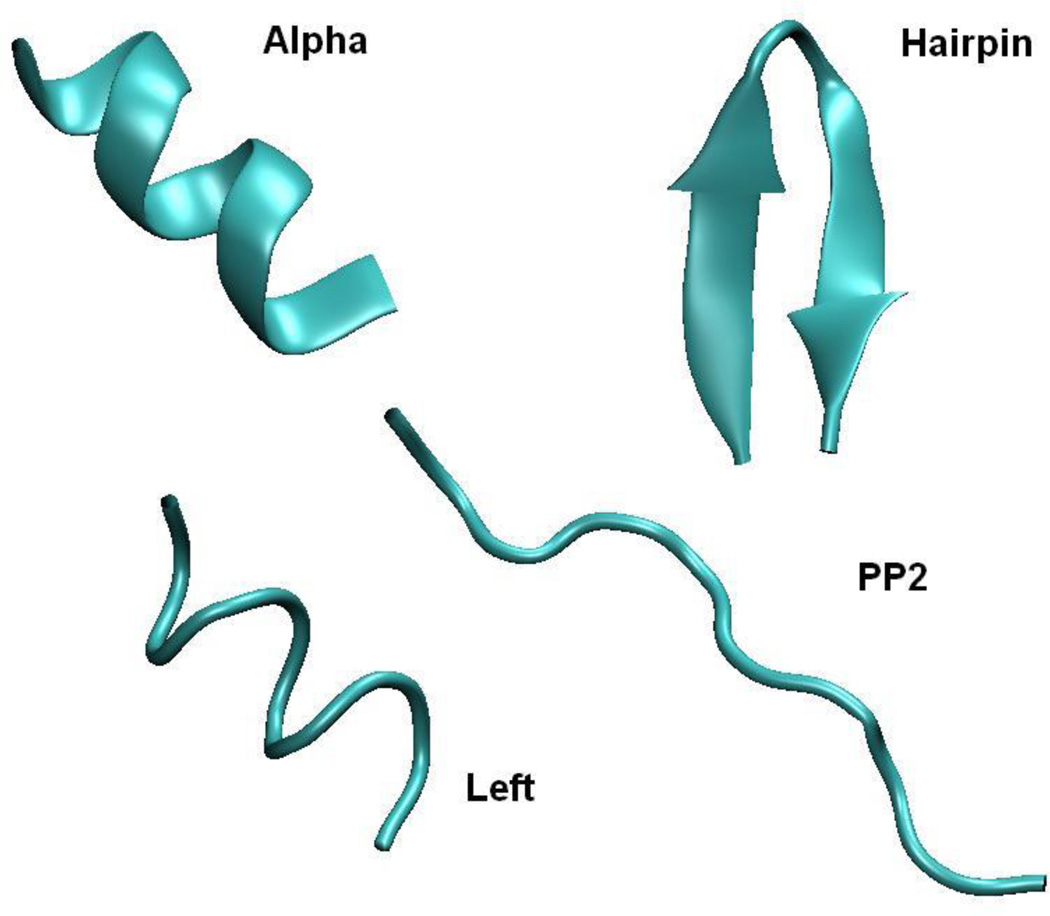
Thermodynamic Integration (TI) calculations were performed with Amber in order to obtain ΔG_Pol values for Ala10 in explicit TIP3P solvent. State 0 had all solute atomic charges off, and state 1 had all solute atomic charges on. Calculations were performed on four different conformations of Ala10: α-helix (Alpha), left-handed α-helix (Left), polyproline II helix (PP2), and β-hairpin (Hairpin). The Alpha, Left, and PP2 conformations were generated with the Leap module of Amber. All φ/ψ dihedrals in these conformations were set to ‘idealized’ values: Alpha = −57.8°/−47.0°, Left = 57.8°/47.0°, PP2 = −75.0°/145°. The Hairpin conformation was generated from the backbone of the β-hairpin peptide Trpzip2⁴⁰ (PDB ID 1LE1). Figure 1 shows cartoon representations of these four conformations.

Figure 1.

Cartoon represenations of the four conformations of Ala10 used in this study. Picture generated with VMD 1.8.4⁵¹.

There are two main considerations in these calculations. One is that over the course of the TI calculation the solute may change conformation, which is not desirable since only ΔG_Pol values for specific conformations are desired. This was dealt with by applying simple positional restraints on all atoms to hold the molecule in the desired conformation. Another consideration is that when the charges in the solute are switched on, there are not only solvent-solute charge interactions but intra-solute charge interactions. This requires that two separate TI calculations be done; one in which the molecule is solvated, and one in which the molecule is in the gas phase. Subtracting the free energy values then not only cancels out the intra-solute charge interactions, but the restraint energies as well.

All conformations were solvated with the same number of TIP3P waters as in the REMD simulations, energy minimized, and TI calculations were run for 0.2, 1.0, or 2.0 ns with 5 or 7 λ values in order to test the sensitivity of the results to TI parameters. Conformations were preserved in TI calculations by use of 10 kcal/mol harmonic restraints on all atoms. Final TI values were obtained from Gaussian integration over all λ values, excluding the first 50 ps of data from each λ value as equilibration

Secondary Structure and Conformational Analysis

Secondary structure values were calculated using DSSP⁴¹ as implemented in the Ptraj module of Amber, which uses patterns of hydrogen bonding to differentiate between different types of secondary structure. In addition, residues were assigned local conformational preferences (Alpha, Left, PP2, Extended) based on their φ/ψ dihedral angle statistics calculated over the REMD trajectories. A residue is considered in the given conformation if it falls within ±30° of the following φ/ψ values, chosen based on approximate boundaries of the free energy basins sampled in the explicit solvent REMD simulation of Ala10: Alpha (−70°/−25°), Left (50°/30°), PP2 (−70°/150°), or Extended (−150°/155°).

Results and Discussion

Secondary Structure and Local Conformational Propensities

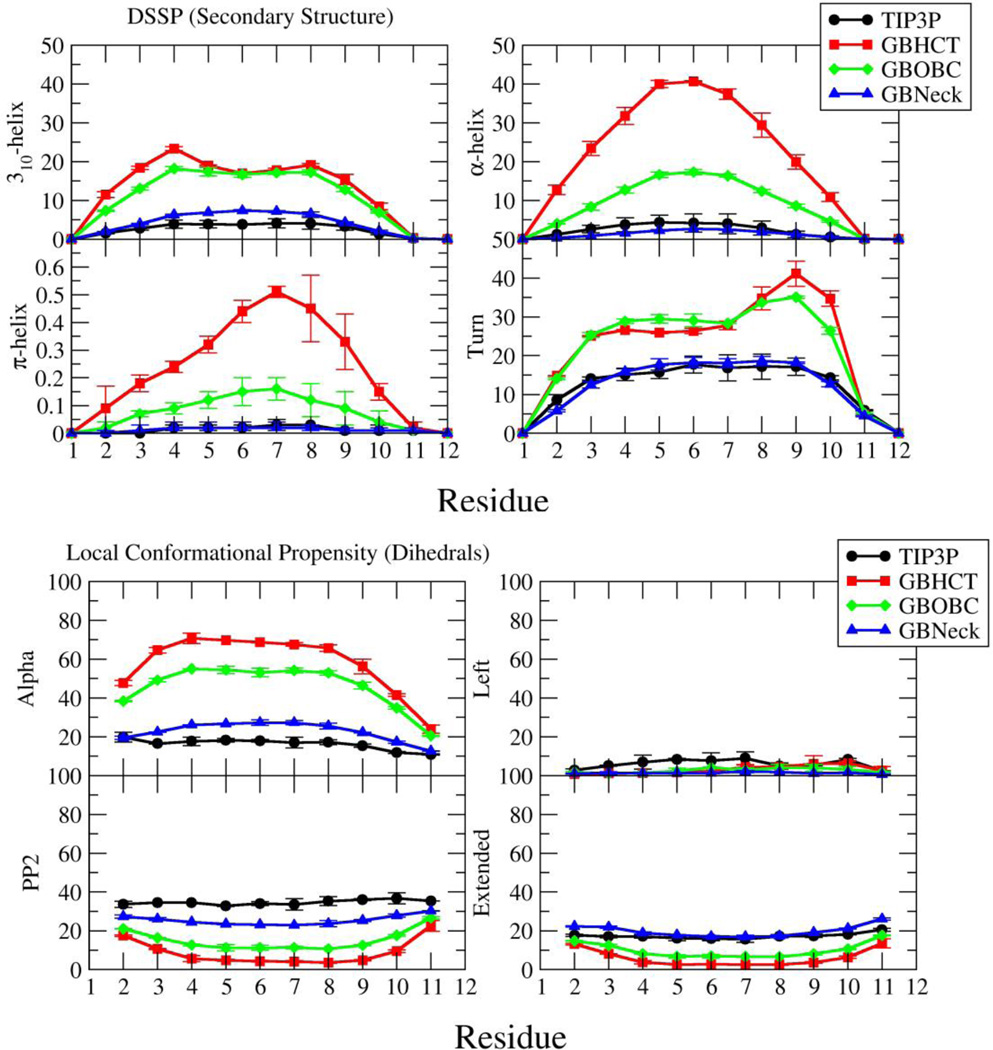
Figure 2 shows secondary structure and local backbone conformational propensities calculated from backbone dihedral angles (see Methods for details) at 300.0 K for all residues of Ala10 calculated from unrestrained REMD simulations conducted using either the TIP3P, GBHCT, GBOBC, or GBNeck solvent model. Local conformational propensity differs from secondary structure propensity in that it is not dependent on the conformation of neighboring residues; for example a particular residue may be in a helical conformation and yet not be part of any regular helical structure (perhaps its neighbors are in a PP2 conformation). The average secondary structure propensities and local conformational preferences of all residues in each simulation are given in Table 1. The overall agreement between independent simulations for each solvent model (as indicated by the small error values) shows that good convergence was achieved for all simulations; excellent convergence for these ensembles has been reported previously²¹.

Figure 2.

Secondary structure and local conformational propensities for each residue of Ala10 from unrestrained REMD simulations using various solvent models at 300.0 K. Residues 1 and 12 are the acetyl and amide N- and C-caps respectively. Error bars are calculated as half the difference of values reported from two independent simulations with the given solvent model, using different initial coordinates.

Table 1.

Average Percent Secondary Structure and Local Conformational Propensities from Ala10 REMD Simulations

A) DSSP (Secondary Structure)
	TIP3P	GBHCT	GBOBC	GBNeck
310-Helix	2.89 ± 0.06	15.01 ± 0.08	12.66 ± 0.07	4.64 ± 0.09
α-Helix	2.45 ± 0.63	24.60 ± 0.06	10.06 ± 0.08	1.37 ± 0.01
π-Helix	0.01 ± 0.01	0.27 ± 0.02	0.09 ± 0.02	0.01 ± 0.01
Turn	14.26 ± 0.18	26.19 ± 0.29	25.54 ± 0.09	14.21 ± 0.30
B) Local Conformational Propensity (Backbone Dihedrals)
	TIP3P	GBHCT	GBOBC	GBNeck
Alpha	16.20 ± 0.33	57.57 ± 0.20	45.85 ± 0.20	22.63 ± 0.15
Left	6.00 ± 0.28	3.06 ± 0.16	2.58 ± 0.03	1.29 ± 0.04
PP2	34.65 ± 0.29	8.73 ± 0.01	15.14 ± 0.09	25.45 ± 0.04
Extended	17.61 ± 0.38	5.91 ± 0.08	9.87 ± 0.10	19.83 ± 0.15

Error is calculated as half the difference of values reported from two independent REMD simulations for given solvent model.

Secondary Structure and Local Conformational Propensities: Explicit Solvent Simulations

The unrestrained REMD simulations of Ala10 with the TIP3P solvent model give results that are consistent with several recent theoretical and experimental studies of related polyalanine peptides. On average, Ala10 residues in the TIP3P simulation are predominantly in the PP2 conformation, consistent with free energy calculations done by Mezei et al.⁴². The average amount of PP2 observed (34.65±0.29%) is in reasonable agreement with values obtained for a similar polyalanine peptide XAO (Ace-X₂A₇O₂-NH₂, X≡diaminobutyrate, O≡ornithine), from both a previous explicit solvent computational study (42–47%⁴³) and from experiment (40±8%⁴⁴). Amide hydrogen atoms are involved in intramolecular hydrogen bonds for about 10% of the TIP3P simulation (data not shown), in close agreement with the value obtained from NMR data by Scheraga et al. (9%⁴⁵) for XAO.

The predominant secondary structure type identified by DSSP for the TIP3P simulation is Turn, indicating that any inter-residue hydrogen bonds that form tend to be in no specific pattern. Although there is a tendency for residues to adopt an Alpha conformation locally (16.20±0.33%), there is almost no α-helical or 3₁₀-helical structure (5.34±0.63% total). There is a similar tendency for residues to adopt Extended conformations locally (17.61±0.38%), but little parallel or anti-parallel β-sheet structure formation (1.54±0.44% total). Residues very rarely adopt the Left conformation locally, consistent with the fact that this conformation is sterically hindered.

Secondary Structure and Local Conformational Propensities: Implicit Solvent Simulations

In the unrestrained REMD simulations with the GBHCT and GBOBC solvent models there is clearly much greater preference for residues to be in the Alpha conformation locally compared to the TIP3P simulation; the GBHCT simulation in particular contains about 10 times the amount of average α-helical structure compared to the TIP3P simulation, and the GBOBC simulation contains about 4 times as much. A qualitative tendency for the GBHCT model to favor helix formation has been reported previously²⁰. Similarly, there are greater amounts of 3₁₀-helical, α-helical, and even π-helical structure present in these simulations. There is also a greater amount of Turn structure in both GB simulations than in the TIP3P simulations, reflecting an increased amount of localized inter-solute interaction. This is consistent with the increased helical populations observed in the GB simulations. In both the GBHCT and GBOBC simulations there is much less tendency to adopt the PP2, Extended, and Left local conformations. Using the GBOBC model with alternate α, β, and γ parameters (igb=2 in Amber) resulted in very similar results to the igb=5 set of α, β, and γ parameters for GBOBC (see supplementary Figure S1); thus the igb=2 variant was not analyzed in further detail.

Compared to the other GB models, the GBNeck simulation shows overall better agreement with the TIP3P simulation results. In particular, the amount of Extended local conformational propensity and percent Turn structure agree quite well with the TIP3P values. However, there is still a slightly larger preference for residues to be in the Alpha conformation locally (22.63±0.15% vs. 16.20±0.33% TIP3P). Also, while the GBNeck simulation contains about twice the amount of 3₁₀-helical structure as the TIP3P simulation, it contains only about half the amount of α-helical structure. As with GBHCT and GBOBC there is much less of a tendency to adopt the PP2 and Left local conformations than in the TIP3P simulations.

These results show that even for a simple system such as Ala10 which has no problematic salt bridges, the choice of solvent model has a large impact on secondary structural propensities and the local backbone dihedral conformation of residues. In particular, the GBHCT and GBOBC solvent models appear to foster the formation of α-helical structure when compared to the TIP3P solvent model, and although the GBNeck model appears to give better agreement with TIP3P solvent, there are still significant deviations.

There are two questions that should be addressed at this point: 1) Are implicit models simply unable to reproduce explicit solvent results, or 2) is the specific form of the implicit model the cause of the bias? Answering yes to the first question implies that fundamental assumption of implicit models – that is, that the bulk properties of water can be represented as a continuum dielectric – is incorrect, at least for Ala10. Studies have shown that the behavior of water near the water-peptide interface can deviate significantly from that of bulk water^46,47. Answering yes to the second question implies that the problem is in the GB model itself, perhaps arising from its approximate nature with respect to PE. We address the first question by comparing the GBHCT, GBOBC, GBNeck, and PE models directly to the TIP3P explicit water model, and the second question by comparing the GB models directly to PE calculations.

Comparison of Free Energies of Solvent Polarization from Explicit and Implicit Solvents

Since the electrostatic component of the solvation free energy (ΔG_Pol) is expected to be dominant, it is desirable to directly compare ΔG_Pol obtained from both implicit and explicit solvent simulations. Since there is no direct calculation of ΔG_Pol in explicit solvent models, other methods must be employed. Thermodynamic Integration (TI) is a method by which the free energy is approximated as the work done in changing a system from one state to another (State 0 → State 1) by way of a switching function, usually represented by f(λ), λ ranges from 0→1⁴⁸. Since ΔG_Pol can be interpreted as the free energy cost associated with perturbing the solvent when the solute goes from an uncharged to a charged state, it can be calculated for a molecule in explicit water via TI by making state 0 and state 1 the uncharged and charged states respectively, as has been done previously⁴⁹.

TI calculations were performed to obtain ΔG_Pol values for four conformations of Ala10; three idealized conformations in which all backbone dihedral angles were approximately equal across all residues (Alpha, Left, and PP2), and an additional conformation generated from the backbone of a model β-hairpin (Hairpin, see Methods for complete details). TI calculations were run with either 5 or 7 λ values and for different lengths of time to test the accuracy and sensitivity of the results, which are given in Table 2.

Table 2.

TI Results (kcal/mol)

	Alpha	PP2	Left	Hairpin
0.2 ns 5 λ	−44.23	−75.62	−51.49	−55.09
1.0 ns 5 λ	−44.10	−76.51	−51.29	−53.87
1.0 ns 7 λ	−44.10	−76.43	−51.19	−54.36
2.0 ns 5 λ	−44.04	−76.22	−51.42	−54.25

The ΔG_Pol values generated from the TI calculations appear well converged; the difference between values is less than 1.0 kcal/mol over all variable changes. Increasing the simulation length from 0.2 ns to 1.0 ns has the largest effect, most likely from allowing the system more time to equilibrate. Because of this, only values from TI simulations 1.0 ns or greater in length are considered in the analysis. Increasing the number of λ values from 5 to 7 has little effect on final results, indicating that for this system 5 λ values is adequate.

Table 3A shows the comparison of ΔG_Pol values from explicit solvent to implicit solvent models for the four conformations of Ala10. The implicit solvent model values were obtained by averaging ΔG_Pol from the set of structures (1000 for each conformation) generated during the 1.0 ns TI calculations. Each solvent model has the same overall trend in terms of which conformation has the most favorable (lowest) solvation free energy; PP2<<Hairpin<Left<Alpha. It is interesting to note that the less solvent exposed the conformation, the more ΔG_Pol values from the various solvent models deviate from each other, as shown in the last column of Table 3A (labeled Stdev). For example, the ΔG_Pol values from both explicit and implicit solvent models are very similar the well-solvated PP2 conformation, as shown by the small standard deviation of ΔG_Pol across all models (0.69 kcal/mol). The differences between the explicit and implicit solvent models show up more clearly in the less solvent-exposed Hairpin, Left, and Alpha conformations, with larger standard deviations of 2.02, 2.83, and 3.56 kcal/mol respectively.

Table 3.

Free Energies of Solvation for Different Conformations of Ala10 (kcal/mol)

A) ΔGPol	TIP3P	PE	GBHCT	GBOBC	GBNeck	Stdev
Alpha	−44.08 ± 0.04	−47.97 ± 0.77	−51.69 ± 1.21	−49.38 ± 1.21	−43.26 ± 0.90	3.56
PP2	−76.39 ± 0.15	−78.05 ± 0.91	−77.35 ± 1.05	−78.07 ± 1.09	−77.59 ± 1.02	0.69
Left	−51.30 ± 0.12	−54.85 ± 0.90	−55.05 ± 1.08	−52.67 ± 1.10	−48.19 ± 0.91	2.83
Hairpin	−54.16 ± 0.25	−57.28 ± 1.13	−57.48 ± 1.45	−56.03 ± 1.47	−52.85 ± 1.29	2.01
B) ΔΔGPol	TIP3P	PE	GBHCT	GBOBC	GBNeck
PP2-Alpha	−32.31	−30.07	−25.67	−28.69	−34.33
PP2-Left	−25.09	−23.19	−22.31	−25.40	−29.40
PP2-Hairpin	−22.23	−20.77	−19.87	−22.03	−24.73
Alpha-Left	7.22	6.88	3.36	3.29	4.93
Alpha-Hairpin	10.08	9.31	5.80	6.66	9.60
Left-Hairpin	2.86	2.43	2.43	3.37	4.67
C) ΔΔGPol RMSD†		PE	GBHCT	GBOBC	GBNeck
Overall		1.39	3.89	2.60	2.51
PP2		1.89	4.37	2.10	3.11
Non-PP2		0.55	3.34	3.02	1.71

^†RMSD from TIP3P ΔΔGPol values.

It is not expected that the results from implicit solvent models will agree directly with the TI results from the TIP3P model since the intrinsic Born radii set used (Mbondi2) has not been optimized to reproduce explicit solvent values for some of these implicit models. It is still useful, however, to compare the differences in ΔG_Pol between different conformations (ΔΔG_Pol), as this has a direct affect on the thermodynamics of the system, and so provides a way to relate individual ΔG_Pol values from various solvent models to the ensembles of structures generated in the REMD runs. The ΔΔG_Pol values between all conformations are given in Table 3B.

The first three sets of ΔΔG_Pol values considered are those between the PP2 conformation and all other conformations. As the PP2 conformation is much more highly solvated and extended compared to the other conformations, these comparisons give insight into the changes in solvation that accompany peptide or protein folding. It is shown in Table 2C that compared to TIP3P, ΔΔG_Pol between the PP2 and Alpha conformations is underestimated by PE, GBOBC, and GBHCT by −2.23, −3.62, and −6.64 kcal/mol respectively. This indicates an insufficient desolvation penalty upon the transition to the Alpha conformation. In contrast, the GBNeck model overestimates ΔΔG_Pol by 2.02 kcal/mol, indicating there is too much of a desolvation penalty upon the transition to Alpha.

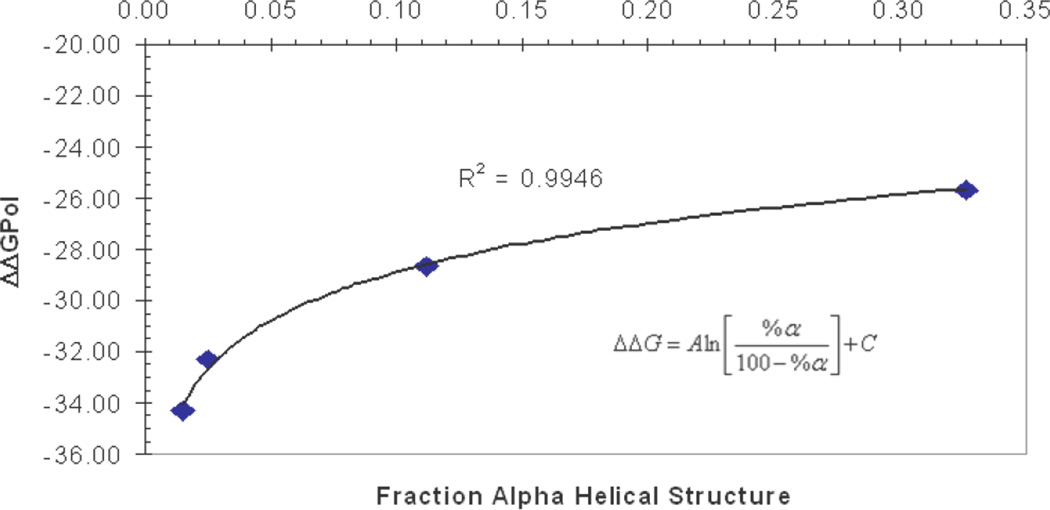
It is interesting to note that the PP2 and Alpha ΔΔG_Pol values from both explicit and implicit solvent models correlate well (natural log fit, R² = 0.9946) with the fractional α-helical structure (%α /[100−%α]) obtained from DSSP analysis of the corresponding REMD simulations (Figure 3). This shows a direct relationship between the change in free energy of solvation of a structure, and how much of that structure is observed in simulation. Based on the fit, the PE ΔΔG_Pol value of − 30.07 kcal/mol would translate into ~6% α-helical structure for an ensemble sampled using PE (which was not computationally feasible for this study). This suggests that even a model based on PE may be slightly too helical compared to TIP3P, although its performance is still much better than GBHCT or GBOBC. Of course this value is simply an extrapolation, and ideally simulations using implicit solvent based on PE will be used in the future to generate well-converged ensembles.

Figure 3.

Plot of fractional α-helical structure (%α/[100−%α]) obtained from DSSP analysis of REMD simulations with various solvent models versus the corresponding ΔΔG_Pol value between the PP2 and Alpha conformations. The data points from right to left are for the GBNeck, TIP3P, GBOBC, and GBHCT solvent models. As the solvation free energy gap in the given solvent model between the PP2 and Alpha structures decreases, the amount of α-helical structure in simulations with that model increases.

The ΔΔG_Pol values between PP2 and Left follow a slightly different trend. Compared to TIP3P values, the PE and GBHCT models underestimate ΔΔG_Pol by −1.89 and −2.78 kcal/mol respectively, which is consistent with the smaller ratio of PP2 to Left conformation (as determined from the values in Table 1) observed in the GBHCT REMD simulation (2.9) compared to the TIP3P simulation (5.8). The GBOBC model is almost an exact match, only overestimating ΔΔG_Pol by 0.31 kcal/mol, consistent with the fact that the ratio of PP2 to Left in the GBOBC REMD simulation (5.9) is quite similar to the TIP3P value. The GBNeck model greatly overestimates ΔΔG_Pol in this case by 4.31 kcal/mol, consistent with the greatly increased ratio of PP2 to Left conformation found in the GBNeck REMD simulation (19.7).

It is noted that while the Left conformation itself is a high energy and not very realistic conformation, adopting a left-helical conformation is important for residues in structures incorporating reverse-turns, such as β-hairpins. It is perhaps unsurprising then that the ΔΔG_Pol values between PP2 and Hairpin follow a similar trend to those between PP2 and Left. The PE and GBHCT models underestimate ΔΔG_Pol by −1.51 and −2.40 kcal/mol respectively. The GBOBC model is again almost exact, underestimating by only −0.24 kcal/mol. The GBNeck model overestimates ΔΔG_Pol by 2.46 kcal/mol.

The last three sets of ΔΔG_Pol values considered are between the Alpha, Hairpin, and Left conformations, which are less solvated and have more favorable internal contacts compared to the PP2 conformation. The performance of PE in all three cases is superb; the largest deviation from TIP3P is ΔΔG_Pol between Alpha and Hairpin, just 0.73 kcal/mol.

The overall performance for all three GB models for these compact structures is markedly worse than PE. All three GB models overestimate ΔΔG_Pol between Alpha and Left; GBHCT and GBOBC by about 3.9 kcal/mol, and GBNeck by about 2.3 kcal/mol. The desolvation penalty between these two conformations being too large is consistent with the increased ratio of Alpha to Left conformational propensity observed in the GBHCT, GBOBC, and GBNeck REMD simulations (~18) compared to the ratio from the TIP3P REMD simulation (~3).

The remaining comparisons show no consistent pattern and serve only to highlight how the performance of each GB model depends on conformation. The GBOBC and GBHCT models overestimate ΔΔG_Pol between Alpha and Hairpin by 4.28 and 3.42 kcal/mol respectively, while GBNeck only overestimates by 0.44 kcal/mol. In contrast, the GBNeck model underestimates ΔΔG_Pol between Left and Hairpin by 1.79 kcal/mol, while the GBOBC and GBHCT models are within 0.5 kcal/mol of the TIP3P value.

It is clear that the performance of implicit solvent models is dependent on the conformation of Ala10. As a way to gauge the overall performance of each implicit solvent model with respect to the TIP3P solvent model, the RMSD from TIP3P ΔΔG_Pol values for each implicit solvent model was calculated (Table 3C). The best overall performance is from PE, with an overall RMSD of 1.39 kcal/mol. The next best performance is by the GBNeck and GBOBC models, with RMSDs of 2.51 and 2.60 kcal/mol respectively. The worst performance is from the GBHCT model, with an overall RMSD of 3.89 kcal/mol. For reproducing the difference between PP2 and more compact states (analogous to folding, PP2 column in Table 3C), PE again has the best performance (1.89 kcal/mol), with GBOBC coming in a close second (2.10 kcal/mol). GBNeck and GBHCT perform worse, with RMSDs of 3.11 and 4.37 kcal/mol. For reproducing the differences between compact states themselves (Non-PP2 column in Table 3C), PE is clearly superior to all of the GB models, with a RMSD of 0.55 kcal/mol. GBNeck is a distant second with a RMSD of 1.71 kcal/mol, while GBOBC and GBHCT have RMSDs of 3.02 and 3.34 respectively.

The overabundance of helical structure in the REMD ensembles obtained with the GBHCT and GBOBC solvent models can now be rationalized. Essentially, these models over-stabilize α-helices because not enough of a desolvation penalty is paid for forming the α-helical structure; the already favorable internal energy of the α-helix is accompanied by an overly favorable solvation free energy. In contrast, the desolvation penalty for formation of α-helical structure with the GBNeck model is comparable to PE and TIP3P, and α-helical structure is not overly-abundant in the REMD simulations with this model.

Overall, PE is the best of the implicit models at reproducing the differences in ΔG_Pol between different conformations of Ala10, while all GB models perform considerably worse. PE and GBOBC are both good at reproducing the differences between PP2 and the more compact conformations. Although PE is clearly superior to all GB models at reproducing the differences between the compact conformations, it should be noted that GBNeck is still much better at this than GBHCT or GBOBC. It is interesting to point out that in particular all GB models have difficulty reproducing the difference between the right-handed and left-handed alpha helix.

The reason for the relatively poor performance of these GB models compared to the PE model, especially for reproducing ΔΔG_Pol between the more compact structures (Alpha, Left, and Hairpin) is not clear at this point. In the next section, this problem is explored by comparing the effective radii and energy calculations of these three GB models to effective Born radii and energy calculated with PE.

Direct Comparison of GB to PE: Effective Radii

All implicit models rely on an accurate description of the dielectric boundary for good performance⁴. In this study, the model based on PE (DelPhi 2.0) calculates this boundary based on the molecular surface accessible to a probe with a radius comparable to that of a water molecule (1.4 Å), which is then mapped onto a cubic lattice. In these GB models, instead of a specific dielectric boundary, each atom is assigned an effective Born radius (R_GB), which is essentially a measure of how well solvated the atom is. For atoms that are well-solvated (i.e. atoms that have a more favorable solvation free energy) this radius is small, reflecting the damping effect that a solvent with high dielectric has on atomic charge. The relationship between R_GB and atomic solvation free energy (Self Energy) can be seen clearly from Equation 6.

The fundamental difference between the GBHCT, GBOBC, and GBNeck models discussed here is in the calculation of R_GB (see Methods for more details). Onufriev et al. showed that when R_GB is calculated from atomic ΔG_Pol obtained using PE, the resulting ‘perfect’ Born radii (R_PE) improve the accuracy of both GB Self and Interaction energy terms, and improve overall agreement with PE²². Since out of all the implicit models, PE had the best performance in reproducing explicit solvent ΔΔG_Pol values, examining the deviation between ‘perfect’ radii obtained via PE and those calculated with the various GB models may provide insight into areas where GB is deficient, and reveal specific areas to improve.

Effective Born radii were calculated with PE (R_PE), and compared to R_GB obtained from the GBHCT, GBOBC, and GBNeck implicit solvent models using a subset of the last 500 structures from the Alpha, Left, and Hairpin TI calculation trajectories, and a subset 100 structures (frames 500–599) from the PP2 TI calculation trajectories. A subset of structures was chosen since derivation of R_PE for many structures is particularly time consuming as it requires a PE calculation for every atom in every structure. Fewer structures were used for PP2 as the PE calculations for these structures are particularly time-consuming (because of the large solvent-exposed surface area of this conformation).

Table 4A–I shows the RMSD of R_GB from R_PE for each of the GB solvent models across all residues of Ala10 for the given atom type, averaged over all structures used in the ΔG_Pol analysis shown in Table 3. The atom types considered are amide hydrogen (H), carbonyl oxygen (O), amide nitrogen (N), carbonyl carbon (C), α carbon (CA), β carbon (CB), α hydrogen (HA), backbone atoms (BB, representing H, O, N, C, and CA), and all atom types. Table 4J shows the average RMSD value over all conformations for the given solvent model. Table 5 shows the average difference instead of RMSD for each atom type, to convey whether R_GB is under-estimated or over-estimated with respect to R_PE. The data in Table 5 are also presented graphically for individual residues in each conformation; see supplementary Figures S2–5.

Table 4.

GB Effective Radii Average RMSD from Perfect (PE) Radii (Ǻ)

A) All	GBHCT	GBOBC	GBNeck	F) C	GBHCT	GBOBC	GBNeck
alpha	0.25 ± 0.01	0.19 ± 0.01	0.22 ± 0.02	alpha	0.16 ± 0.01	0.19 ± 0.02	0.42 ± 0.03
hairpin	0.18 ± 0.01	0.16 ± 0.01	0.12 ± 0.01	hairpin	0.08 ± 0.01	0.20 ± 0.01	0.25 ± 0.02
left	0.20 ± 0.01	0.20 ± 0.01	0.32 ± 0.03	left	0.12 ± 0.01	0.29 ± 0.03	0.58 ± 0.04
pp2	0.06 ± 0.00	0.11 ± 0.01	0.04 ± 0.00	pp2	0.07 ± 0.01	0.09 ± 0.01	0.05 ± 0.01
B) BB	GBHCT	GBOBC	GBNeck	G) CA	GBHCT	GBOBC	GBNeck
alpha	0.35 ± 0.02	0.26 ± 0.01	0.31 ± 0.03	alpha	0.05 ± 0.01	0.34 ± 0.02	0.26 ± 0.02
hairpin	0.20 ± 0.02	0.20 ± 0.01	0.16 ± 0.01	hairpin	0.09 ± 0.01	0.26 ± 0.01	0.12 ± 0.01
left	0.27 ± 0.02	0.26 ± 0.02	0.45 ± 0.04	left	0.07 ± 0.01	0.36 ± 0.02	0.37 ± 0.03
pp2	0.06 ± 0.00	0.12 ± 0.01	0.05 ± 0.00	pp2	0.03 ± 0.01	0.18 ± 0.01	0.04 ± 0.01
C) H	GBHCT	GBOBC	GBNeck	H) CB	GBHCT	GBOBC	GBNeck
alpha	0.71 ± 0.04	0.29 ± 0.04	0.19 ± 0.06	alpha	0.03 ± 0.00	0.03 ± 0.00	0.12 ± 0.01
hairpin	0.39 ± 0.04	0.19 ± 0.03	0.15 ± 0.03	hairpin	0.04 ± 0.00	0.04 ± 0.00	0.08 ± 0.00
left	0.50 ± 0.04	0.13 ± 0.02	0.43 ± 0.06	left	0.01 ± 0.00	0.02 ± 0.00	0.10 ± 0.00
pp2	0.04 ± 0.00	0.10 ± 0.01	0.02 ± 0.00	pp2	0.03 ± 0.00	0.04 ± 0.00	0.05 ± 0.00
D) O	GBHCT	GBOBC	GBNeck	I) HA	GBHCT	GBOBC	GBNeck
alpha	0.16 ± 0.01	0.09 ± 0.01	0.20 ± 0.02	alpha	0.07 ± 0.00	0.19 ± 0.01	0.04 ± 0.01
hairpin	0.16 ± 0.01	0.08 ± 0.01	0.11 ± 0.02	hairpin	0.34 ± 0.03	0.23 ± 0.02	0.12 ± 0.03
left	0.18 ± 0.01	0.07 ± 0.01	0.24 ± 0.02	left	0.10 ± 0.01	0.21 ± 0.01	0.11 ± 0.02
pp2	0.03 ± 0.00	0.02 ± 0.00	0.04 ± 0.00	pp2	0.08 ± 0.00	0.18 ± 0.01	0.02 ± 0.00
E) N	GBHCT	GBOBC	GBNeck
alpha	0.26 ± 0.01	0.30 ± 0.03	0.37 ± 0.04
hairpin	0.16 ± 0.01	0.21 ± 0.02	0.11 ± 0.02
left	0.27 ± 0.02	0.31 ± 0.03	0.52 ± 0.05
pp2	0.08 ± 0.01	0.13 ± 0.01	0.07 ± 0.01
J) Overall Averages
	GBHCT	GBOBC	GBNeck		GBHCT	GBOBC	GBNeck
All	0.17	0.16	0.17	C	0.11	0.19	0.33
BB	0.22	0.21	0.24	CA	0.06	0.29	0.20
H	0.41	0.18	0.20	CB	0.03	0.03	0.09
O	0.13	0.06	0.15	HA	0.15	0.20	0.08
N	0.19	0.24	0.27

Table 5.

GB Effective Radii Average Difference from Perfect (PE) Radii (Ǻ)

A) H	GBHCT	GBOBC	GBNeck	E) CA	GBHCT	GBOBC	GBNeck
alpha	0.59 ± 0.38	0.18 ± 0.19	−0.11 ± 0.12	alpha	0.03 ± 0.03	−0.33 ± 0.07	−0.23 ± 0.11
hairpin	0.18 ± 0.34	−0.02 ± 0.18	0.03 ± 0.13	hairpin	0.05 ± 0.07	−0.25 ± 0.07	−0.09 ± 0.07
left	0.39 ± 0.30	−0.01 ± 0.10	−0.37 ± 0.20	left	0.05 ± 0.05	−0.35 ± 0.09	−0.32 ± 0.18
pp2	−0.04 ± 0.02	−0.10 ± 0.02	0.00 ± 0.02	pp2	0.02 ± 0.02	−0.18 ± 0.03	0.03 ± 0.02
B) O	GBHCT	GBOBC	GBNeck	F) CB	GBHCT	GBOBC	GBNeck
alpha	0.12 ± 0.10	0.06 ± 0.06	−0.17 ± 0.10	alpha	0.00 ± 0.03	0.00 ± 0.03	−0.11 ± 0.03
hairpin	0.08 ± 0.13	0.03 ± 0.07	−0.09 ± 0.06	hairpin	0.02 ± 0.03	0.03 ± 0.03	−0.08 ± 0.02
left	0.15 ± 0.11	0.02 ± 0.05	−0.20 ± 0.12	left	0.00 ± 0.01	0.01 ± 0.01	−0.10 ± 0.03
pp2	−0.01 ± 0.03	−0.01 ± 0.02	−0.04 ± 0.01	pp2	0.02 ± 0.02	0.03 ± 0.02	−0.05 ± 0.01
C) N	GBHCT	GBOBC	GBNeck	G) HA	GBHCT	GBOBC	GBNeck
alpha	0.24 ± 0.10	−0.26 ± 0.13	−0.30 ± 0.21	alpha	−0.05 ± 0.04	−0.18 ± 0.03	−0.03 ± 0.03
hairpin	0.11 ± 0.11	−0.16 ± 0.12	−0.06 ± 0.09	hairpin	0.13 ± 0.31	−0.07 ± 0.21	0.04 ± 0.10
left	0.24 ± 0.11	−0.27 ± 0.14	−0.43 ± 0.29	left	−0.04 ± 0.09	−0.20 ± 0.05	−0.09 ± 0.05
pp2	0.07 ± 0.04	−0.11 ± 0.07	0.05 ± 0.04	pp2	−0.08 ± 0.01	−0.18 ± 0.04	0.02 ± 0.01
D) C	GBHCT	GBOBC	GBNeck
alpha	0.14 ± 0.07	−0.17 ± 0.08	−0.37 ± 0.21
hairpin	0.03 ± 0.07	−0.17 ± 0.10	−0.21 ± 0.13
left	0.10 ± 0.06	−0.26 ± 0.11	−0.50 ± 0.28
pp2	0.04 ± 0.05	−0.07 ± 0.04	−0.02 ± 0.04
H) Overall Averages
	GBHCT	GBOBC	GBNeck		GBHCT	GBOBC	GBNeck
H	0.28	0.01	−0.11	CA	0.04	−0.28	−0.15
O	0.08	0.02	−0.13	CB	0.01	0.02	−0.08
N	0.17	−0.20	−0.18	HA	−0.01	−0.16	−0.02
C	0.08	−0.17	−0.27

Two trends are readily apparent from the effective radii RMSDs shown in Tables 4A for all atom types and 4B for all backbone atom types: 1) The largest deviations of R_GB from R_PE are in backbone atoms, and 2) the deviation of R_GB from R_PE in PP2 conformations is significantly smaller than for the more compact Alpha, Left, and Hairpin conformations across all GB models. These two observations are consistent with the idea that the performance of GB models decreases the more buried an atom is, and also consistent with previously published comparisons of R_GB with R_PE^20,22. The corresponding average differences in Tables 5A and 5B show that in general the GBOBC and GBNeck models tend to overestimate R_GB (and thus underestimate solvation), while the GBHCT model underestimates R_GB.

Each GB model shows different behavior across different atom types and conformations (Tables 4C–I and 5A–G). The largest deviation in the GBHCT model is from the amide hydrogens (H), which has an average RMSD across all residues of 0.41 Å; this is the worst of all three GB models. A detailed look at the H atoms confirms that the deviation is greatest when the atoms are buried, such as when involved in hydrogen bonding. For example, the H atom of residue A1 in the hairpin structure (which is solvent exposed) shows almost no deviation, while R_GB for the H atom of the very next residue (which is involved in a hydrogen bond) is underestimated by 0.70 Å (Data not shown).

The average deviations across the Alpha, Hairpin, and Left structures seen in Table 5A indicate that in the GBHCT model R_GB is always underestimated for H atoms, meaning that they are considered more solvent exposed than they should be according to PE. In addition, R_GB is also underestimated for carbonyl oxygen (O) atoms in these conformations. This leads to the conclusion that in this model, backbone hydrogen bonding between H and O atoms will be over-stabilized due to an insufficient desolvation penalty, consistent with the overabundance of helical structures observed in the unrestrained REMD structural ensembles.

R_GB is underestimated in general for all other atom types in GBHCT, particularly the amide nitrogen (N) atoms (average RMSD of 0.19 Å). However, the performance for carbonyl carbon (C) and α carbon (CA) atoms is the best of all the GB models (average RMSDs of 0.11 and 0.06 Å respectively). Overall, the performance of this model for Ala10 becomes progressively worse the less solvated the structure becomes. This behavior is consistent with previous observations of this GB model^23,38.

The behavior of the GBOBC model is slightly more varied. The R_GB for H and O atoms is still underestimated, particularly when these atoms are buried, but to a much lesser extent than in GBHCT (average RMSDs of 0.18 and 0.06 Å respectively). In fact, the GBOBC model has the best performance for O atoms out of any of the GB models. This indicates that backbone hydrogen bonds between H and O atoms may still be over-stabilized, but to a lesser extent than in GBHCT. It is also interesting to note that the deviation of R_GB for H atoms in the Left conformation is quite small compared to the other two GB models. However, R_GB is overestimated for N, HA, C, and CA atoms (average RMSDs of 0.24, 0.20 Å, 0.19, 0.29, and respectively). The deviation for CA atoms is particularly large compared to that for GBHCT; in fact GBOBC has the worst performance for CA atoms out of the three GB models. As with the GBHCT model, the performance for the GBOBC model is worse for less well-solvated structures.

The performance of GBNeck for H atoms is comparable to that of GBOBC (overall RMSD of 0.20), except for the Left conformation, where it has deviations as large as those of GBHCT. The performance of GBNeck for O atoms is also about as poor as GBHCT (overall RMSD of 0.15). In contrast to GBHCT and GBOBC however, GBNeck overestimates R_GB for H and O atoms, the net result of which is a destabilization of hydrogen bonds between these two atoms due to an increased desolvation penalty. In fact, the GBNeck model in general overestimates R_GB for all atom types. The performance of GBNeck for C atoms is particularly bad compared to the other two GB models (overall RMSD of 0.33), as is its performance for β carbon (CB) atoms. The only atom type for which GBNeck performs well compared to the other GB models is α hydrogen (HA) atoms (overall RMSD of 0.08). Like the GBHCT and GBOBC models, the performance of the GBNeck model is worse for less well-solvated structures, except it has more deviation for the Left conformation than the Alpha conformation; the reason for this is not clear.

It is seen here that each GB model has significant deviations in calculation of R_GB for various atom types, and the differences are in general not consistent between the GB models. The only real consistency is that R_GB approaches R_PE for well-solvated structures. In terms of overall R_GB RMSD from R_PE, each model performs about equally, except for the GBNeck model and the Left conformation as noted above. The differences between the GB models will be further examined by translating the effective radii into actual solvation free energies.

Direct Comparison of GB to PE: Solvation Free Energy

Equation 6 shows that the effective Born radius of an atom is directly related to its solvation free energy; this is the Self energy portion of the GB equation (sum of terms in Equation 1 when i=j). However, it is important to note that this energy is also highly dependent on the charge of the atom. The magnitude of the differences between the GB and PE effective Born radii shown in Tables 4 and 5 will be strongly modified by the charges on the atoms. For each of the three GB solvent models, the average RMSD of PE self energies from GB self energies across all residues of Ala10 for various atom types are shown in Table 6. The data in Table 6 is also presented graphically for individual residues in each conformation; see supplementary Figures S6–9.

Table 6.

GB Atomic Self Energy RMSD from Perfect (PE) Atomic Self Energy (kcal/mol)

A) All	GBHCT	GBOBC	GBNeck	F) C	GBHCT	GBOBC	GBNeck
alpha	0.90 ± 0.03	0.65 ± 0.03	1.11 ± 0.08	alpha	1.29 ± 0.09	1.39 ± 0.14	2.69 ± 0.18
hairpin	0.70 ± 0.04	0.73 ± 0.04	0.79 ± 0.06	hairpin	0.81 ± 0.08	1.78 ± 0.12	2.10 ± 0.14
left	0.83 ± 0.04	0.75 ± 0.05	1.37 ± 0.08	left	0.98 ± 0.09	1.97 ± 0.16	3.47 ± 0.18
pp2	0.32 ± 0.02	0.39 ± 0.03	0.30 ± 0.02	pp2	0.71 ± 0.08	0.87 ± 0.08	0.52 ± 0.06
B) BB	GBHCT	GBOBC	GBNeck	G) CA	GBHCT	GBOBC	GBNeck
alpha	1.28 ± 0.05	0.93 ± 0.05	1.59 ± 0.11	alpha	0.00 ± 0.00	0.01 ± 0.00	0.01 ± 0.00
hairpin	1.00 ± 0.05	1.04 ± 0.05	1.13 ± 0.08	hairpin	0.00 ± 0.00	0.01 ± 0.00	0.00 ± 0.00
left	1.19 ± 0.05	1.07 ± 0.07	1.96 ± 0.11	left	0.00 ± 0.00	0.01 ± 0.00	0.01 ± 0.00
pp2	0.45 ± 0.03	0.56 ± 0.04	0.43 ± 0.03	pp2	0.00 ± 0.00	0.01 ± 0.00	0.00 ± 0.00
C) H	GBHCT	GBOBC	GBNeck	H) CB	GBHCT	GBOBC	GBNeck
alpha	1.35 ± 0.06	0.49 ± 0.06	0.24 ± 0.06	alpha	0.03 ± 0.00	0.03 ± 0.01	0.14 ± 0.01
hairpin	0.82 ± 0.06	0.47 ± 0.04	0.30 ± 0.04	hairpin	0.05 ± 0.01	0.05 ± 0.01	0.09 ± 0.01
left	1.03 ± 0.06	0.31 ± 0.04	0.64 ± 0.07	left	0.02 ± 0.00	0.02 ± 0.00	0.12 ± 0.01
pp2	0.18 ± 0.02	0.40 ± 0.03	0.10 ± 0.02	pp2	0.03 ± 0.00	0.05 ± 0.00	0.07 ± 0.00
D) O	GBHCT	GBOBC	GBNeck	I) HA	GBHCT	GBOBC	GBNeck
alpha	1.86 ± 0.08	1.00 ± 0.11	1.92 ± 0.15	alpha	0.03 ± 0.00	0.07 ± 0.00	0.02 ± 0.00
hairpin	1.73 ± 0.10	0.94 ± 0.10	1.16 ± 0.12	hairpin	0.09 ± 0.01	0.07 ± 0.00	0.02 ± 0.01
left	1.94 ± 0.09	0.72 ± 0.09	2.00 ± 0.16	left	0.04 ± 0.00	0.08 ± 0.00	0.04 ± 0.00
pp2	0.50 ± 0.05	0.38 ± 0.06	0.68 ± 0.05	pp2	0.03 ± 0.00	0.07 ± 0.00	0.01 ± 0.00
E) N	GBHCT	GBOBC	GBNeck
alpha	1.07 ± 0.06	1.00 ± 0.09	1.10 ± 0.10
hairpin	0.76 ± 0.07	0.98 ± 0.08	0.53 ± 0.07
left	1.07 ± 0.07	1.03 ± 0.09	1.46 ± 0.11
pp2	0.45 ± 0.04	0.69 ± 0.05	0.38 ± 0.04
J) Overall Averages
	GBHCT	GBOBC	GBNeck		GBHCT	GBOBC	GBNeck
All	0.69	0.63	0.89	C	0.95	1.50	2.19
BB	0.98	0.90	1.28	CA	0.00	0.01	0.00
H	0.84	0.42	0.32	CB	0.03	0.04	0.10
O	1.51	0.76	1.44	HA	0.05	0.07	0.02
N	0.84	0.92	0.87

There is of course a direct relationship between deviations in effective radii and deviations in Self solvation free energy; an atom whose effective radius has been underestimated will have an overestimated solvation free energy, and vice versa. What is less clear is the relationship between the magnitude of deviation of effective radii and magnitude of deviation of self solvation free energy. It is apparent that the relatively small (for the most part < 0.5 Å) deviations in effective radii in Tables 4 and 5 can translate into significant differences in Self energy on the order of ~1.0 kcal/mol, but this is highly dependent on the charge of the atom. For example, in the GBHCT model even though the average radii RMSD for H atoms was about three times as large as the average radii RMSD for O atoms, the average self energy RMSD for H atoms is only about half as large. As expected, radii deviations for atoms with small charges become almost insignificant in terms of energy. For example, although large deviations in the effective radius were observed for CA atoms in the GBOBC model, the energy differences are negligible (< 0.01 kcal/mol).

Of course, the Self energy is just part of the GB model; only the Total GB energy can be directly related to observed structural ensembles, so it is important to calculate the Interaction energy as well (sum of terms in Equation 1 when i≠j). Table 7 shows the Self, Interaction, and Total GB energies computed with effective radii obtained with the GBHCT, GBOBC, and GBNeck models (R_GB), and PE derived effective radii (Perfect radii, R_PE) for the structures used in the analysis shown in Tables 4–6. Note the excellent agreement of the Total ΔGPol values in Table 7 with ΔGPol values in Table 3A, showing that choosing a subset of structures for the effective radii analysis has not adversely affected the results.

Table 7.

Total, Self, and Interaction Components of Solvation Free Energy for Ala10 (kcal/mol)

Total	PE	Perfect	GBHCT	GBOBC	GBNeck
alpha	−47.96 ± 0.77	−47.42 ± 0.77	−51.64 ± 0.94	−49.38 ± 0.98	−43.27 ± 0.82
hairpin	−57.28 ± 1.15	−57.70 ± 1.04	−57.45 ± 1.17	−56.02 ± 1.19	−52.83 ± 1.05
left	−54.85 ± 0.90	−52.45 ± 0.82	−55.05 ± 0.90	−52.70 ± 0.93	−48.24 ± 0.08
pp2	−78.00 ± 0.92	−81.22 ± 0.97	−77.26 ± 0.94	−77.99 ± 0.95	−77.48 ± 0.92
Self	PE	Perfect	GBHCT	GBOBC	GBNeck
alpha	−763.77 ± 1.68	−763.77 ± 1.68	−813.34 ± 2.91	−748.18 ± 4.85	−703.92 ± 5.51
hairpin	−822.96 ± 2.96	−822.96 ± 2.96	−843.65 ± 2.23	−798.59 ± 3.55	−787.25 ± 3.58
left	−754.11 ± 1.86	−754.11 ± 1.86	−798.61 ± 3.00	−724.13 ± 5.15	−676.81 ± 5.54
pp2	−882.27 ± 1.45	−882.27 ± 1.45	−885.93 ± 1.47	−862.55 ± 2.12	−875.09 ± 1.52
Interaction	PE†	Perfect	GBHCT	GBOBC	GBNeck
alpha	715.81	716.36 ± 1.75	761.70 ± 2.48	698.80 ± 4.34	660.65 ± 5.17
hairpin	765.68	765.26 ± 2.94	786.20 ± 1.89	742.57 ± 3.07	734.42 ± 3.22
left	699.26	701.66 ± 2.03	743.56 ± 2.75	671.43 ± 4.85	628.57 ± 5.35
pp2	804.27	801.05 ± 1.44	808.67 ± 1.32	784.56 ± 1.86	797.61 ± 1.36

^†Calculated from PE(Total) - PE(Self)

In Table 7 it is apparent that although the deviations in the Total energy between PE and each GB model are on the order of a few kcal/mol, there are significant differences in the Self and Interaction GB energies which end up cancelling in the Total solvation free energy. This behavior for GB models has been observed previously^22,23.

As was noted by Onufriev et al.²², use of effective Born radii calculated via PE improves the quality of interaction energies as well as self energies; surprisingly, this improvement is not always reflected in the Total energy, where other GB models may happen to have better agreement with PE results due to fortuitous cancellation of error. For example, although perfect radii give the lowest Total energy deviation for the Alpha conformation (−0.55 kcal/mol), it does not for the Left conformation (−2.40 kcal/mol); in that case the lowest deviation is from the GBHCT model (0.20 kcal/mol).

As in the previous section, the differences in Total, Self, and Interaction energies shown in Table 7 between different conformations are considered (Table 8) in order to better compare the performance of each implicit model. Here it is seen that despite the fact that using perfect effective radii brings the Self and Interaction GB energies much closer to those calculated with PE, the use of perfect radii shows no improvement over other GB effective radii calculations in terms of reproducing the solvation free energy differences between different conformations of Ala10. This finding is consistent with that from a study by Stultz, who suggested that agreement with PE alone may be an inadequate way to parameterize GB models for the purpose of calculating free energy differences⁵⁰.

Table 8.

Differences in Components of ΔGPol (from Table 7) Between Conformations of Ala10 (kcal/mol)

A) ΔΔGPol Total
	P-A	P-L	A-L	P-H	A-H	L-H
PE	−30.03	−23.15	6.89	−20.72	9.32	2.43
Perfect	−33.80	−28.77	5.03	−23.52	10.28	5.25
GBHCT	−25.62	−22.21	3.41	−19.81	5.80	2.40
GBOBC	−28.61	−25.29	3.32	−21.97	6.64	3.32
GBNeck	−34.21	−29.25	4.97	−24.66	9.56	4.59
B) ΔΔGPol Self
	P-A	P-L	A-L	P-H	A-H	L-H
PE	−118.49	−128.15	−9.66	−59.31	59.18	68.84
Perfect	−118.49	−128.15	−9.66	−59.31	59.18	68.84
GBHCT	−72.58	−87.32	−14.74	−42.28	30.30	45.04
GBOBC	−114.37	−138.42	−24.05	−63.96	50.41	74.45
GBNeck	−171.17	−198.28	−27.11	−87.85	83.33	110.43
C) ΔΔGPol Interaction
	P-A	P-L	A-L	P-H	A-H	L-H
PE	88.46	105.01	16.55	38.59	−49.87	−66.42
Perfect	84.69	99.39	14.69	35.79	−48.90	−63.59
GBHCT	46.97	65.11	18.14	22.47	−24.50	−42.64
GBOBC	85.76	113.13	27.37	42.00	−43.76	−71.14
GBNeck	136.96	169.04	32.08	63.19	−73.77	−105.84
D) RMSD from PE
	Total	Self	Interaction
Perfect	3.32	0.00	3.32
GBHCT	2.76	30.25	28.24
GBOBC	2.19	8.75	6.60
GBNeck	3.62	43.06	39.63

A=Alpha, P=PP2, L=Left, H=Hairpin

Conclusions

In this study, we directly compared the TIP3P explicit solvent model to results from PE and three GB solvent models. Well-converged REMD simulations using either the TIP3P solvent model or each of the three GB solvent models revealed that simulations with GB models show markedly different conformational and structural preferences. In particular, the GBHCT and GBOBC models contained an overabundance of helical structure compared to explicit solvent results and experiment. Thus the different solvent models not only provide ensembles with different secondary structure populations, but the “native” structure in each solvent model (as defined by the dominant conformation in the ensemble) differs depending on the solvent model used for the simulation. This result has significant implications for the use of these GB models for structure prediction or characterization of folding landscapes.

Using the TIP3P model as the standard, we directly compared free energies of solvent polarization from each model for four different conformations of Ala10; right-handed α-helix (Alpha), left-handed α-helix (Left), β-hairpin (Hairpin), and polyproline II helix (PP2). The performance of implicit models was found to be dependent on conformation; in general, agreement with TIP3P results was best for the well-solvated PP2 conformation, growing progressively worse for more compact conformations (Hairpin, Left, and Alpha). PE was found to have the best overall performance in terms of reproducing differences in solvation free energy between the different conformations. It was also found that the amount of α-helical structure in the unrestrained REMD simulations is correlated to the solvation free energy gap between the PP2 (unfolded model) and Alpha conformations; in the GBHCT and GBOBC solvent models this gap was too small, which is related to the observed overabundance of helical structure in the REMD simulations.

One difference between the TIP3P and GB REMD simulations reported here is the lack of a specific term for ΔG_Nonpol in the GB simulations. In addition to the ΔG_pol term that was our main focus, the absence of this term could also impact the ability of the GB simulations to reproduce ensembles from explicit water simulations. The errors in ΔG_Pol from the various GB models as compared to explicit water charging free energy calculations correlate well with trends in deviations of structure populations from the REMD simulations, suggesting that ΔG_Pol dominates the current errors in solvation free energy. It is of course likely that a quantitative agreement between implicit and explicit solvent models will require careful consideration of ΔG_nonpol as well as ΔG_pol.

The effective Born radius calculation of each GB model (R_GB) was then compared to effective Born radii calculated with PE (R_PE). While small deviations in effective radii were found for PP2, significant deviations were found for the more compact conformations. It is likely that backbone hydrogen bonds are too stable in the GBHCT and GBOBC models because R_GB is underestimated for amide hydrogen (H) and carbonyl oxygen (O) atoms, leading to an insufficient desolvation penalty for hydrogen bonds. Likewise, the GBNeck model overestimates R_GB for these atoms, leading to unstable hydrogen bonds and a lower helical population.

As has been reported by others, we note that substantial errors in the Self and Interaction GB energies tend to cancel in the net Total energies. The significant cancellation of error that we observe supports the idea that individual GB energy components should be considered when comparing total GB energies to results from PE, as is often done during development or validation of GB models.

As has been seen before, using R_PE in the GB function improves the agreement between Self and Interaction energies compared to PE. However, this improvement does not translate into overall better performance; so-called ‘perfect’ radii are no better at capturing the difference between the conformations here than any other GB model that we tested. This may suggest a limit to how much GB models can be improved solely through optimization of the effective Born radius calculation.