The uncertain role of diversity dependence in species diversification and the need to incorporate time-varying carrying capacities

Abstract

There is no agreement among palaeobiologists or biologists as to whether, or to what extent, there are limits on diversification and species numbers. Here, we posit that part of the disagreement stems from: (i) the lack of explicit criteria for defining the relevant species pools, which may be defined phylogenetically, ecologically or geographically; (ii) assumptions that must be made when extrapolating from population-level logistic growth to macro-evolutionary diversification; and (iii) too much emphasis being placed on fixed carrying capacities, rather than taking into account the opportunities for increased species richness on evolutionary timescales, for example, owing to increased biologically available energy, increased habitat complexity and the ability of many clades to better extract resources from the environment, or to broaden their resource base. Thus, we argue that a more effective way of assessing the evidence for and against the ideas of bound versus unbound diversification is through appropriate definition of the relevant species pools, and through explicit modelling of diversity-dependent diversification with time-varying carrying capacities. Here, we show that time-varying carrying capacities, either increases or decreases, can be accommodated through changing intrinsic diversification rates (diversity-independent effects), or changing the effects of crowding (diversity-dependent effects).

1. Introduction

The idea of a carrying capacity, or equilibrium diversity, has been of particular interest to palaeontologists and neontologists alike. For palaeontologists, who confront the controls on biodiversity directly as they document biodiversity change in deep time, two fundamental models have been proposed to describe diversity dynamics. The first, building on MacArthur & Wilson [1], proposes the existence of an equilibrium diversity that the biota, or portions of the biota, can achieve, [2–4], while others have assessed the impact of extinction on the extent to which this equilibrium is realized [5]. The second, representing a radical departure from the first, proposes that diversity is not limited by any carrying capacity, or if it is, that the biosphere is so far from the equilibrium diversity that we can effectively ignore it [6–9]. Establishing whether there are diversity limits is also of central interest to neontologists, on both evolutionary and ecological timescales, where there is similar disagreement over the importance, or even existence, of a carrying capacity [10,11].

Below we assess the extent to which the disagreement over the existence and importance of equilibrium diversities is a consequence of different temporal, spatial and taxonomic views of biodiversity. Recognizing that different approaches might bring their own definitions of a carrying capacity, we develop a quantitative framework for incorporating time-varying carrying capacities, emphasizing that while equilibria and equilibrial processes might operate in the biosphere, individual clade or total biosphere diversity may be fundamentally non-equilibrial.

(a). Motivation for the idea of a species carrying capacity

The seminal work of MacArthur & Wilson [1,12], and the empirical studies of island biogeography that followed (e.g. [13]) had a deep influence on the notion of a carrying capacity in both shallow and deep time. The observation of species–area relationships, of an isolation effect on island diversities, and the fact that islands can quickly recolonize followed by a period of species turnover, are usually interpreted as evidence for a limit on diversity. In island biogeography theory, the equilibrial diversity can be described as the balance between the immigration and speciation rate and extinction rate, where these rates depend on island area and distance and nature of the species source pool. Key to theory of island biogeography is the notion that as species richness increases in an island (ecosystem), immigration and speciation rates decrease and extinction rates increase, in accordance with the classic view of a logistic growth.

This model directly inspired palaeontological analysis of biodiversity dynamics in deep time [2–4]. However, there are many differences between colonization of islands and the evolution of the Earth's biota (putting aside the fact that Sepkoski's pioneering work was at the family level), which might render the use of simple logistic models in deep time inadequate. Moreover, there are differences between palaeontological, phylogenetic and ecological ways of defining the relevant species pools, which translate into differences in the extent to which these views of biodiversity might be expected to fit a model of logistic growth, the population growth of a single population in a small, circumscribed, environment (i.e. in a flask). Here, we compare the assumption of these different domains and discuss their implications to the debate of bound and unbound diversity dynamics.

(b). Palaeontological and neontological evidence for bound diversification

At the heart of MacArthur & Wilson's [1,12] notion of a dynamic equilibrium is the idea that immigration (extended to include speciation on evolutionary timescales) balances extinction and the idea that immigration and extinction rates might be diversity-dependent. However, the living biota represent a snapshot in time, and thus it is not possible to determine directly whether immigration, speciation and extinction rates are in fact diversity-dependent. By contrast, the dynamics of diversity change can be measured directly with rich fossil records, by determining the extent to which origination and extinction rates are correlated with change in diversity as one proceeds from one stratigraphic interval to the next.

One might reasonably ask whether the fossil record is up to this task? In some cases, the answer is a resounding yes. In the case of the 19 Cenozoic mammalian clades analysed by Quental & Marshall [14], the average genus-level preservation rate was 89% at a temporal resolution of the geological stage, while for planktonic forams the Cenozoic fossil record is 81% complete at the species level at a temporal resolution of 1 Myr [15]. Thus, for some groups, the fossil record is essentially complete on evolutionary timescales.

Analysis of the fossil record has revealed strong evidence of diversity dependence in rates of origination [2,16,17], with evidence for both diversity dependence and independence in rates of extinction [15,16]. Furthermore, the recovery of mass extinction events are usually associated with elevated rates of origination (e.g. [7]), which has also been interpreted as evidence for diversity dependence [18]. Additionally, diversity trajectories themselves sometimes fit a logistic model ([4], for marine families) or show a temporal decrease in speciation and an increase in extinction rates, a trend that is consistent with diversity dependence [19]. While the early palaeontological literature, and much of the current literature as well (e.g. [20,21]), is restricted to analyses of higher taxa, there are now an increasing number of species-level studies which also show diversity-dependent rates of origination and/or extinction [15,16,22]. These recent species-level studies are particularly relevant for the ‘bound versus unbound diversification’ debate, given that this is the taxonomic level typically used in phylogenetic and ecological studies. Lastly, studies at the level of local assemblages typically suggest that variation in species richness is constrained on timescales of approximately 1 to 20 Myr [23] and hence can also be interpreted as evidence against a model of unbound diversification dynamics [18].

The neontological literature on bound diversification has several threads, including the study of adaptive radiations [24] and the use of models that explicitly fit diversity-dependence dynamics [25,26]. Although most neontological evidence for a limit on diversity is indirect, a considerable number of molecular phylogenies show evidence of decrease in diversification rates as one proceeds up the phylogeny ([27,28]; but see [29] for alternative possibilities).

While there is empirical evidence in the fossil and neontological records of diversity dependence at play, we should note that diversity-dependence rates, although necessary, are not sufficient evidence to demonstrate the existence of a fixed carrying capacity [14,18,30,31]. In fact the results shown by Morlon et al. [32] based on several molecular phylogenies suggest that although rates of diversification consistently decrease over time, diversity for those same phylogenies are probably still expanding.

(c). How to view the carrying capacity: an instructive example from the fossil record

The idea of a carrying capacity evokes a series of important issues that need to be evaluated in the debate over the usefulness of the equilibrium model. The work of Sepkoski [4] embodies the central issues involved. Sepkoski employed a coupled-logistic equation to model Phanerozoic marine family-level data, where each of three ‘faunas' has its own intrinsic diversification rate and equilibrium diversity, but where the diversity trajectory of each ‘fauna’ is influenced by the diversity of all the ‘faunas' (inset, figure 1). We have put the word ‘fauna’ in quotes because they are not directly defined spatially or ecologically, but are simply groups of classes that had similar temporal family-level diversity trajectories [33].

Figure 1.

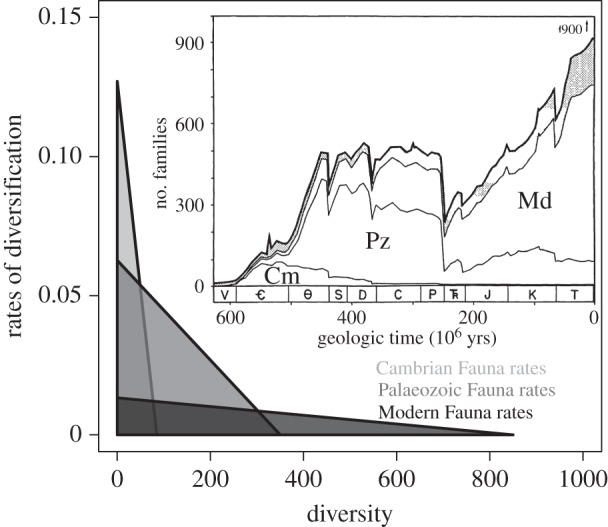
Depiction of the intrinsic per lineage rate of diversification (intercepts on the y-axis) and carrying capacities (intercepts on the x-axis) for the three ‘faunas' Sepkoski [4] used to model the diversity trajectory of marine Phanerozoic families (inset; used with permission from the Paleontological Society).

Thus, in Sepkoski's model, while each pool of taxa (each ‘fauna’) has its own logistic growth, other pools influence its diversity trajectory. However, while the dynamics of each ‘fauna’ is portrayed as fixed (which could be viewed as either an error or a retrospective convenience) we see that for the entire marine biota the realized average intrinsic diversification rate and the strength of the diversity dependence (which is inversely proportional to the carrying capacity) change with time. The Phanerozoic begins with the fast diversifying but low equilibrium-diversity Cambrian Fauna, but by the latter part of the Cenozoic the marine biota is dominated by the more slowly diversifying, but more diverse Modern Fauna (figure 1).

This time-evolution in the intrinsic rate of diversification and effective carrying capacity can be interpreted as the impact of evolutionary innovation within the later ‘faunas', which effectively changed the total carrying capacity as these faunas, or at least some of their constituent clades, exploited new resources, and/or partitioned resources in different ways.

Sepkoski's formulation also embodies the idea that interaction between ‘faunas' can drive groups to extinction. Thus, even though the Cambrian and Palaeozoic Faunas have fixed carrying capacities in Sepkoski's model, interaction with each other and the Modern Fauna leaves them with realized diversities that are far below their equilibrium values. Thus, similar to Quental & Marshall's [14] analysis of individual mammalian clades, realized diversity trajectories need not be fixed nor fully determined by their intrinsic dynamics. Carrying capacities might not only expand with time (e.g. in Sepkoski's' model [4], if you take into account the fact that some of the most diverse clades in the Modern Fauna had later times of origin than the Fauna itself), but also shrink.

Sepkoski's work (figure 1) also raises a series of related questions of how we measure carrying capacities, and what are the mechanisms that drive changes in carrying capacities. First, are the patterns, and therefore the underlying mechanisms, seen for higher taxa good proxies for what happens at the species level? Second, Sepkoski's model is constructed through the eyes of logistic growth, and thus it evokes competition as a central force behind the observed diversity dynamics. But are there other biotic and abiotic factors that are equally or more important? Lastly, the decision to model the dynamics as a three-phase coupled logistic equation implies that competition might exist not only between groups within a given ‘fauna’, but also between faunas. This last point raises the possibility that solely looking for the evidence of equilibrium diversity within a focal clade (e.g. as is implicitly assumed when fitting logistic models to the phylogeny of a given clade) might not be appropriate given that diversity-dependent mechanisms may also operate beyond the focal clade.

Analysis of Sepkoski's seminal work highlights the importance of carefully defining and understanding the appropriate pool of taxa for which we might expect to see a carrying capacity, and raises questions about the nature of that group's equilibrium diversity.

(d). The case against the carrying capacity

Arguments against a potential cap on species diversity have been made at different spatial and temporal levels, from population studies at shallow timescales, up to deep time studies using the fossil record. It is generally assumed that a limit to diversity should manifest itself in different ‘domains', e.g. from local to global, for shorter or longer periods of time [11]. When looking at bird populations, Ricklefs [34] noted that an increase in local species richness does not appear to affect either local population density or niche breadth. Similarly, the observation that many local communities are amenable to the invasion of exotic species without driving the extinction of local species has been argued as evidence for uncapped diversity at the local scale [11].

A lack of support for a macroevolutionary diversity-dependent model has also been argued for larger spatial, temporal and taxonomic scales, such as the whole biota [6,7]. For the terrestrial vertebrate fossil record, the evidence is that the observed diversity trajectory does not show any sign of an asymptote towards the present [6]. For the marine fossil record, the exact shape of the genus-level diversity curve is hotly debated, the lowest taxonomic level analysed to date, with some arguing for an asymptote [35], while others argue for an exponential increase [7]. The debate over the shape of the marine fossil record has stalled on how to best take into account a multitude of time-varying sampling biases [35–37], although the most recent analysis suggests that marine diversity steadily increased from the Jurassic to the present [38]. Interestingly, in the marine realm Stanley [7] was unable to find a solution to a coupled logistic equation that adequately describes the observed genus-level diversity curve when the genera are grouped according to Sepkoski's three Faunas. However, in his analysis, there is typically increased diversification rates at the genus level after mass extinctions ([7], fig. 22), and the overall trend across the entire Phanerozoic is one of decreasing rates of diversification. While these both point to the presence of a carrying capacity, Stanley also points out that in the recovery from extinction events, the rates at the short timescales do not decrease. Thus, the genus-level fossil record shows signatures of both limits to diversification, as well as of an expanding carrying capacity.

2. The importance of identifying the ‘correct’ species pool

Although the observations described immediately above appear to negate the idea of a carrying capacity, we note that equilibrium processes might take a long time to realize; the carrying capacity might change faster than the ability of the biota to keep up with it, as appears to be the case during the decline of the 19 mammalian clades analysed by Quental & Marshall [14]; or it might be taxon specific. Further, the carrying capacity might not be perceived if we lump together species that do not directly affect each other, or if we have not considered all the relevant taxa.

When performing an analysis, whether it is directed at identifying or rejecting the hypothesis of a carrying capacity, we explicitly or implicitly make a statement about the appropriate species pool and the temporal-spatial scale relevant to the hypothesized diversity-dependent process. For example, at a local scale, the effect of new species, exotic or not, might take time to impact the ecological balance expected under an equilibrium model. When considering the ease with which invasive bird species can infiltrate ecosystems, it is important to recognize that typically the resource base may have also expanded, e.g. with the introduction and maintenance of exotic plant species. Alternatively, different communities might be continuously suffering local extinctions and hence might be amenable to the recolonization of species, exotic or not.

At a global scale, lumping many different taxonomic groups into one single pool of species (e.g. the whole biota), when looking for the evidence of a carrying capacity, might represent the wrong phylogenetic or spatial scale given that diversity-dependent processes could operate within a species pool at smaller spatial and/or taxonomic scales. Furthermore, evolutionary innovation may lead to an ever-increasing carrying capacity even while individual groups reach their carrying capacities.

To better appreciate the need for an explicit and appropriate delineation of the species pool, it is instructive to revisit the ways palaeontologists and neontologists have defined their species pools.

(a). Defining the species pool: the palaeontological perspective

Palaeontologists, in part driven by the incompleteness of the fossil record, have typically addressed this question at global and broad taxonomic scales. This represents a ‘supra ecosystem’ approach, which pulls all the available data from as many different taxa as the fossil record permits (e.g. largely skeletonized taxa). If a carrying capacity is assumed, or evidence of its existence tested for, it is typically for a single fixed global carrying capacity (but see discussion above, where we argue that Sepkoski's approach can be viewed as encapsulating a time-varying carrying capacity). An important question is what the global pool of species (or higher taxa) might mean, and for which species pool(s) we might expect to see a bound diversification dynamics.

Given the huge preservational heterogeneity among different lineages it might be naive to expect to see a cap on the observed diversity, as we might be missing some important components of the ecosystems. Similarly, by lumping together a set of disparate taxonomic groups, we might be pooling species with very different ecologies that do not affect each other's dynamics in a diversity-dependent manner. Nonetheless, at the truly global scale, i.e. if all taxa are accounted for, we expect to find clear evidence of a carrying capacity if the taxa present are resource limited (e.g. by space). Thus, one does not need to restrict oneself to pools of interacting species to see evidence of a carrying capacity, as long as the species pool consists of sub-pools that each have their own carrying capacities. However, at broad temporal and taxonomic scales, it seems unreasonable to assume that the carrying capacity is fixed—over time we might expect evolutionary innovation to expand the total carrying capacity [8,9]. By contrast, if we limit the taxonomic scope (e.g. brachiopods), we might leave out ecologically relevant competitors [21].

Our point here is simply that by pooling all the available taxa and looking for evidence of an equilibrium model (e.g. diversity dependence) palaeontologists have implicitly assumed that, with respect to biotic interactions which are ultimately at the heart of any cap on diversity, the selected pool of taxa effectively represent all relevant taxa, and that the signal of a bounded diversity should emerge for this global collection of species. This might not be the case if the lineages are not directly connected in any important ecological way, or if key elements are missing from the palaeontological sampling.

(b). Defining the species pool: the phylogenetic perspective

A taxonomically less inclusive view of a carrying capacity is exemplified by the work of neontologists who use molecular phylogenies to study diversity dynamics, and palaeontologists who examine single clades in the fossil record. This approach usually consists of picking a clade of interest and looking for evidence of carrying capacities, either through indirect evidences such as decreases in diversification rate [28] or by explicitly modelling changes in speciation (or extinction) as diversity-dependent [25,26]. The underlying assumption of phylogenetically defined species pools is that the species within the monophyletic clade of interest includes all (or most) of the relevant players for the diversity-dependent dynamics.

Surveys of molecular phylogenies provide ample evidence for a drop in diversification rate with time for many extant groups [27,32]. Given the Darwinian tenet that closely related species might compete more intensely against each other, this is perhaps not too surprising, and the interpretation that decreasing diversification rates as evidence of diversity dependence is not unreasonable. However, decreasing diversification is also compatible with other dynamics [39], for example with the initial phases of an extinction process [29,40]. Thus, the dynamics of a clade exhibiting a drop in diversification rate might be driven by the time-varying interactions with the abiotic environment, or with species outside the clade of interest [22], in which case a more appropriate species pool should be defined ecologically rather than phylogenetically if one expects to see evidence for bound diversity.

3. Back to basics: scaling up the population-level logistic process to the macroevolutionary scale

Given the complexity introduced by the differing ways of defining species pools, and the lack of agreement in even the existence of a carrying capacity, it is instructive to examine the assumptions required to scale up the relatively straightforward process of logistic growth of a population in a limiting environment to multi-species systems. In macroevolutionary terms, the number of individuals at the population level are equated with the number of species (or the number of genera or families which are often used proxy for species), while the strength of competition, which for population growth is referred to as density dependence, refers to the crowding effect felt by species. Density dependence is referred to as diversity dependence at the macroevolutionary scale. The logistic model of population growth posits a limit in the population size, which is referred to as the carrying capacity (K), which represents the maximum number of individuals a given environment can sustain. When scaled up to a macroevolutionary level, the carrying capacity is usually defined as the maximum number of species, or higher taxa, that can co-exist.

The scaling up of the logistic model of population growth to a macroevolutionary perspective makes a series of assumptions (figure 2) that require evaluation [9,41,42]. While there is no disputing the value of the extrapolation of logistic population growth to macroevolutionary scales, it is instructive to look at the differences between the two. In population biology, the assumptions of the logistic model are clear, and the domain and pool of interacting individuals are typically easily defined and represent a reasonable simplification of the real system. At the population level, the individuals are assumed to be equal with respect to the relevant ecological interactions, and to remain so throughout the whole process. Therefore, it assumes no evolution. It also assumes that the individuals overlap in time and space. Perhaps more importantly, the simple population view assumes that the resources required to sustain a given population are limited and unchanging, i.e. it assumes a constant environment. In effect, the demarcation of the physical space and rate of input of resource establishes the existence of a carrying capacity irrespective of the presence of the population, and the strength of the density-dependence (the effects of crowding) can be viewed as a by-product of the carrying capacity and the intrinsic rate of growth.

Figure 2.

Assumptions and their implications when extending the population-level notion of logistic growth to species-level logistic growth. Left: phylogenetic/single-clade approach. (a) Simple scaling up of population level logistic growth makes some assumptions that are unrealistic when viewing evolution in deep time. (b) Relaxing the assumption of a fixed carrying capacity renders the phylogenetic approach more reasonable, and allows for a role for diversity dependence even if non-equilibrial processes dominate. Right: whole biota approach. (c) This approach makes some simple assumptions that are valid on short timescales. (d) To use the approach on longer timescales, it is necessary to include speciation as a relevant process. (e) Palaeontologists have co-opted the whole biota island biogeography approach, where the whole Earth is viewed as an island. In addition, they have used it hierarchically. In both approaches, the use of a logistic formulation becomes more reasonable once one incorporates the idea that the carrying capacity might change through time.

Scaling up the population-level process to the macroevolutionary scale requires a re-interpretation of the meaning of the core parameters. First, evolution happens, which affects the intrinsic reproductive rate of the species in the species pool, their ability to speciate in the absence of competitors. Evolutionary change also influences their ability to compete with others for resources, which influences the crowding effect. Second, the assumption that the ‘individuals', the different species, can be considered equal with respect to the relevant ecological interactions is at best controversial. While it is unclear the extent to which closely related species are ecologically equivalent, it has long been known that there are ecological differences between closely related species (e.g. [43]), with each species seeing many of the available resources in a different way. However, Hubbell's [44] model posits ecological equivalence, and it is possible that for some species groups the assumption of ecological equivalence may hold. Third, on longer timescales, the available resources are unlikely to be fixed, either abiotically (e.g. due to changes in physical habitat size, temperature or rainfall), or due to evolutionary innovation that might lead to an increase in resource availability [20,45], and/or render previously inaccessible resources available, including habitat space. Examples include microhabitats created with the development of complex coral reefs, or suitable habitat for arboreal epibionts with the increased species richness and complexity of tiering in especially angiosperm-dominated forests. Other potential examples include the evolution of new dentitions that open up more feeding opportunities, or the other side of the plant–herbivore arms race where the evolution of plant defences might lead to less food for herbivores.

Thus, one might expect abiotic environmental change and evolutionary innovation to change the carrying capacity. The scaling up of the population process leads naturally to the notion of a time-varying carrying capacity.

(a). Scaling up population-level logistic growth when species pools are defined phylogenetically

The phylogenetic perspective assumes that the relevant pool of species belong to the clade of interest. However, this delineation of the species pool may be inappropriate if there are ecologically similar species that are not part of the focal monophyletic group—in fact, competitive interaction is not necessarily more prevalent among closely related species [46,47]. We see evidence that in deep time, diversity dependence might operate between species belonging to different lineages, for example, between different groups of North American carnivores [22]. Thus, the appropriate species pool may very well be a polyphyletic group.

Given that spatial overlap is required for ecological interaction, even if all the ecologically relevant taxa belong to the same monophyletic group, the assemblage of interacting species may be a geographically delineated paraphyletic subset of that monophyletic group. Thus, even in this situation, uncritical analysis of the whole clade might lead one astray when looking for evidence of diversity dependence.

(b). Scaling up population-level logistic growth when species pools are defined palaeontologically

The simple population view of a logistic growth has also been co-opted by palaeontologists in the analysis of the large-scale patterns of diversity change, and is thus similar to the traditional view of island biogeography to the extent that the whole Earth can be viewed as an island (except that when working on geological timescales we anticipate multiple evolutionary innovations and there is no external source pool; figure 2). We also refer to this view as the ‘whole biota approach’, while recognizing that palaeontologists also employ clade-based approaches. Here, the species pool is not phylogenetically constrained but rather intended to represent all species that temporally coexist. In rare cases, most species in the community appear to be preserved, for example, in the soft-bodied Chengjiang and Burgess Shale Cambrian marine faunas, or the Eocene Messel Oil Shale in Germany, where 700 taxa have now been placed in food webs [48]. But typically, the ‘whole biota’ in reality consists of just the relatively abundant, readily fossilized, geographically widespread portions of the whole biota (e.g. skeletonized marine invertebrates).

(c). Defining the species pool: the central importance of thinking ecologically

In both the phylogenetic and ‘whole biota’ palaeontological views, there is often a mismatch with the classic logistic description, where the bounded logistic growth emerges from explicit ecological interaction and resource limitation. Thus, either analyses over deep time need to incorporate an explicit link to the relevant ecological interactions and players, or explain why one might expect logistic growth given other considerations. It is ecological identity not the phylogenetic (or taxonomic) identity, per se, that matters for strictly bound dynamics. It is in the ecological domain that we should expect to see the signal of a carrying capacity, if such a cap on diversity exists, an observation emphasized by Cornell [31] in his discussion of regional species pools.

By only looking at just one lineage, we might wrongly infer the underlying process governing the diversity dynamics. For example, the regional diversity of clade might be observed in the fossil record, or inferred from a molecular phylogeny, to be increasing and thus one might reject the hypothesis that logistic processes are operating. But it might be the case that the clade is expanding at the expense of an ecologically similar clade, so that collectively they are in fact evolving under simple logistic growth, for example as appears to be the case for North American Cenozoic carnivores [22,49].

There are two ways of approaching the ecological delineation of the species pool. The first is simply to identify the pool regionally, analysing the full set of interacting species [31], or at least those that are known. The second is to work within a defined guild, the approach used by Hubbell [44] in his neutral theory of biodiversity. In some cases, analysis of monophyletic clades might map well onto guilds, but in other cases they might not. A simple way forward would be to simultaneously analyse multiple phylogenetically defined species pools (e.g. multiple clades) if one expects the ecological arena to encompass a larger collection of lineages. One such example is the work of Silvestro et al. [22], which considered competition for food resources to be a main driver of interaction between clades. We note that using an ecological framework for analysing bound species dynamics is not well represented in current macroevolutionary approaches, especially those using molecular phylogenies to study the diversification dynamics.

4. A unifying framework centred on a time-varying carrying capacity

(a). Special insight offered by the fossil record

While the living biota represent a snapshot in time of the outcomes of a potentially diverse set of evolutionary and ecological dynamics, the fossil record enables us to directly follow the diversity change of groups of species. Several clades, or more typically groups defined taxonomically, show patterns of diversity change that do not fit the simple dichotomy of unbound versus bound diversification. For example, particularly at lower taxonomic levels, a pattern of waxing followed by waning diversity is consistently found for many groups [14,50,51]. We note, however, that waxing and waning are not incompatible with a role of diversity dependence. Thus, for example, Quental & Marshall [14] argue for the role of diversity dependence in the rise and fall of the Cenozoic mammalian clades they analysed, but they also note that the role of the diversity dependence was secondary.

Additionally, the observation that the demise of a given clade is sometimes followed by the rise of an ecologically similar one [49] has also motivated the idea that, similar to Sepkoski's marine family dynamics, the dynamics of individual clades might be coupled. Perhaps one of the best examples of this is evidence of competitive displacement among post-Palaeozoic cyclostome and cheilostome bryozoans [52]. This view reinforces the idea that the carrying capacity need not operate within a single phylogenetic domain but should be delineated ecologically. In fact, a recent study of mammalian carnivore clades [22] suggests that changes in speciation and extinction rates of declining clades are more related to changes in the diversity of a potential competitor clade than to the diversity within the clade itself.

Key to these palaeontological examples is the observation that clades often diversify and then decline—for some of these clades diversity-dependent origination and extinction rates have been established [15,22], but their carrying capacities are not fixed even if the relevant guild's carrying capacity might be.

(b). A middle ground between bound versus unbound diversification

As pointed out by Cornell [31], the disagreement between the opposing views on bounded versus unbounded diversification suggests we need another approach to accommodate the lack of unequivocal support for either of the two opposing views. Cornell's solution was that we consider a new ‘damped increase diversity’, the idea that ‘diversity generally increases through time but that its rate of increase is often slowed by ecological constraint’ [31].

We extend this idea, arguing that explicit incorporation of a time-varying carrying capacity (sensu [14]) into the debate solves many of the problems encountered when only considering the two extreme hypotheses. Specifically, we propose a framework that allows for the possibility of both expansion and contraction of the carrying capacity. This approach focuses attention on the critical issues of the extent to which biotas fill the ecological space available to them, and identifies the appropriate species pool when considering damped diversification. The approach also aids in the investigation of the roles of biotic and abiotic forces in diversification (and extinction). Lastly, it is compatible with the pragmatic phylogenetic and ‘whole biota’ (palaeontological) ways of viewing diversification.

The notion of a time-varying carrying capacity is certainly not new [8,9,41] and from a palaeontological perspective there is plenty of evidence for major changes in the abiotic and biotic conditions that in turn have had an impact on the biosphere's carrying capacity. Most of the biotic changes are driven by major innovations that increased the available resources in space, resources at the base of the foodweb, or increased the ability to extract nutrients higher up the food web, e.g. the rise to dominance of eukaryotic plankton in the oceans during the Mesozoic [45]; the origin of the first forests in the mid-Paleozoic, which increased energy capture in the terrestrial realm; the angiosperm radiations that further increased energy uptake in terrestrial ecosystems, providing fruits and nectar for insects, birds and mammals, as well as new habitats that led to a radiation of epiphytic ferns [53]; the creation of microhabitats in reefs, etc.

Incorporation of time-varying carrying capacities also makes it easier to ‘rescue’ clade-based approaches [22] and enables extension of Sepkoski-style ‘whole biota’ approaches to formulating the dynamics of diversity change.

(c). Two way of thinking about logistic growth

Before presenting a formal incorporation of time-varying carrying capacities, we feel it is instructive to examine two different ways of thinking about logistic growth. The first focuses on the carrying capacity itself, which might be interpreted as the number of niches (e.g. [11]). The second focuses on the strength of the effect of crowding on reducing the diversification rate. This second perspective sees the carrying capacity as an equilibrium state of a dynamic process, an epiphenomenon of the intrinsic growth rate (e.g. the difference between immigration and extinction in MacArthur and Wilson) and the strength of the diversity dependence.

(d). The core elements of bounded diversification and their macroevolution meaning

The mathematical description of bounded diversification in macroevolutionary studies is an extrapolation of the logistic equation from studies of population growth ([54]; see also [55]; figure 3). The core elements are: the intrinsic (unconstrained or diversity-independent) growth rate (r₀); the strength of the diversity dependence on the rate of diversification (γ), i.e. the effect of crowding; and the carrying capacity (K), which is the ratio of the diversity-independent (r₀) and diversity-dependent (γ) components of logistic growth.

Figure 3.

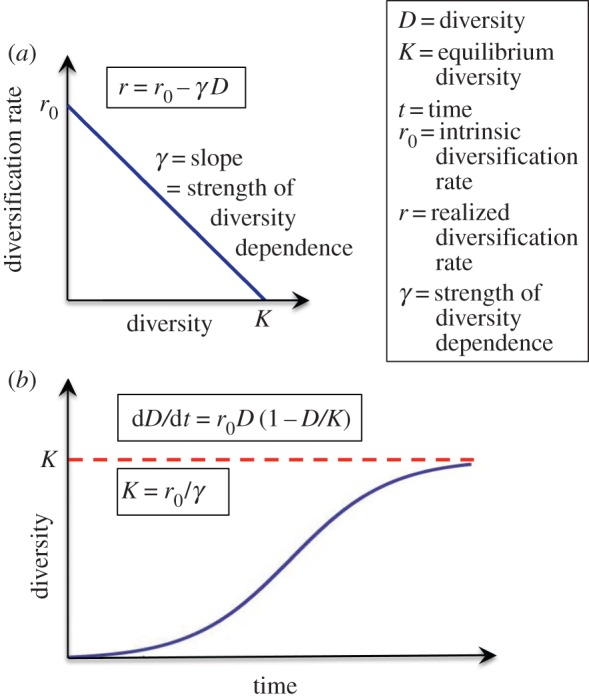
Simple logistic growth. Essential elements of logistic growth, including the relationship between the diversity-independent intrinsic diversification rate (r₀), the strength of the diversity dependence (γ) and the carrying capacity (K). (Online version in colour.)

(e). Two ways of accommodating a time-varying carrying capacity

Given that K equals r₀/γ (figure 3b), there are two simple ways of accommodating a time-varying carrying capacity, either by varying the intrinsic diversification rate with time, r₀(t), or by varying the strength of the diversity dependence with time, γ(t). Here, we quantitatively explore the expected diversity trajectories when the carrying capacity changes linearly with time, either by changing r₀(t) or γ(t) with time. To accommodate linear change in K(t) via a time variable r₀(t), the standard equation for logistic growth (figure 3b) can be re-written as:

4.1

where α′ is a constant, r_0,t=0 is the initial intrinsic diversification rate and D is diversity. To accommodate a linear change in K via a time-varying γ(t), the standard equation for logistic growth (figure 3b) can be re-written as:

4.2

where γ_t=0 is the initial strength of the diversity dependence. Note that α′ in equation (4.1) equals αγ in equation (4.2) (see appendix A). Derivations of equations (4.1) and (4.2) are provided in appendix A.

Of course, both r₀ and γ could change simultaneously, including in such a way that the carrying capacity remains unchanged. Moreover, change need not be linear, or even continuous, with time, but here we simply analyse projected diversity trajectories with linear change in K. Examples where there is evidence of non-linear environmental change influencing species richness include Jaramillo et al.'s study [56] of the relationship between neotropical plant diversity and temperature as viewed through the pollen fossil record from 65 to 20 Ma, and Ezard et al.'s analysis [15] of Cenozoic planktonic foraminiferal diversity change and climate (temperature) change.

(f). Expected diversity trajectories with time-varying carrying capacities

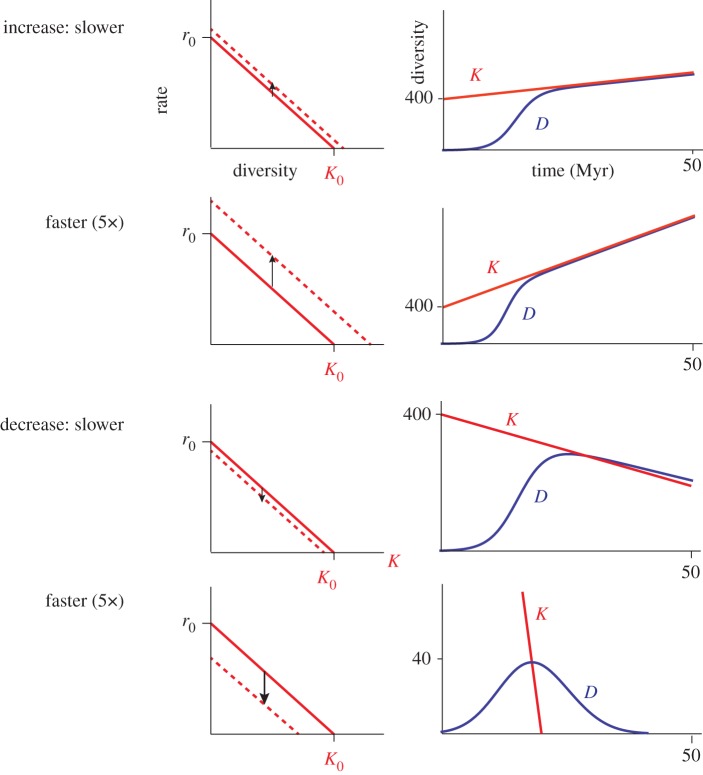
Representative solutions to equations (4.1) and (4.2) are shown in figures 4 and 5. The diversity trajectories when the carrying capacity increases linearly with time are broadly similar, regardless of how fast the carrying capacity increases, or whether the increase is driven by an increase in the intrinsic diversification rate or by decreasing the strength of the diversity dependence. In all cases, the Malthusian principle of exponential growth overtaking linear increase in resource availability prevails—the diversity initially increases exponentially, and then eventually tracks the increasing carrying capacity. In this light, the steady increase seen in genus richness in the marine realm since the Jurassic [38] provides evidence of the existence of a carrying capacity, albeit an increasing one—without a carrying capacity, we would have expected to see exponential growth, which we do not.

Figure 4.

Diversity trajectories (right panels) when the carrying capacity changes linearly with time via an increase or decrease in the intrinsic diversification rate, r₀(t), the ability to generate species with no crowding (left panels). The diversity curves were generated solving equation (4.1) with Mathematica 10.1.0.0. In all cases, the initial diversification rate (r₀) was 0.4 lineages/lineage million years, and the strength of diversity dependence (γ) of 0.001 per lineage million years, yielding an initial carrying capacity (K_t=0) of 400. For the slower rates of change α′ = 0.004 (a 1% change/million years), while the faster rate was fivefold faster with α′ = 0.02 (5% change/million years). (Online version in colour.)

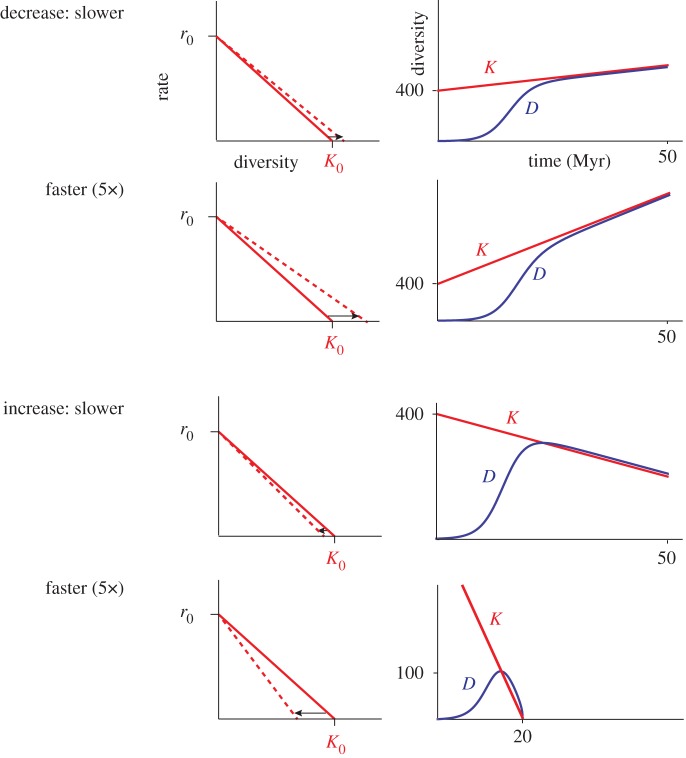
Figure 5.

Diversity trajectories (right panels) when the carrying capacity changes linearly with time via an increase or decrease in the strength of per-species diversity dependence, γ(t), the effect of crowding in inhibiting diversification (left panels). The diversity curves were generated solving equation (4.2) with Mathematica 10.1.0.0. The initial values of r₀, γ, and thus the initial carrying capacity (K_t=0) of 400, were the same as those used in figure 4. Similarly, we used the same α values as in figure 4, which, given that α = α′/γ in equation (4.2) (see appendix A), translated into a value of α = 4 for the slower rates (a 1% change/million years), and α = 20 species for the faster rates (5% change/million years). (Online version in colour.)

The dynamics are more varied when the carrying capacity decreases with time. With slow rates of carrying capacity decrease, the diversity initially increases exponentially, then the rate of increase drops to zero as the diversity reaches the carrying capacity, and then tracks the falling carrying capacity (figures 4 and 5). The realized diversity is slightly higher than the carrying capacity during the decline as expected—there is a time lag between the dropping carrying capacity and the ability of the species pool to respond to the decreased resource availability.

When the carrying capacity drops more rapidly, the mechanism by which the carrying capacity drops has a major influence on the resulting diversity trajectory. When the carrying capacity drops via an increase in the strength of the diversity dependence (figure 5, bottom panels), the decline phase is faster than the growth phase (the diversity trajectory is asymmetrical) and the diversity reaches zero at the same time that the carrying capacity also reaches zero.

By contrast, when the decline in the carrying capacity is fast and driven by a change in the intrinsic diversification rate, the resulting diversity trajectory is roughly symmetrical with time and the diversity increasingly lags behind the carrying capacity—the species pool accumulates a larger and larger extinction debt (figure 4, bottom panels). The reason the diversity trajectory lags so far behind the carrying capacity is that the decreasing intrinsic diversification rate means that the species pool increasingly loses its ability to respond to the decreasing carrying capacity. By contrast, when the carrying capacity drops via an increase in the strength of the diversity dependence (figure 5), the initial intrinsic diversification rate remains unchanged, and thus as diversity drops, the species pool's ability to respond to dropping carrying capacity remains strong.

A steady accumulation of an extinction debt might seem implausible, but note that it makes two strong predictions: the first is that the diversity trajectory is symmetrical. The second stronger prediction is that the final diversification rate is large (and negative), given that at the time of extinction the diversity-dependent extinction rate is much larger than the time-dependent origination rate. This is exactly what was observed for mammals analysed by Quental & Marshall [14], where, averaged over the 19 clades, the final origination rate was as low as the initial extinction rate and the final extinction rate was as high as the original origination rate.

(g). Distinguishing between the mechanisms driving carrying capacity change

The switching in the magnitudes of the speciation and extinction rates is also seen at the species level [22]. While the number of studies conducted to date is small, they suggest that where diversity-dependent rates exist, and when a species pool contracts in diversity, changes in the intrinsic rates may better describe the dynamics than change in the strength of the crowding within the clade. Conversely, if the carrying capacity for a clade is increasing, it may be very difficult to determine using the diversity trajectory alone, or the temporal trajectories of the origination and extinction rates, whether the increasing carrying capacity is due to an increasing intrinsic diversification rate or decreasing crowding (or some combination thereof). An alternative, as yet unexplored, approach to using diversity trajectories to determine which of the two primary mechanisms for changing the carrying capacity might be operating is to try and determine whether the strength of the diversity dependence itself changes with time. This will require particularly high fidelity fossil data.

5. The macroevolutionary drivers of time-varying carrying capacities

While we can easily model a changing carrying capacity in two ways, by changing the slope or the intercept of the diversity-dependent diversification rate, it is harder to unravel the ecological and evolutionary mechanisms that might drive changing carrying capacities. Here, we discuss potential mechanisms from the perspectives of clades and regional species pools. We note that this discussion seems well suited to furthering the integration of ecology into macroevolutionary study [57]. We also note that this integration, and understanding the control on species numbers, constitutes two of biology's hardest problems, ones that we do not pretend to solve here.

When a clade increases its carrying capacity, the key question is whether the increase reflects an increase in the diversity-independent intrinsic diversification rate or a decrease in the per-species crowding effect with respect to the designated species pool. If evolutionary change within the lineage led to access to more resources, e.g. via an expansion of the clade's or guild's trophic capacity, that might result in an increased intrinsic diversification rate if the evolutionary innovation did not affect the per-species crowding. Alternatively, if evolutionary innovation led to increased niche differentiation, with increase resource specialization, this would manifest as decreased crowding, a decrease in the slope of the diversity dependence. Similarly, if the carrying capacity increase is driven by increased habitat area, then one might expect the per-species crowding to remain unchanged, while there would be more opportunities for speciation—thus the increased species richness is most likely mediated through an increase in the intrinsic diversification rate. Increased habitat area could simply be increased geographical area, for example, expansion of a biome such as rainforest, desert or savannah, or a volcanic island [58], but it might also be an increase in the density of suitable or new microhabitats, for example, nooks and crannies as coral reefs develop, or epiphyte perches as tree size and species richness increase as forests evolve. That is, an increased resource base may be the result of evolutionary innovation in other clades.

If there is a decrease in the carrying capacity, if that decrease is simply due to decreased availability of resources, this should result in a decrease in the intrinsic diversification rate, unless these changes also increase the per-species crowding among members of the focal pool. Decreased resources could be due to a variety of different reasons, for example, reduced geographical area (e.g. as a volcano island subsides and erodes [58]), or food availability, increased predation or due to the arrival of competitors via evolutionary change among species outside the focal species pool, or via migration from outside the region (e.g. the invasion of Felidae into North America providing competition with the endemic Borophaginae (Canidae) species [22]).

Most of the discussion above has been framed around changes in the net diversification rate. In the palaeontological literature, where diversification rates have been dissected into their component origination and extinction rates, sometimes origination [15,16] and sometimes extinction [15,22] shows the greatest diversity dependence. We do not know the reason for this, although in the case of Silvestro et al.'s [22] study the diversity dependence seems to be imposed by competition with other clades, which suggests that clade competition might be manifested in the losing clade more strongly through the extinction rate. However, we do not know what controlled diversity change in the Cenozoic mammals of North America [16], nor what drove the declines in the 19 clades studied by Quental & Marshall [14], for example, whether it was competition with other clades, or changing environments, including vegetation change. The steady failure to speciate in all these examples may simply be the result of there simply being no new ecological space to expand into as the focal clade is forced out by changing environments and/or competition.

Finally, we note that a key ingredient to understanding the controls on the number of species is the biosphere's total biomass, as well as the biomass of individual organisms, which are connected to the size of the base of the foodweb (and thus to evolution of forests, for example). In this context, Bambach's [59] observation that marine organisms increase in mass, meatiness and metabolism (see also [60]), the observation that ecospace has become more richly filled [61,62], the fact that local species richness in marine benthic communities has increased on Phanerozoic timescales [36,63,64], and the argument that these trends are driven by increased primary productivity through time [20] is fully consistent with the view that the marine biosphere's carrying capacity has increased with time, and will probably continue to do so.

We suggest that changes in carrying capacity that are driven by a change in slope are primarily driven by evolutionary or ecological changes that act within the clade of interest, while changes resulting from shifts in intercept (r₀) might represent changes occurring either inside or outside the clade of interest. Curiously, when considering the decline phase, a change in the intercept might better represent the Red Queen scenario of a deteriorating environment, where the evolution within the lineage has a passive role on the lineage extinction. This scenario could be seen as a ‘macroevolutionary homicide’, while a change in slope could be viewed as a kind of ‘macroevolutionary suicide’, where evolution within a lineage slows the net production of new species, driving a clade into decline by its ‘own means'. While it is easy to conceive a change in slope driving an expansion of the carrying capacity, it is difficult to imagine an adaptive scenario where a change in slope would result in a steeper crowding effect and hence clade extinction, although one possibility is that within a given lineage one species might become a considerably better competitor and progressively eliminate all other species.

6. Diversity dependence: competition versus other biotic interactions

Diversity dependence and the ensuing carrying capacity are typically discussed from the perspective of resource competition, but one could ask whether diversity dependence can be produced by other types of biotic interaction. In fact, Sepkoski [65] in his discussion of his coupled logistic equations refers to the effect of interference, which could be seen as a broader set of interactions than simply resource competition (see also [66]).

Predation could in theory change the diversity of a given clade. Vermeij [67] suggests that an increase in predation through the Cenozoic could have lead the decline of certain mollusk lineages. Hence if a given lineage faces stronger predation it might eventually decline in diversity. Interestingly, in the same example given by Vermeij [67], he discusses the rise in diversity of lineages with shell traits that made them less susceptible to predation. Therefore in some sense, one could argue that ‘competition for escaping predation’ could be at play. This is similar to what ecologists call ‘apparent competition’, where in deep time the increase in diversity in a prey lineage that evolves more efficient protection could produce an increase in predator abundance, diversity and efficiency, which in turn could adversely affect another less protected lineage, perhaps driving it to extinction.

7. Summary: revisiting the phylogenetic, ecological and palaeontological perspectives on defining species pools

In deep time, each approach has its merits, once they are placed in their appropriate ecological (and evolutionary) contexts. Of prime importance is the recognition of the potentially confounding effects of different ways of defining the species pool in the analysis of the diversity dependence (crowding). Thus, in a sense, the palaeontological debate over the importance of crowding on long-term diversification is misdirected, to the extent that steadily increasing diversity with time may very well reflect a steady increase in K—that is diversity dynamics is still dominated by diversity dependence, even while it is controlled by evolutionary innovation. We emphasize that the importance of crowding, i.e. diversity-dependent diversification, is quite distinct from the question of whether the ark is full, that is whether and when a given species pool is at saturation [18].

One should only expect to see a truly bound diversification if the species pool is defined ecologically and where the timescale is short enough that there is no significant evolutionary innovation, or immigration, as well as a relatively constant climatic regime. Under this scenario, the simple assumptions made by the logistic growth at the population level are adequate for modelling species richness. However, we acknowledge that defining species pools ecologically might be operationally difficult because it can be difficult to describe the ecological properties of many species (especially when using the fossil record). On longer timescales, this becomes more difficult as some taxa (and thus ecological roles) become extinct, and as new ecologies evolve in situ, or migrate into the focal region.

A practical solution to defining species pools is to use the phylogenetic or palaeontological ‘whole biota’ approaches, but these approaches require modification of the way we think about carrying capacities, and requires incorporation of a framework that allows it to change with time. The framework allows one to explicitly look at the diversity dependence and independent aspect of a carrying capacity, and to investigate if and how they change in time. This leads to the recognition that clade diversity might be simultaneously affected by equilibrial and non-equilibrial processes, but that in the long run non-equilibrial processes might be of prime importance. The use of such a framework allows for a much richer integration of palaeontological perspectives into our understanding of the regulators of biodiversity in deep time.

Appendix A. Quantifying diversity trajectories with time-varying carrying capacities

Here we derive equations (4.1) and (4.2) in the text. In our quantitative exploration of the effect of time-varying carrying capacities, K(t), on diversity trajectories we examine the simple case of linear increase or decrease of K with time, viz:

A 1

where K_t=0 is the initial carrying capacity. Positive α leads to an increasing K with time, while negative α leads to a decreasing K with time.

(a) Changing the carrying capacity via change in the intrinsic diversification rate

When K(t) is driven by a changing intrinsic diversification rate r₀(t), the equation for species richness change with time (figure 3b) becomes:

A 2

Further, equation (A 1) becomes

A 3

After rearranging,

A 4

Given that γK_t=0 = r_0,t=0, and if we set α′ = αγ, then:

A 5

Substituting equations (A 1) and (A 5) into equation (A 2) yields:

A 7

Given that K_t=0 = r_0,t=0/γ, and α′ = αγ, equation (A 7) can be rearranged to yield equation (4.1) in the text:

A 8

(b) Changing the carrying capacity via change in the strength of the diversity dependence

When K(t) is driven by a change in the strength of the diversity dependence γ(t), the equation for species richness change with time (figure 3b) becomes:

A 9

where

A 10

Substituting equation (A 10) into equation (A 9) and given that K_t=0 = r₀/γ_t=0, yields equation (4.2) in the text:

A 11

Authors' contributions

The authors shared equally in formulating the ideas, writing the text, and designing and drafting the figures.

Competing interests

We have no competing interests.

Funding

T.B.Q. is funded by Fundação de Amparo à Pesquisa do Estado de Federal São Paulo (FAPESP), grant nos. 2012/04072-3 and 2013/50904-3.