Information use and resource competition: an integrative framework

Abstract

Organisms may reduce uncertainty regarding how best to exploit their environment by collecting information about resource distribution. We develop a model to demonstrate how competition can facilitate or constrain an individual's ability to use information when acquiring resources. As resource distribution underpins both selection on information use and the strength and nature of competition between individuals, we demonstrate interdependencies between the two that should be common in nature. Individuals in our model can search for resources either personally or by using social information. We explore selection on social information use across a comprehensive range of ecological conditions, generalizing the producer–scrounger framework to a wide diversity of taxa and resources. We show that resource ecology—defined by scarcity, depletion rate and monopolizability—determines patterns of individual differences in social information use. These differences suggest coevolutionary processes linking dominance systems and social information use, with implications for the evolutionary demography of populations.

1. Introduction

Organisms must secure resources such as food, mates and safety from predation to ensure survival and reproduction. Variability in the spatio-temporal distribution of these resources means that individuals face uncertainty regarding how best to exploit them. Individuals can thus acquire resources more efficiently by collecting uncertainty-reducing information [1,2]. However, resource distribution also underpins the strength and nature of competition between individuals [3–5]. Despite this convergence in resource distribution as a selective force, very little is known about how competition might facilitate or constrain information use. In this study, we present a general model to predict how resource competition will affect individual information use across a comprehensive range of ecological conditions, generating novel insights into the behavioural processes underlying the evolution of social systems.

Information can be gathered either personally, by direct interaction with the environment, or socially, by observing the behaviours of others [6,7]. The majority of research into information use has focused on two key ways that the costs and benefits of ‘personal’ versus ‘social’ information can differ. First, empirical and theoretical studies have shown that if gathering personal information involves long search times, trial-and-error sampling or risk-taking, collecting social information can reduce these costs by exploiting the efforts of others [8–10]. Second, the usefulness of one type of information over the other will depend on how rapidly each becomes outdated [11–13]. The resultant cost/reliability trade-off between personal and social information suggests that selection should favour strategies that balance adaptively an individual's reliance on each source [7,14].

Individuals may nonetheless be constrained in their ability to use information due to competition with others over resources, but such limitations have received little attention. An individual may be free to collect reliable social information at a relatively low cost, yet its ability to use it may be mediated by certain phenotypic factors, such as competitive ability. For example, if food patches or breeding territories are both limited and monopolizable, then the advantages of using social information may be restricted to socially dominant individuals (e.g. [15–17]). Since social information has been variously implicated as a regulator of population growth [18], a benefit of group living [19] and a facilitator of learning and culture [20,21], constraints on its use may have important ecological and evolutionary consequences.

The producer–scrounger model represents a useful game theoretical framework for exploring the influence that competition over resources can have on the evolutionary dynamics of social information use [9,22]. The model considers groups of individuals searching for and consuming discrete resource patches by using either personal information (‘producing’) or social information (‘scrounging’). When playing ‘producer’, an individual searches for its own resources; when playing ‘scrounger’, it looks for and exploits the discoveries of producers [23]. A well-established insight from producer–scrounger games, relating to one element of resource distribution, is that the ‘finder's share’ should influence optimal levels of social information use within a group [24]. When producers can fully deplete a discovery before the arrival of any scroungers—at which point social information becomes outdated—there is no benefit to scrounging behaviour. By contrast, when depletion time is longer, the finder's share is lower and scrounging becomes more prevalent. Consistent with this, Giraldeau & Livoreil [25] experimentally demonstrated a positive relationship between the finder's share and scrounging behaviour in nutmeg mannikins (Lonchura punctulata).

Two further elements of resource distribution can readily be incorporated into producer–scrounger games, but have received limited attention. First, almost all producer–scrounger models assume that resources are so hard to find that they are only discovered singly and successively, regardless of the number of individuals searching for them as producers. However, it is clear that many organisms inhabit environments in which simultaneous resource discoveries are likely. Those few studies that have varied the difficulty of resource discovery such that simultaneous resource discoveries can occur [26–28] propose that social information use should decrease as finding resources using personal information becomes easier. Second, only one model [29] has explored the effects of resource monopolizability on scrounging behaviour, while others have assumed scramble-like competition between a producer and any scroungers at its discovery. Barta & Giraldeau [29] demonstrated a positive link between dominance and scrounging behaviour when resources were monopolizable.

No study to date has attempted to combine the three elements of resource distribution outlined above to better understand how their influences on the strength and nature of competition might interact to impact individual information use. Such an approach should be of general interest given the range of ecological conditions that different taxa experience when exploiting resources in nature. Here, we expand the producer–scrounger game to develop a general model for how resource ecology should affect individual information use in a social context. We define resource ecology along three axes of variation: (i) the ‘scarcity’ of resource patches, which quantifies how difficult they are to discover using personal information; (ii) the ‘depletion rate’ of resource patches, which quantifies how rapidly social information becomes outdated following discovery; and (iii) the ‘monopolizability’ of resource patches, which quantifies the degree to which competitors can exclude one another based on differences in competitive ability [30]. Within this framework, the classic producer–scrounger game is represented by a specific subset of the environmental conditions considered.

Using this framework, we investigate how individual decisions to use personal or social information may be affected or constrained by ecological conditions and individual phenotype. By considering the interactive effects of three dimensions of resource ecology, we provide general insights into how the relative costs of not just collecting, but also using, personal versus social information should influence individual information use. Furthermore, we demonstrate that the individual benefits of high competitive ability are dependent on more than just resource monopolizability when individuals face uncertainty about the spatio-temporal distribution of resources. As such, patterns of resource ecology may have previously unexpected influences on the character of social systems across taxa.

2. The model

We model groups of N individuals searching for and consuming resource patches. Patches contain F resource units. Individuals can choose to search for patches using one of two mutually exclusive tactics: producing or scrounging. Producers collect and use personal information, sampling their environment asocially. The per capita resource discovery rate for producers in a given ‘time step’ is determined by λ, which ranges from 0 to 1 and represents ‘scarcity’. The lower the value of λ, the more difficult resources are to find. Scroungers, in contrast, collect and use social information. They do not contribute to the group's resource discovery rate, but exploit patches produced by others. The proportion of the group producing and scrounging is denoted by q and (1 − q), respectively.

The total number of patches discovered per time step is given by λqN—the per capita resource discovery rate for producers multiplied by the number of producers in the group. Simultaneous resource discoveries occur if λqN > 1, but individual scroungers can only access a maximum of one discovered patch per time step. Therefore, when λqN ≥ 1, λ represents the ratio of the costs of collecting social versus personal information, since a scrounger can access a patch each time step, whereas a producer discovers a patch only every 1/λ time steps. When λqN < 1, however, scroungers only access a patch every 1/(λqN) time steps. In this case, the ratio of the costs of collecting social versus personal information will be 1/qN, since scroungers access each producer's discovery, while producers only benefit from their own discoveries. Because our parameters and variables do not change across time steps for a given group composition, all resource consumption formulae given below represent rates per time step (i.e. T = 1).

A producer discovering a patch gains a finder's advantage of a resource units before any scroungers arrive [24]. The remaining (F − a) resource units, defined as A, are divided between the producer and any scroungers present in proportion to their relative competitive weights. Patches are fully depleted in the same time step that they are discovered, meaning that the finder's share (a/F) represents the ‘depletion rate’ of a resource patch within that time step. An individual's competitive weight is defined as

2.1

where i denotes an individual's ranked competitive ability relative to others in the group (expressed as an integer, ascending from 1 to N; hereafter ‘social rank’), and c defines the degree to which patches can be monopolized [29].

The exponent c represents resource ‘monopolizability’, and may be best considered as patch area. When c = 0, an individual cannot monopolize a patch regardless of social rank; CW_i is the same for all individuals, and competition at patches is scramble-like. However, as c increases, resources become more defensible and the degree to which social rank influences competitive asymmetry between individuals increases following a power law. When c = 100, the highest-ranking individual in a patch essentially monopolizes A.

If λqN ≤ 1, scroungers are able to access each patch discovery. In this case, the rate of resource consumption for producers and scroungers is equivalent to that given by Barta & Giraldeau [29]. When, in addition to this, c = 0, the model becomes equivalent to the classical producer–scrounger game [23,24]. The rate of resource consumption for the ith-ranking producer with competitive weight CW_i when λqN ≤ 1 is given by

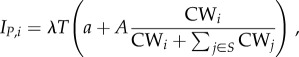2.2

where S is the set of social ranks for all (1 − q)N individuals playing scrounger, and CW_j is the competitive weight of the jth scrounger in the set, making 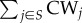the summed competitive weight of all scroungers in the group. The rate of resource consumption for the ith-ranking scrounger, in contrast, is

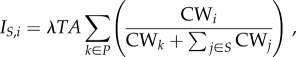2.3

where P is the set of social ranks for all qN individuals playing producer, making CW_k the competitive weight of the kth producer in the set. The summation operator describes a scrounger accessing the discoveries of all qN producers in the group.

When λqN > 1, scroungers cannot access all discoveries, since some discoveries are occurring simultaneously. As such, we assume that the probability of a scrounger exploiting a given producer's discovery in each time step is determined by the total number of discoveries in the group, which we take to be the expected value of λqN. While λqN will in reality also be probabilistic, modelling its expected (i.e. mean) value will not have affected the model's overall predictions, but allowed us to focus on how scroungers may be distributed probabilistically across different producers. A given producer is at risk of being exploited by a total of n = (1 − q)N mutually independent scroungers, where the likelihood of each of these scroungers being present is thus 1/λqN. The probability of a given producer being scrounged by a certain number, l, of the n scroungers is drawn from a binomial distribution. However, the identities of the l scroungers exploiting a producer will influence the cumulative competitive weight of the individuals within a patch. We thus calculate the probability of occurrence and cumulative competitive weight for all 2ⁿ possible combinations of scroungers that can occur at a given producer's discovery. We define a 2ⁿ × n matrix, S_P, which defines the absence (0) or the presence (1) of each scrounger for each combination. The probability of occurrence for each of these combinations is given in a 2ⁿ × 1 column vector, B_P, the elements of which are calculated as

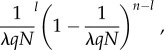2.4

where the value of l for each row is the sum of the elements in the corresponding row in S_P. To calculate the cumulative competitive weight of scroungers for each combination, we multiplied S_P by a n × 1 column vector, C_P, of competitive weights for each individual scrounger, to produce a 2ⁿ × 1 column vector, W_P, of competitive weights summed across scroungers for each possible combination of individual scroungers present.

As such, when λqN > 1, the rate of resource consumption for the ith-ranking producer is given by

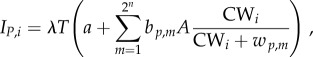2.5

where b_p,m and w_p,m represent the mth elements (i.e. rows) of the B_P and W_P, vectors, respectively, and m ranges from 1 to 2ⁿ.

To calculate the rate of resource consumption for a given scrounger, we must define all of the possible contexts in which it can be when exploiting producers. For each context, we calculate its probability of occurrence and the cumulative competitive weight of individuals present. A scrounger will always exploit one producer when λqN > 1. This may occur alone or in conjunction with a certain number, (l − 1), of the remaining (n − 1) scroungers. The total number of possible combinations of other scroungers occurring alongside a given focal scrounger is 2⁽ⁿ⁻¹⁾. We define a 2⁽ⁿ⁻¹⁾ × (n − 1) matrix, S_S, which records the absence (0) or the presence (1) of the remaining scroungers for each combination. The likelihood of any individual scrounger exploiting a given producer is 1/λqN, making the probability of a given scrounger sharing a resource with a given combination of the remaining scroungers

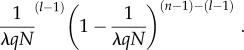2.6

Since the focal scrounger will itself only have a 1/λqN chance of being present at a given producer's discovery, the probability of each of these combinations occurring at a given discovery will be

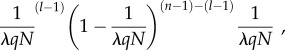2.7

simplified as

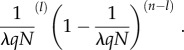2.8

We calculate this probability for each of the 2⁽ⁿ⁻¹⁾ possible combinations to produce a 2⁽ⁿ⁻¹⁾ × 1 column vector, B_S.

The identity of a given focal scrounger will influence the cumulative competitive weight of the (n − 1) remaining scroungers. As such, we define, for each focal scrounger, a separate (n − 1) × 1 column vector, C_Si, of competitive weights for the remaining scroungers, where i is the rank of the focal scrounger. The cumulative competitive weight of remaining scroungers for each of the 2⁽ⁿ⁻¹⁾ combinations is calculated for the ith-ranking scrounger by multiplying the matrix S_S with the column vector C_Si, to generate a 2⁽ⁿ⁻¹⁾ × 1 column vector, W_Si.

When λqN > 1, therefore, the rate of resource consumption for the ith-ranking scrounger is given by

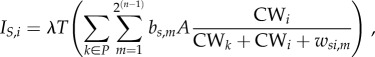2.9

where b_s,m and w_si,m represent the mth elements (i.e. rows) of the B_S and W_Si vectors, respectively, and m ranges from 1 to 2⁽ⁿ⁻¹⁾. The competitive weight of a given producer, CW_k, is defined as above.

We analysed the model—for fixed values of N, a/F, λ and c—by allowing individuals to switch between the producer and scrounger tactic in an attempt to improve their relative rate of resource consumption, or relative fitness. This was calculated for the ith-ranking individual as

2.10

its fitness relative to the group's average. In this way, we searched for Nash equilibria: stable group compositions where no individual could increase its payoff by switching tactic. We generated results numerically across a range of group sizes (4, 8, 16), but our equations relate to groups of any size. Here, we present only those findings where N = 16, since the other group sizes modelled always showed qualitatively similar patterns. The robustness of our findings to increasing group size is corroborated by our analysis of a larger range of group sizes (ranging from 4 to 28) across a pertinent range of the parameter space, the results of which are presented in the electronic supplementary material.

We began each model run by defining a group as a vector of zeros and ones of length N, where the value at position i represents the tactic (0 = producer; 1 = scrounger) of the ith-ranking individual [29]. Initial group composition was generated such that each individual had a 50% chance of starting as a producer or scrounger. The group was then perturbed by randomly selecting one individual to switch tactics. If this individual's payoff increased, the new tactic would be maintained; otherwise, it would revert to its previous tactic. This perturbation was repeated until a Nash equilibrium was reached. Model runs for a given parameter set were replicated up to 10 000 times in order to account for multiple Nash equilibria. We thus calculated—for each group and each individual in each parameter set—the probability of scrounging based on average tactics in the stable group compositions of model replicates. All model analysis was conducted in R v. 3.0.2 [31].

3. Results

Increasing the producer's resource discovery rate (λ) reduced the relative cost of collecting personal information. However, the impact of this relationship on the decision to produce or scrounge was dependent upon resource monopolizability. When individuals were unable to monopolize resources (i.e. c = 0), scrounging became less common if patches were easier to find (higher λ) (figure 1). Under these conditions, there was no between-individual variation in scrounging behaviour (figure 2a). Scrounging ultimately disappeared from the population (i.e. producing became fixed) when resources were sufficiently easy to find using personal information that the associated costs of resource sharing were no longer economical.

Figure 1.

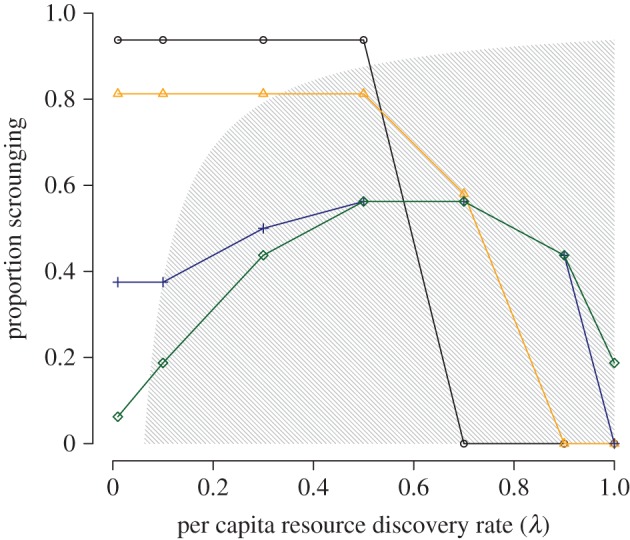
The combined influence of resource scarcity and monopolizability on levels of scrounging in a group. Simultaneous resource discoveries occurred only within the shaded region (i.e. where λqN > 1). Values of c as follows: 0 (black circles), 1 (orange triangles), 10 (blue crosses), 100 (green diamonds). N = 16; a/F = 0.05.

Figure 2.

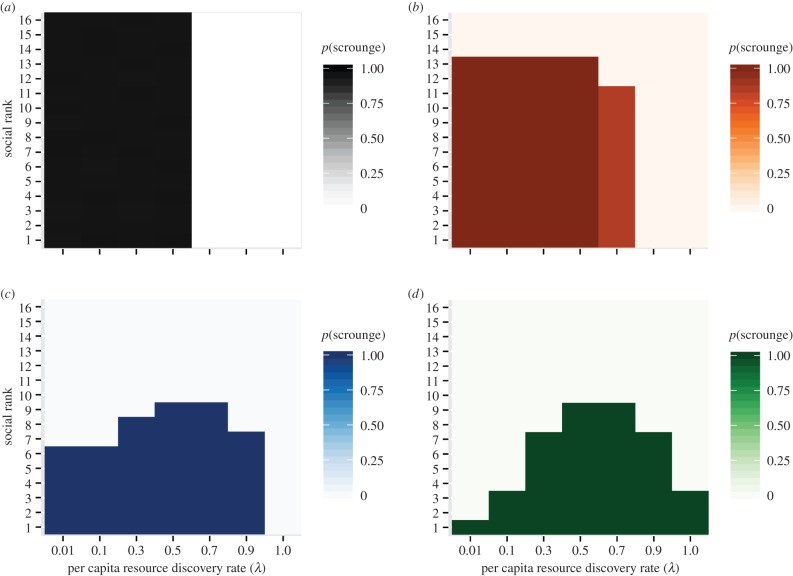
The combined effect of resource scarcity and monopolizability on the probability of scrounging for individuals of different social rank. Resource monopolizability for each panel as follows: (a) c = 0 (black), (b) c = 1 (orange), (c) c = 10 (blue) and (d) c = 100 (green). Colour coding corresponds to that given in figure 1. Note that social rank ranges highest to lowest from 1 to N. N = 16; a/F = 0.05.

As resources became monopolizable (increasing c), the relationship between the discovery rate and the proportion of scrounging in a population changed dramatically. First, when the discovery rate was low, such that no more than one patch was being discovered per time step (λqN ≤ 1), scrounging became less common at higher values of c (figure 1). This occurred because the more effectively every discovery could be monopolized by a single, top-ranked individual playing scrounger, the less profitable this tactic became for others (figure 2a–d, far left columns). Rather, other individuals would benefit more from playing producer: even though patch discoveries would be rare, and would be largely appropriated by the dominant scrounger, producers would at least secure a finder's advantage.

Second, under conditions of strong monopolizability (c ≥ 10), intermediate discovery rates promoted higher levels of scrounging despite the lower relative cost of collecting personal information (figure 1). This was because simultaneous resource discoveries (i.e. λqN > 1) could occur more easily as λ increased. Simultaneous resource discoveries precluded complete monopolization by single individuals, freeing up resources for other individuals to scrounge. Owing to the higher competitive weights of higher-ranking individuals, however, scrounging remained tightly linked to social rank despite more individuals being able to use the tactic (figure 2c,d). Finally, scrounging began to decline once resources became so easy to find that even the highest-ranked individuals would benefit more from producing—thus gaining a finder's advantage—than from monopolizing the discoveries of others (figure 1). The overall result when c ≥ 10 was thus a ‘peaked’ relationship between resource discovery rate and population levels of scrounging.

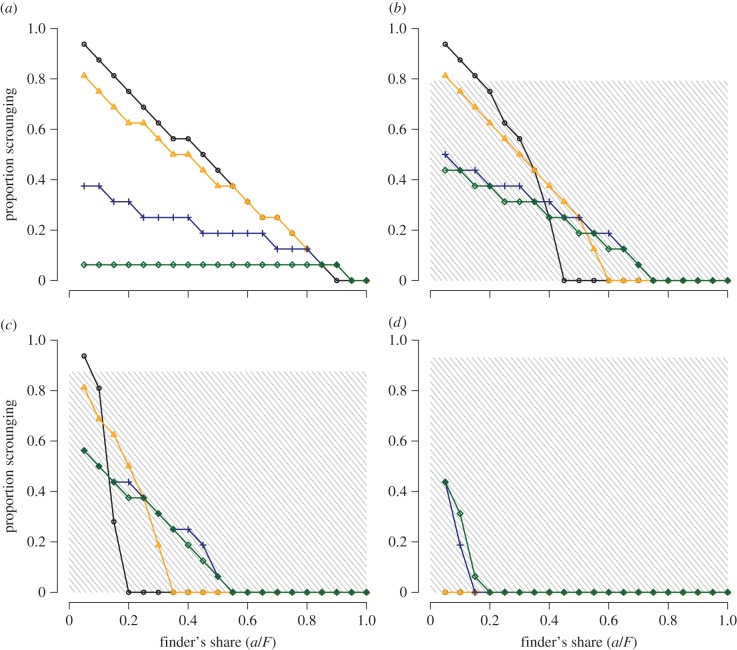
Scrounging was less common when the finder's share was high (figure 3). Individuals were less likely to scrounge as those producing benefited from consuming greater portions of their discoveries, leaving less for scroungers to exploit. The strength of this effect, however, was influenced by both resource discovery rate and monopolizability. While at very small finder's shares the levels of scrounging were usually lower when monopolizability was high, the rate of decline of scrounging with increasing finder's share was actually slower at higher levels of monopolizability (figure 3a–d). This reflects the fact that scroungers able to monopolize patches were more robust to the losses associated with a higher finder's share, because they still secured large proportions of the remaining A resource units. By contrast, the general effect of a higher resource discovery rate was to accelerate the decline in scrounging associated with the finder's share (figure 3a–d). When resources could be discovered more easily, individuals benefited from producing when the finder's share was high.

Figure 3.

The effect of the finder's share on levels of scrounging in a group depends on interactions between resource scarcity and monopolizability. Panels show data for different values of per capita resource discovery rate (λ) as follows: (a) 0.01, (b) 0.3, (c) 0.5 and (d) 0.9. Values of c as follows: 0 (black circles), 1 (orange triangles), 10 (blue crosses), 100 (green diamonds). Simultaneous resource discoveries occurred only within the shaded regions (i.e. where λqN > 1). N = 16; a/F = 0.05.

Finally, high resource monopolizability allowed scrounging to persist at intermediate values of the finder's share when it would otherwise disappear from the population (figure 3b), although this effect persisted only at progressively smaller values of the finder's share as discovery rates increased (figure 3c,d). This was caused by a combination of simultaneous resource discoveries and the robustness of scrounging for individuals of high social rank described above.

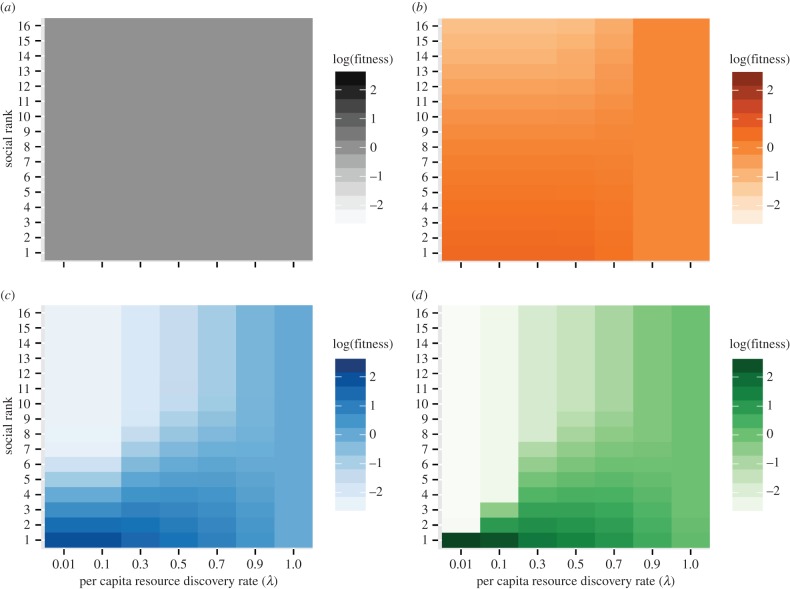
The interactive effects of resource discovery rate and monopolizability on scrounging behaviour had important fitness consequences (figure 4). The exclusivity of scrounging to individuals of high rank when resources were monopolizable but extremely rare resulted in a strong skew in fitness favouring dominant individuals. This increased in proportion with c, and tended towards a single, top-ranked scrounger with a very high relative fitness (figure 4d, far-left column). As resources became easier to find, however, this fitness skew became less dramatic (figure 4d). This was primarily due to the occurrence of simultaneous resource discoveries, which made scrounging behaviour and its benefits more evenly shared across more individuals of relatively high social rank, and lower-ranked producers less prone to being in direct competition with the highest ranked individuals. Low-ranked producers also benefited from more frequent discoveries, and the resulting finder's share benefits, when the discovery rate was high. These findings were in stark contrast to the outcome when resources could not be monopolized (c = 0). In these cases, there was no variation in scrounging propensity between individuals, leading the population to a stable mix of producers and scroungers where all individuals had equal fitness irrespective of social rank or resource scarcity (figure 4a).

Figure 4.

Resource scarcity and monopolizability interact to determine both the skew and strength of the fitness benefits of social rank. Resource monopolizability for each panel as follows: (a) c = 0 (black), (b) c = 1 (orange), (c) c = 10 (blue) and (d) c = 100 (green). Colour coding corresponds to that given in figure 1. Note that social rank ranges highest to lowest from 1 to N. N = 16; a/F = 0.05.

Since scroungers do not contribute to resource discovery, they can reduce a population's average individual resource consumption rate, potentially impacting on various demographic processes. When resources were rare (i.e. low λ), higher values of c resulted in fewer scroungers and therefore greater average intake rates (figure 5). However, as resources became more common this pattern reversed: high values of c led to more scroungers and thus lower average intake rates relative to when c was low.

Figure 5.

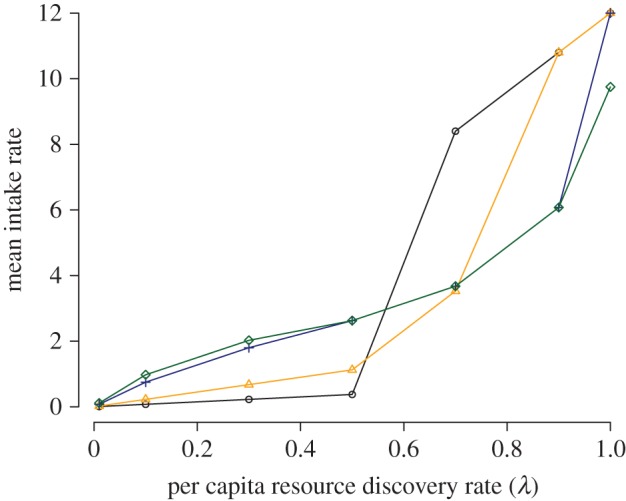
Resource scarcity and monopolizability affects a group's average resource consumption rate through their influence on scrounging behaviour. Values of c as follows: 0 (black circles), 1 (orange triangles), 10 (blue crosses), 100 (green diamonds). N = 16; a/F = 0.05.

4. Discussion

Our aim was to explore the interdependencies between information use and competition over resources, driven by resource distribution as a shared selective force. To do this, we investigated how three key aspects of resource ecology—scarcity, depletion rate and monopolizability—interact to promote or constrain the use of social information when acquiring resources in an uncertain environment. Further, we asked how such influences might lead to variation in fitness between individuals through differential access to resources. Our findings generated two key predictions. First, the effects of resource scarcity on social information use should depend strongly on resource monopolizability. Second, the potential benefits of social dominance should be closely linked to social information use in uncertain environments, determined not just by monopolizability, but all three aspects of resource ecology. Below, we discuss these predictions in the context of previous work and propose avenues for future research. We then raise an important theoretical consideration for the study of social information use, and conclude by outlining the potential evolutionary demographic implications of our research.

Previous producer–scrounger models have proposed that individuals should rely more on social information when the costs of collecting personal information are high (i.e. scrounging increases as valuable resources become harder to find) [26–28,32]. Although this relationship seems intuitive, direct experimental support is surprisingly lacking [14], possibly because the true relationship is dependent on the degree of resource monopolizability. Thus, our results confirmed this pattern when resources were not monopolizable, but predicted a ‘peaked’ relationship when resources were monopolizable, where social information use (scrounging) only increases initially but then declines again as resources become progressively scarcer. Data from Koops & Giraldeau [33] provides circumstantial evidence supporting this explanation. These authors found that scrounging declined in European starlings (Sturnus vulgaris) when novel food patches were more scarce, contrary to conventional wisdom but consistent with the downturn our model predicts at higher levels of resource scarcity and monopolizability. Crucially, starling social groups exhibit a dominance structure [34], and Koops & Giraldeau [33] reported that scroungers in their study were primarily socially dominant starlings with a competitive advantage at resource patches. Our findings thus suggest that resource scarcity, depletion rate and monopolizability should be considered in unison when making predictions about how selection should act on social information use in a given species.

Most research into information use has focused on how individuals optimize their reliance on social versus personal information based on trade-offs between their collection costs and reliabilities [14,20], and their negatively frequency-dependent payoffs [23]. Very little attention has been given to the constraints that competition imposes on an individual's liberty to use social information to access resources. Our findings are consistent with the only previous study to consider systematically how variation in competitive ability might constrain individual social information use due to competition over limited resources [29]: when resources are monopolizable, social information use may become exclusive to dominant individuals, leading to a positive relationship between social rank and resource acquisition rate. However, our model further demonstrates that resource scarcity is critical in determining the degree of this exclusivity. Specifically, it is only under conditions of sequential resource discovery that a single individual can make exclusive use of social information; when resources are discovered simultaneously social information may be exploited by successively lower ranked individuals.

Despite the clear influence that social dominance may play in constraining information use, we know of no studies exploring how social information use varies in response to systematic manipulation of resource monopolizability in taxa exhibiting dominance hierarchies. Liker & Barta [35] showed that dominant house sparrows (Passer domesticus) scrounged more than subordinates when searching for spatially clumped seeds, but did not investigate conditions where resources could not be monopolized. A number of other experimental producer–scrounger studies in birds and primates have reported either a positive relationship or no relationship between social rank and scrounging [17,36,37]. Consistent with our findings, observational studies in chacma baboons have shown that dominance-linked scrounging increases when food patches are monopolizable [16,38]. Our model suggests that predictions (and associated experimental designs) regarding the relationship between social dominance and information use for a given taxon should be guided by an appreciation of resource scarcity, depletion rate and monopolizability. Further empirical work is needed to experimentally test the predictions that resource monopolizability constrains an individual's use of social information according to dominance, leading to differential access to resources, and that the patterns of these constraints is dependent on resource scarcity.

The fact that resource monopolizability influences the benefits of dominance is well established [30,39,40]. However, since there is expected to be uncertainty associated with the spatio-temporal distribution of most resources, our model highlights a crucial role for social information use in capturing the benefits of dominance. As such, selection pressures on dominance will depend on multidimensional aspects of resource ecology (e.g. scarcity, depletion rate and monopolizability) that influence both the benefits of social information use and competition between individuals. This does not mean that we predict the ecology of any single resource to lead to any particular information use phenotype or social system, since organisms must exploit many different resources to survive and reproduce. Overall selection on these phenotypes and systems will be driven by the combined pressures of multiple resources ecologies through space and time [41].

Our findings also highlight an important theoretical issue that requires development if we are to fully understand the evolutionary ecology of social information use. We only consider the acquisition of ephemeral resources that are fully depleted upon discovery. Like most previous theory, we thus assume that any information generated by the discovery of a resource becomes useless upon its depletion. Yet, it is clear that many organisms exploit resources that exhibit at least some spatio-temporal predictability, such that previous experience, or prior information, can be used to inform future decisions [10,42–44]. When information is reusable or generalizable in this way, the relationship between social information use and competition over resources may change dramatically. Specifically, social information use may be decoupled from the context in which it was collected in a way that would not be possible with unpredictable, ephemeral resources (where information must be used as soon as it is collected). For example, an individual may be able to collect social information in a highly competitive situation and then use it in a less competitive one. In this way, competitive constraints on social information use may be relaxed or altered. Since the fitness benefits of information use are generally expected to be associated with improvements in resource exploitation, research is needed to more formally define the links between information acquisition and resource acquisition, and to explore how these links can vary.

Our model may have important evolutionary demographic implications. Coolen et al. [18] showed that social information use can regulate population dynamics. They argued that, because individuals forgoing personal information in favour of social information (i.e. scroungers) do not contribute to per capita food discovery rates, higher levels of scrounging could reduce average population birth rates [18]. Our results thus suggest that demographic rates may differ for different systems of social dominance—ranging from egalitarian to despotic—driven by differences in levels of scrounging behaviour within groups, in turn driven by differences in resource ecology. For example, when simultaneous resource discoveries occur, we predict scrounging to be more prevalent if resources are monopolizable, resulting in lower average resource consumption rates. We predict the opposite pattern when resources are discovered sequentially. It is widely accepted that population-level processes such as density dependence and trait-mediated interference are often driven by underlying behavioural mechanisms [45–47]. Better understanding of the relationships between resource ecology, information use, social dominance and fitness should thus strengthen our understanding of the differences in population dynamics across environments and taxa, and improve our ability to predict population responses to environmental change.

Data accessibility

Data are available to download from Dryad: http://dx.doi.org/10.5061/dryad.mn36c.

Authors' contributions

A.E.G.L. conceived the study, designed and analysed the model, and drafted the manuscript. J.P.O., T.C. and J.M.R. provided conceptual input, assisted mathematically and helped draft the manuscript. G.C. conceived and coordinated the study, and helped draft the manuscript.

Competing interests

We have no competing interests.

Funding

This study was supported by an NERC Quota Studentship (NE/J500409/1) awarded to A.E.G.L.